Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 May 8;15(19):5243–5249. doi: 10.1021/acs.jpclett.4c00686

Pathway to Polyradicals: A Planar and Fully π-Conjugated Organic Tetraradical(oid)

Sergi Betkhoshvili †, Ibério de P R Moreira ‡, Jordi Poater †,, Josep Maria Bofill †,*
PMCID: PMC11103692  PMID: 38718211

Abstract

graphic file with name jz4c00686_0006.jpg

In this work, we provide a general strategy to stabilize the ground state of polyradical(oid)s and make higher spin states thermally accessible. As a proof of concept, we propose to merge two planar fully π-conjugated diradical(oid)s to obtain a planar and cross-conjugated tetraradical(oid). Using multireference quantum chemistry methods, we show that the designed tetraradical(oid) is stabilized by aromaticity and delozalization in the π-system and has six thermally accessible spin states within 1.72 kcal/mol. Analysis of the electronic structure of these six states of the tetraradical(oid) shows that its frontier π-system consists of two weakly interacting subsystems: aromatic cycles and four unpaired electrons. Conjugation between unpaired electrons, which favors closed-shell structures, is mitigated by delocalization and the aromaticity of the bridging groups, leading to the synergistic cross-coupling between two diradical(oid) subunits to stabilize the tetraradical(oid) electronic structure.

Purely organic magnetic materials are emerging as promising candidates to substitute scarce and environmentally harmful transition metal and lanthanide compounds for many applications in organic electronics. This new generation of organic materials shows magnetic properties with potential applications in flexible organic electronics,1,2 photonics,2−5 spintronics,6−8 and organic quantum devices.9 The magnetic properties of these materials arise from molecular entities (isolated molecules or defined groups in a polymeric structure) with unpaired electrons, usually called radical centers. The synthesis of stable polyradicals with large spin angular momentum is still a major challenge due to their high chemical reactivity. The stability of the radical centers can be enhanced by surrounding bulky groups such as in the sterically hindered triphenylmethyl radical10 or nitronyl/nitroxide polyradicals.11−13 However, this strategy usually leads to difficulties in connecting radical centers close enough to form small polyradicals. Another strategy for the stabilization of unpaired electrons is through delocalization via π-conjugation in planar molecular structures.1,8,13−22 This approach is effective to design systems with any number of unpaired electrons and can lead to singlet or doublet ground states with thermally accessible high-spin states (polyradicals) or singlet or doublet ground states with a little higher-lying high-spin states (polyradicaloids). The most widely studied polyradical(oid)s are diradical(oid)s with potential applications in organic electronics and spintronics, n-channel or ambipolar field effect transistors (FETs), organic magnetic materials, molecular switches, singlet fission with solar energy conversion capability, batteries, nonlinear optics, functional dyes, and photodynamic therapy.1,6,23−37 The history of higher-order polyradicals starts in 1964 with the first synthesized triradical38 and tetraradical,39 after which many experimental and theoretical studies followed.11−21,40−55

When discussing polyradicals, we must distinguish between two extremes: the first is a polymer of monoradicals, which can be a chain of repeating radical units, and the second is a single molecule with several unpaired electrons. Our focus of this work is to devise a strategy to generate single molecules with several unpaired electrons. Motivated by the difficulties in stabilizing high spin states in organic molecules, in this Letter, we present a new and general strategy of designing polyradical(oid) molecules with thermally accessible (i.e., within 2 kcal/mol from the ground state) spin states. Through a suitable unification of two fully π-conjugated and planar diradical(oid)s, we propose a new cross-conjugated tetraradical(oid) with six thermally accessible spin states of two singlets, three triplets and one quintet. This strategy envisages generating more complex planar π-conjugated polyradical(oid)s. Since we cannot be experimentally certain that a quintet state is thermally accessible, we use the term “tetraradical(oid)” to express generality.

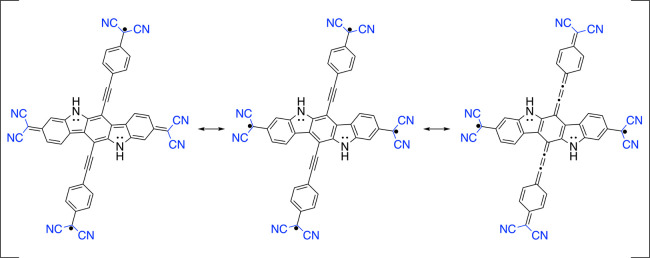
The tetraradical(oid) we designed is inspired from the diradical(oid)s that are either already synthesized or resemble the structures of well-known diradical(oid)s. The diradical(oid) 2,2′-(5,11-dihydroindolo[3,2-b]carbazole-3,9-diyl)dimalononitrile (S) shown in Figure 1a has been synthesized and computationally studied. Its trivial derivative is also a diradical(oid) that dimerizes readily, proving its significant diradical character.56,57 Since diradical(oid) S has its substituteable hydrogens in para positions from one another in the central benzene ring, we could substitute both of them with radicals to obtain a tetraradical(oid). It is more pertinent to complete the building of the tetraradical(oid) from S by merging it with structures that are stable diradical(oid)s. Such known diradical(oid)s are homologous Thiele’s (n = 1), Chichibabin’s (n = 2) or Müller’s (n = 3) hydrocarbons with structure Ph2C=(Ph)n=CPh2, with the latter having the highest diradical character.58−60 If we insert acetylene residues between benzene rings of Müller’s hydrocarbon, we avoid the steric hindrance without changing the topology of the π-conjugation. Furthermore, since S has cyano terminal groups and it is still a diradical(oid), we could substitute terminal phenyl groups of the Müller’s hydrocarbon with cyano groups. Upon such changes, we obtain 2,2′-((1,4-phenylenebis(ethyne-2,1-diyl))bis(4,1-phenylene))dimalononitrile (L) shown in Figure 1b, which represents the additional diradical(oid) component toward building a tetraradical(oid) LS. As shown in Figure 1, for both diradical(oid)s S and L, Ovchinnikov’s rule61 predicts a singlet open-shell ground state (G.S.), as the antiferromagnetic coupling is transmitted via an antiferromagnetic coupling unit (ACU).24 For S this is corroborated by experiments, and for L this could be extrapolated from Müller’s hydrocarbon, which has a singlet G.S. Ovchinnikov’s rule also predicts that the system obtained from the (approximate) conceptual union of L and S, the tetraradical(oid) 2,2′-(6,12-bis((4-(dicyanomethyl)phenyl)ethynyl)-5,11-dihydroindolo[3,2-b]carbazole-3,9-diyl)dimalononitrile (LS) given in Figure 2, should also have a singlet open-shell G.S., as verified in this Letter.

Figure 1.

Figure 1

Open in a new tab

Demonstration of Ovchinnikov’s rule with antiferromagnetic coupling units (ACUs) to determine the ground state of each diradical(oid) substructure (a) S and (b) L that conceptually makes up the tetraradical(oid) LS.

Figure 2.

Figure 2

Open in a new tab

Resonance structures of the 2,2′-(6,12-bis((4-(dicyanomethyl)phenyl)ethynyl)-5,11-dihydroindolo[3,2-b]carbazole-3,9-diyl)dimalononitrile LS. On the left, S is quinoidal and L diradical; this resonance structure is referred to as LDSQ. In the middle, both S and L are diradical, thus referred as LDSD. On the right, S is diradical and L is quinoidal, thus referred as LQSD.

Since polyradical species are very difficult to isolate, quantum chemical calculations are important tools for studying and analyzing their electronic structure properties. The geometry for each of the structures, L, S and LS, was optimized with the Slater-type all-electron triple-ζ basis set (TZP)62 with the BLYP exchange-correlation functional63,64 within unrestricted Kohn–Sham (UKS) density functional theory (DFT).65 It must be remarked that a planar structure with C2h symmetry results for LS whether the starting geometry is planar or not (refer to section S2.1 in the Supporting Information for details). After geometry optimization, LS was tested by broken-symmetry unrestricted Hartree–Fock (UHF) and found to be a possible tetraradical(oid) (see section S2.3 and Figure S3 in the Supporting Information). Moreover, single-point energy UKS DFT benchmark with hybrids of PBE66,67 showed UKS DFT was insufficient for the description of all spin states of LS (section S4 in the Supporting Information).

For an appropriate description of an electronic structure of a tetraradical(oid), a qualitatively correct wave function can be obtained by multiconfigurational self-consistent field (MCSCF) methods such as complete active space SCF (CASSCF), also known as full optimized reaction space (FORS),68−75 which describes the so-called nondynamic correlation. CASSCF calculations were run from UHF natural orbitals (see below) guess as they are one of the best guess orbitals for CASSCF calculations.76 In order to explore the wave function of the LS system in greater detail, CAS configuration interaction (CASCI) calculations with (4,4) and (16,16) active spaces were performed (see section S2.4 in the Supporting Information for details). All calculations other than geometry optimizations were done with Dunning’s correlation-consistent double-ζ basis set cc-pVDZ.77

According to CASSCF(14,14) and CASCI(14,14) or CASCI(16,16) calculations,78L has greater diradical character than S, and CASSCF(14,14) calculations show that both have a singlet open-shell ground state with singlet–triplet gaps (ΔES–T) of 1.63 kcal/mol for S and 0.11 kcal/mol for L (section S7 in the Supporting Information).

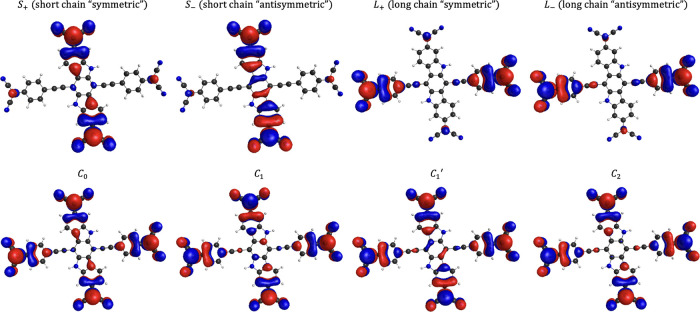
Referring to diradical(oid)s as S and L translates into referring to singly occupied natural orbitals (SONOs) given in Figure 3 for the description of the spin states of LS given in Table1. Natural orbitals (NOs) are eigenvectors of first-order density matrix operators, and a corresponding eigenvalue to the particular NO is its occupation number79 (denoted as nNO). The highest occupied NO (HONO) is defined as the orbital that has the lowest occupation number nNO among NOs with nNO ≥ 1. The lowest unoccupied NO (LUNO) is defined as the orbital that has the highest nNO among NOs with nNO ≤ 1.

Figure 3.

Figure 3

Open in a new tab

Symbolic assignations to singly occupied natural orbitals that appear for frontier orbitals in the CASSCF and CASCI solutions. Orbitals are shown as isosurfaces with a value of 0.015.

Table 1. CASSCF(16,16) Resultsa with Energy Gaps from the Ground State (G.S.)b.

state symmetry HONO – 1 HONO LUNO LUNO + 1 ΔE from G.S. (cm–1)
S0 Ag S+ 1.221 L+ 1.043 L– 0.955 S– 0.781 0.00
T0 Bu S+ 1.222 L– 1.000 L+ 0.998 S– 0.780 56.76
T1 Bu L+ 1.058 S+ 0.997 S– 0.995 L– 0.948 532.93
S1 Ag C0 1.059 C1 1.011 C′1 0.977 C2 0.951 534.77
T2 Ag C0 1.043 C1 1.021 C′1 0.975 C2 0.959 549.13
Q0 Ag C0 1.002 C2 0.999 L– 0.999 S– 0.997 602.74
Open in a new tab
a

Detailed data for CASSCF are given in Tables S1–S4 in the Supporting Information for CASSCF(4,4), CASSCF(10,10), CASSCF(14,14), and CASSCF(16,16), respectively.

b

Under columns HONO–LUNO are CASSCF NO identities from Figure 3 and their occupation numbers.

Remarkable qualitative consistency is observed throughout CASSCF(4,4), (10,10), (14,14), and (16,16) results (Tables S1–S4 in section S3.1 of the Supporting Information). CASSCF description of LS for every active space size shows four nearly singly occupied NOs for six spin states in the low-energy spectrum. Thus, LS is indeed a tetraradical(oid). Comparing the extremes, CASSCF(4,4) results given in Table S1 (Supporting Information) and CASSCF(16,16) results given in Table 1 show that we have six spin states of LS within 283.41 and 602.74 cm–1 (0.810 and 1.723 kcal/mol), respectively. Both sets of calculations show qualitatively the same picture for each state, as demonstrated by inspecting Table S1 (Supporting Information) and Table 1 with orbitals notations given in Figure 3. Notable differences are that energy gaps from ground state for each state are about twice as much for CASSCF(16,16) as for CASSCF(4,4) and the ordering between S1 and T1 is switched. However, the energy gap between S1 and T1 is 2.77 cm–1 (0.0079 kcal/mol) for CASSCF(4,4) and 1.84 cm–1 (0.0053 kcal/mol) for CASSCF(16,16), which are much smaller than the error scale of the employed method. Overall, the CASSCF method unequivocally points to the high tetraradical character of LS.

For planar polyradicals, interactions between spin centers can be approximately characterized by the Heisenberg–Dirac–van Vleck Hamiltonian (ĤHDVV = −∑i<jJijŜi·Ŝj),80−83 which describes open-shell systems as particle-per-site model of spin centers. Moreover, one must also build an effective Hamiltonian84,85 for the system and correspond it to ĤHDVV to obtain exchange-coupling constants. CASCI(16,16) results run with a neutral determinant basis of Sz = 0 subspace showed that the exchange-coupling constant (J) for radical centers in subsystem S is JS = 312.06 cm–1 (positive value means an antiferromagnetic interaction), while in subsystem L it is JL = 43.34 cm–1 (see Tables S7 and S8 in section S3.1 and section S3.2 in the Supporting Information for details and theoretical background). Furthermore, there is quite a strong coupling between the radical center of S with the radical center of L on the opposite side of indole nitrogen with value Ja = 59.92 cm–1 and a weaker coupling between the radical center of S with the radical center of L on the same side of the indole nitrogen with value Jb = 12.92 cm–1. We note that the reason Ja is much greater than Jb is because Ja is a coupling between spin centers arising from the unpaired electrons that are conjugated directly so that they could pair up to close the shell, while electrons giving rise to spin centers coupled via Jb could not (see LRSR and LRSR′ resonance structures of LS in Figure S1 of the Supporting Information). Ja is the interaction that most reflects the synergy between S and L to form tetraradical(oid) LS. The relative strengths of exchange-coupling constants are given in Figure 4a, and the energy spectrum of its spin states is given in Figure 4b. Upon inspection of results in Tables S1–S8 in section S3.1 of the Supporting Information, we see that CASCI(4,4) and CASCI(16,16) calculations parallel each other in terms of the determinantal build of the wave function and energy ordering of spin states and show remarkable qualitative consistency with CASSCF results. With CASCI(16,16), we find that in the description of the wave function of LS the aromaticity of the molecule86,87 is important (see Table S8 in section S3.1 of the Supporting Information). Hence, it can be claimed that the frontier π-electronic system of LS consists of two subsystems. The first of these is aromatic π-subspace, which is mostly delocalized within an indolo[3,2-b]carbazole aromatic moiety and two phenyl rings. The second of these subsystems is a set of four unpaired electrons that form the tetraradical(oid) electronic structure. These subsystems interact weakly but substantially enough to affect the energy spectrum of spin states.

Figure 4.

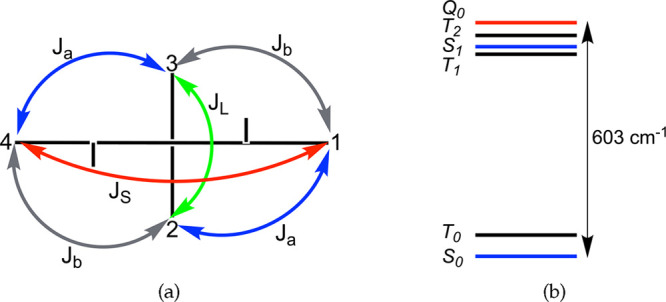
Figure 4

Open in a new tab

(a) Scheme of the strength of exchange-coupling interactions in the tetraradical(oid) LS. Red is the strongest, blue is the second strongest, closely followed by green, and the weakest is gray. Rods sticking out from the horizontal line (1–4) correspond to the indole nitrogens. (b) Low-energy sectrum of the tetraradical(oid) LS.

The possible reasons for the stabilization of this tetraradical(oid) electronic structure are symmetry, a high degree of conjugation and delocalization, the presence of bridging groups between radical centers involving locally aromatic benzenoid rings (Clar’s π-sextets), and the potential for so-called “global aromaticity” of the indolo[3,2-b]carbazole backbone. Upon investigation of the anisotropy of induced current density (ACID) of singlet and quintet states, which describes the response of electron currents on a perpendicular magnetic field that leads to flow of electron current around the aromatic rings,88 we detected continuous electron flow around the perimeter of the indolo[3,2-b]carbazole backbone and two phenyl rings bonded to the central benzene ring of the indolo[3,2-b]carbazole as given in Figure 5 for a singlet state, which is almost indistinguishable from a quintet state in this aspect (Figure S8 in section S5 of the Supporting Information). Hence, in addition to evidence from CASSCF and CASCI calculations, we have other demonstrations for the aromatic stabilization of this tetraradical(oid). These results are also corroborated by another measure of aromaticity, the multicenter index (MCI).89,90 MCI values show that benzenoid rings within LS, for which results are given in Table S10 of the Supporting Information, are indeed aromatic. To explain the maintenance of open shells, we should also note that diradical resonance structures possess three more Clar’s aromatic π-sextets91,92 than closed-shell quinoidal structures for L (Figure S12 in the Supporting Information) and S (Figure S13 in the Supporting Information), which stabilizes the diradical form over the quinoidal form. This is also maintained in the tetraradical(oid) LS, for which the resonance structure (from Figure 2) LDSD has three more Clar’s aromatic π-sextets than the resonance forms LDSQ and LQSD (and LRSR/LRSR′ structures given in Figure S1 of the Supporting Information). Notably, subunits S and L based on nNO of their frontier NOs maintain their respective diradical(oid) structure quite closely in the tetraradical(oid) LS. For demonstration, we can compare S0 states from CASSCF(14,14) for S, L, and LS (Tables S17, S20, and S3, respectively, in the Supporting Information). Occupation numbers in the S0 state change from nHONO = 1.047–1.051 and nLUNO = 0.958–0.947 for L, while occupation numbers in the S0 state change from nHONO = 1.205–1.192 and nLUNO = 0.801–0.813 for S. If we view this tetraradical(oid) LS from the modular perspective of L and S, it would not necessarily (and usually) be expected to combine these diradical(oid) structures in some way and still maintain electrons unpaired to form tetraradical(oid), which is usually successively more difficult as the number of unpaired electrons increases. Nonetheless, this is what we observed for LS. Hence, there is a synergy between L and S substructures within LS that maintains all the open shells and achieves the diradical(oid) + diradical(oid) + coupling = tetraradical(oid) structure, as manifested by Ja = 59.92 cm–1. Evidently, the conceptual union of these two diradical(oid)s produces tetraradical(oid) LS, which is indeed one of the smallest planar and fully π-conjugated organic tetraradical(oid)s that has been described in the scientific literature to date. Our work predicts that LS is a genuine tetraradical with six thermally accessible spin states in the low-energy spectrum, which can be experimentally validated by electron paramagnetic resonance (EPR) spectroscopy.

Figure 5.

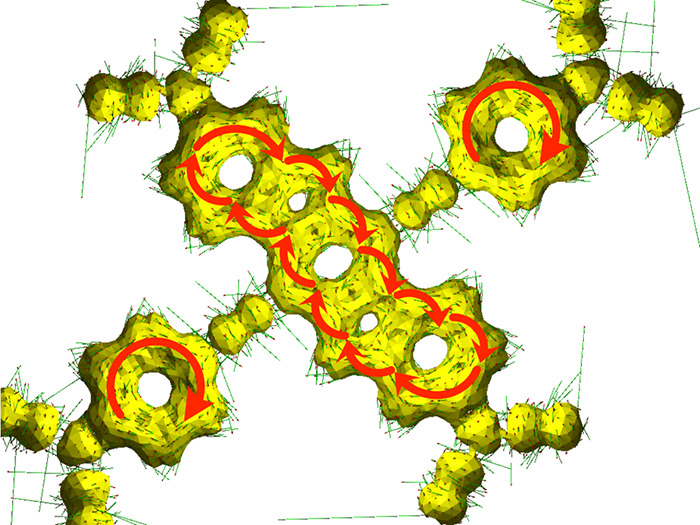
Figure 5

Open in a new tab

An ACID plot for a singlet state of LS calculated with the PBE0/cc-pVDZ level of theory. See the full version of the ACID plot in Figure S8a in the Supporting Information. Isosurface with value of 0.030.

Our general approach can be summarized in the following way: (1) If the polyradical is built from merging diradicals or other polyradicals, one must ensure that π-conjugation is maintained throughout the resulting structure. (2) Within a given polyradical, each diradical subunit must have an aromatic stabilization with at least two or (more favorably) three benzene rings. (3) Aromatic rings can be shared between different subunits, similarly as the central benzene ring is shared between L and S subunits within tetraradical(oid) LS. (4) Upon the design of a polyradical, one can take advantage of cross-conjugation to restrict the lower bound of polyradical character, as we did to restrict the minimal polyradical character of tetraradical(oid) LS to 2.

To conclude, we provide a general strategy to design polyradicals with thermally accessible high spin electronic states. Thus, 2,2’-(6,12-bis((4-(dicyanomethyl)phenyl)ethynyl)-5,11-dihydroindolo[3,2-b]carbazole-3,9-diyl)dimalononitrile (LS) is built with this approach as a merger of L and S diradical(oid) constituents. Diradical(oid)s are merged in a way that retains π-conjugation and allows for inner electron delocalization, which is a source of stabilization. Such a mechanism can be used to stabilize hexaradicals, octadecaradicals, and higher polyradicals. Hence, this frontier toward higher polyradical(oid)s is being actively explored further by our group.

Acknowledgments

Authors acknowledge the financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades, project nos. PID2019-109518GB-I00 and PID2022-138861NB-I00, and Spanish Structures of Excellence María de Maeztu program through Grant CEX2021-001202-M. This work was supported by Agència de Gestió d’Ajuts Universitaris i de Recerca of Generalitat de Catalunya, project nos. 2021SGR00354 and 2021SGR00442.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.4c00686.

  • Optimized geometries, computational details of geometry optimization, methodology of the open-shell character test, computational details of CASSCF and CASCI, details of the model and effective Hamiltonian, results of CASSCF and CASCI calculations, results from the broken-symmetry DFT and HF benchmark, results from ACID and MCI, and study of constituent diradical(oid)s (PDF)

  • Transparent Peer Review report available (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz4c00686_si_001.pdf (11MB, pdf)
jz4c00686_si_002.pdf (371KB, pdf)

References

  1. Hu X.; Wang W.; Wang D.; Zheng Y. The electronic applications of stable diradicaloids: present and future. J. Mater. Chem. C 2018, 6, 11232–11242. 10.1039/C8TC04484H. [DOI] [Google Scholar]
  2. Cui Z.; Abdurahman A.; Ai X.; Li F. Stable Luminescent Radicals and Radical-Based LEDs with Doublet Emission. CCS Chem. 2020, 2, 1129–1145. 10.31635/ccschem.020.202000210. [DOI] [Google Scholar]
  3. Dong S.; Ong A.; Chi C. Photochemistry of various acene based molecules. J. Photochem. Photobiol., C 2019, 38, 27–46. 10.1016/j.jphotochemrev.2018.12.002. [DOI] [Google Scholar]
  4. Teki Y. Excited-State Dynamics of Non-Luminescent and Luminescent π-Radicals. Chem.-Eur. J. 2020, 26, 980–996. 10.1002/chem.201903444. [DOI] [PubMed] [Google Scholar]
  5. Ji L.; Shi J.; Wei J.; Yu T.; Huang W. Air-Stable Organic Radicals: New-Generation Materials for Flexible Electronics?. Adv. Mater. 2020, 32, 1908015. 10.1002/adma.201908015. [DOI] [PubMed] [Google Scholar]
  6. Sanvito S. Molecular spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. 10.1039/c1cs15047b. [DOI] [PubMed] [Google Scholar]
  7. Gopalakrishna T. Y.; Zeng W.; Lu X.; Wu J. From open-shell singlet diradicaloids to polyradicaloids. Chem. Commun. 2018, 54, 2186–2199. 10.1039/C7CC09949E. [DOI] [PubMed] [Google Scholar]
  8. Chen Z.; Li Y.; Huang F. Persistent and Stable Organic Radicals: Design, Synthesis, and Applications. Chem. 2021, 7, 288–332. 10.1016/j.chempr.2020.09.024. [DOI] [Google Scholar]
  9. Slota M.; Keerthi A.; Myers W. K.; Tretyakov E.; Baumgarten M.; Ardavan A.; Sadeghi H.; Lambert C. J.; Narita A.; Müllen K.; et al. Magnetic edge states and coherent manipulation of graphene nanoribbons. Nature 2018, 557, 691–695. 10.1038/s41586-018-0154-7. [DOI] [PubMed] [Google Scholar]
  10. Gomberg M. Triphenylmethyl, ein Fall von dreiwerthigem Kohlenstoff. Ber. Dtsch. Chem. Ges. 1900, 33, 3150–3163. 10.1002/cber.19000330369. [DOI] [Google Scholar]
  11. Catala L.; Le Moigne J.; Gruber N.; Novoa J. J.; Rabu P.; Belorizky E.; Turek P. Towards a Better Understanding of Magnetic Interactions within m-Phenylene α-Nitronyl Nitroxide and Imino Nitroxide Based Radicals, Part III: Magnetic Exchange in a Series of Triradicals and Tetraradicals Based on the Phenyl Acetylene and Biphenyl Coupling Units.. Chem.-Eur. J. 2005, 11, 2440–2454. 10.1002/chem.200400552. [DOI] [PubMed] [Google Scholar]
  12. Olankitwanit A.; Kathirvelu V.; Rajca S.; Eaton G. R.; Eaton S. S.; Rajca A. Calix[4]arene nitroxide tetraradical and octaradical. Chem. Commun. 2011, 47, 6443–6445. 10.1039/c1cc11172h. [DOI] [PubMed] [Google Scholar]
  13. Tretyakov E. V.; Zayakin I. A.; Dmitriev A. A.; Fedin M. V.; Romanenko G. V.; Bogomyakov A. S.; Akyeva A. Y.; Syroeshkin M. A.; Yoshioka N.; Gritsan N. P. A Nitronyl Nitroxide-Substituted Benzotriazinyl Tetraradical**. Chem.-Eur. J. 2024, 30, e202303456 10.1002/chem.202303456. [DOI] [PubMed] [Google Scholar]
  14. Pal A. K.; Datta S. N. Quantum Chemical Investigation of Calix[4]arene-Based Radicals with Bis(biphenylene)methyl Linkers as Precursors of Spin Glass and Superparamagnets. J. Phys. Chem. C 2014, 118, 27599–27610. 10.1021/jp509972m. [DOI] [Google Scholar]
  15. Hu P.; Lee S.; Herng T. S.; Aratani N.; Gonçalves T. P.; Qi Q.; Shi X.; Yamada H.; Huang K.-W.; Ding J.; et al. Toward Tetraradicaloid: The Effect of Fusion Mode on Radical Character and Chemical Reactivity. J. Am. Chem. Soc. 2016, 138, 1065–1077. 10.1021/jacs.5b12532. [DOI] [PubMed] [Google Scholar]
  16. Das S.; Herng T. S.; Zafra J. L.; Burrezo P. M.; Kitano M.; Ishida M.; Gopalakrishna T. Y.; Hu P.; Osuka A.; Casado J.; et al. Fully Fused Quinoidal/Aromatic Carbazole Macrocycles with Poly-radical Characters. J. Am. Chem. Soc. 2016, 138, 7782–7790. 10.1021/jacs.6b04539. [DOI] [PubMed] [Google Scholar]
  17. Lu X.; Gopalakrishna T. Y.; Phan H.; Herng T. S.; Jiang Q.; Liu C.; Li G.; Ding J.; Wu J. Global Aromaticity in Macrocyclic Cyclopenta-Fused Tetraphenanthrenylene Tetraradicaloid and Its Charged Species. Angew. Chem., Int. Ed. 2018, 57, 13052–13056. 10.1002/anie.201807185. [DOI] [PubMed] [Google Scholar]
  18. Ma J.; Zhang K.; Schellhammer K. S.; Fu Y.; Komber H.; Xu C.; Popov A. A.; Hennersdorf F.; Weigand J. J.; Zhou S.; et al. Wave-shaped polycyclic hydrocarbons with controlled aromaticity. Chem. Sci. 2019, 10, 4025–4031. 10.1039/C8SC05416A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Li G.; Han Y.; Zou Y.; Lee J. J. C.; Ni Y.; Wu J. Dearomatization Approach Toward a Superbenzoquinone-Based Diradicaloid, Tetraradicaloid, and Hexaradicaloid. Angew. Chem., Int. Ed. 2019, 58, 14319–14326. 10.1002/anie.201907030. [DOI] [PubMed] [Google Scholar]
  20. Ajayakumar M. R.; Ma J.; Lucotti A.; Schellhammer K. S.; Serra G.; Dmitrieva E.; Rosenkranz M.; Komber H.; Liu J.; Ortmann F.; et al. Persistent peri-Heptacene: Synthesis and In Situ Characterization. Angew. Chem., Int. Ed. 2021, 60, 13853–13858. 10.1002/anie.202102757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Miyazawa Y.; Wang Z.; Hatano S.; Takagi R.; Matsuoka H.; Amamizu N.; Kitagawa Y.; Kayahara E.; Yamago S.; Abe M. Generation and Characterization of a Tetraradical Embedded in a Curved Cyclic Paraphenylene Unit. Chem.-Eur. J. 2023, 29, e202301009 10.1002/chem.202301009. [DOI] [PubMed] [Google Scholar]
  22. Anglada J. M.; Poater J.; Moreira I. d. P. R.; Bofill J. M. Controlling the Diradical Character of Thiele Like Compounds. J. Org. Chem. 2023, 88, 8553–8562. 10.1021/acs.joc.3c00482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Iwamura H. Design of organic molecules and molecular assemblies with electron spin alignment. Pure Appl. Chem. 1987, 59, 1595–1604. 10.1351/pac198759121595. [DOI] [Google Scholar]
  24. Rajca A. The physical organic chemistry of very high-spin polyradicals. Adv. Phys. Org. Chem. 2005, 40, 153–199. 10.1016/S0065-3160(05)40004-0. [DOI] [Google Scholar]
  25. Li Y.; Jia Z.; Xiao S.; Liu H.; Li Y. A method for controlling the synthesis of stable twisted two-dimensional conjugated molecules. Nat. Commun. 2016, 7, 11637. 10.1038/ncomms11637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Nagai H.; Nakano M.; Yoneda K.; Kishi R.; Takahashi H.; Shimizu A.; Kubo T.; Kamada K.; Ohta K.; Botek E.; et al. Signature of multiradical character in second hyperpolarizabilities of rectangular graphene nanoflakes. Chem. Phys. Lett. 2010, 489, 212–218. 10.1016/j.cplett.2010.03.013. [DOI] [Google Scholar]
  27. Smith M. B.; Michl J. Singlet Fission. Chem. Rev. 2010, 110, 6891–6936. 10.1021/cr1002613. [DOI] [PubMed] [Google Scholar]
  28. Wang L.; Shi X.; Feng S.; Liang W.; Fu H.; Yao J. Molecular Design Strategy for Practical Singlet Fission Materials: The Charm of Donor/Acceptor Decorated Quinoidal Structure. CCS Chem. 2022, 4, 2748–2756. 10.31635/ccschem.021.202101199. [DOI] [Google Scholar]
  29. Zimmerman P. M.; Zhang Z.; Musgrave C. B. Singlet fission in pentacene through multi-exciton quantum states. Nat. Chem. 2010, 2, 648–652. 10.1038/nchem.694. [DOI] [PubMed] [Google Scholar]
  30. Cheng W.; Chen H.; Liu C.; Ji C.; Ma G.; Yin M. Functional organic dyes for health-related applications. VIEW 2020, 1, 20200055. 10.1002/VIW.20200055. [DOI] [Google Scholar]
  31. Guo Z.; Park S.; Yoon J.; Shin I. Recent progress in the development of near-infrared fluorescent probes for bioimaging applications. Chem. Soc. Rev. 2014, 43, 16–29. 10.1039/C3CS60271K. [DOI] [PubMed] [Google Scholar]
  32. Abe M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. 10.1021/cr400056a. [DOI] [PubMed] [Google Scholar]
  33. Okamoto Y.; Tanioka M.; Muranaka A.; Miyamoto K.; Aoyama T.; Ouyang X.; Kamino S.; Sawada D.; Uchiyama M. Stable Thiele’s Hydrocarbon Derivatives Exhibiting Near-Infrared Absorption/Emission and Two-Step Electrochromism. J. Am. Chem. Soc. 2018, 140, 17857–17861. 10.1021/jacs.8b11092. [DOI] [PubMed] [Google Scholar]
  34. Morita Y.; Nishida S.; Murata T.; Moriguchi M.; Ueda A.; Satoh M.; Arifuku K.; Sato K.; Takui T. Organic tailored batteries materials using stable open-shell molecules with degenerate frontier orbitals. Nat. Mater. 2011, 10, 947–951. 10.1038/nmat3142. [DOI] [PubMed] [Google Scholar]
  35. Nakano M.; Kishi R.; Nitta T.; Kubo T.; Nakasuji K.; Kamada K.; Ohta K.; Champagne B.; Botek E.; Yamaguchi K. Second Hyperpolarizability (γ) of Singlet Diradical System: Dependence of γon the Diradical Character.. J. Phys. Chem. A 2005, 109, 885–891. 10.1021/jp046322x. [DOI] [PubMed] [Google Scholar]
  36. Minami T.; Nakano M. Diradical Character View of Singlet Fission. J. Phys. Chem. Lett. 2012, 3, 145–150. 10.1021/jz2015346. [DOI] [PubMed] [Google Scholar]
  37. Varnavski O.; Abeyasinghe N.; Aragó J.; Serrano-Pérez J. J.; Ortí E.; López Navarrete J. T.; Takimiya K.; Casanova D.; Casado J.; Goodson T. I. High Yield Ultrafast Intramolecular Singlet Exciton Fission in a Quinoidal Bithiophene. J. Phys. Chem. Lett. 2015, 6, 1375–1384. 10.1021/acs.jpclett.5b00198. [DOI] [PubMed] [Google Scholar]
  38. Neiman M. B.; Rozantsev É. G.; Golubev V. A. First stable triradicals. Bull. Acad. Sci. USSR, Div. Chem. Sci. 1965, 14, 529–530. 10.1007/BF00846621. [DOI] [Google Scholar]
  39. Rozantsev E. G.; Golubev V. A. Free tetraradicals. Bull. Acad. Sci. USSR, Div. Chem. Sci. 1965, 14, 695–697. 10.1007/BF00846732. [DOI] [Google Scholar]
  40. Carilla J.; Julia L.; Riera J.; Brillas E.; Garrido J. A.; Labarta A.; Alcala R. The first isolated carbon tetraradical with a pair of triplets. J. Am. Chem. Soc. 1991, 113, 8281–8284. 10.1021/ja00022a013. [DOI] [Google Scholar]
  41. Rajca A.; Utamapanya S. Poly(arylmethyl) quartet triradicals and quintet tetraradicals. J. Am. Chem. Soc. 1993, 115, 2396–2401. 10.1021/ja00059a039. [DOI] [Google Scholar]
  42. Rajca A.; Rajca S.; Desai S. R. Macrocyclic π-Conjugated Carbopolyanions and Polyradicals Based upon Calix[4]arene and Calix[3]arene Rings.. J. Am. Chem. Soc. 1995, 117, 806–816. 10.1021/ja00107a025. [DOI] [Google Scholar]
  43. Adam W.; van Barneveld C.; Emmert O.; Harrer H. M.; Kita F.; Kumar A. S.; Maas W.; Nau W. M.; Reddy S. H. K.; Wirz J. About monoradicals, triplet diradicals and higher spin states: Understanding electronic substituent effects through EPR and time-resolved UV spectroscopy. Pure Appl. Chem. 1997, 69, 735–742. 10.1351/pac199769040735. [DOI] [Google Scholar]
  44. Nau W. M. Organic Tri- and Tetraradicals with High-Spin or Low-Spin States. Angew. Chem., Int. Ed. Engl. 1997, 36, 2445–2448. 10.1002/anie.199724451. [DOI] [Google Scholar]
  45. Krylov A. I. Triradicals. J. Phys. Chem. A 2005, 109, 10638–10645. 10.1021/jp0528212. [DOI] [PubMed] [Google Scholar]
  46. Winkler M.; Sander W. Triradicals. Acc. Chem. Res. 2014, 47, 31–44. 10.1021/ar4000218. [DOI] [PubMed] [Google Scholar]
  47. Nobusue S.; Miyoshi H.; Shimizu A.; Hisaki I.; Fukuda K.; Nakano M.; Tobe Y. Tetracyclopenta[def,jkl,pqr,vwx]tetraphenylene: A Potential Tetraradicaloid Hydrocarbon. Angew. Chem., Int. Ed. 2015, 54, 2090–2094. 10.1002/anie.201410791. [DOI] [PubMed] [Google Scholar]
  48. Zhang D.; Liu C. Electronic Structures of Anti-Ferromagnetic Tetraradicals: Ab Initio and Semi-Empirical Studies. J. Chem. Theory Comput. 2016, 12, 1714–1727. 10.1021/acs.jctc.6b00103. [DOI] [PubMed] [Google Scholar]
  49. Li Y.; Jia Z.; Xiao S.; Liu H.; Li Y. A method for controlling the synthesis of stable twisted two-dimensional conjugated molecules. Nat. Commun. 2016, 7, 11637. 10.1038/ncomms11637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Hattori Y.; Michail E.; Schmiedel A.; Moos M.; Holzapfel M.; Krummenacher I.; Braunschweig H.; Müller U.; Pflaum J.; Lambert C. Luminescent Mono-, Di-, and Triradicals: Bridging Polychlorinated Triarylmethyl Radicals by Triarylamines and Triarylboranes. Chem.-Eur. J. 2019, 25, 15463–15471. 10.1002/chem.201903007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Chattopadhyay S. Ab Initio Probing of the Ground State of Tetraradicals: Breakdown of Hund’s Multiplicity Rule. J. Phys. Chem. A 2019, 123, 2211–2226. 10.1021/acs.jpca.8b10514. [DOI] [PubMed] [Google Scholar]
  52. Zhang H.; Pink M.; Wang Y.; Rajca S.; Rajca A. High-Spin S = 3/2 Ground-State Aminyl Triradicals: Toward High-Spin Oligo-Aza Nanographenes. J. Am. Chem. Soc. 2022, 144, 19576–19591. 10.1021/jacs.2c09241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Khurana R.; Bajaj A.; Shamasundar K. R.; Ali M. E. High-Spin Blatter’s Triradicals. J. Phys. Chem. A 2023, 127, 7802–7810. 10.1021/acs.jpca.3c02683. [DOI] [PubMed] [Google Scholar]
  54. Zander E.; Bresien J.; Zhivonitko V. V.; Fessler J.; Villinger A.; Michalik D.; Schulz A. Rational Design of Persistent Phosphorus-Centered Singlet Tetraradicals and Their Use in Small-Molecule Activation. J. Am. Chem. Soc. 2023, 145, 14484–14497. 10.1021/jacs.3c03928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Badía-Domínguez I.; Canola S.; Hernández Jolín V.; López Navarrete J. T.; Sancho-García J. C.; Negri F.; Ruiz Delgado M. C. Tuning the Diradical Character of Indolocarbazoles: Impact of Structural Isomerism and Substitution Position. J. Phys. Chem. Lett. 2022, 13, 6003–6010. 10.1021/acs.jpclett.2c01325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Zhang Y.; Ma Y.; Kong L.; Tian Y.; Yang J. A novel indolo[3,2-b]carbazole derivative with D–A structure exhibiting aggregation-enhanced emission and mechanofluorochromic properties.. Dyes Pigm. 2018, 159, 314–321. 10.1016/j.dyepig.2018.06.040. [DOI] [Google Scholar]
  57. Thiele J.; Balhorn H. Ueber einen chinoïden Kohlenwasserstoff. Ber. Dtsch. Chem. Ges. 1904, 37, 1463–1470. 10.1002/cber.19040370245. [DOI] [Google Scholar]
  58. Tschitschibabin A. E. Über einige phenylierte Derivate des p, p-Ditolyls. Ber. Dtsch. Chem. Ges. 1907, 40, 1810–1819. 10.1002/cber.19070400282. [DOI] [Google Scholar]
  59. Müller E.; Pfanz H. Über biradikaloide Terphenylderivate. Ber. Dtsch. Chem. Ges. A/B 1941, 74, 1051–1074. 10.1002/cber.19410740636. [DOI] [Google Scholar]
  60. Ovchinnikov A. A. Multiplicity of the ground state of large alternant organic molecules with conjugated bonds. Theor. Chim. Acta 1978, 47, 297–304. 10.1007/BF00549259. [DOI] [Google Scholar]
  61. Van Lenthe E.; Baerends E. J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
  62. Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  63. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  64. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
  65. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  66. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)].. Phys. Rev. Lett. 1997, 78, 1396–1396. 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
  67. Ruedenberg K.; Sundberg K. R.. MCSCF Studies of Chemical Reactions: Natural Reaction Orbitals and Localized Reaction Orbitals. In Quantum Science: Methods and Structure. A Tribute to Per-Olov Löwdin; Calais J.-L., Goscinski O., Linderberg J., Öhrn Y., Eds.; Springer US: Boston, MA, 1976; pp 505–515. [Google Scholar]
  68. Cheung L. M.; Sundberg K. R.; Ruedenberg K. Dimerization of carbene to ethylene. J. Am. Chem. Soc. 1978, 100, 8024–8025. 10.1021/ja00493a050. [DOI] [Google Scholar]
  69. Cheung L. M.; Sundberg K. R.; Ruedenberg K. Electronic rearrangements during chemical reactions. II. Planar dissociation of ethylene. Int. J. Quantum Chem. 1979, 16, 1103–1139. 10.1002/qua.560160512. [DOI] [Google Scholar]
  70. Roos B. O.; Taylor P. R.; Sigbahn P. E. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
  71. Johnson R. P.; Schmidt M. W. The sudden polarization effect: MC-SCF calculations on planar and 90.degree. twisted methylenecyclopropene. J. Am. Chem. Soc. 1981, 103, 3244–3249. 10.1021/ja00402a002. [DOI] [Google Scholar]
  72. Feller D. F.; Schmidt M. W.; Ruedenberg K. Concerted dihydrogen exchange between ethane and ethylene. SCF and FORS calculations of the barrier. J. Am. Chem. Soc. 1982, 104, 960–967. 10.1021/ja00368a006. [DOI] [Google Scholar]
  73. Ruedenberg K.; Schmidt M. W.; Gilbert M. M.; Elbert S. Are atoms intrinsic to molecular electronic wavefunctions?. I. The FORS model. Chem. Phys. 1982, 71, 41–49. 10.1016/0301-0104(82)87004-3. [DOI] [Google Scholar]
  74. Shepard R. The Multiconfiguration Self-Consistent Field Method. Adv. Chem. Phys. 1987, 69, 63–200. 10.1002/9780470142943.ch2. [DOI] [Google Scholar]
  75. Pulay P.; Hamilton T. P. UHF natural orbitals for defining and starting MC-SCF calculations. J. Chem. Phys. 1988, 88, 4926–4933. 10.1063/1.454704. [DOI] [Google Scholar]
  76. Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. 10.1063/1.470645. [DOI] [Google Scholar]
  77. Bofill J. M.; Pulay P. The unrestricted natural orbital–complete active space (UNO–CAS) method: An inexpensive alternative to the complete active space–self-consistent-field (CAS–SCF) method. J. Chem. Phys. 1989, 90, 3637–3646. 10.1063/1.455822. [DOI] [Google Scholar]
  78. Lowdin P.-O. Present Situation of Quantum Chemistry. J. Phys. Chem. 1957, 61, 55–68. 10.1021/j150547a012. [DOI] [Google Scholar]
  79. Heisenberg W. Zur Theorie des Ferromagnetismus. Z. Phys. 1928, 49, 619–636. 10.1007/BF01328601. [DOI] [Google Scholar]
  80. Dirac P. A. M.; Polkinghorne J. C. The Principles of Quantum Mechanics. Phys. Today 1958, 11, 32–33. 10.1063/1.3062610. [DOI] [Google Scholar]
  81. Van Vleck J. The Theory of Electric and Magnetic Susceptibilities. Nature 1932, 130, 490–491. 10.1038/130490a0. [DOI] [Google Scholar]
  82. de P. R. Moreira I.; Illas F. Ab initio theoretical comparative study of magnetic coupling in KNiF3sand K2NiF4s. Phys. Rev. B 1997, 55, 4129–4137. 10.1103/PhysRevB.55.4129. [DOI] [Google Scholar]
  83. Bloch C. Sur la théorie des perturbations des états liés. Nucl. Phys. 1958, 6, 329–347. 10.1016/0029-5582(58)90116-0. [DOI] [Google Scholar]
  84. des Cloizeaux J. Extension d’une formule de Lagrange à des problèmes de valeurs propres. Nucl. Phys. 1960, 20, 321–346. 10.1016/0029-5582(60)90177-2. [DOI] [Google Scholar]
  85. Ottosson H. Exciting excited-state aromaticity. Nat. Chem. 2012, 4, 969–971. 10.1038/nchem.1518. [DOI] [PubMed] [Google Scholar]
  86. Escayola S.; Tonnelé C.; Matito E.; Poater A.; Ottosson H.; Solà M.; Casanova D. Guidelines for Tuning the Excited State Hückel–Baird Hybrid Aromatic Character of Pro-Aromatic Quinoidal Compounds. Angew. Chem., Int. Ed. 2021, 60, 10255–10265. 10.1002/anie.202100261. [DOI] [PubMed] [Google Scholar]
  87. Geuenich D.; Hess K.; Köhler F.; Herges R. Anisotropy of the Induced Current Density (ACID), a General Method To Quantify and Visualize Electronic Delocalization. Chem. Rev. 2005, 105, 3758–3772. 10.1021/cr0300901. [DOI] [PubMed] [Google Scholar]
  88. Bultinck P.; Ponec R.; Van Damme S. Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. 10.1002/poc.922. [DOI] [Google Scholar]
  89. Feixas F.; Matito E.; Poater J.; Solà M. Quantifying aromaticity with electron delocalisation measure. Chem. Soc. Rev. 2015, 44, 6434–6451. 10.1039/C5CS00066A. [DOI] [PubMed] [Google Scholar]
  90. Clar E.The Aromatic Sextet; Wiley, 1972. [Google Scholar]
  91. Solà M. Forty years of Clar’s aromatic π-sextet rule. Front. Chem. 2013, 1, 22. 10.3389/fchem.2013.00022. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz4c00686_si_001.pdf (11MB, pdf)
jz4c00686_si_002.pdf (371KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES