Building an allocentric traveling-direction signal via vector computation

Abstract

Many behavioral tasks require the manipulation of mathematical vectors, but, outside of computational models^1–7, it is not known how brains perform vector operations. Here we show how the Drosophila central complex, a region implicated in goal-directed navigation^7–10, performs vector arithmetic. First, we describe a neural signal in the fan-shaped body that explicitly tracks a fly’s allocentric traveling angle, that is, the traveling angle in reference to external cues. Past work has identified neurons in Drosophila^8,11–13 and mammals¹⁴ that track an animal’s heading angle referenced to external cues (e.g., head-direction cells), but this new signal illuminates how the sense of space is properly updated when traveling and heading angles differ (e.g., when walking sideways). We then characterize a neuronal circuit that performs an egocentric-to-allocentric (i.e., body- to world-centered) coordinate transformation and vector addition to compute the allocentric traveling direction. This circuit operates by mapping two-dimensional vectors onto sinusoidal patterns of activity across distinct neuronal populations, with the sinusoid’s amplitude representing the vector’s length and its phase representing the vector’s angle. The principles of this circuit may generalize to other brains and to domains beyond navigation where vector operations or reference-frame transformations are required.

Introduction

Insects solve remarkable navigational tasks^15,16 and, like mammals, they have head-direction-like cells, called EPGs, with activity tuned to the fly’s angular heading in reference to external cues⁸. An insect’s heading and traveling angles, however, do not always align, such as when walking or flying sideways (e.g., due to wind) or when simply looking sideways while walking forward. Because it is the traveling direction that is most relevant for forming spatial memories via path integration, perhaps insects explicitly track this variable during navigation? Here we show that a population of neurons that tiles the Drosophila fan-shaped body expresses a bump of activity at a left-right position along this structure that indicates the fly’s traveling, rather than heading, angle in reference to external cues. We further describe a neuronal circuit that computes this external-cue-referenced, or allocentric, traveling-direction signal by explicitly projecting the fly’s egocentric, or body-referenced, traveling vector onto four orthogonal axes, rotating those axes into the allocentric reference frame, and taking a vector sum of the four vectors.

Beyond heading in the central complex

The Drosophila central complex includes the ellipsoid body, protocerebral bridge and fan-shaped body (Fig. 1a–b). Single EPG neurons have a mixed, input/output, ‘dendritic’ terminal in one wedge of the ellipsoid body and an ‘axonal’ terminal in one glomerulus of the protocerebral bridge^17,18 (Fig. 1b, two blue cells). In both walking^8,11,12 and flying flies^10,19, the full population of EPG cells expresses a bump of calcium activity in the ellipsoid body, and copies of this bump in the left and right bridge. These three signals shift in concert along these structures, tracking the fly’s angular heading referenced to external cues^8,11,12.

Figure 1 |. hΔB neurons signal Drosophila’s allocentric traveling direction.

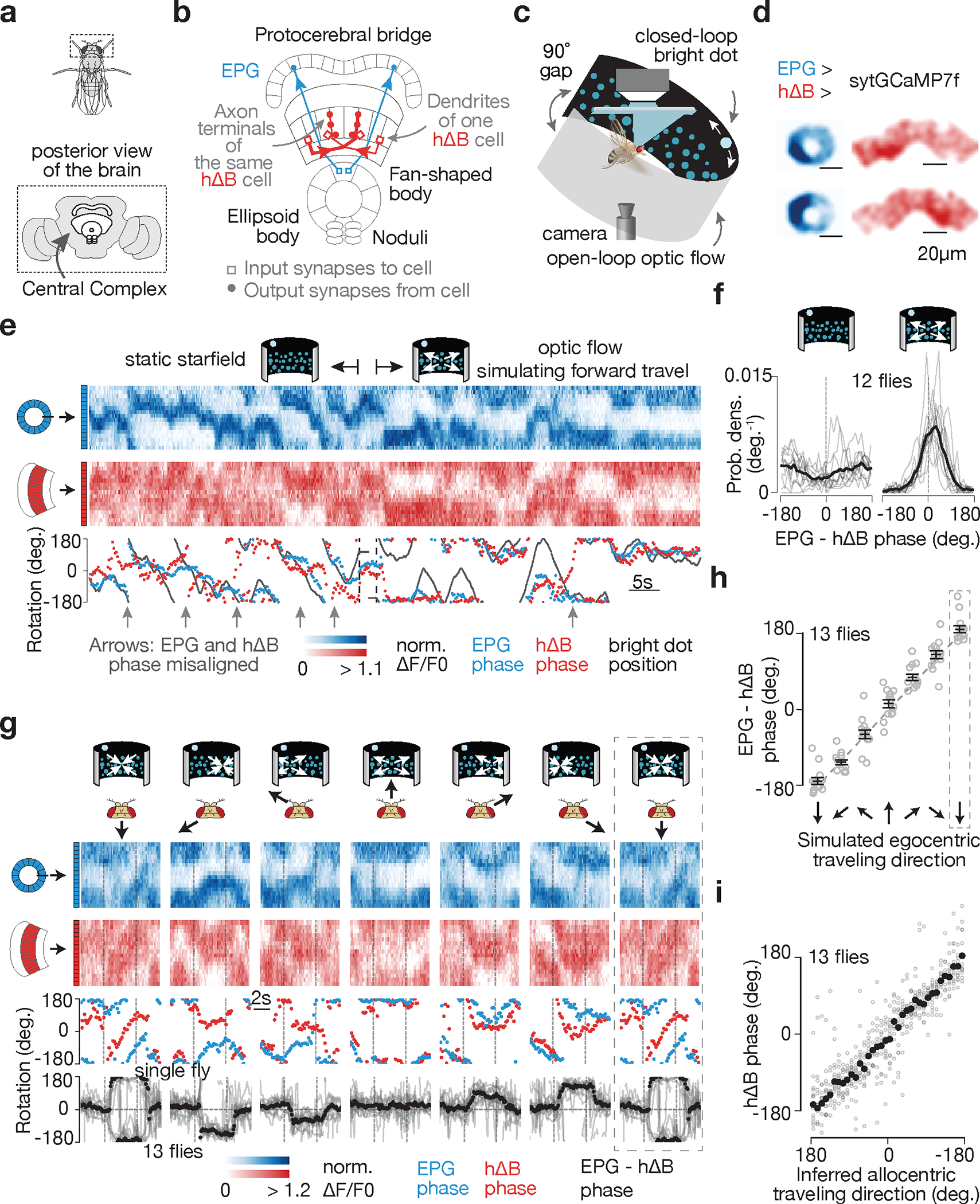
a, Fly brain. b, Two example EPGs and two example hΔBs. Each cell type tiles the central complex c, Imaging neural activity in a flying fly with an LED arena. d, sytGCaMP7f frames of the EPG bump in the ellipsoid body and the hΔB bump in the fan-shaped body. e, Simultaneously recorded sytGCaMP7f signal from EPGs (blue) and hΔBs (red) in a flying fly. Top: [Ca²⁺] signal; bottom: phase estimates and dot position. Gray regions represent the 90° gap in the back of the arena. f, Distributions of EPG – hΔB phase without and with optic flow. Gray: single fly means. Black: population mean. g, Top, EPG (blue) and hΔB (red) sytGCaMP7f signal in a sample flying fly experiencing optic-flow with foci of expansion that simulate the following directions of travel (in the time period delimited by the vertical dashed lines): 180° (backward), −120°, −60°, 0° (forward), 60°, 120°, 180° (backward; repeated). Middle, phases of the sample [Ca²⁺] signals above. Bottom, circular mean of EPG – hΔB phase for a fly population. Gray: single fly means. Black: population mean. Dotted rectangle: repeated-data column. h, EPG – hΔB phase versus the egocentric traveling direction simulated by optic flow. Circular means were calculated in the final 2.5 s of optic-flow presentation. Gray: individual fly means. Black: population mean and s.e.m. Dotted rectangle: repeated-data column. i, hΔB phase versus the inferred allocentric traveling direction, calculated by assuming that the EPG phase indicates allocentric heading and adding to this angle, at every sample point, the optic-flow angle. Same data as in panels g-h. Gray: individual fly means. Black: population mean. (Note flipped x-axis indicating that the hΔB bump tracks the negative of the fly’s traveling direction; Methods).

EPGs represent one of a few dozen sets of columnar neurons in the central complex. Each columnar cell class tiles the ellipsoid body, protocerebral bridge, and/or fan-shaped body. Individual columnar cells or neurite fields can be assigned an angular label between 0°–360° based on their anatomical location^17,18, with neighboring neurites mapping to neighboring angles. hDeltaB cells (hΔBs) are a columnar class whose constituent cells have a ‘dendritic’ arbor in layer 3 of one fan-shaped body column and a mixed, input/output, ‘axonal’ arbor in layers 3, 4, 5 of another column offset by half the width of the fan-shaped body¹⁷ (Fig. 1b, two red cells). We created a split-Gal4 driver line for hΔBs (Extended Data Fig. 1a–d) and a UAS-sytGCaMP7f responder line in which GCaMP7f is fused to the c-terminus of synaptotagmin to bias GCaMP7f to presynaptic compartments²⁰ (Extended Data Fig. 1e–f). Imaging sytGCaMP7f fluorescence in hΔBs of both walking (Extended Data Fig. 1n) and flying (see below) flies revealed a bump of activity that moves left/right along the fan-shaped body in coordination with the movements of the EPG bump around the ellipsoid body. Critically, however, the relative position of the hΔB and EPG bumps were often offset (Extended Data Fig. 1n) suggesting that the hΔB bump position might signal the fly’s traveling, rather than heading, angle.

hΔBs track the allocentric travel angle

To test the hypothesis that the hΔB bump position tracks the fly’s traveling direction, we performed most of our experiments on tethered, flying flies²¹ (Fig. 1c). In flight, insects rely heavily on translational visual motion to assess their direction of travel²². We could thus use visual, starfield stimuli to simulate the flies translating forward, backward or sideways relative to their head/body while simultaneously measuring the EPG and hΔB bump positions via two-photon excitation of sytGCaMP7f (Fig. 1d). A bright dot at the top of the cylindrical LED arena rotated in closed-loop with the fly’s steering behavior, simulating a static, distant cue that the fly could use to infer heading¹⁰. Under these conditions, the flies did not show a consistent, detectable preference for keeping the bright dot at any particular angular position (Extended Data Fig. 1k). A field of dimmer dots (starfield) in the lower visual field was either stationary or moved coherently to generate open-loop optic-flow that simulated the fly translating along different directions relative to its head/body axes^23,24 (Fig. 1c; Methods).

The position of the EPG bump, i.e., its phase, tracked the angular movements of the closed-loop dot (Fig. 1e), though with a lower correlation compared to tethered walking^8,11 (Extended Data Fig. 1g–j) likely because the lack of vestibular feedback on the tether impacts the flies’ ability to register turns more in flight than in walking. With a stationary starfield, the hΔB phase often drifted off the EPG phase (Fig. 1e, left, many gray arrows). In contrast, when we presented optic flow that simulated the fly’s body moving forward, the EPG and hΔB phases became more aligned, both in a single-fly example (Fig. 1e, right, one gray arrow) and across a population of twelve flies (Fig. 1f, Extended Data Fig. 1l, m).

When we varied the expansion point of the optic-flow stimulus to simulate the fly translating along six different directions, we observed that the offset between the EPG and hΔB phases matched the simulated egocentric (i.e., body-referenced) angle of travel (Fig. 1g–h). If we make the standard assumption that the EPG phase signals the fly’s allocentric heading angle^8,10,19, this implies that the hΔB bump position in the fan-shaped body tracks the fly’s allocentric traveling direction (Fig. 1i), which is the angular sum of the egocentric traveling and allocentric heading angles. In flies walking on an air-cushioned ball, rather than flying, we found that the hΔB and EPG phases generally align, but deviate predictably during backward/sideward walking (Extended Data Fig. 1n–p) in a manner consistent with the hΔB phase signaling the allocentric traveling direction during terrestrial locomotion, as in flight.

Computing the traveling angle

How is the hΔB signal built? As we will show and consistent with past work in bees⁷, there exist sets of neurons that provide four motion-related inputs to the central complex. These inputs ––L₁, L₂, L₃ and L₄,_–– represent the projections of the fly’s traveling vector (determined, for example, by optic flow) onto axes oriented ±45° (forward-right and forward-left) and ±135° (backward-right and backward-left) relative to the fly’s head⁷ (Fig. 2a). The fly’s egocentric traveling direction can be computed by adding the four vectors defined by these projection lengths and angles. To turn the egocentric into an allocentric traveling direction, a coordinate transformation must be performed, and, as we will also demonstrate, this is done by referencing the four projection/basis vectors to the fly’s allocentric heading, H, before taking the vector sum (Fig. 2b bottom). The fly then computes its allocentric traveling direction by adding these four allocentric projection vectors with lengths L_1–4 and angles H±45° and H±135°.

Figure 2 |. The allocentric traveling direction can be computed by vector rotation and summation, which can be implemented by phasors.

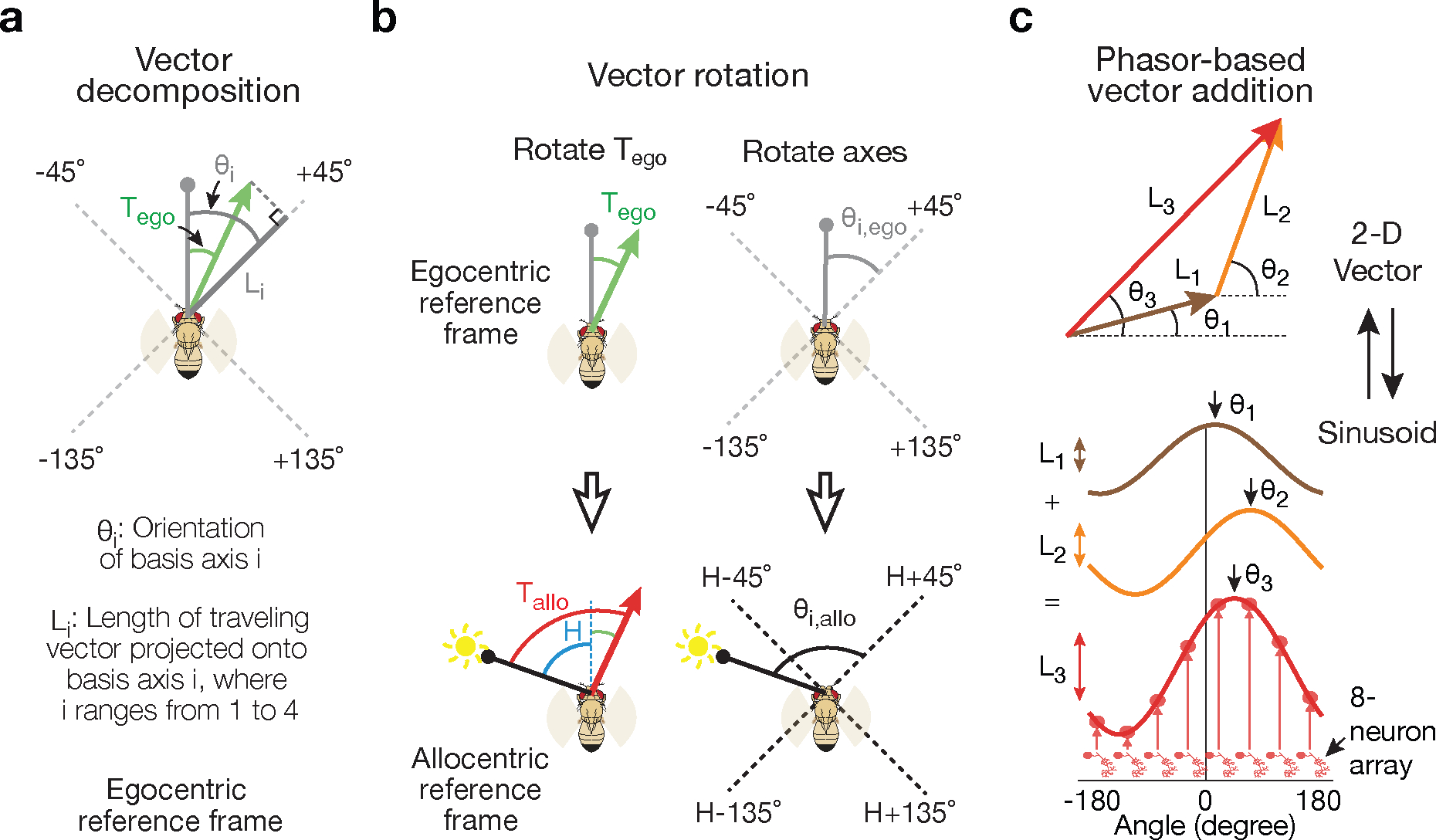
a, The traveling-direction vector (green) for a fly translating at an egocentric traveling angle T_ego, referenced to its head direction (gray line with circle), is projected onto four axes oriented ±45° and ±135° relative to the head, yielding four scalars L_1–4. The +45° projection is shown. The fly’s head direction represents 0° in this egocentric reference frame. Angles are positive clockwise. b, The fly’s allocentric traveling direction, T_allo, can be computed either by rotating the egocentric traveling angle (T_ego) such that it becomes referenced to the external world (i.e., the sun) (top) or, as in the fly circuit, by first referencing the ±45° and ±135° projection axes to the external world (bottom) and then taking the vector sum of the four projection vectors. Egocentric vectors are referenced to the external world by adding H, the fly’s allocentric heading angle, to them. c, Two-dimensional vectors can be represented by sinusoids and adding sinusoids then implements vector addition.

This vector sum can be performed by representing 2D vectors as sinusoids––a phasor representation––where the amplitudes and phases of the sinusoids match the lengths and angles of the corresponding vectors. In such a representation, vectors are added by simply summing their corresponding sinusoids (Fig. 2c). Theoretical models employing phasors have been proposed², including for the fan-shaped body⁷, but here we provide the first comprehensive experimental demonstration of their operation. Connectome-inspired conceptual models in Drosophila (conducted in parallel to our work) have also proposed how phasors could compute the fly’s traveling direction and speed²⁵.

PFN_ds and PFN_vs encode vectors

The phasor model requires neuronal populations with sinusoidal activity patterns whose phases and amplitudes match the allocentric projection vectors. PFN_d and PFN_v cells are columnar neurons that receive synaptic input in the bridge and noduli¹⁸, while also projecting axons to the fan-shaped body where they synapse onto hΔB cells¹⁷ (Fig. 3a, b). Separate arrays of PFN_ds (Fig. 3a) and PFN_vs (Fig. 3b) in the left and right bridge receive extensive mono- and di-synaptic input from EPGs. Co-imaging EPGs and PFNs revealed one activity bump in the left bridge and another in the right bridge for both PFN_ds and PFN_vs, and the phase of these PFN bumps aligned with the EPG bumps (Fig. 3c–e and Extended Data Fig. 2). Thus, left- and right-bridge PFN_ds and PFN_vs together express four copies of the EPG allocentric heading signal. The activity profiles across the bridge of the four PFN populations are well fit by sinusoidal functions (Fig. 3d–e, Methods), consistent with the possibility that the PFN activity patterns represent two-dimensional vectors (Fig. 2c). The sinusoidal shape of PFN bumps in the bridge may originate from the spatially sinusoidal dendritic density in a group of bridge interneurons called Delta7 (Δ7) cells¹⁸, which are interposed between EPGs and many downstream bridge cells, including PFNs (Extended Data Fig. 3 and Supplemental Text).

Figure 3 |. PFN_d and PFN_v cells show physiological and anatomical patterns consistent with them functioning to build the traveling-direction signal in hΔBs.

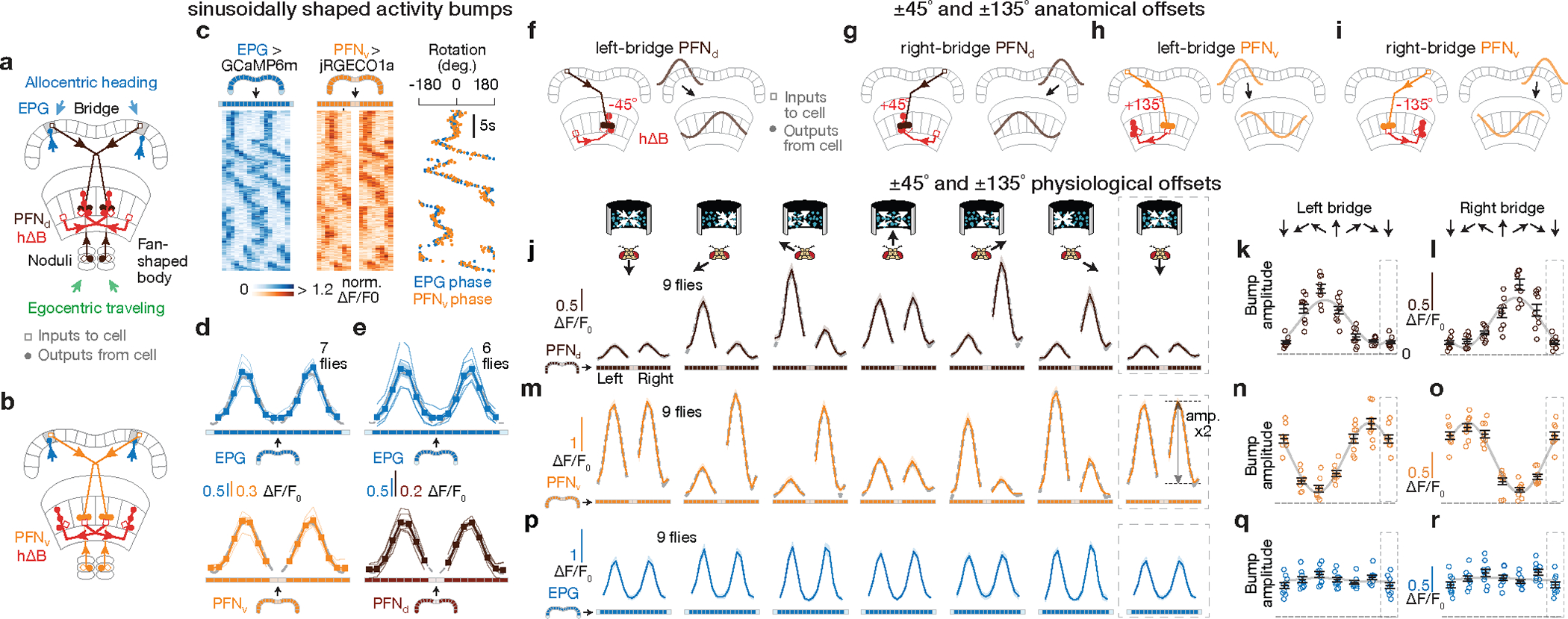
a-b, Sample PFN and hΔB cells (see Text). c, [Ca²⁺] signals and phase estimates of EPG and PFN_v³⁸ bumps simultaneously imaged in the bridge of a flying fly. d, Phase-nulled and averaged EPG and PFN_v activity in the bridge. On each frame, the EPG bumps were rotated to the same position and the simultaneously imaged PFN_v signals were rotated by this EPG-defined angle; coherent PFN_v bumps in these plots thus indicates strong phase-alignment to the EPGs. Thin lines: individual flies. Thick lines: population average. Gray dashed lines: sinusoidal fits (see Methods for details and goodness of fit). e, Same as panel d, but for EPGs and PFN_ds. f-i, schematics of how PFNs promote hΔB axonal activity with ±45° and ±135° offsets (see Text) j, Phase-nulled PFN_d activity in the bridge, averaged in the final 2.5 s of each optic-flow epoch. Dotted rectangle: repeated-data column here and throughout. Gray dashed lines: sinusoidal fits. Closed-loop bright dot was not displayed. k, Single-fly (circles) and population means ± s.e.m. (black bars) of the amplitude of PFN_d activity across the left bridge, averaged in the final 2.5 s of the optic flow epoch. Sinusoidal fit: gray line. l, same as panel k, but right-bridge PFN_ds. m-o, same as panels j-l, but PFN_vs. p-r, same as panels j-l, but EPGs.

The four, sinusoidal, PFN bumps in the bridge are poised to represent the four allocentric projection vectors from Figure 2a–b, except that their phases are not offset by ±45° and ±135° relative to the EPG heading angle, H. Although PFN and EPG bumps share a common phase in the bridge, the projection anatomy of PFNs from the bridge to the fan-shaped body provides a path for the PFN bumps to acquire ±45° and ±135° offsets from H. Corresponding PFN_v and PFN_d cells in the left- and right-bridge send projections to the fan-shaped body that are offset from each other by approximately ±1/8 of the extent of the fan-shaped body¹⁸ (Fig. 3a–b), equivalent to a ±45° angular offset. PFN_ds synapse onto both the axonal and dendritic regions of the hΔBs, but the input to the axonal region is anatomically dominant¹⁷ (Fig. 3f, g). Assuming that the axonal input is thereby physiologically dominant, PFNds can promote hΔB axonal output at fan-shaped-body locations that are offset by ±45° relative to the EPG heading signal in the bridge. PFN_vs project to the fan-shaped body with the same ±45° angular offset as PFN_ds, but PFN_vs target the hΔB dendrites, not axons, nearly exclusively¹⁷ (Fig. 3h, i). As described earlier, the axon terminal region of each hΔB cell is offset from its dendrites by half the width of the fan-shaped body, equivalent to an angular displacement of ~180° (Fig. 3f–i). The result of these two sets of shifts is that left- and right-bridge PFN_vs promote hΔB axonal activity shifted by approximately ±135° relative to their common phase in the bridge. Thus, the anatomy suggests that the four PFN sinusoids in the bridge are transferred to the fan-shaped body with peaks at H±45 and H±135°, matching the angles of the allocentric projection vectors (Fig. 2).Furthermore, these sinusoids appear to be summed at the level of the hΔB axons.

To complete the phasor representation, the amplitudes of the PFN sinusoids should match the expected lengths of the corresponding allocentric projection vectors (L_1–4 in Fig. 2a). We found that the amplitudes of the PFN sinusoidal bumps across the bridge were strongly modulated by the fly’s egocentric traveling direction, i.e., by the optic-flow direction. Specifically, the amplitude of each PFN sinusoid matched the projection of the fly’s inferred traveling direction (from optic flow) onto the four projection axes defined in Figure 2b and 3f–i (Fig. 3j–o). For example, the amplitude of the left-bridge PFN_d sinusoid reaches its maximum when optic flow simulates traveling toward the front left (Fig. 3k, see Extended Data Fig. 4 for details), consistent with the anatomy-based prediction in Figure 3f for the projection axis represented by left-bridge PFN_ds. Anatomical and physiological measurements strongly point to LNO1s, LNO2s and SpsPs as the cell types that cause the modulations of PFN activity based on the fly’s egocentric traveling direction (i.e., based on optic-flow in flight or on efference-copy/proprioception of leg movements in walking) (see Supplemental Text) (Extended Data Fig. 4). In contrast, EPG bumps in the bridge show little amplitude modulation with optic flow (Fig. 3p–r, Methods).

Model-Data comparison

The phasor model predicts that the allocentric traveling direction can be determined by summing the four PFN sinusoids, because this is equivalent to summing the corresponding allocentric projection vectors (Fig. 4a–d and Supplemental Video 1). To test this notion, we modeled the input to hΔBs as four cosine functions shifted by the appropriate angles, representing the expected PFN activity patterns across the fan-shaped body. We multiplied these cosines by the experimentally determined amplitudes measured at different optic-flow angles (Fig. 3j–o) and summed the four amplitude-modulated and shifted sinusoids. The predicted traveling angle calculated in this manner is in excellent agreement with the angular location of the hΔB bump, measured experimentally (Fig. 4e, red circles). This prediction involves no free parameters, but it relies on an assumption that all four PFN types contribute equally to the total hΔB input. We can relax this assumption by adding the four sinusoids weighted by the average number of synapses from each PFN type onto the hΔBs¹⁷ (Methods). We can also extract the angles by which the PFN sinusoids are anatomically shifted between the bridge and fan-shaped body from the hemibrain connectome¹⁷ (Extended Data Fig. 5 and 6), rather than using exactly ±45° and ±135°. The predicted bump location again agrees well with the measured hΔB bump position (Fig. 4e, green diamonds) (see Supplemental Text for more details).

Figure 4 |. A model of how vector computation builds the traveling-direction signal in hΔB cells.

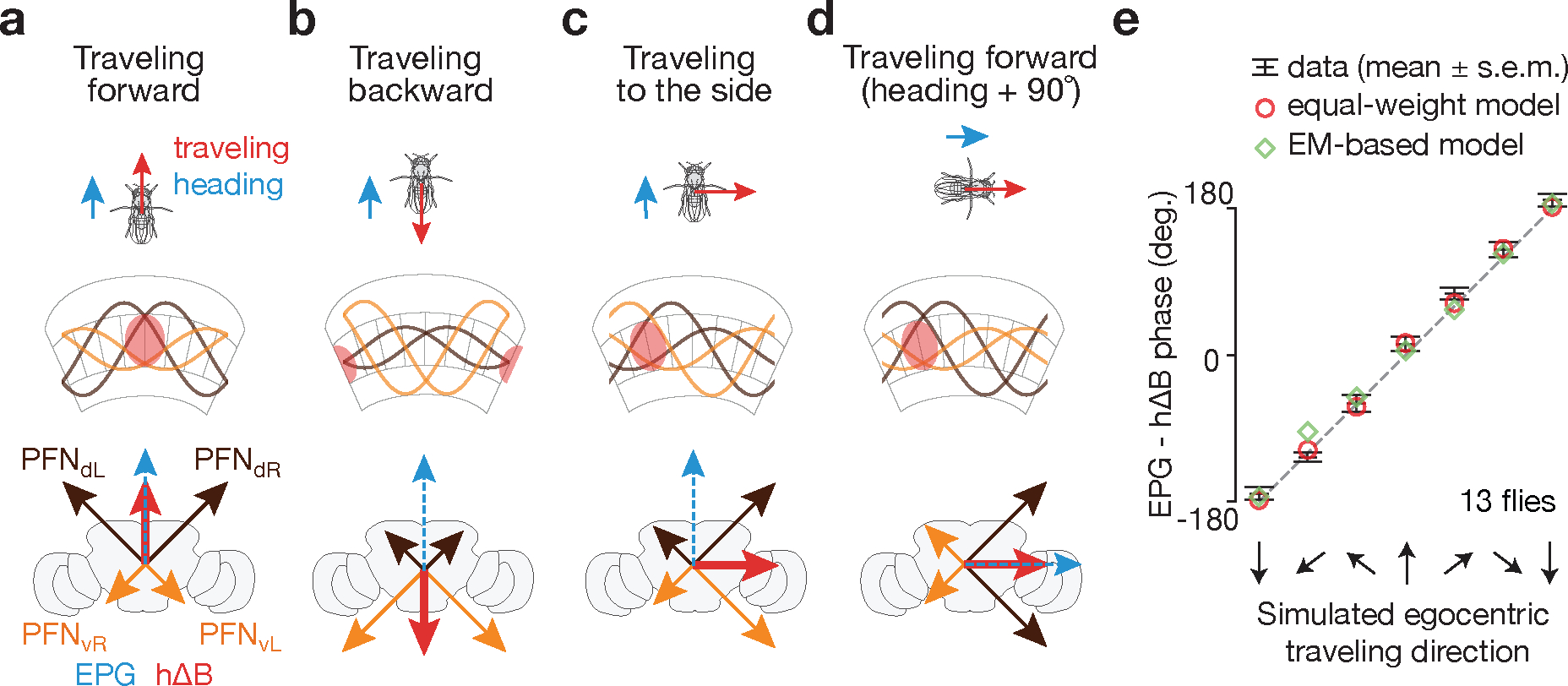
a, When a fly travels forward, both PFN_d sinusoids have large amplitude and both PFN_v sinusoids have small amplitude, leading the sum of the four PFN vectors, i.e., the hΔB (red) vector, to point forward, or in the heading direction (blue EPG vector). b, When a fly travels backward, both PFN_d sinusoids have small amplitude and both PFN_v sinusoids have large amplitude, leading the sum, i.e., the hΔB (red) vector, to point backward, or opposite the heading direction. c, When a fly travels rightward, the right-bridge PFN_d sinusoid and the left-bridge PFN_v sinusoid have larger amplitude than their counterparts on the opposite side of the bridge, leading the sum, i.e., the hΔB (red) vector, to point rightward. d, Same as panel a––fly moving forward––but after the fly has turned clockwise by 90°. This turn rotates all the vectors (i.e., the reference frame) by 90° inside the brain. e, Data from Figure 1h (black bars) and model (diamonds and circles) (see Text).

Perturbations support the vector model

To test the vector model, we manipulated EPG, PFN_d and PFN_v activity while measuring the impact on the fly’s traveling-direction estimate. For technical reasons, in these experiments we imaged the bump position of PFRs, rather than hΔBs, in the fan-shaped body; PFRs are a columnar cell class whose numerically dominant monosynaptic input is from hΔBs¹⁷ (see Supplemental Text). We found that the PFR bump position aligns well with the fly’s traveling direction in flight (Extended Data Fig. 7a–e and Supplemental Video 2) and walking (Extended Data Fig. 7f–o), arguing that the PFR bump can serve as a proxy for the hΔB signal under our experimental conditions. We note that there were consistent, subtle differences between the hΔB and PFR signals (and PFRs receive many more inputs than just from hΔBs) implying that PFRs and hΔBs track different angular variables, although the PFR phase correlated strongly with the fly’s traveling direction here (see Supplemental Text).

First, we inhibited EPG output⁹ by expressing shibire^ts, which abolishes synaptic vesicle recycling at high temperatures²⁶, in EPGs. Without EPG input, the PFN_d, PFN_v, hΔB and PFR bumps should all be untethered from external cues and unable to track the allocentric traveling angle (Fig. 5a). We measured the PFR bump in persistently walking flies where, unlike in flying flies, it was rare to observe large deviations of the hΔB or PFR phase from the angular position of a closed-loop visual cue or the EPG phase (Extended Data Fig. 7f–j). With the EPGs silenced, we still observed a bump in PFRs but its phase did not effectively track the angular position of the closed-loop cue (Fig. 5b–d). Thus, EPG input is indeed necessary for the traveling signal to be yoked to the external world.

Figure 5 |. Neural-activity perturbations induce changes in the traveling-direction signal that are consistent with the vector-sum model.

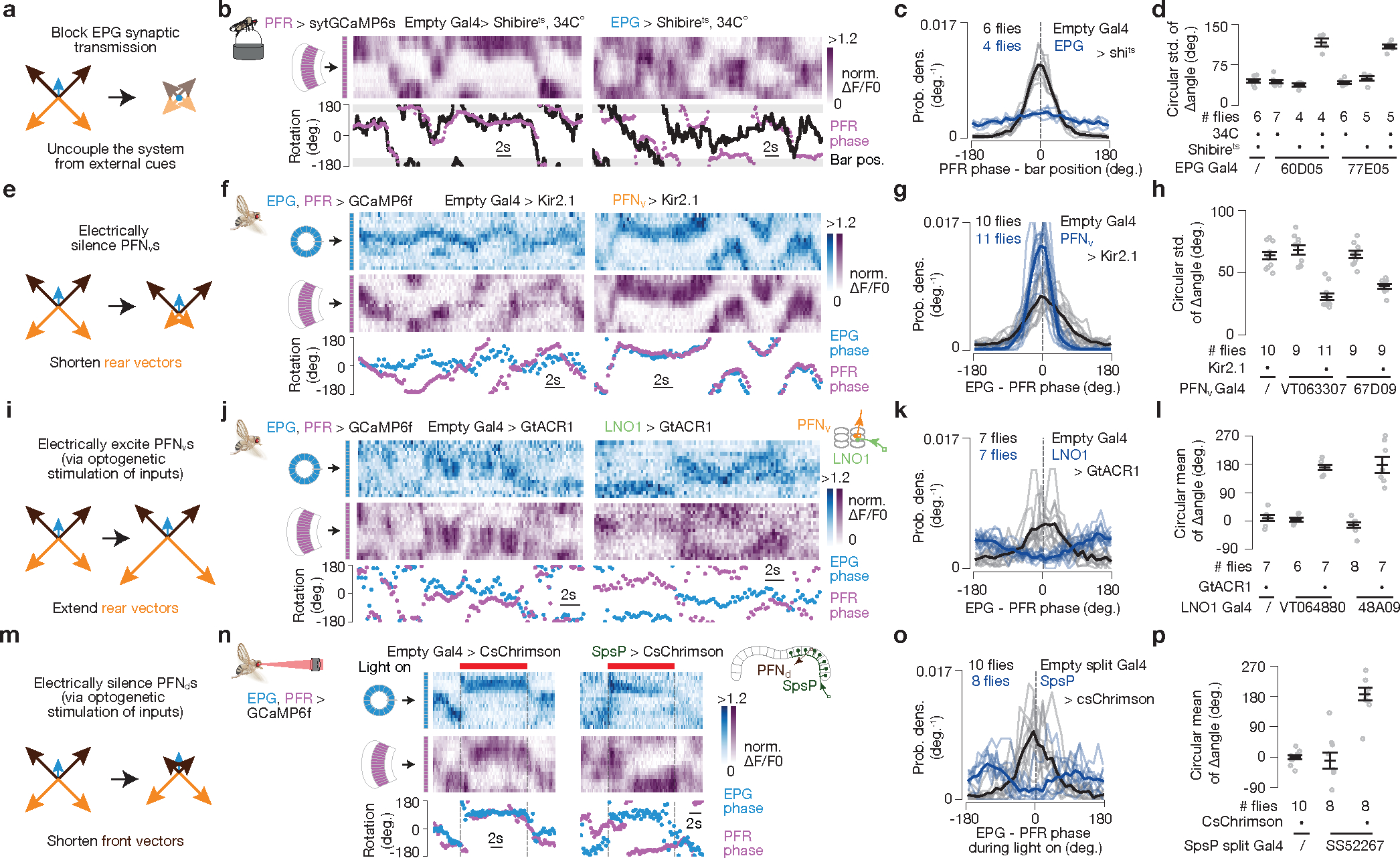
PFR phase used as proxy for hΔB phase here (see Text). a, Prediction. b, PFR bump in the fan-shaped body of a fly walking with a closed-loop bright bar at 34°C, with EPGs expressing (right) or not expressing (left) shibire^ts. c, PFR phase – bar position distributions. Thin lines represent single flies and the thick line represents the population mean (also in panels g,k,o). d, Circular s.d. of PFR phase – bar position distributions for different genotypes. Gray dots represent single flies and black markers represent population means ± s.e.m (also in panels h,l,p). P<2×10⁻⁴ comparing experimental (4th or 7th columns) with any control group (Unpaired two-tailed t-tests). e, Prediction. f, Simultaneous imaging of EPG and PFR bumps in the context of PFN_vs expressing (right) or not expressing (left) Kir2.1. g, EPG – PFR phase distributions. h, Circular s.d. of PFR – EPG phase distributions for different genotypes. P<4×10⁻⁵ comparing experimental (3rd or 5th columns) with any control group (Unpaired two-tailed t-tests). i, Prediction. j, Simultaneous imaging of PFR and EPG bumps in the context of expected optogenetic activation (right) or no activation (left) of PFN_vs. The two-photon laser exciting GCaMP simultaneously excites GtACR1 in LNO1s, which should silence them and thus excite PFN_vs via sign-inverting synapses in the noduli. k, EPG – PFR phase distributions. l, Circular mean of the PFR – EPG phase distributions for different genotypes. P<4×10⁻⁴ comparing experimental (3rd column) with either control group (Watson-Williams multi-sample test). m, Prediction. n, Simultaneous imaging of PFR and EPG bumps in the context of optogenetic activation of SpsP cells expressing (right) or not expressing (left) csChrimson. An external, red laser excites csChrimson in SpsPs, which should activate them and thus inhibit PFN_ds via sign-inverting synapses in the bridge. o, EPG – PFR phase distributions. p, Circular mean of the PFR – EPG phase distributions for various genotypes. P<7×10⁻⁴ when comparing the experimental group (3rd column) with either control group (Watson-Williams multi-sample test). See Methods for exact p values.

Second, we expressed a K⁺ channel, Kir2.1²⁷ in PFN_vs, with the aim of tonically inhibiting them and thus decreasing the contribution of the backward-facing PFN_v sinusoids/vectors to the traveling-direction computation (Fig. 5e). This perturbation yielded an increase in the phase alignment between the EPG and PFR bumps in tethered, flying flies in the context of no optic flow (Fig. 5f–h), consistent with our model.

Third, we used the two-photon laser to optogenetically activate GtACR1 Cl⁻ channels^28,29 in LNO1s³⁰, which are the primary monosynaptic, likely inhibitory (Extended Data Fig. 4), inputs to PFN_vs in the noduli¹⁷. This perturbation should disinhibit the PFN_vs, increasing the amplitudes of their sinusoids, opposite to the previous perturbation (Fig. 5i). This manipulation drove the PFR bump to be ~180° offset from the EPG bump (Fig. 5j–l), consistent with our model.

Finally, we silenced PFN_ds by perturbing one of their strongest inputs, the SpsPs. There are two SpsP cells per side, each innervating all of the ipsilateral PFN_ds, and the vast majority of SpsP output synapses (>80%) target PFN_ds¹⁷. Because the tuning of SpsPs to translational optic flow is opposite that of the PFN_ds, suggesting inhibition (Extended Data Fig. 4d–f), we optogenetically activated SpsPs (with csChrimson³¹) to reduce the amplitude of the front-facing PFN_d sinusoids/vectors. This perturbation drove the PFR bump to be offset by 180°, on average, from the EPG bump (Fig. 5m–p), consistent with this manipulation effectively shortening the two front-facing vectors (Fig. 5m).

Tuning for speed

If the hΔB or PFR bumps were to accurately track the fly’s traveling vector (angle + speed), rather than just the traveling direction, we would expect the amplitude of their sinusoidal activity profiles to scale with speed (Extended Data Figs. 7, 8). Indeed, both the PFRs and hΔBs showed a measurable increase in bump amplitude with faster optic-flow speeds, but this modulation was focused to frontal-travel directions (Extended Data Fig. 8f–i, v–x). Different speed modulation across different travel directions complicates the interpretation of hΔBs as encoding a full traveling-vector, but non-uniform-speed-tuning across traveling directions could get corrected with additional modulation between the hΔBs and putative downstream path integrators.

Discussion

Do mammalian brains have neurons that are tuned to the animal’s allocentric traveling direction as in Drosophila? Although a defined population of traveling-direction-tuned neurons has yet to be highlighted in mammals^32,33, such cells could have been missed because their activity would loosely resemble that of the head-direction cells outside of a task in which the animal is required to sidestep or walk backwards.

Neurons are often modeled as summing their synaptic inputs, but the heading inputs that PFNs receive from the EPG system appear to be multiplied by self-motion (e.g., optic flow) input, resulting in an amplitude or gain modulation. Multiplicative or gain-modulated responses appear in classic computational models for how neurons in area 7a of primate parietal cortex might implement a coordinate transformation^1,4,5, alongside similar proposals in mammalian navigation^34,35. The Drosophila circuit described here strongly resembles aspects of the classic parietal-cortex models (Extended Data Fig. 9). Units that multiply their inputs are also at the core of the ‘attention’ mechanism used, for example, in machine-based language processing³⁶. Our experimental evidence for input multiplication in a biological network may indicate that real neural circuits have greater potential for computation than is generally appreciated.

We describe a traveling-direction signal and how it is built; related results and conclusions appear in a parallel study³⁷. The mechanisms we describe for calculating the traveling direction are robust to left/right rotations of the head (Supplemental Text and Extended Data Fig. 10) and to the possibility of the allocentric projection vectors being non-orthogonal (Supplemental Text and Extended Data Figs. 4, 5, 6). It is possible that the hΔB traveling signal is compared with a goal-traveling direction to drive turns that keep a fly along a desired trajectory^9,10. Augmented with an appropriate speed signal (or if the fly generally travels forward relative to its body), the hΔB signal could also be integrated over time to form a spatial-vector memory via path integration^7,25 (see Supplemental Text). There are hundreds more PFNs beyond the 40 PFN_ds and 20 PFN_vs¹⁷, and thus the central complex could readily convert other angular variables from egocentric to allocentric coordinates via the algorithm described here. Because many sensory, motor and cognitive processes can be formalized in the language of linear algebra and vector spaces, defining a neuronal circuit for vector computation may open the door to better understanding several previously enigmatic circuits and neuronal-activity patterns across multiple nervous systems.

Methods

Fly husbandry

Flies were raised at 25°C with a 12-h light and 12-h dark cycle. In all experiments, we studied female Drosophila melanogaster that were 2–6 days old. Flies were randomly selected for all of experiments. We excluded flies that appeared unhealthy at the time of tethering as well as flies that did not fly longer than 20 s in flight experiments. This meant excluding fewer than 5% of flies for most genotypes. However, in the perturbational experiments shown in Figure 5e–p many flies flew poorly––perhaps because these genotypes all expressed 5–6 transgenes which can affect overall health and flight vigor––and we had to exclude ~70% of flies due to poor tethered flight behavior (i.e., would not maintain continuous flight for > 5 s bouts). The 30% of flies tested in these genotypes flew in bouts that ranged 20 s to many minutes, allowing us to make the necessary EPG/PFR signal comparisons (discussed below). Flies in optogenetic experiments were shielded from green and red light during rearing by placing the fly vials in a box with blue gel filters (Tokyo Blue, Rosco) on the walls. After eclosion, two days or more prior to experiments, we transferred these flies to vials with food that contained 400μM all-trans-retinal.

Cell type acronyms and naming conventions

Each cell type is described in the order of ‘Names in this paper (in hemibrain v1.1 if different)’, ‘Names used in a previous reference³⁰‘, ‘Description of acronym’, ‘References in which cell type is studied or defined’ and ‘Total cell number (in hemibrain v1.1)’, separated by em dash.

EPG -- E-PG -- Ellipsoid body-Protocerebral bridge-Gall -- Lin C, et al³⁹; Wolff T, et al^18,30; Seelig J, et al⁸; Green J, et al¹¹; Turner-Evans D, et al¹² – 46

PFR (PFR_a) -- P-F-R -- Protocerebral bridge-Fan shaped body- Fan shaped body-Round body -- Lin C, et al³⁹; Wolff T, et al^18,30; Shiozaki H, et al¹³ – 29

PFN_v (PFNv) -- P-FN_V -- Protocerebral bridge-Fan shaped body- Nodulus (ventral) -- Lin C, et al³⁹; Wolff T, et al^18,30 -- 20

PFN_d (PFNd) -- P-FN_d -- Protocerebral bridge-Fan shaped body- Nodulus (dorsal) -- Lin C, et al³⁹; Wolff T, et al18,30 -- 40

hΔB (hDeltaB) -- n.a. -- Columnar cell class with lateral projections in layer 3 of the fan-shaped body – n.a. – 19

LNO1 – L-N -- Lateral accessory lobe-Nodulus -- Wolff T, et al³⁰ – 4

LNO2 – n.a. -- Lateral accessory lobe-Nodulus – n.a. – 2

SpsP – Sps-P -- Superior posterior slope- Protocerebral bridge -- Wolff T, et al^18,30 – 4

Δ7 (Delta7) – Delta7 -- Skipping 7 glomeruli in the Protocerebral bridge between two output areas -- Lin C, et al³⁹; Wolff T, et al^18,30; Turner-Evans D, et al⁴⁰ – 42

PEN1 (PEN_a) – P-EN1 -- Protocerebral bridge-Ellipsoid body – Nodulus -- Lin C, et al³⁹; Wolff T, et al^18,30; Green J, et al¹¹; Turner-Evans D, et al¹² -- 20

PEN2 (PEN_b) – P-EN2 -- Protocerebral bridge-Ellipsoid body – Nodulus -- Green J, et al¹¹ -- 22

Fly genotypes

• For simultaneous imaging of EPGs and hΔBs:

  In Fig. 1 and Extended Data Fig. 1, we used + (Canton S, Heisenberg Laboratory); UAS-sytGCaMP7f /72B05-AD (Bloomington Drosophila Stock Center, BDSC # 70939); 60D05-Gal4 (BDSC #39247)/ VT055827-DBD (BDSC # 71851) flies. We created the sytGCaMP7f construct by linking the GCaMP7f and Drosophila synaptotagmin 1 coding sequences using a 33GS linker. We then used this construct to generate transgenic flies by PhiC31-based integration into attp40 site, performed by BestGene.

• For simultaneous imaging of EPGs and PFN_ds:

  In Fig. 3e and Extended Data Figs. 2a–b, 3h (top row), we used +; +; 60D05-LexA (BDSC #52867)/+; LexAop-GCaMP6m, UAS–jRGECO1a (BDSC #44588 & #63794) /47E04-Gal4(BDSC #50311) flies.

• For simultaneous imaging of EPGs and PFN_vs:

  In Fig. 3c–d and Extended Data Figs. 2c–f, 3e (left column), h (middle row), we used +; 60D05-LexA/+; LexAop-GCaMP6m, UAS–jRGECO1a/VT063307-Gal4 (Vienna Drosophila Resource Center, CDRC) flies.

• For simultaneous imaging of EPGs and PFRs:

  In Fig. 5f–h, we used +; 60D05-LexA, LexAop-GCaMP6f (BDSC #44277)/37G12-LexA (BDSC #52765); UAS-Kir2.1 (Leslie Vosshall Laboratory)/VT063307-Gal4 flies and +; 60D05-LexA, LexAop-GCaMP6f/37G12-LexA; UAS-Kir2.1/67D09-Gal4 (BDSC #49618) flies for the experimental groups. For the control groups, we used +; 60D05-LexA, LexAop-GCaMP6f/37G12-LexA; UAS-Kir2.1/empty-Gal4 (BDSC #68384) flies, +; 60D05-LexA, LexAop-GCaMP6f/37G12-LexA; VT063307-Gal4/empty-Gal4 flies, and +; 60D05-LexA, LexAop-GCaMP6f/37G12-LexA; 67D09-Gal4/empty-Gal4 flies.

  In Fig. 5j–l, we used +; 60D05-LexA, LexAop-GCaMP6f /37G12-LexA; UAS-GtACR1-EYFP (Adam Claridge-Chang Laboratory)/VT064880-Gal4 (CDRC) flies and +; 60D05-LexA, LexAop-GCaMP6f /37G12-LexA; UAS-GtACR1-EYFP/48A09-Gal4 (BDSC #50342) flies for the experimental groups. For the control groups, we used +; 60D05-LexA, LexAop-GCaMP6f/37G12-LexA; UAS-GtACR1-EYFP/empty-Gal4 flies, +; 60D05-LexA, LexAop-GCaMP6f/37G12-LexA; VT064880-Gal4/empty-Gal4 flies, and +; 60D05-LexA, LexAop-GCaMP6f/37G12-LexA; 48A09-Gal4/empty-Gal4 flies.

  In Fig. 5n–p, we used UAS-CsChrimson-mVenus (BDSC #55134)/+; 60D05-LexA, LexAop-GCaMP6f/VT019012-AD; VT005534-LexA (Barry Dickson Laboratory)/72C10-DBD (Janelia FlyLight Split-Gal4 Driver Collection, FlyLight SS52267) flies for the experimental groups. For the control groups, we used UAS-CsChrimson-mVenus; 60D05-LexA, LexAop-GCaMP6f/empty-LexA (BDSC #77691); VT005534-LexA/empty-Gal4 flies, and + (Canton-S); 60D05-LexA, LexAop-GCaMP6f/ VT019012-AD; VT005534-LexA (Barry Dickson Laboratory)/72C10-DBD flies.

  In Extended Data Figs. 1i, j, 7b–e, we used +; UAS-GCaMP7f (BDSC #80906)/+; 60D05-Gal4 /37G12-Gal4 (BDSC #49967) flies.

  In Extended Data Fig. 3h (bottom row), we used +; 60D05-LexA/+; LexAop-GCaMP6m, UAS–jRGECO1a/37G12-Gal4 flies.

  In Extended Data Fig. 7g–j, we used +; UAS-GCaMP6m (BDSC #42748)/+; 60D05-Gal4 /37G12-Gal4 flies.

  In Extended Data Fig. 7l–o, we used UAS-CsChrimson-mVenus/+; 60D05-LexA, LexAop-GCaMP6f/ 26A03-AD; VT005534-LexA/54A05-DBD (FlyLight OL0046B) flies.

• For imaging single cell types:

  In Fig. 3j–l and Extended Data Figs. 4e–i, n, o, 5g, i, 8a–c, j, k, r, s, we used +; 15E01-AD (BDSC #70558)/+; UAS-GCaMP7f (BDSC #79031)/47E04-DBD (BDSC #70366) flies for PFN_ds.

  In Fig. 3m–o and Extended Data Figs. 4b, c, i, j, k, 5h, i, 8d, e, l, m, t, u, we used +; +; UAS-GCaMP7f/VT066307-Gal4 flies for PFN_vs.

  In Fig. 3p–r and Extended Data Fig. 5e, f, we used +; +; UAS-GCaMP7f/60D05-Gal4 flies for EPGs.

  In Fig. 5b–d, we used pJFRC99–20XUAS-IVS-Syn21-Shibire-ts1-p10 inserted at VK00005 (referred to here as UAS-shibire^ts) to drive shibire^ts (Rubin Laboratory). We used +; 37G12-LexA/LexAop-sytGCaMP6s (Vanessa Ruta Laboratory); 60D05-Gal4/UAS- shibire^ts flies for the experimental group. For the control groups, we used +; 37G12-LexA/LexAop-sytGCaMP6s; 60D05-Gal4/empty-Gal4 flies and +; 37G12-LexA/LexAop-sytGCaMP6s; UAS- shibire^ts/empty-Gal4 flies.

  In Extended Data Fig. 1e, we used +; +/72B05-AD; UAS-GCaMP7f / VT055827-DBD flies for hΔBs.

  In Extended Data Figs. 1f, 8f, h, i, n, p, q, v, x, we used +; UAS-sytGCaMP7f /72B05-AD; +/ VT055827-DBD flies for hΔBs.

  In Extended Data Fig. 1i, j, we used +; +; UAS-GCaMP6m (BDSC #42750)/60D05-Gal4 flies for EPGs.

  In Extended Data Fig. 4b, c, i, l, m, we used +; VT020742-AD /+; UAS-GCaMP7f/VT017270-DBD (FlyLight SS47398) flies for LNO1s.

  In Extended Data Fig. 4e, f, i, p, q, we used +; VT019012-AD/+; UAS-GCaMP7f/72C10-DBD (FlyLight SS52267) flies for SpsPs.

  In Extended Data Fig. 8g, o, w, we used +; +; UAS-GCaMP7f/37G12-Gal4 flies for PFRs.

Distinguishing PFR subtypes in Gal4 lines

The hemibrain connectome¹⁷ defines two subtypes of PFR cells¹⁸: PFR_a cells and PFR_b cells, which differ in the details of their projections and connectivity in the fan-shaped body. Both PFR_as and PFR_bs are columnar cells that project from the protocerebral bridge to the fan-shaped body. Based on the connectome¹⁷, PFR_as and PFR_bs that innervate 4 of the bridge glomeruli project to the fan-shaped body in the same way and PFR_as and PFR_bs that innervate 12 other bridge glomeruli project to the fan-shaped body in a slightly different way. We used this fact to interrogate the MultiColor Flip-Out (MCFO) single-cell anatomical data set⁴¹ from the FlyLight Generation 1 MCFO Collection to quantify the ratio of each PFR subtype in the two Gal4 driver lines that we used for targeting transgenes to PFRs. For driver line 37G12, we found 10 out of 13 cells in the MCFO data had an innervation pattern that is consistent with PFR_a but not PFR_b and the innervation patterns of the other 3 cells were indistinguishable between the two subtypes. For driver line VT005534, we found 2 out of 3 cells in the MCFO data were consistent with them being PFR_as and not PFR_bs and the third cell had an anatomy that did not allow us to distinguish between subtypes. We observed no cell whose projection pattern matched PFR_b but not PFR_a. These results argue that the majority of the PFR cells targeted by the two Gal4 driver lines we used are PFR_a cells.

Fly preparation and behavioral setup

As described previously, we glued flies to a custom stage for imaging during flight²¹ and to a slightly different custom stage––which allows for more emission light to be collected by the objective––for imaging during walking¹¹. Dissection and imaging protocols followed previous studies¹¹. For tethered flight experiments, each fly was illuminated with 850 nm LEDs with two fiber optics from behind²¹. A Prosilica GE680 camera attached to a fixed-focus Infinistix lens (94-mm working distance, 1.0× magnification, Infinity) imaged the fly’s wing-stroke envelope at 80–100 Hz. The lens also held an OD4 875-nm shortpass filter (Edmund Optics) to block the two-photon excitation laser (925 nm). This camera was connected to a computer that tracked the fly’s left and right wing beat amplitude with custom software developed by Andrew Straw (https://github.com/motmot/strokelitude)²¹. Two analog voltages were output in real time by this software and the difference between the left and right wingbeat amplitude was used to control the angular position of the bright dot on the LED arena in closed-loop experiments (described below). For tethered walking experiments we followed protocols described previously¹¹.

LED arena and visual stimuli

We used a cylindrical LED arena display system⁴² with blue (465 nm) LEDs (BM-10B88MD, Betlux Electronics). The arena was 81° high and wrapped around 270° of the azimuth, with each pixel subtending ~1.875°. To minimize blue light from the LEDs inducing noise in the microscope’s photomultiplier tubes, we reduced the LED intensities, over most of the arena, by covering the LEDs with five sheets of blue gel (Tokyo Blue, Rosco). Over the 16 pixels at the very top of the arena (top ~30°), we only placed two gel sheets, so that the closed-loop dot at the top of the arena was brighter than the optic flow dots at the bottom, which may have helped to promote that the fly interpret the bright blue dot as a celestial cue (like the sun) and the optic-flow at the bottom as ground or side motion. During flight experiments, we held the arena in a ~66° pitched-back position, so that the LED vertical and horizontal axes matched the major ommatidial axes of the eye²⁴. During walking experiments, we typically presented a tall vertical bar––rather than a small dot––in closed loop and we tilted the arena by only ~30° because the ball physically occludes the ventral visual field and a shallower arena tilt made it more likely that the fly could see the closed-loop stimulus over all 270° of the azimuthal positions that it could take.

We adapted past approaches for generating optic flow (starfield) stimuli^23,24. In brief, we populated a virtual 3D world with forty-five, randomly positioned spheres (2.3-cm diameter) per cubic meter. The spheres were bright on a dark background. We only rendered spheres that were within two meters of the fly because spheres further away contributed only minimally to the observed motion and, if rendered, would have overpopulated the visual field with bright pixels. We then calculated the angular projection of each sphere onto the fly’s head and used this projection to determine the pattern to display on the LED arena on each frame. To prevent the size of each sphere from being infinitely large as it approached the fly, we limited each sphere’s diameter on the arena to be no larger than 7.5°. The starfield extended from 4 pixels (~8°) above to 20 pixels (~40°) below the arena’s midline. In all experiments that employed open-loop optic flow (Figs. 1, 3j–r and Extended Data Figs. 1e–m, 2e–f, 4b–i, 5, 7b–e, 8), the optic-flow position was updated at a frame rate of 25 Hz. (Note that the LED refresh rate was at least 372 Hz⁴².) To simulate the optic flow that a fly would experience when it is translating through 3D space, we moved a virtual fly in the desired direction(s) through the virtual world and displayed the resultant optic flow pattern on the arena. We used a translation speed of 35 cm/s in all experiments, except those in Extended Data Figures 7 and 8 where we tested multiple speeds as indicated (ranging from 8.75 to 70 cm/s). Although we report on the translation speed of the virtual fly in metric units, the optic flow experienced by insects translating at 35 cm/s will vary dramatically depending on the clutter of the local environment. We believe that the optic flow stimuli we presented in our study are potentially in an ethologically relevant range because (1) our virtual fly translated at speeds that bracket observed flight speeds in natural environments^43–45 and (2) optic-flow sensitive cells reported on here responded with progressively increasing activity to the presented stimuli/speeds rather than immediately saturating or showing no detectable responses (e.g., Extended Data Fig. 8). That said, our stimuli simulated a dense visual environment and it will be important to test our results in the context of reduced visual clutter in future work.

In flight experiments with a closed-loop dot (Figs. 1, 3c–e and Extended Data Figs. 1g–m, 2, 3e, h, 4b–f, i, 7b–e), the dot subtended 3.75° by 3.75° and was located ~34° above the arena’s midline. We used the difference of the left and right wingbeat amplitudes (L–R WBA) to control the azimuthal velocity of the bright dot on the LED arena. That is, when the right wingbeat amplitude is smaller than the left wingbeat amplitude (indicating that the fly is attempting to turn to the right), the dot rotated to the left, and vice versa. The negative-feedback closed-loop gain was set to 7.3°/s per degree change in L–R WBA. In initial experiments we set the gain to 5.5°/s and we have lumped those data in with the data at 7.3°/s in Fig. 1f and Extended Data Fig. 1g–m because we did not observe obvious differences in any of our analyses. In closed-loop walking experiments with a visual stimulus (Fig. 5b–d and Extended Data Fig. 7f–o), the bright bar was 11.25° wide and spanned the entire height of the arena. We directly linked the azimuthal position of the bright bar on the LED arena to the azimuthal position of the ball under the fly using Fictrac^11,46, as described previously. This closed-loop set up mimics the visual experience of a fly with a bright cue at visual infinity, like the sun. We did not provide translational stimuli in closed loop in this paper.

Calcium imaging

We used a two-photon microscope with a movable objective (Ultima IV, Bruker). The two-photon laser (Chameleon Ultra II Ti:Sapphire, Coherent) was tuned to 1000–1010 nm for simultaneous imaging of GCaMP6m and jRGECO1a (Fig. 3c–e and Extended Data Fig. 2), and was otherwise tuned to 925 nm in all of the other imaging experiments. We used a 40x/0.8 NA objective (Olympus) or 16x/0.8 NA objective (Nikon) for all imaging experiments. The laser intensity at the back aperture was 30–40mW for walking experiments and 40–80mW for flight experiments. Because of light loss through the objective and the fact that the platform to which the fly was attached blocks ~half the light from reaching the fly, we estimate an illumination intensity, at the fly, of ~16–32mW for flight experiments. In walking experiments, the platform to which we attach the fly blocks less light and we expect an illumination intensity, at the fly, of ~24–32mW. A 575 nm dichroic split the emission light. A 490–560nm bandpass filter (Chroma) was used for the green channel PMT and a 590–650nm bandpass filter (Chroma) was used for the red channel PMT. We recorded all imaging data using three to five z-slices, with a Piezo objective mover (Bruker Ext. Range Piezo), at a volumetric rate of 4–10 Hz. We perfused the brain with extracellular saline composed of (in mM) 103 NaCl, 3 KCl, 5 N-Tris(hydroxymethyl) methyl-2-aminoethanesulfonic acid (TES), 10 trehalose, 10 glucose, 2 sucrose, 26 NaHCO3, 1 NaH2PO4, 1.5 CaCl2, 4 MgCl2, and bubbled with 95% O2/5% CO2. The saline had a pH of ~7.3 and an osmolarity of ~280 mOsm. We controlled the temperature of the bath by flowing the saline through a Peltier device and measured the temperature of the bath with a thermistor (Warner Instruments, CL-100).

Optogenetic stimulation

In the optogenetic experiments in Fig. 5j–l, we used the two-photon laser tuned to 925 nm to excite GtACR1, with the same scanning light being used to excite GCaMP. To excite CsChrimson in the optogenetic experiments in Fig. 5n–p and Extended Data Fig. 7k–o), we focused 617nm laser (M617F2, Thorlabs) on to the front, middle of the fly’s head with a custom lens set (M15L01 and MAP10100100-A, Thorlabs). We placed two bandpass filters (et620/60m, Chroma) in the two-photon microscope’s emission path to minimize any of the optogenetic light being measured by the photomultiplier tubes. In flight experiments (Fig. 5n–p), we used pulse-width modulation at 490Hz (Arduino Mega board) with a duty cycle of 0.8 to change the 617 nm laser’s intensity. We measured the laser’s intensity at the fly’s head to be 20.8 μW. In the experiments where we triggered backward walking via activation of csChrimson (Extended Data Fig. 7k–o) in lobula columnar neurons, the duty cycle of the red light was 0.7 and the effective light intensity was 18.2 μW.

In Fig. 5j–l, for two main reasons, rather than directly exciting PFN_vs, we optogenetically inhibited the LNO1 inputs to PFN_vs. First, [Ca²⁺] imaging revealed opposite responses to our optic flow stimuli in the two cell types (Extended Data Fig. 4a–c), as mentioned earlier, arguing for a sign-inverting synapse between them. Second, we tried optogenetically activating the PFN_vs directly (data not shown), which yielded more variable movements of the PFR bump. We believe that stimulating LNO1s yielded more consistent effects on the PFR bump because there are only two LNO1s per side and they synapse uniformly on all PFN_vs within a tiny neuropil (the second layer of the nodulus) on their side¹⁷. The majority of LNO1’s synaptic output goes to PFN_vs in the nodulus, with each LNO1 cell on average forming ~655 synapses on PFN_vs¹⁷. Stimulating GtACR1 in a small volume likely made homogeneous activation of the PFN_v population more feasible.

Similarly, in Fig. 5m–p, rather than directly silencing PFN_ds, we optogenetically excited SpsPs to inhibit PFN_ds. Exciting SpsPs was likely to be an effective way to inhibit PFN_ds for two reasons. First, [Ca²⁺] imaging revealed sign-inverted responses to our optic-flow stimuli in the two cell types (Extended Data Fig. 4d–h), arguing for sign-inverting synapses existing between them. Second, ~80% of SpsP synapses are to PFN_ds in the bridge, with each SpsP cell on forming ~563 synapses on PFN_ds¹⁷, on average. Also, stimulating Chrimson in four copies of SpsP cells likely makes homogeneous inhibition of the PFN_d population more feasible than via direct optogenetic inhibition of the PFN_ds (where some PFN_ds might get more inhibited than others depending on expression level of the opsin and light delivery details).

Immunohistochemistry

Dissection of fly brains, fixation and staining of neuropil and neurons was performed as previously described¹¹. For primary antibodies, we used mouse anti-Brp (nc82, DSHB) at 1:10 and chicken anti-GFP (Rockland, 600–901-215) at 1:1000. For secondary antibodies, we used Alexa Fluor 488 goat anti-chicken (A11039, Invitrogen) at 1:800 and Alexa Fluor 633 goat anti-mouse (A21052, Invitrogen) at 1:400.

Data analysis

Data acquisition and alignment

All data were digitized by a Digidata 1440 (Molecular Devices) at 10kHz, except for the two-photon images which were acquired using PrairieView (Bruker) at varying frequencies and saved as tiff files for later analysis. We used the frame triggers associated our imaging frames (from Prairie View), recorded on the Digidata 1440, to carefully align behavioral measurements with [Ca²⁺] imaging measurements.

Experimental Structure

For Fig. 1d–f and Extended Data Fig. 1g–m, each fly performed tethered flight while in control of a bright dot in closed loop. Each recording was split into two segments, where we first presented a static starfield for 90 s and followed by progressive optic flow for 90 s.

For Fig. 1g–i, we presented each fly with a closed-loop dot throughout. We presented four blocks of six translational optic-flow stimuli (six translational plus two rotational) per block, shown in a pseudorandom order. Each 4 s optic flow stimulus was preceded and followed by 4 s of optic flow that mimics forward travel, which ensured that the EPG and hΔB (or PFR) bumps were aligned––for a stable “baseline”––before and after each tested optic flow stimulus. We presented 4 s of a static starfield between each repetition of the above three patterns. We employed the same protocol for Extended Data Fig. 7b, c and d–e (35cm/s column), but we presented two yaw-rotation optic flow stimuli to each block, whose data we did not analyze for this paper.

For Fig. 3c–e and Extended Data Figs. 2a–d, 3e, h, each fly was presented with a closed-loop dot and static starfield throughout the recording. Recording durations ranged from 1–4 min.

For Fig. 3j–r and Extended Data Figs. 4e–h (PFN_d rows), i (PFN_ds in the noduli, PFN_ds and PFN_vs in the bridge), 5, 8, we did not have a closed-loop dot. We presented four blocks of 24 stimuli (6 translational directions at 4 different speeds) per block, shown in a pseudorandom order. Each stimulus was preceded by 1.2-s of a static starfield, followed by 4 s of optic flow at different directions, and ending with a 1.2-s static starfield.

For Fig. 5b–d, each fly was presented with a tall bright bar in closed-loop throughout. EPG > Shibire^ts flies experienced both 25°C and 34°C trials in these experiments and we waited ~5 min after the bath temperature reached 34°C before imaging in the EPG silenced condition so as to increase the likelihood of thorough vesicle depletion. Recording durations ranged from 6–8 min.

For Fig. 5f–h, j–l, flies performed tethered flight in the context of a dark (unlit) visual display. We recorded data for ~1–4 min and if the fly was flying robustly, we collected a second data set from the same fly.

For Fig. 5n–p, flies performed tethered flight in the context of a dark (unlit) visual display. We recorded data for 2–6 min. and if the fly was flying robustly, we collected a second data set from the same fly. We presented 12 s red light pulses to activate csChrimson every ~20 s.

For Extended Data Figs. 1e, f, 4b, c, e–f (SpsP rows) and i (PFN_vs in the noduli, SpsPs and LNO1s), we presented each fly with a closed-loop dot throughout. We presented four blocks of eight optic-flow stimuli (six translational plus two rotational) per block, shown in a pseudorandom order. Each optic flow stimulus was preceded by 4-s of a static starfield, followed by 4-s of optic flow at different directions, and ending with a 4-s of static starfield.

For Extended Data Fig. 1d was presented with a tall bright bar in closed-loop for the second 2.5 min. of the recording. We recorded data for 5 min., with up to three 5-min. data sets collected per fly.

For Extended Data Figs. 1n–p and 4j–q, each fly was walking in the dark. We recorded data for 5–10 min., with up to three 10-min. data sets collected per fly.

For Extended Data Fig. 2e–f, we presented each fly with a closed-loop dot throughout. We presented four blocks of 3 translational optic-flow per block, shown in a pseudorandom order. Each stimulus was preceded by 1.2-s of a static starfield and 4 s of translational optic flow simulating forward travel, followed by 4 s of optic flow at different directions, and ending with a 4 s of optic flow simulating forward travel.

For Extended Data Fig. 7d and e (17.5cm/s and 70cm/s columns), we presented each fly with a closed-loop dot throughout. We presented three blocks of 18 stimuli per block (6 translational directions at 3 different speeds), shown in a pseudorandom order. Each stimulus was preceded by 1.2-s of a static starfield and 4 s of translational optic flow simulating forward travel, followed by 4 s of optic flow at different directions, and ending with a 4 s of optic flow simulating forward travel.

For Extended Data Fig. 7f–j, each fly was presented with a tall bright bar in closed-loop for the first 5 min. of the recording and was walking in the dark for the second 5 min. of the recording. We recorded data for 10 min., with up to three 10-min. data sets collected per fly.

For Extended Data Fig. 7k–o, each fly was presented with a tall bright bar in closed-loop throughout. We recorded data for 7–10 min., with up to 3 data sets collected per fly. We presented 4 s red light pulses to activate csChrimson every 1–3 min.

Image registration

Before quantifying fluorescence intensities, imaging frames were registered in Python by translating each frame in the x and y plane to best match the time-averaged frame for each z-plane. Multiple recordings from the same fly were registered to the same time-averaged template if the positional shift between recordings was small.

Defining regions of interest

To analyze calcium imaging data, we defined regions of interest (ROIs) in Fiji and Python for each glomerulus (protocerebral bridge), wedge (ellipsoid body) or column (fan shaped body). For the bridge data, we defined ROIs by manually delineating each glomerulus from the registered time-averaged image of each z-plane (Fig. 2 and Extended Data Figs. 2, 3, 4e-h PFN_d row, i PFN_ds and PFN_vs in the bridge, j-k, n-o, 5, 8a-e, j-m, r-u), as described previously¹¹. Because single SpsP neurons innervate the entire left or right side of the protocerebral bridge (Extended Data Fig. 4e, f (SpsP row), p-q), when imaging them we treated the entire left bridge as one ROI and the entire right bridge as another. When imaging PFNs or LNO1s in the noduli (Extended Data Fig. 4b–c, i, l–m), we treated the entire left nodulus as one ROI and the entire right nodulus as another.

For ellipsoid body imaging (Figs. 1, 5 and Extended Data Figs. 1, 7), we defined ROIs by first outlining the region of each z-slice that corresponded to the ellipsoid body. We then radially subdivided the ellipsoid body into 16 equal wedges radiating from a manually defined center, as describe previously⁸. For fan-shaped body imaging (Figs. 1, 5 and Extended Data Figs. 1, 7, 8f–i, n–q, v–x), we defined ROIs by first outlining the region in each z-slice that corresponded to the fan-shaped body. We then defined two boundary lines delineating the left and right edges of the fan-shaped body. When these two edge lines were extended down, they met at an intersection point beneath the fan-shaped body. We subdivided the angle generated by thus intersecting the two fan-shaped body edges––which corresponds to the overall angular width of the fan-shaped body region––into 16, equally spaced, angular subdivisions radiating from the intersection point. We assigned pixels to one of the sixteen fan-shaped body columns based on the pixel needing to (1) reside in the overall fan-shaped region and (2) reside in the radiating angular region associated with the column of interest.

Calculating fluorescence intensities

We used ROIs, defined above, as the unit for calculating fluorescent intensities (see above). If pixels from multiple z-planes corresponded to the same ROI (e.g., the same column in the fan-shaped body), as defined above, then we grouped pixels from the multiple z-planes together for generating single fluorescence signal for that ROI. For each ROI, we calculated the mean pixel value at each time point and then used three different methods for normalization. We call the first method $\mathrm{\Delta }F/F_0$ (Figs. 3d–e, j–r and Extended Data Figs. 1e–f (phase-nulled bump shape), 3, 4i PFN_ds and PFN_ds in the bridge, j, l, n, p, 5, 8), where ${\mathrm{F}}_0$ was defined as the mean of the lowest 5% of raw fluorescence values in a given ROI over time and $\mathrm{\Delta }\mathrm{F}$ was defined as $\mathrm{F}-{\mathrm{F}}_0$. We call the second method normalized $\mathrm{\Delta }F/F_0$ (Figs. 1, 3c, 5, and Extended Data Figs. 1e–f heatmap, g-p, 2, 7), which uses this equation: $\left(\mathrm{F}-{\mathrm{F}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)/\left({\mathrm{F}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{F}}_0\right)$, where ${\mathrm{F}}_0$ was still the mean of the lowest 5% of raw fluorescence values in a given ROI over time and ${\mathrm{F}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ was defined as the mean of the top 3% of raw values in a given ROI over time. This metric normalizes the fluorescence intensity of each glomerulus, wedge or column ROI to its own minimum and maximum and makes the assumption that each column, wedge or glomerulus has the same dynamic range as the others in the structure, with intensity differences arising from technical variation in the expression of indicator or from the number of cells expressing indicator within a column or wedge. We used this method to estimate the phase of heading/traveling signals where it seemed reasonable to make the above assumption for accurately estimating the phase of a bump in a structure. We call the third method z-score normalized $\mathrm{\Delta }F/F_0$ (Extended Data Figs. 4b–h, i, signals in the noduli and SpsPs, k, m, o, q) where we show how many standard deviations each time point’s signal is away from the mean. We calculated the signal as $\mathrm{\Delta }F/F_0$ and then we z-normalized the signal. We used this method to estimate the asymmetry of neural responses to optic flow in the bridge or noduli, where it seemed sensible to normalize the baseline asymmetry (when there are no visual stimuli) to zero. Importantly, none of the conclusions presented in this paper rely on the normalization method used for visualizing and analyzing the data.

Calculating the phase of bumps and aligning phase across structures

To calculate the phase of the joint movement of the calcium bumps in the left and right protocerebral bridge, we first converted the raw bridge signal into a 16-to-18-point vector, with each glomerulus’ signal normalized as described above. Then, for each time point, we took a Fourier transform of this vector and used the phase at a period of 8 glomeruli to define the phase of the bumps, as previously described¹¹. To calculate phase of the EPG bump in the ellipsoid body, we computed the population vector average of the 16-point activity vector, as previously described⁸. To calculate the phase of the hΔB and PFR bumps in the fan-shaped body, we computed the population vector average like in the ellipsoid body, using the following mapping of fan-shaped body columns to ellipsoid body wedges. The leftmost column in the fan-shaped body corresponded to the wedge at the very bottom of the ellipsoid body, just to the left of the vertical bisecting line; the rightmost column in fan-shaped body corresponded to the wedge at the very bottom of the ellipsoid body, just to the right of the vertical bisecting line. We then numbered the fan-shaped body columns 1 to 16, from left to right, just like we numbered the ellipsoid body wedges clockwise around that structure⁸. This mapping is meant to match the expected mapping of signals from anatomy, described previously¹⁸, and as further discussed immediately below.

To align the EPG phase in the ellipsoid body with the hΔB phase or the PFR phase in the fan-shaped body, we used the approach just described (Figs. 1, 5, and Extended Data Figs. 1, 7). To align the EPG and PFN_d and PFN_v phase signals in the protocerebral bridge (Fig. 3c–e, and Extended Data Figs. 2, 3), we used the fact that these neuron populations commonly innervate 14/18 glomeruli in the protocerebral bridge, which allows for an obvious alignment anchor, as done previously¹¹. To calculate the offset between the phase of neural bumps and the angular position of a cue (bright bar or dot) rotating in angular closed loop on our visual display, we computed the circular mean of the difference between the neural phase and the cue angle during the time points when the cue was visible to the fly. We used this difference to provide a constant (non-time-varying) offset to the neural phase signal such that the difference between the phase and cue angles was minimized across the whole measurement window of relevance. This approach is needed because of the past finding that phase signals in the central complex have variable offset angles to the angular position of cues in the external world across flies (and sometimes across time within a fly)^8,11. To calculate the phase offset between neural bump position and visual cue angle, we did not analyze time points when the fly was not flying in all of our flight experiments (Figs. 1–5, and Extended Data Figs. 1–5, 7, 8 except panels h, p, x) nor did we analyze time points when the fly was standing in walking experiments (Fig. 5c, d and Extended Data Fig. 1o, p). For a fly to be detected as standing, the forward speed needed to be less than 2 mm/s, the sideslip speed less than 2 mm/s, and the turning speed less than 30 °/s. We also excluded the first 10 s of each period in Figure 1f to minimize the impact of a changing visual stimulus on the offset estimate.

Comparing data acquired at different sampling rates or with a time lag

When comparing two-photon imaging data (collected at ~5–10 Hz) and behavioral (flight turns or ball walking) data (collected at 50–100 Hz) for the same fly, we subsampled the behavioral data to the imaging frame rate by computing the mean of behavioral signals during the time window in which each imaging data point was collected (Figs. 1f, 5b–d and Extended Data Figs. 1g–j, 4j–q, 7m–o), as previously described¹¹.

Although we collected both the EPG signal in the ellipsoid body and the hΔB (or PFR) signal in the fan-shaped body at the same frame rate, the precise time points in which these two signals were sampled were slightly different because the piezo drive that moves the objective had to travel from the higher fan-shaped body z-levels to the lower ellipsoid body z-levels. Importantly, each z-slice in a such volumetric time series was associated with its own trigger time and we could use this fact to more accurately align the fan-shaped body and ellipsoid body phase signals to each other. Specifically, when comparing EPG and hΔB (or PFR) bump positions over time, we first created a common 10 Hz (100 ms interval) time base. We then assigned phase estimates from the two structures/cell-types to this common time base by linearly interpolating each time series (using its specific z-slice triggers) and we used these interpolated time points, on the common time base, for calculating the phase differences between EPGs and hΔBs, or EPGs and PFRs (Fig. 1g–i, and Extended Data Figs. 1p, 7c–e, m–o). For the histograms and other analyses in Figures 1g, 5g, h, k, l, o, p, and Extended Data Figs. 1l, m, n–p, 7g–j, we simply subtracted the EPG phase and the hΔB phase or the PFR phase measured in each frame, without temporal interpolation. None of our conclusions are altered if we change the interpolation interval or do not interpolate.

Sideslip and backward walking analysis

In Extended Data Fig. 1n–p, we detected time segments where flies walked in three different, broad traveling directions (forward, rightward, and leftward). Forward-walking segments were defined by the flies having a forward velocity between +3 to +10 mm/s and a sideslip velocity between −2 to +2 mm/s. Sideward walking segments were defined by the flies having a forward walking velocity between +2 to −10 mm/s and a sideslip velocity between 3 to 10 mm/s to the relevant side.

We expressed CsChrimson in a group of lobula columnar neurons, LC16, whose activation with red light has been shown to induce flies to walk backward (Extended Data Fig. 7k–o, more details in ‘Optogenetic stimulation’)⁴⁷. Consistent with previous studies in free walking flies⁴⁷, we also observed variable backward walking behaviors mixed with sideward walking and turning in our tethered preparation. To test whether the PFR phase separates from the EPG phase when a fly walks backward, we analyzed optogenetic activation trials based on the following three criteria being met. First, the backward walking speed needed to be larger than 6 mm/s. Second, the duration of continuous backward walking (defined by backward walking speed being above 0.5 mm/s) needed to be longer than 1 s. Third, during the backward walking period, the sideward walking velocity needed to be biased toward one direction; the fraction of optogenetic trials in which the sideward velocity was clearly either positive or negative exceeded 80%. We included this third criterion so that we could split optogenetic trials into those where the PFR phase should have moved to the right and those in which it should have moved to the left in the fan-shaped body (Extended Data Fig. 7k–o).

Phase nulling

To compute the time-averaged shape of the bump in PFNs and EPGs, we followed previous methods¹¹. In brief, we (1) computationally rotated each frame by the estimated phase of the bump on that frame, such that the bump peak was at the same location on all frames and then (2) averaged together the signal from all frames to get an averaged bump, whose shape we could analyze via fits to sinusoids (Fig. 3 and Extended Data Figs. 3, 5, 8a). In this phase nulling process, we first interpolated the GCaMP signal from each frame to 1/10 of a glomerulus, column, or wedge with a cubic spline. We then shifted this interpolated signal by the phase angle calculated for that frame. In both the ellipsoid body and fan-shaped body (Extended Data Fig. 1e, f), we performed a circular shift, such the signals wrapped around the edges of the fan-shaped body. In the protocerebral bridge, we performed this circular shift independently for the left and right bridge. For the protocerebral bridge data, we subsampled the spatially interpolated GCaMP signal back to a 16-glomerulus vector before plotting the data (Fig. 3 and Extended Data Figs. 3, 5, 8a) so as to more accurately reflect, in our averaged signals, what the actual signal in the brain looked like.

To compute the cell-averaged shape of the EPG-to-Δ7 synapse number across the glomeruli of the bridge in Extended Data Figure 3, we followed a similar protocol to the one described above for the imaging data. We treated the EPG-to-Δ7 synapse number profile of each Δ7 cell as the equivalent of one imaging frame, with the synapse number of each glomerulus the equivalent of the fluorescence intensity of a single glomerulus from that frame. The rest of the steps—calculating phase, interpolation, shifting, averaging and subsampling—are the same as those described above.

Statistics and Reproducibility

We performed unpaired two-tailed t-tests (Fig. 5d, h, Extended Data Fig. 1h, i, l, m, 7d, 7j) and Watson-Williams multi-sample tests (two-tailed, Fig. 5l, p, Extended Data Fig. 1p, 2g, 7i, o). See the related Figures and captions for details. All experiments discussed in the paper were conducted once at the conditions shown; no experimental replicate was excluded. For most experiments, data across multiple days were collected and the data across days were consistent. In immunohistochemistry plots (Extended Data Fig. 1a–c), two brains were imaged, but only one is shown. Both imaged brains showed the same qualitative pattern of staining. Note also the fly exclusion criteria described in Fly Husbandry.

In Figure 5d, p values are 2.7e-5, 6.2e-6 and 1.5e-4 comparing 4^th column (from left) with 1^st, 2^nd and 3^rd columns, respectively. P values are 1.6e-6, 2.4e-7 and 1.3e-5 comparing 7^th column (from left) with 1^st, 5^th and 6^th columns, respectively. In Figure 5h, p values are 1.1e-7 and 9.9e-8 comparing 3^rd column (from left) with 1^st and 2^nd columns, respectively. P values are 1.5e-5 and 6.9e-6 comparing 5^th column (from left) with 1^st, and 4^th columns, respectively. In Figure 5l, p values are 7.0e-8 and 2.8e-8 comparing 3^rd column (from left) with 1^st and 2^nd columns, respectively. P values are 4.0e-4 and 2.5e-4 comparing 5^th column (from left) with 1^st, and 4^th columns, respectively. In Figure 5p, p values are 2.0e-6 and 6.6e-4 comparing 3^rd column (from left) with 1^st and 2^nd columns, respectively.

For Fig. 1i, to test if the hΔB bump tracks the allocentric traveling direction (data fall on the diagonal line) better than tracking the allocentric heading direction (data fall on the horizonal line at zero), we calculated the mean circular squared difference between the data and the diagonal line versus the data and the horizontal line at zero. The result was 106 deg² for the diagonal line and 11807 deg² for the horizontal line at zero, demonstrating that the hΔB bump tracks the fly’s allocentric traveling direction better than the allocentric heading direction.

All the sinusoidal fits throughout the paper had three free parameters: baseline, amplitude and phase.

For fitting sinusoids to the activity bumps shown in Fig. 3d, e and Extended Data Fig. 3h, the left- and right-bridge data were fit to sinusoids separately because their amplitudes could vary independently. The period of each sinusoidal fit was 8 glomeruli, with the 1^st and 9^th glomeruli set to the same value (Extended Data Fig. 5). Reduced χ² tests were performed to test goodness of the fit. χ² values per degrees of freedom ranged between 0.17 to 0.83 for all PFN fits, between 0.05 to 0.13 for all PFR fits, and between 0.24 to 1.91 for all EPG fits. The corresponding p values ranged between 0.53 and 0.98 for all PFN fits, between 0.98 to 0.99 for all PFR fits, and between 0.08 to 0.95 for all EPG fits. These fit results mean that we cannot reject the hypothesis that the data are draws from an underlying sinusoidal distribution of activity.

For fitting sinusoids to the tuning curves in Fig. 3k, l, n, o, q, r, chi-squared per degrees of freedom were between 0.15 to 1.20 giving p values between 0.31 and 0.93. Again, the hypothesis that these data are generated by a sinusoidal distribution cannot be rejected. Although the EPG amplitude-tuning-curves to optic flow (Fig. 3q and r) fit well to sinusoids, the amplitude parameters of the fits were very small compared to the baseline parameters. For Fig. 3q, the amplitude and baseline parameters were 0.040 and 0.73 (unit: $\mathrm{\Delta }\mathrm{F}/{\mathrm{F}}_0$), respectively. For Fig. 3r, the amplitude and baseline parameters were 0.024 and 0.76 (unit: $\mathrm{\Delta }\mathrm{F}/{\mathrm{F}}_0$), respectively. By contrast, for the PFN signals in Figure 3k, l, n, o, the amplitude parameters were 0.69, 0.69, 0.30 and 0.33 and the baseline parameters were 0.90, 0.90, 0.43 and 0.42, respectively. We thus conclude that the PFN_v and PFN_d sinusoidal activity patterns in the bridge are strongly modulated by optic flow, whereas the EPG activity pattern is very weakly modulated by optic flow.

The data points in Fig. 3d, e, k, l, n, o, q, r, and Extended Data Fig. 3h, were fit to sinusoids using the method of variance-weighted least-squares. All other fits to sinusoids used the method of least-squares.

For Extended Data Fig. 7d, the null hypothesis is that the PFR bump tracks the allocentric traveling direction (data fall on the diagonal line) equally well than tracking the allocentric heading direction (data fall on the horizonal line at zero). We calculated the mean circular squared difference between the data and the diagonal line versus the data and the horizontal line at zero for the 35cm/s column. The result is 549 deg² for the diagonal line and 7710 deg² for the horizontal line at zero. Thus, the PFR bump tracks the fly’s allocentric traveling direction better than the allocentric heading direction in these experiments.

Modeling

We constructed a model, based heavily on the data, to test whether the observed PFN activity profiles could provide summed input to hΔB neurons that would induce the hΔB bump of activity to indicate the fly’s traveling angle. Neurons in the model are labeled by an angle $\theta$ that indicates their position along the fan-shaped body. In reality, this angle takes discrete values corresponding to the columns of the fan-shaped body but, to simplify the notation, we use a continuous label here. The fly’s allocentric heading angle is denoted by $H$.

The data argue that the PFN activity profiles in the bridge have a sinusoidal shape (Fig. 3d, e, Extended Data Fig. 3) with phases locked to the phase of the EPG bumps (Extended Data Fig. 2), and that the projections of the PFNs from the bridge to the fan-shaped body result in anatomically shifted inputs to the hΔB cells (Fig. 3f–i, Extended Data Fig. 6). The phase of the EPG bump tracks the inverse of the fly’s heading angle, $H$, meaning that when the fly turns clockwise, for example, the bump rotates counterclockwise (when looking at the ellipsoid body from the rear). (To make things hopefully less confusing with regard to this minus sign, we flipped the orientation of the horizontal axis in some of our figures.) On the basis of these observations, we model the PFN activity profiles in the fan-shaped body as

$${\mathrm{P}\mathrm{F}\mathrm{N}}_i\left(\theta \right)=A_i\left(a_i+\mathrm{c}\mathrm{o}\mathrm{s}\left(-H-\theta -{\varphi }_i\right)\right)+c_i,$$

where $i=1,2,3,4$ refers to right-bridge PFN_d, left-bridge PFN_d, right-bridge PFN_v, and left-bridge PFN_v, and $a_i$ and $c_i$ are parameters reflecting amplitude-dependent and amplitude-independent offsets (i.e., mean levels) of the sinusoidal activity patterns (Extended Data Fig. 8). $A_i$ is the amplitude of the sinusoid for PFN $i$, which depends on the egocentric traveling angle (i.e., simulated optic flow; Fig. 3j–o. The angles $\varphi$ are the shifts in the PFN projections from the bridge to the hΔBs (Fig. 3f–i, Extended Data Fig. 6). The total input to the hΔBs, which we call $\mathrm{h}\mathrm{\Delta }\mathrm{B}\mathrm{I}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}(\theta )$, is given by the sum of the PFN activities weighted by factors $g_i$ that reflect the strengths of the PFN connections to the hΔBs,

$$\mathrm{h}\mathrm{\Delta }\mathrm{B}\mathrm{I}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}(\theta )=\sum _{i=1}^4{g}_i{\mathrm{P}\mathrm{F}\mathrm{N}}_i(\theta )=\sum _{i=1}^4{g}_i\left(A_i\left(a_i+\mathrm{c}\mathrm{o}\mathrm{s}\left(-H-\theta -{\varphi }_i\right)\right)+c_i\right).$$

The hΔB bump will appear at the value of $\theta$ for which this summed input is maximal, which occurs at

$${\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}=-\arctan \left(\frac{\sum _{i=1}^4{g}_i{A}_i\sin \left({\varphi }_i\right)}{\sum _{i=1}^4{g}_i{A}_i\cos \left({\varphi }_i\right)}\right)-H.$$

The prediction of the model is that this angle should be equal to the negative of the allocentric traveling angle. Many of the model’s parameters do not appear in this expression, and the overall scale of the $g_i$ values for the different PFNs cancels in the above ratio. We obtained the amplitude factors, $A_i$, directly from the data. For this purpose, we could use the amplitudes measured in the protocerebral bridge (Fig. 3j–o) with good results, but we chose instead to use the measurements from the noduli (Extended Data Fig. 4a–h), which is the site of the sensory input that drives the amplitude modulation of the PFNs. Although the noduli do not have a columnar structure and thus can only provide a measure of mean activity for a given PFN type, we took advantage of the fact that the mean and amplitude of the PFN sinusoids in the bridge show virtually identical modulation (Extended Data Fig. 8) to infer the amplitudes $A_i$. As mentioned in the text, we divided the measured amplitudes by their averages across all the measured simulated motion directions for each PFN type to correct for possible expression and imaging differences.

We set the remaining parameters in the above expression for ${\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ in two ways (both results are shown in Fig. 4e). First, we assumed that the four values of $g$ were the same, meaning equal weighting of the four PFN types, and we took the angles $\varphi$ to be 45°, −45°, −135° and 135°. This resulted in a ‘fit’ to the data that involves assumptions, but no free parameters (Fig. 4e, red circles). To avoid these assumptions, we also used values of these two sets of parameters extracted from a connectome-based analysis¹⁷ (Extended Data Fig. 6). On average, right (left) PFN_ds make 257.3 (260.7) synapse onto the ‘axonal’ region of the hΔBs and 164.4 (162.7) onto the ‘dendritic’ region. Because these regions are 180° apart, implying a subtraction of sinusoidal signals, we took the strengths of these inputs to be $g_1=257.3-164.4=92.9$ and $g_2=260.7-162.7=98$. Right (left) PFN_vs synapse onto the ‘dendritic’ regions with, on average, 67.0 and 74.3 synapses, and we used these numbers as the values of $g_3$ and $g_4$. This assumes that there is no appreciable attenuation between the dendritic and axonal regions of the hΔBs. The angles $\varphi$, up to an overall rotation which we chose to bring these angles in approximate alignment with the set of angles used above, were extracted from the hemibrain data by the procedure shown in Extended Data Fig. 6 and were taken to be 44.5°, −41.5°, −131.5° and 136.5°. This generated the second set of model results shown in Fig. 4e (green diamonds).

Extended Data

Extended Data Figure 1 |. Characterizing the anatomy and physiology of hΔB cells, showing that sytGCaMP and RGECO1a yield similar EPG phase estimates in the ellipsoid body, quantifying the EPG phase tracking of the closed loop dot, and evidence that the hΔB phase tracks the fly’s traveling direction in walking flies.

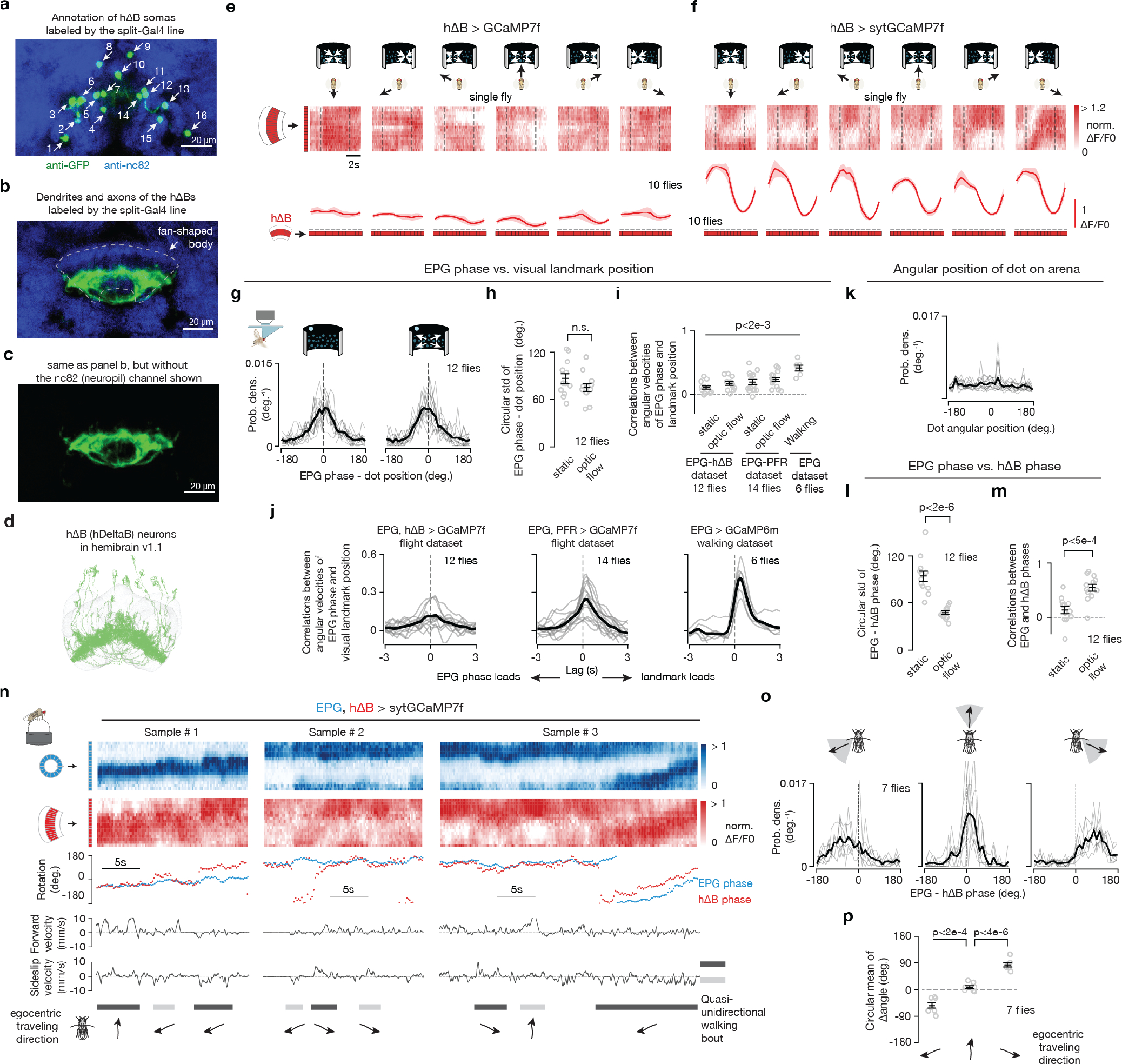
a, At least sixteen somas are labeled by the hΔB split-Gal4 line used in this paper. By comparison, the hemibrain connectome (v1.1) reports nineteen hΔB cells¹⁷. b, GFP expression of the hΔB split Gal4 in the fan-shaped body. c, Same as panel b, but not showing the anti-nc82 neuropil stain. d, hΔB cells from hemibrain connectome v1.1¹⁷. e, Top, hΔB GCaMP7f signal in a tethered, flying fly experiencing optic-flow (in the time window bracketed by the vertical dashed lines) with foci of expansion that simulate the following directions of travel: 180° (backward), −120°, −60°, 0° (forward), 60°, 120°. Bottom, Phase-nulled and averaged hΔB activity patterns in the fan-shaped body, calculated from the above [Ca²⁺] signals in the last 2.5 s of optic flow presentation. Population means with s.e.m. are shown. f, Same as panel e, but with hΔB sytGCaMP7f signal. Note that the single-bump structure in the sytGCaMP7f signal is clear than the structure in the cytoplasmic GCaMP7f signal, which is consistent with sytGCaMP7f biasing GCaMP to axonal compartments of hΔBs. g, Probability distributions of the difference between the EPG phase and the bright dot’s angular position, without and with optic flow. h, Circular standard deviation of the EPG phase – dot position distributions, without and with optic flow. Two-tailed unpaired t-test was performed. i, Correlations between the angular velocities of the EPG phase and the visual landmark position under different conditions. The first two columns use the same data as in panels g and h. The third and fourth columns use data from simultaneous GCaMP7f imaging of EPGs and PFRs in tethered-flying flies with a closed-loop dot. The fifth column use data from GCaMP6m imaging of EPGs in tethered-walking flies with a closed-loop bar. Two-tailed one sample t-tests were performed against zero. P values are 1.7e-3, 1.3e-4, 5.3e-4, 1.2e-5 and 3.6e-4 comparing each column (from left to right) to zero, respectively. The relatively low, but significantly different from zero, r values show that the EPG phase tracks, even if poorly, the rotation of the landmark. The EPG phase measured in walking experiments tracks the closed-loop stimulus better than in tethered flight. See Main Text for possible technical reasons for why one would observe this difference. The fact that EPG-phase tracking of the closed loop dot is better when we co-imaged EPGs and PFRs compared to when we imaged EPGs and hΔBs argues that the flies’ genetic background (and thus how reliably flies perform tethered flight) can also quantitatively impact these measures. j, Angular-velocity correlations of the EPG phase and the visual landmark position under different conditions as a function of the time-lag between the two velocity signals. Same data as in panel i, but data with and without optic flow are lumped together. Correlation is highest at 290 ms, 260 ms and 375 ms for the three panels from left to right, respectively. Thus, we used time lags of 275 ms (mean of 290 and 260) and 375 ms for calculating the correlations in flight and walking experiments in panel i, respectively. k, Probability distribution of the angular position of the dot on the arena. Same data as in panels g and h, but data with and without optic flow are lumped together. We tested the uniformity of the distribution across angles using reduced χ2 test. P value is > 0.995, meaning that we cannot reject the hypothesis that the dot position is not evenly distributed on the arena. l, Circular standard deviation of the EPG phase minus the hΔB phase distributions, without and with optic flow. Same data as in panels g and h. Two-tailed unpaired t-test was performed. P value equals 1.3e-6. m, Correlations between the EPG phase and the hΔB phase. Same data as in panels g, h and l. Two-tailed unpaired t-test was performed. P value equals 3.9e-4. n, Data collected from tethered flies walking on a floating ball in complete darkness are shown in this panel and all subsequent panels in this figure. Sample time series of simultaneously imaged EPG and hΔB Gal4 lines. Top two traces show [Ca²⁺] signals. Third trace shows the phase estimates of the two bumps. Bottom two traces show the forward velocity and sideslip velocity of the fly. Quasi-unidirectional walking bouts are labeled with walking directions indicated. o, Probability distribution of the difference between EPG phase and hΔB phase from time segments where flies were walking in three different general directions (Methods). p, EPG – hΔB phase as a function of the egocentric traveling direction. Gray: individual fly circular means. Black: population circular mean and s.e.m. The sign of EPG – hΔB phase deviations seen here, in walking, are consistent with the signs observed in flight, for the same directions of backward-left and backward-right travel. Watson-Williams multi-sample tests were performed. P values are 1.6e-3 and 2.6e-6 comparing the 1^st and 3^rd columns (from left to right) to the 2^nd column, respectively.

Extended Data Figure 2 |. PFN_d and PFN_v activity bumps in the bridge are phase aligned with the EPG heading signal.

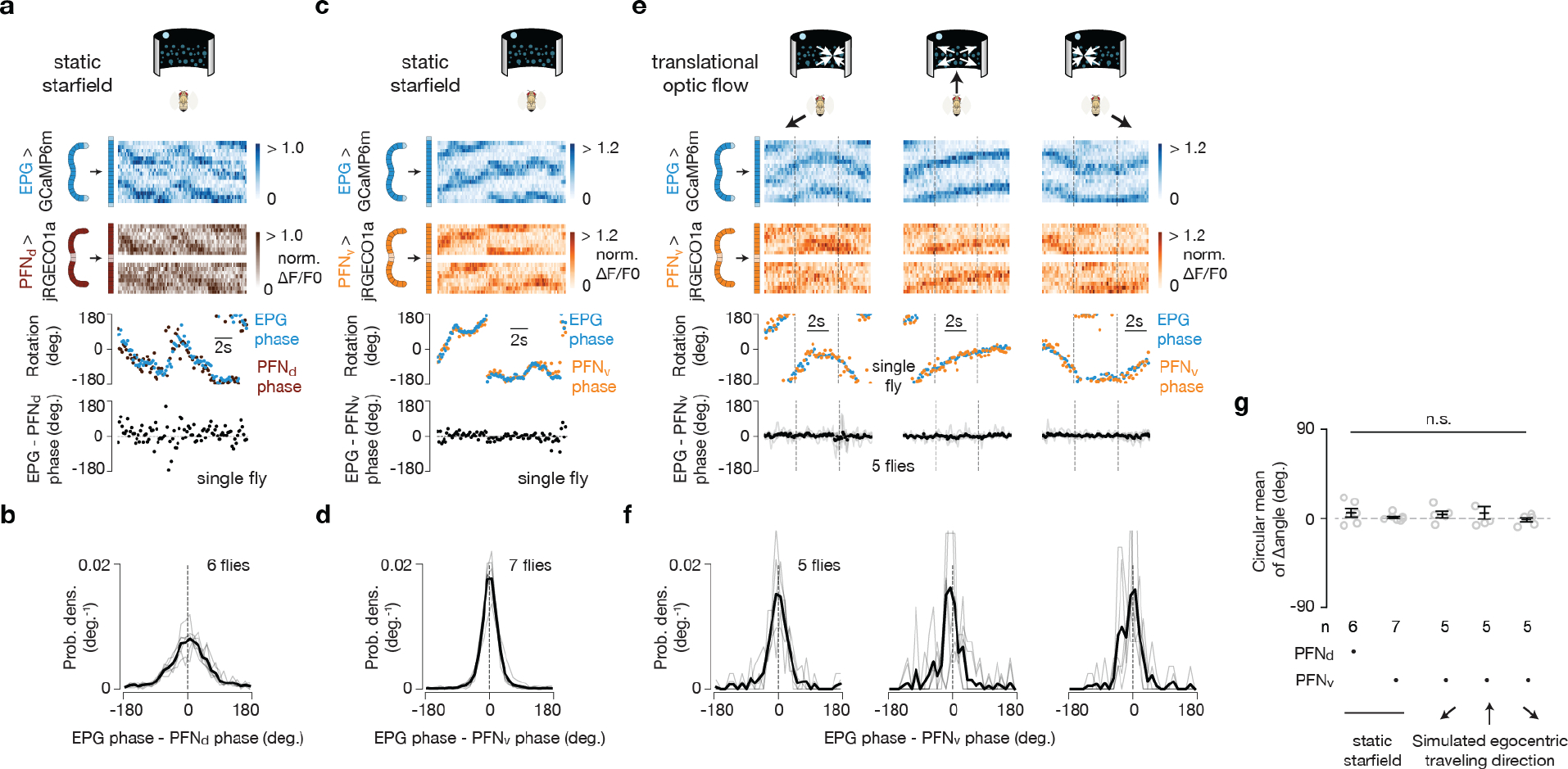
a, Sample trace, in tethered flight without optic flow, of simultaneously imaged GCaMP6m in EPGs and jRGECO1a in PFN_ds reveals that the activity bumps of these two cell classes are phase aligned in the bridge. b, Probability distribution of the EPG - PFN_d phase in tethered flight without optic flow. In this panel and throughout, the single fly data are in light gray and the population mean is in black. c-d, Same as panel a-b, but for GCaMP6m in EPGs and jRGECO1a in PFN_vs. e, Top three rows, sample trace of simultaneously imaged GCaMP6m in EPGs and jRGECO1a in PFN_vs in a tethered, flying fly experiencing optic flow (in the time window bracketed by the vertical dashed lines) with foci of expansion that simulate the following directions of travel: −120°, 0° (forward), 120°. Bottom, circular-mean phase difference between EPGs and PFN_vs. f, Probability distribution of the EPG - PFN_vs phase under three optic flow conditions. g, Circular mean of the EPG – PFN phase ad s.e.m. under different visual stimulus conditions. Watson-Williams multi-sample tests, P>0.66 when comparing any experimental group with 0°. Note that we only collected a full EPG-PFN, dual-imaging data set with optic flow (moving dots) with PFN_vs because, for reasons that are not fully clear, the jRGECO1a signal was too weak in PFN_ds to properly estimate the PFN_d phase outside of the context of stationary dots (i.e., during optic flow). When imaging PFN_ds with a split-Gal4 driver and with GCaMP rather than with jRGECO1a (e.g., Fig. 3j-l), the signal is much brighter.

Extended Data Figure 3 |. Δ7 cells are poised to help create sinusoidally shaped activity bumps in PFN_ds, PFN_vs and PFRs in the protocerebral bridge.

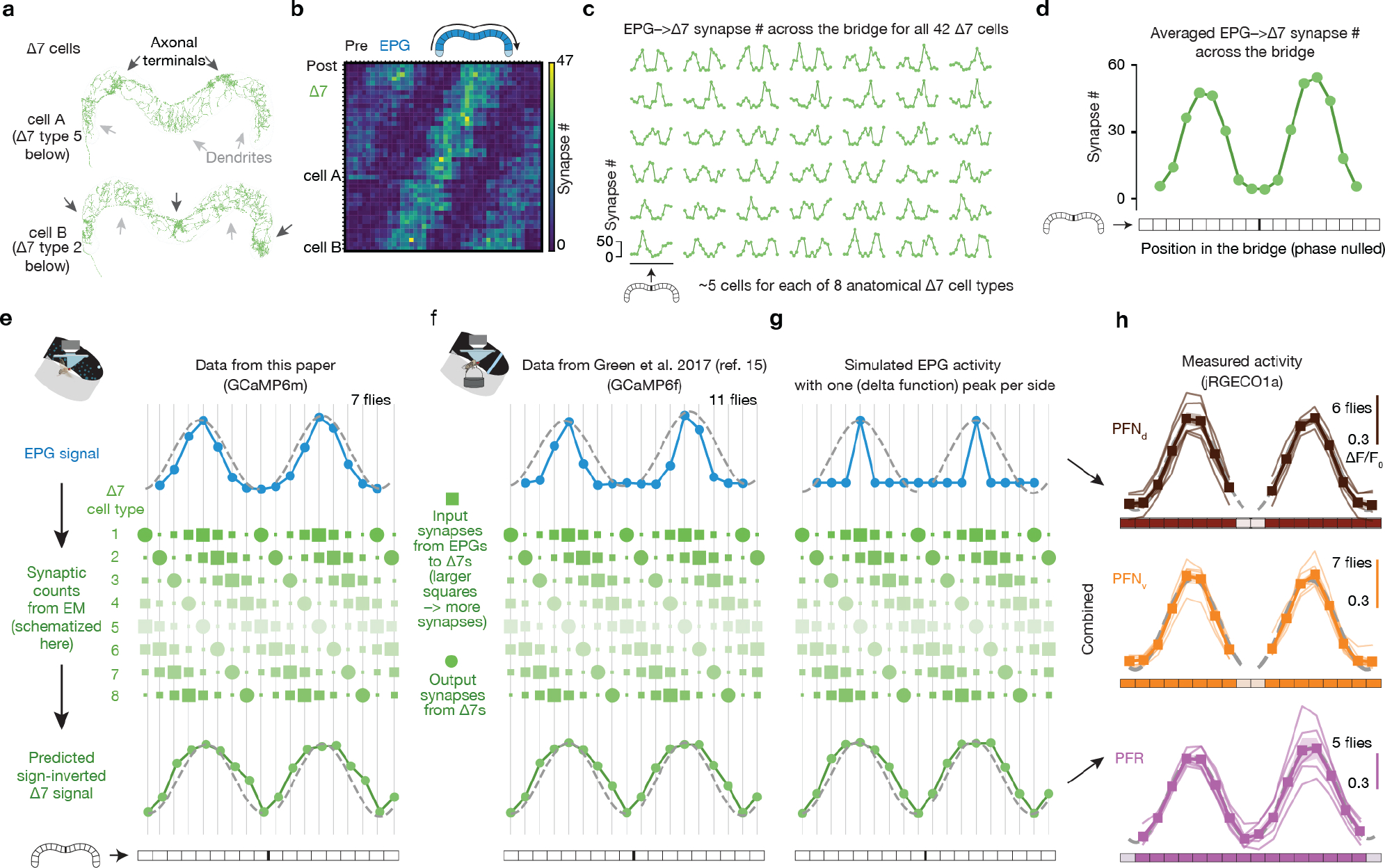
Connectivity data are based on those in neuPrint¹⁷, hemibrain:v1.1. a, Two Δ7 cells from neuPrint reveal a graded increase and decrease in dendritic density across the bridge. b, Synapse-number matrix for detected synapses from EPG cells to Δ7 cells in the protocerebral bridge. Each row represents one Δ7 cell. c, Same data as in panel b, but plotting each Δ7 cell separately. d, Phase-nulled EPG-to-Δ7 synapse # across the glomeruli of the bridge, averaged across all 42 Δ7 cells, based on the data in panel c. The anatomical input strength from EPGs to Δ7s is sinusoidally modulated across the bridge. e, Transforming the EPG activity pattern across the bridge (blue) into a predicted Δ7 activity pattern (green, bottom row) based on the synaptic density profile in panel c (schematized in the middle). We first calculated the dot product between the EPG activity vector and each Δ7 cell’s EPG-to-Δ7 synapse-number vector (panel c). Then, for each glomerulus, we averaged the dot-product-output for all of the Δ7s that have axonal terminals in that glomerulus, thus creating the predicted activity value for that glomerulus. (The size of each green square here schematizes the # of synapses from EPGs to the Δ7 cell of that type in that column; the intensity of each Δ7 row indicates the expected output strength of each Δ7 cell type, after being driven by the EPG signal above.) We plot the inverted, predicted activity output from Δ7s in the bottom row (green) because Δ7s are glutamatergic⁴⁰ and glutamatergic neurons in the Drosophila central nervous system typically inhibit their postsynaptic targets (via Glu-Cl channels). After inverting the Δ7 activity one can then imagine simply averaging the Δ7 predicted-activity row with the EPG activity––with some relative weighting for the Δ7 and EPG curves––to generate the net drive to the many downstream neurons that receive both EPG and Δ7 input¹⁷, like PFNs. Note that the EPG activity bumps are slightly narrower than the sinusoidal fits whereas the Δ7 activity bumps are slightly wider than the sinusoidal fits. f, Same as panel e, but using the phase-nulled, averaged EPG GCaMP activity pattern from a previous study¹¹. Note although the EPG bump is narrower in these data from walking flies than in panel e from flying flies, the shape of the predicted Δ7 output remains similar. g, Same as panel e, but starting with (imagined) EPG activity where there is only one active glomerulus on each side of the bridge. Note that the shape of the predicted Δ7 output remains similar to that in panels e-f. h, Measured, phase-nulled activity profiles from PFN_ds, PFN_vs and PFRs. Thin lines: individual flies. Thick lines: population average. All three activity patterns conform well to their sinusoidal fits (gray dashed lines) (see Methods for goodness of fit). We hypothesize that the sinusoidal activity patterns in bridge columnar cells like PFN_ds, PFN_vs, PFRs arises from the combined impact of EPG and Δ7 input. In other words, we posit that Δ7s “sinusoidalize” the EPG bumps in the bridge –– that is, they function to broaden and smoothen the EPG input to the bridge, to create two sinusoidally shaped bumps in their recipient cells, with these bumps often functioning as explicit, 2D vector signals in the fan-shaped body.

Extended Data Figure 4 |. LNO1 and SpsP cells have [Ca²⁺] responses that are strongly tuned to the fly’s egocentric translation direction––in both walking and flying flies––with responses suggesting that these cells provide sign-inverting input to PFN_v and PFN_d cells, respectively.

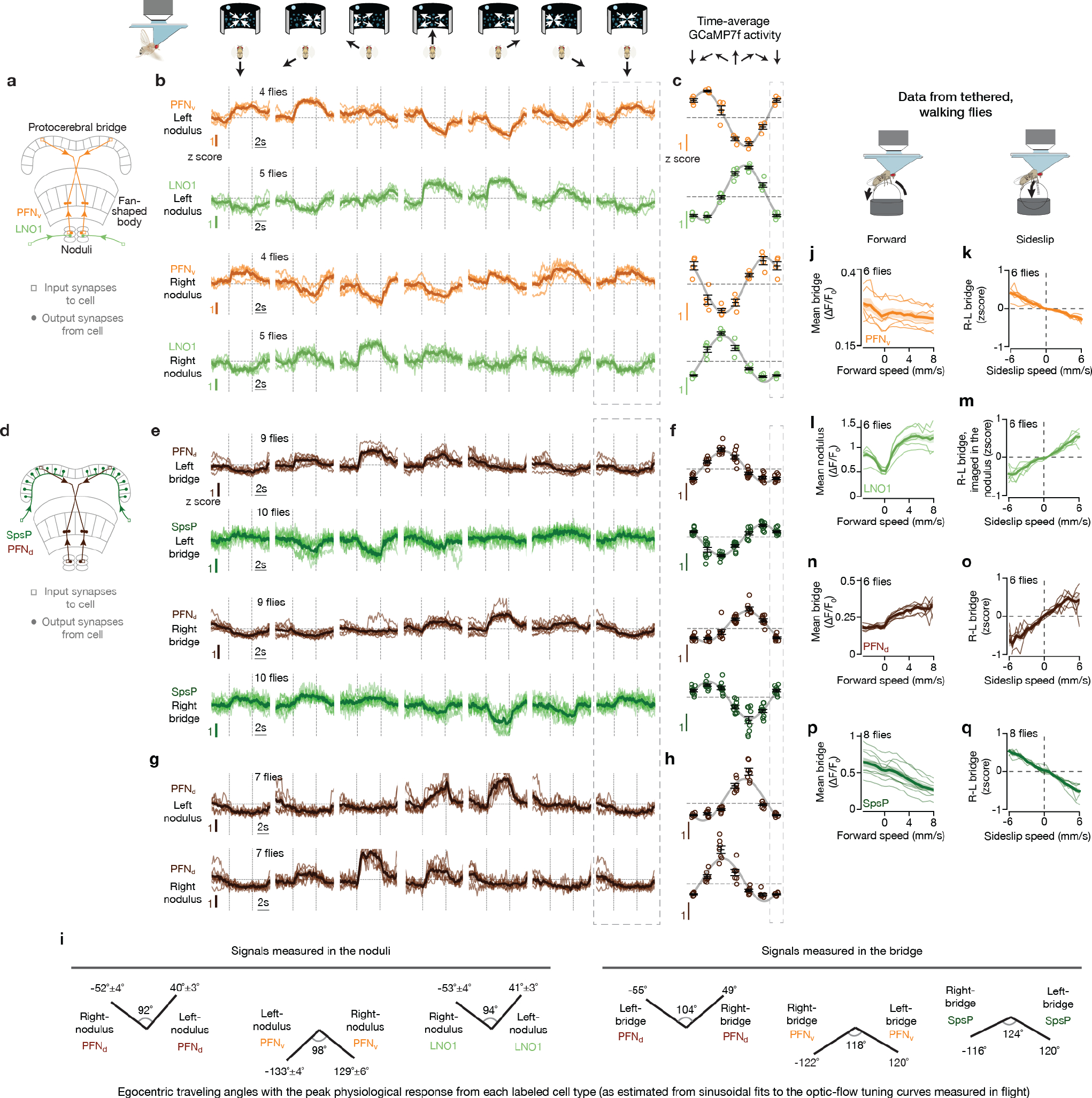
Connectivity data and cell-type names are based on those in neuPrint¹⁷, hemibrain:v1.1. a, LNO1s are a class of cells (two total neurons per side, four per brain) that receive extensive synaptic input outside the central complex and provide extensive synaptic input to PFN_vs in the noduli, with each PFN_v cell on average receive 131 synapses from LNO1s¹⁷. b, Mean GCaMP signals in PFN_vs and LNO1s in the nodulus as a function of the simulated traveling direction of the fly (via open-loop optic flow). Dotted rectangle indicates a repeated-data column, in this panel and throughout. c, Single-fly (colored circles) and population means ± s.e.m. (black bars) of the average signal in the final 2.5 s of the optic flow epoch. Sinusoidal fits shown in this panel (Methods), and throughout. d, Each SpsP cell (two total neurons per side, four per brain) receives extensive synaptic input outside the central complex and provides extensive synaptic input to PFN_ds on one side of the protocerebral bridge, with each PFN_d cell on average receive 56 synapses from SpsPs¹⁷. e, Same as panel b, but mean GCaMP signals in PFN_ds and SpsPs in the bridge as a function of the simulated traveling direction of the fly (via open-loop optic flow). A closed-loop bright dot was not present on the LED display when collecting the PFN_d data. f, Same as panel c, but averaging the bridge signal in panel e. g, Same as panel b, but analyzing the PFN_d signal in the noduli. A closed-loop bright dot was not present on the LED display. h, Same as panel c, but averaging the nodulus signal in panel g. i, The optic-flow-simulated egocentric traveling angle at which the activity of each cell type is strongest is depicted with a line at the associated angle. Note that the left-vs.-right angular differences measured in the noduli are smaller, and closer to 90°, than the left-vs.-right angular differences measured in the bridge. This difference might be a purposeful shift in optic-flow tuning related to the use of orthogonal and non-orthogonal PFN axes under different behavioral contexts (see Supplemental Text) and/or originate from differences in how SpsPs in the bridge and LNO1s in the noduli balance optic-flow with proprioceptive/efference-copy inputs to generate their signals. j, Data collected from tethered flies walking on a floating ball in complete darkness are shown in this panel and all subsequent panels in this figure. Mean PFN_v GCaMP signals in the bridge as a function of the fly’s forward speed. k, Right-minus-left PFN_v GCaMP signals in the bridge as a function of the fly’s sideslip speed. l-m, Same as panel j and k, but analyzing LNO1 signals in the nodulus. n-o, Same as panel j and k, but analyzing PFN_d signals in the bridge. p-q, Same as panel j and k, but analyzing SpsP signals in the bridge. In panel b, e, g, j-q, thin lines represent single-fly means and thick lines represent population means. Note that PFN_vs and LNO1s have sign-inverted responses, and that PFN_ds and SpsPs have sign-inverted responses. The response signs to optic-flow simulating the fly’s body translating forward and leftward (rightward) in flight are the same as the signs of responses to the fly walking forward and side-slipping leftward (rightward) when walking. Thus, these data are consistent with all these neurons being sensitive to the fly’s egocentric translation direction, as assessed via optic flow (dominantly) in flight, and via proprioception or efference-copy (dominantly) in walking.

Extended Data Figure 5 |. Multiple, functionally relevant ways of indexing angles across the protocerebral bridge.

Connectivity data and cell-type names are based on those in neuPrint¹⁷, hemibrain:v1.1. a, The previously described mapping between EPG dendritic locations in the ellipsoid body and axonal-terminal locations in the bridge¹⁸. Numbers ordered based on the location of each EPG cell in the ellipsoid body. b, EPG cells divide the ellipsoid body into 16 wedges, each 22.5° wide. Each glomerulus in the bridge inherits its angle, in our analysis here, based on the EPG projection pattern shown in panel a. The angles of the outer two bridge glomeruli––which do not receive standard EPG input, but only EPGt input¹⁷––were inferred to have angles equal to the middle two glomeruli (0° and 22.5°, respectively) based on how other cell types (e.g., PENs) innervate the bridge, as discussed in past work¹¹. This angular assignment maintains a 45° step size between adjacent glomeruli on each side of the bridge, which seems natural due to symmetry considerations. (Note that EPGt cells map from the ellipsoid body to the outer two glomeruli of the bridge with a small angular offset compared to the pattern set up by the EPGs that target the central 16 glomeruli––as reported by other studies²⁵––a caveat that slightly complicates our angular assignments; however, EPGt cells receive extensive axonal input in the bridge that has the potential to align their output signals with the rest of the bridge system.) Glomeruli are numbered 1 to 18 from left to right, to aid the comparisons made below. c, Two Δ7 cells from neuPrint (and past work¹⁸) reveal that the axonal terminals of each Δ7 cell are 8-glomeruli apart (#5→#13 for cell A and #2→#10→#18 for cell B). This anatomy argues that any two glomeruli 8 apart, such as #5 and #13, will experience Δ7 output of equal strength. Compelling physiological evidence for this statement is available in the [Ca²⁺] signals of the PEN2 (equivalently, PEN_b) columnar cell class in the bridge, which is a strong anatomical recipient of Δ7 synapses¹⁷ and shows [Ca²⁺] activity across the bridge––clearly dissociable from the activity in EPGs––with consistently equal signal strength at glomeruli spaced 8 apart, perfectly following the Δ7 anatomical prediction (orange trace in Fig. 3d and data points in Extended Data Fig. 2i from ref. 15). Note that in the EPG indexing, shown in panel b, glomeruli #5 and #13, as examples, have angular indices that are not identical, but differ by 22.5°. d, Angles assigned to each bridge glomerulus based on the Δ7 axonal anatomy. Because the Δ7 output anatomy requires that any two glomeruli 8 apart, across the whole bridge, have the same angular index assignment, this results in a situation where all neighboring glomeruli have angular assignments that are separated by 45°. Note that almost all neighboring glomeruli are separated by 45° in the EPG mapping as well, except that, critically, in the EPG mapping the middle two glomeruli are separated by only 22.5°. This discontinuity is not evident in the Δ7 output. To create an angular indexing of the bridge for Δ7s that accommodates the anatomical constraints just described––i.e., one that incorporates an additional 22.5° in the bridge representation of angular space and thus “erases” the EPG discontinuity––we shifted the angular index for each glomerulus on the left bridge leftward by 11.25° relative to the EPG indexing and we shifted the angular index for each glomerulus on the right bridge rightward by 11.25° relative to the EPG indexing. e, The EPG indexing in panels a-b predicts that EPG activity in the left bridge (#2→#9) will be left-shifted by 22.5° compared to EPG activity in the right bridge (#10→#17). Indeed, when we overlapped the left- and right-bridge EPG signals we found the two curves are detectably offset from each other. f, To quantify the data from panel e, for each imaging frame in which the fly was flying, we calculated the phase of the EPG bump in the left and right bridge separately (via a population-vector average) and took the difference of these two angles (black bars: population mean and s.e.m.). We then averaged this angular difference across all analyzed frames for the same fly. For EPGs, this angular difference should be −22.5° if it follows the EPG indexing in panel b and it should be 0° if the activity follows the Δ7 indexing in panel d. Across a population of 9 flies, we found the angular difference is close to −22.5°, but shifted toward 0° by 4.6°, consistent with the fact that the EPG signal itself receives strong anatomical input from the Δ7s and thus could be modulated in its shape to follow the Δ7 indexing, in principle¹⁷. It seems that the Δ7 feedback to EPGs reshapes its signal, but incompletely. g-h, Same as panel e, but analyzing the PFN_d and PFN_v activity in the bridge. Because PFNs only innervate the outer 8 glomeruli in each side of the bridge (unlike EPGs, which innervate the inner 8), we compared glomeruli #1→#8 in the left bridge overlapped with glomeruli #11→#18 in the right bridge here (the middle two glomeruli contain no signal for PFNs). i, Same as panel f, but analyzing the PFN_d and PFN_v activity in the bridge. Black bars: population mean and s.e.m. Note that because PFN_ds and PFN_vs innervate (and thus we can only analyze) the outer 8 glomeruli of the bridge, the angular difference in phase estimates between the left- and right-bridge activity should be +67.5° if it follows the EPG indexing (panel b) and +90° if it follows the Δ7 indexing (panel d). We found that the average angular difference in both PFN_ds and PFN_vs is intermediate between +67.5° and +90°, consistent with PFNs receiving functional inputs from both EPGs and Δ7s. We use the angular offsets measured in this panel as the basis for slightly adjusting the PFN_d and PFN_v angular indices in the bridge to an intermediate value between the EPG and Δ7 indexing options, described above. We believe that this approach represents the most careful way to combine the known anatomy and physiology to determine the azimuthal angle that each PFN cell signals with its activity in driving the hΔB neurites in the fan-shaped body, which we analyze in the next figure. j, Angles assigned to each bridge glomerulus for PFN_ds, based on the EPG indices from panel b and the physiologically determined adjustment required, based on the measurements in panel i. k, Same as panel j, but for PFN_vs.

Extended Data Figure 6 |. Computing the angular shift implemented by the PFN-to-hΔB connections.

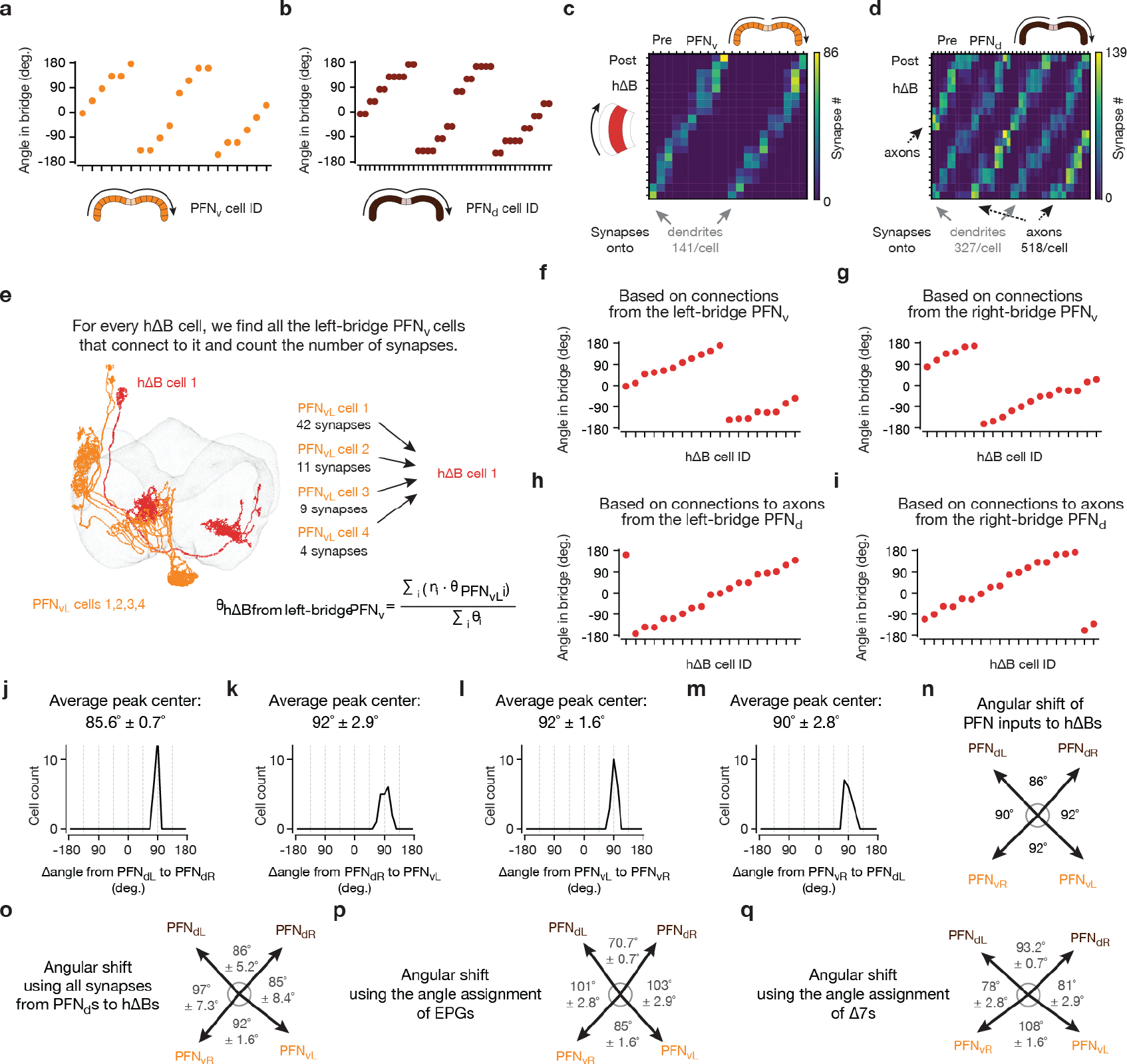
Connectivity data and cell-type names are based on those in neuPrint¹⁷, hemibrain:v1.1. a, The anatomical angle of each PFN_v cell is indicated based on which glomerulus it inervates in the protocerebral bridge, using the indexing described in Extended Data Figure 5k. b, Same as panel a, but for PFN_ds, using the indexing described in Extended Data Figure 5j. c, Synapse-number matrix for detected synapses from PFN_v cells to hΔB cells in the fan-shaped body. Note that the two stripes in the heatmap represent PFN_vs synapsing onto the dendritic regions of hΔBs. d, Same as panel c, but for synapses from PFN_d cells to hΔB cells. Note that two of the five stripes in the heatmap represent PFN_ds synapsing onto the dendritic regions of hΔBs, whereas the other, brighter, three stripes represent PFN_ds synapsing onto the axons of hΔBs. The average # of synapses that each hΔB compartment (axon vs. dendrite) receives from PFN cells is indicated on the bottom. e, Because hΔBs are postsynaptic to both PFN_vs and PFN_ds that project to the fan-shaped body from both sides of the bridge (panel c-d), each hΔB cell can be assigned an anatomical angle in four potential ways. To calculate the angle for an hΔB cell through its connection with the left-bridge PFN_vs, for example, we averaged the anatomical angles of all the left-bridge PFN_vs that connect to the hΔB cell in question, weighted by the number of synapses from that PFN_v cell to the hΔB cell. f, The anatomical angle of each hΔB cell calculated based on its monosynaptic inputs from left-bridge PFN_vs using the method described in panel e and data in panel c. g, Same as panel f, but calculations were made with right-bridge PFN_v inputs to hΔBs. h, Same as panel f, but calculations were made with left-bridge PFN_d inputs to hΔBs, using only the synapses formed on the axonal terminals of hΔBs. (We test the impact of this assumption––of complete functional dominance of PFN_d axonal synapses to hΔBs––below.) i, Same as panel f, but calculations were made with right-bridge PFN_d inputs to hΔBs, using only axonal synapses. j, For each hΔB cell, we calculated the angular difference between the mean left-bridge PFN_d input and the mean right-bridge PFN_d inputs (i.e., the difference between data points in panels h and i) and we plot a histogram of those values. k-m, same as j for the cell types indicated. n, The anatomically predicted angles for the coordinate axes of the four PFN vectors, as projected to the fan-shaped body and interpreted by hΔB axons and dendrites, calculated by averaging the histogram values in panels j-m, respectively. o, Same as panel n, but including all synapses from PFN_ds to hΔBs, not just the axonal ones as in panel n. We weigh dendritic and axonal synapses by PFN_ds to hΔBs equally in the panel-e calculation. Note that the angles between four coordinate-frame axes do not change very much when also including the dendritic synapses from PFN_ds to hΔBs, likely because they are less numerous than the axonal ones and the impact of the dendritic angles also seem to cancel out in their net effect (compare panels o and n). p, Same as panel n, but using the EPG indexing from Extended Data Figure 5 instead of the adjusted PFN_v and PFN_d indexing. Note that the EPG indexing makes the front angle between the left- and right-bridge PFN_d axes smaller. The same is true for the back angle between the left- and right-bridge PFN_v axes. q, Same as panel n, but using the Δ7 indexing from Extended Data Figure 5 instead of the PFN_v and PFN_d indexing. Note that the Δ7 indexing makes the front and back angles broader than 90°, when used in isolation. This analysis suggests that EPG and Δ7 inputs to PFNs are perfectly weighted to create axes that are orthogonal in our experiments in flying flies and also raise the possibility that orthogonality of this 4-vector system can be dynamically modulated via changing the weights of EPG and Δ7 inputs to PFNs (see Supplemental Text).

Extended Data Figure 7 |. PFR neurons track a variable similar to allocentric traveling direction in walking and flying flies.

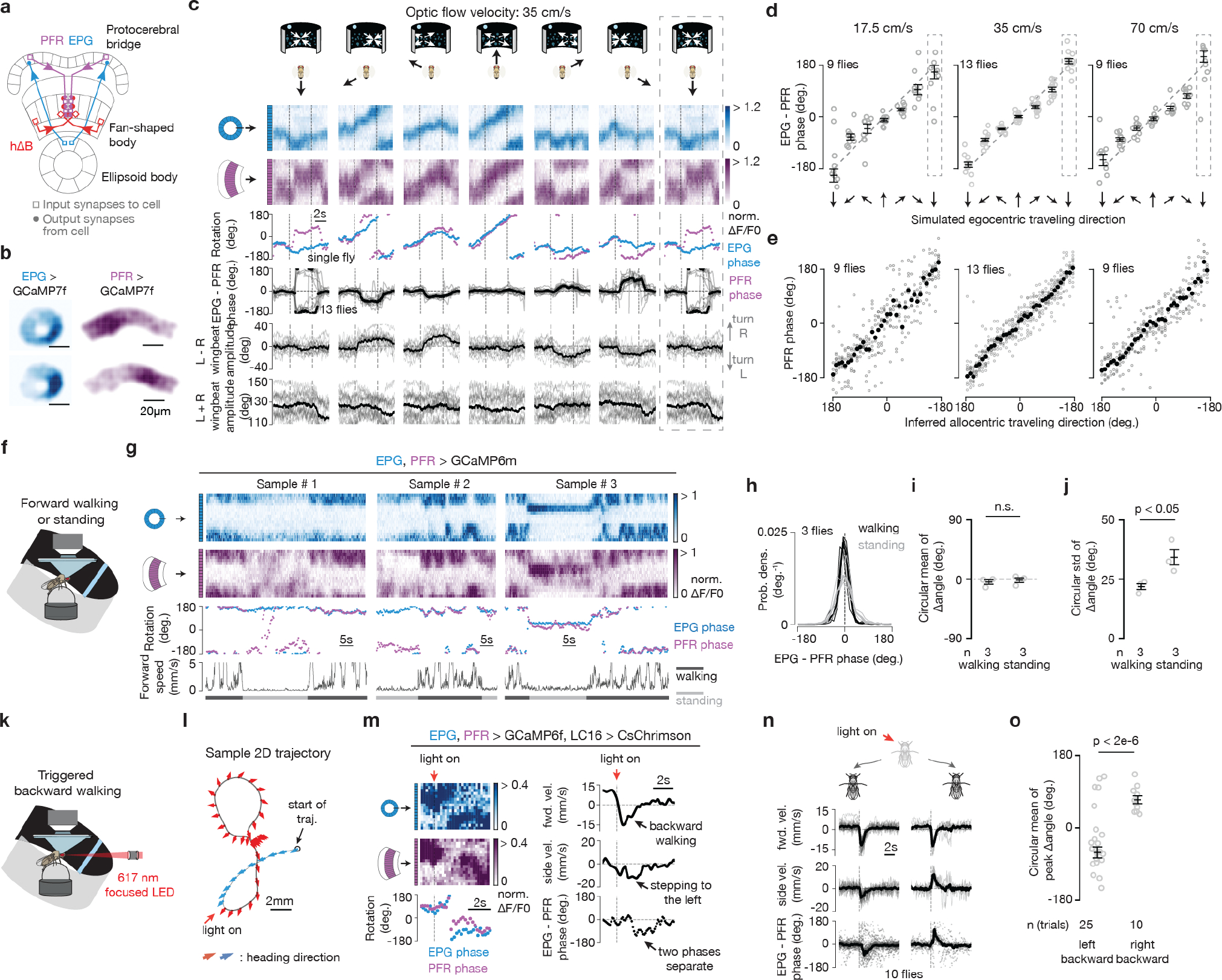
a, Schematics of two example EPG cells, two example PFR cells and two example hΔB cells, which are the anatomically dominant input to PFRs. b, Sample GCaMP7f frames of the EPG bump in the ellipsoid body and the PFR bump in the fan-shaped body. c, Top, EPG (blue) and PFR (purple) GCaMP7f signal in a tethered, flying fly experiencing optic-flow (in the time window bracketed by the vertical dashed lines) with foci of expansion that simulate the following directions of travel: 180° (backward), −120°, −60°, 0° (forward), 60°, 120°, 180° (backward; repeated data). Third row, EPG and PFR phases extracted from the above [Ca²⁺] signals. Fourth row, circular-mean phase difference between EPGs and PFRs. Bottom two rows, average of left-minus-right and left-plus-right wingbeat amplitude. Single fly means: light gray. Population means: black. Dotted rectangle indicates a repeated-data column. d, EPG – PFR phase as a function of the egocentric traveling direction simulated by the optic flow, at three different speeds. Circular means were calculated in the last 2.5 s of optic flow presentation. Gray: individual fly circular means. Black: population circular mean and s.e.m. Dotted rectangle indicates a repeated-data column. (See Methods for how we calculate the optic flow speed.) Note that the data points deviate slightly from the unity line in a manner that means that the PFR phase is slightly shifted away from the traveling direction indicated by the optic flow and toward a frontal heading direction. The hΔB data in Figure 1h does not show this deviation from unity. We performed two-tailed one-sample t-tests against the diagonal line for data points in the ±60° and ±120° columns for the 35 cm/s data from PFRs here and the 35 cm/s data from hΔBs in Figure 1h. For the PFR results on the left of panel d, P values are 4.7e-5, 4.7e-5, 5.4e-4 and 9.1e-3 for the −120°, −60°, +60° and +120° columns, respectively. For the hΔB results in Figure 1h, P values are 0.39, 0.88, 0.058 and 0.44 for the −120°, −60°, +60° and +120° columns, respectively. e, PFR phase as a function of the inferred allocentric traveling direction, calculated by assuming that the EPG phase indicates allocentric heading direction and adding to this angle, at every sample point, the optic-flow angle. Gray: individual fly means. Black: population mean. In panel d and e, data from the middle column (35cm/s) were the same as in panel c. f, Tethered, walking, [Ca²⁺]-imaging setup with a bright blue bar that rotates in closed loop with the fly’s turns. g, Sample time series of simultaneously imaged EPG and PFR bumps in a tethered, walking fly. Top two traces show [Ca²⁺] signals. Third trace shows the phase estimates of the two bumps. Bottom trace shows the forward speed of the fly. h, Probability distributions of the EPG – PFR phase in walking and standing flies. Thin lines: single flies. Thick line: population mean. i, Circular mean of the EPG – PFR phase in walking and standing flies. WatsonWilliams multi-sample tests, P>0.63 when comparing any experimental group with 0°. Gray dots: single fly values. Black bars: population means ± s.e.m. j, Same as panel i, but plotting circular standard deviation. Two-tailed unpaired t-tests were performed. P value equals 0.042. k, Tethered-walking setup where we used a 617 nm LED focused on the center of the fly’s head to optogenetically trigger backward walking via activation of LC16 visual neurons expressing CsChrimson⁴⁷ (Methods). l, An example 2D trajectory of optogenetically triggered backward walking. An arrow is shown every ~0.1 seconds. Red arrows indicate backward walking during the red-light pulse; blue arrows indicate the 1.2 s before the red light turned on. m, Left, time series of EPG (blue) and PFR (purple) bumps and phase-estimates from the trajectory in panel l. Right, time series of forward velocity, sideslip velocity and the difference between the PFR and EPG phase in the trajectory shown in panel l. The ΔF/F heatmap range is more compressed here than in other plots because the PFR signal strength typically dips when the fly initiates backward walking (a phenomenon whose mechanism we have not yet explored). Nevertheless, clear moments where the PFR phase separates from the EPG phase are evident, even after the PFR signal strength has recovered, in this sample trace (and in others). n, Time series of the mean forward velocity, mean sideslip velocity and the circular mean of the difference between the PFR and EPG phase during backward walking, grouped by optogenetic trials in which the fly walked to the back left (left panel) or to the back right (right panel). The sign of PFR-EPG phase deviations seen here, in walking, are consistent with the signs observed in flight, for the same directions of backward-left and backward-right travel. Thin lines and gray dots: individual trials. Thick line and black dot: population mean (circular mean for bottom row). o, Circular mean and s.e.m. of the peak EPG – PFR phase during triggered left-backward and right-backward walking bouts (0.6 s to 1.4 s after the dashed lines in panel n). Watson-Williams multi-sample tests were performed and P value equals 1.6e-6.

Extended Data Figure 8 |. Response-tuning in PFN, PFR and hΔB neurons to the translation speed indicated by our optic-flow stimuli.

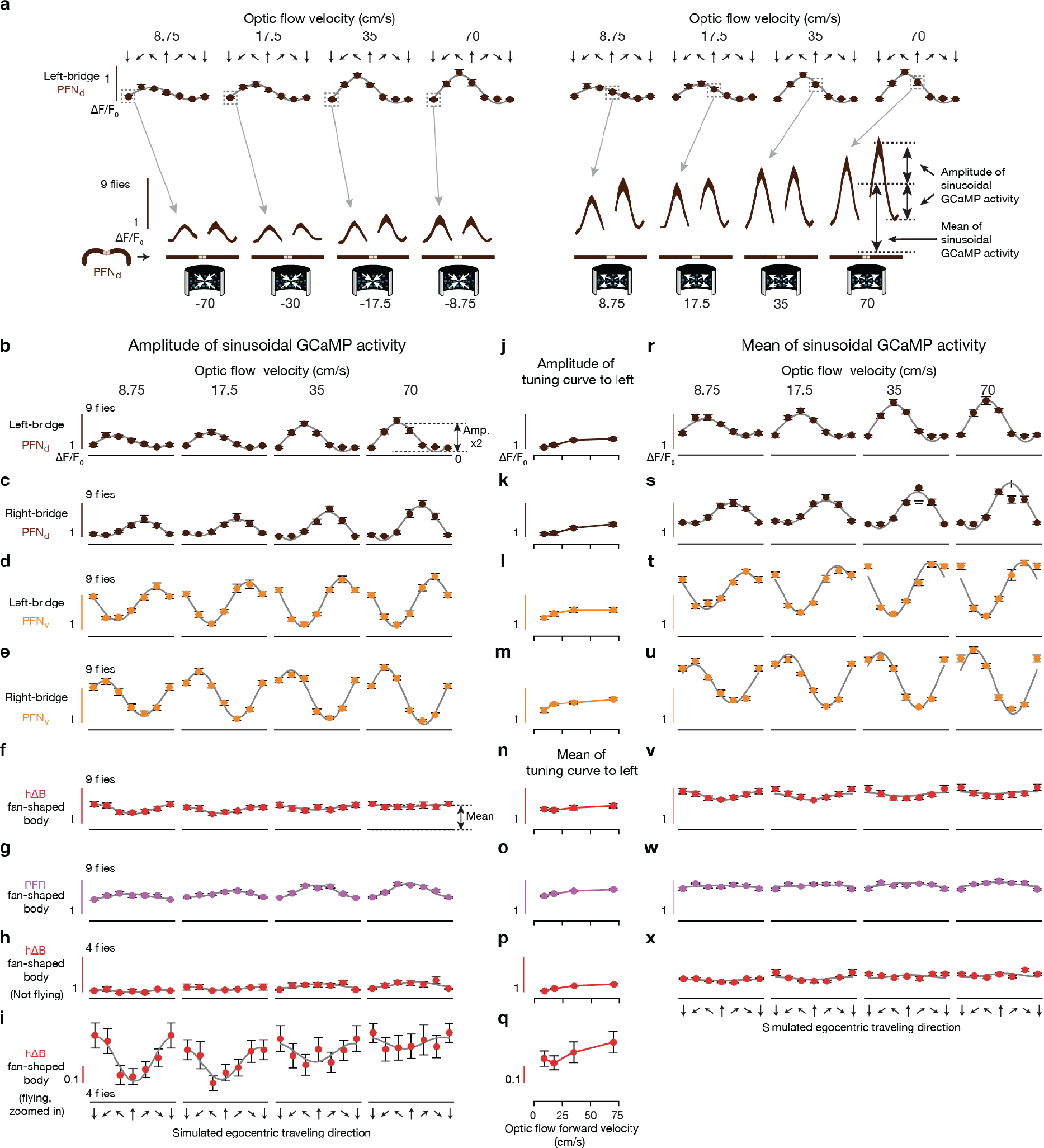
a, Bottom row: phase-nulled PFN_d GCaMP activity across the bridge, averaged in the final 2.5 s of the optic flow epoch. We show responses to optic flow simulating traveling backward at four different speeds (left) and responses to optic flow simulating forward travel at four different speeds (right). The mapping between bridge [Ca²⁺] signals and data points in the plots in subsequent panels is indicated (arrows) for a few example points, using measurements from left-bridge PFN_ds, as an example. How we calculate the mean and amplitude of each bump is schematized. b, The population-averaged amplitude of the phase-nulled left-bridge PFN_d [Ca²⁺] activity in the final 2.5 s of the optic flow epoch, plotted as a function of the egocentric traveling direction simulated by the optic flow. The translational speed of optic flow increases across the four columns, from left to right. Gray lines: sinusoidal fits. S.e.m. are shown in this panel and throughout. c, Same as panel b, but analyzing the right-bridge PFN_d activity_. d, Same as panel b, but analyzing the left-bridge PFN_v activity_. e, Same as panel b, but analyzing the right-bridge PFN_v activity_. f, Same as panel b, but analyzing the hΔB activity in the fan-shaped body_. g, Same as panel b, but analyzing the PFR activity in the fan-shaped body. h, Same as panel b, but analyzing the hΔB activity in the fan-shaped body in non-flying flies. i, Same as panel f, but with a more zoomed-in y-axis. j, Amplitude of the four sinusoids in panel b to indicate how PFN_d responses, overall, scale with optic-flow translation speed. k-m, Same as panel j, but for the plots and cell type shown to the left. Note that the amplitudes of the PFN sinusoidal activity patterns are not only scaled by the traveling direction angle (panel b-e), but also by traveling speed (panel j-m). These plots make sense as a way to quantify the amplitude of sinusoidally modulated responses, like those of PFNs, but we also show, for completeness, the results of the same analysis for hΔBs and PFRs, where this way of quantifying forward-speed tuning makes less sense. n, Mean of the four sinusoids in panel f to indicate how hΔB responses, overall, scale with optic-flow translation speed. o, Same as panel n, but for the PFR plots shown to the left. p, Same as panel n, but for the hΔB plots shown to the left. Note that response-scaling with speed in hΔBs and PFRs was not consistent across all traveling directions (panels f-h). The fact that the speed tuning of hΔBs remains nonuniform across traveling directions in non-flying flies (panel h) suggests that this nonuniform tuning is not entirely due to an efference copy/proprioceptive signal being mismatched with backward optic-flow directions in tethered flight, though the interpretation of this nonuniform tuning will need to be resolved in future work. q, Same as panel n, but for the hΔB plots shown to the left. r, Same as panel b, but analyzing the mean (rather than the amplitude) of the left-bridge PFN_d [Ca²⁺] activity patterns. Gray lines: same sinusoidal fits from panel b with a vertical offset and a scale factor that is constant across all four speeds. The fact that our amplitude fits from panel b also fit the mean responses shown here well supports the hypothesis that the heading input and the optic-flow input to PFN cells are integrated multiplicatively (see Methods). s-x, Same as panel r, but analyzing the cell type indicated on the left side of the figure, for each row. See Methods for how the optic-flow speed was calculated.

Extended Data Figure 9 |. The neural circuit described in this paper implements an egocentric-to-allocentric coordinate transformation.

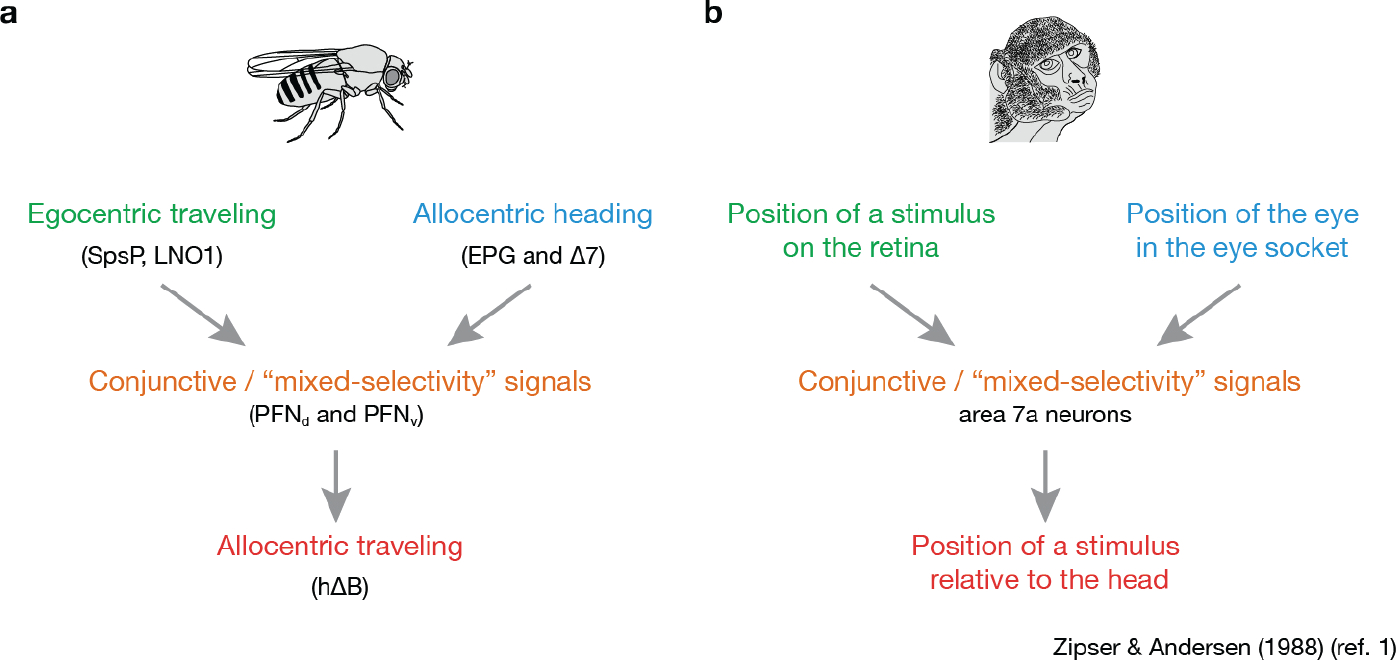
a, Schematic of the computation implemented in the Drosophila central complex. Traveling-direction signals referenced to the body axis (i.e., optic flow signals in SpsP and LNO1s, which indicate the egocentric traveling angle, green) are converted into traveling-angle signals referenced to cues in the world (i.e., the hΔB bump position, which indicates allocentric traveling angle, red). b, Schematic of a very similar computation hypothesized to take place in monkey parietal cortex.

Extended Data Figure 10 |. A traveling-direction signal computed via optic flow is robust to changes in the yaw angle of the fly’s head.

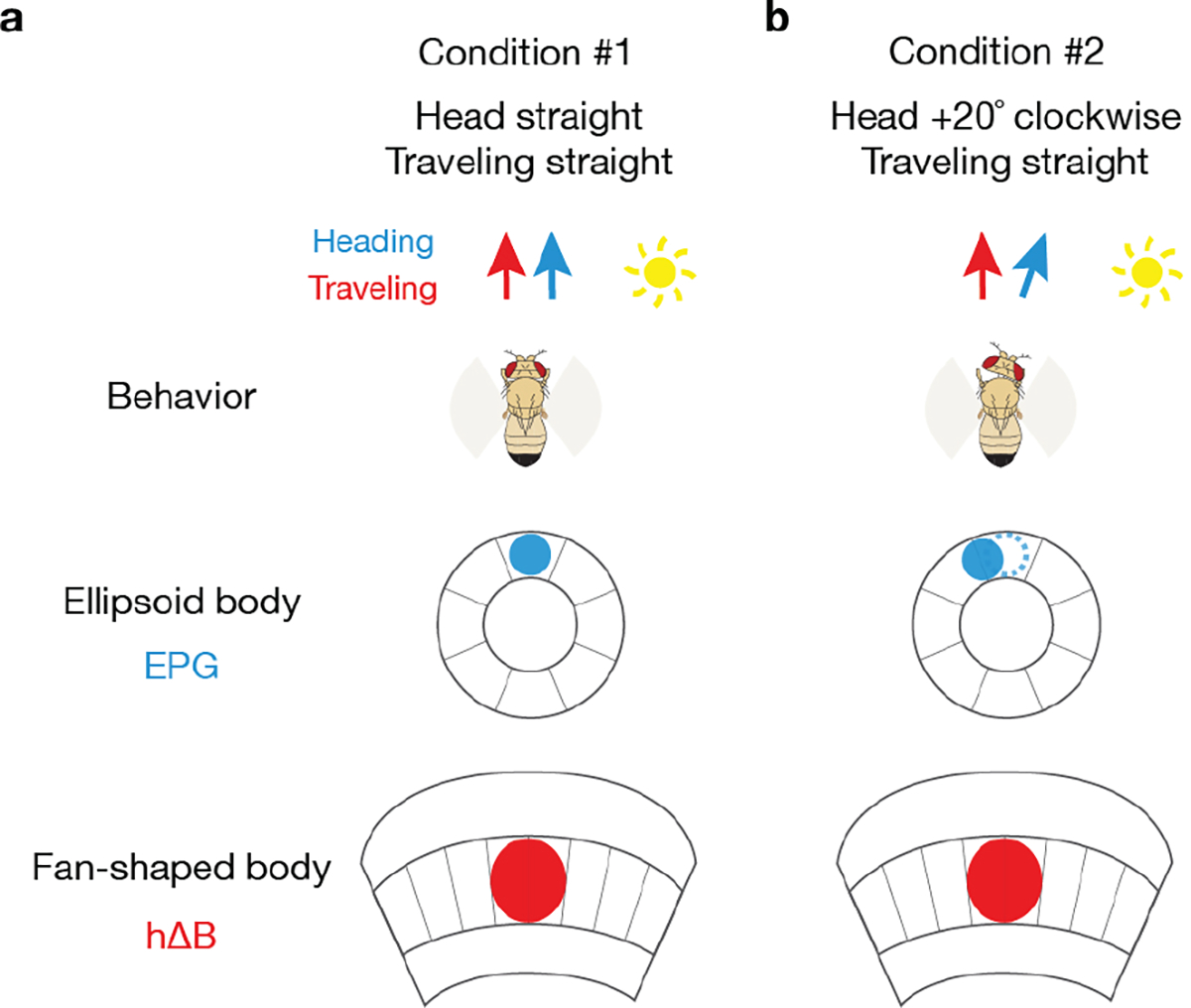
a, Fly flying straight with the head aligned to the body axis. EPG and hΔB signals are aligned in the ellipsoid body and fan-shaped body, respectively. b, Fly flying straight forward with the head rotated 20° to the right. The EPG bump––assuming the EPG bump position tracks the fly’s head (rather than body) direction––will rotate 20° counterclockwise. The hΔB bump, however, will remain pointing in the same allocentric traveling direction because the net effect of the EPG bump rotating 20° in one direction and the ego-motion signal from optic flow (not represented in the diagram) rotating 20° in the opposite direction is that the PFR/hΔB bump stably indicates the same traveling direction throughout.

Data availability

Data for all of the main Figures are available on Dropbox (https://www.dropbox.com/sh/p8bqwavlsyl9ppv/AABz2-vda4Q3gukXqp8Ba2Gwa?dl=0). Other data are available upon request.