Personalized analysis of human cancer multi-omics for precision oncology

Abstract

Multi-omics technologies, encompassing genomics, proteomics, and transcriptomics, provide profound insights into cancer biology. A fundamental computational approach for analyzing multi-omics data is differential analysis, which identifies molecular distinctions between cancerous and normal tissues. Traditional methods, however, often fail to address the distinct heterogeneity of individual tumors, thereby neglecting crucial patient-specific molecular traits. This shortcoming underscores the necessity for tailored differential analysis algorithms, which focus on particular patient variations. Such approaches offer a more nuanced understanding of cancer biology and are instrumental in pinpointing personalized therapeutic strategies. In this review, we summarize the principles of current individualized techniques. We also review their efficacy in analyzing cancer multi-omics data and discuss their potential applications in clinical practice.

1. Introduction

The investigation of human cancer using multi-omics methodologies has emerged as a pivotal area of research, seeking to elucidate cancer mechanisms by integrating diverse biological dimensions. This approach merges data from genomics, epigenomics, transcriptomics, and proteomics to forge a comprehensive molecular portrait of cancer [1]. Genomic analysis focuses on DNA alterations, including mutations and copy number variations, primarily utilizing whole-genome sequencing [2]. Epigenomic research delves into DNA methylation and histone modifications, shedding light on gene regulation [3]. Transcriptomics examines RNA transcripts to reveal gene expression patterns, predominantly through RNA sequencing [4]. Proteomics, employing methods such as mass spectrometry, examines the complete protein set in a sample, thus reflecting the actual functional molecules [5].

Differential analysis is one of the most commonly performed tasks for multi-omics data. Currently, most of these methods were designed for the population-level, offering insights into variances between distinct groups such as tumor and normal samples. The T-test [6] is a statistical method utilized for hypothesis testing to detect differences between continuous data that are approximately normally distributed and have equal variances. DESeq2 [7] identifies differentially expressed genes using a negative binomial distribution model, necessitating biological replicates in the experimental samples to ensure result accuracy. Similarly, edgeR [8] also applies a negative binomial distribution model to identify differentially expressed genes. It accounts for variance in gene expression levels to calculate normalized expression values for each gene across various sample groups.

However, conventional population-level analysis methods often overlook the heterogeneity unique to individual tumors, thereby neglecting patient-specific molecular traits. Therefore, several studies have shifted their focus towards the heterogeneity and individual differences among patients, leading to the development of individualized differential analysis techniques.

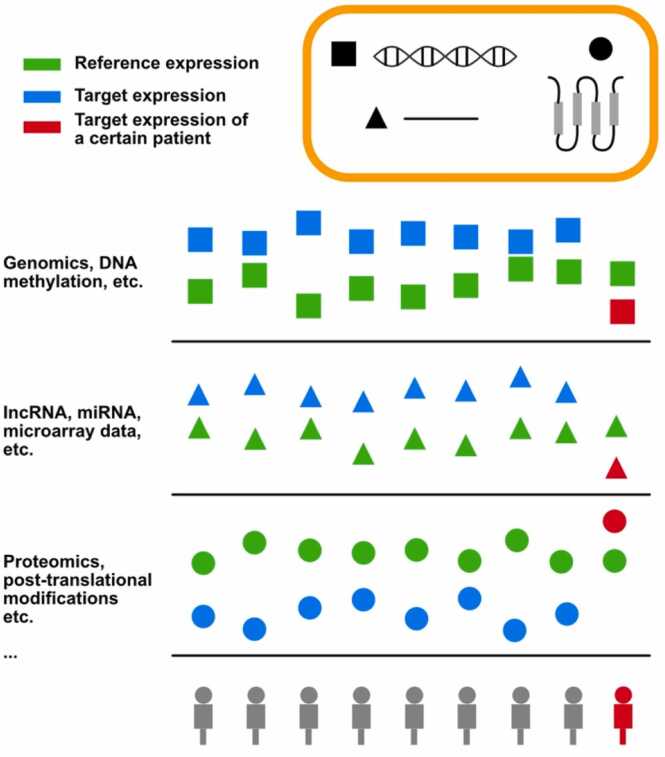
Individualized differential analysis methods are initially designed to identify sample-specific deregulated genes. The assumption of these methods is that the relative expression orderings (REOs) of gene pairs remain consistent in normal tissue types, yet are susceptible to disruptions in diseased tissues. REOs demonstrate robustness, rendering them insensitive to batch effects. By assessing the reversal of REOs in individual diseased samples, personalized analysis effectively identifies differentially expressed genes critical for precision medicine (Fig. 1).

Fig. 1.

Overview of individualized analysis methods for human cancer multi-omics.

Research demonstrates that such personalized tools, encompassing mRNA, miRNA, lncRNA, and proteins, are superior in computational precision and clinical relevance [9], [10], [11], [12], [13], [14]. For instance, Liu et al.'s study in proteomics across various cancers, including lung, gastric, and liver cancer, underscores the superiority of individualized methods in precisely identifying dysregulated proteins over population-level analysis [12]. This review elucidates the principles of various individualized differential analysis methods, summarizing their performance in cancer multi-omics data analysis and their applications in cancer research.

2. Overview of individualized differential analysis methods

2.1. RankCompV1 and RankCompV2

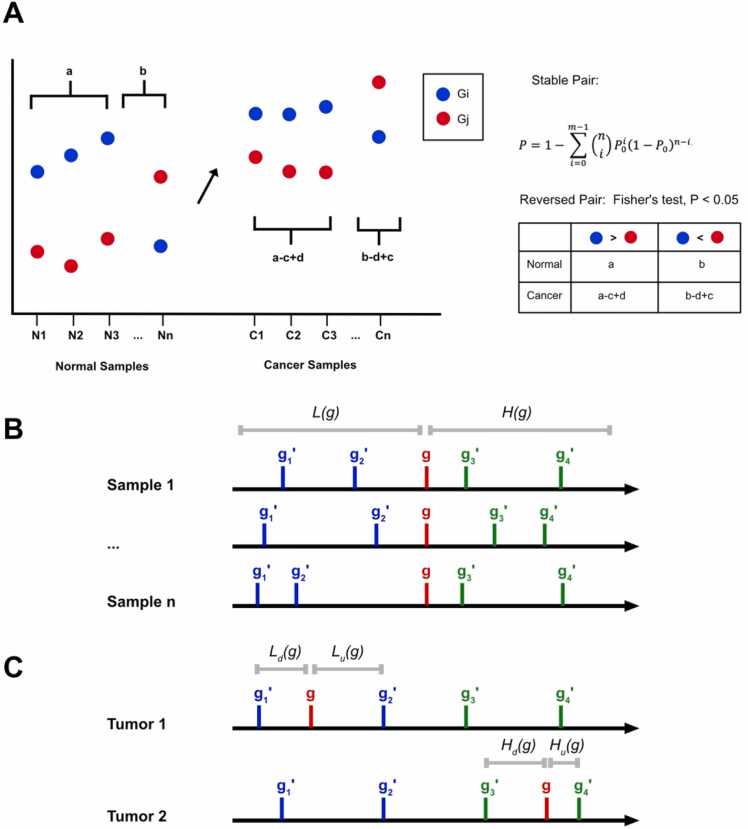
RankCompV1 [13] and RankCompV2 [11] initiate their processes by identifying highly stable gene pairs within normal samples. Subsequently, using the relative rank order of these stable gene pairs in normal samples as a baseline, RankCompV1 and RankCompV2 identify differentially expressed genes distinguished by reversed rankings (Fig. 2A).

• (1)
  Selection of highly stable gene pairs in normal samples: Gene expression data are ranked based on the expression values, with genes having higher values receiving higher ranks, and vice versa for those with lower values. For a specific gene, i (G_i), there are two potential rank order relationships with its partner gene G_j: either G_i > G_j or G_i < G_j. The significance of these relationships is assessed using a P-value derived from the cumulative binomial distribution:

  $$P=1-\sum _{i=0}^{m-1}\left(\genfrac{}{}{0ex}{}{n}{i}\right)P_0^i{\left(1-P_0\right)}^{n-i}$$

  In the formula, 'n' denotes the number of normal tissue samples, while 'm' represents the number of samples exhibiting a specific rank order (G_i > G_j or G_i < G_j). The probability P₀ represents the likelihood of a particular rank order (G_i > G_j or G_i < G_j) occurring randomly in normal samples, which is set at 0.5. The P value is adjusted using the Benjamini-Hochberg method. If the adjusted P value is below a predefined threshold, such as 0.05, the gene pair with this rank order is considered a highly stable gene pair in the normal tissue sample.

• (2)Identification of differentially expressed genes in disease samples: A gene pair is classified as reversed if its ranking in a disease sample is the opposite of its ranking in the highly stable gene pairs identified in normal samples. The presence of a reversed gene pair, compared to a stable pair in normal samples, implies abnormal expression of at least one gene in the pair. The number of cases where G_i > Gj in normal samples is denoted as 'a', while the instances of G_i < G_j are denoted as 'b'. In a specific disease sample, 'c' represents the number of gene pairs that transition from Gi > Gj to Gi < Gj, while 'd' represents the reversals from G_i < G_j to G_i > G_j. If ‘c′ exceeds ‘d′, gene Gi is considered down-regulated in the disease sample; conversely, if 'c' is less than 'd', Gi is considered up-regulated. The statistical significance of these findings is determined using the Fisher test, with the null hypothesis defined as a / (a - c + d) = b / (b - d + c). A p-value below 0.05 leads to the rejection of this hypothesis, indicating a significant up-regulation or down-regulation of gene G_i in the disease sample compared to its expression in normal samples.
• (3)Identification of differential genes in gene pairs: The change in rank order of genes in disease samples may stem from imbalances in gene pairs. Thus, it is essential to alleviate the effects of expression level alterations in these gene pairs. After the initial steps, if the partner gene of gene G_i is identified as a differential gene and its imbalance direction conflicts with that of G_i, this pair of genes is eliminated. Following this, a secondary Fisher test is carried out, which provides the conclusive result for gene G_i.

Fig. 2.

RankComp and Penda methods for individualized analysis. (A) Detection of stable and reversed pairs in RankComp. (B, C) Defining gene lists using the Penda method.

The first three stages of RankCompV2 closely resemble those of RankCompV1, with the key difference lying in the iterative filtering process used in the final stage. In this stage, when a differential gene is identified as the partner gene of gene G_i, the corresponding gene pair - consisting of gene G_i and its partner - is promptly excluded from the reference set. Subsequently, both stable and reversed gene pair counts in normal and diseased samples are recalculated. A Fisher test is then carried out, and this recalculation and testing process continues until the counts of differential genes in the two comparative analyses converge. This convergence point is then established as the definitive criterion for judgment. It is worth noting that RankCompV2 represents a significant enhancement in statistical efficiency compared to RankCompV1.

2.2. Peng

This method enables the identification of differentially expressed long non-coding RNAs (lncRNAs) in individual cancer patients[9]. In step 1, similar to the RankComp method, the absolute expression data of lncRNAs is transformed into a rank spectrum. Using lncRNA-A as an example (Supplementary Figure 1A), a stable pair for lncRNA-A is observed in over 95% of the normal samples. Subsequently, in the cancer samples, the reversed pair of lncRNA-A is identified. The significance of both stable and reversed pairs is then assessed using the Fisher exact test.

In step 2, only the partner lncRNAs in the cancer sample that show the same directional imbalance as lncRNA-A are retained (Supplementary Figures 1B and 1C). Subsequently, in step 3, the coefficient of variation for the ranking of each partner lncRNA across normal and cancer samples is calculated. If the number of partner lncRNAs is three or more, only the top three lncRNAs with the smallest coefficient of variation are kept. Conversely, if there are fewer than three partner lncRNAs, all of them are retained (Supplementary Figure 1D). Finally, in the last step, lncRNA-A is deemed differentially expressed in a patient sample if more than half of its associated lncRNA pairs with reversed directional imbalance are detected in that patient (Supplementary Figure 1E).

2.3. PenDA

In the PenDA method[10], each gene g is associated with two distinct gene lists based on their ranks relative to gene g: H(g) for higher-ranking genes and L(g) for lower-ranking genes. The rank order of both H(g) and L(g) must remain consistent with at least 99% of normal samples with gene g. To ensure comparability among genes with similar expression levels and to improve the PenDA method’s sensitivity, H(g) and L(g) are limited to a subset of l genes whose expression levels closely resemble that of gene g in the normal control sample. The median expression of this subset is chosen for its proximity to the median expression of gene g in the normal sample. The user-defined parameter l regulates the size of the gene lists H(g) and L(g) (Fig. 2B).

In a specific cancer sample T, the PenDA method conducts an iterative individualized differential analysis. The subsequent description outlines the steps undertaken by PenDA to identify differentially expressed genes.

• (1)
  Each gene g’s expression level in cancer sample T is denoted as E(g, T) and compared with genes in the H(g) and L(g) lists. This comparison results in the generation of four distinct and non-overlapping gene set lists (Fig. 2C):

  $${\mathrm{L}}_{\mathrm{d}}=\{{\mathrm{g}}^{\prime }\in \mathrm{L}\left(\mathrm{g}\right)\mathrm{\mid }\mathrm{E}\left({\mathrm{g}}^{\prime },\mathrm{T}\right)<\mathrm{E}\left(\mathrm{g},\mathrm{T}\right)\}$$

  $${\mathrm{L}}_{\mathrm{u}}=\{{\mathrm{g}}^{\prime }\in \mathrm{L}\left(\mathrm{g}\right)\mathrm{\mid }\mathrm{E}\left({\mathrm{g}}^{\prime },\mathrm{T}\right)>\mathrm{E}\left(\mathrm{g},\mathrm{T}\right)\}$$

  $${\mathrm{H}}_{\mathrm{d}}=\{{\mathrm{g}}^{\prime }\in \mathrm{H}\left(\mathrm{g}\right)\mathrm{\mid }\mathrm{E}\left({\mathrm{g}}^{\prime },\mathrm{T}\right)<\mathrm{E}\left(\mathrm{g},\mathrm{T}\right)\}$$

  $${\mathrm{H}}_{\mathrm{u}}=\{{\mathrm{g}}^{\prime }\in \mathrm{H}\left(\mathrm{g}\right)\mathrm{\mid }\mathrm{E}\left({\mathrm{g}}^{\prime },\mathrm{T}\right)>\mathrm{E}\left(\mathrm{g},\mathrm{T}\right)\}$$
• (2)
  A gene g is categorized as a dysregulated gene in cancer sample T only if it meets the specified conditions:

  $$\left(\frac{\left|L_u\right|}{\left|L\right|}\ge h\right)\vee \left(\frac{\left|H_d\right|}{\left|H\right|}\ge h\right)$$

  The cardinality of set L is denoted as |L|, and h represents a user-defined threshold determining the minimum proportion of genes in either H(g) or L(g) needed to change their relative position in comparison to gene g. Gene g is considered down-regulated in cancer sample T if the ratio |L_u|/|L| is greater than or equal to h, and the sum of |L_d| and |H_d| is less than |L|. Conversely, gene g is classified as up-regulated in cancer sample T if the ratio |H_d|/|H| is greater than or equal to h, and the total count of |L_u| and |H_u| is less than |H|. If either the L or H list is empty, the Percentile method, which will be described subsequently, is used to verify the dysregulation of gene g in the cancer sample T.

• (3)To prevent misunderstanding gene g’s dysregulation as a consequence of changes in the relative positions of genes within the H(g) or L(g) lists, rather than being attributed to the inherent dysregulation of gene g, the following approach is proposed: Upon identifying each gene, all previously categorized dysregulated genes are excluded from the H(g) and L(g) sets. Then, the aforementioned steps are repeated iteratively until the list of differentially expressed genes reaches stability.

2.4. Percentile

The Percentile[10] method identifies differentially expressed genes by comparing a gene’s expression level in a test disease sample with its expression in normal reference samples. Specifically, a gene g’s expression value across all normal samples, denoted as E(g, S), is ordered from the lowest to the highest. Subsequently, lower (p_l) and upper (p_u) thresholds are set at the xth and (100-x)th percentiles of the distribution of E(g, S), respectively, where x represents a user-defined percentage (Supplementary Figure 2A). Within a specific cancer sample T, E(g, T) represents the expression level of gene g. If E(g, T) is lower than p_l divided by a factor f, gene g is classified as down-regulated; if E(g, T) exceeds p_u multiplied by f, the gene is classified as up-regulated. The parameter f, which must be equal to or greater than 1, is also user-defined (Supplementary Figure 2B). However, the Percentile method is criticized for its lack of rigorous statistical control and increased subjectivity resulting from the use of arbitrarily determined thresholds.

2.5. DEGdriver

DEGdriver [15] is an innovative approach that identifies driver mutations by examining differential gene expression at the individual level. This method effectively distinguishes between driver genes and passenger genes by utilizing information from protein-protein interaction networks.

2.6. Comparison of five individualized analysis methods

We conducted a brief comparison of five individualized analysis methods, as presented in Table 1. The initial steps for RankCompV1, RankCompV2, and Peng involve the transformation of actual expression quantifications into relative expression orders. RankComp sets itself apart by utilizing a binomial distribution test to evaluate the significance of relationships, while Peng, originally developed for lncRNA data analysis, utilizes Fisher’s exact test to assess relative expression orders. RankCompV2 introduces an iterative filtering step absent in RankCompV1. PenDA enhances the detection sensitivity for differences by employing a comprehensive algorithm that calculates the change proportions in four gene sets associated with the target gene. In contrast, Percentile provides a simple and intuitive method, based on the deviation of gene expression levels in targeted disease samples from those in normal samples.

Table 1.

Comparisons of individualized differential analysis methods.

Method	Url	Principle and advantage	Limitation	References
RankCompV1/2	https://github.com/pathint/reoa	Identification of highly stable gene pairs; Iterative filtering of partner differential genes	Time consuming and memory consumption	Wang, H., et al.[13]; Cai, H., et al. [11]
Peng	https://github.com/FuduanPeng/LncRIndiv	Based on coefficient of variation (CV)	Low accuracy	Peng, F., et al. [9]
Penda	https://github.com/bcm-uga/penda	Based on the local ordering of gene expressions within individual cases; Improved sensitivity	Dependence on parameter settings; Sensitivity to differences in gene expression levels	Richard, M., et al. [10]
Percentile	https://github.com/bcm-uga/penda	Simple and intuitive; Suitable for rapid screening	Without statistical significance; Sensitivity to outliers	Richard, M., et al. [10]

3. Assessment of the performance of individualized differential analysis methods

3.1. Feasibility analysis

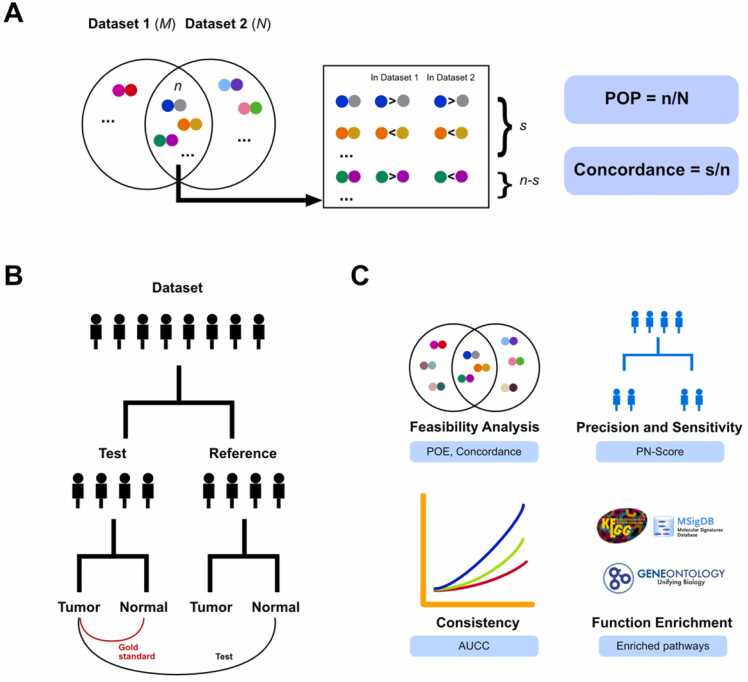
Before applying individualized analysis methods to diverse cancer omics datasets, it is essential to validate the foundational principles of these methods. The individualized analysis algorithm is primarily grounded on the concept of stable pairs identified in normal samples. To assess the reproducibility of these stable pairs across independent datasets, two metrics are utilized: the Percentage of Overlapping Pairs (POP) and Concordance. Assuming there are M and N stable pairs in two datasets, with n pairs common to both. If the relative order of s pairs remains consistent among these n overlapping pairs across both datasets, then the POP is calculated as n/N, and Concordance is determined by s/n (Fig. 3A).

Fig. 3.

Assessing the performance of individualized differential analysis methods. (A) Reproducibility of stable pairs in two independent datasets: POP and concordance analysis. (B) Establishing a gold standard for precision evaluation. (C) Step-by-step overview of performance evaluation.

3.2. Precision and sensitivity

To evaluate the precision of each differential analysis method, directional discrepancies in gene expression between cancer samples and their paired normal samples were established as the gold standard (Fig. 3B). Samples in each dataset are evenly split into a test group and a reference group, both containing an equal number of samples. The reference group, consisting of normal samples, functions as controls to identify differentially expressed genes in the cancer samples of the test group. Various differential analysis methods are employed for this identification. Subsequently, normal tissue samples paired with cancerous tissues in the test group are utilized for comparison. The gene expression patterns in these normal samples adjacent to the cancer set the standard for gene regulation direction. A gene is categorized as showing a positive differential direction if its expression is higher in cancer than in the corresponding normal sample, and negative if the expression is lower. The performance of each differential analysis method is then assessed against this standard using the following precision formula:

$\text{Precision}=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}}$

Precision in differential analysis methods denotes the accuracy with which these methods identify differentially expressed genes. TP (True Positives) represents genes correctly identified as differentially expressed and match the directional difference indicated in the gold standard. Conversely, FP (False Positives) are genes mistakenly labeled as differentially expressed, showing a directional difference that conflicts with the gold standard.

In addition to assessing precision, the total count of differentially expressed genes determined by a differential analysis method plays a crucial role, highlighting the sensitivity of the method. The PN score, which acts as a weighted harmonic mean of both precision and the number of differentially expressed genes, provides a comprehensive evaluation of both the method’s accuracy and the scope of gene identification. The formula for calculating the PN score is presented below:

$$\mathit{PN}-\mathit{score}=\left(1+{\mathrm{\beta }}^2\right)*\frac{\text{Precision}*\text{Number}}{{\mathrm{\beta }}^2*\text{Precision}+\text{Number}}$$

The PN score quantifies the effectiveness of a differential analysis method, with Precision indicating the method’s accuracy in detecting differentially expressed genes, and Number representing the percentage of such genes identified by the method relative to the total gene count. The parameter β functions as a weighting factor, balancing the significance of accuracy with the number of identified differentially expressed genes.

The precision and sensitivity of different differential analysis methods are affected by the quantity of normal tissue samples utilized. This is due to the reliance of these methods on the expression values and the relative gene order within these samples. Therefore, determining the optimal number of normal samples is essential for enhancing the effectiveness of individualized analysis algorithms.

3.3. Consistency

To evaluate the consistency of differentially expressed genes identified by different individualized analysis algorithms, it is essential to compare these algorithms pairwise. The consistency score, as proposed by Liu et al.[12], measures the similarity between the gene sets identified by each algorithm. This is achieved by calculating the intersection of the top k differentially expressed genes for each algorithm, yielding k intersections for each method. This process is conducted for every tumor sample, producing a unique list for each sample that outlines the significant intersections of differential gene expression. These lists contain k intersections each. The mean intersection count is then calculated for each rank across all samples. A consistency curve is plotted, spanning from 1 to k on the x-axis with increments of 1, while the y-axis shows the average intersection count for each k value. The consistency score for two individualized differential methods is determined by calculating the Area Under the Concordance Curve. This score is then normalized by dividing it by k²/2. A normalized score of 1 indicates total alignment between the algorithms, while a score of 0 indicates complete dissimilarity. The standardized consistency score ranges from 0 to 1, reflecting the level of agreement between the methods, where higher scores represent increased consistency and lower scores indicate more significant discrepancies.

3.4. Function enrichment analysis

The gene sets of functional pathways could be downloaded from Gene Ontology[16], Kyoto Encyclopedia of Genes and Genomes[17], and MsigDB[18]. Functional enrichment analysis is usually performed using the following formula:

$$P=\sum _{i=k}^n\left(\genfrac{}{}{0ex}{}{n}{i}\right)P_{\mathit{de}}^i{\left(1-P_{\mathit{de}}\right)}^{n-i}$$

The variable n represents the total number of disease samples, while k indicates the number of samples exhibiting a specific differentially expressed gene. P_de refers to the probability of misclassifying a gene as differentially expressed solely by chance, calculated as the ratio of differentially expressed genes to the total gene count. The p-value is then adjusted using the Benjamini-Hochberg procedure. A p-value less than 0.05 is considered statistically significant, suggesting differential gene expression at the population level.

3.5. Computational cost

The RankComp method documentation specifies that the gene size (number of rows) should not exceed 2097,151, and the sample size (number of columns) should not exceed 255 [11]. However, the computational costs for other methods remain undisclosed. To address this gap, we conducted an assessment of the time required to execute each method on the proteomics dataset, gastric-Ge [19], which consisted of 84 pairs tumor samples. These assessments were conducted on a Linux server, utilizing 10 GB of memory and a single-core CPU. Among the methods evaluated, the Peng method exhibited the highest time requirement, followed by RankComp and PenDA (Table 2).

Table 2.

Time cost of differential analysis methods on gastric-Ge.

Method	RankComp	Penda	Peng	Percentile
Time (Second)	891.28	505.05	67715.05	26.29

3.6. Assessment scheme of individualized methods

We established the fundamental criteria for evaluating the performance of individualized differential analysis methods. Taking the proteomics data of gastric cancer as an example, the first step involves evaluating the robustness of relative expression rankings in normal samples using POP and Concordance metrics across two independent datasets. Subsequently, the precision is determined using the paired tumor-normal tissue group as the gold standard. Ultimately, functional enrichment analysis is used to gain deeper insights into the mechanisms associated with deregulated proteins. The evaluation of consistency among different methods is an optionally subsequent step.

Codes were provided to facilitate the evaluation of individualized analysis methods (https://github.com/Liuliantang223/IDEPA-XMBD).

4. Application of individualized analysis methods on cancer multi-omics

4.1. DNA methylation

The diagnosis and treatment of colorectal cancer (CRC) present a challenge due to its heterogeneity. It is crucial to identify both universal and subtype-specific biomarkers. Yan et al. [20] demonstrated the effectiveness of the RankCompV1 algorithm in identifying stable methylation patterns in normal colorectal tissues and their disruption in CRC tissues. Utilizing datasets from the Gene Expression Omnibus database, RankCompV1 successfully detected numerous differentially methylated CpG sites with a high level of methylation pattern concordance. In a sample of 75 CRC samples from the Cancer Genome Atlas, RankCompV1 identified an average of 4062 differentially methylated CpG sites per sample with 91.34% precision, highlighting its capability to pinpoint both universal and subtype-specific differentially methylated CpG sites in CRC. Key genes such as POU5F1, IRF4, and ADHFE1 demonstrated consistent hypermethylation or hypomethylation patterns in a significant portion of CRC samples and were associated with changes in gene expression. These genes were proposed as critical targets for CRC treatment, given their substantial roles in the pathogenesis and progression of the disease.

4.2. Transcriptomes

Wang, H., et al. [13] evaluated the efficacy of the RankCompV1 algorithm using diverse gene expression datasets. They revealed a notable consistency in the relative expression order of gene pairs across multiple normal tissue samples. RankCompV1 effectively distinguishes genes with varying behaviors in cancerous versus normal samples, displaying increased sensitivity to substantial differences. Nonetheless, this may slightly compromise the algorithm’s error detection capacity. The precision of RankCompV1 in identifying such genes improves with the inclusion of more normal samples, indicating enhanced accuracy with larger datasets. By implementing stringent criteria (99%) for consistent gene pair identification, RankCompV1 minimizes false positives. Moreover, the role of RankCompV1 in identifying differentially expressed genes at both individual and subpopulation levels has been evaluated. The algorithm performs comparably to COPA [21] and outperforms MOST [22] at lower false discovery rates but exhibits reduced effectiveness at higher rates. Additionally, RankCompV1 shows resistance to systematic batch effects.

The Peng method, which is designed to identify differentially expressed lncRNAs in individual cancer patients, has been used to detect prognostic markers in patients with lung adenocarcinoma [9]. To determine the specificity of differentially expressed microRNAs (miRNAs) in particular cancer samples, Yan et al.[14] introduced a novel algorithm, RankMiRNA. This algorithm was evaluated using paired cancer and normal samples, in comparison to stable miRNA expression in normal tissues. In a comparative analysis of RankMiRNA, RankCompV1, and the Peng method in lung and liver cancer samples, RankMiRNA exhibited superior performance, identifying a greater number of differentially expressed miRNAs with higher precision than the Peng method. Conversely, RankCompV1 and the Peng method showed lower efficacy in identifying differentially expressed miRNAs (Supplementary Figure 3A). Furthermore, increasing the number of normal samples improved the performance of RankMiRNA. In their final application, RankMiRNA was utilized to identify has-mir-210 and has-mir-490, which are commonly differentially expressed and correlated with patient survival in lung cancer cases from The Cancer Genome Atlas.

4.3. Proteomes

Liu et al.[12] first applied individualized differential analysis in cancer proteomics by utilizing liquid chromatography-mass spectrometry. Their study revealed a remarkable level of consistency in the Relative Expression Order of stable protein pairs within normal tissue samples, exceeding 99.9% across diverse datasets. This high degree of consistency was maintained even when comparing results obtained through different quantification methods, such as tandem mass tag and label-free techniques. Their research established the feasibility of utilizing stable protein pairs for individual-level analysis of differentially expressed proteins (DEPs). In a comparative evaluation, the PenDA and Percentile methods were identified as the most precise in detecting DEPs, outperforming approaches like RankCompV1/2, Limma, and the t-test. The Peng method exhibited the lowest Type I error rate because of its stringent criteria. On the other hand, conventional methods like the t-test, which failed to consider sample heterogeneity, led to a higher rate of false positives. Notably, the occurrence of false positives in the Percentile method displayed less reliance on mean protein abundance, unlike the PenDA method (Supplementary Figure 3B).

This study also investigated the effect of normal sample size on the performance of DEP detection methods across varied datasets. While the accuracy of DEP detection remained stable regardless of sample size, the number of DEPs identified varied. Methods such as RankComp and the Wilcoxon signed-rank test showed an increased accuracy in DEP identification with larger normal sample sizes, whereas PenDA and the Percentile method exhibited a decreased accuracy, suggesting greater stringency in outlier-based approaches as sample sizes increased. In terms of consistency, RankCompV1 and PenDA outperformed other methods, while RankCompV2 and the Percentile method demonstrated lower consistency, with the latter ranking as the least consistent among the evaluated differential expression analysis methods. Furthermore, Liu et al. have provided a PLOTLY version of IDEPA^XMBD (https://hub.docker.com/r/lylan/idepa)[12], enabling users to conduct DEP identification with their data via a web interface.

5. Discussion and perspectives

The evolving field of individualized differential analysis methods in cancer multi-omics has been thoroughly reviewed. This shift from population-level to personalized analysis methods represents a significant leap forward in identifying unique molecular characteristics at the patient level. However, several limitations warrant attention.

Individualized analysis methods are notably more time-intensive and complex than their population-level counterparts, requiring increased computational resources and expertise. This complexity renders them less feasible for routine clinical application. Additionally, these individual-level methods often exhibit a high Type I error rate. This may be attributed to an overemphasis on inter-individual differences, leading to a misinterpretation of technological variances as biological disparities. Enhanced data quality control measures are imperative.

Current research in tumor heterogeneity increasingly utilizes single-cell and spatial omics technologies [23]. Single-cell transcriptomics, analyzing gene expression at an individual cell level, offers a more intricate understanding of cellular diversity within tumors. This technique can uncover previously unidentified cell types and states pivotal in cancer progression. In parallel, spatial transcriptomics integrates genomic data with locational information, shedding light on the spatial patterns of gene expression within tissues. This approach is key to understanding the interactions between tumor cells and their microenvironment, which are critical for grasping cancer progression and the efficacy of treatments.

However, integrating data across various omics layers presents significant analytical challenges, necessitating advanced computational tools and algorithms. For instance, OmicsNet 2.0 [24] serves as a tool for exploring multi-omics data and accepts either single or multiple lists of mRNA, transcription factors, miRNAs, or metabolites. Researchers may generate personalized biological networks, such as transcriptional regulation networks, by leveraging multiple integrated molecular interaction databases based on lists of patient-specific differential characteristics obtained through individualized analysis. Another strategy, DDK-Linker [25] may also enhance personalized medicine by analyzing individual genetic and proteomic data to identify specific disease signals and potential drug targets. The development of multi-layered networks for omics data integration is imperative, enabling the delineation of complex biological interactions and pathways. Future research should focus on how to effectively incorporate multi-omics analysis in personalized medicine.

CRediT authorship contribution statement

Zan Liu: Writing – original draft. Yachen Liu: Conceptualization, Methodology, Software. Mengsha Tong: Supervision, Writing – review & editing, Writing – original draft. Jiaao Li: Conceptualization, Methodology, Writing – review & editing, Writing – original draft. Jingyi Tian: Conceptualization, Methodology, Writing – original draft.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.