Linear modeling of zonal level crop production in Ethiopia

Abstract

Accounting for zonal-level variations and identifying factors that have linear effects on crop production help to make better decisions and plan new policies for effective crop production and food security. The main objective of this study is to identify potential subsets of covariates and estimate their linear effects on crop production. A linear mixed effects model (random--intercept) is used on agricultural sample survey data for Meher seasons from 2012/13 to 2019/20 to explore and identify the best variance-covariance structure for the longitudinal data on 90 zones with eight repeated observations and different sampling weights. The minimum, mean, and maximum crop production by farmers across the country are 1.616, 8.693, and 147.843 quintals, respectively, and about 98 % of farmers produced less than 25 quintals. There is a small rate of increase in mean and median crop production by farmers across the years, and the variability between zones is highest in the year 2019/20 and in the Somali region. The histogram, kernel density, and P–P plots suggested a common logarithm transformation on the crop production variable. Results from the data exploration and variance-covariance structure selection methods suggested a heterogeneous compound symmetry (CSH) structure. Covariates region, year, proportion of farmers who practice pure-agriculture and other-agriculture types, proportion of farmers who use any type of fertilizer, farmer's age, area used, farmer association crop production, indigenous seed used, improved seed used, UREA fertilizer used, other fertilizers used, and percentage of crop damaged are significant in linearly explaining/affecting log crop production, and among these area used, farmers association crop production, UREA fertilizer used, and indigenous seed used have relatively highest effect on log crop production. Zones Wolayita, North-Shewa (Am), West-Arsi, West-Welega, Dawro, and Guji are top/good performers while zones Southwest-Shewa, Waghimra, Guraghe, South-Omo, Keffa, North-Wello, South-Wello, and Eastern Tigray are bottom/poor performers in crop production. Model assumptions and influence diagnostics results suggested the linearity of the model and normality of random effects and residuals are not violated, even though some zones have influences on either model parameters, precisions of estimates of these parameters, and predicted values.

1. Introduction

The annual survey of agricultural practices by smallholder private farmers at country level is regularly conducted to collect the necessary information on demographic characteristics of the farmers, types of crops cultivated, area in hectare usage, types and amounts of fertilizers and seeds used, supports from agricultural associations, prevention of erosion and crops damage, and other activities that are used for decision-making and policy planning that lead to effective crop production and food security [1]. Making valuable decisions and planning applicable policies require identifying factors that have linear effects on crop production by accounting for the variability due to zonal variations. Eight years’ annually measured observations from zones are considered, which makes the dataset longitudinal, and these repeated observations from the same zone are expected to be more correlated than observations from other zones [[2], [3], [4]]. This behavior of the dataset forces us to use a linear mixed effects model rather than the standard multiple linear regression model for identifying significant factors linearly affecting crop production [[3], [4], [5], [6]].

The application and usage of linear mixed effects models in different fields has increased in recent years, and one of these fields is agriculture [[7], [8], [9], [10], [11]]. Agricultural activities are important in providing foods, job opportunities, and incomes to households, providing inputs for small-scale and large-scale industries, and finally supporting the economy of the country by exporting direct and indirect agricultural products [[12], [13], [14]]. Crop production is one of the agricultural activities that is practiced in all zones of the country, mainly by smallholder private farmers [1].

The use and importance of linear mixed effects models in agricultural experiments are well explained by different authors by comparing them with conventional general linear models, analysis of variance (ANOVA), and experimental design, whenever the dataset to analyze is either hierarchical, multilevel, longitudinal, nested, or unbalanced, and if there are random effects to consider by subject variations with different software (SAS, R, SPSS, and GenStat) [[15], [16], [17], [18], [19], [20], [21], [22]].

This study is focused on crop production at the zonal level by smallholder private farmers, with the main objective of identify the most appropriate subsets of potential covariates and estimating their linear effects on crop production. For the selection of appropriate variance-covariance structures and fitting the best linear mixed effects model, SAS (9.4) software is used.

2. Study area and data

The study areas are all zones in Ethiopia, from which agricultural sample surveys are conducted by the Central Statistics Agency (CSA). These zones are from nine administrative regions (Tigray, Afar, Amhara, Oromia, Somali, Benishangul-Gumuz, Southern Nations Nationalities and Peoples (SNNP), Gambella, and Harari) and one administrative town, Dire Dawa (Fig. 1).

Fig. 1.

Map showing zones in each region and administrative town of Ethiopia.

The data used in this study is from a sample survey on the agricultural activities of smallholder private farmers in each zone for eight Meher seasons (seasons between the months of September and February, and in most cases, crops that are planted in the major rainy season are collected during these seasons), from 2012/13 to 2019/20. These data are averaged (for continuous variables), and proportions or percentages of levels of categorical variables are considered so that we will have repeated measures of the variables at the zonal level for the study period (i.e., a longitudinal dataset for each zone).

3. Methodology

Multiple linear regression models assume the independence of observations and the constant variance of random errors. But, since the dataset used in this study is based on repeated measures of crop production and other factors/covariates in each zone for the successive eight Meher seasons (years) (longitudinal dataset), the assumptions of independence and constant variance required by these models will not be attained. Linear mixed effects models are appropriate for analyzing hierarchical (multilevel), longitudinal, nested, and unbalanced datasets by allowing dependence of observations and non-constant variances and accounting for the variability within and between subjects (zones in our case). So, to attain the objective of this study, a linear mixed effects model is the appropriate method to handle such dataset, and it extends the general linear models by allowing the addition of random effects (which quantify how much variability in the response variable is due to variability in their level values) and permitting the data to exhibit correlation and non-constant variability [3,4,6,23,24].

The linear mixed effects model provides the flexibility of modeling the mean structure and the variance-covariance structure at a time, and this helps us to save degrees of freedom compared to the standard regression model; it models the fixed and random effects as having a linear form such that the response variable is the sum of the fixed and random effects and the random errors. The fixed effects are the mean structures of the model, while both random effects and random errors are the variance-covariance structures of the model, and this expression can be shown using matrix notation as follows [2,4,23,[25], [26], [27]]:

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{Z}\mathit{\gamma }+\mathit{\epsilon }$$

Where:

y is vector of the response variable (n × 1)

X is known design matrix of fixed effects (n × p)

β is vector of unknown fixed/constant effects (p × 1)

Z is known design matrix of random effects (n × q)

γ is vector of unknown random effects (q × 1)

ε is vector of unknown random errors (n × 1)

To select and reduce the dimension of covariates (feature selection), a StepAIC (based on Akaike Information Criteria (AIC), which measures loss or gain of information for each variable dropped or entered at each step or iteration and for each competing model) function in R software is applied using a stepwise (both forward and backward) selection method, beginning with a full model. A competing model with the smallest AIC value is preferred, and the covariates in this model are considered for final analysis [28]. But this method dropped the most important variables like region, household size, improved seed (in kg) and DAP fertilizer (in kg) used, percentage of crop damaged, proportion of female farmers, and proportion of farmers who received advisory services and who participated in extension programs that may have policy implications, so we decided to use all the covariates to estimate their linear effect on crop production.

Following this, the final mixed effects model (random intercept, so we will have one column per zone in the random effects design matrix Z), in which zone is used as a random term (grouping factor) and there are 598 observations from ninety zones to consider for the analysis, is given by:

y_{(598× 1)} = X_{(598× 43)}β_{(43× 1)} + Z_{(598× 90)}γ_{(90× 1)} + ε_{(598× 1)}

3.1. Model assumptions

Like other models, the linear mixed effects model has basic assumptions to be satisfied, and these are stated as follows [4,23,25,27].

• •The random effects and random errors are normally distributed with mean zero and covariance matrices of G and R, respectively; i.e., γ ∼ N (0, G) and ε ∼ N (0, R)

where G is the variance-covariance matrix of random effects (random intercepts and/or one or more random slopes)

R is the variance-covariance matrix of repeated measurements of the same subject over time, space or condition.

• •Random effects and random errors are independent of each other, cov (γ, ε) = 0

→ E $\left[\begin{array}{c}\mathit{\gamma }\\ \mathit{\epsilon }\end{array}\right]$ = $\left[\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right]$ and Var $\left[\begin{array}{c}\mathit{\gamma }\\ \mathit{\epsilon }\end{array}\right]$ = $\left[\begin{array}{cc}\mathbf{G}& \mathbf{0}\\ \mathbf{0}& \mathbf{R}\end{array}\right]$ → $\left(\begin{array}{c}\mathit{\gamma }\\ \mathit{\epsilon }\end{array}\right)$ ∼ N $\left(\begin{array}{ccc}\left[\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right]& ,& \left[\begin{array}{cc}\mathbf{G}& \mathbf{0}\\ \mathbf{0}& \mathbf{R}\end{array}\right]\end{array}\right)$.

• •The expected (mean) values of the responses are linearly related to the predictor variables (i.e., linear in terms of fixed effects parameters), E (y) = Xβ and
• •The variances of responses are Var (y) = Var (Zγ + ε) = ZGZʹ + R, in which ZGZʹ is the between-subjects (level-2) component and R is the within-subject (level-1) component; let the sum equals to V, then we can have y ∼ N (Xβ, ZGZʹ + R) → y ∼ N (Xβ, V)

3.2. Parameters estimation

To estimate the parameters of the linear mixed effects model, we can use generalized least squares for parameters of mean structure (fixed effects) and maximum likelihood or restricted (residual) maximum likelihood for covariance parameters [4].

For the generalized least squares estimation of fixed effects, we differentiate

$$(\mathrm{y}–\mathrm{X}\mathrm{\beta })ʹ{\mathrm{V}}^{‐1}(\mathrm{y}–\mathrm{X}\mathrm{\beta })$$

with respect to the vector β and equate it to zero to get the estimated vector $\hat{\mathit{\beta }}$ given by

$$\hat{\mathrm{\beta }}={(\mathrm{X}ʹ{\mathrm{V}}^{‐1}\mathrm{X})}^{‐1}\mathrm{X}ʹ{\mathrm{V}}^{‐1}\mathrm{y}$$

which requires the vector of responses, the design matrix of fixed effects, and the knowledge of the variance of the response V and hence G and R; otherwise, we need to have reasonable estimates of G and R. To estimate these variance-covariance structures' parameters (G and R), we can use either the maximum likelihood (ML) or restricted/residual maximum likelihood (REML, in which the response vector is linearly transformed by removing the fixed effects (mean structure), and that is why restricted/residual) so that the estimated values of the parameters maximize the likelihood of observing the given dataset [4,25,27].

To estimate the parameters, we use the logarithm of ML or REML function and then derivate these objective functions with respect to G and R (i.e., we find the gradient vector (first derivative) and then the Hessian Matrix (second derivative) for G and R in both cases using the Newton-Raphson and Fisher-Scoring algorithm, which use the second derivative matrix of the logarithm function) [4,27].

Henderson's mixed model equations (MME), following the differentiation and rearrangement of objective functions (logarithm of ML or REML functions given above), can be used to estimate fixed effect β and random effect γ given by Refs. [4,25,27]:

$\left[\begin{array}{cc}{\mathbf{X}ʹ\mathit{R}}^{-1}\mathbf{X}& {\mathbf{X}\mathrm{ʹ}\mathit{R}}^{-1}\mathbf{Z}\\ {\mathbf{Z}\mathrm{ʹ}\mathit{R}}^{-1}\mathbf{X}& {\mathbf{Z}\mathrm{ʹ}\mathit{R}}^{-1}{\mathbf{Z}+\mathit{G}}^{-1}\end{array}\right]\left[\begin{array}{c}\mathit{\beta }\\ \mathrm{\gamma }\end{array}\right]$ = $\left[\begin{array}{c}{\mathbf{X}\mathrm{ʹ}\mathit{R}}^{-1}\mathbf{y}\\ {\mathbf{Z}\mathrm{ʹ}\mathit{R}}^{-1}\mathbf{y}\end{array}\right]$ and from this we can solve for $\mathit{\beta }$ and $\mathrm{\gamma }$.

$\mathit{\beta }$ = (Xʹ $\mathit{V}$⁻¹X)⁻¹Xʹ $\mathit{V}$⁻¹y … … which is best linear unbiased estimator (BLUE) of β

$\mathrm{\gamma }$ = $\mathit{G}$ Zʹ $\mathit{V}$⁻¹(y – X $\mathit{\beta }$) … … which is best linear unbiased predictor (BLUP) of γ

If G and R are both unknown, we use their estimators in the above equation, and the resulting estimators of the fixed effect β and random effect γ become the empirical best linear unbiased estimator (EBLUE) and the empirical best linear unbiased predictor (EBLUP), respectively [4,27].

3.3. Variance covariance structure selection

For valid inferences, the comparison and selection of variance-covariance structures should be done before examining and fitting the fixed effects (mean structure) model that provides a good fit to estimate changes in the response at both the group/population and the subject/individual levels [2,4,6,25,27,[29], [30], [31]].

For repeated measures observed at 4 time points for each subject, the variance-covariance structure of the errors for a given subject can be given in a matrix notation as follows (in general, if we have measures at k time points, there are k-variances at diagonal and k(k-1)/2 covariances at off-diagonal, and a total of k(k+1)/2 variance-covariances parameters to be estimated) [3,4,26,30]:

$${\mathbf{R}}_{\mathrm{i}}=\left[\begin{array}{cccc}{\sigma }_1^2& {\sigma }_{12}& {\sigma }_{13}& {\sigma }_{14}\\ {\sigma }_{21}& {\sigma }_2^2& {\sigma }_{23}& {\sigma }_{24}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_3^2& {\sigma }_{34}\\ {\sigma }_{41}& {\sigma }_{42}& {\sigma }_{43}& {\sigma }_4^2\end{array}\right]$$

As we can see from the matrix, there are a total of 10 different parameters to be estimated, and there are no specific structure considerations about the variances (equal or unequal variances) and covariances (no correlation or common correlation or varying correlation). This type of covariance structure is called unstructured covariance (UN) and is the most complex (as we need many distinct parameters to estimate) and flexible (as it imposes no pattern on the covariances) structure [3,4,31].

Based on the assumptions on the variances and covariances, we can have a number of different variance-covariance structures, like variance components (VC), compound symmetry (CS), first-order autoregressive (AR(1)), and Toeplitz (TOEP), each with different numbers of parameters. Except for the UN structure, the above structures are in their homogeneous form (the same variances along the diagonal), and the heterogeneous versions of these structures are obtained by considering that the variances along the diagonal need not be the same, and this consideration leads to having more parameters to be estimated (i.e., one variance for each measurement). For weighted survey datasets, we have W^−1/2RW^−1/2 in place of R, where W is the diagonal matrix of the weights and R is the full diagonal (which assumes the independence of observations from different subjects and subjects have the same variance-covariance structure) matrix made of symmetric R_i sub-matrices, which are equal to the number of subjects and each with k-by-k dimension [3,4,27].

To identify the potential variance covariance structures, we can use data explorations, literature reviews, and experiences, and to choose the best one, we can use model fit information criteria, which are functions of log likelihood (−2 Res Likelihood, Akaike Information criteria (AIC), corrected AIC, and Bayesian Information Criteria (BIC)) [[2], [3], [4],11,27,[31], [32], [33]]. For models with the same fixed effects (possibly with the most complex mean structure), we compare these criteria for different covariance structures, and the model with the smallest information criteria (usually AICC and BIC) [2,34,35] is the best model to choose. If there are ties or they are very close, we select the simpler (in terms of parameters to estimate) model [2,4,6,31,33].

BIC selects simpler models (which inflate rate of Type I error) compared to AICC, while AICC selects more complicated models (which inflate rate of Type II error and hence inadequate or loss of statistical power); if controlling Type I error is of importance, we may consider AICC, and if loss of power is of more concern, we may consider BIC [2,36].

For a given selection criterion, we may have different competing variance-covariance structures that have closely the minimum values and in this case, we can use chi-square difference test to select the one with simple structure compared to the competing more complex structure in terms of parameters to be estimated using differences of the chi-square values and degrees of freedom.

3.4. Model diagnostics

For model diagnostics, we use the usual residual plots in which these residuals are based on either the marginal means or conditional means of the response vector; for a given linear mixed effects model, the marginal and conditional means are given by:

E (y) = X $\hat{\mathit{\beta }}$ (marginal) and E (y/γ) = X $\hat{\mathit{\beta }}$ + Z $\hat{\mathit{\gamma }}$ (conditional)

and the corresponding marginal residuals (r_mi) and conditional residuals (r_ci) will be the difference between the response vector (y) and marginal mean and conditional mean, respectively [4,37].

Studentized and Pearson residuals are recommended for examining the basic model assumptions and to detect outliers and potentially influential data points in the dataset rather than using the raw residuals. The influence of observations from the same subject (observations of a given zone) on the model is cross-checked by the impact they have on the likelihood functions (Restricted Likelihood Distance, RLD), estimates of fixed effects and variance-covariance parameters (Cook's D), estimates of the precision of these parameters (COVRATIO), and the fitted (DFFITS) and predicted (PRESS Statistics) values. Finally, we will check the normality of the random effects using a density histogram and normal Q-Q plots [4,37,38].

4. Results and discussion

The overall mean and standard deviation of crop production by farmers across all zones and Meher seasons (years) are 8.693 and 8.262 quintals (1 quintal equals 100 kg), respectively; the minimum and maximum crop production observed are 1.616 quintals in the Easter Tigray zone of the Tigray region for 2013/14 Meher season, as this zone is potentially a Belg season crop producing area and it if frequently affected by climate changes, famine and droughts [39], so there is less crop production in Meher season, and 147.843 quintals in the Fafan/Jigjiga zone of the Somali region, which is one of the potential regions for large-scale land/agricultural investments [40,41], for 2019/20 Meher season, respectively.

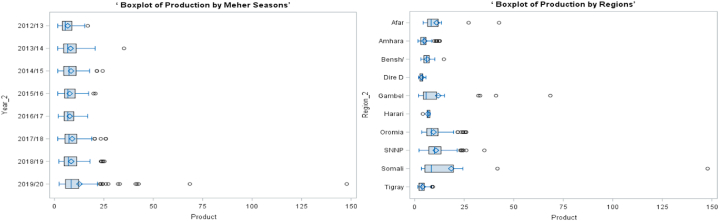
From Fig. 2a and b, we can see a decreased mean crop production in 2015/16 and 2016/17 compared to the previous two Meher seasons due to the abnormal and inadequate rain falls and drought, following the El Nino in the majority parts of the country during 2015/16 [[42], [43], [44]]. For Meher season 2019/20, there is the highest minimum, mean, median, and maximum crop production observed compared to previous Meher seasons as there are more inputs, irrigation, and technologies used by farmers under the recently introduced programs like Agricultural Commercialization Clusters (ACC), in which smallholder private farms are combined in a large farming area so that for specific crop improved seeds, agroecological specific fertilizers, pesticides, irrigations, and heavy harvesting machineries are used under the supervision and support of the Agricultural Transformation Agency (ATA) [[45], [46], [47]].

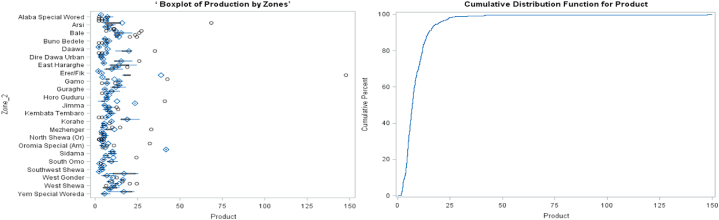
Fig. 2a.

Box Plots of Production in each Year (left) and Region (right) b. Box Plots of Production in each Zone (left) and Cumulative Distribution (right).

On average, there is an increase in mean and median crop production over the study period (the diamonds and lines in the box plots indicate the mean and median crop production, respectively) [48]. Farmers performed differently in the Meher seasons of 2017/18, 2018/19, and 2019/20, as these three years’ box plots are relatively widest, while for the rest years, farmers on average performed in a similar way; farmers from Afar, Gambella, Oromia, SNNP, and Somali regions performed differently, while farmers in the rest regions relatively performed in the same way; the Somali region has the highest mean and maximum crop production; the highest median production is observed in the SNNP region; and the smallest minimum and mean crop production are observed in Tigray region and Dire Dawa town, respectively.

Box plots for zones show that there are different groupings of box plots for different zones indicating dependency of observations within zone and independency of observations between zones and overall there is different performance of crop production between zones (the Eastern Tigray zone from the Tigray region produced the least minimum, mean, median, and maximum crop; the Shebele/Godey zone from the Somali region produced the highest minimum, mean, and median crop; and the Fafan/Jigjiga zone from the Somali region produced the highest maximum crop, followed by Anuak, Gabi Rasu, Shebele, and Itang zones, which are the most potential crop producing areas in the country). From the cumulative distribution plot, we can see that 25 %, 50 %, 75 %, and 98 % of the farmers produced less than 4.72, 6.95, 10.83 and 24.43 quintals, respectively, and this is mainly due to the fact that farmers are using on average 0.104 ha for crop production (the minimum, maximum, mean, and standard deviation of area used in hectares across all zones for the study period are 0.013, 0.519, 0.104, and 0.065, respectively, and half of them are using less than 0.087 ha) which is the most important input for agricultural practices.

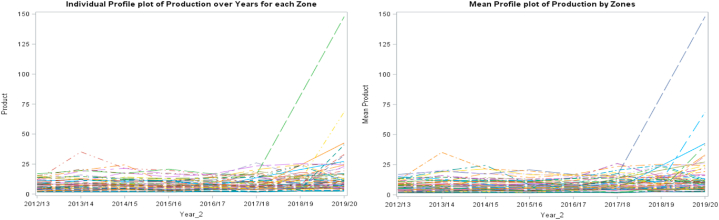
Fig. 3 shows the individual and group mean profile plots for zones, and we can see crop production measurements (individual and mean) for each zone are different each year, and over the years these values are changing differently for some zones, which can be seen from the crossed lines. Based on their slopes over the years, there is a very slow rate of increase in crop production; between zones, variation increases with years (except the middle two years), and this variation is high in the last Meher season (year).

Fig. 3.

Individual Profile plots (left) and Mean Profile plots (right) of Zones over years.

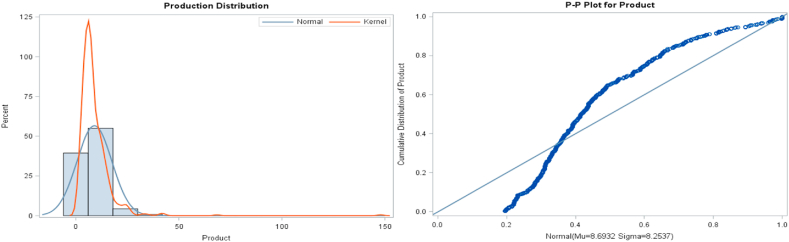
Fig. 4 shows the normal probability plot and kernel density plot for assessing whether or not the response variable, crop production, is approximately normally distributed. From the plot, we can see the response variable is not approximately normally distributed, and we need some kind of transformation on this variable.

Fig. 4.

Kernel Density plot (left) and Normal Probability plot (right) of Crop production.

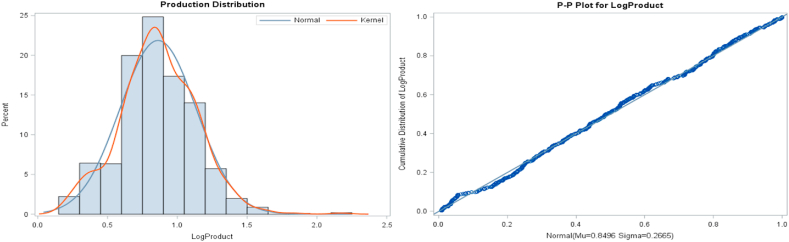
Following the result from Box-Cox transformation (in which zero lambda value was found within 95 % CI), the Common Logarithm Transformation was applied to the response variable crop production to make it approximately normally distributed, and from Fig. 5, we can see the log transformed crop production is approximately normally distributed.

Fig. 5.

Kernel Density plot (left) and Normal Probability plot (right) of log Crop production.

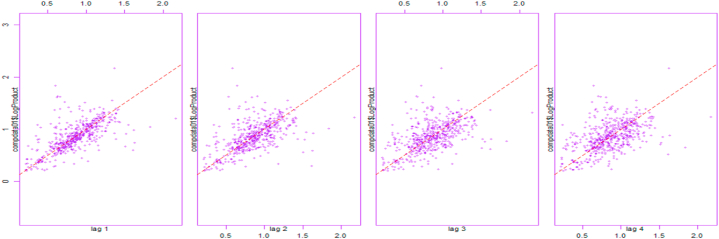
Fig. 6 shows the autocorrelation of the log crop production at four different lags (years), and from the panels, we can see measures of crop production at one year apart (lag 1) are relatively more correlated than measurements at two or more years apart, even though the decrease in correlations is very small as we go to larger lags.

Fig. 6.

Autocorrelation of log Crop production at lag 1, lag 2, lag 3 and lag 4 from left to right, respectively.

The results from the data exploration suggest that there are different and slightly increasing variabilities of crop production by farmers and zones across years (box plots and individual and group profile plots); measures of crop production from near in years are more similar than from further apart in years (autocorrelation plot), and the log transformation of the response variable crop production is normally distributed (kernel density and normal probability plots). So, the model that we will consider for data analysis should considered by zone variation (random effect) of crop production and dependence of observations (correlated observations) from the same zone for the study period.

4.1. Covariance structure selection (for R)

For the selection of variance-covariance structure for the eight repeated measures (R_i, for one Zone), a linear mixed effects model with the same fixed effects (considering all the independent variables to have complex mean structure) is fitted for variance component, unstructured, compound symmetry, first-order autoregressive, and Toeplitz variance-covariance structures, both homogeneous and heterogeneous versions. For each variance-covariance structure's parameters estimation, the default criterion for convergence (1E-8) is met at different numbers of iterations, the estimated parameters are significant at 5 %, and the null model likelihood ration test is significant ([Pr > ChiSq] < 0.0001), indicating that all these fitted covariance structures are better than the ordinary linear model (i.e., the null model assumes identical and independent residuals' variance-covariance structure, Variance Component) [2,27,32,49].

Table 1 given below shows the model fit statistics for each fitted variance-covariance structure, and we can see the information criteria values are relatively the smallest (largest negative values) in all heterogeneous variance-covariance structures, which agree with the patterns indicated in the data exploration parts. Based on the patterns we observed in data exploration and using BIC information criteria (to avoid loss of statistical power), we select the simpler/parsimonious heterogeneous compound symmetry (CSH) using chi-square difference test as a final variance-covariance structure to fit the model and test the mean structures [2,30,50,51].

Table 1.

Summary of Model Fit Statistics (Information Criteria) for each Structure.

Description	VC	UN	CS	CSH	AR1	ARH1	TOEP	TOEPH
−2 Res Log Likelihood	−275.2	−753.4	−424.7	−614.1	−454.3	−601.4	−474.3	−639.1
AIC (Smaller is Better)	−273.2	−681.4	−420.7	−596.1	−450.3	−583.4	−458.3	−609.1
AICC (Smaller is Better)	−273.2	−676.3	−420.7	−595.8	−450.3	−583.1	−458	−608.2
BIC (Smaller is Better)	−270.7	−591.4	−415.7	−573.6	−445.3	−560.9	−438.3	−571.6

4.2. Linear mixed effect (random intercept) model

The random intercept linear mixed effects model, in which zones are allowed to have different intercepts to account for zonal variation in overall crop production while all the covariates in the model are assumed to have the same effects on the crop production for each zone, is fitted using the restricted/residual maximum likelihood (REML) estimation method (the convergence criterion of 1E-8 is met at the 10th iteration number). Table 2a, Table 2ba and 2b given below show the 10 significantly estimated parameters of the two variance-covariance structure matrices of the random effect (G_i, which measure how zones vary around the overall average log crop production) and random residual (R_i for Zone_1, which measures variation of measurements at each Meher season and covariances/correlations between measurements from different Meher seasons), respectively, and Table 2c shows the model fit statistics. As there are many covariates to estimate, the REML estimation method is used because it gives unbiased estimates of the parameters compared to the ML estimation method.

Table 2a.

Estimated variance of G matrix.

Estimated G Matrix (REML, CSH)
Row	Effect	Zone	Col1
1	Intercept	1	0.007244

Table 2b.

Estimated variances, covariances, and correlation for the repeated measures.

Estimated R Matrix for Zone 1 (Weighted by Sample Weight) (REML, CSH)
Row	2012/13	2013/14	2014/15	2015/16	2016/17	2017/18	2018/19	2019/20
1	0.02115	0.01052	0.00371	0.00376	0.00446	0.00564	0.00664	0.0133
2	0.486	0.02216	0.0038	0.00384	0.00457	0.00577	0.0068	0.01362
3	0.486	0.486	0.00276	0.00136	0.00161	0.00204	0.0024	0.0048
4	0.486	0.486	0.486	0.00282	0.00163	0.00206	0.00243	0.00486
5	0.486	0.486	0.486	0.486	0.00399	0.00245	0.00288	0.00578
6	0.486	0.486	0.486	0.486	0.486	0.00637	0.00364	0.0073
7	0.486	0.486	0.486	0.486	0.486	0.486	0.00883	0.0086
8	0.486	0.486	0.486	0.486	0.486	0.486	0.486	0.03544

Table 2c.

Fit statistics (information criteria) with zones as random effect.

Fit Statistics (REML, CSH)
−2 Res Log Likelihood	AIC	AICC	BIC
−653.1	−633.1	−632.7	−608.1

Under Table 2a, we have the between-zones variance (0.007244) of random intercepts, which indicates the variation of zones’ crop production around the overall mean crop production (how much zones differ in crop production from each other), and under Table 2b, we have eight different within-zones variances along the diagonal (among which the last year has the highest variance of 0.03544), the same correlations below the diagonal, and different covariances above the diagonal.

The type III test and solution for fixed effects tables showed a subset of potential significant covariates (year, region, proportion of farmers who practice pure-agriculture and other-agriculture types, proportion of farmers who use any type of fertilizer, farmer's age, area used in hectare, farmer association crop production in quintal, indigenous seed used in kilogram, improved seed used in kilogram, UREA fertilizer used in kilogram, other fertilizers used in kilogram, and percentage of crop damaged) with their linear effects on log crop production besides the significant overall intercept term [52]. SNNP region (region 7), Harari region (region 13), and Oromia region (region 4) have 0.3997, 0.3162, and 0.2634, respectively, increase in log crop production compared to the reference in Dire Dawa town (region 15).

Keeping all other terms in the model constant, a one-year increase in Meher season has a 0.01157 increase in log crop production while a one-year increase in farmers age has a 0.0096 decrease in log crop production, a one percent increase in farmers proportion who practice pure-agriculture has a 0.0021 increase while a one percent increase in farmers proportion who practice other-agriculture has a 0.0015 decrease in log crop production compared to the reference proportion of farmers who practice mixed-agriculture, a one percent increase in farmers proportion who used any type of fertilizer has a 0.001128 increase in log crop production compared to the reference proportion of farmers who do not use any fertilizer, a 1 ha increase in area usage leads to a 1.6111 increase in log crop production, a 1 kg increase in UREA fertilizer used leads to a 0.00566 increase in log crop production, a 1 kg increase in other (except UREA and DAP) fertilizer used leads to a 0.0012 increase in log crop production, a one quintal increase in Farmers association crop production leads to a 0.0101 increase in log crop production, a one percentage increase in crop damage leads to a 0.002 decrease in log crop production, a 1 kg increase in indigenous seed and improved seed used have a positive and negative effects, respectively, in log crop production.

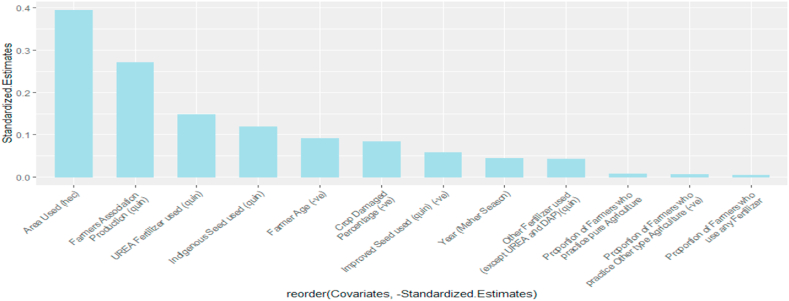
For covariates comparison and ranking based on their relative effect on crop production, their absolute standardized coefficients are used and from Fig. 7 given below, we can see that area used has the highest effect (0.395) followed by farmers association production, UREA fertilizer used, and Indigenous seed used (0.2717, 0.1483, and 0.1186, respectively, in decreasing order) on crop production compared to the effects of other covariates in the model [53].

Fig. 7.

Relative order/rank of covariates affecting log Crop production.

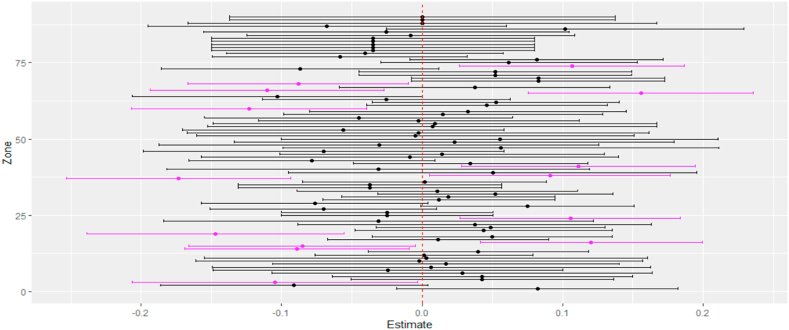
From Table 3 and Fig. 8 given below, we can see that fourteen zones have significant zonal-specific random intercepts (magenta colored) indicating their individual performance in crop production compared to each other and with the overall population crop production. Among all zones, Wolayita (65) from SNNP region, North Shewa (16) from Amhara region, West Arsi (41) and West Welega (24) from Oromia region, Dawro Special wereda (74) from SNNP region, and Guji (38) from Oromia region are the top six good performing zones in crop production (to the right of dashed vertical red line) while Southwest Shewa (37) from Oromia region, Waghimra (19) from Amhara region, Guraghe (60), South Omo (66), and Keffa (68) from SNNP region, North Wello (14) and South Wello (15) from Amhara region, and Eastern Tigray (3) from Tigray region are the bottom eight poor performing zones in crop production (to the left of dashed vertical red line).

Table 3.

Top six and bottom eight performing Zones in Crop Production.

Top Performing Zones in Crop Production					Bottom Performing Zones in Crop Production |
Zone	Estimate	Std Err Pred	t Value	Pr > |t|	Zone	Estimate	Std Err Pred	t Value	Pr > |t|
Wolayita (65)	0.1557	0.04087	3.81	2E-04	Southwest Shewa (37)	−0.1733	0.04081	−4.25	1E-04
North Shewa (16)	0.1204	0.04036	2.98	0.003	Waghimra (19)	−0.1473	0.04666	−3.16	0.002
West Arsi (41)	0.1114	0.04243	2.63	0.009	Guraghe (60)	−0.1231	0.04271	−2.88	0.004
West Welega (24)	0.1054	0.04001	2.63	0.009	South Omo (66)	−0.1104	0.04235	−2.61	0.009
Dawro (74)	0.1066	0.04088	2.61	0.009	Keffa (68)	−0.08818	0.0401	−2.2	0.028
Guji (38)	0.0909	0.04381	2.07	0.039	North Wello (14)	−0.08898	0.04075	−2.18	0.029
					South Wello (15)	−0.08542	0.04104	−2.08	0.038
					Eastern Tigray (3)	−0.1049	0.05179	−2.03	0.043

Fig. 8.

Predicted random intercepts with their 95 % CI of Zones considered.

4.3. Model assumptions and diagnostics

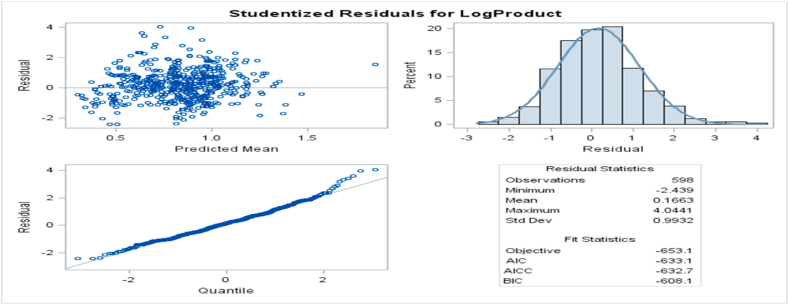
Model assumptions checking and diagnostics are performed for the final fitted model using residuals plot, influence diagnostics, and normal histogram and Q-Q plots; Fig. 9a given below shows the marginal Studentized residual plots, in which residual versus predicted values, histogram with normal density curve, Normal Q-Q plot and residual summary statistics and model fit information criteria values are displayed in four panels; from the panels we can see that the assumption of normality of random errors (from the histograms and Q-Q plots in which residuals falling on the 45-degree reference line) and linearity (from the residual versus Predicted Mean plots, residuals falling randomly around the horizontal reference line of residual = 0) are satisfied.

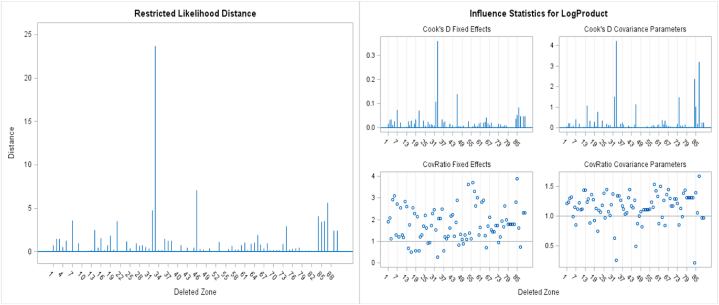
Fig. 9.

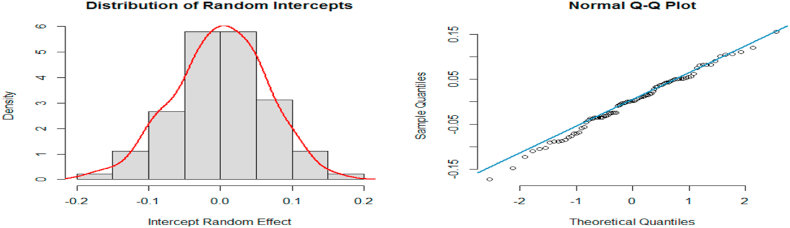
a. Marginal Studentized residuals plots b. Restricted Likelihood Distance (left) and Influence Statistics (right) plots c. Density plot (left) and Normal Q-Q plot (right) of the random intercept.

For influence diagnostics, the 5-iteration method is used for the updates of fixed effects parameters and variance-covariance parameters for checking the impact or influence of a given zone (based on the eight observations); Fig. 9b, given below, shows the overall influence (likelihood displacement) and influence statistics for parameters of fixed effects and variance-covariances of observations from each zone.

From the restricted likelihood distance (RLD) plot (Fig. 9b left), we can see East Hararghe (33) zone has the largest restricted likelihood distance; also zones Fafan/Jigjiga (46), Itang (87), West Hararghe (32), and Anuak (84) have higher likelihood change or displacement (i.e., if the observations from these zones are dropped, one zone at a time, and the estimates obtained are used to replace the full data model's estimates to re-evaluate the log-likelihood function of the full data model and measure the change observed in this objective function), indicating that observations from a zone have jointly influenced all parameters (fixed and variance-covariance parameters, as all are used in the log-likelihood) from the full data estimates.

Influence Statistics plot (Fig. 9b right) shows the impact of zones on parameters of fixed effects and variance-covariances (Cook's D plots) and the precision of estimates of these parameters (CovRatio plots); following the overall influence test (RLD plot), zones East Hararghe (33), Fafan/Jigjiga (46), and West Hararghe (32) have the highest Cook's D values for Fixed Effects and zones East Hararghe (33), Itang (87), and Anuak (84) have the highest Cook's D values for Variance-Covariance Parameters indicating that if the observations of these zones are deleted, one zone at a time, they will have impact/influence on the fixed effects and variance-covariance parameters, respectively.

From the CovRatio plots of fixed effects and covariance parameters, we can see the ratio values of zones East Hararghe (33), North Shewa Am (16), Waghimra (19), and Southwest Shewa (37) and zones Anuak (84), East Hararghe (33), Fafan/Jigjiga (46), and West Hararghe (32) are less than one, indicating the deletion of observations of these zones, one zone at a time, will improve the precision of estimates of fixed effects and variance-covariance parameters, respectively.

Influence of observations from each zone on the predicted value is measured using PRESS Statistic (which is the sum of the squared PRESS residuals for individual observations of each zone and these PRESS residuals are the difference between the observed values and the predicted (marginal) means) and based on this zones Mezhenger (86), Anuak (84), and Itang (87), all from Gambella (12) region, have the highest PRESS Statistic values, 1.437, 1.410, and 0.920, respectively, indicating their relatively higher influence on the predicted values.

East Hararghe (33), West Hararghe (32), and Southwest Shewa (37) zones from Oromia (4) region, Fafan/Jigjiga (46) zone from Somali (5) region, Anuak (84), Mezhenger (86), and Itang (87) zones from Gambella (12) region, and North Shewa (16) and Waghimra (19) zones from Amhara (3) region have influence at least on fixed effects, variance-covariance parameters and/or the precision of estimation of these parameters, and predicted values.

East and West Hararghe zones are frequently affected by drought due to irregular and inadequate rainfalls [[54], [55], [56]] while zones like Fafan, Anuak, Mezhenger, and Itang are among the potential zones for crops production in the country, following the expansion of large-scale agricultural investments in the regions of Somali and Gambella, so the reason for their influences is their inconsistent and high crops productivity, respectively [40,41,[57], [58], [59]].

Fig. 9c shows the density plot and normal Q-Q plot for checking the normality assumption of the random effects, and from the plots we can see the normality assumption is not violated and we conclude random intercepts are normally distributed.

5. Conclusion

Using data exploration and model fit statistics for variance-covariance and mean structure selection, we concluded that a random-intercept linear mixed effects model with heterogenous compound symmetry is the best fit of the longitudinal (repeated measures) data of crops production by zones; the mean crops production is linearly affected by covariates region, year, proportion of farmers who practice pure-agriculture and other-agriculture types both with reference to mixed agriculture, proportion of farmers who use any type of fertilizer, farmer's age, area used in hectare, farmer association crop production in quintal, indigenous seed used in kilogram, improved seed used in kilogram, UREA fertilizer used in kilogram, other fertilizers used (except UREA and DAP) in kilogram, and percentage of crop damaged. Among these, area used has the highest linear effect on log crop production followed by farmer association production, UREA fertilizer used, and indigenous seed used; zones Wolayita, North-Shewa (Am), West-Arsi, West-Welega, Dawro, and Guji are the top six good performers while zones Southwest-Shewa, Waghimra, Guraghe, South-Omo, Keffa, North-Wello, South-Wello, and Eastern Tigray are the bottom eight poor performers in crop production.

To have an increased crop production, farmers should use their farm land in cluster form so that more farm lands can be used for crop production, farmers should be encouraged to practice pure agriculture than mixed agriculture, they should be provided with UREA fertilizer and indigenous seeds to use, farmers associations should be established and supported to motivate other farmers, policies on credit and advisory services, women participations, and educational system should be reconsidered in such a way to motivate more female farmers and educated farmers to participate in crop production activities and credit/loan services should be provided to help farmers in financing their crop production activities. The effectiveness of agricultural extension programs should be evaluated, more private investors should be encouraged to participate in crop production, different agricultural inputs should be provided in quantity and affordable prices, mechanized crop production should be considered so as to reduce wastage and damage of crops and support elderly farmers. Finally, there should be experience sharing between zones and those poor performing zones need to be supported by the stakeholders and policies in these zones need revisions.

The basic model assumptions are not violated even though some zones have influence on the estimation and precision of estimation of the model parameters and predicted values they are retained in model fitting process as they are the potential areas for crop production.

Linear mixed model is used to identify the direction and significance of the relationship between the covariates and log crop production when the relationships are strictly linear by considering by-zone variation as random effect and the dependence of repeated observations from each zone but it has the limitation of assuming the functional relationship between the response variable and covariates is linear, which may not be true for all covariates considered in the model. To relax this linearity assumption, the additive mixed model can be considered in future work, which lets the data decide the true functional relationship between the response variable and covariates.

Ethical approval and consent to participate

The author received the consent of CSA of Ethiopia to use the data for academic purpose.

Funding

Not applicable.

Data availability statement

Data will be made available upon formal request and approval of Central Statistical Agency (CSA) of Ethiopia.

CRediT authorship contribution statement

Yidnekachew Mare: Writing – review & editing, Writing – original draft, Methodology, Formal analysis, Data curation, Conceptualization. Denekew Bitew Belay: Writing – review & editing, Writing – original draft, Validation, Resources, Conceptualization. Temesgen Zewotir: Writing – review & editing, Validation, Supervision, Resources, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.