Abstract
In muscles, the arrays of skeletal myosin molecules interact with actin filaments and continuously generate force at various contraction speeds. Therefore, it is crucial for myosin molecules to generate force collectively and minimize the interference between individual myosin molecules. Knowledge of the elasticity of myosin molecules is crucial for understanding the molecular mechanisms of muscle contractions because elasticity directly affects the working and drag (resistance) force generation when myosin molecules are positively or negatively strained. The working stroke distance is also an important mechanical property necessary for elucidation of the thermodynamic efficiency of muscle contractions at the molecular level. In this review, we focus on these mechanical properties obtained from single-fiber and single-molecule studies and discuss recent findings associated with these mechanical properties. We also discuss the potential molecular mechanisms associated with reduction of the drag effect caused by negatively strained myosin molecules.
Keywords: Skeletal myosin, Stiffness, Working stroke size, Drag force, Nonlinear elasticity, Single molecule
Introduction
Muscle contraction is driven by the cyclical interaction of myosin molecules with actin filaments and is associated with the hydrolysis of ATP molecules. The current view of the muscle force generation mechanism is that myosin molecules bind to actin filaments along with the products of ATP hydrolysis (phosphate and/or ADP), which is followed by conformational changes (working stroke) of the myosin head to produce a sliding movement of actin filaments past myosin filaments [1, 2]. At this point, the distortion of the myosin head stores elastic energy that is a source of mechanical work for use against the external environment. Thus, this elastic distortion of the myosin molecule is characterized as stiffness (inverse of compliance) and has been modeled as an essential mechanical element for the force generation driven by cross-bridges during muscle contractions. In this model, the force was simply determined by multiplying the constant stiffness by the strain in each myosin molecule [3]. At the maximum shortening velocity with zero net force output, the myosin molecules must achieve mechanical equilibrium, in which the negatively strained myosin molecules generate the net drag (negative) forces that are equal in magnitude but in the opposite direction of the net working (positive) forces generated by the positively strained myosin molecules [3]. When force output is required at slower shortening speeds, the detachment rate of myosin must increase in the negative strain direction while the attachment rate of myosin increases in the positive strain direction. In principle, the amount of working and drag forces at a given amount of strain depends on the elasticity of the myosin molecules. Thus, the attachment and detachment rates must be modulated if the elasticity changes at different strain sizes. This adjustment implies the importance of determining the elasticity of myosin molecules to clarify not only the magnitude of force but also the rate of the force generation and the fraction of the myosin molecules attached to the actin filament [4–6].
Another important mechanical property of muscle myosin is the size of the working stroke, defined as the limit of the displacement generated by the conformational changes of the myosin head. This value is important for understanding the energetics of muscle contraction. The mechanical work performed by a single-myosin single-myosin molecule, which is the integral of force over the sliding distance elucidates the mechanical efficiency of muscle, which ranges from 30 to 70 % of the chemical energy input (i.e., free energy of ATP hydrolysis) [7]. Thus, it is intriguing to investigate whether the mechanical efficiency of single-myosin molecules is sufficient to ensure the efficiency of the entire muscle system. In addition, some enhancement mechanism may exist in the myosin motor ensembles and/or other muscle structures.
In this review, we focus primarily on two essential mechanical properties of muscle myosin: the stiffness and the working stroke size. These properties were investigated primarily using single-fiber experiments until optical tweezers and glass needles were introduced to measure the forces and displacements produced by single motors in the 1990s [8–10]. Now, these mechanical properties, measured with single-fiber and single-molecule approaches, are used to gain further insight into the molecular mechanisms of muscle contractions. Thus, the discussion includes the recent findings regarding these parameters obtained from both experimental approaches. The discrepancies in the values obtained within or between these approaches are discussed, and the data most pertinent to understanding the molecular mechanics of muscle contractions will be described. We also compare the elasticity of myosin between positive and negative strain sides and propose a potential molecular design of single-myosin molecules that ensures effective force generation and avoids drag force generation. Finally, we explore the interpretations of how these molecular properties are utilized in the muscle performance observed in physiological muscle activities.
Elasticity of skeletal myosin as determined from single-fiber studies
The elastic properties of myosin were experimentally quantified for the first time by Huxley and Simmons [11], who characterized the quick release of sarcomere length during isometric contractions. Their results indicated a substantial amount of sarcomere compliance (approximately 8 nm per half-sarcomere) and resulted in a cross-bridge stiffness of 0.25 pN/nm being added to the formation of the 1971 cross-bridge model [11]. Their subsequent studies [12], which were performed with a greater speed of length change, led to the interpretation that the cross-bridges were strained by 4 nm on average in isometric contractions by assuming that the majority (approximately 90 %) of the half-sarcomere compliance resided in the cross-bridges. Thus, myofilaments and other sarcomere structures were modeled as rigid segments [13].
However, the existence of myofilament compliance was identified in in vitro experiments with single actin filaments using a glass needle [14]. Moreover, the actin and/or myosin filament compliances in muscle fibers were examined using X-ray diffraction techniques [15, 16] and mechanical measurements [17]. For example, in a quick length release experiment, the elongations of actin and the myosin filament were approximately 3 and 2.1 nm, respectively [16], contributing to an instantaneous half-sarcomere compliance of approximately 6 nm [12]. Thus, in general, the contributions of the actin and myosin filament compliance to the half-sarcomere compliance are approximately 40 and 20–30 %, respectively [16–21], implying that the contribution of the cross-bridge compliance is 30–40 % of the half-sarcomere compliance, in contrast to the originally assigned value of approximately 90 % [13]. Since then, the myofilament compliance has been considered a significant component of the half-sarcomere compliance, resulting in cross-bridge stiffness values on the order of 1–3 pN/nm [5, 6, 22] (e.g., 1.2 pN/nm in the rabbit psoas muscle according to [5], 3.1 pN/nm in the Rana esculenta tibialis anterior muscle according to [22], and 3.3 pN/nm in the Rana temporaria tibialis anterior muscle according to [6]). All these values are much higher than the originally estimated value of 0.25 pN/nm [11]. It has been suggested that the variation in stiffness values between different species and muscles may be subtle if the similarity of the working stroke size is considered [23]. Nevertheless, one may still argue that the higher stiffness observed in frog muscles (i.e., Rana temporaria or Rana esculenta) using an intact fiber preparation compared with the lower stiffness values observed in rabbit muscles using a skinned fiber preparation, which may result in occasional fiber disruptions and the loss of proteins, could be attributable to the preparation method employed. In addition, the variation in the stiffness value may arise from potential errors in the stiffness calculations, as discussed in the following paragraphs. In any case, the contribution of the myofilament compliance is a prerequisite for the calculation of the myosin stiffness obtained from single-fiber preparations.
As noted by Offer and Ranatunga [23], the calculation of the cross-bridge stiffness based on the measurement of the half-sarcomere compliance in single-fibers may have sizable errors due to the accumulation of errors arising from the compliance measurements and the subsequent series of calculations. To calculate the myosin stiffness, the average myosin strain is first derived by subtracting the myofilament (actin + myosin filament) compliance from the half-sarcomere compliance. Then, the total isometric tension (e.g., 230 kPa for a half-sarcomere) is divided by the product of the average myosin strain and the number of myosin heads attached to yield the stiffness of a single-myosin head. In this series of calculations, there are several potential sources of error. First, the actin and myosin filament compliances obtained from the X-ray reflection have appreciable errors, as discussed in detail elsewhere [23]. The myofilament compliances can also be calculated by estimating the slope of the linear fit to the half-sarcomere strain-tension curves, the linear fit of which deviates from the experimental results in the lower tension range due to the curvature of this relationship [6, 24]. Thus, the fitting is applied to the mid-higher tension range, causing variation in the fit results depending on the selected tension range. Moreover, the stiffness calculation is extremely sensitive to the myofilament compliance value. For example, in a study by Linari et al. [5], if the myofilament compliance of 21 nmMPa−1 was increased by 10 %, the average stiffness of the myosin head in rigor (1.21 pN/nm) was increased by 40 %, becoming 1.69 pN/nm. In addition, the typical stiffness calculation requires the input of the number of heads attached to the actin filaments, which is estimated by multiplying the total number of myosin heads (e.g., 300 heads per half-sarcomere) by the fraction of heads attached. The fraction of heads attached is typically obtained by comparing the fiber stiffness values between the experimental condition and the rigor condition based on the assumption that all heads are uniformly attached to actin filaments during rigor and that the change in fiber stiffness is directly proportional to that in the fraction of attached heads [13]. However, as previously described, a substantial proportion of the nonlinear half-sarcomere compliance resides in myofilaments (60–70 %) [15, 17, 24–26], implying that changes in stiffness do not linearly scale with changes in the fraction of heads attached. In addition, several studies based on mechanical [24] and X-ray approaches [27, 28] have demonstrated that the attached heads include both the force-generating and the non-force-generating heads, which contribute to the stiffness but not the force generation, suggesting that the muscle fiber stiffness may not be a direct measure of the number of force-generating heads. Thus, the nonlinear myofilament compliance complicates the interpretation of fiber stiffness as a way to estimate the cross-bridge stiffness, fraction of the attached myosin heads, average force per myosin head, and rate of the attachment and detachment of myosin heads because these properties cannot be obtained in isolation and are dependent on each other in a non-proportional manner [29]. The question of whether the cross-bridge and myofilament elasticities are linear or nonlinear needs to be addressed to understand the fundamental mechanical properties of muscle myosin molecules [23]. We recently demonstrated that the elasticity of myosin changes nonlinearly in both the positive and negative strain directions [30]. This nonlinear elastic behavior of myosin could explain the variation in stiffness of 1–3 pN/nm and the potential mechanism of the reduction of drag force in the negative strain region, as discussed in later sections.
Despite the potential errors in the myosin stiffness values obtained from single-fiber studies, the single-fiber, or myofibril, is the most physiologically relevant system for elucidating the molecular mechanics of muscle contractions given that the single-fiber or myofibril preparation conserves the lattice structure of the myofilaments, contractile protein structures (e.g., titin and nebulin), and regulatory proteins (e.g., troponin, tropomyosin, and myosin-binding protein C). It has been suggested that the lattice formation of myosin, actin filaments [31, 32], and other proteins [33, 34] may play a crucial role in myosin force generation. For example, titin is a molecular spring that spans a half-sarcomere length between the Z-line and the M-band and is responsible for most of the passive force in muscle fibers [35, 36]. In myofibrils, elastic recoil in titin appears to enhance the shortening velocity, which may be advantageous with regard to the shortening onset resulting from greater sarcomere lengths associated with an elongation of titin [33]. More recently, it was observed that active force generated by cross-bridges induces an increase in the passive force at the sarcomere length beyond the overlap between myosin and actin filaments by enhancing the binding of titin to actin filaments [37]. These results imply that the passive force produced by titin may alter the force requirements and kinetics of myosin in cases of longer sarcomere lengths. Nebulin is also known as a passive element in the sarcomere and a large, filamentous F-actin-binding protein that extends along the thin filament. Recent studies have consistently shown that nebulin increases thin filament activation, resulting in an increase in the attachment probability of myosin molecules to actin [38] and, thus, an increase in the force and efficiency of contraction [39]. These effects of passive components on myosin kinetics and force generation are certainly important for understanding sarcomere dynamics and cannot be explored by the isolated single-molecule setup. In addition, the existence of multiple myosin molecules bound to actin filaments in muscle fibers leads to the elucidation of additional features of single-myosin molecules that are technically difficult to test in the isolated single-myosin molecule setup because the typical single-molecule experiments cannot avoid premature detachment of single-myosin molecules due to the low affinity of myosin, which hampers the examination of such features, except during the application of the sophisticated feedback system using optical tweezers [40]. For example, single-fiber studies generally suggest that one of the two heads in a myosin molecule primarily contributes to the force generation during isometric contractions [6], and these studies have revealed additional features of acto-myosin interactions, such as the recruitment of the second head attachment, which contributes to the force enhancement during the active lengthening [41–44] and the enhancement of the force per myosin head (i.e., a transition of the cross-bridge from a non-stereo-specific bound state to a stereo-specific bound state) induced during temperature-jump experiments [22, 27, 45, 46]. Furthermore, the active stretching and shortening of muscle fibers and myofibrils after isometric contractions induces force enhancement [47, 48] and force depression [49, 50] compared with the results obtained under isometric tension at the same post-stretching or post-shortening length. Thus, these findings are extremely informative for understanding the additional features of muscle myosin observed during physiological muscle activities that have not been successfully investigated by isolated single-molecule experiments due to difficulties in the reconstraction of acto-myosin interactions against external perturbations.
Elasticity of skeletal myosin as determined from single-molecule studies
In contrast to the single-fiber studies, single-molecule experiments enable the investigator to directly measure the force and displacement produced by a single molecular motor and thus clarify many of the ambiguities that arise from the assumptions made regarding the muscle fiber system. In this type of measurement, the targeted protein is typically linked via beads manipulated by optical tweezers. The beads can be manipulated by projecting a focused laser [8, 10] such that the forces and displacements produced by these proteins can be obtained by measuring the positions of these beads. However, the values of myosin stiffness are substantially lower, ranging from 0.2–0.6 pN (0.17 pN/nm in [51] and 0.58 pN/nm in [52]), because these values are obtained without accounting for the linkage compliance between the beads and actin filaments caused by the rotations of the beads in the trap and the filament bending near the bead-filament attachments [53]. Thus, the contribution of the linkage compliance to the measured compliance must be mathematically calculated [54, 55]. Nevertheless, the values of stiffness appear to be lower, approximately 0.7 pN/nm (0.65 pN/nm in [54] and 0.69 pN/nm in [55]), than the values obtained from single-fiber studies (e.g., 1.2 pN/nm in [5] and 3.3 pN/nm in [6]). However, recent refinements to single-molecule measurements and analysis techniques have yielded reductions and more accurate estimations of the compliance of bead-protein linkages, with the result that the values of single-myosin stiffness are much more consistent with those obtained from single-fiber studies [30, 40, 56, 57] (e.g., approximately 1.3 pN/nm according to [40], approximately 1.4 pN/nm according to [56], approximately 2.5 pN/nm according to [57], and approximately 2.9 pN/nm according to [30]). For example, Takagi et al. [40] added a feedback system to clamp the bead-actin complex so that the effective stiffness of the actin was increased and higher forces and stiffnesses were detected for the myosin. Lewalle et al. [57] developed a sensitive method to estimate the stiffness of actin-bead linkage and myosin by applying a large-amplitude, triangular wave to both trapped ends of the actin filaments during the acto-myosin interactions and evaluated the ratios of the bead velocities between the bound and unbound conditions. In addition, we used quantum dots attached to the actin filament to represent the position of the myosin head because the actin filament is less extendable than myosin due to the much higher stiffness of the actin filament (approximately 20 pN/nm under our experimental conditions). Thus, the displacements of the myosin molecule can be obtained with minor corrections to the linkage compliance [30].
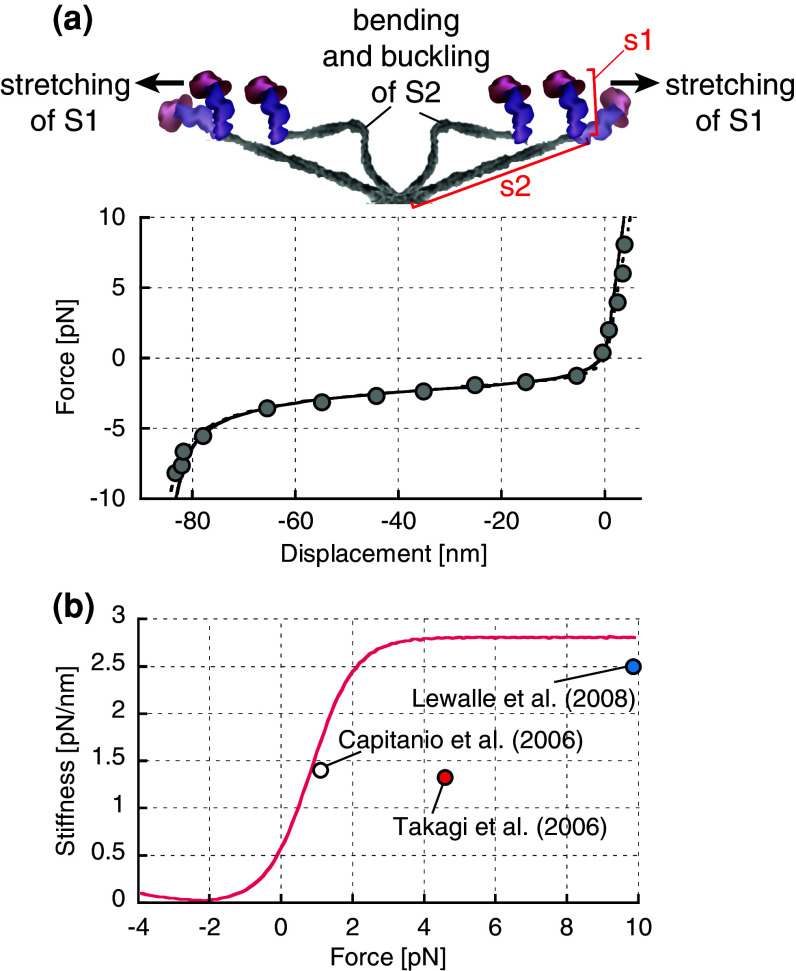
Despite the recent development of experimental approaches that reduce the contribution of the actin-bead linkage compliance, the values of myosin stiffness obtained from single-molecule approaches still vary between 1 and 3 pN/nm. A potential reason for such variations is the nonlinear elasticity of myosin molecules [30]. We found that the elasticity of myosin changes nonlinearly in both the positive and negative directions (Fig. 1a). The slope of the fitting curve of the force–displacement relationships of single-myosin molecules provides the change in stiffness as a function of load (Fig. 1b) and clearly demonstrates that the stiffness changes in both the positive and negative strain directions. Interestingly, the relatively lower stiffness values reported in [56] were obtained from a lower force range (F < 1 pN), while our results of 2.9 pN/nm [30] and 2.5 pN/nm [57] were obtained under a higher force range (F = 4–10 pN). If the stiffness values reported in [58] are plotted on the stiffness-load curve obtained in our study [30], their results appear to be consistent with our stiffness curve (Fig. 1b), implying that the variation in stiffness values could be explained by the nonlinear elasticity in the positive strain direction, which was also observed but not discussed in other single-molecule experiments [52, 55].
Fig. 1.
Nonlinear elasticity of single skeletal myosin molecules. a The elasticity of single skeletal myosin molecules is characterized by the force–displacement relationships obtained from the combination of optical tweezers and single-molecule fluorescent techniques [30]. The stiffness (slope of the curve) is higher in the positive displacement (strain) region and dramatically lower in the negative strain region. Below −80 nm of displacement, the stiffness increases as well. Taken together with the fact that the length of S2 is approximately 40 nm, the higher stiffness (approximately 2.9 pN/nm) observed in the positive strain region and below −80 nm likely represents the elasticity of S1, while S2 is fully stretched and becomes much stiffer (approximately 100 pN/nm), as depicted in the top illustration. In the negative strain region between 0 and −80 nm, the lower stiffness (approximately 0.02 pN/nm) represents the bending stiffness of S2, which is bent and buckled as shown in the top illustration. b The stiffness values are calculated as the slope of the curve in Fig. 1a and plotted as a function of the loads. The stiffness values increase continuously from −2 to 4 pN and are comparable to those reported in previous single-molecule studies. Except for the stiffness obtained in [40], the values in other studies [56, 57] are consistent with our stiffness curve, implying that the variation in stiffness may be explained by the nonlinear elasticity of myosin molecules. Note that data from Fig. 2b in [57] were used here, and the other data are the mean values from those studies [40, 56]
One may argue that the variations in the stiffness values obtained using the single-molecule approaches may be attributed to the difference in myosin preparations, such as single-head (e.g., subfragment 1 (S1) or single-headed myosin) and two-head [e.g., heavy-meromyosin (HMM) or full-length myosin] preparations, if the elastic portion is located on the myosin head rather than the myosin subfragment 2 (S2) portion [59]. Several single-fiber studies have suggested that only one of the two heads primarily contributes to the cross-bridge stiffness in single-fibers during isomeric contractions [60–64] and in rigor, where both heads are attached to the actin filament with two distinct angular distributions of the light-chain domain [65, 66]. Therefore, the variations in stiffness are not likely to be due to variations in the number of heads (one vs. two heads) available for attachment in each molecule. Instead, the variations may be the result of differences in the experimental setups or other possible sources, as discussed in the previous paragraph.
Overall, both the recent single-fiber and single-molecule approaches appear to converge in a similar stiffness range between 1 and 3 pN/nm. However, this range remains a matter of debate due to the intrinsic ambiguities arising from the experimental approaches and the underlying assumptions in both single-fiber and single-molecule studies. The nonlinear elasticity of skeletal myosin molecules appears to explain the variation of stiffness obtained from single-molecule studies. To clarify this issue, the amount of strain in a single-myosin molecule during force generation needs to be directly quantified in the future. Such quantification can be achieved by labeling the different locations of the myosin head with probes, such as fluorescence dyes, quantum dots, and gold nanoparticles (e.g., myosin VI [67]), and simultaneously measuring the displacement of each probe and the forces exerted on the myosin head. This approach requires either the recombination of skeletal myosin molecules [68] or the replacement of the light chain domains with recombinant light chains [69–72].
Nonlinear elasticity of myosin in the negative strain region
The elasticity of myosin is assumed to be linear in both the positive and negative strain regions [3]. This assumption of linear elasticity in both the positive and negative strain regions is based on the linear elasticity observed exclusively in the positive strain region of single-fibers [11, 73] because negative force generation in single-fibers is practically impossible unless a sophisticated protocol is performed involving relaxed or rigor muscle fibers [74, 75]. For single-molecule studies, the linear elasticity was observed in both the positive and negative strain regions for myosin S1 and HMM [55, 57], which are produced by the cleavage of the flexible S2 coiled-coil region from native myosin molecules. However, the elasticity of full-length myosin has not been tested for both strain regions. Thus, we investigated the elasticity of native skeletal myosin molecules using a combination of optical tweezers and a single fluorescence imaging technique [30] and found that the stiffness substantially decreases to 0.02 pN/nm when myosin is negatively strained, compared with the 2.9 pN/nm observed on the positive strain side (Fig. 1b). Interestingly, the lower stiffness value of approximately 0.02 pN/nm of single-myosin molecules observed in the negative strain region is similar to the theoretically estimated bending stiffness of S2 [76] (approximately 0.01 pN/nm), suggesting that the lower stiffness may be associated with a bending or buckling of the S2 portion when myosin molecules are negatively strained. Electron tomography of swollen rigor insect flight muscle fibers revealed a wide range of S2 axial angle distributions, and 17 % of the S2 was found to be oriented perpendicular to the myosin filament (−90°) or more negatively than −90° [77], implying that the bending or buckling of myosin heads may arise from the S2 coiled-coil. These results are consistent with the fact that the elasticity of S1 and HMM myosin molecules is continuously linear, even in the negative strain region [55, 57] because these truncated proteins cannot be softened without the flexible S2 portions. The nonlinear elasticity of native myosin molecules may be attributed to the significant difference in stiffness between the S1 and S2 portions of the myosin head.
The degree of bending or buckling of the S2 portion can be theoretically estimated using a combination of the Principle of the Equipartition of Energy and the beam equation [78]. The persistence length (L p) of S2 with a coiled-coil structure that is 40 nm in length (S) is approximately 100 nm, and the average angle of one end (θ(S)) relative to the other end (θ(0) = 0) caused by thermal fluctuations is approximately 35° according to Eq. (1) [78], indicating that thermal forces are enough to cause the bending of S2.
| 1 |
If the load is continuously applied to one end of the S2 portion and exceeds the buckling load, S2 eventually buckles. Such large deflections can be theoretically predicted by the elastica theory [58, 78]. In the elastica model, the deformations of a single elastic isotropic beam with the axial load, F, can be estimated by solving the following second order ordinary differential equation;
| 2 |
where θ and s are the rotational angle of the cross-section and the path of the cross-section along the main-axis of the beam (Fig. 2a), and EI is flexural rigidity (= 400 × 10−30 N m2) for myosin S2 [78]. The solution of Eq. (2) can be derived by satisfying the boundary condition (see “Appendix” for details) as the following:
| 3 |
where l 0 is the length of S2 (= 40 nm). In Eq. (3), the constant, , is determined by satisfying the following boundary condition at a given load, F,
| 4 |
Fig. 2.
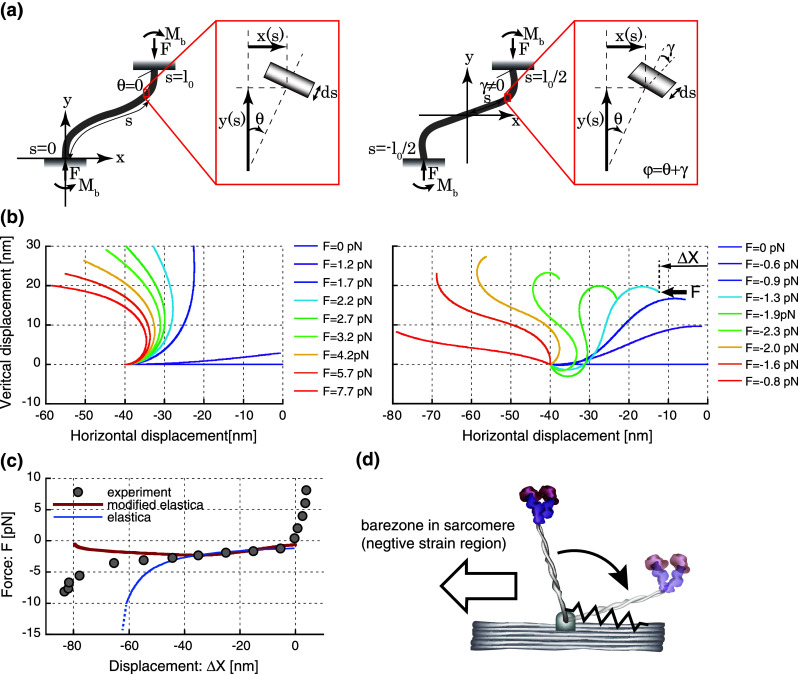
Deflection of the myosin S2 rod under horizontal compressive loads. a The schematic diagram of the regular elastica model (left) and the elastica model (right) modified by adding the angle of shear deformations, γ. b The deflections of the S2 rod are estimated by the elastica model (left) and the modified elastica model (right). One end is fixed at the horizontal position of X = −40 nm, while the other, free end is subject to the horizontal compressive load (F). c The force–displacement relationships in the experiment (gray circles), the elastica model (blue line) and the modified elastica model (red line). In the elastica model, the displacements are calculated as the change in the horizontal displacement from its original position of X = 0, as denoted by in Fig. 2a. The shaded region indicates the difference in curves between the experiment and the modified elastica model below the horizontal displacement of −40 nm. d A schematic diagram of the potential elasticity at the S2 rod-myosin filament junction. This elasticity, depicted by a spring, may contribute to the structural constraint that prevents the excessive rotation of the S2 rod toward the negative strain side, resulting in the discrepancy in the force–displacement relationships between the experiment and the elastica model below −40 nm
Finally, the XY positions of the cross-sectional plain along the path, , are given as,
| 5 |
From Eq. (5) for , the deformations of S2 at a given amount of load, F, are estimated and shown in Fig. 2b. The horizontal displacements, , are calculated by comparing the horizontal positions of the beam end with that at F = 0,
| 6 |
In Fig. 2c, the force–displacement relationships predicted by the elastica model were similar to our experimental results between 0 and −40 nm. However, the predicted buckling loads drastically increased in the negative direction below −40 nm, while the experimental results showed a small change in buckling loads for a wide range of displacement from 0 to −80 nm, suggesting that a large deformation of myosin S2 cannot be modeled by a single elastic isotropic beam used in the elastica model. Such a wide range of stable buckling loads was found in the rubber bearing for base-isolated buildings and can be modeled by the modified elastica model that allows shear deformations [79]. The modified elastica model is composed of two angular components, the angle caused by bending moment, , and the angle of shear deformation, (Fig. 2a). In this model, the solution of Eq. (2) can be expressed in terms of elliptic integrals,
| 7 |
where is the angle of deformation, and is the complete elliptic integral of the first kind for the given parameter, k, and satisfies the following equation,
| 8 |
where is the critical buckling load and and for myosin S2 are the shear modulus and the flexural rigidity, respectively. By incorporating with the boundary conditions (see “Appendix” for details), the following equation can be derived,
| 9 |
where is the elliptic integral of the second kind. By satisfying Eq. (9) with the initial length, l 0, to be 40 nm for myosin S2, the critical buckling load, , can be determined and is substituted into Eq. (8) to obtain the value of . Then, the XY-positions of the cross-sectional plane can be obtained by using Jacobi elliptic functions, cn and dn,
| 10 |
The deformations of myosin S2 were shown in Fig. 2b. The horizontal displacements, , are calculated by comparing the horizontal position of the beam end at by definition in this model (Fig. 2a) and thus,
| 11 |
The force–displacement relationships predicted by the modified elastica model appeared to show a moderate change in buckling loads and resemble our experimental results better than those predicted by the regular elastic model (Fig. 2c). However below −40 nm, the predicted buckling loads gradually decreased toward zero, while the experimental results gradually increased, suggesting that an additional elasticity may exist and contribute to an increase in buckling loads below −40 nm. This idea implies that the S2 rod is constrained somehow, either structurally or by the ionic interactions between S2 and the thick filament backbone [80], to maintain its projection toward the positive strain side, which is the direction opposite to the bare zone of sarcomeres and favorable for force generation (Fig. 2d). The additional elasticity at the S2-myofilament junction can be characterized by calculating the difference between the experimental and theoretical curves in the force–displacement plot (Fig. 2c). The area surrounded by these curves yields 100 pNnm of work with a displacement of 40 nm, as shown in the shaded region in Fig. 2c, suggesting an average stiffness of 0.125 pN/nm Such additional elasticity is sufficient to maintain the orientation of the head toward the positive strain direction against the thermal agitation (k B T). Taken together from these analyses, two things should be pointed out: first, a wide range (almost double length of S2) of the nearly constant buckling loads in the colied-coil S2 can be modeled by implementing the additional deformable component in the elastica model (e.g., shear deformations); second, the additional elastic component may exist possibly at the junction between the S2 and the backbone of myosin filament and maintain the orientation of myosin heads in the positive strain direction. According to Nishimura’s study on the rubber bearing [79], the ratio between the shear modulus and the buckling load is a critical factor to maintain the stable buckling load against a wide range of deformations. Thus, it is very intriguing to imagine that myosin S2 may be evolutionally optimized to avoid a drastic increase in buckling loads against a large amount of deformation possibly by adopting the optimum shear modulus as well as the bending modulus against the buckling loads during muscle contractions.
Working stroke size of skeletal myosin
In this section, three terms associated with displacement generated by myosin molecules are distinctively defined because they have been used ambiguously without distinction in past studies: working stroke size, step size, and interaction distance. Working stroke size is the limit of the displacement generated by the conformational changes of the myosin head. Step size is the observed sliding displacement of actin filaments generated by myosin molecules and can be altered at different velocities and loads. Finally, interaction distance is the sum of the working and drag stroke distance per ATP hydrolysis cycle. In the later part of this section, the relationship between working stroke size and step size is discussed. Interaction distance is discussed in the next section, “Drag effect on force generation.”
A series of studies using crystallography [81–83], electron microscopy [84], and X-ray diffraction [20, 85] claim to have proven the lever arm hypothesis, which states that the generation of force and displacement in muscle is accompanied by a tilting of the light chain domain, referred to as the “lever arm” (approximately 9 nm of the α-helix), with respect to the catalytic domain bound to actin. These reports indicate a 40–70° tilt of the light chain domain, equivalent to 6–10 nm of axial movement of the end of the lever arm. Huxley [1] originally estimated the size of a working stroke to be approximately 16 nm by fitting the theoretical model (cross-bridge model) with the results of heat measurements by Hill [86]. Huxley further experimentally observed a working stroke of 10 nm, which is a synchronous working stroke of myosin molecules during the quick force recovery period when muscle lengths/tensions are quickly released within a few milliseconds [12, 87]. Pate et al. [88] estimated the size of a working stroke by applying realistic cross-bridge kinetics to Huxley’s cross-bridge model [11] and found that the working stroke size is approximately 10 nm. In a motility assay, in which either individual myosin molecules are spread on a cover glass surface [89–91] or myosin-rod cofilaments move along the actin filaments suspended between two optically trapped beads [92], the estimates of the working stroke size vary widely between 10 and 200 nm, presumably due to the use of indirect estimates for the number of myosin heads attached to the actin filament.
Beginning in 1994, several groups successfully measured the displacement of actin filaments generated by single-myosin molecules. Finer et al. [8] used optical tweezers and reported a working stroke size of 11 nm produced by HMM, while Ishijima et al. [9] used glass needles attached to actin filaments that interacted with myosin-rod cofilaments and reported a slightly larger size of 17 nm at near-zero load. Molloy et al. [51] determined a 3–5-nm working stroke size generated by single S1 and HMM by accounting for the randomizing effect of thermal filament fluctuations. Since then, the working stroke sizes of the single-headed S1, the double-headed HMM, and full-length myosin have been measured by several groups and vary from 3 to 20 nm (Table 1). The differences are presumably due to several potential factors, including protein-bead linkage compliances, random orientations of the myosin head relative to actin filaments, low affinity of the myosin heads to actin filaments, and utilization of different step detection techniques (e.g., variance picking and mean–variance analysis). As discussed in the previous section, protein-bead linkage compliance has been experimentally reduced by the refinement of optical systems, such as the optical force-clamp feedback system, resulting in smaller working stroke sizes [40, 56]. Takagi et al. [40] reported a working stroke size of 7 nm for full-length myosin, while Capitanio et al. [56] reported working stroke sizes of 3 and 5 nm for S1 and HMM, respectively. The effect of the orientation of the myosin heads relative to the actin filaments on force and step generation was rigorously tested by Tanaka et al. [93], who found a significant reduction in both the force and step size by increasing the angles between the myosin-rod cofilament and the actin filament from 0 to 90°, suggesting the importance of the orientation of the myosin heads relative to the actin filaments. To increase the affinity of myosin attachment, Kitamura et al. [70] used flexible glass needles that enabled the myosin to continuously stay closer to the actin binding sites, as in muscle. As a result, the myosin molecules displayed several consecutive substeps of 5.5 nm, which were generated during the 9–13-nm steps. The dwell times of each substep were independent of the ATP concentrations, while those of the total step were dependent on ATP, implying that myosin can generate multiple steps per ATP molecule hydrolyzed (i.e., the loose-coupling model). Although this is an extremely intriguing phenomenon to discuss, it is beyond the focus of this review and should be discussed elsewhere.
Table 1.
Summary of the reported mean values for the unitary displacements, maximum forces, stiffnesses of single-myosin molecules, and solution components
| Myosin | Apparatus | Displacement (nm) | Maximum force (pN) | Stiffness (pN/nm) | Assay buffer and temperature | |
|---|---|---|---|---|---|---|
| Single molecules | ||||||
| Ishijima et al. [9] | Full-length in cofilament | Micro needle | 17.0 | 5.7 (~9) | 25 KCl, 20Hep pH 7.6, 27 °C | |
| Guilford [101] | Full-length | Trap | 10.6 | 3.4 | 25 KCl, 25Imi pH 7.4, 25 °C | |
| Kad et al. [94] | Full-length | Trap | 5.0*1, 10.6*2, 6,6*3, 13.7*4 | 25 KCl, 25Imi pH 7.4, 25 °C | ||
| Takagi et al. [40] | Full-length | Trap with force-clamp | 7.0 | 9.0 (~17) | 1.3 | 20 KCl, 10Hep pH 7.0, 25 °C |
| Kaya and Higuchi [30] | Full-length in cofilament | Trap | 4.3–7.9 | 10.4 (~13) | 2.9 | 20 KCl, 10Pip pH 7.1, 25 °C |
| Molloy et al. [51] | S1 & HMM | Trap | 3.0 (S1) 5.0 (HMM) | 1.7 (~5.5) | 0.17 (S1) | 25 KCl, 10Tri pH 7.0, 23 °C |
| Nishizaka et al. [52] | S1 & HMM | Trap | 0.58 | 25 KCl, 25Imi pH 7.4, 28–30 °C | ||
| Steffan et al. [102] | S1 | Trap | 5.4 | 25 KCl, 25Hep pH 7.4, RT | ||
| Capitanio et al. [56] | S1 | Trap | 3.0 + 1.1 (fast) 4.9 + 1.6 (slow) | 0.9–1.4 0.35–0.4 | 25 KCl, 25Hep pH 7.2, 22 °C | |
| Kitamura et al. [70] | S1 | Scanning probe | 9.2 (high load) 13.0 (low load) | 2.0 (~5) | 25 KCl, 20Hep pH 7.8, 20–27 °C | |
| Lewalle et al. [57] | S1 | Trap | 1.79 (~4) | 22 °C | ||
| Finer et al. [8] | HMM | Trap | 11.0 | 3.5 (~7) | 0.4 | 25 KCl, 25Imi pH 7.4, 21 °C |
| Mehta et al. [54] | HMM | Trap | 5.0–6.0 | 0.65 | 25 KCl, 25Imi pH 7.4, 21 °C | |
| Veigel et al. [55] | HMM | Trap | 5.5 | 0.69 | 25 KCl, 25Imi pH 7.4, 23 °C | |
| Tyska et al. [103] | Single and double headed HMM | Trap | 6.8 (single) 11.6 (double) | 0.7 (single) 1.4 (double) | 25 KCl, 25Imi pH 7.4, 25 °C | |
| Ruff et al. [104] | HMM | Trap + needle | 5.5 | 25 KCl, 25Imi pH 7.4, 23 °C | ||
| Ishijima et al. [105] | Single-headed myosin in cofilament | Trap | 13.5 | 25 KCl, 20Hep pH 7.6, 25 °C | ||
| Tanaka et al. [93] | Single-headed myosin in cofilament | Trap | 10.0 | 25 KCl, 20Hep pH 7.6, 20–25 °C | ||
| Single fibers | ||||||
| Huxley and Simmons [11] | Rana temporaria semitendinousus | Length perturbation | 8.0 |
Ringer pH 7.0, 0–4 °C |
||
| Yamada et al. [106] | Rabbit psoas | Unloaded shortening | 10.0 |
200ion pH 7.0, 20–22 °C |
||
| Higuchi and Goldman [4] | Rabbit psoas | Isometric | 11–60** |
200ion pH 7.1, 19–20 °C |
||
| Piazessi et al. [19] | Rana esculenta tibialis anterior | Force/length perturbation | 4–7 | 11.5 | 5.0 |
Ringer pH 7.1, 4 °C |
| Reconditi et al. [20] | Rana temporaria tibialis anterior | Force perturbation | 5.2–8.1 |
Ringer pH 7.1, 4 °C |
||
| Piazessi et al. [6] | Rana temporaria tibialis anterior | Force perturbation + X-ray | 4.0–10 | 6.0 | 3.3*** |
Ringer pH 7.1, 4 °C |
| Linari et al. [5] | Rabbit psoas | Isometric | 6.6 | 1.7 |
200ion pH 7.1, 20 °C |
|
The numbers shown in parentheses are the maximum values observed (e.g., 4 pN/nm for the maximum stiffness values reported by Lewalle et al. [57]). *1 and *2 The step sizes of single-myosin molecules interacting with actin filaments decorated with troponin-tropomyosins (TN/TM) and without TM/TN in the absence of Ca2+. *3 and *4 The sizes of the first and second steps observed in staircase stepping movements when multiple myosin molecules interact with the TM/TN-decorated actin in the absence of Ca2+. ** The unitary displacement includes the working stroke and drag distance. *** The original value was shown as the compliance, which is the inverse of stiffness, in the paper. In the column of “Assay Buffer and Temperature”, all solution concentrations are in mM. Hep, Pip, Tri, and Imi correspond to the buffers HEPES, PIPES, tris, and imidazole, respectively. 200ion indicates that the total ionic strength of solution was kept at 200 mM, but each composition was different for different conditions (e.g., relaxing, activating, and caged ATP). For details, please see the studies listed in the references. Ringer indicates the Ringer solution (115 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl2, 3 mM phosphate buffer)
To the best of our knowledge, only one single-molecule study has investigated the effect of regulatory proteins, namely troponin (Tn) and tropomyosin (Tm), on myosin step size [94]. The step sizes were compared between the interaction of myosin with unregulated (no Tn/Tm) and regulated (with Tn/Tm) actin filaments in the absence of Ca2+. This study revealed that the average step size for regulated actin filaments was 5.0 nm, almost half the 10.6-nm step size observed for unregulated actin filaments. Furthermore, when myosin density was increased twofold for the regulated actin condition, staircase stepping events were more frequently observed because of the interaction between multiple myosin molecules. The sizes of the first and second steps were 6.6 and 13.7 nm, respectively. From these results, the researchers interpreted that the size of the first step is comparable to the step size of a single burst caused by a single-myosin, which interacts with a regulated actin filament, whereas the size of the second step and subsequent steps resembles the step size associated with an unregulated actin filament, suggesting the following scenario: Tn/Tm prevents the optimal interaction of myosin with actin in the absence of Ca2+, possibly by allowing only one of two heads to interact with actin filaments, and produces half the step size as that observed in the first step of staircase stepping. Then, once the first myosin molecule binds to actin, the neighboring Tn/Tm units are activated, allowing the second myosin molecule to interact with actin without the Tn/Tm inhibitory effect, resulting in twice the step size of the first myosin. Thus, this step size alternation model take into account the effect of the cooperative activation of thin filaments on step generation.
In our experimental setup, we synthesized myosin-rod cofilaments by mixing myosin molecules and fluorescently labeled myosin rods at a molar ratio of 1:2 and quickly diluted them with a low ionic solution [30]. As a result, we generated 400–900-nm myosin-rod cofilaments that typically contained 3–5 myosin molecules that could interact with actin filaments. Synthetic myosin-rod cofilaments maintain bi-polar structures [95, 96] such that all of the myosin molecules are orientated in the same direction toward the central region. Thus, the reduction in step generation caused by random orientations of the myosin heads can be avoided. In addition, multiple myosin molecules embedded in the cofilaments hold actin filaments for a number of consecutive acto-myosin interaction cycles, resulting in an increase in the affinity for myosin attachment during processive movements [30]. On the basis of dwell time analysis, we found that the individual steps observed during processive movements are generated by one myosin molecule, and the average working stroke size extrapolated from the step size-load relationship was 8 nm at no load.
Several research groups have shown load-dependent step sizes for single-myosin molecules. Ishijima et al. [9] demonstrated that the observed step sizes produced by single-myosin molecules embedded in myosin-rod cofilaments decreased from 17 to 5 nm when the imposing loads increased from 1.5 to 6 pN. Kitamura et al. [70] also reported that the average ensemble step sizes produced by S1 are 13 nm for a low load (low needle stiffness) and 9 nm for a high load (high needle stiffness). Such load-dependent step sizes are consistently observed in single-fiber studies. Piazessi et al. [19] performed quick tension release experiments to release single-fiber tensions within a few hundred microseconds to avoid the contribution of myofilament compliance and suggested that the working stroke sizes decreased in a load-dependent manner from 7 to 4 nm with increasing loads from zero to the maximum isometric tension. The load-dependent step sizes were further investigated in a quick tension release experiment on muscle fibers using the X-ray-interference technique [20]. The ratio of the M3 X-ray reflection intensities between the higher and lower angle peaks from myosin heads spaced at 14.5 nm in each array is consistent with the concept that the working stroke is generated a few milliseconds after the quick tension release [19]. The researchers suggested that the working stroke size at a low load is likely set by the structural limit, whereas smaller stroke sizes at a high load are caused by the detachment of the motor before reaching this limit [20]. Piazzesi et al. [6] demonstrated that the rate of detachment for the myosin heads increases strongly with an increase in the velocity of shortening, suggesting that the detachment of myosin molecules is primarily governed by the critical conformations. Thus, myosin molecules quickly reach the critical conformations (the full working stroke size) and detach during faster speeds of shortening, while the effective stroke size is reduced at a higher motor force during slower speeds of shortening because the stretching of the elastic portion caused by the higher load induces the transition from one conformation to another.
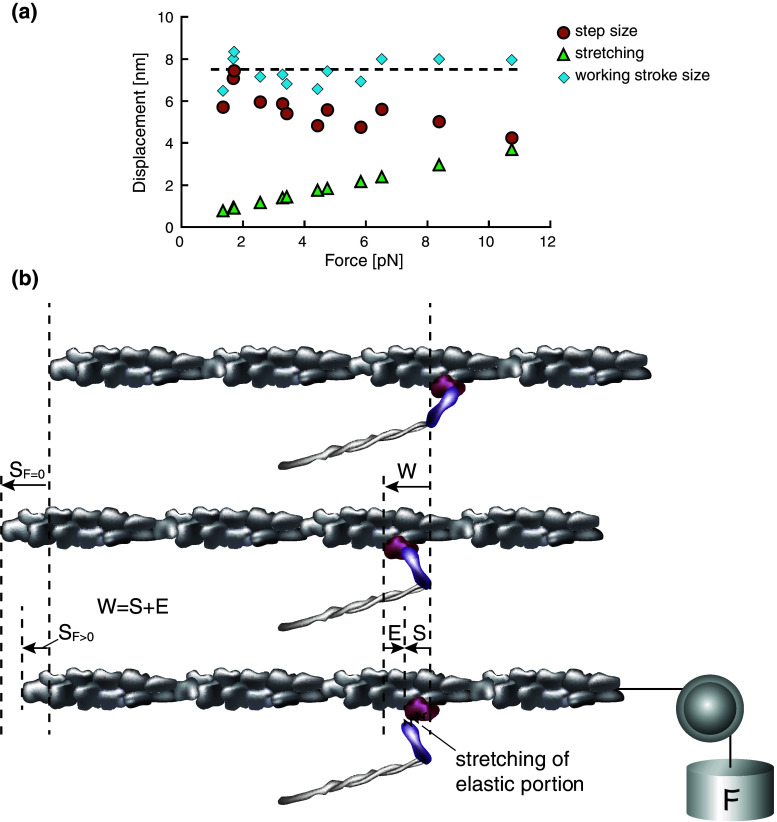
The load-dependent step sizes can also be interpreted from a mechanical perspective. We demonstrated that the load-dependent step sizes of a single-myosin embedded in myosin-rod cofilaments change from 7 to 4 nm in the loading range of 1–12 pN [30]. By incorporating the nonlinear elasticity obtained from the single-molecule elasticity measurements into the load-dependent step sizes, we found that the sums of the amount of elastic elongation of the myosin heads and the observed step size are nearly constant at 8 nm for any load (Fig. 3a). Therefore, we proposed that the working stroke size is the sliding distance generated by the conformational changes of the myosin head, while the apparent decreases in the step sizes with increasing loads are due to the elastic elongations in the myosin head partly cancelling the working stroke of 8 nm (i.e., working stroke size = observed step size + stretch of elastic portion) (Fig. 3b). Our proposed mechanism is consistent with the model proposed by Reconditi et al. [20] in the sense that the working stroke size is the maximum sliding distance of the actin filaments and is limited by the structures of the myosin head. Thus, the observed step sizes at no load are equivalent to the working stroke size. Therefore, we prefer the term “working stroke size” to signify the maximum sliding distance of the actin filament produced by the conformational changes of the myosin head and distinguish it from the observed “step size.” In this definition, the working stroke size is 8–10 nm [6, 30]. Two potential factors have been proposed for the decrease in the step size at higher loads: (1) the detachment of the myosin head before the completion of a full working stroke [6, 20] and (2) the elastic elongation of the myosin head, which partly cancels the full working stroke size [30].
Fig. 3.
Mechanical model of working stroke size. a The step size, the amount of stretching in the elastic portion, and the working stroke size are plotted as a function of load. The observed step sizes (circles) obtained from the optical trap assay decrease with increasing loads [30], while the amount of stretching in the elastic portion of the myosin head (triangles) estimated from the elasticity measurement in the positive strain side of Fig. 1a increases. The working stroke sizes (diamonds), defined as the sum of the step size and the amount of stretching, appear to be consistently approximately 8 nm at any load, suggesting that the working stroke size is 8 nm and that there is a structural limit for myosin conformational changes. b A schematic diagram of the working stroke size, along with the step size and the stretched amount of the elastic portion. At no load (the mid panel), the working stroke of the myosin head (W) is purely translated to the sliding movement of actin, which corresponds to the observed step size (W = S F=0). When a load is applied (the bottom panel), the stretching of the elastic portion of the myosin head (E) partially cancels the working stroke size such that the working stroke size is reduced by E, and the remnant distance is translated to the actin sliding (W − E = S F>0)
The recent results regarding working stroke size obtained from single-fibers and single-myosin molecules reveal values that range between 5 and 10 nm and that are consistent with the axial displacement of the end of the light chain domain estimated from structural studies. Piazzessi et al. [6] suggested that the working stroke sizes change from 5 to 10 nm as the velocity increases from zero to nearly the maximum value, whereas the force produced by the myosin head is relatively insensitive to the shortening velocity. The working stroke size and the force per attached head at a slow shortening velocity are 6 nm and 6 pN, respectively [6], giving an upper bound on mechanical work of W = (1/2 × F × d) = 18 zJ, which is approximately 23 % of the mechanical efficiency. However, by using a force-clamp system to ensure that the force generated by single-myosin molecules was as high as possible, Takagi et al. [40] reported that the mechanical work of a single-myosin molecule can be increased to 32 zJ = (1/2 × 9 pN × 7 nm), which is 40 % of the mechanical efficiency and falls within the range of the 30–70 % thermodynamic efficiency observed in whole muscles [7]. Thus, single-myosin molecules could have a full capacity of mechanical work output that is nearly as large as the whole muscle.
Drag effect on force generation
The muscle force output is a result of the force balance between the working (positive) and drag (negative) forces exerted by myosin molecules and external forces [3]. If the elasticity is assumed to be linear [11], the average working force (distance) at the maximum shortening speed (i.e., no external force) is counterbalanced by the average drag force (distance), given that the net force output is zero [3, 97]. If force output is required at a slower velocity, the working force must overcome the drag force by decreasing the number of drag motors and/or increasing the number of working motors. A decrease in the number of drag motors can naturally occur at a slower velocity because working motors are activated for a longer time and, thus, have a higher probability of detaching before exerting a drag force. In addition, an increase in the number of working motors appeared to be promoted by decreasing the detachment rate of myosin molecules at higher loads (slower velocities), as reported in single-molecule experiments involving smooth muscle myosin and myosin V [98, 99]. Piazzesi et al. [6] argued that in muscle, the detachment rate of skeletal myosin is more sensitive to velocity than force and may be controlled by the myosin motor conformation rather than its load or elastic strain, as proposed by Veigel et al. [98]. Although an increase in the detachment rate at a faster shortening velocity was suggested, myosin motors still have a higher probability of being negatively strained before detachment because the faster sliding of the actin filaments quickly pushes strongly bound myosin molecules into the negative strain region before detachment. For instance, in a simple calculation scheme, the attachment time of myosin at the maximum shortening velocity is approximately 1–2 ms, as estimated from the kinetics in the strongly bound state [78]. Thus, the drag stroke distance could be part of the sliding distance of 7–14 nm (1–2 ms × 7 μm/s), with a maximum shortening velocity of 7 μm/s [4].
Higuchi and Goldman [4] rigorously investigated the interaction distance (D i), which is the sum of the working and drag stroke distance per ATP hydrolysis cycle, and reported a distance of 60 nm between 400 and 700 μM ATP at a shortening velocity of 1.94 μm/s. At the maximum shortening velocity, the extrapolated value of D i is 100–190 nm, which is reduced to 30–60 nm if the significant contribution of thin and thick filament extensibility to the half-sarcomere compliance is approximately 70 % of the sarcomere compliance [16, 17]. Higuchi and Goldman [4] concluded that if the elasticity is assumed to be linear, the working stroke size must be half of 70–130 nm, or 30–60 nm in our estimates, at the maximum shortening, which cannot be compatible with a single tilting motion, suggesting multiple force generation cycles (attachment and detachment) per ATP hydrolysis cycle. However, if the elasticity of single skeletal myosin molecules is considered to be nonlinear, as we have shown [30], a single working stroke size of 10 nm is still feasible, with a remnant distance of 60–120 nm or 20–50 nm in our estimates as the drag stroke distance because the drag force caused by a long drag stroke can be small in the presence of nonlinear elasticity. Such a small drag force can be counterbalanced by the working force generated by the small working stroke size of 10 nm.
Despite a potential increase in drag (resittance) on myosin molecules at the maximum shortening speed, the simple force equilibrium mathematical model can predict that the maximum shortening speed is greatly enhanced by the nonlinear elasticity. In the model, it is assumed that at a steady state, an ensemble of myosin motors moves an actin filament at a speed of v under force equilibrium. Then, the following equation must be satisfied:
| 12 |
where S(x) is the force-extension curve of myosin at the extension of myosin (x), d, and k d are the working stroke size and the dissociation rate constant of myosin, respectively. If the elasticity is linear (i.e., ), the solution of this integral is given as the following:
| 13 |
Thus, the maximum shortening speed is limited by the working stroke distance and the dissociation rate constant [100]. In the case of nonlinear elasticity (i.e., for x ≥ 0 and for x < 0; k 1 > k 2), Eq. (6) can be expanded as the following:
| 14 |
By using the first-order approximation of the exponential term as follows,
| 15 |
the solution of Eq. (8) yields the following:
| 16 |
Compared with Eq. (13) for linear elasticity, the additional term, , indicates that the maximum shortening speed can be increased by the factor of in the case of nonlinear elasticity (i.e., for ) because the sliding speed of an actin filament is accelerated by a reduction of drag force due to the lower stiffness in the negative strain region. In our study, (from the experimental data shown in Fig. 1b, pN/nm for and pN/nm for , on average) and, thus, one would expect the maximum shortening speed of full-length myosin molecules to be approximately three- to fourfold faster than that observed in S1 or HMM, which has a presumably linear elasticity due to the cleavage of the flexible S2 portion. Although such a large increase in shortening speed, in practice, has not been reported, it has been reported that the motility speed of a synthetic myosin filament sliding along an actin filament is approximately 11 μm/s at 27 °C [92] and is 40 % higher than the S1 motility speed of 6.8 μm/s at 29 °C [69]. This small increase in motility speed is possible due to the assumptions of the model, which assumes a large number of myosin molecules with a large drag distance, assumes biphasic elasticity characterized by and (e.g., non-continuous change in stiffness as shown in Fig. 1a), and neglects the load-dependent dissociation rate and other potential factors.
Nonlinear elasticity is obviously an advantage for reducing the drag force during a fast shortening when the myosin molecules remain attached after executing a working stroke and are subsequently strained into the negative strain region as the actin filament is moved by other attaching myosin molecules. Meanwhile, the higher stiffness in the positive strain region ensures the generation of a high working force with a small amount of strain. From an energetic point of view, the nonlinear elasticity reduces the loss of energy more than the linear elasticity. For example, if a single-myosin molecule is negatively strained by 5 nm, the energy loss is calculated to be 36 pNnm in the case of linear elasticity, with a stiffness of 2.9 pN/nm (2.9 × 52/2 = 36). This accounts for 36 % of the total energy utilized by the hydrolysis of a single ATP molecule (approximately 100 pNnm = 10−19 J). In contrast to linear elasticity, the energy loss is only 3 pNnm, or 3 % of the total energy, in the case of nonlinear elasticity, as shown in Fig. 1a. However, one may argue that the nonlinear elasticity would not matter for the reduction of molecular interference in the case of rapid muscle contractions, given that the detachment of the myosin heads increases with the speed of shortening [6]. However, the detachment rates were estimated by dividing the measured shortening velocity by the working stroke size [6] and have not been directly measured by monitoring the individual detached heads, as studied for single smooth myosin and myosin V molecules [98, 99]. Thus, it is still too early to conclude that the drag effect is negligibly small due to the increase in the detachment rate during rapid contractions. The direct measurement of individual myosin heads during muscle contractions must be performed to elucidate the drag effect on muscle contractions.
Molecular mechanisms of muscle contractions elucidated from the mechanical properties of single skeletal myosin molecules
The mechanical properties of single skeletal myosin molecules revealed by single-molecule and single-fiber studies have shed light on the molecular mechanisms of muscle contractions. In our single-molecule study, the force generated by a single-myosin molecule was directly coupled to the external loads imposed by optical tweezers and increased up to 12 pN in a myosin-rod cofilament, which contained approximately five myosin molecules interacting with an actin filament maximally in rigor [30]. This value is also consistent with the high force generated by a single HMM, as observed using the optical force clamp system [40]. Intriguingly, during isometric contractions, the average force per myosin head in single-fibers is thought to be approximately 6 pN [6, 28], which is lower than the maximum force value of approximately 12 pN observed in the recent single-myosin experiments [30, 40]. These results suggest that the force production of single-myosin molecules in muscle may be modulated to maintain the force level below the maximum force capacity. Moreover, the combination of X-ray interference and mechanical measurement techniques on single muscle fibers demonstrated that the force per myosin head is almost constant, approximately 6 pN from the isometric tension (T 0) to 50 % of T 0, while the fraction of myosin heads attached to the actin filament substantially decreases, from 30 to 15 %, in accordance with force demands [6]. Thus, in a large ensemble of myosin motors, individual myosin molecules are modulated to maintain a moderate force output, whereas the net force output of the muscle is sensitively controlled by modulation of the fraction of myosin heads attached. Such modulations may be advantageous for efficient performance of myosin motors against a wide range of external loads.
Concluding remarks
The mechanical properties of single skeletal myosin molecules have been investigated in many single-muscle fiber and single-molecule studies because of the tremendous importance of myosin in understanding the molecular mechanisms of muscle contractions. In this review, we focused on two mechanical properties, elasticity and the working stroke size, investigated in both single-fiber and single-molecule studies. We demonstrated that the elasticity of single-myosin molecules is nonlinear in both the positive and negative strain regions. The variation of the stiffness value in the positive strain direction may be explained by the nonlinear elastic behavior of the myosin head, whereby stiffness increases with increasing loads. In the negative strain direction, the stiffness dramatically decreases due to the buckling of the S2 coiled-coil structures, and this significant reduction in stiffness may play a role in reducing the molecular interference caused by negatively strained myosin molecules. Additional elasticity may exist at the S2-myosin filament junction to prevent the excessive deflection of the myosin head toward the negative strain direction, which is important for maintaining the correct orientation of the myosin head before it attaches to the actin filaments. The working stroke size is 8–10 nm and reflects the maximum sliding distance of the actin filament generated by the conformational changes of the myosin head, while the step size is the apparent sliding distance of the actin filament, which changes in a load-dependent manner. Two mechanisms associated with the load-dependent step size have been proposed: (1) the detachment of the myosin head caused by external loads before the completion of the full working stroke and (2) the elastic elongation of the myosin head caused by external loads, which partially cancels the full working stroke. Recent single-molecule studies have shown that the mechanical efficiency of single skeletal myosin molecules can reach the level observed in muscles; however, the mechanical work output of single-myosin molecules in muscles is modulated in a sophisticated manner that depends on external demands, such as loads and shortening velocities. In the future, accurate measurement of the position of the myosin head will surely reveal the molecular mechanisms associated with acto-myosin interactions in more detail and help address the following questions: (1) what is the strain of the myosin head against a given load?; (2) what is the size of the working stroke and drag stroke distances at various loads per cycle of acto-myosin interactions?; (3) what are the working and drag forces?; and (4) what are the attachment and detachment times and, thus, the duty ratio of the myosin heads?
Appendix
In the elastica model, Eq. (3) can be derived by multiplying at both sides of Eq. (2) as the following:
| 17 |
By integrating Eq. (17), the following equation can be derived as,
| 18 |
The constant, C, can be determined by satisfying the boundary condition, , where is the bending moment and can be given as,
| 19 |
By assuming in Eq. (18), Eq. (3) can be derived.
In the modified elastica model [79], Eqs. (7), (8) and the boundary conditions at the beam end when the beam is buckled (e.g., etc.), the initial length of beam, , can be expressed as,
| 20 |
By substituting from Eq. (8) into Eq. (20), Eq. (9) can be derived.
References
- 1.Huxley AF, Niedergerke R. Structural changes in muscle during contraction; interference microscopy of living muscle fibres. Nature. 1954;173(4412):971–973. doi: 10.1038/173971a0. [DOI] [PubMed] [Google Scholar]
- 2.Huxley H, Hanson J. Changes in the cross-striations of muscle during contraction and stretch and their structural interpretation. Nature. 1954;173(4412):973–976. doi: 10.1038/173973a0. [DOI] [PubMed] [Google Scholar]
- 3.Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- 4.Higuchi H, Goldman YE. Sliding distance per ATP molecule hydrolyzed by myosin heads during isotonic shortening of skinned muscle fibers. Biophys J. 1995;69(4):1491–1507. doi: 10.1016/S0006-3495(95)80020-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Linari M, Caremani M, Piperio C, Brandt P, Lombardi V. Stiffness and fraction of Myosin motors responsible for active force in permeabilized muscle fibers from rabbit psoas. Biophys J. 2007;92(7):2476–2490. doi: 10.1529/biophysj.106.099549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Piazzesi G, Reconditi M, Linari M, Lucii L, Bianco P, Brunello E, Decostre V, Stewart A, Gore DB, Irving TC, Irving M, Lombardi V. Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell. 2007;131(4):784–795. doi: 10.1016/j.cell.2007.09.045. [DOI] [PubMed] [Google Scholar]
- 7.Smith NP, Barclay CJ, Loiselle DS. The efficiency of muscle contraction. Prog Biophys Mol Biol. 2005;88(1):1–58. doi: 10.1016/j.pbiomolbio.2003.11.014. [DOI] [PubMed] [Google Scholar]
- 8.Finer JT, Simmons RM, Spudich JA. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. 1994;368(6467):113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- 9.Ishijima A, Harada Y, Kojima H, Funatsu T, Higuchi H, Yanagida T. Single-molecule analysis of the actomyosin motor using nano-manipulation. Biochem Biophys Res Commun. 1994;199(2):1057–1063. doi: 10.1006/bbrc.1994.1336. [DOI] [PubMed] [Google Scholar]
- 10.Svoboda K, Block SM. Force and velocity measured for single kinesin molecules. Cell. 1994;77(5):773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
- 11.Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233(5321):533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- 12.Ford LE, Huxley AF, Simmons RM. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J Physiol. 1977;269(2):441–515. doi: 10.1113/jphysiol.1977.sp011911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ford LE, Huxley AF, Simmons RM. The relation between stiffness and filament overlap in stimulated frog muscle fibres. J Physiol. 1981;311:219–249. doi: 10.1113/jphysiol.1981.sp013582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kojima H, Ishijima A, Yanagida T. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc Natl Acad Sci USA. 1994;91(26):12962–12966. doi: 10.1073/pnas.91.26.12962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Huxley HE, Stewart A, Sosa H, Irving T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys J. 1994;67(6):2411–2421. doi: 10.1016/S0006-3495(94)80728-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wakabayashi K, Sugimoto Y, Tanaka H, Ueno Y, Takezawa Y, Amemiya Y. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys J. 1994;67(6):2422–2435. doi: 10.1016/S0006-3495(94)80729-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Higuchi H, Yanagida T, Goldman YE. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys J. 1995;69(3):1000–1010. doi: 10.1016/S0006-3495(95)79975-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dobbie I, Linari M, Piazzesi G, Reconditi M, Koubassova N, Ferenczi MA, Lombardi V, Irving M. Elastic bending and active tilting of myosin heads during muscle contraction. Nature. 1998;396(6709):383–387. doi: 10.1038/24647. [DOI] [PubMed] [Google Scholar]
- 19.Piazzesi G, Lucii L, Lombardi V. The size and the speed of the working stroke of muscle myosin and its dependence on the force. J Physiol. 2002;545(Pt 1):145–151. doi: 10.1113/jphysiol.2002.028969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reconditi M, Linari M, Lucii L, Stewart A, Sun YB, Boesecke P, Narayanan T, Fischetti RF, Irving T, Piazzesi G, Irving M, Lombardi V. The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature. 2004;428(6982):578–581. doi: 10.1038/nature02380. [DOI] [PubMed] [Google Scholar]
- 21.Linari M, Piazzesi G, Lombardi V. The effect of myofilament compliance on kinetics of force generation by myosin motors in muscle. Biophys J. 2009;96(2):583–592. doi: 10.1016/j.bpj.2008.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Decostre V, Bianco P, Lombardi V, Piazzesi G. Effect of temperature on the working stroke of muscle myosin. Proc Natl Acad Sci USA. 2005;102(39):13927–13932. doi: 10.1073/pnas.0506795102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Offer G, Ranatunga KW. Crossbridge and filament compliance in muscle: implications for tension generation and lever arm swing. J Muscle Res Cell Motil. 2010;31(4):245–265. doi: 10.1007/s10974-010-9232-7. [DOI] [PubMed] [Google Scholar]
- 24.Colombini B, Nocella M, Bagni MA, Griffiths PJ, Cecchi G. Is the cross-bridge stiffness proportional to tension during muscle fiber activation? Biophys J. 2010;98(11):2582–2590. doi: 10.1016/j.bpj.2010.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bagni MA, Cecchi G, Colombini B, Colomo F. Sarcomere tension-stiffness relation during the tetanus rise in single frog muscle fibres. J Muscle Res Cell Motil. 1999;20(5–6):469–476. doi: 10.1023/a:1005582324129. [DOI] [PubMed] [Google Scholar]
- 26.Edman KA. Non-linear myofilament elasticity in frog intact muscle fibres. J Exp Biol. 2009;212(Pt 8):1115–1119. doi: 10.1242/jeb.020982. [DOI] [PubMed] [Google Scholar]
- 27.Bershitsky SY, Tsaturyan AK, Bershitskaya ON, Mashanov GI, Brown P, Burns R, Ferenczi MA. Muscle force is generated by myosin heads stereospecifically attached to actin. Nature. 1997;388(6638):186–190. doi: 10.1038/40651. [DOI] [PubMed] [Google Scholar]
- 28.Tsaturyan AK, Bershitsky SY, Koubassova NA, Fernandez M, Narayanan T, Ferenczi MA. The fraction of myosin motors that participate in isometric contraction of rabbit muscle fibers at near-physiological temperature. Biophys J. 2011;101(2):404–410. doi: 10.1016/j.bpj.2011.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mansson A. Significant impact on muscle mechanics of small nonlinearities in myofilament elasticity. Biophys J. 2010;99(6):1869–1875. doi: 10.1016/j.bpj.2010.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kaya M, Higuchi H. Nonlinear elasticity and an 8-nm working stroke of single myosin molecules in myofilaments. Science. 2010;329(5992):686–689. doi: 10.1126/science.1191484. [DOI] [PubMed] [Google Scholar]
- 31.Metzger JM, Moss RL. Shortening velocity in skinned single muscle fibers. Influence of filament lattice spacing. Biophys J. 1987;52(1):127–131. doi: 10.1016/S0006-3495(87)83197-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tanner BC, Daniel TL, Regnier M. Sarcomere lattice geometry influences cooperative myosin binding in muscle. PLoS Comput Biol. 2007;3(7):e115. doi: 10.1371/journal.pcbi.0030115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Minajeva A, Neagoe C, Kulke M, Linke WA. Titin-based contribution to shortening velocity of rabbit skeletal myofibrils. J Physiol. 2002;540(Pt 1):177–188. doi: 10.1113/jphysiol.2001.013154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Weith A, Sadayappan S, Gulick J, Previs MJ, Vanburen P, Robbins J, Warshaw DM. Unique single molecule binding of cardiac myosin binding protein-C to actin and phosphorylation-dependent inhibition of actomyosin motility requires 17 amino acids of the motif domain. J Mol Cell Cardiol. 2012;52(1):219–227. doi: 10.1016/j.yjmcc.2011.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Higuchi H. Changes in contractile properties with selective digestion of connectin (titin) in skinned fibers of frog skeletal muscle. J Biochem. 1992;111(3):291–295. doi: 10.1093/oxfordjournals.jbchem.a123752. [DOI] [PubMed] [Google Scholar]
- 36.Linke WA, Popov VI, Pollack GH. Passive and active tension in single cardiac myofibrils. Biophys J. 1994;67(2):782–792. doi: 10.1016/S0006-3495(94)80538-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Leonard TR, Herzog W. Regulation of muscle force in the absence of actin-myosin-based cross-bridge interaction. Am J Physiol Cell Physiol. 2010;299(1):C14–20. doi: 10.1152/ajpcell.00049.2010. [DOI] [PubMed] [Google Scholar]
- 38.Bang ML, Caremani M, Brunello E, Littlefield R, Lieber RL, Chen J, Lombardi V, Linari M. Nebulin plays a direct role in promoting strong actin-myosin interactions. FASEB J: Off Publ Fed Am Soc Exp Biol. 2009;23(12):4117–4125. doi: 10.1096/fj.09-137729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chandra M, Mamidi R, Ford S, Hidalgo C, Witt C, Ottenheijm C, Labeit S, Granzier H. Nebulin alters cross-bridge cycling kinetics and increases thin filament activation: a novel mechanism for increasing tension and reducing tension cost. J Biol Chem. 2009;284(45):30889–30896. doi: 10.1074/jbc.M109.049718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Takagi Y, Homsher EE, Goldman YE, Shuman H. Force generation in single conventional actomyosin complexes under high dynamic load. Biophys J. 2006;90(4):1295–1307. doi: 10.1529/biophysj.105.068429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lombardi V, Piazzesi G. The contractile response during steady lengthening of stimulated frog muscle fibres. J Physiol. 1990;431:141–171. doi: 10.1113/jphysiol.1990.sp018324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Linari M, Piazzesi G, Dobbie I, Koubassova N, Reconditi M, Narayanan T, Diat O, Irving M, Lombardi V. Interference fine structure and sarcomere length dependence of the axial X-ray pattern from active single muscle fibers. Proc Natl Acad Sci USA. 2000;97(13):7226–7231. doi: 10.1073/pnas.97.13.7226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Brunello E, Reconditi M, Elangovan R, Linari M, Sun YB, Narayanan T, Panine P, Piazzesi G, Irving M, Lombardi V. Skeletal muscle resists stretch by rapid binding of the second motor domain of myosin to actin. Proc Natl Acad Sci USA. 2007;104(50):20114–20119. doi: 10.1073/pnas.0707626104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fusi L, Reconditi M, Linari M, Brunello E, Elangovan R, Lombardi V, Piazzesi G. The mechanism of the resistance to stretch of isometrically contracting single muscle fibres. J Physiol. 2010;588(Pt 3):495–510. doi: 10.1113/jphysiol.2009.178137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Goldman YE, McCray JA, Ranatunga KW. Transient tension changes initiated by laser temperature jumps in rabbit psoas muscle fibres. J Physiol. 1987;392:71–95. doi: 10.1113/jphysiol.1987.sp016770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Piazzesi G, Reconditi M, Koubassova N, Decostre V, Linari M, Lucii L, Lombardi V. Temperature dependence of the force-generating process in single fibres from frog skeletal muscle. J Physiol. 2003;549(Pt 1):93–106. doi: 10.1113/jphysiol.2002.038703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Herzog W, Lee EJ, Rassier DE. Residual force enhancement in skeletal muscle. J Physiol. 2006;574(Pt 3):635–642. doi: 10.1113/jphysiol.2006.107748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lee EJ, Herzog W. Effect of temperature on residual force enhancement in single skeletal muscle fibers. J Biomech. 2008;41(12):2703–2707. doi: 10.1016/j.jbiomech.2008.06.007. [DOI] [PubMed] [Google Scholar]
- 49.Bullimore SR, Leonard TR, Rassier DE, Herzog W. History-dependence of isometric muscle force: effect of prior stretch or shortening amplitude. J Biomech. 2007;40(7):1518–1524. doi: 10.1016/j.jbiomech.2006.06.014. [DOI] [PubMed] [Google Scholar]
- 50.Joumaa V, Herzog W. Force depression in single myofibrils. J Appl Physiol. 2010;108(2):356–362. doi: 10.1152/japplphysiol.01108.2009. [DOI] [PubMed] [Google Scholar]
- 51.Molloy JE, Burns JE, Kendrick-Jones J, Tregear RT, White DC. Movement and force produced by a single myosin head. Nature. 1995;378(6553):209–212. doi: 10.1038/378209a0. [DOI] [PubMed] [Google Scholar]
- 52.Nishizaka T, Miyata H, Yoshikawa H, Ishiwata S, Kinosita K., Jr Unbinding force of a single motor molecule of muscle measured using optical tweezers. Nature. 1995;377(6546):251–254. doi: 10.1038/377251a0. [DOI] [PubMed] [Google Scholar]
- 53.Dupuis DE, Guilford WH, Wu J, Warshaw DM. Actin filament mechanics in the laser trap. J Muscle Res Cell Motil. 1997;18(1):17–30. doi: 10.1023/a:1018672631256. [DOI] [PubMed] [Google Scholar]
- 54.Mehta AD, Finer JT, Spudich JA. Detection of single-molecule interactions using correlated thermal diffusion. Proc Natl Acad Sci USA. 1997;94(15):7927–7931. doi: 10.1073/pnas.94.15.7927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Veigel C, Bartoo ML, White DC, Sparrow JC, Molloy JE. The stiffness of rabbit skeletal actomyosin cross-bridges determined with an optical tweezers transducer. Biophys J. 1998;75(3):1424–1438. doi: 10.1016/S0006-3495(98)74061-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Capitanio M, Canepari M, Cacciafesta P, Lombardi V, Cicchi R, Maffei M, Pavone FS, Bottinelli R. Two independent mechanical events in the interaction cycle of skeletal muscle myosin with actin. Proc Natl Acad Sci USA. 2006;103(1):87–92. doi: 10.1073/pnas.0506830102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lewalle A, Steffen W, Stevenson O, Ouyang Z, Sleep J. Single-molecule measurement of the stiffness of the rigor myosin head. Biophys J. 2008;94(6):2160–2169. doi: 10.1529/biophysj.107.119396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Vilfan A. Elastic lever-arm model for myosin V. Biophys J. 2005;88(6):3792–3805. doi: 10.1529/biophysj.104.046763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kohler J, Winkler G, Schulte I, Scholz T, McKenna W, Brenner B, Kraft T. Mutation of the myosin converter domain alters cross-bridge elasticity. Proc Natl Acad Sci USA. 2002;99(6):3557–3562. doi: 10.1073/pnas.062415899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Cooke R, Crowder MS, Thomas DD. Orientation of spin labels attached to cross-bridges in contracting muscle fibres. Nature. 1982;300(5894):776–778. doi: 10.1038/300776a0. [DOI] [PubMed] [Google Scholar]
- 61.Fajer PG, Fajer EA, Brunsvold NJ, Thomas DD. Effects of AMPPNP on the orientation and rotational dynamics of spin-labeled muscle cross-bridges. Biophys J. 1988;53(4):513–524. doi: 10.1016/S0006-3495(88)83131-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pate E, Cooke R. Energetics of the actomyosin bond in the filament array of muscle fibers. Biophys J. 1988;53(4):561–573. doi: 10.1016/S0006-3495(88)83136-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Taylor KA, Schmitz H, Reedy MC, Goldman YE, Franzini-Armstrong C, Sasaki H, Tregear RT, Poole K, Lucaveche C, Edwards RJ, Chen LF, Winkler H, Reedy MK. Tomographic 3D reconstruction of quick-frozen, Ca2+ -activated contracting insect flight muscle. Cell. 1999;99(4):421–431. doi: 10.1016/s0092-8674(00)81528-7. [DOI] [PubMed] [Google Scholar]
- 64.Lidke DS, Thomas DD. Coordination of the two heads of myosin during muscle contraction. Proc Natl Acad Sci USA. 2002;99(23):14801–14806. doi: 10.1073/pnas.232161999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Arata T. Orientation of spin-labeled light chain 2 of myosin heads in muscle fibers. J Mol Biol. 1990;214(2):471–478. doi: 10.1016/0022-2836(90)90194-Q. [DOI] [PubMed] [Google Scholar]
- 66.Hopkins SC, Sabido-David C, van der Heide UA, Ferguson RE, Brandmeier BD, Dale RE, Kendrick-Jones J, Corrie JE, Trentham DR, Irving M, Goldman YE. Orientation changes of the myosin light chain domain during filament sliding in active and rigor muscle. J Mol Biol. 2002;318(5):1275–1291. doi: 10.1016/s0022-2836(02)00189-4. [DOI] [PubMed] [Google Scholar]
- 67.Nishikawa S, Arimoto I, Ikezaki K, Sugawa M, Ueno H, Komori T, Iwane AH, Yanagida T. Switch between large hand-over-hand and small inchworm-like steps in myosin VI. Cell. 2010;142(6):879–888. doi: 10.1016/j.cell.2010.08.033. [DOI] [PubMed] [Google Scholar]
- 68.Resnicow DI, Deacon JC, Warrick HM, Spudich JA, Leinwand LA. Functional diversity among a family of human skeletal muscle myosin motors. Proc Natl Acad Sci USA. 2010;107(3):1053–1058. doi: 10.1073/pnas.0913527107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Iwane AH, Kitamura K, Tokunaga M, Yanagida T. Myosin subfragment-1 is fully equipped with factors essential for motor function. Biochem Biophys Res Commun. 1997;230(1):76–80. doi: 10.1006/bbrc.1996.5861. [DOI] [PubMed] [Google Scholar]
- 70.Kitamura K, Tokunaga M, Iwane AH, Yanagida T. A single myosin head moves along an actin filament with regular steps of 5.3 nanometres. Nature. 1999;397(6715):129–134. doi: 10.1038/16403. [DOI] [PubMed] [Google Scholar]
- 71.Brack AS, Brandmeier BD, Ferguson RE, Criddle S, Dale RE, Irving M. Bifunctional rhodamine probes of Myosin regulatory light chain orientation in relaxed skeletal muscle fibers. Biophys J. 2004;86(4):2329–2341. doi: 10.1016/S0006-3495(04)74290-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Romano D, Brandmeier BD, Sun YB, Trentham DR, Irving M. Orientation of the N-terminal lobe of the myosin regulatory light chain in skeletal muscle fibers. Biophys J. 2012;102(6):1418–1426. doi: 10.1016/j.bpj.2012.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Joumaa V, Rassier DE, Leonard TR, Herzog W. Passive force enhancement in single myofibrils. Pflugers Arch. 2007;455(2):367–371. doi: 10.1007/s00424-007-0287-2. [DOI] [PubMed] [Google Scholar]
- 74.Goldman YE, McCray JA, Vallette DP. Cross-bridges in rigor fibres of rabbit psoas muscle support negative forces. J Physiol. 1988;398:75P. [Google Scholar]
- 75.Burghardt TP, Ajtai K. Effect of negative mechanical stress on the orientation of myosin cross-bridges in muscle fibers. Proc Natl Acad Sci USA. 1989;86(14):5366–5370. doi: 10.1073/pnas.86.14.5366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Adamovic I, Mijailovich SM, Karplus M. The elastic properties of the structurally characterized myosin II S2 subdomain: a molecular dynamics and normal mode analysis. Biophys J. 2008;94(10):3779–3789. doi: 10.1529/biophysj.107.122028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Liu J, Wu S, Reedy MC, Winkler H, Lucaveche C, Cheng Y, Reedy MK, Taylor KA. Electron tomography of swollen rigor fibers of insect flight muscle reveals a short and variably angled S2 domain. J Mol Biol. 2006;362(4):844–860. doi: 10.1016/j.jmb.2006.07.084. [DOI] [PubMed] [Google Scholar]
- 78.Howard J (2002) Mechanics of motor proteins and the cytoskeleton. Sinauer Associates, Inc., Sunderland
- 79.Nishimura I. The effect of geometrical nonlinearity on the buckling load of laminated rubber bearing. J Struct Constr Eng. 2006;579:79–86. [Google Scholar]
- 80.Stewart M, McLachlan AD, Calladine CR. A model to account for the elastic element in muscle crossbridges in terms of a bending myosin rod. Proc R Soc Lond B Biol Sci. 1987;229(1257):381–413. doi: 10.1098/rspb.1987.0002. [DOI] [PubMed] [Google Scholar]
- 81.Rayment I, Rypniewski WR, Schmidt-Base K, Smith R, Tomchick DR, Benning MM, Winkelmann DA, Wesenberg G, Holden HM. Three-dimensional structure of myosin subfragment-1: a molecular motor. Science. 1993;261(5117):50–58. doi: 10.1126/science.8316857. [DOI] [PubMed] [Google Scholar]
- 82.Dominguez R, Freyzon Y, Trybus KM, Cohen C. Crystal structure of a vertebrate smooth muscle myosin motor domain and its complex with the essential light chain: visualization of the pre-power stroke state. Cell. 1998;94(5):559–571. doi: 10.1016/s0092-8674(00)81598-6. [DOI] [PubMed] [Google Scholar]
- 83.Houdusse A, Kalabokis VN, Himmel D, Szent-Gyorgyi AG, Cohen C. Atomic structure of scallop myosin subfragment S1 complexed with MgADP: a novel conformation of the myosin head. Cell. 1999;97(4):459–470. doi: 10.1016/s0092-8674(00)80756-4. [DOI] [PubMed] [Google Scholar]
- 84.Jontes JD, Milligan RA. Brush border myosin-I structure and ADP-dependent conformational changes revealed by cryoelectron microscopy and image analysis. J Cell Biol. 1997;139(3):683–693. doi: 10.1083/jcb.139.3.683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Piazzesi G, Reconditi M, Linari M, Lucii L, Sun YB, Narayanan T, Boesecke P, Lombardi V, Irving M. Mechanism of force generation by myosin heads in skeletal muscle. Nature. 2002;415(6872):659–662. doi: 10.1038/415659a. [DOI] [PubMed] [Google Scholar]
- 86.Hill AV. The effect of load on the heat of shortening of muscle. Proc R Soc Lond B Biol Sci. 1964;159:297–318. doi: 10.1098/rspb.1964.0004. [DOI] [PubMed] [Google Scholar]
- 87.Lombardi V, Piazzesi G, Linari M. Rapid regeneration of the actin-myosin power stroke in contracting muscle. Nature. 1992;355(6361):638–641. doi: 10.1038/355638a0. [DOI] [PubMed] [Google Scholar]
- 88.Pate E, White H, Cooke R. Determination of the myosin step size from mechanical and kinetic data. Proc Natl Acad Sci USA. 1993;90(6):2451–2455. doi: 10.1073/pnas.90.6.2451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Harada Y, Sakurada K, Aoki T, Thomas DD, Yanagida T. Mechanochemical coupling in actomyosin energy transduction studied by in vitro movement assay. J Mol Biol. 1990;216(1):49–68. doi: 10.1016/S0022-2836(05)80060-9. [DOI] [PubMed] [Google Scholar]
- 90.Toyoshima YY, Kron SJ, Spudich JA. The myosin step size: measurement of the unit displacement per ATP hydrolyzed in an in vitro assay. Proc Natl Acad Sci USA. 1990;87(18):7130–7134. doi: 10.1073/pnas.87.18.7130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Uyeda TQ, Kron SJ, Spudich JA. Myosin step size. Estimation from slow sliding movement of actin over low densities of heavy meromyosin. J Mol Biol. 1990;214(3):699–710. doi: 10.1016/0022-2836(90)90287-V. [DOI] [PubMed] [Google Scholar]
- 92.Saito K, Aoki T, Aoki T, Yanagida T. Movement of single myosin filaments and myosin step size on an actin filament suspended in solution by a laser trap. Biophys J. 1994;66(3 Pt 1):769–777. doi: 10.1016/s0006-3495(94)80853-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Tanaka H, Ishijima A, Honda M, Saito K, Yanagida T. Orientation dependence of displacements by a single one-headed myosin relative to the actin filament. Biophys J. 1998;75(4):1886–1894. doi: 10.1016/S0006-3495(98)77629-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Kad NM, Kim S, Warshaw DM, VanBuren P, Baker JE. Single-myosin crossbridge interactions with actin filaments regulated by troponin-tropomyosin. Proc Natl Acad Sci USA. 2005;102(47):16990–16995. doi: 10.1073/pnas.0506326102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Huxley HE. Electron microscope studies on the structure of natural and synthetic protein filaments from striated muscle. J Mol Biol. 1963;7:281–308. doi: 10.1016/s0022-2836(63)80008-x. [DOI] [PubMed] [Google Scholar]
- 96.Reisler E, Cheung P, Oriol-Audit C, Lake JA. Growth of synthetic myosin filaments from myosin minifilaments. Biochemistry. 1982;21(4):701–707. doi: 10.1021/bi00533a018. [DOI] [PubMed] [Google Scholar]
- 97.Pate E, Franks-Skiba K, White H, Cooke R. The use of differing nucleotides to investigate cross-bridge kinetics. J Biol Chem. 1993;268(14):10046–10053. [PubMed] [Google Scholar]
- 98.Veigel C, Molloy JE, Schmitz S, Kendrick-Jones J. Load-dependent kinetics of force production by smooth muscle myosin measured with optical tweezers. Nat Cell Biol. 2003;5(11):980–986. doi: 10.1038/ncb1060. [DOI] [PubMed] [Google Scholar]
- 99.Veigel C, Schmitz S, Wang F, Sellers JR. Load-dependent kinetics of myosin-V can explain its high processivity. Nat Cell Biol. 2005;7(9):861–869. doi: 10.1038/ncb1287. [DOI] [PubMed] [Google Scholar]
- 100.Siemankowski RF, Wiseman MO, White HD. ADP dissociation from actomyosin subfragment 1 is sufficiently slow to limit the unloaded shortening velocity in vertebrate muscle. Proc Natl Acad Sci USA. 1985;82(3):658–662. doi: 10.1073/pnas.82.3.658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Guilford WH, Dupuis DE, Kennedy G, Wu J, Patlak JB, Warshaw DM. Smooth muscle and skeletal muscle myosins produce similar unitary forces and displacements in the laser trap. Biophys J. 1997;72(3):1006–1021. doi: 10.1016/S0006-3495(97)78753-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Steffen W, Smith D, Sleep J. The working stroke upon myosin-nucleotide complexes binding to actin. Proc Natl Acad Sci USA. 2003;100(11):6434–6439. doi: 10.1073/pnas.1231998100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Tyska MJ, Dupuis DE, Guilford WH, Patlak JB, Waller GS, Trybus KM, Warshaw DM, Lowey S. Two heads of myosin are better than one for generating force and motion. Proc Natl Acad Sci USA. 1999;96(8):4402–4407. doi: 10.1073/pnas.96.8.4402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Ruff C, Furch M, Brenner B, Manstein DJ, Meyhofer E. Single-molecule tracking of myosins with genetically engineered amplifier domains. Nat Struct Biol. 2001;8(3):226–229. doi: 10.1038/84962. [DOI] [PubMed] [Google Scholar]
- 105.Ishijima A, Kojima H, Funatsu T, Tokunaga M, Higuchi H, Tanaka H, Yanagida T. Simultaneous observation of individual ATPase and mechanical events by a single myosin molecule during interaction with actin. Cell. 1998;92(2):161–171. doi: 10.1016/s0092-8674(00)80911-3. [DOI] [PubMed] [Google Scholar]
- 106.Yamada T, Abe O, Kobayashi T, Sugi H. Myofilament sliding per ATP molecule in rabbit muscle fibres studied using laser flash photolysis of caged ATP. J Physiol. 1993;466:229–243. [PMC free article] [PubMed] [Google Scholar]