Abstract
Objective:
We designed an automatic, computationally efficient, and interpretable algorithm for detecting ventricular ectopic beats in long-term, single-lead electrocardiogram recordings.
Methods:
We built five simple, interpretable, and computationally efficient features from each cardiac cycle, including a novel morphological feature which described the distance to the median beat in the recording. After an unsupervised subject-specific normalization procedure, we trained an ensemble binary classifier using the AdaBoost algorithm
Results:
After our classifier was trained on subset DS1 of the Massachusetts Institute of Technology-Beth Israel hospital (MIT-BIH) Arrhythmia database, our classifier obtained an F1 score of 94.35% on subset DS2 of the same database. The same classifier achieved F1 scores of 92.06% on the St. Petersburg Institute of Cardiological Technics (INCART) 12-lead Arrhythmia database and 91.40% on the MIT-BIH Long-term database. A phenotype-specific analysis of model performance was afforded by the annotations included in the St. Petersburg INCART Arrhythmia database
Conclusion:
The five features this novel algorithm employed allowed our ventricular ectopy detector to obtain high precision on previously unseen subjects and databases
Significance:
Our ventricular ectopy detector will be used to study the relationship between premature ventricular contractions and adverse patient outcomes such as congestive heart failure and death.
Keywords: Electrocardiogram, Ventricular ectopic beats, Heartbeat classification, Adaptive boosting
Introduction
The relationship between premature ventricular contractions (PVCs) and cardiovascular outcomes is incompletely understood. While PVCs can be benign [1], frequent PVCs and non-sustained ventricular tachycardia (NSVT) have been associated with increased risk of cardiomyopathy [2], sudden cardiac arrest [3,4], and death [5]. Polymorphic PVCs are associated with a higher incidence of mortality, hospitalization, transient ischemic attack, new-onset atrial fibrillation, and new-onset heart failure independent of other clinical risk factors [6]. Ambulatory electrocardiographic monitoring can quantify PVC frequency, timing, and morphology characteristics that convey important prognostic information [7–9]. These ambulatory recordings are usually processed by proprietary automatic ventricular ectopy detection algorithms. Clinicians rely on the accuracy of these PVC detection algorithms as total PVC burden is independently associated with the development of cardiomyopathy [10–12] and informs decision-making about the use of antiarrhythmic medications or catheter ablation in patients with non-ischemic cardiomyopathy [13,14]
A variety of heartbeat classification algorithms have been proposed in the literature. Traditionally, researchers design automatic classification algorithms based on carefully chosen morphological features and heart rate [15–19]. Recently, deep neural networks (DNNs) have been used to classify heartbeats [20–22]. While existing algorithms can help clinicians identify various types of arrhythmias, the classification accuracy for each individual beat type (PVCs, in particular) can be improved. Besides accuracy, limited prior studies [23–26] have focused on providing a computationally efficient PVC detection algorithm based on interpretable features that operates on long-term, single-channel electrocardiogram (ECG) recordings. Our objective is to develop a computationally efficient and interpretable ventricular ectopy detection algorithm that operates on long-term, single-channel ECG signals. The algorithm should be suitable for analyzing large databases of ECG signals and continuing the study of PVCs and their properties
Methods
Annotated databases
Three annotated databases (see Table 1) were used for the purposes of training and validation. Forty-four of the 48 recordings from the MIT-BIH Arrhythmia database [27] were divided into two groups, labeled DS1 and DS2 (four recordings were discarded because they contain paced beats) [15]. We began by considering only the first available lead (usually a modified limb lead II), as our algorithm is designed to operate on a single channel. All 44 recordings were 30 min in length and were sampled at 360 Hz. We also considered all 75 recordings from the St Petersburg INCART 12-lead Arrhythmia Database. In this database, we used the second available lead (limb lead II) because of the low quality of the first available lead. Each recording was 30 min long and sampled at 257 Hz. We also considered all seven recordings from the MIT-BIH Long-term database; these 3-channel recordings were between 14 and 22 h long and were sampled at 128 Hz. We used the first lead in this database (the actual lead configuration is not provided). All three databases are available online at PhysioNet [28]. PhysioNet’s annotation system divides cardiac cycles into 19 subgroups following the Association for the Advancement of Medical Instrumentation (AAMI) standard [29]. Our algorithm distinguishes PVCs (annotation code V) and ventricular escape beats (annotation code E) from all other beat types. This is a binary classification problem; we consider the positive class to be the class consisting of the PVCs and the ventricular escape beats
Table 1.
Annotated Single-lead Electrocardiogram Databases.
| Database | Non-VEB | VEB | Sampling Rate | Recordings | Length |
|---|---|---|---|---|---|
|
| |||||
| MIT-BIH Arrhythmia DS1 | 47,233 | 3788 | 360 Hz | 22 | 30 min |
| MIT-BIH Arrhythmia DS2 | 46,491 | 3221 | 360 Hz | 22 | 30 min |
| St. Petersburg INCART Arrhythmia | 155,888 | 20,011 | 257 Hz | 75 | 30 min |
| MIT-BIH Long-term | 604,640 | 64,095 | 128 Hz | 7 | 14–22 h |
Note: VEB = ventricular ectopic beats; MIT-BIH = Massachusetts Institute of Technology-Beth Israel Hospital; INCART = Institute of Cardiological Technics; Hz = Hertz.
Algorithm derivation
Our proposed algorithm takes as input a raw ECG in units of mV, its sampling rate , and the locations (in samples) of all QRS complexes in the recording. Suppose there are annotated QRS complexes in , and that the i-th QRS marker is located at sample . Our algorithm determines which of the QRS markers correspond to either a PVC or a ventricular escape beat. The first step in our algorithm is a newly proposed standardization of the incoming QRS markers. Ideally, heartbeats with similar morphologies should have similarly demarcated R waves (QRS markers). However, since PVCs vary widely in morphology and can alternate in polarity, discriminating the R wave on a PVC can be ambiguous. Expert annotators or different annotation algorithms may place the QRS marker at different points on the same heartbeat. Our classifier may perform well when the QRS markers are provided by one expert but poorly when the QRS markers are provided by another expert (or annotation algorithm). Manual annotations are additionally troublesome because a QRS marker that is even a few samples away from the ideal location can significantly affect morphological features that depend on heartbeats being suitably aligned with one another. Therefore, when possible, each heartbeat’s original QRS marker is replaced by a new QRS marker that has been obtained using a precise and consistent method. This standardization step is to ensure that our algorithm is not confounded by the method used to obtain the QRS markers. We begin by applying a standard high-accuracy QRS detector to [30]. If the i-th annotated QRS complex location is matched to any of the predicted QRS complex locations provided by the detection algorithm, we replace with that predicted QRS complex location. The heartbeat matching algorithm that we employ is standard in ECG processing [Section 4.3.2, 29]
The second step in our algorithm is a filtering and standardization of the raw ECG signal. (Note that the cited QRS detector carries out its own independent filtering stages.) We apply a bi-directional 3rd order Butterworth bandpass filter to with cutoff frequencies 0.5 Hz and 40 Hz to remove baseline wandering and to suppress noise. We then resample the signal at a sampling rate of [31] to enhance our ability to construct the level sets of each heartbeat (which we will define later). We denote the filtered and resampled signal as . For the detected QRS complexes, we use the notation to denote the location of the i-th QRS complex in the resampled signal. See the top of Fig. 1 for an illustration of the pre-processing and standardization steps. In this case, note that the QRS standardization step makes no visible change to the existing QRS annotations
Fig. 1.
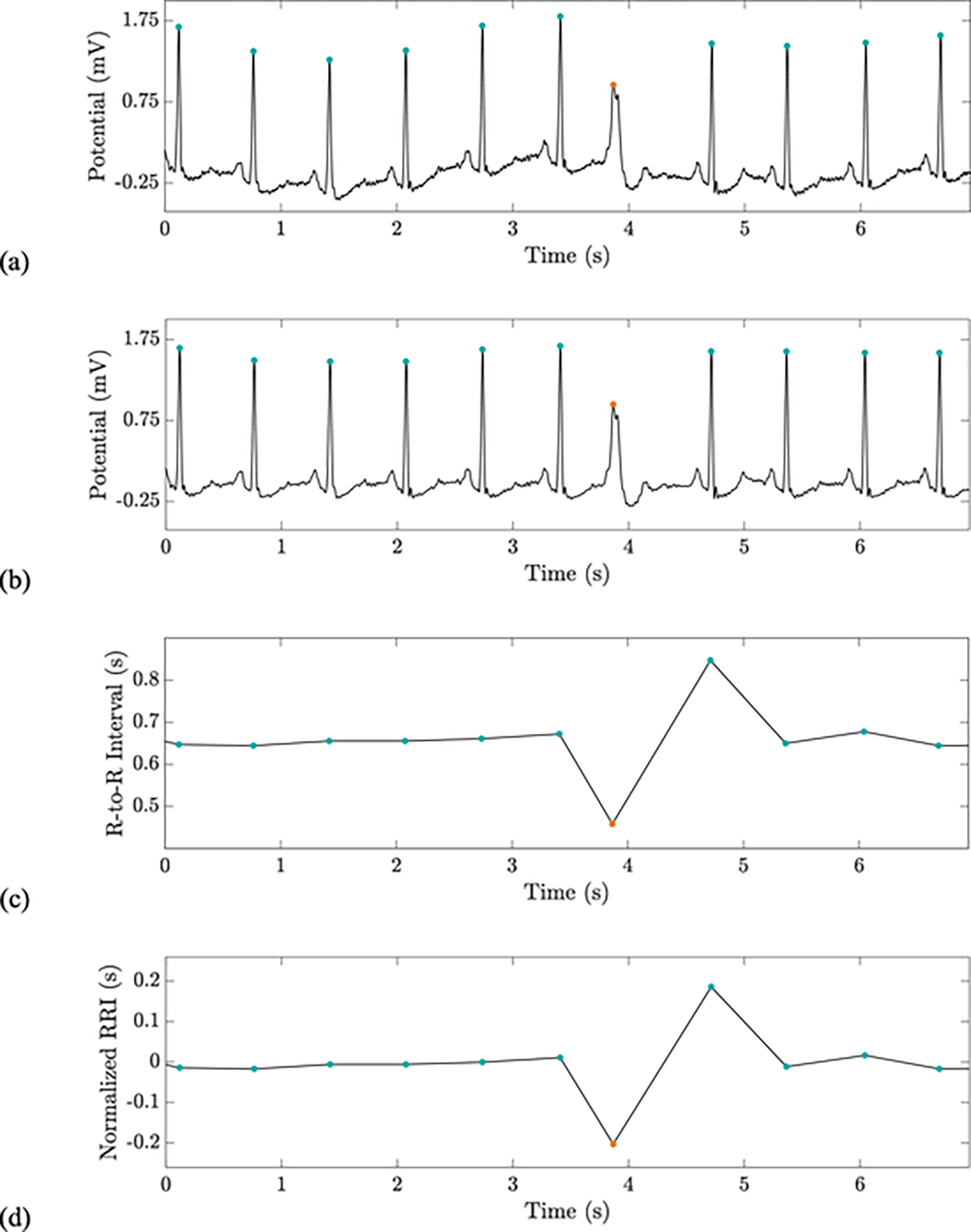
From top to bottom: a raw ECG signal with QRS markers (a); the pre-processed ECG with standardized QRS markers (b); a linear interpolation of the unnormalized feature vector (c); a linear interpolation of the normalized feature vector (d). The second feature is similar to but depicts the RR interval between the current beat and the following beat rather than the prior beat. Orange and blue dots indicate VEBs and non-VEBs, respectively. This recording is record 234 in the MIT-BIH Arrhythmia database. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
We then associate five features to each QRS complex. We build five vectors so that is the value of the j-th feature at the i-th QRS complex. The first two features associated to the i-th QRS complex are based on the heartrate and are constructed in the following way:
the time difference between the current beat and the previous beat, specifically
| (1) |
the time difference between the current beat and the next beat, specifically
| (2) |
We compute and using linear extrapolation. These quantities are normalized by a procedure we call “subject-specific normalization,” resulting in the construction of the features and . This normalization step is also time-specific. In particular, for each and , we define the normalized features for the current recording to be
| (3) |
Note that this operation corresponds to removing the output of a median filter (with window size 1001 heartbeats) from the signal and highlights the beat-specific deviation in R-to-R interval from the local median. See the bottom of Fig. 1 for an illustration of these heartrate-based features and their corresponding normalizations
The final three features are morphological. To calculate these features, we first extract a portion of each cardiac cycle from the recording. Set and . Obtain a data matrix by setting
| (4) |
where is the beat index, and is an integer satisfying . The intention is that the i-th row of corresponds to a large portion of the i-th cardiac cycle. The width of the window is chosen to be 325 ms to accommodate heart rates of up to 180 bpm. We now associate three distances with each cardiac cycle, namely
the squared Euclidean distance to the median beat (see Fig. 2), specifically
Fig. 2.
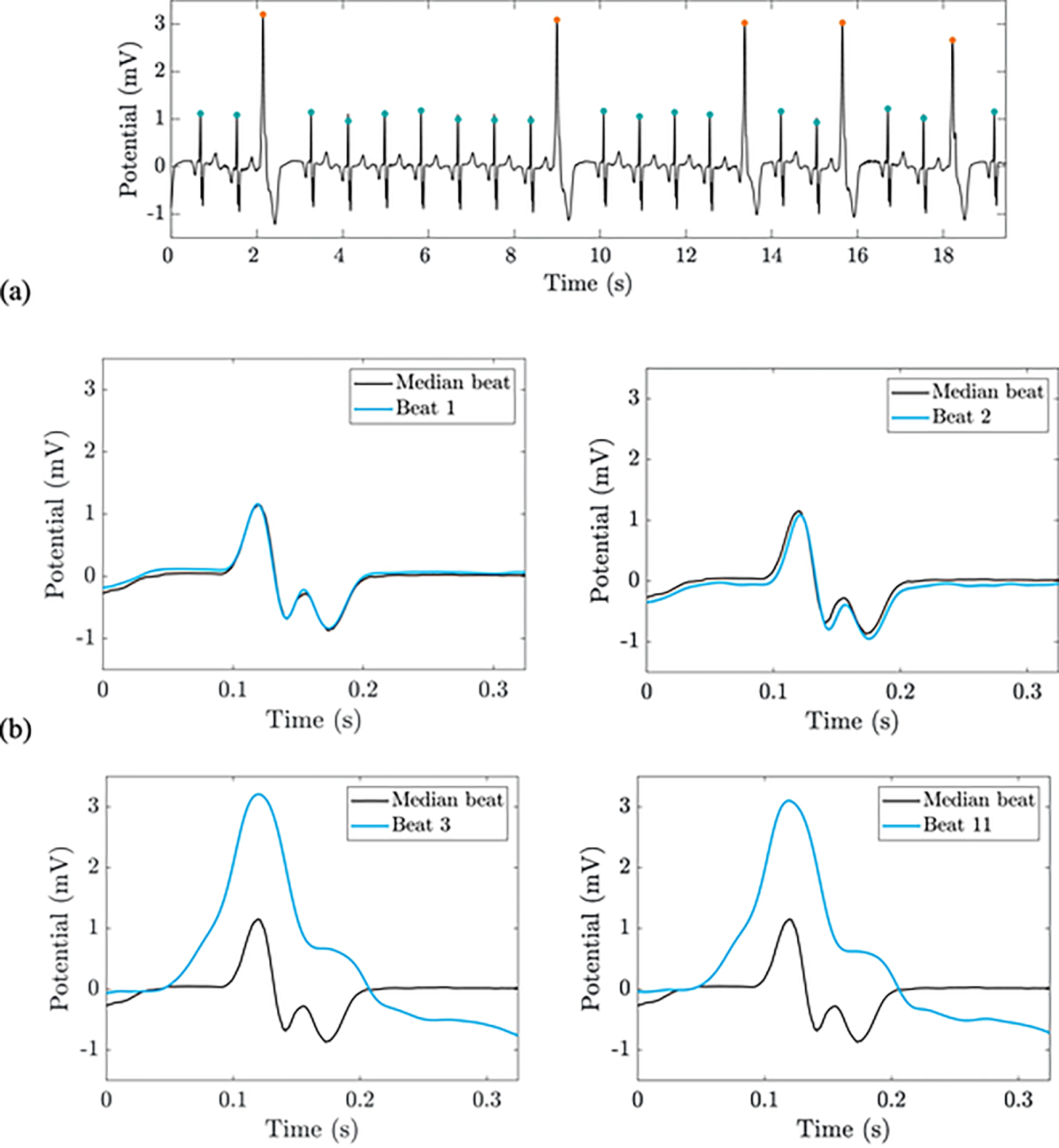
From top to bottom: the pre-processed ECG signal with standardized QRS markers (a); a comparison of four beats to the median of the nearest 1000 heartbeats (b). The third feature in our algorithm is the squared Euclidean distance to the median beat, and the fourth feature is the city block distance to the median beat. Orange and blue dots indicate VEBs and non-VEBs, respectively. This recording is record I75 in the St. Petersburg INCART Arrhythmia database. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
| (5) |
the city block distance to the median beat, specifically
| (6) |
the quadratic form (or cross-bin) distance [32] from the current beat’s level set representation to the median level set representation, which we define below
Note from the above formulas that the median beat is estimated using a median filter with a window size of 1001 heartbeats. Next, we calculate the level set representation of each cardiac cycle. Define a vector of bin edges
| (7) |
and a level set matrix by setting
| (8) |
for each and each . Note that counts the number of samples making up the i-th beat which are greater than or equal to but less than ; that is, the i-th row of is like the histogram of the i-th QRS complex with the respect to the bins determined by , except that we do not normalize it. The high sampling rate of 2000 Hz allows us to accurately estimate the time spent in each voltage bin. See Fig. 3 for an illustration of one heartbeat’s level set representation. Note that the sum of each row of is . The motivation for considering the level set matrix is that it allows the comparison of heartbeats that are not well-aligned. We locally estimate the median level set representation by introducing a new matrix whose entries are
| (9) |
Fig. 3.
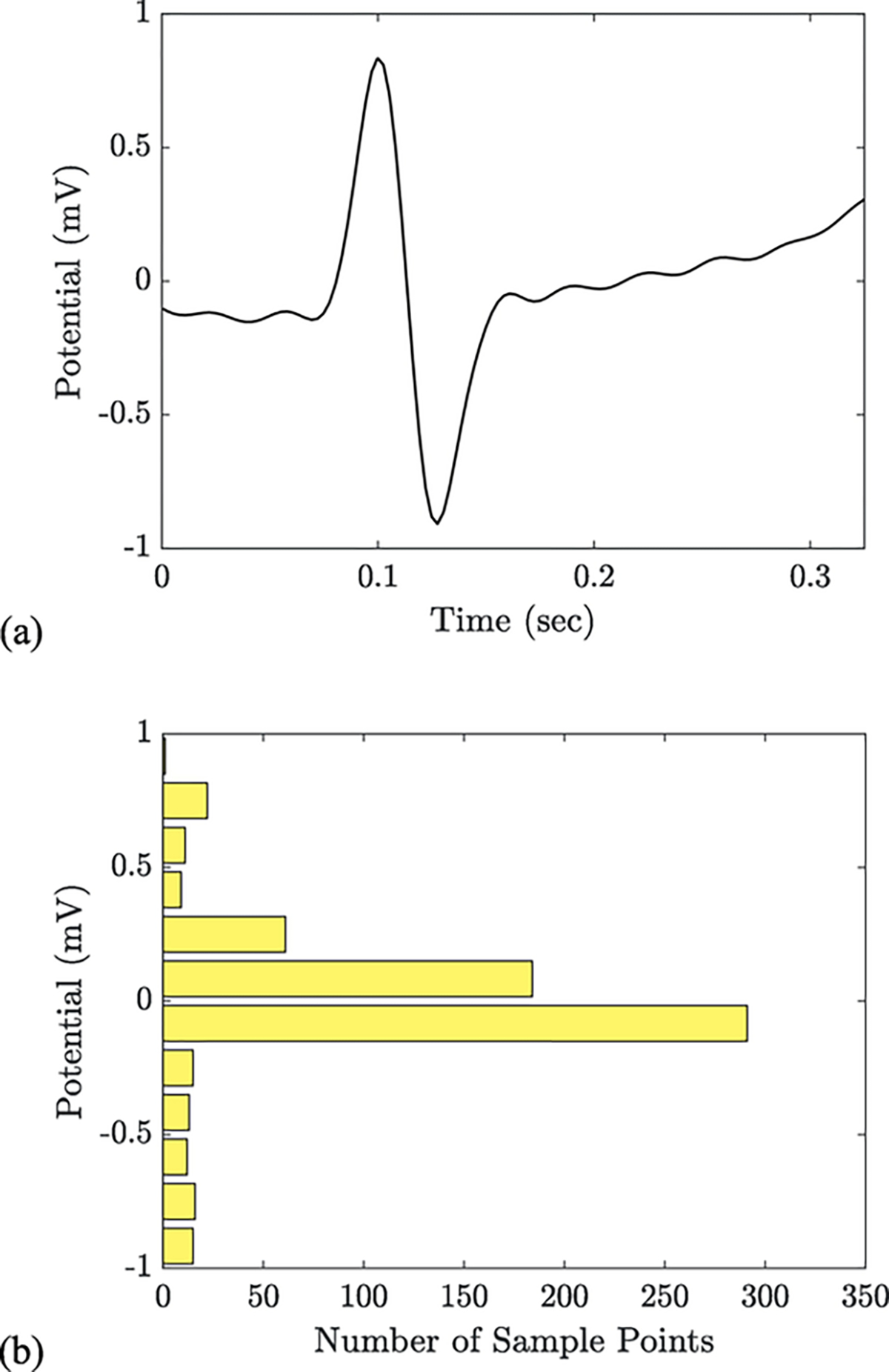
An individual heartbeat (a) extracted from the pre-processed ECG signal (record 117 of the MIT-BIH Arrhythmia database) and its associated level set representation (b). Each bar in this histogram-like plot represents the number of samples that occur near a specific voltage. The largest bars reflect the isoelectric baseline and the ascending T wave; the smaller bars reflect the R and S waves of the QRS complex. The fifth and final feature in our algorithm is the quadratic form (or cross-bin distance) from each beat’s level set representation to the median level set representation
In fact, we obtain by applying a median filter to the columns of . We define a matrix of bin similarities by setting
| (10) |
for all . The fifth and final feature, namely the quadratic form distance from the current beat’s level set representation to the median level set representation , is calculated by the formula
| (11) |
The five features are fed into an ensemble binary classifier to determine if the i-th cardiac cycle is of the positive class (either a PVC or a ventricular escape beat). The classifier consists of 500 binary decision tree learners each with a maximum of 2 splits (built using the CART algorithm with Gini’s diversity index as the splitting criterion), and the ensembling method was the AdaBoost algorithm [33]. In particular, we used the AdaBoostM1 functionality in MATLAB R2019a with exponential loss and the default learning rate of 1. No explicit optimization of the parameters in either the feature design or ensembling stages was carried out in order to avoid over-fitting
Evaluation
We trained an ensemble binary classifier (named Classifier1) on the cardiac cycles in DS1. We then validated the trained classifier on the cardiac cycles in DS2. Note that DS1 and DS2 are independent data sets without overlap and that each subject’s heartbeats are entirely contained in either DS1 or DS2 (but not both). This step was performed to evaluate the model’s ability to correctly classify heartbeats from previously unseen subjects. It also provided the opportunity to compare our algorithm to others that were trained and validated using the same DS1/DS2 splitting convention [15–17,23,34,35]. We also took the opportunity to validate Classifier1 on the St. Petersburg INCART Arrhythmia database and the MIT-BIH Long-term database. To further assess the algorithm, we trained a new classifier (named Classifier2) on all the heartbeats from DS1 and DS2. We evaluated Classifier2 on the cardiac cycles in the St. Petersburg INCART Arrhythmia database to evaluate the model’s ability to accurately process ECG recordings made in different patient populations. The record-wise phenotype annotations included in the St. Petersburg INCART Arrhythmia database were used to build seven homogeneous patient subgroups: the ventricular ectopy, supraventricular ectopy, conduction disease, potential ischemia, irregular rhythm, tachycardia, and bradycardia subgroups. Finally, we trained a third classifier (named Classifier3) on all the heartbeats from DS1, DS2, and the St. Petersburg INCART database, and we validated the trained classifier on the MIT-BIH Long-term database. This step was performed to determine whether increasing the size of the training set would have a positive effect on model performance
To quantify the performance of the two classifiers, we used a number of evaluation metrics derived from the number of true positives (), false positives (), true negatives (), and false negatives (). We calculated the sensitivity (), specificity (), and positive predictive value () using the formulas
| (12) |
| (13) |
| (14) |
The F1 score is the harmonic mean of and and served as our main summary statistic. Due to the strong imbalance between the positive and negative classes, SPE was not as informative as SEN and for assessing model performance
Since a subject’s PVC burden (the percentage of his or her heartbeats that are PVCs) informs decision-making about the use of antiarrhythmic medications or catheter ablation, we designed an additional evaluation metric which captures the ability of our model to accurately estimate the PVC burden of an individual subject. This metric is calculated subject-wise as
| (15) |
(where is the number of heartbeats in the recording) and represents the absolute error between the true percentage of PVCs (and ventricular escape beats) in a recording and the classifier’s estimate for the percentage of PVCs (and ventricular escape beats) in that recording
In addition to the diagnostic performance of these algorithms, the processing time was calculated. All of our calculations were performed in MATLAB R2019a on an Intel i7–4790K processor at 3.60 GHz with 24 GB of RAM. Input file parsing was performed by the WaveForm DataBase (WFDB) Toolbox for MATLAB [36]
Results
After training Classifier1 on DS1, we report in Table 2 a variety of evaluation metrics which describe the classifier’s performance on DS2, the MIT-BIH Long-term database, and the St. Petersburg INCART Arrhythmia database. We also report the performance on the training database (DS1) to show that our model has not been over-fit to the training data. Classifier1 demonstrated a SEN of 93.82%, a PPV of 94.88%, and an F1 score of 94.35%. The confusion matrix is shown in Table 3. Classifier1 obtained values which were less than or equal to 1% for 19 of the 22 recordings in DS2. The median of the 22 values was 0.075% with 95% confidence interval [0, 2.57]; the median absolute deviation was 0.43%. One subject (record 105 of the MIT-BIH Arrhythmia database) whose true PVC burden was 1.6% was incorrectly estimated to be 4.2%, likely because of noise in the recording
Table 2.
Performance of the Ventricular Ectopy Detector Classifier1 Trained on DS1.
| Database | SEN (%) | PPV (%) | SPE (%) | F1 (%) | ρ (%) | Purpose |
|---|---|---|---|---|---|---|
|
| ||||||
| MIT-BIH Arrhythmia DS1 | 93.55 | 93.67 | 99.49 | 93.55 | 0.64 ± 1.12 | Training |
| MIT-BIH Arrhythmia DS2 | 93.82 | 94.88 | 99.65 | 94.35 | 0.36 ± 0.67 | Testing |
| St. Petersburg INCART Arrhythmia | 88.93 | 95.42 | 99.45 | 92.06 | 1.56 ± 3.31 | Testing |
| MIT-BIH Long-term | 88.74 | 94.22 | 99.42 | 91.40 | 1.51 ± 1.80 | Testing |
Note: SEN = sensitivity; PPV = positive predictive value; SPE = specificity; F1 = F1 score; ρ = mean ± standard deviation of all ρ values (absolute PVC burden estimation error); MIT-BIH = Massachusetts Institute of Technology-Beth Israel Hospital; INCART = Institute of Cardiological Technics.
Table 3.
Confusion Matrix for the Ventricular Ectopy Detector Classifier1 Trained on DS1 and Evaluated on DS2.
| Target False | Target True | |
|---|---|---|
|
| ||
| Predicted False | 46,328 | 199 |
| Predicted True | 163 | 3022 |
Note: The positive (true) class consists of premature ventricular contractions and ventricular escape beats.
When Classifier2 was trained on the aggregation of DS1 and DS2 and evaluated on the St. Petersburg INCART Arrhythmia database, the resulting SEN, PPV, and F1 score were 89.16%, 96.03%, and 92.47%, respectively (see Table 4). Also featured in Table 4 is a demonstration of the model’s performance on relatively homogeneous patient subgroups. These subgroups were devised using the record-wise phenotype annotations included by the database contributors. Classifier2 performed well on the ventricular ectopy, tachycardia, and bradycardia subgroups; acceptably on the supraventricular ectopy and conduction disease subgroups; but poorly on the potential ischemia and irregular rhythm subgroups. On the irregular rhythm subgroup (which contained subjects with atrial fibrillation and sinus arrhythmia), PPV was low because the irregular R-to-R interval features lead to many false discoveries. Classifier2 obtained values which were less than or equal to 1% for 53 of the 75 subjects in the St. Petersburg INCART Arrhythmia database. The median of the 75 values was 0.18% with 95% confidence interval [0, 9.48]; the median absolute deviation was 1.88%. The classifier performed poorly on two records in particular, namely I31 and I62, where the value exceeded 10%. Record I31 has a low signal-to-noise ratio, and record I62 has long segments of ventricular rhythm. Three subjects in the St. Petersburg INCART database have PVC burdens larger than 49%; these subjects all had values less than 1.6%
Table 4.
Performance of the Ventricular Ectopy Detector Classifier2 Trained on DS1 and DS2.
| Database | Records | VEBs per Record | SEN (%) | PPV (%) | SPE (%) | F1 (%) | ρ (%) |
|---|---|---|---|---|---|---|---|
|
| |||||||
| St. Petersburg INCART Arrythmia | I01-I75 | 267 | 89.16 | 96.03 | 99.53 | 92.47 | 1.47 ± 3.00 |
| Ventricular ectopy subgroup | I01-I09, I11-I33, I35-I49, I51-I59, I63-I69, I73-I75 | 286 | 90.89 | 97.36 | 99.66 | 94.01 | 1.15 ± 2.23 |
| Supraventricular ectopy subgroup | I07, I20-I22, I26, I33, I34, I70, I73 | 42 | 81.58 | 81.58 | 99.64 | 81.58 | 0.67 ± 0.92 |
| Conduction disease subgroup | I09-I11, I16, I17, I23, I34, I68, I70, I71 | 33 | 98.49 | 64.30 | 99.17 | 77.80 | 1.06 ± 2.17 |
| Potential ischemia subgroup | I03, I06, I12, I15, I24, I40, I50, I59, I60, I62 | 112 | 50.22 | 81.36 | 99.47 | 62.11 | 2.86 ± 5.80 |
| Irregular rhythm subgroup | I41, I47, I49, I50, I71 | 25 | 97.60 | 47.66 | 98.70 | 64.04 | 1.59 ± 2.90 |
| Tachycardia subgroup | I04, I05, I10, I20, I22, I25, I26, I29-I31, I34, I35, I38, I42, I44, I46, I51, I54, I55, I57, I62, I65-I67, I74, I75 | 422 | 85.94 | 97.78 | 99.62 | 91.48 | 2.48 ± 4.33 |
| Bradycardia subgroup | I04, I09, I17, I28, I37, I39, I49, I52, I58, I61, I69, I73, I75 | 152 | 93.70 | 98.73 | 99.90 | 96.15 | 0.45 ± 1.22 |
Note: SEN = sensitivity; PPV = positive predictive value; SPE = specificity; F1 = F1 score; ρ = mean ± standard deviation of all ρ values (absolute PVC burden estimation error); INCART = Institute of Cardiological Technics.
When Classifier3 was trained on the aggregation of DS1, DS2, and the St. Petersburg INCART database and evaluated on the seven subjects in the MIT-BIH Long-term database, the resulting SEN, PPV, and F1 score were 93.97%, 92.18%, and 93.06% (see Table 5). In Fig. 4, we plot both the true PVC burden and the estimated PVC burden for all seven subjects in the MIT-BIH Long-term database. Classifier3’s largest value was obtained on record 14,134 and was 2.1%. On record 14,149, the true PVC burden was 0.2%, but the classifier estimated the PVC burden to be 1.6%; we suspect that this deviation resulted from the subject having atrial fibrillation. Finally, we segmented the seven recordings in the MIT-BIH Long-term database by hour (obtaining 144 h-long segments in total), allowed Classifier3 to process the heartbeats from each of the hour-long recordings, and found that the median of the 144 resultant values was 0.93% with 95% confidence interval [0.02, 4.12]; the median absolute deviation was 0.92%
Table 5.
Performance of the Ventricular Ectopy Detector Classifier3 Trained on DS1, DS2, and INCART.
| Database | SEN (%) | PPV (%) | SPE (%) | F1 (%) | ρ (%) | Purpose |
|---|---|---|---|---|---|---|
|
| ||||||
| MIT-BIH Arrhythmia DS1 | 91.10 | 86.88 | 98.90 | 88.94 | 1.14 ± 1.97 | Training |
| MIT-BIH Arrhythmia DS2 | 96.65 | 93.60 | 99.54 | 95.10 | 0.41 ± 0.55 | Training |
| St. Petersburg INCART Arrythmia | 94.65 | 95.94 | 99.49 | 95.29 | 0.95 ± 1.68 | Training |
| MIT-BIH Long-term | 93.97 | 92.18 | 99.15 | 93.06 | 1.22 ± 1.17 | Testing |
Note: SEN = sensitivity; PPV = positive predictive value; SPE = specificity; F1 = F1 score; ρ = mean ± standard deviation of all ρ values (absolute PVC burden estimation error); MIT-BIH = Massachusetts Institute of Technology-Beth Israel Hospital; INCART = Institute of Cardiological Technics.
Fig. 4.
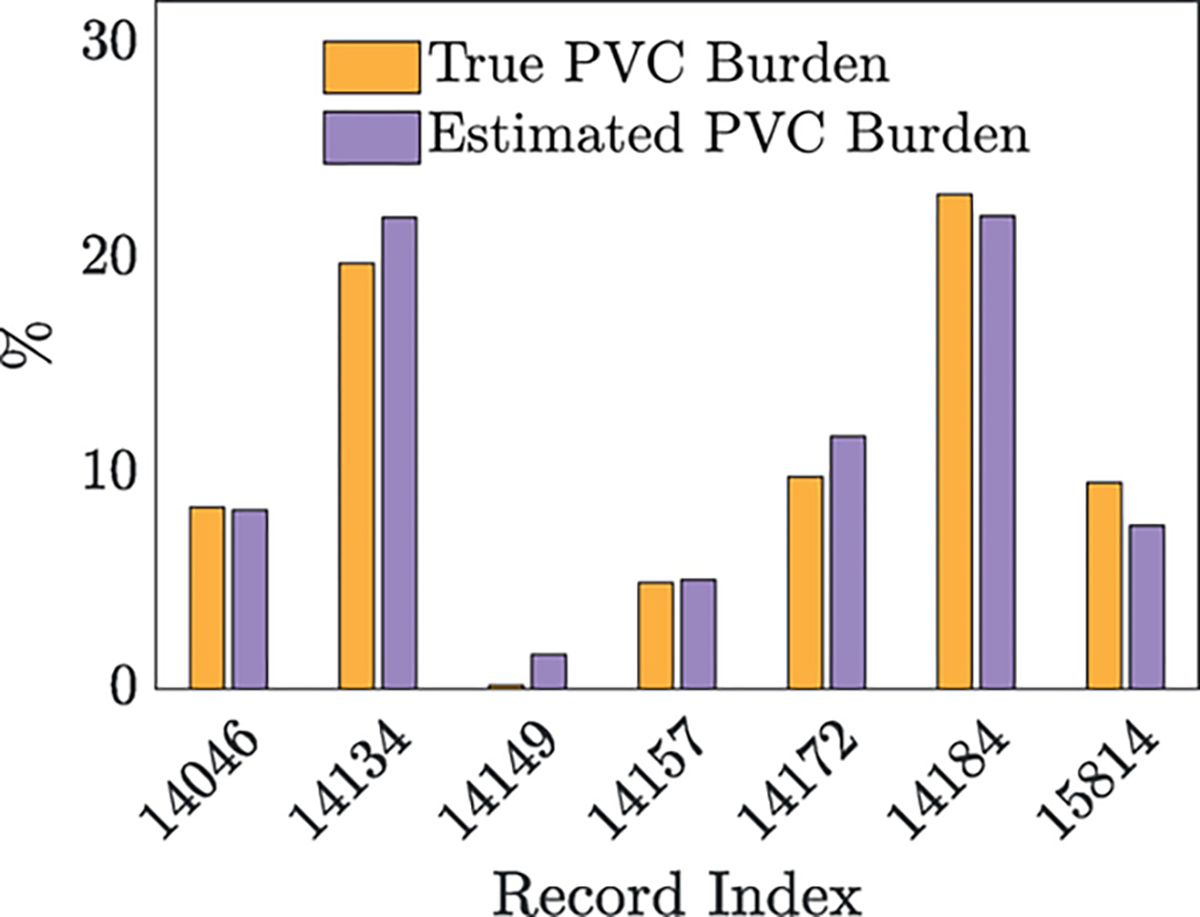
After training Classifier3 on DS1, DS2, and the St. Petersburg INCART Arrhythmia database, we plot the true PVC burden and the estimated PVC burden for all seven subjects in the MIT-BIH Long-term database
Our algorithm was able to perform input file parsing, signal pre-processing, QRS marker standardization, feature calculation, and heartbeat classification (for all 49,712 heartbeats in DS2) in 19.078 ± 0.045 s – approximately 867 ms per 30-min record in DS2
Discussion
In this study, we designed and validated an interpretable and computationally efficient automatic, single-lead ventricular ectopy detector which achieved encouraging F1 scores on different validation databases. We introduced a novel beat morphology feature based on the a priori cardiac electrophysiological knowledge that ventricular ectopic beats are “distant” from the median beat in the recording. To handle the difficulty of inter-individual rhythm classification, the algorithm used a novel subject-specific normalization procedure. We ensured that our algorithm was not confounded by the QRS complex annotation method (whether it be automatic or manual) by, when possible, replacing each QRS complex annotation with one generated by a high-accuracy QRS detector [30]. We also proposed a novel feature to describe heartbeat morphology which involved comparing heartbeat level sets (a histogram-like representation) using the cross-bin distance. The classifier we used to solve the binary classification problem was an ensemble of binary decision trees, aggregated using the AdaBoost algorithm with 500 learning cycles. We proposed a subgrouping of the subjects in the St. Petersburg INCART Arrhythmia database that allowed for a phenotype-specific evaluation of model performance. Finally, we introduced a novel metric for assessing the classifier’s ability to accurately estimate PVC burden from ambulatory recordings
Overall, our initial detector, Classifier1 (which was trained on DS1), worked well on the validation database DS2, achieving an F1 score of 94.35%, and generalized well to other databases, achieving F1 scores of 92.06% on the St. Petersburg INCART Arrhythmia database and 91.40% on the MIT-BIH Long-term database. Our second detector, Classifier2 (which was trained on DS1 and DS2), was validated on phenotype-specific subgroups of the St. Petersburg INCART Arrhythmia database and demonstrated strong performance on patients with ventricular ectopy, tachycardia, and bradycardia. Our third detector, Classifier3 (which was trained on DS1, DS2, and the St. Petersburg INCART database), obtained an F1 score of 93.06% on the first lead of the MIT-BIH Long-term database. These results indicate that our model can generalize well to recordings made on different leads, devices, and patient populations, and that increasing the size of the training set has a beneficial effect on classification performance
Our algorithm is intended to be able to perform on recordings from new systems in mobile health monitoring such as the ZIO® Patch cardiac monitor (iRhythm Technologies, Inc., San Fransisco, California, USA), so it must be both fast and suitable for analyzing long-term signals. Given the need to resample the signal at 2000 Hz, we recommend analyzing the signal in chunks in order to minimize memory usage. The numerically efficiency of our proposed algorithm makes it a great fit for ultra-long-term ECG signal processing, including HRV analysis, PVC quantification, and novel PVC characterizations
This work represents a novel use of the so-called quadratic form distance between histograms. The quadratic form distance between histograms has previously been used in image processing and has a noted comparability with the earth mover’s distance [32,37,38]. The quadratic form distance that we used in this work is a Bregman divergence with a positive-definite kernel, but to the best of our knowledge, its specific theoretical properties have not been studied. The properties it apparently enjoys are a robustness to QRS marker translation and a robustness to measurement noise. Further work is required to verify the properties of this comparison tool, but its usefulness was evident in this application, as discarding this feature lead to Classifer1 achieving less competitive F1 scores of 93.86%, 91.39%, and 89.79% on DS2, the St. Petersburg INCART Arrhythmia database, and the MIT-BIH Long-term database, respectively
Because our algorithm used the distance to the median beat to detect ventricular ectopy, we implicitly assumed that the most common beat in each 1000-beat section of each recording was not a ventricular ectopic beat. We believe that this assumption is warranted for the majority of patients, but we found that our algorithm’s success rate was lower on recordings featuring sustained ventricular rhythm and ventricular bigeminy or trigeminy. The relatively large window size of one thousand beats was chosen to accommodate recordings featuring ventricular rhythm. We also note that our algorithm does not explicitly require at least 1000 beats in the recording, and we believe that, if required, the robustness of the median operator will allow successful results on recordings as short as 10 s provided they are not segments of ventricular rhythm
It is always possible to over-fit a classifier. We experimented with including the height of the R peak as an additional feature; doing so lead to Classifier1 achieving an F1 score of 95.65% on DS2 but lower F1 scores on the INCART database and the MIT-BIH Long-term database. This result confirms that it is always possible to over-fit a model’s hyperparameters to an individual validation database. It is for this reason that we report Classifier1’s performance on both the St. Petersburg INCART Arrhythmia database and the MIT-BIH Long-term database in Table 2. We also experimented with resampling each recording so as to normalize for the effect of heart rate; this experiment did not result in a significant improvement to our algorithm’s performance; this result may be due to the nature of the recordings considered in this work
An advantage to using decision trees to perform classification is that we do not have to map features into a small interval by a process such as z-scoring or min-max scaling before training the classifier. As the problem of ventricular ectopy detection is largely a problem of anomaly detection in which we cannot assume our features are distributed normally (or uniformly) and the number of outliers is high, this kind of normalization step would be inappropriate. Our training algorithm was not subjected to any explicit hyperparameter optimization. Parameters in the feature design stage were selected ad hoc based on the intuition of the authors
Comparison with previous results
A comparison of our algorithm’s performance to the reported performance of previous algorithms is shown in Table 6. Llamedo and Martinez [16] designed an automatic heartbeat classifier using two-lead recordings which divides cardiac cycles into four categories, one of which is the ventricular ectopy class. They selected eight features based on the R-to-R interval time series and the autocorrelation of the discrete wavelet transform of each ECG lead. They employed a linear discriminant classifier and reported a SEN of 82.9% and a PPV of 88.0% on DS2 when identifying the ventricular ectopy class (although three ventricular ectopic beats appear to be missing from the reference set). While their algorithm’s performance is certainly below the performance of our algorithm, the fact that their algorithm was designed to solve a multi-class problem indicates that a lower performance on the ventricular ectopy class is to be expected. Llamedo and Martinez also considered a semi-automatic approach to heartbeat classification [17]. They modified their previously considered model to allow expert assistance. After manually annotating 12 carefully selected beats from each recording, they achieved a SEN of 92.2% and a PPV of 94.8% when detecting PVCs, ventricular escape beats, and fusions of ventricular and normal beats (PhysioNet annotation code F). Since our ventricular ectopy class does not contain the fusion class, these results may not be comparable. Another expert-assisted approach which features the manual annotation of an average of three beats from each 30-min recording in DS2 achieved an F1 score of 94.5% [34] on the same binary classification problem we consider in this work. Oster et al. considered two leads, and they reported that discarding noisy beats (3.2% of all beats in DS2) can improve the F1 score to 98.6%. For ultra-long-term signals (≥14 days) we expect that the number of beats which need to be manually annotated in order to achieve the same performance would increase, making these expert-assisted algorithms impractical
Table 6.
Comparison with previous results on DS2
| Reference | SEN (%) | PPV (%) | F1 (%) | Notes |
|---|---|---|---|---|
|
| ||||
| de Chazal et al. [Table 8, 15] | 77.7 | 81.6 | 79.6 | Multi-class, multi-lead |
| Llamedo & Martinez [Table 6, 16] | 82.9 | 88.0 | 85.4 | Multi-lead, multi-class |
| Llamedo & Martinez [Discussion, 17] | 92.2 | 94.8 | 93.5 | Expert-assisted, multi-lead, multi-class |
| Oster et al. [Table 4, 34] | 92.7 | 96.2 | 94.5 | Expert-assisted, multi-lead |
| Alfaras et al. [Table 7, 23] | 92.7 | 95.7 | 94.2 | |
| Ortin et al. [Table 4, 39] | 95.3 | 88.8 | 91.9 | Augmented training database, validated on DS1 & DS2 |
| Qurraie & Afkhami [Table 4, 35] | 95.4 | 94.1 | 94.8 | Multi-class |
| This work (Classifier1) | 93.8 | 94.9 | 94.4 | |
Note: The computational time is discussed in the Comparison with Previous Results in the Discussion section. SEN = sensitivity; PPV = positive predictive value; F1 = F1 score.
A recent single-lead automatic ventricular ectopy detector which uses ring-topology reservoir computing (echo state networks) achieved a SEN of 92.7% and a PPV of 95.7% when detecting the same set of ventricular ectopic beats that we consider in this work [Table 7, 23]. Alfaras et al. also reported performance on the second available lead in the MIT-BIH Arrhythmia database; they obtained a SEN of 86.1% and a PPV of 75.1% on DS2, compared to our algorithm’s SEN of 74.3% and PPV of 92.7%. They report that, by using the same CPU used in this work, their ensemble of 30 networks (with 1000 nodes each) can classify the heartbeats in DS2 in roughly 3 s [Fig. 6, 23], but it is unclear whether their runtime assessment included stages such as file parsing, signal pre-processing, and feature calculation. Our ensemble of binary decision trees took 2.15 s to classify the 49,712 heartbeats in DS2 using the pre-calculated feature vectors. The F1 score reported by Alfaras et al. is not as strong as what we are able to achieve, and they do not employ interpretable morphological features, choosing rather to pass the raw waveform into the echo state network
Reservoir computing was also used by Ortin et al. to achieve a SEN of 95.3% and a PPV of 88.8% in the ventricular ectopy detection task [Table 4, 39]; however, this result was obtained on the entire MIT-BIH Arrhythmia database after training on a pair of databases not considered in this work. (For this reason, we have noted the difference in Table 6.) Their training strategy lead to strong results on the St. Petersburg INCART Arrhythmia database, in which they used a QRS marker adjustment strategy similar to ours in order to extend their analyses to all twelve leads. Ortin et al.’s twelve features are based on a template-matching approach similar to ours and are equally as interpretable as the features used in this work. They report that their algorithm (implemented in MATLAB R2010b) took 2.2 s to classify the heartbeats in one 30-min record (not including the pre-processing and heartbeat segmentation stages). Our algorithm was able to perform input file parsing, signal pre-processing, QRS marker standardization, feature calculation, and heartbeat classification (for all heartbeats in the recording) in approximately 867 ms per 30-min record. To the best of our knowledge, among the works examined in this section, Alfaras et al. and Ortin et al. are the only authors to report on the computational efficiency of their algorithms
We report one final four-class heartbeat classifier by Qurraie and Afkhami which used time-frequency analysis (the Wigner-Ville distribution) [35]. They achieved a SEN of 95.4% and a PPV of 94.1% on DS2 using only the first lead (although three ventricular ectopic beats appear to be missing from DS2). While this result exceeds ours in terms of F1 score, the algorithm is undoubtedly numerically inefficient due to its use of time-frequency methods. Moreover, since the authors did not validate on multiple databases, their parameters may be over-tuned to perform well on DS2
Many other published works take different approaches to validating their heartbeat classification algorithms; we chose to compare our algorithm to those algorithms which were validated using the inter-subject approach, wherein heartbeats from one subject are not spread across both the training and validation sets. In some cases, the use of the MIT-BIH Arrhythmia database in algorithm design and validation was ambiguous [40], and the most effective comparisons are drawn with those works which use the now popular DS1/DS2 split [15]. Semi-supervised approaches which feature 5-min warm-up periods were also not considered because the number of beats which need to be labeled is high
Limitations and future work
This study has several limitations. First, this study suffers from the size of our labeled data. While there are hundreds of thousands of labeled heartbeats in the publicly available databases we considered in this study, there are relatively few subjects and thus relatively few distinct PVC morphologies and phenotypes. Another limitation of our study is the lack of labeled data obtained from real-world settings. Indeed, all labeled databases we can access are of relatively high quality. In practice, we need an automatic signal quality classifier to identify when the ECG is readable. (Our algorithm made many false detections on noisy records such as record 105 in the MIT-BIH Arrhythmia database.) While developing a suitable signal quality index is out of the scope of this work, this issue should be considered when applying the algorithm in a real-world setting. In our future work, we plan to invite experts to help annotate more ECG signals obtained in real-world settings and further improve the algorithm. We found that our algorithm performed poorly on the Irregular Rhythm and Potential Ischemia subgroups (see Table 4); since developing a phenotype classifier is out of the scope of this work, we will explore the possibility of developing an ectopy detection algorithm suited to these specific patient populations in future work. Yet another limitation is that our algorithm is not designed nor validated in patients who are paced. It would be a clinical important topic to explore when we have an access to database of this kind. Finally, our algorithm was not designed to leverage all of the information present in a multi-lead ECG recording. When multiple leads are available, all of the available information should be considered to further improve the result. Future work will leverage multiple leads with the goal of developing an algorithm with higher precision
Conclusion
The computationally efficient and interpretable ventricular ectopy detection algorithm developed in this work raises the standard for automatic tools that can expedite clinical decision-making and propagate PVC-related research by allowing the complete analysis of large databases of long-term ECG recordings
Footnotes
CRediT authorship contribution statement
John Malik: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing - original draft, Writing - review & editing. Zak Loring: Conceptualization, Investigation, Writing - original draft, Writing - review & editing. Jonathan P. Piccini: Conceptualization, Project administration, Resources, Supervision, Writing - review & editing. Hau-Tieng Wu: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing - review & editing.
References
- [1].Kennedy HL, et al. Long-term follow-up of asymptomatic healthy subjects with frequent and complex ventricular ectopy. N Engl J Med 1985;312(4):193–197. [DOI] [PubMed] [Google Scholar]
- [2].Cha Y-M, et al. Premature ventricular contraction-induced cardiomyopathy: a treatable condition. Circ Arrhythm Electrophysiol 2012;5(1):229–236. [DOI] [PubMed] [Google Scholar]
- [3].Abdalla IS, et al. Relation between ventricular premature complexes and sudden cardiac death in apparently healthy men. Am J Cardiol 1987;60(13):1036–1042. [DOI] [PubMed] [Google Scholar]
- [4].Cheriyath P, et al. Relation of atrial and/or ventricular premature complexes on a two-minute rhythm strip to the risk of sudden cardiac death (the Atherosclerosis Risk in Communities [ARIC] study). Am J Cardiol 2011;107(2):151–155. [DOI] [PubMed] [Google Scholar]
- [5].Bikkina M, Larson MG, Levy D Prognostic implications of asymptomatic ventricular arrhythmias: the Framingham Heart Study. Ann Intern Med 1992;117(12):990–996. [DOI] [PubMed] [Google Scholar]
- [6].Lin C-Y, et al. Long-term outcome of multiform premature ventricular complexes in structurally normal heart. Int J Cardiol 2015;180:80–85. [DOI] [PubMed] [Google Scholar]
- [7].Dukes JW, et al. Ventricular ectopy as a predictor of heart failure and death. J Am Coll Cardiol 2015;66(2):101–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Hamon D, et al. Premature ventricular contraction coupling interval variability destabilizes cardiac neuronal and electrophysiological control: insights from simultaneous cardioneural mapping. Circ Arrhythm Electrophysiol 2017;10(4):e004937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Walters TE, et al. Left ventricular dyssynchrony predicts the cardiomyopathy associated with premature ventricular contractions. J Am Coll Cardiol 2018;72(23):2870–2882. [DOI] [PubMed] [Google Scholar]
- [10].Baman TS, et al. Relationship between burden of premature ventricular complexes and left ventricular function. Heart Rhythm 2010;7(7):865–869. [DOI] [PubMed] [Google Scholar]
- [11].Niwano S, et al. Prognostic significance of frequent premature ventricular contractions originating from the ventricular outflow tract in patients with normal left ventricular function. Heart 2009;95(15):1230–1237. [DOI] [PubMed] [Google Scholar]
- [12].Voskoboinik A, et al. Predictors of adverse outcome in patients with frequent premature ventricular complexes: The ABC-VT risk score. Heart Rhythm 2020;17(7):1066–1074. [DOI] [PubMed] [Google Scholar]
- [13].El Kadri M, et al. Effect of ablation of frequent premature ventricular complexes on left ventricular function in patients with nonischemic cardiomyopathy. Heart Rhythm 2015;12(4):706–713. [DOI] [PubMed] [Google Scholar]
- [14].Lip GY, et al. Stroke prevention in atrial fibrillation: past, present and future. Thromb Haemost 2017;117(7):1230–1239. [DOI] [PubMed] [Google Scholar]
- [15].De Chazal P, O’Dwyer M, Reilly RB Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans Biomed Eng 2004;51(7):1196–1206. [DOI] [PubMed] [Google Scholar]
- [16].Llamedo M, Martínez JP Heartbeat classification using feature selection driven by database generalization criteria. IEEE Trans Biomed Eng 2010;58(3):616–625. [DOI] [PubMed] [Google Scholar]
- [17].Llamedo M, Martínez JP An automatic patient-adapted ECG heartbeat classifier allowing expert assistance. IEEE Trans Biomed Eng 2012;59(8):2312–2320. [DOI] [PubMed] [Google Scholar]
- [18].Ye C, Kumar BVKV, Coimbra MT Heartbeat classification using morphological and dynamic features of ECG signals. IEEE Trans Biomed Eng 2012;59(10):2930–2941. [DOI] [PubMed] [Google Scholar]
- [19].Herry CL, et al. Heart beat classification from single-lead ECG using the synchrosqueezing transform. Physiol Meas 2017;38(2):171. [DOI] [PubMed] [Google Scholar]
- [20].Acharya UR, et al. A deep convolutional neural network model to classify heartbeats. Comput Biol Med 2017;89:389–396. [DOI] [PubMed] [Google Scholar]
- [21].Warrick P, Homsi MN Cardiac arrhythmia detection from ECG combining convolutional and long short-term memory networks. 2017 Computing in Cardiology (CinC); 2017. IEEE. [Google Scholar]
- [22].Xiong Z, et al. ECG signal classification for the detection of cardiac arrhythmias using a convolutional recurrent neural network. Physiol Meas 2018;39(9):094006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Alfaras M, Soriano MC, Ortín S A fast machine learning model for ECG-based heartbeat classification and arrhythmia detection. Front Physics 2019;7:103. [Google Scholar]
- [24].Martinez A, Alcaraz R, Rieta JJ Ectopic beats canceler for improved atrial activity extraction from Holter recordings of atrial fibrillation. 2010 Computing in Cardiology; 2010. IEEE. [Google Scholar]
- [25].Martínez A, Alcaraz R, Rieta JJ Detection and removal of ventricular ectopic beats in atrial fibrillation recordings via principal component analysis. 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society; 2011. IEEE. [DOI] [PubMed] [Google Scholar]
- [26].Martínez A, Alcaraz R, Rieta JJ Ventricular activity morphological characterization: Ectopic beats removal in long term atrial fibrillation recordings. Comput Methods Programs Biomed 2013;109(3):283–292. [DOI] [PubMed] [Google Scholar]
- [27].Moody GB, Mark RG The impact of the MIT-BIH arrhythmia database. IEEE Eng Med Biol Mag 2001;20(3):45–50. [DOI] [PubMed] [Google Scholar]
- [28].Goldberger AL, et al. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation 2000;101(23):e215–e220. [DOI] [PubMed] [Google Scholar]
- [29].AAMI/ANSI EC57 Testing and reporting performance results of cardiac rhythm and ST segment measurement algorithms. 2012. American National Standard, 2012. [Google Scholar]
- [30].Malik J, Soliman EZ, Wu H-T An adaptive QRS detection algorithm for ultra-long-term ECG recordings. J Electrocardiol 2020. [DOI] [PubMed] [Google Scholar]
- [31].Laguna P, Sörnmo L Sampling rate and the estimation of ensemble variability for repetitive signals. Med Biol Eng Comput 2000;38(5):540–546. [DOI] [PubMed] [Google Scholar]
- [32].Hafner J, et al. Efficient color histogram indexing for quadratic form distance functions. IEEE Trans Pattern Anal Mach Intell 1995;17(7):729–736. [Google Scholar]
- [33].Freund Y, Schapire RE A desicion-theoretic generalization of on-line learning and an application to boosting. European conference on computational learning theory. Springer; 1995. [Google Scholar]
- [34].Oster J, et al. Semisupervised ECG ventricular beat classification with novelty detection based on switching Kalman filters. IEEE Trans Biomed Eng 2015;62(9):2125–2134. [DOI] [PubMed] [Google Scholar]
- [35].Qurraie SS, Afkhami RG ECG arrhythmia classification using time frequency distribution techniques. Biomed Eng Lett 2017;7(4):325–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Silva I, Moody GB An open-source toolbox for analysing and processing physionet databases in matlab and octave. J Open Res Software 2014;2(1):e27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Rubner Y, Tomasi C, Guibas LJ The earth mover’s distance as a metric for image retrieval. Int J Comput Vision 2000;40(2):99–121. [Google Scholar]
- [38].Niblack CW, et al. QBIC project: querying images by content, using color, texture, and shape. Storage and retrieval for image and video databases. International Society for Optics and Photonics; 1993. [Google Scholar]
- [39].Ortín S, et al. Automated real-time method for ventricular heartbeat classification. Comput Methods Programs Biomed 2019;169:1–8. [DOI] [PubMed] [Google Scholar]
- [40].Teijeiro T, et al. Heartbeat Classification Using Abstract Features From the Abductive Interpretation of the ECG. IEEE J Biomed Health Inform 2018;22(2):409–420. [DOI] [PubMed] [Google Scholar]


