Probing Renal Microstructure and Function with Advanced Diffusion MRI: Concepts, Applications, Challenges and Future Directions

Abstract

Diffusion measurements in the kidney are affected not only by renal microstructure but also by physiological processes (i.e., glomerular filtration, water reabsorption and urine formation). Because of the superposition of passive tissue diffusion, blood perfusion and tubular pre-urine flow, the limitations of the monoexponential apparent diffusion coefficient (ADC) model in assessing pathophysiological changes in renal tissue are becoming apparent and motivate the development of more advanced diffusion-weighted imaging (DWI) variants. These approaches take advantage of the fact that the length scale probed in DWI measurements can be adjusted by experimental parameters, including diffusion-weighting, diffusion gradient directions and diffusion time. This forms the basis by which advanced DWI models can be used to capture not only passive diffusion effects, but also microcirculation, compartmentalization, tissue anisotropy. In this review, we provide a comprehensive overview of the recent advancements in the field of renal DWI. Following a short introduction on renal structure and physiology, we present the key methodological approaches for the acquisition and analysis of renal DWI data, including intravoxel incoherent motion (IVIM), diffusion tensor imaging (DTI), non-Gaussian diffusion, and hybrid IVIM-DTI. We then briefly summarize the applications of these methods in chronic kidney disease and renal allograft dysfunction. Finally, we discuss the challenges and potential avenues for further development of renal DWI.

Introduction

Chronic kidney disease (CKD) is a long-term condition that affects > 10% of the general global population and has emerged as one of the leading causes of death worldwide(1). In the current clinical practice, CKD is most frequently diagnosed through laboratory testing, usually by estimating glomerular filtration rate (eGFR) from a filtration marker (e.g., serum creatinine (SCr) or cystatin C), or by analyzing the urine for the presence of proteins, such as albumin. But despite their wide availability and comparatively low costs, blood and urine biomarkers of renal function do not allow to differentiate between different pathologies. Further, eGFR values derived from serum creatinine are not accurate in patients with rapidly changing creatinine levels, people at extremes of body size or muscle mass, or those with altered diet patterns(2). This inaccuracy might lead to disease misclassification in populations with renal disease but normal eGFR, such as patients with diabetes mellitus(3). In cases of unexplained deterioration of renal function, renal biopsy remains the gold standard for diagnosis and therapy guidance of renal parenchymal diseases. However, besides being invasive and difficult to obtain in certain patients, biopsy is prone to sampling errors and may therefore lead to unreliable diagnosis(4). These limitations largely prevent the use of renal biopsy for frequent patient monitoring that is necessary for optimizing individualized therapy strategies. Development of better diagnostic and prognostic tools is a well-recognized strategy to resolve these challenges. This is where imaging, especially MRI, can play a significant role.

Assessment of renal morphology, microstructure and function with MRI has been actively explored in the past two decades(5-9). For example, dynamic contrast-enhanced (DCE) MRI using gadolinium chelates has been shown to provide accurate information on single-kidney glomerular filtration rate (GFR) and renal plasma flow (RPF)(10). Nevertheless, the use of DCE MRI in patients with renal impairment is limited(11). By probing the water molecule displacement at the microscopic level, diffusion weighted imaging (DWI) quantified by the apparent diffusion coefficient (ADC) has been recognized as a potentially valuable and sensitive biomarker of renal dysfunction. However, despite growing evidence from multiple studies (e.g., (12-16)), the use of renal DWI in routine clinical settings is still limited. One of the major challenges of this technique is its relatively low biological specificity to underlying pathological changes in diseased kidneys. In fact, it is known that the diffusion measurements in the kidney are affected not only by renal microstructure but also by physiological processes such as glomerular filtration, water reabsorption and urine formation, which involve considerable microscopic flow in blood vessels and tubules. This multifactorial dependence of the DWI contrast complicates the interpretation of the observed signal changes in renal pathologies. For instance, it is still a subject of debate whether the reduced ADC values reported in numerous studies in human CKD reflect predominantly the impaired function (directed water transport in tubules) and reduced blood perfusion (e.g.,(12, 17, 18)), or the degree of fibrotic changes in the kidney (e.g., (13, 19, 20)).

Our limited understanding of the origins of the DWI signal in renal tissue, and awareness of the limitations of the monoexponential ADC model led to the development and application of more advanced DWI variants. These approaches take advantage of the fact that the length scale probed by DWI measurements can be adjusted by experimental parameters, including diffusion-weighting (b-value), diffusion gradient directions and diffusion time (i.e., time interval during which random spin movements are sampled). This forms the basis by which DWI can be used to capture not only passive diffusion effects, but also microcirculation, compartmentalization, and tissue anisotropy(21), to provide additional insights into renal pathophysiology.

In this review, we summarize the recent progress in the field of advanced DWI of the human kidney. We begin with a short introduction of renal anatomy and physiology, followed by an overview of various methodological approaches for the acquisition and analysis of renal DWI data. We then briefly cover the applications of these methods in CKD and renal allograft dysfunction in the past 5 years, complementing a previous review of Caroli et al.(6). Finally, we discuss specific issues and major directions for further development of renal DWI.

Unique Features of Renal Structure and Physiology

The Nephron

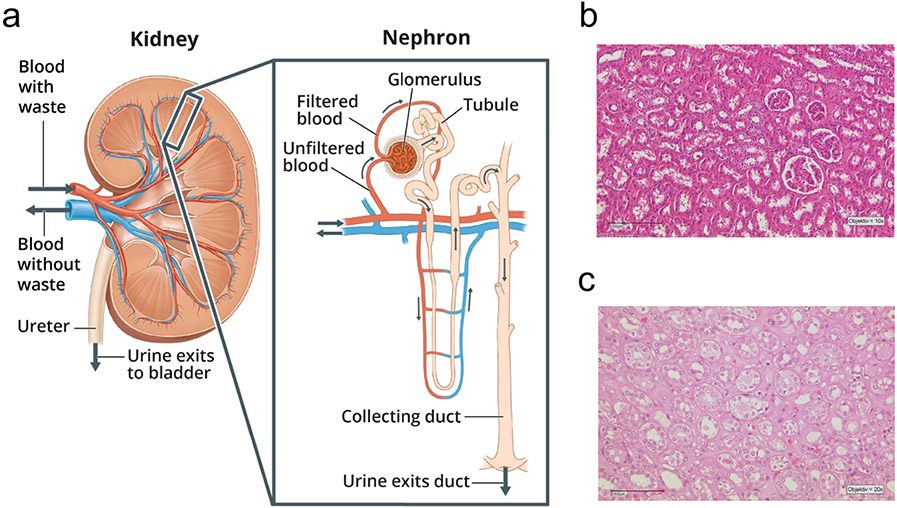
Each human kidney contains up to a million functioning units called nephrons (Figure 1), which carry out three basic functions: glomerular filtration, tubular reabsorption, and tubular secretion. The first step of urine formation is the glomerular filtration, during which water and most solutes of the blood plasma pass through walls of a high-pressure capillary bed called the glomerulus, into the proximal end of the tubule known as the Bowman’s capsule. The product of glomerular filtration, called glomerular filtrate, travels through the remining segments of the nephron to the proximal tubule, loop of Henle, and distal convoluted tubule, before exiting the nephron into the common collecting ducts shared by many nephrons. The walls of these different nephron segments are made of a single layer of epithelial cells that separate the tubular lumen from the interstitial space(22).

Figure 1:

(a) Image of a close up nephron and its place in the kidney, and (b, c) histological sections of a healthy kidney. (b) Normal-appearing cortical tissue with glomeruli, distal and proximal tubules and blood vessels; (c) Outer medulla with vasa recta, proximal tubules, segments of loop of Henle and collecting ducts. Panel (a) image source: National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK), National Institutes of Health (NIH).

During the tubular reabsorption, the epithelial cells lining the tubules and collecting ducts reabsorb nearly all water and various solutes from the glomerular filtrate as it passes through. These reabsorbed substances are subsequently returned to the bloodstream through the peritubular capillaries and vasa recta. During the process of tubular secretion, various substances such as metabolic wastes, drugs, and excess ions are transferred from the peritubular capillaries to the tubular lumen in a tightly regulated manner to be eventually removed from the body as urine(22).

The renal tubules comprise a large fraction of the renal volume (up to approximately 85% of cortical volume(23)). Under various pathophysiological conditions the tubular volume fraction can rapidly change due to (i) changes in glomerular filtration, (ii) changes in tubular outflow towards the pelvis, (iii) modulation of the transmural pressure gradient, and (iv) changes in fluid resorption(24) (v) interstitial expansion or contraction. A common early feature of many progressive renal diseases (e.g., polycystic kidney disease and diabetes) is tubular hypertrophy, which is associated with tubular enlargement and, consequently, an increase in tubular volume fraction. As renal disease progresses, tubular damage leads to tubular atrophy that shows a contraction of the tubular lumen (and reduced tubular volume fraction)(25). Therefore, it is believed that the tubular volume fraction could serve as a diagnostic biomarker of tubular pathology. Owing to its unique sensitivity to restricted water motion within the tubular lumen, DWI is particularly well suited to provide quantitative measures of tubular volume fraction.

Renal Interstitium

The renal interstitium refers to the inter-tubular, extraglomerular and extravascular space of the kidney. It is enclosed by tubular and vascular basement membranes and filled with cells, extracellular matrix (ECM) and interstitial fluid. Distribution of the renal interstitium varies within the kidney, accounting for approximately 8% of the total parenchymal volume in the cortex and up to 40% in the inner medulla(26).

Pathologic remodeling of the interstitium, called “interstitial fibrosis” determines progression of CKD in native kidneys and renal transplants. Chronic progressive kidney injury is associated with a substantial expansion of the interstitium (the relative volume might increase from 5%-10% in normal kidneys to >60% in severely diseased kidney tissue), which is predominantly caused by accumulation of ECM proteins, ECM-producing fibroblasts and mononuclear cells(26). Increased extent of interstitial fibrosis and accompanying tubular atrophy is associated with poor prognosis in a wide range of kidney pathologies(27)(28). Being able to noninvasively measure the extent of renal fibrosis with MRI would be clinically valuable as it could help predict outcome in CKD and renal transplants dysfunction.

Deposition and accumulation of ECM and tubular atrophy are expected to restrict the mobility of water molecules, resulting in lower ADC. However, a fall in renal perfusion and tubular flow in fibrotic kidneys may also lead to decreased ADC (Figure 2). Thus, it has recently been suggested that in vivo ADC is unlikely to be a direct measure of fibrosis but rather reflects renal function and perfusion(29). In this context, the ability of advanced DWI variants to separate the effects of passive diffusion from microcirculation, or to probe the tissue anisotropy may help elucidate the diffusion mechanism in fibrotic kidneys and thereby characterize different pathologies.

Figure 2:

Schematic depictions of a (a) normal and (b) fibrotic kidney. (b) Deposition and accumulation of extracellular matrix and tubular atrophy restrict the mobility of water molecules, elevate macromolecular content and lowers the tubular flow, whereas vascular rarefaction causes a fall in renal perfusion. Redrawn from Jiang et al. (7)

Renal Blood Flow and Glomerular Filtration Rate

Under resting conditions, approximately one-fifth of the cardiac output in humans ends up flowing through the kidneys, organs that constitute less than 0.5% of the total body mass. If considered per tissue weight, the rate of renal blood flow (RBF) of about 400 ml/100 g tissue/min (or about 1 liter per minute) is much higher than that of most other vascular beds, including heart, brain and liver(30). RBF is highly compartmentalized, with the majority of blood flow being delivered to the renal cortex and only a small fraction entering the renal medulla (10% - 15% of total RBF)(31).

Approximately one-fourth of the blood plasma that enters the glomerulus passes through the filtration barrier to ultimately form the glomerular filtrate. The amount of fluid filtered from the glomerulus into Bowman’s capsule per unit time is known as the GFR. In young adults, GFR is about 120 ml/min/1.73 m² and declines in normal individuals with age. Nonetheless, a decrease in GFR may also be a marker of kidney disease and precedes the onset of kidney failure. Therefore, a persistently reduced or declining GFR is a specific diagnostic criterion for CKD(2).

The central role of the kidney in blood filtration, and reductions in filtration rate and blood flow associated with many renal diseases, make it possible to assess kidney function by probing the microscopic motion of water protons with DWI. In this context, separation of the capillary blood perfusion (quantified as RPF) from the pre-urine tubular flow (assessed with GFR, as its closest measurable proxy) remains an ongoing challenge for advanced DWI.

Advanced DWI: Acquisition Techniques

Diffusion-weighted single-shot spin-echo echo planar imaging (DW-SE-ssEPI) is the most widely used acquisition technique in DWI because it enables rapid image acquisition (<100 ms/slice), substantially reducing motion artifacts for a given slice. Unfortunately, ss-EPI is highly sensitive to magnetic susceptibility effects, which typically result in image blurring, geometric distortions of the imaged tissues, and signal dropouts. Hence, diffusion-weighted ss-EPI is particularly challenging in kidney regions adjacent to the bowel or close to boundaries of different tissue types (fat/muscle/skin)(32). One way to reduce distortions in DWI is to alter k-space traversal by using different sampling trajectories. Several approaches have been proposed so far which include, but are not limited to, multi-shot fast SE-DW-EPI with ‘periodically rotated overlapping parallel lines with enhanced reconstruction’ (DW-PROPELLER)(33), DW-PROPELLER combined with split-echo acquisition of FSE signals (DW-SPLICE-PROPELLER)(34), or readout-segmented DWI(35, 36, 20). Both DW-PROPELLER and DW-SPLICE-PROPELLER demonstrated less sensitivity to field inhomogeneities and reduced motion-related artifacts due to intrinsic segmental phase correction and oversampling at the center of k-space compared to DW-SE-ssEPI. In applications where specific absorption rate (SAR) is a limiting factor (e.g., pediatric imaging), readout-segmented EPI might be a promising alternative. Another way to further reduce the image distortions is to use a reduced field of view or zoomed-DW-SE-ssEPI sequence that has been shown to reduce the interference of bowel movement and air-related artifacts on the kidney through small field of view local excitation and associated smaller echo train length(37). In a recent study, it has been demonstrated that zoomed-DWI outperforms both DW-SE-ssEPI combined with different breathing schemes, and readout-segmented DWI as it provided the highest ADC reproducibility, better cortico-medullary contrast-to-noise ratio and good image quality at 3T(38). Another fast and robust method for efficient distortion correction is the “reversed gradient” method(39). Lately, it has been demonstrated that this approach is feasible for ssEPI-based diffusion tensor imaging of the kidney, with good correlation to T2-weighted imaging and no significant impact on diffusion tensor metrics(40).

A crucial issue for the clinical translation of renal DWI is the acquisition time. A common feature of advanced DWI variants and models is that they all require repeated acquisitions of DW images (across a potentially wide range of b-values and/or diffusion gradients directions, or diffusion times), which leads to long examination times and thus the applicability of these methods in clinical routine is limited. According to several previous studies, simultaneous multislice (SMS) DWI seems be a promising acquisition strategy to drastically reduce the scan time by simultaneously exciting multiple slices(41-44). Further, it has been shown that advanced intravoxel incoherent motion (IVIM) imaging combined with SMS accelerated DWI acquisition yields comparable results to a conventional approach with DW-SE-ssEPI(42).

Advanced DWI: Signal Modelling

Intravoxel Incoherent Motion (IVIM)

In biological tissues, molecular diffusion is affected by both microstructure and microdynamics (including blood flow in capillaries, exchange and transport between different tissue compartments). This observation led to the belief that localized information about blood perfusion can be obtained from diffusion-based MR measurements. The intra-voxel incoherent motion (IVIM) model as originally proposed by Le Bihan et al.(45) is based on the postulate that blood flowing in isotropically distributed capillary segments introduces a phase dispersion of the measured MR signal, which leads to increased signal attenuation in DW images. Further, it is assumed that (i) the (pseudo-) diffusion coefficient ${\mathrm{D}}^{\star }$ associated with microcirculation is much larger (at least an order of magnitude) than the molecular diffusion coefficient $\mathrm{D}$, (ii) there is negligible exchange between the vascular and extracellular compartments during the measurements, and (iii) the associated compartmental T2 values are the same. Under these assumptions, it is expected that the signal decay measured at different b-values can be fitted using a biexponential function:

$$S(b)=S_0\left((1-f)\cdot e^{-bD}+f\cdot e^{-b{D}^{\ast }}\right)$$ (Eq. 1)

where $\mathrm{S}(\mathrm{b})$ and ${\mathrm{S}}_0$ are the measured signal intensities with a gradient sensitivity factor $\mathrm{b}$ and $\mathrm{b}=0$, respectively; $\mathrm{D}$ is the molecular (or passive) diffusion coefficient and ${\mathrm{D}}^{\star }$ is assumed to be the pseudo-diffusion coefficient. Parameter $\mathrm{f}$ is believed to reflect blood volume fraction and thus perfusion (or flow) (Figure 3). A reliable estimation of the perfusion fraction $\mathrm{f}$ requires acquiring multiple DW images at sufficiently low b-values (< 200 s/mm²).

Figure 3:

Signal fraction (f) maps from the bi- and triexponential IVIM fits. (a) DW images for b-values from 0 to 700 s/mm2; (b) signal fraction maps in % for the bi- and tri-exponential fit; (c) merged signal fraction maps of the triexponential IVIM fit color coded as red, green and blues for $1-{\mathsf{f}}_{\text{interm}}-{\mathsf{f}}_{\text{fast},2},{\mathsf{f}}_{\text{interm}}$ and ${\mathsf{f}}_{\text{fast},2}$, respectively with the corresponding T2w anatomical images. Figure taken from van Baalen et al.(48) with permission.

Although the principles of IVIM imaging were originally introduced for cerebral applications, the potential of this technique is now being more thoroughly investigated in abdominal organs, which have higher incoherent flow contributions than the brain. With its high blood flow and capillary density, the kidney is expected to exhibit particularly strong IVIM effects. As a consequence, the two-compartment model was shown to better describe the diffusion signal in the kidney than the conventional single compartment model(46-48).

Multicompartment Models

Even though the IVIM term generally describes any type of motion that may contribute to the DW signal, the IVIM model assumes that the fast pseudo-diffusion component is primarily associated with microcirculation. In the kidneys, the incoherent motion can be linked not only to blood perfusion in the renal microvasculature and glomeruli but also to pre-urine flow in the tubules and collecting ducts. One important consequence of this observation is that the IVIM parameters derived from the bi-exponential model may reflect the flow-dependent renal function rather than regional renal blood flow(49). This interpretation is also supported by the fact that D and f were shown to be sensitive to diuretic challenges(50). Recently it has been suggested that the vascular and tubular contributions to the renal DWI signal can be resolved based on their pseudo-diffusion rates. A three-compartment IVIM model was therefore proposed in which a third exponent term with an intermediate decay rate was incorporated into the IVIM model, to account for the tubular water pseudo-diffusion component with a signal fraction f_i, potentially reflecting the tubular volume fraction (Figure 3)(48, 51, 52):

$$S(b)=S_0\left((1-f_i-f_f)\cdot e^{-bD}+f_i\cdot e^{-b{D}_i^{\ast }}+f_f\cdot e^{-b{D}_f^{\ast }}\right)$$ (Eq. 2)

where $\mathrm{D}$ is the diffusion coefficient, and ${\mathrm{f}}_{\mathrm{i}}$ and ${\mathrm{f}}_{\mathrm{f}}$ are the signal fractions corresponding to the intermediate pseudo-diffusion coefficient ${\mathrm{D}}_{\mathrm{i}}^{\star }$ and fast pseudo-diffusion coefficient ${\mathrm{D}}_{\mathrm{f}}^{\star }$, respectively. The three-exponential model was found to adequately fit the DWI signal in the kidney, while providing additional information on the renal structures associated with intermediate flow-related process(48).

An alternative interpretation of the three compartment model (TCM) was recently put forth, in which it was suggested that an unattenuated fat signal acts as an independent compartment and can be incorporated in the IVIM model by adding a third exponential decay term(53):

$$S(b)=S_0\left((1-(C+f))\cdot e^{-b{D}^{\ast }}+C\cdot e^{-bD}+f\right)$$ (Eq. 3)

where $\mathrm{C}$ and $\mathrm{f}$ are the tissue (extratubular/extravascular) and fat-related signal fractions in the DW signal, and the $\mathrm{D}$ and ${\mathrm{D}}^{\star }$ are the diffusion coefficient and pseudo-diffusion coefficient of the flow-related component, respectively. At high b-values, the amplitude of unsuppressed fat signal can become prominent compared to the attenuated water signal, and therefore has a considerable impact on DWI measurements. At the same time, it was suggested that the fat-related fraction component, $\mathrm{f}$, can be reduced by selecting longer TR and optimal TE based on the T2 values of fat and water.

Spectral Diffusion Analysis

A common limitation of the rigid biexponential and triexponential models is that they may not accurately reflect the complex pathophysiological changes in diseased kidneys because the data is forced to conform to a priori assumption on the number of (pseudo-)diffusion compartments(54, 55, 52). Furthermore, their performance is usually highly dependent on the initial parameter values and fit boundaries. To overcome these issues, a data-driven spectral diffusion analysis based on the non-negative least squares (NNLS) algorithm of Hanson and Lawson(56) has recently been proposed. This approach assumes that the diffusion signal decay, y_i can be represented as a sum of exponential functions:

$$y_i={\sum }_{j=1}^M{s}_j{e}^{-b_i{D}_j},i=1,2,\dots ,N$$ (Eq. 4)

where ${\mathrm{s}}_{\mathrm{j}}$ is the relative amplitude for each (pseudo-) diffusion coefficient ${\mathrm{D}}_{\mathrm{i}}$, ${\mathrm{b}}_{\mathrm{i}}$ is the b-value for each data point, $\mathrm{M}$ is the number of logarithmically spaced D-values, and $\mathrm{N}$ represents the total number of data points. The NNLS algorithm is then used to minimize the least-squares ${\chi }^2$ misfit:

$${\chi }_r^2=min\left[{\sum }_{i=1}^N{\mid {\sum }_{j=1}^M{s}_j{e}^{-b_i{D}_j}-y_i\mid }^2+\mu {\sum }_{j=2}^{M-1}{\mid s_{j+1}-2s_j-s_{j-1}\mid }^2\right]$$ (Eq. 5)

where $\mu$ is the regularization factor that acts as a smoothing constraint to improve the robustness of the fit to noise. As an output, spectral diffusion analysis with NNLS yields a diffusion coefficient distribution with distinct peaks, each of which corresponds to a major (pseudo-) diffusion compartment(52).

Considering the experimental evidence provided by recent studies in which NNLS modelling approach was applied, use of the rigid three-compartment model seems to be justified in healthy kidneys(54, 55). This assumption, however, might not be accurate in the case of renal pathologies such as renal fibrosis, polycystic kidney disease, or renal masses(55) that may contain additional (or fewer) sources of renal incoherent water motion.

Generalized IVIM Model (GIVIM)

The concept of continuous pseudo-diffusion, as opposed to the rigid multi-exponential IVIM models, has also been used to formulate the generalized intravoxel incoherent motion (GIVIM) model(57). This model assumes that the perfusion fraction density function follows a Gaussian distribution and so the diffusion signal as a function of b-value can be describe as(57, 58):

$$S(b)=S_0\left((1-f)\cdot e^{-bD}+f\frac{{\int }_0^{+\infty }\text{exp}(-{(D_c-\overline{D})}^2∕2{\sigma }^2)e^{-b(D_c+D)}d{D}_c}{{\int }_0^{+\infty }\text{exp}(-{(D_c-\overline{D})}^2∕2{\sigma }^2)d{D}_c}\right)$$ (Eq. 6)

where ${\mathrm{D}}_{\mathrm{c}}$ is a continuous pseudo-diffusion variable, $\overline{\mathrm{D}}$ is the mean pseudo-diffusivity, $\sigma$ is the pseudo-diffusion dispersion, $\mathrm{f}$ represents the perfusion volume fraction, and $\mathrm{D}$ is the pure tissue diffusion. A combination of the GIVIM model and diffusion tensor imaging (see next section) has recently been proposed to better characterize renal microstructure and microcirculation(58).

Diffusion Tensor Imaging (DTI)

Both the monoexponential ADC and IVIM models assume that tissue diffusion is isotropic (i.e., equal in all directions), and therefore fail to capture the anisotropy of blood vessels, tubules, and collecting ducts that contribute to spatially organized flow patterns in the kidney. In contrast, diffusion tensor imaging (DTI) quantitatively measures and visualizes the directionality and anisotropy imposed on water diffusion measurements by the tissue microstructure. In DTI, diffusion-sensitizing gradients are applied along multiple directions (at least 6) and included in the Gaussian diffusion model. Quantitatively, the degree of direction-dependency of the diffusion signal is represented by the fractional anisotropy $(\text{FA})$ parameter, ranging from 0 (complete isotropy) to 1 (complete anisotropy) and calculated according to the following equation:

$$FA=\sqrt{\frac{3}{2}}\times \frac{\sqrt{{({\lambda }_1-\overline{MD})}^2+{({\lambda }_2-\overline{MD})}^2+{({\lambda }_3-\overline{MD})}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$$ (Eq. 7)

where $\overline{MD}$ is the average of the diffusion coefficients, a DTI-specific ADC equivalent, defined as:

$$MD=\frac{1}{3}({\lambda }_1+{\lambda }_2+{\lambda }_3)$$ (Eq. 8)

where ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ are the eigenvalues of the symmetric diffusion tensor $\overline{D}$ with elements $D_{ij}$ determined by a set of linear equations involving the set of ADC measurements along specified diffusion gradient directions. The primary eigenvalue, known as axial diffusivity, ${\lambda }_{ax}={\lambda }_1$ describes the magnitude of diffusion along the preferential diffusion direction, whereas the radial diffusivity ${\lambda }_{rad}=({\lambda }_1+{\lambda }_2)∕2$ refers to the magnitude of diffusion perpendicular to the principal diffusion direction (Figure 4).

Figure 4:

(a) Model of the tensor and (b-j) renal DT images obtained at 3T. (b) Image at b = 0 s/mm2; (c) $\text{FA}$ map; (d) $\text{MD}$ map; (e) direction-coded color map; (f) principal eigenvector diagram; (g) $\lambda 1$ map; (h) $\lambda 2$ map; (i) $\lambda 3$ map, and (j) ${\lambda }_{\perp }(={\lambda }_{\text{rad}})$ map. Panel (a) redrawn from Moura et al.,(152) and panels (b-j) modified from Sigmund et al.(50) with permission.

DTI of the kidney reveals considerably higher fractional anisotropy and axial diffusivity values in renal medulla compared to cortex, and, conversely, higher mean diffusivity and radial diffusivity values in renal cortex than in medulla. These observations are consistent with the fact that, unlike renal cortex, renal medulla has a well-defined structure with often parallel tubules, collecting ducts, and vessels radially oriented toward the pelvis, in which water molecules move in a preferential direction. In contrast, the pattern of the cortical microcirculation and tubules are more stochastic, promoting radial diffusivity. Several studies to date have demonstrated the ability of DTI to detect structural damage in kidney pathologies based on changes in diffusion anisotropy (e.g., (14, 59-61)).

Hybrid IVIM-DTI Models

While numerous DTI studies to date have reported higher $\text{FA}$ values in the renal medulla compared to cortex, the biophysical underpinnings of this anisotropy remain unclear. Nevertheless, it is reasonable to assume that both (i) active flow in highly oriented tubular and vascular structures, and (ii) structural restrictions to passive diffusion are the two major contributors. In the context of renal disease diagnostics, separating these two effects may be particularly relevant for distinguishing reduced medullary flow (associated with renal function) and irreversible renal tissue damage, for example, in diabetic nephropathy, acute tubular ischemia, or renal allograft dysfunction. To address this issue, several studies proposed using hybrid IVIM-DTI models that jointly assess the structural and flow anisotropy, either by assigning the flow anisotropy to the perfusion fraction, the pseudo-diffusivity, or both(62-66).

One of these joint approaches, known as the intravoxel oriented flow model (IVOF)(65, 66) describes the signal of flowing spins in case where the tissue organization is not isotropic but flow is oriented towards a preferential direction:

$$S(b)=S_0\left(\left(1-\overrightarrow{{\mathit{g}}^{\mathit{T}}}\mathit{f}\overrightarrow{\mathit{g}}\right)\cdot e^{-b\overrightarrow{g^T}D\overrightarrow{g}}+\overrightarrow{{\mathit{g}}^{\mathit{T}}}\mathit{f}\overrightarrow{\mathit{g}}{e}^{-bD{\overrightarrow{g^T}}^{\ast }\overrightarrow{g}}\right)$$ (Eq. 9)

where $\overrightarrow{\mathit{g}}$ is the normalized diffusion gradient vector and $\mathrm{b}$ is a scalar b-value. The IVOF model described by Eq. 9 has six free parameters for each tensor $\mathbf{f}$, $\mathbf{D}$ and ${\mathbf{D}}^{\star }$, yielding 18 free parameters in total. Anisotropic ${\mathrm{D}}^{\star }$ indicates different velocities in different directions, whereas anisotropic $\mathrm{f}$ indicates that tubules and capillaries are not oriented isotropically, but rather are aligned parallel in a certain direction.

An alternative approach, the REFMAP (for “REnal Flow and Microstructure AnisotroPy”)(62-64) methodology combines the separate bi-exponential IVIM and DTI analyses with a cylindrical two-compartment model to quantify the global anisotropies of the diffusion and perfusion components. The REFMAP model yields the mean diffusion $\text{MD}$ and fractional anisotropy $\text{FA}$ for both tissue diffusion compartment $(\mathrm{t})$ and flow compartment $(\mathrm{p})$, assuming cylindrical symmetry $({\lambda }_2={\lambda }_3)$:

$${MD}_t=\frac{1}{3}(D_{t,ax}+2D_{t,rad})$$ (Eq. 10)

$$FA=\sqrt{\frac{3}{2}}\times \frac{\sqrt{{(D_{t,ax}-{MD}_t)}^2+{2(D_{t,rad}-{MD}_t)}^2}}{\sqrt{D_{t,ax}^2+D_{t,rad}^2}}$$ (Eq. 11)

where ${\mathrm{D}}_{\mathrm{t},\text{ax}}$ and ${\mathrm{D}}_{\mathrm{t},\text{rad}}$ are the global tissue diffusivity along the axial and radial direction, respectively. The global pseudo-diffusivity parameters ${\mathrm{D}}_{\mathrm{p},\text{ax}}$ and ${\mathrm{D}}_{\mathrm{p},\text{rad}}$ are obtained with equivalent calculations. This parameter set is termed REFMAP. For a more detailed description of the specific REFMAP analysis steps, please refer to(62, 63).

Regardless of the applied hybrid IVIM-DTI approach, it has been demonstrated that the medullary flow-related component in the kidney is indeed anisotropic. Consistent with those findings, Sigmund et al.(50) found that medullary ${\lambda }_{\text{rad}}$ increases significantly with diuretic challenges, indicating elevated transverse water motion. This increase may likely be attributed to a combination of tubular and vascular mechanisms possibly occurring simultaneously, including (i) tubule dilation (resulting in a lessening of diffusion restriction), (ii) increased trans-tubular flow due to water reabsorption in distal nephron segments, and (iii) increased vascular flow in transverse segments of the vasa recta. In a recent study, the REFMAP was combined with cardiac-gating and flow-compensated gradients to address the challenge of separating the tubular and vascular contributions and further improve our understanding of renal diffusion MR contrast(64).

Models of Diffusional Non-Gaussianity

Both DWI (including IVIM) and DTI assume that the probability for water molecule to travel a certain distance over time follows a Gaussian distribution, which is valid only when water molecules diffuse unrestricted in any direction. In biological tissues, the complex cellular microstructure greatly affects the random movement of water molecules within an imaging voxel, thus leading to a considerable deviation from the normative pattern.

Over the past decades, several non-geometric DWI data modelling approaches that provide quantitative metrics of non-Gaussianity have been proposed. One such model known as the diffusion-kurtosis imaging (DKI) expresses the logarithm of the DW signal as a Taylor-series to estimate excess kurtosis. In general, the kurtosis model extends the DTI model by including a higher order ${\mathrm{b}}^2$ term :

$$S(b)=S_0\left(e^{-b{D}_K+\frac{1}{6}{b}^2{D}_K^2{K}^2}\right)$$ (Eq. 12)

where the diffusion kurtosis, $\mathrm{K}$, describes the deviation from the Gaussian distribution and ${\mathrm{D}}_{\mathrm{K}}$ is the mean diffusion coefficient in the voxel (Figure 5). In the case of Gaussian distribution, $\mathrm{K}=0$. Quantitively, higher kurtosis values suggest greater hindrance and restriction to normal diffusion and thus, higher microstructural complexity of the imaged tissue. Consequently, $\mathrm{K}$ can be considered a measure of intra-voxel diffusion heterogeneity. In contrast to the IVIM effects that are observable at lower b-values (b < 300 s/mm²), the effect of diffusion kurtosis is best appreciated at high b-values (> 600 s/mm²). Further, analogous to DTI, by acquiring DW images at multiple diffusion gradient directions (at least 15), it is possible to estimate the diffusion the axial and radial components of kurtosis.

Figure 5:

(a) Diagram of gaussian and non-gaussian diffusion environment and corresponding diffusion displacement distributions, and (b - d) MK maps of benign and malignant renal tumors. (a) Non-gaussian diffusion is represented with a Kurtosis K > 0; (b) mean kurtosis (MK) maps of a clear cell renal cell carcinoma (ccRCC), (c) renal angiomyolipoma, (AML) and (d) renal oncocytoma (RO). Significantly higher MK was found in AML than ccRCC and RO. Panel (a) redrawn from Zhuo et al. and panels (b-d) taken from Fu et al. with permission(154).

The kurtosis model, in which the Taylor-series is terminated after the quadratic term, is a special case of the cumulant expansion model. A common problem of the cumulant expansion is that convergence of the series may break down by singularities in the complex b-plane(68). This limitation can be overcome by using a Padé approximant that can model singularities. The resulting Padé exponent model can be expressed as(68):

$$S(b)=S_0\left(e^{\frac{-b{D}_P}{1+{\delta }_{1}b}}\right)$$ (Eq. 13)

where ${\delta }_1$ is the amount of non-Gaussianity and ${\mathrm{D}}_{\mathrm{P}}$ is the mean diffusion coefficient in the voxel. In a recent study of Ljimani et al., the Padé exponent model was shown to better describe the renal diffusion signal than the diffusion kurtosis model(69).

The non-monoexponential behavior of the diffusion signal in the kidney can be also quantified using a statistical model with a Gaussian-type distribution function(70, 47). Briefly, this model assumes that (i) because spin packets at different positions within a voxel are confronted with different restrictions and hindrances to their movement, their ADCs are generally different; and (2) the total MR signal can be represented in terms of a Gaussian-type distribution function that describes the fraction of spin packets with a given ADC value:

$$S(b)=S_0\left(e^{-b{D}_{stat}+\frac{1}{2}{\sigma }^2{b}^2}\right)$$ (Eq. 14)

where ${\mathrm{D}}_{\text{stat}}$ is the mean diffusion coefficient and $\sigma$ is the width of the Gaussian-type distribution.

By using a stretched exponential DWI model(68, 71, 72), the water molecular diffusion heterogeneity index $(\alpha )$ and the “distributed diffusion coefficient” (DDC) can be determined using the following equation:

$$S(b)=S_0\left(e^{-{(bDDC)}^{\alpha }}\right)$$ (Eq. 15)

where $\text{DDC}$ is the mean intravoxel diffusion rate and $\alpha$ describes to the intravoxel water molecular diffusion heterogeneity in the range between 0 and 1. Note that high $\alpha$ values represent low intravoxel diffusion heterogeneity (approaching the monoexponential decay).

Each of these non-gaussian DWI approaches has seen application in renal tissue in both health and disease. It is important to note, however, that they assign all nonmonoexponential behavior to microstructural heterogeneity, without separate regard for microcirculation. As indicated above, this assumption may be limiting in the case of renal tissue. Hybrid IVIM/DKI methodologies, which have been applied in oncologic imaging(73-75), may have a role in renal tissue in the future. Regardless, in any use of non-gaussian approaches in renal DWI, care must be taken to ensure sufficient signal-to-noise ratio (SNR) at the higher diffusion weightings required (b>1000 s/mm²) to avoid Rician noise bias.

Advanced DWI: Applications in CKD and Renal Transplants

We identified clinical studies that in the past 5 years applied advanced DWI approaches in human kidney (classified in Table 1). The complete list of identified papers is available as Supporting Information Table 1, 2, and 3. In the following, we will briefly discuss recent findings on the clinical use of IVIM, DTI and DKI in patients with CKD (mixed aetiology) and kidney transplant recipients (please also see Supporting Information Table 4). For a more comprehensive overview of the clinical applications of advanced renal DWI, we refer the reader to several recently published excellent reviews(76-78).

Table 1:

Classification of the clinical studies based on the advanced DWI variants and renal pathology. A full list of these studies is available as Supplementary Material Table 1.

	CKD (mixed aetiology)	Kidney transplants	Renal masses	Diabetic nephropathy	IgA nephropathy	Hyperuricemia	Lupus nephritis	Other
IVIM	7	7	12	3	2	2	0	1
DTI	5	6	4	9	1	2	3	9
DKI	7	1	7	0	3	0	0	1

IVIM: intravoxel incoherent motion; DTI: diffusion tensor imaging; DKI: diffusion kurtosis imaging

Chronic Kidney Disease (CKD)

CKD is a state of progressive loss of renal function, which ultimately leads to end-stage renal failure and a need for renal replacement therapy (dialysis or transplantation). CKD is classified into 5 categories based on GFR (G1 to G5 with G3 split into 3a and 3b). Regardless of the exact aetiology, fibrosis, tubular atrophy, and interstitial inflammation are the structural hallmark of CKD.

IVIM imaging detected decreased diffusion and perfusion in CKD patients. In fact, significant differences in $\mathrm{D}$, $\mathrm{f}$, and ${\mathrm{D}}^{\star }$ values between healthy volunteers and CKD patients with normal (CKD stage G1-G2) and abnormal eGFR (CKD stage G3-G5) were found in several large studies(79-83). Among all IVIM parameters, perfusion fraction $\mathrm{f}$ was identified as the optimal parameter to differentiate healthy volunteers from CKD patients with normal eGFR(79), and patients with normal eGFR from those with abnormal eGFR(79, 80). Notably, f showed better performance than eGFR(79), MK(80) and arterial spin labelling (ASL)-derived RBF(79) in discriminating healthy controls from CKD patients. Further, several studies demonstrated significant correlations between different IVIM parameters and eGFR(79, 81-84), glomerulosclerosis index (GSI)(84, 85), tubulointerstitial fibrosis index(83, 85), serum creatinine(81, 83, 85), cystatin C(81), glomerular injury score(82), tubulointerstitial injury score (TBI)(82, 84), and 24h urinary protein level (24h-UPRO)(83).

Applications of DTI (and its natural extension, DKI) in CKD patients have revealed that medullary $\text{MD}$ and $\text{FA}$ are correlated with eGFR(85) and SCr(85), which is consistent with the fact that the pre-urine flow in anisotropically oriented tubules in the renal medulla is associated with the filtration function of the kidney. One study also found that cortical and medullary $\text{MD}$ and medullary $\text{FA}$ correlate with TBI and GSI scores(85). This suggests that interstitial fibrosis, tubular atrophy, cell infiltration and glomerular scarring lead to more restricted and less anisotropic water diffusion in the extracellular space and, consequently, reduced $\text{MD}$ and medullary $\text{FA}$. In contrast, one study identified cortical $\text{FA}$ and $\text{MD}$ as better markers of structural integrity in CKD(86). This may relate to the importance of anisotropic microstructure along the full nephron path, even in the dominantly isotropic “cortical labyrinth”.

Since accumulation of the ECM in fibrotic kidneys imposes additional obstacles to water diffusion, several studies reported increased cortical MK in CKD patients compared to healthy controls(80, 87-89). This trend was observable regardless of whether eGFR was reduced or not(88), indicating that DKI can reflect tubulointerstitial damage at early stage of CKD. Consistent with this observation, MK also showed significant correlation with tubulointerstitial fibrosis(87) and tubular atrophy score(87). Further, parenchymal MK showed better performance than ADC and MD in differentiating the mild injury group from the medium-to-severe renal injury group(88), and CKD stage G1-G2 group from the CKD stage G3-G5 group(80). In addition to MK, also MD derived from DKI showed significant predictive value for prognosis of CKD(90). Overall, it is expected that DKI might be a particularly effective and promising tool to guide the clinical treatment and monitoring of CKD patients.

Kidney transplants

Kidney transplantation is currently considered the optimal treatment option for patients with end stage renal disease. Minimally invasive measurements of SCr used for monitoring of renal allograft function may not accurately reflect the state of the the allograft. In fact, SCr does not increase until approximately half of the kidney function is lost(91, 92). In addition, approximately one-third of renal allografts show histologic signs of acute rejection in the first 3 months after transplantation, without any change in SCr(93). In clinical practice, transplant renal biopsy is generally performed to provide a definitive confirmation of allograft rejection and only about 20% of the US kidney transplant centers use protocol biopsies to detect subclinical renal allograft pathology(94). Consequently, there is a clinical need for sensitive tools that can identify renal transplant recipients at an early stage of allograft dysfunction, with mild to moderate interstitial fibrosis and tubular atrophy, who are prone to rapid decrease in eGFR(95).

Advanced DWI methods have shown promising results in detecting early renal allograft dysfunction. For example, a decrease in $\mathrm{f}$ (in the cortex(96-98), medulla , and entire parenchyma(96)), $\mathrm{D}$ (in the cortex and medulla(97)), and cortical ${\mathrm{D}}^{\star }$(97) was observed in patients with impaired allograft function. At the same time, combined use of all cortical IVIM parameters was reported to have higher efficacy (sensitivity = 90.6%, specificity = 78.3%) in detecting renal allograft dysfunction than any single parameter(97). In a cohort of patients with delayed graft function, cortical $\mathrm{f}$ was found to be significantly lower in patients with complications (acute tubular necrosis, acute rejection, perirenal fluid collection/hematoma, and vascular occlusion/torsion) compared to those without complications(98). In another study, combined use of medullary $\mathrm{f}$ and cortical $\mathrm{D}$ yielded a specificity of 90.9% in identifying kidney transplant patients who needed clinical intervention(100). In pediatric transplant recipients, medullary $\text{FA}$ values in patients whose renal biopsies prompted a change in clinical management were significantly different compared with the group whose biopsy results did not change clinical management(101). At the same time, similar to native CKD, medullary $\text{FA}$ showed direct correlation with several histopathological scores(102). Several other studies in adult patients also demonstrated the potential of DTI in detecting renal allograft injury and dysfunction(91, 103, 104). For example, cortical and medullary $\text{MD}$ and $\text{FA}$ values were found to be highest in healthy controls, followed by late transplants (more than 3 months post-transplantation), with the lowest values measured for early transplants(91). Among these parameters, medullary $\text{FA}$ showed the highest correlation with eGFR and the amount of interstitial fibrosis and tubular atrophy on renal biopsy(91). Possibly, the observed changes in $\text{FA}$ result from underlying pathological changes, including cell swelling and capillary leakage in early transplants or renal interstitial fibrosis in dysfunctional allografts(91).

In DKI, an increase in medullary and cortical $\text{MD}$ and a gradual decrease in cortical and medullary MK was observed as creatinine increased. In addition, a significant correlation between eGFR and medullary $\text{FA}$, medullary MK and $\text{MD}$(105) was reported.

Advanced DWI: Current Challenges and Future Directions

Motion Artifacts and Flow Compensation

DWI in the kidney is strongly influenced by respiratory, cardiac and peristaltic motion, which cause intravoxel spin dephasing and therefore signal loss that negatively impacts the quality of DW images and estimated diffusion maps. Compared to native kidneys, DWI in transplanted kidney is less susceptible to respiratory motion artifacts due to the extraperitoneal allograft position in the iliac fossa(106). To mitigate the respiratory motion in native kidneys, respiratory-triggered or gated acquisitions are typically used (and recommended by recent consensus-based guidelines for translation of renal DWI(107)). Alternatively, post-hoc registration and advanced model-based approaches that use intrinsic features of the acquired DW data to track and correct motion and motion-dependent distortion, thus allowing free-breathing acquisition, could be a promising option(108-111). However, these methods still require more extensive validation in renal pathologies.

The adverse effects of cardiac-driven pulsation can be avoided using electrocardiogram (ECG)-triggering. However, simultaneous respiratory and cardiac-triggered acquisition is considered impractical in clinical settings due to its low efficiency. As alternatives, motion-compensated diffusion-encoding gradient waveforms have been recently proposed to minimize the motion-related artifacts in DWI of different abdominal organs (e.g., liver³⁴, pancreas(113), and kidney(114)). In the simplest case, a symmetric bipolar waveform can be designed such that the first gradient moment is equal zero, leading to no phase accumulation and therefore no signal loss when spins move with a constant velocity during diffusion encoding. Several studies demonstrated that the so-called flow-compensated diffusion encodings (dual bipolar gradients) significantly mitigate the severity of cardiac-driven pulsation artifact(115, 116). In the context of renal DWI, it has recently been found that the combination of flow-compensated and non-flow compensated data can possibly allow to resolve vascular and tubular contributions in the IVIM signal as only the slower tubular flow is effectively compensated by flow-compensated gradients(64) (Figure 6). Because of its sensitivity to vessel/tubule segment length and flow velocity, flow-compensated IVIM could potentially also be used to reveal pathological changes in microvasculature and tubular structure(117).

Figure 6:

Effects of cardiac cycle and flow compensation on renal perfusion fraction ${\mathsf{f}}_{\mathrm{p}}$ and $\text{FA}$. parameters. (a) T2-weighted anatomical image; (b) phase-contrast MRI magnitude images; (c) renal artery velocity/cortical perfusion fraction ${\mathsf{f}}_{\mathrm{p}}$; (d) ${\mathsf{f}}_{\mathrm{p}}$ maps; (e) $\text{FA}$ maps from REFMAP analysis at different cardiac phases and bipolar/flow compensated sequences in a healthy volunteer. Modified figure from Sigmund et al.(64) with permission.

Cardiac Cycle Dependence of IVIM parameters

Several renal DWI studies found that some of the diffusion metrics (especially those related to pseudo-diffusion) are modulated by the cardiac cycle, with largest values in the systolic phase and smallest values in the diastolic phase(64, 118-122). This is consistent with the pulsatile nature of renal microcirculation. The latter study(64), however, demonstrated that the majority contribution to IVIM-derived perfusion fraction remains constant over the entire cardiac cycle. Nevertheless, cardiac-gated renal DWI can be advantageous for several reasons. First, synchronizing the data acquisition with the instant of maximum blood velocity can potentially increase the sensitivity to the IVIM effect and thereby improve robustness of the IVIM-derived parameters(122). Second, collecting data at one cardiac cycle is expected to increase reproducibility of flow-related parameters. Finally, capturing cardiac cycle dependent variations in the IVIM parameters may allow separation of different contributors to DWI signal in renal tissue (tissue diffusion vs. tubular flow vs. blood perfusion) based on the amount of pulsatility associated with each of them. Indeed, a recent study, in which the REFMAP methodology along with cardiac gating and flow-compensated diffusion gradient was employed(64), suggested a small fast flow fraction with high pulsatility, a larger intermediate fraction with little pulsatility, and a substantial slow fraction with minimal pulsatility. The fast fraction likely reflects highly pulsatile vascular flow, whereas the intermediate one suggests less pulsatile tubular flow. The comparatively large slow fraction is most probably related to parenchymal diffusion and randomized slow flow components (Figure 6). These results are in agreement with those obtained with different multicompartmental approaches(48, 54, 55), suggesting that cardiac gating (combined with flow-compensated diffusion gradients) may inform the interpretation of renal DWI signal.

Diversity of Data Acquisition Protocols

Across the published DWI studies, a broad range of acquisition parameters have been employed to assess diffuse kidney pathologies by renal DWI. A problematic consequence of this diversity of acquisition protocols is a large variability of the reported quantitative renal diffusion parameters. To address this issue, recent efforts have been made to facilitate multi-site consistency through standardized renal DWI data collection and analysis guidelines(6, 107). The full list of recommendations regarding the acquisition parameters, patient preparation (including hydration status and salt intake) and data processing can be found in the work of Ljimani et al.(107).

One of the crucial DWI protocol elements is the diffusion weighting (choice of b-values). A meta-analysis of dozens of renal DWI studies(107), which was performed to generate the technical recommendations, demonstrated that average b-value correlates significantly with tissue diffusivity $\mathrm{D}$ and flow-related signal fraction. On the one hand, it is known that higher b-value ranges provide improved estimates of both slow and fast diffusion components, but on the other hand, if the SNR of images acquired at high b-values is beyond the appropriate level, Rician noise bias can lead to lower $\mathrm{D}$ values and inflate $\mathrm{f}$ values. Based on the consensus paper(107), it is recommended to use the following parameter sets (b-values and number of diffusion directions): for IVIM studies, b = 0, 30, 70, 100, 200, 400, 800 s/mm² and 3 diffusion gradient directions; for DTI studies, b = 0, 200, 800 s/mm² and 12 or more diffusion gradient directions.

Another relevant modulator of the flow-related signal fraction is the echo time TE (or equivalently T₂ weighting factor). This can be explained by the differences in T₂ relaxation times of renal tissue, blood and urine (which are not accounted for in the conventional IVIM approach) that lead to the misassignment of differential T₂ signal decay between compartments(123). It is important to note that longer TE is usually associated with longer diffusion time, a sequence parameter that was shown to affect DTI measurements in the renal tissue(124). Further, longer T₁ recovery time (controlled by repetition time TR) leads to more pronounced flow effects and therefore higher $\mathrm{f}$. Interestingly, a combination of relaxation factors and average b-value demonstrated a negative correlation trend with medullary $\text{FA}$, which is consistent with the effect of flow modulation on diffusion anisotropy. Further studies are needed to better understand the role of diffusion time, T₁- and T₂-weighting factors as well as other aspects that did not reach level of consensus in the most recent standardization iteration.

Diversity of Data Analysis Protocols

Another relevant source of variability of the reported renal DWI parameter values is poor stability and accuracy of the algorithms used for fitting the DWI signal decay(51), especially in the case of IVIM (and multi-compartment) signal modelling. To overcome this limitation, multiple approaches for fitting the IVIM model have been proposed. One of these is the so-called “segmented fitting” or “2-step” method, in which IVIM parameters are estimated stepwise after choosing an empirical threshold b-value separating true diffusion and flow-related pseudo-diffusion effects(125, 126). While the use of the “segmented fitting” was shown to improve the stability of D(127), the estimates of f and D* are likely to be biased depending on the selected threshold above which the flow-induced decay is considered negligible. A simplified version of the “segmented fitting” uses a low number of b-values (3 or 4) for fast and robust measurement of $\mathrm{D}$ and $\mathrm{f}$, however, without attempting to estimate ${\mathrm{D}}^{\star }$.

A particularly promising class of algorithms that have recently been explored for fitting the IVIM model are the Bayesian probability-based methods. Bayesian modelling improves fitting stability by regularizing the fitting problem and assuming either local or global dependencies between the pixels, depending on the prior chosen (e.g., spatial homogeneity prior)(128-131). Due to their high accuracy, precision and low inter-subject variability compared to several “least-squares” and “segmented fitting” approaches, the Bayesian probability algorithms were recommended for IVIM model fitting in upper abdominal organs(132). However, it is still unclear whether the high reproducibility of these approaches in healthy volunteers translates to high sensitivity in kidney patient populations for differentiating between normal and pathological tissue. Besides the Bayesian probability fitting algorithms, the concept of spatial homogeneity has been explored in other works aiming at improving the robustness of the IVIM parameter estimations (including the Partially Constrained Probability Distribution Model of Incoherent Motion (SPIM)(133) and Image Downsampling Expedited Adaptive least-squares (IDEAL)(134) fitting). Previous works showed that accounting for spatial homogeneity not only increases SNR but also enforces regions when these boundaries are present(135, 136). Similar as for the Bayesian methods, these approaches need to be validated in patients with renal pathologies.

Recently, more advanced approaches based on deep learning or deep neural networks (DNNs) were proposed as a viable alternative for IVIM fitting in abdominal organs(137-141). In general, training of these DNNs can either be unsupervised or supervised, depending on the type of input data. In the unsupervised training, the network is optimized on the error between the estimated IVIM signal and the measured signal, whereas in the supervised training the network is optimized on the error between the estimated IVIM parameters and the ground-truth values. A major advantage of DNNs is that they can be used for data analysis immediately after the learning process and improve the time efficiency of the processing pipelines. At the same time, the performance of DNNs for fitting IVIM model is comparable with a Bayesian approach with the advantage of being much faster and providing more visually appealing parameter maps⁵⁴. However, some previous works demonstrated that the accuracy of the DNNs IVIM parameter estimates is affected by the learning rate, network size, training length(142), which can lead to erroneous correlations between estimates of ${\mathrm{D}}^{\star }$ and $\mathrm{f}$(138). With the rapid advances in deep learning, we expect to see substantial progress in DNN-based fitting algorithms for IVIM modelling over the coming years.

Diffusion Time-Dependence

As mentioned above, biological tissues are characterized by non-zero kurtosis, which is a quantitative measure of the degree of diffusion restriction or tissue heterogeneity. Another important consequence of the restricted tissue diffusion is the dependence of diffusion measurements on the effective diffusion time. By varying the diffusion time, diffusion dynamics at different spatial scales can be captured, which can provide sensitivity to unique microstructural parameters, such as cell size, density, and surface-to-volume ratio. Microstructurally, as the diffusion times increase, water molecules interact with more barriers and the apparent diffusion coefficient decreases toward an asymptotic value (Figure 7). Interestingly, an opposite trend has been observed in the kidney where $\text{MD}$ and $\text{FA}$ showed an increase with diffusion time in a broad range between 20 and 125 ms . It has been hypothesized that this time-dependent increase in mean diffusivity and anisotropy can be due to strong vascular and tubular flow contributions, consistent with an at least partially “ballistic” regime of IVIM pseudodiffusion time-dependence(143). While the time dependence of the flow-related components in renal tissue remains to be investigated, it is known that the IVIM signals depend on the average length of capillary segments and the average distance that water molecules travel within the diffusion time(45).

Figure 7:

(a) Simplified physical basis of diffusion time-dependent DWI. (a) Dispersion of the water molecules diffusing across compartments at different timescales $(\Delta )$; (b) random motion of water molecules inside a normal, hypertrophic, and atrophic tubular lumen; (c) the schematic root mean square (RMS) distance of water molecules with respect to $\sqrt{\Delta }$ and (d) corresponding schematic diffusion signals in a normal, hypertrophic, and atrophic tubular lumen as a function of b-value. In the case of hindered diffusion (i.e. Gaussian diffusion, red), the RMS distance increases linearly with $\sqrt{\Delta }$ and the signal decays exponentially with respect to b-value. Redrawn from Mendez et al. and Morozov et al.(25)

Diffusion time considerations could aid the interpretation of hierarchy in the IVIM signals (tubules and collecting ducts vs. blood capillaries) based on the differences in length and flow velocities in different tubular and vascular segments. With advanced microstructural modelling, specific parameters such as tubular diameter and geometry, membrane permeability, and blood and tubular flow velocity could be estimated, which may be particularly sensitive to microstructural changes associated with the progression of renal diseases (e.g., inflammation, tubular hypertrophy, renal fibrosis and tubular atrophy). In a recent study of Sigmund et al., an impermeable cylindrical tubular model along with the Mitra theory(144) was employed to estimate the tubular diameter from radial diffusivities of the slow compartments $({\mathrm{D}}_{\mathrm{t},\text{rad}})$ measured at two different diffusion times. Comparison of experimental $({\mathrm{D}}_{\mathrm{t},\text{rad}})$ with both analytical and simulation estimates of tubular size yielded consistent results suggesting a diameter of ~34 μm, which is within the range of the expected tubular size range(25).

Microanisotropy

Despite its potential to serve as an index of renal microstructure, $\text{FA}$ extracted from the conventional Stejskal-Tanner experiment with linear tensor encoding (LTE) does not fully reflect tissue heterogeneity on the microscopic level due to the orientation dispersion within a voxel. In an LTE acquisition, a single diffusion encoding b-tensor shape is applied leading to situations in which different structures show nearly identical DWI signal behavior. As a result, information on the microscopic anisotropy and orientation dispersion on a sub-voxel level is usually lost. To disentangle these two overlapping effects and obtain independent microscopic fractional anisotropy (mFA) measures, a joint analysis of LTE and spherical tensor encoding (STE) acquisition that provides rotation-invariant diffusion data can be used. The feasibility of this approach in the human kidney has recently been demonstrated by Nery et al(145). Their results showed that in contrast to the $\text{FA}$ maps demonstrating excellent cortical-medullary differentiation, the mFA maps are more homogenous throughout the renal parenchyma. This observation suggests that the high cortical-medullary contrast observed in the conventional DTI-derived $\text{FA}$ maps is enhanced by the orientation dispersion in the renal cortex. This also leads to a hypothesis that mFA may provide a more accurate assessment of microstructural integrity than $\text{FA}$ in tissues that display high levels of orientation dispersion, such as the convoluted tubules in the cortex.

Orientational patterns and heterogeneity

Diffusion anisotropy in medulla is an established feature of renal DWI. Analogous to work in cerebral white matter axons and skeletal muscle myofibers(146) some pilot studies have explored first-order tractography to continuously illustrate nephron integrity and renal function(147-150) , although their interpretation is still ongoing. One aspect of this field that has not yet been extensively pursued in the renal context, related to the orientational dispersion discussed above, is multiple axes of anisotropy within a voxel (i.e. “fiber-crossing” in the neural context)(151). While the radial orientation of the medullary loops of Henle and collecting ducts is the primary anisotropy axis, features such as loop turns and transverse vasa recta vascular segments may present a secondary anisotropy axis if probed with high angular resolution diffusion protocols. This area represents another possible approach to disentangling microstructural and microcirculatory aspects of renal DWI.

Conclusion

In conclusion, advanced DWI techniques that acquire data over an extended range of b-values, diffusion gradient directions, or diffusion times provide the possibility to quantitatively characterize the complexities of renal tissue. While these emerging methods can provide a new class of imaging biomarkers, there are still many unanswered questions regarding the exact relation between the diffusion parameters and specific properties of renal tissue. Answering these questions will require further advancements in diffusion acquisition and modelling strategies together with improved quantitative histology, multimodal image registration and validation methods. Implementations of the advanced variants of DWI to date produced promising results that need to be validated in future large-cohort and multi-center studies. For this, standardization of the acquisition and analysis protocols across different sites and clinical platforms will be crucial. Another important consideration for renal DWI is the intrinsically low sensitivity and specificity of this technique which contributed to some conflicting findings and limits its potential diagnostic accuracy. Given all these challenges, we see tremendous opportunity for further advancing the field.