The Potential of Neural Network Potentials

Abstract

In the next half-century, physical chemistry will likely undergo a profound transformation, driven predominantly by the combination of recent advances in quantum chemistry and machine learning (ML). Specifically, equivariant neural network potentials (NNPs) are a breakthrough new tool that are already enabling us to simulate systems at the molecular scale with unprecedented accuracy and speed, relying on nothing but fundamental physical laws. The continued development of this approach will realize Paul Dirac’s 80-year-old vision of using quantum mechanics to unify physics with chemistry and providing invaluable tools for understanding materials science, biology, earth sciences, and beyond. The era of highly accurate and efficient first-principles molecular simulations will provide a wealth of training data that can be used to build automated computational methodologies, using tools such as diffusion models, for the design and optimization of systems at the molecular scale. Large language models (LLMs) will also evolve into increasingly indispensable tools for literature review, coding, idea generation, and scientific writing.

Introduction

Over the last year, a surge of excitement has arisen around the potentially transformative role of machine learning (ML) or artificial intelligence in many areas of technology, science, and society. This has been driven by the remarkable performance of large language models (LLMs)¹ and image generation diffusion models.²

Given the excitement around these technologies, there is a natural tendency to either assume they will profoundly transform every field or dismiss them as “overhyped”.

A better approach is to be excited about the potential of these technologies while also thinking through as carefully as possible the potential obstructions that may arise to limit their potential, with the goal of identifying the most promising approaches and applications where they are likely to be most useful.

While the recent excitement around LLMs and diffusion models is justified, the potential for ML in science has long been recognized. A pioneering example is the demonstration in 2007 by Behler and Parrinello³ that neural network potentials (NNPs), originally developed in the 1990s,^4,5 could be used to massively accelerate the simulation of liquids by learning the underlying potential energy surface from quantum chemistry calculations.

More recently, AlphaFold2 (AF2)^6,7 has dramatically demonstrated the ability of ML to predict the structure of folded proteins with remarkable accuracy.

In this article, I argue that neural network potentials, AF2, diffusion models, and even LLMs to some extent can all be understood as examples of one fundamental idea: learning and sampling from an underlying energy surface. The recursive application of this fundamental idea will have profound implications for physical chemistry and beyond over the next half-century.

Dirac’s Dream

Using quantum mechanics to predictively understand biology and chemistry has been a dream of physicists for nearly a century since Paul Dirac’s famous statement:

The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations that are much too complicated to be soluble. It therefore becomes desirable that approximate practical methods of applying quantum mechanics should be developed, which can lead to an explanation of the main features of complex atomic systems without too much computation.⁸

Physical chemistry is the natural discipline to home this dream, and much progress has been made on making it a reality. For example, accurate quantum chemistry algorithms, such as density functional theory (DFT)⁹ and coupled-cluster (CC) with single, double, and perturbative triple excitations (CCSD(T)),¹⁰ and advanced simulation techniques have made it possible to build highly accurate models of water¹¹ and resolve challenging scientific questions¹² starting from nothing but Schrödinger’s equation. This pioneering work convincingly demonstrates the feasibility of achieving Dirac’s dream. Now the key scientific challenge becomes making this procedure efficient, automated, generalizable, and scalable. This is a task perfectly suited to ML. Achieving this dream, depicted in Figure 1, would be truly transformative, enabling the predictive understanding of the properties of a vast range of critically important systems throughout materials science, chemistry, biology, and beyond.

Figure 1.

DALL-E’s depiction of the potential of neural network potentials.

Neural Network Potentials

The most promising tool for doing this is neural network potentials (NNPs), which are a class of machine learning interatomic potentials (MLIPs). These tools are rapidly gaining importance and recognition due to their flexibility and efficacy.¹³⁻¹⁸

The concept of NNPs is straightforward yet innovative. Instead of relying on traditional methods, such as specifying Lennard-Jones potentials and bonded terms, to define the potential energy surface (PES) as a function of atomic type and coordinates, NNPs employ more adaptable functions with a larger set of parameters. These parameters are optimized using machine learning algorithms facilitated by automatic differentiation. To avoid the need for large experimental data sets, these models are trained on data from quantum chemistry, predominantly at the DFT level, though increasingly higher levels of theory are being utilized.¹⁹ Traditional molecular dynamics (MD) algorithms can then be used to simulate the direct physical behaviors of gases, liquids, and solids using the trained NNPs.

While NNPs have been under development for some time,¹⁴ recent advancements in ML have significantly enhanced their practical utility. One such critical advancement is the incorporation of equivariance, which encodes the spatial symmetries of 3D space into the neural network.²⁰⁻²³ This feature, also pivotal in the success of AlphaFold2,²⁴ ensures that the neural network’s features rotate in accordance with the rotations of the input coordinates, significantly enhancing model accuracy and reliability. A recent review provides a comprehensive and clear explanation.²⁵

The success of equivariant models is very intuitive, as they use a natural extension of the traditional concepts of intermolecular modeling. More specifically, they use tensors to describe the atomic properties and tensor products for modeling the interactions. This approach mirrors the long-standing practice in physics, where molecular interactions have been described using the multipole expansion, i.e., using monopoles, dipoles, and quadrupoles, which are tensors, interacting via tensor products.

Additional exciting tools such as active and delta learning as well as improved quantum chemistry algorithms have also significantly improved the generalizability and usefulness of NNPs.²⁶ An additional avenue is the development of foundation models, where increasingly larger and more diverse/general training data sets are used to improve a model’s generalizability.²⁷⁻³⁰

These more recent improvements have stepped up NNPs from being an occasionally useful tool to a potentially transformative one. As some recent perspective articles state, this field is undergoing “remarkable/breathtaking progress,” achieving results that would be “unimaginable with conventional methods.”^31,32

The potential of neural network potentials is that they are a tool that provides access to a new spatial and temporal scale that has not yet been observed accurately. Such tool-driven revolutions are a recurring process in the history of science and are inevitably followed by a string of rapid and surprising discoveries. The telescope, the microscope, and the particle collider are famous examples. I believe that NNPs have the potential to approach a comparable level of significance. Initial examples of this are already beginning to emerge. For instance, important new insights into catalysis at high temperatures have already been discovered using NNP-MD simulations.³³ Additionally, NNP-MD is apparently now the state of the art for protein–ligand binding affinity predictions.³⁴

Breaking the Accuracy–Efficiency Trade-off

The promise of NNPs lies in their potential to transcend the long-standing trade-off between accuracy and efficiency in simulations. Specifically, they offer the possibility of achieving quantum mechanics (QM)-level accuracy at the computational cost of classical MD. This breakthrough implies that this technique will become increasingly prevalent.

An important recent advance on this front has been the development of density corrected DFT methods,^9,35 where the computation of the energy and electron density are separated to achieve a better balance of accuracy. These methods have been demonstrated to provide an improved description of aqueous solutions³⁵⁻³⁹ while maintaining affordable computational requirements. They are therefore well-suited to providing training data for NNPs. We have recently shown that accurate and efficient prediction of key electrolyte solution properties is possible by combining this method with an equivariant NNP.^40,41

Remaining Challenges

Although rapid progress is being made, several challenges remain toward fully realizing the potential of NNPs. One example accounts for long-range interactions. These are known to play an important role in many liquid phase phenomena.^42,43 Multiple promising solutions are being explored.⁴⁴⁻⁵² Another is the generation of sufficiently diverse training data sets, where active learning plays a crucial role. In active learning, the uncertainty within the model’s predictions is monitored, and data points with higher uncertainty are added to the training set to enhance its accuracy.⁵³⁻⁵⁵ The use of structural databases generated at lower levels of theory is another promising option.^17,56

The accuracy of the underlying quantum chemical method used to generate the training data is also an issue, but there is significant exciting progress on this front too, as discussed below.

Speed and scalability also present significant hurdles. Equivariant NNPs, while powerful, tend to be slower than classical MD and standard MLIPs. Although they can handle large systems,^57,58 this requires substantial computational resources. One solution is using equivariant NNPs to generate data for training faster non-equivariant architectures. There are many promising architectures from the more general family of MLIPs such as permutation invariant polynomials (PIPs) and Gaussian approximation potentials (GAPs), which generally appear to have similar performance to standard Behler–Parrinello-type NNPs and may be able to provide speed advantages.^59,60 Data augmentation may be able to avoid the need for equivariant models as well.⁶¹ Another possibility is optimizing classical MD potentials against quantum data using automatic differentiation⁶² or algorithmic improvements.^63,64

Recursive Coarse-Graining

Despite the promise of current approaches to improving speed, there are inherent limitations to any simulation that attempts to keep track of the position and motion of every single atom in a system. A more transformative solution lies in coarse-graining, which involves focusing on only the essential degrees of freedom of a system while neglecting the others. This is the essence of physical modeling at all scales. For example, in modeling a macroscopic object, only the center of mass of each atom is considered. The core motivation is that most of the system’s information is often irrelevant for predicting its properties.

In physical chemistry, details such as the exact positions of every solvent molecule are usually not critical for understanding the properties of interest. Thus, continuum or implicit solvent models are used, which are a form of coarse-graining. Currently, these models are developed in a somewhat empirical manner, and a systematic and rigorous approach is needed. ML, with its fundamental focus on finding lower-dimensional representations of high-dimensional data sets, offers an excellent set of tools to address this challenge.⁶⁵⁻⁶⁸

Remarkably, it is precisely the same technique that provides one possible solution: equivariant neural network potentials, as has recently been demonstrated.^41,69−71 It is not surprising in retrospect that these tools are suitable for this task. The goal of coarse-graining is to find the potential of mean force (PMF) for a reduced set of degrees of freedom. This is just an energy surface, technically a free energy, and so this is a task well-suited for NNPs. Here NNPs have the key advantage over fitting a classical force field, as the free energy surfaces modeled by NNPs can capture a more complex-shaped landscape than the typical bonded or Lennard-Jones interactions used in a classical force field. In fact, fitting an NNP to the full PES is a form of coarse-graining itself. It is just the electronic positions that are the degrees of freedom that are being coarse-grained out. Protein folding models such as AF2 and RFdiffusion can actually be interpreted as an NNP that learns a coarse-grained free energy, as discussed below.

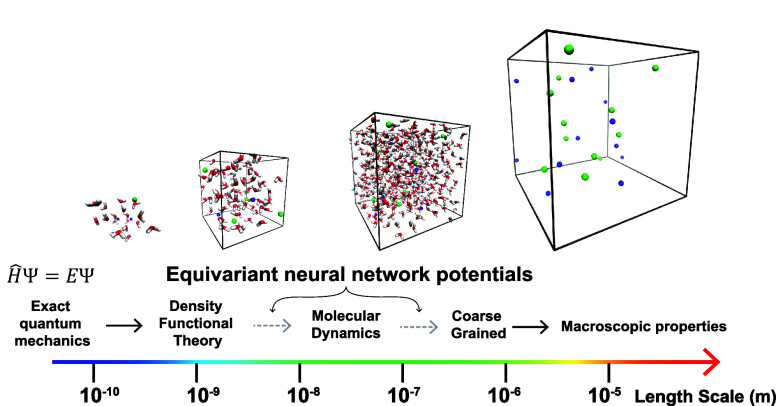
So the promising conclusion of this is that all atom equivariant NNPs trained on QM data can be used to recursively train coarse-grained NNPs.⁴¹ This could enable large-scale biological simulations starting solely from first principles. This process, illustrated in Figure 2, may have a transformative impact on biology and materials science if the remaining challenges can be overcome and may eventually supplant tools like AlphaFold2. We have demonstrated the feasibility of this process of recursively training a coarse-grained equivariant NNP on its own output in a recent preprint for simple electrolyte solutions.⁴¹

Figure 2.

Depiction of a method of connecting the microscopic scale to the macroscopic scale via the recursive application of equivariant neural network potentials.

Currently, coarse-graining with an NNP is applied to relatively small-scale classical systems, such as simplifying water to a single site⁷² or for proteins.^67,69,70,73 However, they could potentially be iteratively applied to increasingly larger scales, perhaps one day encompassing complexes of multiple proteins, cell membranes, etc.

While the core principle of automatically creating reduced-dimensional representations will likely remain constant, advancements may be required in determining which features to retain at a higher resolution, like binding sites, and which to coarse-grain; here again, ML will be a critical tool.⁷⁴

This methodology may even be a general solution to the long-standing and central challenge of molecular simulation, which is how to connect scales, i.e., how to use information from the molecular scale to inform and understand meso- and macroscopic-scale phenomena. It is also possible to reproduce fine-grained representation from the coarse-grained one.⁷⁵

One importance caveat is that coarse-graining does distort the underlying dynamics, but solutions to this problem are being developed.^76,77

Simulating Large-Scale from the Molecular Scale

The goal of this methodology is both ambitious and thrilling. It opens the possibility of simulating large-scale complex systems starting solely from Schrödinger’s equation. We can envisage a future where, through a simple web interface, we input a system of atoms and obtain a highly accurate depiction of their behavior at any desired scale. This would be a more general version of the way AF2 now enables the rapid prediction of the folded structure of a protein with a simple web interface.

Such a tool would be transformative for many areas of science. For a great many scientific problems, the scales at which the most critical and interesting processes occur are too small to observe experimentally either with direct microscopy or with more indirect methods, such as spectroscopy or X-ray diffraction. As a result, we are often left to rely on guess work, intuition, and indirect evidence to infer what is actually happening on the molecular scale. In other words, when it comes to the molecular scale, we are essentially operating in the dark. Accurate and efficient molecular-scale simulations could act as a computational microscope, shedding light on this critically important scale and opening a wealth of new otherwise hidden information by enabling us to simply directly observe the key phenomena that occur at this scale. The application areas span most of biology and much of chemical engineering, such as catalysis and electrochemical energy storage.

Additionally, we can use these simulations in combination with statistical mechanics to calculate key experimental properties. For example, free energies or activities can be directly estimated from molecular-scale simulations using tools such as the Kirkwood–Buff theory. Additionally, diffusivities and other kinetic properties can also be determined. These values can then be fed as parameters into simulations of larger-scale systems, where these parameters are a key source of uncertainty. For example, the activity of ions in solution is a key challenge for predicting solubilities and chemical equilibria. Similarly, climate simulations are currently limited by the lack of information about molecular-scale processes, such as the stability and formation of aerosols. Molecular simulation models that can quickly predict the distribution of aerosol particles could be connected to larger-scale climate simulation models to improve their reliability. These tools therefore have the potential to have an impact on many different areas of science across many different scales of phenomena wherever physical-based modeling is important. Additionally, in combination with automated coarse-grained systems, these can potentially be scaled to simulate systems of ever-increasing size by selectively ignoring aspects of the system that are not considered practically important.

Quantum Chemistry Accuracy

A critical limitation of NNPs is the current accuracy of methods for solving Schrödinger’s equation to generate data for training NNPs. However, the field of quantum chemistry is witnessing substantial progress with exciting developments like density corrected DFT,³⁵ ensemble DFT,⁷⁸ DLPNO–CCSD(T),⁷⁹ large-scale random phase approximation (RPA),⁸⁰ and the density matrix renormalization group.⁸¹ These innovations promise more precise descriptions of molecular-scale systems. Additionally, ML algorithms could also have potentially important applications here by using neural network ansatzes for wave function representation, for example,⁸² or for reducing the cost of traditional methods.^83,84

While DFT functional accuracy is still an issue, a key advantage is that for a great many systems of practical interest, methods such as CCSD(T) can generate very high-quality data on small systems. This means that DFT functionals can be carefully validated and fine-tuned for specific tasks. This means that the problem of DFT functional accuracy is for many cases mainly a practical problem rather than a fundamental scientific challenge. Exciting new tools for automated development of new DFT functionals trained on data from higher-quality quantum chemistry methods is another promising recent development.⁸⁵

However, for some materials, we still lack good benchmark methods. For example, highly multireference states, where fundamental new tools are required. Multireference methods such as complete active space self-consistent field (CASSCF) can be used, but they come with their own set of challenges and limitations, particularly in terms of computational cost and complexity.

Computational Hardware

Another potential avenue for advancement lies in the development of new, powerful hardware specifically designed for molecular simulation and quantum chemistry calculations. While quantum computers are often cited in this context, it is debatable whether using qubits will provide a practically relevant quantum chemistry acceleration.^86,87 Other burgeoning technologies, such as thermodynamic computing, may prove useful instead. Additionally, the ongoing rapid development of new computational hardware for general computing and ML, such as large-memory graphics processing units (GPUs), should be sufficient to provide significant improvements in quantum chemistry and molecular simulation using existing algorithms.

The development of new computing architectures relies on components that are becoming increasingly small and will continue to approach the molecular scale. The design of these components could potentially be significantly advanced through highly accurate molecular simulations, which could be used to predict and optimize important properties such as heat generation, etc. Improvements in molecular simulation enabled by NNPs could therefore lead to a feedback process in which they enable improvements in computing.

Diffusion Models

Accurate molecular simulation is a powerful tool for understanding and predicting the properties of various systems. However, when it comes to generating and designing new systems, an additional new tool from ML is increasingly coming into play: diffusion models. These models, though initially complex to grasp, especially as often presented, are fundamentally about learning a generalized version of a potential energy surface.

To conceptualize diffusion models from a physical point of view, consider the pixel values to represent atomic coordinates. Then, just as certain coordinates have a high probability of being observed in an equilibrium simulation, certain pixel values have a high probability of having certain properties, i.e., being a face.

To generate these high-probability coordinates/pixel values, we evolve the coordinates/pixel values according to equations of motion with a force field, which is learned from the data via a denoising process. In fact, a diffusion model can be trained on molecular coordinates from an equilibrium distribution, which, in turn, reproduces the true underlying force field responsible for that distribution.⁸⁸ Diffusion models then can be considered again as a special case of an NNP, where they are learning a coarse-grained free energy surface. An intriguing aspect of these models is that they can include “forces” for properties other than positions, such as atomic numbers, allowing them to sample from a variety of atomic types. This flexibility enables targeted sampling from specific regions of the probability distribution, akin to biasing MD simulations toward areas of the phase space of particular interest.^89,90 Technically a time-dependent force is used to improve the convergence of the sampling, but this is a technicality.

This methodology is increasingly promising for the generation and design of new materials and molecules. It is already proving capable of protein design, leveraging databases like the Protein Data Bank (PDB) to identify new specific folded protein structures.⁸⁹

AlphaFold2

One potential challenge to the importance of NNPs is AF2. AF2 represents a significant breakthrough in protein structure prediction. Its capability allows anyone to predict the atomically resolved structure of a protein, with accuracy now comparable to that obtained from nuclear magnetic resonance (NMR) techniques,⁹¹ marking a paradigm shift in structural biology. While this is not traditionally considered a core problem of physical chemistry, there are many closely related problems, i.e., predicting the atomic structure of a chemical system in thermodynamic equilibrium. Most significantly, AF2 does not explicitly rely on physical notions of energy and MD. An intriguing question then arises as to whether this approach could be used to revolutionize biology and chemistry without the need for physics-based modeling.

This is highly unlikely, in my opinion. The key to AF2’s success is the extensive, high-quality Protein Data Bank (PDB).⁹² This immediately highlights a challenge to generalizing this approach. The PDB contains high-quality atomic structures of over 100 000 proteins with each one taking significant investment to obtain. This took many decades to build. There are vanishingly few problems of practical scientific interest, especially in physical chemistry, where these kinds of extremely large, high-quality databases exist. This becomes evident as soon as we leave the region of AF2’s success.

For instance, AF2 cannot predict the folding pathway or kinetics of a protein due to its reliance on the static folded structures found in the database.⁹³ Furthermore, the database lacks information on the distributions of many ions near the protein surfaces, limiting AF2’s ability to predict properties influenced by electrolyte concentrations, such as protein agglomeration, ion conductivities, etc.

Additionally, AF2 has a deep conceptual relationship to NNPs. It has been demonstrated that AF2 can be interpreted as using a learned energy landscape to optimize the protein structure;⁹⁴ the main difference is that AF2 is trained on experimental obtained structures rather than quantum chemical data, but experimental structures still contain important information about the energy landscape: they must lie on its minima. As AF2 uses gradient descent to optimize the protein structures, it must have learned an energy landscape with the same energy minima as the true protein energy landscape. The true protein energy landscape can be rigorously described as the coarse-grained free energy surface where the solvent degrees of freedom have been integrated (or marginalized) out. This energy surface may look quite different from the true free energy surface far from a minimum, but this is not an issue for obtaining minimum energy structures, although it is for dynamic information.

For diffusion models trained on the PDB, the connection is even clearer. The score learned by the model is equivalent to the gradient of a coarse-grained free energy. If one could train the diffusion model on the true equilibrium distribution of states occupied by the protein, then one would learn the true coarse-grained free energy. The use of PDB training data means that one is effectively training on coordinates extracted at 0 K; so the off-equilibrium distribution will be wrong, but it will still have the correct minima. In fact, Langevin dynamics are used in diffusion models, which is a common algorithm to perform molecular simulations. Thus, something like RFdiffusion⁸⁹ is actually a coarse-grained MD simulation just on an approximation of the true coarse-grained free energy surface.

The Only Alternative?

The dependence of AF2 on extensive high-quality experimental data sets indicates that the same strategy will not work for predicting a broader range of important phenomena. This situation has a parallel to the development of AlphaGo, an ML algorithm that can play the board game Go, which was trained on data from human games accumulated over many decades. To improve the performance beyond what was learnable from human games, AlphaZero was developed, which does not require any human-generated training data and learns through self-play based only on the rules of the game.⁹⁵ Similar recent breakthroughs in mathematical problem solving use a similar strategy.⁹⁶

A natural question then arises: can we use this same strategy for solving scientific problems to avoid the need for large, hand-curated experimental databases? Doing so would require one to know the fundamental rules of the game that nature obeys. Of course, this is exactly what quantum mechanics is. It can in principle predict the behavior of all biological and chemical systems as captured by Dirac’s dream. NNPs are therefore the best option for using ML to have a broad and significant impact on physical chemistry and beyond.

Robotics and Self-Driving Laboratories

Laboratories will also become increasingly automated as robotics continues to improve, reducing the need for humans in the loop experimentation and enabling automated active learning feedback where errors in computational methods are identified and rectified through iterative exploration of regions of high uncertainty.

End-to-End Differentiability

Another critical advancement, which was also key to the success of AF2, is the concept of end-to-end differentiability. Essentially, this means that it should be possible to take derivatives of any parameter used in modeling a system with respect to the final loss function. This approach is exemplified by graph neural networks, which many modern NNP architectures successfully use. The idea is that rather than imposing arbitrary descriptors of the atomic structure, a flexible and general function can be used with many adjustable parameters that are then optimized using stochastic gradient descent just as the other parameters in a neural network are fitted.⁹⁷

End-to-end differentiability is also showing promise in applications to simulations themselves where gradients can be taken through simulations, allowing the automatic optimization of parameters with respect to output properties of molecular simulations. For example, this can be used to fit interatomic potentials to experimentally obtainable structural data.⁹⁸ It is also an important component of modern generative models for drug discovery.⁹⁹ Finally, this idea is also being applied to DFT functional development, where all of the key parameters used to define a DFT functional are treated as differentiable parameters that can be optimized with respect to some loss.⁸⁵

Large Language Models

An obvious impact of ML in physical chemistry is through large language models (LLMs), e.g., ChatGPT, which have dramatically expanded their capabilities recently. These models can assist in various academic activities, including writing, brainstorming, literature searches, education, and even language translation for non-native English speakers. Their utility is expected to increase as they become more accurate and less prone to producing erroneous outputs (“hallucinations”). Recent articles provide a detailed demonstration of the potential of LLMs in chemistry more generally.^1,100

LLMs will become increasingly integral to scientific meetings and conferences, offering real-time notes, suggestions, and relevant literature based on the extensive training data encoded in their weights. They will play a crucial role in reviewing and improving the scientific literature, making research more accessible and efficient. Moreover, their capability in condensing vast amounts of data will likely foster novel connections and insights in research.

Furthermore, LLMs will be instrumental in programming, aiding researchers with limited coding proficiency in translating their ideas into executable code or converting code across different programming languages. This will significantly enhance scientific productivity and democratize computational tools, making cutting-edge research accessible to a broader spectrum of scientists.

LLMs will help automate the generation of MD trajectories and the building and curation of large databases. LLMs will not only suggest improvements for optimizing system performance but may also autonomously manage simulations, drawing from vast data sets to propose novel research directions.

There is also an intriguing connection between NNPs and LLMs. LLMs use a Boltzmann distribution, via the softmax activation function, to compute probabilities from the output of the transformer during next word prediction. They can therefore be interpreted as predicting an energy for each token in the vocabulary as a function of the previous words in the sentence, i.e., as a series of NNPs. While this is a more tenuous connection than for diffusion models, it hints at the deep connections between statistical mechanics and deep learning, which remain to be fully uncovered.

Longer Term

As we look beyond the next decade, two potential trajectories emerge. One radical possibility is that LLMs continue to improve at the current exponential pace, potentially surpassing human capabilities in 50 years, leading to a future dominated by ML-driven science. Alternatively, these tools might reach a plateau, maintaining their status as invaluable aids but still leaving room for significant human contribution. This latter scenario presents an intriguing landscape for future speculation.

The likelihood of LLMs reaching a developmental plateau arises from three considerations. First, they are trained on Internet text, which, while extensive, inherently limits their capacity to generate novel knowledge. Second, the issue of “hallucinations” or generating false information remains a challenge. While scaling up models and refined training methods (such as reinforcement learning from human feedback) may mitigate this, this may be a more fundamental and challenging problem to resolve. The third reason that LLMs might plateau in performance may be the excessive energy demands of training ever larger models. Here again, advances in materials science to design new, more efficient forms of computing will be key, and improved molecular simulation enabled by NNPs will be a critically useful tool for this.

A More Radical Future

One potential avenue to address the issues of hallucination and generalizing beyond the training data is to enable LLMs to verify or validate their generated knowledge. For example, in the area of physical chemistry, this could be enabled by augmenting an LLM by providing it access to molecular simulation tools such as NNP-MD and quantum chemistry. It could then automatically go about generating the necessary data and validating hypotheses it has generated autonomously. The likelihood of such a transformative leap in ML capabilities is extremely hard to ascertain, but if it does happen and continues to grow exponentially, it will be such a significant shift across all spheres of human society that speculation is only of limited use. In my personal view, while a temporary plateau in ML development might persist for decades, it seems improbable that it will extend for the next 50 years, and so I would expect at some point to witness profound changes in the way science and society operate.

This evolution raises profound and challenging questions both scientifically and ethically. A particularly sobering prospect is the potential redundancy of human involvement in scientific discovery courtesy of highly efficient LLMs or their successors. In such a scenario, the human role might be relegated to determining the tasks we would like ML to solve rather than engaging in direct scientific inquiry.

In the field of physical chemistry, many fundamental questions bear immense practical significance. It might be necessary to leverage ML’s capabilities to address these. However, we could also consider one day preserving certain areas within science as “ML-free zones”, allowing human scientists to explore them independently. Alternatively, we might use ML to develop technologies to enhance our quality of life while deliberately avoiding full comprehension of their workings to preserve a sense of purpose and discovery for ourselves.

While the prospect of ML solving complex scientific problems might initially seem disheartening, especially considering the potential obsolescence of human-led research, it is important to recognize the brighter side. In a world where ML resolves most material challenges, we could exist in a state of near-universal abundance. This shift might mitigate any disappointment stemming from the reduced role of human discovery. Moreover, even in such a world, humans could still find purpose in understanding and replicating ML-derived solutions, thus continuing the quest for knowledge and innovation.

Conclusions

ML is poised to revolutionize physical chemistry, reshaping our approach to solving many long-standing problems. A pivotal advancement facilitated by ML combined with state-of-the-art quantum chemistry is the ability to conduct molecular-scale simulations with unprecedented accuracy and speed. While there are still challenges to be overcome, this is already beginning with equivariant neural network potentials (NNPs) trained on extensive data sets derived from solutions of Schrödinger’s equation. To access increasingly larger scales, these models will be recursively trained to automatically generate good coarse-grained descriptions, i.e., reduced dimension representations, thereby solving the long-standing challenge of connecting the microscopic and macroscopic scales and dramatically widening the scope of applications where first-principles physical simulation plays a critical role.

LLMs will improve efficiency and knowledge discovery. End-to-end differentiable simulations will efficiently compute the thermodynamic and kinetic properties of diverse systems. Diffusion models will be used to automate the generation of new potential candidate molecules and materials with particular properties.

Eventually, upon finalizing a design, it will be synthesized in automated laboratories, robotically produced, and dispatched for testing and further optimization based on experimental data. This vision heralds a new era in our understanding and manipulation of chemical systems, offering boundless opportunities for discovery and innovation.

Finally, it is worth considering the possibility of continued exponential advancements in ML. The implications of such a development are challenging to predict, but they could potentially reduce the field of physical chemistry to a discipline where our primary role is to ask LLMs to teach us complex concepts. The timeline for such a shift, whether it spans decades or centuries, remains an intriguing and open question.

The author declares no competing financial interest.

Special Issue

Published as part of ACS Physical Chemistry Auvirtual special issue “Visions for the Future of Physical Chemistry in 2050”.