Assessment of performance of four mortality prediction systems in a Saudi Arabian intensive care unit

Abstract

Introduction

The purpose of this study is to assess the performance of Acute Physiology and Chronic Health Evaluation (APACHE) II, Simplified Acute Physiology Score (SAPS) II, Mortality Probability Model MPM II₀ and MPM II₂₄ systems in a major tertiary care hospital in Riyadh, Saudi Arabia.

Methods

The following data were collected prospectively on all consecutive patients admitted to the Intensive Care Unit between 1 March 1999 and 31 December 2000: demographics, APACHE II and SAPS II scores, MPM variables, ICU and hospital outcome. Predicted mortality was calculated using original regression formulas. Standardized mortality ratio (SMR) was computed with 95% confidence intervals (CI). Calibration was assessed by calculating Lemeshow–Hosmer goodness-of-fit C statistics. Discrimination was evaluated by calculating the Area Under the Receiver Operating Characteristic Curves (ROC AUC).

Results

Predicted mortality by all systems was not significantly different from actual mortality [SMR for MPM II₀: 1.00 (0.91–1.10), APACHE II: 1.00 (0.8–1.11), SAPS II: 1.09 (0.97–1.21), MPM II₂₄ 0.92 (0.82–1.03)]. Calibration was best for MPM II₂₄ (C-statistic: 14.71, P = 0.06). Discrimination was best for MPM II₀ (ROC AUC:0.85) followed by MPM II₂₄ (0.84), APACHE II (0.83) then SAPS II (0.79).

Conclusions

In our ICU population: 1) Overall mortality prediction, estimated by standardized mortality ratio, was accurate, especially for MPM II₀ and APACHE II. 2) MPM II₂₄ has the best calibration. 3) SAPS II has the lowest calibration and discrimination. The local performance of MPM II₂₄ in addition to its ease-to-use makes it an attractive model for mortality prediction in Saudi Arabia.

Introduction

Mortality prediction systems have been advocated as means of evaluating the performance of intensive care units (ICUs) [1]. These systems allow adjustment to the severity of illness of the patient population. Acute Physiology and Chronic Health Evaluation (APACHE) II and Simplified Acute Physiology Score (SAPS) II measure severity of illness by a numeric score [2,3] based on physiologic variables selected because of their impact on mortality: the sicker the patient, the more deranged the values and the higher the score. The numeric scores are then converted into predicted mortality by using a logistic regression formula developed and validated on populations of ICU patients. Mortality Probability Models (MPM) II differ slightly in that they use categorical variables (with the exception of age) for mortality prediction [4].

Before the clinical application of any of these systems, they must be validated on the population under evaluation [5,6]. These systems have been assessed for validity in several countries [7,8,9]. We report here the result of our validation study of the four systems in ICU population in a tertiary care center in Saudi Arabia.

Methods

King Fahad National Guard Hospital is a 550-bed tertiary care center in Riyadh, Saudi Arabia. The 12-bed medical–surgical ICU has 600 admissions a year. The hospital also has a coronary care unit and a cardiac surgical intensive care unit. Patients admitted to these units were not included in the study. The unit is run by full-time intensivists and has 24-hour immediate access to other medical and surgical specialties. Our nurse-to-patient ratio is approximately 1:1.2. This high ratio has been maintained because of the high acuity of care. Our ICU database was established in March 1999 to record ICU admissions. The present study presents information on all consecutive admissions between 1 March 1999 and 31 December 2000. Data were collected by one of the inten-sivists (Y.A., S.H. or R.G.). To minimize variability in data collection, one physician (Y.A.) coordinated the overall process. In addition, a written reference with the definitions used in original articles was made. Patients aged 16 years or more were eligible for the study with the exception of burn and brain-dead patients. For patients admitted to the ICU more than once in the same hospitalization, data from the first admission were used. Approval from the hospital Ethics Committee was not required because the information had already been collected for clinical reasons.

The following data were collected: demographics, APACHE II and SAPS II scores, and MPM variables. MPM II₀ data were obtained on all admissions, whereas MPM II₂₄, APACHE II and SAPS II data were obtained on patients who stayed for 24 hours or more in ICU. APACHE II and SAPS II scores were calculated in accordance with the original methodology, using the worst physiologic values in the first ICU day [2,3]. The only exception was Glasgow Coma Score (GCS). Many of these patients were under the influence of sedation and the worst GCS would reflect the effect of sedation more than the true underlying mental status. We therefore used the worst GCS value for non-sedated patients and the pre-sedation score for patients under sedation, as described previously [4,10,11,12]. The main reason for ICU admission, whether the admission was after emergency surgery, and the presence of severe chronic illness were documented in accordance with the original definitions [2]. Postoperative patients with sepsis or cardiac arrest were included with non-operative patients with these conditions [2]. ICU and hospital length of stay (LOS) and lead time (the interval from hospital admission to ICU admission) were calculated. Vital status at discharge from the ICU and from the hospital was registered.

Predicted hospital mortality was calculated with the logistic regression formulas described originally [2,3,4]. Standardized mortality ratio (SMR) was calculated by dividing observed hospital mortality by the predicted hospital mortality. The 95% confidence intervals (CIs) for SMRs were calculated by regarding the observed mortality as a Poisson variable, then dividing its 95% CI by the predicted mortality [7].

Validation of the systems was tested by assessing calibration and discrimination. Calibration (the ability to provide risk estimate corresponding to the observed mortality) was assessed by calibration curves and the Lemeshow–Hosmer goodness-of-fit C-statistic [11]. Calibration curves were drawn by plotting predicted against actual mortality for groups of the patient population stratified by 10% increments of predicted mortality. To calculate the C-statistic, the study population was stratified into ten deciles with approximately equal numbers of patients. The predicted and actual number of survivors and non-survivors were compared statistically with the use of formal goodness-of-fit testing to determine whether or not the discrepancy was statistically insignificant (P > 0.05).

Discrimination was tested by receiver operating characteristic (ROC) curves and 2 × 2 classification matrices. ROC curves were constructed as a measure of assessing discrimination with 10% stepwise increments in predicted mortality [14,15]. The four curves were compared by computing the areas under the curves. Classification matrices were performed at decision criteria of 10%, 30% and 50%. Sensitivity, specificity, positive and negative predictive values and overall correct classification rate were calculated.

Minitab for Windows (Release 12.1, Minitab Inc.) was used to perform statistics. Continuous variables were expressed as means ± SD and were compared by standard t-test. Categorical values were expressed in absolute and relative frequencies and were analyzed by χ² test. Linear regression and logistic regression analysis were used when appropriate. P ≤ 0.05 was considered significant.

Results

During the study period there were 1084 admissions to the ICU. Excluded patients were 94 re-admissions, 6 brain-dead patients and 15 with incomplete data.

Patient population

The demographics of the 969 eligible patients are shown in Table 1. It is noteworthy that 32% of all patients had one or more severe chronic illnesses. Severe hepatic disease was the leading chronic illness, followed by immunosuppression, severe respiratory illness, renal illness and cardiovascular illness. Some patients had more than one severe chronic illness. In comparison with survivors, non-survivors were older, had a longer lead time and ICU LOS but shorter hospital LOS. They had higher APACHE II and SAPS II scores. The type of admission was more likely to be medical or emergency surgical in non-survivors, and to be elective surgical in survivors. Severe chronic illness was more common in non-survivors, especially liver disease.

Table 1.

Patients' demographics

Variable	Total	Survivors	Non-survivors	P value*
Total number	969 (100)	659 (100)	310 (100)	-
Number of females	363 (37.46)	246 (37.33)	117 (37.74)	NS
Age in years (mean ± SD)	49.09 ± 20.19	45.78 ± 20.09	56.15 ± 18.53	<0.001
Lead time in days (mean ± SD)	4.08 ± 8.93	3.66 ± 8.04	4.98 ± 10.53	0.05
ICU LOS in days (mean ± SD)	6.58 ± 9.76	5.99 ± 8.80	7.82 ± 11.44	0.01
Hospital LOS in days (Mean ± SD)	31.75 ± 43.80	35.17 ± 43.27	24.45 ± 44.14	<0.001
APACHE II score (mean ± SD)	18.85 ± 9.13	15.75 ± 7.46	25.63 ± 8.80	< 0.001
SAPS II score (mean ± SD)	38.02 ± 19.90	31.20 ± 15.63	52.98 ± 20.11	< 0.001
Type of admission
Medical	662 (68.32)	404 (61.31)	258 (83.23)	<0.001
Elective surgical	173 (17.85)	155 (23.52)	18 (5.81)	<0.001
Emergency surgical	134 (13.83)	100 (15.17)	34 (10.97)	NS
Chronic illness:
Hepatic	121 (12.5)	32 (4.86)	89 (28.71)	<0.001
Cardiovascular	35 (3.62)	24 (3.64)	11 (3.55)	NS
Renal	54(5.58)	32(4.86)	22 (7.10)	NS
Respiratory	68 (7.02)	55 (8.35)	13 (4.19)	0.02
Immunosuppression	85 (8.78)	39 (5.92)	46 (14.84)	<0.001
Any of the above	310 (32.02)	166 (25.19)	144 (46.45)	<0.001
ICU mortality	204 (21.05)	0	204 (65.81)

Figures in parentheses are percentages. ^*Survivors versus non-survivors. LOS, length of stay; NS, not significant.

Mortality predicted by the four systems

Table 2 shows the actual mortality and predicted mortality by all four systems, and also SMRs and their 95% CIs. SMRs for all system were not significantly different from 1, indicating accurate overall mortality prediction.

Table 2.

Mortalities predicted by the four systems

System	N	Actual mortality	Predicted mortality	SMR	95% CI	Survivors	Non-survivors
MPM II0	969	0.320	0.319	1.00	0.91–1.10	0.190 ± 0.205	0.592 ± 0.307*
MPM II24	681	0.316	0.341	0.92	0.82–1.03	0.221 ± 0.220	0.602 ± 0.290*
APACHE II	681	0.316	0.315	1.00	0.89–1.11	0.213 ± 0.211	0.536 ± 0.279*
SAPS II	681	0.316	0.290	1.09	0.97–1.21	0.189 ± 0.215	0.507 ± 0.311*

^*P < 0.001 for survivors versus non-survivors. CI, confidence interval.

Predicted mortality by subgroups

When subgrouped by categories of main reasons for ICU admission (Table 3), SMRs by the four systems were not significantly different from 1, with few exceptions. MPM II₀ and MPM II₂₄ overestimated mortality for the category 'non-operative trauma' admissions, and SAPS II underestimated mortality for the category 'other medical'. When subgrouped by the source of admission, all SMRs were not significantly different from 1 with the exception of the underestimation of mortality of SAPS II for patients admitted from the floor.

Table 3.

Standardized mortality ratios for the four systems by reason of admission and source of admission

	All patients		Patient s with LOS ≥ 24 h		Standardized mortality ratio (95% confidence interval)
Subcategory	N	Died	N	Died	MPM II0	MPM II24	APACHE II	SAPS II
Reason for admission
Respiratory	156	46	132	39	1.21 (0.92–1.50)	1.07 (0.79–1.35)	0.93 (0.69–1.18)	1.29 (0.95–1.63)
Cardiovascular	222	132	152	82	1.07 (0.96–1.19)	0.98 (0.84–1.12)	0.99 (0.84–1.13)	1.05 (0.90–1.21)
Neurological	58	20	43	16	0.91 (0.59–1.23)	0.96 (0.59–1.33)	1.17 (0.72–1.62)	1.39 (0.85–1.93)
Other medical	87	41	63	32	1.02 (0.79–1.25)	1.05 (0.80–1.31)	1.05 (0.79–1.31)	1.32(1.00–1.63)
Non-op. trauma	146	24	126	18	0.73 (0.46–0.99)	0.60 (0.34–0.85)	1.09 (0.62–1.56)	0.73 (0.42–1.04)
Op. trauma	52	11	37	6	0.83 (0.40–1.27)	0.75 (0.20–1.30)	1.21 (0.32–2.10)	0.75 (0.20–1.31)
Post-op.	241	30	127	21	0.79 (0.53–1.05)	0.79 (0.48–1.10)	0.89 (0.54–1.24)	1.04 (0.64–1.45)
Source of admission
Emergency room	312	87	224	53	0.89 (0.73–1.05)	0.77 (0.59–0.95)	0.94 (0.72–1.16)	0.93 (0.71–1.14)
Floor	292	149	228	107	1.11 (0.99–1.24)	1.02 (0.88–1.16)	1.02 (0.88–1.16)	1.18 (1.01–1.34)
Operating room	307	52	179	38	0.89 (0.67–1.11)	0.85 (0.61–1.08)	1.01 (0.72–1.29)	1.06 (0.76–1.36)
Other hospital	58	22	50	17	1.21 (0.81–1.61)	1.21 (0.75–1.68)	1.09 (0.67–1.51)	1.29 (0.79–1.79)

LOS, length of stay.

Calibration

Calibration curves are shown in Figure 1. Of the four systems, SAPS II stands out as deviating from the identity line in most of the strata, including those with large numbers of patients. The SAPS II curve shows an underestimation of mortality in low-risk patients and an overestimation of mortality in high-risk patients, leading to the skewed appearance of its calibration curve. The curves of the other three systems fell on the identity line in the strata with large number of patients and deviated in some other strata.

Figure 1.

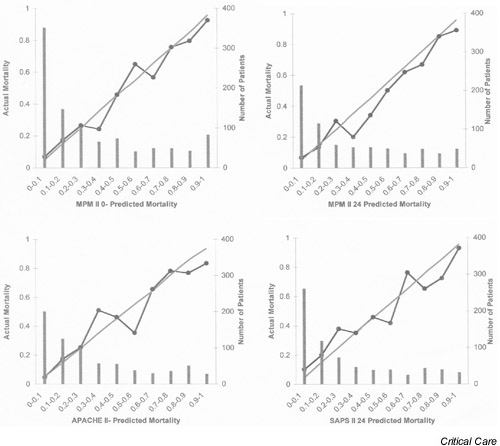
Calibration curves for the four mortality prediction systems.

The results of Lemeshow–Hosmer goodness-of-fit tests are shown in Table 4. The C-statistic was best for MPM II₂₄ (14.71), with P = 0.06. For the other three systems, calibration tested by the C-statistic was poor. These results indicate that, of the four systems, MPM II₂₄ had the least statistically significant discrepancy between predicted and observed mortality across the strata of increasing predicted mortality.

Table 4.

Hosmer-Lemeshow goodness-of-fit tests

MPM II0						MPM II24
Decile	N	PD	AD	PS	AS	Decile	N	PD	AD	PS	AS
1	96	1.46	5	94.54	91	1	68	1.32	1	66.68	67
2	97	3.43	6	93.57	91	2	68	3.04	7	64.96	61
3	97	6.38	10	90.62	87	3	68	5.23	6	62.77	62
4	97	9.48	4	87.52	93	4	69	8.72	7	60.28	62
5	97	15.85	22	81.15	75	5	68	12.60	14	55.40	54
6	97	23.05	26	73.95	71	6	68	19.88	17	48.12	51
7	97	35.47	27	61.53	70	7	68	29.04	21	38.96	47
8	97	50.99	55	46.01	42	8	68	38.89	36	29.11	32
9	97	71.98	68	25.02	29	9	68	50.88	46	17.12	22
10	96	90.39	87	5.61	9	10	68	62.86	60	5.14	8
C-statistic:	26.61		P value:	<0.001		C-statistic:	14.71		P value:	0.06
APACHE II						SAPS II
Decile	N	PD	AD	PS	AS	Decile	N	PD	AD	PS	AS
1	70	1.53	2	68.47	68	1	71	0.74	3	70.26	68
2	68	3.57	2	64.43	66	2	72	2.16	8	69.84	64
3	69	5.82	7	63.18	62	3	65	3.76	8	61.24	57
4	68	9.15	11	58.85	57	4	74	7.13	11	66.87	63
5	66	12.37	18	53.63	48	5	72	10.79	15	61.21	57
6	68	17.28	13	50.72	55	6	63	13.98	21	49.02	42
7	69	24.68	35	44.32	34	7	68	22.09	24	45.91	44
8	66	32.39	25	33.61	41	8	68	33.70	31	34.30	37
9	70	48.57	49	21.43	21	9	64	45.54	42	18.46	22
10	67	59.24	53	7.76	14	10	64	57.24	52	6.76	12
C-statistic:	21.87		P value:	0.005		C-statistic:	43.36		P value:	<0.001

Degrees of freedom = 8. PD, predicted to die; PS, predicted to survive; AD, actually died; AS, actually survived.

Discrimination

Figure 2 shows the receiver operating characteristic (ROC) curves for the four systems. The corresponding areas under the curves were as follows: MPM II₀, 0.85; MPM II₂₄, 0.84; APACHE II, 0.83; SAPS II, 0.79. These reflect the better discriminative power of the first three systems than that of SAPS II.

Figure 2.

Receiver operating characteristic (ROC) curves for the four systems.

The results of the 2×2 classification matrix are shown in Table 5. The overall correct classification rate was highest for MPM II₀ and lowest for SAPS II at the different cutoff points; MPM II₂₄ and APACHE II had intermediate rates. This was consistent with the results of ROC curve testing.

Table 5.

Classification matrix for the four mortality prediction systems

	Died		Survived
System	PD	PS	PD	PS	Sensitivity	Specificity	PPV	NPV	OCCR
Cutoff 10%
MPM II0	286	24	334	324	92 (87–95)	49 (45–53)	46 (42–50)	93 (90–96)	63 (60–66)
MPM II24	201	14	270	196	93 (89–96)	42 (38–47)	43 (38–47)	93 (89–96)	58 (55–62)
APACHE II	206	9	278	188	96 (92–98)	40 (36–45)	43 (38–47)	95 (92–98)	58 (54–62)
SAPS II	189	26	234	232	88 (83–92)	50 (45–54)	45 (40–50)	90 (86–93)	62 (58–65)
Cutoff 30%
MPM II0	235	75	143	515	76 (71–80)	78 (75–81)	62 (57–67)	87 (84–89)	77 (75–80)
MPM II24	169	46	134	332	79 (73–84)	71 (67–75)	56 (50–61)	88 (84–91)	74 (70–77)
APACHE II	161	54	107	359	75 (69–81)	77 (73–81)	60 (54–66)	87 (83–90)	76 (73–80)
SAPS II	140	75	99	367	65 (58–71)	79 (74–82)	59 (52–65)	83 (79–86)	74 (71–78)
Cutoff 50%
MPM II0	189	121	58	600	61 (55–66)	91 (89–93)	77 (71–82)	83 (80–86)	82 (79–84)
MPM II24	142	73	61	405	66 (59–72)	87 (84–90)	70 (63–76)	85 (81–87)	80 (77–83)
APACHE II	110	105	53	413	51 (44–58)	89 (85–91)	67 (60–75)	80 (76–83)	77 (73–80)
SAPS II	109	106	52	414	51 (44–58)	89 (86–92)	68 (60–75)	80 (76–83)	77 (73–80)

Figures in parentheses are 95% confidence intervals. PD, predicted to die; PS, predicted to survive; PPV, positive predictive value; NPV, negative predictive value; OCCR, overall correct classification rate.

Correlation of predicted mortalities by the four systems

On the basis of linear regression analysis, mortalities predicted by all four systems correlated with each other (P < 0.001 for all combinations). The closest correlation was between MPM II₀ and MPM II₂₄ (r² = 0.67) followed by APACHE II and SAPS II₂₄ (r² = 0.66), MPM II₂₄ and SAPS II (r² = 0.62), MPM II₂₄ and APACHE II (r² = 0.56), MPM II₀ and SAPS II (r² = 0.52) and MPM II₀ and APACHE II (r² = 0.48). Figure 3 shows plots for the highest and lowest correlations.

Figure 3.

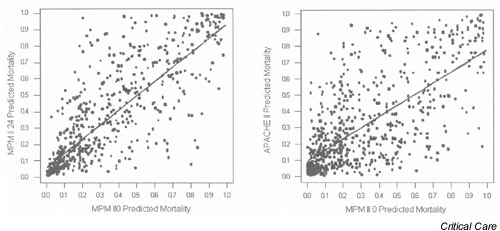
Plots of predicted mortality of the systems with the highest intersystem correlation (MPM II₀ versus MPM II₂₄, left) and the lowest intersystem correlation (MPM II₀ versus APACHE II, right).

The effect of lead time and ICU LOS on hospital mortality

By univariate analysis, lead time was a significant predictor of hospital outcome (odds ratio 1.02, 95% CI 1.00–1.03 per day, P = 0.04). However, when adjusted to the severity of illness estimated from the mortality predicted by any of the four systems, lead time was not an independent predictor of hospital outcome. Similarly, ICU LOS was a significant predictor of hospital outcome by univariate analysis (odds ratio 1.02, 95% CI 1.00–1.03 per day, P = 0.01) but not when adjusted to severity of illness by multivariate analysis.

Discussion

The main findings of this validation study on a Saudi Arabian ICU population can be summarized as follows: (1) overall mortality prediction, estimated by SMR, was reasonably accurate, especially for MPM II₀ and APACHE II; (2) MPM II24 had the best calibration by C-statistic; (3) SAPS II had the lowest calibration and discrimination.

There is great international variability in patient mix and severity of illness [7,8,9,16,17,18]. Some of the differences are inherent in the patient population. For example, patients with cirrhosis have a high severity of illness and poor prognosis when admitted to the ICU [19,20,21]. Case mix is also affected by the type of hospital, for example whether it is primary or tertiary, or a transplant or trauma center. Patients referred from other hospitals have a higher severity of illness and mortality compared with direct admissions [22]. Other factors are practice-related. An important example is the 'do not-resuscitate' (DNR) practice [23,24]. Early (pre-ICU) determination of DNR status reduces the number of futile admissions to the ICU leading to a probable reduction in overall severity of illness. Another example is related to ICU bed availability. It has been documented that physicians tend to be more selective in their ICU admissions at times of bed shortages, with patients with higher severity of illness being admitted [25]. In our study, the relatively high level of severity of illness was probably related to a combination of all these factors. Being a tertiary care center, our hospital receives referrals from other hospitals, some of them directly to ICU (Table 2). Being a transplant center, we have a large population of end-stage liver disease. The concept of DNR is evolving in Saudi Arabia. Our hospital has been leading in the country in this field by establishing a written policy for DNR orders and raising the awareness among physicians about this issue. Nevertheless, there is room for improvement. Frequently the DNR status is discussed at a very late stage or is not discussed at all before admission to the ICU. Consequently, many desperately ill patients are admitted to the ICU with very high severity of illness and no meaningful chance of survival. The nursing shortage in our ICU led to selecting the sicker admissions and decreasing the number of elective admissions.

In this study we showed that the overall mortality prediction was accurate but calibration was inadequate. Potential reasons for insufficient calibration might include the following: (1) factors related to the calibration methodology itself; (2) reasons related to data collection, namely intra-observer and interobserver variability; (3) variability in GCS; (4) differences in case mix; (5) differences in DNR policies; and (6) differences in medical care.

The results of Lemeshow–Hosmer statistics are dependent not only on the calibration of the model but also on patient numbers and the distribution of the estimates [26]. The results of the calibration tests in our study might seem inconsistent with the overall estimate of mortality of the whole population and with the mortality estimates of the subgroups (Table 2). This apparent inconsistency is probably related to the distribution of estimates. The overestimation of mortality in certain strata of severity of illness is 'counterbalanced' by underestimation in other strata (Table 4), leading to 'perfect' estimation when the whole population or a specific subgroup is considered.

Interobserver variability in data collection has been documented in several studies [27,28,29]. This is potentially relevant to our study because data collection was performed by several physicians and over a relatively long period (22 months). We tried to minimize variability by having a written reference of definitions based on the original articles of the various scoring systems and having one person coordinate the process of data collection. Similar approaches have been shown to minimize variability [30,31]. MPM II systems have been documented to have high reproducibility, which might explain the better calibration of MPM II₂₄ in our study [32].

The variability of GCS determination in sedated patients accounts for much of the variability in scoring APACHE II. Several approaches in determining GCS have been used previously. For non-sedated patients we used the worst value in the first 24 hours; for sedated patients we used the pre-sedation GCS. This approach has been shown to be associated with better performance of APACHE II than the approach that assumes normal GCS for sedated patients [10]. This approach also follows the original MPM II article definitions [4] and is consistent with the approach described by Knaus and others [11,12].

Another potential reason for the inadequate calibration is the differences in case mix between our database and the development databases of the mortality prediction systems. Medical patients constitute a larger proportion in our database (68%) than in the development databases (MPM II₀, 45%; MPM II₂₄, 48%; SAPS II, 49%; APACHE II, 58%) [2,3,4]. When the main diagnostic categories in our database are compared with those in the development database of APACHE II, some interesting differences appear. The post cardiac arrest category, which is associated with a high mortality risk (APACHE II diagnostic category weight is 0.393) accounts for 7% of our admissions, compared with 3% in the developmental database of APACHE II. The postoperative category 'peripheral vascular surgery', which is associated with a low mortality risk (APACHE II diagnostic weight is -1.315) accounts for 1.5% of our admissions, compared with 9.82% of the development database. Our database also has more severe chronic illnesses (32%) compared with 5–29% in different participating ICUs in the APACHE II development database. This is partly related to the high percentage of patients with end-stage liver disease admitted to our ICU (12.5% of all patients).

Differences in admission practises to the ICUs might also have an impact on ICU outcome. The delay in DNR orders is mentioned earlier. This factor probably contributes to our high severity of illness and could have affected system calibration.

Finally, one must examine whether the inadequate calibration is related to differences in medical care. However, in our study, overall actual mortality was not different from predicted mortality, as is evident in the SMRs (Table 2). Furthermore, when the calibration curves are examined there is no consistent pattern of overestimation or underestimation of mortality among the four systems in the different strata of severity of illness. This suggests that the inadequate calibration is inherent in these systems when applied to this population and less likely to be related to gross variation in medical care.

Our study has some limitations. First, it is a single-center study, which makes it biased towards a certain case mix. Second, as discussed above, collecting the data over a relatively long period by different physicians has implications for consistency of data collection. The use of a written reference of definitions and assigning a coordinator to oversee the whole process probably decreased variability, as has been shown previously [28,29]. In addition, variability has been found to be random and of little impact on the overall estimates [29]. A multicenter study would have addressed some of these concerns.

In conclusion, the four mortality prediction systems gave accurate overall estimates of mortality, especially MPM II₀ and APACHE II. Calibration was modest for MPM II₂₄ and inadequate for the others. SAPS II had the lowest calibration and discrimination. The local performance of MPM II systems (particularly MPM II₂₄), in addition to their ease of use, makes them attractive models for use in Saudi Arabia. However, a multi-center national study is needed to confirm these findings.

Competing interests

None declared.

Abbreviations

APACHE = Acute Physiology and Chronic Health Evaluation; CI = confidence interval; DNR = 'do not resuscitate'; GCS = Glasgow Coma Score; ICU = intensive care unit; LOS = length of stay; MPM = Mortality Probability Model; ROC = receiver operating characteristic; SAPS = Simplified Acute Physiology Score; SMR = standardized mortality ratio.