Abstract
Proteins fold to a specific functional conformation with a densely packed hydrophobic core that controls their stability. We develop a geometric, yet all-atom model for proteins that explains the universal core packing fraction of found in experimental measurements. We show that as the hydrophobic interactions increase relative to the temperature, a novel jamming transition occurs when the core packing fraction exceeds . The model also recapitulates the global structure of proteins since it can accurately refold to native-like structures from partially unfolded states.
In native solution conditions, globular proteins fold from an extended chain to a compact, specific, and functional state. Protein folding is believed to be an equilibrium collapse process toward a global energy minimum driven primarily by the hydrophobicity of the amino acid sequence [1–7]. In addition, it is well known that proteins possess dense, solvent-inaccessible, or core, regions, which include ~10% of the protein and provide their thermal stability. Focusing on the hard-core atomic interactions, initial calculations of the core packing fraction found that , which is close to the maximum packing fraction in crystalline solids [8–11]. In such hard-particle models, the maximum packing fraction corresponds to a minimum in the potential energy, i.e. . However, we now know that achieving such large values for the packing fraction is not possible for disordered states like protein cores, without causing interatomic overlaps. More recent work shows that the average packing fraction in globular protein cores is [12].
While the fact that each protein folds to a specific conformation suggests an equilibrium process, dense packing in protein cores suggests that non-equilibrium processes also occur. For example, as hard particles are compressed, the system becomes rigid and solid-like, i.e. jammed, at a sufficiently large packing fraction [13]. However, the and mechanical properties depend on the protocol used to generate the particle packings, and thus jamming is a highly non-equilibrium process [14–17]. In addition, vibrational studies of proteins show that they posses a boson peak, or an abundance of low frequency modes in the density of states, which is a prominent feature of non-equilibrium systems, such as glasses [18–21]. Moreover, recent experiments on the dry molten globule state [22–25] suggest that the final stages of core formation take much longer than the initial stages of folding [26]. Thus, it is important to develop a geomertic, yet atomistically accurate model for proteins, which will allow us to rigorously connect the nonequilibrium physics of hard-particle packings [13, 27] to the nearly folded conformational landscape of proteins [28].
In this Letter, we first discuss a hard-sphere (HS) model for proteins with stereochemical constraints and a specific set of atom sizes that recapitulates the allowed backbone and side chain dihedral angle distributions in proteins. We then add attractive atomic interactions that scale with amino acid hydrophobicity (i.e. the HS+HP model) to explore core formation. We find that the HS+HP model collapses as the attractive strength relative to temperature is increased, and similar to jamming, transitions from a floppy to rigid state at . Additionally, we find that the potential energy of atomic overlaps scales as a power-law with packing fraction, with a novel scaling exponent . This result suggests that proteins collapse until the core amino acids reach a mechanically stable state that resists the compression induced by the hydrophobic attractions. Moreover, HS+HP model proteins can refold from partially unfolded states, suggesting that the model can recapitulate the protein conformational landscape.
First, to calculate the core packing fraction, the set of atomic diameters must be defined. However, the literature provides a wide range of possible for the hard-core atomic interactions in proteins [12]. Therefore, we propose that can be selected by validating the atom sizes against a fundamental feature of protein structure. Ramachandran, et al. first demonstrated that by assuming only repulsive, hard-core atomic interactions, plus the stereochemistry of amino acids, one can predict the backbone dihedral angle pairs and that occur in proteins are those pairs that do not cause large atomic overlaps [29, 30]. (See the inset of Fig. 1(c) for the backbone dihedral angle distribution from high-quality -ray crystal structures of proteins.) We have also validated this approach for the distributions of side chain dihedral angles [31–35]. The potential energy for the HS model includes both nonbonded and bonded atomic interactions. For the nonbonded interactions, we employ a purely repulsive linear spring potential to prevent atomic overlaps,
| (1) |
where defines the repulsive energy scale, is the centerto-center distance between atoms and , is their average diameter, and is the Heaviside step-function. (See Fig. 1 (a) and (b).) The total repulsive potential energy includes all atom pairs except those that participate in bonded interactions: , where is the set of nonbonded atom pairs. We add restraints on the bond lengths , bond angles , and dihedral angles with rest values, , , and that occur in each target protein’s high-resolution x-ray crystal structure:
| (2) |
| (3) |
| (4) |
where are the respective spring constants and is the diameter of hydrogen. (Below, all energy scales will be given in units of ) We set the spring constants to be equal to weight nonbonded overlaps and deformations in stereochemistry equally. Additionally, only the dihedral angles needed to maintain high-quality protein stereochemistry are restrained. First, we add restraints to the main chain peptide bond dihedral angle , which due to the peptide bond’s partial double-bonded character, is relatively planar in high-quality protein structures. Second, amino acids with side chains containing double bonds require restraints to maintain their planar geometry, such as in the phenylalanine ring. The total potential energy for the HS model is then , where is the set of bonded atom pairs, is the set of atom triples that defines each bond angle, and is the set of groups of four atoms that define the dihedral angles. All hydrogens are placed using the REDUCE software [36]. When comparing simulation results to experimentally determined protein structures, we use a high-resolution dataset of structures with a resolution <1.8 Å culled from the Protein Data Bank (PDB) [37, 38]. For the HS protein simulations, we carry out Langevin dynamics over range of temperatures using 20 randomly selected, single chain target proteins with no disulfide bonds from the x-ray crystal structure dataset. Sizes range from with an average of amino acids. (PDBIDs are given in Table S1 and examples of the restraints in Eqs. 2–4 are given in Tables S2 and S3 in Supplemental Material (SM).)
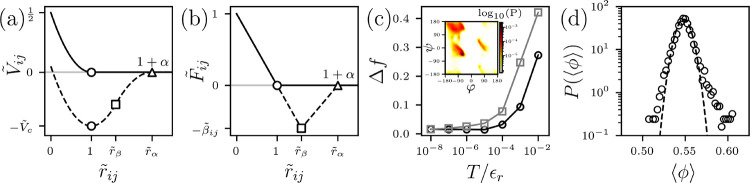
FIG. 1.
The nonbonded dimensionless pair potential plotted versus atomic separation for purely-repulsive interactions (Eq. 1) (solid line) and attractive interactions (Eq. 5) (dashed line) and (b) the corresponding dimensionless force . The symbols represent the onset of repulsive interactions where and (circles), the change in spring constant where and (squares), and the separation above which the interactions are zero (triangles). (c) The difference between the average fraction of backbone dihedral angle outliers (black circles) and side chain dihedral angle outliers (grey squares) between the HS model and proteins from a high-quality x-ray crystal structure database plotted versus the temperature at which the HS model proteins were simulated. Inset: The probability distribution of backbone dihedral angles sampled by high-quality x-ray crystal structures of proteins. The colors from light to dark indicate increasing probability on a logarithmic scale. (d) Probability distribution of the average core packing fraction in high-quality x-ray crystal structures of proteins calculated using the optimized HS atom sizes on a semi-log plot with a Gaussian fit (black dashed line).
Using optimized (Table S4 of SM) [31–35, 39], we compare the backbone and side chain dihedral angles sampled by the HS model and those of high-quality x-ray crystal structures. We use the software package MOLPROBITY to quantify the fraction of backbone and side chain dihedral angle outliers, with respect to a reference set of high quality x-ray crystal structures [40–42]. We compare the fraction of backbone and side chain outliers in the HS simulations to the fraction of outliers in our high-resolution x-ray crystal structure database . We show in Fig. 1 (c) that approaches zero for both backbone and side chain dihedral angles as decreases (and the HS model approaches the hard-core limit). Note that the HS protein model recapitulates the Ramachandran map even though it has fewer restraints than in typical all-atom protein force fields. For example, in an alanine dipeptide, the HS model includes two dihedral angle restraints, whereas current Amber and CHARMM force fields have 41 dihedral angle restraints [43, 44].
With this optimized set of atomic diameters , we can calculate the average core packing fraction in the high-resolution x-ray crystal structure data set as shown in Fig. 1 (d). Core amino acids are those that have relative solvent accessible surface area rSASA <10−3, using the Lee and Richards algorithm with a probe size of a water molecule [45]. As we have previously reported [12, 46], we find . The same result is found for solution NMR structures when only including high quality bundles [47]. An important question naturally arises, why does the folding process give rise to this value for in all globular protein cores?
To study core formation, we can add attractive interactions to the HS protein model, which yields the HS+HP model. For the nonbonded attractive interactions between atoms, we extend the potential in Eq. 1 to and cutoff the interactions at using piecewise harmonic functions of :
| (5) |
where for continuity. defines the attractive range and defines the magnitude of the attractive force. (See Fig. 1(a) and (b).) is the average hydrophobicity associated with atom pairs and , where is the hydrophobicity per amino acid and is assigned to each atom on a given amino acid [48]. (See Table S5 in SM.)
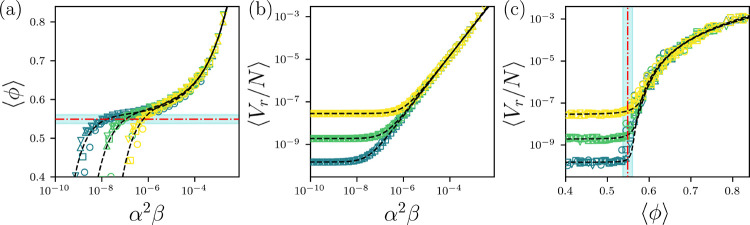
To explore the dynamics of folding for the HS+HP model, we run Langevin dynamics with the HS-energy minimized x-ray crystal structure of a given protein as the initial condition. We consider 20 randomly selected single-chain protein targets from the high-resolution x-ray crystal structure database and study the folowing parameter regimes: , and . In Fig. 2 (a), we show the packing fraction of core residues averaged over the 20 proteins versus increasing attractive strength, quantified using . Plotting versus collapses the data for each temperature . At small , the proteins unfold and . As the attractive interactions increase, a plateau at (i.e. at the average packing fraction of experimentally determined protein cores) occurs for . Increasing the attraction further causes a steep increase in . As is lowered, the HS+HP model behaves as a hard-core system and the plateau extends to smaller versus is well fit by
| (6) |
where and are constants, and the exponents and as .
FIG. 2.
(a) The average core packing fraction plotted versus the attraction strength for the HS+HP protein model for temperatures (yellow), 10−7 (green), and 10−8 (blue) and (circles), 1.0 (squares), 1.5 (upward triangles), and 2.0 (downward triangles). The horizontal red dot-dashed line and cyan shading indicate the average and standard deviation of the core packing fraction in the high-resolution x-ray crystal structure data set. The black dashed lines indicate fits to Eq. 6. (b) The average repulsive potential energy per atom plotted versus . The black dashed lines indicate fits to Eq. 7. (c) plotted versus . The vertical red dot-dashed line and cyan shading indicate the average and standard deviation of the core packing fraction in the high-resolution x-ray crystal structure data set. The black dashed lines indicate fits to Eq. 8.
How are such large values of possible in Fig. 2 (a)? When we plot the average total nonbonded repulsive potential energy per atom versus in Fig. 2 (b), we find that , where for . However, when , increases from the plateau value as a power-law:
where is a constant and as . Thus, we find that when , the total repulsive energy per atom increases strongly, which indicates a jamming transition.
In Fig. 2 (c), we combine data from Figs. 2 (a) and (b). For , . When , increases as a power-law, obtained by combining Eqs. 6 and 7:
| (8) |
where , and . When , Eq. 8 simplifies to , where in the limit. This result is similar to that found for the jamming transition in particle packings, except with a significantly larger exponent than expected from affine compression.
Thus, Fig. 2 shows that the HS+HP model undergoes a jamming transition when the average packing fraction increases above the value observed in x-ray crystal structures of proteins. However, the jamming transition in the HS+HP model has a scaling exponent that is more than a factor of two larger than that found previously for hard-sphere systems and bead-spring polymers [49]. In the SM, we confirm that the collapse transition in bead-spring polymers with the same nonbonded interactions and only bond-length constraints yields , which suggests that the anomalous exponent for the HS+HP model is caused by the unique geometry of amino acids and not from the attractive interactions. A possible source of the anomalous scaling exponent is changes in the number of contacts between amino acids as the core is compressed [50].
Below jamming onset, unjammed systems possess a large number of low frequency, liquid-like modes in the vibrational density of states (VDOS). Near jamming onset, excess intermediate frequencies, known as the boson peak, occur in the VDOS, and as the packing fraction increases above jamming onset the boson peak is suppressed [51, 52]. We calculate the VDOS from the eigenvalues of the displacement correlation matrix , where is the velocity correlation matrix and is the positional covariance matrix, are the atom velocities, are the atom positions, and are the average atom positions. The angle brackets indicate time averages. Each eigenvalue has a corresponding eigenvector . The VDOS is then obtained by binning the frequencies [53, 54], where the frequencies are given in units of , where is the mass of hydrogen.
In Fig. 3 (a), to investigate the rigidification of the HS+HP model, we plot the VDOS of the backbone atoms averaged over the 20 proteins for . We show for all and values in Fig. 2 and as a function of to identify the jamming transition. When the HS+HP proteins are unjammed with , the VDOS possesses a large peak of liquid-like modes in the range , as well as a secondary peak near corresponding to the bonded interactions. As increases, the liquid-like peak decreases and the modes at intermediate frequencies fill-in to form a plateau near . A key sign of the onset of rigidification is the formation of a plateau in the intermediate frequency region of the VDOS, also known as the boson peak [55]. The boson peak is suppressed when the system becomes overcompressed with increasing . (The results for the VDOS of attractive bead-spring polymers are similar, except the liquid-like modes vanish more rapidly with increasing related to the difference in , as shown in SM.)
FIG. 3.
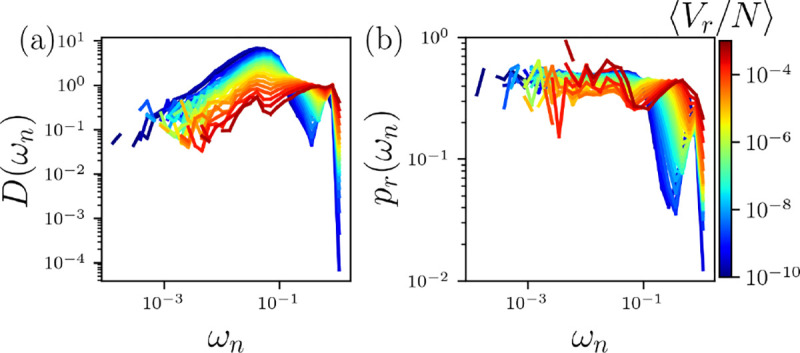
(a) The vibrational density of states (VDOS) , where is the frequency, of the atoms in the HS+HP model at for all and in Fig. 2. (b) Participation ratio plotted versus . The average total nonbonded repulsive potential energy per atom increases from blue to red on a logarithmic scale.
Near jamming onset in packings of spherical particles, the vibrational modes in the VDOS plateau region are quasilocalized, i.e. many particles participate in the eigenmodes, but they are not phonon-like [55]. We investigate the localization of the modes in the platueau region of by calculating the participation ratio for each eigenmode,
| (9) |
where is the contribution of particle to the th eigenvector of [56]. In Fig. 3 (b), we plot the binned at each . A key difference between for the unjammed systems and jammed systems is that there is a strong increase in for frequencies in the range , which indicates the development of quasi-localized modes at intermediate frequencies. As expected, the highest frequencies correspond to local excitations.
We demonstrated that during folding, the HS+HP model for proteins undergoes a jamming transition at the average core packing fraction observed in high-resolution x-ray crystal structures. We now quantify whether the backbone atoms of the HS+HP model deviate from the x-ray crystal structures during the jamming process. To do this, we calculate the rootmean-square-deviations (RMSD) in the positions between the simulated and experimental protein structures,
| (10) |
where and are the positions of the th amino acid from the simulations and x-ray crystal structures, respectively. We find that converges rapidly as a function of time, and thus we focus on at the last time point in the simulations. We plot averaged over the 20 proteins in Fig. 4 (a) for the HS+HP simulations presented above. We find that near jamming onset, confirming that not only the core packing fraction, but also the overall backbone conformation is similar to the x-ray crystal structure near jamming onset.
FIG. 4.
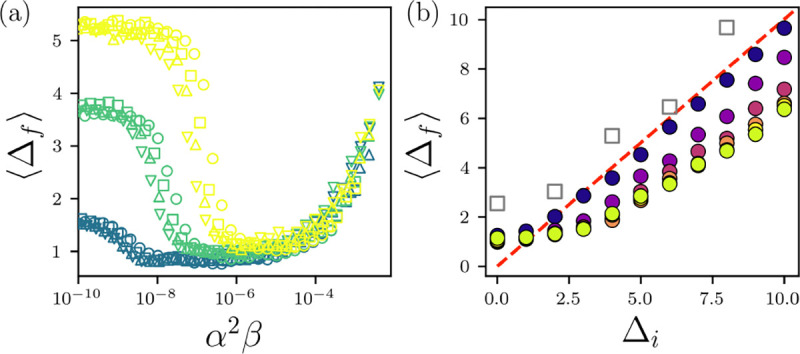
(a) in Å between the HS+HP model proteins and the x-ray crystal structures averaged over 20 proteins plotted versus when starting from the experimental structure for temperature (yellow), 10−7 (green), and 10−8 (blue) and (circles), 1.0 (squares), 1.5 (upward triangles), and 2.0 (downward triangles). (b) Average plotted versus the initial in for . The filled circles are colored by increasing from purple to yellow, and is set so that . All-atom MD simulations of a single protein (PDBID: 2IGP) using the Amber99SB-ILDN force field are shown as grey squares. The red dashed line indicates .
Does the RMSD of the HS+HP model relative to the x-ray crystal structures remain small when the simulations are initialized further from the x-ray crystal structure? To study the ability of the HS+HP model to refold proteins, we initialize the HS+HP simulations with conformations at different values of the RMSD using the HS model conformations, which unfold over time since there are no attractive forces. We then run Langevin dynamics simulations of the HS+HP model at over the range and we set such that .
In Fig. 4 (b), we plot the long-time versus for a range of averaged over all 20 proteins studied. We find that for short attractive ranges (i.e. ), while when starting in the crystal structure can lead to a jamming transition, the HS+HP model cannot refold (i.e. ) above . As is increased, the HS+HP model can refold initial states with to , a threshold that is considered properly folded in all-atom MD simulations of protein folding [57]. In addition, all HS+HP proteins that refold to form a well-defined core possess . We also compared these results to those from all-atom MD simulations using the Amber99SB-ILDN force field in explicit water. We find that when starting near the x-ray crystal structure for PDBID: 2IGP, yet when After running for [43, 58–62]. (More details are found in SM.)
Here, we have developed a quantitatively accurate model for protein structure in which the stereochemistry of the amino acids is preserved and the atom sizes are optimized to recapitulate the experimentally observed backbone (and side chain) dihedral angle distributions. By adding hydrophobic attractive interactions, we showed that a novel jamming transition occurs during folding at the average core packing fraction of protein x-ray crystal structures. We showed that the total repulsive potential energy versus obeys power-law scaling above jamming onset with an anomalous exponent . In addition, the vibrational response indicates that the HS+HP model rigidifies at with quasi-localized vibrational modes at intermediate frequencies. Thus, we have demonstrated that the core packing fraction observed in high quality experimental protein structures is due to the onset of jamming under hydrophobic compression and have provided a theoretical direction for understanding non-equilibrium properties of proteins. In addition, starting from partially unfolded states with , HS+HP proteins can refold to the x-ray crystal structure. We believe that the HS+HP model is well-suited for tackling many open problems in protein science, such as predicting the structural response to amino acid mutations, identifying protein-protein interactions, and understanding protein structure in vivo [63–67]. In addition, the HS+HP model can be used to investigate the effects of folding rate on protein core packing, given that the properties of other jammed systems possess strong cooling rate dependence [68–71].
Acknowledgments
The authors acknowledge support from NIH Training Grant No. T32GM145452 (A. T. G. and C. S. O.), NIH Training Grant No. T15LM007056-37 (J. A. L.) and the High Performance Computing facilities operated by Yale’s Center for Research Computing.
References
- [1].Dill K. A., Dominant forces in protein folding, Biochemistry 29, 7133 (1990). [DOI] [PubMed] [Google Scholar]
- [2].Bryngelson J. D. and Wolynes P. G., Spin glasses and the statistical mechanics of protein folding, Proceedings of the National Academy of Sciences 84, 7524 (1987). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Leopold P. E., Montal M., and Onuchic J. N., Protein folding funnels: A kinetic approach to the sequence-structure relationship, Proceedings of the National Academy of Sciences 89, 8721 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wolynes P. G., Onuchic J. N., and Thirumalai D., Navigating the folding routes, Science 267, 1619 (1995). [DOI] [PubMed] [Google Scholar]
- [5].Onuchic J. N., Luthey-Schulten Z., and Wolynes P. G., Theory of protein folding: The energy landscape perspective, Annual Review of Physical Chemistry 48, 545 (1997). [DOI] [PubMed] [Google Scholar]
- [6].Plotkin S. S. and Onuchic J. N., Understanding protein folding with energy landscape theory part I: Basic concepts, Quarterly Reviews of Biophysics 35, 111 (2002). [DOI] [PubMed] [Google Scholar]
- [7].Pace C. N., Fu H., Fryar K. L., Landua J., Trevino S. R., Shirley B. A., Hendricks M. M., Iimura S., Gajiwala K., Scholtz J. M., and Grimsley G. R., Contribution of hydrophobic interactions to protein stability, Journal of Molecular Biology 408, 514 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Chothia C., Structural invariants in protein folding, Nature 254, 304 (1975). [DOI] [PubMed] [Google Scholar]
- [9].Richards F. M., The interpretation of protein structures: Total volume, group volume distributions and packing density, Journal of Molecular Biology 82, 1 (1974). [DOI] [PubMed] [Google Scholar]
- [10].Richards F. M., Areas, volumes, packing, and protein structure, Annual Review of Biophysics and Bioengineering 6, 151 (1977). [DOI] [PubMed] [Google Scholar]
- [11].Liang J. and Dill K. A., Are proteins well-packed?, Biophysical Journal 81, 751 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Gaines J. C., Smith W. W., Regan L., and O’Hern C. S., Random close packing in protein cores, Physical Review E 93, 032415 (2016). [DOI] [PubMed] [Google Scholar]
- [13].O’Hern C. S., Silbert L. E., Liu A. J., and Nagel S. R., Jamming at zero temperature and zero applied stress: The epitome of disorder, Physical Review E 68, 011306 (2003). [DOI] [PubMed] [Google Scholar]
- [14].Chaudhuri P., Berthier L., and Sastry S., Jamming transitions in amorphous packings of frictionless spheres occur over a continuous range of volume fractions, Physical Review Letters 104, 165701 (2010). [DOI] [PubMed] [Google Scholar]
- [15].Ashwin S. S., Zaeifi Yamchi M., and Bowles R. K., Inherent structure landscape connection between liquids, granular materials, and the jamming phase diagram, Physical Review Letters 110, 145701 (2013). [DOI] [PubMed] [Google Scholar]
- [16].Bertrand T., Behringer R. P., Chakraborty B., O’Hern C. S., and Shattuck M. D., Protocol dependence of the jamming transition, Physical Review E 93, 012901 (2016). [DOI] [PubMed] [Google Scholar]
- [17].Ozawa M., Berthier L., and Coslovich D., Exploring the jamming transition over a wide range of critical densities, SciPost Physics 3, 027 (2017). [Google Scholar]
- [18].Perticaroli S., Nickels J. D., Ehlers G., O’Neill H., Zhang Q., and Sokolov A. P., Secondary structure and rigidity in model proteins, Soft Matter 9, 9548 (2013). [DOI] [PubMed] [Google Scholar]
- [19].Perticaroli S., Nickels J. D., Ehlers G., and Sokolov A. P., Rigidity, secondary structure, and the universality of the boson peak in proteins, Biophysical Journal 106, 2667 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Nakagawa H., Joti Y., Kitao A., Yamamuro O., and Kataoka M., Universality and structural implications of the boson peak in proteins., Biophysical Journal 117, 229 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Mori T., Jiang Y., Fujii Y., Kitani S., Mizuno H., Koreeda A., Motoji L., Tokoro H., Shiraki K., Yamamoto Y., and Kojima S., Detection of boson peak and fractal dynamics of disordered systems using terahertz spectroscopy, Physical Review E 102, 022502 (2020). [DOI] [PubMed] [Google Scholar]
- [22].Baldwin R. L., Frieden C., and Rose G. D., Dry molten globule intermediates and the mechanism of protein unfolding, Proteins: Structure, Function, and Bioinformatics 78, 2725 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Jha S. K. and Udgaonkar J. B., Direct evidence for a dry molten globule intermediate during the unfolding of a small protein, Proceedings of the National Academy of Sciences 106, 12289 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Sarkar S. S., Udgaonkar J. B., and Krishnamoorthy G., Unfolding of a small protein proceeds via dry and wet globules and a solvated transition state, Biophysical Journal 105, 2392 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Neumaier S. and Kiefhaber T., Redefining the dry molten globule state of proteins, Journal of Molecular Biology 426, 2520 (2014). [DOI] [PubMed] [Google Scholar]
- [26].Wilson C. B., Yau W.-M., and Tycko R., Experimental evidence for millisecond–timescale structural evolution following the microsecond–timescale folding of a small protein, Physical Review Letters 132, 048402 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Charbonneau P., Kurchan J., Parisi G., Urbani P., and Zamponi F., Glass and jamming transitions: From exact results to finite-dimensional descriptions, Annual Review of Condensed Matter Physics 8, 265 (2017). [Google Scholar]
- [28].Dill K. A. and MacCallum J. L., The protein-folding problem, 50 years on, Science 338, 1042 (2012). [DOI] [PubMed] [Google Scholar]
- [29].Ramachandran G., Ramakrishnan C., and Sasisekharan V., Stereochemistry of polypeptide chain configurations, Journal of Molecular Biology 7, 95 (1963). [DOI] [PubMed] [Google Scholar]
- [30].Ramakrishnan C. and Ramachandran G., Stereochemical criteria for polypeptide and protein chain conformations. II. Allowed conformations for a pair of peptide units, Biophysical Journal 5, 909 (1965). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zhou A. Q., O’Hern C. S., and Regan L., The power of hard-sphere models: Explaining side-chain dihedral angle distributions of Thr and Val, Biophysical Journal 102, 2345 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Zhou A. Q., O’Hern C. S., and Regan L., Predicting the side-chain dihedral angle distributions of nonpolar, aromatic, and polar amino acids using hard sphere models, Proteins: Structure, Function, and Bioinformatics 82, 2574 (2014). [DOI] [PubMed] [Google Scholar]
- [33].Caballero D., Määttä J., Zhou A. Q., Sammalkorpi M., O’Hern C. S., and Regan L., Intrinsic α-helical and β-sheet conformational preferences: A computational case study of alanine, Protein Science 23, 970 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Caballero D., Virrueta A., O’Hern C., and Regan L., Steric interactions determine side-chain conformations in protein cores, Protein Engineering, Design and Selection 29, 367 (2016). [DOI] [PubMed] [Google Scholar]
- [35].Gaines J. C., Virrueta A., Buch D. A., Fleishman S. J., O’Hern C. S., and Regan L., Collective repacking reveals that the structures of protein cores are uniquely specified by steric repulsive interactions, Protein Engineering, Design and Selection 30, 387 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Word J., Lovell S. C., Richardson J. S., and Richardson D. C., Asparagine and glutamine: Using hydrogen atom contacts in the choice of side-chain amide orientation, Journal of Molecular Biology 285, 1735 (1999). [DOI] [PubMed] [Google Scholar]
- [37].Wang G. and Dunbrack R. L. Jr., PISCES: A protein sequence culling server, Bioinformatics 19, 1589 (2003). [DOI] [PubMed] [Google Scholar]
- [38].Wang G. and Dunbrack R. L. Jr., PISCES: Recent improvements to a PDB sequence culling server, Nucleic Acids Research 33, W94 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Caballero D., Smith W. W., O’Hern C. S., and Regan L., Equilibrium transitions between side-chain conformations in leucine and isoleucine, Proteins: Structure, Function, and Bioinformatics 83, 1488 (2015). [DOI] [PubMed] [Google Scholar]
- [40].Davis I. W., Leaver-Fay A., Chen V. B., Block J. N., Kapral G. J., Wang X., Murray L. W., Arendall I., Bryan W., Snoeyink J., Richardson J. S., and Richardson D. C., MolProbity: All-Atom contacts and structure validation for proteins and nucleic acids, Nucleic Acids Research 35, W375 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Chen V. B., Arendall W. B. III, Headd J. J., Keedy D. A., Immormino R. M., Kapral G. J., Murray L. W., Richardson J. S., and Richardson D. C., MolProbity: All-Atom structure validation for macromolecular crystallography, Acta Crystallographica Section D 66, 12 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Williams C. J., Headd J. J., Moriarty N. W., Prisant M. G., Videau L. L., Deis L. N., Verma V., Keedy D. A., Hintze B. J., Chen V. B., Jain S., Lewis S. M., Arendall III W. B., Snoeyink J., Adams P. D., Lovell S. C., Richardson J. S., and Richardson D. C., Molprobity: More and better reference data for improved all-atom structure validation, Protein Science 27, 293 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lindorff-Larsen K., Piana S., Palmo K., Maragakis P., Klepeis J. L., Dror R. O., and Shaw D. E., Improved side-chain torsion potentials for the Amber ff99SB protein force field, Proteins: Structure, Function, and Bioinformatics 78, 1950 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Huang J., Rauscher S., Nawrocki G., Ran T., Feig M., de Groot B. L., Grubmüller H., and MacKerell A. D., CHARMM36m: An improved force field for folded and intrinsically disordered proteins, Nature Methods 14, 71 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Mitternacht S., FreeSASA: An open source C library for solvent accessible surface area calculations, F1000Res 5, 189 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Mei Z., Treado J. D., Grigas A. T., Levine Z. A., Regan L., and O’Hern C. S., Analyses of protein cores reveal fundamental differences between solution and crystal structures, Proteins: Structure, Function, and Bioinformatics 88, 1154 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Grigas A. T., Liu Z., Regan L., and O’Hern C. S., Core packing of well-defined x-ray and NMR structures is the same, Protein Science 31, e4373 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Smith W. W., Ho P.-Y., and O’Hern C. S., Calibrated langevin-dynamics simulations of intrinsically disordered proteins, Physical Review E 90, 042709 (2014). [DOI] [PubMed] [Google Scholar]
- [49].Grigas A. T., Fisher A., Shattuck M. D., and O’Hern C. S., Connecting polymer collapse and the onset of jamming, Physical Review E 109, 034406 (2024). [DOI] [PubMed] [Google Scholar]
- [50].VanderWerf K., Boromand A., Shattuck M. D., and O’Hern C. S., Pressure dependent shear response of jammed packings of frictionless spherical particles, Physical Review Letters 124, 038004 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Silbert L. E., Liu A. J., and Nagel S. R., Vibrations and diverging length scales near the unjamming transition, Physical Review Letters 95, 098301 (2005). [DOI] [PubMed] [Google Scholar]
- [52].Wyart M., Silbert L. E., Nagel S. R., and Witten T. A., Effects of compression on the vibrational modes of marginally jammed solids, Physical Review E 72, 051306 (2005). [DOI] [PubMed] [Google Scholar]
- [53].Henkes S., Brito C., and Dauchot O., Extracting vibrational modes from fluctuations: A pedagogical discussion, Soft Matter 8, 6092 (2012). [Google Scholar]
- [54].Bertrand T., Schreck C. F., O’Hern C. S., and Shattuck M. D., Hypocoordinated solids in particulate media, Physical Review E 89, 062203 (2014). [DOI] [PubMed] [Google Scholar]
- [55].Liu A. J. and Nagel S. R., The jamming transition and the marginally jammed solid, Annual Review of Condensed Matter Physics 1, 347 (2010). [Google Scholar]
- [56].Arceri F. and Corwin E. I., Vibrational properties of hard and soft spheres are unified at jamming, Physical Review Letters 124, 238002 (2020). [DOI] [PubMed] [Google Scholar]
- [57].Lindorff-Larsen K., Piana S., Dror R. O., and Shaw D. E., How fast-folding proteins fold, Science 334, 517 (2011). [DOI] [PubMed] [Google Scholar]
- [58].Best R. B. and Hummer G., Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides, The Journal of Physical Chemistry B 113, 9004 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Abraham M. J., Murtola T., Schulz R., Páll S., Smith J. C., Hess B., and Lindahl E., GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX 1–2, 19 (2015). [Google Scholar]
- [60].Jorgensen W. L., Quantum and statistical mechanical studies of liquids. 10. Transferable intermolecular potential functions for water, alcohols, and ethers. application to liquid water, Journal of the American Chemical Society 103, 335 (1981). [Google Scholar]
- [61].Mark P. and Nilsson L., Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K, The Journal of Physical Chemistry A 105, 9954 (2001). [Google Scholar]
- [62].Bussi G., Donadio D., and Parrinello M., Canonical sampling through velocity rescaling, The Journal of Chemical Physics 126, 014101 (2007). [DOI] [PubMed] [Google Scholar]
- [63].Xu J., Baase W. A., Baldwin E., and Matthews B. W., The response of T4 lysozyme to large-to-small substitutions within the core and its relation to the hydrophobic effect, Protein Science 7, 158 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Liu R., Baase W. A., and Matthews B. W., The introduction of strain and its effects on the structure and stability of T4 lysozyme, Journal of Molecular Biology 295, 127 (2000). [DOI] [PubMed] [Google Scholar]
- [65].Baase W. A., Liu L., Tronrud D. E., and Matthews B. W., Lessons from the lysozyme of phage T4, Protein Science 19, 631 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Chen J., Sawyer N., and Regan L., Protein–protein interactions: General trends in the relationship between binding affinity and interfacial buried surface area, Protein Science 22, 510 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Davis C. M., Gruebele M., and Sukenik S., How does solvation in the cell affect protein folding and binding?, Current Opinion in Structural Biology 48, 23 (2018). [DOI] [PubMed] [Google Scholar]
- [68].Hu X., Hong L., Dean Smith M., Neusius T., Cheng X., and Smith J. C., The dynamics of single protein molecules is non-equilibrium and self-similar over thirteen decades in time, Nature Physics 12, 171 (2016). [Google Scholar]
- [69].Li J., Xie J., Godec A., Weninger K. R., Liu C., Smith J. C., and Hong L., Non-ergodicity of a globular protein extending beyond its functional timescale, Chem. Sci. 13, 9668 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Liao Q., Berthier L., Zhou H.-J., and Xu N., Dynamic Gardner cross-over in a simple glass, Proceedings of the National Academy of Sciences 120, e2218218120 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Dorbath E., Gulzar A., and Stock G., Log-periodic oscillations as real-time signatures of hierarchical dynamics in proteins, The Journal of Chemical Physics 160, 074103 (2024). [DOI] [PubMed] [Google Scholar]