Significance
Predicting whether two proteins interact physically has become a problem of major interest. Despite recent progress using deep learning approaches to predict PPIs, these methods are still not computationally efficient enough to interrogate the vast number of possible PPIs. We have previously developed the PrePPI algorithm which uses structural information and other sources of evidence to predict whether two proteins interact for most of the human proteome. However, PrePPI does not incorporate evolutionary signals embedded in multiple sequence alignments. The ZEPPI algorithm addresses this problem for defined interfaces and is computationally efficient enough to be applied to millions of putative PPIs. ZEPPI can be used alone, or in conjunction with other methods, to evaluate any structural model of a complex.
Keywords: protein-protein interactions, protein structure, coevolution, protein complex prediction
Abstract
We introduce ZEPPI (Z-score Evaluation of Protein–Protein Interfaces), a framework to evaluate structural models of a complex based on sequence coevolution and conservation involving residues in protein–protein interfaces. The ZEPPI score is calculated by comparing metrics for an interface to those obtained from randomly chosen residues. Since contacting residues are defined by the structural model, this obviates the need to account for indirect interactions. Further, although ZEPPI relies on species-paired multiple sequence alignments, its focus on interfacial residues allows it to leverage quite shallow alignments. ZEPPI can be implemented on a proteome-wide scale and is applied here to millions of structural models of dimeric complexes in the Escherichia coli and human interactomes found in the PrePPI database. PrePPI’s scoring function is based primarily on the evaluation of protein–protein interfaces, and ZEPPI adds a new feature to this analysis through the incorporation of evolutionary information. ZEPPI performance is evaluated through applications to experimentally determined complexes and to decoys from the CASP-CAPRI experiment. As we discuss, the standard CAPRI scores used to evaluate docking models are based on model quality and not on the ability to give yes/no answers as to whether two proteins interact. ZEPPI is able to detect weak signals from PPI models that the CAPRI scores define as incorrect and, similarly, to identify potential PPIs defined as low confidence by the current PrePPI scoring function. A number of examples that illustrate how the combination of PrePPI and ZEPPI can yield functional hypotheses are provided.
The past decade has seen continuing developments in the prediction of protein–protein interactions (PPIs). One can trace these advances to the use of amino acid coevolution to predict interresidue contacts (1, 2). These methods have been used to predict protein structures (3–5) and, more recently, to predict interaction partners and interfacial residues involved in PPIs (6–9). The underlying premise is that functional interactions between two residues in an interface will result in their coevolution, which should be reflected in species-paired multiple sequence alignments (pMSAs) of putative orthologs and detectable through mutual information (MI)–based metrics between the two corresponding positions in the alignment. Since MI measures the mutual dependence between two variables, a complication is that the correlation between two residue positions i and j, i.e., two columns in the MSA, may result from an indirect coupling of i and j through their interaction with a third residue k. To solve this problem, methods such as direct coupling analysis (DCA) (3, 10), sparse inverse covariance (PSICOV) (11), EVcouplings (6, 8), and Gremlin (4, 7) have been developed. However, these methods rely on the availability of deep multiple sequence alignments (MSAs) and thus have almost exclusively been applied to bacterial systems. In contrast, as we demonstrate below, ZEPPI can be applied on a genome-wide scale to eukaryotic proteomes with relatively shallow MSAs.
AlphaFold-Multimer (12) (AFM) has fundamentally changed the landscape of the prediction of structures of multiprotein complexes. There have been continuing improvements in AFM-based methods (13, 14) as is evident from the substantial progress in the recent CASP-CAPRI (15, 16) experiment (17). An underlying problem for MSA-based methods is that for optimal performance on a heterodimeric pair, it is generally necessary to carry out a species-based matching of the two query sequences which limits application to eukaryotic organisms due to the relatively limited number of sequences available for a paired MSA. Recently, RoseTTAFold/AlphaFold was used to screen 4.3 million potential yeast PPIs among proteins comprising 65% of the proteome with paired alignments containing >200 sequences and protein pairs with <1,500 amino acids (18). This was enabled in part by the large number of fungal genomes that contributed to the yeast MSAs. However, applying deep learning to predict whether and how two proteins interact for entire eukaryotic proteomes, for example, 20M and 200M pairwise combinations of yeast and human proteins, remains computationally challenging.
Docking-based methods predict models of protein dimers based on the structures of the constituent monomers (19–22) but have not been applied on a proteome-wide scale or to predict whether two proteins interact. Template-based modeling (23) is an alternate approach where the structures of individual proteins are superimposed on structurally similar proteins that appear in a complex present in the PDB (24). In a series of papers, we reported the PrePPI (Predicting Protein–Protein Interactions) algorithm and database (25–27) which rely on template-based modeling and, through a highly efficient scoring function, leverage structural information on a truly proteome-wide scale. The most recent version of PrePPI which uses AlphaFold models for monomers, effectively screens the ~200 million possible pairwise combinations of 20K human proteins which, in practice, amounts to billions of possible interactions among full-length proteins and individual protein domains. Based on a false positive rate (FPR) of < 0.005, 1.3 million high confidence predictions appear in the PrePPI-AF online database with 370K predicted direct binary interactions (27).
Here, we use PrePPI-predicted complexes in the Escherichia coli and human proteomes (27) to examine the extent to which simple evolution-based metrics are informative even in those cases for which the paired MSA depth is shallow. Once an interface is defined, we expect that MI calculations alone would be sufficient, even for eukaryotic proteins, as the deep pMSAs required for DCA would no longer be necessary. Our method, ZEPPI (for Z-score Evaluation of Protein–Protein Interfaces), uses paired MSAs to determine coevolutionary information across interfaces but also leverages sequence conservation which provides an additional signal as to the reliability of a predicted interface. An essential feature of ZEPPI is the comparison of evolutionary metrics derived from pMSA positions corresponding to residues in predicted interfaces versus positions corresponding to randomly chosen residues.
Our focus on interfacial residues leads to a significant speedup in the evaluation of dimeric complexes that allows us to apply ZEPPI on a proteome-wide scale. Similarly, our finding that DCA is not needed for evaluating heterodimeric complexes effectively removes the need for deep pMSAs. As shown below ZEPPI is extremely effective in distinguishing correct from incorrect protein–protein interfaces as indicated by tests on PDB structures. Tests on a CASP-CAPRI benchmark set (15, 27, 28) indicate that ZEPPI is able to discriminate interfaces from acceptable versus incorrect decoys as defined by CAPRI criteria (15). Most notably, there is a strong inverse correlation between ZEPPI scores and FPRs for PrePPI predictions thus providing strong support for the reliability of ZEPPI’s efficacy in determining whether a PPI occurs for proteome-wide interactomes. We use a combined PrePPI/ZEPPI screen to identify a large number of high-confidence interactions that do not appear in any database. A number of such examples are discussed below.
Results
ZEPPI Overview.
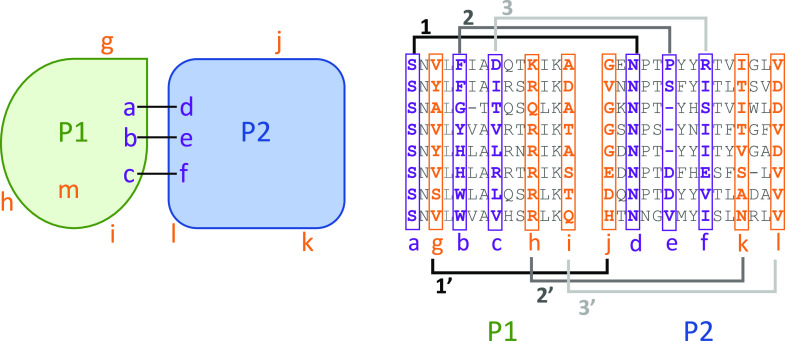
Fig. 1 summarizes the ZEPPI algorithm. The procedure starts with a structural model of a complex between proteins P1 and P2 (left panel) and a pMSA (right panel). Contacting interfacial residues are identified; in this case, P1-a contacts P2-d, P1-b contacts P2-e, and P1-c contacts P2-f. A pMSA is created and used to calculate the following metrics for each of the four interfacial contacts as described in Methods: mutual information (MI), conservation (Con), direct coupling (DCA), and the metric of each after applying the average product correction (APC) (29). The resulting values are then averaged over the interfacial contacts yielding six metrics. In addition, the highest single-contact score for each metric, denoted as “top” is retained, resulting in a total of twelve metrics that characterize a predicted interface. Columns in the pMSA corresponding to contacting interfacial residues are colored in purple. For example, the residues in columns P1-a and P2-d are almost completely conserved and would give a strong Con signal but a weak MI signal. Columns P1-b and P2-e show no obvious Con or MI signal, but P1-c and P2-f show a clear MI signal.
Fig. 1.
Schematic of the ZEPPI algorithm. Two proteins, P1 and P2, form a complex with three interfacial contacts between residues a and d, b and e, as well as c and f (purple; Left), respectively labeled as 1, 2, and 3 in the Right panel. Various evolutionary metrics (see text) are calculated from the corresponding columns in the pMSA (purple; Right). “Fake interfacial contacts” are generated between randomly chosen surface residues outside the interface (orange), shown by 1′, 2′, and 3′ on the Right panel. When the number of surface residues outside the interface does not exceed the number of interfacial residues, buried residues (m) are considered as well. The same metrics are calculated from the corresponding columns in the pMSA (orange; right) for each of 100 samples.
The next step is to carry out the same procedure for a set of randomly chosen surface residues that are not in the interface. These are denoted in orange and are treated as if they were interfacial so that, for example, the metrics calculated between columns P1-a and P2-d are replaced by those between P1-g and P2-j. Each contact in the real interface is replaced in this way by fake contacts as indicated in the figure. Note that when the number of surface residues outside the interface is less than the number of residues in the interface, buried residues, e.g. P1-m, are included in sampling. This occurs for <10% of PPIs evaluated. A hundred fake interfaces with corresponding values for the twelve metrics are generated in this way. A Z-score for the predicted interface is then calculated for each of the metrics based on the values for the real interface as compared to the values obtained for the 100 fake interfaces.
Testing ZEPPI on PDB Complexes.
Dimeric PDB complexes were collected from the first bioassembly, as defined in the PDB structure file, for both bacterial and human complexes (24). We tested performance with both prokaryotic and eukaryotic proteomes which, overall, have very different pMSA depths. As described in Methods, complexes were selected based on resolution, chain length, and the requirement that the proteins in the complex are from the same species. In total, 279 bacterial heterodimers, 247 human heterodimers, 3,976 bacterial homodimers, and 977 human homodimers, for a total of 5,479 dimer structures, were obtained. For each complex, we calculated the 12 metrics (SI Appendix).
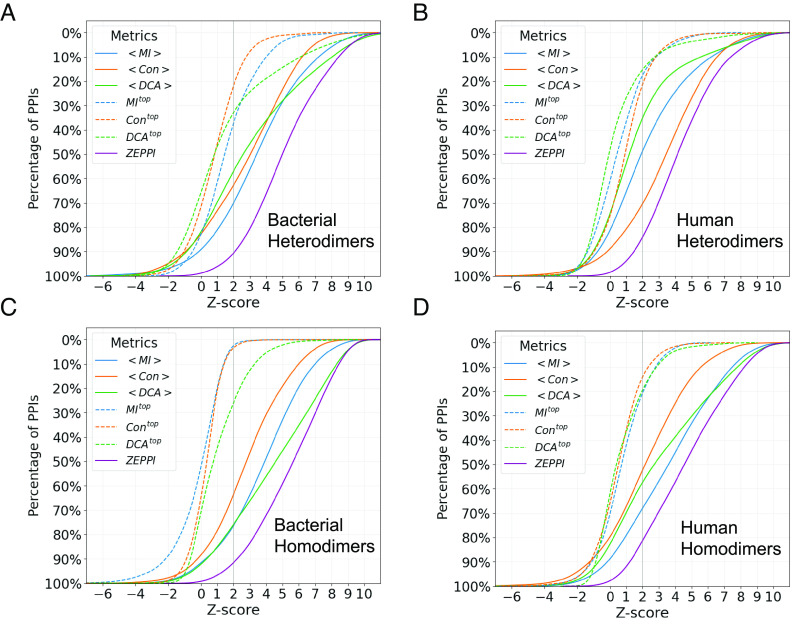
Fig. 2 displays plots of the fraction of PPIs with a Z-score above the threshold denoted along the x-axis for different metrics. The curves are derived from those in SI Appendix, Figs. S1 and S2 which plot, for each of the twelve metrics, the fraction of PPIs with a Z-score above the threshold denoted along the x axis. For example, in SI Appendix, Fig. S1A, at a Z-score of 2, the metric for average APC-corrected MI, <MIAPC>, by itself recovers 60% of bacterial heterodimers, whereas integrating all metrics (Fig. 2, purple curve) recovers 80%. Overall, it is evident that, for heterodimers, the APC correction improves performance relative to raw (uncorrected) metrics for MI and DCA but not for Con (SI Appendix, Fig. S1 A and B). In contrast, for homodimers, the APC-corrected Con metric is more effective than the corresponding raw metric (SI Appendix, Fig. S1 C and D). Further, choosing the top value for each metric is less effective than choosing the value averaged over the entire interface (dashed curves versus solid curves, SI Appendix, Figs. S1 and S2). This is not unexpected since all contacts identified in PDB complexes are presumed to be correct and likely contribute to the total score. However, this is not necessarily the case with docked and predicted complexes as depicted below.
Fig. 2.
Percentage of PDB PPIs as a function of Z-score is shown for bacterial heterodimers (A), human heterodimers (B), bacterial homodimers (C), and human homodimers (D). Colors and line types in the legend indicate curves for different metrics each of which corresponds to the maximum of the raw and APC values for a given PPI. The mean and top metric of all interface contacts are denoted as <>, and top, respectively. The ZEPPI score for a given PPI is the largest Z-score among all metrics (purple). See SI Appendix for details.
The plots in Fig. 2 are similar to those in SI Appendix, Figs. S1 and S2 but, for a given metric, the higher value of raw versus APC-corrected metric is chosen for each complex. The ZEPPI curve (purple) is generated by choosing the metric with the highest score for each complex. For the remainder of the paper, the ZEPPI score for a given complex corresponds to the maximum Z-scores from among the complex’s 12 metrics. For bacterial heterodimers (Fig. 2A), MI is the best-performing metric although DCA is slightly better at high Z-scores and Con performance is similar to both MI and DCA. In contrast, Con is clearly the most important metric for human heterodimers (Fig. 2B). We suggest that the difference in performance for humans and bacteria is the greater coevolutionary divergence underlying bacterial pMSAs as opposed to eukaryotic pMSAs. Of note, the overall ZEPPI performance is very similar for bacterial and human heterodimers with, in both cases, about 80% of the complexes having a ZEPPI score >2 and 65% having a score >4.
For homodimers, the two coevolutionary metrics perform the best with DCA performing better than MI at high Z-scores for bacteria (Fig. 2C) while MI is, overall, the best performer for humans (Fig. 2D). The improved performance of coevolution for homodimers is likely due to the fact that pMSA sequence depth for homodimeric complexes is much larger (reflecting two copies of a single protein) than for heterodimers. It is interesting that in all cases, except for bacterial homodimers, MI performance is comparable to or better than that of DCA, reflecting the existence of a known interface. But even in this case, the differences manifest only at high Z-scores. Most importantly, since DCA contributes very little for human complexes and, given its need for deep pMSAs and the extra computer time required in its use, we use DCA for only homodimers in the work below. Of note, Bitbol et al. have reported that, using an interative pairing algorithm, MI alone performs at least as well as DCA in the sequence-based identification of protein–protein interaction partners (30).
Effect of pMSA depth.
Fig. 3 plots ZEPPI score (red dots) versus the sequence depth of the pMSAs (NMSA). The histogram (green) displays the number of interfaces as a function of NMSA. On average, the ZEPPI score increases with increasing pMSA depth although there are examples where ZEPPI scores >2 are obtained for very shallow pMSA depths (NMSA < 10). Most of these result from significant sequence conservation of interfacial residues but there are cases where even MI yields a significant signal. Although these few cases may well be statistical anomalies, there are many high-scoring interfaces of relatively shallow depths with values of NMSA in the range of 10 to 100. Note that NMSA here is a raw number that does not include the low-weighting of redundant sequences. It is generally accepted that, for most applications, NMSA should be at least the sum of the number of residues in each protein (7, 31–33) and is typically taken to be greater than 500 or 1,000 for predictions of protein–protein interactions (7, 32). Our results highlight the success of ZEPPI in leveraging even shallow pMSAs, made possible by the evaluation of interfacial residues in experimentally determined structures.
Fig. 3.
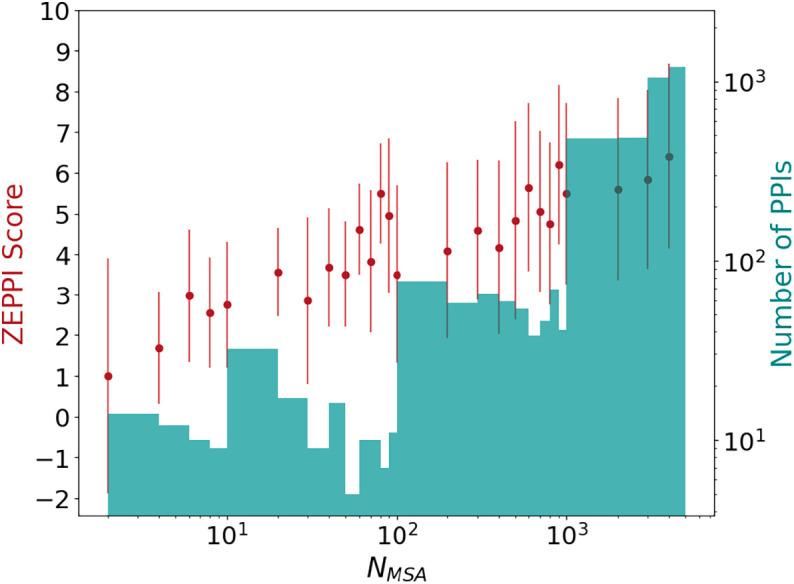
Effect of MSA depth on ZEPPI score for PDB dimers. The ZEPPI score is plotted against pMSA depth, NMSA, where each red dot and error bar correspond to the average and SD of the ZEPPI score for the PPIs in a given bin of NMSA values. A histogram of the numbers of PPIs in each bin is shown in green. Data are plotted on a log scale for NMSA and the number of PPIs. NMSA is the depth of the paired MSAs after checking the coverage of surface residues (Methods).
Test on CAPRI Benchmark Decoys.
To place ZEPPI in the context of other interface prediction methods, we tested the performance of ZEPPI in differentiating good versus poor models in a widely used decoy set, score_set (28), which was derived from targets from the CASP-CAPRI experiment. The score_set contains docking models predicted by 47 participating groups for proteins from bacteria, yeast, vertebrates, and of artificial design. We considered 13 widely studied targets which, overall, have 18,538 corresponding decoys: 10% represent docking predictions of acceptable, medium, or high quality (15, 28). We combine these three categories and annotate them as “acceptable+,” whereas the remaining 90% are annotated as “incorrect”. Even though two of the targets, T53 and T54, contain designed proteins, they both have pMSAs with NMSA values of 2,110 and 198, respectively. SI Appendix, Table S1 reports pMSA depth for all targets along with the number of acceptable+ and incorrect decoys, and the area under the ROC curve (AUROC) for each target (34). In contrast to the results with PDB complexes, the “top” metrics contribute to the ZEPPI score to a greater extent likely because the interfaces for acceptable+ models have inaccuracies. It is clear from the table that shallow pMSA depths (<100) can produce good AUROCs, particularly for T47 which has an AUROC of 0.93 and NMSA of only 24.
SI Appendix, Fig. S3 plots the percentage of all models that have a given ZEPPI score in each of the four categories across targets (SI Appendix, Fig. S3). There is a clear distinction between acceptable+ and incorrect decoys with essentially 90% of the acceptable+ models having Z-score >2 and about half with Z-score >4. Nevertheless, some incorrect decoys do have high Z-scores and some correct decoys have low Z-scores.
Table 1 compares ZEPPI performance across targets to that of other methods (34–39), most of which are based on deep learning and have been trained on docking decoy sets. The data for other methods were taken from figure S9 of Réau et al. (34). ZEPPI, despite not involving training, is essentially tied as the top performer as measured by AUROC and is the best performer based on top 100 Success Rate. However, ZEPPI is outperformed by a number of other methods as measured by top 1 and top 5 Success Rates. Of note, Success Rate measures the ability to identify the best model among a group of presumably other good models. As such it is a meaningful basis for CASP-CAPRI rankings since it evaluates success in identifying the most accurate model. In contrast, a ROC curve measures success in distinguishing acceptable+ models from incorrect ones even if the acceptable model is not particularly accurate. Since the main application we envision for ZEPPI is not to choose among models but, rather, to distinguish among pairs of proteins that interact and those that do not, ROC curve performance may serve as a better indicator of success in this application. Nevertheless, that ZEPPI performs comparably to other methods on CASP-CAPRI decoys suggests that it may also be useful in the scoring of docking models, especially in combination with other methods (40).
Table 1.
Performance of different scoring methods on CAPRI decoys
| Success rates | ||||
|---|---|---|---|---|
| Method | AUROC | Top1 | Top5 | Top100 |
| ZEPPI | 0.72 ± 0.13 | 2/13 | 2/13 | 12/13 |
| HADDOCK | 0.57 ± 0.23 | 2/13 | 3/13 | 9/13 |
| iScore | 0.68 ± 0.21 | 5/13 | 6/13 | 9/13 |
| DeepRank | 0.64 ± 0.19 | 1/13 | 1/13 | 9/13 |
| DOVE | 0.56 ± 0.14 | 1/13 | 2/13 | 10/13 |
| GNN-DOVE | 0.63 ± 0.16 | 1/13 | 6/13 | 8/13 |
| DeepRank-GNN | 0.72 ± 0.19 | 1/13 | 5/13 | 10/13 |
The AUROC in this table is averaged over values for each of 13 targets. Success Rates of Top N indicates the number of targets where there are acceptable or better predictions in the Top N predictions.
It is important to recall in this regard that all targets used in CASP-CAPRI actually form complexes so that, if CASP-CAPRI models are evaluated based on their ability to provide yes/no answers as to whether two proteins form a complex, the experimental answer would always be yes. The CAPRI criteria (15, 28) or the later defined continuous score, dockQ (41) are based in part on the fraction of interfacial contacts and RMSD of the models relative to the native complex. They do not directly account for the number of correctly predicted interfacial residues. As a result, even if many residues on both sides of an interface are correctly predicted, if the contacts are wrong due, for example, to an incorrect orientation between two proteins in a complex, the prediction will be scored as incorrect. This is reasonable for the evaluation of CAPRI models since better models will have more accurate orientations, but the signal for a PPI based on correct prediction of interfacial residues will be lost. Thus, even models deemed to be incorrect may contain evidence for an interaction between two proteins (42).
SI Appendix, Fig. S4 reports the distribution of the fraction of interfacial contacts (SI Appendix, Fig. S4A) and interfacial residues for acceptable+ and incorrect decoys (SI Appendix, Fig. S4B). As expected, the fraction of interfacial contacts maps well to the two categories but the fraction of interfacial residues does not. Rather, we find, in agreement with previous evidence (42) that many incorrect models have a significant number of correctly predicted interfacial residues. This likely accounts for the fact that many incorrect models have high ZEPPI scores (SI Appendix, Fig. S3) which can arise from MI and conservation signals between residues positions not in direct contact in the native structure. These findings then highlight ZEPPI’s ability to provide evidence for an interaction even based on models that do not score well in CAPRI.
Evaluating PrePPI Models with ZEPPI.
In recent work, we reported calculations from our PrePPI algorithm for the human and E. coli interactomes represented by models for the full-length sequences and constituent domains (43). A structural modeling score, SM, was trained on the HINT high-quality literature-curated (HINT-HQ-LC) dataset for human PPIs. HINT-HQ-LC datasets are designed to contain high-confidence binary interactions (44). ROC curves were reported for testing the PrePPI human and E. coli models on the human and E. coli HINT-HQ-LC datasets using 10-fold cross-validation. This yielded AUROC values of 0.83 and 0.88, respectively, thus, attesting to the overall high quality of the predictions.
SI Appendix, Fig. S5 displays violin plots for the range of ZEPPI scores for PrePPI predictions in different bins of FPR (SI Appendix, Fig. S5). For PrePPI predictions of higher confidence (lower FPR), the median ZEPPI score is larger. These results provide a strong consistency check in that better structural models as defined by PrePPI produce stronger evolutionary signals as measured by ZEPPI. For bacterial heterodimers (SI Appendix, Fig. S5A), at FPR < 10−4, the percentage of predicted PPIs with a ZEPPI score >2, 3, 4 is 94%, 81%, and 67%, respectively. The comparable numbers for PDB structures (see discussion of Fig. 2) are 95%, 85%, and 71% suggesting that PrePPI’s highest confidence predictions have ZEPPI scores close to those of PDB structures. Performance deteriorates as FPR increases but there are still many good ZEPPI scores for higher FPR values. The distributions in SI Appendix, Fig. S5 demonstrate that high and low ZEPPI scores are obtained in all FPR bins suggesting that the ZEPPI score can be used as an additional evidence source for prioritizing PrePPI models SI Appendix, Fig. S5.
Binding specificity among homologs.
An issue with PrePPI and other PPI prediction methods is that they encounter difficulties in predicting binding specificity when closely related homologs are involved. However, the evolutionary signals in ZEPPI can be used to address this issue. As shown in Table 2, PrePPI models filtered by ZEPPI score are enriched for observed PPIs. For example, PrePPI predictions with FPR ≤0.01 are almost two times as likely to appear in the experimental PPI databases (DBs, as defined below) when filtered by a ZEPPI score ≥4. A striking example is provided by interactions of the small GTPase, K-Ras, with other GTPases and signaling proteins. Based on the X-ray complex for H-Ras/Grb14 (45) (PDB ID: 4k81), PrePPI makes predictions (FPR ≤ 0.005) for K-Ras interactions with Grb7, Grb11, and Grb14. However, ZEPPI is significant (Z = 3.5) for only KRAS-Grb7 (46), the only partner for which there is evidence of an interaction (in databases as defined above). This is a case where the structural models are too similar to be distinguished from one another by PrePPI scoring but where there is a clear evolutionary signal that ZEPPI detects among interfacial residues.
Table 2.
Number of proteins, PPIs, and novel predictions for different combinations of PrePPI FPRs and ZEPPI-scores for E. coli
| PrePPI FPR (≤) | 0.05 | 0.01 | 0.001 | 0.0001 | ||||
|---|---|---|---|---|---|---|---|---|
| ZEPPI Score (≥) | – | 4 | – | 4 | – | 4 | – | 4 |
| # PPIs | 303,212 | 38,062 | 71,151 | 17,098 | 10,336 | 6,002 | 3,151 | 2,355 |
| # Proteins | 3,941 | 3,671 | 3,557 | 3,030 | 2,464 | 1,993 | 1,605 | 1,350 |
| # PPIs in DBs | 38,916 | 9,069 | 14,580 | 6,090 | 5,289 | 3,528 | 2,386 | 1,837 |
| # Novel PPIs | 264,296 | 28,993 | 56,571 | 11,008 | 5,047 | 2,474 | 765 | 518 |
The E. coli Structural Interactome.
The E. coli K12 proteome contains 4,403 proteins with 97M possible protein–protein pairwise combinations. Table 2 lists the number of E. coli PPIs (out of the 5.4 million for which a model can be built) and the number of proteins that comprise these interactions for different FPRs and ZEPPI scores. At FPR < 0.01, PrePPI predicts 71K PPIs involving 3.5K proteins, and these numbers are significantly decreased when more stringent PrePPI FPRs and ZEPPI scores are applied. 2.3K PPIs satisfy the highly restrictive criteria of FPR < 0.0001 and ZEPPI score > 4.
Table 2 also lists the overlap of ZEPPI-filtered PrePPI predictions with PPIs annotated in experimental databases (DBs). Any PPI that appears in the listed databases (Methods) is considered whether or not the interaction is likely to be direct or indirect so as to determine the number of truly novel PPIs that our methods predict. At the most stringent end of the scale (FPR < 0.0001, ZEPPI score > 4) 518 novel predictions are made. On the other hand, as an example, there are 21,000 novel predictions made for FPR < 0.05 and ZEPPI score > 4 suggesting that using ZEPPI may facilitate the identification of meaningful predictions that might be missed based on PrePPI alone.
The Human Structural Interactome.
The human proteome contains 20,596 proteins with 212M possible protein–protein combinations. Table 3 presents results for the PrePPI-predicted human interactome that parallel those for E. coli (Table 2). In contrast to PrePPI results reported recently, which are based on both structural and nonstructural evidence, Table 3 reports data for structural evidence only, i.e., domain–domain structure-based predictions. A total of 1M PPIs are predicted with an FPR < 0.01 which is an overly tolerant criterion. This number is reduced to only 101K for FPR < 0.001 and only 11K for FPR < 0.0001 (43). ZEPPI provides an alternate filter; for example, ZEPPI = 4 reduces the number of predictions to 184K, 26K, and 7K for FPR < 0.01, 0.001, and 0.0001, respectively.
Table 3.
Number of proteins, PPIs, and novel predictions for different combinations of PrePPI FPRs and ZEPPI-scores for humans
| PrePPI FPR (≤) | 0.05 | 0.01 | 0.001 | 0.0001 | ||||
|---|---|---|---|---|---|---|---|---|
| ZEPPI Score (≥) | – | 4 | – | 4 | – | 4 | – | 4 |
| # PPIs | 6,209,528 | 1,002,052 | 1,271,323 | 228,321 | 130,447 | 30,572 | 11,896 | 7,392 |
| # Proteins | 16,780 | 15,987 | 13,903 | 11,781 | 6,358 | 5,250 | 2,882 | 2,441 |
| # PPIs in DBs | 463,971 | 130,426 | 148,461 | 54,131 | 20,605 | 10,762 | 6,293 | 4,409 |
| # Novel PPIs | 5,745,557 | 871,626 | 1,122,862 | 174,190 | 109,842 | 19,810 | 5,603 | 2,983 |
As is the case for E. coli (Table 2), most PrePPI predictions do not appear in any experimental database nor in STRING, (47) which includes many PPIs inferred from sequence relationships (collectively, “PPIs in DBs”). Although PrePPI provides structural models for many experimentally determined interactions, its value is also in hypothesis generation as many of its predictions are novel. At the highest confidence level (FPR < 0.0001, ZEPPI > 4), there are 2,713 novel human PPI predictions. ZEPPI can be used to discriminate predictions at different PrePPI confidence levels, as indicated in the following examples.
Biological Applications of ZEPPI/PrePPI.
In this section, we highlight examples where ZEPPI can be used to identify PPIs whose PrePPI FPRs are in the range where they would be defined as low-confidence predictions, thus revealing ZEPPI’s ability to extract signal from otherwise uncertain PrePPI predictions.
A possible role for K-Ras in synaptic signaling.
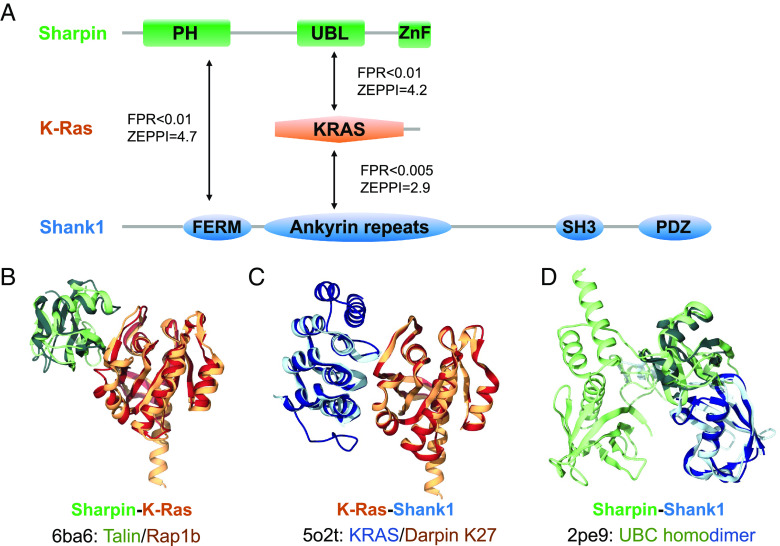
As shown in Fig. 4A, PrePPI predicts interactions among K-Ras, Sharpin (the Shank-interacting protein-like 1), and Shank1 (the SH3 and multiple ankyrin repeat domains protein 1). Structural predictions are shown for 1) the Sharpin ubiquitin-like (UBL) domain and K-Ras (Fig. 4B); 2) K-Ras and Sharpin ankyrin repeats (Fig. 4C); and 3) Sharpin PH domain and Shank1 FERM domain (Fig. 4D). Sharpin has previously been shown to interact with Shank1 and both colocalize at synaptic sites in mature neurons (48). Altogether, our predictions (Fig. 4) and the related experimental evidence suggest a role for K-Ras in synaptic signaling. Indeed, a recent study (49) found that mutant K-Ras increases synaptic transmission in inhibitory neurons, while it promotes the cell death of excitatory neurons.
Fig. 4.
High-confidence PPIs in synaptic signaling. (A) PrePPI and ZEPPI predict interactions among Sharpin (the Shank-interacting protein-like 1, colored in green), the small GTPase K-Ras (orange), and Shank1 (the SH3 and multiple ankyrin repeat domains protein 1, colored in blue). Solid lines between protein domains denote the domains involved in the PPIs which are depicted as backbone ribbons. In B–D, the darker colored ribbons represent the chains from the PDB PPI template and are defined below the query protein names: (B) Sharpin-K-Ras; (C) K-Ras-Shank1; and (D) Sharpin-Shank1. In all but two cases (KRAS-6ba6:B and KRAS-5o2t:A), the pairwise sequence identities between the queries and the respective template chains are less than 25%.
Secreted peptide fragments in the pancreas.
Chymotrypsin-like elastase family member 1 (CELA1) is a secreted elastase with high pancreatic expression. Recent studies have implicated peptides produced from the amyloid precursor protein (APP) in metabolic diseases (50, 51). In particular, human pancreatic islet cells process APP to release secreted fragments of APP (sAPP). The CELA1-APP model (SI Appendix, Fig. S6) suggests a pancreatic-specific mechanism for the production of sAPP.
Role of Cystatins in tumorigenesis.
Cystatins are inhibitors of cysteine peptidases. In tumor development and cancer progression, the balance between cystatins and cysteine peptidases may be disrupted (52). Cathepsin F (CTSF) was observed to have an antitumor effect in lung adenocarcinoma (LUAD) (53) whereas Cystatin-SN (CST1) promotes the epithelial–mesenchymal transition in LUAD cells (54). The CST1-CTSF model (SI Appendix, Fig. S7) suggests that the mechanism of action of CST1, which is highly expressed in LUAD (54), may be to inhibit the antitumorigenic activity of CTSF.
Discussion
Here, we have introduced ZEPPI, a method that uses species-paired MSAs as a basis for scoring predicted models of protein–protein interfaces. ZEPPI’s central feature involves the analysis of evolutionary information involving only contacting residues in a 3D structural model. The relatively limited number of residues to be analyzed results in a major reduction in computer time required to evaluate a model. Moreover, ZEPPI extracts signals from shallow pMSAs enabled in part by its reliance on sequence conservation as well as mutual information. Deep learning methods implicitly leverage both sources of information but since most analyze entire sequences they are more computationally intensive.
In addition to validation on crystal structures, ZEPPI was tested on thirteen CASP-CAPRI targets (28) and its performance was found to be comparable to or better than other interface evaluation approaches (34). We note that evolutionary information has been used for some time in the evaluation of docking models (55–57) but generally in combination with other evidence sources, such as statistical propensities for surface residues to be in protein interfaces. ZEPPI differs from these approaches in its combined use of mutual information and conservation within interfaces and, especially, in its method of calculating Z-scores through the comparison of metrics for positions in the pMSAs corresponding to interfacial residues versus positions in the pMSAs corresponding to randomly chosen surface residues outside an interface. Our results on both PDB and CASP-CAPRI complexes demonstrate that ZEPPI provides a computationally efficient and effective measure of interface quality that can easily be combined with other sources of evidence.
To demonstrate its computational efficiency, we have applied ZEPPI to 5.4 million E. coli PPIs (300,000 with FPR < 0.05 shown in Table 2) and to a total of 6.2 million (FPR < 0.05) human PPIs predicted by PrePPI (27) (Table 3). As suggested by the results in Tables 2 and 3, filtering PrePPI predictions by ZEPPI scores has the potential to increase the reliability of high confidence predictions while identifying low-confidence PrePPI predictions that are worthy of further consideration. An immediate application of ZEPPI is its integration into the PrePPI algorithm with the goal of combining evolutionary signals with a method based entirely on 3D structure. The integration should prove to be quite valuable, especially in applications to the human proteome and other eukaryotic organisms where available sequence information supports alignments of relatively shallow depth.
The vignettes provided above indicate the ability of ZEPPI to aid in the identification of potentially important functional hypotheses. In this regard, PrePPI/ZEPPI can be viewed as a hypothesis-generating method that could be followed up with slower structure prediction methods ranging from docking to AF-multimer to methods based on their combination as evidenced from the most recent CASP-CAPRI experiment (17). Of course, alternatively, ZEPPI can be used independent of PrePPI to evaluate any predicted model of a complex such as generated by AlphaFold-Multimer (12) or AlphaFoldComplex (14).
The combination of PrePPI with ZEPPI suggests a general approach to the proteome-wide prediction of whether and how two proteins interact. It is important to note that AF-related methods are still too slow to provide yes/no predictions on a proteome-wide scale; for humans, this would require evaluation 200 million possible interactions and, as we have done with PrePPI, billions of interactions between full-length proteins and individual domains, and allowing for more than one model per domain. In contrast, Burke et al. (58) have built AF-based models for only 65,000 human PPIs that have been identified with high-throughput methods. Gao et al. (14) have estimated that it would take on the order of 1 million processor hours to run their computationally efficient AlphaFoldComplex algorithm on the entire E. coli proteome (~9 million putative PPIs) while Humphreys et al. (18) arrived at a similar estimate for the time it would take to run AF2 on the 4.3 million paired MSAs they assembled for yeast. Thus, at this stage, PrePPI/ZEPPI appears the only viable option for structure-based proteome-wide studies. These can then be used to provide interactome-wide yes/no answers along with 3D models which, when of interest, can be studied with slower but increasingly accurate deep learning methods.
Methods
Selecting Bacterial and Human PDB Dimer Structures.
Taxonomy and UniProtKB summary files for all PDB chains were downloaded from the Structure Integration with Function, Taxonomy and Sequence (SIFTS) project (59). From the SIFTS PDB chain taxonomy file, PDB chains that correspond to only one taxonomy ID were selected and then filtered to bacterial and human PDB chains, respectively. The taxonomy list of bacteria was collected by searching both the UniProt proteome (60) and the NCBI Taxonomy databases (61). The union of the two searches provided 521,897 unique bacteria taxonomy IDs.
From the SIFTS PDB chain UniProt file, PDB files with only two UniProt IDs for heterodimers and one UniProt ID for homodimers with both chains longer than 30 amino acids are selected. PDBs that have any single chain mapped to ≥2 UniProt IDs are excluded to avoid fusion or chimera proteins. Structure resolution information is obtained through the PDB API service (24). PDBs that are protein-only as the polymer entity type, and either from X-ray with resolution ≤4 Å or from EM with resolution ≤4.5 Å are selected. NMR structures are not used. Further, through reading the PDB file header, PDBs where the oligomer state of the first BioAssembly (BIOMOLECULE annotations) defined as “DIMERIC” by either the author or software with resolved sequence lengths longer than 30 amino acids are selected. Different PDB dimer structures for the same UniProt ID pairs are collapsed by keeping the structures with better structural resolution or longer chain-concatenated length (at least twice as long). Last, to remove closely related homologous protein pairs, we compared the pairwise sequence identities and removed sequence redundant structures where both protein sequences have 90% sequence identity with another structure. The detailed pipeline is provided in SI Appendix.
Defining Protein Surface and Protein–Protein Interface.
The accessible surface area (ASA) of residues for individual chains A and B and their complex AB are obtained using our in-house program of surfv (62). An interface is defined as long as the buried ASA is larger than zero. The interface between proteins A and B consists of contacting residues where the distance between any heavy atoms is less than 6.0 Å. All the residue indices from the PDB are updated after mapping the PDB sequences to their full UniProt sequences using hhalign of the hh-suite package (63).
Generating Random Protein–Protein Interfaces.
The positions of interface residues on proteins A and B in the concatenated MSA are replaced, one by one, with positions for randomly chosen surface residues of the same protein as indicated in Fig. 1. If one protein has more interface residues than surface residues that are not on the interface, the sampling pool goes to the entire protein sequence. To ensure statistical significance of the Z-score calculations, 100 random interfaces are generated for each protein–protein interface.
Generating and Pairing MSAs.
To avoid biased sequence sampling due to overstudied model species, we carried out homolog sequence search on 5,090 representative proteomes that were carefully curated and selected in EggNog 5.0 (64). This database includes 4,445 prokaryotic reference genomes selected from original 25,038 bacteria genomes, and 477 eukaryotic genomes. Homologous sequences are searched using Jackhmmer (hmmer-3.2.1) (65) with five iterations and the default E-value of 0.001. In the final outputted multiple sequence alignment, only the sequence with highest identity to the query is kept as the representative sequence for each species.
The MSAs of two proteins, p1 and p2, are paired based on the shared common species. Sequence rows that cover less than 50% of surface residue positions of p1 or p2 are excluded from the paired MSA. MSA columns, either for interface residue or surface residue positions, that have more than 50% gaps are excluded.
| [1] |
Calculating Mutual Information, Conservation, DCA, and their APC-corrected Terms.
For two positions (a, b) in the paired MSA, their mutual information (MI) is calculated with Eq. 1, where x and y denote one of 20 amino acids, and a gap in the MSA is treated as the 21st amino acid. p(x) and p(y) are the frequencies of a given amino acid type in columns a and b, respectively, and p(x, y) is the frequency of x and y being paired in the MSA. The conservation score between two MSA positions (a, b) is defined through the complement of their normalized joint entropy with
Eqs. 2 and 3, where the p(x, y) is still the joint frequency of (x, y) amino acid pair.
| [2] |
| [3] |
| [4] |
| [5] |
| [6] |
The DCA method (3, 10) yields a value for direct coupling information, DI, used above in the analysis of the curves labeled DCA. DI is calculated with Eq. 4 where p(dir)(x, y) involves only the isolated direct coupling strength of (a, b) obtained from DCA (3). The average product correction (APC) is applied to measurements as denoted throughout the text. Taking MI as an example, the APC term APCMI between position (a, b) (from protein p1 and p2, respectively) is calculated with Eq. 5, where <MI(a,y)> is the average value of MI between position a in protein p1 and any position y in p2. Similarly, <MI(b,x)> is the average value of MI between position b in protein p2 and any position x in p1 and <MI(x,y)> is the average MI between any position x in p1 and position y in p2. The APC-corrected MI is calculated by subtracting the APC-term APCMI from the original MI with Eq. 6. The same correction correspondingly applies to Con, and DCA scores.
Calculating Z-scores of the Interface.
For each interface contact of a given interface between protein p1 and p2 and the generated 100 random interfaces, the following six measurements are calculated: mutual information, conservation, direct coupling information, and their corresponding APC-corrected terms. Of all the interface contacts, we choose the top and the mean as the representative metric for each measurement, denoted as MItop and <MI>, for example. The Z-score of the 12 metrics is then calculated for the given interface versus the generated random interfaces. The larger Z-score of the raw metric versus its APC-corrected metric is taken as the Z-score for this metric. The maximum of all metrics is taken as the final ZEPPI score.
Building the E. coli Experimental PPI Database.
The experimental database of E. coli PPIs is integrated from several major resources including Interactome3D (66), HINT (44), APID (67), STRING (47), and Ecocyc (68), as well as previously known large-scale E. coli PPI high-throughput screening with experimental methods such as APMS (69) and Y2H (70). Another well-known experimental database BioGrid (71) is not included due to the lack of E. coli (NCBI Taxonomy ID: 83333) PPIs included. Before their integration, each database was preprocessed by selecting only E. coli K12 proteins (proteome size: 4391) and sorting the uniport IDs for each pair of PPIs. During the integration, redundant PPIs were removed. Note that Interactome3D also includes homology-modeled PPIs and the STRING database has many inferred PPIs, which are not determined by direct physical interaction experiments but inferred by other methods such as gene-related methods or species PPI transfer. By excluding these two contributions, we also built a purely experimental PPI database of E. coli based on direct physical experiments. In all, there are 565,007 PPIs in the integrated experimental database set and 45,634 PPIs in the physical experimental PPI dataset.
In summary, the integrated experimental database set includes all HINT binary and complex PPIs (updates of 2021/11), all APID PPIs (updates of 2021/11), all Interactome3D PPIs (updates of 2021/11), all STRING PPIs (v11.5), the Y2H PPI set from Rajagopala et al. (70), the high-confidence and median-confidence APMS PPI set from Babu et al. (69), the gold standard dataset and the high-throughput experimental (HTE) PPI set used in Zhang and coworkers’ Threpp work (72), and the EcoCyc and APMS PPIs used in Baker’s 2019 work (73). For the physical experimental PPI dataset, only physical links in the STRING database with experimental score >0 are included; only the PDB subset of Interactome3D is included; the other datasets remain the same as in the integrated experimental database.
Building the Human Experimental PPI Database.
The integrated human experimental PPI database consists of the following resources: all HINT binary and complex PPIs, all Interactome3D PPIs, all APID PPIs, all STRING PPIs (v11.5), all BioGrid (71) PPIs, all HURI (48) PPIs, and the HC-2016 set from PrePPI (26). In total, there are 6,068,248 PPIs collected from the above-mentioned experimental databases with the large majority derived from STRING. For the physical experimental PPI dataset, only the physical-links subset with experimental score >0 from STRING database, the PDB subset from Interactome3D, and the MV-physical from BioGrid are integrated with the other datasets, together contributing to 766,044 PPIs.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
This work was supported by the NIH grant R35-GM139585.
Author contributions
H.Z., D.M., and B.H. designed research; H.Z., D.M., and B.H. performed research; H.Z. contributed new reagents/analytic tools; H.Z., D.P., D.M., and B.H. analyzed data; and H.Z., D.M., and B.H. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
Reviewers: N.B.-T., Tel Aviv University; and J.S., Georgia Institute of Technology.
Contributor Information
Diana Murray, Email: dm527@columbia.edu.
Barry Honig, Email: bh6@columbia.edu.
Data, Materials, and Software Availability
All the data generated in this study are available to download from the online open access repository FigShare with this link https://doi.org/10.6084/m9.figshare.c.6800502.v1 (74). The provided data include the ZEPPI results for Bacterial and Human PDB heterodimer complexes and homodimer complexes, the CASP/CAPRI score_set complexes, and the PrePPI-AF predictions of E. coli and humans with FPR ≤ 0.05. The collected and integrated experimental PPI databases of E. coli and humans are provided as well. The predicted structures of vignette models are available on FigShare while the rest of mentioned PrePPI predictions can be accessed from the PrePPI-AF website https://honiglab.c2b2.columbia.edu/PrePPI/. All other data are included in the manuscript and/or SI Appendix. Code for the ZEPPI method with tutorial examples is available at https://github.com/honig-lab/ZEPPI.
Supporting Information
References
- 1.Göbel U., Sander C., Schneider R., Valencia A., Correlated mutations and residue contacts in proteins. Proteins: Structure, Function, and Bioinformatics 18, 309–317 (1994). [DOI] [PubMed] [Google Scholar]
- 2.Shoemaker B. A., Panchenko A. R., Deciphering protein-protein interactions. Part II. Computational methods to predict protein and domain interaction partners. PLoS Comput. Biol. 3, 595–601 (2007), 10.1371/journal.pcbi.0030043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Morcos F., et al. , Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. U.S.A. 108, E1293–E1301 (2011), 10.1073/pnas.1111471108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kamisetty H., Ovchinnikov S., Baker D., Assessing the utility of coevolution-based residue-residue contact predictions in a sequence- and structure-rich era. Proc. Natl. Acad. Sci. U.S.A. 110, 15674–15679 (2013). Correction in: Proc. Natl. Acad. Sci. U.S.A. 110, 18734–18735 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Marks D. S., et al. , Protein 3D structure computed from evolutionary sequence variation. PLoS One 6, e28766 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hopf T. A., et al. , Sequence co-evolution gives 3D contacts and structures of protein complexes. Elife 3, 1–45 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ovchinnikov S., Kamisetty H., Baker D., Robust and accurate prediction of residue-residue interactions across protein interfaces using evolutionary information. Elife 2014, 1–21 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Green A. G., et al. , Large-scale discovery of protein interactions at residue resolution using co-evolution calculated from genomic sequences. Nat. Commun. 12, 1396 (2021), 10.1038/s41467-021-21636-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bitbol A. F., Inferring interaction partners from protein sequences using mutual information. PLoS Comput. Biol. 14, e1006401 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Weigt M., White R. A., Szurmant H., Hoch J. A., Hwa T., Identification of direct residue contacts in protein-protein interaction by message passing. Proc. Natl. Acad. Sci. U.S.A. 106, 67–72 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jones D. T., Buchan D. W. A., Cozzetto D., Pontil M., PSICOV: Precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics 28, 184–190 (2012). [DOI] [PubMed] [Google Scholar]
- 12.Evans R., et al. , Protein complex prediction with AlphaFold-Multimer. bioXriv [Preprint] (2021). 10.1101/2021.10.04.463034 (Accessed 1 March 2023). [DOI]
- 13.Bryant P., Pozzati G., Elofsson A., Improved prediction of protein-protein interactions using AlphaFold2. Nat. Commun. 13, 1–11 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gao M., Nakajima An D., Parks J. M., Skolnick J., AF2Complex predicts direct physical interactions in multimeric proteins with deep learning. Nat. Commun. 13, 1744 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Janin J., et al. , CAPRI: A critical assessment of PRedicted interactions. Proteins 52, 2–9 (2003). [DOI] [PubMed] [Google Scholar]
- 16.Kryshtafovych A., et al. , New prediction categories in CASP15. Proteins 91, 1550–1557 (2023), 10.1002/prot.26515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Elofsson A., Progress at protein structure prediction, as seen in CASP15. Curr. Opin. Struct. Biol. 80, 102594 (2023). [DOI] [PubMed] [Google Scholar]
- 18.Humphreys I., et al. , Computed structures of core eukaryotic protein complexes. Science 374, eabm4805 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vakser I. A., Protein-protein docking: From interaction to interactome. Biophys. J. 107, 1785–1793 (2014), 10.1016/j.bpj.2014.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Barradas-Bautista D., Rosell M., Pallara C., Fernández-Recio J., Structural prediction of protein–protein interactions by docking: Application to biomedical problems. Adv. Protein Chem. Struct. Biol. 110, 203–249 (2018). [DOI] [PubMed] [Google Scholar]
- 21.Pierce B. G., et al. , ZDOCK server: Interactive docking prediction of protein-protein complexes and symmetric multimers. Bioinformatics 30, 1771–1773 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kozakov D., et al. , The ClusPro web server for protein-protein docking. Nat. Protoc. 12, 255–278 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Petrey D., et al. , Template-based prediction of protein function. Curr. Opin. Struct. Biol. 32, 33–38 (2015), 10.1016/j.sbi.2015.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Berman H. M., et al. , The protein data bank. Nucleic Acids Res. 28, 235–242 (2000), http://www.rcsb.org/pdb/status.html. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang Q. C., et al. , Structure-based prediction of protein-protein interactions on a genome-wide scale. Nature 490, 556–560 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Garzón J. I., et al. , A computational interactome and functional annotation for the human proteome. Elife 5, 1–27 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Petrey D., Zhao H., Trudeau S. J., Murray D., Honig B., PrePPI: A structure informed proteome-wide database of protein-protein interactions. J. Mol. Biol. 435, 168052 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lensink M. F., Wodak S. J., Score_set: A CAPRI benchmark for scoring protein complexes. Proteins 82, 3163–3169 (2014). [DOI] [PubMed] [Google Scholar]
- 29.Dunn S. D., Wahl L. M., Gloor G. B., Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 24, 333–340 (2008). [DOI] [PubMed] [Google Scholar]
- 30.Bitbol A. F., Dwyer R. S., Colwell L. J., Wingreen N. S., Inferring interaction partners from protein sequences. Proc. Natl. Acad. Sci. U.S.A. 113, 12180–12185 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jumper J., et al. , Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mehrabiani K. M., Cheng R. R., Onuchic J. N., Expanding direct coupling analysis to identify heterodimeric interfaces from limited protein sequence data. J. Phys. Chem. B 125, 11408–11417 (2021). [DOI] [PubMed] [Google Scholar]
- 33.Haldane A., Levy R. M., Influence of multiple-sequence-alignment depth on Potts statistical models of protein covariation. Phys. Rev. E 99, 1–15 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Réau M., Renaud N., Xue L. C., Bonvin A. M. J. J., DeepRank-GNN: A graph neural network framework to learn patterns in protein-protein interfaces. Bioinformatics 39, 1–8 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Renaud N., et al. , DeepRank: A deep learning framework for data mining 3D protein-protein interfaces. Nat. Commun. 12, 1–8 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Geng C., et al. , Structural bioinformatics iScore: A novel graph kernel-based function for scoring protein-protein docking models. Bioinformatics 36, 112–121 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dominguez C., Boelens R., Bonvin A. M. J. J., HADDOCK: A protein-protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc. 125, 1731–1737 (2003). [DOI] [PubMed] [Google Scholar]
- 38.Wang X., Flannery S. T., Kihara D., Protein docking model evaluation by graph neural networks. Front Mol. Biosci. 8, 647915 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wang X., Terashi G., Christoffer C. W., Zhu M., Kihara D., Protein docking model evaluation by 3D deep convolutional neural networks. Bioinformatics 36, 2113–2118 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schweke H., et al. , Discriminating physiological from non-physiological interfaces in structures of protein complexes: A community-wide study. Proteomics 23, 1–21 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Basu S., Wallner B., DockQ: A quality measure for protein-protein docking models. PLoS One 11, e0161879 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lensink M. F., et al. , Prediction of protein assemblies, the next frontier: The CASP14-CAPRI experiment. Proteins 89, 1800–1823 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Petrey D., Zhao H., Trudeau S., Murray D., Honig B., PrePPI: A structure informed proteome-wide database of protein-protein interactions. J. Mol. Biol. 435, 168052 (2023), 10.1016/j.jmb.2023.168052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Das J., Yu H., HINT: High-quality protein interactomes and their applications in understanding human disease. BMC Syst. Biol. 6, 1–12 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Qamra R., Hubbard S. R., Structural basis for the interaction of the adaptor protein Grb14 with activated Ras. PLoS One 8, 1–9 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chen K., et al. , Methylation-associated silencing of miR-193a-3p promotes ovarian cancer aggressiveness by targeting GRB7 and MAPK/ERK pathways. Theranostics 8, 423–436 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Szklarczyk D., et al. , The STRING database in 2021: Customizable protein-protein networks, and functional characterization of user-uploaded gene/measurement sets. Nucleic Acids Res. 49, D605–D612 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Luck K., et al. , A reference map of the human binary protein interactome. Nature 580, 402–408 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ryu H. H., et al. , Neuron type-specific expression of a mutant KRAS impairs hippocampal-dependent learning and memory. Sci. Rep. 10, 1–13 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Guo Y., Wang Q., Chen S., Xu C., Functions of amyloid precursor protein in metabolic diseases. Metabolism 115, 154454 (2021). [DOI] [PubMed] [Google Scholar]
- 51.Kulas J. A., Puig K. L., Combs C. K., Amyloid precursor protein in pancreatic islets. J. Endocrinol. 235, 49–67 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Breznik B., Mitrović A., Lah T., Kos J., Cystatins in cancer progression: More than just cathepsin inhibitors. Biochimie 166, 233–250 (2019). [DOI] [PubMed] [Google Scholar]
- 53.Song L., et al. , Expression signature, prognosis value and immune characteristics of cathepsin F in non-small cell lung cancer identified by bioinformatics assessment. BMC Pulm Med. 21, 1–17 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Yang J., et al. , Cystatin SN promotes epithelial-mesenchymal transition and serves as a prognostic biomarker in lung adenocarcinoma. BMC Cancer 22, 1–18 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Meyer M. J., et al. , Interactome INSIDER: A structural interactome browser for genomic studies. Nat. Methods 15, 107–114 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Sanchez-Garcia R., Sorzano C. O. S., Carazo J. M., Segura J., BIPSPI: A method for the prediction of partner-specific protein-protein interfaces. Bioinformatics 35, 470–477 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Quignot C., et al. , InterEvDock3: A combined template-based and free docking server with increased performance through explicit modeling of complex homologs and integration of covariation-based contact maps. Nucleic Acids Res. 49, W277–W284 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Burke D. F., et al. , Towards a structurally resolved human protein interaction network. Nat. Struct. Mol. Biol. 30, 216–225 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Velankar S., et al. , SIFTS: Structure integration with function, taxonomy and sequences resource. Nucleic Acids Res. 41, D483–D489 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bateman A., et al. , UniProt: The universal protein knowledgebase in 2021. Nucleic Acids Res. 49, D480–D489 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Federhen S., The NCBI Taxonomy database. Nucleic Acids Res. 40, D136–D143 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Nicholls A., Sharp K. A., Honig B., Protein folding and association: Insights from the interfacial and thermodynamic properties of hydrocarbons. Proteins 11, 281–296 (1991). [DOI] [PubMed] [Google Scholar]
- 63.Remmert M., Biegert A., Hauser A., Söding J., HHblits: Lightning-fast iterative protein sequence searching by HMM-HMM alignment. Nat. Methods 9, 173–175 (2012). [DOI] [PubMed] [Google Scholar]
- 64.Huerta-Cepas J., et al. , EggNOG 5.0: A hierarchical, functionally and phylogenetically annotated orthology resource based on 5090 organisms and 2502 viruses. Nucleic Acids Res. 47, D309–D314 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Eddy S. R., HMMER User’s Guide Biological Sequence Analysis Using Profile Hidden Markov Models (2020). http://hmmer.org. Accessed 12 December 2022.
- 66.Mosca R., Céol A., Aloy P., Interactome3D: Adding structural details to protein networks. Nat. Methods 10, 47–53 (2013). [DOI] [PubMed] [Google Scholar]
- 67.Alonso-López D., et al. , APID database: Redefining protein-protein interaction experimental evidences and binary interactomes. Database 2019, baz005 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Keseler I. M., et al. , The EcoCyc database: Reflecting new knowledge about Escherichia coli K-12. Nucleic Acids Res. 45, D543–D550 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Babu M., et al. , Global landscape of cell envelope protein complexes in Escherichia coli. Nat. Biotechnol. 36, 103–112 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Rajagopala S. V., et al. , The binary protein-protein interaction landscape of escherichia coli. Nat. Biotechnol. 32, 285–290 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Oughtred R., et al. , The BioGRID interaction database: 2019 update. Nucleic Acids Res. 47, D529–D541 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Gong W., et al. , Integrating multimeric threading with high-throughput experiments for structural interactome of Escherichia coli. J. Mol. Biol. 433, 166944 (2021). [DOI] [PubMed] [Google Scholar]
- 73.Cong Q., Anishchenko I., Ovchinnikov S., Baker D., Protein interaction networks revealed by proteome coevolution. Science 365, 185–189 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Murray D., Zhao H., ZEPPI Supplementary Files. Figshare. 10.6084/m9.figshare.c.6800502.v1. Deposit 22 August 2023. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All the data generated in this study are available to download from the online open access repository FigShare with this link https://doi.org/10.6084/m9.figshare.c.6800502.v1 (74). The provided data include the ZEPPI results for Bacterial and Human PDB heterodimer complexes and homodimer complexes, the CASP/CAPRI score_set complexes, and the PrePPI-AF predictions of E. coli and humans with FPR ≤ 0.05. The collected and integrated experimental PPI databases of E. coli and humans are provided as well. The predicted structures of vignette models are available on FigShare while the rest of mentioned PrePPI predictions can be accessed from the PrePPI-AF website https://honiglab.c2b2.columbia.edu/PrePPI/. All other data are included in the manuscript and/or SI Appendix. Code for the ZEPPI method with tutorial examples is available at https://github.com/honig-lab/ZEPPI.