When can odds ratios mislead?

Odds ratios are a common measure of the size of an effect and may be reported in case-control studies, cohort studies, or clinical trials. Increasingly, they are also used to report the findings from systematic reviews and meta-analyses. Odds ratios are hard to comprehend directly and are usually interpreted as being equivalent to the relative risk. Unfortunately, there is a recognised problem that odds ratios do not approximate well to the relative risk when the initial risk (that is, the prevalence of the outcome of interest) is high.¹,² Thus there is a danger that if odds ratios are interpreted as though they were relative risks then they may mislead.

The advice given in many texts is unusually coy on the matter. For example: “The odds ratio is approximately the same as the relative risk if the outcome of interest is rare. For common events, however, they can be quite different.”³ How close is “approximately the same,” how uncommon does an event have to be to qualify as “rare,” and how different is “quite different”?

Summary points

• If the odds ratio is interpreted as a relative risk it will always overstate any effect size: the odds ratio is smaller than the relative risk for odds ratios of less than one, and bigger than the relative risk for odds ratios of greater than one

• The extent of overstatement increases as both the initial risk increases and the odds ratio departs from unity

• However, serious divergence between the odds ratio and the relative risk occurs only with large effects on groups at high initial risk. Therefore qualitative judgments based on interpreting odds ratios as though they were relative risks are unlikely to be seriously in error

• In studies which show reductions in risk (odds ratios of less than one), the odds ratio will never underestimate the relative risk by a greater percentage than the level of initial risk

• In studies which show increases in risk (odds ratios of greater than one), the odds ratio will be no more than twice the relative risk so long as the odds ratio times the initial risk is less than 100%

This short note quantifies the discrepancy between odds ratios and relative risks in different circumstances, and assesses whether such a discrepancy may seriously mislead if an odds ratio is used as an estimate of the relative risk.

Odds and risk

There is a problem with odds: unlike risks, they are difficult to understand. The risk of an event happening is simply the number of those who experience the event divided by the total number of people at risk of having that event. It is usually expressed as a proportion or as a percentage. In either case the meaning is usually clear.

In contrast, the odds of an event is the number of those who experience the event divided by the number of those who do not. It is expressed as a number from zero (event will never happen) to infinity (event is certain to happen). Odds are fairly easy to visualise when they are greater than one, but are less easily grasped when the value is less than one. Thus odds of six (that is, six to one) mean that six people will experience the event for every one that does not (a risk of six out of seven or 86%). An odds of 0.2 however seems less intuitive: 0.2 people will experience the event for every one that does not. This translates to one event for every five non-events (a risk of one in six or 17%).

A second problem with odds is that, although they are related to risk, the relation is not straightforward. The table shows the odds for various risks. For risks of less than about 20% the odds are not greatly dissimilar to the risk, but as the risk climbs above 50% the odds start to look very different.

Relative risks and odds ratios

The relative risk of one group compared with another is simply the ratio of the risks in the two groups. Thus the relative risk tells us how much risk is increased or decreased from an initial level. Again it is readily understood: a relative risk of 0.5 shows that the initial risk has been halved; a relative risk of 3 shows that the initial risk has been increased threefold.

The odds ratio is calculated in a similar way: it is simply the ratio of the odds in the two groups of interest. We know that if the odds ratio is less than one then the odds (and therefore the risk too) has decreased, and if the odds ratio is greater than one then they have increased. But by how much? How do we interpret an odds ratio of, say, 0.5 or an odds ratio of 3? A lack of familiarity with odds means that many people have no intuitive feel for the size of the difference when expressed in this way.

When the risks (or odds) in the two groups being compared are both small (say less than 20%) then the odds will approximate to the risks and the odds ratio will approximate to the relative risk. Then interpretation is easy. But as the risk in either group rises above 20% the gap between the odds ratio and the relative risk will widen. A recent article in Bandolier concluded that “as both the prevalence [initial risk] and the odds ratio increase, the error in the approximation quickly becomes unacceptable.”² But is this the case? In what circumstances will interpreting an odds ratio as though it were a relative risk lead to serious errors in interpretation?

Odds ratio as an approximation of relative risk

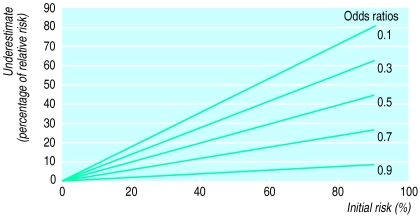
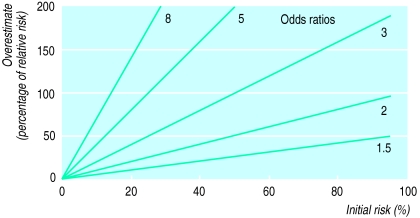
When faced with an odds ratio, we want to know the discrepancy between that odds ratio and the relative risk. Figures 1 and 2 show the extent to which the reported odds ratio underestimates or overestimates the relative risk for different odds ratios and a given level of initial risk (see appendix for calculations).

Figure 1.

 Amount by which odds ratios of <1 underestimate relative risk, for different odds ratios and different levels of initial risk

Figure 2.

 Amount by which odds ratios of >1 overestimate relative risk, for different odds ratios and different levels of initial risk

Figure 1 shows the underestimation of the relative risk by the odds ratio in studies that report odds ratios of less than one (typically studies of benefit from treatment or exposure). Even with initial risks as high as 50% and very large reductions in this risk (odds ratios of about 0.1), the odds ratio is only 50% smaller than the relative risk (0.1 for the odds ratio compared with a true value for the relative risk of 0.2). In fact, the discrepancy between the odds ratio and the true relative risk will never be greater than the initial risk (see appendix for proof).

Figure 2 shows the discrepancy between the odds ratio and the relative risk for studies which report odds ratios of greater than one (typically studies showing harm). Although large discrepancies between the odds ratio and the relative risk are possible, the odds ratio overstates the relative risk by less than 50% for a wide range of both initial risks and effect sizes. For initial risks of 10% or less, even odds ratios of up to eight can reasonably be interpreted as relative risks; for initial risks up to 30% the approximation breaks down when the effect size gives odds ratios of more than about three. As a conservative rule of thumb, if the initial risk multiplied by the odds ratio is less than 100% then the odds ratio will overestimate the relative risk by less than twofold.

Does the discrepancy influence our interpretation?

The figures show that the odds ratio will always exaggerate the size of the effect compared with a relative risk. That is, if the odds ratio is less than one then it is always smaller than the relative risk. Conversely, if the odds ratio is greater than one then it is always bigger than the relative risk. Thus interpreting an odds ratio as though it were a relative risk could mislead us into believing that an effect size is bigger than is actually the case.

Crucially, however, large discrepancies are seen for only large effect sizes. Suppose an odds ratio of, say, 0.2 reflects a true relative risk of 0.4. Such a discrepancy is unlikely to alter your view: this is a large reduction in risk whichever way you look at it. This is particularly so as large discrepancies occur only when the initial risk is high and thus even modest changes in the relative risk will mean substantial gains. So, for studies which show reductions in risk, the odds ratio is unlikely to mislead: either it will be close in value to the relative risk or it represents a substantial effect for groups at high initial risk. Thus any qualitative judgment is unaltered by the discrepancy between the odds ratio and the relative risk (see box).

Example of use of odds ratios

The fortnightly review by Dennis and Langhorne, “So stroke units save lives: where do we go from here?” (BMJ 1994;309:1273-7) reported outcomes after stroke (death or living in an institution) for patients managed in specialist stroke units compared with patients managed on general medical wards. Specialist stroke units had the better outcomes, with a reported odds ratio of 0.66. The authors advised that an “odds ratio of <1.0 indicates that outcome of care in a stroke unit is better,” and concluded that “patients with stroke treated in specialist units were less likely to die than those treated in general medical wards.” No further guidance was given on interpreting the quoted odds ratio.

Because the frequency of a poor outcome was very high (about 55%) there might be concern that the odds ratio is a poor estimate of the relative risk. In fact, the odds ratio of 0.66 corresponds to a relative risk of 0.81—that is, the odds ratio underestimates the relative risk by just 19%. In other words, interpreting the odds ratio as a relative risk suggests a reduction in deleterious outcomes after stroke (death or living in an institution) of about a third compared with a more likely true reduction of about a fifth. Clearly, in either case this represents a substantial reduction in poor outcomes for a patient group with a large initial risk.

The same logic holds for studies which show increases in risk. The discrepancy between the odds ratio and the relative risk becomes large only when there are large effects (a twofold or threefold increase in risk) for groups already at a large initial risk. Although the odds ratio may diverge quite sharply from the relative risk, by the time it does so the message conveyed by the different measures is the same: these are large effects.

Of course, although qualitative judgments may be unaltered by the odds ratio deviating from the relative risk, quantitatively we can still be led astray. Thus if we are interested in assessing the impact of interventions quantitatively (for example, for a cost effectiveness analysis) then, for larger initial risks and substantial odds ratios, the actual relative risk should still be calculated.

Conclusion

The difference between the odds ratio and the relative risk depends on the risks (or odds) in both groups. So for any reported odds ratio, the discrepancy between that odds ratio and the relative risk depends on both the initial risk and the odds ratio itself. This is possibly why textbooks are coy about giving a single figure for risk beneath which it is acceptable to interpret odds ratios as though they were relative risks.

Odds ratios may be non-intuitive in interpretation, but in almost all realistic cases interpreting them as though they were relative risks is unlikely to change any qualitative assessment of the study findings. The odds ratio will always overstate the case when interpreted as a relative risk, and the degree of overstatement will increase as both the initial risk increases and the size of any treatment effect increases. However, there is no point at which the degree of overstatement is likely to lead to qualitatively different judgments about the study. Substantial discrepancies between the odds ratio and the relative risk are seen only when the effect sizes are large and the initial risk is high. Whether a large increase or a large decrease in risk is indicated, our judgments are likely to be the same—they are important effects.

Appendix: Calculation of discrepancy between odds ratios and relative risks

If the proportions of subjects experiencing an event in two groups are P₁ (initial risk) and P₂ (post-intervention risk) then the relative risk is P₂/P₁ and the odds ratio is (1−P₁)/(1−P₂)×relative risk. Simple algebra leads this multiplier to be recast as 1−P₁+(P₁×odds ratio). However, it is convenient to express the discrepancy between the odds ratio and the relative risk as a proportion of the relative risk. Therefore, for studies in which the odds ratio is <1, 1 minus this multiplier is the discrepancy (P₁−(P₁×odds ratio)). For studies in which the odds ratio is >1, the multiplier minus 1 gives the discrepancy ((P₁×odds ratio)−P₁). Figures 1 and 2 plot these discrepancy values (as percentages) for various initial risks and odds ratios.

Netlines

Lest we forget ...

• Andrew Bamji has placed the Plastic Surgery Archives—a collection of material that documents the development of plastic surgery at the beginning of the 20th century, particularly after the first world war—on the web on ourworld.compuserve.com/homepages/Andrew_Bamji/homepage.htm. The site has links to other online material about the first world war, including a medical bibliography of the war (raven.cc.ukans.edu/∼kansite/ww_one/medical/medtitle.htm).

Evidence based medicine

• There are ever more sources of evidence based medicine appearing on the web. The full text of the evidence based medicine journal Bandolier is available free on www.jr2.ox.ac.uk/Bandolier/, the Internet Database of Evidence-Based Abstracts and Articles (IDEA) can be found at www.ohsu.edu/bicc-informatics/ebm/ebm_topics.htm, and the NHS Centre for Reviews and Dissemination is at www.york.ac.uk/inst/crd/. For more comprehensive information, visit Netting the Evidence (www.shef.ac.uk/uni/academic/R-Z/scharr/ir/netting.html), an index of online sources of evidence based medicine, complete with commentaries, produced by Andrew Booth at the School of Health and Related Research (ScHARR), Sheffield.

Online journals: Highwire Press

• With production of the BMJ website all set to change over to Highwire Press next month, it is worth visiting the Highwire Press site (highwire.stanford.edu/ in the United States or intl.highwire.org in Europe) to see how many online journals they are managing now—everything from the American Journal of Respiratory and Critical Care Medicine (www.ajrccm.org) to Science magazine (www.sciencemag.org). Future titles will include the Annual Reviews series and the journals of the American Society for Microbiology and the American Heart Association. All the journals are available as full text online both in HTML and Adobe Acrobat format (www.adobe.co.uk/products/acrobat/main.html) and come with fully searchable archives of past issues. The only snag is that, for most of them, you must have a subscription. In the near future the Highwire Press site will allow you to search all its journals in one go, and will also feature a Medline service.

ER online

• As ER is probably the best medical drama on British television, it is nice to see so much ER related stuff on the internet. A good starting place for exploring it all is the Alt.TV.ER site (www.digiserve.com/er/erdex.html), where you can pick up episode listings, summaries and reviews, and also commentaries on the medical conditions featured in each show. There is also an exhaustive set of links to other ER pages and sites. British viewers can discuss the show on the newsgroup uk.media.tv.er (news:uk.media.tv.er).

He@lth Information on the Internet

• He@lth Information on the Internet (www.wellcome.ac.uk/healthinfo/) is a new bimonthly newsletter from the Wellcome Trust and the Royal Society of Medicine, containing a range of contributed articles and regular features. The first issue is available in full on the web at www.wellcome.ac.uk/healthinfo/be1.html. I am on its editorial board.

Index to Theses

• The Index to Theses site (www.theses.com/) allows you to search an online database of theses accepted for higher degrees by the Universities of Great Britain and Ireland. Abstracts are available for recent theses. To use the site you must be in an institution that subscribes to the “dead-tree” version of the database.

Laparoscopy online

• The laparoscopy.com website (www.laparoscopy.com) features a feast of virtual laparoscopy, including multimedia walk-throughs of procedures, images, an online radio channel, and discussion forums.

The Visible Embryo

• The Visible Embryo (visembryo.ucsf.edu/) is an impressive online tour of the first four weeks of human life. For full appreciation of the site, however, you must have the Shockwave plug-in (available from www.macromedia.com) and plenty of memory allocated to your web browser.

Compiled by Mark Pallen email m.pallen@qmw.ac.uk web page www.medmicro.mds.qmw.ac.uk/∼mpallen

Table 1.

Comparing risks and odds

Risk	Odds
0.05 or 5%	0.053
0.1 or 10%	0.11
0.2 or 20%	0.25
0.3 or 30%	0.43
0.4 or 40%	0.67
0.5 or 50%	1
0.6 or 60%	1.5
0.7 or 70%	2.3
0.8 or 80%	4
0.9 or 90%	9
0.95 or 95%	19