Abstract
Sequential multiple assignment randomized trials (SMARTs) are the gold standard for estimating optimal dynamic treatment regimes (DTRs), but are costly and require a large sample size. We introduce the multi-stage augmented Q-learning estimator (MAQE) to improve efficiency of estimation of optimal DTRs by augmenting SMART data with observational data. Our motivating example comes from the Back Pain Consortium, where one of the overarching aims is to learn how to tailor treatments for chronic low back pain to individual patient phenotypes, knowledge which is lacking clinically. The Consortium-wide collaborative SMART and observational studies within the Consortium collect data on the same participant phenotypes, treatments, and outcomes at multiple time points, which can easily be integrated. Previously published single-stage augmentation methods for integration of trial and observational study (OS) data were adapted to estimate optimal DTRs from SMARTs using Q-learning. Simulation studies show the MAQE, which integrates phenotype, treatment, and outcome information from multiple studies over multiple time points, more accurately estimates the optimal DTR, and has a higher average value than a comparable Q-learning estimator without augmentation. We demonstrate this improvement is robust to a wide range of trial and OS sample sizes, addition of noise variables, and effect sizes.
Keywords: augmentation, Back Pain Consortium, data integration, doubly robust, precision medicine, Q-learning
1. INTRODUCTION
Patient heterogeneity necessitates approaches to clinical medicine and patient care that are tailored to patients’ individual characteristics. The field of precision medicine seeks to leverage new data analysis methods to improve treatment decisions such that the right treatment is given to the right person at the right time (Kosorok and Laber, 2019). Dynamic treatment regimes (DTRs), also known as adaptive treatment strategies or individualized interventions, are sequences of decision rules, one per intervention, that assign treatments to patients based on individual characteristics such as past treatments and evolving disease history (Lavori et al., 2000; Lavori and Dawson, 2004; Chakraborty and Murphy, 2014).
Just as the randomized controlled trial is the gold standard for efficacy trials, a sequential multiple assignment randomized trial (SMART) design is better suited for unbiased estimation of optimal DTRs than observational studies (Murphy, 2005). Using SMART designs to address precision medicine aims has become increasingly common in fields such as mental and behavioral health, oncology, obesity, and smoking cessation, among others. The sequential nature of SMARTs allows the delayed effects of previous treatments to be observed over time, which can guide clinical care. However, the limitation to the sequential design is that a large sample size is needed to estimate optimal DTRs, so many SMARTs are only powered to address primary aims such as comparison of initial treatment options or comparison of second stage treatment options for non-responders (Murphy et al., 2007). Other limitations to conducting SMARTs and other randomized trials are the cost of the trial itself, the complexity of the design and implementation, and potential for drop-out and non-compliance due to the length of the study (March et al., 2010). Therefore, there is a need to improve analysis methods to more efficiently estimate optimal DTRs.
Observational data, such as cohort studies, medical records, and patient databases, have been used to estimate optimal DTRs (Moodie et al., 2012). The advantage of using observational data is that it is less expensive and studies can enroll many more participants than randomized trials. Inclusion and exclusion criteria are generally less strict than trials, so the participant population may be more representative of the true patient population, and heterogeneity of treatments can be better represented. However, using observational data alone is subject to biases, especially due to unmeasured confounding. Combining data from randomized trials and observational studies can allow for analysis of a greater and more heterogeneous pooled participant population, while maintaining the validity of treatment causality due to the randomized nature of the trial.
The Back Pain Consortium (BACPAC), part of the National Institutes of Health (NIH) Helping to End Addiction Long-term (HEAL) Initiative, consists of randomized trials, observational studies, and sites developing experimental new technology to study the etiology of chronic low back pain (cLBP) (NIH HEAL Initiative, 2019). While many effective treatments have been identified for cLBP, little is known about which treatments are best for which patients at which time in their course of chronic disease, especially due to the high degree of patient heterogeneity. Therefore, the Biomarkers for Evaluating Spine Treatments (BEST) trial was designed as a SMART to evaluate and compare multiple treatment sequences across cLBP patients with the goal of estimating optimal DTRs (NCT05396014). Back Pain Consortium has multiple observational studies aiming to characterize cLBP patient phenotypes, and to evaluate which cLBP treatments are most effective for which patient subgroups (Mauck et al., 2023). Consortium-wide longitudinal data collection on participant phenotypes, observed treatment, and outcomes, was harmonized across all studies, facilitating integrability of trial and observational study (OS) data (Batorsky et al., 2023). The participant populations, and response to cLBP treatments, in BEST and the observational studies are expected to be comparable. Data collection for BACPAC studies is currently underway, but the structure of the Consortium and harmonization of data elements across studies provides a motivating example to explore statistical methods to improve efficiency of estimation of optimal DTRs from SMARTs by integrating data from observational studies.
There are several established methods for combining single-stage trial and observational data to improve efficiency of estimates and improve generalizability of treatment effects. These methods include the inverse probability of sampling weighting (IPSW) estimator, stratification, and/or involve creating propensity scores to reduce bias from measured confounders (Colnet et al., 2021). Other methods include G-formula estimators, as proposed by Robins (Robins, 1986). However, these methods do not immediately address the need to improve efficiency, and are not designed to estimate optimal DTRs from multi-stage trials. To date, methods to augment SMART data with stage-wise observational data are lacking in the literature.
In this article, we propose a procedure within the Q-learning framework to combine the data from a SMART and an OS to estimate optimal DTRs. Q-learning is a regression-based method which maximizes the outcome at each sequential stage working backwards to arrive at the optimal treatment rule at each stage (Murphy, 2005). At each stage in the Q-learning estimation, we utilize the framework of the doubly robust augmented IPSW (APISW) estimator, which was originally used for estimating the average treatment effect or heterogeneous treatment effect in a single stage study (Lunceford and Davidian, 2004; Lipkovich et al., 2023). The estimator is doubly robust in that it will give unbiased results as long as either the the outcome model or the probabilities of receiving a given treatment are accurate. We first predict the estimated outcome model parameters using the SMART data, then use these estimated parameters to estimate stage-wise potential outcomes for all trial and OS participants. We use a doubly robust construction of the Q-function for trial participants, then incorporate the contrast of the predicted potential outcomes for OS participants to estimate the optimal treatment rule at each stage. We denote this algorithm the multi-stage augmented Q-learning estimator (MAQE). Due to the doubly robust property of this estimator, it is guaranteed to be unbiased even if the predicted potential outcomes are inaccurate because the treatment randomization probabilities at each stage of the trial are known. Furthermore, the MAQE is expected to have less uncertainty (ie, increased efficiency) because of the data augmentation step.
Notation and assumptions relevant to this method are introduced in Section 2.1, Q-learning is described in Section 2.2, and the details of the algorithm are described in Section 2.3. In Section 3.1, we describe the simulation study motivated by BACPAC. Performance metrics are described in Section 3.2. We then demonstrate the properties of the MAQE using simulated test data when changing various parameters, such as relative and absolute sample sizes, OS sample size, addition of noise variables, and using different effect sizes (Sections 3.3 and 3.4). We also discuss advantages of this method and next steps for future research in Section 4.
2. METHODS
2.1. Notation and basic assumptions
The SMART (henceforth referred to as the trial) of size n and OS of size m both consist of K stages of treatments. Individual data consist of a sequence of K tuples 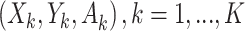 , where
, where 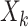 denotes a p-dimensional vector of covariates collected at stage k.
denotes a p-dimensional vector of covariates collected at stage k. 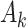 represents the binary, categorical or continuous treatment assigned or observed at stage k. For the purposes of this example A is binary, taking values 0 or 1.
represents the binary, categorical or continuous treatment assigned or observed at stage k. For the purposes of this example A is binary, taking values 0 or 1. 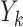 denotes the observed binary or continuous outcome, where a larger value is more beneficial. Let
denotes the observed binary or continuous outcome, where a larger value is more beneficial. Let 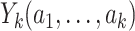 denote a potential outcome at stage k given treatment
denote a potential outcome at stage k given treatment 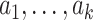 . Participant history by stage k is denoted by
. Participant history by stage k is denoted by 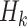 including the intercept, so
including the intercept, so 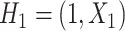 and
and 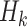 consists sequentially of
consists sequentially of 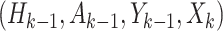 .
.
A DTR is a sequence of decision functions for all K stages, represented by 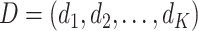 , where stage-wise treatment rule
, where stage-wise treatment rule 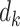 maps
maps 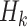 to the domain of
to the domain of 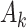 , i.e.,
, i.e., 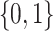 . The corresponding value function of D is defined as
. The corresponding value function of D is defined as 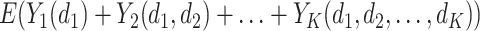 , which is the expected population average value of the outcome measures from stages one to K added together, if all participants were to follow the DTR, D. When analyzing a SMART, the goal is to estimate the optimal DTR, denoted by
, which is the expected population average value of the outcome measures from stages one to K added together, if all participants were to follow the DTR, D. When analyzing a SMART, the goal is to estimate the optimal DTR, denoted by 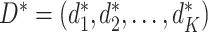 which yields the highest value.
which yields the highest value.
The following assumptions are needed to provide valid estimates of DTRs from SMARTs and are described in more detail by Schulte et al. (2014).
Assumption 1 (consistency and the stable unit treatment value assumption [SUTVA])
.
Assumption 2 (sequential ignorability)
for any
,
is independent of
given
.
Assumption 3 (positivity)
for all
{0,1} and
in the domain of
.
Causal consistency and SUTVA implicitly assume that there exists no interference or non-compliance. The assumption of sequential ignorability, also referred to as exchangeability, implies that due to balanced randomization, there is no unmeasured confounding at each stage k, given participant history 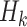 . We note that this assumption holds for the SMART but may not be true for the OS. The third assumption implies that there is a non-zero (ie, positive) probability that a study participant will receive any available treatment at each stage. This assumption holds for SMARTs when randomization probabilities are greater than zero for each treatment at each stage, but may not hold for observational data, where actual or near-positivity violations may occur.
. We note that this assumption holds for the SMART but may not be true for the OS. The third assumption implies that there is a non-zero (ie, positive) probability that a study participant will receive any available treatment at each stage. This assumption holds for SMARTs when randomization probabilities are greater than zero for each treatment at each stage, but may not hold for observational data, where actual or near-positivity violations may occur.
2.2. Q-learning to estimate optimal DTRs
Q-learning is commonly used to estimate optimal DTRs from SMARTs. We refer to the following method of estimation without augmentation as the standard Q-learning estimator (SQE). Let 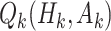 be the Q-function at stage k, which is defined as the expected outcome at stage k given history
be the Q-function at stage k, which is defined as the expected outcome at stage k given history 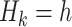 and treatment
and treatment 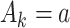 , assuming the participant is treated optimally at all future stages. Analysis using the Q-function for multiple stages uses the Bellman optimality equation (Bellman, 1957):
, assuming the participant is treated optimally at all future stages. Analysis using the Q-function for multiple stages uses the Bellman optimality equation (Bellman, 1957): 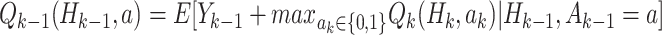 .
.
The optimal treatment for a patient with observed covariate history 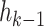 , at stage
, at stage  , is the treatment maximizing the expectation on the right-hand side of the Bellman equation. Q-learning proceeds by estimating stage-wise Q-functions and optimal treatment rules through a backwards algorithm. Let participants from the SMART of size n be modeled by a sequence of K independent random tuples
, is the treatment maximizing the expectation on the right-hand side of the Bellman equation. Q-learning proceeds by estimating stage-wise Q-functions and optimal treatment rules through a backwards algorithm. Let participants from the SMART of size n be modeled by a sequence of K independent random tuples 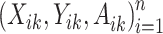 independent and identically distributed (i.i.d.) according to the trial population. In this article, we model the interaction between
independent and identically distributed (i.i.d.) according to the trial population. In this article, we model the interaction between 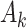 and
and 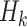 , with form
, with form 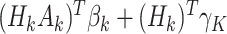 , where
, where 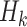 may include interaction terms between past treatments and observed covariates. An extension of this method may replace
may include interaction terms between past treatments and observed covariates. An extension of this method may replace 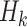 with a nonlinear basis function in the space of
with a nonlinear basis function in the space of 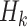 , to allow for a more flexible and nonlinear model for interactions.
, to allow for a more flexible and nonlinear model for interactions.
Start with stage K. Computation for Q-learning minimizes the following objective function to estimate the vector of regression coefficients from n trial participants, which dictate the estimated optimal treatment rule at the last stage, K:
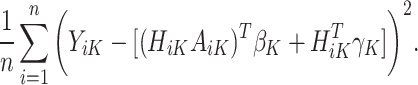 |
(1) |
We denote the estimated coefficients as 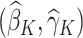 . The estimated optimal treatment rule at stage K,
. The estimated optimal treatment rule at stage K, 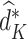 , is used to estimate the optimal treatment for subject i at stage K, the treatment that yields the highest estimated outcome as determined by (2)
, is used to estimate the optimal treatment for subject i at stage K, the treatment that yields the highest estimated outcome as determined by (2)
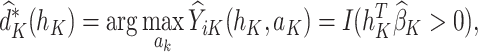 |
(2) |
where 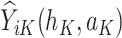 is the predicted outcome from the solution to (1) for
is the predicted outcome from the solution to (1) for 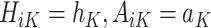 .
.
For each stage working backward, continuing with stage  , the pseudo-outcome,
, the pseudo-outcome, 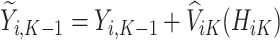 is evaluated, where
is evaluated, where 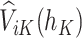 is the maximum of
is the maximum of 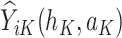 over
over 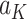 . This allows for estimation of the conditional function at stage
. This allows for estimation of the conditional function at stage  ,
, 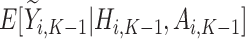 . Then, the following function is minimized
. Then, the following function is minimized
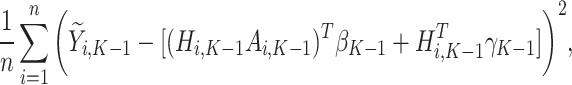 |
(3) |
so that we obtain the estimator for the vector of regression coefficients, denoted by 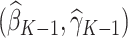 . Thus, for stage
. Thus, for stage  , the estimated optimal treatment rule,
, the estimated optimal treatment rule, 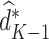 , is used to determine the treatment that yields the highest estimated outcome, as determined by (4)
, is used to determine the treatment that yields the highest estimated outcome, as determined by (4)
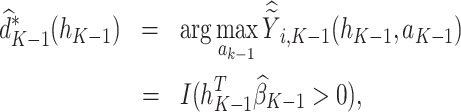 |
(4) |
where 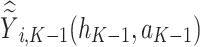 is the predicted outcome from the solution to (3). Estimation of subsequent stage-wise optimal treatment rules (
is the predicted outcome from the solution to (3). Estimation of subsequent stage-wise optimal treatment rules (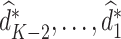 ), and thus the full estimated optimal DTR,
), and thus the full estimated optimal DTR, 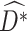 , proceeds using the same algorithm in turn.
, proceeds using the same algorithm in turn.
2.3. Data augmentation with an OS
To improve efficiency of estimates of optimal DTRs using Q-learning, we propose the multi-stage augmented Q-learning estimator (MAQE), which includes an augmentation term, allowing for pooled data analysis of n trial participants and m OS participants for all K stages. In addition to data from n trial participants, we introduce data from m OS participants, modeled by a sequence of K independent random tuples 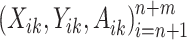 where data from each participant are i.i.d. according to the distribution of the OS population. It is assumed that treatment and outcome are observed for all K stages.
where data from each participant are i.i.d. according to the distribution of the OS population. It is assumed that treatment and outcome are observed for all K stages.
In contrast to the SQE in (1), the MAQE at stage K directly estimates the treatment effect using a contrast between potential outcomes for a given participant if they were to receive treatment 1 vs 0 at stage K. For subject i in the trial data, it is clear that because of Assumptions 1–3, 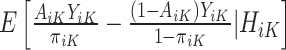 is equal to this contrast, where
is equal to this contrast, where 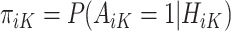 is the known randomization probability to assign treatment
is the known randomization probability to assign treatment 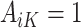 . Therefore, such a contrast is available for the trial participants. However, since there may be unobserved confounders and the treatment assignment probabilities are unknown, in the OS such a contrast is not available and therefore needs to be estimated using the data.
. Therefore, such a contrast is available for the trial participants. However, since there may be unobserved confounders and the treatment assignment probabilities are unknown, in the OS such a contrast is not available and therefore needs to be estimated using the data.
Therefore, as the first step at stage K, we regress 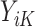 on
on 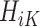 separately for subjects who receive treatment 1 (ie,
separately for subjects who receive treatment 1 (ie, 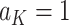 ), or treatment 0 (ie,
), or treatment 0 (ie, 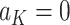 ). These subpopulations are modeled separately to directly model differences in treatment by covariate effects. The regression model is chosen to be a linear model in our analysis, although we can use a nonlinear model by replacing
). These subpopulations are modeled separately to directly model differences in treatment by covariate effects. The regression model is chosen to be a linear model in our analysis, although we can use a nonlinear model by replacing 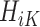 with nonlinear basis functions. We denote the predicted potential outcome for each treatment as
with nonlinear basis functions. We denote the predicted potential outcome for each treatment as 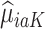 for
for 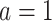 and 0. Due to potential biases in the observational data, the above regression is performed only using the trial data. Once regression parameters from each model (denoted
and 0. Due to potential biases in the observational data, the above regression is performed only using the trial data. Once regression parameters from each model (denoted 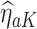 ) are estimated using trial data, the potential outcomes
) are estimated using trial data, the potential outcomes 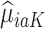 are calculated for all trial and OS participants.
are calculated for all trial and OS participants.
Following the construction of the doubly robust estimator in the literature of heterogeneous treatment effects, we have
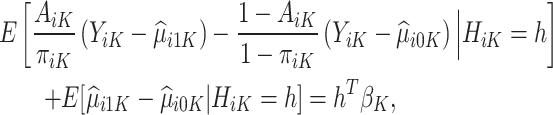 |
assuming that the true treatment effect takes form 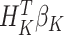 , and that this holds even if the models for
, and that this holds even if the models for 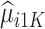 and
and  are not accurate. Note that the first conditional expectation can only be estimated using the trial data, but the second conditional expectation can be estimated using both the trial and OS. Thus, the above equation can be further expressed as
are not accurate. Note that the first conditional expectation can only be estimated using the trial data, but the second conditional expectation can be estimated using both the trial and OS. Thus, the above equation can be further expressed as
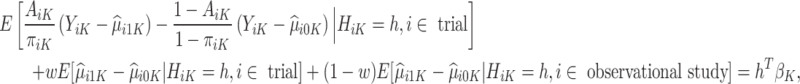 |
(5) |
where w is any value between 0 and 1 and is used to weight the contribution of the contrast term from the trial and OS.
Therefore, for trial participants, we define 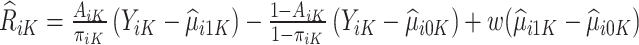 and for OS participants, we let
and for OS participants, we let 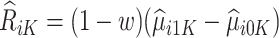 . An estimating equation for
. An estimating equation for 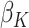 is given by
is given by
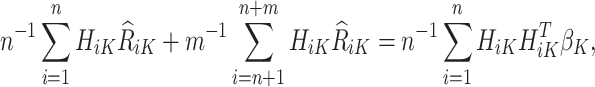 |
with analytical solution,
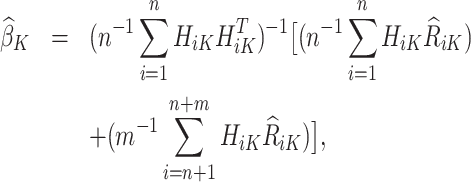 |
where only the trial data contributes to the design matrix.
Then the estimated optimal treatment rule at stage K is 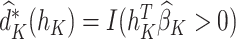 . As a note, when the weight, w, is chosen to be 1, we estimate the conditional mean of the contrast only using the trial data, so
. As a note, when the weight, w, is chosen to be 1, we estimate the conditional mean of the contrast only using the trial data, so 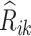 reduces to the doubly robust construction in the literature when there is no OS; when the weight, w, is chosen to be 0, we estimate the conditional mean using the OS.
reduces to the doubly robust construction in the literature when there is no OS; when the weight, w, is chosen to be 0, we estimate the conditional mean using the OS.
To estimate the optimal stage  treatment rule, we must calculate
treatment rule, we must calculate
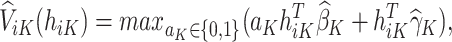 |
(6) |
which is the predicted value of the outcome at stage K if the optimal treatment rule were followed. In the previous step, we estimated 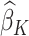 , and therefore the estimated treatment effect is
, and therefore the estimated treatment effect is 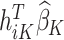 . To calculate the values of
. To calculate the values of 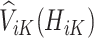 , we estimate the main effects,
, we estimate the main effects, 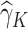 by regressing
by regressing 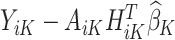 , the residual after removing the estimated treatment effect, on
, the residual after removing the estimated treatment effect, on 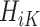 .
.
Next, estimation of the optimal treatment rule for stage  proceeds using a similar algorithm as stage K, but the outcome is the pseudo-outcome given by
proceeds using a similar algorithm as stage K, but the outcome is the pseudo-outcome given by 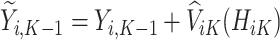 . As such, the predicted contrast function, denoted by
. As such, the predicted contrast function, denoted by 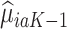 , is estimated using this pseudo-outcome for the trial subjects with treatment
, is estimated using this pseudo-outcome for the trial subjects with treatment 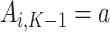 for
for 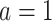 or 0. Similar to stage K, these values are used to estimate
or 0. Similar to stage K, these values are used to estimate 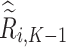 values for trial participants as
values for trial participants as 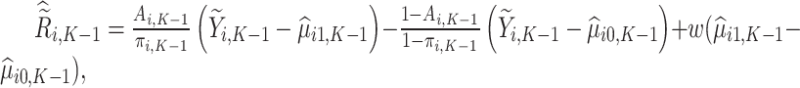 and OS participants as
and OS participants as 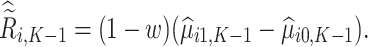
Using the same argument as for stage K, we show
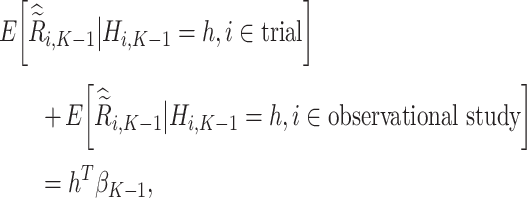 |
assuming that the true treatment effect for the pseudo-outcome takes the same form as the right-hand side. We are therefore able to estimate the optimal treatment rule, 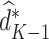 , after solving for
, after solving for 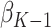 using the estimating equation
using the estimating equation
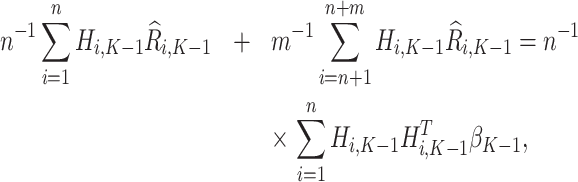 |
with analytical solution,
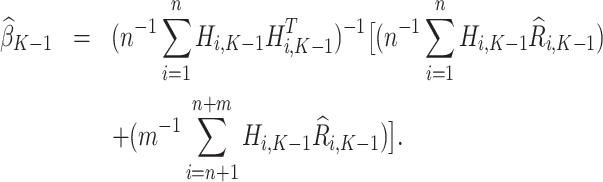 |
The estimated optimal treatment rule at stage  is
is 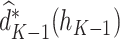 =
= 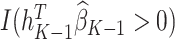 .
.
We continue the same procedure backward from stage 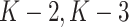 ,..., until stage 1. Finally, we obtain estimation of optimal treatment rules (
,..., until stage 1. Finally, we obtain estimation of optimal treatment rules (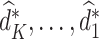 ) sequentially to arrive at
) sequentially to arrive at 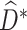 , the estimated optimal DTR. The general algorithm for the MAQE is described in the appendix.
, the estimated optimal DTR. The general algorithm for the MAQE is described in the appendix.
As an example, when K = 2, the estimated optimal DTR is given by the values of 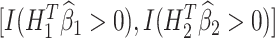 . For a new patient in the clinic, values of a patient’s measured phenotype variables can be multiplied by the regression parameters for stage 1 to determine the optimal treatment for that patient at the first stage. Once the outcome from that treatment is measured, the optimal stage 2 treatment can be determined by multiplying stage 2 covariate history by the regression parameters for stage 2. For each stage, if the sign of the resulting value is positive, the patient should receive treatment A = 1, otherwise they should receive treatment A = 0 (as per Equations 2 and 4).
. For a new patient in the clinic, values of a patient’s measured phenotype variables can be multiplied by the regression parameters for stage 1 to determine the optimal treatment for that patient at the first stage. Once the outcome from that treatment is measured, the optimal stage 2 treatment can be determined by multiplying stage 2 covariate history by the regression parameters for stage 2. For each stage, if the sign of the resulting value is positive, the patient should receive treatment A = 1, otherwise they should receive treatment A = 0 (as per Equations 2 and 4).
3. SIMULATION STUDY AND RESULTS
3.1. Design of the simulation study
Biomarkers for Evaluating Spine Treatments is a two-stage SMART with four stage 1 treatment arms, with the primary aim of estimating an algorithm for optimally assigning cLBP treatments based on an individual’s phenotypic markers and response to treatment. Secondary aims of the trial include assessing long-term effectiveness of the estimated optimal DTRs, and estimating optimal DTRs tailored to patient preferences. Twelve nationally distributed study sites are recruiting cLBP participants for BEST, who have a pain duration over 3 months and pain more than half of the days over the last 6 months, age 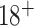 . The target sample size for the study is 630 completers.
. The target sample size for the study is 630 completers.
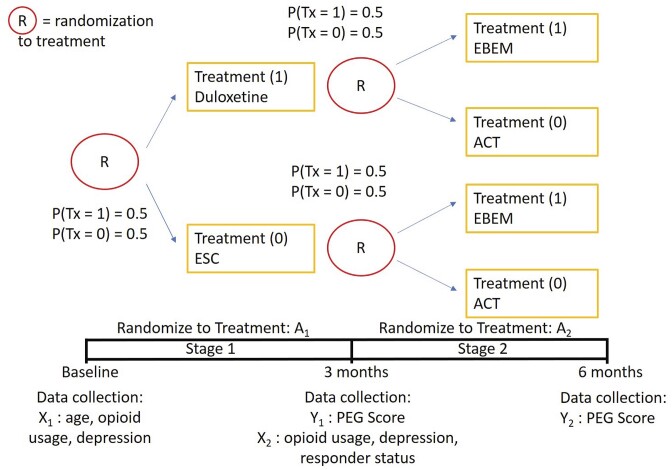
For the purposes of illustration and generalizability to other study designs, we utilize the most basic SMART design for our simulation studies, where randomization to one of two treatment arms occurs at two sequential time points three months apart, instead of randomizing to four treatment arms at both stages (Figure 1). Figure 1 shows the simplified trial design, where participants are randomized with probability 0.5 to either enhanced self-care or duloxetine, coded as 0 and 1, at stage 1, then independent of response status, are randomized with probability 0.5 to either evidence-based exercise and manual therapy or acceptance and commitment therapy, coded as 0 and 1, at stage 2.
FIGURE 1.
Sequential multiple assignment randomized trial design for simulation experiments, including four trial arms, enhanced self-care (ESC), duloxetine, evidence-based exercise and manual therapy (EBEM), and acceptance and commitment therapy (ACT).
The LB3P study at the University of Pittsburgh, one of BACPAC’s mechanistic research centers, is a prospective cohort OS with a target enrollment of 1000 participants (Vo et al., 2023). This study has similar inclusion/exclusion criteria as BEST, and longitudinal cLBP treatment information is captured at similar timepoints as BEST. One of the strengths of BACPAC is that longitudinal data collection was harmonized, whereby the same data elements of the BACPAC Minimum Dataset are required to be collected across all studies at baseline and a 3-month visit to facilitate characterization of cLBP study participants Consortium-wide (Mauck et al., 2023).
Study outcome data elements were also harmonized. The primary outcome for BACPAC studies is the PEG score, which is the average value of three questions about pain severity and pain interference, where for each question, 10 is the worst pain or pain interference imaginable and 0 is no pain or pain interference (Krebs et al., 2009). For simulations, we use a continuous (instead of ordinal) outcome where higher scores are more beneficial, and represent the decrease in pain and/or pain interference between the end of each stage and baseline. Response to first stage treatment (Resp, 1 = yes, 0 = no) for trial and OS participants was defined in simulations as having a stage 1 outcome value higher than the 60th percentile in a simulated dataset comprising 20,000 participants.
One of the goals of the analysis of BEST is to determine which elements of the BACPAC Minimum Dataset could be used as DTR tailoring variables. Tailoring variables are variables used to make treatment decisions, and can be collected at baseline, or during treatment, and may change throughout a treatment sequence (Almirall et al., 2014). In our simulation studies, we use one continuous and two binary variables as tailoring variables for stages 1 and 2. The continuous age variable is denoted by 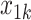 ,
, 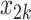 indicates opioid usage (1 = yes, 0 = no), and
indicates opioid usage (1 = yes, 0 = no), and 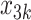 indicates depression symptoms (1 = yes, 0 = no), where k represents the stage number.
indicates depression symptoms (1 = yes, 0 = no), where k represents the stage number.
Table 1 shows selected simulation parameters for the two studies. Opioid usage and depression symptoms at 3 months (start of stage 2) were correlated with baseline values for a given participant. Logistic regression models, with baseline values and stage 1 treatment as model covariates, were used to generate stage 2 (3-month) values. The treatment randomization probabilities at each stage for the OS were based on a logistic regression model using covariates 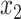 ,
, 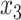 and unobserved confounder, z, at each respective stage.
and unobserved confounder, z, at each respective stage.
TABLE 1.
Selected parameters from simulation study using sequential multiple assignment randomized trial (SMART), observational study (OS), and test datasets.
| SMART | OS | Test Dataset | |
|---|---|---|---|
| Number of participants | 630 | 1000 | 20,000 |
| Age (mean, sd) | 52 (8) | 52 (8) | 52 (8) |
| Opioid usage (Baseline) % | 0.2 | 0.2 | 0.2 |
| Depression symptoms (Baseline) % | 0.3 | 0.3 | 0.3 |
| Opioid usage (3 months) % |
p
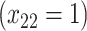 = expit
= expit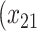 − 0.5 − 0.5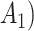
|
p
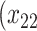 =1) = expit
=1) = expit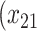 − − 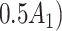
|
p
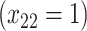 = expit
= expit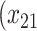 − − 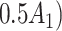
|
| Depression symptoms (3 months) % |
p
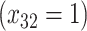 = expit
= expit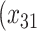 + + 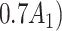
|
p
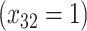 = expit
= expit + + 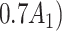
|
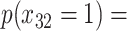 expit
expit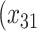 + + 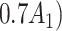
|
| Randomization probabilities at each stage |
p
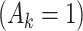 = 0.5
= 0.5 |
p
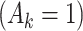 = expit(−0.5
= expit(−0.5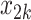 − − 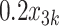 + + 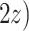
|
p
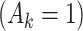 = 0.5
= 0.5 |
The outcome-generating models for stages 1 and 2 are based on main effects of the three selected variables and an unobserved confounder, the interactions of all variables with treatment, as well as interactions of treatment with squared and cubed age terms. At stage 2, the outcome-generating model also includes responder status, an indicator variable for stage 1 treatment, and the interaction between stage 2 treatment and stage 1 treatment. For a full description of the outcome-generating models and rationale, please see Web Appendix A in the Supplementary Materials.
3.2. Evaluation of performance
We evaluate the performance of the MAQE compared with the SQE, an estimator that uses the Q-learning algorithm without data augmentation, introduced in Section 2.2. A 20,000 participant test set was generated using the outcome models and participant covariate distributions from the simulated trial and observational studies, to represent the target population of cLBP patients. For this test set, the probability of a participant being assigned treatment 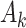 = 1 is 0.5, similar to the trial, instead of using a propensity score model. For a full list of simulation parameters, please see Web Appendix A.
= 1 is 0.5, similar to the trial, instead of using a propensity score model. For a full list of simulation parameters, please see Web Appendix A.
One metric for evaluating performance of the estimators is determining the percentage of test set participants for whom the estimator correctly estimates the optimal treatment sequence, or percent correctly classified (PCC). Because we know the simulation parameters for the outcome models, we are able to record the optimal treatment sequence for test set participants which optimizes the Q-function. For each iteration of the simulation, we use the training SMART and OS datasets to estimate the 2-stage DTRs, then use the regression parameters (ie, estimated optimal DTRs) to estimate the optimal treatment sequence for each participant in the test set. For each simulation run, we record the percentage of test set participants for whom the estimated treatment sequence matches the optimal treatment sequence. We also provide a variance estimate based on running the simulation 500 times.
We also report the value of the MAQE evaluated on the test dataset, where data from the test set consists of treatment 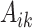 , covariate history
, covariate history 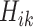 , observed outcome
, observed outcome 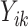 , stage number indexed k from 1 to K, and data from individual i from 1 to N where N = 20 000. As shown in (7), the value of a DTR is defined as the average sum of the outcomes from all stages for participants who followed the estimated optimal treatment rule divided by the probability of receiving that treatment sequence, and is a common metric for comparing DTRs (Chen et al., 2020). The value under the estimated optimal DTR using the MAQE can be compared with the value using other estimators including the SQE. We also compare the results to the value if a one size fits all treatment rule were implemented
, stage number indexed k from 1 to K, and data from individual i from 1 to N where N = 20 000. As shown in (7), the value of a DTR is defined as the average sum of the outcomes from all stages for participants who followed the estimated optimal treatment rule divided by the probability of receiving that treatment sequence, and is a common metric for comparing DTRs (Chen et al., 2020). The value under the estimated optimal DTR using the MAQE can be compared with the value using other estimators including the SQE. We also compare the results to the value if a one size fits all treatment rule were implemented
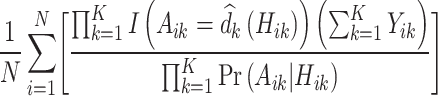 |
(7) |
We denote the estimator where w is equal to the proportion of trial participants, 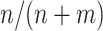 , as the MAQE1 and the estimator where
, as the MAQE1 and the estimator where 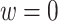 as the MAQE2, the SQE using only OS data as SQE1, the SQE using combined trial and OS data as SQE2, and the SQE using only trial data as SQE3. We demonstrate side by side performance of the MAQE and SQE when varying the sample sizes of the trial and OS relative to each other, and varying the OS sample size when keeping the trial sample size constant.
as the MAQE2, the SQE using only OS data as SQE1, the SQE using combined trial and OS data as SQE2, and the SQE using only trial data as SQE3. We demonstrate side by side performance of the MAQE and SQE when varying the sample sizes of the trial and OS relative to each other, and varying the OS sample size when keeping the trial sample size constant.
3.3. Results of simulation studies
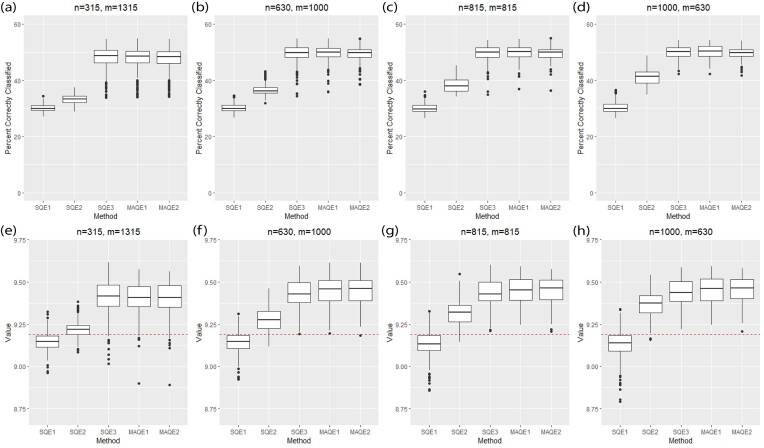
Using the standard simulation parameters (Table 1, Web Appendix A) and the projected sample sizes from BEST and LB3P, the MAQE1 and MAQE2 have a higher PCC and value compared with the SQE1 and SQE2, and similar PCC and value compared with the SQE3 (Table 2, Figure 2b and f). The PCC of the SQEs (30.2%, 36.5%, and 49.6%) and MAQEs (49.7% and 49.4%) can be compared with a mean 25% PCC rate if binary treatments were randomly assigned at each stage without using patient covariates in a decision function. Figure 2 and Table 2 show that for all sample size combinations, the SQE1 using only OS data has poor performance because of unobserved confounding. Naively combining all trial and OS data into the SQE2 gives slightly better performance because the trial data do not have unobserved confounding, but basing estimation solely on the trial data using the SQE3 improves performance dramatically. Figure 2a–d shows that the PCC of the MAQE1 is highest and has smaller variability compared with the SQE3. The MAQE2 has slightly lower PCC compared with the MAQE1 and SQE3 but has smaller variability than either. The slight reduction in accuracy but improvement in variability is likely due to the fact that only the OS data contribute to the contrast term for the MAQE2, compared with the MAQE1 which uses both trial and OS data. Table 2 shows that as the proportion of trial participants increases, the variability of the PCC decreases for the SQE3, MAQE1, and MAQE2, and that the variability of the MAQEs is generally lower than the SQE3, which uses only trial data.
TABLE 2.
Means and standard deviations (sd) of percent correctly classified (PCC) and value of multi-stage augmented Q-learning estimators (MAQE) and standard Q-learning estimators (SQE) with varying sample size ratios where the number of participants in the trial and OS are denoted n and m, respectively. The MAQE1 uses 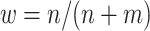 , the MAQE2 uses
, the MAQE2 uses 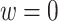 , the SQE1 uses only OS data, the SQE2 uses combined trial and OS data, and the SQE3 uses only trial data.
, the SQE1 uses only OS data, the SQE2 uses combined trial and OS data, and the SQE3 uses only trial data.
| Metric | n | m | SQE1 (mean, sd) | SQE2 (mean, sd) | SQE3 (mean, sd) | MAQE1 (mean, sd) | MAQE2 (mean, sd) |
|---|---|---|---|---|---|---|---|
| PCC | 315 | 1315 | 30.2 (1.19) | 33.2 (1.60) | 48.1 (3.83) | 48.1 (3.62) | 47.9 (3.61) |
| PCC | 630 | 1000 | 30.2 (1.36) | 36.5 (1.76) | 49.6 (2.80) | 49.7 (2.58) | 49.4 (2.27) |
| PCC | 815 | 815 | 30.1 (1.60) | 38.4 (2.36) | 49.8 (2.50) | 50.0 (2.36) | 49.6 (2.31) |
| PCC | 1000 | 630 | 30.3 (1.89) | 41.0 (2.83) | 50.0 (2.27) | 50.2 (2.35) | 49.7 (1.89) |
| Value | 315 | 1315 | 9.15 (0.0485) | 9.22 (0.0482) | 9.41 (0.0939) | 9.41 (0.0881) | 9.41 (0.0893) |
| Value | 630 | 1000 | 9.14 (0.0566) | 9.28 (0.0656) | 9.43 (0.0771) | 9.44 (0.0761) | 9.45 (0.0746) |
| Value | 815 | 815 | 9.14 (0.0705) | 9.32 (0.0735) | 9.44 (0.0734) | 9.45 (0.0743) | 9.45 (0.0726) |
| Value | 1000 | 630 | 9.14 (0.0795) | 9.37 (0.0687) | 9.44 (0.0710) | 9.45 (0.0738) | 9.45 (0.0700) |
FIGURE 2.
Performance of multi-stage augmented Q-learning estimators (MAQE) and standard Q-learning estimators (SQE) with varying trial and observational study (OS) sample size ratios. The MAQE1 uses 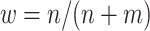 , the MAQE2 uses
, the MAQE2 uses 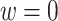 , the SQE1 uses only OS data, the SQE2 uses combined trial and OS data, and the SQE3 uses only trial data. The red dashed line in subfigures (e)–(h) shows the value of the best one size fits all treatment, if all participants follow treatment sequence
, the SQE1 uses only OS data, the SQE2 uses combined trial and OS data, and the SQE3 uses only trial data. The red dashed line in subfigures (e)–(h) shows the value of the best one size fits all treatment, if all participants follow treatment sequence 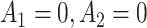 .
.
Figure 2e–h and Table 2 show the MAQE has a higher average value than all versions of the SQE. The values if all participants in the test dataset followed treatment sequences 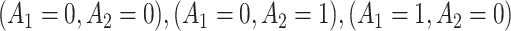 , or
, or 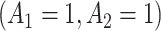 are 9.19, 7.95, 9.01, and 7.92, respectively. The MAQE also has a higher value than if the treatment rule consisted of assigning one of these four sets of treatment sequences to the entire population, ignoring patient characteristics. The red dashed lines in Figure 2e–h show the value of the best one size fits all treatment sequence, if everyone in the test set were to have been assigned treatment sequence
are 9.19, 7.95, 9.01, and 7.92, respectively. The MAQE also has a higher value than if the treatment rule consisted of assigning one of these four sets of treatment sequences to the entire population, ignoring patient characteristics. The red dashed lines in Figure 2e–h show the value of the best one size fits all treatment sequence, if everyone in the test set were to have been assigned treatment sequence 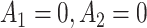 .
.
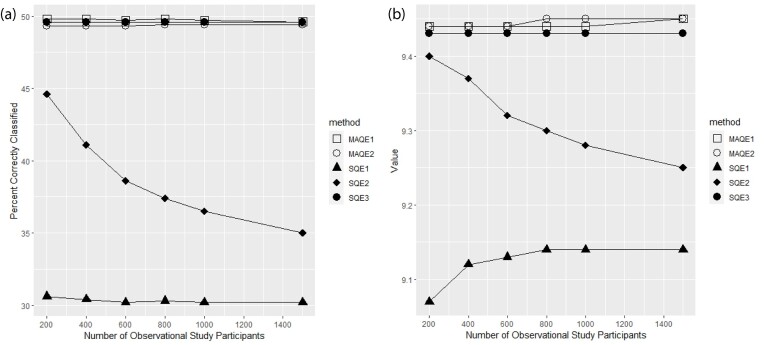
Figure 3 shows that as the number of OS participants increases, the PCC and value of the SQE3, MAQE1, and MAQE2 remain relatively constant but the performance of the SQE2 declines. The performance of the SQE1 stays relatively poor at any OS sample size. We would expect to see this decline in performance of the SQE2 because the higher quality trial data are being diluted by the OS data, which contains an unobserved confounder. The PCC and value for the SQE3 is expected to be constant because it does not use OS data, and due to the nature of the augmented estimator, we would expect the performance of the MAQE to be robust to, and potentially benefit from, addition of OS participants, despite the effects of unobserved confounding in this simulation scenario.
FIGURE 3.
Percent correctly classified and value for the multi-stage augmented Q-learning estimators (MAQE) and standard Q-learning estimators (SQE) as number of observational study (OS) participants varies. The MAQE1 uses 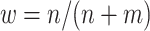 , the MAQE2 uses
, the MAQE2 uses 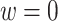 , the SQE1 uses only OS data, the SQE2 uses combined trial and OS data, and the SQE3 uses only trial data.
, the SQE1 uses only OS data, the SQE2 uses combined trial and OS data, and the SQE3 uses only trial data.
It is important to note that the value is generally accepted in the field as the primary metric for evaluating a DTR. Due to covariate profiles, some patients may benefit very little by being assigned an optimal, instead of suboptimal, treatment at a given stage. Therefore, misclassification of these individuals makes less of a difference in the overall outcome for the population.
We can conclude that assigning treatments based on rules estimated from the data results in better outcomes for this patient population than a one size fits all treatment, and that the MAQE has better performance than naively combining the trial and OS data into the SQE when unobserved confounding is expected.
3.4. Sensitivity analyses
For the MAQE to be applicable to a range of real data scenarios, its performance and relative performance compared with other estimators need to be robust to various experimental scenarios. We performed sensitivity analyses to test performance of the MAQE when adding noise variables to the analysis model, changing the magnitude of the treatment effects, and using smaller sample sizes. Results are shown in the Supplementary Materials.
An important consideration when analyzing data is to create an interpretable and parsimonious model by selecting key variables for analysis. Subject matter experts and literature review can provide valuable insight about potential DTR tailoring variables, and model-selection algorithms such as the least absolute shrinkage and selection operator (LASSO) can also be used. All of these sources may be inaccurate, so it is valuable to experiment with the properties of this method in the absence of a reliable variable-selection algorithm. The set of harmonized data elements in BACPAC data includes upward of hundreds of potential tailoring variables that may define cLBP subgroups and could be integral in optimizing DTRs. Web Appendix B describes the parameters for the ten noise variables that were created based in part on variables within the BACPAC Minimum Dataset, with continuous, binary or uniform distributions. Several of the variables are correlated with other variables (Web Appendix B).
Our simulations indicate that as long as the true variables in the outcome-generating model are included in analysis, the performance of the MAQE declines only slightly when including 10 or 20 noise variables (Web Appendix B). Web Figure S1 shows boxplots of the PCC when using noise variables in the analysis model for estimating  and the Q-function. Web Figure S1b shows the reduction in performance of the MAQE is slight, and comparable to the reduction in performance of the SQE, compared with not using these 10 noise variables in the models. We see similar trends in Web Figure S1c, where a further reduction in performance is similar between the MAQE and SQE when including 20 noise variables in the analysis. This shows that the MAQE is reasonably robust to the use of models with noise variables as long as the key variables are also included in the model, and is in all cases an improvement over the SQE1 and SQE2. This is especially useful if the analyst does not have expert opinion for variable selection, or in the absence of a suitable variable selection algorithm.
and the Q-function. Web Figure S1b shows the reduction in performance of the MAQE is slight, and comparable to the reduction in performance of the SQE, compared with not using these 10 noise variables in the models. We see similar trends in Web Figure S1c, where a further reduction in performance is similar between the MAQE and SQE when including 20 noise variables in the analysis. This shows that the MAQE is reasonably robust to the use of models with noise variables as long as the key variables are also included in the model, and is in all cases an improvement over the SQE1 and SQE2. This is especially useful if the analyst does not have expert opinion for variable selection, or in the absence of a suitable variable selection algorithm.
We additionally experiment with simulation parameters where the effect sizes in the trial and OS are smaller or larger than our standard simulation parameters. Web Figure S2 shows boxplots of the PCC when the treatment effect sizes in the trial, OS and test set are 0.5, 1.2, and 2 times that of the standard parameters. As the effect size increases, the accuracy of all estimators also increases, which would be expected. The MAQE has similar or improved performance compared with the SQE regardless of effect size. The improvement in performance when the effect size is smaller is evidence that the MAQE is more efficient than the SQE.
Lastly, we experiment with smaller sample sizes, where the trial has 250 participants and the OS has either 250, 300, or 500 participants. Web Figure S3 shows similar trends for these sample sizes as with the larger sample sizes.
4. DISCUSSION
We show that across various simulation parameters the MAQE consistently performs the same or better than the SQE when used to estimate the optimal treatment sequence for test set participants, and has a higher average value. We demonstrate the performance of the MAQE as compared with the SQE when experimenting with the relative sample size between the trial and OS, total number of trial and OS participants, inclusion of noise variables, and differences in treatment effect sizes.
To apply the MAQE to analysis of BEST, the algorithm can be adapted to analyze a SMART design with more than two treatment options at each stage, and for analysis of other trials, it can be used to analyze more than two treatment stages. The algorithm for the method is amenable to the addition of a large number of potential tailoring variables, and different variable selection method algorithms, such as LASSO, could be applied. This is a key feature of the method since potential tailoring variables may need to be investigated to estimate an optimal DTR for a heterogeneous patient population, such as with cLBP. The use of Q-learning also lends well to interpretability compared with classification-based methods.
The performance of this method depends on the confounding bias in the OS data. We anticipate when there is small bias due to unobserved confounders, integrating OS data with even a small sample size can yield a significant improvement as compared with analyzing the SMART only. Therefore, careful selection of the OS data to minimize differentiable bias between the OS and SMART participants is important for applying this method.
While one goal of developing methods to integrate trial and OS data is to improve efficiency, another is to have greater accuracy when generalizing or transporting a treatment effect or DTR to a target population. In future studies, we will experiment with incorporating established weighting methods into the MAQE to improve generalizability of estimated optimal DTRs to a target population with different covariate distributions. Back Pain Consortium has multiple observational studies with different cLBP patient populations, including BACKhome (University of California San Francisco, 2023), a nation-wide fully remote 3000-participant study coordinated by the University of California San Francisco. Data harmonization and creation of data standards (Batorsky et al., 2023), facilitate longitudinal characterization of cLBP patient phenotypes and integrated analyses across all BACPAC studies. Integrating harmonized data across multiple randomized trials and observational studies can improve efficiency of estimating DTRs and may also improve generalizability to a target population. Spearheaded by the NIH Common Data Elements program (Wandner et al., 2022), it is becoming increasingly common for consortia to have harmonized data collection across multiple randomized trials and observational studies, making methods like the MAQE increasingly useful and easy to implement.
Supplementary Material
Web Appendices, Figures and Tables are available with this paper at the Biometrics website on Oxford Academic. Web Appendix A provides additional details about the simulation parameters referenced in Sections 3.1 and 3.2. Web Appendix B provides descriptions of the simulation studies for the sensitivity analyses and displays the Figures referenced in Section 3.4. R code and accompanying documentation for running the simulations are also included, and are available on Github (https://github.com/abatorsky/MAQE).
ACKNOWLEDGMENTS
We thank the members of the Back Pain Consortium for motivating this research.
Appendix: Algorithm for Multi-stage Augmented Q-learning Estimator
Algorithm 1.
Multi-stage Augmented Q-learning Estimator
Contributor Information
Anna Batorsky, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA.
Kevin J Anstrom, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA.
Donglin Zeng, Department of Biostatistics, School of Public Health, University of Michigan, Ann Arbor, MI 48109, USA.
FUNDING
This work was partly supported by National Institutes of Health grants (R01 GM124104, R01 MH123487, R01 NS073671, and 1-U24-AR076730).
CONFLICT OF INTEREST
None declared.
DATA AVAILABILITY
No new data were generated or analyzed in support of this research.
References
- Almirall D., Nahum-Shani I., Sherwood N. E., Murphy S. A. (2014). Introduction to SMART designs for the development of adaptive interventions: with application to weight loss research. Translational Behavioral Medicine, 4, 260–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batorsky A., Bowden A. E., Darwin J., Fields A. J., Greco C. M., Harris R. E. et al. (2023). The Back Pain Consortium (BACPAC) research program data harmonization: Rationale for data elements and standards. Pain Medicine, 24, S95–S104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellman R. (1957). A markovian decision process. Journal of Mathematics and Mechanics, 6, 679–684. [Google Scholar]
- Chakraborty B., Murphy S. A. (2014). Dynamic treatment regimes. Annual Review of Statistics and Its Application, 1, 447–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Liu Y., Zeng D., Wang Y. (2020). Statistical learning methods for optimizing dynamic treatment regimes in subgroup identification. In: Design and Analysis of Subgroups with Biopharmaceutical Applications, Emerging Topics in Statistics and Biostatistics(eds. Ting N., C. J., Ho S., D.-G. D.), 271–297. Cham: Springer International Publishing. [Google Scholar]
- Colnet B., Mayer I., Chen G., Dieng A., Li R., Varoquaux G. et al. (2021). Causal inference methods for combining randomized trials and observational studies: a review. https://arxiv.org/abs/2011.08047v2. arXiv:2011.08047v2 [stat.ME]. Accessed February 25, 2022.
- Kosorok M. R., Laber E. B. (2019). Precision medicine. Annual Review of Statistics and Its Application, 6, 263–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krebs E. E., Lorenz K. A., Bair M. J., Damush T. M., Wu J., Sutherland J. M. et al. (2009). Development and initial validation of the PEG, a three-item scale assessing pain intensity and interference. Journal of General Internal Medicine, 24, 733–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavori P. W., Dawson R. (2004). Dynamic treatment regimes: practical design considerations. Clinical Trials, 1, 9–20. [DOI] [PubMed] [Google Scholar]
- Lavori P. W., Dawson R., Rush A. J. (2000). Flexible treatment strategies in chronic disease: clinical and research implications. Biological Psychiatry, 48, 605–614. [DOI] [PubMed] [Google Scholar]
- Lipkovich I., Svensson D., Ratitch B., Dmitrienko A. (2023). Overview of modern approaches for identifying and evaluating heterogeneous treatment effects from clinical data. Clinical Trials (London, England), 20, 380–393. [DOI] [PubMed] [Google Scholar]
- Lunceford J. K., Davidian M. (2004). Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Statistics in Medicine, 23, 2937–2960. [DOI] [PubMed] [Google Scholar]
- March J., Kraemer H. C., Trivedi M., Csernansky J., Davis J., Ketter T. A. et al. (2010). What have we learned about trial design from NIMH-Funded pragmatic trials?. Neuropsychopharmacology, 35, 2491–2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauck M. C., Lotz J., Psioda M. A., Carey T. S., Clauw D. J., Majumdar S. et al. (2023). The back pain consortium (BACPAC) research program: structure, research priorities, and methods. Pain Medicine, 24, S3–S12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moodie E. E. M., Chakraborty B., Kramer M. S. (2012). Q-learning for estimating optimal dynamic treatment rules from observational data. The Canadian Journal of Statistics = Revue Canadienne de Statistique, 40, 629–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy S. A. (2005). An experimental design for the development of adaptive treatment strategies. Statistics in Medicine, 24, 1455–1481. [DOI] [PubMed] [Google Scholar]
- Murphy S. A., Lynch K. G., Oslin D., McKay J. R., TenHave T. (2007). Developing adaptive treatment strategies in substance abuse research. Drug and Alcohol Dependence, 88, S24–S30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- NIH HEAL Initiative. (2019). Back Pain Consortium (BACPAC) research program. https://heal.nih.gov/research/clinical-research/back-pain. [Accessed December 4, 2022].
- Robins J. (1986). A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Mathematical Modelling, 7, 1393–1512. [Google Scholar]
- Schulte P. J., Tsiatis A. A., Laber E. B., Davidian M. (2014). Q- and A-learning methods for estimating optimal dynamic treatment regimes. Statistical Science: A Review Journal of the Institute of Mathematical Statistics, 29, 640–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- University of California San Francisco. (2023). Low back pain online study | BACKHOME study. https://backhomestudy.org/. [Accessed December 26, 2022].
- Vo N. V., Piva S. R., Patterson C. G., McKernan G. P., Zhou L., Bell K. M. et al. (2023). Toward the identification of distinct phenotypes: research protocol for the low back pain biological, biomechanical, and behavioral (LB3P) cohort study and the BACPAC mechanistic research center at the University of Pittsburgh. Pain Medicine, 24, S36–S47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandner L. D., Domenichiello A. F., Beierlein J., Pogorzala L., Aquino G., Siddons A. et al. (2022). NIH’s Helping to End Addiction Long-term initiative (NIH HEAL initiative) clinical pain management common data element program. The Journal of Pain, 23, 370–378. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Web Appendices, Figures and Tables are available with this paper at the Biometrics website on Oxford Academic. Web Appendix A provides additional details about the simulation parameters referenced in Sections 3.1 and 3.2. Web Appendix B provides descriptions of the simulation studies for the sensitivity analyses and displays the Figures referenced in Section 3.4. R code and accompanying documentation for running the simulations are also included, and are available on Github (https://github.com/abatorsky/MAQE).
Data Availability Statement
No new data were generated or analyzed in support of this research.