CSTs for Terabyte-Sized Data

Abstract

Generating pangenomic datasets is becoming increasingly common but there are still few tools able to handle them and even fewer accessible to non-specialists. Building compressed suffix trees (CSTs) for pangenomic datasets is still a major challenge but could be enormously beneficial to the community. In this paper, we present a method, which we refer to as RePFP-CST, for building CSTs in a manner that is scalable. To accomplish this, we show how to build a CST directly from VCF files without decompressing them, and to prune from the prefix-free parse (PFP) phrase boundaries whose removal reduces the total size of the dictionary and the parse. We show that these improvements reduce the time and space required for the construction of the CST, and the memory footprint of the finished CST, enabling us to build a CST for a terabyte of DNA for the first time in the literature.

1. Introduction

High-throughput sequencing technologies have allowed many fields—from plant biology [17] to human genetics [16]—to generate pangenomic datasets, which could bring enormous benefits. However, researchers must be able to process terabytes of DNA efficiently for those benefits to be realized, and there are few tools that work well at that scale. Hence, computation is now the bottleneck in pangenomics and we need powerful, general-purpose compressed data structures to catch up with sequencing. Compressed suffix trees (CSTs) could satisfy this need since they offer the same functionality as conventional suffix trees—which have been a standard data structure for nearly 50 years and are used in myriad algorithms and applications (see, e.g., [9,12,13])—but have so far been unable to handle a terabyte of data. Nonetheless, a few CST implementations have recently been proposed for pangenomics—notably Gagie et al.’s [7] based on the r-index and string attractors; Cáceres and Navarro’s [4], based on block trees; and Boucher et al.’s [2] based on prefix-free parsing (PFP), which we refer to as PFP-CST. PFP takes as input a string S and parses S into substrings by sliding a window of length w over the dataset, and introducing a phrase break whenever the hash of the contents of the window are congruent to 0 modulo a parameter p. We refer to such substrings of length w as trigger strings and include them both as a suffix of the preceding phrase and as a prefix of the next phrase. This means that no phrase-suffix of length greater than w is a proper prefix of any other phrase-suffix, giving the parsing its name and allowing us to build a BWT directly from the dictionary of distinct phrases [3]. It was initially developed to build the r-index [3,10], it was later also used to build the XBWT [6] and the eBWT [1].

We present a scalable CST construction algorithm that also uses PFP but with two innovations. First, we develop a method to build the PFP directly from Variant Call Format (VCF) data, which is a compressed form of pangenomics data. A VCF file is obtained by aligning the sequence reads or other genomes to the reference genome and storing the deviations from the reference [5]. This allows for the distribution of the data in a more space-efficient manner, i.e., the 1000 Genomes Project data requires 21GB of space using VCF but requires 6TB when stored uncompressed as FASTA files [16]. Currently, PFP-CST—as well as other current CST implementations—takes as input a set of sequences and, thus, requires decompressing the VCF data before construction. Our first contribution eliminates this.

Next, we develop a method to optimize the dictionary and parse built by PFP. Our algorithm is inspired by Larsson and Moffat’s RePair [11] which repeatedly finds the most common pair of characters in a string and replaces all occurrences of that pair by a new character. Here, we remove trigger strings rather than pairs of characters. Removing a trigger string requires us to remove from the dictionary any phrases for which it is a suffix or prefix, add to the dictionary the concatenation of any pair of phrases such that the first phrase ends with the trigger string and the second starts with it and which appear consecutively in the parse, and merge the phrases in the parse that are separated by the trigger string. This can reduce the total size of the dictionary and parse when the trigger string occurs often in the dataset but only separating a few distinct pairs of phrases. For example, if a common trigger string is the suffix of only one distinct phrase and the prefix of only one other distinct phrase, then it serves no purpose and just makes the parse bigger. We keep a list of trigger strings sorted by how much their removal would change the total size of the dictionary and the parse, and auxiliary data structures that let us update efficiently after removing a trigger string. Our experiments demonstrate that this removal of trigger strings can reduce the combined size of the dictionary and parse substantially.

We refer to our resulting method as RePFP-CST, and demonstrate that it enables us to build a CST for significantly larger datasets than we could before: the largest dataset Boucher et al. considered consisted of 1000 haplotypes of chromosome 19 of the human genome, occupying 60GB in uncompressed FASTA format, for which they built a 20GB PFP-CST in 1 hour using 51GB of peak memory. For comparison, Gagie et al.’s CST based on the r-index and string attractors has never been implemented; Cáceres and Navarro’s CST based on block trees was not able to handle more than 8 haplotypes of chromosome 19; and the CST implementation available in SDSL 2.0 required more than 16 hours and 1TB of memory for only 512 haplotypes of chromosome 19.

In this paper we consider a dataset consisting of chromosomes 17, 18 and 19 from 5000 human haplotypes, for which the FASTA files occupy just over 1TB, and try to build a PFP-CST for it using Boucher et al.’s construction and with RePFP-CST. The files are available for download only in VCF and even just extracting the FASTA files to run Boucher et al.’s construction takes over 3 weeks of CPU time; eventually we gave up and built the PFP from the VCF to test the rest of Boucher et al.’s construction, as well as RePFP-CST. Building the PFP-CST from the unoptimized PFP took 14 hours of CPU time and 900GB of memory and the final CST was 439GB. Optimizing the PFP by removing trigger strings took 5.5 hours of CPU time and 152GB of memory, but then building the RePFP-CST took 7.5 hours of CPU time and 643GB of memory and the final size of the CST was 328GB. As far as we know, no one has built a CST for a terabyte of data before. Our executable and source code is publicly available at: https://github.com/marco-oliva/pfp.

2. Preliminaries

Basic definitions.

A string S is a finite sequence of characters S = S[1..n] = S[1] … S[n] over an alphabet Σ = {c₁, …, c_σ}. We denote by ε the empty string, and the length of S as |S|. We denote by S[i..j] the substring S[i] … S[j] of S starting in position i and ending in position j, with S[i..j] = ε if i > j. For a string S and 1 ≤ i ≤ n, S[1..i] is called the i-th prefix of S, and S[i..n] is called the i-th suffix of S. We call a prefix S[1..i] of S a proper prefix if 1 ≤ i < n. Similarly, we call a suffix S[i..n] of S a proper suffix if 1 < i ≤ n. Lastly, given two strings S = S[1] … S[n] and T = T[1] … T[m] we define as S + T the string obtaining concatenating all the characters from T to S, i.e the string S[1] … S[n]T[1] … T[m].

VCF.

VCF is a widely used text-based file format for distributing and storing pangenomics data, e.g., 1000 Genome Project [16], and 1001 Arabidopsis Project [17]. A VCF file is built by aligning all sequence reads from an individual to the standard reference genome of the species of interest, and the genetic variants and locations of the variants are stored. The FASTA file containing the genome corresponding to the VCF can easily be created by copying the reference genome and replacing each location where there is the variation with the one specified in the VCF.

Review of PFP.

PFP takes as input a string S of length n, and two integers greater than one, which we denote as w and p. It produces a parse of S into overlapping phrases, where each unique phrase is stored in a dictionary. We denote the dictionary as D and the parse as P. As the name suggests, the parse produced by PFP has the property that no suffix of length greater than w of any string in D is a proper prefix of any other suffix in D. The first step of PFP is to append w copies of # to S, where # is a special symbols lexicographically smaller that any element in the Σ and S does not contain w copies of #. For the sake of the explanation we consider the string S′ = #^wS#^w1.

Next, we characterize the set of trigger strings which define the parse of S. Given a parameter p, we construct the set of trigger strings by computing the Karp-Rabin hash, g(t), of substrings of length w, sliding a window of length w over S′ = #^wS#^w, and letting T be the set of substrings t = S′[s..s + w − 1] where g(t) ≡ 0 (mod p) or t = #^w. This set T will be used to parse #^wS#^w. Next, we formally define the dictionary D of PFP.

Given a string S and a set of trigger strings T, we define the dictionary D = {D₁, …, D_|D|} to be the set of substrings of #^wS#^w such that the following holds for each D_i: exactly one proper prefix of D_i is contained in T, exactly one proper suffix of D_i is contained in T, and no other substring of D_i is in T. We can build D by scanning #^wS#^w to find all occurrences of the trigger strings in T and adding to D each substring of #^wS#^w that starts at the beginning of one occurrence and ends at the end of the next one. Lastly, the dictionary is sorted lexicographically.

Given the dictionary D and input string S, we can easily parse S into phrases from D, with consecutive phrases overlapping by w characters. This defines the parse P as a sequence of indices of the phrases in D. We note that S can then be reconstructed from D and P alone. We illustrate PFP using a small example: given w = 2 and #²S#² = ##GATTACAT#GATACAT#GATTAGATA##, we suppose there exists a Karp-Rabin hash that define the set of trigger strings T to be {AC, AG, T#,##}. It follows that the dictionary D is equal to {##GATTAC, ACAT#, AGATA##, T#GATAC, T#GATTAG} and the parse P to be 1, 2, 4, 2, 5, 3.

3. Methods

Here, we describe the algorithmic contributions behind RePFP-CST, namely performing PFP directly from VCF files and filtering trigger strings to compress PFP.

3.1. VCF to PFP

Here we assume to be working on a string S that corresponds to a reference genome, and on a VCF file containing the variations belonging to m sequences S₁, …, S_m. This can easily be generalized to the case where we have multiple references and multiple VCF files. A more detailed explanation will be available in the full version of the paper. The objective here is to obtain the PFP of S, S₁, …, S_m while avoiding parsing phrases of S_i aligned to equal phrases in S (that is, those which do not contain a variation) and only parse those which are different (that is, those which do).

For each sequence S_i, we store its variations in a list $Va{r}_i=\left[v_{i_1},\dots ,v_{i_j}\right]$, where each v_ik is a string over the alphabet {A, C, G, T}. Similarly, we store the positions on the reference of the first character of each variation in a list which we denote as $Po{s}_i=\left[r_{i_1},\dots ,r_{i_j}\right]$, where each $r_{i_k}$ is an integer within [1,|S|] and $r_{i_1}<r_{i_2}<\dots <r_{i_j}$. Lastly we store the number of characters in the reference that the variation is going to change, which we denote as $Le{n}_i=\left[{\ell }_{i_1},\dots ,{\ell }_{i_j}\right]$, where each ${\ell }_{i_k}$ is an integer. These three lists allow us to represent most type of variation commonly stored in a VCF file, i.e. SNPs, insertions, deletions, substitutions and structural variants.

Given w and p, we first parse S using PFP as defined in Section 2. We denote the resulting dictionary, parse, and trigger strings as D_S, P_S, and T_S, respectively. We will now create a dictionary D, parse P, and trigger strings for S and V as follows. First, we add all elements of D_S, P_S, and T_S to D, P, and T, respectively. Next, we generate a parse for S_i using V ar_i, Pos_i, and Len_i for each i = 1, …, m as follows. Starting with the first element of Pos_i (i.e., $r_{i_1}$), we add all elements of P_S to the parse of S_i as long as their position in S is less than $r_{i_1}-w$ , i.e., we add P_S[1], …, P_S[j] to the parse of V_i if $\left|D_{P_S[1]}\right|+\dots +\left|D_{P_S[j]}\right|-jw<r_{i_1}-w$ and $\left|D_{P_S[1]}\right|+\dots +\left|D_{P_S[j+1]}\right|-(j+1)w>r_{i_1}-w$. Let r′ be the last position covered by this parse. We create a temporary string, $S\left[r^{\prime }+1\right],\dots ,S\left[r_{i_1}-1\right]+v_{i_1}+S\left[r_{i_1}+{\ell }_{i_1}+1\right],\dots ,S\left[r^{″}\right]$, where r″ − w is the first position where a new trigger string occurs, and parse it using PFP and discard the temporary string. In general, the temporary string we create may include more than one variation which depends on when the parse stops, e.g., $S\left[r^{\prime }+1\right],\dots ,S\left[r_{i_1}-1\right]+v_{i_1}+S\left[r_{i_1}+{\ell }_{i_1}+1\right],\dots ,S\left[r_{i_k}-1\right]+v_{i_k}+S\left[r_{i_k}+{\ell }_{i_k}+1\right],\dots ,S\left[r^{″}\right].$ Next, we add P_S[j′], …, P_S[j″] to the parse of V_i, where j′ corresponds to the phrase corresponding to S[r″] in P_S, and j″ corresponds to the phrase whose position in S is less than $r_{ik+1}-w$. We parse the temporary string and update the parse, dictionary and trigger strings of V_i as we would with PFP from Section 2. We continue on in this process until all elements of V ar_i have been considered.

This approach lets us avoid re-parsing long substrings of S_i that exactly match the corresponding substrings of S. We store the phrases that occur in S_i but not S in a temporary dictionary, identified by their Karp-Rabin hashes, until we are finished parsing V. At that point we merge the dictionaries and make a pass over the parse, relabelling the phrases with their new lexicographic order. We note that, since it is possible to work on each S_i independently, this process can be easily parallelized using a number of threads less than or equal to m (i.e. the number of sequences in the VCF file).

3.2. Compress PFP via Filtering Trigger Strings

Our method for compressing the dictionary and the parse is inspired by Larsson and Moffat’s RePair. We do not look for the most common pair of phrases to merge, however — which would be the most direct analogue of RePair — and instead we find the trigger string whose removal will decrease the total size of dictionary and parse the most. Moreover, when removing a trigger string we need to merge all the pairs that share said trigger string. To efficiently track the effect of removing a trigger string we formalize the problem as follows and introduce a cost function. We also note that the order of the removal of trigger strings matters.

To describe our algorithm, we begin by assuming that we parsed S into a dictionary D = {D₁, …, D_|D|} and a parse P = [p₁, …, p_|P|]. We aim to derive from D and P a new parse of S, D′ and P′, such that ||D′|| + W|P′| < ||D|| + W|P|, where ||D|| is the sum of the lengths of the phrases in D and W is the size in bytes of one element of the parse. To simplify the notation, given a phrase p_i of the parse, we define |p_i| = |D_pi|. Following from the definition of PFP, we note that each pair of consecutive phrases (p_j, p_j+1) in P overlaps by a trigger string of w characters. Therefore we define a set L_i as the set of pairs of phrases (p_j, p_j+1) for each trigger string T_i, where p_j ends with T_i and p_j+1 starts with T_i. We also define two additional sets $L_{1_i}$ (resp. $L_{2_i}$) that contains the first (resp. second) element of the pairs in L_i, i.e., $L_{1_i}=\left\{p_1\mid \left(p_1,p_2\right)\in L_i\right\}$ and $L_{2_i}=\left\{p_2\mid \left(p_1,p_2\right)\in L_i\right\}$. Furthermore we refer to f(p, q) as the frequency of the pair of phrases (p, q) in P.

Based on the set L_i, we can compute the effect that removing T_i has on the total size of the dictionary and parse. In particular, for each merged pair the size of the parse will reduce by W. The total parse size reduction will amount to W times the number of occurrences of T_i. As for the dictionary, if a pair is merged then its size will increase by the number of characters in the merged phrase, and will decrease by the size of the elements of the pair taken singularly. We can formalize this by defining the following cost functions. We define C_D(T_i) to be the reduction in size of the dictionary due to the removal of T_i, i.e., $C_D\left(T_i\right)={\sum }_{p\in L_{1_i}\cup L_{2_i}}|p|-{\sum }_{\left(p_1,p_2\right)\in L_i}\left(\left|p_1\right|+\left|p_2\right|-w\right)$. Similarly, we define C_P (T_i) as the reduction in the size of the parse, i.e., $C_P\left(T_i\right)={\sum }_{\left(p_1,p_2\right)\in L_i}f\left(p_1,p_2\right)\times W$. We define the total cost of a trigger string T_i as C(T_i) = C_D(T_i) + C_P (T_i).

Hence, the algorithm to derive D′ and P′ consists of finding the trigger string with the highest cost, replacing each pair (p, q) of phrases overlapping in such trigger string with a new symbol u obtained, concatenating to D[p] all the characters of D[q] from position w + 1 on, and updating the frequencies and costs associated with the removal of T_i. The process is repeated until there are no trigger strings with positive cost left.

In order to perform these updates efficiently, we construct and use the following auxiliary data structures. Given the dictionary D and parse P, we construct and store an array A_D for the elements of D, and a double-linked list L_P. Note that, even though A_D start as a sorted array inheriting the ordering from D, during the procedure it looses it’s ordering.

Next, given the set of trigger strings T, we construct an indexed priority queue PQ_T to store the costs C(T_i) for each trigger string T_i in T. The indexed priority queue is a priority queue which allows us to change the priority value of any of the elements in the queue in logarithmic time with respect to the size of the queue [15, Sec. 2.4]. Finally, we construct an array A_T of lists such that for each trigger string T_i in T we store a list of pointers to elements of L_P that end with T_i.

To characterize the running time of the algorithm, we first give the running time of a single iteration in the following lemma.

Lemma 3.1 Given a set of trigger strings T, dictionary D, parse P, data structures PQ_T, L_P, A_T , and A_D, we can remove the trigger string T_i ∈ T that occurs occ times in P, in O(occ log|T| + occ log occ) time and O(occ) additional space, such that the data structures PQ_T′, L_P′, A_T′, and A_D′ are updated, where T′, D′, and P′ are the trigger string set, dictionary and parse obtained by the removal of T_i.

The following paragraphs give an idea of how to achieve the time and space complexity presented in Lemma 3.1, a detailed proof will be included in the full version of the paper. Let ${\text{L}}_{T_i}$ be the list of occ phrases in L_P that end with T_i in L_P order. We construct two arrays A_L and A_R which store the triplets of phrases visited during the process with a trigger string different from T_i on the left or on the right, respectively. For all occurrences $p\in {\text{L}}_{T_i}$, let q be the next element in L_P, that can be obtained in O(1) time. Let T_j and T_k be the trigger strings at the beginning and at the end of p and q respectively, and let ℓ and r be the phrases preceding p and following q in L_P, respectively. Then we insert (p, ℓ, q) in A_L and (q, r, p) in A_R. We will mark the occurrences of deleted phrases from A_D, and append the phrase u in A_D that represents the phrase in D obtained by the concatenation of p and q. Finally, we will remove the occurrence of q and replace the occurrence of p with the concatenated string in L_P. We note that A_T can be updated by ignoring the list of occurrences relative to T_i. Hence, for each occurrence of the trigger string T_i we take O(1) time to update the data structures.

After all the occurrences have been processed, we sort 𝒜_L and 𝒜_R in O(occ log occ) time. This allows to compute for each trigger string T_j the set $L_j^{\prime }=\left\{(p,\ell ,q)\in {\text{A}}_L\mid \right.\ell$ ends with T_j} ∪ {(q, r, p) ∈ A_R | r starts with T_j} of new pairs, the set $L_{{12}_j}=\left\{(p,q)\mid (p,u,q)\in L_j^{\prime }\right\}$ of new single phrases, the set $U_j=\left\{(p,u)\mid (p,u,q)\in L_j^{\prime }\right\}$ of updated pairs, and the set $U_{{12}_j}=\left\{p\mid (p,u,q)\in L_j^{\prime }\right\}$ of updated single phrases from which we can compute the updated costs of $C_D\left(T_j\right)=C_D\left(T_j\right)-{\sum }_{p\in U_{{12}_j}}(|p|)+{\sum }_{(p,q)\in L_{{12}_j}}(|p|+|q|-w)+{\sum }_{(p,u)\in U_j}(|p|+|u|-w)-{\sum }_{(p,u,q)\in L_j^{\prime }}(|p|+|u|+|q|-2w)$ where the second and fourth terms are meant to remove the contribution of the phrases that are going to be merged from the previous value of C_D(T_j), and the third and fifth terms add the contribution of the new phrases obtained by the removal of the trigger string T_i. Furthermore, the scan of the occurrences of T_i in L_P ensure that if a phrase is repeatedly merged with consecutive phrases in L_P then the subsequent operations produces a telescopic sum leading to the correct final cost update. This can happen when we have phrases that starts and ends with the same trigger string T_i. We note that each of the four sets can be obtained by sorting the original arrays A_L and A_R in O(occ log occ) time. Hence, the total time for this phase is O(occ log occ). We then update PQ_T in O(occ log|T|) time. In total we will take O(occ log |T| + occ log occ) time to remove all the occurrences of T_i.

It is also easy to see that by removing all the occurrences of T_i from the parse, and merging all the corresponding phrases, we generate a dictionary D′ and a parse P′ that are a valid prefix-free parsing of the original text S. Next, we present our main theorem. Due to page length, we leave the proof of this theorem to the full version of the paper.

Theorem 3.2 Given a set of trigger strings T, dictionary D, and parse P, we can obtain a new set of trigger strings T′, D′ and P′ such that $C\left(T_i^{\prime }\right)\le 0$ for all $T_i^{\prime }$, in T′ in O(|P|+|D|+|D′| log|D′|+|P| log|P|)) time and O(|P|+|D|+|T| log|T|) space.

4. Experiments and Discussion

Experimental Set-up.

We implemented our method in ISO C++ 2020 and measured the performance using two datasets. Our first set of data was the repetitive corpus from Pizza&Chili [14], which is a collection of repetitive texts characterized by different lengths and alphabet sizes. The second dataset consists of 10 sets of variants of human chromosome 17, 18, and 19 (chr17–19), containing 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, and 5000 distinct sequences where each collection is a superset of the previous one. The smallest of these datasets (chr17–19.500) has size 101.90GB and the largest (chr17–19.5000) has size 1017.16GB with each data point increasing in size by 100GB. The experiments on Pizza&Chili were performed on a server with Intel(R) Xeon(R) CPU E5–2640 v4 @ 2.40GHz with 40 cores and 756GB of RAM, while the experiments on chr17–19 were performed on a server with two AMD(R) EPYC(R) 7702 processors for a total of 128 cores and 1028GB of memory. The running time was recorded with the Unix utility /usr/bin/time and the memory usage with malloc_count². We refer to disk space as the total number of bytes written to disk, including intermediate data. We limited the resources for each run to 2TB of disk space, 1TB of memory and 21 CPU days.

Results on Pizza&Chili.

We first compared the performance using Pizza&Chili and the chromosome 19s from 1000 human haplotypes (chr19.1000). In this experiment, we only evaluated the filtering of the trigger strings, since Pizza&Chili includes multiple collections but none are available in the form of a VCF file. Although the chromosome 19 dataset is available for download only as a VCF, in this experiment we constructed and used the FASTA files for this dataset to make it consistent with Pizza&Chili. We first built the PFP on the input data and then we compressed with the method in Section 3.2 (RePFP). In Table 1, we report the size of the dictionary and parse produced by PFP, and the size of the dictionary and parse produced from RePFP. The space savings on the size of the PFP ranged from 1% to 57%, with the highest compression obtained on einstein.en.txt (57%) and the second and third highest compression obtained on einstein.de.txt and chr19.1000, respectively.

Table 1:

Performance of RePFP for the Pizza&Chili repetitive corpus and 1000 variants of chromosome 19 in FASTA format. We report the alphabet size σ and dataset size n in MB. The size of the dictionary and parse before and after RePFP are given in MB. Lastly, we report the compression ratio and space saving provided by RePFP, where the compression ratio is the ratio of the total size of PFP over the total size of RePFP, while the space saving is 1 minus the reciprocal of the compression ratio expressed in percentage.

	Description		PFP		RePFP		Compression Metrics
Name	σ	n	Dict	Parse	Dict	Parse	Compression	Space Savings
cere	5	461.28	90.34	16.99	91.33	15.26	1.01	1%
einstein.de.txt	117	92.21	1.31	3.49	1.70	0.82	1.90	47%
einstein.en.txt	139	465.24	3.25	17.83	4.91	4.22	2.31	57%
Escherichia_Coli	15	112.68	52.57	4.48	52.63	4.10	1.01	1%
influenza	15	154.80	49.10	6.27	49.43	5.43	1.01	1%
kernel	160	249.51	14.78	9.95	15.03	4.59	1.26	21%
para	5	429.26	84.87	16.34	86.26	14.08	1.01	1%
world_leaders	89	46.90	10.71	1.02	10.70	0.85	1.02	2%
chr19.1000	5	60,110.54	274.57	2219.08	541.09	951.65	1.67	40%

Results on Chromosome 17, 18, 19.

Here, we compare RePFP-CST to PFP-CST [2]. PFP-CST is the most recent CST implementation and was shown to require less memory and time for construction than Cáceres and Navarro’s block tree-based CST [4], and the CST of the SDSL library [8]. While RePFP-CST is able to work directly from a VCF file, PFP-CST requires the input to either be text or FASTA format. Therefore, we first evaluate the CPU time, memory and disk space that would be required to extract FASTA files from VCF using bcftools consenus, and thus, the savings obtained by building the dictionary and parse directly from VCF. This is shown in Table 2. More than 21 CPU days were needed to extract chr17–19.2500 from VCF, hence we were not able to evaluate PFP-CST on any bigger dataset. By building the PFP directly from the VCF we obtain a maximum speedup of 33.4x to build the PFP and of 25.3x on the construction of the whole CST.

Table 2:

Comparison of the CST construction using PFP-CST and RePFP-CST. We compared the CPU time (“Time”), peak memory (“Memory”), and disk space (“Disk”) required to build a CST using PFP-CST and RePFP-CST. PFP-CST requires extraction to FASTA file and building the PFP (“Extraction & PFP”) then construction of CST from PFP (“Construction of CST”). RePFP-CST builds the PFP from VCF, filters trigger strings from the PFP, and builds the CST from the compressed PFP. Memory is in GB. Time is hh:mm::ss.

Sequences of chr17–19	PFP-CST									RePFP-CST
	Extraction & PFP			Construction of CST			Total for PFP-CST			Total for
	Time	Mem	Disk	Time	Mem	Disk	Time	Mem	Disk	Time	Mem	Disk
500	125:52:05	0.94	122.34	00:58:25	85.44	38.80	126:50:30	85.44	161.14	06:08:23	65.31	66.50
1000	251:27:49	1.29	243.19	01:56:03	156.38	69.23	253:23:53	156.38	312.43	10:54:48	121.22	124.14
1500	376:55:26	1.50	363.99	03:08:23	305.37	150.04	380:03:49	305.37	514.04	15:51:24	163.20	232.07
2000	502:23:32	1.84	484.79	4:17:56	380.04	192.95	506:41:28	380.04	677.74	20:20:02	288.34	302.18
2500	NA	NA	NA	NA	NA	NA	NA	NA	NA	25:05:44	360.25	372.29
3000	NA	NA	NA	NA	NA	NA	NA	NA	NA	29:51:21	422.42	441.46
3500	NA	NA	NA	NA	NA	NA	NA	NA	NA	35:00:43	464.20	508.25
4000	NA	NA	NA	NA	NA	NA	NA	NA	NA	39:51:01	540.62	577.48
4500	NA	NA	NA	NA	NA	NA	NA	NA	NA	46:03:01	584.04	645.29
5000	NA	NA	NA	NA	NA	NA	NA	NA	NA	50:30:21	643.81	711.80

Next, in order to fully evaluate the effect filtering the trigger strings has on the CST construction, we eliminated the need for PFP-CST to build from a FASTA file and compared the performance of PFP-CST (using the PFP constructed from the VCF) to RePFP-CST. Figure 1 illustrates the peak memory, CPU time and the size of the CST. Filtering resulted in an average reduction of the size of PFP across all the collections of 36.27%, where the minimum was 34.87% on chr17–19.500 and the maximum was 36.67% on chr17–19.1750. This led to an average reduction of the CPU time required to build the CST of 37.17% with a maximum of 45.41% and a minimum of 28.19%. Furthermore, it led to an average reduction of the peak memory of 27.65% with a maximum of 46.56% and a minimum of 22.48%. Lastly, the reduction on the size of the data structure averaged on 21.11% with a maximum of 25.22% and a minimum of 15.30%. Note that the percentage reduction of CPU time, memory and disk space increased with the number of haplotypes in the collection ranging from 30.65% CPU time, 23.57% memory and 15.30% disk on chr17–19.500 to 45.41% CPU time, 28.45% memory and 25.22% disk on chr17–19.5000.

Figure 1:

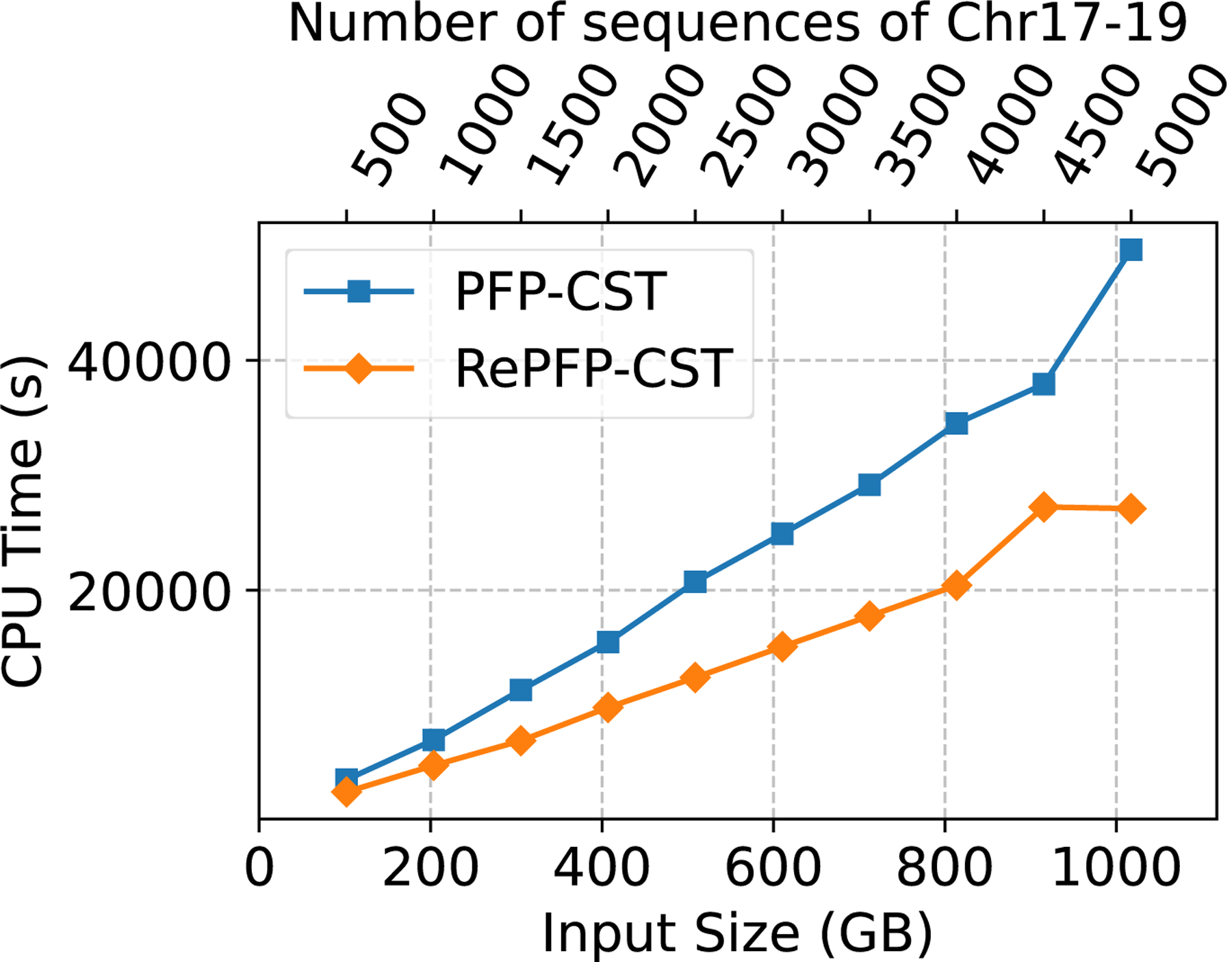
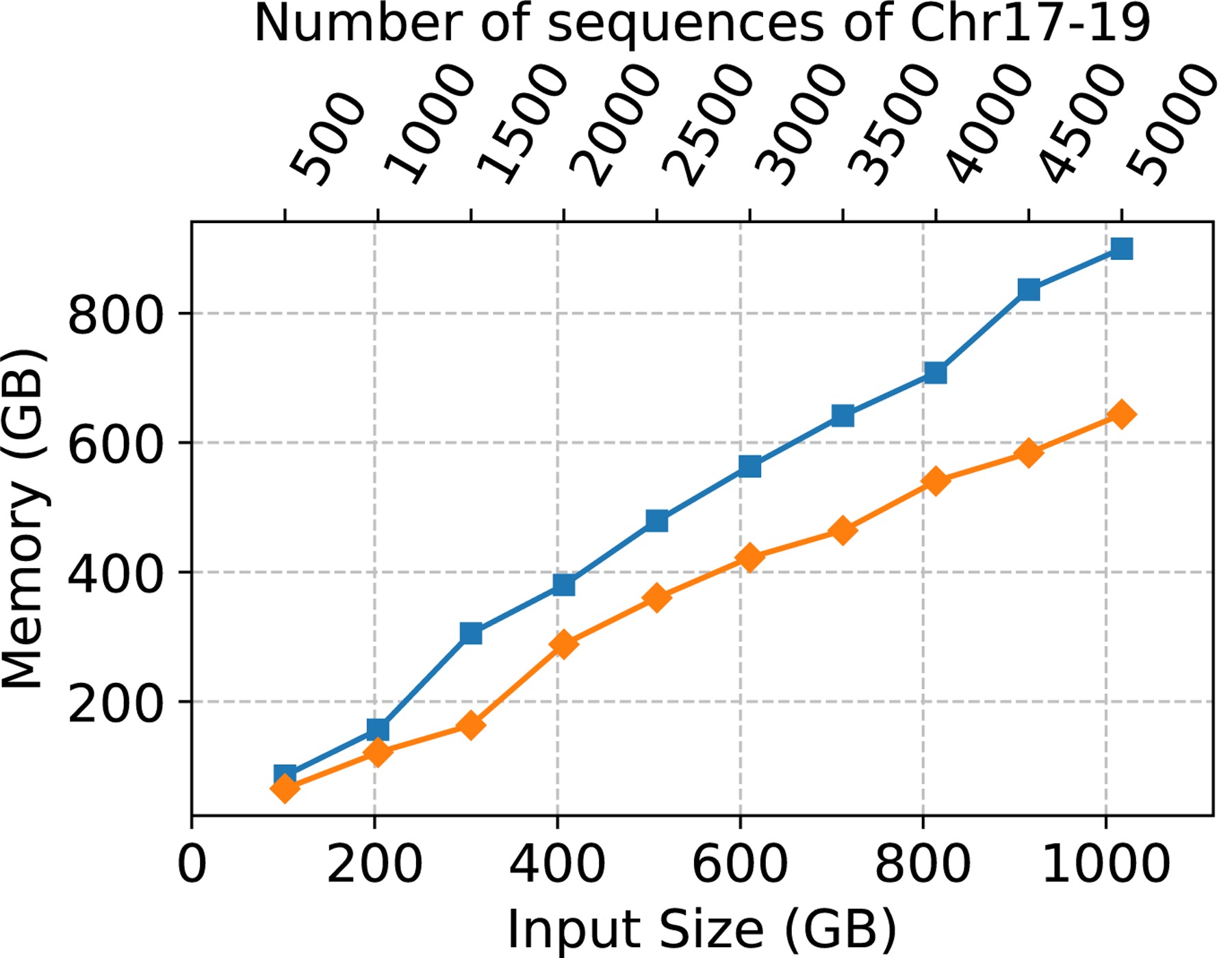
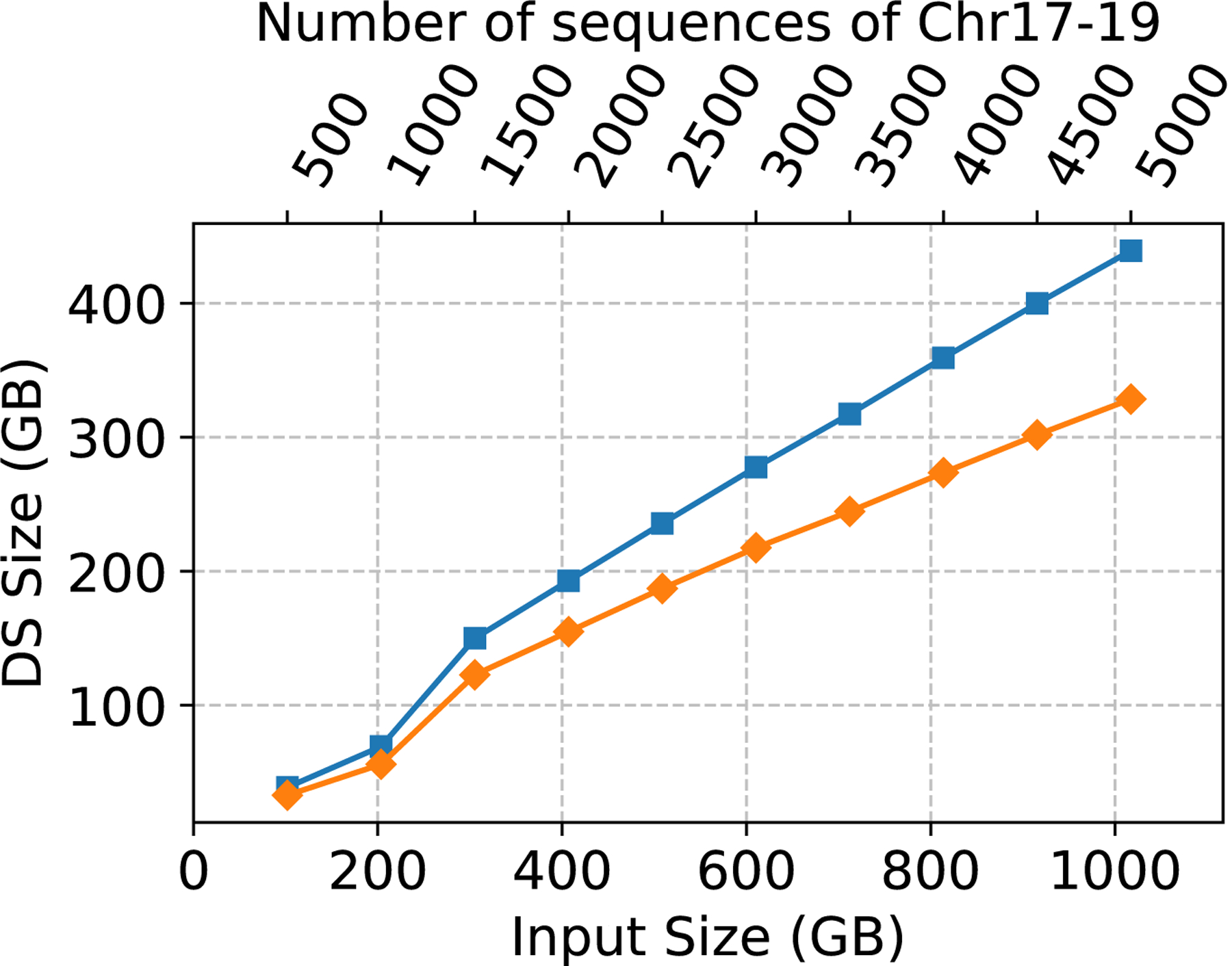
Chromosomes 17–19 construction CPU time (left), peak memory in GB (center), and data structure size in GB (right).