Rethinking Semi-Supervised Medical Image Segmentation: A Variance-Reduction Perspective

Abstract

For medical image segmentation, contrastive learning is the dominant practice to improve the quality of visual representations by contrasting semantically similar and dissimilar pairs of samples. This is enabled by the observation that without accessing ground truth labels, negative examples with truly dissimilar anatomical features, if sampled, can significantly improve the performance. In reality, however, these samples may come from similar anatomical regions and the models may struggle to distinguish the minority tail-class samples, making the tail classes more prone to misclassification, both of which typically lead to model collapse. In this paper, we propose ARCO, a semi-supervised contrastive learning (CL) framework with stratified group theory for medical image segmentation. In particular, we first propose building ARCO through the concept of variance-reduced estimation and show that certain variance-reduction techniques are particularly beneficial in pixel/voxel-level segmentation tasks with extremely limited labels. Furthermore, we theoretically prove these sampling techniques are universal in variance reduction. Finally, we experimentally validate our approaches on eight benchmarks, i.e., five 2D/3D medical and three semantic segmentation datasets, with different label settings, and our methods consistently outperform state-of-the-art semi-supervised methods. Additionally, we augment the CL frameworks with these sampling techniques and demonstrate significant gains over previous methods. We believe our work is an important step towards semi-supervised medical image segmentation by quantifying the limitation of current self-supervision objectives for accomplishing such challenging safety-critical tasks.¹

1. Introduction

Model robustness and label efficiency are two highly desirable perspectives when it comes to building reliable medical segmentation models. In the context of medical image analysis, a model is said to be robust if (1) it has a high segmentation quality with only using extremely limited labels in long-tailed medical data; (2) and fast convergence speed [1, 2, 3]. The success of traditional supervised learning depends on training deep networks on a large amount of labeled data, but this improved segmentation/model robustness often comes at the cost of annotations and clinical expertise [4, 5, 6]. Therefore, it is difficult to adopt these models in real-world clinical applications.

Recently, a significant amount of research efforts [7, 8, 9, 10] have resorted to unsupervised or semi-supervised learning techniques for improving the segmentation robustness. One of the most effective methods is contrastive learning (CL) [11, 12, 13, 14]. It aims to learn useful representations by contrasting semantically similar (positive) and dissimilar (negative) pairs of data points sampled from the massive unlabeled data. These methods fit particularly well with real-world clinical scenarios as we assume only access to a large amount of unlabelled data coupled with extremely limited labels. However, pixel-level contrastive learning with medical image segmentation is quite impractical since sampling all pixels can be extremely time-consuming and computationally expensive [15]. Fortunately, recent studies [16, 17] provide a remedy by leveraging the popular strategy of bootstrapping, which first actively samples a sparse set of pixel-level representation (queries), and then optimize the contrastive objective by pulling them to be close to the class mean averaged across all representations in this class (positive keys), and simultaneously pushing apart those representations from other class (negative keys). The demonstrated imbalancedness and diversity across various medical image datasets, as echoed in [18], show the positive sign of utilizing the massive unlabeled data with extremely limited annotations while maintaining the impressive segmentation performance compared to supervised counterparts. Meanwhile, it can lead to substantial memory/computation reduction when using pixel-level contrastive learning framework for medical image segmentation.

Nevertheless, in practical clinical settings, the deployed machine learning models often ask for strong robustness, which is far beyond the scope of segmentation quality for such challenging safety-critical scenarios. This leads to a more challenging requirement, which demands the models to be more robust to the collapse problems whereby all representations collapse into constant features [14, 13, 19] or only span a lower-dimensional subspace [20, 21, 22, 23], as one main cause of such fragility could be attributed to the non-smooth feature space near samples [24, 25] (i.e., random sampling can result in large feature variations and even annotation information alter). Thus, it is a new perspective: how to sample most informative pixels/voxels towards improving variance reduction in training semi-supervised contrastive learning models. This inspires us to propose a new hypothesis of semi-supervised CL. Specifically, when directly baking in variance-reduction sampling into semi-supervised CL frameworks for medical image segmentation, the models can further push toward state-of-the-art segmentation robustness and label efficiency.

In this paper, we present ARCO, a semi-supervised strAtifed gRoup Contrastive learning framework with two perspectives (i.e., segmentation/model robustness and label efficiency), and with the aid of variance-reduction estimation, realize two practical solutions – Stratified Group (SG) and Stratified-Antithetic Group (SAG) – for selecting the most semantically informative pixels. ARCO is a group-based sampling method that builds a set of pixel groups and then proportionally samples from each group with respect to the class distribution. The main idea of our approach is via first partitioning the image with respect to different classes into grids with the same size, and then sampling, within the same grid, pixels semantically close to each other with high probability, with minimal additional memory footprint.

Subsequently, we show that baking ARCO into contrastive pre-training (i.e., MONA [17]) provides an efficient pixel-wise contrastive learning paradigm to train deep networks that perform well in long-tailed medical data. ARCO is easy to implement, being built on top of off-the-shelf pixel-level contrastive learning framework [13, 14, 26, 27, 28], and consistently improve overall segmentation quality across all label ratios and datasets (i.e., five 2D/3D medical and three semantic datasets).

Our theoretical analysis shows that, ARCO is more label efficient, providing practical means for computing the gradient estimator with improved variance reduction. Empirically, our approach achieves competitive results across eight 2D/3D medical and semantic segmentation benchmarks. Our proposed framework has several theoretical and practical contributions:

• We propose ARCO, a new CL framework based on stratified group theory to improve the label efficiency and model robustness trade-off in CL for medical image segmentation. We show that incorporating ARCO coupled with two special sampling methods, Stratified Group and Stratified-Antithetic Group, into the models provides an efficient learning paradigm to train deep networks that perform well in those long-tail clinical scenarios.

• To our best knowledge, we are the first work to show the benefit of certain variance-reduction techniques in CL for medical image segmentation. We demonstrate the unexplored advantage of the refined gradient estimator in handling long-tailed medical image data.

• We conduct extensive experiments to validate the effectiveness of our proposed method using a variety of datasets, network architectures, and different label ratios. For segmentation robustness/accuracy, we show that our proposed method by demonstrating superior segmentation accuracy (up to 11.08% absolute improvements in Dice). For label efficiency, our method trained with different labeled ratios – consistently achieves competitive performance improvements across all eight 2D/3D medical and semantic segmentation benchmarks.

• Theoretical analysis of ARCO shows improved variance reduction with optimization guarantee. We further demonstrate the intriguing property of ARCO across the different pixel-level contrastive learning frameworks.

2. Related work

Medical Image Segmentation.

Contemporary medical image segmentation approaches typically build upon fully convolutional networks (FCN) [29] or UNet [30], which formulates the task as a dense classification problem. In general, current medical image segmentation methods can be cast into two sets: network design and optimization strategy. One is to optimize segmentation network design for improving feature representations through dilated/atrous/deformable convolutions [31, 32, 33], pyramid pooling [34, 35, 36], and attention mechanisms [37, 38, 39]. Most recent works [40, 41, 6] reformulates the task as a sequence-to-sequence prediction task by using the vision transformer (ViT) architecture [42, 43]. The other is to improve optimization strategies, by designing loss function to better address class imbalance [44] or refining uncertain pixels from high-frequency regions improving the segmentation quality [45, 46, 47, 48, 49]. In contrast, we take a leap further to a more practical clinical scenario by leveraging the massive unlabeled data with extremely limited labels in the learning stage. Moreover, we focus on building model-agnostic, label-efficiency framework to improve segmentation quality by providing additional supervision on the most confusing pixels for each class. In this work, we question how medical segmentation models behave under such imbalanced class distributions and whether they can perform well in those challenging scenarios through sampling methods.

Semi-Supervised Learning (SSL).

SSL aims to train models with a combination of labeled, weakly-labeled and unlabelled data. In recent years, there has been a surge of work on semi-supervised medical segmentation [8, 9, 50, 48, 16, 51, 52, 17, 10, 53, 54], which makes it hard to present a complete overview here. We therefore only outline some key milestones related to this study. In general, it can be roughly categorized into two groups: (1) Consistency regularization was first proposed by [55], which aims to impose consistency corresponding to different perturbations into the training, such as consistency regularization [56, 57], pi-model [58], and mean-teacher [59, 60]. (2) Self-training was initially proposed in [61], which aims at using a model’s predictions to obtain noisy pseudo-labels for performance boosts with minimal human labor, such as pseudo-labeling [7, 62], model uncertainty [8, 63], confidence estimation [64, 65, 66], and noisy student [67]. These methods usually lead to competitive performance but fail to prevent collapse due to class imbalanceness. In this work, we focus on semi-supervised medical segmentation with extremely limited labels since the medical image data is extremely diverse and often long-tail distributed over anatomical classes. We speculate that a good medical segmentation model is expected to distinguish the minority tail-class samples and hence achieve better performance under additional supervision on hard pixels.

Contrastive Self-Supervised Learning.

Self-supervised representation learning is a subclass of unsupervised learning, but with the critical distinction that it incorporates “inherent” supervision from the input data itself [68]. The primary aim of self-supervised representation learning is to enable the model to learn the most useful representations from the large amount of unlabelled data for various downstream tasks. Self-supervised learning typically relies on pretext tasks, including predictive [69, 70, 71], contextual [72, 73], and generative [74] or reconstructive [75] tasks.

Among them, contrastive learning is considered as a popular approach for self-supervised representation learning by pulling the representations of similar instances closer and representations of dissimilar instances further apart in the learned feature space [11, 12, 13, 14]. The past five years have seen tremendous progress related to CL in medical image segmentation [50, 23, 76, 48, 16, 17, 77], and it becomes increasingly important to improve representation in label-scarcity scenarios. The key idea in CL [11, 12, 13, 14] is to learn representations from unlabeled data that obey similarity constraints by pulling augmented views of the same samples closer in a representation space, and pushing apart augmented views of different samples. This is typically achieved by encoding a view of a data into a single global feature vector. However, the global representation is sufficient for simple tasks like image classification, but does not necessarily achieve decent performance, especially for more challenging dense prediction tasks. On the other hand, several works on dense contrastive learning [50, 23], aim at providing additional supervision to capturing intrinsic spatial structure and fine-grained anatomical correspondence, while these methods may suffer from class imbalance issues. Particularly, very recent work [16, 17] for the first time demonstrates the imbalancedness phenomenon can be mitigated by performing contrastive learning yet lacking stability. By contrast, a key motivation of our work is to bridge the connection between model robustness and label efficiency, which we believe is an important and under-explored area. We hence focus on variance-reduced estimation in medical image segmentation, and show that certain variance-reduction techniques can help provide more efficient approaches or alternative solutions for handling collapse issues, and improving model robustness in terms of accuracy and stability. To the best of our knowledge, we are the first to provide a theoretical guarantee of robustness by using certain variance-reduction techniques.

3. Methodology

In this section we set-up our semi-supervised medical segmentation problem, introduce key definitions and notations and formulate an approach to incorporate stratified group theory. Then, we discuss how our proposed ARCO can directly bake in two perspectives into deep neural networks: (1) model robustness, and (2) label efficiency.

3.1. Preliminaries and setup

Problem Definition.

In this paper, we consider the multi-class medical image segmentation problem. Specifically, given a medical image dataset $(𝒳,𝒴)$, we wish to automatically learn a segmentator, which assigns each pixel to their corresponding $K$-class segmentation labels. Let us denote x as the input sample of the student and teacher networks $F(\cdot$)², consisting of an encoder $E$ and a decoder $D$, and $F$ is parameterized by weights ${\theta }_s$ and ${\theta }_t$.

Background.

Contrastive learning aims to learn effective representations by pulling semantically close neighbors together and pushing apart other non-neighbors [11]. Among various popular contrastive learning frameworks, MONA [17] is easy-to-implement while yielding the state-of-the-art performance for semi-supervised medical image segmentation so far. The main idea of MONA is to discover diverse views (i.e., augmented/mined views) whose anatomical feature responses are homogeneous within the same or different occurrences of the same class type, while at the same time being distinctive for different class types.

Hereinafter, we are interested in showing that certain variance-reduction techniques coupled with CL frameworks are particularly beneficial in long-tail pixel/voxel-level segmentation tasks with extremely limited labels. We hence build our ARCO as a simplification of the MONA pipeline [17], without additional complex augmentation strategies, for deriving the model robustness and label efficiency proprieties of our medical segmentation model. Figure 1 overviews the high-level workflow of the proposed ARCO framework. Training ARCO involves a two-phase training procedure: (1) relational semi-supervised pre-training, and (2) anatomical contrastive fine-tuning. To make the discussion self-contained, we defer the full details of ARCO to the appendix E.

Figure 1: Pipeline overview.

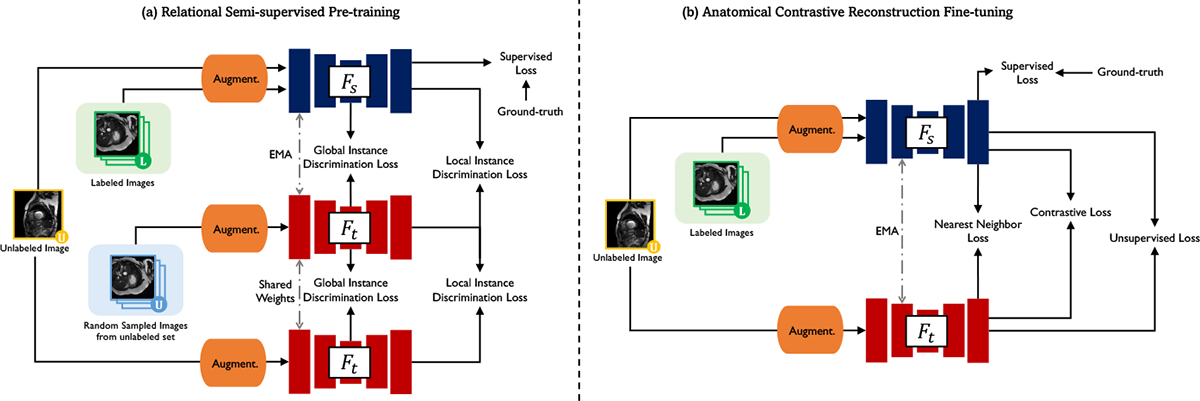
Our semi-supervised segmentation model $F$ takes a 2D/3D medical image $x$ as input and outputs the segmentation map and the representation map. We leverage a simplification of MONA pipeline [17] which is composed of two stages: (1) relational semi-supervised pre-training: on labeled data, the student network is trained by the ground-truth labels with the supervised loss ${ℒ}_{\text{sup}}$; while on unlabeled data, the student network takes the augmened and mined embeddings from the EMA teacher for instance discrimination ${ℒ}_{\text{inst}}$ in the global and local manner, (2) anatomical contrastive reconstruction fine-tuning: on labeled data, the student network is trained by the ground-truth labels with the supervised loss ${ℒ}_{\text{sup}}$; while on unlabeled data, the student network takes the representation maps and pseudo labels from the EMA teacher to give more importance to tail class ${ℒ}_{\text{contrast}}$, exploit the inter-instance relationship ${ℒ}_{\text{nn}}$, and compute unsupervised loss ${ℒ}_{\text{unsup}}$. See Appendix M for details of the visualization loss landscapes.

3.2. Motivation and Challenges

Intuitively, the contrastive loss will learn generalizable, balanced and diverse representations for downstream medical segmentation tasks if the positive and negative pairs correspond to the desired latent anatomical classes [50, 16, 17]. Yet, one critical constraint in real-world clinical scenarios is severe memory bottlenecks [15, 16]. To address this issue, current pixel-level CL approaches [16, 17] for high-resolution medical images devise their aggregation rules by unitary simulators, i.e., Naïve Sampling (NS), that determines the empirical estimate from all available pixels. Despite the blessing of large learning capacity, such aggregation rules are unreliable “black boxes”. It is never well understood which rule existing CL models should use for improved model robustness and label efficiency; nor is it easy to compare different models and assess the model performance. Moreover, unitary simulators, especially naïve sampling, often incur high variances and fail to identify semantically similar pixels [24], limiting CL stability. As demonstrated in Figure 3, regions of similar anatomical features should be grouped together in the original medical images, resulting in corresponding plateau regions in the visualization of the loss landscape. This is consistent with the observations uncovered by the recent empirical findings [79, 80].

Figure 3:

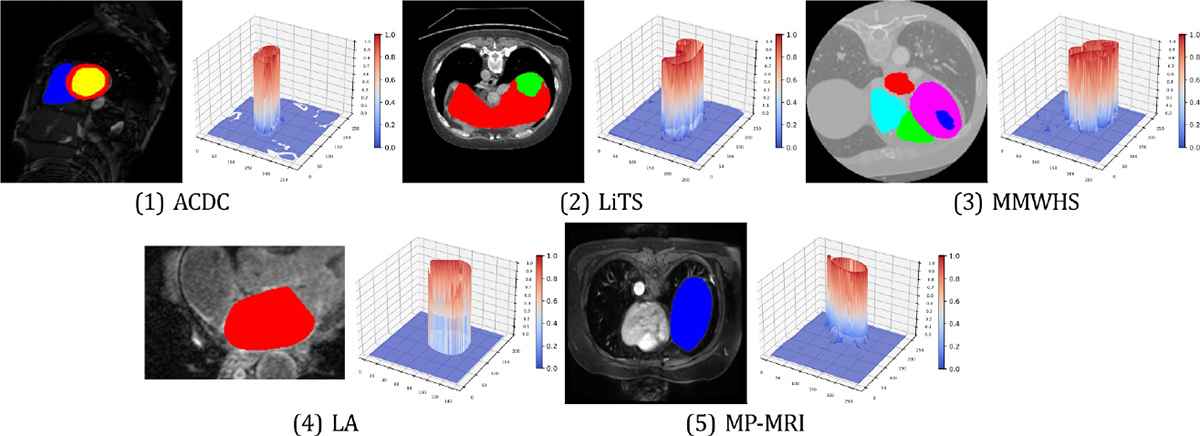
Loss landscape visualization of pixel-wise contrastive loss ${ℒ}_{\text{contrast}}$ with ARCO-SG. Loss plots are generated with same original images randomly chosen from ACDC [81], LiTS [82], MMWHS [83], LA [84], and MP-MRI, respectively. $z$-axis denotes the loss value at each pixel. For each example of the five benchmarks, the left subplot indicates that similar anatomical features are grouped together in the original medical images, as shown by different anatomical regions in different colors.

If we take a unified mathematical perspective, the execution of simulation can be represented either through an adaptive rule, or by a unitary simulation. To tackle the two critical issues, we look back at adaptive rules. We hence propose two straightforward yet effective techniques – Stratified Group (SG) and Stratified-Antithetic Group (SAG) – to mitigate the undesirable high-variance limitation, and turn to the following idea of sampling the most representative pixels from groups of semantically similar pixels. In particular, our proposed solution is based on stratified group simulation to adaptively characterize anatomical regions found on different medical images. This characterization is succinct, and regions with the same anatomical properties within different medical images are identifiable. In practice, we first partition the image with respect to different classes into grids with the same size, and then sampling, within the same grid, the pixels semantically close to each other with high probability, with minimal additional memory footprint (Figure 2).

Figure 2:

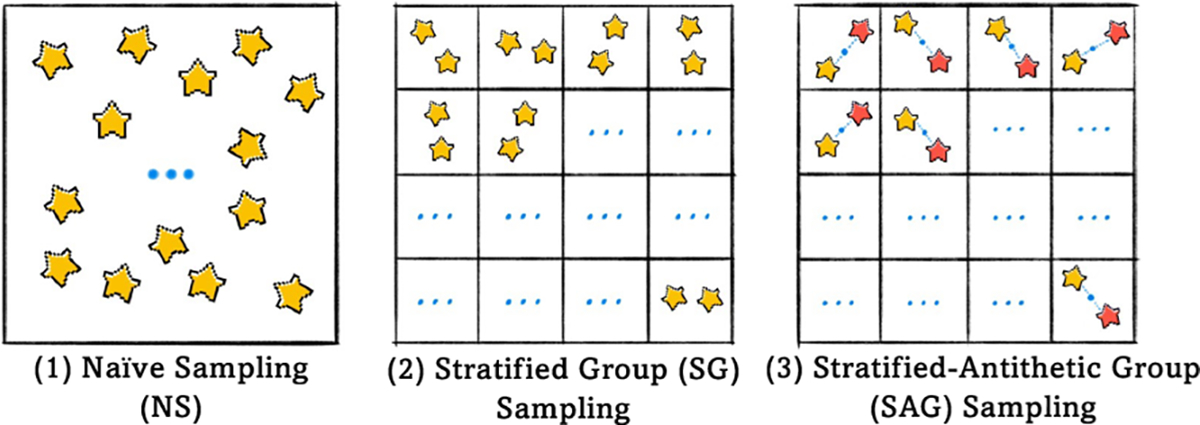
Overview of three sampling methods. (1) Naïve Sampling, (2) Stratified Group Sampling, and (3) Stratified-Antithetic Group Sampling.

In what follows, we will theoretically demonstrate the important properties of such techniques (i.e., SG and SAG), especially in reduced variance and unbiasedness. Here the reduced variance implies more robust gradient estimates in the backpropagation, and leads to faster and stabler training in theory, as corroborated by our experiments (Section 4). Empirically, we will demonstrate many practical benefits of reduced variances including improved model robustness, i.e., faster convergence and better segmentation quality, through mitigating the collapse issue.

3.3. Stratified Group Sampling

To be consistent with the previous notation, we denote an arbitrary image from the given medical image dataset as $\mathbf{x}\in 𝒳$, and $𝒫$ as the set of pixels. For arbitrary function $h:𝒳\times 𝒫\to \mathbb{R}$, we define the aggregation function $H$³ as:

$$H\left(\mathbf{x}\right)=\frac{1}{\left|𝒫\right|}\sum _{p\in 𝒫} h\left(\mathbf{x};p\right).$$ (3.1)

As a large cardinality of $𝒫$ prevents efficient direct computation of $H$, an immediate approach is to compute $H\left(\mathbf{x}\right)$ by first sampling a subset of pixels $𝒟\subseteq 𝒫$ according to certain sampling strategy, and then computing $\widehat{H}(\mathbf{x};𝒟)={\sum }_{p\in 𝒟} h(\mathbf{x};p)/\left|𝒟\right|$. SG sampling achieves this by first decomposing the pixels into $M$ disjoint groups ${𝒫}_m$ satisfying ${\cup }_{m=1}^M{𝒫}_m=𝒫$, and then sampling ${𝒟}_m\subseteq {𝒫}_m$ so that $𝒟={\cup }_{m=1}^M{𝒟}_m$. The SG sampling can then be written as:

$${\widehat{H}}_{\mathrm{S}\mathrm{G}}\left(\mathbf{x};𝒟\right)=\frac{1}{M}\sum _{m=1}^M \frac{1}{\left|{𝒟}_m\right|}\sum _{p\in {𝒟}_m} h\left(\mathbf{x};p\right).$$

SAG, built upon SG, adopts a similar form, except for an additionally enforced symmetry on ${𝒟}_m:\forall m,\exists c_m\in {𝒫}_m$, such that for any $p\in {𝒟}_m$,

$$c_m-p=p^{\prime }-c_m,\text{for}\text{some}{p}^{\prime }\in {𝒟}_m.$$

Here $c_m$ denotes the center of the group ${𝒫}_m$⁴. The implementation of SG and SAG involves two steps: (1) to create groups ${\left\{{𝒫}_m\right\}}_{m=1}^M$, and (2) to generate each ${𝒟}_m\subseteq {𝒫}_m$. For the latter, we consider independent sampling within and between groups, i.e., ${𝒟}_m⫫𝒟m^{\prime }$ for $m\ne m^{\prime }$, and $p⫫p^{\prime }\forall p,p^{\prime }\in {𝒟}_m$, where the variance of SG sampling is as follows.

Lemma 3.1. Suppose in SG sampling, for each $m$, ${𝒟}_m$ is sampled from ${𝒫}_m$ with sampling variance ${\sigma }_m^2$ and sample size $\left|{𝒟}_m\right|=n_m$. Then the variance satisfies $\mathrm{V}\mathrm{a}\mathrm{r}\left[{\widehat{H}}_{\mathrm{S}\mathrm{G}}\right]={\sum }_{m=1}^M {\sigma }_m^2{n}_m/n$, and SAG with the same sample size satisfies $\mathrm{V}\mathrm{a}\mathrm{r}\left[{\widehat{H}}_{\mathrm{S}\mathrm{A}\mathrm{G}}\right]\le 2\mathrm{V}\mathrm{a}\mathrm{r}\left[{\widehat{H}}_{\mathrm{S}\mathrm{G}}\right]$.

To ensure the unbiasedness property, we adopt the setting of proportional group sizes [85, 86], i.e., $\left|{𝒟}_m\right|\propto \left|{𝒫}_m\right|$ for all $m$. It turns out that such setting also enjoys the variance-reduction property.

Theorem 3.2 (Unbiasedness and Variance of SG). SG with proportional group sizes is unbiased, and has a variance no larger than that of NS. That is: $\mathbb{E}\left[{\widehat{H}}_{\mathrm{S}\mathrm{G}}\left(\mathbf{x}\right)\right]=H\left(\mathbf{x}\right)$, and

$$\text{Var}\left[{\widehat{H}}_{\text{SG}}\right]=\text{Var}\left[{\widehat{H}}_{\text{NS}}\right]-\frac{1}{n}\sum _{m=1}^M{\left({\mathbb{E}}_{p\stackrel{\text{uinf}.}{\sim }{𝒫}_m}[h(\mathbf{x};p)]-{\mathbb{E}}_{p\stackrel{\text{uinf}.}{\sim }𝒫}[h(\mathbf{x};p)]\right)}^2.$$

The last term is the intra-group variance, which captures the discrepancy between the pixel groups ${\left\{{𝒫}_m\right\}}_{m=1}^M$. Theorem 3.2 guarantees that the variance of SG is no larger than that of NS, and SG has strictly less variance than NS as long as all the pixel groups do not share an equal mean over $h(\mathbf{x};p)$, which is almost-sure in medical images (See Figure 3). For SAG, Lemma 3.1 guarantees its variance is of the same magnitude as that of SG, and at worst differs by a factor of 2. Since the pixel/voxel-level contrastive loss ${ℒ}_{\text{contrast}}$ is an aggregation function over pixels by definition (E.2), it benefits from the variance-deduction property of SG/SAG. In Section 4.1, we will see that such variance reduction allows ARCO to achieve better segmentation accuracy, especially along the boundary of the anatomical regions (Figure 4).

Figure 4:

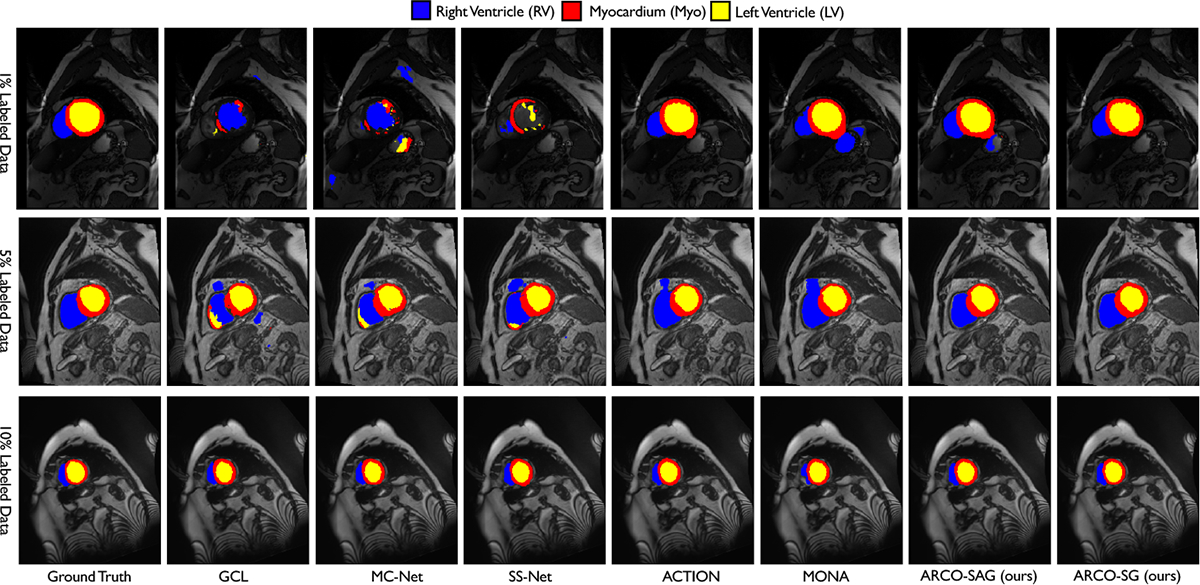
Visual results on ACDC with 1%, 5%, 10% label ratios. ARCO consistently produce more accurate predictions on anatomical regions and boundaries compared to all other SSL methods.

Training Convergence.

We further demonstrate the benefit of variance reduction estimation in terms of training stability. Specifically, leveraging techniques from standard optimization theory [87, 88, 89], we can show that variance-reduced gradient estimator through SG sampling leads to faster training convergence. Suppose we have a loss function $ℒ\left(\theta \right)$ with the model parameter $\theta$, and use stochastic gradient descent (SGD) as the optimizer. A gradient estimate $\left(\theta \right)\approx \nabla ℒ\theta$) is computed at each iteration. It is well-known that the convergence of SGD depends on the quality of the estimate $g\left(\theta \right)$ [87]. Specifically, we make the common assumptions that the loss function is smooth and the gradient estimate has bounded variance (More details in Appendix A.3), which can be formulated as below:

$${∥\nabla ℒ\left(\theta \right)-\nabla ℒ\left({\theta }^{\prime }\right)∥}_2\le L\left({∥\theta -{\theta }^{\prime }∥}_2\right),\mathbb{E}\left[\parallel g\left(\theta \right)-\nabla ℒ\left(\theta \right){\parallel }^2\right]\le {\sigma }_g^2.$$

Under these two assumptions, the average expected gradient norm of the learned parameter satisfies the following:

$$\frac{1}{T}\sum _{t=1}^T \mathbb{E}\left[{∥\nabla ℒ\left({\theta }_t\right)∥}_2^2\right]\le C\left(\frac{1}{T}+\frac{{\sigma }_g}{\sqrt{T}}\right).$$

For general non-convex loss function, the above implies convergence to some local minimum. Importantly, the slow rate $\left({\sigma }_g/\sqrt{T}\right)$ depends on standard deviation ${\sigma }_g$, indicating a faster convergence can indeed be achieved with a more accurate gradient estimate. This indicates our proposed sampling techniques demonstrate universality in variance reduction, as they can be applied to a wide range of scenarios that involve pixel/voxel-level sampling (See Appendix A.3). In Figure 5, we observe that using SG enables faster loss decay with smaller error bar, showing that it outperforms other methods in both convergence speed and stability. See Section 4.2 and Appendix A.3 for more details.

Figure 5:

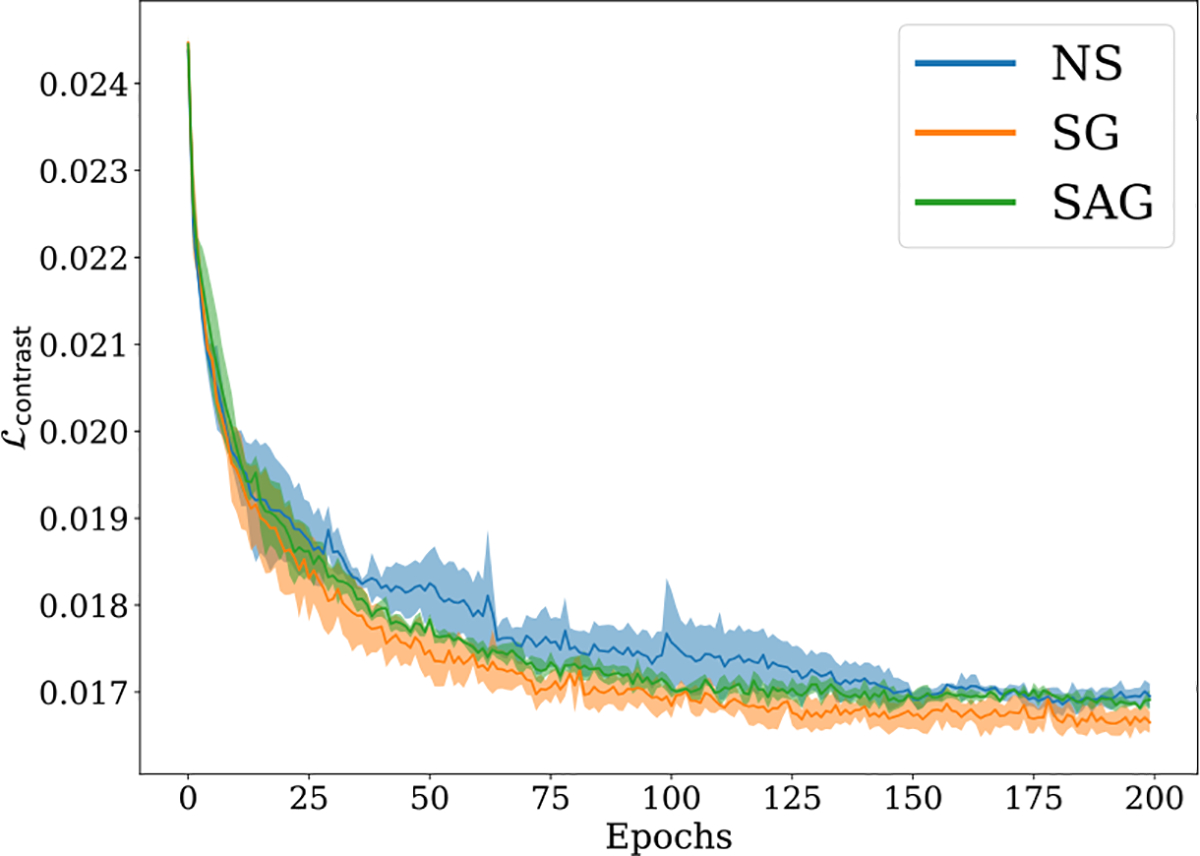
Visualization of training trajectories given by ${ℒ}_{\text{contrast}}$ vs. epochs on ACDC under 10% label ratio. The proposed ARCO is compared in terms of different sampling methods: Naïve Sampling (NS), Stratified Group (SG) Sampling, and Stratified-Antithetic Group (SAG) Sampling. The solid line and shaded area of each sampling method denote the mean and variance of test accuracies over 3 independent trials. Clearly, we observe SG sampling consistently outperforms the other sampling methods in convergence speed and training stability. SAG slightly outperforms NS.

4. Experiments

In this section, we present experimental results to validate our proposed methods across various datasets and different label ratios in Appendix B. We use 2D UNet [30] or 3D VNet [78] as our backbones. Further implementation details are discussed in Appendix C.⁵

4.1. Main Results

In this subsection, we first examine whether our proposed ARCO can generalize well across various datasets and label ratios. Then, we investigate to what extent ARCO coupled with two samplers can realize two essential properties: (1) model robustness; and (2) label efficiency. The quantitative results for all the compared methods on eight popular datasets: (1) Medical image segmentation tasks: three 2D benchmarks (i.e., ACDC [81], LiTS [82], MMWHS [83]), two 3D benchmarks (i.e., LA [84], in-house MP-MRI) under various label ratios (i.e., 1%, 5%, 10%) are collected in Table 1, Table 5 (Appendix G), Table 6 (Appendix H), and Table 9 (Appendix I and J), respectively; (2) General computer vision tasks: To further validate the effectiveness, we experiment on three popular segmentation benchmarks (i.e., Cityscapes [97], Pascal VOC 2012 [98], indoor scene segmentation dataset – SUN RGB-D [99]) in the semi-supervised full-label settings. We follow the identical setting [100] to sample labelled images to ensure that every class appears sufficiently in our three datasets, (i.e., CityScapes, Pascal VOC, and SUN RGB-D). The results are collected in Appendix Section K. Several consistent observations can be drawn from these extensive evaluations with eighteen segmentation networks.

Table 1:

Quantitative comparisons (DSC[%] ↑ / ASD[voxel] ↓) across the three labeled ratio settings (1%, 5%, 10%) on the ACDC benchmark. All experiments are conducted as [30, 90, 91, 92, 93, 8, 94, 9, 57, 95, 62, 50, 59, 96, 53, 16, 17] in the identical setting for fair comparisons. Best and second-best results are coloured blue and red, respectively. UNet-F (fully-supervided) and UNet-L (semi-supervided) are considered as the upper bound and the lower bound for the performance comparison. Note that, Right Ventricle → RV, Myocardium → Myo, Left Ventricle → LV. We adopt the identical data augmentation (i.e., random rotation, random cropping, and horizontal flipping) for fair comparisons.

Method	ACDC
	Average	1 Labeled (1%)			Average	3 Labeled (5%)			Average	7 Labeled (10%)
		RV	Myo	LV		RV	Myo	LV		RV	Myo	LV
UNet-F [30]	91.5/0.996	90.5/0.606	88.8/0.941	94.4/1.44	91.5/0.996	90.5/0.606	88.8/0.941	94.4/1.44	91.5/0.996	90.5/0.606	88.8/0.941	94.4/1.44
UNet-L	40.3/22.7	29.0/25.4	43.6/15.3	48.2/27.5	51.7/13.1	36.9/30.1	54.9/4.27	63.4/5.11	79.5/2.73	65.9/0.892	82.9/2.70	89.6/4.60
EM [90]	43.1/18.1	38.7/23.1	42.0/12.0	48.7/19.4	59.8/5.64	44.2/11.1	63.2/3.23	71.9/2.57	75.7/2.73	68.0/0.892	76.5/2.70	82.7/4.60
CCT [91]	48.6/19.2	38.7/28.0	49.2/14.8	57.9/17.0	59.1/10.1	44.6/19.8	63.2/6.04	69.4/4.32	75.9/3.60	67.2/2.90	77.5/3.32	82.9/4.59
DAN [92]	48.9/17.5	45.4/19.7	41.0/8.88	60.4/23.8	56.4/15.1	47.1/21.7	58.1/11.6	63.9/11.9	76.5/3.01	75.7/2.61	73.3/3.11	80.5/3.31
URPC [57]	43.0/21.1	38.6/22.8	41.7/14.4	48.6/26.0	58.9/8.14	50.1/12.6	60.8/4.10	65.8/7.71	83.1/1.68	77.0/0.742	82.2/0.505	90.1/3.79
DTC [9]	51.7/17.5	39.3/23.3	54.6/9.12	61.3/20.2	56.9/7.59	35.1/9.17	62.9/6.01	72.7/7.59	84.3/4.04	83.8/3.72	83.5/4.63	85.6/3.77
DCT [93]	49.7/16.4	42.4/20.4	48.8/10.6	57.9/18.2	58.5/10.8	41.2/21.4	63.9/5.01	70.5/6.05	78.1/2.64	70.7/1.75	77.7/2.90	85.8/3.26
ICT [95]	42.1/21.0	36.5/18.5	43.4/11.1	46.3/33.5	59.0/6.59	48.8/11.4	61.4/4.59	66.6/3.83	80.6/1.64	75.1/0.898	80.2/1.53	86.6/2.48
MT [59]	42.9/15.1	32.5/21.9	46.2/8.99	50.1/14.7	58.3/11.2	39.0/21.5	58.7/7.47	77.3/4.72	80.1/2.33	75.2/1.22	79.2/2.32	86.0/3.45
UAMT [8]	36.9/15.2	32.5/21.9	46.2/8.99	50.1/14.7	48.3/9.14	37.6/18.9	50.1/4.27	57.3/4.17	81.8/4.04	79.9/2.73	80.1/3.32	85.4/6.07
SASSNet [94]	42.6/24.8	29.8/34.7	45.4/13.3	52.5/26.6	57.8/6.36	47.9/11.7	59.7/4.51	65.8/2.87	84.7/1.83	81.8/0.769	82.9/1.73	89.4/2.99
CPS [62]	51.5/15.3	41.1/17.7	52.0/7.27	61.4/21.0	61.0/2.92	43.8/2.95	64.5/2.84	74.8/2.95	78.8/3.41	74.0/1.95	78.1/3.11	84.5/5.18
GCL [50]	59.7/14.3	49.5/25.3	60.9/6.28	68.8/11.5	70.6/2.24	56.5/1.99	70.7/1.67	84.8/3.05	87.0/0.751	86.9/0.584	81.8/0.820	92.5/0.849
MC-Net [96]	53.4/17.17	43.0/25.3	51.2/7.41	60.8/15.11	62.8/2.59	52.7/5.14	62.6/0.807	73.1/1.81	86.5/1.89	85.1/0.745	84.0/2.12	90.3/2.81
SS-Net [53]	63.4/2.94	64.7/3.32	57.0/1.81	68.4/3.70	65.8/2.28	57.5/3.91	65.7/2.02	74.2/0.896	86.8/1.40	85.4/1.19	84.3/1.44	90.6/1.57
ACTION [16]	81.0/3.45	76.9/3.09	78.4/2.07	87.5/5.17	86.6/1.20	85.2/0.734	84.7/0.909	89.8/1.97	87.2/1.47	86.1/0.976	85.7/1.11	89.7/2.33
MONA [17]	82.6/1.43	80.2/1.57	79.9/1.10	87.8/1.43	86.9/1.07	84.7/1.01	85.4/0.731	90.6/1.48	87.7/1.33	86.9/0.687	85.7/1.70	90.5/2.14
● ARCO-SAG (ours)	84.9/1.47	81.7/1.98	81.9/0.903	90.9/1.52	87.1/0.848	85.6/0.414	85.1/0.930	90.6/1.20	88.5/1.40	87.1/0.635	86.2/1.04	92.2/2.53
○ ARCO-SG (ours)	85.5/0.947	81.8/1.19	83.8/0.801	90.9/0.853	88.7/0.841	88.2/0.618	85.9/0.673	91.9/1.23	89.4/0.776	90.2/0.701	86.5/0.787	91.6/0.839

❶. Superior Performance Across Datasets.

We demonstrate that ARCO achieves superior performance across all datasets and label ratios. In specific, our experiments consider three 2D benchmarks (i.e., ACDC [81], LiTS [82], MMWHS [83]), two 3D benchmarks (i.e., LA [84], in-house MP-MRI), and different label ratios (i.e., 1%, 5%, 10%). As shown in Table 1, Table 5 (Appendix G), Table 6 (Appendix H), and Table 9 (Appendix I and J), we observe that our methods consistently outperform all the compared SSL-based methods by a considerable margin across all datasets and label ratios, which validates the superior performance of our proposed methods in both segmentation accuracy and label efficiency. For example, compared to the second-best MONA, our ARCO-SG under {1%, 5%, 10%} label ratios achieves {2.9%↑, 1.8%↑, 1.7%↑}, {3.3%↑, 1.8%↑, 1.8%↑}, {4.1%↑, 2.0%↑, 1.8%↑}, {0.3%↑, 0.3%↑, 0.5%↑}, {2.2%↑, 0.8%↑, 0.4%↑} in average Dice across ACDC, LiTS, and MMWHS, MP-MRI, and LA, respectively. Our ARCO-SAG achieves {84.9%, 87.1%, 88.5%}, {64.1%, 67.3%, 69.4%}, {86.1%, 88.6%, 89.3%}, {91.5%, 92.5%, 92.6%}, {73.2%, 86.9%, 89.1%} in averaged Dice across ACDC, LiTS, MMWHS, MP-MRI, and LA. These results indicate that our methods can generalize to different clinical scenarios and label ratios.

❷. Across Label Ratios and Robustified Methods.

To further validate the label efficiency property of our ARCO, we evaluate our ARCO-SG and ARCO-SAG with limited labeled training data available (e.g., 1% and 5%). As demonstrated in Table 1, Table 5 (Appendix G), Table 6 (Appendix H), and Table 9 (Appendix I and J), our models under 5% label ratios surpass all the compared SSL methods by a significant performance margin. For example, compared to MONA, we observe our methods to push the best segmentation accuracy higher by 0.3%~2.0% in Dice on ACDC, LiTS, and MMWHS, MP-MRI, and LA, respectively. For example, the best segmentation accuracy on MMWHS rises from 87.3% to 89.3%. This suggests that our SSL-based approaches – without compromising the best achievable segmentation results – robustly improve performance using very limited labels, and further lead to a much-improved trade-off between SSL schemes and supervised learning schemes by avoiding a large amount of labeled data.

Similar to our results under 5% label ratio, our ARCO-SG and ARCO-SAG trained with 1% label ratio demonstrate sufficient performance boost compared to MONA by an especially significant margin, with up to 0.3%~4.1% relative improvement in Dice. Taking the extremely limited label ratio (i.e., 1%) as an indicator: (1) on 3D LA, ARCO-SG achieves 2.2% higher average Dice, and 6.64 lower average ASD than the second best MONA; (2) on LiTS, ARCO-SG achieves 3.3% higher average Dice, and 4.7 lower average ASD than the second best MONA; and (3) considering the more challenging clinical scenarios (i.e., 7 anatomical classes), ARCO-SG achieves 5.1% higher average Dice, and 2.26 lower average ASD than the second-best MONA on MMWHS. It highlights the superior performance of ARCO is not only from improved label efficiency but also credits to the superior model robustness.

❸. Qualitative Results.

We provide qualitative illustrations of ACDC, LiTS, MMWHS, LA, MP-MRI in Figure 4, Figure 6 (Appendix G), Figure 7 (Appendix H), Figure 8 (Appendix I), and Figure 9 (Appendix J), respectively. As shown in Figure 4, we observe that ARCO appears a significant advantage, where the edges and the boundaries of different anatomical regions are clearly more pronounced, such as RV and Myo regions. More interestingly, we found that in Figure 6, though all methods may confuse ambiguous tail-class samples such as small lesions, ARCO-SG and ARCO-SAG still produces consistently sharp and accurate object boundaries compared to the current approaches. We also observe similar results for ARCO on MMWHS in Figure 7 (Appendix H), where our approaches can regularize the segmentation results to be smooth and shape-consistent. Our findings suggest that ARCO improves model robustness mainly through distinguishing the minority tail-class samples.

4.2. Ablation Studies

In this subsection, we conduct various ablations to better understand our design choices. For all the ablation experiments the models are trained on ACDC with 1% labeled ratio.

Importance of Loss Components.

We analyse several critical components of our method in the final performance and conduct comprehensive ablation studies on the ACDC dataset with a 1% label ratio to validate their necessity. First, at the heart of our method is the combination of three losses: ${ℒ}_{\text{contrast}}$ for tailness, and ${ℒ}_{\mathrm{n}\mathrm{n}}$ for diversity (See Section 3 for more details). We deactivate each component and then evaluate the resulting models, as shown in Table 2. As is shown, global contrastive loss ${ℒ}_{\text{contrast}}$ and nearest neighbor loss ${ℒ}_{\mathrm{n}\mathrm{n}}$ can boost performance by a large margin. Moreover, incorporating our methods (i.e., SG and SAG) consistently achieve superior model robustness gains compared to naïve sampling (i.e., NS), both of which suggests the importance of these components. Second, we compare the impact of different loss function (e.g., unsupervised $\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}/{ℒ}_{\text{unsup}}$, global instance discrimination $\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}/{ℒ}_{\text{inst}}^{\text{global}}$, and local instance discrimination $\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\left./{ℒ}_{\text{inst}}^{\text{local}}\right)$. As shown in Table 3, using each loss function consistently achieves significant performance gains, which demonstrates positive contribution of each component to performance gains.

Table 2:

Ablation on component aspect: (1) $\text{tailness}/{ℒ}_{\text{contrast}}$; (2) $\text{diversity}/{ℒ}_{\text{nn}}$.

Method	DSC[%] ↑	ASD[voxel] ↓
Vanilla	49.3	7.11
● ARCO-SAG (ours)	84.9	1.47
w/o tailness-SAG	60.9	4.11
w/o diversity	78.6	1.68
○ ARCO-SG (ours)	85.5	0.947
w/o tailness-SG	60.9	4.11
w/o diversity	79.3	1.26
ARCO-NS	82.6	1.43
w/o tailness-NS	60.9	4.11
w/o diversity	75.2	2.07

Table 3:

Ablation on loss function: (1) unsupervised $\text{loss}/{ℒ}_{\text{unsup}}$; (2) global instance discrimination $\text{loss}/{ℒ}_{\text{inst}}^{\text{global}}$; and (3) local instance discrimination $\text{loss}/{ℒ}_{\text{inst}}^{\text{local}}$.

Method	DSC[%]↑	ASD[voxel]↓
● ARCO-SAG (ours)	84.9	1.47
w/o ${ℒ}_{\text{unsup}}$	81.2	1.87
w/o ${ℒ}_{\text{inst}}^{\text{global}}$	84.0	2.64
w/o ${ℒ}_{\text{inst}}^{\text{local}}$	83.3	2.63
○ ARCO-SG (ours)	85.5	0.947
w/o ${ℒ}_{\text{unsup}}$	81.9	1.04
w/o ${ℒ}_{\text{inst}}^{\text{global}}$	84.1	2.10
w/o ${ℒ}_{\text{inst}}^{\text{local}}$	83.8	2.11

Importance of Augmentation Components.

We further investigate the impact of data augmentation on the ACDC dataset with a 1% label ratio. As is shown in Table 4 (in Appendix), employing each data augmentation strategy consistently results in notable performance improvements, underscoring the efficacy of these data augmentations. Of note, ARCO-SAG/ARCO-SG using all three augmentations and ARCO-SAG/ARCO-SG using no augmentation are considered as the upper bound and the lower bound for the performance comparison. These results show that each augmentation strategy systematically boosts performance by a large margin, which suggests improved robustness.

Stability Analyses.

In Figure 5, we show the stability analysis results on ARCO over different sampling methods. As we can see, our SG and SAG sampling facilitates convergence during the training. More importantly, SG sampling has stable performance with small standard derivations, which aligns with our hypothesis that our proposed sampling method can be viewed as the form of variance regularization. Moreover, loss landscape visualization of different loss functions (Figure 3) reveals similar conclusions.

Extra Study.

More investigations about (1) generalization across label ratios and frameworks in Appendix L; (2) final checkpoint loss landscapes in Appendix M; (3) ablation on different training settings are in Appendix N.

5. Conclusion and Discussion of Broader Impact

In this paper, we propose ARCO, a new semi-supervised contrastive learning framework for improved model robustness and label efficiency in medical image segmentation. Specifically, we propose two practical solutions via stratified group theory that correct for the variance introduced by the common sampling practice, and achieve significant performance benefits. Our theoretical findings indicate Stratified Group and Stratified-Antithetic Group Sampling provide practical means for improving variance reduction. It presents a curated and easily adaptable training toolkit for training deep networks that generalize well beyond training data in those long-tail clinical scenarios. Moreover, our sampling techniques can provide pragmatic solutions for enhancing variance reduction, thereby fostering their application in a wide array of real-world applications and sectors. These include but are not limited to 3D rendering, augmented reality, virtual reality, trajectory prediction, and autonomous driving. We hope this study could be a stepping stone towards by quantifying the limitation of current self-supervision objectives for accomplishing such challenging safety-critical tasks.

Broader Impact.

Defending machine learning models against inevitable variance will have the great potential to build more reliable and trustworthy clinical AI. Our findings show that the stratified group theory can provide practical means for improving variance reduction, leading to realistic deployments in a large variety of real-world clinical applications. Besides, we should address the challenges of fairness or privacy in the medical image analysis domain as our future research direction.