Abstract
Non-invasive imaging of deep blood vessels for mapping haemodynamics remains an open quest in biomedical optical imaging. Although pure optical imaging techniques offer rich optical contrast of blood and have been reported to measure blood flow, they are generally limited to surface imaging within the optical diffusion limit of about one millimeter. Herein, we present photoacoustic vector tomography (PAVT), breaking through the optical diffusion limit to image deep blood flow with speed and direction quantification. PAVT synergizes the spatial heterogeneity of blood and the photoacoustic contrast; it compiles successive single-shot, wide-field photoacoustic images to directly visualize the frame-to-frame propagation of the blood with pixel-wise flow velocity estimation. We demonstrated in vivo that PAVT allows haemodynamic quantification of deep veins at five times the optical diffusion limit (more than five millimeters), leading to vector mapping of blood flow in humans. By offering the capability for deep haemodynamic imaging with optical contrast, PAVT may become a powerful tool for monitoring and diagnosing vascular diseases and mapping circulatory system function.
Introduction
In vivo haemodynamic imaging provides invaluable functional information in tissues and organs. Biomedical optical imaging techniques, such as Doppler-based methods1 (laser Doppler flowmetry2, Doppler optical coherence tomography3), speckle-based methods4 (laser speckle contrast imaging5), and red blood cell tracking methods (confocal microscopy6), have been reported to map the dynamics of blood flow due to their intrinsic optical contrast of blood. However, these techniques suffer from shallow depth penetration due to strong ballistic light attenuation in biological tissue. Thus, imaging blood flow with fine spatial resolution at depths beyond the optical diffusion limit (>1 mm)7 by pure optical imaging remains challenging. Unlike pure optical imaging modalities, photoacoustic tomography (PAT) combines optical absorption contrast with low scattering ultrasonic detection to enable high spatiotemporal resolution and deep tissue imaging of endogenous chromophores, such as hemoglobin8. As such, PAT is uniquely positioned as a functional, anatomical, and molecular imaging modality which can image blood vessels beyond the optical diffusion limit with fine spatial resolution7.
PAT primarily has three main forms of implementation: optical resolution photoacoustic microscopy (OR-PAM), acoustic resolution photoacoustic microscopy (AR-PAM), and photoacoustic computed tomography (PACT)7. While all three techniques have excellent optical contrast for imaging blood vessels, thus far, only OR-PAM has been demonstrated to measure in vivo blood flow9. OR-PAM uses point-by-point scanning of an optical focus to enable transverse spatial resolution on the order of microns7. As such, OR-PAM can measure blood flow by tracking individual red blood cells (RBCs), whose diameters range from 7–8 microns10. However, this measurement is limited to the optical diffusion limit in biological tissue due to the inability to focus light beyond one transport mean free path11. AR-PAM employs raster scanning of an acoustic focus for three-dimensional (3D) imaging at acoustic resolution11. Since the resolution in AR-PAM is sacrificed to image deeper than OR-PAM, deep blood flow measurement is challenging because individual RBCs cannot be resolved. Similar in principle to AR-PAM, acoustic resolution photoacoustic doppler flowmetry (AR-PAF) uses wide-field illumination and a single-element focused transducer to calculate A-line cross-correlations between photoacoustic (PA) waveforms. Previous work has demonstrated that ex vivo whole blood velocity measurement is possible for high center frequency transducers using AR-PAF12, but in vivo blood flow measurement beyond the optical diffusion limit remains an outstanding hurdle. Conversely, PACT uses wide-field illumination coupled with an array of ultrasonic detectors to image vasculature at depths beyond the optical diffusion limit with acoustic resolution13. Generally speaking, measuring blood flow in deep tissue with PACT has been challenging because 1) compared to OR-PAM, PACT has a lower resolution, preventing it from being able to resolve individual RBCs; 2) the photoacoustic signals within the lumen of a vessel are suppressed relative to the signals at the boundaries due to the random summation of absorption signals from millions of RBCs in each lumen imaging voxel, thus rendering PACT as “speckle-free”14. While recent work has utilized PACT speckle field decorrelation to extract velocity measurements in ink phantoms and chicken embryos, direct imaging of blood flow beyond the optical diffusion limit has remained elusive15.
In this article, we present photoacoustic vector tomography (PAVT) as a framework to achieve, to our knowledge, the first vector maps of human blood flow by photoacoustics beyond the optical diffusion limit. The key features of this framework can be summarized as follows: 1) The synergy between the spatial heterogeneity of blood and the photoacoustic contrast produces strong photoacoustic signals in the lumen of the blood vessels. 2) Successive compilation of single-shot, wide-field photoacoustic images allows direct visualization of the blood flow throughout the lumen. 3) Applying pixel-wise motion estimation algorithms to the reconstructed images generates blood flow vector maps with speed and direction quantification. Through simulation and phantom validation, we demonstrated that PAVT blood flow measurement is facilitated by the heterogeneity of the blood. The accuracy of this measurement was assessed through trials on ex vivo blood in which measured flow speeds were validated against known values. We acquired images in the vessels of the hand and arm regions of healthy subjects using a linear ultrasound array probe coupled to an optical fiber bundle. We demonstrated in vivo that vector flow maps could be obtained in blood vessels greater than 5 mm in depth. Moreover, we demonstrated the potential for vector flow imaging to measure unique flow patterns at irregular interfaces in the blood vessel, such as valve regions. Lastly, we measured the in vivo functional PA blood flow responses to the inflation and release of a blood pressure cuff. This work establishes PAVT as a viable imaging technique for monitoring and diagnosing vascular diseases and mapping circulatory system function.
Results
The principle of photoacoustic vector tomography (PAVT) for deep haemodynamic imaging is illustrated in Fig. 1. Fig. 1a shows the schematic of the system. An ultrasonic probe is placed on top of the skin, and a laser delivers light through a fiber bundle to the blood vessels. The hemoglobin content within RBCs absorbs the light and converts it into heat. Based on the known photoacoustic effect, acoustic waves are generated through thermoelastic expansion and detected by the ultrasonic probe. The data are then streamed to the computer through the data acquisition (DAQ) module, and we employ the universal back projection algorithm16 to reconstruct the images. Fig. 1b illustrates the effect of blood heterogeneity (RBC spatial distribution) on the visibility of the signals arising from the lumen region of the blood vessel. For uniform blood, the simulated photoacoustic signals from the lumen region are suppressed relative to the signals at the boundaries (known as the boundary buildup effect14), resulting in little visibility in the lumen region of the image, whereas in nonuniform blood, the simulated photoacoustic signals from the lumen region show an increased amplitude, resulting in heightened visibility in the lumen region relative to the uniform case. Modeling of the spatial heterogeneity of blood and details about the simulation can be found in Methods and Supplementary Fig. 1–3. Fig. 1c is a representative in vivo photoacoustic image of a blood vessel located beyond 1 mm depth. Similar to the simulated image in the nonuniform case, the in vivo image shows detectable signals from the lumen region of the blood vessel. To quantify the heterogeneity of the blood, we define a relative visibility index as , where denotes the mean lumen signal, the mean boundary signal, and the mean background signal (see Methods). The measured relative visibility index for the vessel in Fig. 1c is 0.15 ± 0.01 (n = 10). After acquiring multiple frames of data, we can clearly visualize the propagation of the lumen signals from frame-to-frame (Supplementary Video 1), as shown in the magnified view of the region in the white box in Fig. 1c (further data processing details can be found in Methods). We then apply a pixel-wise flow estimation algorithm to the images, extracting both the direction and magnitude of the blood flow inside the vessel. As shown in Fig. 1d, this map shows a laminar flow pattern in the lumen region that has a higher speed through the center of the vessel and a lower speed at the edges.
Fig. 1 |. Photoacoustic vector tomography (PAVT).
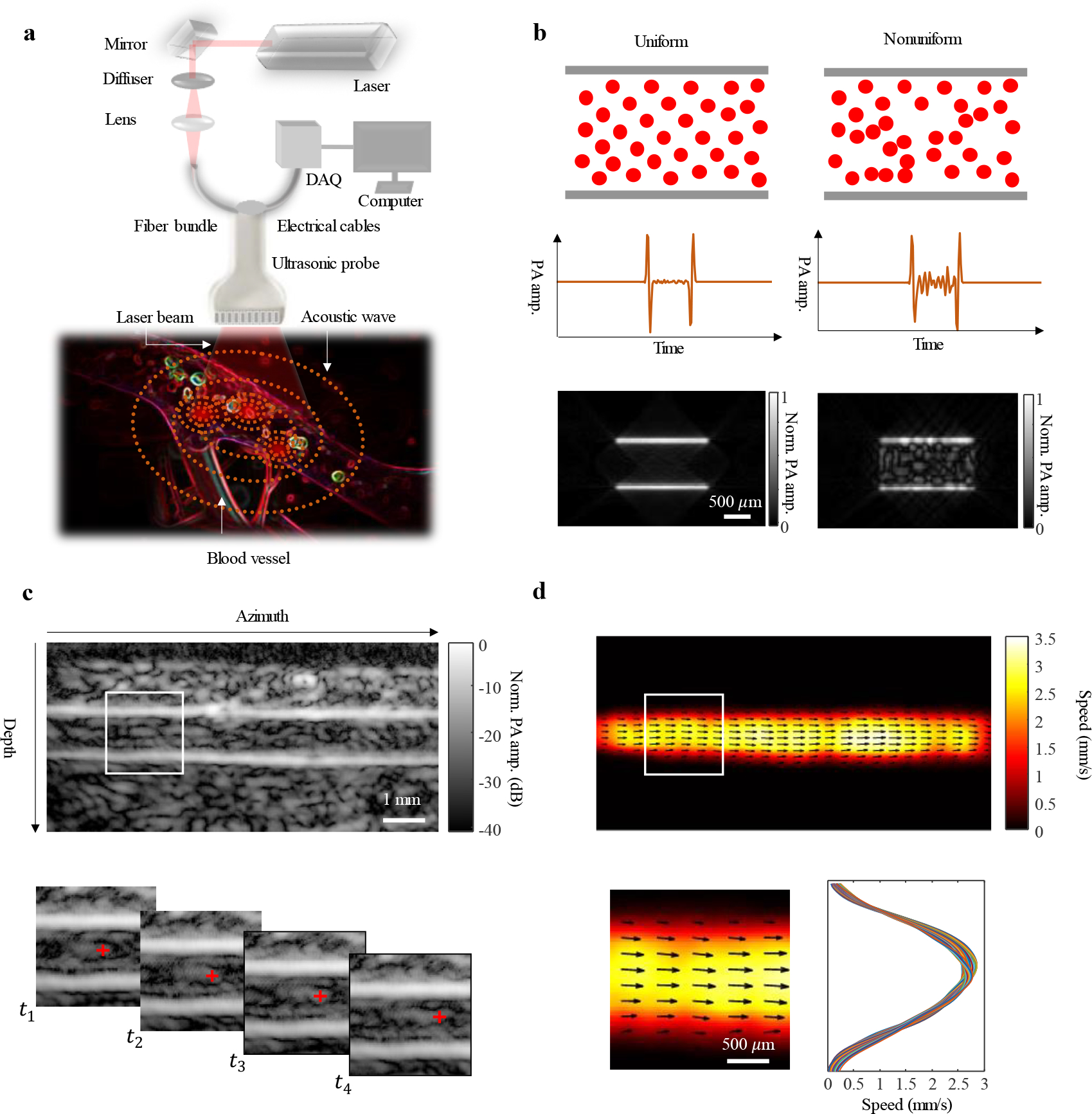
a, Schematic of the imaging system. Light from a laser is delivered to the blood vessel region via a fiber bundle. Photoacoustic waves are generated and then detected by the ultrasonic probe. Photoacoustic signals are streamed to the computer through the data acquisition (DAQ) module. b, Effect of blood heterogeneity on the visibility of the signals arising from the lumen region of the blood vessel. For uniform blood, the simulated photoacoustic signals from the lumen region are suppressed relative to the signals at the boundaries, resulting in little visibility in the lumen region of the image, whereas in nonuniform blood, the simulated photoacoustic signals from the lumen region show an increased amplitude, resulting in heightened visibility in the lumen region relative to the uniform case. c, Structural images of a blood vessel are reconstructed in real-time. Magnified view of the region in the white box in c (top row) shows that the image features in the lumen region (beyond 1 mm depth) can be tracked in successive images at time points to . d, After tracking all of the features in the field of view, a blood flow speed map is reconstructed. Quantitative representation of the flow vector fields is overlayed on the speed map. Magnified view of the region in the white box in d (top row) shows that the flow has a laminar pattern.
To characterize the system resolution, we imaged a lead point source (actual diameter 50 μm). Fig. 2a shows an axial resolution of 125 μm and a lateral resolution of 150 μm. To determine the mechanism for flow detectability and validate the speed estimation accuracy of PAVT, we designed a blood flow phantom to closely mimic in vivo circulation. Fig. 2b shows the set-up for the flow phantom, in which a converging bifurcation is fabricated by two inlet channels (C1 and C2) feeding into an outlet channel (C3). While imaging the outlet channel, five measured speeds were validated against preset syringe flow speeds. The results in Fig. 2c show strong agreement between the measured and preset values for all five speeds. These results were validated against Doppler ultrasound measurements (see Supplementary Fig. 4) as well. Additionally, we tested the limits of speed detection. The slowest measured flow was approximately 0.04 mm/s, while the fastest measured flow was approximately 100 mm/s (see Supplementary Fig. 5). Finally, we found that the speed measurement is unaffected by the angle of the vessel relative to the probe (see Supplementary Fig. 6). The mechanism for flow detectability is demonstrated in Fig. 2 d–i. Fig. 2 d,f,h show the structural images of channels C1, C2, and C3, respectively, before (top) and after (bottom) the induction of pressure fluctuations in the inlet channels, whereas Fig. 2 e,g,i show the corresponding vector flow maps for each channel and scenario. Fig. 2 d–g show suppressed lumen signals and no flow detectability (97% relative error for measured mean speeds of 0.1 mm/s versus ground truth of 3.3 mm/s) in the inlet channels C1 and C2 with and without pressure fluctuations. The measured relative visibility index is 0.003 ± 0.007 (n = 40) for the bottom panel of Fig. 2d. In the top panel of Fig. 2h, the structural image for outlet channel C3 shows a detectable signal in the center of the channel, which likely arises from the mixing of blood from each inlet channel, thus producing a detectable nonuniformity at the center of the outlet channel. The vector flow image in the top panel of Fig. 2i shows weak flow detectability (80% relative error for measured mean speed of 0.6 mm/s versus ground truth of 3.3 mm/s). The measured relative visibility index is 0.098 ± 0.005 (n = 40) for the top panel of Fig. 2h. After the induction of pressure fluctuations in the inlet channels, the structural image in the bottom panel of Fig. 2h shows the nonuniformity dispersed throughout the lumen region (see also Supplementary Video 2), allowing us to clearly track the flow (2.5% relative error for measured mean speed of 3.4 mm/s versus ground truth of 3.3 mm/s) in the vector flow map shown in the bottom panel of Fig. 2i. The measured relative visibility index is 0.128 ± 0.006 (n = 40) for the bottom panel of Fig. 2h. Thus, we conclude that the visibility of the photoacoustic lumen signals is enhanced by spatial heterogeneity in the blood.
Fig. 2. System characterization and phantom validation.
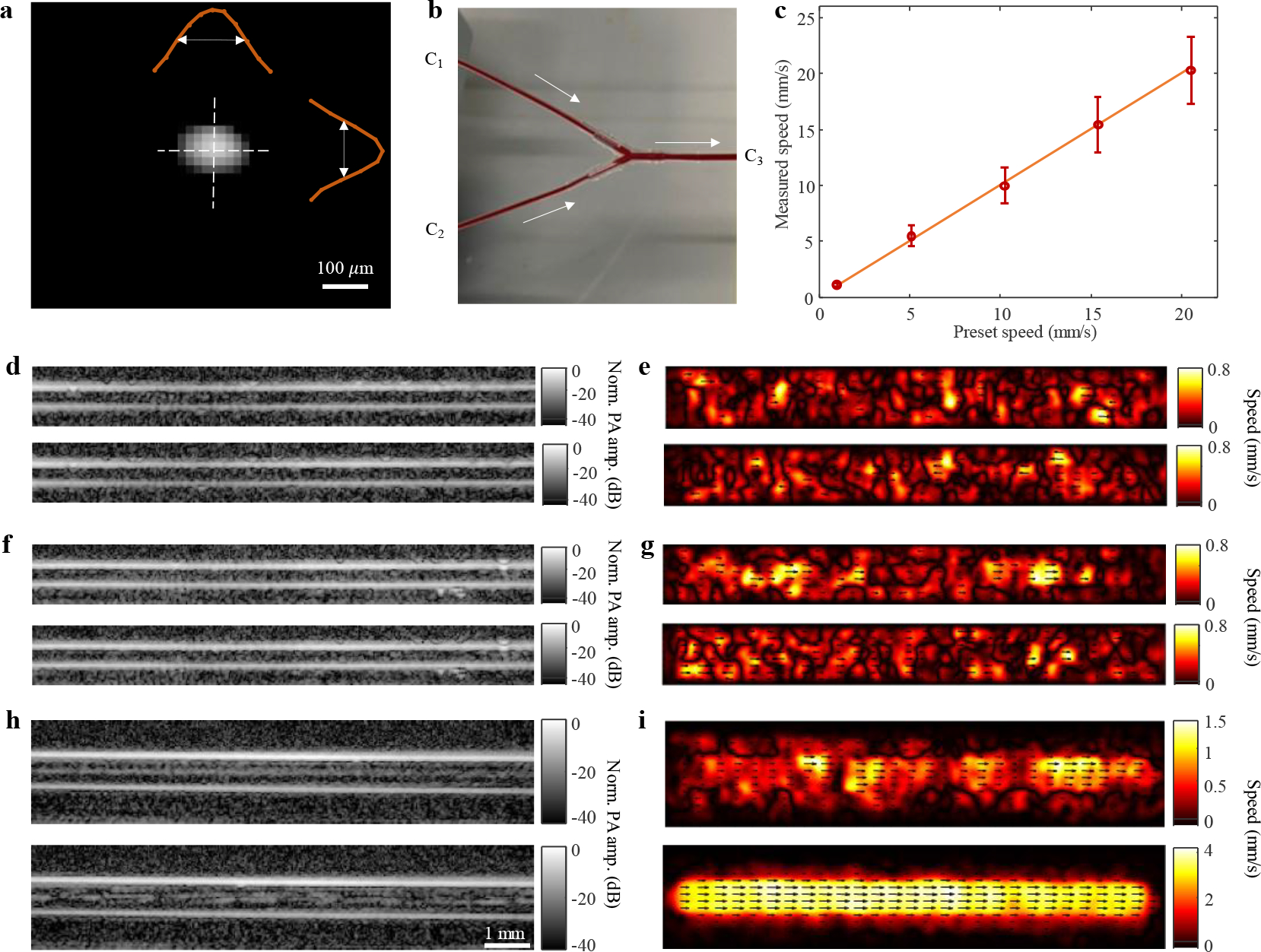
a, Image of a lead point source (actual diameter 50 μm), showing axial and lateral resolutions of 125 and 150 μm, respectively. b, Blood phantom set-up with inlet channels C1, C2, and outlet channel C3. c, Measured flow speeds plotted against preset syringe flow speeds. The mean ± standard deviation (in mm/s) speeds were (from left to right): 1.07 ± 0.21, 5.33 ±0.85, 9.93 ± 1.83, 14.77 ± 2.76, and 20.14 ± 3.17 with relative errors of 4.5, 3.6, 3.4, 4.2, and 2.0 %, respectively (n = 6859). Orange line represents the preset speed, and red circles represent the measured mean speeds. Error bars represent the standard deviation for each measurement. d,f,h, Structural images in channels C1, C2, and C3, respectively, before (top) and after (bottom) the induction of pressure fluctuations. e,g,i, Vector flow maps in channels C1, C2, and C3, respectively, before (top) and after (bottom) the induction of pressure fluctuations.
Representative PAVT images of four blood vessels at depths beyond the optical diffusion limit are shown in Fig. 3. Fig. 3a shows a vessel in the wrist (Supplementary Video 3), imaged at an optical wavelength (λ) of 1,064 nm and a pulse repetition frequency (PRF) of 100 Hz. The vessel has a varying diameter along its longitudinal axis with a high flow speed in the upstream narrower region (likely due to smooth muscle contraction) and a lower flow speed in the downstream dilated region. Fig. 3b shows a vessel in the palmar region imaged at a PRF of 100 Hz with an isosbestic wavelength (805 nm) of oxy- and deoxyhemoglobin (Supplementary Video 4). Demonstration of flow measurements at other wavelengths can be found in Supplementary Fig. 7 and Supplementary Video 5. In Fig. 3c–d, the structural images of two different forearm vessels acquired at λ = 1,064 nm and PRF = 20 Hz show that the distances from the skin surfaces to the axes of the vessels are 3.5 mm and 5.5 mm, respectively, with the vector maps confirming that the blood flow is still detectable (Supplementary Videos 6–7). For Fig. 3c–d, the measured signal-to-noise ratio (SNR) values at the center of vessel lumen regions were 14.1 and 5.8, respectively, whereas the contrast-to-noise ratio (CNR) values were 7.1 and 2.5, respectively. In vivo validation of PAVT with ultrafast Doppler ultrasound can be found in Supplementary Fig. 8.
Fig. 3 |. PAVT vector flow maps.
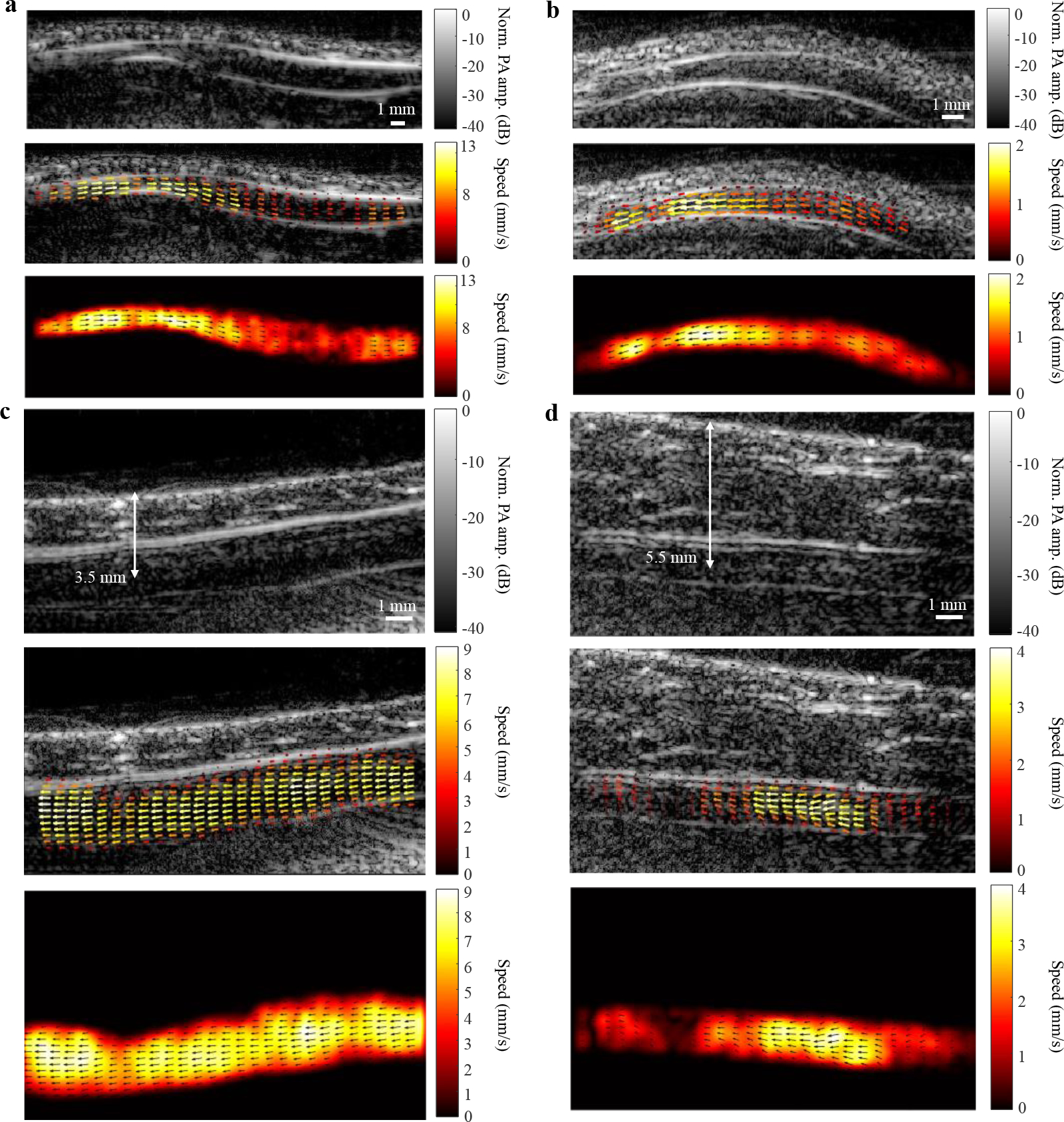
a, Structural image (top), overlayed vector flow map (middle), and vector flow map (bottom) of a vessel in the wrist with a varying diameter. b, Structural and vector maps of a vessel in the palmar region imaged at an isosbestic wavelength for oxygenated and deoxygenated hemoglobin (805 nm). c–d, Structural and vector maps of vessels in the forearm imaged at 3.5 and 5.5 mm depths, respectively.
A carpal tunnel vein with a valve is shown in Fig. 4 (Supplementary Video 8), as indicated by the white circles in Fig. 4a. The vector maps and speed profiles in Fig. 4b–c and Fig. 4d, respectively, indicate a higher speed in the narrow diameter intra-valve region and lower speeds in the wider diameter regions surrounding the valve. In Fig. 4e–f, magnified views of the regions indicated by the white boxes show a converging flow pattern within the valve. Furthermore, the magnified vector maps highlight the sinus pocket regions17 above and below the valve boundaries, as shown by the dashed lines in Fig. 4e–f.
Fig. 4 |. PAVT characterization of haemodynamics around a valve.
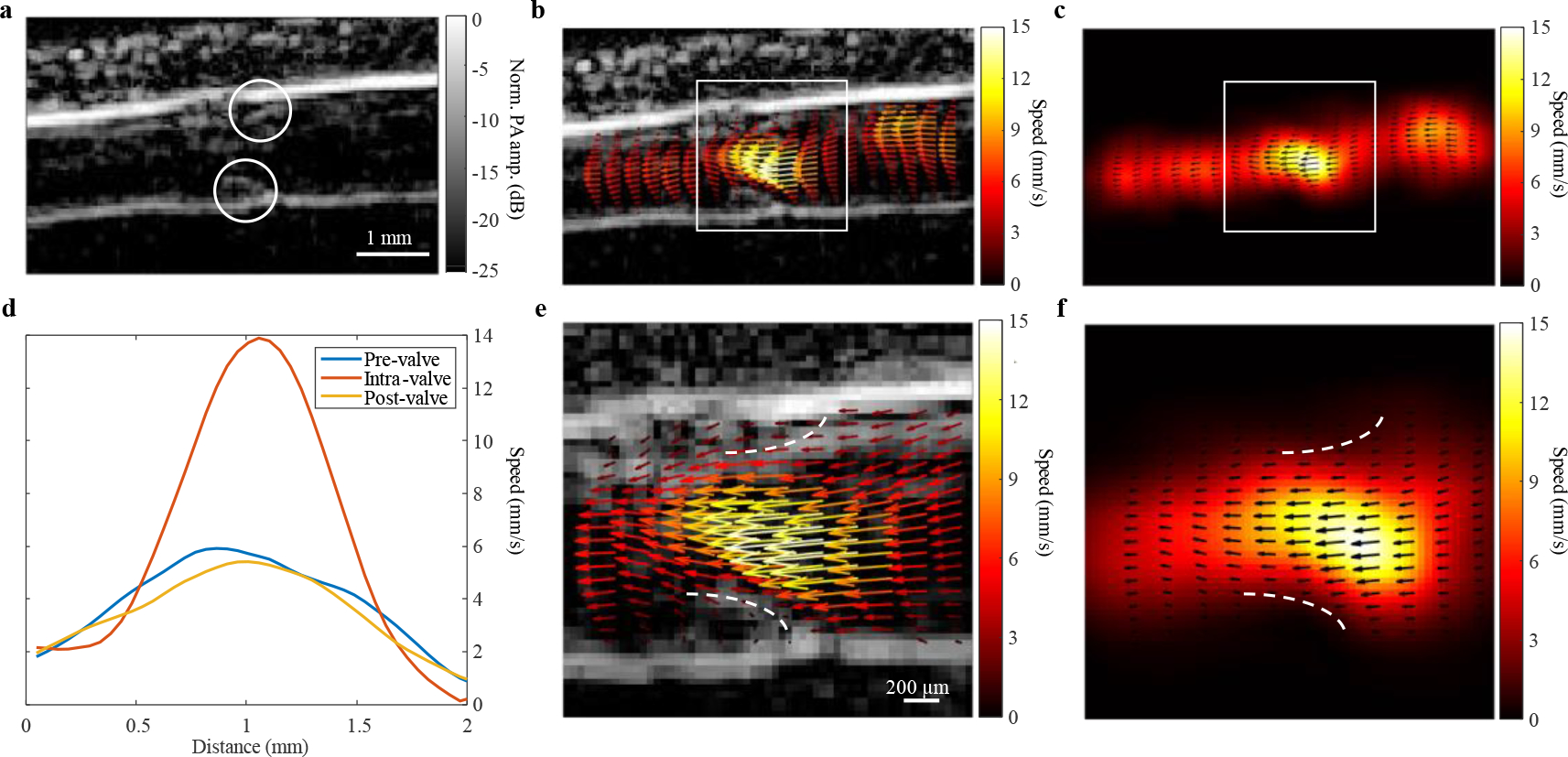
a, A venous valve in the carpal tunnel region in the arm (valve boundaries indicated by white circles). b-c, Vector maps showing a higher speed inside the valve than the vessel regions upstream and downstream to the valve. d, Speed profiles taken upstream, within, and downstream the valve (pre-valve, intra-valve, and post-valve, respectively). e-f, Magnified views of the maps in b-c with the valve boundaries indicated by the dashed white lines.
To evaluate functional changes, we measured a subject’s blood flow before, during, and after inflating a blood pressure cuff. The cuff was placed against the brachial vein in the upper left arm, and the imaged vessel was located in the metacarpal region, distal to the application site of the cuff. Fractional speed changes were measured relative to the baseline flow. Fig. 5 shows a flow speed decrease of approximately 70% while the cuff was inflated, followed by a transient flow speed increase of approximately 350% upon release of the cuff and eventually a steady-state return to the baseline (Supplementary Video 9). The 70% drop can be explained by incomplete cuffing, whereas the transient increase could be due to an immediate pressure release in the metacarpal vessel. This experiment was repeated for multiple subjects, for which the flow speed responses are reported in Supplementary Fig. 9.
Fig. 5 |. Measuring functional responses to a blood pressure cuff.
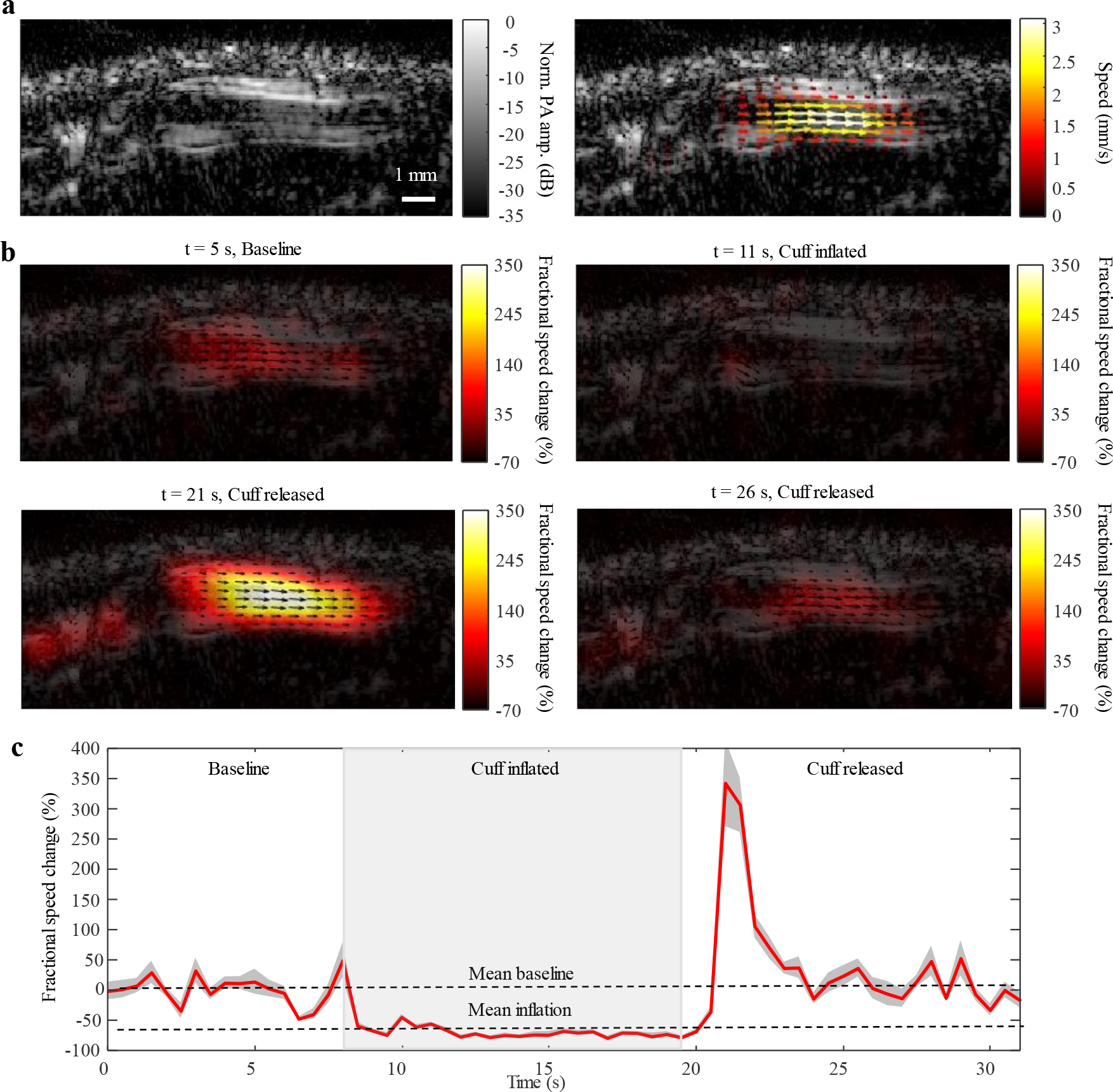
A blood pressure cuff was applied to the upper left arm across the subject’s brachial vein. Baseline flow was measured in a distal metacarpal vein, after which subsequent flow measurements were quantified relative to the mean of this baseline. The cuff was inflated for approximately 10 seconds before release. a, Structural image of the vessel (left) and the vector overlay map for the baseline flow speed (right). b, Vector maps for relative flow measurements at four different time points throughout the experiment: the baseline flow (top left), the flow during cuff inflation (top right), the flow during release (bottom left), and the flow after release (bottom right). c, Discrete-time sequence for relative flow speed changes. The flow speed decreased by approximately 70% during the application of the cuff and increased to approximately 350% upon release before returning to baseline.
Discussion
This study introduces PAVT, which demonstrates the capability of photoacoustics to image human blood flow beyond the optical diffusion limit. Through phantom experiments, we validate the mechanism and accuracy of this measurement. By employing in vivo vector flow analysis, we have demonstrated the versatility of PAVT across laser pulse repetition frequency (PRF), laser wavelength, and depths. Furthermore, we show that in the vicinity of valves, PAVT can measure flow patterns that deviate from typical laminar flow. In tracking the flow speed changes in response to a blood pressure cuff, this work establishes PAVT as a powerful imaging technique that can perform blood flow functional measurements in deep vessels. As such, PAVT outperforms existing pure optical methods for deep haemodynamic imaging and complements ultrasound imaging18–20 by simultaneously providing hemoglobin-based molecular contrast21.
There is an inherent tradeoff between imaging depth and laser PRF. For instance, the American National Standards Institute’s (ANSI) safety limit for skin exposure at a laser wavelength of 1,064 nm is 50 mJ/cm2 and 10 mJ/cm2 at a laser PRF of 20 Hz and 100 Hz, respectively22. Therefore, if one wishes to maximize laser fluence in order to image deep blood vessels with a high signal-to-noise ratio (SNR), one must necessarily decrease the laser PRF to satisfy the ANSI limit. This tradeoff is exemplified in Fig. 3, in which we used a 20 Hz laser PRF to image blood flow at a depth of approximately 5.5 mm (Fig. 3d), whereas we used a 100 Hz laser PRF to image blood flow at a depth of approximately 1.5 mm (Fig. 3a). The effect of the frame rate on speed estimation is further expounded upon in Supplementary Fig. 10. Starting with a dataset acquired at a 100 Hz PRF over 1 second, we downsampled the images at effective frame rates of 50, 20, 10 and 5 Hz. The mean speeds showed reasonable agreement (within one standard deviation of the 100 Hz upsampled mean speed), at frame rates of 50, 20, and 10 Hz, with an underestimation at 5 Hz (relative error of 89%). These results are consistent with Equation 8, in which the calculated flow pattern correlation length and flow speed of approximately 0.6 mm and 2 mm/s, respectively, correspond to a minimum required laser PRF of 6.7 Hz according to the Nyquist sampling theorem23.
To clearly visualize the flow, we employed two post-processing techniques prior to velocity quantification. First, we implemented a singular value decomposition (SVD)-based spatiotemporal filter to the reconstructed photoacoustic images to extract the dynamic features (i.e., blood flow). Next, we applied amplitude-based logarithmic compression24 to the filtered images to highlight the lumen signals. As shown by the dashed lines in Supplementary Fig. 11, each of these steps may be implemented individually or together. The accuracy of these methods is demonstrated in Supplementary Fig. 12, in which we consider a representative phantom dataset. The relative errors for Supplementary Fig. 12a–d were 29, 6.9, 1.4, and 0.3%, respectively, indicating that implementing SVD and logarithmic compression yields the most accurate results, albeit with modest improvement over implementing logarithmic compression without SVD.
Additionally, we applied a pixel-wise noise floor filtering method (see details in Methods) before generating the final vector flow maps. The effect of this procedure is demonstrated in Supplementary Fig. 13, in which we consider a phantom dataset with a mean flow speed of 4.11 mm/s as the ground truth. Supplementary Fig. 13a shows the estimated speed map when averaging across all frames for each pixel, yielding a calculated mean speed of 3.93 mm/s (relative error of 4.5%). This underestimation is because when calculating pixel-wise frame-to-frame motion, low-speed noise measurements may erroneously be incorporated into the velocity quantification due to spatial gaps in the propagating flow pattern (as shown in the bottom panel of Fig. 2h). To avoid this underestimation, we calculated the temporal standard deviation of each pixel’s speed measurements to form a pixel-wise noise floor, below which frames with low speeds (i.e., measurements due to noise) were excluded. Supplementary Fig. 13b shows the estimated speed map when averaging across the remaining frames, yielding a calculated mean speed of 4.07 mm/s (relative error of 0.9%).
An important aspect of PAVT is that it can detect variations in flow patterns throughout the lumen of the blood vessel. Fig. 4 highlights key features regarding the detectability of PAVT in blood vessel regions containing valves. From a structural standpoint, it is important to note that the venous extremities valves, such as the one imaged in this work, are composed of endothelial cells and connective tissue25, for which photoacoustic imaging does not have high contrast relative to hemoglobin. However, like the walls of the blood vessels, the valve can be considered as a sub-boundary of the blood, and we can detect the sub-boundaries of these structures due to the boundary buildup effect. Our PAVT images reveal that we can detect complex vector flow patterns in the regions surrounding the valves, and our speed profiles in Fig. 4d are consistent with that predicted by the continuity equation26, showing a higher speed in the narrow diameter intra-valve region and lower speeds in the wider diameter regions before and after the valve (relative error of 3.2%). We also demonstrated the ability to measure temporal changes in the flow speed due to the application of a blood pressure cuff, thus establishing a basis for detecting functional responses. Furthermore, we observed naturally occurring temporal blood flow changes in a vertically oriented hand, possibly due to the counteracting force of gravity against the venous one-way valves (see Supplementary Video 12).
Here, we consider the most likely hypothesis for the mechanism of blood flow detectability by PAVT. We designed a flow phantom (see Fig. 2) to closely mimic in vivo circulation, consisting of a converging bifurcation that has two inlet channels and an outlet channel with diameters roughly corresponding to Murray’s law27 (i.e., the cubic of the vessel radius is conserved: , where “out” denotes the outgoing branch and “in1” and “in2” denote the two incoming branches, respectively). Because whole blood is uniform, we were unable to image baseline blood flow in either of the inlet channels. However, as shown in the top panel of Fig. 2h, the converging bifurcation produced a detectable nonuniformity of RBC distribution in the center of the outlet channel. Furthermore, inducing pressure fluctuations in the inlet channels resulted in the dispersion of this nonuniformity throughout the lumen of the outlet channel, allowing us to clearly visualize the blood flow. From a physiological perspective, converging bifurcation structures merging dissimilar blood naturally occur throughout the venous system28, and pressure fluctuations can be induced by the opening and closing of one-way valves in the veins, as well as from smooth muscle contractions. In validating the flow speed measurements with the preset syringe flow speeds, we hypothesize that the two aforementioned factors facilitate in vivo flow measurement by inducing blood spatial heterogeneity that is detectable at our probe’s center frequency.
For completeness, we also consider the hypothesis that PAVT flow measurement is facilitated by the propagation of oxygen saturation (sO2) heterogeneities. This hypothesis is reasonable due to PA’s selective contrast to oxy- and deoxyhemoglobin at most wavelengths. However, as shown in Fig. 3, we were able to measure flow even at an isosbestic wavelength of 805 nm, effectively ruling out this hypothesis.
Moreover, we demonstrated that PAVT blood flow measurement is versatile, with consistent speed measurements across three different laser wavelengths (750 nm, 805 nm, and 900 nm) in the near-infrared (NIR) spectral region (see Supplementary Fig. 7) while imaging a palmar vein. indicating that spectral PAVT measurement of blood flow and sO2 is achievable. The sO2 and blood flow maps of vessels in three different regions are shown in Supplementary Fig. 14. Using linear unmixing with surface fluence compensation29 for each vessel, we calculated sO2 values of 66, 73, and 65%, respectively, which agree with accepted literature values in healthy subjects30. While methods such as Doppler ultrasound and pulse oximetry can each individually image blood flow and sense systemic arterial oxygen saturation without imaging, respectively, PAVT can simultaneously image these physiological parameters, which can provide crucial information regarding brain function31 and hallmarks of cancer, such as angiogenesis and hypermetabolism32. In addition to providing simultaneous sO2 and blood flow measurements, PAVT may have clinical advantages over Doppler ultrasound due to its angle independence, as shown in Supplementary Fig. 5. Furthermore, PAVT has the ability to measure extremely slow flow (relative error of 4.3% for measured speed of 0.039 mm/s versus a ground truth of 0.041 mm/s), as shown in Supplementary Fig. 6. Doppler ultrasound, on the other hand is unable to measure flow that is this slow (relative error of >100% for measured speed of 0.41 mm/s versus a ground truth of 0.041 mm/s).
While we demonstrated PAVT to be efficacious in veins, there remains an outstanding hurdle to image blood flow in arteries. Our hypothesis for the inability to measure arterial flow relates to the visibility of the lumen-blood signals. For PAVT flow measurement, two factors are required: 1) a sufficient visibility of the lumen-blood signals and 2) a sufficient imaging frame rate to track the movement. It is known that on average arterial flow is faster than venous flow. While the speed of the blood certainly affects whether we can accurately measure the blood flow at a given imaging frame rate, it is not directly related to the flow visualization. As shown in our arterial images (see Supplementary Fig. 15 and Supplementary Video 10–11), we cannot visualize the lumen signals, which means there would not be a sufficient signal to track even if the blood flow was slowed down. The measured relative visibility indices for the arteries were 0.008 ± 0.010 (n = 10) and 0.002 ± 0.004 (n = 10), respectively, which are much lower than that in the vein, i.e., 0.15 ± 0.010 (n = 10) in Fig.1. These results confirm the insufficient heterogeneity of the arterial lumen signals relative to that of the veins. Furthermore, as shown in our updated phantom experiment (see Supplementary Fig. 5), we measured blood flow as fast as 100 mm/s, which should be sufficient for many arteries in the regions that we imaged. Together, these results support our hypothesis that the limiting factor for PAVT arterial flow measurement is the visibility of the lumen signals, rather than the speed of the blood. From a physiological perspective, this hypothesis is reasonable because by the time blood from the venous circulation returns to the heart and transitions to the arterial circulation, the blood has become well-mixed and more uniform. As such, the spatial heterogeneity that highlights the photoacoustic signals in the venous blood is no longer present.
In its current stage, PAVT may be capable of clinical implementation, as it extends the photoacoustic blood flow measurement to five times beyond the optical diffusion limit. In principle, PAVT is not limited to the linear array probe that we employed in this work. As such, future work may extend this technique to other array geometries such as the ring array and hemispherical array that provide more complete acoustic views for enhanced image quality. Specifically relevant to this study, peripheral vascular diseases such as chronic venous insufficiency33 and varicose veins33 can be diagnosed through imaging blood flow in the extremities. Future studies may also extend this approach to other regions of the human body for applications such as breast cancer34 and functional brain imaging35,36.
Although veins carry approximately 75% of the total blood volume in the circulatory system, measuring blood flow in both veins and arteries provides more complete clinical information for diagnosing and preventing disease. The clinical impact of this technique will be fully realized when we can perform metabolic imaging of physiological systems. The metabolic rate of oxygen consumption (MRO2)37 for a system can be estimated by measuring the blood flow, total hemoglobin concentration, and oxygen saturation of the major input and output vessels (i.e., arteries and veins, respectively). Although in its current state, PAVT can only measure blood flow in veins, the principle of mass conservation can be applied to estimate the arterial inflow rate from the venous outflow rate. As such, metabolic imaging with PAVT may be a not-so-distant clinical possibility. For example, early breast cancer detection can be aided through monitoring tumor-induced changes in MRO234.
Even though PAVT extends the depth of photoacoustic blood flow measurement to five times further than what was previously considered possible, there will always be a clinical need to push this limit even further. In this work, we employed a 15 MHz probe to image blood flow within a 5 mm depth. Extending this depth further is primarily limited by the acoustic attenuation arising from the high center frequency of our probe, as well as the fact that the vessel lumen signal is weaker than the boundary signal. Future work should therefore explore the implementation of lower frequency probes to image blood flow at centimeter-level depth at the expense of lower resolution. If the blood spatial heterogeneity becomes unresolvable, its detectability may decrease. As such, PAVT may eventually provide simultaneous measurement of cerebral blood flow, hemoglobin concentration, and oxygen saturation for functional human brain imaging. Furthermore, such a depth would enable imaging of both the carotid artery and the jugular vein, thus making cerebral metabolic imaging possible.
Methods
System construction.
We employed a 256-element linear ultrasonic transducer array (LZ250, VisualSonics Inc.) for photoacoustic signal detection at a center frequency of 15 MHz. The transducer array has a size of 23 mm × 3 mm, and each element of the array has a cylindrical focus with a 15 mm focal length. The ultrasound probe was directly connected to the 256 DAQ channels of the Verasonics Vantage 256 system (Verasonics Inc.; 14-bit A/D converters; 62.5 MHz sampling rate; programmable gain up to 51 dB) through a UTA 360 connector. The photoacoustic signals were acquired and digitized into local memory and then transferred to a host computer via PCI express.
For light delivery, we incorporated an optical fiber bundle with the ultrasound probe. The fiber bundle and the array were coaxially aligned to maximize the system’s performance. In the front end of the fiber bundle, a 1,064 nm wavelength laser beam (Quantel Brilliant B pulsed YAG laser; 10 Hz; 5–6 ns pulse width; Quantel Q-Smart 450 laser; 20 Hz; 5–6 ns pulse width) or a 670 nm – 1070 nm laser beam (SpitLight EVO III, InnoLas Laser Inc.; 100 Hz; 5–8 ns pulse width) was utilized to pass through the fiber bundle and was delivered to the imaging target. The angle of incidence of the beam was 30 degrees relative to the imaging plane. The optical fluences were approximately 50 mJ/cm2 for the 1,064 nm wavelength at 10 Hz PRF, 30 mJ/cm2 at 20 Hz PRF, and 6 mJ/cm2 at 100 Hz PRF, which were less than the safety limit set by the American National Standards Institute (ANSI) (100 mJ/cm2, 50 mJ/cm2, 10 mJ/cm2, respectively, and 1000 mW/cm2)22.
To synchronize the system, the laser’s external trigger was used to trigger the DAQ for photoacoustic signal acquisition. For each laser pulse, we acquired both the signal from the ultrasound probe surface and the signal from the imaging target. We then corrected the delay and jitter between the DAQ and the laser system using the acquired surface signal. The preprocessed raw signals were then backprojected to reconstruct the two-dimensional (2D) photoacoustic image.
Data acquisition.
For the human imaging set-up, we prepared a portable water tank and placed it on top of the table. The ultrasound probe was mounted on a three-dimensional linear stage with its surface immersed in the water tank. The human hand/arm region was placed below the probe surface and coupled in water with the ultrasound probe. We implemented the photoacoustic imaging sequence to monitor the blood vessel in real-time. We achieved a frame rate of 10 Hz, 20 Hz or 100 Hz corresponding to the laser PRF. In the blood pressure cuff experiment, a blood pressure cuff device (GF Health Products, Inc) was placed on the upper arm region. The total acquisition took 30 s, with a baseline of ~5 s at the beginning, a cuff period of ~10 s following, and a release of ~15 s.
In the phantom validation experiments, the flow phantom was constructed using micro-renathane tubing (BrainTree Scientific). Each inlet channel had an inner diameter of 0.6 mm, and the outlet channel had an inner diameter of 1.0 mm. The phantom was perfused with 45% hematocrit whole bovine blood (QuadFive). Pressure fluctuations were induced by gently squeezing the inlet channels.
Ultrafast ultrasound Doppler imaging was implemented by coherent plane wave compounding38,39 with seven tilted plane waves from −14 degrees to +14 degrees at a pulse repetition frequency of 10,000 Hz. The Doppler flow maps were generated using a vector projectile imaging framework40,41. Briefly, for each plane wave angle, we obtained the conventional color Doppler image, after which we used least-squares multi-angle Doppler estimators to form the final flow images. In the ultrasound validation experiment, the ultrafast ultrasound data were immediately acquired after the PAVT imaging sequence to ensure the same state in the region of interest.
Data processing.
To visualize the blood flow and obtain the vector flow map from the acquired raw photoacoustic signals, we used the following procedure for data processing as shown in Supplementary Fig. 11. We first applied a universal back projection image reconstruction algorithm16 to the raw photoacoustic signals to reconstruct the images. We then logarithmically compressed the reconstructed structure images of the blood vessel (i.e., structure images in Fig. 1–5) to directly visualize the blood flow (i.e., the top panel of Supplementary Videos 1, 3, 4, 6–7, 8, 10–11). For clearer blood flow visualization, we applied a singular value decomposition (SVD)-based spatiotemporal filter to the reconstructed images and then performed logarithmic compression on the filtered images (i.e., the bottom panel of Supplementary Videos 1, 3, 4, 6–7, 8, 10–11). Lastly, we used a pixel-wise flow estimation method (see below) and noise floor filtering to obtain the velocity of the blood flow. For each pixel, the frame-to-frame velocity was estimated to form a 3D velocity structure with two spatial axes (ultrasound probe azimuthal direction and axial direction ) and one time axis (time ). The temporal standard deviation of each pixel’s speed measurements was calculated to form a pixel-wise noise floor, below which frames with low speeds (i.e., measurements due to noise) were excluded. The final velocity map was constructed from averaging the remaining frames across the temporal domain. For all calculations of speed standard deviations performed in the manuscript, an region of interest in the vessel was segmented into profiles, with each profile parallel to the vessel’s longitudinal axis. We then calculated the spatial standard deviation along each profile and found the final standard deviation () by taking the mean of the profiles’ standard deviations: .
In PAVT, a spatiotemporal filter is used to extract the blood component from the structural images. In our case, the spatiotemporal structure dataset has three dimensions with two spatial axes (ultrasound probe azimuthal direction and axial direction ) and one time axis (time ). We first reshape the 3D dataset into a 2D space-time matrix . Then we use singular value decomposition (SVD)42 to decompose the data matrix as follows:
| (1) |
where is the rank of the data matrix, is the singular value, is the conjugate transpose, corresponds to the spatial domain, and corresponds to the temporal domain. The static or slow-moving components (i.e., tissue) correspond to the first few larger singular values. Therefore, the relatively fast-moving blood components can be extracted as
| (2) |
where is the cutoff of the singular values for extracting the blood component. Finally, the filtered 2D space-time matrix is reshaped back to 3D with the same size as the original 3D dataset.
For flow estimation, the Farneback method43 for optical flow was employed. Briefly, the Farneback method approximates pixel neighborhoods as polynomial expansions. By assuming a constant intensity of the displaced neighborhoods between adjacent frames, the displacement field is estimated as follows. Let the pixel neighborhood in Frame 1 at position vector be approximated as:
| (3) |
in which the coefficients (a symmetric matrix), (a vector), and (a scalar) are estimated by a weighted least squares fit of the signal. Now, let the displaced pixel neighborhood in Frame 2 be approximated as:
| (4) |
in which is the displacement vector to be estimated. By equating the coefficients
| (5) |
| (6) |
we solve for :
| (7) |
Implementations of the Farneback method can be found in OpenCV and the Computer Vision Toolbox of MATLAB. Final flow maps were masked according to the pertinent vessel structure.
In order to track the movement of the blood using PAVT, the imaging frame rate should satisfy the Nyquist sampling theorem23,44, as determined by the equation below:
| (8) |
where is the correlation length of the blood signals, and is the blood flow speed. In other words, we must sample at least twice within the propagation time associated with the correlation length.
Spatial heterogeneity.
Here, heterogeneity refers to the nonuniformity of the spatial distribution of red blood cells (RBCs) in the vessel lumen. The concept of spatial heterogeneity is illustrated in Fig. 1b, in which we consider two scenarios. In the first scenario, as shown in the left column of Fig. 1b, we model the spacing between the RBCs to be uniform and randomly distributed, yielding a weak lumen signal relative to the boundary signal in the PA image. In the second scenario, as shown in the right column of Fig. 1b, the RBC spatial distribution is altered to be nonuniform and random. Without altering the global RBC concentration in the vessel, we induce local pockets of dense and sparse regions of the RBC distribution, yielding a more detectable lumen signal in the PA image. The variability in the heterogeneity is achieved by adjusting the local concentration differentials between the dense and sparse regions within the vessel. In detail, to model, simulate, and measure the spatial heterogeneity of the blood, we define our region of interest as a 3D volume with a size of in the azimuthal, elevational, and axial directions, respectively, of the ultrasonic probe (see Supplementary Fig. 1). The spatial resolution cell is , in the corresponding directions, respectively. We can consider in the linear array probe case. Therefore, the number of divided sub-volumes is
| (9) |
In the uniform case, the concentration of the RBCs in the sub-volumes are the same. Therefore, for a physiological concentration, , of RBCs in a typical adult, and a number concentration, , of RBCs for each sub-volume, we have
| (10) |
Conversely, in the nonuniform case, the concentration of the RBCs in sub-volumes are different. Based on the hematocrit, , of a typical adult, we can obtain the number concentration of RBCs for each sub-volume as
| (11) |
Thus, , with
| (12) |
We can model as a uniform random distribution with mean and scale parameter . Then we obtain
| (13) |
where is considered as the index for heterogeneity ranging from 0 to 1, and is a uniform random distribution ranging from to . According to the typical hematocrit of a healthy adult, we choose , thus
| (14) |
where is a uniform random distribution from −1 to 1.
In the simulation study, we chose our total red blood cell concentration to match a typical physiological value of ~ 4.2 × 106 red blood cells per microliter of blood in the total lumen region of the vessel (1 mm in diameter) for both the uniform blood and nonuniform blood cases. The RBCs are distributed in a 2 mm × 1 mm × 1 mm 3D volume, which corresponds to the probe’s azimuthal, elevational, and axial directions, respectively. For the uniform blood case, the photoacoustic sources were randomly and uniformly distributed with . Conversely, in the case of nonuniform blood, the photoacoustic sources were randomly and nonuniformly distributed in the lumen region, with dense and sparse local regions, which are determined by the heterogeneity index . The simulation assumed a linear array ultrasound probe with the same center frequency (15 MHz) and element arrangement (256 elements, 23 mm aperture size), as in the experimental case. We divided the 3D volume into 200 sub-volumes with 100 μm × 100 μm × 1000 μm, based on the spatial resolution of the ultrasound probe.
We defined the relative visibility of the lumen signal as
| (15) |
where is the mean of the lumen signal, is the mean of the boundary signal, and is the mean of the background signal outside the vessel region. The results in Supplementary Fig. 1 show that the relative visibility index obtained from the photoacoustic images has a linear one-to-one mapping relationship with the heterogeneity index , which determines the distribution of the RBCs. Thus, the measured visibility index was used to characterize the spatial heterogeneity from the phantom and in vivo experimental data.
To study the effect of varying the heterogeneity index and vessel diameter on the relative visibility, we simulated the following two cases. In the first case, we held the diameter of the vessel constant at 1.0 mm, while varying the heterogeneity index across 12 levels from 0 to 1 (see Supplementary Fig. 2). In the second case, we varied the diameter in 0.5 mm increments from 0.5 to 2.0 mm at heterogeneity indices of 0 and 0.5 for each diameter (see Supplementary Fig. 3). The results show that the detected visibility of the lumen signal changes with the spatial heterogeneity condition of the blood but does not change with the vessel diameter.
Imaging protocols.
The experiments on human extremities were performed in a dedicated imaging room. All experiments were performed according to the relevant guidelines and regulations approved by the Institutional Review Board of the California Institute of Technology (Caltech). Eight healthy subjects were recruited from Caltech. Written informed consent was obtained from all the participants according to the study protocols.
Supplementary Material
Acknowledgments
We thank Konstantin Maslov, Lei Li, and Rui Cao for their discussions about the flow mechanism. We thank Steven L. Spitalnik and Paul Buehler for their discussions about blood physiology. We thank Sam Davis and Byullee Park for discussion on the potential improvement of flow visualization. We thank Lei Li for the suggestion about fiber coupling and assistance in light alignment. This work was sponsored by the United States National Institutes of Health (NIH) grants U01 EB029823 (BRAIN Initiative) and R35 CA220436 (Outstanding Investigator Award).
Footnotes
Competing interests
L.V.W. has a financial interest in Microphotoacoustics Inc., CalPACT LLC, and Union Photoacoustic Technologies Ltd., which, however, did not support this work.
Code availability
The reconstruction algorithm and data processing methods can be found in Methods. The reconstruction code is not publicly available because it is proprietary and is used in licensed technologies.
Reporting Summary. Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data that support the findings of this study are provided within the paper and its supplementary material.
References
- 1.Won R Mapping blood flow. Nat. Photonics 5, 393–393 (2011). [Google Scholar]
- 2.Rajan V, Varghese B, van Leeuwen TG & Steenbergen W Review of methodological developments in laser Doppler flowmetry. Lasers Med. Sci. 24, 269–283 (2009). [DOI] [PubMed] [Google Scholar]
- 3.Leitgeb RA, Werkmeister RM, Blatter C & Schmetterer L Doppler Optical Coherence Tomography. Prog. Retin. Eye Res. 41, 26–43 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Qureshi MM et al. Quantitative blood flow estimation in vivo by optical speckle image velocimetry: publisher’s note. Optica 8, 1326–1326 (2021). [Google Scholar]
- 5.Boas DA & Dunn AK Laser speckle contrast imaging in biomedical optics. J. Biomed. Opt. 15, 011109 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cinotti E et al. Quantification of capillary blood cell flow using reflectance confocal microscopy. Skin Res. Technol. 20, 373–378 (2014). [DOI] [PubMed] [Google Scholar]
- 7.Wang LV & Hu S Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science 335, 1458–1462 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang LV Tutorial on Photoacoustic Microscopy and Computed Tomography. IEEE J. Sel. Top. Quantum Electron. 14, 171–179 (2008). [Google Scholar]
- 9.Yao J et al. High-speed label-free functional photoacoustic microscopy of mouse brain in action. Nat. Methods 12, 407–410 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kinnunen M, Kauppila A, Karmenyan A & Myllylä R Effect of the size and shape of a red blood cell on elastic light scattering properties at the single-cell level. Biomed. Opt. Express 2, 1803–1814 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang LV Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics 3, 503–509 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Brunker J & Beard P Velocity measurements in whole blood using acoustic resolution photoacoustic Doppler. Biomed. Opt. Express 7, 2789–2806 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yao J & Wang LV Photoacoustic brain imaging: from microscopic to macroscopic scales. Neurophotonics 1, 011003 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Guo Z, Li L & Wang LV On the speckle-free nature of photoacoustic tomography. Med. Phys. 36, 4084–4088 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pakdaman Zangabad R et al. Photoacoustic flow velocity imaging based on complex field decorrelation. Photoacoustics 22, 100256 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xu M & Wang LV Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E 71, 016706 (2005). [DOI] [PubMed] [Google Scholar]
- 17.Lurie F, Kistner RL, Eklof B & Kessler D Mechanism of venous valve closure and role of the valve in circulation: a new concept. J. Vasc. Surg. 38, 955–961 (2003). [DOI] [PubMed] [Google Scholar]
- 18.Szabo TL Diagnostic ultrasound imaging: inside out. (Academic press, 2004). [Google Scholar]
- 19.Tanter M & Fink M Ultrafast imaging in biomedical ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61, 102–119 (2014). [DOI] [PubMed] [Google Scholar]
- 20.Errico C et al. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 527, 499–502 (2015). [DOI] [PubMed] [Google Scholar]
- 21.Wang LV & Wu H Biomedical optics: principles and imaging. (John Wiley & Sons, 2012). [Google Scholar]
- 22.ANSI Z136.1–2014 - American National Standard for Safe Use of Lasers. https://webstore.ansi.org/Standards/LIA/ANSIZ1362014. [Google Scholar]
- 23.Grenander U The Nyquist frequency is that frequency whose period is two sampling intervals. Probab. Stat. Harald Cramér Vol. 434, (1959). [Google Scholar]
- 24.Lee Y, Kang J & Yoo Y Automatic dynamic range adjustment for ultrasound B-mode imaging. Ultrasonics 56, 435–443 (2015). [DOI] [PubMed] [Google Scholar]
- 25.Fernández-Colino A & Jockenhoevel S Advances in engineering venous valves: the pursuit of a definite solution for chronic venous disease. Tissue Eng. Part B Rev. 27, 253–265 (2021). [DOI] [PubMed] [Google Scholar]
- 26.Petrila T & Trif D Basics of fluid mechanics and introduction to computational fluid dynamics. vol. 3 (Springer Science & Business Media, 2004). [Google Scholar]
- 27.Murray CD The Physiological Principle of Minimum Work. Proc. Natl. Acad. Sci. U. S. A. 12, 207–214 (1926). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wiedeman MP Dimensions of blood vessels from distributing artery to collecting vein. Circ. Res. 12, 375–378 (1963). [DOI] [PubMed] [Google Scholar]
- 29.Li L et al. Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution. Nat. Biomed. Eng. 1, 1–11 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Keys A The oxygen saturation of the venous blood in normal human subjects. Am. J. Physiol.-Leg. Content 124, 13–21 (1938). [Google Scholar]
- 31.Na S, Zhang Y & Wang LV Cross-Ray Ultrasound Tomography and Photoacoustic Tomography of Cerebral Haemodynamics in Rodents. Adv. Sci. 2201104 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yao J, Maslov KI & Wang LV In vivo photoacoustic tomography of total blood flow and potential imaging of cancer angiogenesis and hypermetabolism. Technol. Cancer Res. Treat. 11, 301–307 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Beebe-Dimmer JL, Pfeifer JR, Engle JS & Schottenfeld D The Epidemiology of Chronic Venous Insufficiency and Varicose Veins. Ann. Epidemiol. 15, 175–184 (2005). [DOI] [PubMed] [Google Scholar]
- 34.Lin L & Wang LV The emerging role of photoacoustic imaging in clinical oncology. Nat. Rev. Clin. Oncol. 19, 365–384 (2022). [DOI] [PubMed] [Google Scholar]
- 35.Na S et al. Massively parallel functional photoacoustic computed tomography of the human brain. Nat. Biomed. Eng. 1–9 (2021) doi: 10.1038/s41551-021-00735-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang Y et al. Transcranial photoacoustic computed tomography of human brain function. ArXiv Prepr. ArXiv220600248 (2022). [Google Scholar]
- 37.Yao J, Maslov KI, Zhang Y, Xia Y & Wang LV Label-free oxygen-metabolic photoacoustic microscopy in vivo. J. Biomed. Opt. 16, 076003 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Montaldo G, Tanter M, Bercoff J, Benech N & Fink M Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 489–506 (2009). [DOI] [PubMed] [Google Scholar]
- 39.Zhang Y, Guo Y & Lee W-N Ultrafast Ultrasound Imaging With Cascaded Dual-Polarity Waves. IEEE Trans. Med. Imaging 37, 906–917 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Yiu BY, Lai SS & Alfred CH Vector projectile imaging: Time-resolved dynamic visualization of complex flow patterns. Ultrasound Med. Biol. 40, 2295–2309 (2014). [DOI] [PubMed] [Google Scholar]
- 41.Dong J, Zhang Y & Lee W-N Walled vessel-mimicking phantom for ultrasound imaging using 3D printing with a water-soluble filament: design principle, fluid-structure interaction (FSI) simulation, and experimental validation. Phys. Med. Biol. 65, 085006 (2020). [DOI] [PubMed] [Google Scholar]
- 42.Demené C et al. Spatiotemporal Clutter Filtering of Ultrafast Ultrasound Data Highly Increases Doppler and fUltrasound Sensitivity. IEEE Trans. Med. Imaging 34, 2271–2285 (2015). [DOI] [PubMed] [Google Scholar]
- 43.Farnebäck G Two-frame motion estimation based on polynomial expansion. in Scandinavian conference on Image analysis 363–370 (Springer, 2003). [Google Scholar]
- 44.Leis JW Digital signal processing using MATLAB for students and researchers. (John Wiley & Sons, 2011). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are provided within the paper and its supplementary material.


