glmmPen: High Dimensional Penalized Generalized Linear Mixed Models

Abstract

Generalized linear mixed models (GLMMs) are widely used in research for their ability to model correlated outcomes with non-Gaussian conditional distributions. The proper selection of fixed and random effects is a critical part of the modeling process, where model misspecification may lead to significant bias. However, the joint selection of fixed and random effects has historically been limited to lower dimensional GLMMs, largely due to the use of criterion-based model selection strategies. Here we present the R package glmmPen, one of the first to select fixed and random effects in higher dimension using a penalized GLMM modeling framework. Model parameters are estimated using a Monte Carlo expectation conditional minimization (MCECM) algorithm, which leverages Stan and RcppArmadillo for increased computational efficiency. Our package supports the Binomial, Gaussian, and Poisson families and multiple penalty functions. In this manuscript we discuss the modeling procedure, estimation scheme, and software implementation through application to a pancreatic cancer subtyping study. Simulation results show our method has good performance in selecting both the fixed and random effects in high dimensional GLMMs.

Introduction

Generalized linear mixed models (GLMMs) are widely used in scientific research, with applications spanning the social sciences (Schmidt-Catran and Fairbrother, 2016), biomedical sciences (Fitzmaurice et al., 2012), public health and epidemiology (Szyszkowicz, 2006; Kleinman et al., 2004; Dean and Nielsen, 2007), natural sciences including ecology and evolution (Bolker et al., 2009), and economics (Langford, 1994). GLMMs are generalized linear models where the predictors within the model can have “fixed” or “random” effects. Coefficients corresponding to fixed effects predictors can be considered to describe population-level relationships between the predictor and the outcome. Random effects predictors pertain to variables whose relationships with the outcome are presumed to vary randomly across “groups” of observations within the data, leading to group-specific coefficient estimates (Fitzmaurice et al., 2012). In practical applications, these “groups” may pertain to clusters of samples, repeated measures within the same individual, or observations resulting from nested designs. Multiple studies have shown that omitting important random effects can lead to bias in the estimated variance of the fixed effects, and including unnecessary random effects may lead to computational difficulties (Thompson et al., 2017; Gurka et al., 2011; Bondell et al., 2010). As a result, proper specification of fixed and random effects is an important and critical step in the application of GLMMs.

In many low dimensional settings, researchers may have advanced knowledge about which variables are fixed or random. For instance, researchers may reasonably expect treatment effects in certain multi-site clinical trials to vary by site (Feaster et al., 2011). However, in high dimensional settings, it is often unknown a priori which variables should be specified as fixed or random in the model. In such settings, the feature space may also be sparse with many variables unrelated to the outcome. Therefore, variable selection approaches are employed to evaluate candidate models. R packages such as lme4 (Bates et al., 2015), mcemGLM (Archila, 2020), and MCMCglmm (Hadfield, 2010) allow users to fit a set of pre-specified models, which may then be compared using model selection criteria such as the profile conditional AIC (Donohue et al., 2011), the BIC-ICQ criterion (Ibrahim et al., 2011), the hybrid Bayesian information criterion, BICh (Delattre et al., 2014), or criteria developed for mixed effects models. However, criterion-based all-subsets selection or direct model comparison strategies are not feasible even in small dimensions, as with $p$ predictors there are $2^{2_p}$ possible combinations of fixed and random effects to be evaluated.

Packages such as glmnet (Friedman et al., 2010), ncvreg (Breheny and Huang, 2011), and grpreg (Breheny and Huang, 2015) avoid this limitation for GLMs via coordinate-descent based penalized likelihood methods for variable selection, and are therefore much more scalable with respect to $p$. Unfortunately, none of these methods can account for random effects during their variable selection procedure. Other packages such as glmmLasso (Groll, 2017) and glmmixedLASSO (Schelldorfer et al., 2014) alternatively allow the inclusion of random effects in the model while performing variable selection, but only allow for variable selection on the fixed effects. Prior work has shown that simultaneous selection of fixed and random effects is advantageous because improper specification of the random effects can significantly affect the selection of the fixed effects, and vice versa (Bondell et al., 2010). In addition, there may not be a priori knowledge of which variables may vary randomly across groups in their effects. Therefore, the specification of random effects may be difficult in practical applications, particularly as the dimension of the data grows.

To address these limitations in performing variable selection in high-dimensional GLMMs, we present the glmmPen R package. This package allows for the simultaneous selection of fixed and random effects predictors in higher dimensions through the use of penalized generalized linear mixed models (pGLMMs). Similar to ncvreg and glmnet, this package focuses on variable selection for the purpose of creating prediction models, and does not provide statistical inference. The package leverages Monte Carlo expectation conditional minimization (MCECM) in combination with several techniques to improve the computational efficiency of the algorithm. In the MCECM E-step, glmmPen utilizes the Stan software implemented in the rstan package to efficiently sample from the posterior distribution of the random effects, and a Majorization-Minimization coordinate descent algorithm is utilized to update model parameters in the M-step. The glmmPen package utilizes the fast looping capabilities within Rcpp and RcppArmadillo in order to recalculate large matrices pertaining to intermediate quantities without necessitating their storage, improving memory usage and scalability. The glmmPen package is also able to improve the speed of the overall variable selection procedure by strategic coefficient initialization (see Section “Initialization and convergence”) and strategic restriction of random effects (see Section “Tuning parameter selection strategy”).

The main estimation functions of the package are glmmPen and glmm, where the latter can be used to fit traditional generalized linear mixed models without penalization. The user interface and output of the glmmPen and glmm functions were designed to be very similar to those from the functions lmer and glmer to facilitate ease of use. Specifically, glmmPen outputs a pglmmObj object which, like the merMod object from lme4, can facilitate the application of common S3 method functions used by lme4 such as logLik, fixef, ranef, and others. In addition, multiple types of penalties and information criteria for selecting optimal penalties are available in the package, and the package supports the Binomial, Gaussian, and Poisson distributional families.

Our manuscript is organized as follows. We begin by reviewing the pGLMMs modeling framework, first described in Rashid et al. (2020). The second section describes the MCECM algorithm used by glmmPen to fit pGLMM models. The third section describes the variable selection procedure of the package and the Bayesian information criterion (BIC) type selection criteria available for use. The fourth section illustrates a practical application of the glmmPen R package using data from a recent cancer subtyping study. The fifth section provides some simulation results. Finally, we provide concluding comments. The package is available from the Comprehensive R Archive Network (CRAN) at https://cran.r-project.org/package=glmmPen. The replication of all code content, tables, and figures presented in this paper can be found in the GitHub repository https://github.com/hheiling/paper_glmmPen_RJournal. Supplementary results mentioned but not reported in this paper can also be found in this GitHub repository.

Generalized linear mixed models

We review the notation and model formulation of our approach, first introduced in Rashid et al. (2020). We consider the case where we want to analyze data from $K$ independent groups of any kind. For instance, we could be interested in analyzing data from $K$ different studies, or we could be interested in analyzing longitudinal data from $K$ individuals. For each group $k=1,\dots ,K$, there are $n_k$ observations for a total sample size of $N={\sum }_{k=1}^K{n}_k$. For the $k^{th}$ group, let ${\mathit{y}}_k={\left(y_{k1},\dots ,y_{k{n}_k}\right)}^{\top }$ be the vector of $n_k$ independent responses, let ${\mathit{x}}_{ki}={\left(x_{ki,1},\dots ,x_{ki,p}\right)}^{\top }$ be the $p$-dimensional vector of predictors, and let ${\mathit{X}}_k={\left({\mathit{x}}_{k1},\dots ,{\mathit{x}}_{k{n}_k}\right)}^{\top }$. Although the glmmPen package allows for different $n_k$ for the $K$ groups, we will set ${\left\{n_k\right\}}_{k=1}^K=n$ for simplicity of notation in future equations. In GLMMs, we assume that the conditional distribution of ${\mathit{y}}_k$ given ${\mathit{X}}_k$ belongs to the exponential family and has the following density:

$$f\left({\mathit{y}}_k\mathit{|}{\mathit{X}}_k,{\mathit{\alpha }}_k;\theta \right)=\prod _{i=1}^{n}c\left(y_{ki}\right)\exp \left[{\tau }^{-1}\left\{y_{ki}{\eta }_{ki}-b\left({\eta }_{ki}\right)\right\}\right],$$ (1)

where $c\left(y_{ki}\right)$ is a constant that only depends on $y_{ki}$, $\tau$ is the dispersion parameter, $b(\cdot )$ is a known link function, and ${\eta }_{ki}$ is the linear predictor. The glmmPen algorithm currently allows for the Gaussian, Binomial, and Poisson families with canonical links.

In the GLMM, the linear predictor has the form

$${\eta }_{ki}={\mathit{x}}_{ki}^{\top }\mathit{\beta }+{\mathit{z}}_{ki}^{\top }\mathbf{\Gamma }{\mathit{\alpha }}_k,$$ (2)

where $\mathit{\beta }={\left({\beta }_1,\dots ,{\beta }_p\right)}^{\top }$ is a $p$-dimensional vector for the fixed effects coefficients (including the intercept), ${\mathit{\alpha }}_k$ is a $q$-dimensional vector of unobservable random effects (including the random intercept), ${\mathit{z}}_{ki}$ is a $q$-dimensional subvector of ${\mathit{x}}_{ki}$, and $\mathbf{\Gamma }$ is a lower triangular matrix. In this notation, ${\mathit{z}}_{ki}$ represents the random effects predictors, i.e. the subset of the total predictors (${\mathit{x}}_{ki}$) that have predictor effects that randomly vary across levels of the grouping variable.

In Rashid et al. (2020), the random effects vector ${\mathit{\alpha }}_k$ is assumed to follow $N_q(\mathbf{0},\mathit{I})$ so that $\mathbf{\Gamma }{\mathit{\alpha }}_k$ follows $N\left(\mathbf{0},\hspace{0.33em}\mathbf{\Gamma }{\mathbf{\Gamma }}^{\top }\right)$. In this way, the random component of the linear predictor has variance $\text{Var}\left(\mathbf{\Gamma }{\mathit{\alpha }}_k\right)=\mathbf{\Gamma }{\mathbf{\Gamma }}^{\top }$.

To simplify the procedure of estimating $\mathbf{\Gamma }$, we consider a vector $\mathit{\gamma }$ containing all of the nonzero elements of $\mathbf{\Gamma }$ such that ${\mathit{\gamma }}_t$ is a $t\times 1$ vector consisting of nonzero elements of the $t^{th}$ row of $\mathbf{\Gamma }$ and $\mathit{\gamma }={\left({\mathit{\gamma }}_1^{\top },\dots ,{\mathit{\gamma }}_q^{\top }\right)}^{\top }$. We can then reparameterize the linear predictor (Chen and Dunson, 2003; Ibrahim et al., 2011) to

$${\eta }_{ki}={\mathit{x}}_{ki}^{\top }\mathit{\beta }+{\mathit{z}}_{ki}^{\top }{\mathbf{\Gamma }}_{{\mathit{\alpha }}_k}=\left({\mathit{x}}_{ki}^{\top }\hspace{1em}{\left({\mathit{\alpha }}_k\otimes {\mathit{z}}_{ki}\right)}^{\top }\hspace{1em}{\mathit{J}}_q\right)\left(\begin{array}{c}\mathit{\beta }\\ \mathit{\gamma }\end{array}\right)$$ (3)

where ${\mathit{J}}_q$ is a matrix that transforms $\mathit{\gamma }$ to $\text{vec}(\mathbf{\Gamma })$ such that $\text{vec}(\mathbf{\Gamma })={\mathit{J}}_q\mathit{\gamma }$. ${\mathit{J}}_q$ is of dimension $q^2\times q(q+1)\text{/}2$ when the random effects covariance matrix $\mathbf{\Gamma }{\mathbf{\Gamma }}^{\top }$ is unstructured; alternatively, ${\mathit{J}}_q$ is of dimension $q^2\times q$ when the random effects covariance matrix has an independence structure (i.e., diagonal). The vector of parameters $\mathit{\theta }={\left({\mathit{\beta }}^{\top },\hspace{0.33em}{\mathit{\gamma }}^{\top },\hspace{0.33em}\tau \right)}^{\top }$ are the main parameters of interest. We denote the true value of $\mathit{\theta }$ as ${\mathit{\theta }}^{\ast }={\left({\mathit{\beta }}^{\ast \top },\hspace{0.33em}{\mathit{\gamma }}^{\ast \top },{\tau }^{\ast }\right)}^{\top }={\mathrm{argmin}}_{\mathit{\theta }}{\text{E}}_{\mathit{\theta }}[-\ell (\mathit{\theta })]$ where $\ell (\mathit{\theta })$ is the observed marginal log-likelihood across all $K$ groups such that $\ell (\mathit{\theta })={\sum }_{k=1}^K{\ell }_k(\mathit{\theta })$, ${\ell }_k(\mathit{\theta })=(1\text{/}n)\log \int f\left({\mathit{y}}_k\mathit{|}{\mathit{X}}_k,{\mathit{\alpha }}_k;\mathit{\theta }\right)\varphi \left({\mathit{\alpha }}_k\right)d{\mathit{\alpha }}_k$.

Let us consider the high dimensional case where we want to select the true nonzero fixed effects and true nonzero random effects. In other words, we aim to identify the set

$$S=S_1\cup S_2=\left\{j:{\beta }_j^{\ast }\ne 0\right\}\cup \left\{t\hspace{0.33em}:\hspace{0.33em}{‖{\mathit{\gamma }}_t^{\ast }‖}_2\ne 0\right\},$$

where the set $S_1$ represents the selection of true nonzero fixed effects and the set $S_2$ represents the selection of true nonzero random effects. When ${\mathit{\gamma }}_t=\mathbf{0}$, this sets row $t$ of $\mathbf{\Gamma }$ entirely equal to 0, indicating that effect of covariate $t$ is fixed across the $K$ groups.

We aim to solve the following penalized likelihood:

$$\widehat{\mathit{\theta }}={\mathrm{argmin}}_{\mathit{\theta }}-\ell (\mathit{\theta })+{\lambda }_0\sum _{j=1}^p{\rho }_0\left({\beta }_j\right)+{\lambda }_1\sum _{t=1}^q{\rho }_1\left({‖{\gamma }_t‖}_2\right),$$ (4)

where $\ell (\mathit{\theta })$ is the observed marginal log-likelihood for all $K$ groups defined earlier, ${\rho }_0(t)$ and ${\rho }_1(t)$ are general folded-concave penalty functions, and ${\lambda }_0$ and ${\lambda }_1$ are positive tuning parameters. In the glmmPen package, the ${\rho }_0(t)$ penalty function options include the least absolute shrinkage and selection operator (LASSO) $L_1$ penalty, the smoothly clipped absolute deviation (SCAD) penalty, and the minimax concave penalty (MCP) (Friedman et al., 2010; Breheny and Huang, 2011). For the ${\rho }_1(t)$ penalty, we treat the elements of ${\mathit{\gamma }}_t$ as a group and penalize them in a groupwise manner using the group LASSO, group MCP, or group SCAD penalties presented by Breheny and Huang (2015). These groups of ${\mathit{\gamma }}_t$ are then estimated to be either all zero or all nonzero. In this way, we select covariates to have varying effects $\left({\widehat{\mathit{\gamma }}}_{\mathit{t}}\ne \mathbf{0}\right)$ or fixed effects $\left({\widehat{\mathit{\gamma }}}_{\mathit{t}}\text{=0}\right)$ across the $K$ groups.

Similar to other variable selection packages such as package ncvreg (Breheny and Huang, 2011), in glmmPen we standardize the fixed effects covariates matrix $\mathit{X}={\left({\mathit{X}}_1^{\top },\dots ,{\mathit{X}}_K^{\top }\right)}^{\top }$ such that ${\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\mathit{x}}_{ki,j}=0$ and $N^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\mathit{x}}_{ki,j}^2=1$ for $j=1,\dots ,p$; this process is performed automatically within the algorithm. Although the package grpreg (Breheny and Huang, 2015) orthogonalizes grouped effects, we have found through simulations during early package testing that first standardizing the fixed effects and then using subsets of these standardized fixed effects for the random effects (recall: ${\mathit{z}}_{ki}$ is a $q$-dimensional subvector of ${\mathit{x}}_{ki}$) is sufficient. During the selection procedure, the fixed effects intercept and the variance of the random effects intercept remain unpenalized.

MCECM algorithm

We solve Equation 4 for a specific $\left({\lambda }_0,\hspace{0.33em}{\lambda }_1\right)$ penalty parameter combination using a Monte Carlo expectation conditional minimization (MCECM) algorithm (Garcia et al., 2010). The MCECM algorithm described in this section uses many of the steps and assumptions described in Rashid et al. (2020), but here we provide further practical details about the E-step, M-step, initialization, and convergence. Additionally, the implementation outlined in this paper has several improvements to the implementation used in Rashid et al. (2020). In glmmPen, the E-step allows for several possible sampling schemes, including the fast and efficient No-U-Turn Hamiltonian Monte Carlo sampling procedure (NUTS) from the Stan software (Carpenter et al., 2017; Hoffman and Gelman, 2014). The glmmPen package was also able to reduce the required memory usage of the MCECM algorithm. In the M-step, we utilized the fast looping capability of packages Rcpp and RcppArmadillo to allow for fast recalculation of large matrices (see Step 3 of the M-step presented in Algorithm 1) and avoid their storage, improving model scalability.

During the MCECM algorithm, we aim to evaluate (E-step) and minimize (M-step) the following penalized Q-function in the $s^{th}$ iteration of the algorithm:

$$\begin{array}{l}{Q}_{\lambda }\left(\theta \mathit{|}{\theta }^{(s)}\right)=\sum _{k=1}^{K}E\left\{-\log \left(f\left({\mathit{y}}_k,X_k,{\alpha }_k;\theta \mathit{|}{D}_0;{\theta }^{(s)}\right)\right)\right\}+{\lambda }_0\sum _{j=1}^p{\rho }_0\left({\beta }_j\right)+{\lambda }_1\sum _{t=1}^q{\rho }_1\left(\parallel {\mathit{\gamma }}_t{\parallel }_2\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}=Q_1\left(\theta \mathit{|}{\theta }^{(s)}\right)+Q_2\left({\theta }^{(s)}\right)+{\lambda }_0\sum _{j=1}^p{\rho }_0\left({\beta }_j\right)+{\lambda }_1\sum _{t=1}^q{\rho }_1\left(\parallel {\mathit{\gamma }}_t{\parallel }_2\right),\end{array}$$ (5)

where $\left({\mathit{y}}_k,{\mathit{X}}_k,{\alpha }_k\right)$ gives the complete data for group $k$, ${\mathit{D}}_o$ represents the entirety of the observed data, and ${\mathit{D}}_{k,o}=\left({\mathit{y}}_k,{\mathit{X}}_k\right)$ gives the observed data for group $k$. In other words, we aim to evaluate and minimize the penalized expectation of the negative joint log-likelihood with respect to the observed data. From Rashid et al. (2020), the expectation can be written as the sum of the following terms:

$$Q_1\left(\theta \mathit{|}{\theta }^{(s)}\right)=-\sum _{k=1}^K\int \log \left[f\left(y_k\mathit{|}{\mathit{X}}_k,{\alpha }_k;\theta \right)\right]\varphi \left({\alpha }_k\mathit{|}{\mathit{D}}_{k,0};{\theta }^{(s)}\right)d{\alpha }_k,$$ (6)

$$Q_2({\theta }^{(s)})=-\sum _{k=1}^K\int \log \left[\varphi \left({\alpha }_k\right)\right]\varphi \left({\alpha }_k\mathit{|}{D}_{k,0};{\theta }^{(s)}\right)d{\alpha }_k$$ (7)

The $Q_1\left(\theta \mathit{|}{\theta }^{(s)}\right)$ function expresses the conditional model of the observed data given the latent (random) variables and integrates over the latent variables. Using the $Q_1\left(\theta \mathit{|}{\theta }^{(s)}\right)$ function, we aim to derive the fixed and random effect coefficient estimates during the M-step of the algorithm. During the E-step, we aim to approximate the integral in the $Q_1\left(\theta \mathit{|}{\theta }^{(s)}\right)$ function by incorporating samples from the posterior distribution of the latent variables.

Monte Carlo E-step

The integrals in the Q-function do not have closed forms when $f\left({\mathit{y}}_k\mathit{|}{X}_k,\hspace{0.17em}{\alpha }_k^{(s,m)};\hspace{0.17em}\theta \right)$ is assumed to be non-Gaussian, and become difficult to approximate as $q$ increases. Consequently, we approximate these integrals using a Markov chain Monte Carlo (MCMC) sample of size M from the posterior density $\varphi \left({\alpha }_k\mathit{|}{D}_{k,o};\hspace{0.33em}{\theta }^{(s)}\right)$. The glmmPen package can draw samples from this posterior using one of several techniques: the No-U-Turn Hamiltonian Monte Carlo sampling procedure (NUTS) implemented by the Stan software, which glmmPen calls using the rstan package (Carpenter et al., 2017) (default, and strongly recommended for its speed and efficiency); Metropolis-within-Gibbs with an adaptive random walk sampler (Roberts and Rosenthal, 2009); and Metropolis-within-Gibbs with an independence sampler (Givens and Hoeting, 2012). Each sampler type uses a standard normal candidate distribution. Let ${\alpha }_k^{(s,m)}$ be the $m^{th}$ simulated value, $m=1,\dots ,M$, at the $s^{th}$ iteration of the algorithm for group $k$. The integral in Equation 6 can then be approximated as

$$Q_1\left(\theta \mathit{|}{\theta }^{(s)}\right)\approx -\frac{1}{M}\sum _{m=1}^M\sum _{k=1}^K\log f\left({\mathit{y}}_k\mathit{|}{\mathit{X}}_k,{\alpha }_k^{(s,m)};\theta \right).$$

Although the optimal number of MCMC samples $M^{(s)}$ in the E-step at EM iteration $s$ is not well defined, the general consensus is that a smaller sample size of the posterior is suitable for the start of the algorithm but larger sample sizes are needed later in the algorithm (Booth and Hobert, 1999). We set the default number of MCMC samples in the first iteration of the MCECM algorithm $M^{(1)}=250$ when $q\le 10$, and $M^{(1)}=100$ otherwise. (We decrease the initial sampling size when the number of random effects predictors is large in order to help speed up the algorithm). Then, in a manner similar to the mcemGLM package (Archila, 2020), the MCMC sample size is increased by a multiplicative factor $v$ at each step of the algorithm such that $M^{(s)}=v\times M^{(s-1)}$ until either the value of $M^{(s)}$ reaches its maximum allowed value or the EM algorithm converges. In glmmPen, the default maximum allowed value is dependent on the the number of random effects in the model, $q$; see the documentation of optimControl for more details. For the first 15 iterations of the EM algorithm, the value of $v$ is set to 1.1. For the remaining steps of the algorithm, $v$ is set to 1.2.

M-step

In the M-step of the algorithm, we aim to minimize

$$Q_{1,\lambda }\left(\theta \mathit{|}{\theta }^{(s)}\right)=Q_1\left(\theta \mathit{|}{\theta }^{(s)}\right)+{\lambda }_0\sum _{j=1}^p{\rho }_0\left({\beta }_j\right)+{\lambda }_1\sum _{t=1}^q{\rho }_1\left(\parallel {\gamma }_t{\parallel }_2\right)$$ (8)

with respect to $\theta ={\left({\mathit{\beta }}^{\top },{\gamma }^{\top },\tau \right)}^{\top }$. The minimization of Equation 8 with respect to $\mathit{\beta }$ and $\gamma$ is performed using a Majorization-Minimization approach. For the general exponential family, Rashid et al. (2020) suggested minimizing with respect to $\tau$ using the standard optimization algorithm Newton-Raphson. In glmmPen, the only family implemented with a dispersion parameter is the Gaussian family, and the variance ${\sigma }^2$ can be estimated directly from a derivation of the Q function conditional on the most recent updates of ${\mathit{\beta }}^{(s)}$ and ${\gamma }^{(s)}$:

$${\sigma }^2=\frac{1}{M\times N}\sum _{m=1}^M\sum _{k=1}^K\sum _{i=1}^{n_k}{\left(y_{ki}-{\eta }_{ki}^{(s,m)}\right)}^2,$$ (9)

where ${\eta }_{ki}^{(s,m)}$ is the linear predictor ${\eta }_{ki}$ evaluated with ${\mathit{\beta }}^{(s)}$, ${\gamma }^{(s)}$, and sample ${\alpha }_k^{(s,m)}$.

Let $s$ represent the iteration of the MCECM algorithm, and $h$ represent the iteration within a particular M-step of the MCECM algorithm. The M-step of the $s^{th}$ iteration of the MCECM algorithm proceeds as in Algorithm 1.

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm}}\hspace{0.33em}\mathbf{\text{1}}\hspace{0.33em}\text{M-step}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}s\text{-th}\hspace{0.17em}\text{iteration}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{MCECM}\hspace{0.17em}\text{algorithm}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}\\ \hspace{1em}\text{1.}\hspace{0.33em}\text{The parameters}\hspace{0.17em}{\theta }^{(s,0)}\hspace{0.17em}\text{forM-step}\hspace{0.17em}\text{iteration}\hspace{0.17em}h=0\hspace{0.17em}\text{are}\hspace{0.17em}\text{initialized}\hspace{0.17em}\text{using}\hspace{0.17em}\text{the}\hspace{0.17em}\text{results}\hspace{0.17em}\text{from}\\ \hspace{1em}\hspace{1em}\text{the}\hspace{0.17em}\text{previous}\hspace{0.17em}\text{M-step,}\hspace{0.17em}{\theta }^{(s-1)}\text{.}\\ \hspace{1em}\text{2.}\hspace{0.33em}\text{Conditional}\hspace{0.17em}\text{on}\hspace{0.17em}{\mathit{\gamma }}^{(s,h-1)}\hspace{0.17em}\text{and}\hspace{0.17em}{\tau }^{(s-1)},\hspace{0.17em}\text{each}\hspace{0.17em}{\beta }_j^{(s,h)}\hspace{0.17em}\text{for}\hspace{0.17em}j=\{1,\dots ,p\}\hspace{0.17em}\text{is}\hspace{0.17em}\text{given}\hspace{0.17em}\text{a}\hspace{0.17em}\text{single}\hspace{0.17em}\text{update}\\ \hspace{1em}\hspace{1em}\text{using}\hspace{0.17em}\text{the}\hspace{0.17em}\text{Majorization-Minimization}\hspace{0.17em}\text{algorithm}\hspace{0.17em}\text{specified}\hspace{0.17em}\text{by}\hspace{0.17em}\text{Breheny}\hspace{0.17em}\text{and}\hspace{0.17em}\text{Huang}\left(\text{2015}\right).\\ \hspace{1em}3.\hspace{0.33em}\text{For}\hspace{0.17em}\text{each}\hspace{0.17em}\text{group}\hspace{0.17em}\text{k}\hspace{0.17em}\text{in}\hspace{0.17em}k=\{1,\dots ,K\}\hspace{0.17em}\text{the}\hspace{0.17em}\text{augmented}\hspace{0.17em}\text{matrix} \hspace{0.17em}{\tilde{z}}_{ki}=\left({\tilde{\alpha }}_k^{(s)}\otimes {\mathit{z}}_{ki}\right)J_q\hspace{0.17em}\text{is}\hspace{0.17em}\text{created}\\ \hspace{1em}\hspace{1em}\text{for}\hspace{0.17em}i=1,\dots ,n_k\hspace{0.17em}\text{where}\hspace{0.17em}{\tilde{\alpha }}_k^{(s)}={\left({\left({\alpha }_k^{(s,1)}\right)}^{\top },\dots ,{\left({\alpha }_k^{(s,M)}\right)}^{\top }\right)}^{\top }\text{.}\hspace{0.17em}\text{This}\hspace{0.17em}\text{augmented}\hspace{0.17em}\text{matrix}\hspace{0.17em}\text{is}\hspace{0.17em}\text{used}\hspace{0.17em}\text{in}\\ \hspace{1em}\hspace{1em}\text{the}\hspace{0.17em}\text{random}\hspace{0.17em}\text{effect}\hspace{0.17em}\text{portion}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{linear}\hspace{0.17em}\text{predictor}\hspace{0.17em}\text{specified}\hspace{0.17em}\text{in}\hspace{0.17em}\text{Equation}\hspace{0.17em}\text{2.}\hspace{0.17em}\text{The}\hspace{0.17em}\text{dimension}\hspace{0.17em}\text{of}\\ \hspace{1em}\hspace{1em} {\tilde{\mathit{z}}}_{ki}\hspace{0.17em}\text{is}\hspace{0.17em}M\times q(q+1)\text{/}2\hspace{0.17em}\text{for}\hspace{0.17em}\text{an}\hspace{0.17em}\text{unstructured}\hspace{0.17em}\text{covariance}\hspace{0.17em}\text{matrix}\hspace{0.17em}\text{and}\hspace{0.17em}M\times q\hspace{0.17em}\text{for}\hspace{0.17em}\text{an}\hspace{0.17em}\text{independent}\\ \hspace{1em}\hspace{1em}\text{covariance}\hspace{0.17em}\text{matrix.}\hspace{0.17em}\text{This}\hspace{0.17em}\text{augmented}\hspace{0.17em}\text{matrix}\hspace{0.17em}\text{is}\hspace{0.17em}\text{used}\hspace{0.17em}\text{to}\hspace{0.17em}\text{calculate}\hspace{0.17em}\text{Equation}\hspace{0.17em}\text{2.9}\hspace{0.17em}\text{in}\hspace{0.17em}\text{Breheny}\\ \hspace{1em}\hspace{1em}\text{and}\hspace{0.17em}\text{Huang}\hspace{0.17em}\left(\text{2015}\right).\\ \hspace{1em}4.\hspace{0.33em}\text{Conditional}\hspace{0.17em}\text{on}\hspace{0.17em}\text{the}\hspace{0.17em}{\tau }^{(s-1)}\hspace{0.17em}\text{and}\hspace{0.17em}\text{the}\hspace{0.17em}\text{recently}\hspace{0.17em}\text{updated}\hspace{0.17em}{\mathit{\beta }}^{(s,h+1)}\text{,}\hspace{0.17em}\text{each }\hspace{0.17em}{\mathit{\gamma }}_t^{(s,h)}\hspace{0.17em}\text{or}\hspace{0.17em}t=\{1,\dots ,q\}\\ \hspace{1em}\hspace{1em}\text{is}\hspace{0.17em}\text{updated}\hspace{0.17em}\text{using}\hspace{0.17em}\text{the}\hspace{0.17em}\text{Majorization-Minimzation}\hspace{0.17em}\text{coordinate}\hspace{0.17em}\text{descent}\hspace{0.17em}\text{grouped}\hspace{0.17em}\text{variable}\\ \hspace{1em}\hspace{1em}\text{selection}\hspace{0.17em}\text{algorithm}\hspace{0.17em}\text{specified}\hspace{0.17em}\text{by}\hspace{0.17em}\text{Breheny}\hspace{0.17em}\text{and}\hspace{0.17em}\text{Huang}\hspace{0.17em}\left(\text{2015}\right)\text{,}\hspace{0.17em}\text{except}\hspace{0.17em}\text{the}\hspace{0.17em}\text{residuals}\hspace{0.17em}\text{are}\hspace{0.17em}\text{not}\\ \hspace{1em}\hspace{1em}\text{updated}\hspace{0.17em}\text{after}\hspace{0.17em}\text{every}\hspace{0.17em}{\mathit{\gamma }}_t^{(s,h)}\hspace{0.17em}\text{coefficient}\hspace{0.17em}\text{update}.\\ \hspace{1em}5.\hspace{0.33em}\text{Steps}\hspace{0.17em}\text{2}\hspace{0.17em}\text{through}\hspace{0.17em}\text{4}\hspace{0.17em}\text{are}\hspace{0.17em}\text{repeated}\hspace{0.17em}\text{until}\hspace{0.17em}\text{the}\hspace{0.17em}\text{M-step}\hspace{0.17em}\text{convergence}\hspace{0.17em}\text{criteria}\hspace{0.17em}\text{are}\hspace{0.17em}\text{reached}\\ \hspace{1em}\hspace{1em}\left(\text{Equation10}\right)\hspace{0.17em}\text{or}\hspace{0.17em}\text{until}\hspace{0.17em}\text{the}\hspace{0.17em}\text{M-step}\hspace{0.17em}\text{reaches}\hspace{0.17em}\text{its}\hspace{0.17em}\text{maximum}\hspace{0.17em}\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{iterations:}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\max \left\{\underset{j}{\max }\left|{\beta }_j^{(s,h+1)}-{\beta }_j^{(s,h)}\right|,\underset{t,l}{\max }\left|{\gamma }_{tl}^{(s,h+1)}-{\gamma }_{tl}^{(s,h)}\right|\right\}<\delta ,\hspace{1em}\hspace{1em}\hspace{1em}(10)\\ \hspace{1em}\hspace{1em}\text{where}\hspace{0.17em}{\gamma }_{tl}\hspace{0.17em}\text{is}\hspace{0.17em}\text{an}\hspace{0.17em}\text{individual}\hspace{0.17em}\text{element}\hspace{0.17em}\text{of}\hspace{0.17em}{\mathit{\gamma }}_t\text{.}\hspace{0.17em}\text{The}\hspace{0.17em}\text{default}\hspace{0.17em}\text{value}\hspace{0.17em}\text{of}\hspace{0.17em}\delta \hspace{0.17em}\text{is}\hspace{0.17em}0\text{.0005.}\\ \hspace{1em}\text{6.}\hspace{0.33em}\text{Conditioning}\hspace{0.17em}\text{on}\hspace{0.17em}\text{the}\hspace{0.17em}\text{newly}\hspace{0.17em}\text{updated}\hspace{0.17em}{\mathit{\beta }}^{(s)}\hspace{0.17em}\text{and}\hspace{0.17em}{\mathit{b}}^{(s)}\text{,}\hspace{0.17em}{\tau }^{(s)}\hspace{0.17em}\text{is}\hspace{0.17em}\text{updated}\hspace{0.17em}\text{(generically,}\hspace{0.17em}\text{using}\\ \hspace{1em}\hspace{1em}\text{the}\hspace{0.17em}\text{Newton-Raphson}\hspace{0.17em}\text{algorithm;}\hspace{0.17em}\text{for}\hspace{0.17em}\text{Gaussian}\hspace{0.17em}\text{family,}\hspace{0.17em}\text{using}\hspace{0.17em}\text{Equation}\hspace{0.17em}\text{9).}\end{array}}}$$

Algorithm 1 recomputes the augmented matrices ${\tilde{\mathit{z}}}_{ki}$ for $k=1,\dots ,K$ and $i=1,\dots ,n_k$ in step 3 of every M-step iteration $h$ for several reasons. These repeat calculations prevent the M-step from having to store the augmented matrix $\tilde{\mathit{Z}}={\left({\tilde{\mathit{Z}}}_1^{\top },\dots ,{\tilde{\mathit{Z}}}_K^{\top }\right)}^{\top }$ where ${\tilde{\mathit{Z}}}_k={\left({\tilde{\mathit{z}}}_{k1}^{\top },\dots ,{\tilde{\mathit{z}}}_{k{n}_k}^{\top }\right)}^{\top }$. This full augmented matrix is of dimension $(M\times N)\times q(q+1)\text{/}2$ or $(M\times N)\times q$ depending on whether the random effect covariance matrix is unstructured or independent, respectively. As the MCMC sample size increases throughout the MCECM algorithm and as $q$ increases, saving this $\tilde{\mathit{Z}}$ becomes more and more memory prohibitive even when utilizing large matrix implementation tools such as the package bigmemory (Kane et al., 2013). During testing, we found that recomputing the ${\tilde{\mathit{z}}}_{ki}$ matrices during each M-step iteration utilizing Rcpp (Eddelbuettel and François, 2011) and RcppArmadillo (Eddelbuettel and Sanderson, 2014) significantly reduced the time and memory required to compute each M-step.

In step 4 of the M-step, the residuals are not updated after every update to the random effects coefficients ${\mathit{\gamma }}_t^{(s,h)}$ for $t=1,\dots ,q$ in order to speed up computation. Otherwise, this would require re-calculation of the augmented matrix specified in step 3 for each random effect $(q)$ for each M-step iteration. When $q$ is large, this makes the M-step prohibitively time-consuming. Based on early package testing, simplifying step 4 with no residual updates speeds up the computation time in high dimensional settings and was found to have negligible impact on estimation accuracy.

The full MCECM algorithm then proceeds in Algorithm 2.

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm}}\hspace{0.33em}\mathbf{\text{2}}\hspace{0.33em}\text{Full}\hspace{0.33em}\text{MCECM}\hspace{0.33em}\text{algorithm}\hspace{0.33em}\text{for}\hspace{0.33em}\text{single}\hspace{0.33em}\left({\lambda }_0,{\lambda }_1\right)\hspace{0.33em}\text{penalty}\hspace{0.33em}\text{combination}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}\\ \text{1.}\hspace{0.33em}\text{Fixed}\hspace{0.33em}\text{and}\hspace{0.33em}\text{random}\hspace{0.33em}\text{effects}\hspace{0.33em}{\beta }^{(0)}\hspace{0.33em}\text{and}\hspace{0.33em}{\mathit{\gamma }}^{(0)}\hspace{0.33em}\text{are}\hspace{0.33em}\text{initialized}\hspace{0.33em}\text{as}\hspace{0.33em}\text{discussed}\hspace{0.33em}\text{in}\hspace{0.33em}\text{Section}\hspace{0.33em}″\text{Initializa-}\\ \text{tion}\hspace{0.33em}\text{and}\hspace{0.33em}\text{convergence}″.\\ \text{2.}\hspace{0.33em}\text{E-step:}\hspace{0.33em}\text{In}\hspace{0.33em}\text{each}\hspace{0.33em}\text{E-step}\hspace{0.33em}\text{for}\hspace{0.33em}\text{EM}\hspace{0.33em}\text{iteration}\hspace{0.33em}s\text{,}\hspace{0.33em}\text{a}\hspace{0.33em}\text{burn-in}\hspace{0.33em}\text{sample}\hspace{0.33em}\text{from}\hspace{0.33em}\text{the}\hspace{0.33em}\text{posterior}\hspace{0.33em}\text{distribution}\\ \text{of}\hspace{0.33em}\text{the}\hspace{0.33em}\text{random}\hspace{0.33em}\text{effects}\hspace{0.33em}\text{is}\hspace{0.33em}\text{run}\hspace{0.33em}\text{and}\hspace{0.33em}\text{discarded.}\hspace{0.33em}\text{A}\hspace{0.33em}\text{sample}\hspace{0.33em}\text{of}\hspace{0.33em}\text{size}\hspace{0.33em}{M}^{(s)}\hspace{0.33em}\text{from}\hspace{0.33em}\text{the}\hspace{0.33em}\text{posterior}\hspace{0.33em}\text{is}\\ \text{then}\hspace{0.33em}\text{drawn}\hspace{0.33em}\text{and}\hspace{0.33em}\text{retained}\hspace{0.33em}\text{for}\hspace{0.33em}\text{the}\hspace{0.33em}\text{M-step}\hspace{0.33em}\text{(see}\hspace{0.33em}\text{Section}\hspace{0.33em}″\text{Monte}\hspace{0.33em}\text{Carlo}\hspace{0.33em}\text{E-step}″\text{).}\\ \text{3.}\hspace{0.33em}\text{M-step:}\hspace{0.33em}\text{Parameter}\hspace{0.33em}\text{estimates}\hspace{0.33em}{\beta }^{(s)},{\mathit{\gamma }}^{(s)}\text{,}\hspace{0.33em}\text{and}\hspace{0.33em}{\tau }^{(s)}\hspace{0.33em}\text{are}\hspace{0.33em}\text{then}\hspace{0.33em}\text{updated}\hspace{0.33em}\text{as}\hspace{0.33em}\text{described}\hspace{0.33em}\text{in}\\ \text{Algorithm }\hspace{0.33em}1.\\ \text{4.}\hspace{0.33em}\text{Steps}\hspace{0.33em} 2\hspace{0.33em}\text{and}\hspace{0.33em}3\hspace{0.33em}\text{are}\hspace{0.33em}\text{repeated}\hspace{0.33em}\text{until}\hspace{0.33em}\text{the}\hspace{0.33em}\text{convergence}\hspace{0.33em}\text{condition}\hspace{0.33em}\text{is}\hspace{0.33em}\text{met}\hspace{0.33em}\text{a}\hspace{0.33em}\text{pre-specified}\\ \text{consecutive}\hspace{0.33em}\text{number}\hspace{0.33em}\text{of}\hspace{0.33em}\text{times}\hspace{0.33em}\text{or}\hspace{0.33em}\text{until}\hspace{0.33em}\text{the}\hspace{0.33em}\text{maximum}\hspace{0.33em}\text{number}\hspace{0.33em}\text{of}\hspace{0.33em}\text{EM}\hspace{0.33em}\text{iterations}\hspace{0.33em}\text{is}\hspace{0.33em}\text{reached}\\ \text{(see}\hspace{0.33em}\text{Section}\hspace{0.33em}″\text{Initialization}\hspace{0.33em}\text{and}\hspace{0.33em}\text{convergence}″\text{).}\\ \text{5.}\hspace{0.33em}\text{Using}\hspace{0.33em}\text{the}\hspace{0.33em}\text{estimates}\hspace{0.33em}\text{of}\hspace{0.33em}\mathit{\beta },\hspace{0.33em}\mathit{\gamma }\text{,}\hspace{0.33em}\text{and}\hspace{0.33em}\tau \hspace{0.33em}\text{at}\hspace{0.33em}\text{EM}\hspace{0.33em}\text{convergence,}\hspace{0.33em}\text{a}\hspace{0.33em}\text{final}\hspace{0.33em}\text{sample}\hspace{0.33em}\text{from}\hspace{0.33em}\text{the}\hspace{0.33em}\text{posterior}\\ \text{distribution}\hspace{0.33em}\text{of}\hspace{0.33em}\text{the}\hspace{0.33em}\text{random}\hspace{0.33em}\text{effects}\hspace{0.33em}\text{is}\hspace{0.33em}\text{drawn}\hspace{0.33em}\text{for}\hspace{0.33em}\text{use}\hspace{0.33em}\text{in}\hspace{0.33em}\text{the}\hspace{0.33em}\text{calculation}\hspace{0.33em}\text{of}\hspace{0.33em}\text{the}\hspace{0.33em}\text{marginal}\\ \text{log-likelihood}\hspace{0.33em}\text{as}\hspace{0.33em}\text{well}\hspace{0.33em}\text{as}\hspace{0.33em}\text{for}\hspace{0.33em}\text{diagnostics}\hspace{0.33em}\text{of}\hspace{0.33em}\text{the}\hspace{0.33em}\text{MCMC}\hspace{0.33em}\text{chain.}\hspace{0.33em}\text{The}\hspace{0.33em}\text{marginal}\hspace{0.33em}\text{log-likelihood}\\ \text{is}\hspace{0.33em}\text{used}\hspace{0.33em}\text{for}\hspace{0.33em}\text{model}\hspace{0.33em}\text{selection}\hspace{0.33em}\text{and}\hspace{0.33em}\text{is}\hspace{0.33em}\text{discussed}\hspace{0.33em}\text{in}\hspace{0.33em}\text{detail}\hspace{0.33em}\text{in}\hspace{0.33em}\text{Section 2.4.}\end{array}}}$$

Initialization and convergence

The initial values of the fixed effects ${\mathit{\beta }}^{(0)}$ and the Cholesky decomposition of the random effects covariance matrix ${\mathit{\gamma }}^{(0)}$ for iteration $s=0$ are chosen in one of two ways. We discuss first the initialization procedure used when the package glmmPen is used to fit a single model (glmm function) or the first model in the sequence of models fit for variable selection (glmmPen function). In this scenario, the fixed effects ${\mathit{\beta }}^{(0)}$ are initialized by fitting a ‘naive’ model using the coordinate descent techniques of Breheny and Huang (2011) assuming no random effects, and the random effects covariance matrix is initialized as a diagonal matrix with positive variance. This approach is similar to the mcemGLM package.

By default, this starting variance is initialized in an automated fashion. First, a GLMM composed of only a fixed and random intercept is fit using the lme4 package. The random intercept variance from this model is then multiplied by 2, and this value is set as the starting values of the diagonal of the random effects covariance matrix. We use this approach so that the starting variance of the random effects is sufficiently large, which helps improve the stability of the algorithm (Misztal, 2008).

The E-step MCMC chain, used to approximately sample from the posterior density $\varphi \left({\alpha }_k\mathit{|}{D}_{k,0};{\theta }^{(s)}\right)$ for groups $k=\{1,\dots ,K\}$, is initialized in iteration $s=1$ with random draws from the standard normal distribution. For all following iterations $s>1$, the MCMC chain is initialized with the last draw from the previous EM iteration $s-1$.

When the algorithm performs variable selection using the glmmPen function, the model pertaining to the first tuning parameter combination evaluated is initialized using approach described above. For all subsequent tuning parameter combinations evaluated in the sequence, the fixed effects, random effects covariance matrix, and random effects MCMC chain are initialized using results from a previous tuning parameter fit. More details about initialization for variable selection is discussed in Section “Tuning parameter selection”.

The EM algorithm is considered to have converged when the following condition is met at least 2 consecutive times (default) or until the maximum number of EM iterations is reached:

$$\parallel {\left({\mathit{\beta }}^{(s)\top },\hspace{0.33em}{\mathit{\gamma }}^{(s)\top }\right)}^{\top }-{\left({\mathit{\beta }}^{(s-t)\top },\hspace{0.33em}{\mathit{\gamma }}^{(s-t)\top }\right)}^{\top }{\parallel }_2^2\text{/}{c}^{s-t}<ϵ$$ (11)

where the superscript $\left(s-t\right)$ indicates the EM iteration $t$ iterations prior, $\parallel \cdot {\parallel }_2^2$ represents the $L_2$ norm, and $c^{s-t}$ equals the total number of non-zero ${\left({\mathit{\beta }}^{\top },\hspace{0.33em}{\gamma }^{\top }\right)}^{\top }$ coefficients in iteration $\left(s-t\right)$. In other words, the algorithm computes the average Euclidean distance between the current coefficient vector ${\left({\mathit{\beta }}^{\top },\hspace{0.33em}{\gamma }^{\top }\right)}^{\top }$ and the coefficient vector from $t$ EM iterations prior (default $t=2$) and compares it with $ϵ$, which has a default value of 0.0015.

This MCECM algorithm is able to handle much larger dimensions of $p$ and $q$ relative to prior methods for simultaneous fixed and random effects variable selection (Bondell et al., 2010; Ibrahim et al., 2011). When the number of random effect predictors is greater than or equal to 10, we recommend approximating the random effect covariance matrix $\mathbf{\Gamma }{\mathbf{\Gamma }}^{\top }$ as a diagonal matrix. In the mixed model setting, Fan and Li (2012) demonstrated both theoretical and empirical advantages to estimating the random effects covariance matrix in this manner as $q$ grows. Empirically, they found that this approximation had a relatively low impact on the overall bias of the coefficients and resulted in a relatively large reduction of accumulated estimation error since many fewer covariance parameters needed to be estimated. This simplification also has the advantage of enabling the package to have greater computational efficiency when fitting higher-dimensional models. The above-mentioned recommendation to switch from an unstructured to an independent random effect covariance matrix at the 10 random effect predictor mark is an ad hoc recommendation determined by our experience creating and testing this package.

The MCECM algorithm outlined in Algorithm 2 describes how the glmmPen package estimates the model parameters for a single set of penalty parameters $({\lambda }_0,\hspace{0.33em}{\lambda }_1)$. Section “Tuning parameter selection” discusses how the package chooses optimal set of tuning parameters during the model selection procedure.

Tuning parameter selection

This section provides details on how the glmmPen function selects the set of optimal tuning parameters from a prespecific grid of values. Section “Software” provides further details on how to use both the glmmPen and glmm functions, where the latter function allows the user to fit a single model without performing variable selection on the fixed and random effects.

For glmmPen, we generally recommend that the user specify the ‘full model’, i.e., set the random effects predictors equal to the total considered fixed effects predictors, and let the algorithm select the best fixed and random effects using the procedure outlined in this section. However, if the user has some prior knowledge about the form of the random effects, they can restrict the random effects considered to an appropriate subset. As discussed in the previous section, the package requires that the random effects be a subset of the fixed effects.

Penalty sequence specification

The glmmPen package calculates default sequences of penalty values for ${\lambda }_0$ (penalizing the fixed effects $\mathit{\beta }$) and ${\lambda }_1$ (penalizing the random effects $\mathit{\gamma }$), but allows users to enter their own penalty sequences if desired. We define the penalty parameter sequences for the fixed and random effects as ${\mathit{\lambda }}_0=\left({\lambda }_{0,1},\dots ,{\lambda }_{0,{\omega }_0}\right)$ and ${\mathit{\lambda }}_1=\left({\lambda }_{1,1},\dots ,{\lambda }_{1,{\omega }_1}\right)$, respectively, where ${\omega }_0$ and ${\omega }_1$ are the length of the fixed and random effect penalty sequences. These sequences are ordered from the minimum penalty (${\lambda }_{0,1}={\lambda }_{0,min}$ and ${\lambda }_{1,1}={\lambda }_{1,min}$) to the maximum penalty (${\lambda }_{0,{\omega }_0}={\lambda }_{0,max}$ and ${\lambda }_{1,{\omega }_1}={\lambda }_{1,max}$). By default, these sequences are calculated in a similar manner to the approach used by the package ncvreg (Breheny and Huang, 2011). The maximum penalty parameter ${\lambda }_{max}$ is calculated using the same procedure as ncvreg; this value is assumed to penalize all fixed and random effects coefficients to 0. We then set the sequence of penalty parameters ${\mathit{\lambda }}_0={\mathit{\lambda }}_1$ such that ${\lambda }_{0,max}={\lambda }_{1,max}={\lambda }_{max}$ and ${\lambda }_{0,min}={\lambda }_{1,min}={\lambda }_{min}$, where the minimum penalty parameter ${\lambda }_{min}$ is a small portion of the ${\lambda }_{max}$. More details about these default sequences are given in Section “Software”. In Section “Tuning parameter selection strategy”, we consider a generic case where the ${\mathit{\lambda }}_0$ and ${\mathit{\lambda }}_1$ sequences do not need to be equal.

Tuning parameter selection strategy

By default, the algorithm runs a computationally efficient two-stage approach to pick the optimal set of tuning parameters. In the first stage, the algorithm fits a sequence of models where the fixed effect penalty is kept constant at the minimum value of ${\mathit{\lambda }}_0$, ${\lambda }_{0,min}$, and the random effects penalty proceeds from the minimum value of ${\mathit{\lambda }}_1$, ${\lambda }_{1,min}$, to the maximum value ${\lambda }_{1,max}$. The optimal tuning parameter from this first stage is then identified using Bayesian inforamation criterion (BIC) type selection criteria, described in more detail later in this section. This first stage identifies the optimal random effect penalty value, ${\lambda }_{1,opt}$. In the second stage, the algorithm fits a sequence of models where the random effects penalty is kept fixed at ${\lambda }_{1,opt}$ and the fixed effects penalty ${\mathit{\lambda }}_0$ proceeds from ${\lambda }_{0,min}$ to ${\lambda }_{0,max}$. The overall best model is chosen from the models in the second stage. In both stages, the results from each model are used to initialize the coefficients in the subsequent model in the sequence.

Unlike other packages that perform variable selection, such as ncvreg and grpreg, we run the ${\mathit{\lambda }}_0$ and ${\mathit{\lambda }}_1$ sequences from their minimum value to their maximum value and not the traditional progression from their maximum value to their minimum value. In this mixed model setting, this approach provides better initialization of subsequent models in the tuning parameter sequence, giving an overall better performance to the algorithm and improving algorithm speed. This progression of penalty sequences also speeds up the overall variable selection procedure by restricting the random effects considered during later penalty combinations within the variable selection procedure. In stage one, if a previous tuning parameter in the grid penalized out a set of random effects from the model, the following model in the tuning parameter sequence will automatically ignore these random effects. In stage two, the random effects considered are restricted to the non-zero random effects from the best model in stage one.

In the original MCECM algorithm implementation given in Rashid et al. (2020), the authors searched for the best model by performing a ‘full grid search’ and evaluating all possible combinations of ${\mathit{\lambda }}_0$ and ${\mathit{\lambda }}_1$. (We sometimes refer to the two-stage approach as the ‘abbreviated grid search’). While the glmmPen package can perform this full grid search, we strongly recommend the two-stage abbreviated grid search. Compared with the full grid search, the two-stage grid search significantly reduces the required time to complete the algorithm, particularly when the number of random effects predictors is large. Furthermore, we have found that the two-stage grid search works very well in practice (see Section “Simulations” for performance results).

If users wish to perform a full grid search, the path of solutions is initialized by fitting a model using the minimum penalty for both the fixed and random effects $\left({\lambda }_{0,1}={\lambda }_{0,min},\hspace{0.33em}{\lambda }_{1,1}={\lambda }_{1,min}\right)$. The algorithm then proceeds to estimate models over the full grid of ${\mathit{\lambda }}_0$ and ${\mathit{\lambda }}_1$. For each value of ${\lambda }_{1,h}\in {\mathit{\lambda }}_1$ that penalizes the random effects, the fixed effects penalty parameter sequence proceeds from the minimum value ${\lambda }_{0,min}$ to the maximum value ${\lambda }_{0,max}$ while keeping ${\lambda }_{1,h}$ fixed. Each model is initialized using the result from the model fit with the previous tuning parameter combination in the sequence. The algorithm then updates the penalty parameter to the next ${\lambda }_{1,h+1}$ and repeats the process. The model with the penalty parameter combination $({\lambda }_{0,min},\hspace{0.33em}{\lambda }_{1,h+1})$ is initialized using the model from the previous $({\lambda }_{0,min},\hspace{0.33em}{\lambda }_{1,h})$ penalty parameter combination.

Optimal tuning parameter selection

Once models have been fit pertaining to all tuning parameter combinations within the first and second stages of the tuning parameter search strategy (or over the full tuning parameter grid search), the glmmPen package chooses the best model from one of several BIC-type selection criteria options. For simplification of notation, consider the generic penalty parameter combination $\lambda =\left({\lambda }_0,\hspace{0.33em}{\lambda }_1\right)$ that penalizes the fixed and random effects, respectively. By default, the package uses the BIC-ICQ criterion (Ibrahim et al., 2011), where the abbreviation ICQ stands for “Information Criterion based on the Q-function”. This BIC-ICQ criteria is expressed below:

$$\begin{array}{l}\text{BICq}\left({\theta }_{\lambda }\right)=2\left\{Q_1\left({\theta }_{\lambda }\mathit{|}{\alpha }_0\right)+Q_2\left({\alpha }_0\right)\right\}+d_{\lambda }\log (N)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\approx \left\{-\frac{2}{M}\sum _{m=1}^M\sum _{k=1}^K\left[\log f\left(y_k\mathit{|}{\mathit{X}}_k,{\alpha }_{0,k}^{(m)};\hspace{0.33em}{\theta }_{\lambda }\right)+\log \varphi \left({\alpha }_{0,k}^{(m)}\right)\right]\right\}+d_{\lambda }\log (N),\end{array}$$ (12)

where ${\theta }_{\lambda }$ are the coefficients of the model fit with the penalty $\lambda =\left({\lambda }_0,{\lambda }_1\right)$, ${\alpha }_0$ are the posterior samples from a “minimal penalty model”—the model with either no penalty (when the number of random effects predictors is less than 5) or a minimum penalty used on the fixed and random effects—and ${\alpha }_{0,k}^{(m)}$ is the $m^{th}$ posterior sample for group $k$ from such a minimal penalty model, $Q_1$ and $Q_2$ were defined in Section “MCECM algorithm”, $d_{\lambda }$ is the number of nonzero coefficients for the model (all nonzero $\mathit{\beta }$ plus all nonzero $\mathit{\gamma }$), and $N$ is the total number of observations in the data $(N_{obs})$.

The package can also calculate the traditional BIC criterion as specified below:

$$\text{BIC}\left({\theta }_{\lambda }\right)=-2\ell \left({\theta }_{\lambda }\right)+d_{\lambda }\log (N),$$

where ${\mathit{\theta }}_{\lambda }$ are the coefficients of the penalization model, $\ell ({\mathit{\theta }}_{\lambda })$ is the marginal log-likelihood for the model, $d_{\lambda }$ is the number of nonzero coefficients for the model, and $N$ can be either the total number of observations in the data $(N_{obs})$ or the total number of independent observations (i.e., number of levels within the grouping factor, $N_{grps}$) in the data. The marginal log-likelihood is as follows:

$$\ell (\theta )=\sum _{k=1}^K{\ell }_k(\theta )=\sum _{k=1}^K\frac{1}{n_k}\log \int f\left(y_k\mathit{|}{\mathit{X}}_k,{\alpha }_k;\theta \right)\varphi \left({\alpha }_k\right)d{\alpha }_k.$$ (13)

There is a lack of consensus regarding the use of $\text{log}(N_{obs})$ versus $\log (N_{grps})$ in the BIC penalty term for mixed models. For instance, the $\text{log}(N_{obs})$ penalty is used in the R package nlme (Pinheiro et al., 2021), and the $\log (N_{grp})$ penalty is used in SAS proc NLMIXED (SAS Institute Inc., 2008; Delattre et al., 2014). In practice, the performance of the different versions of the BIC penalty term may depend on the true underlying model (Lorah and Womack, 2019; Delattre et al., 2014), with Delattre et al. (2014) observing that the $\text{log}(N_{obs})$ penalty performed better when the true model had very few random components, and the $\log (N_{grp})$ penalty performed better when the true model had a large number of random components. Both Delattre et al. (2014) and Lorah and Womack (2019) suggest using some combination of these sample size definitions.

To this point, the package also allows the best model to be selected using a ‘hybrid’ BICh selection criteria developed by Delattre et al. (2014):

$$\text{BICh}\left({\theta }_{\lambda }\right)=-2\ell \left({\theta }_{\lambda }\right)+d_{\lambda ,\beta }\log \left(N_{obs}\right)+d_{\lambda ,\gamma }\log \left(N_{grps}\right),$$ (14)

where $d_{\lambda ,\beta }$ and $d_{\lambda ,\gamma }$ are the number of nonzero fixed and random effect coefficients, respectively.

In simulations not shown here (see content in GitHub repository https://github.com/hheiling/paper_glmmPen_RJournal for details), we found that the BIC-ICQ gave the best performance in choosing the correct set of fixed and random effects. The BIC and BICh methods tended to underestimate the number of true fixed effects compared to BIC-ICQ in the simulations we considered. However, in order to calculate the BIC-ICQ, a minimal penalty model needs to be fit using a small penalty (i.e., ${\lambda }_{min}$) on the fixed and random effects. Posterior samples from this minimal penalty model are then used to calculate the BIC-ICQ value for each model fit in the variable selection procedure. Depending on the size of the full model with all fixed and random effects predictors, this calculation can be time-intensive since fitting the model with a small penalty will keep many fixed and random effects predictors in the model.

Alternatively, the calculation of the BIC and BICh criteria require a calculation of the marginal log-likelihood $\ell (\mathit{\theta })$ for each model. Since the integrals within $\ell (\mathit{\theta })$ are intractable, we estimate the marginal log-likelihood using the corrected arithmetic mean estimator (CAME) described by Pajor (2017). We have found this CAME estimator to be relatively quick and easy to calculate, as well as consistent with the marginal log-likelihood estimate calculated by the package lme4 (Bates et al., 2015) for a range of conditions (see content in GitHub repository https://github.com/hheiling/paper_glmmPen_RJournal for details).

To calculate the CAME, we focus on a single group $k$ and define a set $A_k\subseteq \text{Θ}$ as a subset of the parameter space of the random effects for group $k$, where $P\left(A_k\right)$ and $P\left(A_k\mathit{|}{y}_k,X_k;\theta \right)$ are nonzero probabilities. We first start with the knowledge

$$\begin{array}{l}P\left(A_k\mathit{|}{\mathit{y}}_k,X_k;\theta \right)={\int }_{A_k}\varphi \left({\alpha }_k\mathit{|}{\mathit{y}}_k,X_k;\theta \right)d{\alpha }_k\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}={\int }_{\text{Θ}}\frac{1}{f\left(y_k\mathit{|}{X}_k;\theta \right)}f\left(y_k\mathit{|}{X}_k,{\alpha }_k;\theta \right)\varphi \left({\alpha }_k\right)I\left({\alpha }_k\in A_k\right)d{\alpha }_k,\end{array}$$ (15)

where $\text{I}(.)$ is an indicator function, $f\left(y_k\mathit{|}{X}_k;\theta \right)\int f\left(y_k\mathit{|}{X}_k,{\alpha }_k;\theta \right)\varphi \left({\alpha }_k\right)d{\alpha }_k$ is the marginal likelihood for group $k$, and all other terms are described in Section “Generalized linear mixed models”. The above relationship allows us to obtain the result:

$$\begin{array}{l}f\left({\mathit{y}}_k\mathit{|}{X}_k;\theta \right)=\frac{1}{P\left(A_k\mathit{|}{y}_k,X_k;\theta \right)}{\int }_{\text{Θ}}f\left(y_k\mathit{|}{X}_k,{\alpha }_k;\theta \right)\varphi \left({\alpha }_k\right)I\left({\alpha }_k\in A_k\right)d{\alpha }_k\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\frac{1}{P\left(A_k\mathit{|}{\mathit{y}}_k,{\mathit{X}}_k;\theta \right)}{\int }_{\text{Θ}}\frac{f\left({\mathit{y}}_k\mathit{|}{X}_k,{\alpha }_k;\theta \right)\varphi \left({\alpha }_k\right)I\left({\alpha }_k\in A_k\right)s\left({\alpha }_k\right)d{\alpha }_k}{s\left({\alpha }_k\right)},\end{array}$$ (16)

where $s(.)$ is an importance sampling function.

Suppose at the end of the MCECM algorithm we obtain $M$ samples from the posterior distribution of the random effects for group $k$, ${\tilde{\alpha }}_k={\left({\left({\alpha }_k^{(1)}\right)}^{\top },\dots ,{\left({\alpha }_k^{(M)}\right)}^{\top }\right)}^{\top }$. Let us set $A_k={\tilde{\alpha }}_k$; this reduces $P\left(A_k\mathit{|}{y}_k,X_k;\theta \right)$ to 1. Let us also set the importance sampling function $s(.)$ to be a multivariate normal distribution with a mean vector equal to the mean of the posterior samples $\frac{1}{M}{\sum }_{m=1}^M{\alpha }_k^{(m)}$ and a covariance matrix equal to the covariance matrix of a thinned subset of the posterior samples (to obtain a pseudo-independent set of samples). If we draw $M^{\star }$ samples ${\alpha }_k^{\star }={\left({\left({\alpha }_k^{\star (1)}\right)}^{\top },\dots ,{\left({\alpha }_k^{\star \left(M^{\star }\right)}\right)}^{\top }\right)}^{\top }$ from this importance sampling function, then Equation 16 indicates that we can estimate the marginal likelihood for group $k$ as

$$f\left(y_k\mathit{|}{X}_k;\theta \right)\approx \frac{1}{M^{\star }}\sum _{m=1}^{M^{\star }}\frac{f\left(y_k\mathit{|}{X}_k,{\alpha }_k^{\star m};\theta \right)\varphi \left({\alpha }_k^{\star m}\right)I\left({\alpha }_k^{\star m}\in A_k\right)}{s\left({\alpha }_k^{\star m}\right)}.$$ (17)

We repeat the estimation in Equation 17 for all $K$ groups in order to calculate the full desired marginal log-likelihood $\ell (\mathit{\theta })$. This final marginal log-likelihood is then used in the previously mentioned BIC and BICh calculations for each fitted model across the ${\mathit{\lambda }}_0$ and ${\mathit{\lambda }}_1$ grid search. We refer to this marginal log-likelihood as the Pajor log-likelihood in later sections of the paper.

Software

The main function of the glmmPen package is glmmPen, which is used to perform fixed and random effects variable selection after specification of a full model with all possible fixed and random effects. The glmmPen package is also capable of fitting a GLMM with pre-specified fixed and random effects (under no penalization) using the function glmm. Here we will use the basal dataset (Rashid et al., 2020) to illustrate the use of the glmmPen function in practical applications.

Data example

The basal dataset is composed of four studies that contain gene expression data and tumor subtype information from patients spanning three cancer types (Moffitt et al., 2015; Weinstein et al., 2013). Two of these datasets contain gene expression data for subjects with Pancreatic Ductal Adenocarcinoma (PDAC), one dataset contains data for subjects with Breast Cancer, and the last contains data for subjects with Bladder Cancer. While each cancer type has separate sets of defined subtypes, all share a common subtype defined as “basal-like”, which was shown to be similar in character across cancer types and have an impact on survival (Moffitt et al., 2015). The goal of the original study was to select features that are relevant in predicting the basal-like subtype. To increase the sample size, it was proposed that samples were merged from each study into one large dataset.

Multiple approaches have been proposed to integrate gene expression data from multiple studies to improve the accuracy of downstream prediction models (Riester et al., 2014; Ma et al., 2018; Patil and Parmigiani, 2018). The pGLMM methodology from Rashid et al. (2020) was originally motivated by the need to select genes that are predictive of cancer outcome, where the effects of genes may vary randomly across studies. It was shown that accounting for this heterogeneity improved the performance of gene selection after data merging.

Using glmmPen package, we fit a pGLMM that can accommodate a large number of features in the model and account the hetereogeneity in gene effects across studies. It is unclear a priori which features truly have a non-zero association with the outcome and which features truly have variation in their effects across studies. Therefore, we will use the glmmPen function to simultaneously select fixed and random effects from a set of candidate features. Rashid et al. (2020) integrated gene expression data from each study using a binary rank transformation technique (Top Scoring Pairs or TSPs), which we use as our covariates in this example. To illustrate the concept of TSPs, let $g_{ki,A}$ and $g_{ki,B}$ be the raw expression of genes $A$ and $B$ in subject $i$ of group $k$. For each gene pair $\left(g_{ki,A},\hspace{0.33em}{g}_{ki,B}\right)$, the TSP is the indicator $I\left(g_{ki,A}>g_{ki,B}\right)$ which specifies which gene of the two has higher expression in the subject. We denote a TSP predictor as “GeneA_GeneB”. A total of 50 binary TSP covariates are provided in the basal dataset available in the package. For illustration purposes, we randomly select 10 TSP covariates. Our goal is to identify TSPs that are associated with patient tumor subtype while accounting for study-level heterogeneity in gene effects. In each study subtype is defined a binary variable with two levels: basal-like or non-basal-like. Therefore, for this example, our example dataset consists of our matrix of covariates $X$, our subtype vector $y$ (a factor with two levels), and our study membership vector (a factor with four levels).

Summary information about the data is included below.

> library(“glmmPen”)
> data(“basal”)
> y = basal$y
> set.seed(1618)
> idx = sample(1:50, size = 10, replace = FALSE)
> idx = idx[order(idx)]
> X = basal$X[,idx]
> colnames(X)
[1] “GPR160_CD109” “SPDEF_MFI2” “CHST6_CAPN9” “SLC40A1_CDH3”
[5] “PLEK2_HSD17B2” “GPX2_ERO1L” “CYP3A5_B3GNT5” “LY6D_ATP2C2”
[9] “MYO1A_FGFBP1” “CTSE_COL17A1”
> group = basal$group
> levels(group)
[1] “UNC_PDAC” “TCGA_PDAC” “TCGA_Bladder” “UNC_Breast”

We will fit a penalized random effects logistic regression model using the glmmPen function to model patient subtype, as it is unclear which of the 10 TSPs should be included in the model, and which may also randomly vary across studies in their effects. We perform variable selection using the following code:

> set.seed(1618)
> fitB = glmmPen(formula = y ~ X + (X | group),
+        family = “binomial”, covar = “independent”,
+        tuning_options = selectControl(BIC_option = “BICq”,
+                       pre_screen = TRUE,
+                       search = “abbrev”),
+        penalty = “MCP”, BICq_posterior = “Basal_Posterior_Draws”)

Here we utilize the pre-screening and abbreviated grid search options, as well as select the optimal tuning parameter using the BIC-ICQ model selection criteria (denoted “BICq”). Further details about the pre-screening procedure is described in the Section “selectControl arugments” and the consequences of this pre-screening procedure are illustrated through simulations and discussed in Section “Pre-screening performance”. If we were instead interested in fitting a GLMM utilizing all 10 TSPs as fixed effects and assuming a random effect for each (without penalization), we could run the following code:

> set.seed(1618)
> fit_glmm = glmm(formula = y ~ X + (X | group),
+         family = “binomial”, covar = “independent”,
+         optim_options = optimControl())

The set of random effects specified does not necessarily have to be equal to the set of fixed effects as in the above example. Because of the number of random effects that we are considering in the model, we approximate the random effects covariance matrix as an independent, or diagonal, matrix, which we specify by using the argument option covar = “independent”. Our reasoning for such an approximation, as well as a discussion of the pros and cons of such an approximation, are given in Section “Initialization and convergence.”

In the following subsections, we will discuss in detail the glmmPen (and glmm) arguments and relevant output. We will also examine the output from the variable selection procedure given by the glmmPen example.

Full model specification

The syntax for specifying the full model formula (the model with all relevant fixed and random effects predictors) using the formula argument closely follows the formula syntax of the lme4 package (Bates et al., 2015). The formula follows the form response ~ fix_expr + (rand_expr | factor) where the fix_expr specifies the variables to use as the fixed effects, the rand_expr specifies the variables to use as the random effects, and the factor specifies the grouping factor of the observations. When a data frame is given for the data argument, the fixed and random effects can be specified using the column names of the data frame. For higher-dimensional data, users may find it easier to directly specify the matrix containing the covariates of interest and the response vector, such as the y ~ X + (X | group) formula given in the earlier glmmPen fit example. No specification of the data argument is needed in this case. Similar to ncvreg, an intercept is always assumed and required, and therefore an intercept column need not be specified in X or explicitly in the model formula.

Regarding the specification of random effects in formula, the glmmPen package currently does not allow for multiple grouping factors. In addition, the random effects must be a subset of the fixed effects, and a random intercept is always assumed and required in the model. Lastly, the structure of the random effects covariance matrix is determined by the covar argument, which may take on the value of ‘unstructured’ or ‘independent’ (diagonal). By default, the covar parameter is set to NULL. This automatically selects the ‘independent’ option if the number of random effect predictors is 10 or more and selects ‘unstructured’ otherwise. For a large number of random effect predictors, it is strongly recommend that the covariance structure to ‘independent’ in order to improve computational efficiency.

The glmmPen algorithm allows the Binomial, Gaussian, and Poisson families with canonical links.

Penalization and optimal tuning parameter selection

In glmm, the default is to fit the single model with user-specified fixed and random effects with no penalization. Although it is generally not recommended, users have the option to specify a single penalty parameter combination using tuning_options = lambdaControl(lambda0,lambda1). In glmmPen, the arguments penalty, gamma_penalty, alpha, fixef_noPen, and tuning_options all play a part in the variable selection process. The following subsections discuss these argument options in detail and how the arguments impact variable selection.

Penalty, gamma penalty, alpha parameters

To perform variable selection, glmmPen allows the fixed effect coefficients to be penalized using the minimax concave penalty (MCP) (default), smoothly clipped absolute deviation (SCAD), or least absolute shrinkage and selection operator (LASSO) penalties (Breheny and Huang, 2015, 2011; Friedman et al., 2010) via the penalty argument, which takes as input the character strings “MCP”, “SCAD”, or “lasso”. The glmmPen algorithm restricts both the fixed and random effects to be penalized using the same type of penalty (e.g., MCP used to penalize fixed effects and (grouped) MCP used to penalize random effects).

In addition to the previously discussed penalty parameters $({\lambda }_0,\hspace{0.33em}{\lambda }_1)$, the MCP and SCAD penalties also use a scaling factor (Breheny and Huang, 2011, 2015). The argument gamma_penalty specifies this scaling factor, with the default of 3 and 4 for the MCP and SCAD penalties, respectively. Additionally, the argument alpha allows for the elastic net estimator, controlling the relative contribution of the MCP/SCAD/LASSO penalty and the ridge, or L2, penalty. Setting alpha to 1, the default, is equivalent to the regular penalty with no L2 contribution.

selectControl arguments

The grid search over the fixed effects and random effects penalty parameters ${\mathit{\lambda }}_0$ and ${\mathit{\lambda }}_1$ is controlled by the arguments in selectControl(). The user can specify particular sequences for ${\mathit{\lambda }}_0$ (fixed effects penalty parameters) and ${\mathit{\lambda }}_1$ (random effects penalty parameters) using the arguments lambda0_seq and lambda1_seq, respectively; by default, a sequence of penalty parameters (of length nlambda, default 10) are automatically calculated within glmmPen. These default sequences are calculated using the method discussed in Section “Tuning parameter selection”. The minimum penalty ${\lambda }_{min}$ is a small fraction of the ${\lambda }_{max}$ value; the argument lambda.min controls what fraction is used. By default, lambda.min = 0.01 so that ${\lambda }_{min}=0.01$ (${\lambda }_{max}$).

The structure of the optimal tuning parameter search is specified by the argument search. If search = “abbrev” (default), the algorithm performs the abbreviated two-stage tuning parameter search specified in Section “Tuning parameter selection”. If search = “full_grid”, the algorithm looks over the full grid search of length(lambda0_seq)×length(lambda1_seq) models before picking the best model.

After all of the tuning parameters have been evaluated, the optimal combination of tuning parameters can be selected using a BIC-type selection criteria, which can be specified using the selectControl() argument BIC_option. Using the BIC_option argument, the user can select one of four BIC-type selection criteria, given in Table 1, to select the best model.

Table 1:

BIC-type model selection criteria options for argument BIC_option.

Selection criteria	Description
BICq	(Default) BIC-ICQ selection criteria (Ibrahim et al., 2011); requires fitting the minimal penalty model
BICh	Alternative BICh selection criteria specified by Delattre, Lavielle, and Poursat (2014)
BIC	Traditional BIC whose penalty term sets $N$ to the number of total observations in the data
BICNgrp	Traditional BIC whose penalty term sets $N$ to the number of independent observations (i.e., number of levels of the grouping factor)

Refer to the discussion in Section “Tuning parameter selection” for further details about these BIC-type options as well as their respective pros and cons.

The argument pre_screen allows users to screen out some random effects at the start of the algorithm. When pre_screen is set to TRUE (the default) and the number of random effects predictors is 5 or more, a minimal penalty model is fit using a small penalty for the fixed and random effects and relatively lax convergence criteria. If at the end of the pre-screening procedure the variance of a random effect is penalized to 0 or is estimated to be less than 10⁻², that predictor is restricted to have a zero-valued random effect variance for all models fit by the algorithm. The pre-screening procedure is not implemented if the number of random effects is less than five. This threshold of five random effect predictors is an ad hoc choice by the authors; the purpose of the pre-screening procedure is to allow the user to speed up the variable selection procedure when the full model contains a large number of random effects.

The argument lambda.min.presc adjusts the value of the random effect penalty parameter ${\lambda }_1$ used in the pre-screening step and the minimal penalty model fit for the BIC-ICQ calculation, where the minimum penalty used for the random effects is lambda.min.presc ×${\lambda }_{max}$. See package documentation for further details about this argument and other minor arguments not discussed here.

Additional selection arguments in glmmPen

The default variable selection procedure assumes that we have no prior knowledge of which fixed effects should not be penalized during the model fitting procedure. In order to indicate that a covariate should not be subject to penalization (and therefore always remain in the model), one can use the fixef_noPen argument. See the glmmPen function documentation for further details.

After running an initial grid search over the default fixed and random effects penalty parameters, users may desire to re-run the variable selection procedure using alternative settings, such as different penalty sequences (e.g. a finer grid search) or different convergence criteria.

The computation of the minimal penalty model for the BIC-ICQ criterion calculation can be time-consuming. In order to save the minimal penalty model posterior samples to be used for a BIC-ICQ calculation after a subsequent tuning parameter selection grid search, the user can save the posterior samples as a file-backed big.matrix using the argument BICq_posterior = “file_location/file_name”. This saves the backing file and the descriptor file as ‘file_location/file_name.bin’ and ‘file_location/file_name.desc’, respectively. If the file name is not specified, then the posterior samples are automatically saved to the working directory with the file name “BICq_Posterior_Draws”. These saved posterior samples can then be re-loaded in R as a big.matrix using the attach.big.matrix function from the package bigmemory (Kane et al., 2013). In secondary calculations using glmmPen, the recalculation of this minimal penalty model fit can be avoided and these posterior samples can be used by calling BICq_posterior = “file_location/file_name”.

Examination of output

The glmm and glmmPen functions all output a reference class object of class pglmmObj. A full list of the methods available pertaining to pglmmObj are provided in Table 2. These methods and their output were designed to be very similar to the merMod methods and output provided by the lme4 package. Further information about the output provided in a pglmmObj object and additional methods documentation is available in the glmmPen package documentation (see ?pglmmObj).

Table 2:

List of currently available methods for objects of class pglmmObj.

Generic	Brief description of return value
BIC	Numeric vector returning the BIC, BICh, BICNgrp, and, if specified for model selection, BIC-ICQ selection criteria evaluations for a fitted glmm model or model pertaining to the optimal tuning parameters in glmmPen
coef	Matrix reporting the sum of the fixed effects coefficients and the posterior modes of the random effects for each variable at each level of the grouping factor
fitted	Numeric vector of fitted values (the values of the linear predictor) based on either the fixed effects only (recommended for most applications) or both the fixed effects and the posterior modes of the random effects for each level of the grouping factor (potentially useful for diagnostics)
fixef	Numeric vector of the fixed effects coefficient estimates $\widehat{\mathit{\beta }}$
formula	The mixed-model formula of the fitted model
logLik	Estimated log-likelihood for the best model of the glmmPen procedure or the final model from glmm evaluated using the Pajor (2017) marginal likelihood calculation discussed in Section “Tuning parameter selection”
model.frame	A data.frame object containing the output and predictors used to fit the model
model.matrix	The fixed-effects model matrix
ngrps	Number of levels in the grouping factor
nobs	Number of total observations
plot	Diagnostic plots for mixed-model fits
predict	Predicted values based on either the fixed effects only (recommended) or the combined fixed effects and posterior modes of the random effects for each variable and each level of the grouping factor
print	Basic printout of mixed-model objects
ranef	Matrix of posterior modes of the random effects for each variable and each level of the grouping factor
residuals	Numeric vector of residual values: deviance (default), Pearson, response, or working residuals
sigma	Random effect covariance matrix ($\mathbf{\Gamma }{\mathbf{\Gamma }}^{\top }$)
summary	Summary of the mixed model results

When the pglmmObj object is created using the glmm function, the output from the methods listed in Table 2 pertains to the single model fit specified by the glmm arguments. When the pglmmObj object is created using the glmmPen function, the output from the methods pertains to the best model chosen during the model selection procedure. Additional information about each model fit can be found in the results_all field of the pglmmObj object. Using the basal output object fitB from the glmmPen function, we illustrate the use of several of these methods in the remainder of this section.

Model summary

The summary method output the function call information such as the sampler used in the E-step (in this case, Stan), the family, the model formula, the estimates of the fixed effects, the variance and standard deviation estimates of the random effects, and a summary of the deviance residuals. (Note: Due to the style of our formula specification using a matrix instead of column names of a data.frame, all variable names begin with the name of the matrix, X.)

> summary(fitB)
Penalized generalized linear mixed model fit by Monte Carlo Expectation
 Conditional Minimization (MCECM) algorithm (Stan) [‘pglmmObj’]
 Family: binomial ( logit )
Formula: y ~ X + (X | group)

Fixed Effects:

(Intercept)	XGPR160_CD109	XSPDEF_MFI2	XCHST6_CAPN9	XSLC40A1_CDH3
−1.1530	−0.7099	−0.7355	0.5082	−0.5831
XPLEK2_HSD17B2	XGPX2_ERO1L	XCYP3A5_B3GNT5	XLY6D_ATP2C2	XMYO1A_FGFBP1
0.4337	−0.5895	0.0000	0.4620	−0.7411
XCTSE_COL17A1
0.0000

Random Effects:

Group Name	Variance	Std.Dev.
group (Intercept)	0.8193	0.9052
group XGPR160_CD109	0.2036	0.4512
group XSPDEF_MFI2	0.684	0.827
group XCHST6_CAPN9	0	0
group XSLC40A1_CDH3	0	0
group XPLEK2_HSD17B2	0.0804	0.2835
group XGPX2_ERO1L	0.0842	0.2901
group XCYP3A5_B3GNT5	0	0
group XLY6D_ATP2C2	0	0
group XMYO1A_FGFBP1	0.1551	0.3938
group XCTSE_COL17A1	0.7596	0.8715

Number Observations: 938, groups: group, 4

Deviance residuals:

Min	1Q	Median	3Q	Max
−2.9338	−0.4026	−0.1512	0.3457	2.9630

We see that the best model included 9 TSPs with non-zero fixed effects and 6 TSPs with non-zero random effects (i.e., 6 TSPs with varying predictor effects across the studies). The print method supplies very similar information to the summary method minus the summary of the residuals.

The individual components of the print and summary outputs can be obtained using several accessory functions described in Table 2. Similar to the package lme4, the fixed effects can be summarized using fixef and the group-specific random effects can be summarized using ranef. The random effect covariance matrix is summarized using sigma. In the case of the Gaussian family, sigma also provides the residual standard error.

> fixef(fitB)
> ranef(fitB)
> sigma(fitB)

The residuals for the final model can be called using the residuals method. The different type options for the residuals include “deviance”, “pearson”, “response”, and “working”, which correspond to the deviance, Pearson, response, and working residuals, respectively.

> residuals(fitB, type = “deviance”)

Predictions and fitted values

Using the predict method, we can make predictions using only the population level information (i.e., the fixed effects only) or the group-specific level information (i.e., the fixed and random effects results). The glmmPen package restricts predictions on new data to only use the fixed effects. The predict method has the following arguments:

• object: an object of class pglmmObj output from glmm or glmmPen.

• newdata: a data frame of new data that contains all of the fixed effects covariates from the model fit. The variables provided in newdata must match the fixed effects used in the model fit.

• type: a character string specifying whether to output the linear predictor (“link”, default) or the expected mean response (“response”).

• fixed.only: boolean value specifying if the prediction is made with only the fixed effects (TRUE, default) or both the fixed and random effects (FALSE). Predictions are restricted to fixed.only = TRUE for new data predictions.

The fitted method also includes the fixed.only argument, allowing the fitted values of the linear predictor to be estimated with or without the random effects estimates.

> predict(object = fitB, newdata = NULL, type = “link”, fixed.only = TRUE)
> fitted(object = fitB, fixed.only = TRUE)

Diagnostics

The glmmPen package provides methods to perform diagnostics on the final model fit object. The plot method plots the residuals against the fitted values. The plot function defaults to plotting the Pearson residuals for the Gaussian family, and deviance residuals otherwise.

> plot(object = fitB)

The plot_mcmc function performs graphical MCMC diagnostics on the random effect posterior samples. This command has six arguments with the first argument specifying the pglmmObj output object. The second argument plots is used to specify which diagnostics plots to produce. The plots argument is capable of creating sample path plots (“sample.path”, default), autocorrelation plots (“autocorr”), cumulative sum plots (“cumsum”), and histograms (“histogram”) of the posterior samples. The plots are output as faceted ggplots with the graphics arranged by groups in the columns and variables in the rows. As ggplots, they are capable of being edited as any other ggplot. The plots argument can specify a vector of multiple plot types or the choice of “all”, which automatically produces all four types of diagnostic plots. The function outputs a list object containing the plots specified. The third and fourth arguments grps and vars allow the user to restrict which groups and/or variables are examined in the diagnostic plots. The default values of “all” for these arguments give the results for all groups and variables. To request specific groups and variables, provide vectors of character strings specifying the variable or group names. The argument numeric_grp_order tells the function to order the group levels numerically (default FALSE), and bin_width allows the user to manipulate the bin widths of the histograms (default NULL results in geom_histogram defaults, only relevant if the “histogram” plot is requested).

The example code below specifies the names of three of TSP predictors with non-zero random effects across the studies and then uses the plot_mcmc function to produce the sample path plots and autocorrelation plots for the corresponding posterior samples. Some plot aesthetics are adjusted using the ggplot2 package (Wickham, 2016). These sample path and autocorrelation plots can be seen in Figure 1.

Figure 1:

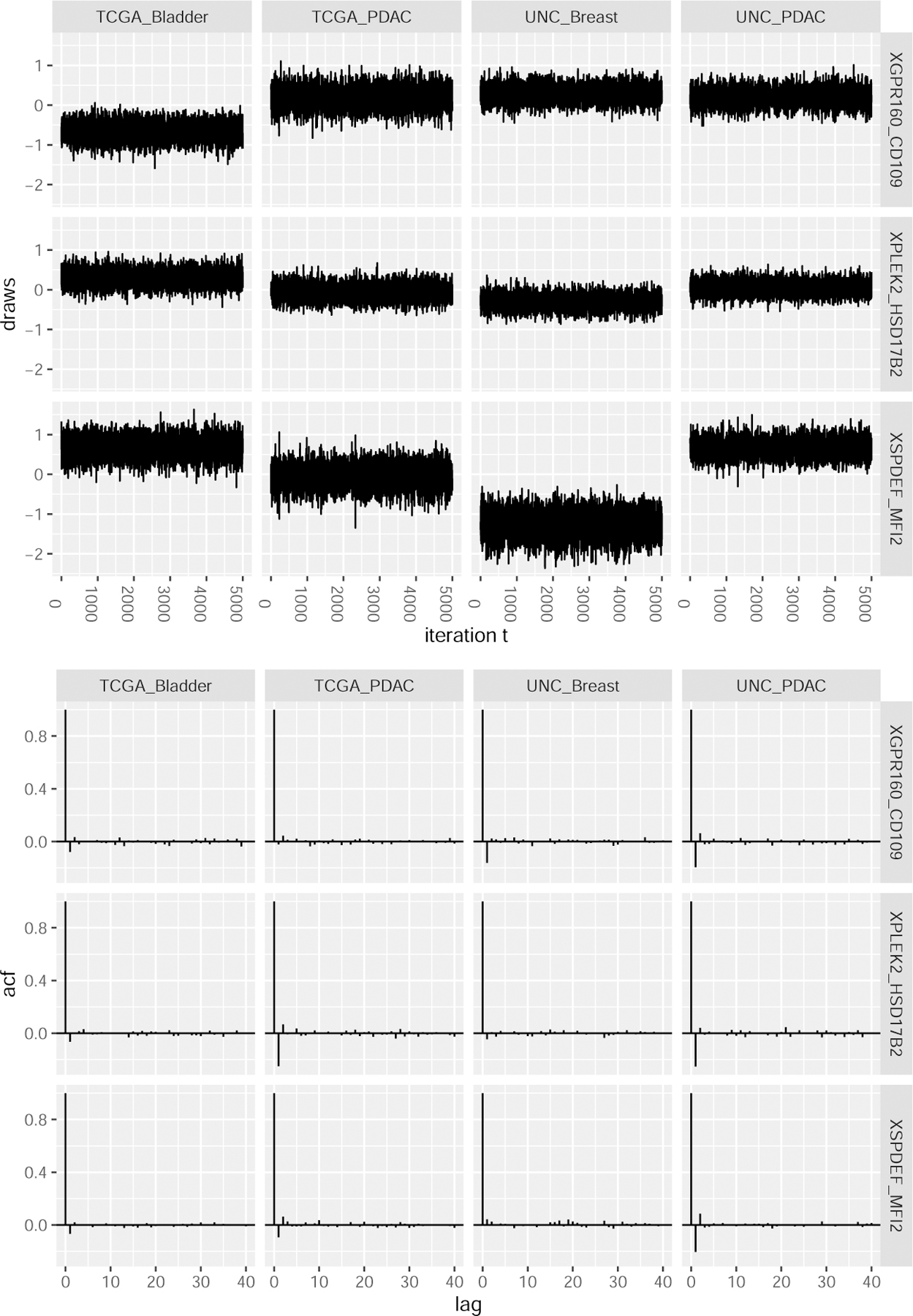
MCMC diagnostic plots for the basal best model results, created using the plot_mcmc function. Top: Sample path plots for the random slopes of three TSP covariates. Bottom: Autocorrelation plots for the random slopes of three TSP covariates.

> TSP = c(“XGPR160_CD109”, “XSPDEF_MFI2”, “XPLEK2_HSD17B2”)
> plot_diag = plot_mcmc(object = fitB, plots = c(“sample.path”,”autocorr”),
+ grps = “all”, vars = TSP)
> library(“ggplot2”)
> plot_diag$sample_path + theme(axis.text.x = element_text(angle = 270))
> plot_diag$autocorr

Optimization

Additional control options can be passed to the glmm and glmmPen functions using the optim_options argument and the optimControl() control structure. Some default settings in optimControl depend on the family of the data or the number of random effects. Descriptions of several of the main optimControl() arguments and their defaults are listed below:

sampler: a character string specifying the sampling type used in the E-step of the MCECM algorithm. The default sampler is “stan”, which requests the No-U-Turn Hamiltonian Monte Carlo sampling performed by the rstan package (Stan Development Team, 2020; Carpenter et al., 2017). We strongly recommend using this sampling method due to its speed and efficiency. Other options include “random_walk”, which requests the Metropolis-within-Gibbs adaptive random walk sampler (Roberts and Rosenthal, 2009), or “independence”, which requests the Metropolis-within-Gibbs independence sampler (Givens and Hoeting, 2012).

var_start: either a character string “recommend” (default) or a positive numeric value. This argument specifies the initial starting variance of the random effects covariance matrix. If var_start is set to “recommend”, the function fits a fixed and random intercept only model using the lme4 package and sets the starting variance to the random intercept variance multiplied by 2. The random effects covariance matrix is initialized as a diagonal matrix with the value of var_start as the diagonal elements.

var_restrictions: either a character string “none” (default) or the character string “fixef”. This argument can be used to restrict which random effects are considered at the start of the algorithm. If this argument is set to “none”, then all random effect predictors are initialized to have a non-zero variance in the random effect covariance matrix. If this argument is set to “fixef”, then only the random effect predictors that are initialized to have non-zero fixed effects estimates during the fixed effects initialization procedure are given non-zero variances when initializing the random effect covariance matrix. In effect, this restricts predictors that are initialized with zero-valued fixed effects coefficients to not have random effects. See glmmPen simulation results utilizing this feature within the GitHub repository https://github.com/hheiling/paper_glmmPen_RJournal. By using this restriction, the user assumes that predictors penalized out of the naive model do not have random effects. While this could be a strong assumption, using this restriction can be helpful in speeding up the algorithm by removing excessive random effects at the start of the variable selection procedure.

conv_EM: a positive numeric value specifying the convergence threshold for the EM algorithm. The argument conv_EM specifies the value of $ϵ$ in Equation 11. The default value is 0.0015.

t: a positive integer that specifies the value of $t$ in the EM algorithm convergence criteria specified in Equation 11. The convergence critera is based on the average Euclidean distance between the most recent coefficient estimate and the coefficient estimate from t EM iterations back. Default value is set to 2.

mcc: a positive integer indicating the number of times the EM convergence criteria must be met before the algorithm is seen as having converged (mcc short for ‘meet condition counter’). Default value is set to 2, and mcc is restricted to be no less than 2.

maxitEM: The maximum number of EM iterations allowed by the algorithm. When the default value of NULL is input, maxitEM is set to a value that depends on the family type of the data. For the Binomial and Poisson families, the default is set to 50. For the Gaussian family, the default is set to 100 (we have observed that the Gaussian family data generally takes longer to converge).

Additional optimization parameters include M-step convergence parameters (conv_CD, maxit_CD), parameters specifying the number of posterior samples to acquire for the E-step throughout the algorithm (nMC_burnin, nMC_start, and nMC_max), the number of posterior samples needed to calculate the log-likelihood (M), and the number of posterior samples to save for diagnostics (nMC_report). Additional details about these parameters and their defaults can be found in the glmmPen documentation of the function optimControl.

Simulations

In this section, we present results from simulations in order to examine the performance of our package. We use the glmmPen package to perform variable selection and examine the resulting fixed effects estimates as well as the true and false positives for the fixed and random effects. All simulations are performed using the default optimization settings discussed in Section “Optimization”. While the performance of the original implementation of the pGLMM algorithm was demonstrated in Rashid et al. (2020), here we confirm the performance of the computational improvements made since then as well as newer features such as the pre-screening procedure.

Simulation set-up

We simulated binary responses from a logistic mixed-effects regression model with $p$ predictors. Of $p$ total predictors, we assume that two predictors have truly non-zero fixed and random effects, and the other $p-2$ predictors have zero-valued fixed and random effects. Our aim in the simulations was to select the true predictors.

In these simulations, we consider the following situations: predictor dimensions of $p=\{10,\hspace{0.33em}50\}$, sample size $N=500$, number of groups $K=\left\{5,10\right\}$, and standard deviation of the random effects $\sigma =\{1, \sqrt{2}\}$. As discussed in Section “Generalized linear mixed models”, we approximate the covariance matrix of the random effects as a diagonal matrix for these higher dimensions. We further consider the scenarios of moderate predictor effects, where the true fixed effects are $\mathit{\beta }={(0,1,1)}^{\top }$.

For group $k$, we generated the binary response $y_{ki}$, $i=1,\dots ,n_k$ such that $y_{ki}\sim Bernoulli\left(p_{ki}\right)$ where $p_{ki}=P\left({\mathit{y}}_{ki}=1\mathit{|}{\mathit{x}}_{ki},{\mathit{z}}_{ki},{\alpha }_k,\theta \right)=\exp \left({\mathit{x}}_{ki}^{\top }\mathit{\beta }+z_{ki}^{\top }{\alpha }_k\right)\text{/}\left\{1+\exp \left({\mathit{x}}_{ki}^{\top }\mathit{\beta }+{\mathit{z}}_{ki}^{\top }{\alpha }_k\right)\right\}$, and ${\alpha }_k\sim N_3\left(0,{\sigma }^2{I}_3\right)$. The fixed effect coefficients were set to $\mathit{\beta }={(0,1,1)}^{\top }$ (moderate predictor effects). We also simulated imbalance in sample sizes between the groups. Of the $N$ samples, $N\text{/3}$ samples were given to study $k=1$ and the remaining $2N\text{/3}$ samples were evenly distributed among the remaining studies. Each condition was evaluated using 100 total simulated datasets.

For individual $i$ in group $k$, the vector of predictors for the fixed effects was ${\mathit{x}}_{ki}={\left(1,x_{ki,1},\dots ,x_{ki,p}\right)}^{\top }$, and we set the random effects ${\mathit{z}}_{ki}={\mathit{x}}_{ki}$, where $x_{ki,j}\sim N(0,1)$ for $j=1,\dots ,p$.

Setting the input random effects equal to the fixed effects represents the worst-case scenario where we have no idea what predictors do or do not have random effects. This is an extreme assumption; in many real-world scenarios, users will have reason to set the input random effects to a strict subset of the fixed effects.

In all of these simulations, we use the default settings discussed earlier, which includes using the default ${\mathit{\lambda }}_0$ and ${\mathit{\lambda }}_1$ penalty sequences, BIC-ICQ for the selection criteria, pre-screening, and the MCP penalty. For all simulations, we performed the abbreviated two-stage grid search as described in Section “Tuning parameter selection”. The results for these simulations are presented in Table 3. These results include the average coefficients, the average true positive and false positive percentages for both fixed and random effects, and the median time for the simulations to complete. The true positive percentages reflect the average percent of the true predictors included in the best models chosen by the BIC-ICQ model selection criteria, which should ideally be near 100%. Likewise, the false positive percentages reflect the average percent of the false predictors included in the best models, which should ideally be near 0%. All simulations were completed on the UNC Longleaf computing cluster (CPU Intel processors between 2.3Ghz and 2.5GHz).

Table 3:

Variable selection simulation results with moderate predictor effects (slopes equal to 1). Results include the estimated coefficients for true non-zero fixed effects, true positive (TP) percentages for fixed and random effects, false positive (FP) percentages for fixed and random effects, and the median time in hours for the algorithm to complete.

$N$	$p$	$K$	$\sigma$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	TP % Fixed	FP % Fixed	TP % Random	FP % Random	$T^{median}$(hours)
500	10	5	1	1.02	1.12	89.0	2.1	90.5	3.5	0.20
			$\sqrt{2}$	1.12	1.18	83.0	1.4	96.0	3.6	0.26
		10	1	0.99	1.04	99.0	3.0	95.0	4.8	0.24
			$\sqrt{2}$	1.02	1.11	91.0	1.8	99.5	7.0	0.32
500	50	5	1	1.18	1.14	84.5	1.2	83.5	2.2	8.07
			$\sqrt{2}$	1.42	1.43	75.5	2.5	89.0	2.5	12.20
		10	1	1.12	1.11	95.0	1.8	93.0	3.9	10.67
			$\sqrt{2}$	1.33	1.31	84.5	2.4	95.5	6.2	15.75

By examining the simulation results, we can observe that the performance of the variable selection procedure in glmmPen is impacted by the underlying structure of the data. As the magnitude of the random effect variance increases, the true positive percentage of the fixed effects decreases and the true positive percentage of the random effects increases. Additionally, as the number of groups $K$ increases, the true positive percentage of both the fixed and random effects increases. We see that as the dimension of the total number of predictors increases ($p=10$ to $p=50$), the true positive percentages of both the fixed and random effects decreases. In regards to the run time, Table 3 shows that increases in the number of groups and increases in the variance of the random effects generally increases the time for the algorithm to complete.

In simulations not shown, we saw that increases to the magnitude of the fixed effects (e.g., increasing the true slope to 2, see content in GitHub repository https://github.com/hheiling/paper_glmmPen_RJournal for details) increased the true positive fixed effects and generally decreased the true positive random effects.

Pre-screening performance

The time it takes the package to complete the tuning parameter selection procedure depends strongly on the number of random effects considered by the algorithm. Therefore, the pre-screening procedure, which reduces the number of random effects considered within the variable selection algorithm, speeds up the algorithm. Table 4 summarizes the performance of the pre-screening algorithm for the variable selection simulations described above. This table reports the average percent of true positive and false positive random effect predictors that remain under consideration within the variable selection procedure after the pre-screening step has completed. The pre-screening settings were the default settings described in Section “Software”, which include specifying lambda.min.presc = 0.01 for $p=10$ and lambda.min.presc = 0.05 for $p=50$ such that the minimum penalty on the random effects is lambda.min.presc ×${\lambda }_{max}$. We note that there are currently no methods that are capable of scaling to values of $q$ evaluated in our simulation for estimating and performing variable selection in GLMMs.

Table 4:

Pre-screening results for variable selection simulations with moderate predictor effects (slopes equal to 1). Results include the true positive percentages and false positive percentages of the random effects remaining after pre-screening.

$N$	$p$	$K$	$\sigma$	TP %	FP %
500	10	5	1	98.0	25.8
			$\sqrt{2}$	100.0	26.1
		10	1	100.0	33.0
			$\sqrt{2}$	100.0	32.2
500	50	5	1	96.0	24.6
			$\sqrt{2}$	96.5	25.7
		10	1	97.5	25.9
			$\sqrt{2}$	98.5	27.3

Using this higher penalty in the $p=50$ simulations helps reduce the false positive percentage of the random effects after pre-screening and consequently helps speed up the time of the algorithm to complete. However, we can see by comparing the $p=50$ and $p=10$ simulations that this approach can also slightly decrease the true positive percentage. In general, increasing lambda.min.presc will help decrease the number of false positive non-zero random effects in the pre-screening step, but it may also decrease the number of true positive non-zero random effects. Decreasing lambda.min.presc will generally have the opposite effect. We also see that the true positive percentage for the selection of the random effects after pre-screening is generally higher when the magnitude of the true random effect variance is higher.

Conclusion

This paper introduces the R package glmmPen for fitting penalized generalized linear mixed models, including Binomial, Gaussian, and Poisson models. The glmmPen package’s main advantage over other packages that estimate GLMMs is that it can perform variable selection on the fixed and random effects simultaneously. The algorithm utilizes a Monte Carlo Expectation Conditional Minimization (MCECM) algorithm. Several established MCMC sampling techniques are available for the E-step, and a Majorization-Minimization coordinate descent algorithm is used in the M-step. The package utilizes the established methods of Stan and RcppArmadillo to increase the computational efficiency of the E-step and M-step, respectively. As a result, the glmmPen package can fit models with higher dimensions compared to other packages that fit GLMMs, supporting models with 50 or more fixed and random effects.

The glmmPen package employs several additional techniques to improve the speed of the algorithm. Such techniques include initialization of subsequent models with the coefficients from the previous model fit and pre-screening to remove unnecessary random effects.

The glmmPen package has several attributes that make it user-friendly. For one, the package was designed to have an interface that is similar to the well-known lme4 package. Additionally, the glmmPen package has several automated processes that make it user-friendly. The package provides automated data-dependent initialization of the random effect covariance matrix. The package also provides automated recommendations for the penalization parameters.

A unique aspect of the package is the calculation of the marginal log-likelihood. The corrected arithmetic mean estimator (CAME) calculation described by Pajor (Pajor, 2017) is relatively simple and fast to calculate, and we have found that it performs well when compared with the log-likelihood estimate used in the lme4 package (see content in the GitHub repository https://github.com/hheiling/paper_glmmPen_RJournal). This marginal log-likelihood calculation allows the algorithm to perform tuning parameter selection using traditional BIC selection criterion as well as other BIC-derived selection criteria. This gives users the option to forgo calculating the BIC-ICQ selection criterion, which requires the minimal penalty model fit where a minimum penalty is applied to both the fixed and random effects.

In its current implementation, the glmmPen R package can apply to Binomial, Gaussian, and Poisson families with canonical links. In the future, we plan to extend the application of this package to survival data, the existing families with non-canonical links, and additional families such as the negative binomial family.