Inequality in Reading and Math Skills Forms Mainly before Kindergarten: A Replication, and Partial Correction, of “Are Schools the Great Equalizer?”

Abstract

When do children become unequal in reading and math skills? Some research claims that inequality grows mainly before school begins. Some research claims that schools cause inequality to grow. And some research−including the 2004 study “Are Schools the Great Equalizer?”−claims that inequality grows mainly during summer vacations. Unfortunately, the test scores used in the Great Equalizer study suffered from a measurement artifact that exaggerated estimates of inequality growth. In addition, the Great Equalizer study is dated and its participants are no longer school-aged. In this article, we replicate the Great Equalizer study using better test scores in both the original data and a newer cohort of children. When we use the new test scores, we find that variance is substantial at the start of kindergarten and does not grow but actually shrinks over the next two to three years. This finding, which was not evident in the original Great Equalizer study, implicates the years before kindergarten as the primary source of inequality in elementary reading and math. Total score variance grows during most summers and shrinks during most school years, suggesting that schools reduce inequality overall. Changes in inequality are small after kindergarten and do not replicate consistently across grades, subjects, or cohorts. That said, socioeconomic gaps tend to shrink during the school year and grow during the summer, while the black-white gap tends to follow the opposite pattern.

The social sciences are deeply conflicted about the origins of inequality in children’s cognitive skills. A long tradition of research builds on the idea that much of inequality is caused by the structure and practices of schools (Bowles and Gintis 1976; Kozol 1992; Lucas 1999; Oakes 2005; Orfield, Kucsera, and Siegel-Hawley 2012). Yet an equally venerable research tradition argues that schools contribute little to inequality−or even reduce it−and that the bulk of inequality is due to differences between families (Coleman et al. 1966; Downey and Condron 2016; Jencks 1972). Among research that attributes inequality to families, there is further disagreement. Some research suggests that inequality between families affects children’s cognitive skills primarily during the early years of life, before schooling begins (Duncan and Magnuson 2011; Farkas and Beron 2004; Heckman and Masterov 2007). Yet other research argues that inequality between families continues to impact children’s cognitive skills heavily after schooling begins−especially when schools let out for summer vacations (Alexander, Entwisle, and Olson 2001; Downey, von Hippel, and Broh 2004; Hayes and Grether 1983; Heyns 1978; Murnane 1975).

Unfortunately, testing and measurement artifacts make it difficult to resolve these disagreements. Many test scores−especially those used in older research−violate the assumption of vertical interval scaling, which is needed to tell whether inequality is greater at one age than another. Without vertical interval scaling, research can reach mistaken conclusions about whether inequality grows or shrinks as children progress through different school years and summer vacations (Reardon 2008; von Hippel and Hamrock 2016). Past research has reached varying conclusions about how unequal children’s skills are when schooling begins and about how much inequality grows or shrinks during later school years and summer vacations. These varying conclusions are confusing and often have little to do with inequality between children. Instead, they often have more to do with the properties of the test scores with which children are compared (von Hippel and Hamrock 2016).

In this article, we replicate a well-known study of growth in cognitive inequality: the article “Are Schools the Great Equalizer?” which has been cited nearly 800 times since it was published in 2004 by the American Sociological Review (Downey et al. 2004). We carry out the same analyses as in the original study, but we use betterscaled test scores that can more plausibly compare inequality at different ages. In addition, we update the Great Equalizer study with evidence from a younger cohort of children who started kindergarten 13 years after the original participants.

The major conclusions of the original Great Equalizer study were these:

1. Inequality in reading and math scores grew substantially between the start of kindergarten and end of first grade.

2. Inequality growth was faster during summer vacations than the school years.

These conclusions held for total variance in test scores, for the score gap between children of different socioeconomic status (SES), and for the gap between Asian and white children. But the pattern was different for the gap between black and white children, which grew faster during the school years than during the first summer vacation. There was no difference in the school and summer growth of gaps between Hispanic, non-Hispanic white, and Native American children, and there was no difference between the school and summer growth of gaps between boys and girls.

When we switch to the new test scores, however, we find that Conclusion 1 no longer holds. Inequality in test scores does not grow; it slightly shrinks between the start of kindergarten and the end of first or second grade. This is true for total variance in test scores, for the SES gap, and for most racial and ethnic gaps. This pattern implicates early childhood as the primary source of inequality in reading and math−an implication that was not evident in the original Great Equalizer study, which used flawed test scores.

Since inequality displays no net growth after the start of kindergarten, the question of when inequality grows fastest needs to be reframed. Instead of asking when inequality grows fastest, we should ask when inequality shrinks, when it grows, and by how much. On this question, our conclusions are closer to those of the original Great Equalizer study−but not entirely unchanged. We find that total variance in test scores shrinks during the kindergarten, first-, and second-grade school years and grows during the first summer vacation−but inequality does not grow during the second summer vacation. Likewise, we find that the SES score gap shrinks during kindergarten and grows during the first summer vacation−but the pattern does not replicate consistently in later school years and summers in the new cohort. Racial and ethnic patterns are murky and do not replicate consistently across school years, summers, or cohorts. With inequality changing so little after the start of kindergarten, it is harder−and less important−to say whether inequality changes more during school or during summer.

DO SCHOOLS CAUSE INEQUALITY?

A long tradition of research builds on the idea that much of inequality is caused by schools. It is not hard to see where this idea comes from. Despite the progress made toward racial desegregation in the 1970s and 1980s, schools remain highly segregated by race and income: Poor, black, and Hispanic children often attend different schools than wealthier, white, and Asian children (Reardon and Owens 2014). And schools primarily serving poor, black, and Hispanic children have less advanced curricula, less advanced technology, and more difficulty attracting and retaining experienced teachers (Phillips and Chin 2004). In addition, the very practice of concentrating disadvantaged children in certain schools may reduce their achievement by depressing morale and limiting their exposure to classmates who have advanced skills and middle-class aspirations and norms (Jencks 1972; Kozol 1992).

Even when advantaged and disadvantaged children attend the same schools, they may not receive equal treatment. Teachers have lower expectations and feel less responsibility for the success of poor, black, and Hispanic children than they do for more affluent, white, and Asian children, even in the same classroom (Diamond, Randolph, and Spillane 2004; Roscigno and Ainsworth-Darnell 1999). In middle and high school, poor, black, and Hispanic students are more likely to be assigned inexperienced teachers and lower curricular tracks (Gamoran 2010; Kalogrides and Loeb 2013; Lucas 1999; Oakes 2005).

For these reasons and others, many scholars and many in the general public subscribe to the belief that “inequalities in the school system” are “important in reproducing the class structure from one generation to the next” (Bowles 1971:137).

DO FAMILIES CAUSE INEQUALITY?

Despite longstanding concerns about schools, an equally venerable research tradition argues that schools contribute relatively little to inequality and that the bulk of inequality is due to non-school influences, especially the family. Indeed, family characteristics−including income, wealth, parental education, race and ethnicity, number of siblings, and number of parents in the home−are far more strongly and consistently associated with children’s academic success than any characteristics of schools (Coleman et al. 1966; Jencks 1972).

How could this be? One reason is that family resources are distributed more unequally than school resources−and school resources are distributed more equally than we often recognize. For example, inequality in family income is far greater than inequality in school spending−and inequality in school spending has shrunk since the 1970s while income inequality among families with children has grown (Corcoran et al. 2004; Western, Bloome, and Percheski 2008). Likewise, the ratio of children to parents at home is far more unequal than the ratio of students to teachers at school. Poor children have about the same average class size as middle-class children (Phillips and Chin 2004), but poor children tend to have larger families with several siblings competing for the attention of a single parent (Lichter 2007). Experience and credentials are also more unequal among parents than teachers. The difference between a novice teacher with a bachelor’s degree and a teacher with 10 years’ experience and a master’s degree is far smaller than the difference between a 30-year-old mother with a professional degree and a teen mother who dropped out of high school.

Another reason why schools may contribute less to inequality is that the effects of many school resources are small. For example, teachers with a master’s degree, who are more common in schools serving affluent children, are not, on average, more effective than teachers with only a bachelor’s degree (Clotfelter, Ladd, and Vigdor 2007; Hedges, Laine, and Greenwald 1994). It is true that poor children have less experienced and effective teachers than non-poor children, but the difference adds only 1 percentile point to the gap between poor and non-poor children’s test scores (Isenberg et al. 2013). Poor, black, and Hispanic adolescents are more likely to be assigned to lower curricular tracks, yet evidence on the effects of tracking on achievement is mixed. In some studies, low track assignment appeared to depress achievement (Lucas 1999; Oakes 2005), yet in some more recent studies, tracking has raised test scores for low- and high-scoring children alike (Duflo, Dupas, and Kremer 2008) while elimination of tracking has increased rates of course failure and dropout (Allensworth et al. 2009). Teacher expectations, too, may have less influence on children than was once thought (Jussim and Harber 2005).

Some school resources even favor the disadvantaged. For example, poor and black children are more likely to attend kindergarten for a full day, while more affluent and white children are more likely to attend only half the day (Lee et al. 2006; see our results as well). In one survey, teachers reported spending more time and effort helping “struggling students” than helping “advanced students,” whose success they may take for granted (Duffett, Farkas, and Loveless 2008). For these reasons, it may be that schools are not just neutral with respect to inequality but actually help reduce it.

Family Inequality before School Begins

If the bulk of inequality does come from families, the question arises: When does family inequality matter most? One body of work holds that most of the effects of family inequality play out during gestation and early childhood, before kindergarten or even preschool begin (Downey and Condron 2016; Duncan and Magnuson 2011; Farkas and Beron 2004; Heckman and Masterov 2007).

One argument for why family inequality matters most in the early years is that these are the years when children have most contact with their families. Children get more family care before school begins than afterward, and poor, black, and Hispanic families are especially reliant on family care (Duncan and Magnuson 2011; Uttal 1999). Children’s early language development is shaped primarily by their mothers’ speech, and poorer, less educated mothers speak to their children less and with more limited vocabulary than more affluent and educated mothers (Hart and Risley 1995; Hoff 2003).

Another argument for the importance of the early years is that the child’s brain is most sensitive to its environment during early childhood. “Sensitivity to environmental stimuli, positive and negative, is heightened during periods of rapid brain development” (Johnson, Riis, and Noble 2016:2), and both the number of neurons and number of synapses in the cerebral cortex grow most rapidly during early childhood, especially before the age of two (Johnson et al. 2016). The slowing of brain development after the preschool years is evident in reading and math scores, whose rate of growth decelerates from kindergarten through eighth grade (von Hippel and Hamrock 2016).

Family Inequality after School Begins

Yet another body of research argues that family inequality continues to have substantial effects after schooling begins−both during the school year and especially during summer vacations (Alexander et al. 2001).

One argument for these later effects is that the brain’s development is not over when schooling begins. Although growth in the number of neurons and synapses is fastest in early childhood, other aspects of neural development, such as pruning and myelination, continue throughout childhood and adolescence. Different parts of the brain have periods of faster growth and heightened sensitivity at different ages; for example, “the prefrontal cortex . . . which supports cognitive self-regulation and executive function, develops rapidly in the first 2 years of life, at 7 to 9 years of age, and again in the midteens, with continued myelination in the third decade” (Johnson et al. 2016:2). Presumably, development of the prefrontal cortex is sensitive to family inequality in the later sensitive periods as well as the earlier ones.

The neurological evidence is consistent with cognitive evidence that children continue to build skills as they progress through school. While basic reading and math skills reach a point of diminishing returns in elementary school, more advanced technical, rhetorical, and organizational skills develop later. Although some cognitive skills are most impacted by early poverty, others are most impacted by poverty in adolescence (Guo 1998; Wagmiller et al. 2006). Perhaps the age at which poverty matters for a skill depends on the age at which that skill develops.

Another reason why family inequality might matter after school begins is that more educated parents tend to be more involved in their children’s schooling (Lareau 2000; Robinson and Harris 2014). Yet the effects on test scores of parental involvement are inconsistent and often small (Patall, Cooper, and Robinson 2008; Robinson and Harris 2014). Perhaps the more important mechanisms by which families affect test scores are more indirect.

SEASONAL RESEARCH DESIGNS

Does inequality in cognitive skills originate primarily at school or at home? If it originates at home, does it emerge primarily in early childhood, or does out-of-school inequality continue to accumulate through later summers, weekends, and evenings? Do schools exacerbate inequality, do they reduce it, or are they neutral?

While the evidence that we have discussed sheds some light on these questions, many of the influences on children’s development are unknown or difficult to conceptualize and measure. It is unlikely that we can list and measure all the school and family variables that matter for children’s cognitive development, and the variables that we measure most often, such as family income and school spending, may be only proxies for the behaviors, resources, and endowments that matter most. There is always some danger that much of the available evidence is missing something essential about families, schools, or both.

A source of evidence that can capture some of these unobserved factors is the longitudinal seasonal research design. Ideally, a longitudinal seasonal design first tests children very early in their school career−in first grade, kindergarten, or even pre-K−so that we can gauge how much inequality children bring with them from early childhood. After that, a seasonal design tests children near the beginning and end of consecutive school years so that we can compare changes in inequality during the school year and during summer when school is out for vacation.

The comparison between school year and summer is important because school year learning is shaped by a mix of school and non-school factors, while summer learning is shaped by non-school factors almost alone (Heyns 1978). So seasonal designs clarify the relative importance of school and non-school environments in shaping inequality. Seasonal designs do not require a comprehensive list of school and non-school factors that might shape inequality. This is a strength in the sense that nothing is left out, but it is also a limitation in that seasonal work does not tell us which specific school or non-school practices exacerbate or reduce inequality.

Seasonal research can yield several possible patterns of results.

• 1If inequality grows faster during the school years than during the summers, then we may conclude that schools exacerbate inequality.
• 2Conversely, if inequality grows faster during the summer than during the school years, we may conclude that schools reduce inequality−at least in the relative sense that they prevent inequality from growing as fast as it otherwise might.

These are the two patterns that were emphasized in past seasonal studies, but they are not the only possibilities.

• 3It is also possible for inequality to shrink during the school year, in which case, we may conclude even more strongly that schools reduce inequality. If inequality also shrinks during summer vacation, the interpretation becomes more challenging, but we can still ask whether inequality shrinks faster during school or during summer.
• 4Finally, it is possible that inequality changes very little during the school year or the summer. Instead, the inequality that children display at the start of kindergarten may simply persist. In that case, we may conclude that inequality originates mainly before kindergarten and that later school and non-school factors contribute little to inequality.

We can be fairly broad here about what we mean by inequality. Most seasonal research has defined inequality as the gap in average test scores between children from advantaged and disadvantaged groups−for example, the gap between white and black children, between children of high or low SES, or between girls and boys. However, race, ethnicity, gender, and SES explain only a quarter to a third of the variance in children’s test scores (Downey et al. 2004; Koretz, McCaffrey, and Sullivan 2001) and only 1 percent of the variance in summer learning (Downey et al. 2004). With so much of the variance unexplained, it is reasonable to ask whether total variance in test scores, including unexplained variance, grows faster (or shrinks slower) during the school year or during summer vacation.

MEASUREMENT ARTIFACTS

While the interpretation of seasonal results may seem fairly clear, a seasonal design can only offer an unbiased comparison of inequality at different times if children’s achievement levels are measured on a vertical interval scale. An interval scale uses equal-sized units to compare students at lower and higher levels of reading and math skill. A vertical interval scale is one whose units do not change as children progress from one grade to the next. Unfortunately, the test scores used in most seasonal research−including the Great Equalizer study−suffered from measurement artifacts that violated the assumptions of vertical interval scaling. Some artifacts exaggerated the growth of inequality as children grew older, and some artifacts also exaggerated the extent to which inequality growth occurs during the summer (von Hippel and Hamrock 2016).

One measurement artifact relates to changes in test form. Older seasonal research used fixed-form testing, in which children filled out the same paper test form in fall and spring and then switched to a new test form, with new questions and scoring, when they started the next grade in the fall. Since these studies used different test forms before and after the summer, differences between test forms confounded estimates of summer learning (von Hippel and Hamrock 2016). Seasonal results that were vulnerable to change-of-form artifacts include the “Summer Setback” findings for Baltimore students in the 1980s (Entwisle and Alexander 1992) and older summer learning studies from Atlanta, New Haven, and New York City (e.g., Entwisle and Alexander 1992, 1994; Hayes and Grether 1969, 1983; Heyns 1978, 1987; Murnane 1975)−in fact, practically all the summer learning studies reviewed in a 1996 meta-analysis (Cooper et al. 1996).

Modern seasonal studies are less vulnerable to change of form artifacts because they less often rely on fixed form tests. Instead, modern studies increasingly use adaptive testing, which gives different students different questions calibrated to their individual abilities rather than their grade in school (Gershon 2005). Adaptive testing minimizes the artifacts associated with abrupt changes in test form at the end of each summer (von Hippel and Hamrock 2016).

A second measurement artifact pertains to test score scaling, which is the mathematical method by which a child’s pattern of right and wrong answers is transformed into a test score. Older seasonal research relied on methods that yielded scales whose variance grew substantially with age so that the gaps between low- and high-achieving students grew substantially as well. By contrast, modern practice favors ability scales (or theta scales), constructed using item response theory (IRT), whose variance typically changes relatively little with age (von Hippel and Hamrock 2016; Williams, Pommerich, and Thissen 1998). IRT ability scales have a plausible though not ironclad claim to vertical interval scaling and are designed to reward the gains of higher and lower ability students more equally.

REPLICATING THE GREAT EQUALIZER STUDY

The Great Equalizer study was not vulnerable to change-of-form artifacts because it used adaptive testing. But it did use a poorly aligned scale, which later analysis showed was not a vertical interval measure of children’s abilities (Reardon 2008; von Hippel and Hamrock 2016). The scale used in the Great Equalizer paper exaggerated the growth of gaps with age and also exaggerated the extent to which higher-scoring children pulled away from lower-scoring children early in the study (von Hippel and Hamrock 2016). In addition, the original Great Equalizer study was limited to just two school years (kindergarten and first grade) and the summer between. Finally, the Great Equalizer has become somewhat dated; its children started kindergarten in 1998−20 years ago−and are no longer school-aged.

Fortunately, we can now replicate the Great Equalizer study in a way that addresses some of the original study’s flaws and limitations. This opportunity exists because the data used in the original Great Equalizer study have been rereleased with better-scaled test scores. In addition, similar data have recently been collected on a more recent cohort of children who started kindergarten in 2010 and were tested seasonally, not just in kindergarten and first grade but in second grade as well. In sum, our replication improves or extends three dimensions of the original study:

1. We replace the original test scores with better-scaled scores that can more plausibly estimate changes in inequality over time.

2. We supplement the original cohort, who started kindergarten in 1998, with a new cohort who started kindergarten in 2010.

3. We extend the study, which originally ended in first grade, through the end of second grade. However, we can do this only in the new cohort.

Note that each dimension of the replication serves a different purpose. By replacing the original test scores, we aim to find out whether the Great Equalizer study suffered from measurement artifacts so severe that some of its conclusions were incorrect. By adding a new cohort and school year, we are not aiming to find out whether the original study was incorrect, but whether its findings generalize to later grades and a more recent cohort.

We are not the first to analyze some of these data with seasonal questions in mind. Earlier work highlighted the importance of scaling artifacts in the data used by the Great Equalizer study (Reardon 2008; von Hippel and Hamrock 2016), and Quinn et al. (2016) analyzed seasonal patterns in the new cohort. However, each of these studies conducted different analyses than the Great Equalizer study and so do not permit an apples-to-apples comparison to the 2004 results. In addition, past studies were limited to a single cohort. We will compare our results to earlier studies in the Discussion.

DATA

We compare two cohorts of US children from the nationally representative Early Childhood Longitudinal Study, Kindergarten class (ECLS-K)−an older cohort that started kindergarten in 1998–1999 (ECLS-K:1999) and a newer cohort that started kindergarten in 2010–2011 (ECLS-K:2011). The ECLS-K:1999 was analyzed in the 2004 Great Equalizer article. The ECLS-K:2011 was conducted later.

Reading and Math Tests

Test schedule.

Children were tested repeatedly in reading and math. In both cohorts, children took tests in the fall and spring of kindergarten and the fall and spring of first grade. In the new cohort, children also took tests in the fall and spring of second grade. In first and second grade, fall tests were only given in a 30 percent subsample of participating schools. The reduced fall sample size reduces statistical power but does not introduce bias since the schools were subsampled at random.

Tests were not given on the first or last day of school. While the average school year started in late August and ended in early June, test dates varied across schools, with most fall tests in September-November and most spring tests in April and May. The mean and SD of school start dates, test dates, and school end dates are summarized in Table A1 in the Appendix.

Both ECLS-K cohorts also took tests in the springs of third and fifth grades, and the newer cohort took tests in the spring of fourth grade as well. The older cohort took tests in the spring of eighth grade, and the newer cohort will do so in spring 2019. Our analyses do not include these later tests since they were given at intervals of one to three years and cannot support separate estimates of school and summer learning rates.

Test scaling (ability or theta scores).

Tests drew items from a large item bank containing between 70 and 150 items depending on the grade, cohort, and subject. The tests proceeded in two stages. In Stage 1, a routing test presented items across a wide range of difficulties and used children’s answers to produce an initial estimate of ability. In Stage 2, the initial ability estimate was used to assign students to a test of low, high, or (in some grades) medium difficulty. This approach is known as two-stage adaptive assessment.

Students’ abilities were estimated using a three-parameter logistic (3PL) item response model in which the probability that child $c$ answers item $i$ correctly is a scaled inverse cumulative logistic function of the child’s ability ${\mathrm{\text{θ}}}_c$ and the item’s difficulty $d_i$, discrimination $a_i$, and guessability $c_i$ (Lord and Novick 1968):

$$P(correct)=c_i+\left(1-c_i\right)logi{t}^{-1}\left(a_i\left({\mathrm{\text{θ}}}_c-d_i\right)\right).$$ (1)

By fitting this model, psychometricians working on the ECLS-K produced estimates ${\widehat{\mathrm{\text{θ}}}}_c$ of each child’s ability, known as theta scores (Najarian, Pollack, and Sorongon 2009; Tourangeau et al. 2017).

Theta scores are vertical interval measures of ability, at least in the technical sense that they are linear in the logit, or log odds, that different students will correctly answer an item of given difficulty, discrimination, and guessability. However, the mean and variance of theta scores is arbitrary and can be changed without changing our ability to interpret theta scores as linear in the log odds of a correct answer.¹ We standardize the theta scores around the mean and SD at the fall of kindergarten so that later changes in the theta scores can be interpreted in SD units.

Although the theta scores offer a vertical interval scale of ability within each cohort, the theta scores have not been aligned between cohorts. That is, we can use the theta scores to compare different tests in the same cohort, but we cannot use them to make certain comparisons between the old and new cohorts. For example, while we can say that, in both cohorts, learning rates are slower and more variable in the summer than during the school year, we cannot say whether summer learning rates are more or less variable in the old cohort than the new cohort. It is possible to put the theta scores from both cohorts on a common scale, but it is not clear when or whether that will be done.²

The estimated ability score ${\widehat{\mathrm{\text{θ}}}}_c$ of child $c$ consists of the child’s true ability ${\mathrm{\text{θ}}}_c$ at the time of the test, plus independent measurement error $e_c:{\widehat{\mathrm{\text{θ}}}}_c={\mathrm{\text{θ}}}_c+e_c$. So across children, the variance of estimated abilities is equal to the variance of true abilities (true variance) plus the variance of the measurement error (error variance):

$$Var\left({\widehat{\mathrm{\text{θ}}}}_c\right)=Var\left({\mathrm{\text{θ}}}_c\right)+Var\left(e_c\right).$$ (2)

The ratio of true variance to total variance is the reliability of the scores:

$$\rho =Var\left({\mathrm{\text{θ}}}_c\right)/Var\left({\widehat{\mathrm{\text{θ}}}}_c\right).$$ (3)

Table A1 in the Appendix gives the reliability of the ability scores on each occasion, as estimated in the ECLS-K psychometric reports (Najarian et al. 2009; Tourangeau et al. 2017). From the reliability and variance of the observed scores ${\widehat{\mathrm{\text{θ}}}}_c$, we can use Equation 2 to calculate the variance of the true scores ${\mathrm{\text{θ}}}_c$ and the variance of the measurement error $e_c$. In every round, the estimated reliability of the tests exceeds .90, which is plausible since the correlation between fall and spring test scores (which cannot exceed the reliability) ranges from .73 to .90.

“Scale” scores and measurement artifacts.

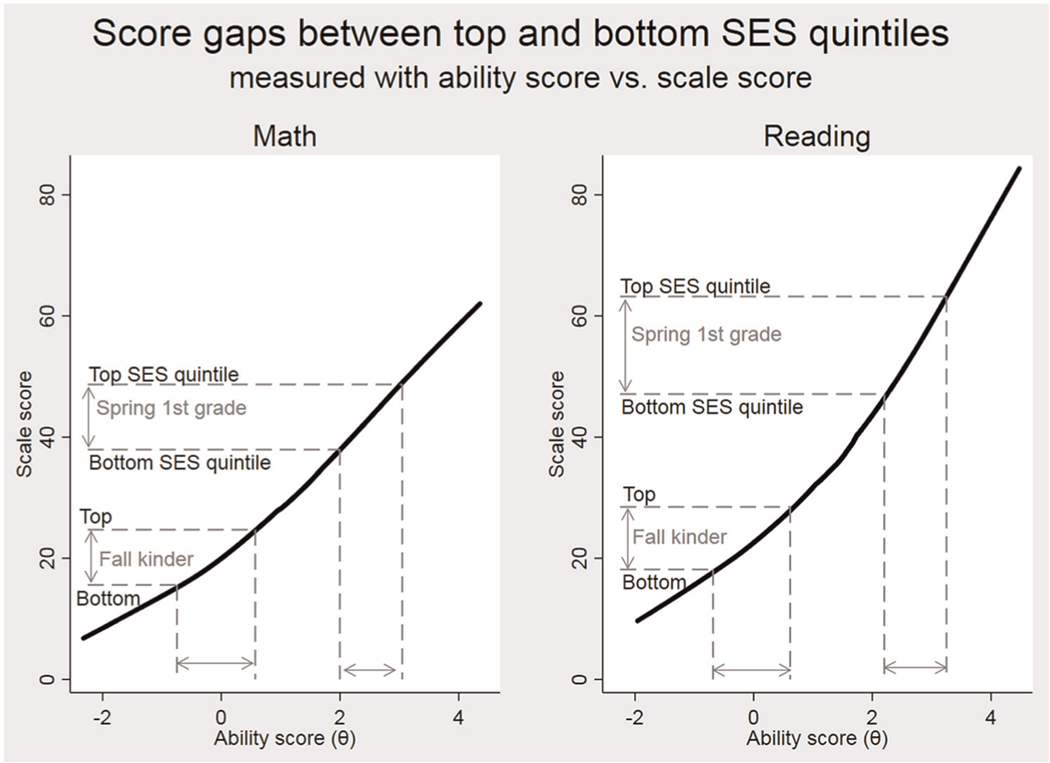
Early releases of data from the old ECLS-K cohort did not include theta scores but instead presented “scale scores,” which estimated the number of items that the student would have answered correctly had they responded to every item in the item bank (instead of just the sample of items on the Stage 1 and Stage 2 assessments). The scale score is not an interval measure of student ability. It is a function of ability, but it is also a function of the difficulty, discrimination, and guessability of the items in the item bank (Reardon 2008; von Hippel and Hamrock 2016). Figure 1 graphs scale scores against ability scores obtained in the first two years of the ECLS-K:2011 (for similar graphs, see Reardon 2008; von Hippel and Hamrock 2016). The relationship is nonlinear, implying that if the ability score is an interval measure of ability, the scale score cannot be.

Figure 1.

One implication of the nonlinear relationship between ability scores (theta) and scale scores in the Early Childhood Longitudinal Study, Kindergarten (ECLS-K:1999). Between the fall of kindergarten and the spring of first grade, the gap between the top and bottom socioeconomic status quintiles shrinks using the theta scores but grows using the scale scores.

Inferences about inequality growth are very different if we use scale scores than if we use ability scores. Typically, the scale score gives an impression of growing inequality, but the ability score does not. For example, in the ECLS-K:1999, the SD of the scale score approximately doubled between the fall of kindergarten and spring of first grade, but the SD of the ability score shrank by over 10 percent. Figure 1 shows why: In the early rounds, the scale score is an accelerating function of the theta score so that children who start out ahead will appear to pull away more quickly on the scale score than the ability score. For example, between the fall of kindergarten and spring of first grade, the gap between the mean scores of the top and bottom SES quintile grew on the scale score but shrank on the ability score (Figure 1).

Many researchers used scale scores anyway (e.g., Condron 2009; Downey et al. 2004; Downey, von Hippel, and Hughes 2008; Reardon 2003; von Hippel 2009). The disadvantages of scale scores were not widely appreciated, and ability scores were not included in early releases of the ECLS-K:1999. Theta scores were included in later releases of the ECLS-K:1999 and in all data releases of the ECLS-K:2011.

We use theta scores in our primary analyses. To confirm fidelity of replication, we also replicated analyses of the older cohort using scale scores. Our results matched the 2004 results closely (Appendix, Tables A2 and A3). The scale scores that we used for our replication were those from the K–1 data release of the ECLS-K:1999−the release that was used for the 2004 article. In later releases, the scale scores changed because the item bank grew larger. The sensitivity of scale scores to the size and characteristics of the item bank is one demonstration that the scale scores are not a pure measure of student ability.

Sample

Each ECLS-K cohort began with a nationally representative probability sample of the US kindergarten population. Both cohort studies used a multistage sample design, sampling children within schools and schools within primary sampling units (PSUs), where each PSU was a large county or a group of adjacent and demographically similar small counties. Both studies were stratified into public and private schools. Both studies oversampled Asian/Pacific Islander children, and the older cohort study oversampled private schools as well. We used sampling weights in our descriptive statistics to compensate for oversampling and nonresponse, but we did not weight our regressions since the weights were correlated with some regressors (Winship and Radbill 1994). We dropped the 3 percent of children who attended year-round schools that stay in session for part of the summer (von Hippel 2016) since our seasonal analysis assumes that summer is a non-school period.

In addition to test scores, the key variables in the analysis are children’s race/ethnicity (six groups), gender, and SES, where SES is defined by the ECLS-K as a weighted average of household income, parents’ education level, and parents’ occupational status. Missing SES values were imputed by the National Center for Education Statistics as part of the ECLS-K release. Replicating the 2004 Great Equalizer study, we averaged SES values across the first two years and standardized the average.

Table 1 summarizes the demographics of the two cohort samples. The samples are similar in size, with few missing values on SES³ and almost none on race and ethnicity. The new cohort has slightly more Asians and many more Hispanics than the older cohort−which makes sense given the high immigration and birth rates of both Hispanic and Asian Americans. Both Asian and Native American children had notably higher SES in the new cohort than the old; in fact, Asian Americans went from having lower SES than white children in the old cohort to having higher SES than white children in the new cohort. While this could be due to the recent influx of highly educated Chinese and Indian immigrants, we should caution that the ECLS-K:2011 user manual reported “operational problems [which] prevented the study from conducting data collection activities in some areas of the country where Asian . . . and American Indian/Alaska Native students sampled for the study resided” (Tourangeau et al. 2017). (Similar problems were not reported for the old ECLS-K:1999.) It is possible that the Asian and Native American samples are not entirely representative in the new cohort.

Table 1.

Sample Demographics.

Race/Ethnicity	1998–2000			2010–2013
	N	Percentage	Mean Socioeconomic Status (standardized)	N	Percentage	Mean Socioeconomic Status (standardized)
Black (non-Hispanic)	2,466	15	−.48	2,350	13	−.39
Hispanic (nonwhite)	2,779	16	−.49	4,404	25	−.57
Asian	1,200	7	.14	1,630	9	.42
Native American	318	2	−.52	167	1	−.32
White	9,733	57	.30	8,376	47	.32
Mixed	401	2	.17	806	5	.17
Total	16,897			17,733

Note: In the older cohort, .3 percent of the analytic sample is missing race and none is missing SES. In the newer cohort, .03 percent of the analytic sample is missing race and 7 percent are missing SES.

English language learners were tested differently in the two cohorts. In the new cohort, all available children took the English reading test, but in the old cohort, it was only given to children who passed an initial screen for English proficiency. So the new cohort includes English reading scores for children who would not have been tested in the old cohort, and this limits the comparability of English language learners, who were predominantly Hispanic and Asian American, across cohorts. This is primarily an issue for the fall kindergarten reading test. It is less of an issue for later reading tests, where fewer students were excluded as English language learners in the older cohort. It is not an issue for the math tests in either cohort.

The 2004 Great Equalizer paper used a complex multiple imputation procedure, but in this replication, we found that imputation was unnecessary, at least for our HLM models, since we can closely replicate the 2004 results using listwise deletion (Appendix, Tables A2 and A3). This is not surprising since listwise deleted estimates are typically similar to multiple imputation estimates when the X variables (i.e., race, ethnicity, gender, SES) are nearly complete and missingness is concentrated among the Y values (here test scores) (von Hippel 2007).

METHODS AND RESULTS

Descriptive Results

Strong and robust patterns are often visible in simple descriptive graphs and tables. For example, in the “Summer Setback” study of Baltimore students in the 1980s, key patterns were plainly visible in a simple graph showing the mean test scores of high- and low-SES students at the beginning and end of each school year (Alexander et al. 2001, 2007; Entwisle and Alexander 1992). The graph appeared to show that low-SES children fell behind high-SES children every summer from first through fifth grades but kept pace during the school years. Though we now know these patterns were distorted by measurement artifacts (von Hippel and Hamrock 2016), they were visually compelling; stylized versions appeared in Time magazine (von Drehle 2010) and became the public face of summer learning loss. They pass the “interocular trauma test”: they hit you between the eyes (Edwards, Lindman, and Savage 1963).

The 2004 Great Equalizer paper included few descriptive results. There was only one graph, and its content was somewhat abstract, showing model-predicted trajectories for different racial and ethnic groups, holding SES constant (Downey et al., 2004, Figure 2). In this section, we will describe our data more transparently, presenting simple descriptive statistics in graphs and tables.

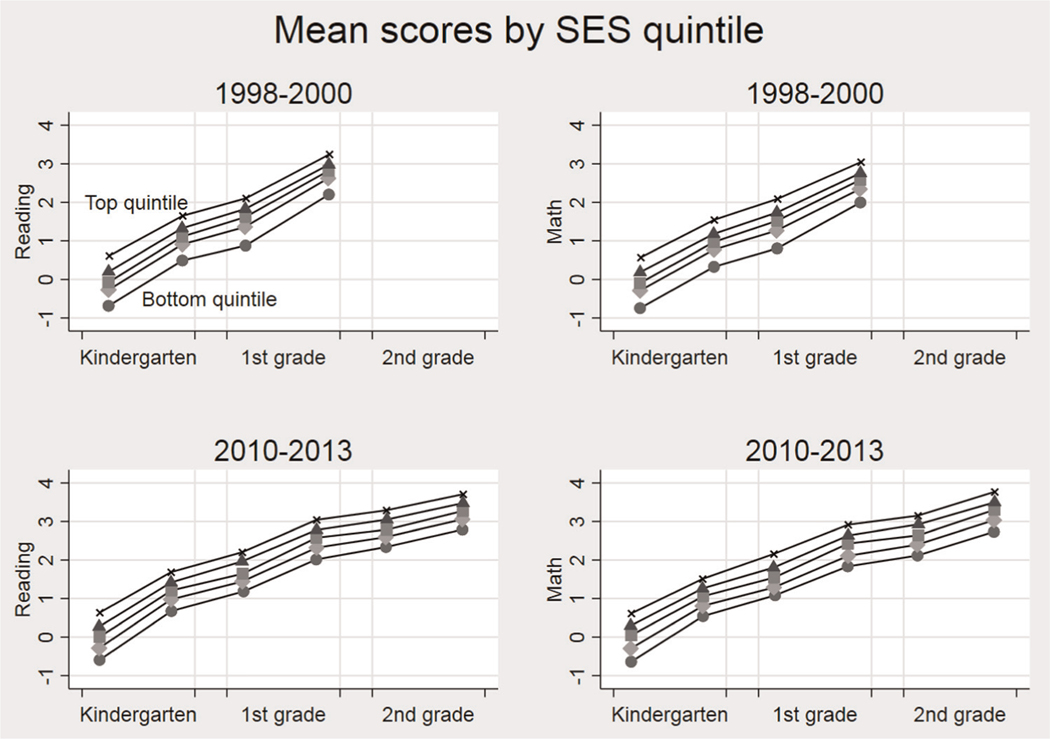
Figure 2.

Mean test scores for children in each quintile of socioeconomic status (SES).

Total variance.

Although most summer learning studies focus on race and SES gaps, it is important to remember that race, ethnicity, gender, and SES explain only about a quarter of the variance in children’s test scores and much less of the variance in learning rates. This implies that children of the same gender, race/ethnicity, and SES can have very different learning environments, especially when they are out of school. We would overlook a substantial part of the inequality story if we imagined that all Hispanic girls’ home environments, for example, were practically the same in their impact on learning.

For that reason, the original Great Equalizer study introduced the idea of examining total test score variance and changes in variance during school and summer. To summarize total variance, Table 2 gives the SD of test scores on each test occasion and the change in the SD (ΔSD) from one test occasion to the next. Table 2 presents the SD of the observed scores and the SD of the “true” scores that would be observed if no measurement error were present. (The true SD is obtained by multiplying the observed SD by the square root of the reliabilities, which are given in Table A1 in the Appendix.)

Table 2.

Standard Deviation (SD) of Test Scores in the Fall and Spring of Each School Year and Change in SD (ΔSD) from One Test Occasion to the Next.

Grade	Season	1998–2000				2010–2013
		Reading		Math		Reading		Math
		SD	ΔSD (percentage)	SD	ΔSD (percentage)	SD	ΔSD (percentage)	SD	ΔSD (percentage)
SD of observed scores
K	Fall	1.00		1.00		1.00		1.00
K	Spring	.97	−3	.96	−4	.92	−8	.83	−17
1	Fall	1.00	3	.98	2	.94	2	.90	9
1	Spring	.88	−12	.87	−11	.89	−5	.92	2
2	Fall					.79	−11	.92	0
2	Spring					.75	−5	.89	−4
SD of true scores (net of measurement error)
K	Fall	.96		.95		.97		.96
K	Spring	.95	−1	.93	−3	.90	−8	.81	−16
1	Fall	.98	3	.95	2	.91	2	.87	8
1	Spring	.86	−12	.85	−11	.86	−6	.89	2
2	Fall					.76	−11	.89	0
2	Spring					.72	−6	.86	−3

Note: If schools are equalizers and summers are disequalizers, then the SD will grow during the summers and shrink (or at least grow more slowly) during the school years. ΔSD values that are consistent with this prediction are bolded; ΔSD values that are inconsistent with the prediction are italicized.

If schools were equalizers, the SD would grow over the summers and shrink (or at least grow more slowly) during the school years. From spring to fall, ΔSD would be positive, but from fall to spring, ΔSD would be negative (or at least would have a smaller positive value).

Most of the ΔSD values follow this pattern, though there are exceptions. Out of 16 ΔSD values, 13 (in bold in Table 2) are consistent with the hypothesis that schools equalize and summers disequalize−but the remaining 3 ΔSD values (in italics in Table 2) are inconsistent with that hypothesis. This is true for the observed SD and for the true SD. During the school years, the SD shrinks in both subjects and all three grades−except for math in first grade. The SD grows in Summer 1 in both cohorts, but in the new cohort, the SD does not grow during Summer 2. Instead, in Summer 2, the SD stays constant in math and actually shrinks in reading.

One pattern that is consistent across cohorts is that the SD shrinks as children get older. By the spring of first grade, the SD is 12 to 14 percent smaller than it was in the fall of kindergarten. By the spring of second grade, the SD is 25 to 28 percent smaller. Most or all of the shrinkage takes place during the school year. This is consistent with the idea that schools reduce inequality.

The shrinking SD of test scores is evident in our results because they use ability scores. Shrinking SDs were not evident in the 2004 Great Equalizer study, which used scale scores whose variance grew, spuriously, with age. Now that we are using ability scores, it seems that the seasonal question should not be: When does inequality grow fastest? It should be: When does inequality shrink?

Race, ethnicity, and SES.

While the total variance patterns are vital, it is also important to examine the variance associated with race/ethnicity and SES. Figure 2 shows mean test scores for children in each quintile of SES. Mean test scores are graphed over mean measurement dates, with vertical reference lines indicating the beginning and end of each school year and summer.

The clearest pattern is that gaps are present in the fall of kindergarten, and gaps do not grow−in fact, they shrink−over the next two or three years. In the old cohort, the reading and math gaps between the top and bottom SES quintile shrink by 20 percent between the fall of kindergarten and the spring of first grade. In the new cohort, between the fall of kindergarten and the spring of second grade. the reading gap between the top and bottom SES quintile shrinks by 25 percent, and the math gap shrinks by 17 percent.

All of the shrinkage in SES gaps occurs during the school years. In some school years, the bottom SES quintile gains on the other quintiles; in some school years, it is the middle quintiles that gain on the top; and in some school years, gaps do not visibly shrink at all. During the summers, by contrast, there is no shrinkage−and, in some summers, growth−in SES gaps. This is most obvious for math in the summer after kindergarten, when children in the top SES quintile continue learning almost as quickly as they did during the school year, while lower-quintile children learn more slowly and fall behind.

Figure 3 presents trends in mean scores for each racial and ethnic group. Here again, the most conspicuous pattern is that gaps are present at the start of kindergarten and grow little−in fact, they mostly shrink−over the next two to three years. In the old cohort, the gap between the highest and lowest scoring racial/ethnic groups shrinks by 13 percent in reading and 23 percent in math between the fall of kindergarten and the spring of first grade. In the new cohort, the gap between the highest and lowest scoring groups shrinks by 41 percent in reading and grows by just 12 percent in math between the fall of kindergarten and spring of second grade.

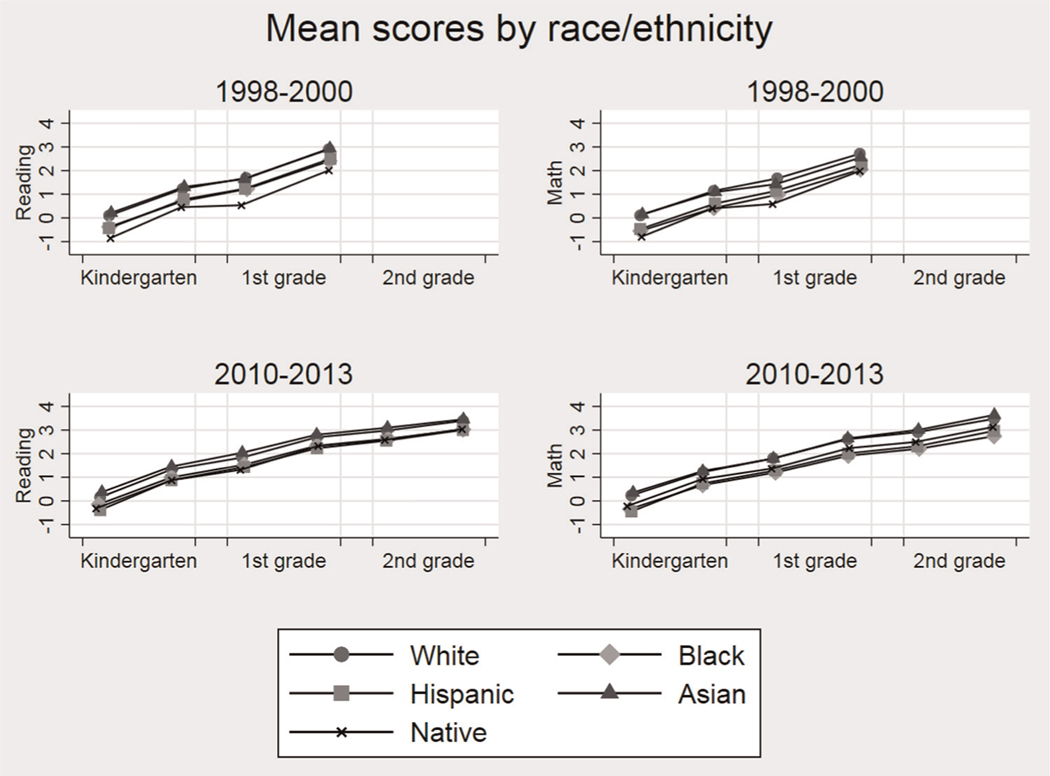
Figure 3.

Mean test scores for children from five different racial/ethnic groups.

Seasonality in racial and ethnic gaps is generally subtle. The only conspicuous exception occurs in the older cohort, where Native American children fall behind during summer in both reading and math. But this pattern does not replicate to the less disadvantaged Native Americans of the new cohort. And there is little visible seasonality in the gaps between other racial and ethnic groups.

We also examined the score gaps between girls and boys, but the results were so simple that we do not need a graph. There was no math gap between boys and girls, and the reading gap, which favored girls, was less than .2 SD. Neither gap changed much after the start of kindergarten, and neither displayed much seasonality.

Overall, the figures do not overwhelm us with evidence that disadvantaged children fall behind during summer. If they do, the tendency is slight and not consistent across subjects, summers, cohorts, or types of disadvantage. When seasonal gap changes exist, most are subtle. You have to squint to see them.

The most consistent pattern in these graphs is not seasonal at all. The most consistent pattern is that gaps are present at the start of kindergarten and change little during later school years and summers. This pattern is clear in our results because the analyses uses IRT ability scores. The pattern was not evident in the original Great Equalizer study because that study used non-interval scale scores that exaggerated gap growth.

Unconditional Growth Model

While our graphs are revealing, they are somewhat limited. They lack estimates of uncertainty (e.g., standard errors and p values), and they give a misleading impression of summer learning. While summer learning occurs in June, July, and August, the graphs compare tests taken in October and May. The October-May period includes over two months of school, and attributing these school months to the summer will exaggerate summer learning.

We address these issues by fitting statistical models that adjust for the difference between the test dates and the first and last days of school. Following the original Great Equalizer study, we estimate a three-level hierarchical linear model. Test scores (Level 1) are nested within children (Level 2), and children are nested within schools (Level 3) (Raudenbush and Bryk 2001). At Level 1, the growth model is

$$\begin{gathered} {\widehat{\text{θ}}}_{sct}={\alpha }_{0sc}+{\alpha }_{1sc}G{0}_{sct}+{\alpha }_{2sc}S{1}_{sct}+{\alpha }_{3sc}G{1}_{sct} \\ +{\alpha }_{4sc}S{2}_{sct}+{\alpha }_{5sc}G{2}_{sct}+e_{sct} \end{gathered}$$ (4)

Here ${\alpha }_{0sc},\dots ,{\alpha }_{3sc}$ are estimated from the kindergarten and first grade tests, which were given to both cohorts, while ${\alpha }_{4sc},{\alpha }_{5sc}$ require second-grade tests that were only given to the later cohort. On occasion $t=1,\dots ,6,Y_{sct}$ is the score of child $c$ in school $s$; $G{0}_{sct},G{1}_{sct},G{2}_{sct}$ are the number of months that the child has been exposed to Grades 0 (kindergarten), 1, and 2; and $S{1}_{sct},S{2}_{sct}$ are the number of months that the child has been exposed to Summers 1 and 2. Exposure to each school grade and summer varies across test occasions and across children. Children were not tested on the first and last days of the school year, nor were all children tested on the same date, and the model accounts for this. For example, on a typical school calendar, a child tested in October of first grade would have $G{0}_{sct}=9.3$ months of exposure to kindergarten, $S{1}_{sct}=2.7$months of exposure to Summer 1, over $G{1}_{sct}=1$ month of exposure to first grade, and no exposure (yet) to later summers or school years. The model implicitly extrapolates beyond the test dates to the scores that would have been achieved on the first and last day of the school year.

The slopes ${\alpha }_{1sc},\dots ,{\alpha }_{5sc}$ are child $c$’s monthly learning rates during each school year and summer. The intercept ${\alpha }_{0sc}$ is the score that would be expected if the child were tested on the first day of kindergarten instead of October, when the first test was most commonly given; since children gain skills during the first months of kindergarten, ${\alpha }_{0sc}$is typically lower than the fall test score. $e_{sct}$is test measurement error, whose variance, which must be fixed to identify the model, can be estimated by multiplying the test score variance by $1-\text{ρ}$, where $\text{ρ}$ is the reliability of test scores. (Reliabilities are reported in the Appendix, Table A1.⁴)

The model assumes that ability grows at a linear rate during each school year and this assumption is untestable in the ECLS-K, which gives only two tests per school year (the minimum needed to identify a linear learning rate). However, other data, where theta-scaled tests were given three times per school year, suggest that learning during the school year is approximately linear (von Hippel and Hamrock 2016).

At Levels 2 and 3, the growth parameter vector ${\mathbf{\alpha }}_{sc}={\left[{\alpha }_{0sc},{\alpha }_{1sc},\dots {\alpha }_{5sc}\right]}^T$ varies across children and schools:

$$\begin{array}{l}{\mathbf{\alpha }}_{sc}=\mathbf{\text{μ}}+{\mathbf{r}}_s+{\mathbf{r}}_c\hfill \\ \left[\begin{array}{l}{\alpha }_{0sc}\hfill \\ {\alpha }_{1sc}\hfill \\ {\alpha }_{2sc}\hfill \\ {\alpha }_{3sc}\hfill \\ {\alpha }_{4sc}\hfill \\ {\alpha }_{5sc}\hfill \end{array}\right]=\left[\begin{array}{l}{\text{μ}}_0\hfill \\ {\text{μ}}_1\hfill \\ {\text{μ}}_2\hfill \\ {\text{μ}}_3\hfill \\ {\text{μ}}_4\hfill \\ {\text{μ}}_5\hfill \end{array}\right]+\left[\begin{array}{l}{r}_{0s}\hfill \\ r_{1s}\hfill \\ r_{2s}\hfill \\ r_{3s}\hfill \\ r_{4s}\hfill \\ r_{5s}\hfill \end{array}\right]+\left[\begin{array}{l}{r}_{0c}\hfill \\ r_{1c}\hfill \\ r_{2c}\hfill \\ r_{3c}\hfill \\ r_{4c}\hfill \\ r_{5c}\hfill \end{array}\right]\hfill \end{array}.$$ (5)

Here $\mathbf{\text{μ}}$ is a parameter vector representing the grand mean of ${\mathbf{\alpha }}_{sc}$, while $r_s$ and $r_c$ are independent random effect vectors representing school-level departures from the grand mean and child-level departures from the school means. These random effect vectors have covariance matrices ${\mathbf{\Sigma }}_s$ and ${\mathbf{\Sigma }}_u$, which represent the variances and covariances among parameters such as initial achievement ${\alpha }_{0sc}$ and kindergarten learning ${\alpha }_{1sc}$.⁵

Estimates.

Table 3 estimates math and reading growth models in the older cohort, and Table 4 estimates them in the new cohort. In both cohorts, average learning rates are much slower during summer vacations than during the school years. Average summer learning rates are near zero. Depending on the summer and cohort, the estimated summer learning rate varies from a gain of .05 SD per month to a loss of −.02 SD per month. Note that learning rates near zero are not well described by popular phrases such as “summer learning loss,” “summer setback,” or “summer slide.” Near zero learning rates would be better described by a phrase like “summer slowdown” or “summer stagnation.”

Table 3.

Mean and Variability of Achievement and Learning Rates, in 1998–2000.

	Mean	Total SD	School Level				Child Level
			SD	Correlations			SD	Correlations
				Initial	Kindergarten	Summer		Initial	Kindergarten	Summer
Reading
Initial points	−.45*** (.019)	1.08*** (.017)	.52*** (.015)				.95*** (.006)
Points per month, kindergarten	.19*** (.001)	.09*** (.001)	.04*** (.001)	−.34***			.08*** (.001)	−.50***
Points per month, summer	.00 (.004)	.13*** (.005)	.05*** (.004)	.26***	−.69***		.12*** (.003)	.16***	−.33***
Points per month, first grade	.18*** (.001)	.06*** (.002)	.03*** (.001)	−.41***	−.09	−.14	.06*** (.001)	−.32***	−.07***	−.24***
Contrast: Summer minus school year average	−.17*** (.004)	.06*** (.005)	.02*** (.004)				.05*** (.003)
Math
Initial points	−.45*** (.019)	1.04*** (.016)	.51*** (.015)				.91*** (.006)
Points per month, kindergarten	.17*** (.001)	.07*** (.001)	.03*** (.001)	−.35***			.06*** (.001)	−.45***
Points per month, summer	.05*** (.004)	.15*** (.006)	.06*** (.004)	.11	−.62***		.13*** (.004)	.12***	−.37***
Points per month, first grade	.15*** (.001)	.06*** (.001)	.02*** (.001)	−.44***	.15*	−.37***	.05*** (.001)	−.31***	.03	−.37***
Contrast: Summer minus school year average	−.10*** (.005)	.07*** (.006)	.03*** (.004)				.07*** (.004)

Note: At both the school level and the child level, learning rates have twice the SD during the summer as the school years. Initial achievement is positively correlated with summer learning but negatively correlated with school year learning. All these patterns are consistent with the idea that schools equalize and summers disequalize.

^*p < .05.

^**p < .01.

^***p < .001. Standard errors in parentheses.

Table 4.

Mean and Variability of Achievement and Learning Rates, in 2010–2013.

	Mean	Total SD	School Level						Child Level
			SD	Correlations					SD	Correlations
				Initial	Kindergarten	Summer 1	First Grade	Summer 2		Initial	Kindergarten	Summer 1	First Grade	Summer 2
Reading
Initial points	−.31*** (.018)	1.04*** (.016)	.47*** (.015)						.93*** (.006)
Points per month
Kindergarten	.20*** (.002)	.09*** (.002)	.04*** (.001)	−.52***					.08*** (.001)	−.50***
Summer 1	−.01* (.005)	.17***(.006)	.10***(.005)	.19**	−.72* **				.15*** (.004)	.24***	−.55***
First grade	.13*** (.002)	.05*** (.002)	.02*** (.002).	−.08	.06	−.38***			.05*** (.001)	−.28***	.06*	−.21 ***
Summer 2	−.02*** (.003)	.09*** (.006)	.04*** (.004)	−.27**	−.17	.47***	−.65***		.08*** (.004)	−.26***	−.15***	.06	−.35***
Second grade	.07*** (.001)	.03*** (.002)	.01*** (.001)	−.25*	.04	−.22	.38**	−.19	.02*** (.001)	−.23***	.06	−.25***	.05	.09
Contrast: Summer average minus school year average	−.15*** (.004)	.11*** (.004)	.06*** (.003)						.08*** (.003)

	Mean	Total SD	School Level						Child Level
			SD	Correlations					SD	Correlations
				Initial	Kindergarten	Summer 1	First Grade	Summer 2		Initial	Kindergarten	Summer 1	First Grade	Summer 2
Math
Initial points	−.27*** (.019)	1.06*** (.016)	.48*** (.015)						.94*** (.006)
Points per month	.17*** (.001)	.07*** (.001)	.04*** (.001)	−.64***					.07*** (.001)	−.64***
Kindergarten
Summer 1	.03*** (.005)	.16*** (.007)	.09*** (.005)	.24***	−.54***				.13*** (.004)	.37***	−.5***
First grade	.12*** (.002)	.05*** (.002)	.02*** (.002)	.14	−.15	−.4***			.04*** (.001)	−.04	.02 −	.29***
Summer 2	−.02*** (.004)	.11*** (.006)	.04*** (.005)	0	−.13	.43***	−.61***		.10*** (.004)	−.03	.08*	−.21***	−.39***
Second grade	.09*** (.001)	.04*** (.002)	.02*** (.002)	−.24**	.18*	−.26*	.04	−.19	.03*** (.001)	−.22***	.08*	−.07	−.06	−.23**
Contrast: Summer average minus school year average	−.12*** (.005)	.09*** (.005)	.06*** (.004)						.07*** (.003)

Note: Learning rates have over twice the SD during summers as during the school years. Initial achievement is positively correlated with kindergarten learning rates but negatively correlated with learning during summer 1. These patterns are consistent with the idea that schools equalize and summers disequalize. After Summer 1, though, the pattern of correlations is not as clear.

^*p < .05.

^**p < .01.

^***p < .001. Standard errors in parentheses.

If schools are equalizers, we would predict that children’s learning rates will be more variable in the summer than during the school years. The results confirm this prediction. In both cohorts and both subjects, the SD of learning rates is about twice as large in each summer as it was in the school year before. This is true for the school-level SD, child-level SD, and total SD, which combines variability across children and schools.⁶ Variability in learning rates is substantial. Even during the school year, when variability is reduced, the total SD of learning rates is one-third to one-half of the mean.

If schools are equalizers, we would also predict that the correlation between learning rates and initial achievement levels will change across seasons. In particular, initial achievement will be negatively correlated with school year learning but positively correlated with summer learning. This pattern of correlations implies that the gaps between initially high- and low-scoring children shrink during the school year but grow during the summer.

Results for the older cohort follow this pattern. Initial achievement has a positive correlation with learning during Summer 1 but a negative correlation with learning during kindergarten and first grade. This is true in both math and reading at both the child level and the school level. This pattern of correlations is similar to the pattern reported in the original Great Equalizer study.

Results for the newer cohort are less clear. Through the first year, the new cohort looks much like the old cohort: Initial achievement is negatively correlated with kindergarten learning but positively correlated with learning during Summer 1. But after Summer 1, the pattern of correlations changes. In reading, initial achievement has about the same correlation with learning during second grade as during Summer 2−and the correlation during Summer 2 is negative, not positive, as we would expect if schools were equalizers.

Conditional Growth Model

In addition to the unconditional growth model, we also fit a conditional growth model that estimated the association between growth rates and children’s race, ethnicity, SES, and gender. Level 1 of the conditional model is the same as it was for the unconditional model (Equation 4). Levels 2 and 3 are also the same except for a vector $X_{sc}$ containing $K$child characteristics, including SES (standardized), a dummy for female gender, and dummies for children of different races and ethnicities (black, Hispanic, etc.):

$$\begin{array}{l}{\mathbf{\alpha }}_{sc}=\mathbf{\text{μ}}+\mathbf{\text{β}}{X}_{sc}+{\mathit{r}}_s+{\mathit{r}}_c\\ \left[\begin{array}{c}{\alpha }_{0sc}\\ {\alpha }_{1sc}\\ {\alpha }_{2sc}\\ {\alpha }_{3sc}\\ {\alpha }_{4sc}\\ {\alpha }_{5sc}\end{array}\right]=\left[\begin{array}{l}{\text{μ}}_0\hfill \\ {\text{μ}}_1\hfill \\ {\text{μ}}_2\hfill \\ {\text{μ}}_3\hfill \\ {\text{μ}}_4\hfill \\ {\text{μ}}_5\hfill \end{array}\right]+\left[\begin{array}{c}{\mathrm{\text{β}}}_{01}{\mathrm{\text{β}}}_{02}\dots {\mathrm{\text{β}}}_{0(K-1)}{\mathrm{\text{β}}}_{0K}\\ {\mathrm{\text{β}}}_{11}{\mathrm{\text{β}}}_{12}\dots {\mathrm{\text{β}}}_{1(K-1)}{\mathrm{\text{β}}}_{1K}\\ {\mathrm{\text{β}}}_{21}{\mathrm{\text{β}}}_{22}\dots {\mathrm{\text{β}}}_{2(K-1)}{\mathrm{\text{β}}}_{2K}\\ {\mathrm{\text{β}}}_{31}{\mathrm{\text{β}}}_{32}\dots {\mathrm{\text{β}}}_{3(K-1)}{\mathrm{\text{β}}}_{3K}\\ {\mathrm{\text{β}}}_{41}{\mathrm{\text{β}}}_{42}\dots {\mathrm{\text{β}}}_{4(K-1)}{\mathrm{\text{β}}}_{4K}\\ {\mathrm{\text{β}}}_{51}{\mathrm{\text{β}}}_{52}\dots {\mathrm{\text{β}}}_{5(K-1)}{\mathrm{\text{β}}}_{5K}\end{array}\right].\\ \left[\begin{array}{c}Black\\ Hispanic\\ \dots \\ Female\\ SES\end{array}\right]+\left[\begin{array}{c}{r}_{0s}\\ r_{1s}\\ r_{2s}\\ r_{3s}\\ r_{4s}\\ r_{5s}\end{array}\right]+\left[\begin{array}{c}{r}_{0c}\\ r_{1c}\\ r_{2c}\\ r_{3c}\\ r_{4c}\\ r_{5c}\end{array}\right]\end{array}$$ (6)

With these characteristics, the intercept $\mathbf{\text{μ}}$ contains the mean growth parameters for non-Hispanic, white, middle-class boys. Then $\mathbf{\text{β}}$ is a matrix whose components represent the expected difference for each growth parameter between girls and boys, children who are black or white (also Hispanic or white, Asian or white, Native American or white), and children whose SES differs by one SD.

Because all child characteristics enter the model at once, they must be interpreted conditionally. The parameter ${\mathrm{\text{β}}}_{01}$, for example, does not represent the start-of-kindergarten gap between black and white children. Instead, it represents the start-of-kindergarten gap between black and white children of the same SES. When SES is held constant, the black-white gap is of course smaller than the difference when SES is not controlled. This distinction should be borne in mind as we interpret the results.

Contrasts.

If schools were equalizers, we would predict that gaps will grow faster (or shrink slower) during summer vacations than during the academic years. To test this prediction, we estimate contrasts between school year and summer learning gaps. For example, in our model, the parameter ${\mathrm{\text{β}}}_{01}$ represents the initial gap between black and white children, while the parameters ${\mathrm{\text{β}}}_{11},{\mathrm{\text{β}}}_{21},{\mathrm{\text{β}}}_{31},{\mathrm{\text{β}}}_{41},{\mathrm{\text{β}}}_{51}$ represent the black-white gap in learning rates during kindergarten, Summer 1, first grade, Summer 2, and second grade. So the question of when gaps grow fastest (or shrink slowest) is addressed by the following contrasts:

• Contrast K–1. The average difference between school and summer learning gaps over the two-year period between grades K and 1 is ${\mathrm{\text{β}}}_{21}-\frac{1}{2}\left({\mathrm{\text{β}}}_{11}+{\mathrm{\text{β}}}_{31}\right)$.

• Contrast 1–2. The average difference over the two-year period between Grades 1 and 2 is ${\mathrm{\text{β}}}_{41}-\frac{1}{2}\left({\mathrm{\text{β}}}_{31}+{\mathrm{\text{β}}}_{51}\right)$.

• Contrast K–2. The average difference over the full three-year period between grades K and 2 is $\frac{1}{2}\left({\mathrm{\text{β}}}_{21}+{\mathrm{\text{β}}}_{41}\right)-\frac{1}{3}\left({\mathrm{\text{β}}}_{11}+{\mathrm{\text{β}}}_{31}+{\mathrm{\text{β}}}_{51}\right)$.

The interpretation of the contrasts depends on the sign of the initial gap. If the initial gap is negative (e.g., the gap ${\mathrm{\text{β}}}_{01}$ between black and white children), then a positive contrast implies that the gap grows faster (or shrinks slower) during the school year. But if the initial gap is positive (e.g., the gap between children of high and low SES), then a positive contrast implies that the gap grows faster (or shrinks slower) during the summers. Since the signs of contrasts can be confusing, we will label each contrast verbally, indicating in words whether a particular gap grows fastest (or shrinks slowest) during the school years or during summer vacations.

Estimates.

Estimates and contrasts for the conditional growth model are given in Tables 5 through 7.

Table 5.

Coefficients from Conditional Growth Model.

	Reading				Math
	1998–2000		2010–2013		1998–2000		2010–2013
	Coefficient	(SE)	Coefficient	(SE)	Coefficient	(SE)	Coefficient	(SE)
Initial points
Reference group	−.47	(.02)	−.32	(.02)	−.36	(.02)	−.32	(.02)
SES	.39***	(.01)	.39***	(.01)	.37***	(.01)	.38***	(.01)
Black	−.17***	(.03)	−.10***	(.03)	−.33***	(.03)	−.29***	(.03)
Hispanic	−.33***	(.03)	−.24***	(.02)	−.36***	(.03)	−.36***	(.02)
Asian	.02	(.04)	.17***	(.03)	−.03	(.04)	.13***	(.03)
Native American	.48***	(.07)	−.19*	(.09)	−.52***	(.07)	−.28**	(.09)
Mixed race	−.10	(.05)	.08*	(.04)	−.16***	(.05)	.01	(.04)
Female	.17***	(.02)	.12***	(.02)	.02	(.02)	.01	(.02)
R2 (percentage)	23		22		23		23
Points per month, kindergarten
Reference group	.18***	(.002)	.20***	(.002)	.17***	(.002)	.17***	(.002)
SES	−.008***	(.001)	−.010***	(.001)	−.007***	(.001)	−.013***	(.001)
Black	−.010***	(.003)	.011***	(.003)	−.011***	(.003)	−.006*	(.003)
Hispanic	.014***	(.003)	.004	(.003)	.009**	(.003)	.019***	(.002)
Asian	.006	(.004)	.000	(.004)	−.002	(.004)	−.006	(.003)
Native American	.016*	(.007)	−.010	(.010)	.026***	(.007)	.018*	(.009)
Mixed race	.008	(.005)	−.004	(.004)	−.002	(.005)	−.004	(.004)
Female	.004*	(.002)	.004*	(.002)	−.004*	(.002)	.000	(.002)
R2 (percentage)	3		3		4		9
Points per month, Summer 1
Reference group	.00	(.005)	−.02**	(.007)	.04***	(.006)	.06***	(.007)
SES	.012***	(.003)	.007*	(.004)	.004	(.003)	.022***	(.004)
Black	.014	(.009)	.022	(.012)	.011	(.010)	−.007	(.013)
Hispanic	−.004	(.008)	.020*	(.009)	−.007	(.009)	−.035***	(.009)
Asian	.018	(.011)	.036**	(.013)	.033**	(.012)	−.030*	(.013)
Native American	−.044*	(.019)	.032	(.026)	−.054*	(.022)	−.034	(.026)
Mixed race	.006	(.014)	.005	(.015)	.004	(.016)	−.013	(.015)
Female	.004	(.005)	−.008	(.006)	.002	(.006)	−.018**	(.006)
R2 (percentage)	2		3		2		9
Points per month, first grade
Reference group	.18***	(.002)	.13***	(.002)	.15***	(.002)	.12***	(.003)
SES	−.008***	(.001)	.000	(.001)	−.004***	(.001)	.000	(.001)
Black	−.002	(.003)	−.007	(.004)	.000	(.003)	−.015***	(.004)
Hispanic	.004	(.003)	−.006*	(.003)	.011**	(.003)	−.002	(.003)
Asian	−.004	(.004)	−.016***	(.004)	−.013**	(.004)	.010*	(.005)
Native American	.006	(.007)	.002	(.009)	.011	(.008)	.013	(.009)
Mixed race	.000	(.005)	−.005	(.005)	.002	(.005)	−.001	(.005)
Female	−.004**	(.002)	.006***	(.002)	−.004*	(.002)	−.006**	(.002)
R2 (percentage)	4		2		4		2
Points per month, Summer 2
Reference group			−.02**	(.005)			−.02*	(.006)
SES			−.017***	(.003)			−.007	(.003)
Black			.006	(.010)			.021	(.011)
Hispanic			.011	(.007)			−.003	(.008)
Asian			.004	(.010)			.007	(.012)
Native American			.016	(.020)			−.019	(.023)
Mixed race			.001	(.013)			.009	(.015)
Female			−.007	(.005)			.000	(.006)
R2 (percentage)			6				6
Points per month, second grade
Reference group			.07***	(.002)			.09***	(.002)
SES			.000	(.001)			−.001	(.001)
Black			−.001	(.003)			−.007	(.004)
Hispanic			.001	(.002)			.008**	(.003)
Asian			−.010**	(.003)			.007	(.004)
Native American			−.007	(.007)			.001	(.008)
Mixed race			.000	(.004)			.000	(.005)
Female			−.001	(.002)			−.001	(.002)
R2 (percentage)			0				0

Note: SEs are robust. SES = socioeconomic status.

^*p < .05.

^**p < .01.

^***p < .001.

Table 7.

Contrasts of Summer Versus School Year Gap Growth in the 2011 Cohort Only: Theta Scores.

Gap	K–1		1–2		K–2
	Contrast (SE)	Gap Grows Faster (shrinks slower) in	Contrast (SE)	Gap Grows Faster (shrinks slower) in	Contrast (SE)	Gap Grows Faster (shrinks slower) in
Reading
SES	.011** (.004)	Summer	−.015*** (.003)	School	−.001 (.003)	NS
Black-white	.028* (.014)	School	.009 (.011)	NS	.018+ (.010)	School
Hispanic-white	.020* (.010)	School	.012+ (.007)	School	.026** (.010)	School
Asian-white	.040** (.013)	Summer	.015 (.012)	NS	.015* (.007)	Summer
Native-white	.034 (.025)	NS	.017 (.023)	NS	.027 (.020)	NS
Female-male	−.012+ (.007)	School	−.009+ (.006)	School	.004 (.013)	NS
Math
SES	.028*** (.005)	Summer	−.006 (.004)	NS	.011** (.004)	Summer
Black-white	.002 (.015)	NS	.031* (.013)	School	.016 (.011)	NS
Hispanic-white	−.043*** (.011)	Summer	−.006 (.010)	NS	−.016*** (.012)	Summer
Asian-white	−.032* (.017)	School	−.001 (.014)	NS	−.027** (.008)	School
Native-white	−.049+ (.026)	Summer	−.026 (.023)	NS	−.037* (.019)	Summer
Female-male	−.015* (.007)	School	.003 (.007)	NS	.000 (.014)	NS

Note: SES = socioeconomic status.

⁺p < .10.

^*p < .05.

^**p < .01.

^***p < .001.

SES gaps.

We begin with SES gaps among children of the same race and ethnicity. At the start of kindergarten, the standardized SES gap is remarkably consistent across cohorts and subjects: a 1 SD advantage in SES is associated with a lead of .37 to .39 SD. In the old cohort, SES gaps shrink during kindergarten, grow during Summer 1, and shrink during first grade−results consistent with the idea that schools are equalizers. In the new cohort, SES gaps also shrink during kindergarten and grow during Summer 1, but then the pattern changes: Reading and math gaps do not change during first or second grade and do not grow during Summer 2 (when math gaps are constant and reading gaps shrink).

In both cohorts and subjects, through kindergarten and Summer 1, all the SES patterns are consistent with the hypothesis that schools are equalizers. But after Summer 1, the results are inconsistent and do not replicate across subjects or cohorts.

When seasonal changes in the SES gap are significant, they are not trivial in size. For example, during kindergarten, the SES coefficient is −.006 to −.013 SD per month−implying that, over the 9.3 months of kindergarten, the initial SES gap shrinks by 17 to 33 percent. If this rate of shrinkage were sustained, SES gaps would close completely in three to six years. In reality, though, gap shrinkage is not sustained into later school years, and gap shrinkage during kindergarten is partly undone by gap growth during Summer 1.

Racial and ethnic gaps.

We continue by reviewing racial and ethnic gaps among children of the same SES. Some gaps are similar across cohorts. At the start of kindergarten, black children lag white children by at least .1 SD in reading and about .3 SD in math, while Hispanic children lag white children by .35 SD in math and .24 to .36 SD in math.

Other gaps differ across cohorts. Native American children start well behind white children of the same SES, but the gap is twice as large in the old cohort (.5 SD) as the new. Asian children start at parity with white children in the old cohort, but in the new cohort, Asian children lead white children by about .15 SD in both subjects.

There is no consistent answer to the question of whether racial/ethnic gaps grow faster in school or out. The seasonal patterns are different for different racial/ethnic groups, and within each group, the patterns often differ across subjects, cohorts, or grades.

We begin with the black-white gap. During kindergarten, the gap between black and white children of the same SES grows slowly, by about .01 SD per month. But during later summers and school years, the gap displays almost no significant changes. (The one exception occurs during first grade, when the gap grows, but only in math and only in the new cohort.) In interpreting these estimates, remember that they apply to black and white children of the same SES. Since black children have lower SES than white children, any opening of the SES-adjusted black-white gap during kindergarten is countered by the closing of the SES gap. If SES were omitted from the model,⁷ estimated kindergarten growth in the black-white gap would be only one-third to one-half as large. This helps explain why Figure 3, which shows gaps that have not been adjusted for SES, gives no visible evidence of the black-white gap growing during kindergarten.

Seasonal patterns in the gap between Hispanic and white children of the same SES are even less consistent. In reading, the gap opens faster during the school year, but in math, the gap opens faster during the summer. Both these patterns are limited to the new cohort; in the old cohort, there was no difference between school and summer gap growth in the Hispanic-white gap.

Seasonal patterns are also inconsistent for the Asian-white gap. In the old cohort, at baseline there was no gap between white and Asian students of the same SES. In the new cohort, Asians start ahead of whites, and the gap grows faster during summer for reading but during school for math. These patterns hold only for grades K–1; afterward, in Grades 1–2, there is no significant difference between school and summer growth of the Asian-white gap.

Seasonal patterns are more consistent for the gap between Native Americans and whites. In the old cohort, both reading and math gaps grew faster during summer than during school. In the new cohort, the gap also grows faster during summer than during school, but only in math, not in reading, and only in Grades K–1, not in Grades 1–2.

A challenge to interpreting racial/ethnic gaps is that the samples of some racial/ethnic groups are not entirely comparable across cohorts. The Asian and Hispanic populations grew and changed between the old cohort and the new, and the new cohort study had operational difficulties sampling from areas with large Asian and Native American populations. Finally, English language learners−who are disproportionately Asian and Hispanic−were given tests of English reading in the new cohort but not the old. For these reasons, when comparing cohorts, it would be conservative not to compare Asians and Native Americans. It would also be conservative to compare Hispanics in math but not in reading.

Explained variance.

Table 5 gives R² values showing how much of the variance is explained by race/ethnicity, gender, and SES. There are separate R² values for scores at the start of kindergarten and for learning rates during each school year and summer.⁸

Race/ethnicity, gender, and SES explain nearly a quarter of the variance in ability at the start of kindergarten, but the same variables explain only 0 to 9 percent of the variance in learning rates during later periods of school and summer. This result has several implications. First, it supports our general conclusion that the bulk of inequality is present at the start of kindergarten and changes little over the next few years. Second, it implies that over three-quarters of the variance in test scores−the bulk of inequality−lies between children of the same race/ethnicity, gender, and SES. Finally, it implies that the random variability of learning rates, as summarized by the child and school random effects, is almost as large for the conditional growth model as for the unconditional model summarized in Tables 3 and 4. That is, net of race/ethnicity, gender, and SES, it remains the case that the variability in learning rates is at least twice as high during summer vacations as during the school years.

A hypothesis motivated by the Great Equalizer narrative might be that race/ethnicity, gender, and SES predict learning rates more strongly during summer vacations than during the academic years. The results do not bear this out. In general, R² values for learning rates are very small, and they are no higher during summer than during school. Summer learning is more variable than school year learning, but little of the variance in summer or school year learning can be explained by race/ethnicity, gender, or SES.

Half-day kindergarten.

Why do SES gaps shrink during kindergarten? One possible reason is that low-SES children are more likely to attend kindergarten for a full day instead of a half day. Table 8 confirms that children attending full-day kindergarten have lower average SES. They are also disproportionately black, and in the new cohort, they are disproportionately Hispanic as well. Given their demographic profile, it is not surprising that full-day kindergarteners have lower average math scores in both cohorts, and lower average reading scores in the new cohort.

Table 8.

Distribution of Full- and Half-day Kindergarten by Race, Ethnicity, and Socioeconomic Status.

	1998–1999		2010–2011
	Full-day	Half-day	Full-day	Half-day
Percentage of children	55	45	83	17
Mean socioeconomic status	.02	.21	−.07	.33
Percentage white	62	74	52	67
Percentage black	18	6	16	4
Percentage Hispanic	13	14	24	17
Percentage Asian	2	3	4	7
Percentage mixed	2	2	4	5
Mean reading, fall kindergarten	.00	.00	−.02	.08
Mean math, fall kindergarten	−.03	.04	−.03	.13

Table 8 also shows that participation in full-day kindergarten increased substantially between the two cohorts. In 1998–99, 55 percent of children attended full-day kindergarten; by 2010–11, this had risen to 82 percent. The potential of full-day kindergarten to reduce gaps may be decreasing as it becomes more nearly universal. In addition, full-day kindergarten probably cannot explain why black children, who are overrepresented in full-day kindergarten, fall further behind white children of the same SES during the kindergarten year.

Table 9 reports how much the kindergarten coefficients change when we add a dummy for full-day kindergarten to Level 2 of our multilevel growth model. The coefficients change very little−by just .000 to .002, or just 0 to 2 thousandths of an SD per month. The changes are in the expected direction−the coefficient for SES gets smaller, and the coefficient for black race gets bigger−but the changes are miniscule, suggesting that the distribution of full-day kindergarten does very little to explain why gaps change during kindergarten. The coefficient for full-day kindergarten itself is more substantial, at .015 SD per month in reading and .012 in math, consistent with other findings that full-day kindergarten increases learning, though some of the benefit fades after kindergarten (Cooper et al. 2010).

Table 9.

How Much Do Kindergarten Coefficients Change When the Model Adds Full-day Kindergarten?

Points per Month, Kindergarten	Reading						Math
	1998–2000			2010–2013			1998–2000			2010–2013
	Coefficient	(SE)	Change in Coefficient (vs. Table 5)	Coefficient	(SE)	Change in Coefficient (vs. Table 5)	Coefficient	(SE)	Change in Coefficient (vs. Table 5)	Coefficient	(SE)	Change in Coefficient (vs. Table 5)
Reference group	.174***	(.002)		.184***	(.004)		.164***	(.002)		.159***	(.003)
SES	−.008***	(.001)	.000	−.009***	(.001)	.000	−.006***	(.001)	.001	−.013***	(.001)	.001
Black	−.012***	(.003)	−.002	−.013***	(.004)	−.002	−.012***	(.003)	−.001	−.007*	(.003)	−.001
Hispanic	.013***	(.003)	−.001	.004	(.003)	.001	.008**	(.004)	−.001	.019***	(.003)	.000
Asian	.008	(.004)	.002	−.001	(.004)	−.001	−.002	(.003)	.000	−.006	(.003)	.000
Native American	.015*	(.007)	−.001	−.011	(.008)	−.001	.025***	(.007)	−.001	.019**	(.007)	.001
Mixed race	.007	(.005)	−.001	−.004	(.004)	.000	−.001	(.005)	.001	−.005	(.003)	−.001
Female	.003*	(.002)	−.001	.004*	(.002)	.000	−.004*	(.002)	.000	.000	(.001)	.000
Full-day kindergarten	.015***	(.003)		.015***	(.004)		.012***	(.002)		.012***	(.003)

Note: SEs are robust. Change represents the difference between the coefficients here and those in Table 5. SES = socioeconomic status.

^*p < .05.

^**p < .01.

^***p < .001

DISCUSSION: WHAT’S NEW?

What changed in our replication? Which conclusions of the original Great Equalizer study stood up to replication and which collapsed?

The biggest change relates to total change in inequality after the start of kindergarten. In the original Great Equalizer study, the SD of reading and math scores at least doubled between the fall of kindergarten and spring of first grade−and SES, racial, and ethnic gaps grew commensurately. But this was an artifact of the scale scores used in that study, which lacked the vertical interval scaling needed to compare inequality at different ages. In our replication, which uses ability scores with a more plausible claim to vertical interval scaling, we find that the SD and most score gaps actually shrink after the fall of kindergarten, typically by about 20 percent over two to three years. Practically all of the inequality that we observe at the end of first or second grade was already present at the start of kindergarten. That is why we titled this article “Inequality in Reading and Math Skills Forms Mainly before Kindergarten.”

Although our replication finds relatively little change in inequality after the start of kindergarten, some of the seasonal patterns in inequality are similar to those observed in the original study. In the original study, the total variance of learning rates was greater during summer than during the school years. In the replication, this is still true. The total variance of test scores grows during most summer vacations and actually shrinks during most school years. So both the original study and the replication found that schools reduced total inequality relative to the inequality growth that was observed over the summer−but the replication has an even stronger finding: schools reduce inequality absolutely in the sense that total variance shrinks during the school year.

In the original study, SES gaps grew during both school and summer, at least in reading, but gap growth in the summer was faster. In the replication, SES gaps grew during the first summer vacation and shrank or held steady in the kindergarten and first grade school years. Again, both the original study and the replication suggest that schools tend to make children of different SES more equal than they are out of school, but only the replication suggests that gaps actually shrink during the school year.

The black-white results replicated only partly. In the original study, the black-white math and reading gaps grew faster during the school year than summer vacation. But in the replication, using data from the original cohort, there was very little growth in the black-white gap overall. To the degree that the black-white gap grew, in the replication it remained the case that most of the gap growth occurred during school−but only in reading, not in math.

Some patterns for other ethnic groups changed more. In the original study, it appeared that the Asian-white gap grew fastest during summer in both reading and math. But in the replication, using data from the original cohort, the Asian-white reading gap grew fastest during the school year, and the Asian-white math gap displayed no seasonality at all. In the original study, there was no seasonality in the gap between whites and Native Americans. But in the replication, using data from the original cohort, Native Americans clearly fell behind in the summer and caught up in the school year. In the original study, there was no seasonality in the Hispanic-white gap, and that remained the case in the replication, at least in the original cohort.

The replication includes a new cohort, and we can ask whether patterns in the new cohort resemble those in the original cohort. Some do. In the new cohort, it remains the case that total variance and SES gaps shrink with age, and it remains the case that most of the shrinkage takes place during the school years rather than summer vacations. Patterns for the black-white gap also replicate in the new cohort, but most patterns for other ethnic groups do not. It is complicated to compare ethnic groups across cohorts. The Hispanic and Asian populations changed substantially due to immigration, and the survey team had operational difficulties sampling Asians and Native Americans in the new cohort but not the old. In addition, English language learners took English reading tests in the new cohort but not the old. Finally, the scores are not aligned between cohorts, so we cannot ask whether there is more inequality in the new cohort or the old.

The new cohort has data for an additional grade, so we can ask whether patterns from kindergarten and first grade replicate in second grade and whether patterns from the first summer replicate in the second. The seasonal patterns do not replicate. After first grade, there is hardly any seasonality−in fact, there is hardly any change in gaps between groups defined by SES or race/ethnicity during school or summer. But that means that the more important pattern does replicate to second grade: Inequality does not grow.

Our results overlap and extend those presented by Quinn et al. (2016). They analyzed ECLS-K:2011 data from kindergarten through second grade and, like us, found mixed results. They noted that compensatory patterns are most evident during the kindergarten year but then attenuate in later years. They also found that schools are more compensatory with respect to math than reading. Finally, Quinn et al. distinguished between inequality measured by whether one group gained more skills (on an interval-level scale) between Times 1 and 2 and the relative position of one group versus another. The two approaches can produce somewhat different results when the variances change over time, and they found that schools’ compensatory power was more evident when analyzing skill gaps versus changes in relative position.

Our study differs from Quinn et al. (2016) in two important ways. Most importantly, we emphasize the magnitude of inequality at kindergarten entry. While testing whether achievement gaps increase faster when school is out versus in is important for understanding schools’ theoretical role, the practical reality is that nearly all of the inequality “action” occurs prior to school entry. Second, once we focus on how schools matter, we supplement our study of achievement gaps with a more inclusive analysis of overall variance. Studying achievement gaps across social groups runs the risk of overlooking important heterogeneity within social categories. For example, we would miss a substantial part of the inequality story if we imagined that all Hispanic girls’ home environments were practically the same in their impact on learning. Analyzing overall variance moves us away from this limited view of inequality and allows us to assess schools’ influence more comprehensively.

CONCLUSION

Our results suggest that inequality in basic reading and math skill originates mainly in early childhood, before kindergarten begins. We find that total variance in reading and math scores−and most score gaps associated with SES and race/ethnicity−do not grow and often shrink over the two to three school years after the start of kindergarten.

Some readers may shrug at these results, claiming that we already knew cognitive inequality came from early childhood. This is true in a sense, but we also “knew” some things that turn out not to be true. As discussed in the introduction, it is widely believed that schools contribute substantially to inequality in cognitive skills−yet our results provide little support for this narrative. To the contrary, we find that the standard deviation of reading and math scores typically shrinks during the kindergarten, first grade, and second grade school years. SES gaps also shrink during kindergarten and either shrink or hold steady during first and second grades. Racial and ethnic gaps display inconsistent patterns across subjects and years but in general are no more likely to grow than shrink. Gender gaps in reading and math are miniscule and change hardly at all during the school years.

These observations put a certain frame around studies that estimate the effect on inequality of individual school resources, such as funding, class size, teacher quality, teacher expectations, or ability grouping. Some studies find that a particular resource contributes very little to inequality, either because the resource is distributed equitably or because the resource has little effect. Such findings are easy to reconcile with our finding that schools contribute little to inequality. Other studies, however, suggest that a particular school resource, such as teacher quality or class size, contributes substantially to inequality. These studies are harder to reconcile with our findings. One possibility is that the estimated effects of some unequally distributed resources are biased in some studies. Another possibility is that the inequality-producing effects of some resources are counterbalanced by the inequality-reducing effects of other resources, which are less studied (Downey and Condron 2016). One inequality-reducing resource is the fact that black and low-SES children are more likely to attend kindergarten for a full day rather than just half the day. But in our analyses, full-day kindergarten explains very little of the tendency for kindergarten to reduce SES gaps. It may be that the low to moderate level of the kindergarten curriculum helps reduce gaps because it exposes disadvantaged children to skills and concepts that are new to them but familiar to more advantaged children. While this is good from the perspective of reducing inequality, it also implies that many advanced children are not being challenged in kindergarten.

Another idea challenged by our results is the notion that inequality in cognitive skills grows substantially during summer vacation. To be sure, we do find that SES gaps grow during Summer 1, as does the total variance in test scores. This finding is directionally interesting since it contrasts with the shrinkage of variance and SES gaps during the kindergarten school years. But the growth in inequality during Summer 1 is small, and no growth in inequality is observed during Summer 2. Gaps associated with race and ethnicity display inconsistent summer patterns, with most changing little during summer or during school.

Whether gaps appear to grow or shrink depends heavily on how reading and math skills are measured. Some past results suggesting that inequality grows substantially during summer−or during the school year−were distorted by measurement artifacts (von Hippel and Hamrock 2016). The 2004 Great Equalizer study is one example. It scored reading and math with a non-interval scale, which made it appear that score gaps grew dramatically from kindergarten through first grade. This replication shows that the apparent gap growth in the Great Equalizer study was an artifact of scaling. When we measure reading and math ability with something closer to a vertical interval scale, gaps grow very little. While the contrast between school and summer still suggests that schools do something to equalize children, the amount of equalization now seems rather small compared to the inequality that exists at the start of kindergarten.

Our results, though nationally representative, are limited to reading and math skills, and limited to the period from kindergarten through second grade. Results elsewhere, using a variety of data sets, suggest that reading and math gaps continue to change little through eighth grade (von Hippel and Hamrock 2016). Yet it may be that schools exacerbate inequality in more advanced skills, particularly in the later years when the curriculum differentiates and the tasks required of advanced students become more complex and harder to measure with tests. In addition, schools may exacerbate socioeconomic gaps in college enrollment (Jennings et al. 2015), perhaps by offering high-SES high school students more guidance in applying to college.

When it comes to gaps in elementary reading and math skills, though, there is something to the old Jesuit maxim, “Give me a child until he is seven, and I will show you the man” (quoted in Apted 1964). In fact, it appears that the bulk of inequality in reading and math skills is present by the time children are five, and this is true for girls as well as for boys.

The finding that inequality comes mainly from early childhood does not mean that nothing can be done to reduce inequality later. The KIPP and Harlem Children’s Zone charter schools, for example, cut achievement gaps in half during the three years of middle school (Dobbie and Fryer 2009; Tuttle et al. 2015), but they do this in part by substantially increasing the time that children spend in school and reducing the time they spend at home and elsewhere. The success of these programs supports the view that school exposure can be a great equalizer. Summer and after school programs for low-achieving students can also reduce achievement gaps, provided they are well attended and offer enough time for learning (Borman and Dowling 2006; Borman, Goetz, and Dowling 2009; Lauer et al. 2006; Matsudaira 2008). However, the success of summer programs does not necessarily mean that without summer programs disadvantaged children will fall further behind during summer. Our results suggest that summer gap growth is minimal, but summers still offer lower-achieving students a chance to catch up when higher-achieving students are taking a breather.

Sociologists of education have put greater effort into the question of how schools influence inequality than into the broader question of why children are unequal in general. Our study highlights the risk of a school-centric approach, which may distort our understanding of what causes gaps and what we might do to reduce them. Heckman (2008:290) argues that “the longer society waits to intervene in the life cycle of a disadvantaged child, the more costly it is to remediate disadvantage.” By the time kindergarten begins, gaps have already emerged, and later school or summer interventions must be viewed as remediating gaps rather than preventing them. It might be more cost-effective to reduce inequality between children, and between parents, before kindergarten begins.

Table 6.

Contrasts of Summer Versus School Year Gap Growth in Grades K–1.

Gap	1998–2000		2010–2013
	Contrast (SE)	Gap Grows Faster (shrinks slower) in	Contrast (SE)	Gap Grows Faster (shrinks slower) in
Reading
SES	.020*** (.002)	Summer	.013** (.004)	Summer
Black-white	.022* (.005)	School	.031* (.013)	School
Hispanic-white	−.012 (.005)	NS	.022* (.009)	School
Asian-white	.018 (.007)	NS	.043** (.012)	Summer
Native-white	−.056* (.011)	Summer	.036 (.022)	NS
Female-male	.004 (.003)	NS	−.014+ (.006)	School
Math
SES	.009** (.004)	Summer	.028*** (.005)	Summer
Black-white	.015 (.012)	NS	.002 (.015)	NS
Hispanic-white	−.015 (.012)	NS	−.043*** (.011)	Summer
Asian-white	.041** (.013)	School	−.032* (.017)	School
Native-white	−.072** (.028)	Summer	−.049+ (.026)	Summer
Female-male	.007 (.006)	NS	−.015* (.007)	School

Note: SES = socioeconomic status.

⁺p < .10.

^*p < .05.

^**p < .01.

^***p < .001.

Author Biographies

Paul T. von Hippel is an associate professor at the LBJ School of Public Affairs, University of Texas, Austin.

Joseph Workman is an assistant professor in the Department of Sociology at the University of Missouri, Kansas City.

Douglas B. Downey is a professor in the Department of Sociology at the Ohio State University, Columbus. Downey and von Hippel were coauthors, with Beckett Broh, of the original “Great Equalizer” study in 2004.

APPENDIX

Table A1.

Dates and Reliabilities of Tests, with Dates for the Start and End of Each School Year.

		1998–2000				2010–2013
		Dates		Test Reliability		Dates		Test Reliability
		Mean	SD (days)	Reading	Math	Mean	SD (days)	Reading	Math
Kindergarten	School starts	August 25, 1998	10			August 25, 2010	10
	Fall test	October 30, 1998	17	.92	.95	October 14, 2010	27	.91	.92
	Spring test	May 4, 1999	16	.95	.95	April 6, 2011	22	.93	.94
	School ends	June 5, 1999	11			June 6, 2011	11
First grade	School starts	August 24, 1999	10			August 24, 2011	10
	Fall test	October 9, 1999	16	.96	.95	October 12, 2011	24	.94	.93
	Spring test	May 4, 2000	18	.96	.93	April 6, 2012	23	.94	.93
	School ends	June 3, 2000	11			June 4, 2012	11
Second grade	School starts					August 24, 2012	9
	Fall test				.93	September 29, 2012	23		.92
	Spring test				.91	August 10, 2013	19		.94
	School ends					June 5, 2013	10

Note: Approximately 90 percent of the variance in test dates lies between schools, and 10 percent lies between children within schools.

Table A2.

Using the K–1 Reading Scale Scores ThatWere Available in 2004,We Approximately Replicate the Results of Model 1 from Downey, von Hippel, and Broh (2004, Table 2).

	Mean	School Level				Child Level
		SD	Correlations			SD	Correlations
			Initial Points	Kindergarten Gains	Summer Gains		Initial Points	Kindergarten Gains	Summer Gains
Downey et al. (2004)
Initial points	19.34***	3.83***				7.47***
	1.65***	.38***	.16***			.78***	−.08***
Points per month, summer	−.01	.57***	.38***	−.32***		1.52***	.18***	−.06*
Points per month, first grade	2.52***	.43***	.12*	−.04	−.23**	.94***	−.12***	−.08***	−.30***
Replication
Initial points	19.40***	3.77***				7.43***
Points per month kindergarten	1.63***	.38***	.16***			.75***	−.06***
Points per month, summer	.01	.56***	.37***	−.31***		1.54***	.17***	−.04
Points per month, first grade	2.49***	.40***	.07	−.07	−.24*	.96***	−.13***	−.06***	−.34***

Note: Standard errors were not displayed in Downey et al. (2004).

^*p < .05.

^**p < .01.

^***p < .001.

Table A3.

Using the K–1 Reading Scale Scores That Were Available in 2004, We Approximately Replicate the Coefficients from Model 2 in Downey, von Hippel, and Broh (2004, Table 3).

	Downey et al. (2004)	Replication
Initial points
Reference group	19.29***	19.23***
SES	2.92***	2.97***
Asian	.70*	.65*
Black	−.86***	−.89***
Hispanic	−2.09***	−2.16***
Mixed	−.59	−.55
Native	−2.30***	−3.04***
Female	.99***	1.04***
Points per month, kindergarten Reference group	1.61***	1.60***
SES	.07***	.07***
Asian	.13**	.10*
Black	−.15***	−.16***
Hispanic	.02	.02
Mixed	.05	.05
Native	−.02	−.02
Female	.11***	.10***
Points per month, Summer 1 Reference group	−.08	−.07
SES	.16***	.17***
Asian	.41**	.35*
Black	.13	.13
Hispanic	.08	.04
Mixed	.05	.14
Native	−.09	−.23
Female	.06	.06
Points per month, first grade Reference group	2.57***	2.52***
SES	.05**	.04**
Asian	−.17**	−.08
Black	−.19***	−.17***
Hispanic	−.13**	−.08*
Mixed	−.06	−.06
Native	−.10	−.24*
Female	.03	.05*

Note: Standard errors were not displayed in Downey et al. (2004). SES = socioeconomic status.

^*p < .05.

^**p < .01.

^***p < .001.