SABER: Statistical Identification of Loci of Interest in GWAS Summary Statistics using a Bayesian Gaussian Mixture Model

Abstract

Genome-wide association studies (GWAS) remain a popular method for identifying novel genetic associations with human phenotypes and have provided many insights into the etiology of many diseases. However, GWAS provide limited support for how a genetic association might contribute to disease due to inherent limitations, such as linkage disequilibrium. As such, many methods that operate on GWAS summary statistics have been developed to generate evidence for functional pathways or for variants of interest, but they require defining the genomic region bounds for loci of interest. At present, there are limited methods for determining these bounds in a rigorous, reproducible way. We present a novel statistical method, Statistical Analysis for Bayesian Estimation of Regions (SABER), that uses Bayesian Gaussian mixture models to reproducibly generate ratios that quantify whether particular genomic positions represent the bounds of loci of interest and can be used to delineate genomic regions for downstream analyses.

1. Introduction

1.1. Genome-Wide Association Studies and Limitations

Genome-wide association studies (GWAS) are a popular method for analyzing the association of genetic variations or alterations with disease or other human phenotypes¹. Their popularity exploded with the advent of consortium science (of many people working together across continents) and with the increasing affordability of genetic sequencing technologies².

However, GWAS do not provide insight into the functional mechanism by which a genetic mutation or variant can contribute to disease - they can only offer support for an association without any evidence for how that association occurs^3,4. This is problematic as it makes it difficult to identify actionable variants, understand molecular underpinnings of disease, or, in the long term, target pathways or mutations with medications or other therapies.

Furthermore, GWAS is, at its core, a method that essentially performs independent association tests of every variant with the phenotype⁵. Most GWAS methods, even to the present day, test these associations entirely independently; however, the assumption that genetic variants are independent of each other is not concomitant with actual human biology⁶. Many genetic variants are inherited with each other, in an observed mechanism called linkage disequilibrium that results from recombination (shuffling of variants between parental chromosomes) not occurring uniformly across the genome^7,8.

This means that a variant that is linked to a causal or functional variant may be mistakenly identified as causing disease, when in reality it is merely likely to be inherited alongside the true causal variant⁹. Generally, variants that are close to each other are likely to be inherited together (though there are exceptions to this rule), which leads to an abundance of signals that may or may not truly be actionable or useful. These often occur in genomic regions (“loci”) called “recombination hotspots”, within which multiple variants may be shown to have a significant association if any one does^10,11.

1.2. Post-GWAS Analyses and Requirements

As such, people have developed downstream analysis methods that make use of GWAS results to try to identify specific causal variants or identify the functional underpinnings of their effect on disease within these loci. These are often referred to as “Post-GWAS Analyses” and include things such as genomic colocalization analyses, fine-mapping, Mendelian randomization, and meta-analyses, among many others¹². However, many of these analyses require users to define the bounds of specific regions of the genome that they would like to assess, and these bounds can have quite significant impacts on the results of these downstream analyses.

For example, some commonly-used tools such as eCAVIAR and HyPrColoc rely on predefined genomic regions to operate on for the purposes of performing colocalization analyses, and the bounds of these loci can often affect the results due to the inclusion or exclusion of specific single nucleotide polymorphisms (SNPs)^13,14. In fine-mapping, many methods compute credible sets for causal variants for specific loci, and the bounds of such loci are important as including additional variants can greatly increase the search space of credible sets to consider^15,16.

However, there remains a lack of rigorous methods for defining and identifying the genomic regions that contain multiple significant variants from summary statistics alone. Often, very basic thresholding after accounting for multiple testing is used to identify significant variants, and then regions containing many variants are often selected based on arbitrary windows (such as 500 kilobases¹⁷ or 1 megabase¹⁸). This has many issues, including the loss of variants that may be causal and detectable in downstream analyses but not significant in the GWAS due to low sample sizes. Conversely, if a region is defined in an overly inclusive way, then many variants that are irrelevant may be included, reducing the power of downstream analyses. Ultimately, this leads to poor reproducibility due to a lack of standardization on window sizes or how to select regions.

This has become increasingly problematic as GWAS protocols develop, particularly as meta-analyses and consortium science become increasingly popular. In these cases, often only summary statistic-level data can be provided due to data sharing limitations, making it difficult to rely on metrics obtainable only from genotype data such as linkage disequilibrium calculations. This is often further complicated by the increased inclusion of multiple different ancestry groups and individuals of admixed ancestry into studies, as while this provides substantial improvements in power and understanding, genomic structures can vary from population to population, leading to different rates of linkage disequilibrium and differences in observed recombination hotspots^11,19,20.

There thus exists a current and growing need for more rigorous and reproducible methods for selecting regions of interest from GWAS summary statistics. This project proposes one such method using Bayesian Gaussian mixture models, called Statistical Analysis of Bayesian Estimation of Regions (SABER), that allows the computation of a quantitative metric associated with each position in the genome representing the likelihood of that region being the start or end of a significant locus.

2. Methods

2.1. Data Acquisition and Generation

To evaluate the proposed novel method, Statistical Analysis of Bayesian Estimation of Regions (SABER), and its ability to identify genomic region bounds for some loci of interest, we obtained publicly available summary statistics from two large genome-wide association studies.

2.1.1. GIANT Consortium Human Height GWAS/Meta-Analysis

One set of summary statistics was sourced from the GIANT Consortium from their 2022 study by Yengo et al. that presented a saturated map of common variants for human height²¹. They performed a meta-analysis on 5,380,080 individuals to produce summary statistics for 1,377,305 unique variants, and they report the loci that they identified in their meta-analysis in their Supplementary Table 12. The resulting summary statistics and identified loci corresponding to the final analysis across all populations were used in this paper for evaluation (summary statistics downloaded from https://www.joelhirschhornlab.org/giant-consortium-results).

2.1.2. UKBB Osteoarthritis GWAS

Another set of summary statistics was acquired from the 2019 study by Tachmazidou et al. that performed a GWAS for arthritis in the UK BioBank¹⁸. They analyzed four phenotypes relating to osteoarthritis including knee, hip, combined knee/hip, and any osteoarthritis on 77,052 cases and 378,169 controls across over 17 million variants. The summary statistics from the analysis for hip osteoarthritis GWAS, downloaded from the NHGRI-EBI GWAS Catalog²² (study accession ID: GCST007091; PubMed ID: 30664745), were used for evaluation.

2.2. Bayesian Gaussian Mixture Model

2.2.1. Theoretical Framework

Statistical Analysis of Bayesian Estimation of Regions (SABER) uses a two-component Bayesian (multivariate) Gaussian mixture model to fit the data using the absolute value of the BETA values and the P values of each variant as features. To improve convergence and efficiency, a user-specified significance threshold is used to subsample the data to include only variants that meet this threshold and a randomly sampled, equal number of variants that failed to meet the threshold, providing an approximate 50/50 ratio of significant to insignificant variants for the fitting process. Three different initializations of the component centroids were used in the fitting process and the best-fitting resultant model is used in later steps.

Each (Gaussian) component of the resulting model is intended to represent different aspects of the data: generally, one component represents the “insignificant” variants (those with no association with the phenotype) and the other component represents the “significant” variants (those that are associated with the phenotype). Note that in practice the centroids of these Gaussians do not necessarily perfectly line up with such definitions due to the relative infrequency of “significant” variants for most genome-wide association studies.

In principle with this mixture model, individual variants are modeled as having been generated from one or the other component based on whether they are “significant” or “insignificant”, and as such, it is possible to compute the relative probability of whether a particular data point was generated from one component or the other by using the probability density function for a multivariate normal distribution:

$$p(y\mid \mu ,\Sigma )=\frac{\exp \left(-\frac{1}{2}{(y-\mu )}^T{\Sigma }^{-1}(y-\mu )\right)}{\sqrt{{(2\pi )}^k\left|\Sigma \right|}}$$

for a data point y and component defined by mean μ and covariance ∑. The values of μ and ∑ for each component are determined by the Bayesian Gaussian Mixture model fitting process.

2.2.2. Code Implementation

To implement SABER, we used the BayesianGaussianMixture model in the scikit-learn Python package (version 1.3.0)²³ using Python 3.8.3 with some default parameters (such as a Dirichlet prior and a full covariance matrix computation). Certain parameters were modified to improve performance, including increasing the number of initializations (n_init) to 3 to increase the likelihood of model parameter convergence and changing the BayesianGaussianMixture default initialization of the parameters of the components (init_params) to use k-means++ instead of k-means to encourage initial parameter estimates to be increasingly distinct.

The model was then fit using scikit-learn’s standard procedure using the per-variant BETA absolute value (ABS(BETA)) and p-values (P) as previously described. The predict_proba function in scikit-learn was subsequently used with the fitted model to compute the relative densities for every data point, scaled to be probabilities of assignment to each component, and the component that ostensibly generated a higher number of variants was assigned as the majority, “insignificant” component, relying on the assumption that the vast majority of variants in any given GWAS are insignificant.

2.3. Position-Based Analysis

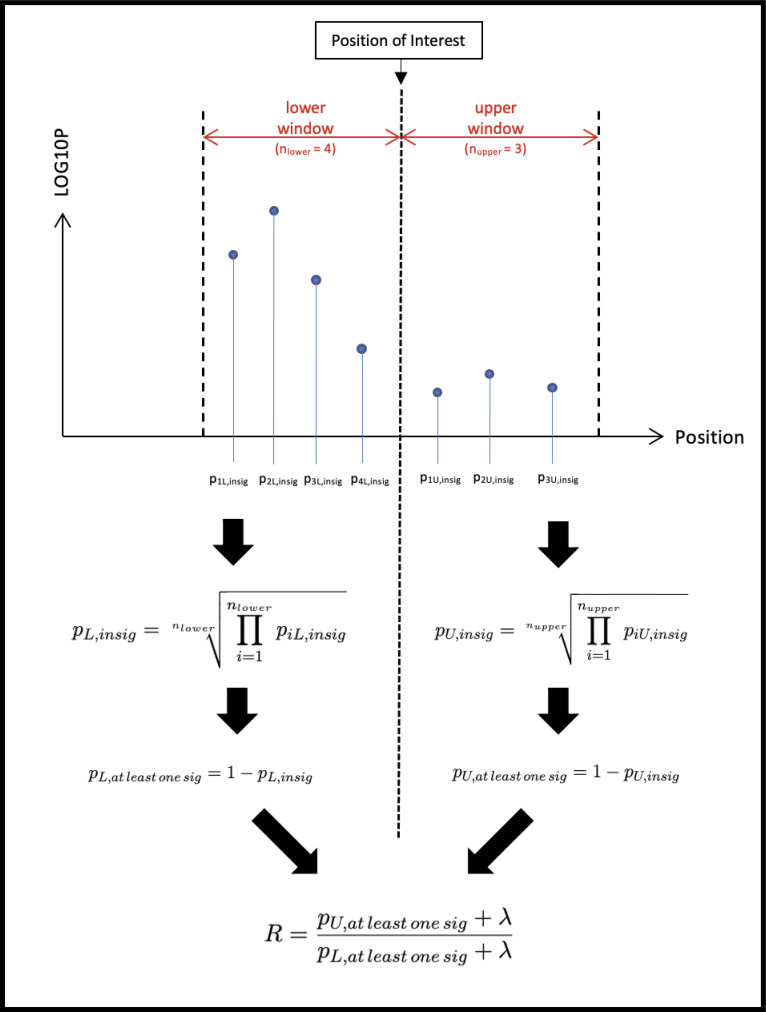
After fitting the data to the Bayesian Gaussian mixture model and computing component-based probabilities for every variant as above, a secondary processing step was performed to get positional information within chromosomes that would be useful in determining the bounds of loci. First, at each position within each chromosome, two sets of variants were identified: an “upper” set, consisting of variants within a window that fell subsequent to the position, and a “lower” set, consisting of variants within a window of the same size that fell prior to the position (with any variants at the position itself being included in the “upper” set). The user-defined window for looking forward and backward position-wise in this study was implemented as a user-definable parameter and was defined for each dataset based on memory limits. Figure 1 below illustrates how windows were defined.

Figure 1.

A visual description of the computations done to calculate positional ratios. The log (base e) of the ratio R (log(R)) is used in subsequent plotting. λ here refers to a regularization factor that helps provide a soft constraint to the values of the log ratio and is usually set to 1e-8.

Subsequently, the computed probabilities of each set containing only variants belonging to the “insignificant component” as computed using scikit-learn’s predict_proba function was found by taking the geometric mean of all of the corresponding variant “insignificant” component probabilities. The geometric mean was taken to avoid imbalances in subsequent calculations due to differences in the number of variants in each set. The complement of the resulting value represents the probability that at least one variant belongs to the “significant” component (that is, 1 - the probability that every variant belongs to the “insignificant” component).

To reduce issues associated with floating point precision for ratios that are extremely large or extremely small, a small regularization factor of 1e-8 was added to the complement probabilities computed for the upper and lower sets. A ratio of these regularized complement probabilities between the upper and lower sets was then computed, representing a ratio of the likelihood that the position in question represented the boundary of a significant locus. The natural log of this ratio was used for plotting and computing of relative bound predictions. A visual representation of this computation process can be found below in Figure 1.

A positive value of the log-ratio implies that the upper set is more likely to have a significant variant than the lower set, while a negative value of the log-ratio indicates the opposite. Values close to zero represent limited differences between the upper and lower sets, while higher-magnitude values indicate increased differences in the enrichment of significant variants.

2.4. Evaluation

We evaluated our method on two real-world GWAS datasets, for which the summary statistics are publicly available, as described in Section 2.1. As there is a limited “ground truth” to validate this model against, we identified several loci with bounds that were demarcated by this method and found the corresponding loci in the studies. We then compared our results qualitatively to these loci to determine whether the bounds identified differed from those in the studies, indicating that our approach might potentially be able to refine the boundaries in question. In particular, we focused on loci that were defined in relatively simple ways (such as by taking a window centered on a lead variant) as these are the most likely to benefit from increased rigor in how such loci are defined for downstream analyses.

3. Results

Results with a ratio-calculating window size of 100KB from the GIANT Consortium human height GWAS²¹ for two regions with a high density of significant SNPs on chromosome 22 can be seen in Figure 2. To compare, we identified whether these regions corresponded to defined loci within the study; note that in this study, many loci were defined by simply selecting 35KB around lead SNPs, and so many bounds are rudimentary.

Figure 2.

Examples from the GIANT Consortium’s GWAS of human height on chromosome 22, showing loci with genome-wide significant variants (cutoff p=5e-8, denoted by the green vertical highlights), variants that met the ratio computation threshold (cutoff p=1e-5, denoted by the yellow vertical highlights), and their respective ratios (plotted in blue) with red vertical highlights of positions with ratios that fall outside the 90% interval for all nonzero positional ratios within the chromosome.

The first of these two images shows a region that corresponds to the 7151:METAFE locus in the study and provides a potentially more refined boundary for this locus as compared to the study definition of a 70 kilobase (KB) region (35634441-35704441) centered on the lead SNP. The second of these two images has a region (the one that is centered, as opposed to the one offset to the left) that corresponds with the 7158:METAFE locus that was defined in the same way - as a 70KB region centered on the lead SNP (37061927-37131927). However, as the image shows, the region in question may actually be wider than thought, encompassing a region closer to ~37000000-37200000, over double the size of the nominal locus defined in the original study²¹.

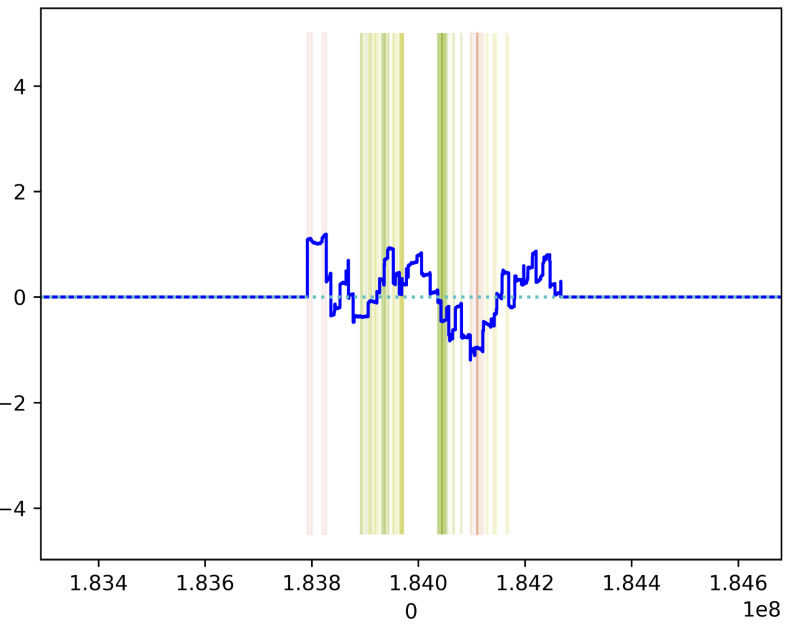
We further evaluated our approach on the UKBB Osteoarthritis GWAS¹⁸, also using a ratio-calculating window size of 100KB on one region on chromosome 1. The corresponding figure can be seen in Figure 3. To compare, we found the lead SNP from the study that corresponded to this region, which has an accession of rs11583641 (chromosome 1, position 183937111, mapped to gene COLGALT2; position identical in GRCh38 and GRCh37). The apparent bounds of the locus around this variant as defined by SABER are not definitive, likely due to there being a relatively smaller density of significant variants in this region as compared to the GIANT GWAS, but possible bounds could be reasonably inferred as 183800000 to 184100000 from the ratio computations and considering the ratios outside the inner 90% interval of all nonzero ratios as possibly boundary locations.

Figure 3.

Example from the GWAS of hip osteoarthritis performed in the UK BioBank on chromosome 1, showing loci with genome-wide significant variants (cutoff p=5e-8, denoted by the green vertical highlights), variants that met the ratio computation threshold (cutoff p=1e-5, denoted by the yellow vertical highlights), and their respective ratios (plotted in blue) with red vertical highlights of positions with ratios that fall outside the 90% interval for all nonzero positional ratios within the chromosome. This particular locus corresponds to a lead SNP identified in the study (rs11583641).

Per the original study, for downstream analyses they used methods that simply take a 1MB region around the lead variant, which in this case would be 183437111 to 184437111, a much wider region that likely includes several other variants that may modify the results of downstream analyses. This particular variant mapped to a gene COLGALT2 that was found to be highly implicated as a result of their downstream analyses and was found to be a novel finding, further lending credence to the possibility that locus boundary refinement could improve or modify results in these circumstances¹⁸.

3.1. Tool Availability and Parameters

The SABER approach described in this paper has been made available in the form of a tool with ongoing development that can be found at a GitHub repository at https://github.com/rachitk/bayesian-mixture-gwas. The tool is very lightweight, requiring just four primary and publicly available Python packages and their dependencies: pandas (to load and parse the data), scikit-learn (to construct and fit the model), numpy (to perform certain mathematical operations), and matplotlib (to plot the data). The primary user-facing script is found in bmm_code.py, which can be run in a terminal by executing it with Python (`python bmm_code.py [parameters]`). The tool was designed to be highly user-configurable through command-line options.

Several command-line parameters have been provided for users to modify various hyperparameters of the tool, and the primary ones of interest are described below:

• --window: determines the size of the window in bases to look forward and backward at each position (default is 100KB, or 100000) for the computation of the ratios.

• --chr: allows the user to select a specific chromosome to analyze (default is all chromosomes, denoted by a value of -1). Note that all variants in the data file provided are candidates for fitting the model, not just the ones on a selected chromosome.

• --sig-thresh: allows the user to define the genome-wide significance threshold if they should choose (default is 5x10^-8). Used for identifying “significant variants” for the mixture model fitting and for highlighting positions of significant SNPs in green, as seen in the results images.

• --ratio-cutoff: allows the user to select the interval outside which they would like ratios to be highlighted. The default is 90% (meaning that any ratios that fall outside the inner 90% interval of ratios will be highlighted in red, as seen in the results images).

• --[beta/p/chr/pos]-col: these arguments allow users to define the names of the columns that correspond to these values in their dataset and are included to support GWAS summary statistics from a wide variety of tools and harmonization approaches, many of which have differing column names.

• --out-dir: the directory where results should be saved. Individual chromosome data will be saved in subfolders of this directory.

Additionally, several modifying parameters are made available:

• --no-filtered-fit: disables the filtering done before fitting the BMM (default behavior is to filter the set of variants used to fit the BMM model to only significant variants and an equal number of randomly sampled “insignificant” variants, determined by the --sig-thresh argument). This can be useful for data where there are a very large number of significant variants already, but it is generally not recommended.

• --ratio-regularization: allows the user to set the value that is used for regularization/constraining of the ratios computed to avoid computing the log of infinity or the log of 0, which can occur indirectly due to computational precision limits. By default, this is 1e-8.

• --ratio-thresh: allows one to set the p-value threshold for selecting variants around which ratios are computed (separate from the significance threshold --sig-thresh). This will determine the number of positions for which ratios are computed (which will essentially be the window around all variants that meet this threshold). These variants will also be highlighted in yellow in the final plots. The default is a nominal threshold of 1e-5. Positions not included by this method will be given a default value of 0.

• --out-per-sig: a toggle that allows the user to decide whether they would like plots that are windowed around every significant variant determined by --sig-thresh (with adjacent variants having their visual windows fused).

• --out-per-ratio-thresh: a toggle that allows the user to decide whether they would like plots that are windowed around every variant that was used as an index for ratio computation, determined by --ratio-thresh (with adjacent variants having their visual windows fused).

• --seed: a value that can be passed by the user for reproducibility, both in the random sampling of the data done for fitting and in the actual fitting process itself. By default, this is 9 (as such, two runs of the tool without setting the seed should produce the same result).

The tool’s primary outputs are the actual computed ratios, which are placed into chromosome-specific directories located at the user-specified output location in the form of CSV files. These CSV files can be used to plot the ratios as an overlay on standard Manhattan plots or on top of other tools such as LocusZoom and can also be accessed directly to identify cutoff points for loci of interest.

4. Discussion

This tool provides a more statistically rigorous method for identifying the boundaries surrounding significant loci from GWAS summary statistics whilst redefining the bounds of significant loci, rather than relying on user-selected windows, which can lead to bias in downstream analyses. This is particularly important for fine mapping, colocalization, and Mendelian randomization, all of which assess predefined regions of the genome. There is presently little standardization regarding the definition of these regions, which can lead to significantly different results depending on the window sizes selected by researchers. This can result in biasing the results towards certain variants while missing others that may be deemed causal in functional analyses but undetected due to window size. This is a critical issue, as analyses such as fine-mapping and colocalization are often used in functionally validating statistically significant genome or transcriptome associations and should not be subject to such bias. SABER yields a more systematic and reproducible way of identifying these bounds, which should lead to less bias in these types of studies.

The model relies on there being a “critical mass” of significant variants across the whole genome, as the fitting procedure of the two components may otherwise not converge to good values or may find a local minimum. As such, the model may not perform optimally on GWAS with very low numbers of SNPs or very low sample sizes, as there would not be enough significant variants under a predefined significance threshold to fit the model, even with the corresponding downsampling of insignificant variants. Some of the present limitations of SABER include its reliance on there being a high density of SNPs in regions of interest; the multiplicative computation means that a region containing only a small number of significant SNPs may not generate a substantial shift in the ratio compared to one with no significant SNPs. Furthermore, an individual SNP may not always be recognized as significant by the “significant” component of the mixture model, even if it truly is significant, though this is unlikely to occur as the number of significant SNPs in a region increases. This means that ratios are far more reliable for regions containing many significant SNPs. Additionally, due to the fitting of the model using the absolute value of the BETA and p-values as features, the GMM may have difficulty assigning variants to a particular component - in particular, variants that were found on association to have a low BETA value are more likely to be identified as insignificant, even if they have a low p-value as well.

Improvements to the speed of the tool will be explored in future work, as will providing a better understanding of the hyperparameters of the BGMM - namely the window size and significance thresholds and how these impact the results of SABER and the ratios computed. Furthermore, at present, SABER cannot handle multiallelic variants that share the same position due to computational assumptions relating to positional uniqueness that were made to improve the speed of ratio computation, and at present the tool simply drops such multiallelic variants before performing the analysis. Future directions may include support for the handling of multiallelic variants through an alternative computation of the ratios when such variants are desired for inclusion.

Moreover, there is a need to evaluate the impact of SABER in improving downstream analyses such as colocalization or fine-mapping. While the tool was shown to identify regions that corresponded to defined loci in real GWAS and worked to refine the boundaries of some regions, as shown, the impact of refining the boundaries of the regions identified on downstream analyses could not be explored in this paper. As there are several different methods that make use of user-defined window sizes, SABER has the potential to impact a wide range of analysis techniques by refining the definition of loci that such methods use in determining causal variants. Future directions would include performing colocalization, fine-mapping, and Mendelian randomization studies, and measuring the improvements in performance of these functional analyses.

Ultimately, SABER provides a new statistically rigorous method for identifying the boundaries of genomic regions from GWAS summary statistics alone by using Bayesian mixture models. This represents an improvement to the current state of the field, which currently consists of studies identifying such regions for downstream post-GWAS analyses in a variety of ways that often leads to poor reproducibility out of necessity, including defining preset windows of sizes that may vary from study to study. SABER will thus further enable consortium science, especially in circumstances where only summary-level data can be shared for collaborations, and it will enable and encourage greater reproducibility across GWAS and post-GWAS analyses.