PFERM: A Fair Empirical Risk Minimization Approach with Prior Knowledge

Abstract

Fairness is crucial in machine learning to prevent bias based on sensitive attributes in classifier predictions. However, the pursuit of strict fairness often sacrifices accuracy, particularly when significant prevalence disparities exist among groups, making classifiers less practical. For example, Alzheimer’s disease (AD) is more prevalent in women than men, making equal treatment inequitable for females. Accounting for prevalence ratios among groups is essential for fair decision-making. In this paper, we introduce prior knowledge for fairness, which incorporates prevalence ratio information into the fairness constraint within the Empirical Risk Minimization (ERM) framework. We develop the Prior-knowledge-guided Fair ERM (PFERM) framework, aiming to minimize expected risk within a specified function class while adhering to a prior-knowledge-guided fairness constraint. This approach strikes a flexible balance between accuracy and fairness. Empirical results confirm its effectiveness in preserving fairness without compromising accuracy.

Introduction

Fairness is a critical concern in machine learning (ML), particularly in high-impact domains such as healthcare, finance, and criminal justice [1, 2, 3]. In these fields, ML models often make decisions with significant consequences for individuals’ lives, necessitating fairness to prevent discrimination against specific groups. While there is no universal definition of fairness in ML, two common criteria are frequently used: Demographic Parity and Equalized Odds. Demographic Parity [4, 5, 6] requires that a model’s predicted scores be independent of an individual’s protected attribute, such as race or gender. This means that the model should not make different predictions for people with the same characteristics but different races or genders. On the other hand, Equalized Odds [2, 3] demands that the model’s positive predictive value (PPV) be consistent across all groups, ensuring unbiased predictions for all races or genders. Both criteria are crucial, but their suitability depends on the specific context. For instance, if one group is more likely to be positive than another, Demographic Parity may not be the best choice, making Equalized Odds more appropriate. The choice of fairness criterion should be carefully considered based on the application and relevant fairness concerns.

However, different groups often have varying prevalence ratios (positive rates), and enforcing strict fairness can significantly harm accuracy [7]. For example, research has shown that Alzheimer’s disease (AD) is more prevalent in women than in men. In the age group 65-69 years, 0.7% of women and 0.6% of men have the disease, with increasing frequencies of 14.2% and 8.8% in individuals aged 85-89 years [8]. It would be fairer for each individual if females had a higher chance of treatment. Specifically, when the disease status is unknown for both females and males, we hope the classifier assigns a higher positive rate to females instead of providing the same predictive score. This way, females have a better chance of getting treated based on classification results.

The question at hand is: How many additional predictive scores should we allocate to females? This decision can be guided by the prevalence ratio among different groups. For instance, if the prevalence ratio indicates that females have a 2% chance of having AD, while males have a 1% chance, it means that females are twice as likely to have AD as males. It is imperative that we incorporate this information, which we refer to as prior knowledge, into the fairness constraint.

In this paper, we incorporate this prior knowledge into the fairness constraint for Empirical Risk Minimization (ERM). We empirically demonstrate that as the gap in the prevalence ratio between two groups widens, a typical ERM framework with a fairness constraint like FERM [5] severely sacrifices accuracy. To address this issue, we define the ratio of the positive rate of one group to the other as the prior knowledge π. We develop a Prior-knowledge-guided Fair ERM (PFERM) framework that aims to minimize expected risk within a prescribed function class while adhering to a prior-knowledge-guided fairness constraint. Due to the non-convex nature of the PFERM constraint, we propose a surrogate convex PFERM problem, related to the original goal of minimizing misclassification error under a relaxed fairness constraint. As a specific example within this framework, we explain how kernel methods such as support vector machines (SVMs) can be enhanced to satisfy the prior-knowledge-guided fairness constraint. We observe that a specific instance of the fairness constraint, when ϵ = 0, reduces to an orthogonality constraint. To enhance flexibility, we introduce a trade-off parameter λ to fine-tune the incorporation of prior knowledge into the fairness constraint. Extensive empirical results on synthetic and real data validate the effectiveness of our proposed method.

Our contributions can be summarized as follows:

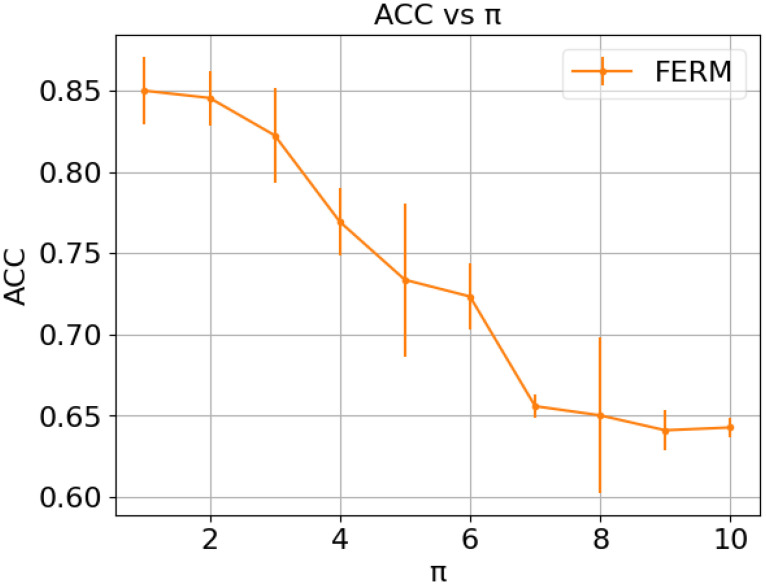
• Empirical Evidence of Prevalence Ratio Impact: Our empirical analysis vividly illustrates the profound impact of widening prevalence ratios between two protected groups on the performance of the FERM [5] framework. We systematically examine how increasing disparity between these ratios, denoted as π, correlates with a substantial degradation in accuracy, highlighting the real-world implications of this phenomenon. See Figure 1 for an illustration.

• Prior-knowledge-guided Fair ERM: To address the challenges posed by varying prevalence ratios, we introduce the Prior-knowledge-guided Fair ERM (PFERM) framework. Within this new framework, we develop a concrete algorithm tailored for SVMs that effectively incorporates prior knowledge to guide fairness constraints. This enhancement allows for a more nuanced and adaptive approach to fairness-aware classification.

• Empirical Validation Across Diverse Data Sources: We have performed a comprehensive evaluation of the PFERM method using a diverse set of datasets, encompassing ten synthetic datasets, four benchmark datasets, and three AD datasets. The empirical results not only confirm the effectiveness of our approach in preserving fairness without compromising accuracy but also underscore its robustness and applicability across various settings.

Figure 1:

Accuracy (ACC) versus π for FERM [5] on synthetic data. Here, π represents the ratio of the positive rate between one group and another group as defined in Eq. (2). Larger values of π result in a significant decrease in accuracy.

Preliminary

Notations

For any integer n ≥ 1, let [n] := {1, … , n}. We denote the data by D = {(x₁, s₁, y₁), … , (x_n, s_n, y_n)}, which consists of n samples drawn independently from an unknown probability distribution µ over X × S × Y. Here, Y = {-1, +1} represents the set of binary output labels, S = {a, b} indicates group membership among two groups (e.g., a for “female” and b for “male”), and X is the input space. It is worth noting that x ∈ X can either include or exclude the sensitive attribute s ∈ S. We also denote the data from group g as D^g = {(x_i, s_i, y_i) : s_i = g} for g ∈ {a, b} and n^g = |D_g |, where | · | denote the cardinality of the set. Similarly, data from both group g and the positive class are denoted as D^g,+ = {(x_i, s_i, y_i) : s_i = g, y_i = 1}, and n^g,+ = |Dg,+|.

Consider a model $f:X\to ℝ$ chosen from a set of possible models . The error (risk) of distribution f in approximating µ is measured using a predefined loss function $\ell :ℝ\times y\to ℝ$. The risk of f is defined as L(f ) = E[ℓ(f (x, y))]. The primary objective of a learning process is to discover a model that minimizes this risk. Typically, we employ the empirical risk $\widehat{L}(f)=\widehat{\text{E}}[\ell (f(x,y))]$ as a surrogate for the true risk since the real risk cannot be computed due to the unknown probability distribution µ. This approach is commonly referred to as ERM.

As previously mentioned, the literature offers various definitions of model fairness [1, 2, 3], yet consensus on the most suitable definition remains elusive. In this paper, we explore a comprehensive fairness concept that incorporates previous definitions, as outlined below.

Definition 1 [5] Let $L^{+,g}(f)=\text{E}[\ell (f(x),y)|y-1,s=g]$ represent the risk of positive labeled samples in the g-th group, and let $\epsilon \in [0,1]$. We define a function f as ϵ-fair if $|L^{+,a}(f)-L^{+,b}(f)|\le \epsilon$.

This definition signifies that a model is fair when it demonstrates roughly equal error rates on the positive class, irrespective of group membership. In simpler terms, the conditional risk L^+,g remains relatively consistent across both groups.

Fairness Definitions

The literature presents a range of fairness definitions [1, 2, 3], yet achieving a consensus on the most suitable definition remains a challenge [6]. In this paper, we focus primarily on two widely adopted notions: Demographic Parity [4] and Equalized Odds [2].

Demographic Parity (DP): This condition posits that the model’s predicted score should be independent of group membership, and it can be formally expressed as:

$$\text{P}\{f(x)>0|s=a\}=\text{P}\{f(x)>0|s=b\}.$$ (DP)

Demographic Parity, in essence, focuses on ensuring that different groups receive similar treatment, irrespective of their attributes. While it provides a straightforward and intuitive notion of fairness, it may not always be the most suitable choice, especially when there are substantial disparities in the prevalence of outcomes among groups. In addition, we derive the difference of DP (DDP) as a fairness measurement

$$\text{P}\{f(x)>0|s=a\}-\text{P}\{f(x)>0|s=b\}.$$ (DDP)

Equalized Odds (EO): This condition asserts that the model’s output should be uncorrelated with group membership, conditioned on the label being positive. In other words, it stipulates that the true positive rate should be the same across all groups, and it can be mathematically formulated as follows:

$$\text{P}\{f(x)>0|y=1,s=a\}=\text{P}\{f(x)>0|y=1,s=b\}.$$ (EO)

Equalized Odds goes a step further by ensuring that not only are groups treated equally in terms of predicted outcomes, but also in terms of predictive accuracy. It aims to eliminate disparities in false positives and false negatives among different groups. However, achieving Equalized Odds can be challenging, especially when the prevalence of positive cases varies significantly between groups. The difference of EO (DEO) is derived as

$$\text{P}\{f(x)>0|y=1,s=a\}-\text{P}\{f(x)>0|y=1,s=b\}.$$ (DEO)

Fair Empirical Risk Minimization

Fair Risk Minimization (FRM) [5] endeavors to minimize risk while adhering to a fairness constraint. Specifically, FRM formulates the problem as follows:

$$\min L(f):f\in F\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}sub.\hspace{0.17em}to\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}|L^{a,+}(f)-L^{b,+}(f)|\le \epsilon ,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\epsilon \in [0,1].$$ (1)

Here, ϵ ∈ [0, 1] represents the acceptable level of unfairness and $L^{a,+}(f)-L^{b,+}(f)$ are defined in Definition 1.

However, since the groundtruth distribution µ is typically unknown, deterministic risks are replaced with their empirical counterparts called Fair ERM (FERM). Thus, Problem (1) becomes:

$$\text{min\hspace{0.17em}}\widehat{L}(f):f\in F\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}sub.\hspace{0.17em}to\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}|{\widehat{L}}^{a,+}(f)-{\widehat{L}}^{b,+}(f)|\le \widehat{\epsilon },\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\widehat{\epsilon }\in [0,1].$$ (FERM)

FERM aims to make the risk of different groups with respect to the positive class equal or closely related. However, when ${\widehat{L}}^{a,+}$ and ${\widehat{L}}^{b,+}$ differ significantly, enforcing strict fairness can harm the overall performance. To address this issue, we incorporate the ratio of the prevalence (proportion of positive samples) between two groups, known as prior knowledge, into the fairness constraint. However, when considering this prior knowledge, we no longer consider the condition on the positive class. For instance, even if females have a higher risk of developing AD than males in ADNI data, the sensitivity (true positive rate) can be the same for both genders. Given an equal number of males and females with AD, we expect our fair classifier to correctly classify the same number of females and males, resulting in an equivalent true positive rate for both genders. On the other hand, when dealing with individuals whose disease status is not revealed, we hope the classifier predicts a higher positive rate for females, providing them with more opportunities for treatment. This higher positive rate can be guided by the ratio of prevalence between the two groups. We denote this prior knowledge as π, calculated as follows:

$$\pi =\frac{n^{a,+}/n^a}{n^{b,+}/n^b}.$$ (2)

With this prior knowledge, our PFERM (Prior-knowledge-guided FERM) can be formulated as follows:

$$\min \widehat{L}(f):f\in F\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}sub.\hspace{0.17em}to\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}|{\widehat{L}}_l^a(f)-\pi \times {\widehat{L}}_l^b(f)|\le \widehat{\epsilon },\widehat{\epsilon }\in [0,1],\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\pi =\frac{n^{a,+}/n^a}{n^{b,+}/n^b}.$$ (PFERM)

Note that (PFERM) is a challenging nonconvex, nonsmooth problem, and it is more convenient to solve a convex relaxation problem. Thus, we replace the hard loss in the risk with a convex loss function ℓ_c (e.g., the Hinge loss ℓ_c = max{0,ℓ_l} where ℓ_l is a linear loss) and the hard loss in the constraint with the linear loss ℓ_l. This way, we can solve the convex PFERM problem as follows:

$$\text{min\hspace{0.17em}}{\widehat{L}}_c(f):f\in F\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}sub.\hspace{0.17em}to\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}|{\widehat{L}}_l^a(f)-\pi \times {\widehat{L}}_l^b(f)|\le \widehat{\epsilon },\widehat{\epsilon }\in [0,1],\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\pi =\frac{n^{a,+}/n^a}{n^{b,+}/n^b}.$$

Proposed Method

We assume that the underlying space of models for our PFERM is a reproducing kernel Hilbert space (RKHS). We denote $\kappa :\chi \times \chi \to ℝ$ as a positive definite kernel and $\varphi :\chi \to \text{H}$ as an induced feature mapping, such that $\kappa (x,x\text{'})=〈\varphi (x),\varphi (x\text{'})〉$ for all $x,x\text{'}\in \chi$, where H represents the Hilbert space of square summable sequences. Functions in the RKHS can be parametrized as follows:

$$f(x)=〈w,\varphi (x)〉,x\in \chi ,$$ (3)

where $w\in \text{H}$ is a vector of parameters. For simplicity, we omit the bias term here, but it can be handled by adding an extra feature with a constant value of 1; see [5] for further discussions on (3).

Let u_g be the barycenter in the feature space for group g ∈ {a, b}, defined as:

$$u_g=\frac{1}{n^g}{\displaystyle \sum _{i\in {\mathcal{I}}^g}\varphi (x_i),}$$ (4)

where ${\mathcal{I}}^g=\{i\in [n]:s_i=g\}$.

Using (4), we can express the constraint in (PFERM) as $\left|〈w,u_a-\pi \times u_b〉\right|\le \epsilon$. In practice, we solve the Tikhonov regularization problem:

$$\underset{w\in \text{H}}{\min }{\displaystyle \sum _{i=1}^n\mathcal{l}(〈w,\varphi (x_i)〉,y_i)+\gamma \left|\right|w\left|{|}^2\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}subj.\hspace{0.17em}to\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\right|〈w,u〉}|\le \epsilon ,$$ (5)

where u = u_a − π × u_b, and γ is a positive trade-off parameter controlling model complexity.

When ϵ = 0, the constraint in Eq. (5) reduces to an orthogonality constraint, which has a geometric interpretation. It requires the vector w to be orthogonal to the vector formed by the difference between the scaled barycenters of the input samples in the two groups.

By the representer theorem [9], the solution to Problem (5) is a linear combination of the feature vectors ϕ(x₁), … , ϕ(x_n) and the vector u. In our case, u itself is a linear combination of the feature vectors. Therefore, w is a linear combination of the input points, i.e., $w={\displaystyle {\sum }_{-=1}^n{\alpha }_i\varphi (x_i)}$. The corresponding prediction function is given by $f(x)={\displaystyle {\sum }_{-=1}^n{\alpha }_i\kappa (x_i,x)}$. Let K the Gram matrix, and the vector of coefficients α can be found by solving:

$${\min }_{\alpha \in {ℝ}^n}{\displaystyle \sum _{i=1}^n\mathcal{l}}\left({\displaystyle \sum _{j=1}^n{K}_{ij}}{\alpha }_j,y_i\right)+\gamma {\displaystyle \sum _{i,j=1}^n{\alpha }_i}{\alpha }_j{K}_{ij}\text{\hspace{1em} subj. to \hspace{1em}}\left|{\displaystyle \sum _{i=1}^n{\alpha }_i}\left[\frac{1}{n^a}{\displaystyle \sum _{j\in {\mathcal{I}}^a}{K}_{ij}}-\frac{\pi }{n^b}{\displaystyle \sum _{j\in {\mathcal{I}}^b}{K}_{ij}}\right]\right|\le ϵ\text{. }$$ (6)

To enhance the algorithm’s flexibility, we introduce a trade-off parameter λ [0, 1] to control the incorporation of prior knowledge. If λ = 0, it implies full utilization of prior knowledge, and if λ = 1, it will change back to Eq. (6).

$$\underset{\alpha \in {ℝ}^n}{\min }{\displaystyle \sum _{i=1}^n\mathcal{l}}\left({\displaystyle \sum _{j=1}^n{K}_{ij}}{\alpha }_j,y_i\right)+\gamma {\displaystyle \sum _{i,j=1}^n{\alpha }_i}{\alpha }_j{K}_{ij}\text{\hspace{1em} subj. to \hspace{1em}}\left|{\displaystyle \sum _{i=1}^n{\alpha }_i}\left[\frac{1}{n^a}{\displaystyle \sum _{j\in {\mathcal{I}}^a}{K}_{ij}}-\frac{(1-\lambda )\pi +\lambda }{n^b}{\displaystyle \sum _{j\in {\mathcal{I}}^b}{K}_{ij}}\right]\right|\le ϵ\text{. }$$

Experiments

Datasets and Settings

In our experiment, we use ten synthetic datasets, four benchmark datasets, and three AD datasets.

The synthetic datasets are generated by multivariate Gaussian distributions with specific means and variances. Each sample is a two-dimensional vector following these distributions:

$$\begin{array}{l}{x}^{a,+}~\aleph ([-1,-1],\text{\hspace{0.17em}diag\hspace{0.17em}}([0.8,0.8])),x^{a,-}~\aleph ([1,1],\text{\hspace{0.17em}diag\hspace{0.17em}}([0.8,0.8])),\\ x^{b,+}~\aleph ([0.5,0.5],\text{\hspace{0.17em}diag\hspace{0.17em}}([0.5,0.5])),x^{b,-}~\aleph ([0.5,0.5],\text{\hspace{0.17em}diag\hspace{0.17em}}([0.5,0.5])).\end{array}$$

Here, x^a,+ represents a sample from group a and the positive class. Similar interpretations apply to the other sample notations. “diag([0.8,0.8])” denotes transforming the vector [0.8, 0.8] into a 2-by-2 diagonal matrix with a diagonal of [0.8,0.8]. In group a, we set the number of negative samples to be 200, while the number of positive samples is π × 200. In group b, the number of positive samples is set to be 200, and the number of negative samples is π × 200. This ensures that $\frac{n^{a,+}/n^a}{n^{b,+}/n^b}=\pi$. We generate ten synthetic datasets by varying π as an integer from 1 to 10.

Four benchmark datasets were gathered from different sources including Kaggle and the University of California Irvine Machine Learning Repository. Their detailed statistics are summarized in Table 1.

Table 1:

Statistics of four benchmark datasets including Adult, Credit, Diabetes and Student.

Dataset	Sample Size	Number of Features	Number of Females	Number of Males	π
Adult	45222	13	14695	30527	0.3635
Credit	30000	23	18112	11888	0.8597
Diabetes	520	16	192	328	2.0105
Student	395	30	208	187	0.8736

• The Adult dataset (https://archive.ics.uci.edu/dataset/2/adult) originally comprises 45,222 samples. However, the code allows for generating a smaller version of the data containing 14,289 samples. This dataset contains demographic information of adults in the United States to determine whether a person makes over 50K a year. Therefore, the binary target variable is income ( 50K = 0, >50K = 1). Some of the 13 predictor variables include occupation, workclass, race, among others.

• The Credit dataset (https://archive.ics.uci.edu/dataset/350/default+of+credit+card+clients) looks at customers’ default payments in Taiwan. The binary target variable is default payment next month (Yes = 1, No = 0), with 23 predictor variables such as marriage, education, BILL AMT1, defined as the amount of bill statement in September, among others. The original dataset has 30,000 samples but in order to reduce running time, 5% of the data was used which yields 1,500 samples.

• The Student dataset (https://archive.ics.uci.edu/dataset/320/student+performance) provides data on student achievement in Mathematics in secondary education of two Portuguese schools. The target variable is G3 which is the final year grade (issued at the 3rd period). Two predictor variables included in the original dataset, G1 and G2, which are first and second period grades respectively, have strong correlations with G3. For that reason, they were omitted as explanatory variables. Furthermore, given that the final grade G3 is numeric and ranges from 0 to 20, to create a binary classification problem, students with grades between 0 and 10 inclusive were labeled 0 and students with grades between 11 to 20 inclusive were labeled 1. Some of the 30 predictor variables include school, address, freetime, among other variables.

• The Diabetes dataset (https://www.kaggle.com/datasets/alakaaay/diabetes-uci-dataset) contains data collected using direct questionnaires from the patients of Sylhet Diabetes Hospital in Sylhet, Bangladesh. The dataset has a binary target named class (Positive = 1, Negative = 0) indicating whether a patient has diabetes. The 16 predictor variables include sudden weight loss, Alopecia, Obesity, among others.

The Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.usc.edu) is a comprehensive repository tailored for facilitating Alzheimer’s disease research [10, 11]. Within the scope of this investigation, three distinct imaging modalities are utilized: AV45, indicative of amyloid deposition [12]; FDG, reflective of glucose metabolism [13]; and VBM, representing gray matter concentration [14]. Three modalities contain 1,650, 1,960, and 2,018 samples, respectively. Each modality presents 119 distinct features. Subjects from the ADNI cohort are categorized into three diagnostic groups: Alzheimer’s Disease (AD), Mild Cognitive Impairment (MCI), and Cognitively Normal (CN). Subsequently, this study focuses on three binary classification tasks, including CN vs. MCI, CN vs. AD, and MCI vs. AD classifications [15, 16]. Their detailed statistics are summarized in Table 2.

Table 2:

Statistics of three ADNI data including AV45, FDG and VBM.

Dataset	Binary Classification Task	Sample Size	Number of Features	Number of Females	Number of Males	π
AV45	CN vs. MCI	686	119	346	340	0.8821
	CN vs. AD	417	119	217	200	0.7865
	MCI vs. AD	547	119	257	290	0.9629
FDG	CN vs. MCI	799	119	368	431	0.8668
	CN vs. AD	498	119	236	262	0.7504
	MCI vs. AD	663	119	278	385	0.9361
VBM	CN vs. MCI	815	119	374	441	0.8583
	CN vs. AD	520	119	244	276	0.7285
	MCI vs. AD	683	119	282	401	0.9159

All datasets include a binary predictor variable referred to as either Sex or Gender, which is used as the sensitive feature to divide the subjects into two groups. As part of the pre-processing stage, for ADNI and the other benchmark datasets, the values of the target variable are modified so that 0 becomes -1 and 1 remains 1. Essentially, our target variables all have the value of -1 for Negative and 1 for Positive. Moreover, the features or predictor variables are standardized using scikit-learn [17]’s StandardScaler. Splitting the data into training and testing sets is also performed using scikit-learn through train test split with test size=0.2 and stratify=target. The trade-off hyperparameter λ is grid searched in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]. We use five different seeds to split the data and report the average and standard deviation results.

The measures used in our experiments are Accuracy (ACC), DEO (defined in Eq. (DEO)) and DDP (defined in Eq. (DDP)) scores. To demonstrate the effectiveness of our PFERM, we choose SVMs and FERM [5] as our baselines.

Ethical Consideration

In conducting our research, we have diligently adhered to stringent ethical standards, recognizing the paramount importance of ethical considerations in academic research, especially when it involves data analysis. The datasets employed in our study were carefully selected from well-established, public sources, recognized for their adherence to ethical principles including, but not limited to, privacy, consent, and data integrity. These datasets are widely accepted in the scientific community and are known for being gathered and shared in compliance with ethical guidelines, ensuring that individual privacy is respected and that data is used responsibly and transparently. Additionally, our methodology was designed to avoid any potential misuse of data, strictly focusing on the analytical objectives without infringing on individual rights or data confidentiality. We ensured that all data handling, processing, and analysis were conducted in accordance with the highest ethical standards, maintaining the integrity of the data subjects and respecting the ethical guidelines established by our academic and scientific community. This commitment to ethical research practices underpins our entire study, reflecting our dedication to responsible and conscientious scientific inquiry.

Results on Synthetic Data

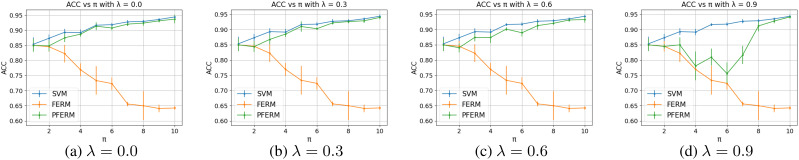
We have 10 synthetic datasets with π values ranging from 1 to 10. To illustrate the performance variation across different π values, we present the results for all π values in a single figure. Figures 2, 3, and 4 show the ACC, DEO, and DDP results, respectively. To demonstrate the impact of the trade-off parameter λ, we report results for various λ values selected from [0.0, 0.3, 0.6, 0.9]. Notably, when λ = 0.0, it signifies full utilization of prior knowledge. As λ increases, the influence of prior knowledge decreases, and at λ = 1.0, no prior knowledge is incorporated, reverting PFERM to FERM. Figure 2 reveals that our PFERM consistently achieves higher accuracy than FERM across all cases. Specifically, when λ = 0.0, which signifies full consideration of prior knowledge, PFERM exhibits performance nearly on par with SVMs. Achieving superior accuracy to SVMs is challenging, given that we impose a fairness constraint atop SVMs, which typically compromises accuracy performance.

Figure 2:

Accuracy versus π.

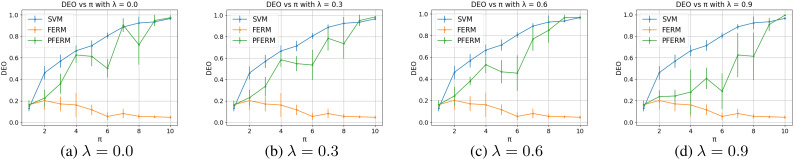
Figure 3:

DEO versus π.

As λ increases, we can see that the accuracy of PFERM also decreases but it is still better than FERM. An interesting phenomenon is that the accuracy does not decrease monotonically as λ increases. For example, when λ = 0.9, the accuracy increases when π becomes larger than 6. This indicates that even a small amount of prior knowledge can change the final situation if the disparity of prevalence between different groups is sufficiently large.

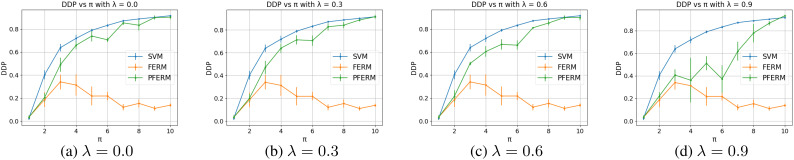
Figure 3 and Figure 4 give similar results. All three curves start from a similar point because the data is balanced when π = 1. SVMs can have a good performance under fairness measurements. When π becomes larger than 1, the data will be imbalanced and SVMs will increase its DEO and DDP, which means it cannot give a fair prediction. FERM gives good and steady DEO and DDP results when π increases. Our PFERM can provide better DEO and DDP results than SVMs. We can see that when π becomes larger, the performance of PFERM also becomes worse. However, in reality, the ratio of the prevalence of one group to another group will not get too big such as larger than 5. According to the statistics in the seven real datasets, π is usually between 1 to 2 (you can take the reciprocal if it is smaller than 1 because we consider the ratio within a pair and the algorithm is symmetric). From Figure 3 and Figure 4 we can see that the fairness performance of PFERM is very close to FERM when π is small and we can even narrow the gap by fine-tuning λ.

Figure 4:

DDP versus π.

Results on Real Data

To further demonstrate the effectiveness of the proposed method, we conduct the experiments on seven real datasets including four benchmark datasets and three ADNI datasets shown in Table 3 and Table 4. We report the best results with the help of fine-tuning λ. In Table 3 for each dataset and each metric, our PFERM outperforms the baselines 5 times out of 12 cases and achieve the second best performance for all the remaining cases. In Table 4, our PFERM outperforms the baseline 15 times out of total 27 cases and get the second place 8 times for the remaining 12 cases. These results demonstrate the effectiveness of the proposed method where our method can preserve fairness without compromising accuracy. It is worthy to emphasize that we do not need to let our PFERM outperform both SVMs and FERM. It would be sufficient if we can let PFERM perform in between them so that we can have an option for a better decision.

Table 3:

Mean Std of Accuracy, DEO and DDP results comparisons for Adult, Credit, Diabetes and Student datasets. The best and the second best results for each dataset and each metric are bold and underlined, respectively.

Dataset	λ Value	Method	Measurement
			ACC	DEO	DDP
Adult	0.7	SVM	0.8241±0.0063	0.1847±0.1178	0.1581±0.0429
		FERM	0.8166±0.0062	0.1521±0.0428	0.0845±0.0421
		PFERM	0.8218±0.0053	0.0391±0.0261	0.1131±0.0143
Credit	0.6	SVM	0.8200±0.0141	0.0644±0.0184	0.0313±0.0135
		FERM	0.8260±0.0139	0.0615±0.0423	0.0372±0.0163
		PFERM	0.8267±0.0158	0.0589±0.0446	0.0281±0.0112
Diabetes	0.4	SVM	0.9731±0.0094	0.0232±0.0343	0.4188±0.0332
		FERM	0.8019±0.0289	0.1845±0.0726	0.0927±0.0348
		PFERM	0.8269±0.0385	0.1147±0.0746	0.1475±0.1033
Student	0.6	SVM	0.6329±0.0615	0.1554±0.1651	0.1852±0.0994
		FERM	0.6380±0.0728	0.1496±0.1022	0.1272±0.0811
		PFERM	0.6380±0.0728	0.1523±0.1001	0.1292±0.0787

Table 4:

Mean Std of Accuracy, DEO and DDP results comparisons on ADNI datasets including AV45, FDG and VBM. The best and the second best results for each dataset and each metric are bold and underlined, respectively.

Dataset	λ Value	Binary Classification Task	Method	Measurement
				ACC	DEO	DDP
AV45	0.7	CN vs. MCI	SVM	0.6681±0.0269	0.0257±0.0244	0.0599±0.0311
			FERM	0.6594±0.0279	0.0481±0.0488	0.0447±0.0368
			PFERM	0.6609±0.0302	0.0481±0.0488	0.0483±0.0334
	0.6	CN vs. AD	SVM	0.8524±0.0358	0.1259±0.0678	0.1078±0.0714
			FERM	0.8667±0.0372	0.1580±0.0999	0.0423±0.0353
			PFERM	0.8690±0.0405	0.1867±0.1333	0.0413±0.032
	0.5	MCI vs. AD	SVM	0.7509±0.0204	0.0509±0.0807	0.0432±0.043
			FERM	0.7618±0.0253	0.0942±0.0833	0.0565±0.0305
			PFERM	0.7618±0.0253	0.0942±0.0833	0.0565±0.0305
FDG	>0.2	CN vs. MCI	SVM	0.6288±0.0175	0.0962±0.095	0.1560±0.0863
			FERM	0.6150±0.0129	0.0211±0.0166	0.0496±0.0382
			PFERM	0.6213±0.0161	0.0164±0.0222	0.0390±0.0435
	0.9	CN vs. AD	SVM	0.8900±0.0228	0.1116±0.0797	0.1084±0.0464
			FERM	0.8900±0.0228	0.0950±0.0596	0.0998±0.0546
			PFERM	0.8920±0.0194	0.0950±0.0596	0.0963±0.0560
	0.4	MCI vs. AD	SVM	0.8481±0.0204	0.0982±0.0556	0.0417±0.0198
			FERM	0.8586±0.0153	0.1548±0.1115	0.0560±0.0362
			PFERM	0.8602±0.0162	0.1482±0.1232	0.0597±0.0342
VBM	0.3	CN vs. MCI	SVM	0.6294±0.0247	0.1330±0.0614	0.1500±0.0147
			FERM	0.6135±0.0269	0.0635±0.0399	0.0472±0.0257
			PFERM	0.5963±0.0131	0.0484±0.0421	0.0248±0.0285
	0.7	CN vs. AD	SVM	0.8615±0.0441	0.0663±0.0402	0.0836±0.0399
			FERM	0.8404±0.0373	0.0718±0.0532	0.0670±0.0397
			PFERM	0.8308±0.0353	0.0568±0.0258	0.0631±0.0256
	0.1	MCI vs. AD	SVM	0.7504±0.0169	0.1747±0.1021	0.0653±0.0293
			FERM	0.7533±0.0233	0.1719±0.1093	0.0827±0.0481
			PFERM	0.7547±0.0188	0.1363±0.1088	0.0659±0.0441

Conclusion and Discussion

We studied prior knowledge for fairness in supervised machine learning, addressing fairness while maintaining classifier accuracy. This Prior-knowledge-guided Fair ERM (PFERM) framework strikes a balance by incorporating prevalence ratio information into fairness constraints within the ERM framework. Empirical results confirm its effectiveness in preserving fairness without compromising accuracy.

Our PFERM framework has far-reaching implications in diverse sectors where fairness and accuracy in machine learning are critical. In healthcare, PFERM can enhance the fairness of diagnostic and treatment models, particularly benefiting groups historically underrepresented in medical research. In finance, it could revolutionize credit scoring and loan processing, ensuring equitable decisions across different socioeconomic groups. In the realm of social media, PFERM promises to make content recommendation and advertising algorithms fairer, reducing biases against specific user demographics. These examples highlight the framework’s potential to foster ethical AI practices, enhancing trust in automated systems. Crucially, PFERM’s adaptability in integrating various types of prior knowledge opens the door for its application in numerous other fields, potentially transforming the landscape of fair decision-making in AI.

While PFERM offers groundbreaking advancements in fairness-centric machine learning, it’s crucial to address its potential limitations and computational challenges. The framework’s effectiveness hinges on the accuracy and representativeness of the prior knowledge used. Misguided or biased prior information can inadvertently introduce new biases, defeating the purpose of fairness. The complexity of tuning PFERM’s parameters also poses a challenge, necessitating a delicate balance between fairness and accuracy. This is especially critical in scenarios with highly imbalanced data or uncertain prevalence ratios. Moreover, computational challenges arise when applying PFERM to large-scale datasets. The framework’s scalability and efficiency can be affected by the size and complexity of data, requiring innovative strategies for optimization. Developing more efficient algorithms, employing parallel computing techniques, and leveraging cloud-based resources are potential avenues to enhance PFERM’s scalability. Acknowledging these limitations and challenges is key, as it guides the careful application of PFERM and informs future advancements, aiming to make the framework more robust and versatile in various applications.