Abstract
The investigation into the distinctive difference of gait is of significance for the clinical diagnosis of neurodegenerative diseases. However, human gait is affected by many factors like behavior, occupation and so on, and they may confuse the gait differences among Parkinson’s disease, amyotrophic lateral sclerosis, and Huntington’s disease. For the purpose of examining distinctive gait differences of neurodegenerative diseases, this study extracts various features from both vertical ground reaction force and time intervals. Moreover, refined Lempel–Ziv complexity is proposed considering the detailed distribution of signals based on the median and quartiles. Basic features (mean, coefficient of variance, and the asymmetry index), nonlinear dynamic features (Hurst exponent, correlation dimension, largest Lyapunov exponent), and refined Lempel–Ziv complexity of different neurodegenerative diseases are compared statistically by violin plot and Kruskal–Wallis test to reveal distinction and regularities. The comparative analysis results illustrate the gait differences across these neurodegenerative diseases by basic features and nonlinear dynamic features. Classification results by random forest indicate that the refined Lempel–Ziv complexity can robustly enhance the diagnosis accuracy when combined with basic features.
Keywords: Parkinson’s disease, Amyotrophic lateral sclerosis, Gait analysis, Random forest
Introduction
The clinical diagnosis of neurodegenerative diseases like Parkinson’s disease (PD), amyotrophic lateral sclerosis (ALS), and Huntington’s disease (HD) is of significance for healthcare (Hou et al. 2019). All these neurodegenerative diseases have the symptoms of abnormal movements like gait disorder, and the disorder patterns are different due to that the loss of brain cells located in different regions. Nonetheless, as a multifactorial appearance of physical, behavioral, cognitive, and environmental reasons for walking, gait signal is influenced by many factors (Cicirell et al. 2021). Therefore, determining the relationship between gait features and pathology of basal ganglia (i.e., PD and HD) and motoneuron (i.e., ALS) is critical.
Comprehensive statistical analysis of gait temporal features like stride interval, swing interval, and so on was discussed for detecting neurodegenerative diseases (Khajuria et al. 2018). Topological motion analysis was also performed to analyze the gait fluctuations in the stance, swing, and stride time interval series (Yan et al. 2020). The stride interval time series of the left foot and the right foot were utilized together for the assessment of movement symmetry, and the results showed that the canonical correlation analysis and joint independent component analysis can classify different kinds of neurodegenerative diseases (Ren et al. 2018a, b). In addition to the spatio-temporal, kinematic and kinetic features (Das et al. 2022) in time-domain, gait data were also analyzed in the frequency domain. The transient artifact reduction method based on the low-frequency components of the signal was proposed for the diagnosis of neurodegenerative diseases (Al-Daffaie et al. 2020). Empirical mode decomposition demonstrated that patients with neurodegenerative diseases are less homogeneous in frequency distributions of gait rhythms and there were more high-frequency components (Ren et al. 2016).
Different nonlinear measures such as Lyapunov exponent, phase space reconstruction were introduced to the detection of Parkinson’s disease (Al-Daffaie et al. 2020). Poincaré sections were employed to model the impairment stages of Parkinson’s disease (Pérez-Toro et al. 2020). Since the temporal characteristics of a step were strongly dependent on the previous steps, the linear relevant index like the coefficient of variance was complemented with nonlinear indices like Hurst exponent and fractal dimension in neurodegenerative diseases diagnosis (Dierick et al. 2021). The improved rescaled range analysis was developed to obtain the Hurst exponent, and it was found that patients with Parkinson’s disease have lower Hurst exponent than aged healthy subjects (Jian-Jun et al. 2008). Scale invariance of the time series was calculated to find that the patients had a larger average of scaling exponent than the healthy subjects (Ren et al. 2018a, b). Multifractal detrended cross-correlation analysis indicated that the stride interval fluctuation between the left and the right foot are almost identical and was greater for healthy individuals compared to the patients with ALS (Chatterjee 2020).
Complexity was also widely used due to its stability in short data series analysis. Sample entropy and permutation entropy were exploited to analyze independent sources extracted from time intervals of different gait phases (Heydarzadeh et al. 2017; Zhao et al. 2020). Multiscale approximate entropy of the ground reaction force indicated that HD patients had the highest complexity while ALS patients had the lowest complexity (Liu et al. 2019). Compared to the ALS, HD, PD, the healthy subjects had the maximum phase synchronization and minimum conditional entropy of stride time, swing time, stance time, swing time proportion, and stance proportion (Ren et al. 2015). The complexity of postural sway was measured by the multiscale entropy analysis for detecting early changes in the motor system, and it provided evidence of a functional decline in fragile X premutation carriers (O’Keeffe et al. 2019). In addition to these entropy measures, Lempel–Ziv (L–Z) complexity proposed in 1976 by Lempel–Ziv (Lempel et al. 1976) was employed for the detection of diseases (Sapina et al. 2021, Borowska et al. 2021, Tanabe et al. 2022, Lahmiri et al. 2022, Mengarelli et al. 2021, Kamath et al. 2016). L–Z complexity has several advantages (Ibáñez-Molina et al. 2015) such as it can be applied to any type of time series no matter how short they are even if they are non-stationary signals. The calculation process of L–Z complexity is simple due to the 0–1 encoding process and it produces a loss of information from the original signal. Since L–Z complexity has been rarely applied to gait analysis for the diagnosis of neurodegenerative disease (Sun et al. 2020), this study employed L–Z complexity and developed a refined L–Z complexity to dig more inherent information of gait affected with neurodegenerative disease.
Though various features and methods have been developed for the diagnosis of neurodegenerative disease, their performance are isolated. Moreover, the significant differences and underlying regularities have not been comprehensively figured out for the clinical diagnosis. To address this problem, basic features and classic nonlinear dynamic features are compared statistically. The contributions of this study are as follows: (1). Nonlinear dynamic features and L–Z complexity are introduced to the gait analysis for the diagnosis of various neurodegenerative diseases; (2). Significantly distinctive features have been illustrated by the comparison of features, and the differences are demonstrated; (3). A refined L–Z complexity considering median and quartiles is developed and it helps to enhance the diagnosing performance of neurodegenerative diseases.
Materials and methods
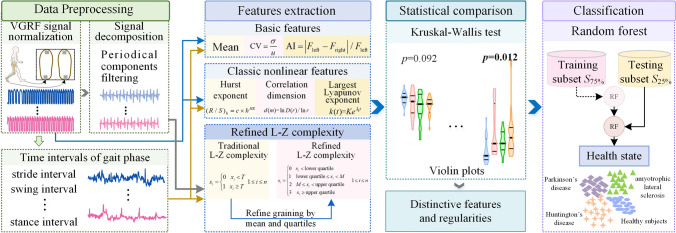
As walking is quasi-periodic activity influenced by many factors, the gait has nonlinear characteristics. Therefore, except for the generally used basic features, the classic nonlinear dynamics are adopted. Moreover, a refined L–Z complexity is developed. To identify the distinctive differences and regularities, features are compared by the violin plots, and the significance are tested by the Kruskal–Wallis test. Finally, the health state is classified by the random forest to validate the accuracy and robustness of the features. The entire process is depicted in Fig. 1.
Fig. 1.
The frame of the diagnosis of neurodegenerative diseases with nonlinear dynamic features and refined Lempel–Ziv complexity
Gait data and preprocessing
The data used are from PhysioNet (https://www.physionet.org/content/gaitndd/1.0.0/) (Hausdorff et al.2000). There are 64 subjects in total, including 13 ALS patients (mean age: 54.9 years, range 36–70), 15 PD patients (mean age: 66.8 years, range 44–80), 20 HD patients (mean age: 47.7 years, range 29–71), and 16 healthy controls (mean age: 39.3 years, range 20–74) respectively. All subjects walked at their preferred speed along a 77-m-long hallway for 5 min. The raw data were obtained from the force-sensitive resistors, and the outputs were proportional to the vertical ground reaction force (VGRF). Except for the raw VGRF signals, the dataset also provides the time series of both left and right stride interval, swing interval, swing interval (% of stride), stance interval, stance interval (% of stride), double support interval, and double support interval (% of stride). These time intervals are derived from the raw VGRF signals and are indicated as “time intervals of gait phase” in this study.
To decrease the influence of individual differences from body weight, raw signals VGRF signals are normalized by body weight and denoted as VGRF/BW. The first and the last 10 s of the original voltage signals are removed to minimize the start-up and the end effects. It is known that PD patients and ALS patients have the symptom of FOG (freezing of gait), and when it appears, the VGRF/BW approximately remains in a value without apparent changes. If the VGRF/BW keeps unchanged for more than 4 s, or if the time intervals are 3 times larger than the median of the series, they will be deleted as outliers.
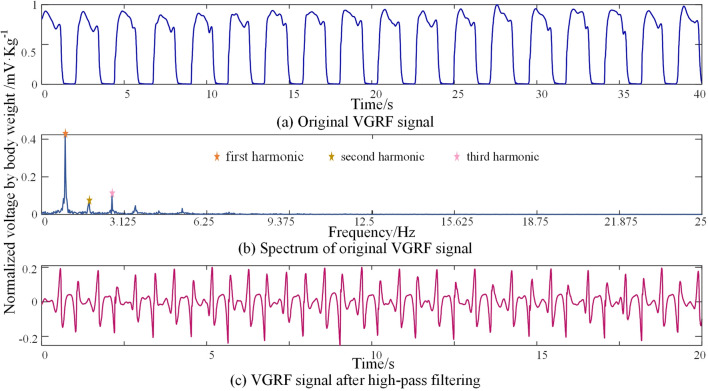
The VGRF signals have similar values during each swing phase and each stance phase respectively as shown in Fig. 2a. This will submerge the fluctuation that contains complex information in each period. To employ the components that have more complexities, the signal will be decomposed in the frequency domain. The spectrum of the VGRF is shown in Fig. 2b, and it can be observed that the first three harmonics account for most of the signal. To avoid the inherent periodic components, the raw signals are filtered by high-pass filtering. The cut-off frequency is selected as the frequency of the third harmonic. Thus components with a frequency higher than the third harmonic are chosen for further analysis. The detailed fluctuation after high-pass filtering is demonstrated in Fig. 2c.
Fig. 2.
The VGRF signals. a The original VGRF signal, b The spectrum of the original VGRF signal, c The VGRF signal after high-pass filtering
Basic features
The features that contain original information directly are important for the diagnosis of neurodegenerative diseases. Therefore, both the VGRF/BW signals and time intervals of gait phase from the database are used. The mean, coefficient of variance and asymmetry are extracted as basic features to keep consistent with previous research (Zhao et al. 2021). The coefficient of variance is calculated as
| 1 |
where is the standard deviation, denotes the mean value. The asymmetry index is derived as
| 2 |
where refers to the parameters of left foot, corresponds to the parameters of right foot.
Classical nonlinear dynamic features
Hurst exponent
The Hurst exponent can be used to estimate the long-term dependencies of a dynamic system. The rescaled range method was commonly used for the calculation of the Hurst exponent (Mandelbrot et al. 1969). For a time sequence that has n continuous values, calculating their logarithm and conducting once differential computation as
| 3 |
Then the logarithm sequence is divided into ‘A’ adjacent subsets with the length of . The mean and the standard deviation of each subspace is denoted as and respectively. In each subset, the accumulated intercept of mean for each former k points is
| 4 |
The fluctuating range of each subset can be derived as
| 5 |
the rescaled range is written as
| 6 |
Increasing the value of h to obtain the rescaled range of subsets with different lengths. Based on the definition that Hurst exponent describes the proportional relation between and as
| 7 |
where, c is a constant, HE represents the Hurst exponent. Therefore, the Hurst exponent can be estimated by plotting the values of log((R/S)h) versus log(h), and the slope of the fitting line represents the Hurst exponent.
Correlation dimension
The correlation dimension is an important parameter to describe fractal characteristics, and it is widely used in the quantitative description of nonlinear systems. It can be computed by the Grassberger-Procaccia algorithm (Grassberger 2007). The process of correlation dimension calculation can be summarized as follows:
Step 1: The time sequence is reconstructed by a small number m0 of embedding dimension to construct a new sequence .
Step 2: The correlation integral is calculated.
Step 3: For the certain range of values of r, the dimension d of the attractor and the cumulative distribution function should satisfy the log-linear relationship as
| 8 |
therefore, the least square fitting can be used to estimate the correlation dimension d(m0) corresponding to m0.
Step 4: Increasing the embedding dimension m0, repeating step 2 and step 3 until the change of estimated dimension d(m0) is no longer changed with the increase of m0.
Largest Lyapunov exponent
Largest Lyapunov exponent illustrates the rate of exponential divergence over time for two near points in the phase space (Rosenstein et al. 1993):
| 9 |
where, k(t) is the divergent distance, K represents the initial distance, and is the largest Lyapunov exponent. Indeed, largest Lyapunov exponent measures the sensitivity of a dynamical system to its initial conditions.
The refined L–Z complexity algorithm
L–Z complexity represents the velocity of the new pattern that appeared in the signal. The detailed steps of the L–Z complexity are as follows: Firstly, the gait time series are grained, the most common method is to choose one threshold value (always the mean) to divide the signal into two parts, the data which is larger than the threshold value will be assigned as 1, and the data smaller than the threshold will be assigned to 0 as follows:
| 10 |
| 11 |
Thus, the gait time series is grained as . Then, the subsequences S and Q from are connected as SQ. For example,, , , and is the sequence that subtracted the last element from . If Q is not the subset of the , Q is the new subsequence; if Q is the subset of the , Q is then reconstructed as . The times that Q is the new subsequence is denoted by . Then the complexity can be normalized as:
| 12 |
Since the coarse-graining in the type of binary ignored details of the original signal, the refined graining is developed. Median and quartiles can objectively indicate the specific distribution of the series, they are used as the boundary points in the graining process to divide the signal into four regions as follows:
| 13 |
where, M represents the median. Then, the complexity is calculated as the process of traditional L–Z complexity. Finally, the refined L–Z complexity can be represented as:
| 14 |
Statistical comparison of features
The basic features, nonlinear dynamic features, and the refined L–Z complexity of all the groups are demonstrated by the violin plot to figure out the underlying regularities across various neurodegenerative diseases. In addition, Kruskal–Wallis test is exploited to distinguish the significant differences across the health controls, HD, PD, and ALS patients, and the significance level is set at 0.05.
Classification with random forest
To recognize the efficiency of the basic features, nonlinear dynamics, and the refined L–Z complexity, the random forest is applied to classify patients with different neurodegenerative diseases. During the classification process, the data augmentation is conducted by dividing the signals into smaller segments with the length of 10 s without overlap. For each kind of feature, 75% of samples are used randomly for training and 25% are used for testing. To obtain reliable results, each classification is conducted 30 times, and their average accuracy are obtained to evaluate the classification performance.
Results of statistical comparisons for features
Comparison of the basic features
For each extracted feature, the Kruskal–Wallis tests are performed across 4 groups to identify the discernibility of features. Both the feature extraction and Kruskal–Wallis tests are carried out by Matlab R2019a. The p-values are added to the violin plot as shown in Fig. 3. It can be observed from Fig. 3a that the p-values of VGRF/BW are larger than 0.05 for both the left and the right foot, nevertheless, PD patients have the largest mean and asymmetry index of VGRF/BW.
Fig. 3.
Violin plot and p-values of basic features. a Basic features extracted from VGR/BW; b Basic features extracted from time intervals; c Basic features extracted from proportion to stride
For features extracted from time intervals as illustrated in Fig. 3b, the mean value and coefficient of variance for all the time intervals are significant. ALS patients have the largest stride interval, stance interval, and double support interval, while the health controls are the smallest. Moreover, HD patients have the largest coefficient of variance for almost all the time intervals and PD patients have the largest asymmetry index in stance intervals. As for proportions to stride, it can be seen in Fig. 3c that healthy controls have the largest swing proportion while the lowest stance proportion and double support proportion compared to patients with neurodegenerative diseases. In addition, the coefficient of variance and asymmetry index of the healthy controls is the lowest. HD patients have the largest coefficient of variance for proportion to stride than other groups.
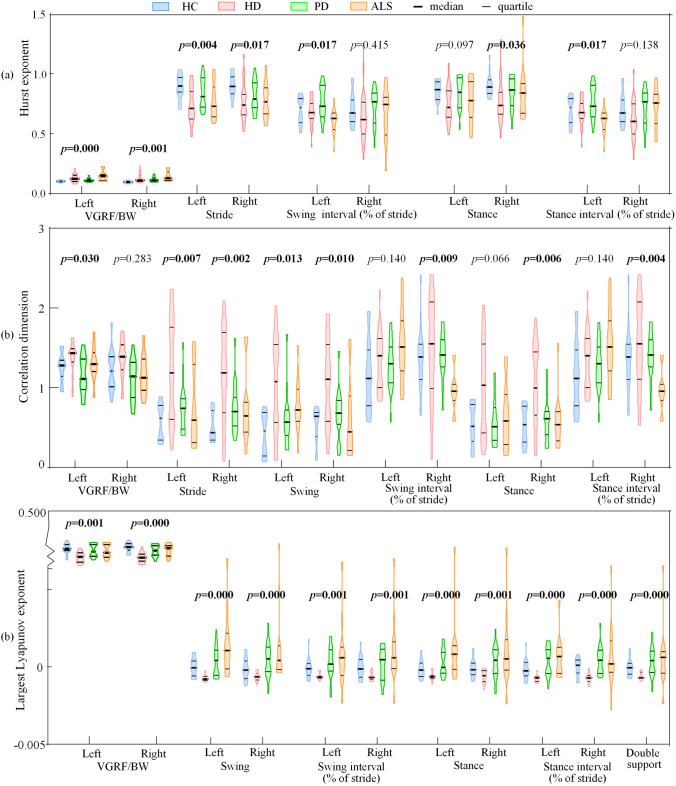
Comparison of nonlinear dynamic features
The Hurst exponent, correlation dimension, and largest Lyapunov exponent of all the subjects are displayed and compared in Fig. 4. Moreover, the p-values of Kruskal–Wallis tests of the 4 groups are displayed on the top of feature distributions. For features whose p-values are larger than 0.05, they are not displayed in the figure. For Hurst exponent calculated from VGRF/BW, ALS patients are larger than other groups and healthy controls are smaller. For Hurst exponent obtained from the stride intervals, healthy controls are the largest followed by PD patients and ALS patients, while HD patients are the lowest.
Fig. 4.
Violin plot and p-values of classic nonlinear dynamics. a Hurst exponent of each series; b Correlation dimension of each series; c Largest Lyapunov exponent of each series
For correlation dimension, HD patients are larger than healthy controls while PD and ALS patients have no regular difference when calculated from VGRF/BW. When calculated from time interval, both the stride interval and the swing phase interval have distinctive differences, and their correlation dimension are the lowest for the healthy controls. In general, HD patients have the highest correlation dimension.
For largest Lyapunov exponent features, all of them are distinctive because their p-values are both lower than 0.05. When calculated from VGRF/BW, healthy controls are higher while HD patients are lower. When largest Lyapunov exponent are calculated from time interval, HD patients are the lowest, while healthy controls are higher than HD patients but lower than PD and ALS patients.
Some regularities can be comprehensively summarized. For nonlinear dynamics calculated from VGRF/BW, the healthy controls have lower Hurst exponent and higher largest Lyapunov exponent than neurodegenerative diseases patients, while HD patients have the highest correlation dimension and the lowest largest Lyapunov exponent. Additionally, for nonlinear dynamics calculated from time interval, the HD patients have the larger correlation dimension but lower largest Lyapunov exponent than healthy controls, PD patients, and ALS patients.
Comparison of L–Z complexity features
The traditional L–Z complexity and the refined L–Z complexity of the filtered VGRF/BW and time intervals are shown in Fig. 5. The p-values of Kruskal–Wallis tests of the 4 groups are shown on the top of feature distributions. It is worth noting that the L–Z complexity distribution of the right foot is not similar to the left foot. The traditional L–Z complexities calculated from VGRF/BW are not significant while the refined L–Z complexity of right foot has a significant difference.
Fig. 5.
Violin plot and p-values of the L–Z complexity
The refined L–Z complexity distribution trend of each group is also different from the traditional L–Z complexity. The traditional L–Z complexity is significant at the right stride interval and the left swing phase. The refined L–Z complexity has a significant difference at the right swing phase and the right stance phase proportion. This also implies that the refined L–Z complexity provides different distinctive features from the traditional L–Z complexity.
The diagnosing results of neurodegenerative diseases
The diagnosis performance of the features
To recognize the efficiency of the basic features, NLD features, and the refined L–Z complexity, the random forest is applied to classify the four groups: health, HD, PD, and ALS. Holdout method is applied to evaluate the diagnosing performance, in which 75% of samples are randomly used for training and 25% are used for testing. The random forest is conducted 30 times randomly, and the mean of training accuracy and the testing accuracy are shown in Table 1.
Table 1.
The 4-class classification accuracy of the random forest with different kinds of features
| Basic features | CD | HE | LLE | L–Z | Refined L–Z | |
|---|---|---|---|---|---|---|
| Training (%) | 100 | 100 | 100 | 100 | 99.93 | 100 |
| Testing (%) | 79.96 | 42.44 | 32.32 | 49.60 | 31.70 | 34.21 |
CD Correlation dimension, HE Hurst exponent, LLE Largest Lyapunov exponent
To further identify the diagnosing ability across the four groups, the L–Z complexity and the nonlinear dynamic features are combined with basic features respectively. The corresponding diagnosing accuracies are shown in Table 2.
Table 2.
The 4-class classification accuracy of the random forest with different kinds of features
| Basic features | Basic + HE | Basic + CD | Basic + LLE | Basic + L–Z | Basic + refined L–Z | |
|---|---|---|---|---|---|---|
| Accuracy (%) | 79.96 (1.99) | 80.62 (2.13) | 80.48 (2.06) | 79.84 (1.91) | 85.21 (1.68) | 86.56 (1.85) |
CD Correlation dimension, HE Hurst exponent, LLE Largest Lyapunov exponent
It can be observed that the refined L–Z complexity combined with basic features achieves the best performance when diagnose different neurodegenerative diseases and healthy controls. The confusion matrix of the diagnosis by the basic feature combined refined L–Z complexity is shown in Fig. 6.
Fig. 6.

Confusion matrix of diagnosis by the basic feature combined refined L–Z complexity
To diagnose the neurodegenerative diseases between each two groups specifically, the refined L–Z complexity combined with basic features are employed to 2-class classification, and the classification results are illustrated in Table 3. It can be seen that the refined L–Z complexity combined with basic features can efficiently diagnose neurodegenerative diseases from healthy controls and can distinguish different kinds of neurodegenerative diseases.
Table 3.
The testing accuracy between each two groups
| Health-patient | HC-HD | HC-PD | HC-ALS | PD-ALS | PD-HD | HD-ALS | |
|---|---|---|---|---|---|---|---|
| Accuracy (Sd) % | 92.87 (2.42) | 91.71 (2.78) | 91.68 (2.65) | 95.72 (1.87) | 91.41 (2.75) | 91.67 (2.33) | 93.01 (2.24) |
CD Correlation dimension, HE Hurst exponent, LLE Largest Lyapunov exponent
The performance of the refined L–Z complexity on another dataset
To validate the generality and efficiency of the refined L–Z complexity in the diagnosis of human neurodegenerative disease, another gait dataset named ‘Gait in Aging and Disease Database’ (https://physionet.org/content/gaitdb/1.0.0/) is employed. It contains the walking stride interval time series from 15 subjects: 5 healthy young adults (23–29 years old), 5 healthy old adults (71–77 years old), and 5 older adults (60–77 years old) with Parkinson's disease (Goldberger et al. 2000). Since this dataset only contains the stride interval series of the subjects, the stride interval, nonlinear dynamic features, and refined L–Z complexity features are tested.
Each kind of feature used singly and used together with stride intervals for the classification of the young health, old health, and PD health are compared and shown in Table 4. When features are singly used in the classification, the accuracy is low with large standard deviation. When stride intervals are combined with the Hurst exponent, correlation dimension, and largest Lyapunov exponent, their diagnosing accuracy increased. The L–Z complexity achieves better diagnosis performance than others when both singly used and combined with stride interval. Moreover, the refined L–Z complexity achieves the higher accuracy than the traditional L–Z complexity.
Table 4.
The testing accuracy for the diagnosis of young, old subjects, and PD patients
| Single features | Stride interval | L–Z | Refined L–Z | HE | CD | LLE |
|---|---|---|---|---|---|---|
| Accuracy (Sd) % | 62.61 (9.47) | 73.50 (8.14) | 73.68 (7.54) | 57.24 (14.7) | 43.67 (12.03) | 55.17 (12.20) |
| Combined features | Stride interval + HE | Stride interval + CD | Stride interval + LLE | Stride interval + L–Z | Stride interval + refined L–Z |
|---|---|---|---|---|---|
| Accuracy (Sd) % | 68.27 (12.17) | 74.94 (11.22) | 73.56 (11.61) | 83.66 (7.62) | 85.30 (7.22) |
CD Correlation dimension, HE Hurst exponent, LLE Largest Lyapunov exponent
The results demonstrate that the refined L–Z complexity helps for a more efficient diagnosis of neurodegenerative diseases though the amount of both sample and feature are small. In addition, the results verified the robustness of the refined L–Z complexity when it is applied for diagnosis of neurodegenerative diseases.
Discussion
Statistical comparisons demonstrate significant differences of features between various kinds of neurodegenerative diseases. Healthy controls have the highest swing proportion while the lowest stance interval and stance proportion, double support proportion, coefficient of variance, and the lowest asymmetry index. HD patients have a lower largest Lyapunov exponent while a larger correlation dimension than other groups. For the traditional L–Z complexities, ALS patients are larger than other groups. The refined L–Z complexity features at the right swing interval for PD patients are lower while larger at right stance proportion than HD patients. Moreover, ALS patients have lower refined L–Z complexity of right swing interval and stance proportion than HD patients.
As for the diagnosis of neurodegenerative diseases, the highest diagnosing accuracy can be achieved when refined L–Z complexity used with basic features. While nonlinear dynamic features combined with basic features obtain lower diagnosing accuracy though the nonlinear dynamic features are distinctive themselves. This may be because that the Hurst exponent, correlation dimension, and largest Lyapunov exponent are calculated based on the sequence itself which contains amplitude information that basic features also contain. While the refined L–Z complexity is calculated by the distribution of the signal which the basic features do not involve. Thus the refined L–Z complexity can supply more information to the basic features. Additionally, the refined L–Z complexity spends less calculating time than nonlinear dynamic features since the calculation of L–Z complexity involves the simplification of data.
Neurodegenerative diseases affect balance and gait. The neurons in basal ganglia influence the regulation of muscular motor control such as balance and sequencing of movements (Scafetta et al. 2009). As typical disorders of basal ganglia, PD and HD are associated with gait sequences, the L–Z complexity which characterizes the sequence is reasonable to be affected. Researches also imply that the dynamic evolution such as the stride-to-stride variability of successive strides is mostly affected and the walking becomes more random (Hausdorff 2009). The L–Z complexity can describe this random and it has been widely employed to characterize the EEG (electroencephalogram) of several mental and neurological disorders (Sun et al. 2020). However, L–Z complexity of gait intervals hasn’t been comprehensively explored for the diagnosis of neurodegenerative diseases. While this study found that the refined L–Z complexity of both VGRF and time intervals plays an important role in diagnosis of neurodegenerative diseases. Moreover, the refined L–Z complexity helps a more accurate and robust performance.
The diagnosis results of this study are compared to the existing research as shown in Table 5.
Table 5.
A comparison of this study and certain state-of-the-art researches using the same data
| References | Features | Data augmentation | Classifier | Accuracy (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HC-PD | HC-HD | HC-ALS | HD-PD | HD-ALS | PD-ALS | HC-NND | 4-class | ||||
| Daliri (2012) | Static features of time series | all trained and all tested | SVM | 89.33 | 90.28 | 96.79 | – | – | – | – | – |
| Zeng et al. (2015) | Stance and swing time intervals | all trained and all tested | DL | 87.1 | 83.33 | 89.66 | – | – | – | 93.75 | – |
| Xia et al. (2015) | Statistical features | – | SVM | 100 | 100 | 96.55 | 91.18 | 96.88 | 96.43 | 96.83 | – |
| Pham (2017) | Texture features of fuzzy recurrence plots transformed from time intervals | – | LS-SVM | 100 | 100 | 100 | – | – | – | – | – |
| Gupta et al. (2019) | Auto-correlation, mean and standard deviation | – | DT | 80.0 | 80.0 | 90.0 | – | – | – | 73.3 | – |
| Lin et al. (2020) | Recurrence plot of VGRF |
10 s time window with 6.66 s overlap (5248 samples) |
CNN | 93.55 | 77.78 | 96.55 | 82.86 | 87.88 | 71.43 | 89.06 | – |
| Beyrami et al. (2020) | Statistical features and ApEn | 10 s time window without overlap | SVM | 86.00 | 91.76 | 95.84 | 93.79 | 92.06 | 87.34 | 80.20 | – |
| Ghaderyan et al. (2020) | Symmetric features of time interval | – | NNLS | 97 | 95 | 98 | – | – | – | 91 | – |
| Erdaş et al. (2021) | QR code of time intervals | – | ConvLSTM/3DCNN | 94.04 | 92.91 | 97.68 | – | – | – | 95.73 | 86.05 |
| Setiawan et al. (2021) | Time–frequency spectrogram and neural network | 10 s time window 1920 samples | CNN | 97.42 | 100 | 100 | – | – | – | 98.44 | – |
| Saljuqi et al. (2021) | Linear and nonlinear of matching pursuit | – | NNLS | 93 | 97 | 94 | – | – | – | – | – |
| Tobar et al. (2022) | Transition times of VGRF–static features | – | RF | – | – | – | – | – | – | – | 91–63 |
| Faisal et al. (2023) | VGRF and their integral, derivative, second derivative | 1 gait cycle, 14,412 samples | ConvMixer network | 94 | 97 | 100 | – | – | 96 | 83 | |
| This study | Basic features and refined L–Z complexity | 10 s time window without overlap, 1004 samples | RF | 91.68 (2.6) | 91.71 (2.7) | 95.72 (1.8) | 91.67 (2.3) | 93.01 (2.2) | 91.41 (2.7) | 92.87 (2.4) | 86.56 (1.9) |
HC Health controls, DL Deterministic learning, SVM Support vector Machines, LS-SVM Least squares support vecor machines, DT Decision tree, CNN Convolutional Neural Networks, KNN k-nearest neighbor, NNLS Non-negative least-squares, RF Random forest
Statistical features such as mean, maximum, minimum, skew, and so on extracted from time intervals were usually employed to the diagnosis of neurodegenerative diseases (Daliri 2012; Xia et al. 2015; Gupta et al. 2019; Prabhu et al. 2020; Beyrami et al. 2020; Erdaş et al. 2021). Recurrence plots from time intervals (Pham2017) and original VGRF signals (Lin et al. 2020) also had been used to extract features. Time-dependent spectral features extracted from time intervals were firstly employed to gait analysis (Mengarelli et al 2022). In this study, basic features, nonlinear dynamic features, and refined L–Z complexity from both time intervals and VGRF signals have been analyzed to explore the gait differences of neurodegenerative diseases.
For the diagnosing performance of disease, the detection of ALS patients from the healthy control has the highest accuracy not only in most of the existing research but also in this study. This implies that the gait of ALS patients has more distinct characteristics as demonstrated by the feature comparisons in this study. Although some existing researches achieve high accuracy, some of these reported accuracy are from the best or highest trial of leave one out cross validation or tenfold across validation (Xia et al. 2015; Pham2017; Prabhu et al. 2020; Saljuqi et al. 2021). While most of the studies hadn’t clarified whether the accuracy is the best one from many classifying trials or is the average accuracy. As for machine learning methods (classifiers), each classifying trial has different results, and the best accuracy is insufficient to represent the classifying performance. To obtain high classifying accuracy, data augmentation approaches were involved. The all-training and all testing classification was conducted by dividing time series of each subject into two series, one for training and one for testing (Daliri 2012; Zeng et al. 2015). Dividing the original signal by time window into many segments as samples was also generally used (Lin et al. 2020; Beyrami et al. 2020; Setiawan et al. 2021; Faisal et al. 2023). In this study, signals were also divided into small segments with 10 s time window without overlap in the classification process. This enhanced the comparability of the obtained accuracy.
These previous researches were limited to the analysis of the classification, and the distinctive differences between neurodegenerative diseases and healthy controls have not been comprehensively explored. This study reports the distinct differences between each type of neurodegenerative disease by the violin plot and statistical analysis. In the future, the intrinsic influences of neurodegenerative disease on the gait model (Ma et al. 2016) and the diagnosis of severity levels (Zhao et al. 2022) will be investigated.
Conclusion
For the purpose of detecting the distinctive differences of gait caused by neurodegenerative diseases, basic features such as mean, coefficient of variance and asymmetry index of VGRF/BW and stride intervals have been extracted. Different nonlinear dynamic features like Hurst exponent, correlation dimension, and the largest Lyapunov exponent have been employed to extract the nonlinear characteristics. Moreover, a refined L–Z complexity is applied by considering the detailed distribution of the original signal to obtain the distinctive gait feature.
Basic features, nonlinear dynamic features, and refined L–Z complexity have been compared statistically. Results show some distinctive differences across the healthy subjects and patients affected with different neurodegenerative diseases. Healthy controls have the highest swing proportion while the lowest stance interval and proportion, double support proportion, coefficient of variance, and the lowest asymmetry. Healthy subjects also have a higher Hurst exponent and a lower correlation dimension. HD patients have a higher correlation dimension while a lower Hurst exponent and a lower largest Lyapunov exponent. When compared to PD patients, ALS patients have a lower correlation dimension and a higher largest Lyapunov exponent.
More importantly, the refined L–Z complexity robustly contributes to a higher diagnostic accuracy of neurodegenerative diseases. When using refined L–Z complexity and basic features together, the random forest can accurately diagnose neurodegenerative diseases with an average accuracy of 86.56%. Furthermore, when the refined L–Z complexity is used, the diagnosis accuracy of PD patients from healthy young and healthy old subjects can be increased by 22.69% in average.
Acknowledgements
This work was supported by the National Key Research and Development Program of China [Grant No. 2021YFE0203400], and Innovation and Technology Commission under Mainland-Hong Kong Joint Funding Scheme (MHKJFS), the Hong Kong Special Administrative Region, China [Project No. MHP/043/20].
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Al-Daffaie K, Al-Ghayab HR. Transient artifact reduction and statistical method based classification of neurodegenerative diseases. Int J Agric Stat Sci. 2020;16(1):1391–1399. [Google Scholar]
- Beyrami SMG, Ghaderyan P. A robust, cost-effective and non-invasive computer-aided method for diagnosis three types of neurodegenerative diseases with gait signal analysis. Measurement. 2020;156:107579. doi: 10.1016/j.measurement.2020.107579. [DOI] [Google Scholar]
- Borowska M. Multiscale permutation LempeL–Ziv complexity measure for biomedical signal analysis: Interpretation and Application to Focal EEG Signals. Entropy. 2021;23:832. doi: 10.3390/e23070832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvajal-Castaño HA, Lemos-Duque JD, Orozco-Arroyave JR. Effective detection of abnormal gait patterns in Parkinson's disease patients using kinematics, nonlinear, and stability gait features. Hum Mov Sci. 2022;81:102891. doi: 10.1016/j.humov.2021.102891. [DOI] [PubMed] [Google Scholar]
- Chatterjee S. Analysis of the human gait rhythm in Neurodegenerative disease: a multifractal approach using Multifractal detrended cross correlation analysis. Phys A Stat Mech Appl. 2020;540:123154. doi: 10.1016/j.physa.2019.123154. [DOI] [Google Scholar]
- Cicirelli G, Impedovo D, Dentamaro V, Marani R, Pirlo G, D’Orazio TR. Human gait analysis in neurodegenerative diseases: a review. IEEE J Biomed Health. 2021;26(1):229–242. doi: 10.1109/JBHI.2021.3092875. [DOI] [PubMed] [Google Scholar]
- Daliri MR. Automatic diagnosis of neuro-degenerative diseases using gait dynamics. Measurement. 2012;45(7):1729–1734. doi: 10.1016/j.measurement.2012.04.013. [DOI] [Google Scholar]
- Das R, Paul S, Mourya GK, Kumar N, Hussain M. Recent trends and practices toward assessment and rehabilitation of neurodegenerative disorders: insights from human gait. Front Neurosci. 2022;16:85929. doi: 10.3389/fnins.2022.859298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dierick F, Vandevoorde C, Chantraine F, White O, Buisseret F. Benefits of nonlinear analysis indices of walking stride interval in the evaluation of neurodegenerative diseases. Hum Movement Sci. 2021;75:102741. doi: 10.1016/j.humov.2020.102741. [DOI] [PubMed] [Google Scholar]
- Erdaş ÇB, Sümer E, Kibaroğlu S. Neurodegenerative disease detection and severity prediction using deep learning approaches. Biomed Signal Proces. 2021;70:103069. doi: 10.1016/j.bspc.2021.103069. [DOI] [Google Scholar]
- Faisal MAA, Chowdhury ME, Mahbub ZB, Pedersen S, Ahmed MU, Khandakar A, AbdulMoniem M (2023) NDDNet: a deep learning model for predicting neurodegenerative diseases from gait pattern. Appl Intell 1–13
- Ghaderyan P, Beyrami SMG. Neurodegenerative diseases detection using distance metrics and sparse coding: a new perspective on gait symmetric features. Comput Biol Med. 2020;120:103736. doi: 10.1016/j.compbiomed.2020.103736. [DOI] [PubMed] [Google Scholar]
- Goldberger AL, Amaral LA, Glass L, Hausdorff JM, Ivanov PC, Mark RG, Stanley HE. PhysioBank, physiotoolkit, and physionet: components of a new research resource for complex physiologic signals. Circulation. 2000;101(23):e215–e220. doi: 10.1161/01.CIR.101.23.e215. [DOI] [PubMed] [Google Scholar]
- Grassberger, P. (2007). Grassberger-Procaccia algorithm. Scholarpedia, 2(5), 3043. 10.4249/scholarpedia.3043
- Gupta K, Khajuria A, Chatterjee N, Joshi P, Joshi D. Rule based classification of neurodegenerative diseases using data driven gait features. Heal Technol. 2019;9:547–560. doi: 10.1007/s12553-018-0274-y. [DOI] [Google Scholar]
- Hausdorff JM. Gait dynamics in Parkinson’s disease: common and distinct behavior among stride length, gait variability, and fractal-like scaling. Chaos Interdiscip J Nonlinear Sci. 2009;19(2):026113. doi: 10.1063/1.3147408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hausdorff JM, Lertratanakul A, Cudkowicz ME, Peterson AL, Kaliton D, Goldberger AL. Dynamic markers of altered gait rhythm in amyotrophic lateral sclerosis. J Appl Physiol. 2000;88:2045–2053. doi: 10.1152/jappl.2000.88.6.2045. [DOI] [PubMed] [Google Scholar]
- Heydarzadeh M, Tan CT, Nourani M, Ostadabbas S. Gait variability assessment in neuro-degenerative patients by measuring complexity of independent sources. Annu Int Conf IEEE Eng Med Biol Soc. 2017;2017:3186–3189. doi: 10.1109/EMBC.2017.8037534. [DOI] [PubMed] [Google Scholar]
- Hou Y, Dan X, Babbar M, Wei Y, Hasselbalch SG, Croteau DL, Bohr VA. Ageing as a risk factor for neurodegenerative disease. Nat Rev Neurol. 2019;15(10):565–581. doi: 10.1038/s41582-019-0244-7. [DOI] [PubMed] [Google Scholar]
- Ibáñez-Molina AJ, Iglesias-Parro S, Soriano MF, Aznarte JI. Multiscale LempeL–Ziv complexity for EEG measures. Clin Neurophysiol. 2015;126(3):541–548. doi: 10.1016/j.clinph.2014.07.012. [DOI] [PubMed] [Google Scholar]
- Jian-Jun Z, Xin-Bao N, Xiao-Dong Y, Feng-Zhen H, Cheng-Yu H. Decrease in Hurst exponent of human gait with aging and neurodegenerative diseases. Chin Phys B. 2008;17:852–856. doi: 10.1088/1674-1056/17/3/021. [DOI] [Google Scholar]
- Kamath C. Analysis of altered complexity of gait dynamics with aging and Parkinson's disease using ternary LempeL–Ziv complexity. Cogent Eng. 2016;3(1):1177924. doi: 10.1080/23311916.2016.1177924. [DOI] [Google Scholar]
- Khajuria A, Joshi P, Joshi D. Comprehensive statistical analysis of the gait parameters in neurodegenerative diseases. Neurophysiology. 2018;50:38–51. doi: 10.1007/s11062-018-9715-5. [DOI] [Google Scholar]
- Lahmiri S, Bekiros S. Complexity measures of high oscillations in phonocardiogram as biomarkers to distinguish between normal heart sound and pathological murmur. Chaos Solitons Fract. 2022;154:111610. doi: 10.1016/j.chaos.2021.111610. [DOI] [Google Scholar]
- Lempel A, Ziv J. On the complexity of finite sequences. IEEE T Inform Theory. 1976;22(1):75–81. doi: 10.1109/TIT.1976.1055501. [DOI] [Google Scholar]
- Lin CW, Wen TC, Setiawan F. Evaluation of vertical ground reaction forces pattern visualization in neurodegenerative diseases identification using deep learning and recurrence plot image feature extraction. Sensors-Basel. 2020;20:3857. doi: 10.3390/s20143857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu AB, Lin CW. Multiscale approximate entropy for gait analysis in patients with neurodegenerative diseases. Entropy. 2019;21:934. doi: 10.3390/e21100934. [DOI] [Google Scholar]
- Ma H, Liao WH. Human gait modeling and analysis using a semi-Markov process with ground reaction forces. Ieee T Neur Sys Reh. 2016;25:597–607. doi: 10.1109/TNSRE.2016.2584923. [DOI] [PubMed] [Google Scholar]
- Mandelbrot BB, Wallis JR. Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence. Water Resour Res. 1969;5(5):967–988. doi: 10.1029/WR005i005p00967. [DOI] [Google Scholar]
- Mengarelli A, Tigrini A, Fioretti S, Verdini F. Identification of neurodegenerative diseases from gait rhythm through time domain and time-dependent spectral descriptors. IEEE J Biomed Health Inform. 2022;26(12):5974–5982. doi: 10.1109/JBHI.2022.3205058. [DOI] [PubMed] [Google Scholar]
- Mengarelli A, Tigrini A, Fioretti S, et al. (2021) Recurrence quantification analysis of gait rhythm in patients affected by Parkinson’s Disease. In: 2021 IEEE EMBS international conference on biomedical and health informatics (BHI). IEEE, pp 1–4
- O’Keeffe C, Taboada LP, Feerick N, Gallagher L, Lynch T, Reilly RB. Complexity based measures of postural stability provide novel evidence of functional decline in fragile X premutation carriers. J Neuroeng Rehabil. 2019;16(1):1–8. doi: 10.1186/s12984-019-0560-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Toro PA, Vásquez-Correa JC, Arias-Vergara T, Nöth E, Orozco-Arroyave JR. Nonlinear dynamics and Poincaré sections to model gait impairments in different stages of Parkinson’s disease. Nonlinear Dyn. 2020;100:3253–3276. doi: 10.1007/s11071-020-05691-7. [DOI] [Google Scholar]
- Pham TD. Texture classification and visualization of time series of gait dynamics in patients with neuro-degenerative diseases. IEEE Trans Neural Syst Rehabil Eng. 2017;26(1):188–196. doi: 10.1109/TNSRE.2017.2732448. [DOI] [PubMed] [Google Scholar]
- Prabhu P, Karunakar AK, Anitha H, Pradhan N. Classification of gait signals into different neurodegenerative diseases using statistical analysis and recurrence quantification analysis. Pattern Recogn Lett. 2020;139:10–16. doi: 10.1016/j.patrec.2018.05.006. [DOI] [Google Scholar]
- Ren P, Zhao W, Zhao Z, Bringas-Vega ML, Valdes-Sosa PA, Kendrick KM. Analysis of gait Rhythm Fluctuations for neurodegenerative diseases by phase synchronization and conditional entropy. IEEE T Neur Sys Reh. 2015;24:291–299. doi: 10.1109/TNSRE.2015.2477325. [DOI] [PubMed] [Google Scholar]
- Ren P, Tang S, Fang F, Luo L, Xu L, Bringas-Vega ML, Valdes-Sosa PA. Gait rhythm fluctuation analysis for neurodegenerative diseases by empirical mode decomposition. IEEE T Bio-Med Eng. 2016;64:52–60. doi: 10.1109/TBME.2016.2536438. [DOI] [PubMed] [Google Scholar]
- Ren H, Yang Y, Gu C, Weng T, Yang H. A patient suffering from neurodegenerative disease may have a strengthened fractal gait rhythm. IEEE T Neur Sys Reh. 2018;26:1765–1772. doi: 10.1109/TNSRE.2018.2860971. [DOI] [PubMed] [Google Scholar]
- Ren P, Hu S, Han Z, Wang Q, Yao S, Gao Z, Valdes-Sosa PA. Movement symmetry assessment by bilateral motion data fusion. IEEE T Bio-Med Eng. 2018;66(1):225–236. doi: 10.1109/TBME.2018.2829749. [DOI] [PubMed] [Google Scholar]
- Rosenstein, M. T., Collins, J. J., & De Luca, C. J. (1993). A practical method for calculating largest Lyapunov exponents from small data sets. Physica D: Nonlinear Phenomena, 65(1–2), 117–134. 10.1016/0167-2789(93)90009-P
- Saljuqi M, Ghaderyan P. A novel method based on matching pursuit decomposition of gait signals for Parkinson’s disease, Amyotrophic lateral sclerosis and Huntington's disease detection. Neurosci Lett. 2021;761:136107. doi: 10.1016/j.neulet.2021.136107. [DOI] [PubMed] [Google Scholar]
- Šapina M, Karmakar CK, Kramarić K, Kośmider M, Garcin M, Brdarić D, Yearwood J. (2021), LempeL–Ziv complexity of the pNNx statistics–an application to neonatal stress. Chaos Solitons Fract. 2021;146:110703. doi: 10.1016/j.chaos.2021.110703. [DOI] [Google Scholar]
- Scafetta N, Marchi D, West BJ. Understanding the complexity of human gait dynamics. Chaos Interdiscip J Nonlinear Sci. 2009;19(2):026108. doi: 10.1063/1.3143035. [DOI] [PubMed] [Google Scholar]
- Setiawan F, Lin CW. Identification of neurodegenerative diseases based on vertical ground reaction force classification using time-frequency spectrogram and deep learning neural network features. Brain Sci. 2021;11(7):902. doi: 10.3390/brainsci11070902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Wang B, Niu Y, Tan Y, Fan C, Zhang N, Xiang J. Complexity analysis of EEG, MEG, and fMRI in mild cognitive impairment and Alzheimer’s disease: a review. Entropy. 2020;22(2):239. doi: 10.3390/e22020239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanabe S, Parker M, Lennertz R, et al. Reduced electroencephalogram complexity in postoperative delirium. J Gerontol Ser A. 2022;77(3):502–506. doi: 10.1093/gerona/glab352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobar C, Rengifo C, Muñoz M. Petri net transition times as training features for multiclass models to support the detection of neurodegenerative diseases. Biomed Phys Eng Express. 2022;8(6):065001. doi: 10.1088/2057-1976/ac8c9a. [DOI] [PubMed] [Google Scholar]
- Xia Y, Gao Q, Ye Q. Classification of gait rhythm signals between patients with neuro-degenerative diseases and normal subjects: Experiments with statistical features and different classification models. Biomed Signal Process Control. 2015;18:254–262. doi: 10.1016/j.bspc.2015.02.002. [DOI] [Google Scholar]
- Yan Y, Omisore OM, Xue YC, Li HH, Liu QH, Nie ZD, Wang L. Classification of neurodegenerative diseases via topological motion analysis—a comparison study for multiple gait fluctuations. Ieee Access. 2020;8:96363–96377. doi: 10.1109/ACCESS.2020.2996667. [DOI] [Google Scholar]
- Zeng W, Wang C. Classification of neurodegenerative diseases using gait dynamics via deterministic learning. Inf Sci. 2015;317:246–258. doi: 10.1016/j.ins.2015.04.047. [DOI] [Google Scholar]
- Zhao H, Cao J, Wang R, Lei Y, Liao WH, Cao H. Accurate identification of Parkinson’s disease by distinctive features and ensemble decision trees. Biomed Signal Proces. 2021;69:102860. doi: 10.1016/j.bspc.2021.102860. [DOI] [Google Scholar]
- Zhao H, Wang R, Lei Y, Liao WH, Cao H, Cao J. Severity level diagnosis of Parkinson’s disease by ensemble K-nearest neighbor under imbalanced data. Expert Syst Appl. 2022;189:116113. doi: 10.1016/j.eswa.2021.116113. [DOI] [Google Scholar]
- Zhao H, Yu J, Cao J, Liao WH (2020) Refined weighted-permutation entropy: a complexity measure for human gait and physiologic signals with outliers and noise, Springer International Publishing, Cham, pp 223–231