Complexity decline of hippocampal CA1 circuit model due to cholinergic deficiency associated with Alzheimer’s disease

Abstract

A hallmark of Alzheimer’s disease (AD) is cholinergic system dysfunction, directly affecting the hippocampal neurons. Previous experiments have demonstrated that reduced complexity is one significant effect of AD on electroencephalography (EEG). Motivated by these, this study explores reduced EEG complexity of cholinergic deficiency in AD by neurocomputation. We first construct a new hippocampal CA1 circuit model with cholinergic action. M-current $I_M$ and calcium-activated potassium current $I_{\mathit{AHP}}$ are newly introduced in the model to describe cholinergic input from the medial septum. Then, by enhancing $I_M$ and $I_{\mathit{AHP}}$ to mimic cholinergic deficiency, how cholinergic deficiency influences the model complexity is investigated by sample entropy (SampEn) and approximate entropy (ApEn). Numerical results show a more severe cholinergic deficit with lower model complexity. Furthermore, we conclude that the decline of SampEn and ApEn is due to the greatly diminished excitability of model neurons. These suggest that decreased neuronal excitability due to cholinergic impairment may contribute to reduced EEG complexity in AD. Subsequently, statistical analysis between simulated AD patients and normal control (NC) groups demonstrates that SampEn and auto-mutual-information (AMI) decrease rates significantly differ. Compared to NC, AD patients have a lower SampEn and a less negative AMI decline rate. These imply a low rate of new-generation information in AD brains with cholinergic deficits. Interestingly, the statistical correlation between SampEn and AMI is analyzed, and they have a large negative Pearson correlation coefficient. Thus, AMI reduction rates may be a complementary tool for complex analysis. Our modeling and complex analysis are expected to provide a deeper understanding of the reduced EEG complexity resulting from cholinergic deficiency.

Introduction

Alzheimer’s disease (AD), the predominant form of dementia (50–75%), is a common neurodegenerative disease in the central nervous system (Bogdanovic et al. 2020). This disease is clinically characterized by memory disorders, cognitive impairment, and ambiguous expression, leading to loss of autonomy (Van et al. 2016). The neuropathological hallmarks of AD include severe neuronal loss, intracellular neurofibrillary tangles, and extracellular senile plaques (NFTs) in the brain histology (Swerdlow 2007; Small and Gangy 2006). To understand AD pathogenesis, neurobiological mechanisms underlying AD have been a top priority, among which the cholinergic hypothesis is noteworthy (Sanabria et al. 2017). According to cholinergic theory, AD is caused by damaged cholinergic neurons in AD patients, which reduces the concentration of acetylcholine in the brain, leads to a disturbance of the central cholinergic nerve system, and subsequently impairs memory and recognition (Swerdlow 2007).

Acetylcholine, a significant neurotransmitter in the central nervous system, plays a crucial role in the dynamic control of the brain's network during cognitive processes. Since 1906, many studies have proved that insufficient acetylcholine in the brain is a vital cause of cognitive impairment in many neurological diseases such as Alzheimer’s disease, Lethargy, and Parkinson’s (Hasselmo 2006). For example, Bartus et al. (1982) have found that Alzheimer’s patients have apparent cholinergic system dysfunction, and specific cholinergic stimulation can reliably improve the memory of AD patients. Further, the pathological process of AD is a progressive degeneration that selectively damages cholinergic neuronal populations in the hippocampus, cortex, nucleus basalis of Meynert (NBM), and medial septum (MS), resulting in decreased cholinergic concentrations (Serge et al. 1986). Pearson et al. have revealed that the basal nucleus in the AD brain has the persistence of shrunken cholinergic neurons compared with age-sex-matched normal brains (Pearson et al. 1983). In 1982, Whitehouse et al. used autoradiography to detect that the number of nicotinic acetylcholine (nAch) receptors in the cerebral cortex of AD patients is significantly reduced (Whitehouse et al. 1982). These findings have confirmed that the dysfunction of the cholinergic system is closely related to AD. Most importantly, it has been shown that the hippocampus is one of the earliest and more specific brain regions in AD development. Meanwhile, cholinergic neurons in the MS are the primary source of cholinergic input to the hippocampus in the cholinergic system (Knox and Keller 2016).

The above studies have suggested that AD may affect cholinergic concentrations in the hippocampus, which might impact the dynamic behavior of neurons there. Moreover, the clinical pathological features are obtained mainly by autopsy. Electroencephalography (EEG) is widely used to record and analyze the brain’s electrical activity to improve the quality of diagnosis. Many previous works have demonstrated that one of the primary EEG characteristics of AD is a decreased level of EEG complexity. Complexity analysis is a nonlinear analysis used to reflect the nonlinear dynamical processes of the brain (Stam et al. 2005). Various complexity metrics have been used to quantify the complexity of EEG signals, among which entropy is a powerful tool for analyzing complexity. In this context, entropy is the rate of generation of new information. EEG with large entropy has a high rate of newly generated information; in contrast, EEG with small entropy corresponds to a low level of freshly generated information (Lake et al. 2002). In recent decades, the EEG activity of AD patients has been researched using entropy techniques. The expected results have revealed that the EEG of AD patients is more regular (i.e., less complex) than age-matched control subjects. For example, Hornero et al. (2009) have reported that EEG and MEG background activities in AD patients are less complicated and more regular than that in healthy control subjects by statistical analysis of approximate entropy (ApEn), sample entropy (SampEn), and multiscale entropy. Woon et al. (2007) calculated EEG complexity to distinguish AD patients from age-matched controls by SampEn. Dauwels et al. (2010) have detected that the auto-mutual information (AMI) throughout the cerebrums of AD patients decreased more slowly with a delay than the AMIs of normal controls. Therefore, the reduced EEG complexity has been considered one of the essential electrophysiological features of AD. Altan et al. (2020) have applied deep learning to study diseases, and this study will apply complexity analysis to AD. Most of the complexity analysis on AD is used for statistical analysis of EEG in AD, and rarely is complexity analysis applied to neurocomputational models. Multiple complexity analysis methods can significantly improve the reliability of experimental conclusions. Motivated by these, this study analyzes the newly constructed neurocomputational model with three complexity methods (e.g., ApEn, SampEn, AMI). These three complexity measures can well quantify the regularity of the signal, and the algorithms are relatively simple and efficient (Dauwels et al. 2010; Aydın et al. 2019; Çetin et al. 2022).

At the same time, constructing neural computational models at the molecular level has been an essential topic in the study of AD. In particular, neuronal modeling in the hippocampus is a high priority, for it can help us to understand the changes in physiological characteristics of EEG signals on AD. Note that the neural firing model for a single neuron is basic to studying neural electrophysiological activity. Based on the effect of $K^{+}$ and ${\mathit{Na}}^{+}$ ionic currents in cell membranes on action potentials (Hodgkin and Huxley 1952), the pioneers of Hodgkin and Huxley proposed the famous H–H model in 1952 to describe action potential generation and conduction in nerve cell membranes. Based on previous results and experimental data, Golomb et al. (2006) have established a single-compartment model of hippocampal CA1 pyramidal cells. This nine-dimensional computational model can simulate some of the experimental electrophysiological results of hippocampal CA1 pyramidal neurons. Then this nine-dimensional one-compartment complex model was simplified by a dimensionality reduction technique to obtain a two-dimensional simplified neuron model for the first time. It is helpful to know the dynamic characteristics of the hippocampal neuron (Peng et al. 2011, 2016). Zou et al. have constructed a hippocampal-septal network, and then the work has discussed how the reduction of a-type $K^{+}$ current ion conductance Aβ-induced affects theta-band power (Zou et al. 2011, 2012). Dong et al. (2022) have used a comprehensive DG-CA3 network model of the hippocampus to explore the neuronal correlation between AD-related glutamatergic synaptic loss and abnormal firing rhythms. Jiang et al. (2020) have introduced cholinergic effects into the hippocampal neuron to construct a modified CA1 pyramidal neuron model, and then the impact of acetylcholine deficiency and beta-amyloid accumulation on the neuronal dynamics are investigated in terms of theta band power and spiking frequency. However, the interactions of neurons in hippocampal brain regions are not taken into account in the computational model. Therefore, a neuronal diversity-leading comprehensive hippocampal network model with cholinergic actions is required to gain insight into the reduced EEG complexity of cholinergic acetylcholine deficiency in AD patients.

Note that cholinergic action affects the hippocampal neurons significantly. Drever et al. (2011) have reported that cholinergic fibers of the medial septal nucleus (MS) can activate muscarinic receptors in CA1 pyramidal and basket neurons by releasing acetylcholine. When activated, muscarinic receptors, a type of acetylcholine receptor, can suppress M-current $I_M$, which is a voltage and muscarine-sensitive $K^{+}$ current (Adams et al. 1982). Benardo et al. (1982) have also found that acetylcholine can effectively block calcium ion-activated potassium ion current $I_{\mathit{AHP}}$, significantly inhibiting AHP current. What is more, Madison et al. have revealed that carbachol (a cholinergic agonist) significantly can reduce the two currents of $I_M$ and $I_{\mathit{AHP}}$; furthermore, the higher the concentration of carbachol is, the more $I_M$ and $I_{\mathit{AHP}}$ are blocked (Madison et al. 1987). Thus, the direct effects of acetylcholine on the hippocampal CA1 neurons are mediated by the blockade of M-current $I_M$ and calcium ion-activated potassium ion current $I_{\mathit{AHP}}$, which implies that acetylcholine deficiency in AD pathology may potentiate these two currents.

As stated above, some hippocampus computational models such as the hippocampal CA1 pyramidal neuron, the hippocampal septal network, and DG-CA3 computational model have been proposed in AD research. These computational models have helped us understand the pathogenic mechanisms of AD. Previous physiological results have verified that AD may damage the cholinergic system in AD patient; meanwhile, EEG experimental studies have revealed that one of AD’s main electrophysiological features is reduced EEG complexity. Unfortunately, the underlying dynamical mechanisms behind these changes have remained puzzling. Motivated by these findings and issues, a neuronal diversity-leading comprehensive hippocampal network model with cholinergic actions is required for a deep understanding of the reduced complexity of EEG in the environment of cholinergic acetylcholine deficiency in AD patients. Therefore, this study focuses on building a more physiologically plausible hippocampal CA1 circuit model with the action of acetylcholine, wherein three kinds of pyramidal cell, basket cell, and OLM cell are interconnected by chemical synaptic coupling. Two new currents, M-current $I_M$ and calcium-activated potassium current $I_{\mathit{AHP}}$, are introduced to the pyramidal and basket cells to describe the cholinergic action of MS cholinergic cells. The condition of acetylcholine deficiency in AD patients is simulated by increasing the conductance of M-current and AHP current in this model. For the exploration of complexity analysis applied to neurocomputational models, this study uses three complexity measures (SampEn, ApEn, and AMI) for the analysis of neuronal membrane potentials in models, aiming to provide some new insights into the underlying dynamical mechanisms of reduced complexity of EEG in AD.

The work is structured as follows: firstly, in the “Model presentation and complexity measures” section a new hippocampal CA1 circuit model with cholinergic action is constructed and three complexity measures are addressed; secondly, in the “Result” section how cholinergic deficit influences the complexity is discussed by SampEn and ApEn; and significant differences of AMI and SampEn between the AD patients group and the normal control (NC) group are simulated; finally, in “Conclusion and Discussion” section a clear summary and discussion of the whole work are presented.

Model presentation and complexity measures

In this section, a new hippocampal CA1 circuit model under the action of acetylcholine is firstly constructed. Then, three complexity measures including SampEn, ApEn and AMI are presented.

A new hippocampal CA1 circuit model with cholinergic action

We construct a new hippocampal CA1 circuit model with cholinergic action based on Hodgkin-Huxley-type formalisms because the H–H model can better simulate the electrophysiological properties of hippocampal neurons (Hodgkin and Huxley 1952). Many existing neurocomputational models provide reliability for this study (Zou et al. 2011, 2012; Peng et al. 2016; Jiang et al. 2020). According to anatomical studies, there are three typical neurons in the CA1 region of the hippocampus, i.e., pyramidal, basket, and OLM cells. As illustrated in the schematic diagram of Fig. 1, this model includes three typical hippocampal CA1 neurons, i.e., pyramidal, basket, and OLM cells. The pyramidal cell acts on basket and OLM cells via excitatory AMPA and NMDA synapses. Basket and OLM cells release inhibitory signals to other postsynaptic cells via the inhibitory GABA_A synapse. According to the physiological experiments (Drever et al. 2011), the pyramidal and basket cells receive cholinergic energy from the MS cholinergic system.

Fig. 1.

Schematic diagram of the hippocampal CA1 circuit model. | The model consists of three types of neurons, i.e., pyramidal, basket, and OLM cells. The red solid line represents the excitatory AMPA and NMDA synaptic connection. The black dash line indicates the inhibitory GABA_A synaptic connection. The direction of the arrow shows the synapse pathway. Cholinergic action of the MS cholinergic system acts directly on pyramidal and basket cells in hippocampal CA1

On the basis of the modified AD hippocampal CA1 pyramidal neuronal model (Peng et al. 2016; Jiang et al. 2020), the mathematical equation of the pyramidal cell in this hippocampal CA1 circuit model is described as follows:

$$Pramidal:C\times \frac{d{V}_P}{\mathit{dt}}=-I_L-I_{\mathit{Na}}-I_K-I_A-I_M-I_{\mathit{AHP}}-I_{\mathit{syn}}+I$$ 1

in which the currents of $I_M$ and $I_{\mathit{AHP}}$ are introduced in order to describe the cholinergic input sourced from the medial septum system (Drever et al. 2011).

In addition to the hippocampal CA1 pyramidal cell, the basket cell in this hippocampal CA1 circuit model is also affected by cholinergic action from the medial septum system (Grigorov et al. 2014). Thus, the basket cell is constructed based on CA1 pyramidal neuronal model (Grigorov et al. 2014; Peng et al. 2016). The mathematical equation of the basket cell with two newly introduced currents of $I_M$ and $I_{\mathit{AHP}}$ is described as follows:

$$Basket:C\times \frac{d{V}_B}{\mathit{dt}}=-I_L-I_{\mathit{Na}}-I_K-I_M-I_{\mathit{AHP}}-I_{\mathit{syn}}+I$$ 2

The mathematical equation governing the OLM cell in this hippocampal CA1 circuit model is as follows (Wang and Buzsaki 1996; Wang 2002; Zou et al. 2011, 2012):

$$OLM:C\times \frac{d{V}_O}{\mathit{dt}}=-I_L-I_{\mathit{Na}}-I_K-I_{\mathit{syn}}+I$$ 3

In the above equations, $V$ denotes the membrane potential (the subscript $P$, $B$ and $O$ denote pyramidal, basket and OLM cells, respectively). $C$ represents the membrane capacitance. $I_A$ is a kind of transient potassium current, $I_{\mathit{Na}}$ and $I_K$ denote spike generating currents and $I_L$ represents leakage current. The synaptic current $I_{\mathit{syn}}$ represents the synaptic interactions from other cells in this new hippocampal CA1 circuit model. $I$ is the injected direct current (DC). Details of the currents and relative parameters are attached in the Appendix.

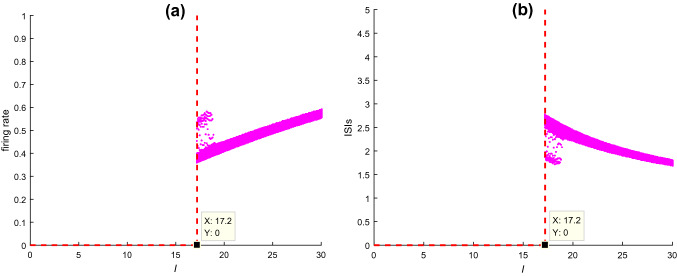
The injected DC current $I$ greatly affects the dynamical behavior of neurons. Here how this injected DC current influences the dynamics of hippocampal CA1 pyramidal cell is analyzed in Fig. 2, in which the firing rate and the bifurcation graph of interspike intervals (ISIs) of pyramidal cell are depicted. From this figure, one can observe that the pyramidal neuron can’t fire initially and starts to discharge when $I\approx 17.2mA$, after that it fires more frequently with a steadily increased firing rate (Fig. 2a) and a steadily decreased ISIs (Fig. 2b) upon further increasing stimulation current $I$. In this study, the injected DC current is set as $I=20mA$ in order to guarantee the neurons in the hippocampal CA1 circuit model to discharge.

Fig. 2.

a The firing rate and b ISIs of CA1 pyramidal cell upon increasing the injected DC current $I$ when $g_{M\_PY}=0.10mS/{\mathit{cm}}^2$, $g_{AHP\_PY}=0.15mS/{\mathit{cm}}^2$,$g_{M\_basket}=0.10mS/{\mathit{cm}}^2$ and $g_{AHP\_basket}=0.15mS/{\mathit{cm}}^2$

Complexity measure: SampEn

SampEn is a classical tool to measure the complexity of time series. It assigns a non-negative number to the time series, with larger value corresponding to more irregularity of the data (Raúl et al. 2010). N data points from a time series $\{x(n)\}=x(1),x(2),\cdots ,x\left(N\right)$ are supplied and its SampEn can be estimated by the following steps (Hornero et al. 2009). Note that two input parameters, the run-length $m$ and the tolerance window $r$, need to be specified firstly.

To calculate the SampEn(m,r,N) from a time series, $\{x(n)\}=x(1),x(2),\cdots ,x\left(N\right)$, one should follow these steps:

1. Define a series of m-vectors $X_m\left(1\right),X_m\left(2\right),\cdots ,X_m\left(N,-,m,+,1\right)$, in which $X_m\left(i\right)=[x\left(i\right),x\left(i,+,1\right),\cdots ,x\left(i,+,m,-,1\right)]$,$i=1,\cdots ,N-m+1$. The distance between $X_m\left(i\right)$ and $X_m\left(j\right)$ is supposed to be

   $$d\left[X_m\left(i\right),X_m\left(j\right)\right]=max\left(\left|x\left(i+k-1\right)-x\left(j+k-1\right)\right|\right)\left(k=1,\dots ,m\right)$$ 4
2. For $X_m\left(i\right)$, denote the number of j ($1\le j\le N-m+1,j\ne i$) as $B_i$ if the distance between $d\left[X_m,\left(i\right),,,X_m,\left(j\right)\right]\le r$. Then, for $1\le i\le N-m+1$,

   $$B_i^m\left(r\right)=\frac{1}{N-m}{B}_i$$ 5
3. Define $B^m\left(r\right)$ as

   $$B^m\left(r\right)=\frac{1}{N-m+1}\sum _{i=1}^{N-m+1}{B}_i^m\left(r\right)$$ 6

Here $B^m\left(r\right)$ is the probability of two sequences matching $m$ points under the tolerance window $r$.

• (d)
  Increase the dimension to $m+1$, and denote the number of j ($1\le j\le N-m,j\ne i$) as $A_i$ such that the distance between $d\left[X_{m+1},\left(i\right),,,X_{m+1},\left(j\right)\right]\le r$. Define $A_i^m\left(r\right)$ as

  $$A_i^m\left(r\right)=\frac{1}{N-m-1}{A}_i$$ 7
• (e)
  Set $A^m\left(r\right)$ as

  $$A^m\left(r\right)=\frac{1}{N-m}\sum _{i=1}^{N-m}{A}_i^m\left(r\right)$$ 8

where $A^m\left(r\right)$ is the probability of two sequences matching $m+1$ points under the tolerance window $r$.

• (f)
  Define the SampEn by

  $$SampEn\left(m,r,N\right)=-ln\left[\frac{A^m\left(r\right)}{B^m\left(r\right)}\right]$$ 9

As suggested in Ref (Pincus 2001), the two specified parameters can be set as $m=1$ or 2, and $r=0.1,0.15,0.2$ and $0.25$ times the standard deviation (SD) of the original data sequence. In this study, using the membrane potentials of pyramidal neuron as the interested time series, we investigate the complexity of the hippocampal CA1 circuit model by measuring SampEn of this time series. In the following, the SampEn is estimated with $m=2$ and $r=0.25$ times the SD of the considered time series.

Complexity measure: ApEn

ApEn is introduced as a quantification of regularity in sequences and time series. Moreover, ApEn is scale-invariant and model-independent (Pincus 2001). ApEn assigns a non-negative number to a time series, with larger values corresponding to more irregularity in the data. It is important to consider $ApEn\left(m,,,r,,,N\right)$, where $N$ is the number of points of the time series, as a family of characterizing measures: comparisons between time series can only be made with the same values of $m$, $r$ and $N$ (Pincus 2001).

Formally, Given $N$ data points from a time series $\left\{x,\left(n\right)\right\}=x\left(1\right),x\left(2\right),\cdots ,x\left(N\right)$, one should follow these steps to compute ApEn:

1. Form $N-m+1$ vectors $X(1),X(2),\cdots ,X\left(N,-,m,+,1\right)$ defined by:$X\left(i\right)=\left[x,\left(i\right),,,x,\left(i,+,1\right),,,\cdots ,,,x,\left(i,-,m,+,1\right)\right],i=1,\cdots ,N-m+1.$

2. Define the distance between $X\left(i\right)$ and $X\left(j\right)$, $d\left[X,\left(i\right),,,X,\left(j\right)\right],$ as the maximum absolute between their respective scalar component. Thus, $d\left[X,\left(i\right),,,X,\left(j\right)\right]$ is defined as

   $$d\left[X\left(i\right),X\left(j\right)\right]=max\left(\left|x\left(i+k-1\right)-x\left(j+k-1\right)\right|\right)\left(k=1,\dots ,m\right)$$ 10
3. For a given $X\left(i\right)$, count the number of j ($1\le j\le N-m+1,j\ne i$) so that $d\left[X,\left(i\right),,,X,\left(j\right)\right]\le r$,denoted as $N^m\left(i\right)$. Then, for $1\le i\le N-m+1$,

   $$C_r^m\left(i\right)=\frac{N^m\left(i\right)}{N-m+1}$$ 11
4. Compute the natural logarithm of each $C_r^m\left(i\right)$, and average it over $i$,

   $${\mathrm{\Phi }}^m\left(r\right)=\frac{1}{N-m+1}\sum _{i=1}^{N-m+1}ln{C}_r^m\left(i\right)$$ 12

5. Increase the dimension to $m+1$. Repeat steps a)-d) and find $C_r^{m+1}\left(i\right)$ and ${\mathrm{\Phi }}^{m+1}\left(r\right)$

6. Theoretically, ApEn is defined as

   $$ApEn\left(m,r\right)=\underset{N\to \infty }{lim}\left[{\mathrm{\Phi }}^{m+1}\left(r\right)-{\mathrm{\Phi }}^m\left(r\right)\right]$$ 13
7. In practice, the muber of data points N is finite. We implement this formula by defining the stastic:

   $$ApEn\left(m,r,N\right)=\left[{\mathrm{\Phi }}^{m+1}\left(r\right)-{\mathrm{\Phi }}^m\left(r\right)\right]$$ 14

As suggested in Ref (Pincus 2001), the two specified parameters can be set as $m=1$ or 2, and $r=0.1,0.15,0.2$ and $0.25$ times the standard deviation (SD) of the original data sequence. In this study, similar to SampEn, using the membrane potentials of pyramidal neuron as the interested time series, we investigate the complexity of the hippocampal CA1 circuit model by measuring ApEn of this time series. In the following, the ApEn is estimated with $m=2$ and $r=0.25$ times the SD of the considered time series.

Complexity measure: AMI

Mutual information (MI) is a concept in information theory used to measure the statistical correlation between two time series (Pompe et al. 1998). The MI between two time series $x_i$ and $y_i$ is the amount of information that the former provides about the latter. AMI is a special form of MI between a time series and a delayed version of itself (Jeong et al. 2001). In general, AMI estimates the degree to which $x(t+\tau )$ can be predicted from $x(t)$ (Fraser and Swinney 1986), which can detect linear and nonlinear dependence in the time series, usually depicting the complexity of a time series.

The AMI between $x(t)$ and $x(t+\tau )$ is defined as (Jeong et al. 2001):

$$I_{X{X}_{\tau }}=\sum _{x\left(t\right),x\left(t+\tau \right)}{P}_{X{X}_{\tau }}\left[x\left(t\right),x\left(t+\tau \right)\right]\times {log}_2\left\{\frac{P_{X{X}_{\tau }}\left[x\left(t\right),x\left(t+\tau \right)\right]}{P_X\left[x\left(t\right)\right]P_{X_{\tau }}\left[x\left(t+\tau \right)\right]}\right\}$$ 15

In which $P_X[x\left(t\right)]$ and ($P_{X_{\tau }}[x(t+\tau )]$) are the probability density of the time series $x\left(t\right)$ and x(t + τ), respectively. $P_{{\mathit{XX}}_{\tau }}[x\left(t\right),x(t+\tau )]$ is the joint probability density for the time series of x(t) and $x(t+\tau )$.

The AMI is based on the amplitude distributions of $x(t)$ on different time scales (David et al. 2004). Based on the AMI curve, the AMI rate of decrease is estimated by the slope of AMI curve from the time delay 0 to the time delay where the first relative minimum of AMI is obtained. The more negative the AMI rates of decrease, the more irregular and complex of the series. Similar to Sect. ”Complexity measure: SampEn”, using the membrane potentials of pyramidal neuron as the interested time series, we also investigate the complexity of the hippocampal CA1 circuit model by measuring AMI of this time series. In the following, the AMI is estimated over a time delay from 0 to 0.5 s and is further normalized so that $AMI(\tau =0)=1$.

Result

In this section, firstly, we explore how the cholinergic deficiency resulting from AD influences the complexity in this constructed hippocampal CA1 circuit model by estimating SampEn and ApEn. Then the SampEn and AMI statistical analysis between the simulated AD patients and the normal control (NC) group is investigated. In addition, the statistical correlation between SampEn and AMI is also discussed.

Decline of SampEn and ApEn by acetylcholine deficiency

As stated in the Introduction, the positive effects of acetylcholine on the hippocampal CA1 neurons are mediated by the blockade of M-current $I_M$ and calcium ion-activated potassium ion current $I_{\mathit{AHP}}$, which implies that acetylcholine deficiency in AD pathology may potentiate these two currents. Thus, by enhancing the currents $I_M$ and $g_{\mathit{AHP}}$ to simulate AD condition in this hippocampal CA1 circuit model, how the increases of ionic conductance in these two currents in pyramidal neuron influence the SampEn and ApEn are respectively discussed in the following. Please note that our further simulations show that potentiating currents $I_M$ and $I_{\mathit{AHP}}$ in the basket cell can produce the similar effect on the complexity of SampEn and ApEn. To save space, it is not necessary to list them in detail.

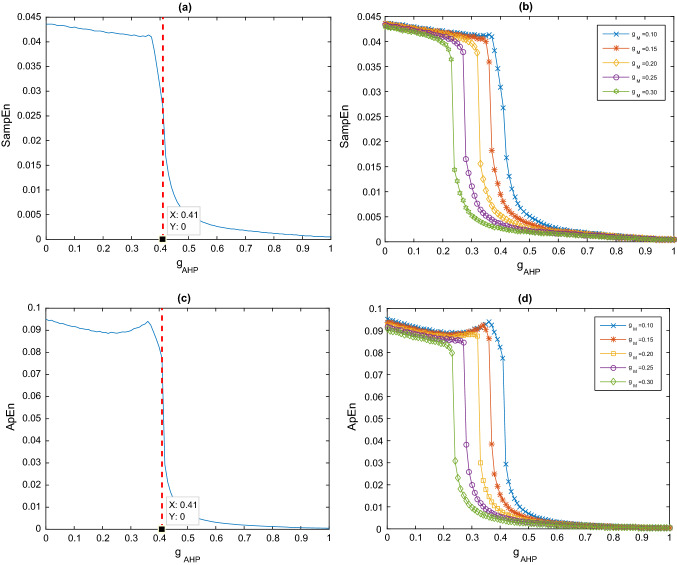
Taking the ionic conductance of current ${\mathit{I}}_{\mathit{M}}$ as control parameter

In this subsection, by fixing the ionic conductance $g_{\mathit{AHP}}$ of current $I_{\mathit{AHP}}$ in the pyramidal cell at $0.15mS/{\mathit{cm}}^2$, how the enhanced current $I_M$ influences the SampEn and ApEn in this hippocampal CA1 circuit model are respectively discussed by taking the ionic conductance $g_M$ of current $I_M$ in the pyramidal cell as a control parameter. Figure 3a depicts the evolution of SampEn in the hippocampal CA1 circuit model as the ionic conductance $g_M$ is increased. It can be clearly seen that upon increasing the parameter $g_M$ slowly from 0 to 1, the SampEn decreases significantly. In detail, the SampEn decreases steadily as the initial increase of $g_M$, suddenly it drops sharply at a critical value $g_M\approx 0.392mS/{\mathit{cm}}^2$, after that it decreases steadily again till it approaches zero with the further increase of $g_M$. Moreover, these above-mentioned interesting results still appear when ApEn analyses model. Figure 3c depicts the decrease of ApEn in the model as the ionic conductance $g_M$ slowly increases from 0 to 1. ApEn similarly decreases steadily with the initial increase in$g_M$. Suddenly it drops sharply at the same critical value $g_M\approx 0.392mS/{\mathit{cm}}^2$, after which ApEn drops steadily again until it approaches 0. This phenomenon implies that the more severe the cholinergic deficit (corresponding to large $g_M$) in AD patients, the lower the complexity of the hippocampal CA1 circuit model. These simulated results are consistent with previous experiment where the complexity of EEG in AD patients decreases significantly compared to the age-match human (Ab´asolo et al. 2006). Given that entropy is the rate of nascent information (Lake et al. 2002), the decrease in entropy values of AD patients also reflect a decrease in information processing flexibility in the damaged brain caused by cholinergic deficits. Model simulations are consistent with the general hypothesis that complexity is reduced when brain cholinergic function is impaired. Cholinergic deficits in AD likely cause a decreased information processing flexibility in the damaged brain.

Fig. 3.

a Dependence of SampEn on the ionic conductance $g_M$ when $g_{\mathit{AHP}}=0.15mS/{\mathit{cm}}^2$. b Dependence of SampEn on the ionic conductance $g_M$ for different $g_{\mathit{AHP}}$. c Dependence of ApEn on the ionic conductance $g_M$ when $g_{\mathit{AHP}}=0.15mS/{\mathit{cm}}^2$. d Dependence of ApEn on the ionic conductance $g_M$ for different $g_{\mathit{AHP}}$

Further simulations demonstrate that the above phenomenon can still appear when the ionic conductance $g_{\mathit{AHP}}$ of current $I_{\mathit{AHP}}$ is fixed at other values. Figure 3b illustrates the dependence of SampEn on $g_M$ for several different ionic conductance, such as$g_{\mathit{AHP}}=0.0,0.1,0.15,0.2,0.3$. For comparison, the case of $g_{\mathit{AHP}}=0.15$ is also included in this figure. One can observe that for each fixed $g_{\mathit{AHP}},$ the SampEn first decreases slowly, then falls abruptly at some critical value of $g_M$, it decreases steadily with the further increase of $g_M$. Obviously, the variation of SampEn with $g_M$ is similar with the case of $g_{\mathit{AHP}}=0.15,$ which shows that the decline of SampEn induced by the increase of $g_M$ is robust to the ionic conductance$g_{\mathit{AHP}}$. Figure 3d presents the dependence of ApEn on $g_M$ for different ionic conductivities $g_{\mathit{AHP}}$ such as $g_{\mathit{AHP}}=0.0,0.1,0.15,0.2,0.3$. Again, the decrease in ApEn caused by an increase of $g_M$ is robust to the ionic conductance $g_{\mathit{AHP}}$. In addition, as $g_{AHP\_PY}$ is increased, the SampEn and ApEn curves are clearly shifted to the left respectively, together with a gradually degraded critical value of$g_M$. That is to say, the compexity of the hippocampal CA1 circuit model is more likely to decrease as the ionic conductance $g_{\mathit{AHP}}$ increases.

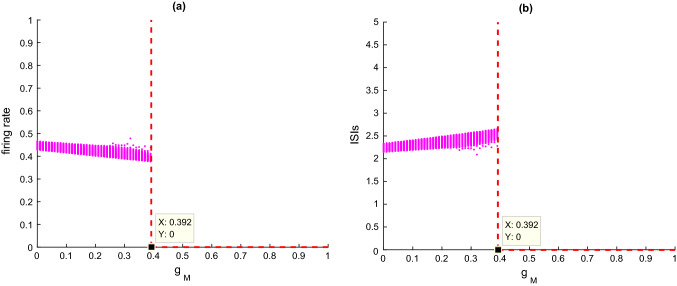
Next, the dynamical mechanism underlying the decline of SampEn and ApEn by the enhancement of current $I_M$ in the hippocampal CA1 circuit model is investigated by nonlinear dynamics analysis. Figure 4a and b portray the variation of firing rate and the corresponding ISIs with the parameter $g_M$, respectively. It can be clearly seen that as $g_M$ increases, firstly the firing rate decreases slowly in Fig. 4a and the ISIs increases slightly in Fig. 4b, while the firing rate and ISIs suddenly drop when the parameter $g_M$ is near the critical value of $0.392mS/{\mathit{cm}}^2$.

Fig. 4.

a The firing rate and b ISIs of CA1 pyramidal cell upon increasing the ionic conductance $g_M$ when $g_{\mathit{AHP}}=0.15mS/{\mathit{cm}}^2$

These results show that enhancement of M current reduces the excitability of model neurons, which also suggests that cholinergic deficiency can degrade the excitability of the hippocampal CA1 circuit model. It is consistent with the experimental finding that the higher the concentration of the cholinergic blocker atropine, the lower the excitability of hippocampal CA1 neurons (Greget et al. 2016). Meanwhile, Fig. 5 depicts some typical phase orbits in the V–n phase plane and the corresponding membrane potentials simulated by this hippocampal CA1 circuit model when $g_M$ is taken as $0.15,0.30,0.391,0.393,0.40$ and $0.75.$ It can be seen that when $g_M$ is less than the critical value of $0.392mS/{\mathit{cm}}^2$ (please see Fig. 5A-C), the phase orbits in the V–n phase plane are in limit cycle attractor mode and the membrane potentials are in a continuous discharge state. When $g_M$ is greater than the critical value $0.392mS/{\mathit{cm}}^2$ (please see Fig. 5D-F), the phase orbits of this model transit to the point attractor mode, and the membrane potentials shift to a resting state. Combined with the simulation analysis in Figs. 4 and 5, one can conclude that an increase in $g_M$ diminishes the excitability of model neurons, which may lead to a decrease of SampEn and ApEn in the hippocampal CA1 circuit model. These results suggest that cholinergic deficits resulting in reduced neuronal excitability may contribute to the reduced EEG complexity in AD patients.

Fig. 5.

The phase orbits in V–n phase plane and the corresponding membrane potential when the ionic conductance $g_M$ from (A) to (F) is successively chosen as $0.15,0.3,0.391,0.393,0.40\mathrm{and}0.75mS/{\mathit{cm}}^2$. The (A1-F1) subplot manifests the stable phase orbit after discarding the transient states

Taking the ionic conductance of current ${\mathit{I}}_{\mathit{A}\mathit{H}\mathit{P}}$ as control parameter

In Sect. “Taking the ionic conductance of current I_M as control parameter”, it can be seen that the SampEn and ApEn of the hippocampal CA1 circuit model decreases with increasing M-current, so does the AHP-current cause the similar phenomenon? Therefore, in this subsection, $g_M$ is fixed at $0.10mS/{\mathit{cm}}^2$, and then the ionic conductance $g_{\mathit{AHP}}$ of the current $I_{\mathit{AHP}}$ in pyramidal cells is used as the control parameter to discuss how the enhanced current $I_{\mathit{AHP}}$ affects the SampEn of this hippocampal CA1 circuit model. Figure 6a shows that when $g_{\mathit{AHP}}$ increases from 0, the curve of SampEn first decreases slowly, but SampEn decreases rapidly when $g_{\mathit{AHP}}$ is around 0.41 $mS/{\mathit{cm}}^2$; then SampEn decreases slowly to about 0 as $g_{\mathit{AHP}}$ continues to increase to 1. Figure 6c shows the decline in ApEn when the ionic conductance $g_{\mathit{AHP}}$ steadily rises from 0 to 1 in the model. The critical value of $g_{\mathit{AHP}}$ is also 0.41 $mS/{\mathit{cm}}^2$. These phenomena are similar to the result obtained in Sect. “Taking the ionic conductance of current I_M as control parameter”, which can also imply that the more severe the cholinergic deficit in AD patients (corresponding to larger $g_{\mathit{AHP}}$), the lower the complexity in the hippocampal CA1 circuit model. This result of numerical simulation is consistent with the experimental finding that AD patients have EEG with low complexity (Ab´asolo et al. 2006).

Fig. 6.

a Dependence of SampEn on the ionic conductance $g_{\mathit{AHP}}$ when $g_M=0.10mS/{\mathit{cm}}^2$. b Dependence of SampEn on the ionic conductance $g_{\mathit{AHP}}$ for different $g_M$. c Dependence of ApEn on the ionic conductance $g_{\mathit{AHP}}$ when $g_M=0.15mS/{\mathit{cm}}^2$. d Dependence of ApEn on the ionic conductance $g_{\mathit{AHP}}$ for different $g_M$

Further numerical simulations reveal that, even for different values of ${\mathrm{g}}_{\mathrm{M}}$, the phenomenon of SampEn and ApEn reduction resulting from the enhanced current of $I_{\mathit{AHP}}$ persists in the hippocampal CA1 circuit model. Figures 6b and 7d depict the variation curves of SampEn (see Fig. 6b) and ApEn (see Fig. 6d) with ${\mathrm{g}}_{\mathrm{AHP}}$ for different ${\mathrm{g}}_{\mathrm{M}}$(such as ${\mathrm{g}}_{\mathrm{M}}=0.1,0.15,0.2,0.25\mathrm{and}0.3).$ It can be clearly seen that for different ${\mathrm{g}}_{\mathrm{M}}$, these curves of SampEn and ApEn all fall slowly at first, then abruptly decrease around a critical value, finally drop slowly again to near 0 as ${\mathrm{g}}_{\mathrm{AHP}}$ continues to increase. These curves with similar pattern indicate that the decrease of SampEn and ApEn caused by an increase of ${\mathrm{g}}_{\mathrm{AHP}}$ are robust to the ionic conductance ${\mathrm{g}}_{\mathrm{M}}$. More importantly, as ${\mathrm{g}}_{\mathrm{M}}$ increases, there is a significant leftward shift in SampEn and ApEn curves, meanwhile the ${\mathrm{g}}_{\mathrm{AHP}}$ critical value becomes smaller. This result suggests that the complexity in the hippocampal CA1 circuit model prefers to decrease with increasing ionic conductance ${\mathrm{g}}_{\mathrm{M}}$.

Fig. 7.

a The firing rate and b ISIs of CA1 pyramidal cell upon increasing the ionic conductance $g_{\mathit{AHP}}$ when $g_M=0.10mS/{\mathit{cm}}^2$

In what follows, the underlying dynamical mechanism behind the decrease of SampEn by the enhancement of current $I_{\mathit{AHP}}$ in the hippocampal CA1 circuit model is discussed by nonlinear dynamics analysis. Figures 7a and b show how the firing rate and the corresponding ISIs change as the parameters $g_{\mathit{AHP}}$ increases. Clearly, with increasing $g_{\mathit{AHP}}$, the firing rates initially fall, and ISIs rise slightly. Interestingly, the firing rate and ISIs suddenly drop when the parameter $g_{\mathit{AHP}}$ increase to the critical value of $0.41mS/{\mathit{cm}}^2$. According to these findings, we can conclude that increasing current $I_{\mathit{AHP}}$ decreases the excitability of the neuron model, which implies that cholinergic shortage suppresses neuronal excitability in the hippocampal CA1 circuit model. Meanwhile, Fig. 8 depicts some typical phase orbits in the V–n phase plane and the corresponding membrane potentials simulated by this hippocampal CA1 circuit model when $g_{\mathit{AHP}}$ takes different values (i.e., $g_{\mathit{AHP}}=0.15,0.40,0.42$ and $0.75$). It is not difficult to see that for some $g_{\mathit{AHP}}$ values (i.e. $g_{\mathit{AHP}}=0.15,0.40$) less than the critical value of $0.41mS/{\mathit{cm}}^2$, the stable phase orbit in the V–n phase plane is the limit cycle attractor, and the corresponding membrane potential is in a continuous firing state. For some $g_{\mathit{AHP}}$ values (i.e., $g_{\mathit{AHP}}=0.42,0.75$) that exceed the critical value, the stable phase orbit in the V–n phase plane is an equilibrium point, and the corresponding membrane potential turns into a resting state. In conjunction with the simulation analysis shown in Figs. 8 and 9, it can be seen that an increase in $g_{\mathit{AHP}}$ speeds up the emergence of a stable equilibrium state in the hippocampal CA1 circuit model. This suggests that SampEn and ApEn decline resulting from the enhancement of current $I_{\mathit{AHP}}$ may be due to a reduction of neuronal excitability in the hippocampal CA1 circuit model.

Fig. 8.

Different $g_{\mathit{AHP}}$ in some phase orbits in V–n phase plane and corresponding membrane potential: the ionic conductance $g_{\mathit{AHP}}$ from A to D is successively chosen as $0.15,0.40,0.42\mathrm{and}0.75mS/{\mathit{cm}}^2$. The (A1-D1) subplot manifests the stable phase orbit after discarding the transient states

Fig. 9.

The significant differences of SampEn a and AMI b between the simuated AD and NC groups

Statistical analysis of SampEn and AMI simulated by the model

The above results in Sect. ”Decline of SampEn and ApEn by acetylcholine deficiency” shows that the complexity of SampEn and ApEn sharply decrease when the ionic conductance of current $I_M$ or $I_{\mathit{AHP}}$ goes beyond the critical value ($g_M\approx 0.392mS/{\mathit{cm}}^2,g_{\mathit{AHP}}\approx$ 0.41 $mS/{\mathit{cm}}^2$). As indicated above, we mimic acetylcholine deficiency in AD patients by enhancing currents of $I_M$ and $I_{\mathit{AHP}}$. Thus, in this section, using the ionic conductance of current $I_M$ or $I_{\mathit{AHP}}$ less than (more than) the critical value to simulate the normal control (NC) group (the AD patients), statistical analysis of SampEn as well as AMI between the simulated AD patients and the normal group is firstly investigated. Then, the statistical correlation of SampEn and AMI is also discussed.

Significant difference of SampEn and AMI between the simulated groups

For further statistical analysis of the complexity of SampEn, we choose 20 sets of different model parameters $g_M$ and $g_{\mathit{AHP}}$ to simulate the NC group and the AD patients. As indicted in Figs. 3a and 6a, the parameters of fixing $g_{\mathit{AHP}}=0.15$ and $g_M>0.392$( here $g_M=0.45,0.5,0.55,0.6,0.65$), together with fixing $g_M=0.1$ and $g_{\mathit{AHP}}>0.41$( here $g_{\mathit{AHP}}=0.45,0.5,0.55,0.6,0.65$) are to mimic the AD patients. On the contrary, the parameters of fixing $g_{\mathit{AHP}}=0.0$ and $g_M<0.392$( here $g_M=0.0,0.05,0.1,0.15,0.2$), together with fixing $g_M=0.0$ and $g_{\mathit{AHP}}<0.41$( here $g_{\mathit{AHP}}=0.0,0.05,0.1,0.2,0.25$) are to mimic the NC group. All these simulated parameters are displayed in Table 1, on the same time, the corresponding SampEn of the two groups is also summarized in Table 1. Now, A one-way Analysis of Variance (ANOVA) is employed to assess the statistical differences between the SampEn of the two groups. The result of analysis is showed in Fig. 10a, in which one can see the SampEn values in AD patients are obviously lower compared to the NC group, i.e., there is significant difference between SampEn of the two simulated groups ($p<0.001$). This result is in agreement with the physiological experiment that there are lower EEG sample entropy values in AD patients and a significant difference between the EEG of AD patients and NC human (Ab´asolo et al. 2006). SampEn reflects the rate of new pattern generation when the dimension decreases from m + 1 to m (Richmann and Moorman 2000). A lower SampEn in AD means the chance of new pattern generation is less than in NC. It is possible to obtain the model with the cholinergic deficit, i.e., when the cholinergic function of the brain is impaired, the chance of newly generated information in AD patients decreases.

Table 1.

20 sets of different model parameters $g_M$ and $g_{\mathit{AHP}}$  to simulate the NC group and the AD patients group. The corresponding SampEn and the AMI decline of the two groups is also summarized in Table 1

AD	$g_M$	$g_{\mathit{AHP}}$	SampEn	the AMI rates of decrease	NC	$g_M$	$g_{\mathit{AHP}}$	SampEn	the AMI rates of decrease
1	0.45	0.15	0.0062	− 15.7464	1	0.00	0.00	0.0437	− 23.8977
2	0.50	0.15	0.0034	− 13.5866	2	0.00	0.05	0.0433	− 27.6913
3	0.55	0.15	0.0022	− 12.4016	3	0.00	0.10	0.0431	− 24.1190
4	0.60	0.15	0.0017	− 16.8786	4	0.00	0.15	0.0429	− 23.7886
5	0.65	0.15	0.0007	− 12.0885	5	0.00	0.20	0.0426	− 24.1402
6	0.10	0.45	0.0089	− 14.5727	6	0.05	0.00	0.0437	− 24.0604
7	0.10	0.50	0.0051	− 13.5427	7	0.10	0.00	0.0436	− 24.0792
8	0.10	0.55	0.0035	− 13.0957	8	0.15	0.00	0.0436	− 27.9566
9	0.10	0.60	0.0026	− 13.2700	9	0.20	0.00	0.0434	− 24.1470
10	0.10	0.65	0.0021	− 11.8393	10	0.25	0.00	0.0433	− 24.1893

Fig. 10.

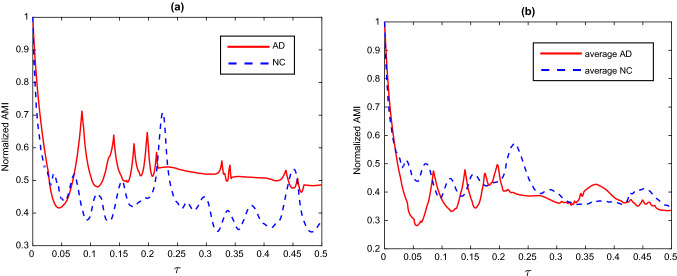
a Two of the normalized AMI curves, one obtained randomly from the AD patient group and the other from the NC group and b The average AMI curves for the NC and AD groups

Next, statistical analysis of the complexity of AMI is carried out. Following the definition of AMI introduced in Sect. ”Complexity measure: AMI”, our simulations show the normalized AMI decrease instantaneously with the initial increase of time delay $\tau$, then it fluctuates up and down and gradually decays upon further increasing $\tau$. To depict vividly, Fig. 11a illustrates two normalized AMI curves, where one is sourced randomly from the AD patient group and the other is sourced randomly from the NC group. In addition, the averaged AMI curves for the NC and AD groups are also respectively depicted in Fig. 11b, whose evolutions are similar with the case of single normalized AMI curve. The AMI rate of decrease is estimated by the slope of AMI curve from the time delay 0 to the time delay where the first relative minimum of AMI is obtained. All the AMI rates of decrease for the two groups are included in Table 1. Statistical differences between the AMI rate of decrease of the two groups are checked by the method of ANOVA, and the result is displayed in Fig. 10b. We can observe that AMI declines more slowly in AD patients compared to the NC group, i.e., there is significant difference between the AMI rate of decrease of the two simulated groups ($p<0.001$). The simulated result accord with the statistical analysis of EEG experiments, in which AD patients’ EEG-AMI declines more slowly with time delay compared to controls (Ab´asolo et al. 2008). The AMI can reveal the information flow of the signal (Jeong at el. 2001). The slower rate AMI of decline in AD patients suggests that the cholinergic deficit in AD patients affects the brain’s information flow and generation.

Fig. 11.

SampEn values versus the AMI rates of decrease for the simulated subjects in Table 2 sets (star) as well as the simulated AD patients (circle) and the simulated NC group (square) in Table 1. Pearson correlation coefficient between SampEn values and the AMI rates of decrease is $\rho =-0.9424$. The straight-line fits the data in a least-squares sense has been plotted

Statical correlation of SampEn and AMI

The above results demonstrate that both the SampEn and the AMI rate of decrease are significantly different between the simulated AD patients and the NC group. Compared with the NC group, the SampEn is obvious lower and the AMI rate of decrease is less negative in the AD patients, which suggests that the complexity of brain rhythm in AD patients is more lower than that of normal human. In fact, the two complexity measures of SampEn and AMI are intrinsically correlated. To reveal the statistical correlation between these two measures, 10 sets of model parameters near the critical values (in Figs. 3a and 6a) are also chosen to mimic the subjects of AD patients and NC. The detailed parameters of ionic conductance $g_{\mathit{AHP}}$ and $g_M$, as well as the corresponding SampEn and the AMI rates of decrease are summarized in Table 2. Combining the data in Tables 1 and 2, the SampEn values versus the AMI rates of decrease are depicted in Fig. 11, from which a negative correlation between them is obvious and the Pearson correlation coefficient is $\rho =-0.9424$. As described in Sect. ”Complexity measure: SampEn” and “Complexity measure:AMI”, this negative correlation is due to the fact SampEn assigns larger values to more complex time series, in which a more negative value of the AMI rates of decrease is associated with higher complexity. This strong statistical correlation indicates that the AMI rates of decrease can be considered as a complementary tool to estimate the complexity of time series for the AMI can inspect time series at different time scales.

Table 2.

The estimated SampEn and the AMI rate of decrease for the other 10 sets of model parameters near the critical values

	$g_M$	$g_{\mathit{AHP}}$	SampEn	The AMI rates of decrease
1	0.3921	0.15	0.0201	− 18.6426
2	0.3922	0.15	0.0190	− 20.1904
3	0.3923	0.15	0.0185	− 20.2594
4	0.3924	0.15	0.0181	− 21.4060
5	0.3925	0.15	0.0178	− 21.0989
6	0.10	0.415	0.0193	− 17.4660
7	0.10	0.420	0.0168	− 16.3164
8	0.10	0.425	0.0147	− 15.4271
9	0.10	0.430	0.0131	− 15.4512
10	0.10	0.435	0.0117	− 15.2815

Conclusion and discussion

As indicated in the Introduction, AD may affect the cholinergic concentration in the hippocampus, thereby altering the dynamic behavior of neurons in the hippocampal region. Studying computational models is also vital for understanding the pathogenic mechanisms of AD. Moreover, the interactions between hippocampal neurons are still not considered in the neurocomputational model with cholinergic effects. Meanwhile, experimental EEG studies have revealed that one of the main electrophysiological effects of AD is reduced EEG complexity. Most complexity analyses on AD are used for statistical analysis of AD patients’ EEG, and rarely complexity analysis is applied to neurocomputational models.

Motivated by these findings and analyses, the work presents a new neuronal diversity-leading comprehensive CA1 circuit model with cholinergic effects based on the Hodgkin-Huxley (HH) model neurons, using complexity analysis to explore the reduced EEG complexity of cholinergic deficiency in AD. This model includes three kinds of neurons of pyramidal cell, basket cell and OLM cell, in which they are interconnected by chemical synaptic coupling. Two new currents of M-current $I_M$ and calcium-activated potassium current $I_{\mathit{AHP}}$ are newly introduced to the pyramidal and basket cells to depict the cholinergic input received from the medial septal nucleus.

Then, by potentiating currents $I_M$ and $I_{\mathit{AHP}}$ to mimic cholinergic deficiency in AD, we explore how the cholinergic deficiency resulting from AD influences the complexity in this constructed model by estimating SampEn and ApEn. SampEn and ApEn are embedding entropy, and they can better quantify the regularity of the signal (Dauwels et al. 2010; Aydın et al. 2019; Çetin et al. 2022). The numerical results indicate that larger ionic conductance of currents $I_M$ and $I_{\mathit{AHP}}$ (corresponding to a more severe cholinergic deficit in AD patients) can induce lower SampEn and ApEn in this hippocampal CA1 circuit model. The simultaneous use of both entropy metrics enriches the reliability of the conclusion that the cholinergic deficit leads to a decrease in model complexity. In an extension of this work, we also analyze the model complexity under cholinergic deficiency using both permutation entropy and fuzzy entropy. The conclusions are similar in the more severe the cholinergic deficit is, the more these entropy values decrease. These phenomena suggest that the more severe the cholinergic deficit in AD patients, the less complex the hippocampal CA1 circuit model is. The decreased entropy values in AD patients also reflect a decreased information processing flexibility in the impaired brain caused by the cholinergic deficit. Model simulations are consistent with the general hypothesis that complexity decreases when brain cholinergic function is impaired. At the same time, the dynamical mechanism behind the decreased SampEn and ApEn is discussed by nonlinear dynamical analysis. We find that an increase in ionic conductance can diminish the excitability of model neurons, which may lead to a decrease of SampEn in the hippocampal CA1 circuit model. The result is consistent with the experimental finding that the higher the concentration of the cholinergic blocker atropine, the lower the excitability of hippocampal CA1 neurons (Greget et al. 2016). These results suggest that cholinergic deficits resulting in reduced neuronal excitability may contribute to the reduced EEG complexity in AD patients.

Next, using the ionic conductance of current $I_M$ or $I_{\mathit{AHP}}$ less than (more than) the critical value to simulate the NC group (the AD patients), statistical analysis of SampEn and AMI between the simulated AD patients and the simulated normal group are investigated. The results imply that compared with the NC group, the SampEn is obviously lower and the AMI rate of decrease is less negative in the AD patients. Moreover, both the SampEn and the AMI rate of decrease are significantly different between the simulated groups. Entropy is the rate of new information generated (Lake et al. 2002). The model with small SampEn corresponds to a low level of newly generated information. AMI can reveal the information flow of the signal (Jeong et al. 2001). These reveal that cholinergic deficits in AD patients affect brain information flow and generation, which may also explain the impaired cognitive function in AD patients due to cholinergic deficits. In addition, the statistical correlation of SampEn and AMI is carried out by the Pearson correlation method, from which an apparent negative correlation between them is revealed with the Pearson correlation coefficient $\rho =-0.9424$. This strong statistical correlation indicates that the decrease of AMI rate can be considered as a complementary tool to estimate the complexity of time series, for the AMI can inspect time series at different time scales.

The above-simulated results accord well with the characteristics of EEG complexity in previous physiological EEG experiments in AD patients and the age-match human (Ab´asolo et al. 2006, 2008). Our modeling and complex analysis are expected to provide a deeper understanding of the reduced EEG complexity resulting from cholinergic deficiency; at the same time, they may provide new insights into the pathogenesis of AD in the cholinergic hypothesis.

Appendix

The model is constructed as stated in Model Preparation, and the parameters of the model are as follows. All of the ionic currents are modelled by the Hodgkin–Huxley type, thus the gating variable $x$ satisfies the following first-order kinetics ($x$ can be $h,n,z,r$ and $b$):

$$\frac{\mathit{dx}}{\mathit{dt}}={\phi }_x\frac{x_{\infty }\left(V\right)-x}{{\tau }_x}$$ A1

This equation will be used to calculate all of the gating variables. $V$ are initially set as $V=-65$.

Neuronal dynamics

The Pyramidal cell model is based on the work of Peng et al. (2016) and Jiang et al. (2020), whose governing equations are as follows:

$$Pramidal:C\times \frac{d{V}_P}{\mathit{dt}}=-I_L-I_{\mathit{Na}}-I_K-I_A-I_M-I_{\mathit{AHP}}-I_{\mathit{syn}}+I$$

Channel	Definition	Explicit expression
$I_L$	$g_L(V-E_L)$
$I_{\mathit{Na}}$	$g_{\mathit{Na}}{m}_{\infty }^{3}h(V-E_{\mathit{Na}})$	$m_{\infty }\left(V\right)=1/(1+\exp (-\frac{V+30}{9.5}))$ $h_{\infty }\left(V\right)=1/(1+\exp ((V+45)/7))$ ${\tau }_h\left(V\right)=0.1+0.75(1/(1+\exp (V+40.5)/6))$
$I_K$	$g_K{n}^4(V-E_{\mathit{Na}})$	$n_{\infty }\left(V\right)=1/(1+\exp (-(V+43.1)/7.3))$ ${\tau }_n\left(V\right)=0.1+0.5(1/(1+\exp (V+27)/15))$
$I_M$	$g_{M}z(V-E_{\mathit{Na}})$	$z_{\infty }\left(V\right)=1/(1+\exp (-(V+39)/5))$ ${\tau }_z=75ms$
$I_{\mathit{AHP}}$	$g_{\mathit{AHP}}q(V-E_K)$	$r_{\infty }\left(V\right)=1/(1+\exp (-(V+20)/10))$ $\frac{d{[{\mathit{Ca}}^{2+}]}_i}{\mathit{dt}}=-v{g}_{\mathit{Ca}}{r}^2\left(V,-,E_{\mathit{Ca}}\right)-\frac{{[{\mathit{Ca}}^{2+}]}_i}{{\tau }_{\mathit{Ca}}}$ $\frac{\mathit{dq}}{\mathit{dt}}=\frac{q_{\infty }\left({\left[{\mathit{Ca}}^{2+}\right]}_i\right)-q}{{\tau }_q}$ $q_{\infty }\left({\left[{\mathit{Ca}}^{2+}\right]}_i\right)=1/(1+16/({\left({\left[{\mathit{Ca}}^{2+}\right]}_i\right)}^4))$ ${\tau }_{\mathit{Ca}}=13ms;{\tau }_q=450ms;{\tau }_r=1ms$ $v=0.13\frac{{\mathit{cm}}^2}{ms-\mu A}$
$I_A$	$g_A{a}_{\infty }^{3}b(V-E_K)$	$a_{\infty }\left(V\right)=1/(1+\exp (-(V+50)/20))$ $b_{\infty }\left(V\right)=1/(1+\exp ((V+80)/6))$ ${\tau }_b=15ms$

The values of the other parameters are $\varphi =1$, $g_L=0.05$, $g_{\mathit{Na}}=35$, $g_K=10,{g_{\mathit{Ca}}=0.02,g}_A=1,E_L=-50,E_{\mathit{Na}}=55,E_K=-90,E_{\mathit{Ca}}=120$.

The basket cell model is based on the work of (Wang and Buzsaki 1996; Wang 2002; Zou et al. 2011, 2012) and the two new introduced currents $I_M$ and $I_{\mathit{AHP}}$ of our work, whose governing equations are as follows:

$$Basket:C\times \frac{d{V}_B}{\mathit{dt}}=-I_L-I_{\mathit{Na}}-I_K-I_M-I_{\mathit{AHP}}-I_{\mathit{syn}}+I$$

Channel	Definition	Explicit expression
$I_L$	$g_L(V-E_L)$
$I_{\mathit{Na}}$	$g_{\mathit{Na}}{m}_{\infty }^{3}h(V-E_{\mathit{Na}})$	${\alpha }_m\left(V\right)=-0.1(V+35)/\exp [-0.1\left(V,+,35\right)-1]$ ${\beta }_m\left(V\right)=4\exp [-\left(V,+,60\right)/18]$ $m_{\infty }=\frac{{\alpha }_m}{{\alpha }_m+{\beta }_m}$ ${\alpha }_h\left(V\right)=0.07\exp [-\left(V,+,58\right)/20]$ ${\beta }_h\left(V\right)=1/\exp [-0.1\left(V,+,28\right)+1]$ $h_{\infty }=\frac{{\alpha }_h}{{\alpha }_h+{\beta }_h}$
$I_K$	$g_K{n}^4(V-E_{\mathit{Na}})$	${\alpha }_n\left(V\right)=-0.01(V+34)/\exp [-0.1\left(V,+,34\right)-1]$ ${\beta }_n\left(V\right)=0.125\exp [-\left(V,+,44\right)/80]$ $n_{\infty }=\frac{{\alpha }_n}{{\alpha }_n+{\beta }_n}$
$I_M$	$g_{M}z(V-E_{\mathit{Na}})$	$z_{\infty }\left(V\right)=1/(1+\exp (-(V+39)/5))$ ${\tau }_z=75ms$
$I_{\mathit{AHP}}$	$g_{\mathit{AHP}}q(V-E_K)$	$r_{\infty }\left(V\right)=1/(1+\exp (-(V+20)/10))$ $\frac{d{[{\mathit{Ca}}^{2+}]}_i}{\mathit{dt}}=-v{g}_{\mathit{Ca}}{r}^2\left(V,-,E_{\mathit{Ca}}\right)-\frac{{[{\mathit{Ca}}^{2+}]}_i}{{\tau }_{\mathit{Ca}}}$ $\frac{\mathit{dq}}{\mathit{dt}}=\frac{q_{\infty }\left({\left[{\mathit{Ca}}^{2+}\right]}_i\right)-q}{{\tau }_q}$ $q_{\infty }\left({\left[{\mathit{Ca}}^{2+}\right]}_i\right)=1/(1+16/({\left({\left[{\mathit{Ca}}^{2+}\right]}_i\right)}^4))$ ${\tau }_{\mathit{Ca}}=13ms;{\tau }_q=450ms;{\tau }_r=1ms$ $v=0.13\frac{{\mathit{cm}}^2}{ms-\mu A}$

The values of the other parameters are $\varphi =1$, $g_L=0.1$, $g_{\mathit{Na}}=35$, $g_K=9,g_M=0.1,{g_{\mathit{Ca}}=0.02,g}_{\mathit{AHP}}=0.15,E_L=-65,E_{\mathit{Na}}=55,E_K=-90,E_{\mathit{Ca}}=120$.

The OLM cell model is based on the work of (Wang and Buzsaki 1996; Wang 2002; Zou et al. 2011, 2012), whose governing equations are as follows:

$$OLM:C\times \frac{d{V}_O}{\mathit{dt}}=-I_L-I_{\mathit{Na}}-I_K-I_{\mathit{syn}}+I$$

Channel	Definition	Explicit expression
$I_L$	$g_L(V-E_L)$
$I_{\mathit{Na}}$	$g_{\mathit{Na}}{m}_{\infty }^{3}h(V-E_{\mathit{Na}})$	${\alpha }_m\left(V\right)=-0.1(V+35)/\exp [-0.1\left(V,+,35\right)-1]$ ${\beta }_m\left(V\right)=4\exp [-\left(V,+,60\right)/18]$ $m_{\infty }=\frac{{\alpha }_m}{{\alpha }_m+{\beta }_m}$ ${\alpha }_h\left(V\right)=0.07\exp [-\left(V,+,58\right)/20]$ ${\beta }_h\left(V\right)=1/\exp [-0.1\left(V,+,28\right)+1]$ $h_{\infty }=\frac{{\alpha }_h}{{\alpha }_h+{\beta }_h}$
$I_K$	$g_K{n}^4(V-E_{\mathit{Na}})$	${\alpha }_n\left(V\right)=-0.01(V+34)/\exp [-0.1\left(V,+,34\right)-1]$ ${\beta }_n\left(V\right)=0.125\exp [-\left(V,+,44\right)/80]$ $n_{\infty }=\frac{{\alpha }_n}{{\alpha }_n+{\beta }_n}$

The values of the other parameters are $\varphi =1$, $g_L=0.1$, $g_{\mathit{Na}}=35$, $g_K=9,E_L=-65,E_{\mathit{Na}}=55,E_K=-90$.

The synaptic connection definition is based on the work of (Wang and Buzsaki 1996; Wang 2002; Zou et al. 2011, 2012), there are three types of synaptic neurotransmitters, the inhibitory GABA_A, the excitatory NMDA and AMPA.

The GABA_A inhibitory post synaptic current is described as

$$GAB{A}_A:I_{\mathit{GABA}}=g_{\mathit{syn}}s\left(V-E_{\mathit{GABA}}\right)$$

where the activation variable $s$ is calculated by $ds/dt=\alpha F\left(V_{\mathit{pre}}\right)\left(1,-,s\right)-\beta s.$ The $V_{\mathit{pre}}$ is the presynaptic neuron membrane potential, $F\left(V_{\mathit{pre}}\right)=1/\left[1,+,\exp ,\left(-,V_{\mathit{pre}},/,K\right)\right].$ Parameters for different neurons couples are: $\alpha =10,\beta =0.1,K=2,$ $E_{GAB{A}_A}=-80,g_{\mathit{syn}}=2.76$ in $\mathrm{basket}-\mathrm{pyramidal};\alpha =20,\beta =0.1,K=2$, $E_{GAB{A}_A}=-80$, $g_{\mathit{syn}}=1.76$ in OLM-basket;$\alpha =20,\beta =0.1,K=2,$ $E_{GAB{A}_A}=-85,g_{\mathit{syn}}=1.76$ in OLM-pyramidal.

The AMPA and NMDA excitatory post synaptic currents are described as

$$AMPA:I_{\mathit{AMPA}}=g_{\mathit{AMPA}}s\left(V-E_{\mathit{AMPA}}\right)$$

$$NMDA:I_{\mathit{NMDA}}=g_{\mathit{NMDA}}B\left(V\right)s\left(V-E_{\mathit{NMDA}}\right)$$

s is updated as $\frac{\mathit{ds}}{\mathit{dt}}=\alpha [T]\left(1,-,s\right)-\beta s$, $\left[T\right]=T_{\mathit{max}}/[1+\exp \left(-,V_{\mathit{pre}},+,V_p\right)/K_p],$ $V_p=2,$ $K_p=5,B\left(V\right)$ is calculated by $B\left(V\right)=1/\{1+\exp \left(-,0.062,V\right)\left[{\mathit{Mg}}^{2+}\right]/3.5\}$,where $\left[{\mathit{Mg}}^{2+}\right]=1mM$ by default. The $\alpha$ and $\beta$ for AMPA and NMDA are $\alpha =1.1,\beta =0.19$ and $\alpha =0.072,\beta =0.0066,$ respectively. $E_{\mathit{NMDA}}=E_{\mathit{AMPA}}=0.$ From pyramidal to basket neurons $g_{\mathit{AMPA}}=0.1$, and from pyramidal to OLM neurons $g_{\mathit{AMPA}}=1.35$ and$g_{\mathit{AMPA}}=0.625$.

The membrane capacitance $C=1\mu F/{\mathit{cm}}^2$ for all equations, therefore it will be ignored. The τ in ($\mathit{ms}$); $E$ and $V$ in ($\mathit{mV}$); $I$ in ($\mu A/{\mathit{cm}}^2$); $g$ in ($mS/{\mathit{cm}}^2$); $\alpha$ and $\beta$ in (${\mathit{ms}}^{-1}$); $K$ in ($\mu M$) and the rest are dimensionless. The numerical simulation method for all equations is to Euler solver in Matlab R2015a simulating environment, using a time step of 0.01 ms.

Author contributions

Li YZ and Yang XL built the model; Li YZ and Yang XL performed the study; Yan SL and Sun ZK compiled and analyzed the data; Li YZ and Yang XL wrote the paper; Yan SL and Sun ZK reviewed and edited.

Data availability

Not applicable.

Declarations

Conflict of interest

The authors declare no conflict of interest or competing interests.