Abstract
Traditionally considered a homogeneous cell type, hippocampal pyramidal cells have been recently shown to be highly diverse. However, how this cellular diversity relates to the different hippocampal network computations that support memory-guided behavior is not yet known. We show that the anatomical identity of pyramidal cells is a major organizing principle of CA1 assembly dynamics, the emergence of memory replay, and cortical projection patterns in rats. Segregated pyramidal cell subpopulations encoded trajectory and choice-specific information or tracked changes in reward configuration respectively, and their activity was selectively readout by different cortical targets. Furthermore, distinct hippocampo-cortical assemblies coordinated the reactivation of complementary memory representations. These findings reveal the existence of specialized hippocampo-cortical subcircuits and provide a cellular mechanism that supports the computational flexibility and memory capacities of these structures.
Introduction
Neural ensemble interactions in the hippocampus and associated cortical structures support learning and memory. Hippocampal principal cells are tuned to specific locations in the environment (’place cells’)1. The same cells that encoded recent spatial experiences are reactivated during sleep and rest periods, coordinated by synchronous network events known as sharp-wave ripples (SWRs)2. The sequential activation of hippocampal place cell ensembles during behavior and their subsequent reactivation during rest periods are considered one of the cellular hallmarks of memory, that generalizes beyond the spatial domain to other types of episodic memory 3–7. Ensemble reactivation during SWRs, generated in the CA1 area of the hippocampus, broadcasts memory representations to the rest of the brain, a process that supports memory consolidation, retrieval, planning, prospective, and retrospective coding2,8–14.
Despite this multiplicity of functions, the hippocampus has been traditionally conceived as being composed of functionally homogenous principal cells in each of its subregions. Contrary to this notion, recent studies have highlighted that hippocampal pyramidal cells are indeed very diverse in their molecular, developmental, anatomical, and physiological characteristics15–23. CA1 principal cell heterogeneity strongly correlates with their radial (depth) position within the pyramidal layer. Neurons located in either the deep, closer to the stratum oriens, or superficial, closer to the stratum radiatum, sublayers of CA1 differ in their embryological origins, morphology, electrophysiological properties, and connectivity15,20–22,24–31. To date, it is not yet understood how this cellular diversity relates to the different computational operations and functional correlates displayed by the hippocampus during navigation and learning. Different processing modules within the CA1 region could enable the formation of complementary representations of behaviorally relevant information that can be flexibly combined and routed to different downstream target areas to support memory-guided behaviors.
To investigate how hippocampal cellular heterogeneity supports diverse memory functions, we examined the dynamic organization and behavioral correlates of large neuronal ensembles in the hippocampus and two of its major targets, the medial entorhinal (MEC) and prefrontal (PFC) cortices in rats during memory tasks and sleep. We analyzed the firing dynamics of ∼ 10, 000 hippocampal pyramidal cells and found that anatomically related neurons (from the same sublayer) formed functional assemblies, reactivated together during SWRs, and had similar spatial tuning and functional correlates. While deep CA1 pyramidal cells were the major contributors to SWRs and assemblies, superficial CA1 cells were specifically recruited during the replay of novel experiences and drove memory formation. Deep CA1 pyramidal cells were a major source of monosynaptic inputs to the PFC and likely drove the reactivation of prefrontal ensembles during memory consolidation. On the other hand, superficial CA1 pyramidal cells projected preferentially to MEC and determined the temporal dynamics of entorhinal reactivation during SWRs. These two hippocampal subpopulations encoded and reactivated different types of information during memory-guided behavior. Superficial CA1 place cells preferentially encoded context identity and displayed prospective coding of trajectory and choice, while deep CA1 place cells tracked changes in reward configuration. These two hippocampal subpopulations, in coordination with either PFC or MEC assemblies, formed complementary representations of task variables. We propose that SWRs carry a multiplexed code in which different types of task-related information are encoded conjunctively but preferentially routed to different cortical target areas by deep and superficial CA1 pyramidal cells.
Results
Anatomical organization of hippocampal assembly dynamics and memory replay
To map the functional diversity of pyramidal cells along the radial axis of CA1, we examined a large number of simultaneously recorded neurons using high-density silicon probes in rats (Fig. 1A). The stereotypical depth profile of SWRs in CA1 and the precise electrode geometry of silicon probes allowed us to divide the pyramidal layer into deep, middle, and superficial sublayers and classify all recorded cells accordingly (Fig. 1B and Fig. S1; cells in 49 rats, Table S122,32). In agreement with previous reports, we found that deep (CA1deep) and superficial (CA1sup) pyramidal cells differ in some of their physiological properties such as bursting, average firing rate, and theta phase firing preference during REM-sleep (Fig. S1,22,23,27,28,31).
Figure 1: Anatomical organization of hippocampal assembly dynamics.
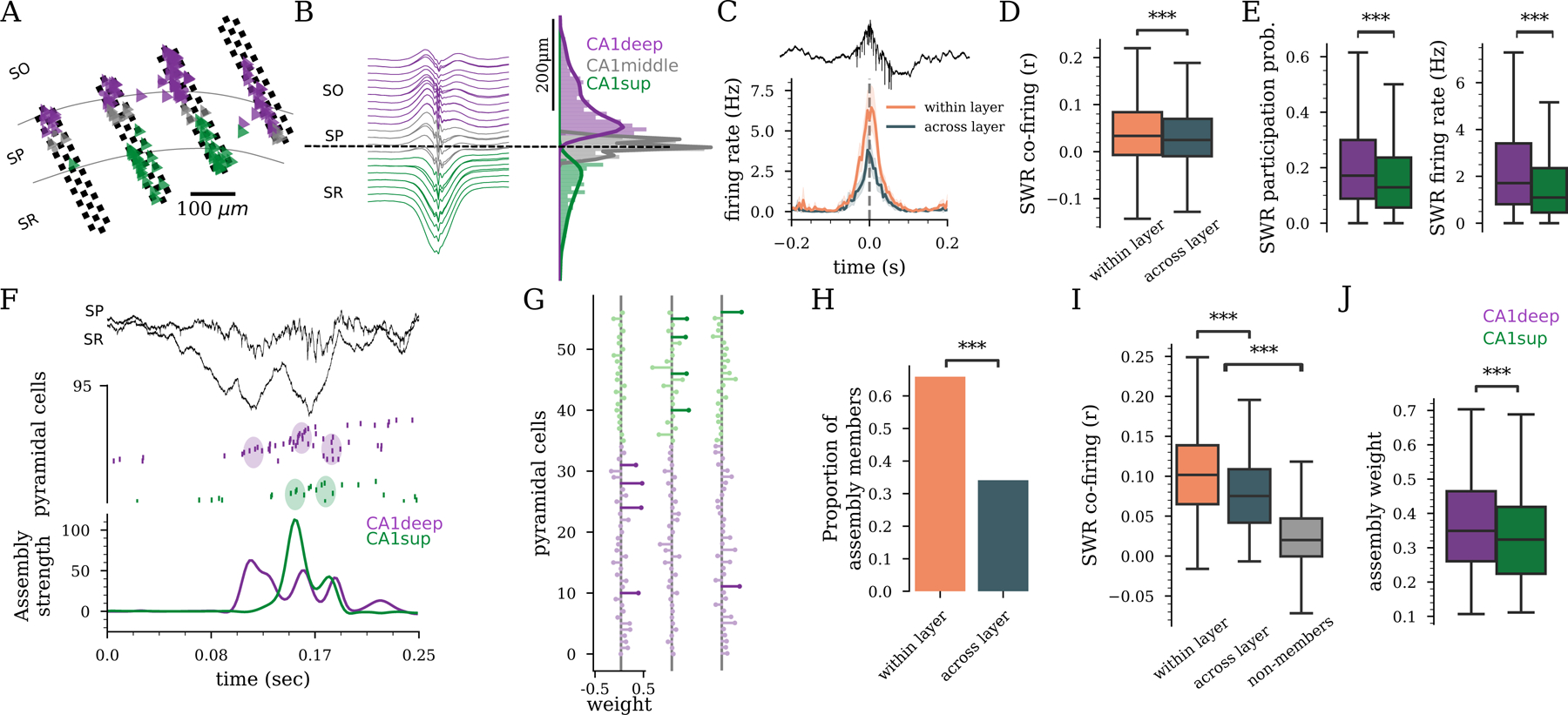
A) Schematic of a 128-channel probe across CA1 sublayers: stratum oriens (SO), pyramidal layer (SP), stratum radiatum (SR) with an overlay of pyramidal cell’s soma’s (triangles) from deep (purple) to superficial (green). B) Left: Average SWR profile. Right: distribution of CA1deep, CA1middle, and CA1sup pyramidal cells. C) Example SWR cross-correlogram of cells pairs within and across sublayers. D) Within and across sublayer SWR pairwise co-firing (771,414 cell pairs, 0.033 vs. 0.024 median r, , Linear mixed-effects model (LME)). E) SWR participation probability and firing rate for CA1deep and CA1sup (, LME). F) SWR (LFP on top) with cell firing (middle raster) and activation of a CA1deep and a CA1sup assembly (bottom). Color circles indicate spikes corresponding to peaks in assembly activation. G) Example assembly weights. Length indicates weight. Assembly members are darker. H) Fraction of assemblies in which all members belonged to the same sublayer (’within layer’) or to different ones (’across layer’) (n=436 assemblies, ,). I) SWR co-firing of assembly members from the same or different CA1 sublayers and non-member neurons (500,968 cell pairs, , LME). J) Contribution to assembly (weight) for CA1deep and CA1sup member neurons (, LME). B-J) CA1deep (3,851), CA1middle (2,878), and CA1sup (1,966) pyramidal cells in 49 rats.
In cortical areas, neurons with similar receptive fields and co-activity patterns tend to cluster anatomically 33–35. On the other hand, the hippocampus has been traditionally conceived as having a ’salt-and-pepper’ or random organization, where the correlated firing dynamics of its principal cells are independent of their anatomical location 36–38. To investigate whether CA1deep and CA1sup cells are functionally correlated, we first analyzed their firing during SWRs, as these are events of enhanced network synchrony39. We found that pyramidal cells of the same sublayer were more likely to fire together during SWRs compared to cells of different sublayers (Fig. 1C–D)21. Although both CA1deep and CA1sup cells were strongly recruited during SWRs, CA1deep had a higher participation probability and fired more during SWRs compared to CA1sup (Fig. 1E). These findings provide evidence that CA1 firing dynamics are influenced by the anatomical location of pyramidal cells.
The synchronous co-activation of pyramidal cells that form functional ”assemblies” has been proposed as the building block of hippocampal and cortical representations37,40–42. To analyze CA1 pyramidal cell assemblies, we performed unsupervised detection of recurrent co-activity firing patterns during task and resting epochs using previously established methods (Fig. 1F;3,41,43,44. We found a strong anatomical bias in assembly cellular composition (Fig. 1F–H). In two-thirds of assemblies, all members belonged to the same sublayer (Fig. 1G–H). Pairs of assembly members from the same sublayer co-fired during SWRs more often than members of different sublayers or non-member cells (Fig. 1I). These results were replicated when we excluded cell pairs from the same shank (Fig. S2). Overall, CA1deep contributed more to assembly activation than CA1sup cells (Fig. 1J). We found similar results when applying these analyses to theta activity during behavior, rather than SWRs (Fig. S2), indicating that a higher synchronization between cells from the same sublayer is a general principle across brain states and behaviors. Taken together, these results indicate that deep and superficial CA1 pyramidal cells preferentially synchronize with cells of the same type, suggesting that their anatomical identity plays an important role in the functional organization of hippocampal network dynamics.
The reactivation of hippocampal place cell sequences during SWRs (’replay’) recapitulates recent experiences and supports memory processes 45,46. To assess the contribution of CA1deep and CA1sup to memory, we analyzed SWR-associated replay during the exploration of mazes and subsequent sleep sessions (Table S2). We trained a Bayesian decoding algorithm on place cell activity on the linear track (Fig. 2A and Fig. S3) and applied it to all SWR-associated spiking sequences to identify trajectory replay events (Fig. 2B and Fig. S3). Given the higher SWR participation of CA1deep (Fig. 1E,J), we expected CA1deep cells to also dominate replay events. Surprisingly, it was CA1sup cells that were specifically recruited and fired more during replay events than CA1deep, (Fig. 2C–F). We separately confirmed the replay participation and firing rate results with an alternative replay detection technique 47 and found similar results (participation:, firing rate:). To more directly test the contribution of CA1deep and CA1sup to replay sequences, we applied a cell-specific shuffling approach as previously described 48. On average CA1sup had a higher per-cell contribution to replay than CA1deep (Fig. 2E). This effect is also demonstrated by the faster replay quality decrease by progressively removing individual CA1sup cells compared to CA1deep cells (Fig. 2F). As a complementary approach, we analyzed the reactivation of cell assemblies during SWRs in the sleep following the task. We found a stronger reactivation of CA1sup compared to CA1deep assemblies (Fig. 2G), in line with the previous replay results.
Figure 2: Anatomical organization of hippocampal memory replay.
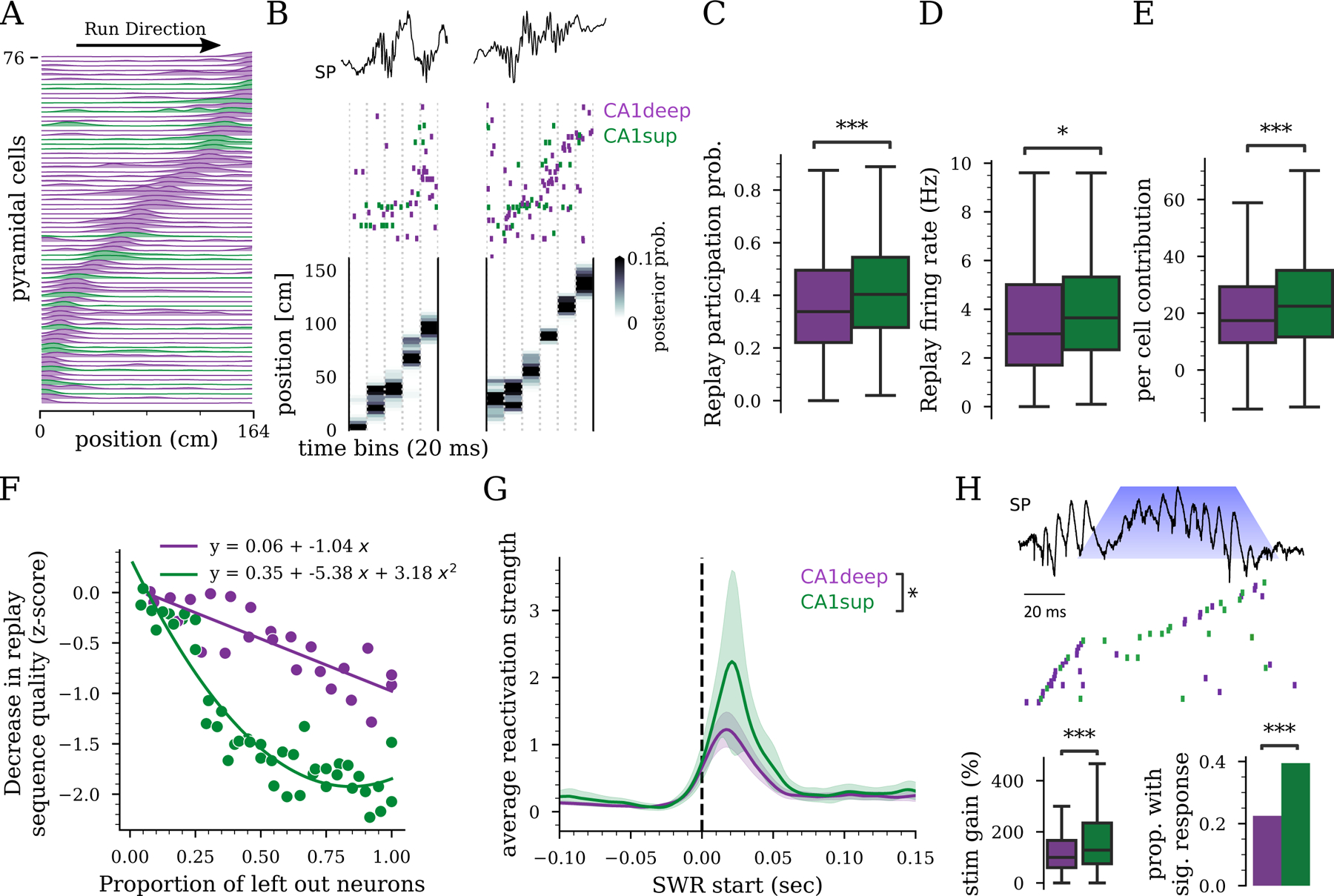
A) Place fields on a linear track sorted by the location of the peak firing rate. B) Example raster (middle) during a SWR (CA1 on LFP top) and decoded animal position (bottom) for two replay events. Units in the raster (one per row) were sorted according to the position of their place fields in the maze (A). C) Probability of participation in replay events (CA1deep vs. CA1sup , GLM, Fig. S2). D) Firing rate in replay events (, rank-sum test). E) Per cell contribution to replay (CA1deep vs. CA1sup , rank-sum test). F) Example showing how leaving out CA1deep or CA1sup cells decrease replay sequence quality differently. G) SWR-triggered average reactivation strength in post-task sleep for CA1deep and CA1sup assemblies (, rank-sum test, 197 assemblies). The shaded band indicates 95% confidence intervals. H) Top: optogenetically prolonged SWR and cell sequence in delayed alternation memory task 49. Blue cone indicates when light was delivered (100ms pulse), triggered by the detection of a SWR. Bottom left: Firing rate increase in prolonged SWR vs. baseline (n=467 CA1deep / 289 CA1sup, 5 rats, , LME). Bottom right: Proportion of CA1deep and CA1sup recruited by stimulation (n=1074 events, ,). C-E,G) n = 685 CA1deep, 248 CA1sup, 12 rats
This preferential recruitment of CA1sup cells led to the hypothesis that CA1sup cells are preferentially involved in memory formation. Given that we have previously shown that optogenetic prolongation of SWRs during learning improves rats’ performance in a delayed alternation memory task49, we analyzed whether this improvement was mediated by CA1sup cells. Animals learned a spatial alternation delayed memory task in an M-maze for 10 days49. We analyzed the recruitment of CA1 cells during closed-loop optogenetic SWR stimulation during the task. Indeed, our optogenetic manipulation prolonged spontaneous SWRs by preferentially recruiting CA1sup cells, rather than CA1deep cells, into the ongoing spiking sequence (Fig. 2H). Optogenetic stimulation tended to recruit almost exclusively cells that did not fire previously in the same SWR (Fig. S3F), thus increasing the total fraction of cells that participate in the sequence. Such differences between the optogenetic recruitment of CA1sup and CA1deep cells were not observed in response to similar pulses delivered at random times (Fig. S3G). These effects were not due to differences in the expression of channelrhodopsin within CA1deep or CA1sup cells (Fig. S3H). Together, these findings are consistent with the hypothesis that the CA1sup cell population preferentially contributes to memory processes.
Hippocampo-cortical circuits for selective routing of information
CA1 broadcasts hippocampal memory representations to multiple areas of the brain during SWRs10,12,13,50–54. To investigate whether CA1deep and CA1sup selectively interact with different downstream target areas, we focused on two hippocampal main output regions implicated in memory-guided behavior: MEC and PFC. First, we examined dorsal hippocampal projections to these regions using fluorescent retrograde tracers (Fig. 3A and Fig. S4). Most monosynaptic inputs from CA1 to MEC originated in the superficial sublayer, while most inputs to PFC (much sparser) originated from deep pyramidal cells (Fig. 3B–C and Fig. S4). To validate the anatomical distribution of CA1 cells targeting MEC and PFC, we performed immunostaining against a known marker of CA1sup cells, calbindin55. The majority of MEC targeting CA1 cells were co-labeled with calbindin, but not PFC targeting CA1 cells (Fig. S4E–F), supporting our observation that CA1sup inputs largely target the MEC, whereas the PFC receives primarily CA1deep inputs. Furthermore, we found a larger proportion of MEC than PFC-projecting pyramidal cells and only a small minority of dual-projecting ones (Fig. 3C), suggesting that these segregated subpopulations may support selective communication with different target areas.
Figure 3: CA1deep and CA1sup have divergent projections to downstream cortical areas.
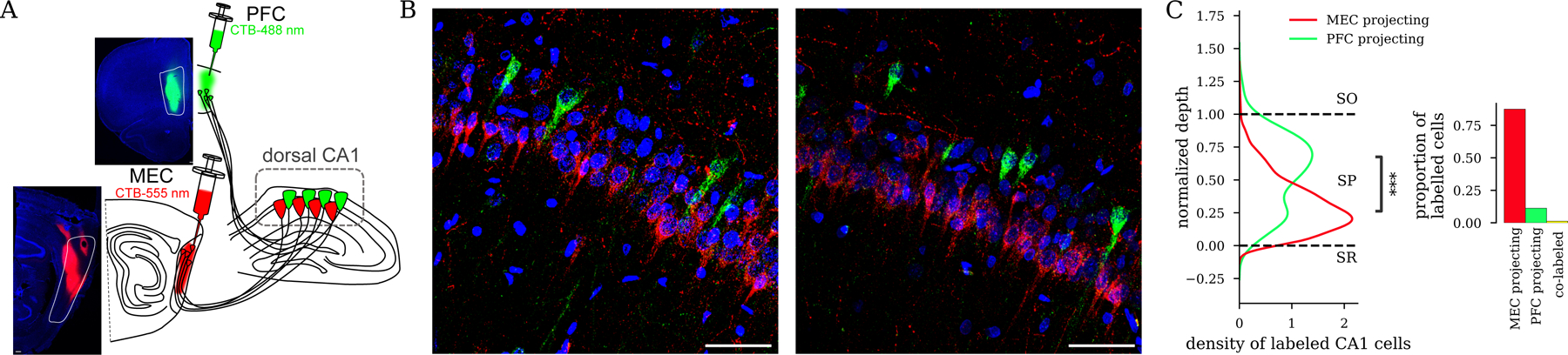
A) Green and red fluorescent retrograde tracers (Alexa Fluor-CTB conjugates) were injected in PFC and MEC to label hippocampal projecting cells in the same hemisphere. B) Representative histology from the same animal as A with CA1deep-PFC projecting (green) and CA1sup-MEC projecting (red) cells labeled in the dorsal hippocampus. Blue: DAPI, Red: CTB-555, Green: CTB488. C) Quantification of soma location for labeled cells ( PFC projecting / 2,167 MEC projecting / 31 co-labeled cells in 3 rats, , rank-sum test, PFC-projecting vs. MEC-projecting depth).
To analyze the functional implications of our anatomical findings, we performed simultaneous ensemble recordings in CA1, PFC, and MEC (Fig. 4A). Pyramidal neurons in the three regions were strongly entrained by SWRs (Fig. 4B–C;50,56). Using a linear model trained on cortical SWR responses, we found that cortical ensembles discriminate the anatomical distribution of CA1 cells participating in SWRs (i.e., the relative fraction of CA1deep and CA1sup cells in each SWR, Fig. 4D). Next, we examined the magnitude of cortical activity during SWRs as a function of their relative ’cell content’. A larger proportion of MEC cells were recruited and fired more in response to SWRs with predominantly CA1sup content (Fig. 4E–F). Likewise, a larger proportion of PFC cells were recruited and fired more in response to SWRs with predominant CA1deep content (Fig. 4E–F). We then examined if MEC and PFC ensembles preferentially responded to the firing patterns of CA1deep and CA1sup cells. Importantly, we found significantly higher mutual information between the activity of CA1sup and MEC cells and between CA1deep and PFC cells during SWRs (Fig. 4G; CA1sup and MEC , CA1deep and PFC , LME). To test the extent to which hippocampal ensemble activity predicted cortical population responses during individual SWRs, we performed reduced rank regression (Fig. 4H). This method finds the latent factors in a multidimensional input (CA1deep or CA1sup SWR firing patterns) that predict the largest fraction of variance in MEC or PFC population dynamics during SWRs. We obtained better predictions of MEC responses from CA1sup SWR patterns and of PFC responses from CA1deep patterns (Fig. 4I), in agreement with our anatomical tracing results. These results suggest that PFC and MEC preferentially readout the information encoded by either CA1deep or CA1sup neurons during SWRs, although this does not imply that they are completely segregated communication channels. These analyses also suggest that distinct aspects of SWR content (e.g. identity or firing rates of participating hippocampal cells) could have different impact on downstream responses, potentially constituting a way of ”multiplexing” information.
Figure 4: CA1deep and CA1sup preferentially coordinate with different downstream cortical areas during SWR.
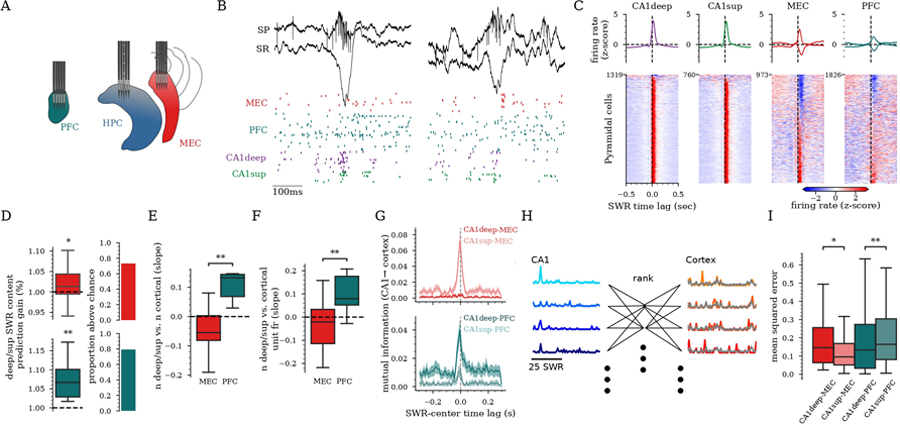
A) Recording schematic of three silicon probes implanted in PFC, dorsal CA1, and MEC of a rat. B) Example unit responses (bottom, each row is one neuron, color-coded by brain region) to SWR (top) in each region. C) Peri-SWR firing rate responses for all pyramidal cells in each region for rats with multi-region implants (n=14 rats, Table S1). Average responses (±95% CI) (top) (positive and negative responses separated for cortex) and individual units (below). D) Left: Prediction gain of the ratio of (CA1deep/CA1sup) for cells active in SWRs calculated from cortical responses vs. shuffle distributions (dashed line) (MEC:, PFC:, t-test). Right: Proportion of sessions with the prediction accuracy above chance. E-F) Regression slopes between SWR relative content of CA1deep vs. CA1sup cells. E) and number of cortical units that responded (, rank-sum), and F) cortical firing rate responses in SWRs (, rank-sum). G) Examples of peri-SWR mutual information between cross-region cell pairs (mean±95%CI). H) Schematic of reduced rank regression used to predict neural activity in cortex from neural activity in CA1 during SWRs. Traces on the left and right reflect cell firing during SWRs. I) Mean squared error of predictions of cortical SWR responses from CA1 activity patterns using reduced rank regression ( for CA1deep/sup versus MEC, for CA1deep/sup vs. PFC, LME). D-F,I) 44 sessions, 9 rats.
CA1 deep and superficial place cells encode different task-related representations
To determine whether CA1deep and CA1sup encode different task-related information and selectivity coordinate with PFC and MEC, we analyzed their activity during behavior. First, we examined place cell dynamics across multiple environments on the same day (Fig. 5A and Fig. S5). Animals explored different types of mazes, in different rooms or locations (see Methods). All mazes lack prominent local cues. Similar to previous reports, we found a larger proportion of place cells among CA1deep compared to CA1sup (Fig. 5B;22,23,28,29). CA1deep cells were more likely to develop fields in multiple environments than CA1sup cells, while the firing of CA1sup cells were more informative about specific environment identity and they had lower ratemap correlations across mazes (Fig. 5C–D and Fig. S5B–D). While spatial information content and place field width was similar, the peak firing rate of CA1deep place cells was higher than CA1sup place cells (Fig. 5E–H). Additionally, CA1deep place cells were more likely to express multiple place fields compared to CA1sup (Fig. 5H). Together, these findings suggest that CA1sup cells, while possessing similar place field quality, are more context selective.
Figure 5: Differential context coding by CA1deep and CA1sup place cells.
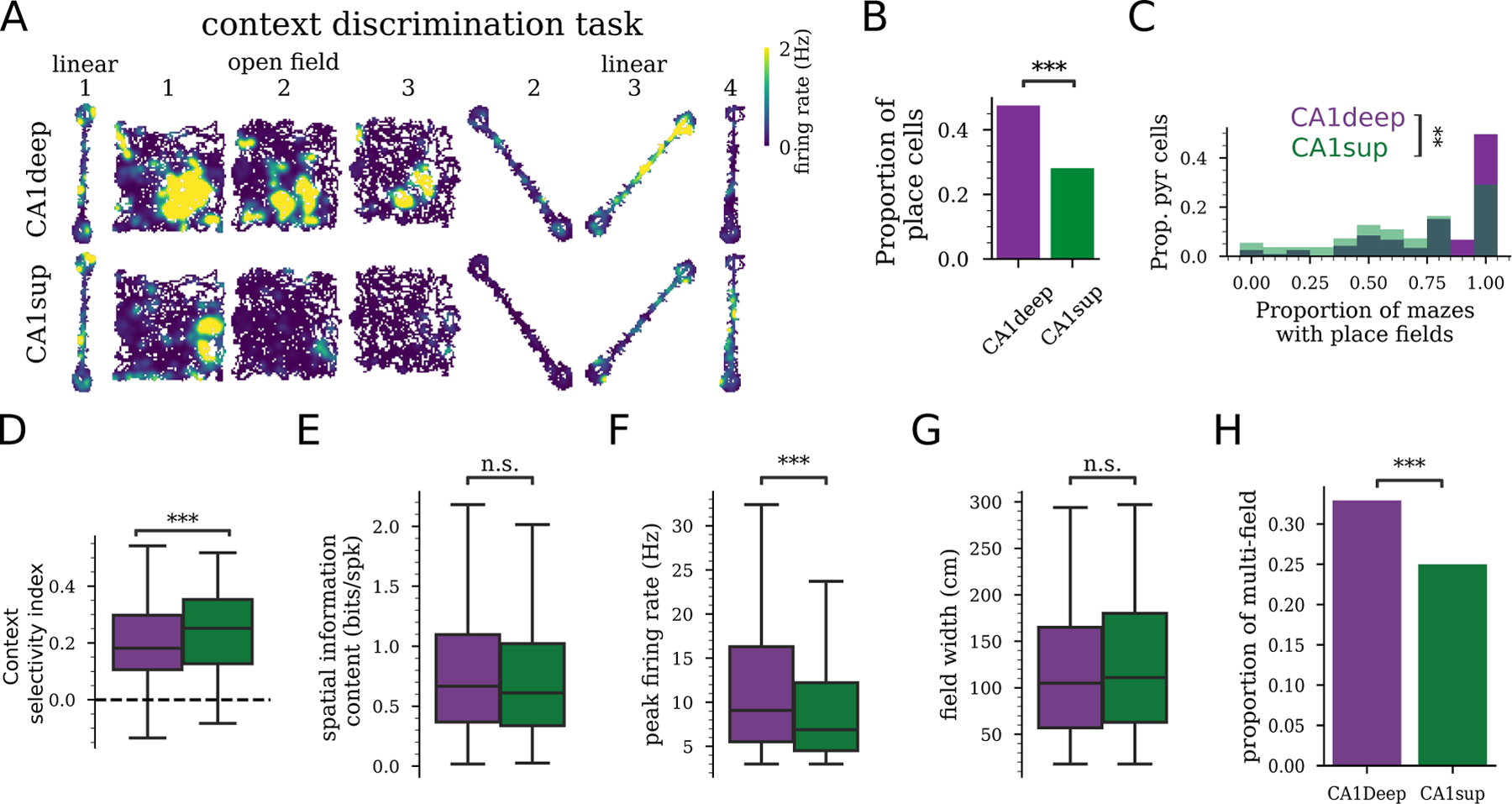
A) Example rate maps for a CA1deep and CA1sup cell in two different mazes across different contexts (different maze locations and cues). B) Proportion of pyramidal cells with at least one place field in a recording session (CA1sup 322/1,146 versus CA1deep 1,183/2,490, ,). C) Fraction of mazes where a cell expressed a place field was higher for CA1deep than CA1sup (, rank-sum). D) Context selectivity index was higher for CA1sup cells compared to CA1deep cells (). E-H) CA1deep and CA1sup place cell properties from place cell on linear track sessions. E) Place cell spatial information content was not significantly different between CA1deep and CA1sup (, LME). F) Place field peak firing rates were higher CA1deep compared to CA1sup (). G) Place field widths were not significantly different between CA1deep and CA1sup (). H) The proportion of place cells with more than one detected place field was higher in CA1deep than CA1sup (,). B-H) CA1deep, 1,146 CA1sup, from 25 rats.
To investigate whether memory demands affect the spatial coding properties of CA1deep and CA1sup, we recorded rats on a delayed alternation task on an M-maze (Fig. 6A; n = 7 rats;49,57,58). The task has two phases. In the ’outbound’ phase, animals start in the center arm and, after a 20-second delay, must navigate to the side arm opposite to the one visited in the previous trial to obtain a sugar-water reward. In the ’inbound’ phase, animals must return from either of the side arms to the center arm to obtain an additional reward. Outbound trajectories require animals to remember previous choices and thus are more memory-demanding than inbound trajectories. We found that CA1sup place cells (n = 325) tended to be more trajectory-specific (i.e., expressing a place field in only one of the four possible trajectories in the maze; Fig. 6B–C) than CA1deep place cells (n = 296), which developed fields along multiple trajectories (Fig. 6B and Fig. S6). This difference in trajectory selectivity was only present in the outbound phase, suggesting a memory-dependent phenomenon (Fig. 6C. Trajectory selectivity index CA1deep vs CA1sup: outbound/ 0.89 inbound, rank-sum test). A signature of trajectory-specific coding is the firing rate modulation in a common location of some place cells depending on an animal’s future choice (’splitter cells’; 57,59). To analyze this phenomenon, we focused on cells with place fields in the center arm of the maze. CA1sup place cells exhibited more choice selective firing (measured as the difference in firing rate in the center arm for left arm versus right arm trajectories) compared to CA1deep place cells in outbound but not inbound trials (’prospective splitter cells’; Fig. 6D and Fig. S6). Additionally, we found an over-representation of the choice point (as a higher density of place fields compared to the rest of the maze) during outbound trials by CA1sup but not CA1deep place cells (Fig. 6E). Finally, we looked at the representation of reward locations at the end of the three maze arms. We found that CA1deep cells had a larger proportion of place fields and higher firing rates around reward locations compared to CA1sup (Fig. 6F).
Figure 6: Differential context, choice, and reward coding by CA1deep and CA1sup place cells.
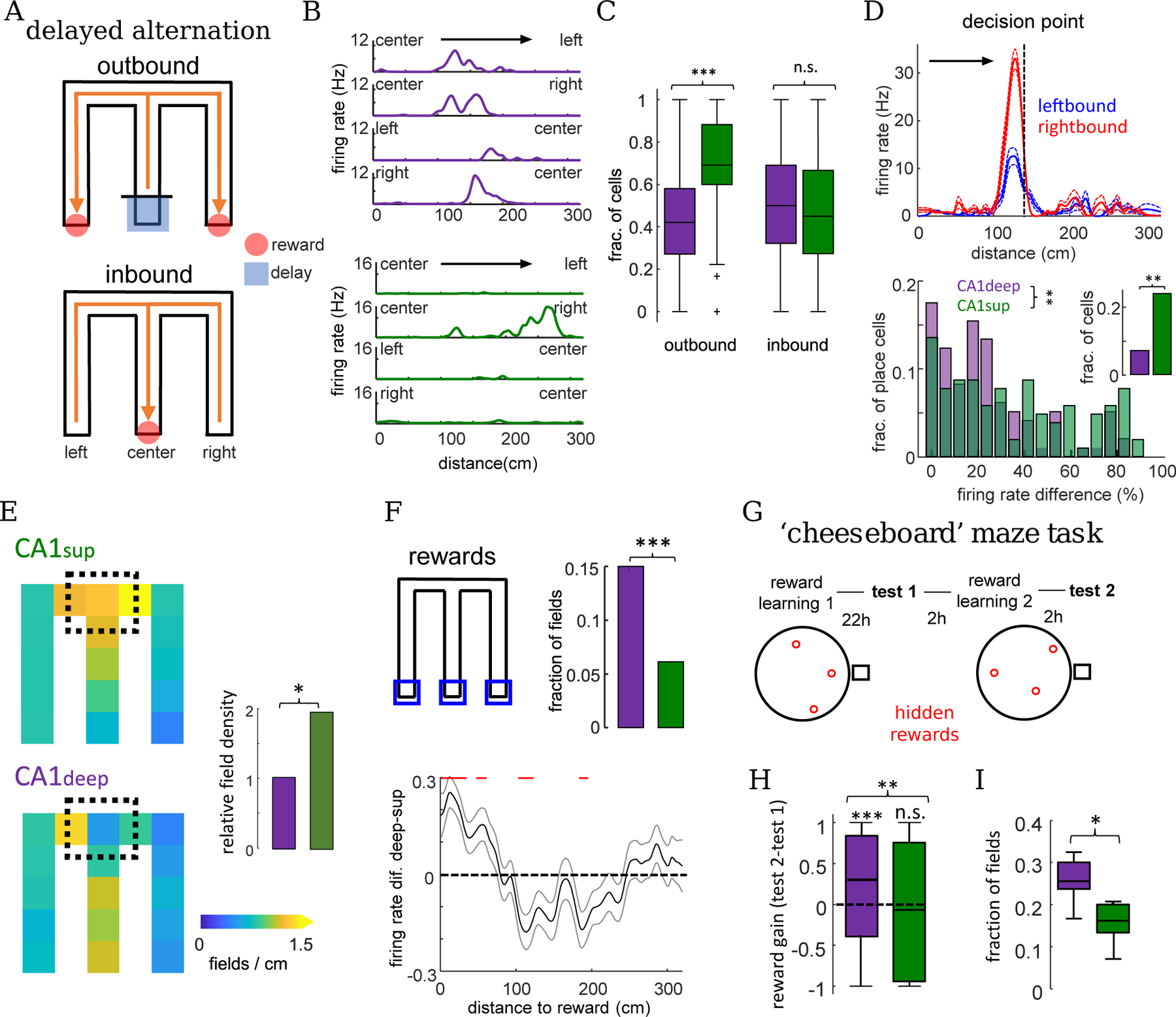
A) Depiction of delayed alternation task in M-maze. B) Example rate maps across the four M-maze trajectories for a CA1deep (top) and CA1sup (bottom) place cell. C) Fraction of place cells with fields in either one of two different trajectories in outbound (CA1deep vs CA1sup, , rank-sum) and inbound () trials. D) Top: rate maps for a splitter cell for left and right outbound trials. Note different firing rates within its place field in the center arm for left-bound and right-bound trials. Bottom: distribution of firing rate difference for left and right outbound trials for cells with overlapping fields in the central arm (n = 97 CA1deep / 104 CA1sup;) and the fraction of splitter cells (inset;, Fisher’s test). E) Aggregated place field density maps for CA1deep and CA1sup place cells in outbound trials (n=398 CA1deep / 422 CA1sup fields). Right: place field density around decision point (black square) / density in rest of maze (, Fisher’s test) F) Top: Fraction of cells with fields around reward locations (blue squares; n=50 CA1deep / 24 CA1sup fields;). Bottom: firing rate difference of CA1deep-CA1sup place cells as a function of distance to reward (mean±SEM: the three arms were averaged together). Red lines indicate significant differences (, t-test with Bonferroni correction). G) Depiction of ’cheeseboard’ maze task schedule and example reward configurations. H) Increase in firing rate around newly learned reward locations from test 1 to test 2 (&; CA1deep and 174 CA1sup place cells; sign-rank test, CA1deep vs. CA1sup , rank-sum). I) Fraction of place fields around reward locations in test 2 (, rank-sum). Only one primary place field for each cell was considered for this analysis.
To analyze reward coding, we recorded animals in a “cheeseboard” maze task in which they had to learn new reward locations every day (Fig. 6G; rats;44,60). At the beginning of the day, animals were allowed to explore the maze for ∼ 20 minutes without any reward (’test 1’). Next, animals ran successive trials in which they had to discover the new locations of three hidden water rewards. Each trial started with the animal in the home box and ended when they retrieved the three rewards and came back to the box. Two hours later, they were put back in the maze again for ∼ 20 minutes without any rewards present (’test 2’). Learning was measured by both a decrease in latency to collect all rewards during learning trials and an increase in the time around previously rewarded locations during probe test sessions 44,60. We analyzed the representation of newly learned reward locations by comparing spatial firing in pre- and post-learning ’test’ sessions without rewards present. CA1deep but not CA1sup place cells selectively increased their firing rates around new reward locations (Fig. 6H) and a larger proportion of CA1deep than CA1sup expressed place fields around new reward locations after learning (Fig. 6I and Fig. S6). To account for potential confound of immobility or low-speed movement around reward locations, all place cell analyses were conducted excluding periods in which animal speed was below 4cm/s. In addition, both CA1deep and CA1sup fired less during immobility than running periods (Fig. S1K), contrary to what has been reported for some CA2 cells23,61. Taken together, these results indicate that CA1sup and CA1deep place cells encoded qualitatively different types of task-related information: CA1sup cells encoded specific context, future trajectories, and choices, while CA1deep cells tracked learned reward locations.
To investigate whether CA1deep and CA1sup preferentially route different task-related information to PFC and MEC, respectively, we detected synchronous assembly patterns across these structures during memory tasks, in the same way as before for only hippocampal neurons (Fig. 1). We found that ∼ 10% of the assemblies that emerged during behavior had both hippocampal and cortical members, while the rest were restricted to a single structure (Fig. 7A–B). Out of the detected assembles the proportion of layer-specific hippocampo-cortical assemblies were: CA1deep-MEC: 8%, CA1sup-MEC: 8%, CA1deep-PFC: 18%, and CA1sup-PFC: 12%. Hippocampo-cortical assembly members, but not non-member cells, displayed high spike synchrony in a ∼ 50ms time window (Fig. 7C). When centered on the activation of hippocampal assembly members, MEC pyramidal cell firing peaked ∼ 15 ms later and PFC firing ∼ 35ms later, indicating the propagation of information from the hippocampus to the cortex (Fig. 7D).
Figure 7: Hippocampo-cortical assemblies encode and reactivate complementary task representations.
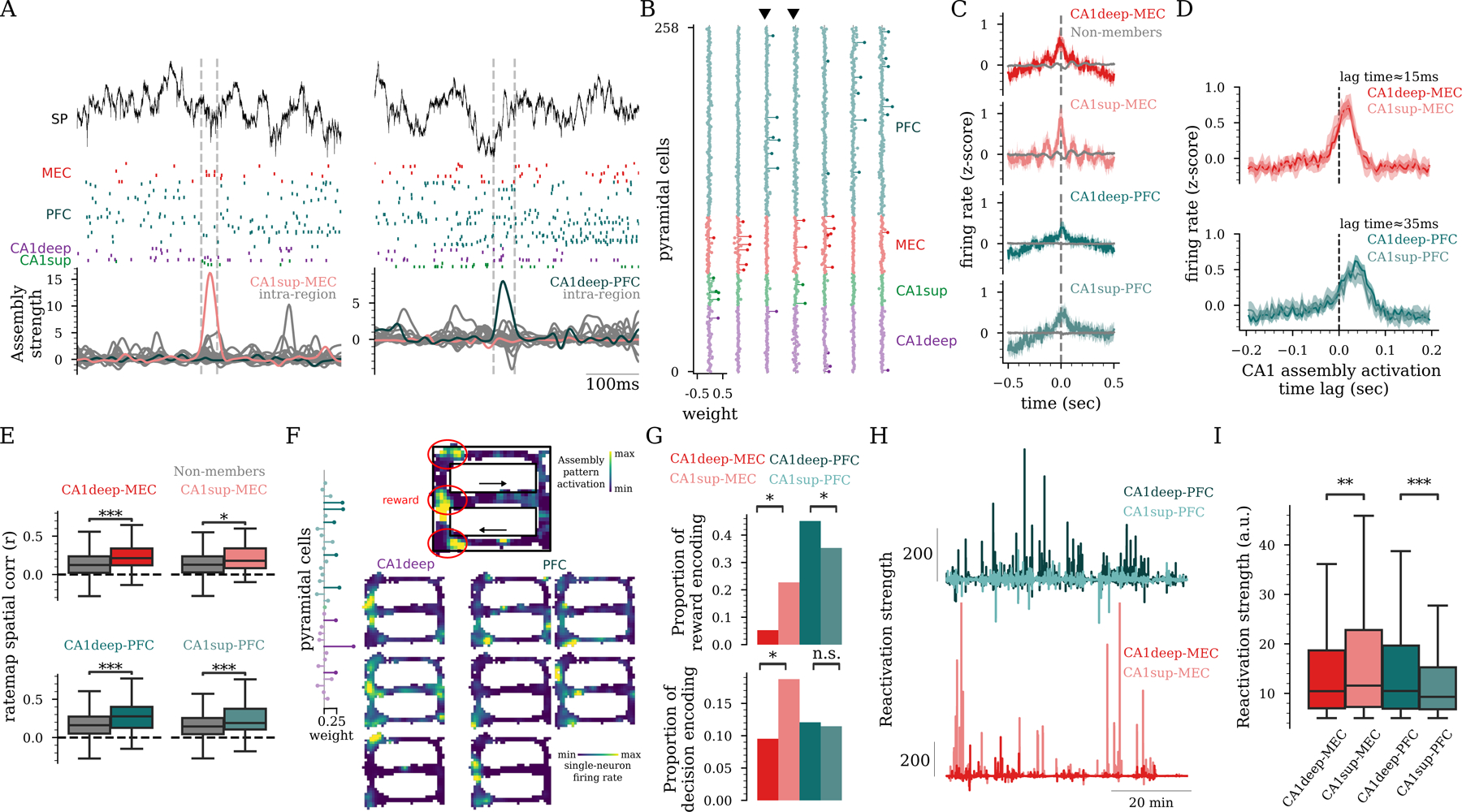
A) Hippocampal LFP (top), unit firing from MEC, PFC, and CA1 (middle), and assembly activation (bottom) during behavior. Dashed lines mark the activation of hippocampo-cortical assemblies (colored curves). B) Example assembly weights, including hippocampo-cortical assemblies (marked by black triangles) and single-region assemblies. C) Cross-correlograms between spike trains of hippocampo-cortical assembly members (colored curves) showed stronger spike synchrony than for non-members (grey curves) during behavior (). D) Firing of MEC (top) & PFC (bottom) units center around the discharge of CA1 assemblies (mean CA1-MEC lag = 15ms; CA1-PFC lag = 35ms). E) Rate map spatial correlation for assembly members was higher than for non-members ( rank-sum test). F) Example rate maps for a CA1deep-PFC assembly activation (top) and its individual members firing (bottom) in a delayed alternation T-maze task. Note the elevated activation of both the assembly and its individual member neurons around reward locations (red circles) indicate reward locations. G) Fraction of assemblies encoding reward locations (top; CA1deep-MEC vs. CA1sup-MEC , , CA1deep-PFC vs. CA1sup-PFC ) and decision point in the maze (bottom; CA1deep-MEC vs. CA1sup-MEC:, , 8 rats from the T-maze task). H) Example assembly reactivation strength during SWRs for representative hippocampo-cortical assemblies. I) Reactivation strengths of hippocampo-cortical assemblies in post-task sleep SWRs (CA1deep-MEC vs. CA1sup-MEC ; CA1deep-PFC vs. CA1sup-PFC , LME). C-E,I) n = 1,319 CA1deep, 760 CA1sup, 973 MEC, 1,826 PFC pyramidal cells, from 14 rats. C,E,G,I) n = 170 cross-region assemblies out of 1,700 total assemblies.
We next analyzed the functional correlates of hippocampo-cortical assemblies. Cortical cells had higher spatial firing correlations with hippocampal cells that were members of the same assembly than with other non-member hippocampal cells (Fig. 7E). Some assemblies were active at all reward locations in the maze while their members fired only at individual reward locations (Fig. 7F), suggesting that cross-regional assemblies can encode generalized representations. Overall, CA1deep-PFC assemblies displayed the highest reward coding among all assembly types (Fig. 7F). On the other hand, CA1sup-MEC assemblies displayed higher activation around the decision point of the maze than any other assembly type (Fig. 7G).
Finally, we examined the reactivation of cross-regional assemblies during sleep following learning tasks. MEC cells reactivated more strongly with CA1sup than with CA1deep partners, while PFC cell’s reactivation was stronger with CA1deep rather than CA1sup (Fig. 7H–I). This observation is in agreement with our previous anatomical and physiological results (Fig. 3 and 4), which together suggest that CA1deep and CA1sup cells encoding different aspects of learning tasks selectively synchronize with either PFC or MEC neurons during behavior and reactivate together during SWRs. It is important to note that representations of different task aspects are not mutually exclusive, nor only restricted to specific cell types in these circuits and can be also found in other hippocampal target areas such as nucleus accumbens or retrosplenial cortex52,62,63.
Discussion
Experimental and theoretical work has suggested that biological and artificial neural networks composed of diverse elements constitute more efficient memory systems than similar networks integrated by homogeneous units64,65. Hippocampal pyramidal cells exhibit a large molecular, anatomical, and physiological diversity15–18,22–25,49 rooted in development20,21; however, hippocampal memory models have not fully considered this diversity. Our findings demonstrate that the functional heterogeneity of CA1 pyramidal cells is a major contributor to the flexible computational capabilities of the hippocampus during memory-guided behavior.
Previous research showed that SWRs entrain ensemble reactivation in numerous downstream areas 10,12,51,51,52,54,63,66. In particular, multiple neocortical regions such as the PFC12,50,67–70, MEC66,71, retrosplenial62,72,73, visual74 or auditory 75 cortices show robust ensemble reactivation during hippocampal SWRs. However, until now, it was not known if memory representations broadcasted by SWRs are similarly readout in all cortical target regions or if these show selective responses. We reported a divergent anatomical and functional connectivity pattern between dorsal CA1, PFC, and MEC. Monosynaptic projections from dorsal CA1 to MEC originated mainly from CA1sup cells, while much sparser projections to PFC originated from CA1deep cells, with minimal overlap between the two subpopulations. Moreover, our physiological data showed that MEC responds preferentially to SWRs enriched in CA1sup spikes, while PFC responds preferentially to SWRs dominated by CA1deep activity. Furthermore, the temporal dynamics of MEC and PFC ensemble reactivation were better predicted by the activity of CA1sup and CA1deep respectively, indicating selective cortical responses to SWRs depending on the anatomical distribution of the hippocampal cells generating them. While our analysis focused on the propagation of activity from the hippocampus to the cortex during SWRs, cortical activity can also precede and influence hippocampal SWR generation 75–77. Further studies are needed to elucidate the mechanisms and functional significance of bidirectional hippocampo-cortical SWR interactions across brain states and behaviors.
The dense direct projection from dorsal CA1 to MEC has been extensively documented in different species 78. In comparison, direct inputs from dorsal CA1 to PFC are much sparser, and their density gradually increases towards the ventral pole 79. Despite this, previous studies in both mice 80,81 and rats79,82 have reported monosynaptic inputs from dorsal CA1 to the PFC using retrograde tracing strategies. The divergent projection pattern we described here for dorsal CA1 deep and superficial neurons was not reported before, possibly because most previous studies did not perform dual MEC/PFC labeling or attempted to quantify the radial distribution of CA1 projection cells. Two previous studies also reported that a large majority of CA1 to PFC projections arise from the deep sublayer in both the dorsal80 and ventral24 mice hippocampus. However, in other studies, also in mice, dorsal CA1 deep versus superficial differences in projections to PFC81 and MEC83 were not apparent. A potential factor that could explain differences across studies is the exact locations of cortical injections and hippocampal imaging. Hippocampal efferent projections vary not only along the radial, but also transverse and longitudinal axes78,79. Disentangling the interaction between projection gradients along those three axes still requires additional investigation. In addition, CA1 axons target different layers across cortical areas and different types of both excitatory and inhibitory neurons (e.g., Ahrlund-Richter et al., 80). In our tracing experiment, we injected large amounts of tracer spanning MEC layers and PFC subregions. Further experiments with more localized injections are needed to unveil the fine-grain organization of these projections in terms of subregion, layer, and cell type-specific targeting. A limitation of our study is that we only examined two projection targets, while it is well known that dorsal CA1 neurons project to multiple other cortical (e.g., lateral entorhinal and retrosplenial cortex) and subcortical (e.g., lateral septum and nucleus accumbens) areas. Given the sparse projection from CA1deep to PFC, it remains to be determined what are their major downstream targets. It is important to highlight that interactions between CA1 and PFC or MEC can also be mediated by polysynaptic circuits. This is particularly relevant when considering functional interactions, such as those described in this work, between dorsal CA1 and PFC. Areas such as the subiculum and retrosplenial cortex with dense connectivity with both CA1 and PFC are likely candidates to mediate interactions between these two structures, an interpretation that is compatible with the longer delay observed on average between CA1 and PFC spiking (Fig. 7D). Future experiments, using optogenetic tagging to verify projection targets of recorded cells are needed to directly relate CA1 pyramidal cell functional responses to anatomical projection patterns19,84.
Contrary to a common tenet that assumes a random cellular organization of hippocampal spatial and memory representations36–38, we found that pyramidal cells from the same sublayer formed functional assemblies, reactivated together during SWRs and had more similar spatial tuning and functional correlates 21. Deep pyramidal cells were more active across brain states and behaviors than superficial ones. A larger proportion of active place cells was found among the CA1deep subpopulation, and they were more likely to express place fields across different environments than CA1sup cells. Despite their lower overall SWR participation, CA1sup cells were more recruited and fired more during post-experience memory replay than CA1deep. Furthermore, CA1sup cells tend to only express place fields in one of the multiple environments, and their firing was more predictive of context identity than that of CA1deep cells. These observations suggest that CA1deep and CA1sup cells may play complementary roles in memory formation. Highly active CA1deep cells may form the ’backbone’ of hippocampal spatial and memory representations. On the other hand, CA1sup cells may be recruited after experience and confer higher specificity and discriminability to hippocampal spatial maps and SWR-associated sequences. These two subpopulations can thus support the rapid encoding and the sparsification of memory representations, respectively.
Our findings can also explain previous observations on the heterogeneous contribution of hippocampal cells to memory replay48,85,86. Previous reports identified a subset of CA1 pyramidal cells with high firing rates whose reactivation dynamics after a new experience or during learning remained relatively unaltered48,49,85,86. On the other hand, a different subset of low-firing CA1 pyramidal cells were selectively recruited into post-experience memory replay48,49,85,86, as well as long SWRs that emerge during memory tasks and optogenetically prolonged SWRs that result in enhanced memory performance 49. Our results suggest that the ’plastic’ low firing subpopulation is composed preferentially of CA1sup cells while the more rigid and excitable one by CA1deep cells. It is important to highlight that CA1deep and CA1sup are not completely homogeneous cellular populations and that they exhibit considerable variability in their physiological and plastic properties. An advantage of our large dataset of more than 10,000 neurons is the ability to resolve differences between these subpopulations. For example, previous studies with smaller cell samples reported conflicting observations regarding the properties of CA1deep and CA1sup cells during SWRs (e.g. Valero et al.,27 reported higher SWR participation of CA1sup while Mizuseki et al., 22 did not). These differences can be partially explained by the lack of resolution due to small samples but also by differences in animal behavior (since novel experiences will induce more replay and therefore more CA1sup recruitment) or brain state (e.g., under urethane anesthesia hippocampal physiology differs from natural sleep).
Previous works reported several differences between the properties of deep and superficial CA1 place cells. These differences included an overall larger proportion of place cells among CA1deep22, higher rate map stability and context discrimination in CA1sup but an increased stability of CA1deep during goal-oriented behavior29, landmark-related place fields in CA1deep28,30, better spatial rate coding in CA1sup in cue-poor environments, and better phase coding in CA1deep in cue-rich environments28. Our current results extend these observations, by demonstrating that CA1deep and CA1sup place cells encode and reactivate complementary task representations during memory-guided behavior. In the working memory phase of a spatial learning task, a larger fraction of CA1sup than CA1deep place cells developed trajectory-selective firing and overrepresented the decision point in the maze. Furthermore, future choices strongly modulated the firing of CA1sup place cells with fields in the central arm of the maze (i.e. ’splitter cells’; 57,59). These results suggest that CA1sup place cells may be specialized in prospective coding, which together with their enhanced participation in replay can support a role in behavioral planning. Of note, the mazes employed in this study did not have prominent local landmarks. The inclusion of intra-maze cues could affect hippocampal place cell properties and animal navigation strategies, as previously reported 28,60,87.
On the other hand, CA1deep place cells preferentially encoded reward locations and specifically remapped when animals learned a novel spatial configuration of hidden rewards. This difference between CA1sup and CA1deep cells can clarify previous conflicting observations that reported varying degrees of reward-related remapping, as they may have sampled from different CA1 subpopulations29,60,88,89. A recent study related CA1deep cells with reverse theta sequences and enhanced participation in reverse replay90. Together with our present findings, this suggests that CA1deep cells may specialize in retrospective coding, that could be used to incorporate reward information into hippocampal spatial and memory representations. These differences in coding properties between CA1deep and CA1sup cells were also reflected in the dynamic expression of cross-regional assemblies formed by the synchronization of firing among hippocampal and cortical neurons. A surprising observation was that, CA1deep, the subpopulation with stronger connections with PFC had the least amount of trajectory specificity and decision-related responses. Previous studies showed that this information is also represented in the PFC in coordination with the CA110, so it is possible that indirect inputs from CA1 (e.g. through subiculum or retrosplenial cortex) convey these signals to the PFC or that a subset choice-selective CA1sup cells also project to PFC.
Further research is also needed to elucidate the mechanisms that underlie these functional differences among CA1deep and CA1sup cells. One possibility is the difference in inputs to these two subpopulations. CA1sup cells receive stronger inputs from CA3 and the lateral entorhinal cortex27,91 while CA1deep are more strongly innervated by inputs from the MEC and CA226,92. An interesting observation is that direct MEC inputs (from layer III) target preferentially CA1deep cells, but hippocampal outputs to the MEC (layer V) arise predominantly from CA1sup, which receive stronger indirect MEC inputs relayed by CA3. Thus, CA1deep cells may mediate the direct flow of information from MEC to PFC while CA1sup may be more involved in an entorhinal-hippocampal recurrent circuit. CA1 pyramidal cells also differ in their connectivity with local interneurons. CA1sup cells preferentially recruit parvalbumin-expressing basket cells that in turn exert stronger inhibition over CA1deep cells 24,27, providing a potential mechanism for segregating CA1sup and CA1deep neuronal assemblies. Another important factor could be the differences in synaptic plasticity between these two hippocampal subpopulations. While the relation between experience-dependent synaptic strength changes and neural dynamics has been poorly studied, a recent report showed that CA1 superficial but not deep cells exhibit potentiated post-synaptic responses to CA3 inputs after a novel experience 93.
Taken together, our results suggest that SWRs carry a multiplexed code in which different types of task-related information are encoded simultaneously but selectively routed to different target areas by deep and superficial pyramidal cells. The existence of parallel hippocampo-cortical subcircuits for selective encoding, routing, and replay of complementary memory representations confers this system with enhanced flexibility and the capability to simultaneously implement different types of computations in support of memory-guided behaviors. These results highlight the importance of incorporating cellular diversity in models of hippocampo-cortical learning and memory functions.
STAR methods
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for reagents and resource may be directed to, and will be fulfilled by the Lead Contact, Antonio Fernandez-Ruiz (afr77@cornell.edu) & Azahara Oliva aog35@cornell.edu.
Materials availability
This study did not generate new unique reagents.
Data and code availability
Newly generated data reported in this paper will be shared by the lead contact upon request. As well, this paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
Original code has been deposited at https://github.com/ayalab1 and https://github.com/ryanharvey1/ripple_heterogeneity and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Fluoroshield with DAPI | Sigma-Aldrich | SKU: F6057 |
| Calbindin-D28K Monoclonal Antibody | Proteintech | Cat# 66394–1-Ig |
| Bacterial and virus strains | ||
| AAV5-CaMKIIa- hChR2-EYFP | UNC Vector Core | NA |
| Biological samples | ||
| Chemicals, peptides, and recombinant proteins | ||
| Cholera Toxin Subunit B, Alexa Fluor™ 488 Conjugate | Invitrogen | Cat# C22841 |
| Cholera Toxin Subunit B, Alexa Fluor™ 594 Conjugate | Invitrogen | Cat# C22842 |
| Cholera Toxin Subunit B, Alexa Fluor™ 647 Conjugate | Invitrogen | Cat# C34778 |
| Critical commercial assays | ||
| Deposited data | ||
| Hippocampal data | http://crcns.org/data-sets/hc/hc-3 | http://dx.doi.org/10.6080/K09G5JRZ |
| Hippocampal and prefrontal data | http://crcns.org/data-sets/pfc/pfc-2 | http://dx.doi.org/10.6080/K01V5BWK |
| Hippocampal data | https://crcns.org/data-sets/hc/hc-11 | http://dx.doi.org/10.6080/K0862DC5 |
| Hippocampal data | https://crcns.org/data-sets/hc/hc-14 | http://dx.doi.org/10.6080/K0MS3QXD |
| Experimental models: Cell lines | ||
| Experimental models: Organisms/strains | ||
| Rat: Long-Evans | Charles River | Cat#: Crl:LE 006 |
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and algorithms | ||
| Analysis tools | https://github.com/ayalab1/neurocode | https://zenodo.org/badge/latestdoi/398122107 |
| Analysis tools | https://github.com/ryanharvey1/ripple_heterogeneity | https://zenodo.org/badge/latestdoi/388846280 |
| MATLAB | MathWorks | https://www.mathworks.com/products/matlab.html |
| Python | Python Software Foundation | https://www.python.org/ |
| R | R Foundation for Statistical Computing | https://www.R-project.org/ ; RRID: SCR_001905 |
| RStudio | RStudio, PBC | https://www.rstudio.com/ ; RRID: SCR_00043 |
| Vscode | Microsoft | https://code.visualstudio.com/ |
| Cell Explorer | https://cellexplorer.org/ | https://doi.org/10.1016/j.neuron.2021.09.002 |
| Nelpy | https://github.com/nelpy/nelpy | https://zenodo.org/badge/latestdoi/77548623 |
| Seaborn | https://seaborn.pydata.org/ | https://doi.org/10.21105/joss.03021 |
| Scikit-learn | https://scikit-learn.org/stable/ | https://zenodo.org/badge/latestdoi/21369/scikit-learn/scikit-learn |
| Matplotlib | https://matplotlib.org/ | 10.1109/MCSE.2007.55 |
| Numpy | https://numpy.org/ | 10.1038/s41586-020-2649-2 |
| Other | ||
| Silicon probes | Neuronexus | https://neuronexus.com/ |
| Intan RHD2000 | Intan technologies | http://intantech.com/files/Intan_RHD2000_eval_system.pdf |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Rats (adult male Long-Evans, 300–500 g, 3–6 months old) were kept in the vivarium on a 12-hour light/ dark cycle and were housed 2 per cage before surgery and individually after it. All experiments conformed to guidelines established by the National Institutes of Health and have been approved by the Cornell University Institutional Animal Care and Use Committee.
METHOD DETAILS
Electrode Implantation and Surgery
Silicon probe implantation was performed as described previously44,49. Animals were anesthetized with isoflurane anesthesia and craniotomies were carried out under stereotaxic guidance. Silicon probes (NeuroNexus, Cambridge Neurotech, or Diagnostic Biosignals) were mounted on custommade 3D-printed micro-drives to allow precise adjustment of the vertical position of sites after implantation. The probes were inserted above the target region. Craniotomies were sealed with sterile wax. Two stainless steel screws were placed bilaterally over the cerebellum to serve as ground and reference electrodes. Several additional screws were driven into the skull and covered with dental cement to strengthen the implant. Finally, a copper mesh mounted on a 3D-printed resin base was attached to the skull with dental cement and connected to the ground screw to act as a Faraday cage, attenuating the contamination of the recordings by environmental electric noise and protecting the headgear. After post-surgery recovery, probes were moved gradually in 50 to 150 µm steps per day until the desired position was reached. Hippocampal, prefrontal cortex, and entorhinal cellular layers were identified physiologically by unit activity and characteristic LFP patterns26,32.
A variety of different silicon probes were implanted in the dorsal hippocampus (−4.5–4.0mm antero-posterior from Bregma - AP and 2.6mm from midline; ML), the medial entorhinal cortex (-9.0mm AP, 4.0mm ML), and prefrontal cortex (3.0mm AP, 0.7mm ML). Data from some of the animals included in this study have also been included in previous studies, and surgical procedures have been described in more detail there26,44,48,49,51,94–99.
Optogenetic experiments
The optogenetic experiments analyzed here were performed as part of a previously published study by Fernandez-Ruiz et al., 49. Briefly, rats (n = 5) were injected with AAV5-CaMKIIa-hChR2(H134R)- EYFP from UNC Vector Core (a gift from Dr. Karl Deisseroth). Three injections of 150 nL each were performed along the longitudinal axis of both dorsal hippocampi, right above the CA1 pyramidal layer. Histological verification showed that CA1 pyramidal cells in a volume of ∼1 mm3 were densely labeled. After injection, craniotomies were sealed and animals recovered in the vivarium for three weeks. Following this period, a second surgical procedure for implanting optic fibers and electrodes was performed. 200 µm core multi-mode optic fibers (Thor Labs) were implanted in the same craniotomies used previously for virus injection, right above the CA1 pyramidal layer. Optic fibers were directly coupled to 460 nm blue light-emitting laser diodes (PL-450, Osram). A 64-channel silicon probe was also implanted targeting the CA1 region.
A closed-loop system was used in order to detect SWR during behavior and trigger light stimulation. Once a SWR was detected, a small amplitude, 100-ms, trapezoidal light pulse was delivered simultaneously through all fibers. The intensity was manually adjusted in each animal during a test session in the home cage by gradually increasing light power until a clear ripple was evoked. Pulses were delivered every time a SWR was detected while the animal was performing the task in the M-maze (see below).
Behavioral recordings
After surgery, the animals were handled daily and accommodated to the experimenter, recording room, and cables for one week before the start of the experiments. Prior to the start of the behavioral experiment, the animals were water restricted. Physiological signals were recorded during five different tasks.
Supplemental Table S1 contains a list of all animals with the tasks in which they were recorded. The number of animals that contributed to specific analysis can be found in the corresponding figure legend or main text.
All the behavioral apparatus used were devoid of intra-maze cues (e.g., objects or other prominent landmarks), thus they were ”cue poor”28. Animals have to rely on global cues (always present in the walls and curtains around mazes) and path integration for navigation.
In the linear or circular track, rats were trained to run back and forth to collect a small water reward. After the first one or two days, all animals performed 40–80 trials per day. The session was terminated when the animal was satiated, typically for one hour. The linear track was placed one meter above the floor and were 160–300 cm long and 7 cm wide with 5–10 cm walls. The circular track was 100 cm in diameter. Water rewards were delivered in a predetermined position only when the animals had performed a full clockwise run.
In the M-maze experiment, rats were first pre-trained to collect sugar-water rewards in the linear track. Once they were used to running and obtaining rewards, the M-maze recordings started49. In the M-maze, rats were rewarded with sugar water each time they reached the end of the three arms in the correct task sequence (center-left-center-right-center). The two components of the task (outbound and inbound) were evaluated separately to assess task performance 49. The animal was confined at the end of the central arm for 20 s after each inbound trial. Animals performed the task for 10 days. Two 30-minute sessions were conducted in the morning and afternoon, separated by 5 h and preceded and followed by ∼ 1 h sleep recording sessions. For all analysis purposes, outbound trials start after the delay period and finish when animals crossed the sensor right before the reward ports on the side arms. Inbound trials end when animals crossed the sensor in the central arm before the delay period starts. The maze was placed one meter above the floor and had 140 cm length (for the central and side arms) and 110 cm width (for the lateral connecting arms), with 5cm walls.
Cheeseboard Maze (120 cm diameter), where the animals learned to find 3 goal wells that contained water rewards. A trial was completed once the animal had retrieved all rewards and returned to the start box to collect an additional food pellet reward. The locations of the goal wells changed daily but were fixed within a session. This strategy required the animals to update their memory for the new goal locations in each session but in an otherwise familiar environment. Note that between trials, there was always a delay of approximately 30 seconds. In the animals used for assessing place field changes before and after learning (n = 4; Fig. 6), a pre-probe session (’test 1’), without rewards present, was run every day to assess whether the animal remembered the previous day’s positions. Following the learning session, a post-probe session (’test 2’), also without rewards, was also conducted to examine whether the animal remembered the newly learned locations. In other animals, the probe sessions consisted of 5 trials with the same reward configuration as the preceding learning sessions. Place fields in these probe sessions were not analyzed due to the impact of reward presence on animal behavior. The inclusion of data for the analysis required that the animal be pre-trained for a week. In addition, the rat’s performance in each included session had to show a trend of learning across trials and memory performance in probe sessions was above chance levels. Sleep sessions were recorded before and after each learning session. The cheeseboard maze was placed in a rotating platform (’lazy Susan’) 1m above the floor and had no walls.
In the rectangular figure-8 maze (or ’T-maze’) animals were trained to alternate between right and left arms to collect water rewards. At the beginning of the trial, the rats were confined in the start box for 15 s. After opening the door that led to the central arm, the animals ran through the central arm and chose to turn right or left. If the choice was correct (opposite arm than visited in the previous trial), they would find a water reward at the end of the side arm; if incorrect, the reward port would remain empty. Only sessions when animals had been trained in the task for at least one week and performed above 70% correct trials were included. The maze was placed one meter above the floor and had 160 cm in length (for the central and side arms) and 134 cm in width (for the lateral connecting arms).
Open field environment (180 cm × 180 cm, or 120 cm × 120 cm), where the animals (n=10) randomly foraged for pieces of randomly placed sugar pellets until they completely sampled the entire environment (∼30 minutes). Open fields had ∼30cm walls with a large cue card in at least one of them.
Plus maze environment (100 cm × 100 cm), where the animals in which the rats were motivated to run to the ends of four corridors, where water was given every 30 s.
Novelty sessions took place in a different room never visited before by the animal. The ’familiar’ and ’novel’ rooms had unique prominent distal cues. Different behavioral apparatuses (described above) were used during novelty sessions: linear and circular tracks, open field, T-maze, and cheeseboard maze. Animals were trained to run in these mazes to collect water or food rewards until they were satiated, typically 30–60 minutes. All animals were trained for multiple days in the familiar room and behavioral apparatus, which differed from those used in novelty sessions for each animal.
For all mazes, the position of the animal was recorded with an overhead camera (Basler) and tracked with DeepLabCut100 or custom software.
In the datasets obtained from the CRCNS repository (http://crcns.org/data-sets/hc/hc-3, http://crcns.org/data-sets/pfc/pfc-2, https://crcns.org/data-sets/hc/hc-11, https://crcns.org/data-sets/hc/hc-14), animals were also recorded during the linear track, open field, and T-maze alternation task that have been described in detail previously48,51,97–99,101–103.
Tissue processing and immunohistochemistry
Following the termination of the experiments, animals were deeply anesthetized and perfused transcardially first with 0.9% saline solution followed by 4% paraformaldehyde solution. The brains were sectioned into 70-µm thick slices (Leica Vibratome). The sections were washed and mounted on glass slides with a fluorescence medium (Fluoroshield with DAPI - F6057, Sigma, USA). Sections stained with Calbindin were done by first permeabilizing with 0.5% Triton-X-100 for 1.5 hours. After permeabilizing, slices were blocked with 10% donkey serum albumin (DSA) plus 0.5% Triton-X-100. Next, slices were incubated in primary antibody (Calbindin-D28K Monoclonal Antibody - 66394, Proteintech, USA) containing blocking solution overnight. After primary antibody incubation, secondary antibody (Donkey anti-Mouse IgG Alex Fluor 647 - A-31571, Thermo Fisher, USA) for 4 hours before DAPI staining. A confocal microscope (Zeiss LSM 800) was used to obtain high-quality photos.
Retrograde tracing experiments
For CTB retrograde studies, 330nl of conjugated CTB (Life Technologies, Carlsbad, CA) was injected into the prefrontal cortex (PFC, CTB Alex Fluor 488) and the Medial Entorhinal Cortex (MEC, CTB Alex Fluor 555) in the same animal in one surgery 104. For each site, there were 10 injections of 33nl at 23 nl/sec with a 15-sec delay. Injection sites (in mm from bregma) for PFC were AP +3.0, ML +1.0, DV −1.5, −1.8, −2.0, −2.3, −2.7, −3.1, −3.6, −4.1, −4.5, −5,0. Injection sites (in mm from bregma) for MEC (1) AP −7.7, ML + 4.6, DV −4.7; (2) AP −8.0, ML +4.6 DV −4.3, −4.8, −5.3; (3) AP −9.1, ML +4.6, DV −3.2, −3.7, −4.2, −4.5, −4.7, −5.2. PFC injections were centered in the prelimbic cortex but also affected anterior cingulate and infralimbic areas. MEC injections cover dorsal and intermediate portions of MEC, and both superficial and deep layers. Animals were perfused transcardially 7 days after injection, first with 0.9% saline followed by 4% paraformaldehyde solution. The brains were sectioned in 70-µm thick slices (Leica Vibratome), then washed with DAPI (Thermo Fisher Scientific), and mounted on glass slides. Images were taken on Confocal microscopes (Zeiss LSM 800 for quantification; Zeiss LSM880 i880 for high-resolution images (Cornell University Biotechnology Resource Center Imaging Core)). Injection sites were verified for both PFC and MEC (Fig. 3 and Fig. S4).
Quantification was performed first in ImageJ by taking CA1 segments from slices AP −3.2 to −4.5 mm and rotating the layer horizontally (Fig. S4). The border between the stratum radiatum (SR) and the pyramidal layer (SP) and the border between the stratum oriens (SO) and the SP were then marked according to the DAPI staining marking in alignment with the Rat Brain Atlas105 (Fig. S4). The distance between SR-SP and SO-SP was taken as the pyramidal layer thickness. The distance of each cell (Alex Fluor 488-PFC+ and Alex Fluor 555 MEC+) from the SR-SP. the border was divided by the pyramidal layer thickness to calculate the normalized depth of all labeled cells within the CA1 pyramidal cell layer 21.
Recording and data processing
Recordings were conducted using the Intan RHD2000 interface board or Intan Recording Controller, sampled at 20 kHz. Amplification and digitization were done on the head stage. Data were visualized with Neurosuite software, Neuroscope. All local field potential (LFP) analyses (SWR detection, state scoring, etc.) were conducted on the 1,250-Hz down-sampled signal.
QUANTIFICATION AND STATISTICAL ANALYSIS
Spike sorting and unit classification
Spike sorting was performed semi-automatically with KiloSort106 (https://github.com/cortex-lab/KiloSort), followed by manual curation using the software Phy (github.com/kwikteam/phy) and custom designed plugins (https://github.com/petersenpeter/phy-plugins) to obtain well-isolated single units. Cluster quality was assessed by manual inspection of waveforms and auto-correlograms, and by the isolation distance metric. Multiunit, noise clusters or poorly isolated units were discarded for analysis. Well-isolated units were classified into putative cell types using the Matlab package Cell Explorer (petersenpeter.github.io/Cell-Explorer107). Spiking characteristics, including the autocorrelograms, spike waveforms, and putative monosynaptic connections derived from short-term cross correlograms, were used to select and characterize well-isolated units. Three cell types were assigned: putative pyramidal cells, narrow, and wide waveform interneurons. Two key metrics used for this separation were burst index and trough-to-peak latency (Fig. S1). Burst index was determined by calculating the average number of spikes in the 3–5 ms bins of the spike autocorrelogram divided by the average number of spikes in the 200–300 ms bins. To calculate the trough-to-peak latency, the average waveforms were taken from the recording site with the maximum amplitude for the averaged waveforms of a given unit.
Classification of deep and superficial CA1 pyramidal cells
To classify all recorded CA1 pyramidal cells based on the radial position of their soma, the relative depth of each electrode across the pyramidal layer was first determined. This classification was based on the stereotypical depth profile of SWRs as the probe transects the pyramidal layer. The slow envelope of the SWR has a positive polarity above the pyramidal layer and reverts that polarity right across the middle of the layer 23,26. Below the middle of the pyramidal layer (superficial sublayer), SWR envelope has a negative polarity. The amplitude of this envelope gradually increases, peaking in the middle of the stratum radiatum (the sharp-wave). The relative depth of each electrode was determined in relation to the channel of polarity reversal (the middle of the layer: 0 µm), considering the know inter-electrode distance. The classification assigned three labels: deep, middle, and superficial defined as deep: < −30µm, middle: −−30µm < 30µm, superficial: > 30µm. The position of the soma of each pyramidal cell was determined as the electrode with the largest amplitude waveforms across the shank.
SWR detection
To detect SWRs, the wide-band signal was band-pass filtered (difference-of-Gaussians; zero-lag, linear phase FIR), and instantaneous power was calculated by clipping at 4 SD, rectified, and low-pass filtered32. The low-pass filter cut-off was at a frequency corresponding to p cycles of the mean bandpass (for 80–250 Hz band-pass, the low-pass was 55 Hz). Subsequently, the power of the non-clipped signal was computed, and all events exceeding 4 SD from the mean were detected. The events were then expanded until the (non-clipped) power fell below 1 SD; short events (< 15ms) were discarded. Sharp waves were detected separately using LFP from a CA1 str. radiatum channel, filtered with band-pass filter boundaries (5–40 Hz). LFP events of a minimum duration of 20 ms and a maximum of 400 ms exceeding 2.5 SD of the background signal were included as candidate SPWs. Only if a sharp wave was simultaneously detected with a ripple was a CA1 SPW-R event retained for further analysis.
SWR spike content analysis
Well-isolated putative units with at least 100 spikes in a given session were included in the analysis. Within-SWR firing rate was calculated as the number of spikes within SWRs divided by the cumulative SWR duration for the session. The probability of participation of individual units in SWRs was defined as the number of events in which a neuron fired at least one spike during the SWR divided by the total number of SWR detected. Cross-correlograms (CCG) were constructed with within-SWR spikes as a function of the latency binning them into 5 ms size bins. Spike counts in CCGs of all pairs in each category were z-scored. For peri-SWR firing histograms, single unit firing rates were z-scored, averaged, and plotted with ± 95% confidence intervals.
Place cell analysis
Spiking data and the tracked animal’s position were binned into 3-cm wide segments of the camera field projected onto the maze floor, generating raw maps of spike counts and occupancy hlfor cells with at least 100 spikes. A Gaussian kernel (SD = 3 cm) was applied to both raw maps of spike and occupancy, and a smoothed rate map was constructed by dividing the spike map by the occupancy map. Independent rate maps were constructed for the different running directions in the mazes. Only periods in which the animal velocity was greater than 4 cm/s were included. A place field was defined as a continuous region of at least 15cm2, where the mean firing rate was above 10% of the peak rate in the maze, and the peak firing rate was > 3Hz. We calculated the spatial information encoded in place cell firing rates using the method of108 to calculate spatial information in bits per spike as follows:
| 1 |
Where the environment is divided into spatial bins , is the occupancy probability of bin , is the mean firing rate for bin , and is the overall mean firing rate of the cell.
In the delayed alternation task, a ’trajectory selectivity index’ (TSI) was calculated similarly to previous reports (e.g.10). First, rate maps were constructed separately for left and right-bound trials. Then the firing rate difference between different trajectories was compared (i.e., center-to-left versus center-to-right outbound trajectories, and left-to-center versus right-to-center inbound trajectories) as:
| 2 |
where is the firing rate in the -th spatial bin on the stem during left trials (i.e., center-to-left trial for outbound, or left-to-center trial for inbound), and is for the right trials.
For all place cell analyses, only sessions containing CA1deep and CA1sup pyramidal cells that passed our criteria for place cell definition were included. In some of these sessions, place cells from other hippocampal regions were also recorded but were not included in the analysis. In the case of memory tasks (e.g., M-maze and cheeseboard), only sessions where memory performance was above chance were included.
To identify ’splitter cells’ place cells with fields in the central arm of the maze were selected. If the cell had overlapping place fields in both directions with an average peak firing rate difference of at least 50% it was considered a splitter cell.
For reward location of decision point-related analysis, place fields were considered if their peak fell within 20 cm of those landmarks. ’Reward gain’ in the cheeseboard maze was calculated as the firing rate of a cell in a 20 cm radius around previously rewarded locations divided by the firing in the rest of the maze.
Cell assembly analyses
Cell assemblies were identified as previously described 3,41,43,44,109,110. Significant co-firing patterns were detected using an unsupervised statistical method based on independent component analysis (ICA). The spike trains for each neuron were binned into time windows (25-ms for inter-hippocampal in Fig. 1 and 50-ms for inter-region in Fig. 7) and z-score transformed to eliminate biases due to differences in average firing rates. Next, a principal component analysis was applied to the binned spike matrix (). The correlation matrix of was given by and the eigenvalue decomposition of C was given by:
| 3 |
where is the jth eigenvalue of C and pj is its corresponding eigenvector. The Marcenko-Pastur law was used to estimate the number of significant patterns embedded within . For a matrix, an eigenvalue exceeding , defined by , signifies that the pattern given by the corresponding principal component explains more correlation than would be expected if the neurons were independent of each other 111. The number of eigenvalues exceeding was defined as NA and therefore represents the minimum number of distinct significant patterns in the data12,43. The significant principal components were then projected back onto the binned spike data
| 4 |
where is the matrix with the NA principal components as columns.
Independent component analysis (ICA), using the fast ICA algorithm 112, was then applied to the matrix . That is, an unmixing matrix W was found such that the rows of the matrix were as independent as possible. The unmixing matrix W was then used to derive each cell’s weight within each assembly .
Cell assembly members were identified using Otsu’s method109,113 to divide the absolute weights into two groups that maximized inter-class variance. Neurons in the group with greater absolute weights were classified as members. The goodness of separation was quantified using Otsu’s effectiveness metric, namely the ratio of the inter-class variance to the total variance. This procedure yielded a set of vectors Ci representing the detected cell assemblies.
To determine the strength of the expressed assemblies, we tracked each assembly pattern over time by:
| 5 |
where z(t) is a smooth vector-function containing for each neuron its z-scored instantaneous firing-rate and Pk is the matrix projecting z(t) to the activation-strength of the assembly pattern k at time t. To increase the temporal resolution, z(t) was obtained by convolving the spike-train of each neuron with a Gaussian kernel () and then z-scoring each trace. w was set to 25 ms to match the bin size used to identify the assembly patterns. Assembly activations were defined as peaks exceeding .
To determine the spatial encoding of assemblies, time-resolved assembly activations were aggregated over spatial 3-cm bins which created 1-D and 2-D assembly maps (Fig. 7F). 2-D assembly maps were used for visualization and 1-D maps were used for quantification of spatial coding properties. In Fig. 7A–B, assemblies were detected using all pyramidal cells simultaneously recorded from CA1, PFC, and MEC. Sessions were not included if no assemblies were detected. For the analysis of assembly reactivation in Fig. 2, assemblies were detected independently using only CA1 pyramidal cells. As well, only sessions with post-task NREM sleep were included in this analysis in order to assess reactivation. Sessions were not included if no assemblies were detected.
Detection of brain states
State scoring was performed as previously described in Levenstein et al., 114. Briefly, the local field potential (LFP) was extracted from wide-band data by lowpass filtering (sinc filter with a 450 Hz cut-off band) and downsampling to 1250Hz. Broadband LFP, narrow-band theta frequency LFP, and estimated electromyogram (EMG) were used for state scoring. Spectrograms were computed from broadband LFP with a Fast Fourier transform in 10s sliding windows (at 1s), and a principle component analysis was computed after a Z-transform. The first principle component reflected power in the low (<20Hz) frequency range, with oppositely weighted power at higher (>32Hz) frequencies. Theta dominance was quantified as the ratio of powers in the 5–10Hz and 2–16Hz frequency bands. EMG was estimated as the zero-lag correlation between 300–600Hz filtered signals between recording sites115. Soft sticky thresholds on these metrics were used to identify states. High LFP principal component 1 and the low EMG were considered NREM, the high theta and low EMG were considered REM, and the remaining data were taken to reflect the waking state.
Detection of replay
A Bayesian decoding approach (see116 for the original method) was used to detect and analyze replay events (see46–48,117–119 for the use cases of this method to investigate replay). Spike counts from each SWR were first binned into 20ms time bin t from N units (200ms time bins were used for active behavior decoding). Then the posterior probability distributions for each t over binned positions (3 cm) along the linear track were calculated using Bayes’ rule:
| 6 |
Where xp is the center of the p − th position bin. Because we assumed Poisson firing, the prior probability, , for the firing of each unit n is equal to
| 7 |
where is the duration of time (20 ms) and is the mean firing rate of the n − th unit in the p − th position. We assumed a uniform prior distribution Pr(xp) over the position bins. This implementation of Bayesian decoding was carried out using tools in the Python package Nelpy120.
Each replay candidate was considered a significant replay event if the series of decoded positions were more consistent with an ordered trajectory compared to a surrogate distribution. A weighted-correlation was used to score each candidate event48. As an alternative approach, we reproduced replay analyses using linear regression to fit a line to the posterior probability distribution. A Bayesian replay score for a given event was defined as the sum probability mass under the fit line within a bandwidth (21 cm)47. For each candidate event, we generated 1000 surrogates of the posterior probability distribution by circularly shifting each column of the posterior probability matrix by a random amount. A Monte Carlo p-value for each event was obtained from the number of surrogate events with replay scores higher than the observed score. The threshold for significance was held at 0.05. Replay events were identified from events with at least 5 active pyramidal cells with a peak firing rate of ≥ 1Hz and a peak-to-mean firing rate ratio of 1. In addition, candidate events with many (> 50%) inactive spike count bins were discarded. Recording sessions were not included if they had less than 5 CA1 pyramidal cells or if no significant replay was detected.
This Bayesian decoding algorithm was also used to estimate the animal’s location during active running (speed > 4 cm/s), similar to previous studies47,121–123.
Recording sessions with poor decoding accuracy of the animal’s position were excluded from the replay analysis. Decoding accuracy was assessed with a surrogate analysis, where the spike times of each unit were circularly shifted by a random amount. This was done to preserve the temporal components of each spike-train, but to randomize the spike times relative to the position in which they fired. Linear regressions between the real and decoded position of the animals were calculated, and a Monte Carlo p-value for each recording session was obtained using the R2 values of each regression. Only sessions with a significant Monte Carlo p-value < 0.05 and also had a median decoding error of < 25cm were used to quantify replay.
Per Cell Contribution (PCC) Analysis
Per cell contribution was calculated according to and described in detail in Grosmark and Buzaski48. For each cell, 1,000 shuffled spatial tuning curves were made, in which only that cell’s tuning curve was randomly circularly translated. For each event that the cell participated in (fired at least one spike), sequence scores (rZ) were assessed using these 1,000 cell-specific circularly shuffled spatial tuning curves:
| 8 |
where rZ was defined as the absolute value of its weighted-correlation48 as a z-score relative to its absolute null weighted correlation distribution derived from circular shuffling. For a given replay event e, a given cell’s c contribution was estimated as the ’degradation’ of sequence score caused by the shuffling of that cell’s spatial tuning, normalized by the number of participating cells in this event:
| 9 |
where specifies the number of cells that participated in event e. This corrects for the influence each cell may have on the sequence score in events with few participating cells.
Predicting downstream neural activity
To predict neural activity from cortical regions downstream of CA1, we used kernel reduced rank regression (Fig. 4,124–128). This is a form of regularized linear regression, with the prediction weights matrix restricted to a specific rank, reducing the number of parameters and making it more robust to overfitting. For analyses where cortical activity was predicted from CA1 during SWRs, spike counts were binned −50ms to +200ms from the start and stop of the SWR respectively to allow for synaptic lag times (Fig. 4C and Fig. 7D). A 5-fold cross-validated grid search on held-out data (60% training data, 40% testing data) was used to locate the optimal rank parameter per recording session using GridSearchCV from scikit-learn112. Recording sessions with at least 5 CA1deep or 5 CA1sup and 5 cortical pyramidal cells were included in this analysis.
To predict the relative proportion of CA1deep and CA1sup neurons that were active in each SWR, cross-validated ridge regression (RidgeCV from scikit-learn112) was used for its robustness to highly collinear predictors. Briefly, a binary spike matrix X (n-units by n SWRs) was constructed from cortical (PFC or MEC) activity ± 100ms around each SWR. Dimensionality reduction was then applied to X using PCA to reduce the explained variance of X to 80% in order to control for different numbers of units from session to session and between cortical regions. From here, the resulting matrix was split into testing and training sets (40/60 split) and used to predict the relative proportion of CA1deep and CA1sup neurons that were active in each SWR (y). The accuracy of this prediction was then compared to the accuracy from a shuffled model where the SWR identify was randomly permuted 1000 times resulting in a prediction gain metric (Fig. 4D). Recording sessions with at least 5 CA1deep, 5 CA1sup, and 5 cortical pyramidal cells were included in this analysis.
Another approach was used to predict the relative proportion of CA1deep and CA1sup neurons that were active in each SWR. The slopes from a linear regression that modeled the relationship between the relative proportion of CA1deep and CA1sup neurons and the number of active cortical neurons in each SWR were compared between MEC and PFC (Fig. 4E). Similarly, the slopes from a regression that modeled the relationship between the relative proportion of CA1deep and CA1sup neurons and the average firing rate of cortical neurons in each SWR were compared between MEC and PFC (Fig. 4F). For both metrics, if the number of CA1deep neurons was positively related to downstream firing, slopes would be positive. Likewise, if the number of CA1sup neurons was positively related to downstream firing, slopes would be negative. Recording sessions with at least 5 CA1deep, 5 CA1sup, and 5 cortical pyramidal cells were included in this analysis.
Mutual information was used to measure the relation between CA1deep/CA1sup and cortical activity. Briefly, firing rates within SWRs from CA1deep, CA1sup, MEC, and PFC pyramidal cells were calculated, and pairwise mutual information was calculated between the resulting vectors. Time-series mutual information between the two vectors x and y was calculated according to Cover & Thomas129 as:
| 10 |
Theta-cycle detection
As theta phase shifts along the radial CA1 axis130, a channel located above the center of the pyramidal layer was selected for consistency of the extracted phases across recordings. Theta cycles were calculated similarly to previous studies 131. To the broadband LFP, downsampled at 1250 Hz, we applied a broad bandpass filter (1–80 Hz) and determined local minima and maxima in the theta range. Local minima and maxima were used to determine the duration of the ascending and descending parts of the theta cycle to calculate the asymmetry index. Cycles below 100 ms and above 200 ms were discarded. From this, local minima and maxima were determined to extract the waveform phase by linear interpolation between them, with minima equaling 0° and maxima equaling 180°. With this approach, regardless of the length of the ascending and descending parts of the theta cycle, each part always covers 180°.
Co-firing analysis
The spike count was calculated in each interval (either a SWR or a theta cycle), resulting in a vector of spike counts for each pyramidal neuron. Pearson’s correlation coefficients between spike count vectors of different neurons were calculated to estimate the SWR and theta-cycle co-firing of each pair.
Context-selectivity index
To estimate how well individual neurons were able to differentiate different environments, a classifier model (ExtraTreeClassifier in scikit-learn112,132) was used. Briefly, binned spike-trains (, smoothing , standardized to lessen bias of high firing units) were used to predict which environment they were sampled for recording sessions with at least 2 environments. The accuracy obtained from the test set (33% of the data) was then compared to the chance levels (Fig. 5C). For example, if 70% of bins were accurately predicted and there were 2 environments for the recording session, giving a chance level of 50%, the context selectivity index was 0.2. This analysis was preferred over other methods, such as the population vector correlation 133, as it made no assumptions about the spatial layout of each environment. Alternative context-selectivity index methods used included pairwise ratemap correlations across re-introductions to the maze and taking the max peak firing rate divided by the average peak firing rate across epochs per cell (also computed with the average firing rate in addition to the peak firing rate). Pairwise ratemap correlations were computed using the Pearson product-moment correlation coefficients for each pair of ratemaps which both had significantly more spatial information content compared to a null shuffled distribution.
Statistical analysis
Statistics were calculated using R, Python, and Matlab. Using R packages lme4134 and lmerTest 135, linear mixed-effects models were used to assess group differences as they account for correlated data, such as many neurons and sessions from the same rat when conducting statistical modeling and hypothesis testing136. The basic model used was . The normality and independence of the errors were visually inspected and corrected with an appropriate transform if the errors were skewed. Model assumptions were also inspected using the R package DHARMa137. When appropriate, a rank-sum test was used. No data were excluded based on statistical tests. Group differences in proportion were modeled using generalized linear models with mixed effects and fit using the glmer() function with family = ”binomial”. When appropriate, a Chi-square () or Fisher’s exact test was used. The significance threshold was set at unless otherwise noted.
Boxplots were generated with the python package Seaborn 138, where the central mark indicates the median; the bottom and top edges of the box indicate the 25th and 75th percentiles,
No specific analysis to estimate minimal population sample or group size was used, but the number of animals, sessions, recorded cells, and SWR events were larger or similar to those employed in previous related works10,12,23,29,30,42,44,49,66. The unit of analysis was typically identified as single cells or SWR events. In some cases, the unit of analysis was sessions or animals, and this is stated in the text.
Supplementary Material
Highlights
Superficial CA1 pyramidal cells are the main contributors to memory replay
CA1 superficial cells encode spatial context and future choices and project to MEC
CA1 deep cells track reward configuration and project to PFC
Hippocampo-cortical assemblies reactivate complementary memory representations.
eTOC Blurb
Harvey et al. show the existence of segregated hippocampo-cortical subcircuits that support the selective encoding, routing, and replay of complementary memory representations. These results highlight the contribution of pyramidal cell diversity to the flexible computational capabilities of the hippocampus during learning and memory.
Acknowledgments
The authors thank Joe Fetcho, Wenbo Tang, Ralitsa Todorova, Laura Berkowitz, Hongyu Chang, Jesse Goldberg, Lucas Sjulson, and Nilay Yapici for useful comments on the manuscript and Melissa Warden for providing access to the confocal microscope. The authors also thank Roman Huzsar and Yunchang Zhang for advice on histological quantification, and Mazen Kheirbek for advice on retrograde tracing experiments. Funding: This work was supported by NIH grant 4R00MH120343, Sloan Fellowship, Whitehall Research Grant and Klingenstein-Simons Fellowship (AFR), NIH grant 4R00MH122582, BBRF NARSAD Award (AO), NYSTEM C029155, and NIH S10OD018516 (Cornell University BRC Imaging Facility).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing interests.
References
- 1.O’Keefe J and Nadel L (1978). The Hippocampus as a Cognitive Map (Oxford: Clarendon Press; ). [Google Scholar]
- 2.Buzsáki G (2015). Hippocampal sharp wave-ripple: A cognitive biomarker for episodic memory and planning. Hippocampus 25, 1073–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Oliva A, Fernández-Ruiz A, Leroy F, and Siegelbaum SA (2020). Hippocampal CA2 sharp-wave ripples reactivate and promote social memory. Nature 587, 264–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wilson M and McNaughton B (1994). Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679. [DOI] [PubMed] [Google Scholar]
- 5.Pavlides C and Winson J (1989). Influences of hippocampal place cell firing in the awake state on the activity of these cells during subsequent sleep episodes. Journal of Neuroscience 9, 2907–2918. Publisher: Society for Neuroscience Section: Articles. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Skaggs WE and McNaughton BL (1996). Replay of Neuronal Firing Sequences in Rat Hippocampus During Sleep Following Spatial Experience. Science 271, 1870–1873. [DOI] [PubMed] [Google Scholar]
- 7.Buzsáki G and Moser EI (2013). Memory, navigation and theta rhythm in the hippocampal-entorhinal system. Nature Neuroscience 16, 130–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Foster DJ (2017). Replay Comes of Age. Annual Review of Neuroscience 40, 581–602. [DOI] [PubMed] [Google Scholar]
- 9.Joo HR and Frank LM (2018). The hippocampal sharp wave–ripple in memory retrieval for immediate use and consolidation. Nature Reviews Neuroscience 19, 744–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shin JD, Tang W, and Jadhav SP (2019). Dynamics of Awake Hippocampal-Prefrontal Replay for Spatial Learning and Memory-Guided Decision Making. Neuron 104, 1110–1125.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pfeiffer BE (2020). The content of hippocampal “replay”. Hippocampus 30, 6–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Peyrache A, Khamassi M, Benchenane K, Wiener SI, and Battaglia FP (2009). Replay of rule-learning related neural patterns in the prefrontal cortex during sleep. Nature Neuroscience 12, 919–926. [DOI] [PubMed] [Google Scholar]
- 13.Vaz AP, Inati SK, Brunel N, and Zaghloul KA (2019). Coupled ripple oscillations between the medial temporal lobe and neocortex retrieve human memory. Science (New York, N.Y.) 363, 975–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Maingret N, Girardeau G, Todorova R, Goutierre M, and Zugaro M (2016). Hippocampo-cortical coupling mediates memory consolidation during sleep. Nature Neuroscience 19, 959–964. [DOI] [PubMed] [Google Scholar]
- 15.Slomianka L, Amrein I, Knuesel I, Sørensen JC, and Wolfer DP (2011). Hippocampal pyramidal cells: the reemergence of cortical lamination. Brain Structure and Function 216, 301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Graves AR, Moore SJ, Bloss EB, Mensh BD, Kath WL, and Spruston N (2012). Hippocampal pyramidal neurons comprise two distinct cell types that are countermodulated by metabotropic receptors. Neuron 76, 776–789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cembrowski MS, Bachman JL, Wang L, Sugino K, Shields BC, and Spruston N (2016). Spatial Gene-Expression Gradients Underlie Prominent Heterogeneity of CA1 Pyramidal Neurons. Neuron 89, 351–368. [DOI] [PubMed] [Google Scholar]
- 18.Yao Z, van Velthoven CTJ, Nguyen TN, Goldy J, Sedeno-Cortes AE, Baftizadeh F, Bertagnolli D, Casper T, Chiang M, Crichton K, et al. (2021). A taxonomy of transcriptomic cell types across the isocortex and hippocampal formation. Cell 184, 3222–3241.e26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ciocchi S, Passecker J, Malagon-Vina H, Mikus N, and Klausberger T (2015). Selective information routing by ventral hippocampal CA1 projection neurons. Science 348, 560–563. [DOI] [PubMed] [Google Scholar]
- 20.Cavalieri D, Angelova A, Islah A, Lopez C, Bocchio M, Bollmann Y, Baude A, and Cossart R (2021). CA1 pyramidal cell diversity is rooted in the time of neurogenesis. eLife 10, e69270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huszár R, Zhang Y, Blockus H, and Buzsáki G (2022). Preconfigured dynamics in the hippocampus are guided by embryonic birthdate and rate of neurogenesis. Nature Neuroscience 25, 1201–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mizuseki K, Diba K, Pastalkova E, and Buzsáki G (2011). Hippocampal CA1 pyramidal cells form functionally distinct sublayers. Nature Neuroscience 14, 1174–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Oliva A, Fernández-Ruiz A, Buzsáki G, and Berényi A (2016). Spatial coding and physiological properties of hippocampal neurons in the Cornu Ammonis subregions. Hippocampus 26, 1593–1607. [DOI] [PubMed] [Google Scholar]
- 24.Lee SH, Marchionni I, Bezaire M, Varga C, Danielson N, Lovett-Barron M, Losonczy A, and Soltesz I (2014). Parvalbumin-Positive Basket Cells Differentiate among Hippocampal Pyramidal Cells. Neuron 82, 1129–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Soltesz I and Losonczy A (2018). CA1 pyramidal cell diversity enabling parallel information processing in the hippocampus. Nature Neuroscience 21, 484–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fernández-Ruiz A, Oliva A, Nagy GA, Maurer AP, Berényi A, and Buzsáki G (2017). Entorhinal-CA3 Dual-Input Control of Spike Timing in the Hippocampus by Theta-Gamma Coupling. Neuron 93, 1213–1226.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Valero M, Cid E, Averkin RG, Aguilar J, Sanchez-Aguilera A, Viney TJ, Gomez-Dominguez D, Bellistri E, and de la Prida LM (2015). Determinants of different deep and superficial CA1 pyramidal cell dynamics during sharp-wave ripples. Nature Neuroscience 18, 1281–1290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sharif F, Tayebi B, Buzsáki G, Royer S, and Fernandez-Ruiz A (2021). Subcircuits of Deep and Superficial CA1 Place Cells Support Efficient Spatial Coding across Heterogeneous Environments. Neuron 109, 363–376.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Danielson NB, Zaremba JD, Kaifosh P, Bowler J, Ladow M, and Losonczy A (2016). Sublayer-Specific Coding Dynamics during Spatial Navigation and Learning in Hippocampal Area CA1. Neuron 91, 652–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Geiller T, Fattahi M, Choi JS, and Royer S (2017). Place cells are more strongly tied to landmarks in deep than in superficial CA1. Nature Communications 8, 14531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Navas-Olive A, Valero M, Jurado-Parras T, de Salas-Quiroga A, Averkin RG, Gambino G, Cid E, and de la Prida LM (2020). Multimodal determinants of phase-locked dynamics across deep-superficial hippocampal sublayers during theta oscillations. Nature Communications 11, 2217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Oliva A, Fernández-Ruiz A, Buzsáki G, and Berényi A (2016). Role of Hippocampal CA2 Region in Triggering Sharp-Wave Ripples. Neuron 91, 1342–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.DeYoe EA and Van Essen DC (1985). Segregation of efferent connections and receptive field properties in visual area V2 of the macaque. Nature 317, 58–61. [DOI] [PubMed] [Google Scholar]
- 34.Bonhoeffer T and Grinvald A (1991). Iso-orientation domains in cat visual cortex are arranged in pinwheel-like patterns. Nature 353, 429–431. [DOI] [PubMed] [Google Scholar]
- 35.Stensola H, Stensola T, Solstad T, Frøland K, Moser MB, and Moser EI (2012). The entorhinal grid map is discretized. Nature 492, 72–78. [DOI] [PubMed] [Google Scholar]
- 36.Treves A and Rolls ET (1994). Computational analysis of the role of the hippocampus in memory. Hippocampus 4, 374–391. [DOI] [PubMed] [Google Scholar]
- 37.Harris KD, Csicsvari J, Hirase H, Dragoi G, and Buzsáki G (2003). Organization of cell assemblies in the hippocampus. Nature 424, 552–556. [DOI] [PubMed] [Google Scholar]
- 38.Redish AD, Battaglia FP, Chawla MK, Ekstrom AD, Gerrard JL, Lipa P, Rosenzweig ES, Worley PF, Guzowski JF, McNaughton BL, et al. (2001). Independence of Firing Correlates of Anatomically Proximate Hippocampal Pyramidal Cells. Journal of Neuroscience 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Csicsvari J, Hirase H, Czurkó A, Mamiya A, and Buzsáki G (1999). Oscillatory Coupling of Hippocampal Pyramidal Cells and Interneurons in the Behaving Rat. Journal of Neuroscience 19, 274–287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hebb DO (1949). The organization of behavior; a neuropsychological theory. The organization of behavior; a neuropsychological theory (Oxford, England: Wiley; ). [Google Scholar]
- 41.van de Ven GM, Trouche S, McNamara CG, Allen K, and Dupret D (2016). Hippocampal Offline Reactivation Consolidates Recently Formed Cell Assembly Patterns during Sharp Wave-Ripples. Neuron 92, 968–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Farooq U, Sibille J, Liu K, and Dragoi G (2019). Strengthened Temporal Coordination within Pre-existing Sequential Cell Assemblies Supports Trajectory Replay. Neuron 103, 719–733.e7. Publisher: Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lopes-dos Santos V, Ribeiro S, and Tort AB (2013). Detecting cell assemblies in large neuronal populations. Journal of Neuroscience Methods 220, 149–166. [DOI] [PubMed] [Google Scholar]
- 44.Fernández-Ruiz A, Oliva A, Soula M, Rocha-Almeida F, Nagy GA, Martin-Vazquez G, and Buzsáki G (2021). Gamma rhythm communication between entorhinal cortex and dentate gyrus neuronal assemblies. Science 372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nádasdy Z, Hirase H, Czurkó A, Csicsvari J, and Buzsáki G (1999). Replay and Time Compression of Recurring Spike Sequences in the Hippocampus. The Journal of Neuroscience 19, 9497–9507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wu X and Foster DJ (2014). Hippocampal Replay Captures the Unique Topological Structure of a Novel Environment. Journal of Neuroscience 34, 6459–6469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Davidson TJ, Kloosterman F, and Wilson MA (2009). Hippocampal Replay of Extended Experience. Neuron 63, 497–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Grosmark AD and Buzsáki G (2016). Diversity in neural firing dynamics supports both rigid and learned hippocampal sequences. Science 351, 1440–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fernández-Ruiz A, Oliva A, Oliveira E.F.d., Rocha-Almeida F, Tingley D, and Buzsáki G (2019). Long-duration hippocampal sharp wave ripples improve memory. Science 364, 1082–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jadhav S, Rothschild G, Roumis D, and Frank L (2016). Coordinated Excitation and Inhibition of Prefrontal Ensembles during Awake Hippocampal Sharp-Wave Ripple Events. Neuron 90, 113–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Girardeau G, Inema I, and Buzsáki G (2017). Reactivations of emotional memory in the hippocampus–amygdala system during sleep. Nature Neuroscience 20, 1634–1642. [DOI] [PubMed] [Google Scholar]
- 52.Sosa M, Joo HR, and Frank LM (2020). Dorsal and Ventral Hippocampal Sharp-Wave Ripples Activate Distinct Nucleus Accumbens Networks. Neuron 105, 725–741.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.van der Meer MAA, Johnson A, Schmitzer-Torbert NC, and Redish AD (2010). Triple Dissociation of Information Processing in Dorsal Striatum, Ventral Striatum, and Hippocampus on a Learned Spatial Decision Task. Neuron 67, 25–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ji D and Wilson MA (2007). Coordinated memory replay in the visual cortex and hippocampus during sleep. Nature Neuroscience 10, 100–107. [DOI] [PubMed] [Google Scholar]
- 55.Baimbridge KG, Peet MJ, McLennan H, and Church J (1991). Bursting response to current-evoked depolarization in rat ca1 pyramidal neurons is correlated with lucifer yellow dye coupling but not with the presence of calbindin-D28k. Synapse 7, 269–277. [DOI] [PubMed] [Google Scholar]
- 56.Roth FC, Beyer KM, Both M, Draguhn A, and Egorov AV (2016). Downstream effects of hippocampal sharp wave ripple oscillations on medial entorhinal cortex layer V neurons in vitro. Hippocampus 26, 1493–1508. [DOI] [PubMed] [Google Scholar]
- 57.Frank LM, Brown EN, and Wilson M (2000). Trajectory Encoding in the Hippocampus and Entorhinal Cortex. Neuron 27, 169–178. [DOI] [PubMed] [Google Scholar]
- 58.Jadhav SP, Kemere C, German PW, and Frank LM (2012). Awake hippocampal sharp-wave ripples support spatial memory. Science 336, 1454–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wood ER, Dudchenko PA, Robitsek RJ, and Eichenbaum H (2000). Hippocampal Neurons Encode Information about Different Types of Memory Episodes Occurring in the Same Location. Neuron 27, 623–633. [DOI] [PubMed] [Google Scholar]
- 60.Dupret D, O’Neill J, Pleydell-Bouverie B, and Csicsvari J (2010). The reorganization and reactivation of hippocampal maps predict spatial memory performance. Nature Neuroscience 13, 995–1002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kay K, Sosa M, Chung JE, Karlsson MP, Larkin MC, and Frank LM (2016). A hippocampal network for spatial coding during immobility and sleep. Nature 531, 185–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Alexander AS, Rangel LM, Tingley D, and Nitz DA (2018). Neurophysiological signatures of temporal coordination between retrosplenial cortex and the hippocampal formation. Behavioral Neuroscience 132, 453–468. [DOI] [PubMed] [Google Scholar]
- 63.Sjulson L, Peyrache A, Cumpelik A, Cassataro D, and Buzsáki G (2018). Cocaine Place Conditioning Strengthens Location-Specific Hippocampal Coupling to the Nucleus Accumbens. Neuron 98, 926–934.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Perez-Nieves N, Leung VCH, Dragotti PL, and Goodman DFM (2021). Neural heterogeneity promotes robust learning. Nature Communications 12, 5791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Gjorgjieva J, Drion G, and Marder E (2016). Computational implications of biophysical diversity and multiple timescales in neurons and synapses for circuit performance. Current Opinion in Neurobiology 37, 44–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ólafsdóttir HF, Carpenter F, and Barry C (2016). Coordinated grid and place cell replay during rest. Nature Neuroscience 19, 792–794. [DOI] [PubMed] [Google Scholar]
- 67.Tang W and Jadhav SP (2019). Sharp-wave ripples as a signature of hippocampal-prefrontal reactivation for memory during sleep and waking states. Neurobiology of Learning and Memory 160, 11–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Tang W, Shin JD, Frank LM, and Jadhav SP (2017). Hippocampal-Prefrontal Reactivation during Learning Is Stronger in Awake Compared with Sleep States. Journal of Neuroscience 37, 11789–11805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kaefer K, Nardin M, Blahna K, and Csicsvari J (2020). Replay of Behavioral Sequences in the Medial Prefrontal Cortex during Rule Switching. Neuron 106, 154–165.e6. [DOI] [PubMed] [Google Scholar]
- 70.Klee JL, Souza BC, and Battaglia FP (2021). Learning differentially shapes prefrontal and hippocampal activity during classical conditioning. eLife 10, e65456. Publisher: eLife Sciences Publications, Ltd. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.O’Neill J, Boccara CN, Stella F, Schoenenberger P, and Csicsvari J (2017). Superficial layers of the medial entorhinal cortex replay independently of the hippocampus. Science 355, 184–188. [DOI] [PubMed] [Google Scholar]
- 72.Nitzan N, McKenzie S, Beed P, English DF, Oldani S, Tukker JJ, Buzsáki G, and Schmitz D (2020). Propagation of hippocampal ripples to the neocortex by way of a subiculum-retrosplenial pathway. Nature Communications 11, 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Opalka AN, Huang W.q., Liu J, Liang H, and Wang DV (2020). Hippocampal Ripple Coordinates Retrosplenial Inhibitory Neurons during Slow-Wave Sleep. Cell Reports 30, 432–441.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Sugden AU, Zaremba JD, Sugden LA, McGuire KL, Lutas A, Ramesh RN, Alturkistani O, Lensjø KK, Burgess CR, and Andermann ML (2020). Cortical reactivations of recent sensory experiences predict bidirectional network changes during learning. Nature Neuroscience 23, 981–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Rothschild G, Eban E, and Frank LM (2017). A cortical–hippocampal–cortical loop of information processing during memory consolidation. Nature Neuroscience 20, 251–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Karimi Abadchi J, Nazari-Ahangarkolaee M, Gattas S, Bermudez-Contreras E, Luczak A, Mc-Naughton BL, and Mohajerani MH (2020). Spatiotemporal patterns of neocortical activity around hippocampal sharp-wave ripples. eLife 9, e51972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Battaglia FP, Sutherland GR, and McNaughton BL (2004). Hippocampal sharp wave bursts coincide with neocortical “up-state” transitions. Learning & Memory 11, 697–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Witter MP, Wouterlood FG, Naber PA, and Van Haeften T (2000). Anatomical Organization of the Parahippocampal-Hippocampal Network. Annals of the New York Academy of Sciences 911, 1–24. [DOI] [PubMed] [Google Scholar]
- 79.Hoover WB and Vertes RP (2007). Anatomical analysis of afferent projections to the medial prefrontal cortex in the rat. Brain Structure & Function 212, 149–179. [DOI] [PubMed] [Google Scholar]
- 80.Ährlund Richter S, Xuan Y, van Lunteren JA, Kim H, Ortiz C, Pollak Dorocic I, Meletis K, and Carlén M (2019). A whole-brain atlas of monosynaptic input targeting four different cell types in the medial prefrontal cortex of the mouse. Nature Neuroscience 22, 657–668. [DOI] [PubMed] [Google Scholar]
- 81.Rajasethupathy P, Sankaran S, Marshel JH, Kim CK, Ferenczi E, Lee SY, Berndt A, Ramakrishnan C, Jaffe A, Lo M, et al. (2015). Projections from neocortex mediate top-down control of memory retrieval. Nature 526, 653–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Ye X, Kapeller-Libermann D, Travaglia A, Inda MC, and Alberini CM (2017). Direct dorsal hippocampal–prelimbic cortex connections strengthen fear memories. Nature Neuroscience 20, 52–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Roy DS, Kitamura T, Okuyama T, Ogawa SK, Sun C, Obata Y, Yoshiki A, and Tonegawa S (2017). Distinct Neural Circuits for the Formation and Retrieval of Episodic Memories. Cell 170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Kitanishi T, Umaba R, and Mizuseki K (2021). Robust information routing by dorsal subiculum neurons. Science Advances 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Chenani A, Sabariego M, Schlesiger MI, Leutgeb JK, Leutgeb S, and Leibold C (2019). Hippocampal CA1 replay becomes less prominent but more rigid without inputs from medial entorhinal cortex. Nature Communications 10, 1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Gava GP, McHugh SB, Lefévre L, Lopes-dos Santos V, Trouche S, El-Gaby M, Schultz SR, and Dupret D (2021). Integrating new memories into the hippocampal network activity space. Nature Neuroscience, 1–5. [DOI] [PMC free article] [PubMed]
- 87.Geiller T, Sadeh S, Rolotti SV, Blockus H, Vancura B, Negrean A, Murray AJ, Rózsa B, Polleux F, Clopath C, et al. (2021). Local circuit amplification of spatial selectivity in the hippocampus. Nature, 1–5. [DOI] [PMC free article] [PubMed]
- 88.Duvelle E, Grieves RM, Hok V, Poucet B, Arleo A, Jeffery KJ, and Save E (2019). Insensitivity of Place Cells to the Value of Spatial Goals in a Two-Choice Flexible Navigation Task. Journal of Neuroscience 39, 2522–2541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Pfeiffer BE and Foster DJ (2013). Hippocampal place-cell sequences depict future paths to remembered goals. Nature 497, 74–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Wang M, Foster DJ, and Pfeiffer BE (2020). Alternating sequences of future and past behavior encoded within hippocampal theta oscillations. Science 370, 247–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Masurkar AV, Srinivas KV, Brann DH, Warren R, Lowes DC, and Siegelbaum SA (2017). Medial and Lateral Entorhinal Cortex Differentially Excite Deep versus Superficial CA1 Pyramidal Neurons. Cell Reports 18, 148–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Kohara K, Pignatelli M, Rivest AJ, Jung HY, Kitamura T, Suh J, Frank D, Kajikawa K, Mise N, Obata Y, et al. (2014). Cell type-specific genetic and optogenetic tools reveal hippocampal CA2 circuits. Nature Neuroscience 17, 269–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Berndt M, Trusel M, Roberts TF, Volk LJ, and Pfeiffer BE (2022). Bidirectional synaptic changes in deep and superficial hippocampal neurons following in vivo activity. bioRxiv . [DOI] [PMC free article] [PubMed]
- 94.Fujisawa S, Amarasingham A, Harrison MT, and Buzsáki G (2014). Simultaneous electrophysiological recordings of ensembles of isolated neurons in rat medial prefrontal cortex and intermediate CA1 area of the hippocampus during a working memory task CRCNS.org.
- 95.Mizuseki K, Sirota A, Pastalkova E, and Buzsáki G (2009). Multi-unit recordings from the rat hippocampus made during open field foraging CRCNS.org.
- 96.Mizuseki K, Sirota A, Pastalkova E, Diba K, and Buzsáki G (2013). Multiple single unit recordings from different rat hippocampal and entorhinal regions while the animals were performing multiple behavioral tasks CRCNS.org.
- 97.Mizuseki K, Sirota A, Pastalkova E, Diba K, Peyrache A, and Buzsáki G (2014). Extracellular recordings from multi-site silicon probes used for clustering of neuron responses in rat hippocampal and entorhinal regions CRCNS.org.
- 98.Grosmark A, Long J, and Buzsáki G (2016). Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning CRCNS.org.
- 99.Girardeau G, Inema I, and Buzsaki G (2017). Simultaneous large-scale recordings in dorsal hippocampus, basolateral amygdala and neighbouring deep nuclei and structures in rats performing a spatial aversive task and sleeping CRCNS.org.
- 100.Mathis A, Mamidanna P, Cury KM, Abe T, Murthy VN, Mathis MW, and Bethge M (2018). DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nature Neuroscience 21, 1281–1289. Number: 9 Publisher: Nature Publishing Group. [DOI] [PubMed] [Google Scholar]
- 101.Mizuseki K, Sirota A, Pastalkova E, and Buzsáki G (2009). Theta Oscillations Provide Temporal Windows for Local Circuit Computation in the Entorhinal-Hippocampal Loop. Neuron 64, 267–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Mizuseki K, Royer S, Diba K, and Buzsáki G (2012). Activity dynamics and behavioral correlates of CA3 and CA1 hippocampal pyramidal neurons. Hippocampus 22, 1659–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Fujisawa S, Amarasingham A, Harrison MT, and Buzsáki G (2008). Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nature Neuroscience 11, 823–833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Jimenez JC, Su K, Goldberg AR, Luna VM, Biane JS, Ordek G, Zhou P, Ong SK, Wright MA, Zweifel L, et al. (2018). Anxiety Cells in a Hippocampal-Hypothalamic Circuit. Neuron 97, 670–683.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Paxinos G and Watson C (2009). The rat brain in stereotaxic coordinates. Compact 6. ed edition (Amsterdam: Elsevier, Academic Press; ). [Google Scholar]
- 106.Pachitariu M, Steinmetz N, Kadir S, Carandini M, and Kenneth D, H. (2016). Kilosort: realtime spike-sorting for extracellular electrophysiology with hundreds of channels. preprint, Neuroscience.
- 107.Petersen PC, Siegle JH, Steinmetz NA, Mahallati S, and Buzsáki G (2021). CellExplorer: A framework for visualizing and characterizing single neurons. Neuron [DOI] [PMC free article] [PubMed]
- 108.Skaggs W, McNaughton B, Gothard K, and Markus E (1993). An Information-Theoretic Approach to Deciphering the Hippocampal Code. Advances in neural information processing systems, 1030–1037.
- 109.Boucly CJ, Pompili MN, Todorova R, Leroux EM, Wiener S, and Zugaro M (2022). Flexible communication between cell assemblies and ’reader’ neurons
- 110.Oberto VJ, Boucly CJ, Gao H, Todorova R, Zugaro MB, and Wiener SI (2022). Distributed cell assemblies spanning prefrontal cortex and striatum. Current Biology 32, 1–13.e6. [DOI] [PubMed] [Google Scholar]
- 111.Peyrache A, Benchenane K, Khamassi M, Wiener SI, and Battaglia FP (2010). Principal component analysis of ensemble recordings reveals cell assemblies at high temporal resolution. Journal of Computational Neuroscience 29, 309–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. (2011). Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 12, 2825–2830. [Google Scholar]
- 113.Otsu N (1979). A Threshold Selection Method from Gray-Level Histograms. IEEE Transactions on Systems, Man, and Cybernetics 9, 62–66. [Google Scholar]
- 114.Levenstein D, Buzsáki G, and Rinzel J (2019). NREM sleep in the rodent neocortex and hippocampus reflects excitable dynamics. Nature Communications 10, 2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Schomburg E, Fernández-Ruiz A, Mizuseki K, Berényi A, Anastassiou C, Koch C, and Buzsáki G (2014). Theta Phase Segregation of Input-Specific Gamma Patterns in Entorhinal-Hippocampal Networks. Neuron 84, 470–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Zhang K, Ginzburg I, McNaughton BL, and Sejnowski TJ (1998). Interpreting Neuronal Population Activity by Reconstruction: Unified Framework With Application to Hippocampal Place Cells. Journal of Neurophysiology 79, 1017–1044. [DOI] [PubMed] [Google Scholar]
- 117.Johnson A and Redish AD (2007). Neural Ensembles in CA3 Transiently Encode Paths Forward of the Animal at a Decision Point. Journal of Neuroscience 27, 12176–12189. Publisher: Society for Neuroscience Section: Articles. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Dragoi G and Tonegawa S (2011). Preplay of future place cell sequences by hippocampal cellular assemblies. Nature 469, 397–401. Number: 7330 Publisher: Nature Publishing Group. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Pfeiffer BE and Foster DJ (2015). Autoassociative dynamics in the generation of sequences of hippocampal place cells. Science 349, 180–183. Publisher: American Association for the Advancement of Science Section: Report. [DOI] [PubMed] [Google Scholar]
- 120.Ackermann E (2021). Nelpy: Neuroelectrophysiology object model, data exploration, and analysis in Python. GitHub
- 121.Ambrose RE, Pfeiffer BE, and Foster DJ (2016). Reverse Replay of Hippocampal Place Cells Is Uniquely Modulated by Changing Reward. Neuron 91, 1124–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Farooq U and Dragoi G (2019). Emergence of preconfigured and plastic time-compressed sequences in early postnatal development. Science 363, 168–173. Publisher: American Association for the Advancement of Science Section: Report. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Ólafsdóttir HF, Carpenter F, and Barry C (2017). Task Demands Predict a Dynamic Switch in the Content of Awake Hippocampal Replay. Neuron 96, 925–935.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Semedo JD, Gokcen E, Machens CK, Kohn A, and Yu BM (2020). Statistical methods for dissecting interactions between brain areas. Current opinion in neurobiology 65, 59–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Izenman AJ (1975). Reduced-rank regression for the multivariate linear model. Journal of Multivariate Analysis 5, 248–264. [Google Scholar]
- 126.Kobak D, Brendel W, Constantinidis C, Feierstein C, Kepecs A, Mainen Z, Qi XL, Romo R, Uchida N, and Machens C (2016). Demixed principal component analysis of neural population data. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Mukherjee A and Zhu J (2011). Reduced rank ridge regression and its kernel extensions. Statistical Analysis and Data Mining: The ASA Data Science Journal 4, 612–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 7893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Cover TM and Thomas JA (1991). Elements of information theory. Wiley series in telecommunications (New York: Wiley; ). [Google Scholar]
- 130.Buzsáki G (2002). Theta Oscillations in the Hippocampus. Neuron 33, 325–340. [DOI] [PubMed] [Google Scholar]
- 131.Belluscio MA, Mizuseki K, Schmidt R, Kempter R, and Buzsáki G (2012). Cross-Frequency Phase–Phase Coupling between Theta and Gamma Oscillations in the Hippocampus. Journal of Neuroscience 32, 423–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Geurts P, Ernst D, and Wehenkel L (2006). Extremely randomized trees. Machine Learning 63, 3–42. [Google Scholar]
- 133.Leutgeb S, Leutgeb JK, Barnes CA, Moser EI, McNaughton BL, and Moser MB (2005). Independent Codes for Spatial and Episodic Memory in Hippocampal Neuronal Ensembles. Science 309, 619–623. [DOI] [PubMed] [Google Scholar]
- 134.Bates D, Mächler M, Bolker B, and Walker S (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software 67, 1–48. [Google Scholar]
- 135.Kuznetsova A, Brockhoff PB, and Christensen RHB (2017). lmerTest Package: Tests in Linear Mixed Effects Models. Journal of Statistical Software 82, 1–26. [Google Scholar]
- 136.Yu Z, Guindani M, Grieco SF, Chen L, Holmes TC, and Xu X (2022). Beyond t test and ANOVA: applications of mixed-effects models for more rigorous statistical analysis in neuroscience research. Neuron 110, 21–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Hartig F and Lohse L (2022). DHARMa: Residual Diagnostics for Hierarchical (Multi-Level / Mixed) Regression Models. CRAN.R-project.
- 138.Waskom ML (2021). seaborn: statistical data visualization. Journal of Open Source Software 6, 3021. [Google Scholar]
- 139.Holt GR, Softky WR, Koch C, and Douglas RJ (1996). Comparison of discharge variability in vitro and in vivo in cat visual cortex neurons. Journal of Neurophysiology 75, 1806–1814. [DOI] [PubMed] [Google Scholar]
- 140.Kloosterman F (2012). Analysis of Hippocampal Memory Replay Using Neural Population Decoding. In Neuronal Network Analysis: Concepts and Experimental Approaches, Fellin T and Halassa M, eds., Neuromethods (Totowa, NJ: Humana Press; ), pp. 259–282. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Newly generated data reported in this paper will be shared by the lead contact upon request. As well, this paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
Original code has been deposited at https://github.com/ayalab1 and https://github.com/ryanharvey1/ripple_heterogeneity and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Fluoroshield with DAPI | Sigma-Aldrich | SKU: F6057 |
| Calbindin-D28K Monoclonal Antibody | Proteintech | Cat# 66394–1-Ig |
| Bacterial and virus strains | ||
| AAV5-CaMKIIa- hChR2-EYFP | UNC Vector Core | NA |
| Biological samples | ||
| Chemicals, peptides, and recombinant proteins | ||
| Cholera Toxin Subunit B, Alexa Fluor™ 488 Conjugate | Invitrogen | Cat# C22841 |
| Cholera Toxin Subunit B, Alexa Fluor™ 594 Conjugate | Invitrogen | Cat# C22842 |
| Cholera Toxin Subunit B, Alexa Fluor™ 647 Conjugate | Invitrogen | Cat# C34778 |
| Critical commercial assays | ||
| Deposited data | ||
| Hippocampal data | http://crcns.org/data-sets/hc/hc-3 | http://dx.doi.org/10.6080/K09G5JRZ |
| Hippocampal and prefrontal data | http://crcns.org/data-sets/pfc/pfc-2 | http://dx.doi.org/10.6080/K01V5BWK |
| Hippocampal data | https://crcns.org/data-sets/hc/hc-11 | http://dx.doi.org/10.6080/K0862DC5 |
| Hippocampal data | https://crcns.org/data-sets/hc/hc-14 | http://dx.doi.org/10.6080/K0MS3QXD |
| Experimental models: Cell lines | ||
| Experimental models: Organisms/strains | ||
| Rat: Long-Evans | Charles River | Cat#: Crl:LE 006 |
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and algorithms | ||
| Analysis tools | https://github.com/ayalab1/neurocode | https://zenodo.org/badge/latestdoi/398122107 |
| Analysis tools | https://github.com/ryanharvey1/ripple_heterogeneity | https://zenodo.org/badge/latestdoi/388846280 |
| MATLAB | MathWorks | https://www.mathworks.com/products/matlab.html |
| Python | Python Software Foundation | https://www.python.org/ |
| R | R Foundation for Statistical Computing | https://www.R-project.org/ ; RRID: SCR_001905 |
| RStudio | RStudio, PBC | https://www.rstudio.com/ ; RRID: SCR_00043 |
| Vscode | Microsoft | https://code.visualstudio.com/ |
| Cell Explorer | https://cellexplorer.org/ | https://doi.org/10.1016/j.neuron.2021.09.002 |
| Nelpy | https://github.com/nelpy/nelpy | https://zenodo.org/badge/latestdoi/77548623 |
| Seaborn | https://seaborn.pydata.org/ | https://doi.org/10.21105/joss.03021 |
| Scikit-learn | https://scikit-learn.org/stable/ | https://zenodo.org/badge/latestdoi/21369/scikit-learn/scikit-learn |
| Matplotlib | https://matplotlib.org/ | 10.1109/MCSE.2007.55 |
| Numpy | https://numpy.org/ | 10.1038/s41586-020-2649-2 |
| Other | ||
| Silicon probes | Neuronexus | https://neuronexus.com/ |
| Intan RHD2000 | Intan technologies | http://intantech.com/files/Intan_RHD2000_eval_system.pdf |


