Retrospective assessment of accuracy of nine intraocular lens power calculation formulae in eyes with axial myopia

Abstract

Purpose:

To compare the accuracy of nine conventional and newer-generation formulae in calculating intraocular lens power in eyes with axial myopia.

Setting:

Tertiary eye care center, Bengaluru, India.

Design:

Retrospective cross-sectional, comparative study conducted in India.

Methods:

Patients undergoing uneventful phacoemulsification in eyes with axial length >26 mm were included. Preoperative biometry was done using Lenstar LS 900 (Haag-Streit AG, Switzerland). Single eye of patients undergoing bilateral implantation was randomly selected. Optimized lens constants were used to calculate the predicted postoperative refraction of each formula, which was then compared with the actual refractive outcomes to give the prediction errors, following which subgroup analysis was performed. The Kane formula, Barrett universal II, Emmetropia Verifying Optical (EVO) 2.0, Hill Radial Basis Function (Hill RBF) 3.0, Olsen formula, along with Wang Koch–adjusted four formulae, that is, Sanders Retzlaff Kraff/Theoretical (SRK/T), Holladay 1, Haigis, and Hoffer Q formula, were compared for intraocular lens power calculations.

Results:

One hundred and sixty-five eyes that fulfilled all the inclusion criteria were studied. Hill RBF 3.0 had the lowest mean and median absolute prediction errors (0.355 and 0.275, respectively) compared to all formulas. In subgroup analysis (26–28, >28–30, and >30 mm), significant difference was seen only in extremely long eyes (>30 mm). The Hill RBF 3.0 formula generated the maximum percentage of eyes with refractive errors within ±0.25, ±0.5, ±0.75, and ±1 D (46%, 76.2%, 89.9%, and 95.8%, respectively).

Conclusion:

This is the first study evaluating all the formulas exclusively in the myopic eyes. Hill RBF 3 was found to be superior in accuracy to all other formulas.

Cataract surgery has now become a refractive procedure with advances in intraocular lens (IOL), phacoemulsification techniques, biometry, and IOL power calculation formulas.[1] However, anatomical variations in myopic eyes lead to unsatisfactory outcomes with previous generation formulas.[2] Most of these formulas tend to give hyperopic refractive surprise, thereby reducing patient satisfaction.[3] Recent studies have shown that the Barrett universal II (BU II), Haigis, and Olsen formulas are more accurate than other formulas in eyes with an axial length of 26 mm or more.[4] On comparing these three formulae, BU II was found to be better than the other two in extremes of myopia.[1]

The newer artificial intelligence (AI) formulas like Hill Radial Basis Function (Hill RBF), Emmetropia Verifying Optical (EVO) 2.0, and Kane formula have shown better prediction accuracy in recent studies.[5] Darcy et al.,[6] in their study on a small number of eyes, have shown that Kane formula is more accurate than other formulas in cases with axial length more than 26 mm. However, this study included eyes with axial length less than 27 mm.[6] Wang Koch (WK) adjustment for axial length has been recommended for calculating IOL powers in patients with high axial length for better prediction accuracy when using Haigis, Holladay, Sanders Retzlaff Kraff/Theoretical (SRK/T), and Hoffer Q formulas.[7] A recent study on a small number of eyes by Khatib et al.[8] has shown that the EVO formula had the same accuracy as the BU II and Hill RBF 2.0 formulas across all range of axial lengths, but this study also did not include patients with axial length >28 mm (mean 23.5 ± 1.96). Lin et al.,[9] in their study, have found EVO 2.0 and Kane formula to be better than Haigis, BU II, and SRK/T in cases with high axial myopia. In the current study, we evaluated conventional as well as newer-generation formulas for their prediction accuracy in Indian patients having axial myopia, undergoing routine cataract surgery.

Methods

This retrospective analysis was approved by the institutional research and ethics committee and conducted in accordance with the tenets of the Declaration of Helsinki. A signed informed consent for the use of their clinical data was obtained from subjects before cataract surgery. Eyes with an axial length more than 26 mm, undergoing uneventful microincision phacoemulsification (2.4 mm) from January 2014 to November 2020, with implantation of Sensar three-piece foldable hydrophobic IOL (AR40E; Advanced Medical Optics Inc, Santa Ana, CA, USA) were included. In eyes with bilateral implantation, one eye was randomly selected to avoid correlation bias.[10] Biometry was performed using optical low coherence reflectometry device (Lenstar LS 900; Haag-Streit AG, Bern, Switzerland). Postoperative refraction was done at 1-month visit by a senior optometrist using log of minimum angle of resolution (LogMAR) chart at a distance of 4 m.

Eyes with previous keratorefractive procedures, keratoconus or other corneal ectasias, intra- or postoperative complications, pre- or postoperative retinal surgeries, and absence of manifest refraction done by a senior optometrist at 1 month following surgery were excluded from the study. Patients with axial lengths measured on immersion ultrasound were also excluded. Eyes with posterior staphyloma and/or best corrected visual acuity less than 20/40 were excluded. Eyes with axial length greater than 35 mm were excluded as these were beyond the range of the Kane formula calculations. Similarly, eyes which were beyond the range of Hill RBF 3.0 and BU II, where the anterior chamber depth (ACD) was not captured, were also excluded.

The IOL power was calculated using WK-adjusted conventional formulae, that is, Holladay 1, Haigis, SRK/T, and Hoffer Q, along with BU II, Olsen formula, Hill RBF ver. 3.0, EVO ver. 2.0, and Kane formula.[1,3,11,12,13] The refractive prediction error (PE) was calculated as the difference between the actual measured and the formula-predicted postoperative refractive spherical equivalent.[10] Lens constant optimization was done by zeroing out the arithmetic mean error as suggested by Wang et al.[10] The mean absolute prediction error (MAE), median absolute prediction error (MedAE), and their standard deviations (SDs) were calculated and compared. The percentage of eyes that had a PE within ±0.25 D, >0.25 to ± 0.5 D, >0.5 to ± 0.75 D, >0.75 to ±1 D, and >1 D was calculated for each formula. The subgroup analysis was done based on the axial length as group I (>26–28 mm), group II (>28–30 mm), and group III (>30 mm).

Statistical analysis was performed using IBM Statistical Package for the Social Sciences (SPSS) statistics software (version 22). The normality of data was assessed using Kolmogorov–Smirnov test. Since the data distribution was not normal, nonparametric Friedman test with Bonferroni’s correction was used to assess the differences in absolute prediction errors (AbPEs). PE was evaluated using Wilcoxon signed rank test.[10] AbPEs were compared using Freidman test, and the number of eyes within a certain PE was calculated.[10] A P-value less than 0.001 was regarded as statistically significant (Bonferroni’s correction).

Results

The study included 165 Indian myopic eyes that fulfilled all inclusion as well as exclusion criteria. Seven eyes whose axial length was more than 35 mm and two eyes whose ACD was not captured were excluded from the analyses. The demographic information of these populations is summarized in Table 1.

Table 1.

Demographics of the patient cohort

Demographic		Mean		Standard deviation		Minimum		Maximum
Axial length (mm)		30.04		1.74		26.01		33.64
Anterior chamber depth (mm)		3.54		0.34		2.7		4.85
Keratometry (D)		44.89		1.87		40.07		51.25
Lens thickness (mm)		4.15		0.40		3.07		4.98
Central corneal thickness (μm)		514.20		36.12		429		614

The mean age of the patients on the day of surgery was 53.22 years (range 21–90 years). There were more women (n = 104) than men (n = 61) and less right eyes (n = 76) than left eyes (n = 89). The sample size was adequate for myopic eyes as per the recent criteria given by Hoffer and Savini.[12] The distribution of AbPE of all formulae is shown in Fig. 1.

Figure 1.

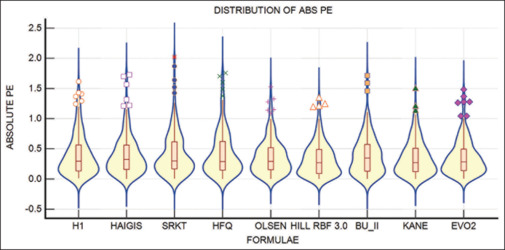
Violin with box and whiskers plot of the absolute prediction error across all formulae. The distribution is more concentrated in Olsen, Hill RBF, Kane, and EVO 2.0 formulae. EVO = Emmetropia Verifying Optical, Hill RBF = Hill Radial Basis Function

Table 2 shows MAE, SD, MedAE, and the minimum and maximum values for all formulas. Freidman test with Bonferroni’s correction revealed a statistically significant difference among AbPEs from various formulas (P < 0.001). The Hill RBF 3 formula was found to have the lowest MAE (0.33), MedAE (0.27), and SD (0.27) among all the formulae.

Table 2.

Absolute prediction error for different formulas

		MAE		SD		MedAE		Min		Max
H1		0.4		0.34		0.29		0.01		1.62
Haigis		0.4		0.34		0.33		0		1.73
SRK/T		0.42		0.37		0.3		0		2.02
HFQ		0.42		0.37		0.29		0		1.76
Olsen		0.37		0.29		0.29		0		1.53
Hill RBF 3.0		0.33		0.28		0.27		0		1.35
BU II		0.39		0.32		0.35		0		1.71
Kane		0.35		0.29		0.27		0		1.51
EVO 2.0		0.36		0.3		0.29		0.01		1.49

The outcomes for all patients sorted by MAE, SD, MedAE, Min, and Max values. BU II=Barrett universal II, EVO=Emmetropia Verifying Optics, H1=Holladay 1, HFQ=Hoffer Q, Hill RBF=Hill Radial Basis Function, MAE=mean absolute error, Max=maximum, MedAE=median absolute error, Min=minimum, SD=standard deviation, SRK/T=Sanders Retzlaff Kraff/Theoretical

The number of eyes within AbPEs of ±0.25, ±0.5, ±0.75, ±1 D, and above is shown in Fig. 2. Hill RBF had the maximum number of eyes within the lowest range of PE among all formulae.

Figure 2.

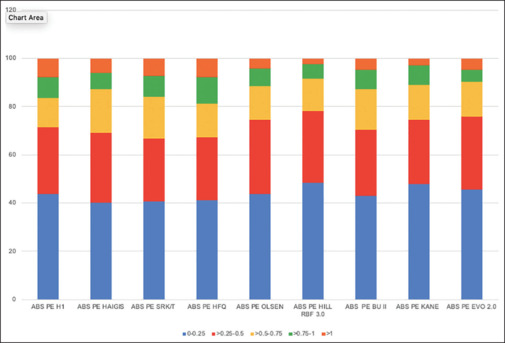
Comparison of the percentage of eyes achieving a prediction error within ±0.25, ±0.5, ±0.75, ±1, and >1 D of absolute prediction error using different intraocular lens formulae

As per the signed rank test [Table 3], Hill RBF had significantly better prediction accuracy compared to BU II, WK-adjusted Holladay 1, WK-adjusted Hoffer Q, and WK-adjusted SRK/T formulas. Though better than Kane and EVO 2.0, the results were not statistically significant (P > 0.05). Thus, the formulas incorporating AI for calculations edged out the other formulas.

Table 3.

Outcomes of rank test for all formulas

Variable AbPE		Mean rank		Different (P<0.001) from variable
Holladay 1		5.2909		(6)
Haigis		5.1091
SRK/T		5.4303		(6)
Hoffer Q		5.3758		(6)
Olsen		5.0121
Hill RBF 3.0		4.1576		(1) (3) (5) (9)
Barrett universal II		5.2848		(6)
Kane		4.6485
Emmetropia verifying optics 2.0		4.6909

The outcomes of signed rank test for AbPE of all formulae. P value less than 0.001 was considered significant. AbPE=absolute prediction error, Hill RBF=Hill Radial Basis Function, SRK/T=Sanders Retzlaff Kraff/Theoretical

Comparisons within different axial length groups

MAE and MedAEs in the three axial length groups calculated with the nine formulas are shown in Table 4. In group 3, significant difference was found in AbPE of the nine formulas (Freidman test, P < 0.0001). The Hill RBF formula performed the best with lowest PEs having the smallest MAE and MedAE. It also had higher prediction accuracy with the largest percentage of eyes under ±0.25 D (45.23%) and least number of patients with >1 D (2.38%) of residual refraction compared to the other formulae [Fig. 3]. Results were not significantly different in the other two groups.

Table 4.

Outcomes of subgroup analysis

		Group 1 26–28 mm				Group 2 >28–30 mm				Group 3 >30 mm
		MAE±SD		MedAE		MAE±SD		MedAE		MAE±SD		MedAE
Holladay 1		0.33±0.31		0.21		0.37±0.32		0.31		0.44±0.33		0.33
Haigis		0.36±0.26		0.35		0.36±0.33		0.28		0.44±0.36		0.36
SRK/T		0.30±0.27		0.24		0.39±0.37		0.27		0.48±0.38		0.38
HFQ		0.34±0.30		0.27		0.40±0.38		0.28		0.46±0.34		0.34
Olsen		0.37±0.32		0.25		0.32±0.26		0.27		0.40±0.35		0.35
Hill RBF 3.0		0.38±0.35		0.23		0.29±0.23		0.24		0.34±0.28		0.28
Barrett universal II		0.45±0.37		0.41		0.31±0.26		0.24		0.43±0.34		0.40
Kane		0.34±0.35		0.23		0.31±0.27		0.23		0.38±0.29		0.32
Emmetropia Verifying Optics 2.0		0.37±0.35		0.24		0.32±0.26		0.27		0.39±0.30		0.33

The overall refractive outcomes of patients in different axial length groups obtained by each formula. HFQ=Hoffer Q, Hill RBF=Hill Radial Basis Function, MAE=mean absolute error, MedAE=median absolute error, SD=standard deviation, SRK/T=Sanders Retzlaff Kraff/Theoretical

Figure 3.

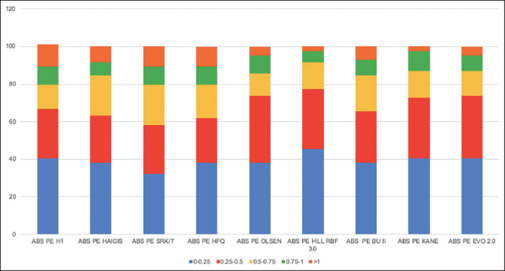
Stacked graphs demonstrating a comparison of the percentage of eyes achieving a prediction error within ±0.25, ±0.5, ±0.75, ±1, and >1 D of absolute prediction error in extremely long eyes (>30 mm axial length) using different intraocular lens formulas

Discussion

Patients with high myopia develop cataract at an earlier age as compared to the general population.[13] Since they need surgery during their active years, giving the best results becomes paramount. The IOL power calculations for highly myopic eyes is not as easy as for emmetropic eyes. The SRK/T formula was known to give good results in these eyes when optimized A constants were used.[12,14] Recently published studies have reported good performance of BU II as well.[1,15] With the advent of newer formulas, the prediction accuracy has significantly improved for myopic eyes. In this study, we evaluated the accuracy of the new AI formulas, namely, Hill RBF 3, Kane formula, EVO 2.0, and Olsen formula, in comparison to BU II, WK-adjusted Holladay 1, Haigis, SRK/T, and Hoffer Q formulas in axial myopia. To our knowledge, this is the first study to assess the accuracy of all these formulas in extreme myopic eyes in the Indian population.

The SRK/T formula was developed in 1990 by Retzlaff et al.[16] using a theoretical eye model and linear regression. However, it does not consider the effective lens plane for IOL power prediction, which affects its outcomes. The Holladay 1 formula is a third-generation formula that utilizes axial length and keratometry for IOL power prediction and uses an assumed ACD, which leads to errors in its predictions.[17] It was the first two-variable formula. The Hoffer Q formula was developed as a personalized theoretical formula to predict the postoperative ACD using axial length (AL), keratometry (K), and personalized ACD.[18] The Haigis formula uses preoperative ACD in regression analysis for postoperative effective ACD prediction.[19] We used WK adjustment for axial length with these conventional formula as it has shown to improve accuracy.[7] The Barrett universal formula, first published in 1993 by Dr. Graham D Barrett,[20] was later modified in 2010 and called BU II. It uses a theoretical model in which ACD is related to axial length and keratometry. It uses ACD and a lens constant to estimate IOL principal plane position and thus predict the effective lens position (ELP).[21] ELP is dependent on five variables: keratometry, AL, ACD, lens thickness, and white-to-white distance. It is freely accessible on www.apacrs.org. EVO 2.0 is a newer thick lens formula that is based on the theory of emmetropization and uses AI.[19] It is freely available online at https://www.evoiolcalculator.com/calculator.aspx. The Hill RBF formula is also an AI-based formula that utilizes data from a patient group and its postoperative refraction to develop IOL power prediction.[22] It collects data from Lenstar LS900 and uses Alcon SN60WF IOL implantation for outcome calculation, and claims to be free from calculation bias. Its version 2.0 has been developed with larger sample of population across a larger range of axial lengths.[23] The Kane formula was created in September 2017 using high-performance cloud-based computing. This is freely available online at https://www.iolformula.com. Variables used in the formula are axial length, keratometry, ACD, lens thickness, central corneal thickness, and patient’s biological sex.

Our sample size was 165 eyes, which is adequate for myopic eyes as per the guidelines given in a recent article by Hoffer and Savini.[12,14] One eye was randomly selected to avoid correlational bias.[12,24] There were more females than males as myopia is more prevalent in female gender.[25] Gender is also an important variable in Kane formula. Though the measurement accuracy of immersion scan is comparable to optical biometers and can be used as a good alternative, we excluded the patients whose axial length was calculated by the immersion A-scan for the sake of uniformity.[26] All our statistical tests were performed adhering to the guidelines given for IOL power calculation studies.[9,27] In our cohort, Hill RBF 3.0 along with Kane and EVO 2.0 formulae were the most accurate, with Hill RBF 3.0 being the best among them. It had the lowest MAE, SD of error, and highest percentage of eyes with low residual error postoperatively.

SD of PE is now the recommended parameter for statistical analysis of spherical equivalent PE to evaluate the performance of different formulas.[28] Chen et al.[13] compared the accuracy of the Kane, Hill RBF 2.0, BU II, and EVO formulas in extreme myopic eyes. In their study also, Hill RBF 2.0 outperformed all other formulae. However, they did not perform A constant optimization. In addition to optimizing A constants, we compared other formulae and used the latest version of Hill RBF (3.0) and EVO 2.0 in our study. A study done by Darcy et al.[6] found BU II formula to be second to Kane in terms of lowest MAE in their long axial length group, which is consistent with our findings. However, they did not compare all the other formulas. Our results were different from those of Paritekar et al.,[29] who found SRK/T and BU II to have lower MedAE and MAE than Kane formula for myopic eyes. This could be because they compared only 59 eyes in the myopic group (which they defined as AL >24 mm) and compared data at the end of 1 week instead of 1 month postoperatively. Guo et al.[30] compared the accuracy of six different formulae in IOL power prediction in eyes with AL >29 mm and obtained results similar to ours. They found the accuracy of EVO 2.0, Kane formula, Olsen, and BU-II to be significantly better than SRK/T and Haigis formulas. They recommended the use of any of the above four formulae for IOL power calculation in high myopic eyes. None of the previous studies used WK adjustment for AL correction while comparing with the older formulas.[3,4,6,8,15,19]

The superiority of Hill RBF could be due to its unique calculation pattern, entirely inbound data-driven methodology, and freedom from calculation bias.[22] It is independent of a distinct ELP calculation and is free from standard calculation errors derived from ocular biometry.[31] Our study is limited by the fact that we used the data from multiple surgeons and refractions performed by different optometrists. There might be some bias due to difference in operating styles and techniques. However, recent studies have shown that this might impact results only minimally.[32] Another limiting factor could be that we used patients implanted with only one type of IOL.

Conclusion

IOL power calculation formulas have improved considerably in the last two decades. With each passing generation, the accuracy of these formulas has improved. The AI-based formulas performed better than the basic regression- and theoretical-based formulas. Thus, Olsen, Hill RBF, Kane, and EVO 2.0 are one of the latest techniques for predicting IOL power using multiple variables with theoretical and regression optics along with AI. Thus, the future may be shaped with increasing use of AI-based formulas.

Financial support and sponsorship:

Nil.

Conflicts of interest:

There are no conflicts of interest.