Abstract
The behavioral and neural effects of the endogenous release of acetylcholine following stimulation of the nucleus basalis (NB) of Meynert have been recently examined in two male monkeys (Qi et al., 2021). Counterintuitively, NB stimulation enhanced behavioral performance while broadening neural tuning in the prefrontal cortex (PFC). The mechanism by which a weaker mnemonic neural code could lead to better performance remains unclear. Here, we show that increased neural excitability in a simple continuous bump attractor model can induce broader neural tuning and decrease bump diffusion, provided neural rates are saturated. Increased memory precision in the model overrides memory accuracy, improving overall task performance. Moreover, we show that bump attractor dynamics can account for the nonuniform impact of neuromodulation on distractibility, depending on distractor distance from the target. Finally, we delve into the conditions under which bump attractor tuning and diffusion balance in biologically plausible heterogeneous network models. In these discrete bump attractor networks, we show that reducing spatial correlations or enhancing excitatory transmission can improve memory precision. Altogether, we provide a mechanistic understanding of how cholinergic neuromodulation controls spatial working memory through perturbed attractor dynamics in the PFC.
Keywords: acetylcholine, attractor, neural network, neural tuning, working memory
Significance Statement
Acetylcholine has been thought to improve cognitive performance by sharpening neuronal tuning in the prefrontal cortex (PFC). Recent work has shown that electrical stimulation of the cholinergic forebrain in awake-behaving monkeys reduces neural tuning in PFC under stimulation conditions that improve performance. To reconcile these divergent observations, we provide network simulations showing that these derive consistently from specific conditions in prefrontal attractor dynamics: firing rate saturation leads to increased storage precision and reduced neural tuning upon cholinergic activation via an increase in neural excitability, a reduction in neural correlations, and an increase in excitatory transmission. Our study integrates previously reported data into a consistent mechanistic view of how acetylcholine controls spatial working memory via attractor network dynamics in the PFC.
Introduction
Understanding how neuromodulatory systems affect associative cortex dynamics during cognitive function is fundamental to acquiring insights into cognitive control processes. Such understanding is also essential for advancing hypotheses for the network mechanisms underlying neuropsychiatric disorders, often characterized by subtle cognitive processing alterations. In this regard, working memory (WM) is of particular relevance. For one, WM is known to be modulated by the dopaminergic, noradrenergic, and cholinergic systems (Cools and Arnsten, 2021). Besides, it is closely associated with network activity in the prefrontal cortex (PFC), for which computational models have successfully linked network dynamics with behavior (Compte et al., 2000; Wimmer et al., 2014; Inagaki et al., 2019; Barbosa et al., 2020). Furthermore, WM is affected in most neuropsychiatric disorders (Forbes et al., 2009). However, the causal chain from cellular neuromodulation to changes in network dynamics and behavioral performance in WM remains largely unknown, even for simple behavioral readouts, such as spatial memory precision in delayed response tasks (Stein et al., 2021).
A series of recent studies have investigated how the release of endogenous acetylcholine through the stimulation of the nucleus basalis (NB) of Meynert impacts cognitive functions, including spatial and color WM and sustained attention (Blake et al., 2017; Liu et al., 2017; Qi et al., 2021). Remarkably, they reported that NB stimulation leads to better behavioral performance, an uncommon observation upon interference with neuromodulatory systems. In addition, they investigated the neural correlates of improved performance in the PFC (Qi et al., 2021). Unexpectedly, they found that NB stimulation induced a general increase in excitability and a widening of neuronal tuning curves and memory fields. A decrease in selectivity has been observed due to cholinergic stimulation applied iontophoretically with high doses of cholinergic agonists (Major et al., 2018; Vijayraghavan et al., 2018; Galvin et al., 2020b). However, this effect has been assumed to correspond to the descending section of an inverted-U function, representing a regime over which cholinergic agonists impair performance (Galvin et al., 2020a). The effectiveness of drugs targeting other neurotransmitter systems, for example, dopamine, is often interpreted as increased stimulus selectivity (Williams and Goldman-Rakic, 1995). Thus, dopamine agonists are known to “sculpt” neuronal activity and improve spatial selectivity at low doses, which is assumed to confer the beneficial effect of dopamine in behavior (Vijayraghavan et al., 2007) as the result of more efficient coding (Fitzpatrick et al., 1997). The concurrent improvement in performance and broadening of tuning raises the question of how weaker memory code at the neural level can lead to better behavioral performances. An answer to this question requires a mechanistic understanding to link PFC dynamics with behavior consistently.
Bump attractor models (Wilson and Cowan, 1972; Amari, 1977; Compte et al., 2000) have successfully explained complex aspects of behavior in spatial WM tasks (Wimmer et al., 2014; Barbosa et al., 2020). In such models, a neural population represents a continuous feature by localized elevated activity (bump attractor) self-sustained through the mnemonic delay period. Continuous bump attractor dynamics are usually investigated in idealized settings with network homogeneity and perfectly symmetric connectivity. However, their more plausible biological implementations must deal with inhomogeneities and asymmetries that can significantly alter the dynamical features of the bump attractor (Renart et al., 2003; Hansel and Mato, 2013; Seeholzer et al., 2019; Darshan and Rivkind, 2022).
Here, we first use a homogeneous, symmetric firing rate bump attractor network model (Amari, 1977)—which we will refer to as the continuous bump attractor model—to build a mechanistic understanding of how increased excitability in the network can explain the effects of NB stimulation in the PFC and its behavioral outcomes in monkeys engaged in a spatial WM task (Qi et al., 2021). We show that bump attractor models can combine broader neural tuning during the delay and improve overall performance in the task, provided that neurons undergo firing rate saturation during the dynamics. Behavioral improvement is due to a reduction in bump diffusion, confirmed in the experiments' behavioral data. Finally, we investigate how these ideal attractor-like qualities can emerge in more realistic, heterogeneous, and asymmetric networks of spiking neurons (discrete bump attractor networks; Hansel and Mato, 2013). We find that heterogeneity per se does not alter our conclusions. Still, when considering network dynamics of strongly recurrent excitatory and inhibitory populations, the cholinergic activation in such discrete bump attractor networks must include other mechanisms than just enhanced excitability to reproduce the experimental data, such as reduced network spatial correlations (Thiele et al., 2012; Chen et al., 2015; Minces et al., 2017).
Materials and Methods
Electrophysiology
The experimental data included here were previously reported (Qi et al., 2021). Two adult male rhesus monkeys (Macaca mulatta) were implanted with a stimulating electrode targeting the anterior portion of the NB. Intermittent stimulation of the NB was applied for 15 s at 80 pulses per second, followed by ∼45 s with no stimulation. The stimulation was applied during the intertrial interval of the behavioral task (below). In addition, neural recordings were obtained from arrays of 1–4 electrodes over areas 8a and 46 of the dorsolateral PFC and were previously reported by Qi et al. (2021).
Task
Monkeys were trained to perform a variation of the oculomotor delayed response task, where two visual stimuli appeared in sequence (Qi et al., 2021). They learned to remember the location of either the first (Remember first) or the second (Remember second) stimulus and make an eye movement to its location depending on the color of the fixation point (white Remember first/blue Remember second). The task was distributed in blocks. Remember first blocks include retrospective distractors (monkeys had to remember the first and ignore the second). Remember second blocks contained prospective distractors (monkeys had to ignore the first and remember the second stimulus). Trial blocks included two null conditions in which either the first or the second stimulus is omitted (Remember first/Absent second and Remember second/Absent first).
After a 1 s fixation period, the first stimulus was presented for 0.5 s. After a 1 s delay (Delay 1), the second stimulus was presented for 0.5 s. Monkeys had to respond with a saccade after another 1 s delay (Delay 2). The monkeys were rewarded with juice after reporting the correct location. Gaze deviation beyond the fixation window led to immediate trial termination without reward.
Each stimulus was displayed at one of eight locations arranged along a circular ring (separated by 45°). The angular distance between the target stimulus and the distractor could be 0, 45, 90, or 180°. Additional details regarding the task structure can be found in the original article (Qi et al., 2021).
Continuous bump attractor network
Our first model consists of a homogeneous bump attractor network of a single population of rate neurons, similar to that proposed by Amari (1977).
Rate dynamics
The equation that defines the evolution of the rates of the neurons in our model is the following:
| (1) |
where we fixed .
Where explicitly indicated, we consider a threshold linear transfer function
| (2) |
in all other cases we assume that the input/output neural transfer function is a sigmoid-like function that saturates for large input values:
| (3) |
where is the saturation threshold of the neural activity and .
Connectivity
The network consists of fully interconnected neurons. Neurons lie on a ring and present selectivity to stimulus locations ( for ). Neurons with similar preferred locations are more strongly connected than neurons coding for distant locations.
We model this with a connectivity profile that follows a cosine shape:
| (4) |
In the simulations, we chose and ; therefore, all connections are negative.
In the case of the heterogeneous bump attractor network, we add an extra noisy term to the connections:
| (5) |
where are random and independently distributed values with zero mean and unit variance, and σHeter controls the magnitude of the heterogeneities.
Recurrent inputs
The recurrent input to neuron is given by the following:
| (6) |
Feedforward (FF) input
Neurons in the network receive an external input that is a FF input with mean, , and temporal variance, :
| (7) |
where we introduce an attention switch, for or 0 otherwise, which turns on upon stimulus presentation and remains on for the rest of the simulation. is white noise. In the simulations, we took and .
Stimulus input
During stimulus presentation, neurons receive an additional tuned input:
| (8) |
where is the strength of the stimulus, is the stimulus modulation, and the stimulus location. In the simulations, we took and .
Moreover, to simulate the effect of distraction in Remember first trials, we assume that is drawn for each trial from a truncated Gaussian distribution with mean and standard deviation ; the negative values of are set to zero.
NB stimulation
Since the release of acetylcholine in the PFC is thought to result in the depolarization of excitatory pyramidal neurons through activation of depolarizing nonspecific cation currents (Andrade, 1991; Haj-Dahmane and Andrade, 1996; Yan et al., 2009; Zhang and Séguéla, 2010; Baker et al., 2018), we modeled NB stimulation as an increase of the constant external input to the excitatory neurons, . In the simulations, we selected . With this parametric choice, baseline firing rate went from 4.8 to 10 Hz with NB stimulation (compared with 10.9 to 13.4 Hz in the experimental data of Qi et al., 2021).
Bump dynamics
In analyzing the simulation results of the different models, we measure changes in the network selectivity by referring to the relative amplitude of the bump. We define it as the ratio between the first and zero moments of the discrete Fourier transform of the rate population vector:
| (9) |
| (10) |
where |.| is the modulus operator.
Moreover, we compute the center of mass of the bump as follows:
| (11) |
and we compute population tuning curves by smoothing the population rate vector, , with a rolling average over nearby neurons.
Model performance
In the attractor rate model, errors in the model can have two components:
- Distraction and heterogeneities systematically bias the bump center endpoint affecting the accuracy of the response. By computing the bump center deviation from S1 averaged over trials and stimulus conditions at the end of the delay (t=tend), we can estimate this bias as follows:
where is the average operator.(12)
In the continuous attractor model with no distraction, there are no response biases.
However, in trials with distraction, the distractor shifts the response in a distance-dependent manner. We define a measure for this shift in a signed manner as follows:
| (13) |
2.
The diffusion of the bump on the ring around the location of the stimulus affects the precision of the response.
By computing the bump center endpoint deviation from its mean over trials,
| (12) |
we can define the average variance in model responses by the following:
| (13) |
The average standard error in responses is as follows:
| (14) |
and the definition of the diffusivity of the random process is as follows:
| (15) |
Quantitative and statistical analysis of saccadic errors
Response bias and variance
In the data, we decompose saccades in a similar manner. For each monkey, we compute a saccade response bias, , as the deviation of the saccade location, , to the target stimulus, θTarget, averaged over trials with the same stimuli pair:
| (16) |
We estimate the saccade response variance by computing the deviation of the saccade to the mean saccade averaged over trials with the same stimuli pair:
| (17) |
Saccade bias and variance were estimated for saccades within 30° of the reported stimulus.
We tested how task conditions affected the saccade response variance in a linear model:
| (18) |
where for control or NB-stimulated trial, for Remember first or Remember second trial, for each monkey, and is assumed to be a Gaussian random variable.
We fitted the model's coefficients with an ordinary least squares scheme. We did not find significant interactions between NB and the monkey factor, so we only included the main factor, “monkey,” in subsequent analyses. In the main text, we report the coefficients and p-values of the interaction between NB stimulation and task .
Distraction bias
In our analysis of the effect of distraction on response accuracy, we tested the dependency of distractor biases with the absolute distance between S1 and S2 with the following linear model:
| (19) |
where for and for .
Moreover, we tested the dependency of the response variance with the distance between stimuli with the following linear model:
| (20) |
We fitted the coefficients of the model with an ordinary least squares scheme. We report in the main text the coefficient and p-value of the interaction between NB stimulation and distance .
Discrete attractor spiking network
Our more realistic spiking model consists of a two-population network of strongly recurrent leaky integrate-and-fire neurons.
Leaky integrate-and-fire neuronal dynamics
The dynamics of the membrane potential of the i-th neuron in population A, , is given by the following:
| (21) |
where is the membrane potential, the recurrent input, the FF input, and the stimulus input into neuron .
Reset condition: if at time the membrane potential, , of neuron crosses the threshold, , the neuron fires a spike, and its voltage is reset to its resting potential, .
In the simulations, we chose for the leak conductances and .
Connectivity
The connectivity between population and is a random matrix with probability and 0 otherwise. On average, neurons in each population receive inputs from neurons in the presynaptic population . varies with the difference in the preferred location between the neurons (Van Vreeswijk and Sompolinsky, 2005):
| (22) |
where determines the spread of the projections from population to population . Here is the preferred location of neuron .
In the simulations, we selected for the number of neurons, for the average number of inputs, and for the spread of the projections, and we assumed that I to E connections were slightly less tuned: (Kerlin et al., 2010; Hofer et al., 2011).
Recurrent inputs
The recurrent input to neuron from its presynaptic neurons in population B is given by the following:
| (23) |
| (24) |
where excitatory synapses form a mixture of fast (AMPA) and slow (NMDA) synapses on other excitatory and inhibitory cells, and all inhibitory synapses are fast (GABA). is the time at which neuron has emitted its spike and the sum is over all the spikes emitted by neuron before time . describes the dynamics of individual postsynaptic currents:
| (25) |
where is the synaptic time constant of the interactions between neurons in population and , and is the Heaviside step function.
In the simulations, we took , , , , , , , , , and .
Synaptic plasticity
is the amount of synaptic resources available at the synaptic terminals of neuron before the spike , and is the fraction of these resources used by this spike. The dynamics of these two variables are responsible for the short-term plasticity experienced by the synapses. We model them as in the following (Hansel and Mato, 2013):
| (26) |
| (27) |
where is the interspike interval for neuron between spikes and .
In the simulations, we took , for the maximal utilization parameter.
FF input
At each time point, we assume that the FF input, , into neuron , is weakly tuned with a random phase . This leads to the emergence of spatial correlations in the recurrent layer. We model this as follows:
| (28) |
where is the strength of the external input, at each time step, is drawn uniformly between and , and controls the strength of the FF correlations. In the simulations, we choose , , , and when not mentioned otherwise.
Since correlations in the recurrent input are quite small in strongly recurrent networks (Darshan et al., 2018), most of the correlations in the net input to a neuron come from the FF contribution:
| (29) |
where is the distance between neurons on the ring.
Stimulus input
During stimulus presentation, the excitatory population receives an additional tuned input:
| (30) |
where is the location of the stimulus, is the strength of the stimulus, and is the footprint of the stimulus. The inhibitory population receives no stimulus.
In the simulation, we took and .
Bump dynamics and model responses
We compute bump amplitude, center, diffusivity, and endpoint deviations in the same way we did for the rate model.
NB stimulation
We model NB stimulation's main effect as an increase of the mean FF input to the excitatory neurons: . In our last analyses, we also consider the cases where, in addition to an increase in the FF input, (1) the excitatory synaptic strength, , increases; (2) the inhibitory presynaptic strength, , decreases; and (3) the modulation of the spatial FF correlations to the E neurons, , decreases.
Code accessibility
Custom code used for simulations of the models and for analysis of behavioral data can be accessed at https://github.com/comptelab/NB_ODR_JNeurosci_24.
Results
Homogeneous, continuous attractor models
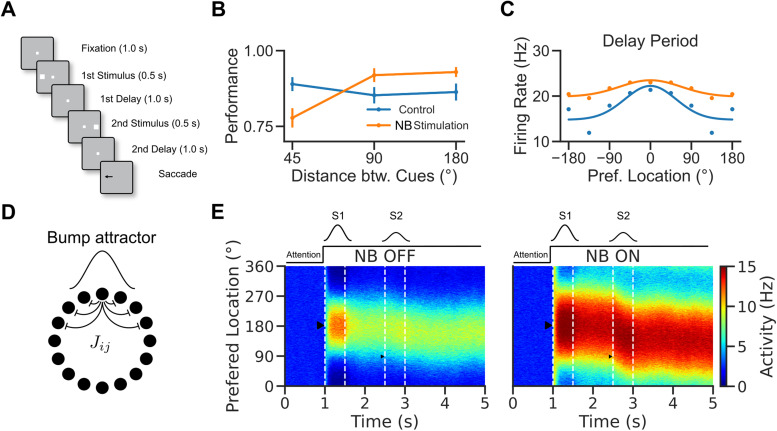
We used numerical simulations to investigate the network mechanisms underlying the reported cholinergic neuromodulation of the prefrontal activity in a visuospatial WM task (Qi et al., 2021). In this task (Fig. 1A), monkeys were trained to saccade to the location of one of two sequentially presented visual cues following a delay period. In alternating blocks of trials, the color of the fixation dot signaled to the monkey whether a reward would be given for an accurate saccade to the remembered location of the first target S1 (Remember first trial) or the second target S2 (Remember second trial). Here, we used a computational approach to reconcile evidence collected during the distractor condition (Remember first; Qi et al., 2021). Monkeys showed a general increase in performance in this task following NB stimulation, except for trials when S2 appeared close to S1, where NB stimulation impaired performance (Fig. 1B). This general increase in performance by NB stimulation was mirrored at the neural level by erosion of PFC neural tuning to the stimulus (Fig. 1C). We developed a simple continuous bump attractor rate model to understand the conditions for this modulation of neuronal tuning by NB stimulation (Fig. 1D; Amari, 1977; Ben-Yishai et al., 1997; Itskov et al., 2011). In the model, following the presentation of a location-tuned stimulus (S1, S2), the network maintains information about the stimulus' spatial location through a localized and persistent increase in activity (Fig. 1E; Wilson and Cowan, 1972; Compte et al., 2000). We model distraction with a second stimulus weaker than the first on average (see Material and Methods) to simulate variable attentional filtering mechanisms occurring in upstream areas. In the model, the network goes from an unstructured low-activity state to a selective high-activity state after stimulus presentation. This is because the network has different stable attractors before and after stimulus presentation, which is achieved by an untuned attentional input to all neurons (marked as “Attention” in Fig. 1E; Itskov et al., 2011). In addition, we modeled NB stimulation (Fig. 1E, right panel) as a nonspecific increase in the excitability of the excitatory neurons in the circuit through slight upregulation of FF inputs to the network.
Figure 1.
A rate model to reconcile cholinergic modulation of behavior and neural tuning in a visuospatial WM task task. A, Visuospatial WM task with distraction (Qi et al., 2021). B, Performance of the monkeys in control and NB-stimulated trials. Performance was measured as percent of trials with responses within 7° visual angle of the target stimulus. C, Average prefrontal neuron location selectivity in the delay period (adapted from Qi et al., 2021). Blue: control trials. Orange: NB-stimulated trials. Dots: data. Lines: fits. D, Network scheme. The network consists of a population of 1,000 rate units with tuned connections. E, Activity versus neurons versus time, left: NB OFF condition, right: NB ON condition ( simulates increased excitability induced by NB stimulation). After 1 s in baseline activity, neurons receive a tuned stimulus, S1, and a nonspecific attention signal is switched on. The activity becomes structured into a bump. The bump is only slightly perturbed by a second weak stimulus, S2, so the bump maintains a location around S1. Triangles show the locations of the stimuli.
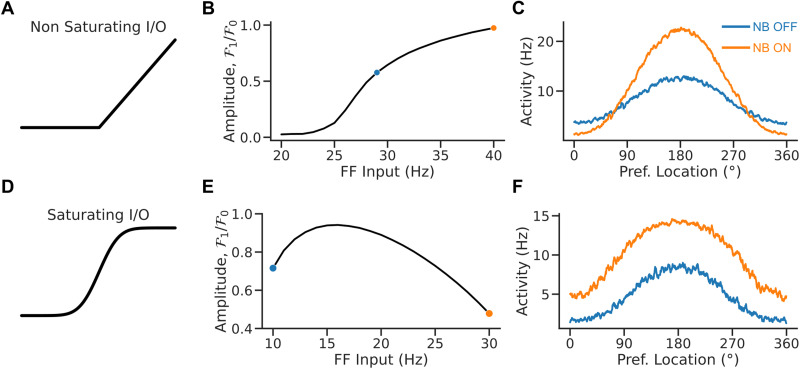
Figure 2 depicts the relationship between the FF input and the network's tuning in the bump state for two neuronal input/output (I/O) functions. When the neuronal I/O function is nonsaturating (Fig. 2A), the network's tuning increases monotonically with the input (Fig. 2B). Figure 2C plots the population tuning curves for two values of the FF input. As the input increases, neurons at the center of the bump increase the activity, inhibiting neurons on the edge and sharpening tuning. This appears qualitatively inconsistent with the observation that NB stimulation (modeled here by an increase in FF input) results in broader PFC tuning (Qi et al., 2021). However, tuning becomes nonmonotonic in the FF input when the neuronal I/O function saturates (Fig. 2D). It decreases with the external drive for sufficiently large inputs (Fig. 2E). Figure 2F plots the network's population tuning curves for two simulated conditions: NB OFF and NB ON. NB ON differs from NB OFF by an increase in the strength of the FF input that simulates the cholinergic activation. As the neurons at the center of the bump reach saturation, neurons on the edges increase their activity, and the tuning broadens. Therefore, the saturated continuous bump attractor model can display population responses qualitatively similar to the neural responses observed in the PFC following NB stimulation (Qi et al., 2021).
Figure 2.
Rate saturation accounts for the broadening of tuning following NB stimulation. A, Nonsaturating I/O function. B, Relative bump amplitude (i.e., the ratio of Fourier modes F1/F0 of the population rate vector; see Materials and Methods) versus the strength of the FF input. Tuning sharpens with stronger FF inputs. C, Population tuning curve for NB ON and NB OFF conditions (matching colors in B). D, Saturating I/O function (saturation occurs at ). E, Relative bump amplitude versus FF input. Tuning broadens with stronger FF input values. F, Population tuning curve for NB ON and NB OFF conditions (matching colors in E).
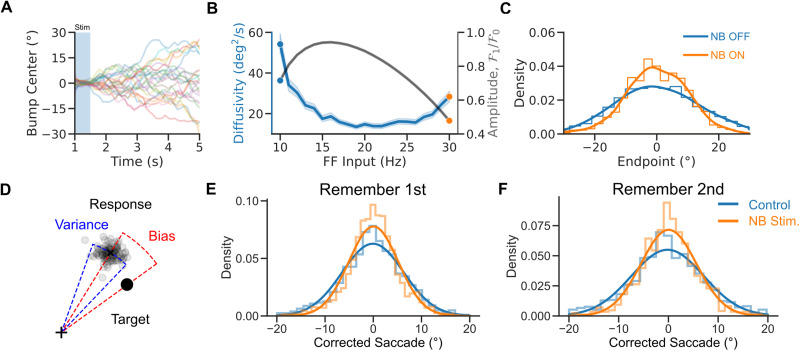
To better understand the network mechanisms underlying the balance between enhanced cognitive function and reduced tuning under neuromodulation, we analyzed the behavior generated by our model in repeated network simulations. Specifically, we investigated how changes in network excitability, modeled through changes in the strength of the FF input, affected network performance. In the bump attractor model, errors can arise from the diffusion of the bump's center. This can occur due to stochastic fluctuations in the net inputs into the neurons that change randomly and might shift the bump's center of mass. We assessed the relationship between FF input strength and the diffusion of the bump's location from 1,000 simulations with different stochastic noise realizations (Fig. 3A). In the bump attractor model with saturation, we found that the diffusivity of the bump decreases in an intermediate range of FF inputs (Fig. 3B). Figure 3C shows the distributions of bump centers around the presented targets at the end of the simulated trials. The bump center distribution narrows for larger FF inputs, indicating more precise storage of the target's location and better network performance. These findings are consistent with the general improvement in behavioral performance following NB stimulation (Qi et al., 2021). This shows how, in a bump attractor model of this spatial WM task, reduced neural tuning (Fig. 2F) can be associated with improved performance (Fig. 3C), provided neurons have saturating responses. Increased performance is explained by a reduction of bump diffusion upon network depolarization. For low FF inputs, neuronal responses are not saturating, and the increase in network performance occurs parallel to neural tuning enhancement (Fig. 3B).
Figure 3.
A diffusion process underlies NB stimulation-induced improved performance. A, Bump center versus time for 50 network initializations (for a cue presented at 0°). The bump center follows a random walk. B, Diffusivity versus FF input. Diffusion decreases for strong enough FF inputs. Shaded area: bootstrapped 95% confidence intervals. Gray line, relative bump amplitude (see Materials and Methods). C, Distributions of bump centers’ endpoint location for two different values of the FF input (for 1,000 initial conditions). Lines are kernel density estimates. D, Two sources of errors in the experimental data: response bias and response variance. E, F. Distributions of saccades (i.e., mean corrected saccadic endpoint; see Materials and Methods) in Remember first and Remember second trials in the data. NB stimulation leads to a sharper distribution of endpoints (see regression analysis, Materials and Methods). Line are Gaussian fits. Blue: control. Orange: NB-stimulated trial.
This insight from the computational model led us to examine whether the improvement in the behavioral performance of the monkeys after NB stimulation (Qi et al., 2021) could be attributed to a reduction in diffusive errors, that is, an increase in memory precision. To test this hypothesis, we analyzed saccadic endpoint distributions in control and NB-stimulated trials in the behavioral data of (Qi et al., 2021). In the dataset, responses exhibit two distinct sources of errors (Fig. 3D). The first, the “response bias,” is a characteristic offset between the mean response to a fixed target stimulus and this target, and it quantifies the memory accuracy. The second, the “response variance,” measures memory precision computed as the dispersion of the reported locations around the mean response. The continuous bump attractor model predicted that this response variance should be reduced following NB stimulation. Figure 3E and F shows the distribution of response variance in control and NB-stimulated trials, that is, saccadic endpoints corrected from response biases. Remarkably, we found that the distribution of these corrected reported locations was significantly sharper in NB-stimulated than in control trials for both Remember first and Remember second trials (corrected saccades: standard deviations and for control and NB stimulation in Remember first, Levene's test , ; and for Remember second, Levene's test , , errors are 95% confidence intervals; regression analysis of squared corrected saccade: , , , ; see Materials and Methods). This suggests that a reduction in diffusive errors could explain the observed improvement in task performance. Our model explains the counterintuitive performance enhancement seen in the behavioral data: reduced neuronal selectivity can still be associated with improved performance if a reduced bump diffusion characterizes network dynamics during the delay period. Our simulations show this is a reasonable condition in bump attractor network models (Figs. 2F, 3C).
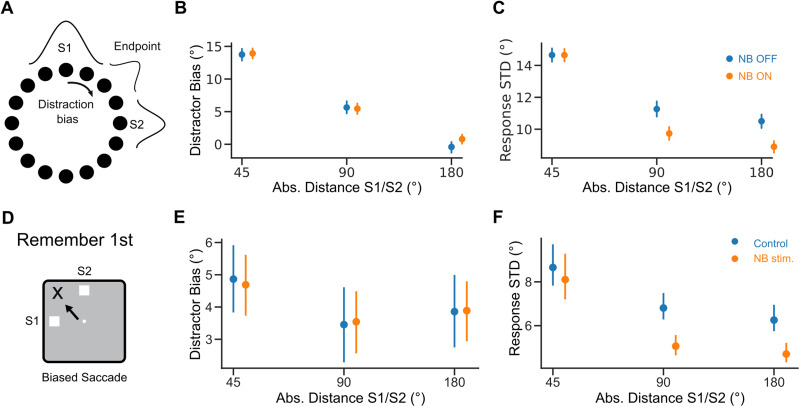
Next, we investigated if our model could explain how performance modulation by NB stimulation depended on how far S2 was presented from S1 (Fig. 1B; Qi et al., 2021). In our network simulations, we tested the effect of distractor proximity on bump dynamics (Fig. 4A–C). Distractors have been reported to attract memory bumps toward their locations (Herwig et al., 2010; Almeida et al., 2015; Lorenc et al., 2018). We found a similar attractive effect in the simulations. Still, these distractor biases did not differ in NB OFF and NB OFF trials (Fig. 4B). Moreover, we found that distraction also affected bump diffusion. In particular, nearby distractors increased response variance compared with far distractors ( , ). This was particularly accentuated in NB ON trials (Fig. 4C). This pattern was also reflected in the saccadic responses of monkeys. Firstly, distractors biased the distribution of saccadic errors in control and NB-stimulated trials similarly (Fig. 4E, regression analysis, , ; see Materials and Methods). Secondly, close distractors increased response variance similarly for NB-stimulated and control trials, with comparable bias in both conditions (Fig. 4F, regression analysis, , ; see Materials and Methods). Finally, response variance was significantly lower in NB-stimulated trials than in control trials for far distractors (±90, ±180°, Fig. 4F, regression analysis, , ; see Materials and Methods). This suggests that a specific reduction in bump diffusion in distant distractor conditions underlies improved task performance following NB stimulation.
Figure 4.
Distraction effect on response variance is distance dependent. A, Distraction by S2 shifts model responses (distraction bias). B, Distraction bias versus absolute distance between S1 and S2. C, Response standard deviation (SD), computed as the square root of the response variance, versus the absolute distance between S1 and S2. We estimated distraction bias and response SD for responses within 30° of S1. Blue: NB OFF condition . Orange: NB ON condition . D, Distractor shifts responses in the task. E, Distraction bias versus absolute distance between S1 and S2 in Remember first trials in the data. F. Same but for response SD. Error bars 95% bootstrapped confidence interval. Orange dots are shifted on the x-axis for visibility.
Inhomogeneous attractor models
Having shown that the findings of Qi et al. (2021) are compatible with a simple continuous attractor network model formulation, we wondered about the generality of our results in more realistic network realizations. There are theoretical arguments to expect possible differences. It has been shown that bump diffusivity in an attractor network depends directly on the noise magnitude and the spatial correlations of the inputs and inversely on bump strength (Kilpatrick and Ermentrout, 2013; Krishnan et al., 2018). In the continuous bump attractor network model with neural saturation, NB stimulation modeled as an increase in cellular excitability does not significantly affect the magnitude of noisy fluctuations because recurrent currents in all-to-all homogeneous networks contribute little noise compared with external inputs. Thus, the primary effect of depolarization in this network is increased bump size, which promotes inertia against diffusion (Kilpatrick and Ermentrout, 2013; Krishnan et al., 2018). However, increased excitability in more realistic network implementations where neurons are connected inhomogeneously to their neighbors may result in changes in the properties of noisy inputs or in distortions of the attractor landscape (Tsodyks and Sejnowski, 1995; Zhang, 1996; Seung et al., 2000; Renart et al., 2003; Itskov et al., 2011; Kilpatrick and Ermentrout, 2013; Kilpatrick et al., 2013) and induce qualitatively different memory diffusion properties.
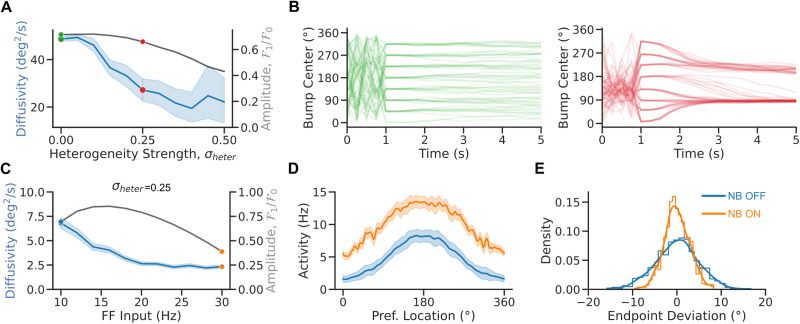
Indeed, Figure 5 shows how structural heterogeneities impact the diffusion of the bump. Diffusivity decreases markedly with heterogeneity in the network connectivity (Fig. 5A; Kilpatrick and Ermentrout, 2013; Kilpatrick et al., 2013). Figure 5B, left (resp. right), plots the time course of the bump's center for different network initializations of the homogeneous (resp. heterogeneous) bump attractor network. Strong heterogeneities modify the diffusion properties of the bump. This is because, in the presence of heterogeneity, the network undergoes symmetry breaking: the attractor goes from continuous to discrete with only a few stable fixed-point locations (Fig. 5B, right; Zhang, 1996). At the fixed point, the bump diffuses weakly in a small basin of attraction instead of being free to diffuse on the entire ring attractor. Nevertheless, even in the presence of strong heterogeneity, tuning and diffusivity of the bump are nonmonotonic, with changes with the FF input (Fig. 5C–E) qualitatively similar to the homogeneous attractor model, albeit much weaker for the case of diffusivity.
Figure 5.
Heterogeneities impair bump diffusion. A, Diffusivity versus heterogeneity strength (averaged over 8 cues and 25 initial conditions per cue and 100 network realizations). B, Bump center versus time in the homogeneous (left panel) and heterogeneous (right panel) bump attractor network (for 8 cues and 10 initial conditions per cue for 1 network realization). C, Diffusivity (averaged over 8 cues and 250 initial conditions per cue, blue) and bump amplitude (black) versus FF input in the heterogeneous network model (averaged over 8 cues and 125 initial conditions per cue and 1 network realization, ; see Materials and Methods). D, Population tuning curve for NB ON and NB OFF (matching colors in C). E, Bump endpoint deviation (i.e., mean corrected endpoint) for NB ON and NB OFF. Lines: kernel density estimates. Error bands 95% confidence intervals.
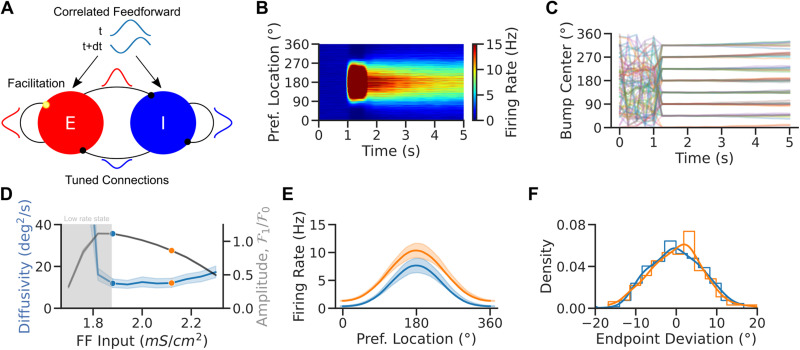
The marked impact that connection heterogeneities have on memory diffusion made us consider how more realistic networks might respond to changes in excitability. In these networks, the conditions to observe lower memory diffusion following increased excitability may depend on the specific biophysical mechanisms that help maintain a quasicontinuous attractor dynamical regime (Stein et al., 2021). We investigated these mechanisms in a biologically realistic model of spiking neurons. The model consists of two populations—excitatory (E) and inhibitory (I)—of strongly recurrent leaky integrate-and-fire neurons with tuned connections (Van Vreeswijk and Sompolinsky, 2005). We assumed that the excitatory-to-excitatory synapses are facilitating (Markram et al., 1998; Tsodyks et al., 1998). Facilitation has been shown to promote persistent activity states with highly heterogeneous neural activity (Mongillo et al., 2012; Hansel and Mato, 2013). The network exhibits multistability with an unstructured baseline and structured persistent states (Fig. 6B). Additionally, short-term synaptic facilitation has been shown to significantly improve the robustness of WM by slowing down the drift of bump activity in heterogeneous networks (Itskov et al., 2011; Hansel and Mato, 2013). In our current context, we reasoned that short-term plasticity might serve as a potential synaptic saturation mechanism to regulate network activity and tuning in responses to changes in excitability, such as those induced by NB stimulation.
Figure 6.
Enhanced excitability weakens network tuning but weakly impacts bump diffusion in spiking attractor networks. A, Network scheme. Spiking EI network with tuned connections (ring model) and facilitating E-to-E synapses. Neurons receive a weakly tuned FF input with a random phase at each time step to induce spatial correlations. B, Local average firing rate versus time versus preferred location for one trial in the NB OFF condition. C, Population activity center of mass in 30 simulations for eight different cue locations. D, Diffusivity (blue) and tuning amplitude (black) versus FF input at time t = 5 s in the simulations of panel C (averaged over 8 cues and 60 random initializations per cue). E, Population tuning curves averaged over trials at the end of the delay period (tuning curves were recentered before averaging). Increased excitability leads to weaker tuning in the NB ON condition. F, Endpoint deviations (mean corrected endpoint). Colors match dots in D. Lines are kernel density estimates. Error bands 95% confidence intervals.
In a strongly recurrent framework, the network dynamically evolves into a state where strong excitation is balanced by strong inhibition such that the net input into the neurons is comparable to their thresholds (van Vreeswijk and Sompolinsky, 1996, 1998). Neurons exhibit temporally irregular spiking patterns and heterogeneous firing rates and tuning. However, diffusion in the bump state is particularly weak, as previously observed in sparsely coupled spiking networks (Hansel and Mato, 2013; Stein et al., 2021) and consistent with the effect of heterogeneity in rate-model networks (Fig. 5; Kilpatrick et al., 2013; Kilpatrick and Ermentrout, 2013). To recover a sizable amount of diffusion, we assumed that the network receives spatially correlated FF inputs that simulate inputs from other areas (Fig. 6A). As a result of these correlated inputs, the network exhibited weak spatiotemporal activity patterns during baseline activity, and self-sustained bumps in the network showed pronounced memory diffusion, consistent with experimental observations (Wimmer et al., 2014; Stein et al., 2020).
We performed extensive simulations to investigate how parameters affect the model's dynamics. Figure 6B shows population activity through a single simulated trial for parameters for which the network is multistable: The network goes from an unstructured low-rate baseline state to a structured high-rate bump state after stimulus presentation. In the bump state, bumps exhibit little drift and diffuse around the cue's location (Fig. 6C). We investigated how network excitability affected the bump tuning and the bump diffusion in this network by systematically varying the strength of FF tonic inputs onto excitatory neurons (Fig. 6D). Bump tuning and diffusivity changed with excitability in a qualitatively similar way as observed in the simpler continuous attractor rate model (Fig. 3B). Short-term plasticity is the saturation mechanism leading the spiking model to nonmonotonic bump width and diffusion in a range of FF inputs. Note that for weak network excitability, multistability was lost, and only the low-rate state remained stable (Fig. 6D, gray area; for short simulations, 5 s in our case, the network still exhibited transient tuning after stimulus presentation due to the dynamics of short-term plasticity). Diffusivity varied only weakly in the bump state of the network, even when tuning changed significantly. As a result, also for this more biophysically detailed network model, we observed a broadening of population tuning curves upon increasing network excitability (Fig. 6D), but this was not accompanied by a significant difference in the distributions of bump center endpoint locations corrected for response biases (Fig. 6E). This is consistent with the sharp reduction in endogenously generated bump diffusion caused by network heterogeneity (Fig. 5). In realistic EI networks, the mere depolarization of the circuit is unable to reproduce the increased memory precision that would explain task performance improvements upon NB stimulation, which may thus depend on additional cholinergic effects in the circuit.
Modeling cholinergic neuromodulation solely as an increase in excitatory neuron excitability neglects important impacts of acetylcholine release in the cortex. Indeed, acetylcholine has been reported to intricately affect multiple cortical mechanisms (Picciotto et al., 2012; Thiele et al., 2012; Minces et al., 2017; Colangelo et al., 2019). We selected a set of specific mechanisms with particular prevalence in the neocortex to test our network model. In particular, in addition to the cellular depolarization of pyramidal neurons that we modeled so far (McCormick and Prince, 1986; Andrade, 1991; Haj-Dahmane and Andrade, 1996), acetylcholine modulates cortical function through (1) increased synaptic excitatory transmission (Nuñez et al., 2012; Fernández de Sevilla et al., 2021), (2) reduced GABA release (Salgado et al., 2007; Nuñez et al., 2012), and (3) reduced neuronal correlations (Thiele et al., 2012; Minces et al., 2017).
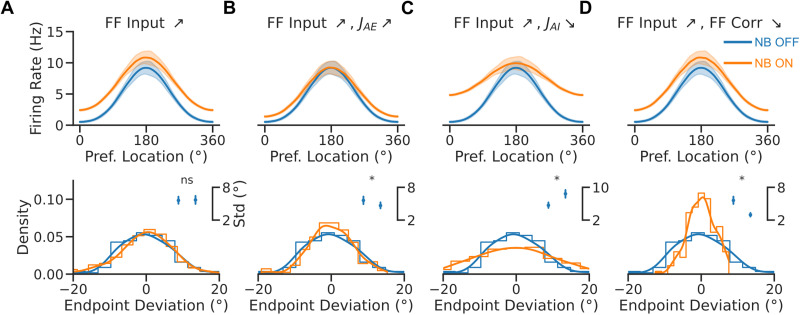
Therefore, we investigated how, in addition to a change in excitability, changes in synaptic strength or correlations impacted tuning and diffusion in the spiking network model (Fig. 7). In the model, increasing excitatory synaptic strength (to both excitatory and inhibitory neurons) had a minimal effect on tuning but instead significantly reduced bump diffusion (Fig. 7B, inset). The reduction of inhibitory synaptic strengths had instead the opposite effect, enhancing bump diffusion (Fig. 7C, inset). Finally, reducing spatial correlations in the FF input in the NB ON condition led to comparable tuning and a marked reduction in bump diffusion (Fig. 7D, inset). We conclude that the interplay between strengthened excitatory synaptic transmission, diminished neuronal correlations, and increased neuronal excitability reflects the cholinergic modulations responsible for Qi et al.'s neural and behavioral observations following NB stimulation (Fig. 3E,F).
Figure 7.
Cholinergic synaptic neuromodulation impacts bump tuning and diffusion, while cholinergic input decorrelation decreases bump diffusion. A–D, Top, population tuning curves (averaged over 8 cues after recentering, with 20 trials per cue) at the end of the delay period. Bottom, endpoint deviation (mean corrected endpoint). Blue: NB OFF condition . Orange: NB ON condition ( ). The NB ON condition has additional modulations in B–D: in B and are doubled; in C and are decreased by 20%; and in D FF correlation modulation, , is divided by half. Inset, response SD in the two conditions. Error bars are 95% bootstrapped confidence intervals.
Our simulations, thus, support the association between reduced neuronal tuning and improved memory precision based on attractor dynamics, which is the basis of our interpretations in the bump attractor model simulations. In addition, the model proposes a role for the cholinergic reduction of neuronal correlations in achieving behavioral improvements in WM.
In summary, bump attractor dynamics in inhomogeneous ring networks with short-term plasticity, which effectively causes saturation in recurrent inputs, naturally explain the contrasting effects of NB stimulation on monkey behavioral and neural responses: response variance is generally reduced, while neural tuning broadens.
Discussion
Here, we show how bump attractor models can reconcile the dynamics of PFC neurons and the behavior of monkeys performing a visuospatial WM task under cholinergic neuromodulation (Qi et al., 2021). We explain how behavior correlates with PFC neural data: cholinergic neuromodulation of the PFC reduces neural tuning while reducing bump diffusion, thus enhancing decoding precision and behavioral performance in the task. We found that network depolarization can lead to broader tuning and reduced diffusion in bump attractor models with cellular or synaptic saturation, which can be enhanced by other synaptic and population effects associated with acetylcholine. Our results provide a mechanistic understanding of how elevated prefrontal excitability, possibly combined with other cholinergic mechanisms, impacts spatial WM through changes in bump attractor dynamics in the PFC. Our model interpretation is strengthened by the match with the specific distractor condition dependencies observed by Qi et al. (2021). NB stimulation improved or impaired WM depending on the distance between the target and the distractor. Our model associates impairments in nearby distractor filtering with a broadening of the bump activity that is not counteracted by reduced bump diffusion upon network depolarization. Conversely, increased performance for distant distractors results from robust reductions in bump attractor diffusion.
Nonmonotonic cholinergic neuromodulation of prefrontal neurons
The effects of acetylcholine on neuronal activity have been investigated in nonhuman primates with microiontophoresis and systemic drug administration. Cholinergic agonists generally increase the activity of prefrontal neurons (Yang et al., 2013; Sun et al., 2017; Dasilva et al., 2019). Conversely, systemic administration of the muscarinic antagonist scopolamine reduces prefrontal activity (Zhou et al., 2011), as does microiontophoresis of muscarinic and nicotinic-α7 inhibitors (Yang et al., 2013; Major et al., 2015; Galvin et al., 2020b). However, the increase in activity by agonists is selective for the preferred location of the neuron so that tuning is enhanced, in contrast to the effect of NB stimulation observed by Qi et al. (2021). This discrepancy may be resolved by noting that the sharpening of prefrontal neurons' tuning takes place with low doses of cholinergic agonists, while high doses of carbachol or M1R allosteric inhibitors lead to broader tuning in WM tasks (Major et al., 2018; Vijayraghavan et al., 2018; Galvin et al., 2020b). The continuous bump attractor model provides a mechanistic explanation for this nonmonotonic relationship between neural tuning and cholinergic modulation. Figure 2E shows that progressive depolarization of the network initially renders neural tuning sharper but then makes it progressively broader when neurons start engaging the saturating part of their input–output function. Under this framework, intrinsic cholinergic neuromodulation through the stimulation of NB represents a strong release of acetylcholine that mimics the effect of high-dose agonists. A direct empirical exploration of the nonmonotonic dependence predicted by our model could be achieved with graded activation of NB, possibly using optogenetic approaches.
Cholinergic neuromodulation of prefrontal circuits and performance
The decrease in selectivity by cholinergic overstimulation (Major et al., 2018; Vijayraghavan et al., 2018; Galvin et al., 2020b) has been assumed to correspond to the descending section of an inverted-U function, representing a regime over which cholinergic agonists would impair performance (Galvin et al., 2020a). This interpretation is based on robust behavioral results with drugs targeting the dopamine system, showing parallel inverted-U dose–response of dopaminergic drugs at the behavioral and neural levels (Arnsten, 2011). However, the behavioral impact of cholinergic drugs needs to be clarified. Available evidence from the manipulation of intrinsic acetylcholine release suggests that WM performance may depend monotonically on acetylcholine prefrontal concentration: prefrontal cholinergic input depletion leads to selective WM impairment (Croxson et al., 2011), while electrical stimulation of NB leads to WM performance enhancement (Blake et al., 2017; Liu et al., 2017; Qi et al., 2021). Our network model is consistent with this apparent monotonic relationship. Still, it predicts that a finer sampling of cholinergic modulation of prefrontal circuits should reveal a nonmonotonic component in the behavioral dose–response curve (Fig. 3B). Notably, our network simulations in Figure 3B show that the nonmonotonic dose–response relationships for neural tuning and behavior are not aligned in their maximum/minimum, thus breaking the intuition that neural tuning maps directly to behavioral performance.
Relationship between neural tuning and behavioral performance
Sharper tuning is typically associated with increased performance. This is particularly clear for conditions in which decoding precise stimulus information is essential, as in discrimination tasks after perceptual learning (Li et al., 2004; Yang and Maunsell, 2004; Raiguel et al., 2006; Sanayei et al., 2018). Theoretical studies have shown, however, that broader tuning curves can produce either worse or better performance depending on the task and noise conditions in the network (Pouget et al., 1999; Zhang and Sejnowski, 1999; Butts and Goldman, 2006; Ma et al., 2006a). For conditions in which stimuli are highly discriminable, and performance depends on the ability to filter distractors or other intervening noise during a memory period, our modeling shows that broader prefrontal tuning can be associated with better memory performance. The connection between reduced neural tuning and increased WM precision depends on specific network implementations and may not generalize to other behavioral readouts in WM tasks. Indeed, previous studies have investigated how improved selectivity can lead to better performance in WM tasks (Yang and Maunsell, 2004; Compte and Wang, 2005; Raiguel et al., 2006; Busse et al., 2008; Sanayei et al., 2018). A network far from saturation shows this tendency. Optimizing mechanisms to increase signal durability during delays may occur at the cost of accuracy, and a stability–accuracy trade-off may determine performance in a task. Unlike the effects of perceptual learning, learning to perform a WM task also induces a broadening of neural selectivity (Qi et al., 2011; Qi and Constantinidis, 2013).
Based on our model, we propose that NB stimulation leads to reduced bump diffusion in the PFC, resulting in a more precise neural code at the end of the delay. This could be tested with large population recordings in the PFC during this task. We predict contrasting results of decoders trained on the activity of simultaneously recorded neurons compared with decoders trained on the activity of pseudopopulations of neurons. Decoders trained on pseudopopulations of neurons pooled from different sessions would show reduced accuracy after NB stimulation, likely reflecting the broadening of neural tuning. In contrast, decoding from a true population of simultaneously recorded neurons should show higher accuracy in NB-stimulated trials due to lower levels of correlated noise within the population.
Circuit mechanisms controlling memory diffusion and neural tuning
Weaker tuning in our continuous attractor network framework can lead to better performance when it is concomitant with a reduction of the noisy diffusion of the memory traces (Pouget et al., 1999; Zhang and Sejnowski, 1999; Butts and Goldman, 2006; Ma et al., 2006b; Stein et al., 2021). How these two components are integrated into attractor dynamics depends on specific network implementations. We explored here several different network implementations, which have been extensively studied in the literature in relation to the formation of bump attractors in rate models (Wilson and Cowan, 1972; Amari, 1977) and in spiking models (Compte et al., 2000; Hansel and Mato, 2013), diffusion of the bump (Zhang, 1996; Compte et al., 2000; Kilpatrick and Ermentrout, 2013; Wimmer et al., 2014; Krishnan et al., 2018), sensitivity to distractors (Compte et al., 2000), or the impact of heterogeneities (Hansel and Mato, 2013; Kilpatrick and Ermentrout, 2013; Kilpatrick et al., 2013; Seeholzer et al., 2019). We specifically asked how neural excitability jointly affects bump diffusion and tuning in these models. In idealized homogeneous networks, the mere depolarization of the network close to saturation provides both broader tunings and reduced diffusion; in heterogeneous networks, however, additional mechanisms are required to observe a significantly reduced bump diffusion. Our modeling selects a set of possible mechanisms: decreased inhibition reduces neural tuning strongly, but increases diffusivity, while enhanced excitation can contribute to reduced tuning and diffusivity mildly. However, only reduced spatial correlations are able to induce a marked reduction in bump diffusion (Fig. 7). It is plausible that NB stimulation produces a combination of effects in PFC circuits.
A marked role for a reduction in spatial correlations in modulating bump diffusion is consistent with results in the literature. Indeed, changes in neuronal correlations significantly impact the diffusion of bump attractors (Kilpatrick and Ermentrout, 2013), and bump diffusion is a determinant of behavioral imprecisions in these tasks (Wimmer et al., 2014). A role for modulation of neuronal correlations in our data is plausible since cholinergic activation is known to reduce neuronal correlations in multiple brain areas (Thiele et al., 2012; Minces et al., 2017). Furthermore, a reduction in correlated variability between neurons has been linked to increased attention (Cohen and Maunsell, 2009; Mitchell et al., 2009; Herrero et al., 2013), typically associated with improved cognitive performance.
We do not view our modeling approach as a commitment to a specific mechanistic basis for neuromodulating neuronal correlations. Previous computational work has explored the effect of FF excitation on correlations in recurrent E–I networks (Rosenbaum et al., 2017), showing that fluctuations in the FF inputs can drive correlated activity. Here, we implemented a similar mechanism but did not explore in depth the possible role of recurrent dynamics on the neuromodulation of neural correlations. Indeed, Darshan et al. (2018) have shown that recurrent structural motifs can generate collective network activity. How specific neuromodulation of such motifs might impact correlations induced by recurrent circuitry remains an open question. From this point of view, the mechanisms analyzed in Figure 7 may not be independent. Synaptic effects of NB stimulation may alter spatial correlations in more complex network architectures. This could be further disentangled with targeted optogenetic manipulations of circuit elements (e.g., inhibitory connections) during NB stimulation.
A methodological approach to identifying mechanisms of behavioral alterations
The challenge of relating cellular or synaptic mechanism modulations with changes in cognitive function using biological neural network models has been pointed out before (Stein et al., 2021). To constrain network models, obtaining neural-level information about how the considered cellular changes affect neural circuits implicated in the behavioral readout is crucial. We applied this approach by constraining our models with neural tuning curves obtained with and without NB stimulation and testing their behavioral predictions. This has allowed us to identify a role for neural saturation dynamics, excitatory synaptic transmission, and neural covariability in determining cholinergic WM improvements. This approach is necessary to advance toward a circuit-level understanding of how alterations in neuromodulators and receptors underlie cognitive dysfunctions, so efforts must be put into generating relevant neural-level data upon hypothesized cellular and synaptic perturbations.
In sum, we show that the bump attractor model can provide a causal link between PFC electrophysiology and the complex pattern of behavioral improvement and impairment in WM caused by endogenous acetylcholine release. The relevant mechanisms in these network models are cholinergic cellular depolarization, cholinergic excitatory synaptic enhancement, neuronal saturation, and cholinergic reduction of input correlations. Our evidence supports that attractor dynamics in the PFC are under the neuromodulatory control of cholinergic centers to improve cognitive performance in WM.
References
- Almeida R, Barbosa J, Compte A (2015) Neural circuit basis of visuo-spatial working memory precision: a computational and behavioral study. J Neurophysiol 114:1806–1818. 10.1152/jn.00362.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amari S (1977) Dynamics of pattern formation in lateral-inhibition type neural fields. Biol Cybern 27:77–87. 10.1007/BF00337259 [DOI] [PubMed] [Google Scholar]
- Andrade R (1991) Cell excitation enhances muscarinic cholinergic responses in rat association cortex. Brain Res 548:81–93. 10.1016/0006-8993(91)91109-E [DOI] [PubMed] [Google Scholar]
- Arnsten AFT (2011) Catecholamine influences on dorsolateral prefrontal cortical networks. Biol Psychiatry 69:e89–e99. 10.1016/j.biopsych.2011.01.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker AL, O'Toole RJ, Gulledge AT (2018) Preferential cholinergic excitation of corticopontine neurons. J Physiol 596:1659–1679. 10.1113/tjp.2018.596.issue-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbosa J, Stein H, Martinez RL, Galan-Gadea A, Li S, Dalmau J, Adam KCS, Valls-Solé J, Constantinidis C, Compte A (2020) Interplay between persistent activity and activity-silent dynamics in the prefrontal cortex underlies serial biases in working memory. Nat Neurosci 23:1016–1024. 10.1038/s41593-020-0644-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Yishai R, Hansel D, Sompolinsky H (1997) Traveling waves and the processing of weakly tuned inputs in a cortical network module. J Comput Neurosci 4:57–77. 10.1023/A:1008816611284 [DOI] [PubMed] [Google Scholar]
- Blake DT, Terry AV, Plagenhoef M, Constantinidis C, Liu R (2017) Potential for intermittent stimulation of nucleus basalis of Meynert to impact treatment of Alzheimer’s disease. Commun Integr Biol 10:e1389359. 10.1080/19420889.2017.1389359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busse L, Katzner S, Tillmann C, Treue S (2008) Effects of attention on perceptual direction tuning curves in the human visual system. J Vis 8:2–2. 10.1167/8.9.2 [DOI] [PubMed] [Google Scholar]
- Butts DA, Goldman MS (2006) Tuning curves, neuronal variability, and sensory coding. PLoS Biol 4:e92. 10.1371/journal.pbio.0040092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen N, Sugihara H, Sur M (2015) An acetylcholine-activated microcircuit drives temporal dynamics of cortical activity. Nat Neurosci 18:892–902. 10.1038/nn.4002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Maunsell JHR (2009) Attention improves performance primarily by reducing interneuronal correlations. Nat Neurosci 12:1594–1600. 10.1038/nn.2439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colangelo C, Shichkova P, Keller D, Markram H, Ramaswamy S (2019) Cellular, synaptic and network effects of acetylcholine in the neocortex. Front Neural Circuits 13:24. 10.3389/fncir.2019.00024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compte A, Brunel N, Goldman-Rakic PS, Wang X-J (2000) Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cereb Cortex 10:910–923. 10.1093/cercor/10.9.910 [DOI] [PubMed] [Google Scholar]
- Compte A, Wang X-J (2005) Tuning curve shift by attention modulation in cortical neurons: a computational study of its mechanisms. Cereb Cortex 16:761–778. 10.1093/cercor/bhj021 [DOI] [PubMed] [Google Scholar]
- Cools R, Arnsten AFT (2021) Neuromodulation of prefrontal cortex cognitive function in primates: the powerful roles of monoamines and acetylcholine. Neuropsychopharmacology 47:309–328. 10.1038/s41386-021-01100-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croxson PL, Kyriazis DA, Baxter MG (2011) Cholinergic modulation of a specific memory function of prefrontal cortex. Nat Neurosci 14:1510–1512. 10.1038/nn.2971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darshan R, Rivkind A (2022) Learning to represent continuous variables in heterogeneous neural networks. Cell Rep 39:110612. 10.1016/j.celrep.2022.110612 [DOI] [PubMed] [Google Scholar]
- Darshan R, van Vreeswijk C, Hansel D (2018) Strength of correlations in strongly recurrent neuronal networks. Phys Rev X 8:031072. 10.1103/PhysRevX.8.031072 [DOI] [Google Scholar]
- Dasilva M, Brandt C, Gotthardt S, Gieselmann MA, Distler C, Thiele A (2019) Cell class-specific modulation of attentional signals by acetylcholine in macaque frontal eye field. Proc Natl Acad Sci U S A 116:20180–20189. 10.1073/pnas.1905413116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández de Sevilla D, Núñez A, Buño W (2021) Muscarinic receptors, from synaptic plasticity to its role in network activity. Neuroscience 456:60–70. 10.1016/j.neuroscience.2020.04.005 [DOI] [PubMed] [Google Scholar]
- Fitzpatrick DC, Batra R, Stanford TR, Kuwada S (1997) A neuronal population code for sound localization. Nature 388:871–874. 10.1038/42246 [DOI] [PubMed] [Google Scholar]
- Forbes NF, Carrick LA, McIntosh AM, Lawrie SM (2009) Working memory in schizophrenia: a meta-analysis. Psychol Med 39:889–905. 10.1017/S0033291708004558 [DOI] [PubMed] [Google Scholar]
- Galvin VC, Arnsten AFT, Wang M (2020a) Involvement of nicotinic receptors in working memory function. In: Behavioral pharmacology of the cholinergic system (Shoaib M, Wallace TL, eds), Current topics in behavioral neurosciences 45, pp. 89–99. Cham, Switzerland: Springer International Publishing. [DOI] [PubMed] [Google Scholar]
- Galvin VC, et al. (2020b) Muscarinic M1 receptors modulate working memory performance and activity via KCNQ potassium channels in the primate prefrontal cortex. Neuron 106:649–661.e4. 10.1016/j.neuron.2020.02.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haj-Dahmane S, Andrade R (1996) Muscarinic activation of a voltage-dependent cation nonselective current in rat association cortex. J Neurosci 16:3848–3861. 10.1523/JNEUROSCI.16-12-03848.1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel D, Mato G (2013) Short-term plasticity explains irregular persistent activity in working memory tasks. J Neurosci 33:133–149. 10.1523/jneurosci.3455-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrero JL, Gieselmann MA, Sanayei M, Thiele A (2013) Attention-induced variance and noise correlation reduction in macaque V1 is mediated by NMDA receptors. Neuron 78:729–739. 10.1016/j.neuron.2013.03.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herwig A, Beisert M, Schneider WX (2010) On the spatial interaction of visual working memory and attention: evidence for a global effect from memory-guided saccades. J Vis 10:8. 10.1167/10.5.8 [DOI] [PubMed] [Google Scholar]
- Hofer SB, Ko H, Pichler B, Vogelstein J, Ros H, Zeng H, Lein E, Lesica NA, Mrsic-Flogel TD (2011) Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex. Nat Neurosci 14:1045–1052. 10.1038/nn.2876 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inagaki HK, Fontolan L, Romani S, Svoboda K (2019) Discrete attractor dynamics underlies persistent activity in the frontal cortex. Nature 566:212–217. 10.1038/s41586-019-0919-7 [DOI] [PubMed] [Google Scholar]
- Itskov V, Hansel D, Tsodyks M (2011) Short-term facilitation may stabilize parametric working memory trace. Front Comput Neurosci 5:40. 10.3389/fncom.2011.00040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerlin AM, Andermann ML, Berezovskii VK, Reid RC (2010) Broadly tuned response properties of diverse inhibitory neuron subtypes in mouse visual cortex. Neuron 67:858–871. 10.1016/j.neuron.2010.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilpatrick ZP, Ermentrout B (2013) Wandering bumps in stochastic neural fields. SIAM J Appl Dyn Syst 12:61–94. 10.1137/120877106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilpatrick ZP, Ermentrout B, Doiron B (2013) Optimizing working memory with heterogeneity of recurrent cortical excitation. J Neurosci 33:18999–19011. 10.1523/JNEUROSCI.1641-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan N, Poll DB, Kilpatrick ZP (2018) Synaptic efficacy shapes resource limitations in working memory. J Comput Neurosci 44:273–295. 10.1007/s10827-018-0679-7 [DOI] [PubMed] [Google Scholar]
- Li W, Piëch V, Gilbert CD (2004) Perceptual learning and top-down influences in primary visual cortex. Nat Neurosci 7:651–657. 10.1038/nn1255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu R, Crawford J, Callahan PM, Terry AV Jr, Constantinidis C, Blake DT (2017) Intermittent stimulation of the nucleus basalis of Meynert improves working memory in adult monkeys. Curr Biol 27:2640–2646.e4. 10.1016/j.cub.2017.07.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenc ES, Sreenivasan KK, Nee DE, Vandenbroucke ARE, D’Esposito M (2018) Flexible coding of visual working memory representations during distraction. J Neurosci 38:5267–5276. 10.1523/JNEUROSCI.3061-17.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma WJ, Beck JM, Latham PE, Pouget A (2006a) Bayesian inference with probabilistic population codes. Nat Neurosci 9:1432–1438. 10.1038/nn1790 [DOI] [PubMed] [Google Scholar]
- Ma Y, Hu H, Berrebi AS, Mathers PH, Agmon A (2006b) Distinct subtypes of somatostatin-containing neocortical interneurons revealed in transgenic mice. J Neurosci 26:5069–5082. 10.1523/JNEUROSCI.0661-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Major AJ, Vijayraghavan S, Everling S (2015) Muscarinic attenuation of mnemonic rule representation in macaque dorsolateral prefrontal cortex during a pro- and anti-saccade task. J Neurosci 35:16064–16076. 10.1523/JNEUROSCI.2454-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Major AJ, Vijayraghavan S, Everling S (2018) Cholinergic overstimulation attenuates rule selectivity in macaque prefrontal cortex. J Neurosci 38:1137–1150. 10.1523/jneurosci.3198-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Wang Y, Tsodyks M (1998) Differential signaling via the same axon of neocortical pyramidal neurons. Proc Natl Acad Sci U S A 95:5323–5328. 10.1073/pnas.95.9.5323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Prince DA (1986) Mechanisms of action of acetylcholine in the guinea pig cerebral cortex in vitro. J Physiol 375:169–194. 10.1113/jphysiol.1986.sp016112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minces V, Pinto L, Dan Y, Chiba AA (2017) Cholinergic shaping of neural correlations. Proc Natl Acad Sci U S A 114:5725–5730. 10.1073/pnas.1621493114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg KA, Reynolds JH (2009) Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. Neuron 63:879–888. 10.1016/j.neuron.2009.09.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mongillo G, Hansel D, van Vreeswijk C (2012) Bistability and spatiotemporal irregularity in neuronal networks with nonlinear synaptic transmission. Phys Rev Lett 108:158101. 10.1103/PhysRevLett.108.158101 [DOI] [PubMed] [Google Scholar]
- Nuñez A, Domínguez S, Buño W, Fernández de Sevilla D (2012) Cholinergic-mediated response enhancement in barrel cortex layer V pyramidal neurons. J Neurophysiol 108:1656–1668. 10.1152/jn.00156.2012 [DOI] [PubMed] [Google Scholar]
- Picciotto MR, Higley MJ, Mineur YS (2012) Acetylcholine as a neuromodulator: cholinergic signaling shapes nervous system function and behavior. Neuron 76:116–129. 10.1016/j.neuron.2012.08.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouget A, Deneve S, Ducom JC, Latham PE (1999) Narrow versus wide tuning curves: what’s best for a population code? Neural Comput 11:85–90. 10.1162/089976699300016818 [DOI] [PubMed] [Google Scholar]
- Qi X-L, Constantinidis C (2013) Neural changes after training to perform cognitive tasks. Behav Brain Res 241:235–243. 10.1016/j.bbr.2012.12.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi X-L, Liu R, Singh B, Bestue D, Compte A, Vazdarjanova AI, Blake DT, Constantinidis C (2021) Nucleus basalis stimulation enhances working memory by stabilizing stimulus representations in primate prefrontal cortical activity. Cell Rep 36:109469. 10.1016/j.celrep.2021.109469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi X-L, Meyer T, Stanford TR, Constantinidis C (2011) Changes in prefrontal neuronal activity after learning to perform a spatial working memory task. Cereb Cortex 21:2722–2732. 10.1093/cercor/bhr058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raiguel S, Vogels R, Mysore SG, Orban GA (2006) Learning to see the difference specifically alters the most informative V4 neurons. J Neurosci 26:6589–6602. 10.1523/JNEUROSCI.0457-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renart A, Song P, Wang X-J (2003) Robust spatial working memory through homeostatic synaptic scaling in heterogeneous cortical networks. Neuron 38:473–485. 10.1016/S0896-6273(03)00255-1 [DOI] [PubMed] [Google Scholar]
- Rosenbaum R, Smith MA, Kohn A, Rubin JE, Doiron B (2017) The spatial structure of correlated neuronal variability. Nat Neurosci 20:107–114. 10.1038/nn.4433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salgado H, Bellay T, Nichols JA, Bose M, Martinolich L, Perrotti L, Atzori M (2007) Muscarinic M2 and M1 receptors reduce GABA release by Ca2+ channel modulation through activation of PI3K/Ca2+-independent and PLC/Ca2+-dependent PKC. J Neurophysiol 98:952–965. 10.1152/jn.00060.2007 [DOI] [PubMed] [Google Scholar]
- Sanayei M, Chen X, Chicharro D, Distler C, Panzeri S, Thiele A (2018) Perceptual learning of fine contrast discrimination changes neuronal tuning and population coding in macaque V4. Nat Commun 9:4238. 10.1038/s41467-018-06698-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeholzer A, Deger M, Gerstner W (2019) Stability of working memory in continuous attractor networks under the control of short-term plasticity. PLoS Comput Biol 15:e1006928. 10.1371/journal.pcbi.1006928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seung HS, Lee DD, Reis BY, Tank DW (2000) Stability of the memory of eye position in a recurrent network of conductance-based model neurons. Neuron 26:259–271. 10.1016/S0896-6273(00)81155-1 [DOI] [PubMed] [Google Scholar]
- Stein H, et al. (2020) Reduced serial dependence suggests deficits in synaptic potentiation in anti-NMDAR encephalitis and schizophrenia. Nat Commun 11:4250. 10.1038/s41467-020-18033-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein H, Barbosa J, Compte A (2021) Towards biologically constrained attractor models of schizophrenia. Curr Opin Neurobiol 70:171–181. 10.1016/j.conb.2021.10.013 [DOI] [PubMed] [Google Scholar]
- Sun Y, Yang Y, Galvin VC, Yang S, Arnsten AF, Wang M (2017) Nicotinic α4β2 cholinergic receptor influences on dorsolateral prefrontal cortical neuronal firing during a working memory task. J Neurosci 37:5366–5377. 10.1523/jneurosci.0364-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiele A, Herrero JL, Distler C, Hoffmann K-P (2012) Contribution of cholinergic and GABAergic mechanisms to direction tuning, discriminability, response reliability, and neuronal rate correlations in macaque middle temporal area. J Neurosci 32:16602–16615. 10.1523/JNEUROSCI.0554-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks M, Pawelzik K, Markram H (1998) Neural networks with dynamic synapses. Neural Comput 10:821–835. 10.1162/089976698300017502 [DOI] [PubMed] [Google Scholar]
- Tsodyks MV, Sejnowski T (1995) Rapid state switching in balanced cortical network models. Network 6:111. 10.1088/0954-898X_6_2_001 [DOI] [Google Scholar]
- van Vreeswijk C, Sompolinsky H (1996) Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274:1724–1726. 10.1126/science.274.5293.1724 [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H (1998) Chaotic balanced state in a model of cortical circuits. Neural Comput 10:1321–1371. 10.1162/089976698300017214 [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H (2005) Irregular activity in large networks of neurons. In: Methods and models in neurophysics (Chow CC, Gutkin B, Hansel D, Meunier C, Dalibard J, eds), pp. 341–406. Amsterdam, The Netherland: Elsevier. [Google Scholar]
- Vijayraghavan S, Major AJ, Everling S (2018) Muscarinic M1 receptor overstimulation disrupts working memory activity for rules in primate prefrontal cortex. Neuron 98:1256–1268.e4. 10.1016/j.neuron.2018.05.027 [DOI] [PubMed] [Google Scholar]
- Vijayraghavan S, Wang M, Birnbaum SG, Williams GV, Arnsten AFT (2007) Inverted-U dopamine D1 receptor actions on prefrontal neurons engaged in working memory. Nat Neurosci 10:376–384. 10.1038/nn1846 [DOI] [PubMed] [Google Scholar]
- Williams GV, Goldman-Rakic PS (1995) Modulation of memory fields by dopamine D1 receptors in prefrontal cortex. Nature 376:572–575. 10.1038/376572a0 [DOI] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD (1972) Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12:1–24. 10.1016/S0006-3495(72)86068-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wimmer K, Nykamp DQ, Constantinidis C, Compte A (2014) Bump attractor dynamics in prefrontal cortex explains behavioral precision in spatial working memory. Nat Neurosci 17:431–439. 10.1038/nn.3645 [DOI] [PubMed] [Google Scholar]
- Yan H-D, Villalobos C, Andrade R (2009) TRPC Channels Mediate a Muscarinic Receptor-Induced Afterdepolarization in Cerebral Cortex. J Neurosci 29:10038–10046. 10.1523/JNEUROSCI.1042-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang T, Maunsell JHR (2004) The effect of perceptual learning on neuronal responses in monkey visual area V4. J Neurosci 24:1617–1626. 10.1523/JNEUROSCI.4442-03.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Paspalas CD, Jin LE, Picciotto MR, Arnsten AFT, Wang M (2013) Nicotinic α7 receptors enhance NMDA cognitive circuits in dorsolateral prefrontal cortex. Proc Natl Acad Sci U S A 110:12078–12083. 10.1073/pnas.1307849110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K (1996) Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensemble: a theory. J Neurosci 16:2112–2126. 10.1523/JNEUROSCI.16-06-02112.1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Séguéla P (2010) Metabotropic induction of persistent activity in layers II/III of anterior cingulate cortex. Cereb Cortex 20:2948–2957. 10.1093/cercor/bhq043 [DOI] [PubMed] [Google Scholar]
- Zhang K, Sejnowski TJ (1999) Neuronal tuning: to sharpen or broaden? Neural Comput 11:75–84. 10.1162/089976699300016809 [DOI] [PubMed] [Google Scholar]
- Zhou X, Qi X-L, Douglas K, Palaninathan K, Kang HS, Buccafusco JJ, Blake DT, Constantinidis C (2011) Cholinergic modulation of working memory activity in primate prefrontal cortex. J Neurophysiol 106:2180–2188. 10.1152/jn.00148.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]