Deep neural network heatmaps capture Alzheimer’s disease patterns reported in a large meta-analysis of neuroimaging studies

Abstract

Deep neural networks currently provide the most advanced and accurate machine learning models to distinguish between structural MRI scans of subjects with Alzheimer’s disease and healthy controls. Unfortunately, the subtle brain alterations captured by these models are difficult to interpret because of the complexity of these multi-layer and non-linear models. Several heatmap methods have been proposed to address this issue and analyze the imaging patterns extracted from the deep neural networks, but no quantitative comparison between these methods has been carried out so far. In this work, we explore these questions by deriving heatmaps from Convolutional Neural Networks (CNN) trained using T1 MRI scans of the ADNI data set and by comparing these heatmaps with brain maps corresponding to Support Vector Machine (SVM) activation patterns. Three prominent heatmap methods are studied: Layer-wise Relevance Propagation (LRP), Integrated Gradients (IG), and Guided Grad-CAM (GGC). Contrary to prior studies where the quality of heatmaps was visually or qualitatively assessed, we obtained precise quantitative measures by computing overlap with a ground-truth map from a large meta-analysis that combined 77 voxel-based morphometry (VBM) studies independently from ADNI. Our results indicate that all three heatmap methods were able to capture brain regions covering the meta-analysis map and achieved better results than SVM activation patterns. Among them, IG produced the heatmaps with the best overlap with the independent meta-analysis.

1. Introduction

Alzheimer’s disease (AD) is the most common brain dementia (Schneider et al., 2009). In 2020, 5.8 million Americans age 65 and older were living with AD, and this number is expected to reach 13.8 million by 2050 (AD, 2020). Considerable efforts have been made to tackle the challenges raised by this issue and, in particular, research early neuroimaging biomarkers and prognosis tools (Habes et al., 2016a; 2016b; Li et al., 2019; Rathore et al., 2017). The most recent Deep Learning frameworks were involved in these efforts and showed promising achievements in AD classification (Ebrahimighahnavieh et al., 2020).

Unfortunately, these machine learning frameworks rely on complex architectures, which make it difficult to understand what neurological changes are modeled by the deep networks as typical dementia signatures, markers of disease progression, and clues for differential diagnosis between dementia (Levakov et al., 2020; Montavon et al., 2018).

In recent years, a new field of research dedicated to the explanation of deep learning models has emerged: Explainable Artificial Intelligence (XAI) (Barredo Arrieta et al., 2020; Longo et al., 2020; Miller, 2019). In that field, heatmaps have emerged as a popular visualization tool to interpret Deep Learning models working on images. A heatmap indicates what part of an input image contributes the most to a deep network output (Simonyan et al., 2014; Zhang and Zhu, 2018; Zhou et al., 2016). In other words, a heatmap reflects the importance of imaging features extracted from an image by a deep neural network to support its decision and how much local image patterns contribute to these important features. The first heatmaps introduced in the literature, the saliency maps, were produced by back-propagating the gradients of a network output through all the layers of the model until reaching the input layers (Simonyan et al., 2014). This core idea was improved and generalized several times in the following years, such as in the Guided Backpropagation method that builds on the Deconvolution network (Zeiler et al., 2010) and where only positive gradients are propagated through ReLU network layers (Nair and Hinton, 2010; Springenberg et al., 2015). In the Class Activation Maps (CAM), network activations are considered instead of back-propagated gradients (Zhou et al., 2016). The Integrated Gradient (IG) approach consists of averaging gradient maps generated from multiple scaled inputs (Sundararajan et al., 2017). In the Layer-wise Relevance Propagation (LRP) method, a set of preservation rules are applied when back-propagating a network’s activations and, in particular, treating positive and negative neural network activations in different ways (Bach et al., 2015; Binder et al., 2016; Montavon et al., 2017). These strategies are also implemented in the DeepLift method (Shrikumar et al., 2017), where baseline activations are subtracted from neuron activations during propagation. These baseline activations are generated by passing task-specific reference images to the networks (Shrikumar et al., 2017). The most recent approaches combine multiple methods to generate fine visualizations that can be produced at different network depths, such as the Guided Grad CAM method that combines guided back-propagated gradients with class-activation maps generated from output gradients (Selvaraju et al., 2017; Springenberg et al., 2015; Zhou et al., 2016). Heatmaps methods can be selected based on their implementation invariance (Sundararajan et al., 2017), their robustness for input perturbations (Samek et al., 2016), model weight randomization (Adebayo et al., 2018), and the relevant information they capture in the saliency maps they produce (Dabkowski and Gal, 2017). In the studies where no ground truth is available to estimate the quality of the heatmaps, this evaluation is particularly difficult to conduct (Böhle et al., 2019).

In the neuroimaging field, clinical studies have been conducted for decades to establish how brain dementia affects the brain (Ashburner and Friston, 2000; 2001). A considerable number of voxel-based morphometry studies (VBM) have been conducted to discover which brain atrophies observed in the aging brain can be imputed to an underlying Alzheimer’s disease (Busatto et al., 2008; Chételat et al., 2008; Mueller et al., 2010a; Testa et al., 2004; Villain et al., 2008). When a meta-analysis is conducted, these VBM studies are often summarized into a single brain map indicating what brain regions are affected by the disease (Di et al., 2014; Minkova et al., 2017; Schroeter et al., 2009). VBM studies capture the univariate significance of local tissue changes: they indicate how much a brain disorder such as AD has impacted local brain tissues. This ‘decoding’ approach reverses the ‘encoding’ approach adopted by neural networks, where local tissue changes are aggregated into non-linear features used to predict patient diagnosis. However, under the assumptions that AD only affects localized brain regions (Busatto et al., 2008; Chételat et al., 2008; Mueller et al., 2010a; Testa et al., 2004; Villain et al., 2008) and that neural networks focus on a restricted set of relevant brain regions when diagnosing AD, VBM and heatmaps should overlap to highlight brain regions associated with and predictive of the disease. Since the different heatmap methods capture imaging pattern contributions in various ways, the overlap between heatmaps and Alzheimer’s disease VBM patterns is also expected to depend on the heatmap calculation; some methods focusing on high-level features are more difficult to relate to voxel-wise VBM results. Lastly, it is unclear how well heatmaps derived from a restricted data set would replicate in larger AD neuroimaging cohorts and if that overlap between univariate significance and neural network features’ importance would be preserved.

As far as we know, none of these questions have been explored so far. We propose to address them at the same time, in this work, by quantifying the amount of overlap that can be reached between a “ground truth” univariate significance map provided by a large VBM meta-analysis and heatmaps derived by the most advanced methods from a convolutional neural network achieving state-of-the-art classification performance for Alzheimer’s disease classification on an independent sample of MRI scans. More specifically, we evaluate the ability of three prominent heatmap methods, the Layer-wise Relevance Propagation (LRP) method (Bach et al., 2015), the Integrated Gradients (IG) method (Sundararajan et al., 2017), and the Guided grad-CAM (GGC) (Selvaraju et al., 2017) method, to capture Alzheimer’s disease effects by training 3D CNN classifiers using T1-weighted MRI scans part of the ADNI data set, and measuring the overlap between their heatmaps and a binary brain map derived from a meta-analysis of voxel-based morphometry studies conducted on other T1 MRI scans. Figure 1 summarizes our approach.

Fig. 1.

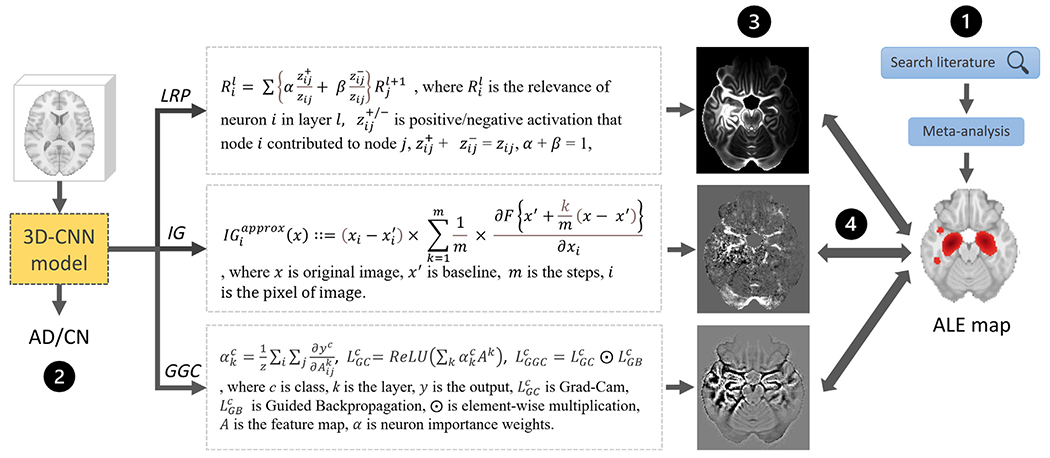
An overview of the present study. (1) A VBM meta-analysis was conducted to derive an Activation Likelihood Estimation (ALE) map summarizing AD effects on the brain visible in T1-weighted MRI scans. (2) 3D CNNs were trained to classify AD and CN ADNI T1-weighted MRI scans. (3) Three heatmap methods were applied to the CNN models with the highest cross-validation accuracy. (4) The heatmaps were compared with the meta-analysis map.

2. Materials and methods

2.1. ADNI study participants

A total of 502 ADNI participants were included in this study. 250 participants were diagnosed with AD and 252 controls. 170 participants were part of the ADNI1 study (92 controls, 78 AD), 298 were enrolled in the ADNI2 study (160 controls, 138 AD), and the last 34 participants were recruited for ADNI3 (0 controls, 34 AD). Study participant demographics are reported in Table 1.

Table 1.

ADNI participants selected in this work. Fisher’s exact test detected no significant difference in the proportion of men in the two groups (p = 0.25) and no significant difference in the proportion of scans acquired with a 3 Tesla MRI scanner (p = 0.22). The T-test detected no significant mean age difference (p = 0.41), while mini-mental state examination (MMSE) values (Jack et al., 2008) were significantly worse in the AD group. Education information was only available for 220 AD study participants and 211 controls and indicated significantly longer education in the AD group.

	Controls	AD	p-value
Study participants (n)	252	250
MRI B0 field (1.5T/3T)	92/160	78/172	0.22
Sex (M/F)	131/121	143/107	0.25
Mean age (std)	74.41 (6.00)	74.93 (8.01)	0.41
Mean MMSE (std)	29.06 (1.25)	22.95 (2.23)	<0.001
Mean years of education (std)	15.25 (2.95)	16.35 (2.65)	<0.001

2.2. ADNI data and processing

For each participant, a raw structural T1-weighted MRI scan was downloaded from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). As a preparation for the present study, the scans were further processed as follows.

First, the multi-atlas brain segmentation pipeline (MUSE) was used for skull-stripping the T1-weighted MRI scans and generating a gray matter map (Doshi et al., 2016). This automated processing pipeline starts by denoising the T1 scans using the N4 bias field correction (Tustison et al., 2010) provided as part of the Advanced Normalization Tools software library (ANTs, version 2.2.0) (Avants et al., 2011). Then, the denoised scans are registered using ANTS nonrigid SyN registration (Avants et al., 2008; 2011) and DRAMMS (Yangming and Davatzikos, 2009) to a set of 50 brain atlases where brain masks have been manually segmented. These registrations are used to warp the atlas brain masks into the space of the T1 scan to process, where they are combined by majority voting to produce an accurate brain mask (Doshi et al., 2016). The brain is then segmented into white matter, gray matter, and cerebrospinal fluid using FSL FAST (version 5.0.11) (Jenkinson et al., 2012), and parcellated into regions of interest by registering a set of 50 manually segmented brain atlases (Doshi et al., 2016). Then, the skull-stripped T1 scans produced by MUSE were registered to the 1 mm resolution 2009c version of the ICBM152 MNI atlas (Collins et al., 1999; Fonov et al., 2011; 2009) using the non-rigid registration method SyN part of the ANTs library (ANTs version 2.3.4) (Avants et al., 2008; 2011). Lastly, each T1 scan was normalized individually by dividing the T1 intensities by the maximum intensity within the brain.

2.3. Convolutional neural networks

A convolutional neural network (CNN) consists of a set of convolutional layers applying convolution operators to gradually condense input data into a set of high-level features that are passed through fully connected layers to produce the final output of the network (Krizhevsky et al., 2017). This output is usually a single value scaled between 0 and 1 when the CNN is used for binary classification (Krizhevsky et al., 2017). Convolutional layers are often combined with the ReLU activation layer filtering negative outputs (Nair and Hinton, 2010), max-pooling layers reducing the dimension of the data (Krizhevsky et al., 2017), and batch normalization layers helping the neural network model optimization (Ioffe and Szegedy, 2015).

In this work, five different 3D CNN architectures of varying complexity were compared. The first architecture, which will be referred to as ModelA, was made of five convolutional layers with decreasing kernel sizes: one layer with a kernel size of 7 ×7 ×7 × c, two layers with kernel sizes of 5 ×5 ×5 × c, and two layers with kernel sizes of 3 ×3 ×3 × c, where c denotes the number of channels, and it was fixed for each CNN separately. ModelB had five convolutional layers with the same kernel size of 3 ×3 ×3 × c. ModelC had four convolutional layers with the same kernel size of 5 ×5 ×5 × c. ModelD was made of three convolutional layers with the same kernel size of 7 ×7 ×7 × c. All convolutional layers were followed by a batch normalization layer, a ReLU activation layer (Nair and Hinton, 2010), and a max-pooling layer (Krizhevsky et al., 2017). For each architecture, the number of channels varied from 24 to 52 to build networks of increasing numbers of parameters. On top of these convolutional layers, all the CNNs were completed by two fully connected layers separated by a ReLU layer (Nair and Hinton, 2010) and a dropout layer fixed to 0.5 to prevent overfitting (Srivastava et al., 2014). The first fully connected layer was obtained by flattening the features produced by the last convolutional layer. The second layer was set to contain 64 neurons and to produce a continuous output corresponding to the AD diagnosis. ModelE is adapted from residual network architectures (He et al., 2016). Residual networks (ResNets) are the first neural networks consisting of hundreds of layers and have achieved huge success in image recognition. The key component of a ResNet is the residual block which concatenates one layer to the next. We tested ModelE of increasing numbers of layers (from 4 to 28) with varying numbers of channels (from 4 to 32). All five CNN architectures are summarized in Fig. 2.

Fig. 2.

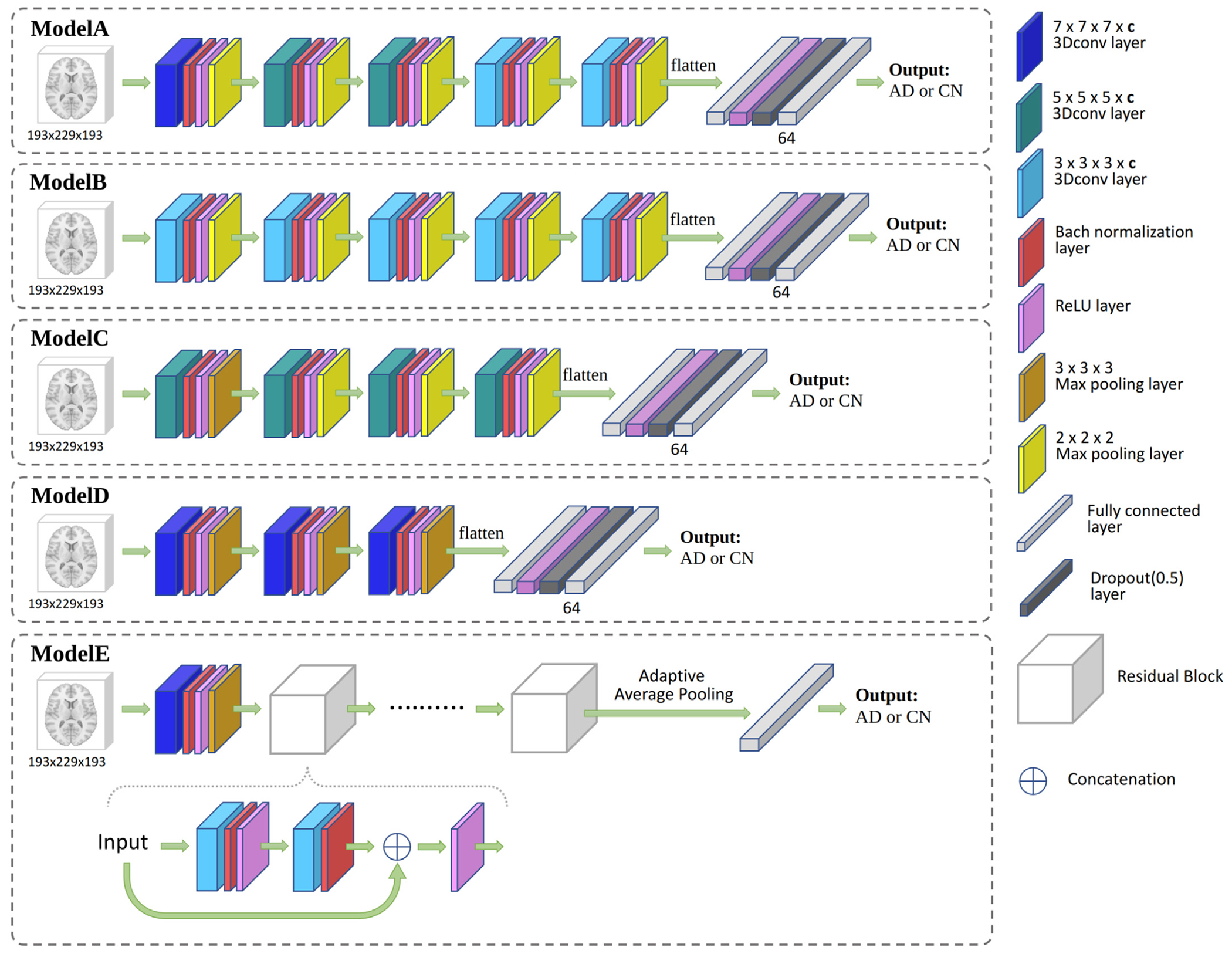
CNN models used in this study to classify ADNI AD participants and controls. For each architecture, several numbers of channels c were tested. The number of channels c corresponds to the number of 3D convolutional kernels used in each convolutional layer. Increasing numbers of layers were tested for ModelE. The Residual Block used in ModelE concatenates its input with the output of two 3 ×3 ×3 × c convolutional layers.

These networks were trained to distinguish between the MRI scans of AD and control in our ADNI data set. Cross-entropy was used as a loss function for the classification, and that loss was minimized using the Adam optimizer with a learning rate of 0.0001 and a weight decay of 0.0001 (Kingma and Ba, 2015). CNN accuracy was evaluated via 5-fold cross-validation by splitting the data set five times into a training set of 322 scans, a validation set of 80 scans, a test set of 100 scans for the first four folds, and a training set of 322 scans, a validation set of 78 scans, a test set of 102 scans for the last fold. An early stopping criterion was implemented by monitoring the validation loss and forcing the training process to stop after ten epochs producing no improvements in the validation loss. These CNN architectures and their optimizers were selected to match standard architectures and their default optimization parameter values and, in particular, state-of-the-art Alexnet (Krizhevsky et al., 2017) and Google net (Szegedy et al., 2015).

All the models were trained on a high-performance computing system equipped with Nvidia v100 GPUs. The training required 32 GB of RAM and was completed within 3 h to 8 h for each fold, depending on the model complexity. The proposed network was built with Pytorch (Paszke et al., 2019).

The classification accuracy obtained for all the CNNs tested was compared with the classification accuracy of linear SVMs with the following set of SVM-C parameters (Pedregosa et al., 2011; Smola and Schölkopf, 2004): 10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 10⁻¹, 1, 10, 10², 10³, 10⁴. An SVM activation patterns map was then calculated for the SVM model with the best accuracy (Haufe et al., 2014). SVM activation patterns maps correspond to SVM coefficients weighted by the covariance of the data, and they were shown to better capture brain changes than unweighted SVM coefficient maps (Haufe et al., 2014). The CNN model with the best cross-validated accuracy was then retained to compute heatmaps highlighting the brain regions selected by the model to distinguish AD and control brains.

2.4. CNN heatmap methods

In this study, three prominent CNN heatmap methods are selected, the Layer-wise Relevance Propagation (LRP) method (Bach et al., 2015), the Integrated Gradients (IG) method (Sundararajan et al., 2017), and the Guided Grad-CAM (GGC) (Selvaraju et al., 2017) method. These methods were used to produce a heatmap for each test scan and then averaged to produce a single heatmap for each heatmap method indicating what brain regions were used the most by the selected CNN when classifying the brain scans to distinguish AD and control ADNI participants (Bach et al., 2015; Selvaraju et al., 2017; Sundararajan et al., 2017).

The Layer-wise Relevance Propagation (LRP) method produces a heatmap by estimating a relevance score for each input pixel passed to a CNN model. The relevance score is computed by propagating CNN outputs backward in the network according to a specific set of rules (Bach et al., 2015). These rules are designed to preserve relevance scores from layer to layer. They are often modified to reduce the noise in relevance scores, improve their sparsity, or treat positive and negative neural network activations differently (Bach et al., 2015; Binder et al., 2016; Montavon et al., 2017). In this work, we used the β-rule LRP algorithm implemented by Binder et al. (2016); Böhle et al. (2019). The β parameter aiming at balancing the relevance scores associated with positive and negative neural network activations was set to 0.5 to account for both activations in a similar manner (Bach et al., 2015). Since the standard LRP implementation cannot handle the 3D adaptive average pooling layers in the residual blocks of our ModelE architecture, only GGC and IG could be used to derive heatmaps for these deep networks (LRP, 2023).

The Integrated Gradients (IG) method was introduced to guarantee two desirable heatmap properties: sensitivity and implementation invariance (Sundararajan et al., 2017). Sensitivity refers to the ability of a heatmap method to produce null relevance scores for network inputs that are not contributing to the network output. Most of the methods published before IG either did not satisfy the sensitivity requirement, such as Guided Backpropagation (Springenberg et al., 2015), Deconvolution networks (Zeiler et al., 2010), and DeepLift (Shrikumar et al., 2017), or were not invariant to the neural network implementation, such as LRP (Bach et al., 2015), and DeepLift (Shrikumar et al., 2017). The Integrated Gradients (IG) method produces the heatmap of an input image by multiplying the input with a scaling factor uniformly selected between 0 and 1 several times in a row, computing the gradient for each scaled input via backpropagation, and then averaging these gradients (Sundararajan et al., 2017). The IG implementation used in this work will be available on https://github.com/UTHSCSA-NAL/CNN-heatmap/.

Guided Grad-Cam (GGC) combines Grad-CAM and Guided Backpropagation (Selvaraju et al., 2017; Springenberg et al., 2015). Grad-CAM is a generalization of the Class Activation Mapping (CAM) (Zhou et al., 2016) that can be implemented for any CNN without model changes or re-training. Grad-CAM generates a heatmap for a CNN layer by applying a ReLU function (Nair and Hinton, 2010) to a linear combination between the activations obtained at that layer and the backpropagated gradients from subsequent layers (Selvaraju et al., 2017). In Guided Grad-CAM, these Grad-CAM heatmaps are up-sampled to the resolution of the input data and element-wise multiplied with a heatmap generated by Guided Backpropagation to produce heatmaps with the same resolution as the input data (Selvaraju et al., 2017; Springenberg et al., 2015). During our experiments, we only considered Guided Grad-CAM heatmaps based on the Grad-CAM maps computed for the last convolutional layer of our CNNs, as suggested in the original GGC publication (Selvaraju et al., 2017). GGC was implemented as part of the Captum PyTorch library https://captum.ai/.

2.5. Meta-analysis ALE map

The meta-analysis map was produced by reprocessing a set of voxel-based morphometry (VBM) studies collected from a prior meta-analysis (Ashburner and Friston, 2000). We produced a brain map by applying the activation likelihood estimation (ALE) method (Eickhoff et al., 2012; 2016; Turkeltaub et al., 2002; 2012) implemented in the GingerALE software (version 3.0.2) (Eickhoff et al., 2009; GingerAle, 2022) to combine the selected VBM studies into a single ALE map indicating what atrophies observed in the brain were likely to be associated with Alzheimer’s disease (Turkeltaub et al., 2002). More specifically and following (Müller et al., 2018; 2017), GingerALE was running for a cluster-forming p-value of 0.001 and a cluster-level significance level of 0.05. Cluster significance was estimated by conducting a thousand random permutations. The continuous map generated by GingerALE, where all non-significant brain locations had been assigned null values, was thresholded at its smallest non-zero value to produce a binary map suitable for a comparison with the thresholded CNN heatmaps.

2.6. Evaluation metrics

The ability of the CNN heatmap methods presented in the previous section to capture brain alterations associated with Alzheimer’s disease was estimated by measuring the Dice overlap between binary maps obtained by smoothing and thresholding the heatmaps with the binary brain map derived from a large meta-analysis that summarized the brain regions affected by Alzheimer’s disease in T1 MRI scans.

More specifically, CNN heatmap values were replaced by their absolute values. The heatmaps were then smoothed by sixteen different Gaussian kernels of full width at half maximum (FWHM) ranging from 1 mm to 32 mm (1 mm, 2 mm, 3 mm, 4 mm, 5 mm, 6 mm, 7 mm, 8 mm, 9 mm, 10 mm, 12 mm, 16 mm, 20 mm, 24 mm, 28 mm, 32 mm). For each smoothed heatmap and the original heatmaps, 50 values were evenly selected between the minimum and the maximum heatmap value to threshold the heatmaps. The reason to smooth a heatmap is to make it comparable to a meta-analysis map since the ALE algorithm inherently adds Gaussian smoothing to the locations of reported foci. The 850 binary maps obtained in this way were compared with the meta-analysis map by computing a Dice overlap. This approach was chosen to explore and mitigate spatial resolution discrepancies between the CNN heatmaps and the meta-analysis map.

2.7. Additional synthetic validation

The methods presented in this work were validated by processing two synthetic data sets. The first data set, the “single-subject” data set, made of 10,000 images, was generated from a single healthy control subject MRI scan (mean MRI intensity = 2600, std = 756) from our ADNI data set and was downsampled to a size of 65 ×77 ×65 voxels to reduce the computational burden. In half of the images, the MRI intensity in the hippocampus regions was increased by a random value ranging between 0 and 2500 and simulating a disease effect on grey matter tissue. Then, Gaussian noise (mean = 0, std = 2000) was added to all synthetic images, and a Gaussian smoothing of 4 mm FWHM was applied. The second data set, the “whole-cohort” data set, also made of 10,000 images, was generated using 250 healthy controls from our ADNI data set and downsampled to 65 ×77 ×65 voxels. Each healthy control scan was used to generate 40 images. In half of these images, the MRI intensity in the hippocampus regions was increased by a random disease effect between 0 and 2500. Then, Gaussian noise (mean = 0, std = 2000) was added to all synthetic images, and a Gaussian smoothing of 4 mm FWHM was applied.

Eleven linear SVMs were trained to distinguish the synthetic scans with and without disease effect, for the parameters tested with the clinical data (SVM-C parameter in 10⁻⁶ , 10⁻⁵ , 10 ⁻⁴ , 10⁻³ , 10⁻² , 10⁻¹ , 1, 10, 10² , 10³ , 10⁴) (Pedregosa et al., 2011; Smola and Schölkopf, 2004). Then, CNN models similar to the models shown in Fig. 2 were trained: a ModelA containing one 7 ×7 ×7 × c and one 5 ×5 ×5 × c convolutional layers, where the number of channels c was set to 4 (ModelA4l2), a ModelB containing two 3 ×3 ×3 × c convolutional layers (ModelB4l2), a ModelC containing two 5 ×5 ×5 × c convolutional layers (ModelC4l2), and a ModelD containing two 7 ×7 ×7 × c convolutional layers (ModelD4l2). The number of convolutional layers in these CNNs was reduced, compared to the original CNN architectures used for classifying ADNI scans, to fit the size of the downsampled synthetic images. More specifically, max-pooling layers have the effect of largely reducing the spatial size of the data, and two layers would have reduced our synthetic data to a size that is smaller than the kernel size, which would be insufficient to reach another convolutional layer. Since the residual block in ModelE does not quip with the max-pooling layer, the layer of ModelE need not be modified for synthetic data. They were trained for a cross-entropy classification loss that was minimized using the Adam optimizer with a learning rate of 0.0001 and a weight decay of 0.0001 (Kingma and Ba, 2015) for a hundred epochs. Please refer to Fig. 2 for their detailed architecture. For each data set, LRP, IG, and GGC were used to compute a heatmap for the CNN model reaching the best five-fold cross-validated accuracy. The activation patterns of the best SVM and the heatmap values were then compared with the binary map of the hippocampus by computing Dice overlaps at different spatial smoothing levels, as explained in the previous Sections.

3. Results

3.1. Classification performance in synthetic data

For both synthetic data sets, the ModelD4l2 reached the best five-fold cross-validated accuracy, with 91% accuracy for the single-subject data and 90.1% for the whole-cohort data, and systematically outperformed the best SVM models, that were obtained for both data sets by setting SVM-C parameter to 0.1 (87% accuracy for single-subject data set and 87.5% accuracy for whole-cohort data set). More specifically, for the single-subject data set, ModelA4l2 also outperformed the best SVM, with an accuracy of 90%, but ModelC4l2 and ModelB4l2 produced worse classification results, with respectively 81% and 74% accuracy. For the whole-cohort data set, on the contrary, ModelB4l2 was the second-best model with 90.06% accuracy, followed by ModelA4l2 (89.9%) and ModelC4l2 (87.9%) and all CNN models were more accurate than the best SVM tested. We tested ModelE with 4, 6, 8, 10, and 18 layers and 4, 8, 10, 12, 16, 20, 24, 28, and 32 channels. For the single-subject data set, the best five-fold cross-validated accuracy was 89.83% and achieved by the 8 layers ModelE with 12 channels (ModelE8-12). For the whole-cohort data set, the best five-fold cross-validated accuracy was 89.91% and was achieved by the 8 layers ModelE with 28 channels (ModelE8-28).

3.2. Heatmaps derived from synthetic data

The Dice overlaps between heatmaps and the binary hippocampus map are shown in Fig. 3. All smoothing results are reported in Supplementary materials (Section 1). For the single-subject data set, the best Dice overlap measured for LRP, IG, GGC using ModelD4l2 is 0.581 when the LRP heatmap was smoothed by a 1 mm FWHM Gaussian smoothing, 0.703 for the IG heatmap with a 1 mm smoothing, 0.593 for GGC heatmap with a 1 mm smoothing. The best Dice overlap measured for IG, GGC using ModelE8-12 is 0.433 when IG heatmap was smoothed at 4 mm and 0.202 when GGC heatmap was smoothed at 12 mm. The best dice overlap for SVM activation patterns is 0.749 without smoothing.

Fig. 3.

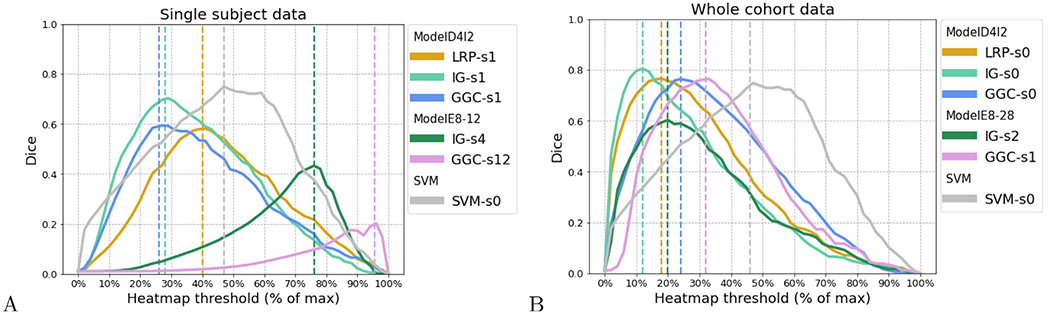
Dice curves reaching the best overlap between the brain region altered in the synthetic data for heatmaps and SVM activation patterns; (A) for the single subject data set, and (B) for the whole cohort data set. ModelD4l2 achieved the best accuracy for both datasets. ModelE8-12 achieved the best accuracy among the residual networks for single subject data and ModelE8-28 for whole cohort data. Only the best SVM model is shown. s0 indicates a heatmap that was unsmoothed, s1 indicates a heatmap smoothed by a Gaussian kernel of 1 mm FWHM, and s2 indicates a 2 mm FWHM smoothing.

For the whole-cohort data set, the best Dice overlap measured for LRP, IG, GGC, using ModelD4l2 is 0.766 for the LRP heatmap without Gaussian smoothing, 0.804 for the IG heatmap without smoothing, 0.763 for GGC without smoothing. The best dice overlap measured for IG, GGC using ModelE8-28 is 0.602 when IG heatmap was smoothed by 2 mm smoothing and 0.748 when GGC heatmap was smoothed by 1 mm smoothing. The best dice overlap for SVM activation patterns is 0.748 without smoothing.

Their corresponding heatmaps achieved the best overlap with the hippocampus map and the heatmaps thresholded at 5% of their maximum values are shown in Supplementary materials (Section 1). Those plots indicate that IG heatmaps have a better focus on the hippocampus than GGC and LRP heatmaps.

These results demonstrate the ability of CNN heatmaps to capture localized and specific brain alterations on a synthetic data set and, in particular, when the hippocampus is affected similarly as in real clinical data.

3.3. Classification performance in ADNI

The 5-fold cross-validation accuracy of ModelA, ModelB, ModelC, ModelD and SVM models tested during this work is reported in Table 3. The best CNN accuracy was achieved by ModelB with 44 channels (ModelB44) and reached 87.25%. This accuracy is six percent better than the cross-validated accuracy obtained with the best SVM model(SVM-C parameter 0.001), which is close to 81.2% and that was obtained through grid search for a set of SVM-C parameters: 10⁻⁶ , 10⁻⁵ , 10⁻⁴ , 10⁻³ , 10⁻² , 10⁻¹ , 1, 10, 10² , 10³ , 10⁴ . The 5-fold cross-validation accuracy of all the ModelE tested is reported in Table 4. For ModelE, we obtained the best accuracy at 81.08% with 18 layers and 20 channels (ModelE18-20).

Table 3.

5-fold cross-validation accuracy for the classification of ADNI participants, for ModelA ModelB ModelC and ModelD with all numbers of channels c, and the best Linear SVM. The number of channels corresponds to the number of 3D convolutional kernels used in each CNN convolutional layer.

c	ModelA	ModelB	ModelC	ModelD
24	76.41%	82.65%	75.47%	58.59%
28	83.85%	84.45%	65.59%	54.78%
32	78.86%	85.44%	84.45%	58.20%
36	83.84%	86.05%	72.18%	55.80%
40	78.05%	86.25%	58.18%	47.21%
44	61.80%	87.25%	55.65%	52.99%
48	59.81%	86.45%	64.45%	55.48%
52	61.41%	86.46%	62.64%	47.81%

Best SVM-C parameter 0.001, accuracy 81.19%.

Table 4.

5-fold cross-validation accuracy for the classification of ADNI participants, for all ModelE and all numbers of channels c. The number of channels corresponds to the number of 3D convolutional kernels used in each layer. ModelE28 refers to ModelE with 28 layers.

c	ModelE28	ModelE24	ModelE22	ModelE20	ModelE18	ModelE16	ModelE10	ModelE8
8	61.12%	70.09%	66.91%	58.12%	67.91%	64.53%	65.17%	49.40%
10	58.53%	73.90%	72.67%	65.31%	73.08%	62.80%	67.11%	56.41%
12	68.33%	60.37%	60.02%	78.08%	51.22%	72.51%	63.86%	53.41%
14	60.27%	71.09%	62.29%	62.74%	67.90%	59.41%	61.01%	59.56%
16	66.47%	72.61%	56.38%	65.47%	72.29%	75.87%	72.87%	54.35%
20	54.09%	61.21%	69.69%	62.79%	81.08%	75.09%	63.01%	54.38%
24	56.58%	69.46%	58.81%	64.16%	66.00%	71.09%	62.89%	57.56%
28	60.98%	68.86%	60.61%	66.30%	67.41%	66.60%	62.07%	56.01%

3.4. Meta-analysis ALE maps

The demographics of the participants included in the meta-analysis are reported in Table 2. There was no statistically significant difference between the control group and the AD/MCI group for mean age and men/women proportions (at a significance level of 0.05 after Bonferroni correction; a Fisher exact test was conducted to compare gender proportions and an unpaired T-test to compare group mean ages). Figure 4 presents the ALE map used in this work. The structural MRI ALE map summarizes 77 neuroimaging studies reporting 773 locations in the brain affected by Alzheimer’s disease, discovered by analyzing the neuroimaging data of a total of 3817 study participants around the world (2118 controls, 1699 MCI or AD). The complete list of publications combined in this map is reported in Supplementary materials (Section 2).

Table 2.

The meta-analysis ALE map summarizes 77 VBM studies published in 58 articles. Gender information was missing in 3 MRI VBM studies. A Fisher exact test was conducted to compare men/women counts, and an unpaired T-test was conducted to compare group mean ages. After Bonferroni correction for two tests, none of the differences observed was significant at level p = 0.05.

	n	Men/women	Mean age
CN	2118	853/1127	69.9
AD/MCI	1699	725/882	71.6
p-value		0.224	0.03

Fig. 4.

Meta-analysis ALE maps in the MNI152 template space.

3.5. Overlaps between heatmaps and meta-analysis

The five ModelB44 models trained during the 5-fold cross-validation were used to generate heatmaps. For each model, a heatmap was generated for each test scan and each heatmap method: LRP, IG, and GGC. The 502 individual heatmaps obtained for each method were averaged into a single heatmap that was compared with the binary meta-analysis map to evaluate the performance of the method. In addition, an SVM activation patterns map was produced by training a linear C-SVM using all the data and by retaining the weight of this model to create a brain map. The C parameter of this SVM was set to the value producing the best five-fold cross-validated accuracy (C = 0.001).

Figure 5 reports all the Dice measured between the heatmaps and the meta-analysis map. The best Dice overlap measured for LRP, IG, and GGC, using ModelB44 was 0.502 when the LRP heatmap was smoothed by a 7 mm FWHM Gaussian smoothing, 0.550 for the IG heatmap with a 4 mm smoothing, 0.540 for GGC with an 8 mm smoothing. The best Dice overlap measured for IG, and GGC, using ModelE18-20 was 0.152 for the IG heatmap with a 26 mm smoothing and 0.338 for the GGC heatmap with a 32 mm smoothing. SVM activation patterns achieved a dice of 0.363 with a 12 mm smoothing. The heatmaps with the best overlaps with the meta-analysis are shown in Fig. 6. Figure 7 displays the unsmoothed heatmaps. The LRP heatmaps select more regions than the other maps and appear to be noisier. On the other hand, IG heatmaps have a better focus on the regions highlighted by the meta-analysis, but the unsmoothed IG map presents an unrealistic scatter. IG produced a map that was simultaneously more relevant than the LRP heatmap and less scattered than the GGC heatmap. In comparison, the unsmoothed SVM activation patterns map covers most of the grey matter. The linear SVM produced slightly larger weight amplitudes in the regions relevant for the diagnosis, but an aggressive smoothing was required to make this effect emerge in Fig. 6.

Fig. 5.

For each heatmap method, the Dice curve of ADNI data corresponding to the spatial smoothing reaches the best overlap with the meta-analysis. ModelB44 achieved the best accuracy and ModelE18-20 achieved the best accuracy among residual networks. Linear SVM with SVM-C parameter of 0.001 achieved the best accuracy among tested SVMs. LRP-s7 corresponds to the LRP heatmap after 7 mm FWHM Gaussian smoothing, and similarly for other methods.

Fig. 6.

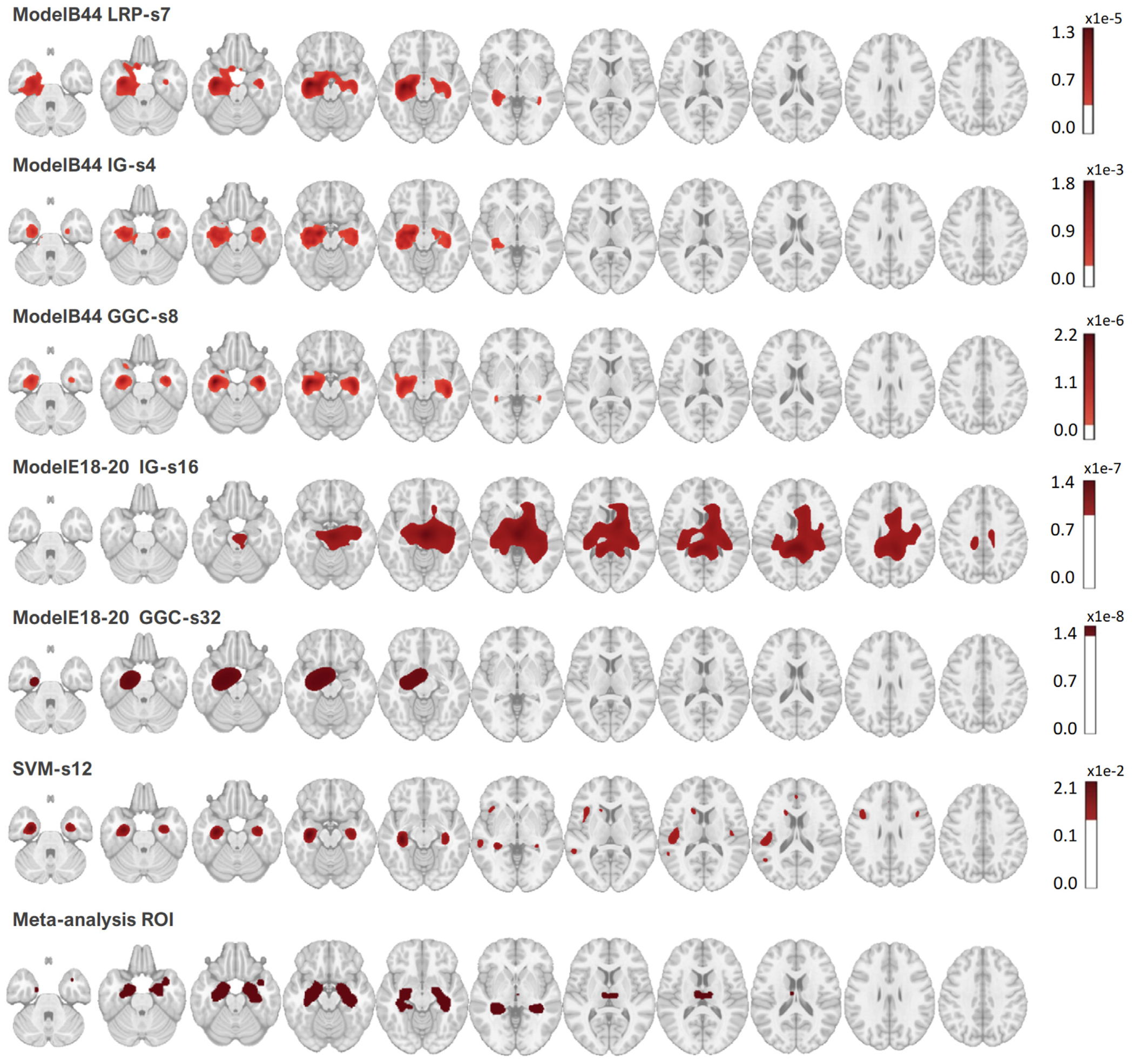
Heatmaps corresponding to the best Dice overlap with the meta-analysis map, for all the CNN heatmaps methods tested in this work and the best linear SVM. The meta-analysis map is binary. ModelB44 achieved the best accuracy and ModelE18-20 achieved the best accuracy among tested residual networks.

Fig. 7.

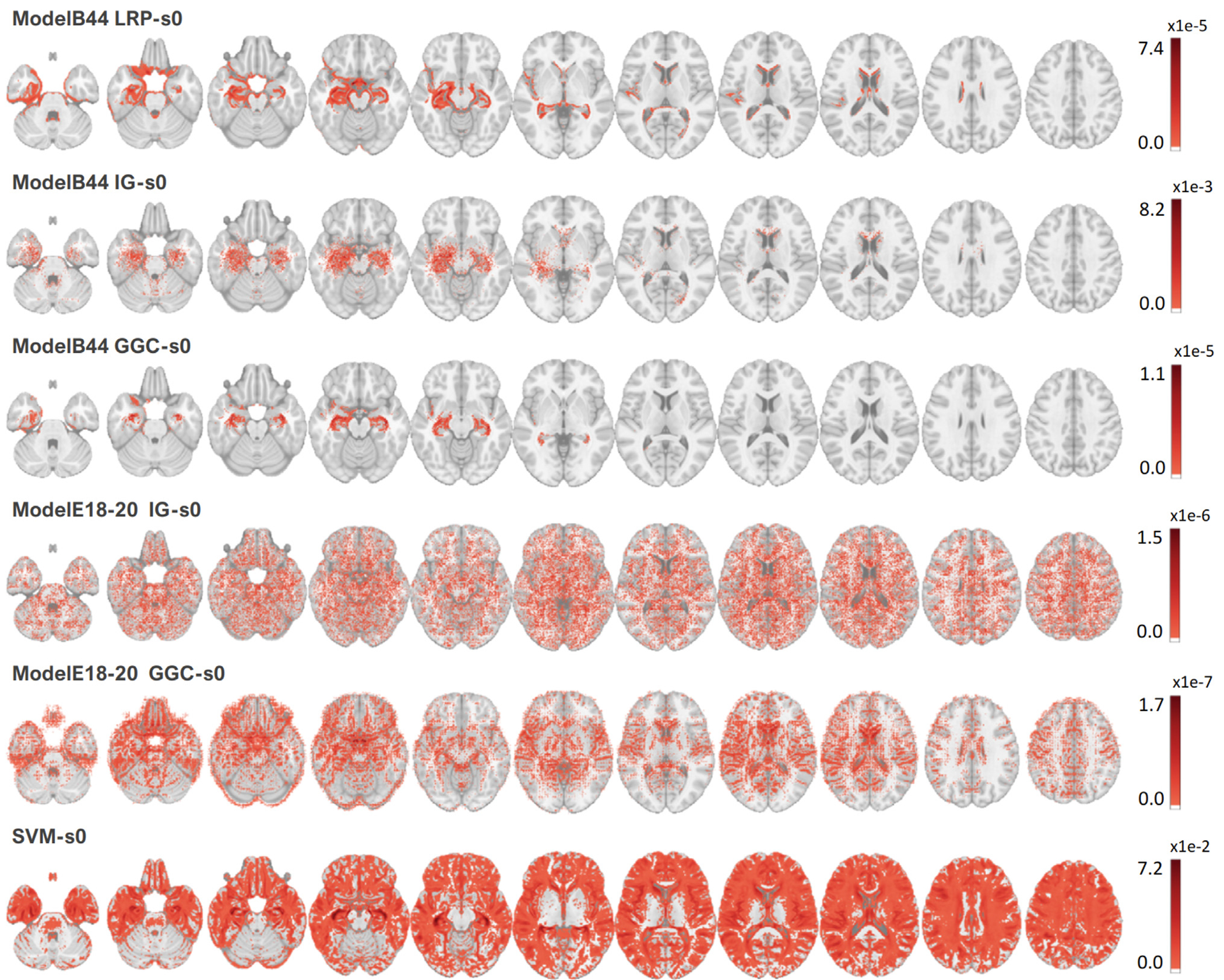
Heatmaps without smoothing, thresholded at 5% of their maximum value. ModelB44 achieved the best accuracy and ModelE18-20 achieved the best accuracy among tested residual networks.

4. Discussion

In the present study, we reported the first data-driven validation, for the study of Alzheimer’s disease, of three prominent CNN heatmap methods: Layer-wise Relevance Propagation (LRP), Integrated Gradients (IG), and Guided Grad-CAM (GGC). The heatmaps produced by these methods, for a CNN classifier producing the best AD classification among a large set of CNN architectures tested using ADNI T1-weighted MRI scans, were compared with a binary meta-analysis ALE map obtained by combining 77 Alzheimer’s disease VBM studies. Our results indicate that the CNN heatmaps captured brain regions that were also associated with AD effects on the brain in the meta-analysis.

4.1. Best deep learning-based classification model

The best 5-fold cross-validation accuracy (87.25%) was obtained for a ModelB with 44 channels. Overall, ModelB accuracy was stable when the number of channels was varied, varying only between 83% and 87%. ModelA and ModelC were less stable: their accuracy ranged between 60% and 84% and 63% and 84%, respectively. ModelD produced only poor classifications, for an accuracy ranging between 47% and 59%. We think that these differences can be explained by overfitting, as we noticed that ModelD usually contains more trainable parameters than ModelC of a similar number of channels. ModelC usually contains more parameters than ModelA, and ModelB is the smallest model. For 44 channels, for instance, ModelD required the training of 1,569,058 parameters, ModelC 957,502 parameters, ModelA 705,866, and ModelB only 436,410 parameters. Some ModelDs were unable to fit the data, as reported in Supplementary Materials Section 3. These observations could support the hypothesis that large networks cannot be trained using our limited sample of scans. The complete list of model sizes is reported in this section. For ModelE, we achieved the best classification accuracy at 81.08% with 18 layers and 20 channels (ModelE18-20).

The classification accuracy reached by our best model, ModelB44, is on par with recent ADNI studies. An accuracy of 84.82% was reported for a 3D CNN trained to classify T1-weighted hippocampus MRI scans extracted from ADNI (Huang et al., 2019). Another study reported a balanced accuracy between 75.5% and 88.3% for distinguishing AD and controls ADNI participants using 3D CNN (Dyrba et al., 2021).

4.2. Explainable AI and neuroimaging

The neuroimaging field has developed meta-analysis brain maps to summarize domain knowledge (Fox et al., 2005; Vanasse et al., 2018), which we use to evaluate the CNN heatmaps. Contrary to prior studies, where the quality of heatmaps was visually or qualitatively assessed (Binder et al., 2016; Jo et al., 2020; Samek et al., 2016; 2021), we obtained precise quantitative measures by computing overlaps with a ground-truth map derived from a large-scale meta-analysis. We explored a broad range of heatmaps’ spatial smoothing intensities, and we found that the heatmaps overlapped the most with the meta-analysis for Gaussian smoothing kernels between 4 mm and 8 mm FWHM. These Gaussian kernels are similar to the kernels usually applied by GingerALE when producing meta-analysis maps (Eickhoff et al., 2009; GingerAle, 2022).

4.3. Heatmaps evaluation

For all the CNN heatmap methods derived for ModelB44, the best heatmaps indicated that changes in the hippocampus regions in both hemispheres were a crucial pattern during the classification of ADNI participants with AD and healthy controls. These results are perfectly in line with the literature, where the effect of Alzheimer’s disease on the hippocampus has been well-characterized (Habes et al., 2016b; Jack et al., 2013; Mueller et al., 2010b; Ohnishi et al., 2001; Shi et al., 2009). We obtained moderately good Dice overlaps between heatmaps and the meta-analysis ground-truth, ranging from 0.5 for the best heatmap generated by the LRP method to 0.55 for the best IG heatmaps.

Direct analysis of the heatmaps, without spatial smoothing, established that all CNN heatmaps were better at focusing on relevant brain regions than linear SVM activation patterns. IG and LRP produced scattered heatmaps that benefited the most from spatial smoothing, gaining up to 0.19 and 0.18 in Dice overlap with the ground truth as the size of the Gaussian kernels was varied. GGC Dice overlap was only improved by 0.16 at most. In comparison, the SVM activation patterns map was so scattered and noisy that a Dice improvement larger than 0.3 was observed when the map was smoothed. We refer the readers to the Supplementary Materials for the complete set of Dice overlaps measured during this experiment (Section 3). The LRP heatmap was the noisiest and produced the least symmetric results by selecting more voxels in the left hemisphere, as reported in prior studies (Böhle et al., 2019).

IG produced the heatmaps with the largest overlaps with the meta-analysis, and that overlap required less spatial smoothing. These results suggest that the IG heatmap, while being more scattered than other heatmaps, was overall less noisy. All heatmap methods produced brain maps closer to the meta-analysis map than the map derived from the baseline support vector machine and were better focused on brain regions impacted by the disease than the SVM activation patterns. The additional overlap measures presented in Supplementary materials (Section 4) also indicate a better overlap between the IG heatmaps and the meta-analysis ground truth, and these results are in line with the synthetic results, where IG also outperformed other heatmap methods.

The heatmaps derived for the best ResNet exhibited a very low overlap with the meta-analysis map. This low overlap was associated with a lower classification performance, slightly worse than the best SVM. So, we think that our ResNets were unable to precisely capture the brain regions impacted by AD, and this failure was reflected in their heatmaps.

4.4. Data augmentation

Various techniques could be used to improve classification performance, such as data augmentation, which is used to enhance performance by enlarging the training set (Rashid et al., 2021). In this work, we did not employ data augmentation as we were aiming to capture biology-informed patterns, and the most standard form of data augmentation, the inclusion of translated and rotated copies of the training scans (Rashid et al., 2021), would have blurred the boundaries of the brain regions that the CNN heatmaps were aiming to capture. In the future, we will check whether the use of more advanced data augmentation methods, such as the introduction of realistic noises that preserve the boundaries between grey matter and white matter in the MRI scans, could be used to carry out a data augmentation that retains the boundaries of the regions of interest.

4.5. Evaluation metrics

Multiple metrics could be used to measure the overlap between the binary meta-analysis map provided by GingerALE, the continuous SVM activation patterns, and the continuous brain maps generated by the heatmap methods. In this work, we decided to threshold the absolute value of the continuous heatmaps, and we used a well-established metric to measure the overlap between brain regions, the Dice overlap. Since the meta-analysis ALE map was produced by thresholding a map combining Gaussian kernels of various sizes (Eickhoff et al., 2009; GingerAle, 2022), we considered that the thresholded heatmap had to be smoothed, and we explored a broad range of thresholds and smoothings to search for the best possible match between meta-analysis and heatmaps. This kind of grid search is not common in the literature, but we think that it was justified to account for the unknown level of smoothing incorporated in the VBM studies and during their combination by GingeALE.

5. Conclusion

In this work, we evaluated the ability of three prominent CNN heatmap methods, the Layer-wise Relevance Propagation (LRP) method, the Integrated Gradients (IG) method, and the Guided Grad-CAM (GGC) method, to capture Alzheimer’s disease effects in the ADNI data set by training CNN classifiers and measuring the overlap between their heatmaps and a brain map derived from a large-scale meta-analysis. We found that the three heatmap methods capture brain regions that overlap fairly well with the meta-analysis map, and we observed the best results for the IG method. All three heatmap methods outperformed linear SVM models. These results suggest that the analysis of deep nonlinear models by the most recent heatmap methods can produce more meaningful brain maps than linear and shallow models. Further work will be required to replicate our results and extend our models to investigate other tasks, such as other neurodegenerative disorders and healthy aging.

Data availability

Data will be made available on request.