The Role of Momentum Partitioning in Covariance Ion Imaging Analysis

Abstract

We present results from a covariance ion imaging study, which employs extensive filtering, on the relationship between fragment momenta to gain deeper insight into photofragmentation dynamics. A new data analysis approach is introduced that considers the momentum partitioning between the fragments of the breakup of a molecular polycation to disentangle concurrent fragmentation channels, which yield the same ion species. We exploit this approach to examine the momentum exchange relationship between the products, which provides direct insight into the dynamics of molecular fragmentation. We apply these techniques to extensively characterize the dissociation of 1-iodopropane and 2-iodopropane dications prepared by site-selective ionization of the iodine atom using extreme ultraviolet intense femtosecond laser pulses with a photon energy of 95 eV. Our assignments are supported by classical simulations, using parameters largely obtained directly from the experimental data.

Introduction

Molecular photoabsorption of short-wavelength light in the extreme ultraviolet (XUV) or X-ray region typically ejects an electron from a highly localized core orbital, enabling ultrafast photochemistry to be either triggered¹⁻³ or probed⁴ in a site-selective fashion. Time-resolved X-ray photoelectron spectroscopy, an example of the latter, offers sensitivity to changes in local charge density during a photochemical reaction⁵ and promises to offer new dynamical insights compared to previous approaches that employ valence ionization from delocalized molecular orbitals.⁶ In species containing light elements, the highly excited ion produced upon core ionization typically relaxes by Auger–Meitner (AM) decay, ejecting further electron(s). The resulting polycation may then undergo a wide range of photofragmentation processes,^7,8 involving the cleavage of multiple bonds on different time scales to yield charged and neutral fragments. Photoisomerization, for instance, involving the migration of hydrogens, may also occur en route to fragmentation.^9,10

These processes can be studied in intricate detail using coincidence counting techniques, which simultaneously detect the momenta of multiple products.^7,11 With advances in short-wavelength light sources, such techniques have driven forward the understanding of the fragmentation dynamics of molecular polycations. However, it must be emphasized that, given the population of a broad spectrum of polycation states following inner-shell ionization, as well as the possibility of ultrafast nuclear motion prior to AM decay, a comprehensive understanding of the photodynamics of these species remains an ambitious goal.³ Given the ongoing advances in free-electron laser (FEL) technology, enabling a whole host of novel X-ray techniques to study structure and ultrafast dynamics,^4,5,12−20 the continued study of inner-shell ionization and polycation dynamics is of great interest.

In coincidence studies, a low count rate is employed to ensure that the species detected in the same experimental cycle come from the same initial ionization/fragmentation event. This leads to a rich data set, containing reaction channel-resolved information, in the form of correlations between the three-dimensional (3D) momenta of different ionic photoproducts. These correlations reveal substantial detail about the underlying fragmentation process, such as the nuclear dissociation dynamics and the time scales over which these dynamics evolve.²¹ Covariance imaging²²⁻²⁵ is a complementary method that allows experiments to be performed at higher count rates (i.e., under conditions in which many molecules are ionized in a given experimental cycle) while still extracting physically meaningful multiparticle correlations through statistical analysis.²⁶⁻³⁰ This method is particularly well suited to experiments at current low-repetition rate FEL sources, where conducting experiments at a higher count rate can greatly expedite data acquisition.

In the present work, covariance analysis is coupled with 3D velocity-map imaging (VMI)³¹ to study the photoionization and photofragmentation dynamics of 1- and 2-iodopropane (referred to as 1-IP/2-IP from here on) following interaction with XUV photons with energy above the iodine 4d ionization edge. We focus on the dynamics of the molecular dication, which is observed to undergo a range of fragmentation pathways, many of which produce the same ionic products via different mechanisms. Being able to distinguish between such processes is an important goal in the field of reaction dynamics. For this purpose, we demonstrate a refined covariance imaging analysis procedure that considers the momentum partitioning between the fragment ions. In the original incarnation of covariance ion imaging, the covariance map is calculated between a pair of ion fragments whose momenta are unrestricted.^23,32 Our previous work introduced the concept of constraining the momentum of one of the fragment ions in a covariance calculation to separate signals arising from different fragmentation channels.²⁸ The current method builds upon this further by constraining the momentum of both of the ions in a covariance calculation, based on their expected momentum relationship for a specific fragmentation channel. This offers a more systematic and precise method of identifying and separating overlapping contributions to a covariance map from different dissociation channels.

The results build on our previous work on the isomers of iodopropane,²⁸ which investigated the dynamics of a single fragmentation channel of the molecular trication. Here, each dissociation pathway of the molecular dication is interrogated in detail. The methods we present allow different fragmentation channels leading to the same products to be disentangled and independently investigated, as well as further interrogation of the dynamics of rotationally excited intermediates. The interpretation of the observed fragment momentum correlations is supported by comparisons with classical simulations of the fragmentation process. Despite their simplicity, these are found to accurately reproduce the experimental results and provide physical insight into the dynamics of sequential fragmentation. This includes how the orientation of the metastable intermediate ion—relative to the trajectory of a primary ion—affects the momentum partitioning between the secondary products upon further breakup.

Collectively, these results shed light on the fragmentation behavior of 1/2-IP polycations and demonstrate the usefulness of covariance imaging analysis to study nuclear dynamics induced by inner-shell ionization. Given the recent developments in extending statistical correlation techniques to higher order correlations (involving four or more particles^25,33,34) and the progress in high-repetition-rate FELs,^8,35,36 we anticipate that this approach will yield a highly sensitive probe of the many-body fragmentation dynamics of highly charged polycations. Such a probe is the basis for Coulomb explosion imaging, generated by either deep single-photon inner-shell ionization of heavy elements³⁷ or multiphoton ionization in intense fields.^{27,35,36,38−40}

Methods

Experimental Section

Ion-imaging experiments were carried out at the SPring-8 Å Compact free electron LAser (SACLA, Japan), using the soft X-ray beamline (BL1). A schematic of the beamline and VMI³¹ ion spectrometer is given in previous work.^28,41 The XUV pulses used in the present study had a central photon energy of 95 eV (selected to coincide with the maximum of the I 4d photoionization cross section⁴²), an average bandwidth of ∼2%, a pulse duration of ∼30 fs,⁴³ a polarization parallel to the detector plane, and a repetition rate of 60 Hz. The mean pulse energy was determined to be 33 μJ, which was attenuated to 3.9 μJ at the molecular sample by the expected transmission of the beamline (90%) and a 0.6 μm Zr filter (13%). The XUV pulse energy was recorded on a shot-to-shot basis using a gas intensity monitor.⁴⁴ A Kirkpatrick-Baez mirror system focused the XUV pulses down to a spot size of approximately 10 μm (1/e²), resulting in a Gaussian intensity of 3.3 × 10¹⁴ W cm^–2.

Neat gaseous samples of 1-IP or 2-IP were expanded into the spectrometer chamber using a pulsed gas jet (general valve) and passed through a skimmer to produce a pulsed molecular beam. The molecular beam and XUV laser propagate parallel to the face of the detector, defined as the xy-plane and intersect at 45° within the center of the VMI spectrometer. XUV pulses site-selectively ionized target molecules above the iodine 4d edge. Electrostatic optics accelerated the nascent ions in the z direction along a time-of-flight (TOF) tube and onto the time- and position-sensitive detector, comprising a pair of stacked microchannel plates coupled to a hexanode delay line detector.

Covariance Analysis

To extract the relative momenta of ion pairs arising from the same fragmentation event, we employ 3D covariance imaging as described in ref (24). The inherent shot-to-shot fluctuation in the energy of the FEL pulses generated by self-amplified spontaneous emission will cause the yield of all species to rise and fall as one, introducing false contributions to the calculated covariance. The original method developed to correct this effect is partial covariance,^45,46 where a correction term that accounts for correlation between the signal of interest and the fluctuating parameter is included in the covariance calculation. The current work employs an alternative approach known as contingent covariance,^47,48 which gives an equivalent result but is more straightforward to implement, as it does not require the calculation of this correction term. Raw data were grouped into 10 subsets based on the FEL pulse energy distribution, covariance was calculated for each separately, and the resulting covariance maps were summed to give the final result.

Momentum filtering is regularly exploited in coincidence studies. For example, if the fragments of a dissociation together constitute the original molecule, the true coincidences can be isolated by selecting only those combinations of ions whose momenta sum to zero.⁴⁹ In our previous work,²⁸ we demonstrated the ability to isolate signals between the same pairs of ion species arising from different fragmentation channels by carefully constraining the momentum of one of the ions in the covariance calculation. The sequential and concerted fragmentation channels of tricationic 1/2-IP into I⁺ + C₂H⁺₄ + CH⁺₃ were respectively studied by selecting only those (I⁺, CH⁺₃) ion pairs for which the I⁺ momentum was above or below a defined threshold. Here, we apply a more advanced approach to disentangle the different sequential three-body breakup mechanisms of molecular dications that lead to the same product species. Specifically, we consider the sequential dissociation process where the primary step is a Coulomb explosion between two charged fragments

1

one of which is an unstable intermediate ion that further dissociates by ejecting a neutral fragment

2

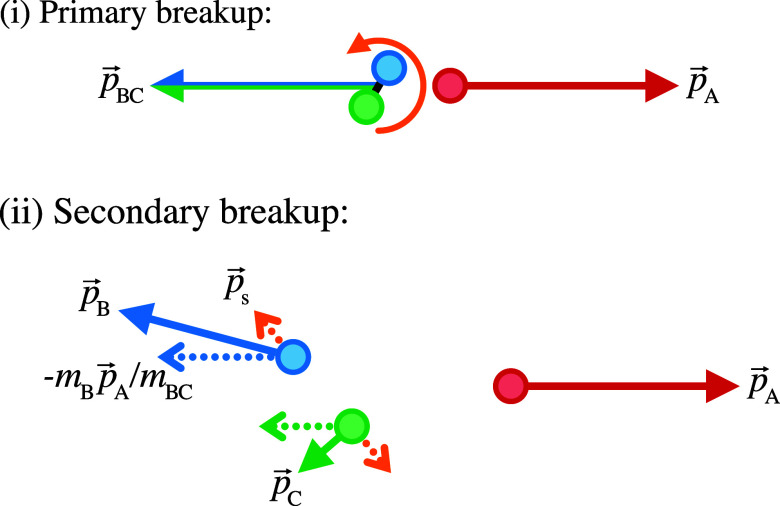
This process is illustrated schematically in Figure 1. The intermediate BC⁺ gains momentum equal and opposite to the primary product A⁺ during the initial step, which is then partitioned between the secondary products according to their masses. Neglecting the impulse of the secondary bond dissociation, which is expected to be significantly smaller than the primary step driven by Coulombic repulsion, the relationship between the momenta of the primary and secondary products can be approximated as

3

Hence, the signal in a covariance map corresponding to a specific fragmentation channel can be separated by applying the constraint that the momenta of the ion pair must obey eq 3, within some range, to account for the impulse of the secondary bond dissociation. Further details are provided in the Supporting Information.

Figure 1.

Schematic diagram for the three-body sequential dissociation scheme described in eqs 1 and 2. Panels (i) and (ii) illustrate the primary and secondary steps, respectively. Solid arrows are used to denote the momenta of the products and dotted-line arrows indicate contributions to the total momenta of the secondary products (B⁺ + C). The primary Coulomb explosion step induces rotation of the intermediate BC⁺, which, in the limit that the intermediate lifetime exceeds its rotational period, will randomly distribute the direction of the secondary dissociation impulse 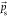relative to the recoil of the primary product (A⁺).

To demonstrate how our approach works, we consider the 2-fold covariance between the (I⁺, CH⁺₃) ion pair. This is plotted in a Newton diagram representation in panels a and b of Figure 2 for 1- and 2-IP, respectively. Here, the recoil direction of I⁺ is oriented along the positive x-axis, the relative momentum of CH⁺₃ is plotted in the upper half, and the relative momentum of the additional fragment(s), deduced through momentum conservation in this frame, is plotted in the lower half. The calculated covariance contains contributions from three fragmentation regimes: (I) sequential and (II) concerted three-body breakup of IP³⁺, which have been discussed in detail previously,²⁸ and (III, IV) sequential three-body breakup of IP²⁺. This latter mechanism involves cleavage of a C–I and C–C bond, but the order in which they occur gives rise to two distinct channels

III

IV

Figure 2.

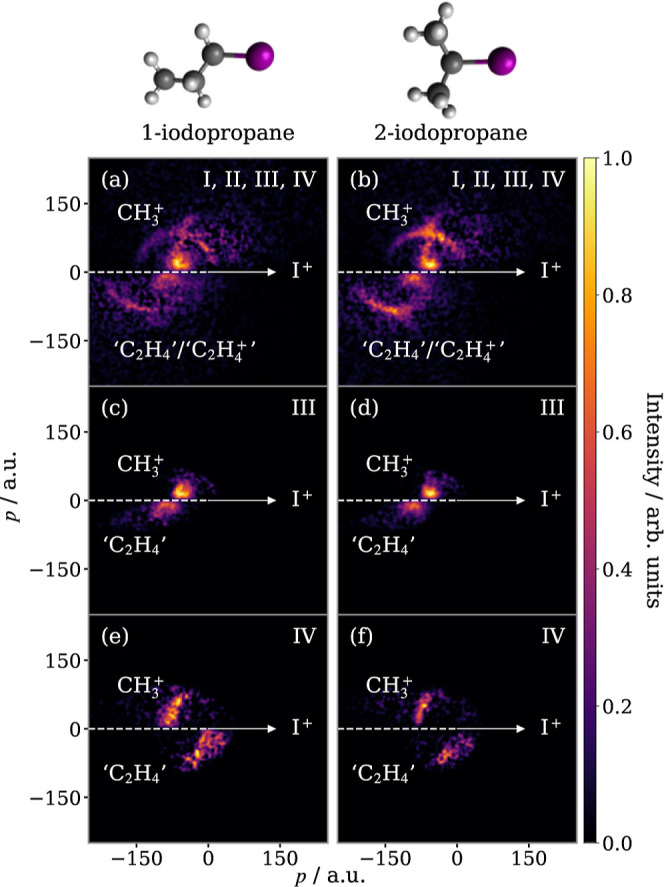
Newton diagrams for the breakup of (a) 1-IP^2+/3+ and (b) 2-IP^2+/3+ into (I⁺ + CH⁺₃ + C₂H₄/C₂H⁺₄). The correlation of I⁺ and CH⁺₃ has been calculated using a 2-fold contingent covariance analysis, wherein the momentum of the third fragment is deduced through momentum conservation in the center-of-mass (COM) frame. Three dissociation channels that contribute are²⁸ (I) sequential and (II) concerted three-body breakup of IP³⁺ and (III, IV) sequential three-body breakup of IP²⁺. In panels (c,d), the signals from the (III) sequential breakup of IP²⁺, where I⁺ is the primary fragment, have been separated while (e,f) show the isolated signals that correspond to (IV) sequential breakup of IP²⁺ with a primary CH⁺₃ product. Each panel is normalized separately.

Using the momentum constraint described above and assigning (A⁺ = I⁺, B⁺ = CH⁺₃), with a range of acceptance of 30 au (atomic units of momentum) to account for the impulse of the C–C bond fission, the signal from channel III can be isolated, as shown in panels c and d. (For a point of reference, an iodine atom with 1 eV of kinetic energy has a momentum ∼130 au.) Note that, although the propyl cation intermediate will be rotationally excited by the initial step, the momenta of both secondary products are roughly in the opposite direction to that of the primary I⁺ product, with only a small component along the vertical axis since the impulse of the primary Coulomb explosion step is much greater than that of the secondary bond dissociation step. The momenta of the secondary products along the horizontal axis are unequal because the momentum they maintain from the primary step is partitioned according to their masses. By exchanging the assignment of I⁺ and CH⁺₃ (i.e., A⁺ = CH⁺₃, B⁺ = I⁺), the covariance corresponding to channel IV is instead separated, shown in panels e and f.

Although the dynamics associated with the sequential breakup of the trication (I) show considerable dependence on the isomer, owing to the different rovibrational dynamics of the intermediate (see ref (28)), the sequential breakup of the dication (III, IV) gives rise to near-identical fragment momentum correlations for the two isomers. Since the initial step is a two-body Coulomb explosion, the outcome must necessarily be back-to-back recoil, in both cases. The rovibrational dynamics of the intermediate are expected to be different because of differing positions of the iodine atom relative to the plane of the carbon chain. However, as we will later demonstrate using simulation, when the dissociation of the intermediate releases little kinetic energy compared to the initial Coulomb explosion, the fragment momentum correlation is nearly identical for this pair of isomers.

Simulations

Classical trajectory calculations of point charges interacting under Coulomb’s law can provide a useful guide for interpreting Coulomb explosion images.^29,32,50,51 A model that assumes instantaneous fragmentation and purely electrostatic repulsion is generally only a good approximation for the Coulomb explosion of highly charged polycations, which fragment promptly into exclusively ionic products.⁵² However, through modifications that build on this basic framework, more complex fragmentation processes can be modeled, such as the three-body sequential breakup.^28,53,54 Here, we extend this methodology to simulate the three-body sequential breakup of a molecular dication, which yields ionic and neutral products.

The simulation is executed in two steps that replicate the primary and secondary fragmentation steps outlined in eqs 1 and 2 and illustrated in panels (i) and (ii) of Figure 1, respectively. The primary Coulomb explosion is initiated from the neutral ground-state geometry of the molecule, in its lowest energy, fully staggered conformation, and the charge on each fragment is located at its COM. We assume the limiting case where the intermediate lifetime is sufficiently long that the two fragmentation steps are isolated events. The ion trajectories are therefore propagated until they have approximately reached their terminal velocities. The intermediate ion is then replaced in space by the secondary ion fragment (the secondary neutral fragment is omitted as the experiment only detects charged species), with an additional velocity component added onto its recoil velocity to account for the impulse of the secondary bond dissociation. The magnitude of the velocity component is determined from the experimentally measured impulse associated with the secondary dissociation step. To simulate the rotation of the intermediate induced by the primary step, this velocity component is rotated. The axis of rotation is determined by considering an impulse along the broken bond, acting at the COM of the intermediate. The magnitude of the rotation is sampled from a uniform distribution to reflect the long intermediate lifetime relative to its rotational period.

Results and Discussion

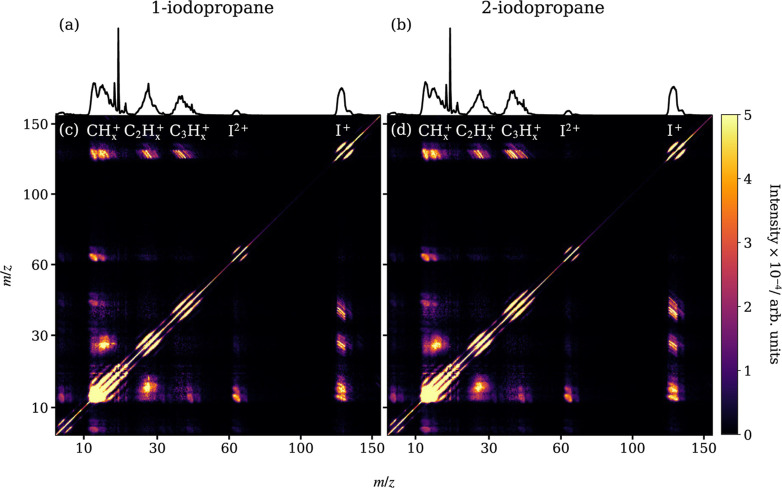
The TOF covariance maps, shown in Figure 3, reveal which pairs of ions are formed in the same fragmentation event. Note that the scale along each axis does not extend to zero as no covariances involving H⁺ were observed. H⁺ is formed with very high velocity, is mostly focused beyond the edges of the detector by the VMI ion optics, and is not detected. Displayed along the top edge of each panel is the mass spectrum measured for that isomer. The intense feature along the positive diagonal in each covariance map is the autocovariance, while the correlated ion signals appear as off-diagonal elements, with a negative gradient. This is because, for a pair of ions arising from a two-body breakup, if one is accelerated toward the detector, the other must be projected away.⁵⁵ This gives rise to several sharp lines of covariance between I⁺ and C₃H⁺_x, resolved by the number of hydrogen atoms remaining on the C₃H⁺_x ion. By contrast, the (I⁺, CH⁺₃) covariance feature is diffuse because it arises from many-body dissociation, in which significant momentum is carried by other (unidentified) heavy fragments.

Figure 3.

Mass spectra obtained for (a) 1-IP and (b) 2-IP. Contingent TOF covariance maps are shown for (a) 1-IP and (b) 2-IP. Note the nonlinear scaling of the m/z axes. Each covariance map is normalized separately.

The three-body fragmentation dynamics of parent trications into (I⁺ + CH⁺₃ + C₂H⁺₄) have previously been described in depth.²⁸ Here we focus on those fragmentation channels that yield only two heavy charged fragments. For each channel, the covariance between the pair of ionic products has been calculated by considering the momentum partitioning of the products, as outlined above. Assuming a uniform detection efficiency for all ionic fragments, the intensity of the covariance associated with a given fragmentation pathway is proportional to the yield of that process.⁵⁵ In Figure 4, the relative intensities for the set of covariance maps (shown in Figures S9–S11 of the Supporting Information) are plotted together. While the absolute detection efficiency for different ion species cannot easily be determined for these data, it is expected to be of similar magnitude for all those listed in Figure 4. Furthermore, the detection efficiency of each ion species is expected to be the same in the data sets recorded for each isomer as they were acquired under otherwise identical conditions.

Figure 4.

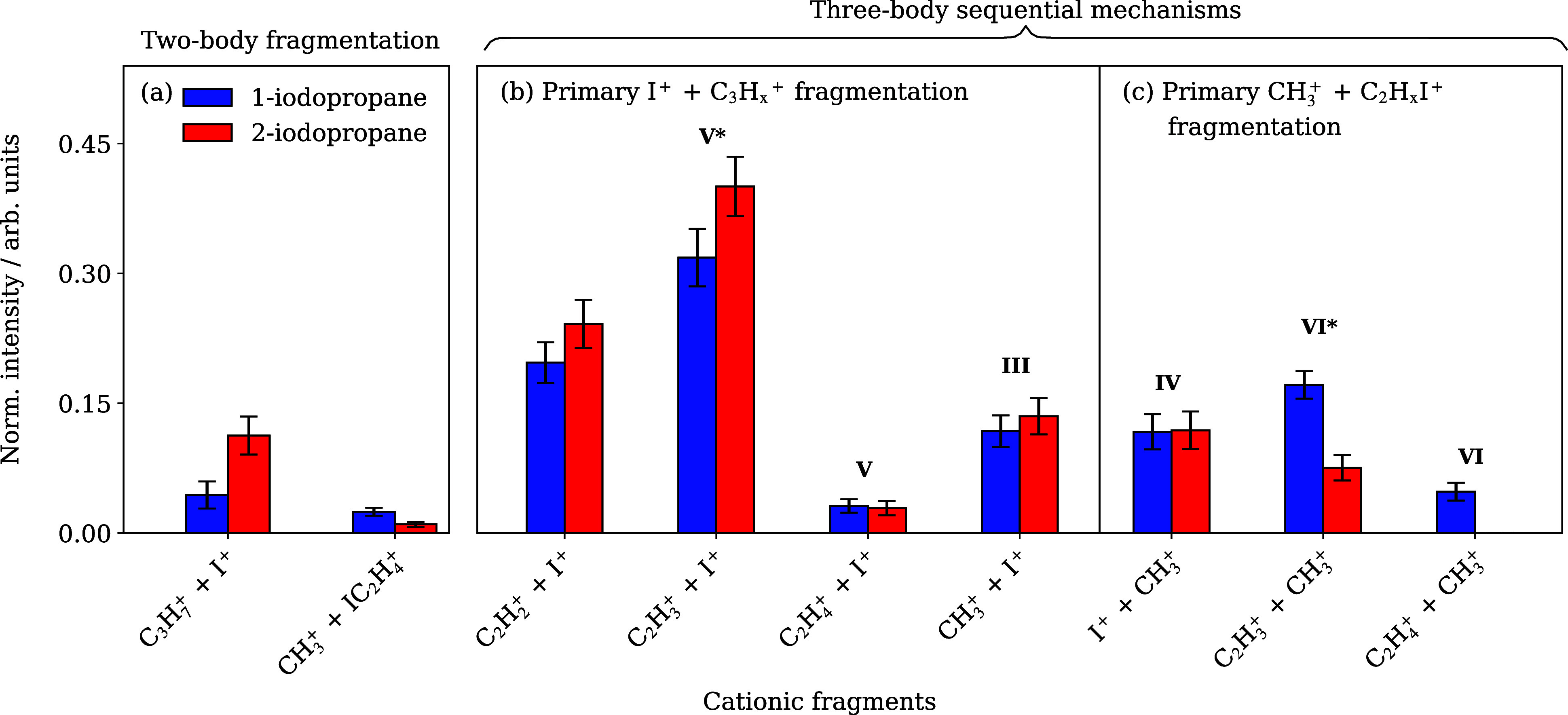
Integrated covariance intensity for all observed fragmentation pathways of the parent dication, including (a) two-body fragmentation and (b) three-body sequential fragmentation where the primary step is the Coulomb explosion into I⁺ + C₃H⁺₇ or (c) CH⁺₃ + C₂H₄I⁺. The data are normalized to the summed intensity of all channels for each isomer. No statistically significant covariance was observed for the (C₂H⁺₄, CH⁺₃) channel in 2-IP. Error bars are given by the standard deviation obtained from a bootstrap fitting method, performed on 100 sample sets of 50,000 experimental cycles. Individual channels of interest are discussed within the text and labeled accordingly, and covariance maps for all ion pairs are given in the Supporting Information.

The two-body breakup channels listed in panel (a) must correspond to the dissociation of the parent dication. 1-IP is likely to breakup via C–C bond cleavage or C–I bond cleavage, whereas breakup of 2-IP occurs predominantly via C–I bond cleavage. This can be attributed to differences between isomer geometries, which influence the range of charge generation and redistribution processes accessible through AM decay. Three-body breakup of the molecular dication is always observed to occur via a sequential mechanism involving cleavage of a C–I and a C–C bond, in either order, such as for channels III and IV. Following dissociation of the intermediate, either secondary product can retain the charge, which gives rise to another two distinct channels

V

VI

In panels b and c of Figure 4, these processes are separated by whether the primary step is the Coulomb explosion to (I⁺ + C₃H⁺₇) or (CH⁺₃ + C₂H₄I⁺). We note that no intensity for channel VI in 2-IP is listed in Figure 4c as no covariance signal was observed above the noise level, though this does not confirm that the channel does not occur for 2-IP.

Several ion pairs are listed in Figure 4b,c that presumably arise from the fragmentation of the parent molecule into more than three bodies and for which the initial charge state is uncertain. These have been included because they act as pseudo-three-body processes and show fragmentation dynamics comparable to the breakup of parent dications. For example, consider the fragmentation pathway that yields (CH⁺₃ + C₂H⁺₃). Both I and H are unaccounted for, though it cannot be determined from the data whether they are bound or isolated, i.e., whether the process is three- or four-body. We label this channel VI* as our analysis suggests that the fragmentation mechanism is analogous to that of channel VI. If we compare the fragment momentum correlations for this pair of channels (see Figure S6 of the Supporting Information), we find that they are similar. This indicates that if H is ejected in the breakup into (CH⁺₃ + C₂H⁺₃), though we cannot determine at what point in the sequential mechanism this occurs, the nuclear dynamics are not meaningfully altered, i.e., the dissociation may be treated as pseudo-three-body. Similarly, if any other subtle dynamics are involved in channel VI*, for example H migration, our experiment is not sensitive to them.

As discussed in connection with Figure 3, because not all H⁺ ions reach the detector, there is also the possibility that channel VI* produces H⁺ and therefore corresponds to the breakup of a parent trication. Because H is so light relative to the other fragments, if a proton is ejected prior to or simultaneously with the Coulomb explosion into (CH⁺₃ + C₂H₃I⁺), it is not expected to significantly affect the kinetic energy of other fragments or meaningfully alter the dynamics compared to the breakup of the parent dication via channel VI.

The C₂H_yI⁺ intermediate can, in theory, fragment by C–I or C–C bond cleavage. However, no significant covariance was observed between pairs of ions that would arise from secondary C–C bond cleavage, e.g., (CH⁺₃, CH_xI⁺) or (CH⁺₃, CH⁺_x). Notably, for 1-IP, several other possible fragmentation pathways could occur via primary cleavage of a C–C bond closer to iodine (see Figure S1 in the Supporting Information), but no such processes were observed. Because significant (I⁺, CH⁺_x) and (C₂H⁺_y, CH⁺_x) covariance is only observed for x = 3, it implies that (in the absence of H migration) the C–C bond furthest from the iodine atom is cleaved in the primary step, and hence breakup into CH⁺₃ + C₂H_yI⁺ is a more favorable process. For 2-IP, cleavage of either C–C bond as the primary step also yields CH⁺₃ + C₂H_yI⁺.

Primary I⁺ + C₃H⁺₇ Fragmentation

Initial dissociation of the molecular dication by ejection of I⁺ is the main pathway for both isomers. This is unsurprising given that ionization occurs site-selectively at iodine. The fact that no significant isomer-dependent intensity is observed for any of the channels listed in Figure 4b suggests that the dissociation dynamics are similar for the C₃H⁺_x intermediates and independent of the parent isomer. This behavior could arise for several reasons. For example, the two isomeric forms of C₃H⁺₇ could interconvert through H migration prior to secondary fragmentation.

The Newton diagrams for the sequential three-body breakup of the molecular dication via channel III, which gives rise to a pair of (I⁺, CH⁺₃) ions, have been reproduced in Figure 5a,b. To extract the total kinetic energy release of the secondary dissociation step (KER_s), we transform into the native frame²¹ of this step, which is the COM frame of the C₃H⁺₇ intermediate. Mathematically, this is performed by calculating the momenta imparted to the secondary fragments from the first dissociation step using eq 3 and subtracting these contributions. The result is the set of Newton diagrams plotted in Figure 5c,d. The measured mean KER_s, determined directly from the momenta of the secondary fragments in this frame, is equal within errors for the pair of isomers at 0.22 ± 0.08 and 0.15 ± 0.06 eV for 1-IP and 2-IP, respectively. The high uncertainty in these values derives from the limited momentum resolution of the VMI spectrometer (see the Supporting Information for details).

Figure 5.

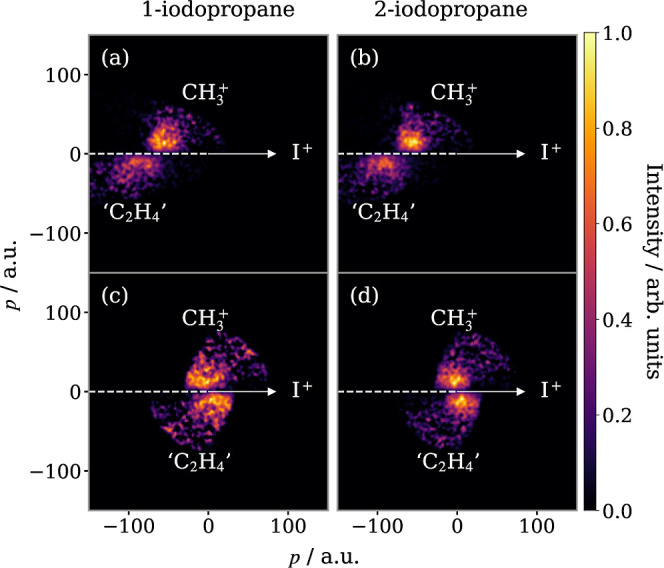
Newton diagrams for channel III—the sequential breakup of 1-IP²⁺ (left column) and 2-IP²⁺ (right column) that yields I⁺ + CH⁺₃ and involves the Coulomb explosion into I⁺ + C₃H⁺₇ as the primary step. Fragment momenta are plotted in the COM frame of the parent ion in panels (a,b) and in the COM of the C₃H⁺₇ intermediate in panels (c,d), i.e., the native frame of the secondary dissociation step. Each panel is normalized separately.

The three-body sequential breakup that yields a pair of (I⁺, C₂H⁺₃) ions is, by contrast, an example of the charge remaining on the ethyl fragment following the breakup of the propyl intermediate. The mechanism for this fragmentation pathway is equivalent to channel V, with the additional loss of H/H⁺ or the formation of CH₄ doing little more than slightly blurring the covariances presented in this paper, hence we refer to it as channel V*. From Figure 4b, it is apparent that channel V* is far more prominent than channel V. Corresponding Newton diagrams for channel V* are analogous to those obtained for channel III and can be found in Figure S10 of the Supporting Information. The total kinetic energy release of the primary Coulomb explosion (KER_p) for channels III and V* is equal, measured at 4.6 ± 0.5/5.0 ± 0.4 eV for 1/2-IP, where the uncertainty in each of these values reflects the standard deviation of a Gaussian distribution. Because the Coulomb explosion product momenta are sensitive to the charge separation, assuming purely Coulombic repulsion, this implies an equivalent charge distribution in the molecular ion leading to both pathways.

The observed KER_s for channel V* (0.17 ± 0.07 eV for 1-IP and 0.15 ± 0.06 eV 2-IP) are within the error of the values obtained for channel III. While it is difficult to comment on how the dynamics of channels III and V* compare due to the large errors associated with the extracted values, it is assumed that the same C–C bond in the propyl cation intermediate is broken in both processes. Because the charge is located on different secondary fragments, it implies the involvement of different electronic states, which may be populated directly from different AM decay processes or through nonadiabatic effects en route to dissociation. Though the similar KER_p values suggest that charge is initially distributed similarly on the propyl intermediate, it can redistribute differently during the lifetimes of the corresponding populated excited states. A highly vibrationally excited intermediate ion in a given electronic state could also decay via various pathways. Ultimately both processes may play a role.

Primary CH⁺₃ + C₂H₄I⁺ Fragmentation

Sequential three-body breakup via the Coulomb explosion into CH⁺₃ + C₂H₄I⁺ is generally less common than sequential three-body breakup via the Coulomb explosion into I⁺ + C₃H⁺₇. The occurrence of channel VI, which produces a (CH⁺₃, C₂H⁺₄) ion pair and a neutral iodine fragment, at first sounds surprising, given the very high cross section for I 4d ionization at 95 eV.⁴² However, while the initial core hole generated by I 4d ionization is well-localized, AM decay can populate a broad range of electronic and internal energy states of the resultant dication. Given the rapid rate of AM decay relative to photofragmentation, it is the character of these dication states that dictates the fragmentation dynamics and thus product species. Prior work has demonstrated that, in some cases, the dication fragmentation dynamics are largely independent of the initial core-hole site, instead being determined by the electronic character of the two valence-hole states of the dication³ or the partitioning of internal energy among vibrational modes.⁵⁶

It is also possible that dications that give rise to these photofragmentation dynamics are formed by other photoionization processes not involving I 4d ionization, such as single-photon double ionization⁵⁷ or successive single (inner) valence ionizations. However, the cross sections for these processes would be expected to be significantly lower than that for I 4d ionization, followed by single AM decay. For instance, Olney et al. previously reported a photoabsorption cross section of ∼30 Mb at 95 eV in CH₃I, with an estimated contribution from valence photoionization of just ∼1 Mb.⁵⁸ The photoabsorption cross section of CH₄ at this photon energy is ∼0.5 Mb,⁵⁹ and the contribution of single-photon double ionization relative to single ionization is believed to be on the order of 1%.⁶⁰ As such, the prominent photofragmentation channels observed from the molecular dication (including those yielding neutral iodine fragments) are most likely initiated by I 4d ionization. Future observation of photoelectrons and/or AM electrons produced in correlation with these fragment ions would provide unambiguous evidence for the precise photoionization process leading to these fragmentation channels.

Channels VI and VI* are the only sequential three-body breakup channels in Figure 4 that exhibit significantly different intensities for the two isomers. Channel VI is an insignificant pathway for 2-IP but is common for 1-IP. It is difficult to reason why this should be the case with the available information. If, following the primary breakup step, the charge on the C₂H_yI⁺ intermediate is located on the C that has cleaved a bond, this would place the charge further from the iodine substituent for the case of 1-IP and could make the subsequent breakup to yield a neutral iodine cofragment more likely. Ultimately, the dissociation of the dications of both isomers likely takes place on different potential energy surfaces, with topography influenced by various factors that determine the final quantum yield of the processes involved.

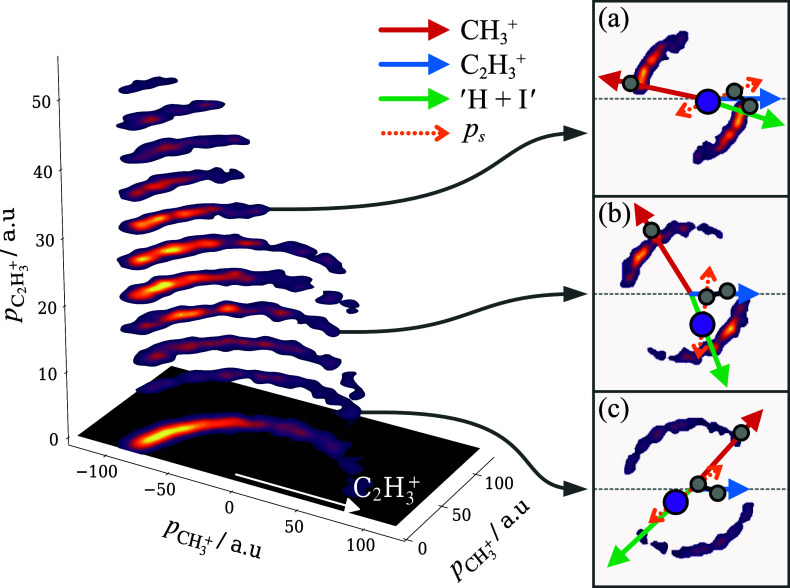
As discussed earlier, channel VI* yields (CH⁺₃ + C₂H⁺₃) by an equivalent mechanism to channel VI, as the loss of H/H⁺ or formation of HI does not measurably alter the dynamics. Again, this channel is more prominent in 1-IP than 2-IP. For both isomers, channel VI* is a more significant dissociation pathway than channel VI. Perhaps this is because the loss of neutral iodine is stabilized by the formation of HI, although the current experiment is insensitive to the nature of the neutral fragment(s) formed. Newton diagrams for channel VI* with the primary CH⁺₃ product as the reference species are shown in panels a,b of Figure 6. Due to the large mismatch in the mass of the secondary products, C₂H⁺₃ retains only a small amount of momentum from the initial Coulomb explosion event, the result being that its momentum is localized around the origin. It is helpful to instead construct the Newton diagrams by selecting C₂H⁺₃ as the reference ion, as shown in panels c,d. This representation makes it easier to visualize the dynamics, as the CH⁺₃ ions have greater momenta, which are better resolved by the spectrometer and offer a better comparison with simulated results (covered in the following section).

Figure 6.

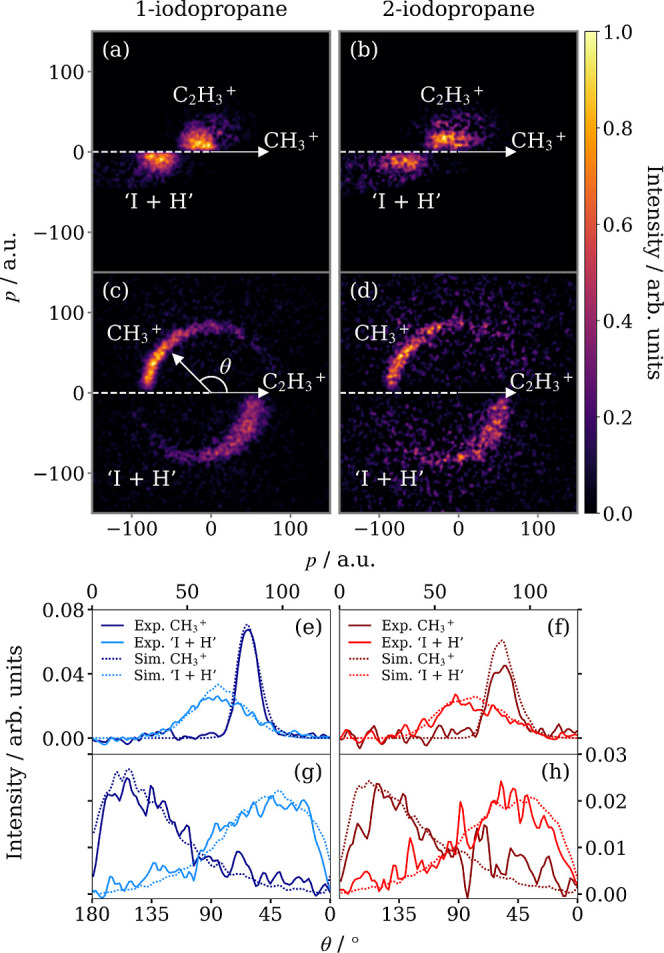
Newton diagrams for channel VI*—the sequential breakup of 1-IP²⁺ (left column) and 2-IP²⁺ (right column), which yields CH⁺₃ + C₂H⁺₃ and involves the Coulomb explosion into CH⁺₃ + C₂H₄I⁺ as the primary step. Panels (a,b) display the momentum distribution of C₂H⁺₃ relative to the recoil direction of CH⁺₃, and vice versa in (c,d). Each panel is normalized separately. Below are displayed the integrated CH⁺₃ and ‘I + H’ momentum distributions (e,f) and angular distributions relative to the recoil direction of C₂H⁺₃ (g,h), normalized to unit area. Experimental data, shown by solid lines, are overlaid with data simulated using a classical model of the sequential dissociation process, indicated by dashed lines.

The CH⁺₃ feature in panels c and d is a wide arc with a uniform radius, as shown by the integrated momentum distributions (solid lines) in e and f. The CH⁺₃ momentum is determined solely by the primary process, whereas the ‘I + H’ momentum distribution is broader because it is the sum of two components, which are not aligned (illustrated in Figure 1). The C₂H₄I⁺ intermediate is rotationally excited in the initial dissociation event and, if its lifetime far exceeds its rotational period, it will be randomly oriented relative to its recoil direction when it dissociates. However, this would not distribute the secondary ethyl and iodine products over a uniform angular range relative to the primary methyl product if the secondary dissociation barely perturbs the iodine cofragment. In such a dissociation, the iodine cofragment retains the majority of the momentum of the intermediate, and so its recoil direction remains roughly back-to-back with CH⁺₃, as seen in panels a and b of Figure 6. The same impulse has a much greater impact on the trajectory of C₂H⁺₃ as it imparts only slightly less momentum than the fragment retains as a fraction of the intermediate’s momentum. This is not enough to reverse the direction of travel of C₂H⁺₃ but can significantly redirect it, resulting in a broad angular distribution (panels g and h) that peaks at ∼180^°.

Simulating Sequential Fragmentation Dynamics

To support the assigned fragmentation mechanism for channel VI*, a series of classical simulations were conducted using the model described in the Methods section. In panel a of Figure 7, the experimental (C₂H⁺₃, CH⁺₃) Newton diagram covariance for 1-IP has been reproduced as a function of recoil angle relative to C₂H⁺₃. The neighboring panels are the outputs of the simulation as successive modifications are implemented, which incorporate more tunable parameters. To fully reproduce the experimentally observed dynamics, values for many of these parameters were determined from the experimental data.

Figure 7.

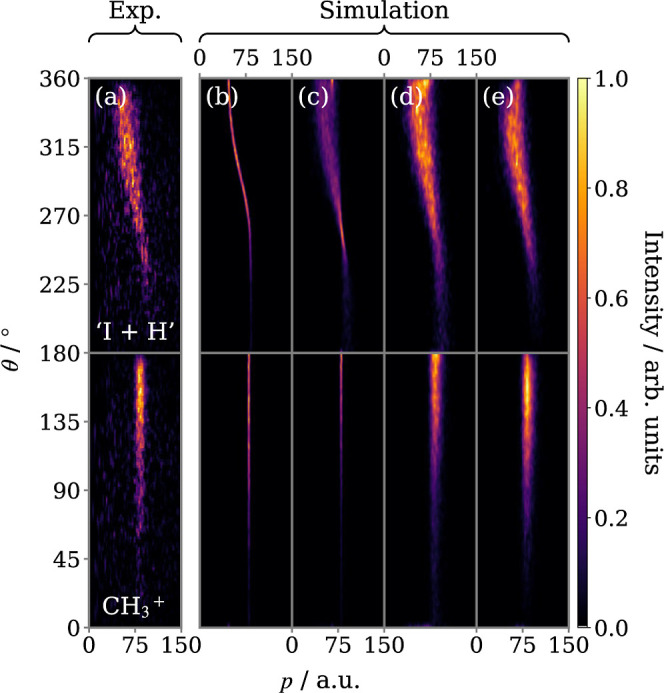
(a) Newton diagram from Figure 6c displayed in polar coordinates, where θ is the angle relative to the recoil direction of C₂H⁺₃. (b–e) Simulated covariance maps for channel VI*—the sequential breakup of 1-IP²⁺, which yields CH⁺₃ and C₂H⁺₃ and involves the Coulomb explosion into CH⁺₃ + C₂H₄I⁺ as the primary step. (b) was produced by the model outlined in the Methods section, (c) incorporates a distribution for the secondary dissociation KER, (d) uses an effective charge separation distribution for the primary step, and (e) also includes a small degree of out-of-plane rotation.

A Gaussian fitting to the experimental data in the native frame of the C₂H₄I⁺ intermediate was used to extract a secondary dissociation impulse (p_s) of 18 ± 9 au in the first iteration of the model (Figure 7b), the mean p_s was used to determine the magnitude of the velocity component v_s superimposed onto the secondary ion product to simulate the dissociation of C₂H₄I⁺. A demonstration of how the simulated result varies as a function of p_s is given in Figure S7 of the Supporting Information. Even in this simple form, the model captures the form of the angular distribution well. This supports our interpretation of the dissociation mechanism, i.e., the intermediate is randomly oriented at the instant of secondary breakup, but the secondary products are not uniformly distributed relative to the recoil direction of the primary product as the greater portion of their momenta derives from the primary Coulomb explosion step.

However, because the KERs of both steps are single-valued, they do not reproduce the momentum distribution of the products. In panel c of Figure 7, the p_s width has been used to generate a v_s distribution. A second Gaussian fitting to the experimental CH⁺₃ momentum distribution in Figure 6e was used to calculate a KER_p of 3.8 ± 0.3 eV for the Coulomb explosion event and combined with Coulomb’s law to calculate an effective separation of the charges on the CH⁺₃ and C₂H₄I⁺ moieties of 3.8 Å. This effective separation has been incorporated into the simulation in panel d.

Finally, to account for potential rotational excitation of the intermediate about different axes relative to the rotation induced by the initial fragmentation, we applied a normal distribution of rotation with a narrow width of 10° about a perpendicular rotational axis. This drives the angular distribution toward 90/270° (panel e), reproducing the decreased intensity at 180/360° in the experimental plot. Integrated angular and radial distributions from the final simulation are overlaid with the experimental data in panels e and g of Figure 6 and show strong agreement. Despite the simplicity of such a model, it is possible to recreate the fragmentation dynamics of a relatively low-charge molecular polycation using parameters directly obtained from experimental data. This is a showcase for the general applicability of the classical point charge model for simulating Coulomb explosion processes, even in the low parent ion charge-state regime.

The model was also used to simulate the same fragmentation channel in 2-IP, with analogous parameters extracted from the 2-IP experimental data used as input (see Figure S8 in the Supporting Information). The output is overlaid with experiment in panels f and h of Figure 6 and, though the 2-IP experimental data for this fragmentation channel has limited statistics compared to 1-IP, the agreement between experimental and simulation is, once again, excellent. It is worth remarking again on the resemblance between fragment correlations for 1- and 2-IP²⁺, which has been observed in all fragmentation channels discussed here. The same resemblance is observed in the simulated data. Interestingly, it was important to consider the different axes of rotation of the intermediate for each isomer, otherwise the predicted angular distributions were very different. This suggests that it is in spite of different intermediate dynamics that this pair of isomers produces closely matching final fragment momentum correlations.

Direct Imaging of Product Momentum Exchange

Our approach of considering the momentum partitioning between an ion pair (used as an input for a covariance calculation) has so far been applied to disentangle signals arising from the same pairs of ion species generated by different fragmentation channels. This can be taken a step further and used to directly interrogate the dynamics of molecular fragmentation more generally. To demonstrate, we again consider the sequential breakup of 1-IP²⁺ via a Coulomb explosion into CH⁺₃ and C₂H₄I⁺, producing the (CH⁺₃, C₂H⁺₃) pair. 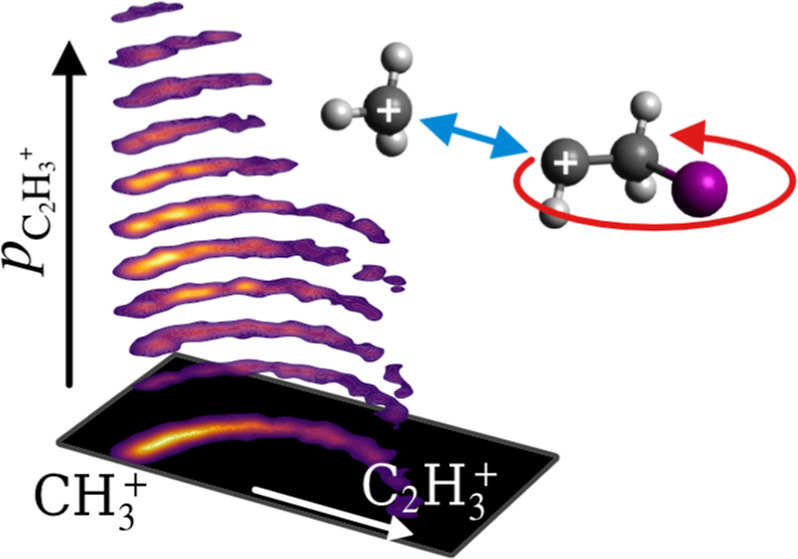In Figure 8, the momenta of the primary CH⁺₃ products (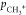), relative to secondary C₂H⁺₃, are plotted as a function of the magnitude of the momentum of this reference ion (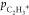). The (CH⁺₃, C₂H⁺₃) data were split into subsets based on the momentum of C₂H⁺₃, and each slice was calculated from a different subset. The sum of these slices is projected onto the xy-plane and exactly equals the data plotted in the top half of Figure 6.

Figure 8.

Momentum distribution of CH⁺₃ relative to the recoil direction of C₂H⁺₃ for channel VI*—the sequential breakup of 1-IP²⁺ involving Coulomb explosion into CH⁺₃ + C₂H₄I⁺ as the primary step. Ascending vertical slices correspond to increasing absolute momentum of C₂H⁺₃. The projection onto the xy-plane is the sum of these vertical slices. Complete Newton diagrams are shown for several slices, with cartoons superimposed to demonstrate how the rotation of the intermediate prior to secondary fragmentation produces the observed fragment momentum distribution. Vectors are shown in the same colors as their corresponding counterparts in Figure 1.

When the C₂H⁺₃ has minimal momentum (the lowest slice), the angular distribution of CH⁺₃ (θ_{(C2H3⁺,CH3⁺)}) sweeps out a broad range. As the momentum of the secondary products increases, the angular distribution becomes focused toward 180°. This shift is a direct visualization of the rotation of the intermediate. Due to the long lifetime of C₂H₄I⁺ relative to its rotational period, each intermediate ion is effectively randomly orientated relative to the recoil direction of CH⁺₃ at the instant of secondary dissociation. However, the exact orientation of the intermediate affects the momentum exchange in the secondary products. To help illustrate this, complete Newton diagrams for several slices are shown, with schematic vector diagrams overlaid.

The relationship between θ_{(C2H3⁺,CH3⁺)} and 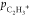is not directly linear because the momentum release of the secondary dissociation takes a range of values. For the orientation of the intermediate illustrated in panel c, if p_s is large, it is enough to redirect the trajectory of C₂H⁺₃, resulting in a pair of ions that recoil at an acute angle. If p_s is small, the momentum that C₂H⁺₃ retains from the primary dissociation dominates, and the ion’s trajectory remains roughly opposite to CH⁺₃. The angular distribution contracts toward 180° in the upper slices because C₂H⁺₃ can only be produced with maximum momentum when p_s is at its greatest and the intermediate is orientated such that p_s aligns with the initial direction of travel. While, fundamentally, the Newton diagrams in Figure 6a,c contain the same information as Figure 8, this representation provides a more intuitive visualization of nuclear dynamics and direct insight into the relationships between fragment momenta and relative recoil angle.

Once more, our arguments are corroborated by simulation. To give a clear-cut comparison of the experimental and simulated data, the 3D covariance map in Figure 8 has been transformed into a 2D representation by radially integrating each slice to produce the θ_{(C2H3⁺,CH3⁺)} distribution as a function of 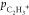, shown in the top panel of Figure 9. In the panel below is the simulated data, first presented in Figure 7e, now shown in the same representation. It captures the general form of the experimental data well, with a broad distribution that tapers toward 180° with increasing 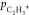and also reproduces the maxima around ∼160^° and ∼30 au. Our simple model of the fragmentation process therefore remains a good approximation that offers detailed insight into the sequential breakup dynamics.

Figure 9.

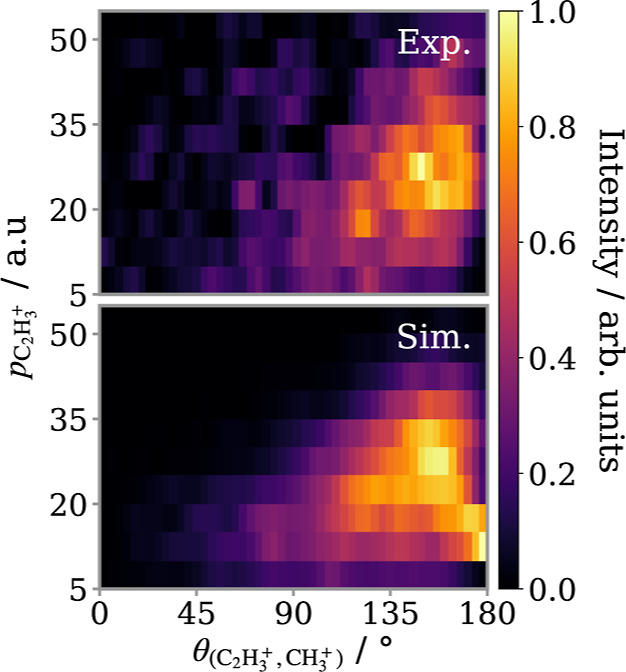
(a) Angular distribution of CH⁺₃ relative to the recoil direction of C₂H⁺₃ as a function of the absolute momentum of C₂H⁺₃, integrated from the vertical slices in Figure 8. (b) Simulated data set, presented in Figure 6e,g, processed in the same manner.

Conclusions

We have demonstrated the utility of incorporating considered momentum constraints into covariance imaging analysis and the high sensitivity such an approach can provide to details of the dissociation dynamics. By exploiting the expected momentum partitioning between the products of a three-body breakup, we have disentangled the wide array of different fragmentation channels for 1- and 2-IP dications. Taking this approach further, we studied the momentum exchange relationship between the products of a sequential breakup, by calculating the covariance map as a function of the momenta of one of the products. The results provide direct insight into how the rotational dynamics of the intermediate manifests in the measured signal. Fragment momentum correlation maps were interpreted with the aid of classical simulations. Despite their simplicity, the simulations reproduced the experimental results with impressive accuracy, demonstrating the worth of a classical point charge model for simulating a variety of Coulomb explosion processes.

In the present work, the molecular dication predominantly dissociates to give I⁺. However, the significant and isomer-dependent intensity observed for covariances between CH⁺₃ and C₂H⁺₃ (generated with a neutral iodine-containing cofragment) shows that the range and probability of different charge redistribution processes occurring depends on the geometry of the target molecule. A future study would benefit from recording the AM electrons in correlation with the fragment ions in order to be sensitive to the excited electronic states of the dication accessed by the ionization process. This electronic information would allow the relationship between ionization and fragmentation dynamics to be explored. The dissociation pathways could then be analyzed in terms of energetics, concerning the internal energy partitioning in the primary and secondary products and the barriers to dissociation. In particular, this could aid in explaining the branching ratios of the various channels listed in Figure 4 and hence the reasons for the isomeric differences. Similarly, photoelectron-photoion coincidence experiments ionizing above the carbon K-edge would likely shed further information on the extent of any site-selectivity in the dication fragmentation dynamics.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.4c00999.

• Diagram of all potential fragmentation pathways on the parent dication; details on covariance calculation; method for determining the momentum resolution; comparison of (CH⁺₃, C₂H⁺_3/4) covariance maps for 1-IP; simulation results as a function of secondary dissociation impulse; simulation of channel VI* in 2-IP²⁺; and Newton diagram covariance maps for all pairs of product ions (PDF)

Author Contributions

^⊥ T.W. and J.W.M. contributed equally.

The authors declare no competing financial interest.