Abstract
Multivariate analysis is becoming central in studies investigating high-throughput molecular data, yet, some important features of these data are seldom explored. Here, we present MANOCCA (Multivariate Analysis of Conditional CovAriance), a powerful method to test for the effect of a predictor on the covariance matrix of a multivariate outcome. The proposed test is by construction orthogonal to tests based on the mean and variance and is able to capture effects that are missed by both approaches. We first compare the performances of MANOCCA with existing correlation-based methods and show that MANOCCA is the only test correctly calibrated in simulation mimicking omics data. We then investigate the impact of reducing the dimensionality of the data using principal component analysis when the sample size is smaller than the number of pairwise covariance terms analysed. We show that, in many realistic scenarios, the maximum power can be achieved with a limited number of components. Finally, we apply MANOCCA to 1000 healthy individuals from the Milieu Interieur cohort, to assess the effect of health, lifestyle and genetic factors on the covariance of two sets of phenotypes, blood biomarkers and flow cytometry–based immune phenotypes. Our analyses identify significant associations between multiple factors and the covariance of both omics data.
Keywords: statistics, covariance, correlation, multivariate analysis, biomarkers
Introduction
Human cohorts commonly collect high-dimensional phenotypic data, including high-throughput omics, extended medical information and biomarkers [1, 2]. A variety of multivariate approaches have been developed to leverage this wealth of data [3–6]. The joint analysis of multiple outcomes can increase statistical power to detect associations [7, 8], help in deciphering complex biological processes through clustering approaches [9] or improve the prediction accuracy of an outcome of interest [10]. Regarding association testing, existing methods and application have mostly focused on testing the impact of predictors of interest on the mean of a multivariate outcome, typically using a composite null hypothesis such as implemented in a multivariate ANOVA (MANOVA). Conversely, methods to investigate other components of multivariate outcomes remain sparse. One of such components of multivariate outcomes is correlation, which is commonly present in omics data. Although methods to investigate predictors associated with the correlation between multiple outcomes exist [11–14], their performance and robustness have not been assessed, and their efficiency in large-scale agnostic screenings remains unknown. Moreover, they carry substantial inherent limitations, including restriction to binary factors and no adjustment for covariates.
Here, we present a new approach, named MANOCCA (Multivariate ANalysis Of Conditional Covariance), that enables the identification of both categorical and continuous predictors associated with changes in the covariance matrix of a multivariate outcome while allowing for covariates adjustment. We first introduce the key principles and the main characteristics of the approach and demonstrate that, in most realistic scenarios, MANOCCA can outperform existing approaches showing stronger power and robustness. We then describe the challenges faced when analysing high-dimensional data and present a robust solution based on principal components analysis (PCA). We next investigate the power of MANOCCA conditional on alternative parametrizations, providing guidelines for real data application across various settings. Finally, we illustrate the method by studying health, lifestyle and genetic factors associated with variability of blood biomarkers and flow cytometry-based immune phenotypes using data from 1000 healthy subjects from the Milieu Intérieur (MI) cohort.
Methods
The MANOCCA approach
Previous work [15] showed that variability in the correlation between two standardized outcomes 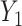 and
and 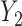 can be investigated through the element-wise product of those outcomes. The Pearson correlation coefficient between
can be investigated through the element-wise product of those outcomes. The Pearson correlation coefficient between 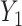 and
and 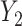 is expressed as
is expressed as 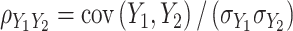 , with
, with 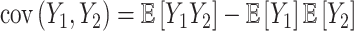 . For standardized outcomes and a sample size
. For standardized outcomes and a sample size  , it can be re-expressed as the average of the element-wise product across individuals:
, it can be re-expressed as the average of the element-wise product across individuals:  . It follows that the effect of a predictor
. It follows that the effect of a predictor  on
on 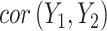 can be tested using a standard least-squares regression framework where
can be tested using a standard least-squares regression framework where  is treated as a predictor and the product
is treated as a predictor and the product 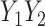 as the outcome. One can easily demonstrate that, under reasonable assumptions, this test is independent of mean and variance effect. Consider the following models:
as the outcome. One can easily demonstrate that, under reasonable assumptions, this test is independent of mean and variance effect. Consider the following models: 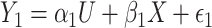 and
and 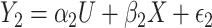 , where
, where 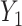 and
and 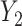 are random variables correlated through an unmeasured normally distributed variable
are random variables correlated through an unmeasured normally distributed variable 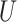 , and depend linearly on a binary predictor
, and depend linearly on a binary predictor 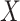 , inducing an effect on the means of
, inducing an effect on the means of 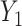 and
and 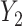 . The conditional covariance between
. The conditional covariance between 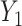 and
and 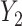 can be expressed as
can be expressed as 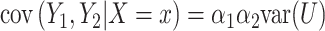 and does not depend on
and does not depend on 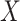 . Consider the alternative models:
. Consider the alternative models: 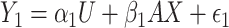 and
and 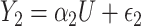 , where
, where 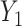 and
and 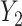 are correlated, and the variance of
are correlated, and the variance of 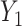 depends on the product of a latent continuous variable
depends on the product of a latent continuous variable 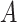 multiplied by the binary predictor
multiplied by the binary predictor 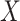 . The conditional covariance can again be expressed as
. The conditional covariance can again be expressed as 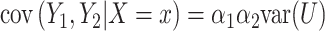 and does not depend on
and does not depend on 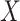 . Finally, consider the models:
. Finally, consider the models: 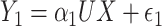 and
and 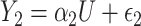 , where
, where 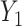 and
and 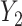 are correlated, with the strength of the correlation depending on the predictor
are correlated, with the strength of the correlation depending on the predictor 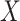 . The covariance can now be expressed as
. The covariance can now be expressed as  and does depend on
and does depend on 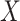 . Further details on those approximations are provided in the Supplementary Notes.
. Further details on those approximations are provided in the Supplementary Notes.
The approach can easily be extended to more than two outcomes by deriving an 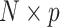 matrix of products between centered outcomes, defined as
matrix of products between centered outcomes, defined as 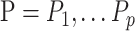 , with
, with 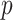 , the number of products, equals
, the number of products, equals 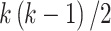 where
where 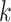 is the number of outcomes and
is the number of outcomes and 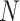 the sample size. The association between a predictor
the sample size. The association between a predictor 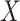 and
and 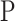 can then be derived by applying a standard two-way analysis of variance (MANOVA), that is
can then be derived by applying a standard two-way analysis of variance (MANOVA), that is 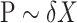 . While valid, this approach is limited to situations where the effective sample size
. While valid, this approach is limited to situations where the effective sample size 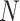 is substantially larger than the number of products
is substantially larger than the number of products 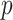 . When this criterion is not met, we use PC analysis to reduce the dimension of the product matrix and use the top
. When this criterion is not met, we use PC analysis to reduce the dimension of the product matrix and use the top 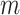 PCs to form an
PCs to form an 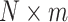 matrix
matrix 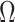 used as input in our test. Given the independence between the PCs, we first considered using a sum of univariate PC tests to form a joint test; however, this approach was not calibrated (see Results and Figures S1 and S2). Instead, we used a MANOVA, that is,
used as input in our test. Given the independence between the PCs, we first considered using a sum of univariate PC tests to form a joint test; however, this approach was not calibrated (see Results and Figures S1 and S2). Instead, we used a MANOVA, that is, 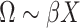 . For fast computation, the joint effect estimates
. For fast computation, the joint effect estimates 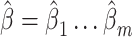 of association between each PC
of association between each PC 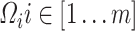 and the predictor
and the predictor 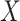 are first derived using a single matrix operation:
are first derived using a single matrix operation: 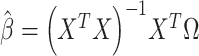 . The Wilks’ lambda statistics,
. The Wilks’ lambda statistics, 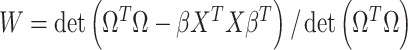 is derived in a second step. Under the null hypothesis of no association,
is derived in a second step. Under the null hypothesis of no association, 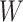 follows a Fisher distribution
follows a Fisher distribution 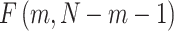 . Figure 1 presents an overview of the steps for applying the approach. Note that the Wilk’s Lambda statistics can be sensitive to the normality assumption of the outcome data analysed [16]. However, as discussed further in the Results section, we implemented in the final version of MANOCCA a systematic rank-inverse normal transformation of the input data ensuring that the normality assumption is met.
. Figure 1 presents an overview of the steps for applying the approach. Note that the Wilk’s Lambda statistics can be sensitive to the normality assumption of the outcome data analysed [16]. However, as discussed further in the Results section, we implemented in the final version of MANOCCA a systematic rank-inverse normal transformation of the input data ensuring that the normality assumption is met.
Figure 1.
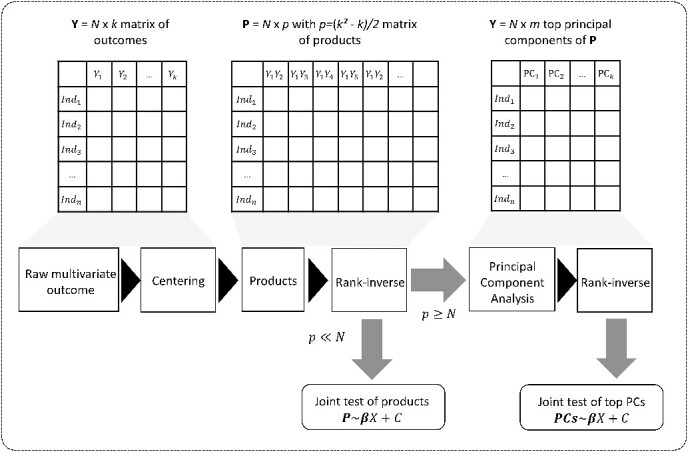
Overview of the MANOCCA approach. Starting with a multivariate outcome matrix of 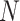 samples and
samples and 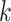 variables, the data are first centred. The pairwise product of each of the
variables, the data are first centred. The pairwise product of each of the 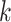 outcomes is computed, generating a high-dimensional matrix of size
outcomes is computed, generating a high-dimensional matrix of size 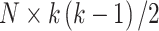 . If
. If 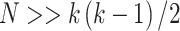 , a joint test of all products can be derived; otherwise, the dimension of the product matrix is reduced using a PCA, to form a PC space of size
, a joint test of all products can be derived; otherwise, the dimension of the product matrix is reduced using a PCA, to form a PC space of size 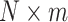 . The final test, including covariates, can be performed on the products or the top
. The final test, including covariates, can be performed on the products or the top 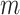 PCs using a Wilk’s lambda test.
PCs using a Wilk’s lambda test.
In a standard MANOVA, potential confounding factors 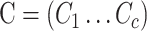 can be incorporated as covariate:
can be incorporated as covariate: 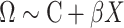 . Again, for fast computation, we used a two-step procedure that consists in adjusting a priori both the outcome and the predictor for the covariates:
. Again, for fast computation, we used a two-step procedure that consists in adjusting a priori both the outcome and the predictor for the covariates: 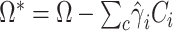 , where
, where 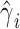 is a vector of estimated effect of
is a vector of estimated effect of 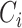 on
on 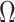 , and
, and 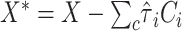 , where
, where 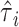 is the estimated effect of
is the estimated effect of 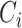 on
on 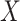 , and applying the MANOVA on the residual variables:
, and applying the MANOVA on the residual variables: 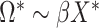 .
.
Type I error rate simulation
The statistical robustness of any covariance test likely depends on the distributional assumptions of the multivariate outcome studied, including the distribution of the outcomes, the number of outcomes analysed jointly, the strength of the correlation across outcomes, the sample size over the number of outcomes ratio and the distribution of the predictors considered (binary or continuous, etc.). We investigated the validity of both MANOCCA and other existing approaches conditional on these factors.
We first assess the calibration under the null of MANOCCA and four existing approaches, the Mantel test [11], the Fisher method [12], the Jennrich test [13] and the BoxM test [14], using fully simulated data and simple scenarios (Fig. 2). We drew a series of 10 000 replicates with a sample size of 1000, each including a multivariate outcome 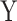 and a binary predictor
and a binary predictor 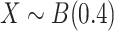 drawn independently of
drawn independently of  under two different models. Note that we used a binary predictor as the four existing approaches do not allow for the analysis of continuous predictors. In the first model, replicates included five outcomes drawn from a multivariate normal with modest pairwise correlation. In the second model, replicates included 30 highly correlated non-normal outcomes drawn from a multivariate chi-square distribution. The overall calibrations of all tests were derived by testing for association between
under two different models. Note that we used a binary predictor as the four existing approaches do not allow for the analysis of continuous predictors. In the first model, replicates included five outcomes drawn from a multivariate normal with modest pairwise correlation. In the second model, replicates included 30 highly correlated non-normal outcomes drawn from a multivariate chi-square distribution. The overall calibrations of all tests were derived by testing for association between 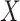 and the correlation between
and the correlation between 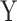 variables and conducting a visual inspection of the P-value distribution.
variables and conducting a visual inspection of the P-value distribution.
Figure 2.
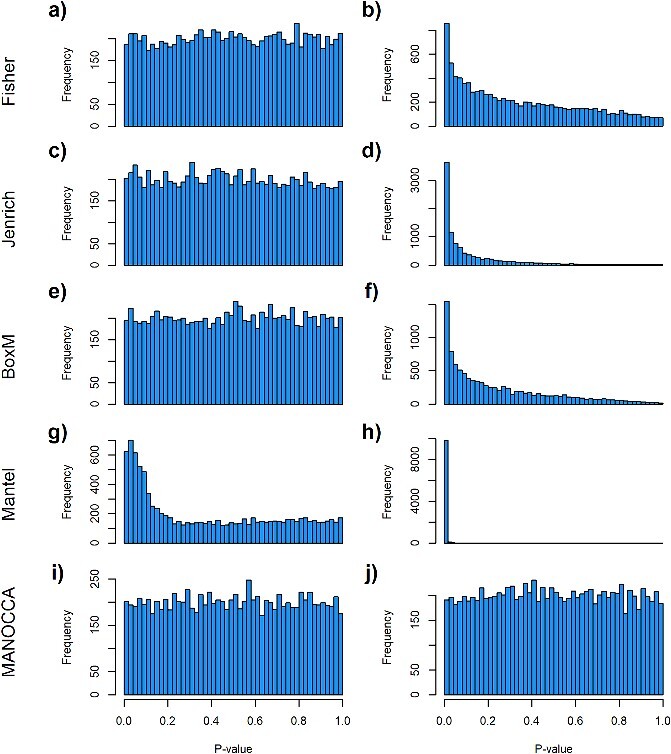
Limitation of existing methods. We assessed the calibration under the null of four approaches representing the state of the art for covariance matrix comparison: the Fisher method (A, B), the Jenrich test (C, D), BoxM (E, F) and Mantel test (G,H), against the proposed MANOCCA approach (I, J). Note that we applied MANOCCA directly on the product matrix thanks to the high sample size compared to the number of products. We simulated a series of 10 000 replicates, with a sample size of 1000 each, under two different null models. In the first model (A, C, E, G, I), replicates included five outcomes  drawn from a multivariate normal with modest pairwise correlation. In the second model (B, D, F, H, J), closer to the expected distribution of omics data, replicates included 30 non-normal outcomes with high correlation. Calibration was derived by splitting each replicate in two random sets according to a random binary variable
drawn from a multivariate normal with modest pairwise correlation. In the second model (B, D, F, H, J), closer to the expected distribution of omics data, replicates included 30 non-normal outcomes with high correlation. Calibration was derived by splitting each replicate in two random sets according to a random binary variable  and testing for association between
and testing for association between  and the correlation between
and the correlation between 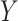 variables. The panels present the distribution of the P-values, expected to be uniformly distributed under this null model, for the five approaches and the two models.
variables. The panels present the distribution of the P-values, expected to be uniformly distributed under this null model, for the five approaches and the two models.
We next assessed the robustness of MANOCCA under a wider range of scenarios, while modifying some of the modelling parameters. We first compared performance when using a binary or a continuous predictor (Figure S3 available online at http://bib.oxfordjournals.org/). We simulated a series of 100 replicates, each including 1000 individuals and a multivariate outcome 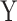 including 400 variables drawn from a multivariate chi-square distribution with a point mass at 0 including 0–50% of the data. For each replicate, we drew 1000 predictors, either from a normal or binary distribution, and applied MANOCCA while varying the number of PCs used and applying no transformation, a rank-inverse normal transformation on the product matrix, the PC matrix or both. The validity of MANOCCA was assessed using a Kolmogorov–Smirnov test for deviation from a uniform [0,1] distribution of the P-values across the 1000 predictors tested. We then conducted simulations using real covariance matrices derived from the MI 169 flow cytometry–based variables and for ranging sample sizes from 1000 to 5000 to draw guidelines on the parametrization of MANOCCA (Figures S6 and S7). For predictors, we considered not only binary predictors with frequencies in [0.01; 0.40] but also categorical ones mimicking genetic variants with minor allele frequency in [0.01; 0.40], both generated independently of the multivariate outcome
including 400 variables drawn from a multivariate chi-square distribution with a point mass at 0 including 0–50% of the data. For each replicate, we drew 1000 predictors, either from a normal or binary distribution, and applied MANOCCA while varying the number of PCs used and applying no transformation, a rank-inverse normal transformation on the product matrix, the PC matrix or both. The validity of MANOCCA was assessed using a Kolmogorov–Smirnov test for deviation from a uniform [0,1] distribution of the P-values across the 1000 predictors tested. We then conducted simulations using real covariance matrices derived from the MI 169 flow cytometry–based variables and for ranging sample sizes from 1000 to 5000 to draw guidelines on the parametrization of MANOCCA (Figures S6 and S7). For predictors, we considered not only binary predictors with frequencies in [0.01; 0.40] but also categorical ones mimicking genetic variants with minor allele frequency in [0.01; 0.40], both generated independently of the multivariate outcome 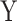 .
.
Power simulation
To investigate power, we drew a series of 50 replicates with sample size of 1000 including a binary exposure 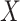 with frequency of 0.5 and a multivariate outcome
with frequency of 0.5 and a multivariate outcome 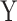 including 50–169 variables (Fig. 4). For each replicate, we used two covariance matrices, one for the exposed (
including 50–169 variables (Fig. 4). For each replicate, we used two covariance matrices, one for the exposed (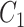 ) and the other for the unexposed (
) and the other for the unexposed (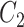 ), and tested the association between
), and tested the association between 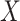 and
and 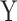 using MANOCCA. We generated the outcome from a multivariate normal and real covariance matrix (
using MANOCCA. We generated the outcome from a multivariate normal and real covariance matrix (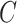 ) derived from the MI flow cytometry data under three scenarios. In scenario (i),
) derived from the MI flow cytometry data under three scenarios. In scenario (i), 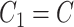 and
and 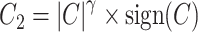 , inducing a covariance with similar pattern among exposed but variability in the magnitude of covariance. In scenario (ii),
, inducing a covariance with similar pattern among exposed but variability in the magnitude of covariance. In scenario (ii), 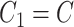 and
and 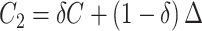 , where
, where 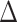 is a random covariance generated using the R randcorr package [17], thus inducing random noise between exposed and unexposed. In scenario (iii), we first drew
is a random covariance generated using the R randcorr package [17], thus inducing random noise between exposed and unexposed. In scenario (iii), we first drew 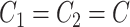 and then attenuated the covariance in an arbitrary chosen subset
and then attenuated the covariance in an arbitrary chosen subset 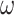 of
of 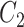 , so that
, so that 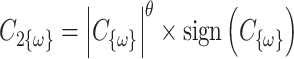 . We arbitrarily set
. We arbitrarily set 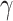 to 1.5,
to 1.5, 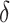 to 0.2 and
to 0.2 and 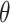 to 0.5, as it allowed for a similar average power across scenarios given the other simulation parameters.
to 0.5, as it allowed for a similar average power across scenarios given the other simulation parameters.
Figure 4.
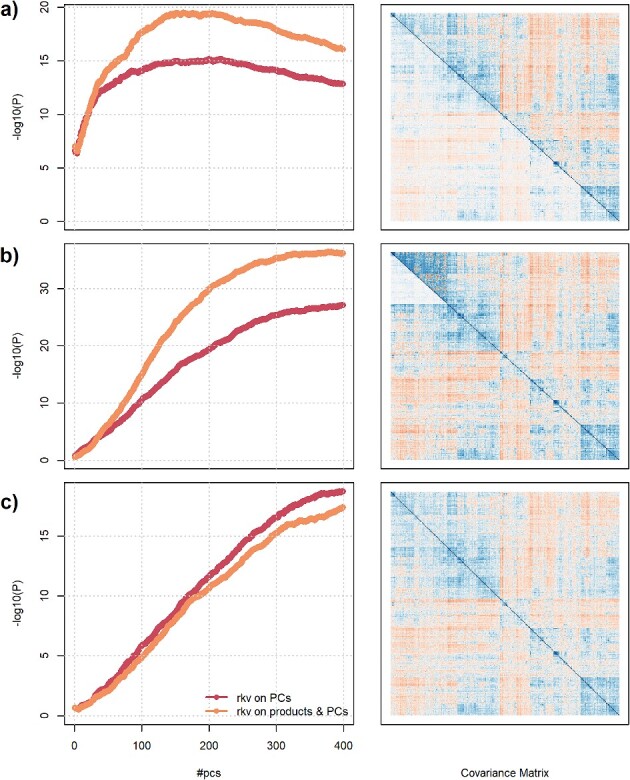
Impact of transformation and number of PCs on statistical power. Power of MANOCCA as a function of the number of PCs retained in the joint test (2–400), while applying two different pre-processings: a rank-inverse normal (rkv) on the PC only or a rank-inverse normal on the PCs and the products. We drew series of 50 replicates with sample size 1000, including a binary exposure with frequency of 0.5 and 30–169 outcomes. For each replicate, we drew two covariance matrices, one for the exposed and one for the unexposed. We generated the outcome under three scenarios using a multivariate normal and covariance derived from real data. In (A), the two matrices are similar but with attenuated covariances among exposed. In (B), random noise is added to the covariance of the exposed group. In (C), the two matrices are equal, except for a subset of outcomes where the covariances have been attenuated. Left panels show the average over the 100 replicates of the −log10(P-value) derived using MANOCCA for the two pre-processings. Right panels present the matrix produced for each scenario using data from an arbitrarily chosen replicate, with upper and lower triangles showing the true covariance in unexposed and exposed, respectively.
MANOCCA association screening in MI
The MI Consortium is a population-based cohort initiated in September 2012 [18]. It comprises 1000 healthy volunteers from western France, with a 1:1 sex ratio. The cohort collected a broad range of variables, including genomic, immunological, environmental and clinical outcomes. We conducted systematic MANOCCA screenings for environmental effects on the covariance of two sets of data: 169 flow cytometry–based immune cell phenotypes [19] and 33 health-related blood biomarkers, including 22 metabolites and 11 cell counts [18] (Tables S1 and S2 available online at http://bib.oxfordjournals.org/). We focused on two types of predictors: health and lifestyle factors collected from questionnaires and genome-wide variants. Health and lifestyle factors included demographics, medical and vaccination history, psychological traits, socio-professional information, smoking habits, physiological measurements and nutrition measured as part of the Nutrinet [20] study (Table S3 available online at http://bib.oxfordjournals.org/). After the filtering of ancestral outliers individuals [21, 22], the genetic screening was conducted in 894 participants for a total of 5 667 803 variants after filtering and imputation using IMPUTE2 [23]. Except when used as predictor, all analyses were adjusted for age, sex and body mass index (BMI). For blood metabolites, the number of products allowed for a direct analysis of the products without requiring the PCA step, and we considered both the products and the PCs as outcomes. For comparison purposes, we also conducted, for each screening, a standard MANOVA on the mean of the multivariate outcome (see Supplementary Notes).
Human samples
Samples came from the MI Cohort, which was approved by the Comité de Protection des Personnes—Ouest 6 (Committee for the protection of persons) on 13 June 2012 and by French Agence nationale de sécurité du médicament (ANSM) on 22 June 2012. The study is sponsored by Institut Pasteur (Pasteur ID-RCB Number: 2012-A00238-35) and was conducted as a single centre interventional study without an investigational product. The original protocol was registered under ClinicalTrials.gov (study# NCT01699893). The samples and data used in this study were formally established as the MI biocollection (NCT03905993), with approvals by the Comité de Protection des Personnes—Sud Méditerranée and the Commission nationale de l’informatique et des libertés (CNIL) on 11 April 2018. All donors gave written informed consent. All data used in this study are available at https://dataset.owey.io/.
Results
Method comparison and MANOCCA characteristics
We identified four existing approaches allowing to test for the effect of a predictor on the covariance matrix of a multivariate outcome: (i) the Mantel test [11], which consists of deriving a distance metric between two square matrices of the same dimension and comparing this distance to an empirical distribution derived through permutation; (ii) the Fisher method [12], which builds a statistic based on the sum of the squared correlations over all cells from the covariance matrix; (iii) the Jennrich test [13], which, in its simplest form, consists of estimating the statistic based on the Hadamard product of a given correlation matrix and the inverse of a second matrix of the same dimension; and (iv) the BoxM test [14], which extends the Levene’s test of homogeneity of variance, an approach often used in human genetics [24]. Further description of each of the four approaches is provided in Supplementary Notes. We conducted a series of simulations to assess their statistical robustness under the null using a binary predictor and no covariates, as these approaches cannot handle continuous predictors and do not allow adjustment for covariates. Except for the Mantel test, all methods performed relatively well for a simple model with a few normally distributed outcomes. Conversely, they all displayed severe type I error rate inflation when confronted with non-normal correlated variables, mimicking omics data (Fig. 2A–H). In comparison, when applied to the same simulated data, MANOCCA was correctly calibrated in all simulations (Figure 2I and J).
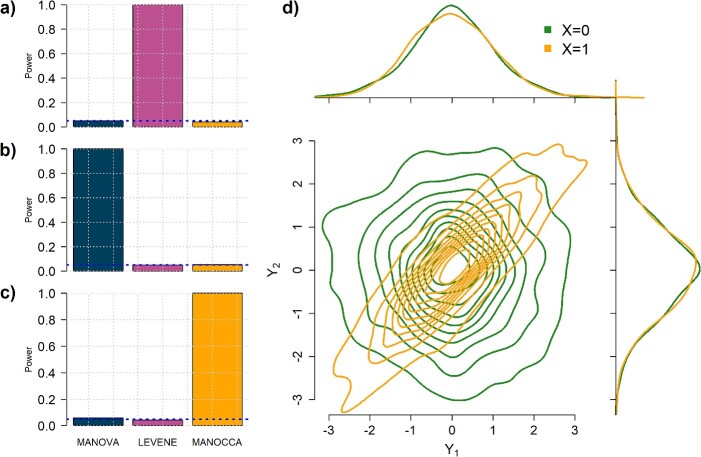
The effect of the predictor on the covariance, the mean and the variance of a set of outcomes are expected to be statistically independent (see Supplementary Notes). We confirmed this orthogonality between mean (derived using a two-way MANOVA), variance (Levene’s test) and the proposed covariance tests through simulation. Figure 3 shows that, under realistic modelling assumptions, the MANOCCA test captures only effects on the covariance and can therefore identify effects missed by both mean and variance-based approaches. Figure 3D further illustrates bivariate data where a binary predictor 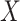 is associated with covariance but neither the mean nor the variance of the outcomes. Importantly, the independence of the three tests does not imply signal across the three approaches will necessarily be uncorrelated in real data. Indeed, one can easily draw scenarios with, e.g. effect of a predictor on both the mean and covariance of a multivariate outcome. Also, unless specified otherwise, we modelled the effect of a predictor on the covariance through an interaction with a latent variable associated shared across the outcomes tested (see Methods). Under this modelling, effects on the covariance can in general be transposed to effects on the correlation. However, when the predictor has an effect on the variance of either outcome, this equality is not valid anymore, as the correlation will depend on
is associated with covariance but neither the mean nor the variance of the outcomes. Importantly, the independence of the three tests does not imply signal across the three approaches will necessarily be uncorrelated in real data. Indeed, one can easily draw scenarios with, e.g. effect of a predictor on both the mean and covariance of a multivariate outcome. Also, unless specified otherwise, we modelled the effect of a predictor on the covariance through an interaction with a latent variable associated shared across the outcomes tested (see Methods). Under this modelling, effects on the covariance can in general be transposed to effects on the correlation. However, when the predictor has an effect on the variance of either outcome, this equality is not valid anymore, as the correlation will depend on 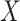 , while the covariance will not (Supplementary Notes).
, while the covariance will not (Supplementary Notes).
Figure 3.
Orthogonality between MANOCCA and other tests. We simulated a series of datasets under three models where a binary predictor 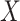 influences orthogonally either the mean, the variance or the covariance of a bivariate outcome
influences orthogonally either the mean, the variance or the covariance of a bivariate outcome 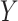 . In model (A), each outcome
. In model (A), each outcome 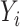 is drawn from a standard additive model:
is drawn from a standard additive model: 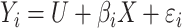 , where
, where 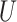 is a normally distributed variable shared across
is a normally distributed variable shared across 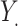 and
and 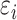 are independent normal residuals. In model (B), each
are independent normal residuals. In model (B), each 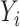 is drawn from
is drawn from 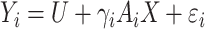 , where
, where 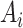 is normally distributed variables producing heterogeneity in the variance of
is normally distributed variables producing heterogeneity in the variance of 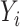 conditional on
conditional on 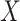 . In model (C), each
. In model (C), each 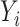 is drawn from the interaction model
is drawn from the interaction model 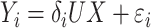 , which produces heterogeneity in the correlation across
, which produces heterogeneity in the correlation across 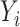 conditional on
conditional on 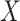 . For each model, we derived the power at the P-value threshold of 0.05 for a joint mean effect test (MANOVA), a test of variance for a randomly selected
. For each model, we derived the power at the P-value threshold of 0.05 for a joint mean effect test (MANOVA), a test of variance for a randomly selected 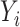 (LEVENE) and the proposed covariance test (MANOCCA). The parameters
(LEVENE) and the proposed covariance test (MANOCCA). The parameters 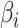 ,
, 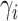 and
and 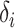 were chosen to maximize the power of the at least one of the three tests. The dashed line indicates the P-value threshold of 0.05. (D) shows an example of a bivariate distribution where
were chosen to maximize the power of the at least one of the three tests. The dashed line indicates the P-value threshold of 0.05. (D) shows an example of a bivariate distribution where 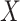 is not associated with the mean and variance of the two outcomes but with their covariance.
is not associated with the mean and variance of the two outcomes but with their covariance.
Extension to high-dimension data
MANOCCA is readily applicable to the matrix of outcome product in all scenarios where 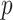 , the number of products, is substantially smaller than the sample size
, the number of products, is substantially smaller than the sample size 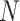 . When this criterion is not met, we used PCA to reduce the dimension of
. When this criterion is not met, we used PCA to reduce the dimension of 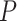 , using the top PCs as the primary outcome. As for all linear models, the maximum number of PCs that can be analysed jointly remained bounded by the sample size. More generally, high-dimension outcomes data bring the question of the latent space dimension, that is, the number of PCs kept in the analysis to achieve maximum power while maintaining a correct type I error rate. Moreover, by construction, both products and PCs tend to display kurtotic distributions, especially for omics-like data, which might also impact performance. We conducted a series of simulations to investigate the robustness of the MANOCCA conditional on these two components. Specifically, we measured the type I error rate while varying the number of top
, using the top PCs as the primary outcome. As for all linear models, the maximum number of PCs that can be analysed jointly remained bounded by the sample size. More generally, high-dimension outcomes data bring the question of the latent space dimension, that is, the number of PCs kept in the analysis to achieve maximum power while maintaining a correct type I error rate. Moreover, by construction, both products and PCs tend to display kurtotic distributions, especially for omics-like data, which might also impact performance. We conducted a series of simulations to investigate the robustness of the MANOCCA conditional on these two components. Specifically, we measured the type I error rate while varying the number of top 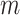 PCs selected, and applying (i) no transformation, or a rank-inverse normal transformation on (ii) the product, (iii) the PCs or (iv) both products and PCs. As shown in Figure S3a available online at http://bib.oxfordjournals.org/, if the predictor being tested is continuous, MANOCCA shows strong robustness conditional on the outcome’s distribution, remaining well calibrated regardless of the transformation applied and allowing for the use of a large number of PCs. Conversely, when analysing binary predictors, the test systematically requires a normalization of the PCs, only allowing a limited number of PCs to be analysed jointly (Figure S3b available online at http://bib.oxfordjournals.org/). Figures S4 and S5 available online at http://bib.oxfordjournals.org/ further presents the results from extended simulations, providing guidelines to determine the number of PCs that can be analysed jointly conditionally on the predictor frequency and the cohort sample size. From an application perspective, when the predictors to be tested include both continuous and non-continuous variables, we recommend using a systematic rank-inverse normal transformation of the PCs, so that the results from either type of predictors can be interpreted on the same scale.
PCs selected, and applying (i) no transformation, or a rank-inverse normal transformation on (ii) the product, (iii) the PCs or (iv) both products and PCs. As shown in Figure S3a available online at http://bib.oxfordjournals.org/, if the predictor being tested is continuous, MANOCCA shows strong robustness conditional on the outcome’s distribution, remaining well calibrated regardless of the transformation applied and allowing for the use of a large number of PCs. Conversely, when analysing binary predictors, the test systematically requires a normalization of the PCs, only allowing a limited number of PCs to be analysed jointly (Figure S3b available online at http://bib.oxfordjournals.org/). Figures S4 and S5 available online at http://bib.oxfordjournals.org/ further presents the results from extended simulations, providing guidelines to determine the number of PCs that can be analysed jointly conditionally on the predictor frequency and the cohort sample size. From an application perspective, when the predictors to be tested include both continuous and non-continuous variables, we recommend using a systematic rank-inverse normal transformation of the PCs, so that the results from either type of predictors can be interpreted on the same scale.
We next evaluated the power of MANOCCA across different scenarios in which the true covariance depends on a binary predictor 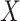 with a frequency of 0.5. We tested up to 400 PCs, and normalized either the products and PCs or the PCs only, the two transformations that display a calibrated null distribution (Figure S3 available online at http://bib.oxfordjournals.org/). The optimal number of PCs varied substantially across the simulated scenarios. Figure 4 illustrates three complementary cases. When
with a frequency of 0.5. We tested up to 400 PCs, and normalized either the products and PCs or the PCs only, the two transformations that display a calibrated null distribution (Figure S3 available online at http://bib.oxfordjournals.org/). The optimal number of PCs varied substantially across the simulated scenarios. Figure 4 illustrates three complementary cases. When 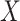 acts as a global scaling factor of the covariance, the maximum power is observed when using a limited number of top PCs and decreases after reaching that optimum (Fig. 4A). When
acts as a global scaling factor of the covariance, the maximum power is observed when using a limited number of top PCs and decreases after reaching that optimum (Fig. 4A). When 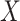 affects only a subset of outcomes, the maximum power is reached when including a fairly large number of PCs and converge afterwards (Fig. 4B). As expected, when
affects only a subset of outcomes, the maximum power is reached when including a fairly large number of PCs and converge afterwards (Fig. 4B). As expected, when 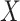 induces random noise in the covariance matrix, the power increases continuously with the number of PCs (Fig. 4C). Among the scenarios we considered, the double normalization (on products and PCs) produced on average larger power, and this transformation was therefore used in all subsequent analyses.
induces random noise in the covariance matrix, the power increases continuously with the number of PCs (Fig. 4C). Among the scenarios we considered, the double normalization (on products and PCs) produced on average larger power, and this transformation was therefore used in all subsequent analyses.
Efficient implementation
The MANOCCA approach requires multiple steps that can be computationally expensive in large-scale data. The main limiting step is the computation of the product matrix followed by the PCA transformation, but it is a one-time cost regardless of the number of predictors tested. With 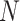 the sample size,
the sample size, 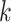 the number of outcomes and
the number of outcomes and 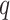 the number of predictors to test, the computation time is divided in
the number of predictors to test, the computation time is divided in 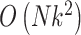 for the computation of the product matrix,
for the computation of the product matrix, 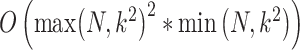 for the computation of the PCA and
for the computation of the PCA and 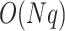 for the test of
for the test of 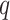 predictors (Fig. 5). Most steps were implemented with limited usage to exterior libraries, but ground-proofed against multiple existing tools. The approach is implemented in a Python package with dependencies to numpy, scipy for the fisher distribution, scikit-learn for the PCA and pandas for dataframe integration, but all computations are performed under numpy array to increase performance. Each step was optimized to minimize computational time and, given that most steps are independent, especially the product matrix, the python version allows for a user-friendly parallel computing implementation if multiple cores are available. An R version, though less optimized, is also available and was used to verify our results.
predictors (Fig. 5). Most steps were implemented with limited usage to exterior libraries, but ground-proofed against multiple existing tools. The approach is implemented in a Python package with dependencies to numpy, scipy for the fisher distribution, scikit-learn for the PCA and pandas for dataframe integration, but all computations are performed under numpy array to increase performance. Each step was optimized to minimize computational time and, given that most steps are independent, especially the product matrix, the python version allows for a user-friendly parallel computing implementation if multiple cores are available. An R version, though less optimized, is also available and was used to verify our results.
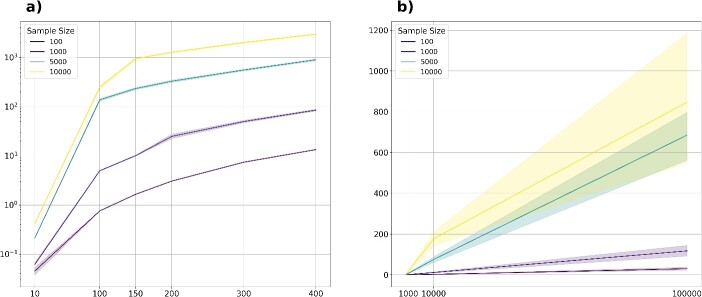
Figure 5.
Computational efficiency. Computational time for running MANOCCA on varying sample sizes, numbers of outcomes and numbers of predictors tested. Over 1000 simulations each time, we simulated multivariate normal distributions of various sizes and computed the product matrix > rank transform > PCA > rank transform using sequential computation. (A) displays the running time to transform the outcome matrix into the reduced covariance matrix for the test, as a function of the number of outcomes (10, 100, 150, 200, 300, 400) and sample size (100, 1000, 5000 and 10 000). Y-axis is in log10-scale. (B) displays the running time for the testing part for a ranging number of sample sizes (100, 1000, 5000 and 10 000) and ranging number of predictors (1000, 10 000, 100 000).
Application to MI omics data
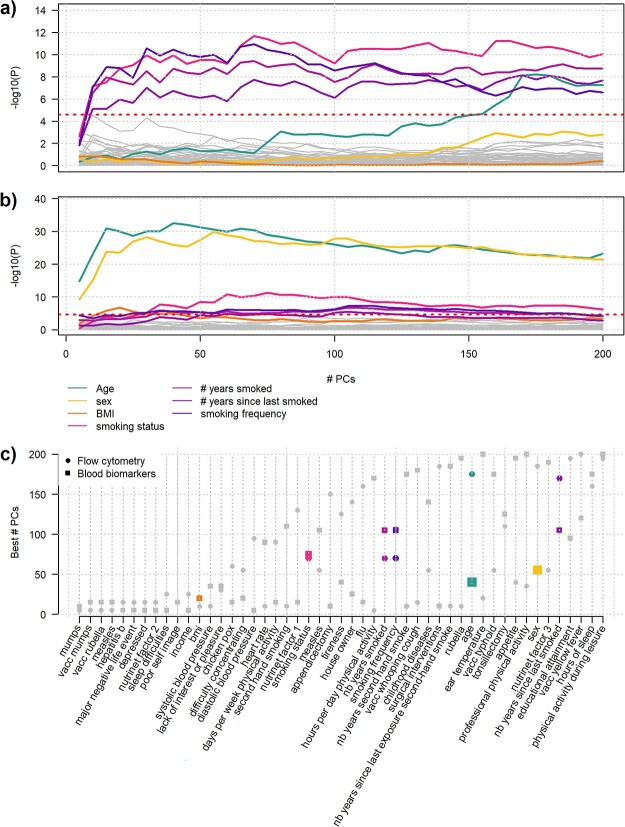
We applied MANOCCA in 1000 healthy individuals from the MI cohort to screen for factors associated with changes in the covariance of 33 blood biomarkers and 169 flow cytometry–based immune phenotypes (Tables S1–S3 available online at http://bib.oxfordjournals.org/). Both datasets display high correlation, ranging from −0.71 to 0.99 for the flow cytometry data and from 0.08 to 0.98 for the biomarkers (Figure S6 available online at http://bib.oxfordjournals.org/). We first investigated the effect of 49 health-related and lifestyle factors using a subset of 992 participants with complete data. We applied the proposed PCA reduction and investigated power when using 5–200 top PCs with a step of 5, resulting in 40 tests per variable. As shown in Fig. 6A and B, multiple features were associated at a stringent Bonferroni-corrected significance level (P < 2.5 × 10−5 accounting for 1960 tests). Flow cytometry–based phenotypic covariance was associated with age (P < 6.0 × 10−9) and all smoking variables: smoking status (P < 2.1 × 10−12), smoking frequency (P < 1.2 × 10−11), number of years smoked (P < 3.8 × 10−10) and number of years since last smoke (P < 7.5 × 10−9). Likewise, blood biomarkers covariance was strongly associated with age (P < 3.5 × 10−33) and sex (P < 1.3 × 10−30), and to a lesser extent with BMI (P < 1.6 × 10−7) and smoking variables (minimum P < 5.5 × 10−12, for smoking status). Except for the age–flow cytometry association, the maximum association signal was almost reached when including the top 50 PCs and display only modest improvement when including more PCs (Fig. 6).
Figure 6.
Screenings for host factors screenings for effect of 49 health and lifestyle factors on the covariance of 169 flow cytometry-based immune phenotypes (A) and 33 blood biomarkers (B) using the MANOCCA approach. We ran each screening using 5−200 PCs with a step of 5. Variables with a P-value below the adjusted Bonferroni threshold (2.6 × 10−5, dashed line) for each screening are displayed in colour: age, sex, body mass index and smoking. (C) presents the list of predictors considered and displays the number of PCs corresponding to the minimum P-value observed.
Thanks to a limited number of outcomes, the blood biomarker dataset could also be analysed by applying MANOCCA directly on the 528 pair-wise products. To investigate the value of using the PCA in such situations, we applied MANOCCA on the product and compared results against the PCA-based approach. Note that the product-based test should be approximately equivalent to the test of all PCs, which was confirmed for these data (Figure S7 available online at http://bib.oxfordjournals.org/). Comparing the minimum P-value across the 40 PCA-based test 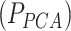 against the P-value from product-based test (
against the P-value from product-based test (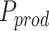 ), we observed a substantial gain for the PCA-based approach, even when accounting for the multiple testing cost of the PCA approach. The product-based test identified only five of the seven signals from the PCA-based approach (Fig. 7). For the strongest signals, the association P-value from the best PCA-based test was several orders of magnitude larger than for the product-based test (e.g. for age, P = 3.5 × 10−33 and 2.6 × 10−11, respectively). These results have three implications. First, it confirms the relevance of using PCA when the dimensionality of the data does not allow the analysis of the product matrix. Using only a subset of top PCs can capture a substantial fraction of the variance of the raw products (e.g. we observed a correlation of 0.85 and higher between the products-based test and the PC-based test, even when using a minimum of 5 PCs, Figure S7). Second, this suggests that, despite the sample size allowing for the full analysis of the product matrix, using PCA remains relevant, with the potential for notable power increase. Third and last, the benefit of testing multiple sets of PCs to search for an optimal threshold can strongly outpace the statistical cost of multiple testing.
), we observed a substantial gain for the PCA-based approach, even when accounting for the multiple testing cost of the PCA approach. The product-based test identified only five of the seven signals from the PCA-based approach (Fig. 7). For the strongest signals, the association P-value from the best PCA-based test was several orders of magnitude larger than for the product-based test (e.g. for age, P = 3.5 × 10−33 and 2.6 × 10−11, respectively). These results have three implications. First, it confirms the relevance of using PCA when the dimensionality of the data does not allow the analysis of the product matrix. Using only a subset of top PCs can capture a substantial fraction of the variance of the raw products (e.g. we observed a correlation of 0.85 and higher between the products-based test and the PC-based test, even when using a minimum of 5 PCs, Figure S7). Second, this suggests that, despite the sample size allowing for the full analysis of the product matrix, using PCA remains relevant, with the potential for notable power increase. Third and last, the benefit of testing multiple sets of PCs to search for an optimal threshold can strongly outpace the statistical cost of multiple testing.
Figure 7.
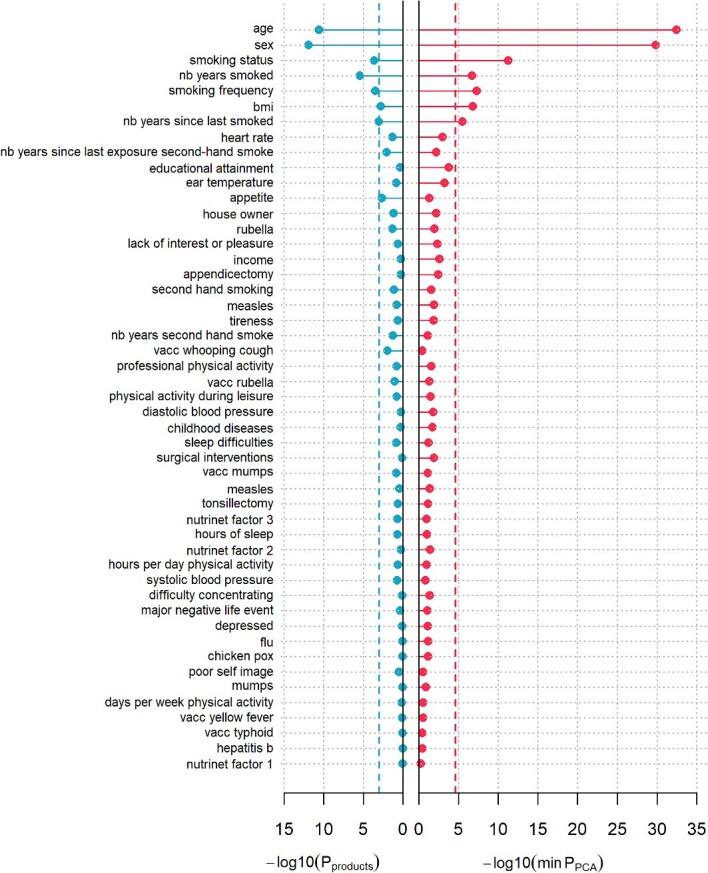
Comparison of PCA-based and product-based MANOCCA screening comparison for covariance signal using MANOCCA on the 33 blood biomarkers as outcomes and using the health and lifestyle electronic case report form (eCRF) questionnaire data as predictors. We ran the MANOCCA screening using the full 528 pair-wise biomarkers products (left) and the PCs derived from the product matrix (right). For the latter, we kept the min(P-value) out of 40 models including 5–200 PCs with a step of 5 PCs. The corresponding Bonferroni correction threshold (dashed line) was derived for each approach based on the number of tests conducted (P-value threshold of 1.0 × 10−3 and 2.6 × 10−5, respectively).
When comparing the MANOCCA results to a standard MANOVA applied to both datasets, MANOVA identified significant associations (P < 1.0 × 10−3 to account for the 49 tests conducted) with 8 and 13 predictors associated in the flow cytometry data and the blood biomarkers data, respectively (Table S4 available online at http://bib.oxfordjournals.org/). These associations included all associations detected by MANOCCA. More generally, while the two tests are expected to be independent, we observed a strong correlation between association signal as measured by the −log10(P-value) (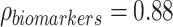 ,
, 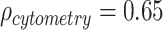 ), suggesting that many of the predictors are associated with effects on both the mean and variance of the outcome studied (Figure S8 available online at http://bib.oxfordjournals.org/). However, several predictors display discordant associations, with a significant effect on the mean but no effect on the covariance. This includes, for example, systolic blood pressure (
), suggesting that many of the predictors are associated with effects on both the mean and variance of the outcome studied (Figure S8 available online at http://bib.oxfordjournals.org/). However, several predictors display discordant associations, with a significant effect on the mean but no effect on the covariance. This includes, for example, systolic blood pressure (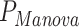 = 2.6 × 10−11,
= 2.6 × 10−11, 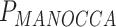 = 0.14) and heart rate (
= 0.14) and heart rate (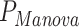 = 4.9 × 10−24,
= 4.9 × 10−24, 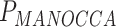 = 0.001) effect on blood biomarkers. On the other hand, one predictor, the number of years of second-hand smoking, displays suggestive significance with MANOCCA on the flow cytometry data, but did not display the mean effect (
= 0.001) effect on blood biomarkers. On the other hand, one predictor, the number of years of second-hand smoking, displays suggestive significance with MANOCCA on the flow cytometry data, but did not display the mean effect (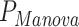 = 0.31,
= 0.31, 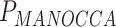 = 3.0 × 10−5).
= 3.0 × 10−5).
Finally, we conducted genome-wide association studies (GWASs) for both blood biomarkers and flow cytometry datasets, testing 5 699 237 genetic variants with a minor allele frequency (MAF) > 5% in up to 894 samples where both genetic and phenotypic data were available. All tests were adjusted for age, sex, BMI and the 10 first genetic PCs of the genotyping matrix. Note that for this genetic screening, we only applied the adjustment on the outcomes. Two-sided adjustment has already been used for mean effect tests in GWAS to account for relatedness [21], but would require further investigation to be extended in the MANOCCA test. Following the results from our simulations for genetic variants with an MAF 5% or larger, the type I error will remain robust only for up to 50 PCs (Figure S4c available online at http://bib.oxfordjournals.org/), resulting in 10 GWASs per dataset. MANOCCA did not detect any genome-wide significant signals at a stringent Bonferroni-corrected threshold (P = 5 × 10−9, Figure S9 available online at http://bib.oxfordjournals.org/). Yet, 46 genetic variants from 11 loci show suggestive significance association (P = 5 × 10−7, Table S5 available online at http://bib.oxfordjournals.org/). We conducted a phenome-wide association study on each variant using the ieu database API [25]. Most variants showed strong association with multiple phenotypes from this database (Table S6 available online at http://bib.oxfordjournals.org/). In particular, 4 out of the 11 loci harboured genetic variants that were expression quantitative trait loci (eQTL) for one or multiple genes (Table S7 available online at http://bib.oxfordjournals.org/), suggesting that our covariance-based approach might capture variants involved in the regulation of gene expression.
Perspective on future applications
Covariance is a feature that is expected to arise commonly in large multidimensional data, including in particular molecular and biomarker data. In general, the relevance of our approach to assess the effect of predictors on such data depends on the a priori assumptions of the underlying causal model. To help guiding future applications, we showcase in Figure S10 different models prone to induce or not covariance signals. For clarity, in these simulations, we simply derived the covariance between two outcomes 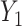 and
and 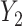 across fixed ranged of values of a given predictor
across fixed ranged of values of a given predictor 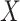 . In general, when the generative model involves the mediation effect, the pleiotropic effect with or without a latent shared factor, the predictor is not expected to produce an effect on the covariance (Figure S10a–c). All models producing a variability of the covariance between
. In general, when the generative model involves the mediation effect, the pleiotropic effect with or without a latent shared factor, the predictor is not expected to produce an effect on the covariance (Figure S10a–c). All models producing a variability of the covariance between 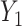 and
and 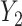 conditional on
conditional on 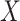 involved some form of interaction (Figure S10d–f), impacting the association between a latent variable and either ones or both of the outcomes or impacting the association between the two outcomes. The latter generative models can be easily connected to known biological mechanisms. For instance, the model from Figure S10f is fairly appropriate to describe an enzymatic or transporter effect, where
involved some form of interaction (Figure S10d–f), impacting the association between a latent variable and either ones or both of the outcomes or impacting the association between the two outcomes. The latter generative models can be easily connected to known biological mechanisms. For instance, the model from Figure S10f is fairly appropriate to describe an enzymatic or transporter effect, where 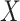 acts as a catalyzer of the transformation between an outcome
acts as a catalyzer of the transformation between an outcome 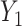 into
into 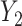 . The model from Figure S10d and e can correspond to scenarios where the relationship between a factor or resource shared by both
. The model from Figure S10d and e can correspond to scenarios where the relationship between a factor or resource shared by both 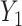 into
into 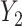 is impacted by
is impacted by 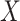 . There is increasing work in the field of microbiology [26, 27], metabolites [28] and gene expression [29] investigating such relationships and where the proposed MANOCCA approach might be of interest.
. There is increasing work in the field of microbiology [26, 27], metabolites [28] and gene expression [29] investigating such relationships and where the proposed MANOCCA approach might be of interest.
Finally, for most statistical models, the relationship between a predictor and an outcome is expected to vary when non-linear transformations are applied to either variable. Here, we devised a pre-processing pipeline that includes some non-linear transformation in order to ensure the statistical robustness of our approach whatever the input outcomes that are analysed. Conversely, the transformation of the raw outcome before deriving the product terms, which might impact both the results and the interpretation of the proposed covariance, remains at the discretion of the user. As for any statistical test, including assessing mean, variance or covariance effect, such transformations will depend on the investigator knowledge about which scale is most relevant to describe the potential underlying biological mechanisms.
Discussion
Covariance is a fundamental feature of omics data. Covariances might be explained by multiple factors, including shared biological mechanisms, shared environmental risk factors or causal effects between the outcomes measured. However, our understanding of the factors involved in covariance has been very limited, partly due to the lack of adapted methodologies and software allowing for systematic screening of large-scale omics datasets. Here, we present MANOCCA, a robust and computationally efficient approach for the identification of predictors associated with the covariance of a multivariate outcome. We show that MANOCCA outperforms existing covariance methods and that, given the appropriate parametrization, it can maintain a calibrated type I error in a range of realistic scenarios when analysing highly multidimensional data. The application of MANOCCA to the MI dataset demonstrates the validity and relevance of our approach, identifying multiple health-related and lifestyle factors significantly associated with the covariance of blood biomarkers and immune phenotypes.
The results from our screenings are in agreement with the existing literature suggesting a role of age, sex, BMI and smoking on the outcomes studied. The marginal association between molecular and cellular biomarkers and ageing has been studied for years and remains topical [30]. There are extensive evidence from clinical and epidemiology studies in healthy individuals that demonstrated associations between age and circulating metabolites [31–33], blood count [31, 33–35] and flow cytometry−based immune phenotypes [36–38]. Association of biomarkers with smoking habits [39] and BMI [40] have been widely described, showing, for example, an impact on platelets glycoprotein [41] and platelet function [42]. Several studies using the same biomarker in MI data have also been conducted, deciphering the short- and long-term effects of smoking on immunity-related biomarkers [43] and describing sexual dimorphism of immunity-related flow cytometry phenotypes [44]. Finally, and more directly related to our work, a recent study suggested association of age and sex with plasma metabolite association networks in healthy subject using correlation approach technics [45].
The MANOCCA approach has four main limitations. First, we used PCA to address situations where the number of covariance terms is larger than the sample size. We defined guidelines that constrain the maximum number of PCs that can be used to ensure the validity of the test when analysing binary or categorical predictors. Regarding power, both simulation and empirical data analyses show that the optimal number of PCs to be included to maximize power can vary substantially conditional on the true covariance association pattern. Here, we use systematic screenings testing a range of PCs and corrected the association results for multiple testing. Our analyses suggest that the benefit of this strategy largely overcomes its statistical cost. Note that this correction strategy might be further improved as it does not account for correlation between each PC test. Second, our extensive simulation analyses show that when reaching high dimensions, the validity of the test relies on a strong data pre-processing to circumvent the non-normal distribution of products and PCs. Future work is required to identify a refined modelling of these non-normal distributions and avoid this pre-processing. Third, we investigated the performance of our approach on two types of omics data (blood flow cytometry and metabolites) and confirmed its validity and power in these data. Omics data from other sources (e.g. RNAseq) might carry additional complexity that would have to be investigated by simulations before conducting real data applications. Fourth, though applicable to any type of ordinal predictor, MANOCCA is currently restricted to continuous outcomes and unstructured observations. Other fields of application interested in changes in outcome relationships, such as the study of mutation mechanisms in genomic sequences [46], the study of longitudinal data (changes of covariances across different timepoints) or covariances across related individuals, would require further work to be studied using MANOCCA.
Given the increasing number of high-dimensional omics data available in existing human cohorts, our approach provides opportunities to investigate multivariate outcomes from a new perspective. Because MANOCCA is built on a standard linear framework, the approach can be extended in many directions, including the derivation of the individual contribution of outcomes and the development of predictive models. Altogether, we expect the application of our method to produce novel insights on the complex structure linking highly intertwined omics data.
Key Points
There exist many methods and software to assess the effect of a predictor on the mean and the variance of omics data. Conversely, there is a lack of methodology and tools to assess the effect of predictors on the covariance of multivariate outcomes.
Under reasonable assumptions on the data distribution, covariance signal is expected to be orthogonal to mean and variance signals and thus can be missed by such approaches.
MANOCCA provides a robust and scalable test to evaluate the effect of a predictor on the covariance of a multivariate outcome that outperforms the state of the art.
Our approach identified several significant associations for covariance signal of human metabolites and blood biomarkers with regard to environmental factors.
Supplementary Material
Acknowledgements
The Milieu Intérieur Consortium¶ is composed of the following team leaders: Laurent Abel (Hôpital Necker), Andres Alcover, Hugues Aschard, Philippe Bousso, Nollaig Bourke (Trinity College Dublin), Petter Brodin (Karolinska Institutet), Pierre Bruhns, Nadine Cerf-Bensussan (INSERM UMR 1163—Institut Imagine), Ana Cumano, Christophe D’Enfert, Ludovic Deriano, Marie-Agnès Dillies, James Di Santo, Gérard Eberl, Jost Enninga, Jacques Fellay (EPFL, Lausanne), Ivo Gomperts-Boneca, Milena Hasan, Gunilla Karlsson Hedestam (Karolinska Institutet), Serge Hercberg (Université Paris 13), Molly A Ingersoll (Institut Cochin and Institut Pasteur), Olivier Lantz (Institut Curie), Rose Anne Kenny (Trinity College Dublin), Mickaël Ménager (INSERM UMR 1163—Institut Imagine), Frédérique Michel, Hugo Mouquet, Cliona O’Farrelly (Trinity College Dublin), Etienne Patin, Sandra Pellegrini, Antonio Rausell (INSERM UMR 1163—Institut Imagine), Frédéric Rieux-Laucat (INSERM UMR 1163—Institut Imagine), Lars Rogge, Magnus Fontes (Institut Roche), Anavaj Sakuntabhai, Olivier Schwartz, Benno Schwikowski, Spencer Shorte, Frédéric Tangy, Antoine Toubert (Hôpital Saint-Louis), Mathilde Touvier (Université Paris 13), Marie-Noëlle Ungeheuer, Christophe Zimmer, Matthew L. Albert (In Sitro), Darragh Duffy§, Lluis Quintana-Murci§,
¶ unless otherwise indicated, partners are located at Institut Pasteur, Paris
§ co-coordinators of the Milieu Intérieur Consortium
Additional information can be found at: http://www.milieuinterieur.fr
Author Biographies
Christophe Boetto is a PhD student in the field of biostatistics.
Arthur Frouin is a postdoc working on bacterial GWAS.
Léo Henches is a research engineer in the field of statistical genetics.
Antoine Auvergne is a PhD student working on multivariate analysis related to the genetics of psychiatric disorders.
Yuka Suzuki is a postdoc in the field of biostatistics.
Etienne Patin is a research scientist in the field of human evolutionary genetics.
Marius Bredon is a postdoc in the field of metagenomics.
Alec Chiu is a PhD student in the field of biostatistics.
Srirarm Sankararaman is a professor in computer science.
Noah Zaitlen is a professor in machine learning.
Sean P. Kennedy is a researcher in the field of clinical metagenomics.
Lluis Quintana-Murci is a professor in human evolutionary genetics.
Darragh Duffy is a research director in the field of translational Immunology.
Harry Sokol is a professor specialized on the human gut microbiome.
Hugues Aschard is a research director in the field of statistical genetics.
Contributor Information
Christophe Boetto, Department of Computational Biology, Institut Pasteur, Université Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France.
Arthur Frouin, Department of Computational Biology, Institut Pasteur, Université Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France.
Léo Henches, Department of Computational Biology, Institut Pasteur, Université Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France.
Antoine Auvergne, Department of Computational Biology, Institut Pasteur, Université Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France.
Yuka Suzuki, Department of Computational Biology, Institut Pasteur, Université Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France.
Etienne Patin, Human Evolutionary Genetics Unit, Institut Pasteur, Université Paris Cité, CNRS UMR2000, 25-28 rue Dr Roux, 75015 Paris, France.
Marius Bredon, Sorbonne Université, INSERM, Centre de recherche Saint-Antoine, CRSA, Microbiota, Gut and Inflammation Laboratory, Hôpital Saint-Antoine (UMR S938) Sorbonne Université, 27 rue Chaligny, 75012 Paris, France.
Alec Chiu, Department of Human Genetics, University California Los Angeles, 695 Charles E. Young Drive South, Box 708822, Los Angeles, CA 90095-7088, United States.
Sriram Sankararaman, Department of Human Genetics, University California Los Angeles, 695 Charles E. Young Drive South, Box 708822, Los Angeles, CA 90095-7088, United States.
Noah Zaitlen, Department of Human Genetics, University California Los Angeles, 695 Charles E. Young Drive South, Box 708822, Los Angeles, CA 90095-7088, United States.
Sean P Kennedy, Department of Computational Biology, Institut Pasteur, Université Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France.
Lluis Quintana-Murci, Human Evolutionary Genetics Unit, Institut Pasteur, Université Paris Cité, CNRS UMR2000, 25-28 rue Dr Roux, 75015 Paris, France; Chair of Human Genomics and Evolution, Collège de France, 11 Pl. Marcelin Berthelot, 75005 Paris, France.
Darragh Duffy, Translational Immunology Unit, Institut Pasteur, Université de Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France.
Harry Sokol, Sorbonne Université, INSERM, Centre de recherche Saint-Antoine, CRSA, Microbiota, Gut and Inflammation Laboratory, Hôpital Saint-Antoine (UMR S938) Sorbonne Université, 27 rue Chaligny, 75012 Paris, France; Paris Center for Microbiome Medicine, Fédération Hospitalo-Universitaire, 184 rue du Faubourg Saint-Antoine, 75571 PARIS Cedex 12, France; Gastroenterology Department, AP-HP, Saint Antoine Hospital, 184 rue du faubourg Saint-Antoine, 75012 Paris, France; INRAE Micalis & AgroParisTech, UMR1319, Micalis & AgroParisTech, 4 avenue Jean Jaurès, 78352 Jouy en Josas, France.
Hugues Aschard, Department of Computational Biology, Institut Pasteur, Université Paris Cité, 25-28 rue du Dr Roux, 75015 Paris, France; Department of Epidemiology, Harvard TH Chan School of Public Health, 677 Huntington Ave, Boston, MA 02115, United States.
Funding
This research was supported by the Agence Nationale pour la Recherche (ANR-20-CE15-0012-01). This work has been conducted as part of the INCEPTION program (Investissement d’Avenir grant ANR-16-CONV-0005). The Milieu Interieur consortium was also supported by the Agence Nationale pour la Recherche (ANR-10-LABX-69-01).
Code availability
All codes are available in Python and R at: https://gitlab.pasteur.fr/statistical-genetics/manocca.
Data availability
Data have been deposited in the European Genome-Phenome Archive under accession code EGAC00001001785.
References
- 1. Perez-Riverol Y, Zorin A, Dass G, et al. Quantifying the impact of public omics data. Nat Commun 2019;10:3512. 10.1038/s41467-019-11461-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Wolfe KH, Li WH. Molecular evolution meets the genomics revolution. Nat Genet 2003;33(Suppl):255–65. 10.1038/ng1088. [DOI] [PubMed] [Google Scholar]
- 3. Worley B, Powers R. Multivariate analysis in metabolomics. Curr Metabolomics 2013;1:92–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Hasin Y, Seldin M, Lusis A. Multi-omics approaches to disease. Genome Biol 2017;18:83. 10.1186/s13059-017-1215-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Rahnenfuhrer J, De Bin R, Benner A, et al. Statistical analysis of high-dimensional biomedical data: a gentle introduction to analytical goals, common approaches and challenges. BMC Med 2023;21:182. 10.1186/s12916-023-02858-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Bartel J, Krumsiek J, Theis FJ. Statistical methods for the analysis of high-throughput metabolomics data. Comput Struct Biotechnol J 2013;4(5):e201301009. 10.5936/csbj.201301009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Turley P, Walters RK, Maghzian O, et al. Multi-trait analysis of genome-wide association summary statistics using MTAG. Nat Genet 2018;50:229–37. 10.1038/s41588-017-0009-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Julienne H, Lechat P, Guillemot V, et al. JASS: command line and web interface for the joint analysis of GWAS results. NAR Genom Bioinform 2020;2:lqaa003. 10.1093/nargab/lqaa003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Julienne H, Laville V, McCaw ZR, et al. Multitrait GWAS to connect disease variants and biological mechanisms. PLoS Genet 2021;17:e1009713. 10.1371/journal.pgen.1009713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Buergel T, Steinfeldt J, Ruyoga G, et al. Metabolomic profiles predict individual multidisease outcomes. Nat Med 2022;28:2309–20. 10.1038/s41591-022-01980-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Mantel N. The detection of disease clustering and a generalized regression approach. Cancer Res 1967;27:209–20. [PubMed] [Google Scholar]
- 12. Steiger JH. Testing pattern hypotheses on correlation matrices: alternative statistics and some empirical results. Multivar Behav Res 1980;15:335–52. 10.1207/s15327906mbr1503_7. [DOI] [PubMed] [Google Scholar]
- 13. Jennrich RI. An asymptotic |chi<sup>2</sup> test for the equality of two correlation matrices. J Am Stat Assoc 1970;65:904–12. [Google Scholar]
- 14. Box GEP. A general distribution theory for a class of likelihood criteria. Biometrika 1949;36:317–46. 10.1093/biomet/36.3-4.317. [DOI] [PubMed] [Google Scholar]
- 15. Lea A, Subramaniam M, Ko A, et al. Genetic and environmental perturbations lead to regulatory decoherence. elife 2019;8. 10.7554/eLife.40538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Ates C, Kaymaz O, Kale HE, et al. Comparison of test statistics of nonnormal and unbalanced samples for multivariate analysis of variance in terms of type-I error rates. Comput Math Methods Med 2019;2019:2173638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Pourahmadi M, Wang X. Distribution of random correlation matrices: hyperspherical parameterization of the Cholesky factor. Stat Probabil Lett 2015;106:5–12. 10.1016/j.spl.2015.06.015. [DOI] [Google Scholar]
- 18. Thomas S, Rouilly V, Patin E, et al. The Milieu Interieur study - an integrative approach for study of human immunological variance. Clin Immunol 2015;157:277–93. 10.1016/j.clim.2014.12.004. [DOI] [PubMed] [Google Scholar]
- 19. Hasan M, Beitz B, Rouilly V, et al. Semi-automated and standardized cytometric procedures for multi-panel and multi-parametric whole blood immunophenotyping. Clin Immunol 2015;157:261–76. 10.1016/j.clim.2014.12.008. [DOI] [PubMed] [Google Scholar]
- 20. Chaltiel D, Adjibade M, Deschamps V, et al. Programme National Nutrition Sante - guidelines score 2 (PNNS-GS2): development and validation of a diet quality score reflecting the 2017 French dietary guidelines. Br J Nutr 2019;122:331–42. 10.1017/S0007114519001181. [DOI] [PubMed] [Google Scholar]
- 21. Price AL, Patterson NJ, Plenge RM, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet 2006;38:904–9. 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 22. Novembre J, Stephens M. Interpreting principal component analyses of spatial population genetic variation. Nat Genet 2008;40:646–9. 10.1038/ng.139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Howie BN, Donnelly P, Marchini J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet 2009;5:e1000529. 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Pare G, Cook NR, Ridker PM, et al. On the use of variance per genotype as a tool to identify quantitative trait interaction effects: a report from the Women's genome health study. PLoS Genet 2010;6:e1000981. 10.1371/journal.pgen.1000981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Ben E, Lyon MS, Alexander T, et al. The MRC IEU OpenGWAS data infrastructure. bioRxiv 2020.08.10.244293 2020. [Google Scholar]
- 26. Layeghifard M, Hwang DM, Guttman DS. Disentangling interactions in the microbiome: a network perspective. Trends Microbiol 2017;25(3):217–28. 10.1016/j.tim.2016.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Chen L, Collij V, Jaeger M, et al. Gut microbial co-abundance networks show specificity in inflammatory bowel disease and obesity. Nat Commun 2020;11:4018. 10.1038/s41467-020-17840-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Smith CJ, Sinnott-Armstrong N, Cichońska A, et al. Integrative analysis of metabolite GWAS illuminates the molecular basis of pleiotropy and genetic correlation. elife 2022;11. 10.7554/eLife.79348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Amariuta T, Siewert-Rocks K, Price AL. Modeling tissue co-regulation estimates tissue-specific contributions to disease. Nat Genet 2023;55:1503–11. 10.1038/s41588-023-01474-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Moqri M, Herzog C, Poganik JR, et al. Validation of biomarkers of aging. Nat Med 2024;30:360–72. 10.1038/s41591-023-02784-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Sebastiani P, Thyagarajan B, Sun F, et al. Age and sex distributions of age-related biomarker values in healthy older adults from the long life family study. J Am Geriatr Soc 2016;64:e189–94. 10.1111/jgs.14522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Adav SS, Wang Y. Metabolomics signatures of aging: recent advances. Aging Dis 2021;12:646–61. 10.14336/AD.2020.0909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Bortz J, Guariglia A, Klaric L, et al. Biological age estimation using circulating blood biomarkers. Commun Biol 2023;6:1089. 10.1038/s42003-023-05456-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Crimmins E, Vasunilashorn S, Kim JK, et al. Biomarkers related to aging in human populations. Adv Clin Chem 2008;46:161–216. 10.1016/S0065-2423(08)00405-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Nakamura E, Miyao K. A method for identifying biomarkers of aging and constructing an index of biological age in humans. J Gerontol A Biol Sci Med Sci 2007;62:1096–105. 10.1093/gerona/62.10.1096. [DOI] [PubMed] [Google Scholar]
- 36. Larbi A, Pawelec G, Wong SC, et al. Impact of age on T cell signaling: a general defect or specific alterations? Ageing Res Rev 2011;10:370–8. 10.1016/j.arr.2010.09.008. [DOI] [PubMed] [Google Scholar]
- 37. Lin Y, Kim J, Metter EJ, et al. Changes in blood lymphocyte numbers with age in vivo and their association with the levels of cytokines/cytokine receptors. Immun Ageing 2016;13:24. 10.1186/s12979-016-0079-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Valiathan R, Ashman M, Asthana D. Effects of ageing on the immune system: infants to elderly. Scand J Immunol 2016;83:255–66. 10.1111/sji.12413. [DOI] [PubMed] [Google Scholar]
- 39. Yanbaeva DG, Dentener MA, Creutzberg EC, et al. Systemic effects of smoking. Chest 2007;131:1557–66. 10.1378/chest.06-2179. [DOI] [PubMed] [Google Scholar]
- 40. Nimptsch K, Konigorski S, Pischon T. Diagnosis of obesity and use of obesity biomarkers in science and clinical medicine. Metabolism 2019;92:61–70. 10.1016/j.metabol.2018.12.006. [DOI] [PubMed] [Google Scholar]
- 41. Nair S, Kulkarni S, Camoens HM, et al. Changes in platelet glycoprotein receptors after smoking – a flow cytometric study. Platelets 2001;12:20–6. 10.1080/09537100120046020. [DOI] [PubMed] [Google Scholar]
- 42. Inoue T. Cigarette smoking as a risk factor of coronary artery disease and its effects on platelet function. Tob Induc Dis 2004;2:27–33. 10.1186/1617-9625-2-1-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Saint-Andre V, Charbit B, Biton A, et al. Smoking changes adaptive immunity with persistent effects. Nature 2024;626:827–35. 10.1038/s41586-023-06968-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Marquez EJ, Chung C-h, Marches R, et al. Sexual-dimorphism in human immune system aging. Nat Commun 2020;11:751. 10.1038/s41467-020-14396-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Vignoli A, Tenori L, Luchinat C, et al. Age and sex effects on plasma metabolite association networks in healthy subjects. J Proteome Res 2018;17:97–107. 10.1021/acs.jproteome.7b00404. [DOI] [PubMed] [Google Scholar]
- 46. Sun N, Zhao X, Yau SS. An efficient numerical representation of genome sequence: natural vector with covariance component. PeerJ 2022;10:e13544. 10.7717/peerj.13544. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data have been deposited in the European Genome-Phenome Archive under accession code EGAC00001001785.