Abstract
Heteroaromatic molecules are found in areas ranging from biochemistry to photovoltaics. We analyze the n,π* excited states of 6π-electron heteroaromatics with in-plane lone pairs (nσ, herein n) and use qualitative theory and quantum chemical computations, starting at Mandado’s 2n + 1 rule for aromaticity of separate spins. After excitation of an electron from n to π*, a (4n + 2)π-electron species has 2n + 2 πα-electrons and 2n + 1 πβ-electrons (or vice versa) and becomes πα-antiaromatic and πβ-aromatic. Yet, the antiaromatic πα- and aromatic πβ-components seldom cancel, leading to residuals with aromatic or antiaromatic character. We explore vertically excited triplet n,π* states (3n,π*), which are most readily analyzed, but also singlet n,π* states (1n,π*), and explain which compounds have n,π* states with aromatic residuals as their lowest excited states (e.g., pyrazine and the phenyl anion). If the πβ-electron population becomes more (less) uniformly distributed upon excitation, the system will have an (anti)aromatic residual. Among isomers, the one that has the most aromatic residual in 3n,π* is often of the lowest energy in this state. Five-membered ring heteroaromatics with one or two N, O, and/or S atoms never have n,π* states as their first excited states (T1 and S1), while this is nearly always the case for six-membered ring heteroaromatics with electropositive heteroatoms and/or highly symmetric (D2h) diheteroaromatics. For the complete compound set, there is a modest correlation between the (anti)aromatic character of the n,π* state and the energy gap between the lowest n,π* and π,π* states (R2 = 0.42), while it is stronger for monosubstituted pyrazines (R2 = 0.84).
1. Introduction
Approximately two-thirds of all compounds that were known at the end of the last century are fully or partially aromatic, and about half are heteroaromatic.1 The latter find applications in a wide array of areas including pharmaceutical chemistry, agrochemistry, and organic electronics.1−8 Thus, it is important to understand their electronic structures, and this applies to their singlet ground states (S0) as well as the first electronically excited states of singlet and triplet multiplicities (S1 and T1), where the latter states normally determine the photophysical and photochemical features. One characteristic is their extent of (anti)aromaticity,1 and in the lowest π,π* excited states, (anti)aromaticity is often given by Baird’s rule.9−18 This rule tells that annulenes with 4n π-electrons are aromatic in these states while those with 4n + 2 are antiaromatic. However, this form of excited state (anti)aromaticity is not valid for heteroaromatics with n,π* states as S1 and/or T1 states, e.g., pyrazine and s-triazine. Thus, how to assess and rationalize the potential aromatic or antiaromatic character of the n,π* states of heteroaromatics? Does the (anti)aromatic character influence which state is the lowest in energy, the n,π* or the π,π* state?
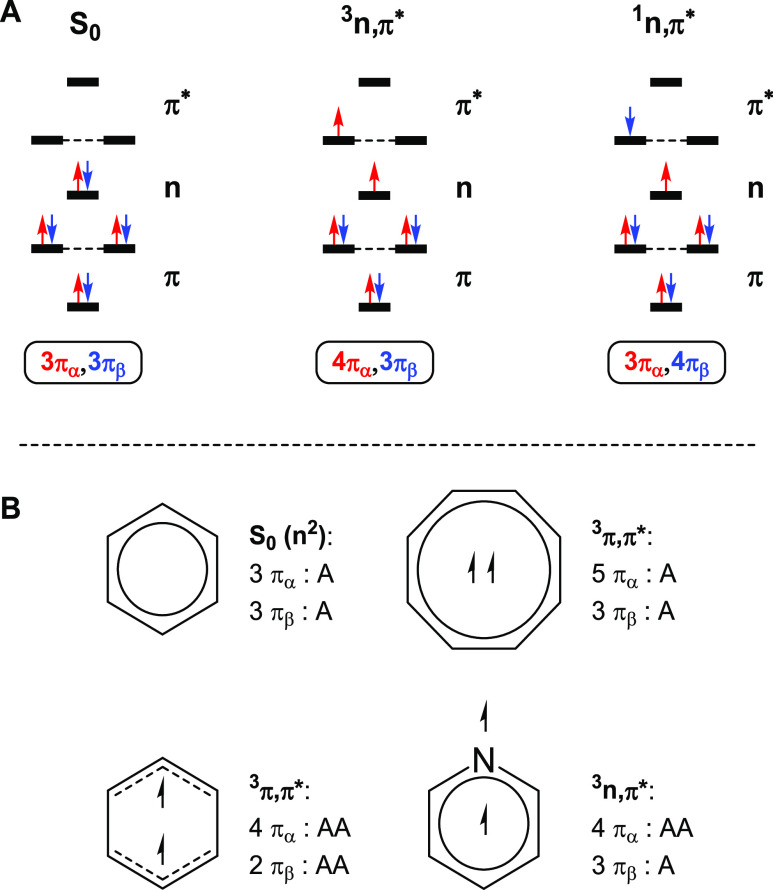
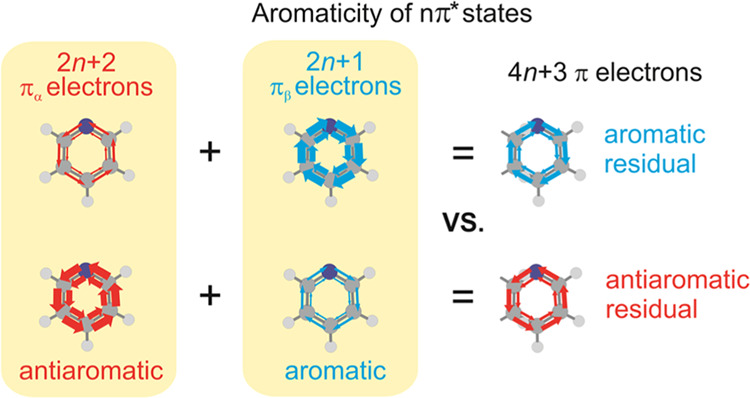
A heteroaromatic molecule with six π-electrons in S0 (three of each spin) will in its n,π* state, where n is an in-plane orbital, have four π-electrons of one spin (α spin) and three of the other (β spin), and this applies to both the singlet and triplet n,π* state (Figure 1A). To understand their aromatic, nonaromatic, or antiaromatic characters, we utilize Mandado’s 2n + 1 rule for aromaticity of separate spins.19 With this rule, Hückel’s 4n + 2 rule for closed-shell singlet state aromaticity is fractioned into a 2n + 1 πα-electron part and a 2n + 1 πβ-electron part (Figure 1B), while Baird’s 4n rule for the lowest π,π* triplet state of [4n]annulenes is fractioned into a 2n + 1 πα-electron and a 2n – 1 πβ-electron part, all four numbers corresponding to aromaticity for separate spins. Conversely, the lowest π,π* triplet state of a species with 4n + 2 π-electrons is antiaromatic, having 2n + 2 πα- and 2n πβ-electrons. A similar rule, derived by Valiev et al., tells that molecules are aromatic (antiaromatic) when having an odd (even) number of doubly and singly occupied π-orbitals,20 suggesting that Mandado’s rule should apply also to singlet excited states with the same electron configuration as the π,π* triplet state.
Figure 1.
(A) Orbital occupancies in the S0 state (n2) and the triplet and singlet n,π* states, with α-electrons in red and β-electrons in blue. (B) Illustrations of Mandado’s rule for (anti)aromaticity of separate spins with aromaticity (A) and antiaromaticity (AA) components in the S0 and the triplet π,π* (T1) states of benzene, the triplet π,π* (T1) state of cyclooctatetraene, and the triplet n,π* state of pyridine.
We have recently revealed the difficulty in proper assessment of excited state aromaticity through molecules which instead of Baird-aromatic are Hückel-aromatic or Hückel-Baird hybrid-aromatic in their lowest excited states.21−23 The situation also becomes more complex in heteroaromatics with in-plane lone pairs (nσ, herein labeled n). The n,π* state of such a (4n + 2)π-electron molecule has 2n + 2 πα- and 2n + 1 πβ-electrons (or vice versa), and would at first glance be nonaromatic if the aromatic πβ-component exactly cancels the antiaromatic πα-component. Yet, can the two parts combined instead lead to aromatic or antiaromatic residuals?
Although the (anti)aromatic characters of various heteroaromatics in their lowest excited states have been analyzed earlier through computations,24−27 the (anti)aromaticity of the n,π* states has to the best of our knowledge not been addressed, neither through qualitative theory nor quantitative computations. Such information can be important to rationalize characteristics of n,π* states. Compounds with n,π* states with aromatic residuals may have these as their T1 and S1 states, with potentially lower excitation energies and higher photochemical stabilities than (isomeric) compounds with n,π* states having non- or antiaromatic residuals. However, a number of additional factors also impact, as can be expected because the relative orbital energies and positions of the heteroatoms in the rings should also play a role.
Here, two recent computational findings are noteworthy. In the first, Foroutan-Nejad points out the lack of correlation between paratropicity and aromatic stabilization energy in monocyclic π-conjugated hydrocarbon radicals,28 and in the second, Zhu et al. uses the concept of adaptive aromaticity in 16- as well as 18-electron metallaaromatic compounds with lowest excited states of π,σ* or σ,π* character.29−33 Both monocyclic π-conjugated hydrocarbon radicals and the metallaaromatics in the states under consideration differ by one electron in the πα- versus πβ-electron counts. Can our analysis approach be extended to these and other species with odd total numbers of πα- and πβ-electrons? If so, one may utilize the analysis to species which are not traditionally regarded as heteroaromatics, e.g., carbenes of relevance for astrochemistry or as ligands in complexes for catalysts, or molecules with charge transfer states composed of cyclic radical cationic and anionic moieties.
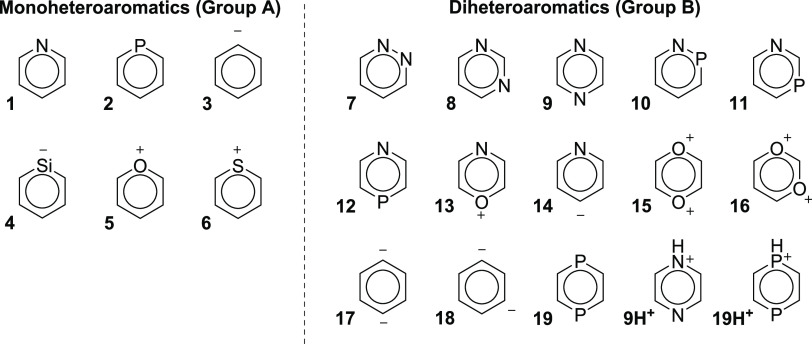
The extent of aromaticity in the S0 state of many heteroaromatics has already been reported.34,35 The compounds now investigated in their n,π* states (Figure 2) are grouped so as to allow us to explore the effects of heteroatom electronegativity, the number of heteroatoms, and their relative positions. We focus on six-membered ring (6-MR) heterocycles as we find that 5-MR heteroaromatics (e.g., furan and imidazole) always have n,π* states of high energies placed well above their first π,π* states, making them difficult to observe experimentally.36 Hence, the latter species are only discussed in the Supporting Information (SI, Section S3.7). Among the 6-MR species, the phenyl anion and dianions (3, 17, and 18) are not heterocycles, but we consider the anionic sp2 hybridized C atoms with in-plane lone pairs as heteroatoms. Thus, even though most of the compounds are common heterocycles, we included species that allow us to identify general trends. We focus on heteroaromatics with n,π* states among the lowest few excited states, whereby they are photochemically relevant. Yet, the n,π* states are not necessarily T1 and S1 for all compounds as that allows us to reveal trends. As far as we know, no investigation into which heteroaromatics have n,π* states as their lowest excited states and which ones have π,π* states has earlier been reported. Thus, the main objectives of our study are to resolve (if possible) which heteroaromatics have n,π* states as their lowest excited states and which ones have π,π* states as these states, and to what extent (anti)aromaticity plays a role for this.
Figure 2.
6-Membered ring (6-MR) heteroaromatics investigated herein. For a selection of 5-membered ring (5-MR) heteroaromatics and an analysis of their frontier orbital energies, see the SI (Section S3.7).
As will be shown, by considering the residuals between the two spin components of (anti)aromaticity, we rationalize features of the heteroaromatics in their n,π* states, e.g., when these states are the lowest excited states. Hence, we provide a theoretical framework for the (anti)aromatic character of n,π* states that can be generalized to states with even πα- and odd πβ-electron counts (or vice versa). We pinpoint why excited state (anti)aromaticity investigations require both quantitative computations and qualitative theory if one is to arrive at conclusions that are correct and comprehensive. Such fundamental knowledge should allow for more insightful design of molecules with targeted properties and applications, especially if linked to machine-learning approaches.
2. Qualitative Theory
Before discussing computational results, we describe the qualitative theoretical framework, and we focus on the triplet n,π* state as this is more readily analyzed computationally than the singlet n,π* state (vide infra). We foremost explore vertical triplet excitations because in the vertical n,π* state the πβ-component should, viewed simplistically (Figure 1A), remain as aromatic as in S0, while the πα-component with four πα-electrons should be antiaromatic. Factors that may perturb this description are (i) a difference in electrostatics within the π-orbital frameworks of the S0 and n,π* states as there will be an increased Coulomb repulsion in the π-system due to the additional π-electron in the n,π* state, and (ii) a difference in the exchange interaction between the two states resulting from the change in the number of πα- and πβ-electrons. A residual that tends toward aromaticity of a vertically excited n,π* state will result if there is a higher degree of aromaticity in the πβ-component compared to the S0 state and/or a low degree of antiaromaticity in the πα-component. Similarly, a residual that tends toward antiaromaticity can stem from a lower aromaticity in the πβ-component than in S0 and/or a high degree of antiaromaticity in the πα-component.
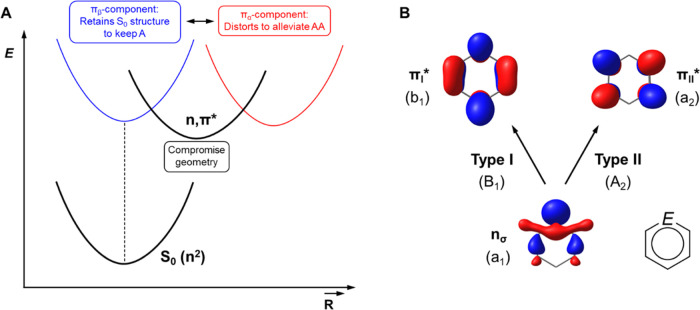
Next, when the molecule relaxes from the vertically excited n,π* state one can postulate that there will be a tug-of-war between the aromatic πβ- and the antiaromatic πα-components. The first seeks to retain the (planar) S0 state geometry and the second strives to alleviate its antiaromaticity through geometric distortions (Figure 3A), i.e., to obtain a more bond length alternated and/or puckered structure. Thus, if the residual between the πα- and πβ-(anti)aromaticity components corresponds to some aromatic character, we postulate that the molecule will be more prone to retain a planar and/or bond length equalized structure in the n,π* state, while it will pucker and/or become more bond length alternated if it has a residual with antiaromatic character. Yet, there can be factors that counteract these features, e.g., a preference of a particular heteroatom to have a more acute bond angle than the planar structure allows for. Hence, by jointly regarding the aromatic-antiaromatic character of the vertically excited n,π* state, we probe the hypothesis that molecules with n,π* states with aromatic residuals between the πα- and πβ-components distort less while those with antiaromatic residuals distort more.
Figure 3.
(A) Illustration of the tug-of-war between the aromatic (A) πβ-component (blue) and the antiaromatic (AA) πα-component (red) in influencing the structure of the n,π* state. (B) The two general types of n,π* excitations for a heteroaromatic molecule with C2v symmetry that can be the lowest n,π* state, as well as the orbital and state symmetries.
There are also various types of n,π* states with different state symmetries as there are two π* orbitals (the b1 and a2 orbitals, Figure 3B), which are degenerate in benzene. As the b1 π* orbital has a lobe at the E atom while the a2 π* orbital has a node there, it is apparent that the orbital energy gap and the energies of the two n,π* states (E(n,π*)) are affected differently by the electronegativity of atom E. This indicates that the n,π* excitation energies of heteroaromatic compounds will be affected by several features, where the extent of n,π* state (anti)aromaticity is only one, others being the S0 state (anti)aromaticity and differences in electrostatic repulsion, exchange interaction, and strain within the molecule when going from S0 to the excited state. Thus, a correlation between the (anti)aromatic residual of an n,π* state and the excitation energy is unlikely. Still, correlations may be observed within closely related compounds, e.g., among isomers or substituted derivatives of a specific heteroaromatic.
The situation becomes more complex with two (or further) heteroatoms E and E′ with in-plane lone-pair electrons because the excitation can be out of either the in-phase or out-of-phase combination of the local n(E) and n(E′) orbitals. Throughout we discuss the lowest n,π* state, yet in a few cases we explore also the second lowest to establish an unambiguous comparison between analogous n,π* states of a subset of the mono- and diheteroaromatics. Moreover, the lowest 3n,π* state is not necessarily the T1 state. Here, we found that 6-MR heteroaromatics often have T1 states of n,π* or π,π* character, while the T1 state of 5-MR heteroaromatics (as mentioned above) mainly are of π,π* character as the in-plane n orbitals are of lower and the π* orbitals of higher energy than in the 6-MR heteroaromatics (see Section S3.7, SI).
3. Results and Discussion
The mono- and diheteroaromatics of Figure 2 were analyzed separately. We primarily explored their lowest triplet n,π* state (3n,π*) as this allows us to use a larger portfolio of aromaticity descriptors. Yet, we also calculated several compounds in their singlet n,π* states (1n,π*) to probe if trends are the same for singlet and triplet n,π* states. Emphasis is placed on electronic aromaticity indices as these are readily separated into α- and β-components, although the spin-separate magnetically induced current densities (MICDs) were also analyzed.37,38 For electronic indices, we computed (spin-separated) multicenter indices (MCI) and electron density of delocalized bonds (EDDB),39−42 with focus on results from MCI known to provide the most accurate predictions in a series of aromaticity tests.35,43 We further computed nucleus-independent chemical shifts (NICS)44−46 for the 3n,π* states, although not spin-separated (see the Computational Details in the SI). Thereby, the NICS values cannot explain the cause of the (anti)aromatic character of an n,π* state as the magnitudes of the individual spin components are unknown. For some 3n,π* states, we also analyzed geometry-based parameters and the relaxation energies when going from the vertically excited to the relaxed 3n,π* states: Do they reflect the drive to relieve antiaromaticity of the πα-component or the strive of the πβ-component to retain aromaticity? The analysis of this tug-of-war (Figure 3A) is done jointly on the mono- and diheteroaromatic compounds in a final section on generalizations.
Computations for the 3n,π* states were mainly performed with the long-range corrected CAM-B3LYP functional47 in the unrestricted Kohn–Sham (KS) formalism, but calculations with the B3LYP and BLYP functionals,48−51 as well as CCSD, BD,52 and CASSCF, were performed for selected compounds (see Sections S1, S2.1, S3.1, and S3.6, SI). Recently, the long-range corrected CAM-B3LYP and ωB97X-D functionals, and the Minnesota functional M06-2X, among 10 different functionals were found to perform best for the lowest excited states of benzene, pyridine, and the diazines.24 For the 1n,π* states, we used time-dependent (TD) density functional theory (DFT).53
3.1. Assessment Criteria
For essentially all compounds, the σ-contributions to the MCI are negligible and do not modify the conclusions (Table S14, SI), and thus, we consider the σ- and π-components combined. We explored for which compounds the MCIβ-components of the 3n,π* states are smaller (less aromatic) than in S0 (i.e., half of the total MCI value in S0), and for which compounds they are larger. The MCIα-component will decrease to a very low value as it becomes antiaromatic, yet its antiaromatic character cannot be assessed as easily as the aromatic character of the MCIβ-component. The residual of the 3n,π* state is the combined MCIα- and MCIβ-components (MCI(3n,π*)tot) minus half the S0 value (MCI(S0)tot); for a nonaromatic 3n,π* state, the MCI(3n,π*)tot should be close to half the total value in S0, provided that the MCIα-component is nearly zero while the MCIβ-component remains as in S0. Moreover, we label the 3n,π* state to lean toward aromaticity if the MCI(3n,π*)tot is at least 10% higher than half the MCI(S0)tot, and toward antiaromaticity if 10% lower.
We consider a 6-MR molecule to be aromatic in S0 if its MCI value is at least half the MCI value of benzene in S0 (i.e., 0.0716/2 = 0.0358). However, the vertically excited lowest triplet π,π* state of benzene is multiconfigurational and is therefore not (easily) comparable to those of the lower-symmetry heterocycles. Instead, we used the MCI and EDDB values of the lowest 3π,π* state of pyridine, which is single-configurational and antiaromatic. This state is an antiaromatic reference with a total MCI value of −0.0005, and MCIα- and MCIβ-components of 0.0023 and −0.0028, respectively.
Thus, in the (anti)aromaticity assessments of the n,π* states of a compound, we use two measures; (i) the ratio between the MCI(3n,π*)tot and MCI(S0)tot of a specific compound and its deviation from 50%, representing nonaromaticity, and (ii) a comparison of the S0 or n,π* state of a specific heteroaromatic with the aromaticity of benzene in S0 (aromatic reference) and the antiaromaticity of the triplet π,π* state of pyridine (antiaromatic reference).
3.2. Monoheteroaromatic 6-MRs (Group A)
As postulated above, the split in energy between the two π* orbitals, b1 and a2, increases with the electronegativity of heteroatom E as the b1 orbital is lowered more. The 13B1 state is the lowest 3n,π* state for all 6-MR monoheteroaromatics, yet, the computed energy difference to the other 3n,π* state (13A2) varies from 0.20 eV for 3 to 2.05 eV for 5 (and similarly for the 1n,π* states, except for 3 where 11A2 is 0.42 eV below 11B1). It is, however, notable that the lowest 3n,π* states of 5 and 6 have multiconfigurational character (see T1 diagnostics, Table S22, SI).54−56 Yet, despite this, the ratios between the MCI values in the 3n,π* and S0 states of 5 and 6 obtained from (U)CAM-B3LYP, (U)CCSD, and (U)BD calculations are quite similar (see Tables S1, S4, and S5 in the SI), clarifying that (U)CAM-B3LYP produces reliable estimates of the decrease in aromaticity when going from S0 to the 3n,π* states of these species (see further Section S3.6 in the SI).
The lowest 3n,π* states of the phenyl and silaphenyl anions (3 and 4) have residuals with MCI that lean toward aromaticity; their MCIβ-components are significantly higher than the corresponding S0 values (Figure 4A), and the MCIα-components resemble that of pyridine (1) in its lowest 3π,π* state (0.0026, 0.0011, and 0.0023 for 3, 4, and 1, respectively). In contrast, the lowest 3n,π* states of 1 and the thiopyrylium cation (6) have residuals that lean toward antiaromaticity, while for phosphinine (2) the MCIβ-component of its 3n,π* state resembles that of S0 and should be categorized as nonaromatic. In S0, the pyrylium cation (5) is nonaromatic because its MCI value is lower than our aromaticity threshold (0.0358). However, in its first 3n,π* state, the MCIβ-component is somewhat higher than in the S0 state. Still, it is the lowest among the 6-MR monoheteroaromatics, and 5 in its 3n,π* state should be labeled nonaromatic. Looking instead at the MCIα-components of the lowest 3n,π* states, it is notable that these are similar or just slightly higher (0.0011–0.0030) than the corresponding components in the antiaromatic 3π,π* state of these compounds (the MCIα-components with four electrons are in the range of −0.0012–0.0034, Table S6, SI). Thus, the πα-components of the 3n,π* states are as antiaromatic as the corresponding component of the 3π,π* state of 1 acting as our antiaromaticity reference.
Figure 4.
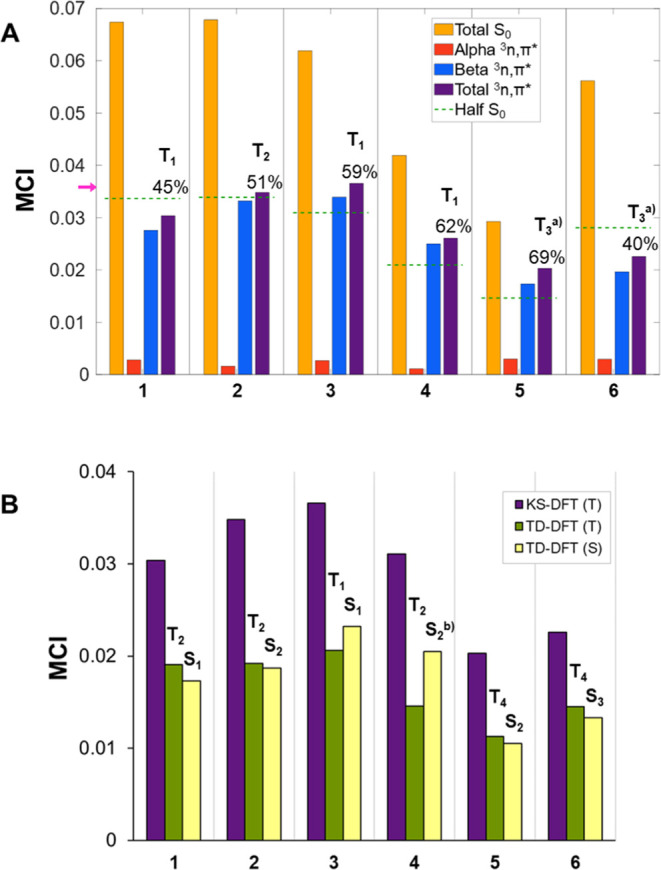
MCI results (in a.u.) of 6-MR monoheteroaromatics in (A) their n,π* triplet states (spin-separated MCI values) with KS-UDFT and (B) their singlet (S) and triplet (T) n,π* states at TD-DFT level, as well as the KS-UDFT results for the 3n,π* states for comparison. The purple arrow in (A) indicates the aromaticity threshold (0.0358). The state orders (Tn and Sn, n = 1, 2, 3,···) given above the bars represent the n,π* states. aT3 or higher. bMixed state. See SI Sections S1, S2.1, S3.1, and S3.2 for further details.
For the lowest 1n,π* states, we used TD-DFT, for which spin-separation is not possible. Therefore, to assess the quality of the results from TD-DFT, we computed MCI values for the 3n,π* states using both the KS-UDFT and the TD-DFT formalisms and found that MCI values from TD-DFT are consistently lower by a third to half of the values from KS-UDFT (Figure 4B). This trend is ascribed to the nature of the associated wavefunction in TD-DFT (see Computational Methods in the SI).
Despite this, the trends observed in the TD-DFT results for the lowest 3n,π* states are very similar to those of KS-UDFT, both in terms of excitation energies and relative (anti)aromaticity assessed by MCI. Thus, we are confident that the 1n,π* and 3n,π* states are explored on comparable footings.
The energetic order of the vertical 1n,π* states matches well that of the corresponding 3n,π* states, and the total MCI values show that the (anti)aromatic characters in the two states are similar for most 6-MR monoheteroaromatics. The exceptions are 3 and 4 for which the 1n,π* states are more aromatic than the 3n,π*, yet, further analysis is impossible as the MCIα- and MCIβ-components cannot be separated in results from TD-DFT computations. Still, for 4 the lowest 1n,π* state (the S2 state) is of mixed n,π*/Rydberg character in contrast to the lowest 3n,π* state which is a pure valence excited state. On the other hand, for 3 the first 1n,π* state is the 11A2 (Type II, Figure 3B), opposite to the other 6-MR monoheteroaromatics for which the lowest 1n,π* states are 11B1. In summary, the extent of (anti)aromaticity of the lowest singlet and triplet n,π* states is similar in four of the six 6-MR monoheteroaromatics.
Now, are n,π* states with highly aromatic residuals normally T1 states, while the T1 and S1 states are of π,π* character for heteroaromatics which have lowest n,π* states with non- or antiaromatic residuals? Figure 4 clarifies that for 6-MR monoheteroaromatics this is the case for some, e.g., 3 with an aromatic residual and T1 and S1 states of n,π* character, and 6 with an antiaromatic residual and T1 and S1 states of π,π* character. However, 1 with a residual that leans toward antiaromaticity also has T1 and S1 states of n,π* nature. Noteworthy, the order between the lowest 3n,π* and 3π,π* transitions, as well as the type of 3n,π* state (B1 or A2), are nearly always the same with UDFT and TD-DFT (Tables S21 and S27, SI), except for 1 and 4 for which the order of 3n,π* and 3π,π* transitions are switched. In summary, the electronegativity of the heteroatom influences the order and energy difference between the b1 and a2 symmetric π* orbitals (see below), and consequently, it has a great impact on the order of the 3n,π* and 3π,π* transitions.
In the Introduction, we asked if a more aromatic (antiaromatic) residual of the 3n,π* state correlates with a lower (higher) vertical excitation energy. However, this hypothesis oversimplifies as the vertical excitation energy also depends on (de)stabilizing features of the S0 state, including (anti)aromaticity and several other factors (see Section 2). Still, the monoheteroaromatics with residuals that lean toward aromaticity (3 and 4) are the two with lowest E(3n,π*) (2.6 and 2.9 eV, respectively), while thiopyrylium (6), with its antiaromatic residual, and the S0 nonaromatic pyrylium (5) have E(3n,π*) of 5.5 and 5.8 eV, respectively. The same relationship is observed for the 1n,π* states (3.1 (3), 3.8 (4), 5.1 (1), 5.1 (2), 5.7 (5), and 6.1 eV (6)). However, the E(n,π*) values also vary with the n orbital energies as this orbital is of very low energy for 5 and 6 being the second below the highest occupied molecular orbital (HOMO–2) at 2.09 and 1.78 eV below the highest occupied π-orbital (HOMO), but high for 3 and 4 (for 3 it is as much as 1.89 eV above the highest occupied π-orbital, which is HOMO–1). Also, the highest π and lowest π* orbital energies vary between the heteroaromatics (Table S47, SI). As a result, for 3 the energy differences between the n and the b1 π* orbital versus the highest π and the b1 π* orbital are 7.77 and 9.66 eV, while for 5 these energy differences are 10.44 and 8.36 eV, respectively. Thus, electronegativity variations among the E atoms impact strongly on the n,π* excitation energies, and these are not necessarily related to (anti)aromatic character.
For the 3n,π* states, EDDB results (Figure 5A) are consistent with the MCI findings. The πβ-components of 3 and 4 are slightly larger than half of the total π-S0 value, indicating aromatic character of the residuals of their 3n,π* states. In contrast, for the remaining 6-MR monoheteroaromatics, the πβ-component is lower in the 3n,π* state than in S0. More comprehensive EDDB results, specifically dissecting σ and π contributions, are provided in Section S2.2 in the SI.
Figure 5.
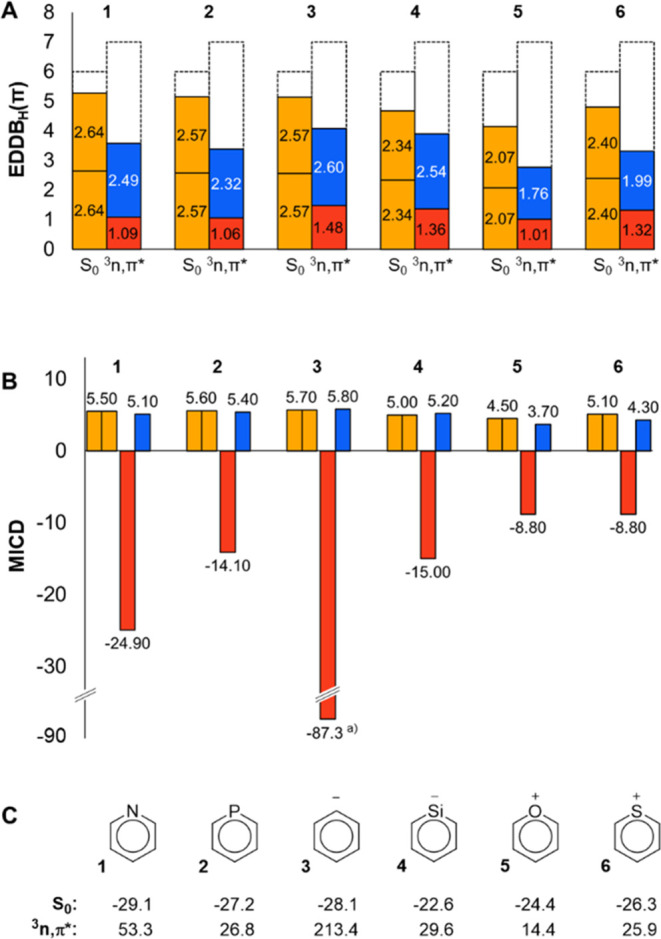
Aromaticity of the monoheteroaromatics in their S0 and 3n,π* states at the UCAM-B3LYP/6-311+G(d,p) level; (A) π-EDDB values (units are electrons), where red and blue bars correspond to, respectively, α- and β-electrons (as references, the total π-EDDB value is 5.33 e for benzene in its aromatic S0 state and 2.77 e for pyridine in its antiaromatic 3π,π* state, see Section S2.2 in the SI for more details, especially on spin-separated reference values). The dashed line bars show the total number of π-electrons in that state. (B) π-Electron bond current strengths (in nA T–1) calculated as the average of all bonds in the given ring, where red and blue bars represent α- and β-electron contributions, respectively. (C) NICS(1)zz values (in ppm).
The trend in MICD results (Figure 5B) resembles that of the electronic indices, but the values are markedly offset toward antiaromaticity since the πα-components give strong paratropic influences. As an illustration, Figure 6 displays the spin-separated π-electron MICD maps of the S0 and 3n,π* states of 1, as well as the orbital transition scheme which provides a qualitative rationalization.57−59 In S0, the π-electrons of all monoheteroaromatics induce diatropic currents due to translational transitions between the occupied b1 and a2 orbitals and the unoccupied b1 and a2 orbitals (blue arrows, Figure 6E).60 Analogous transitions are found within the πβ-electron stack of the 3n,π* state, giving diatropic current contributions. However, the πα-electrons induce strongly paratropic currents arising from the rotational transition from the highest occupied b1 orbital (the α-SOMO) to the empty a2 orbital (red arrow). Although the α-SOMO-1 (a2) and α-SOMO-2 (b1) contribute to diatropic currents through translational transitions to the unoccupied a2 orbital, these contributions are small in comparison to the paratropic current contributions.
Figure 6.
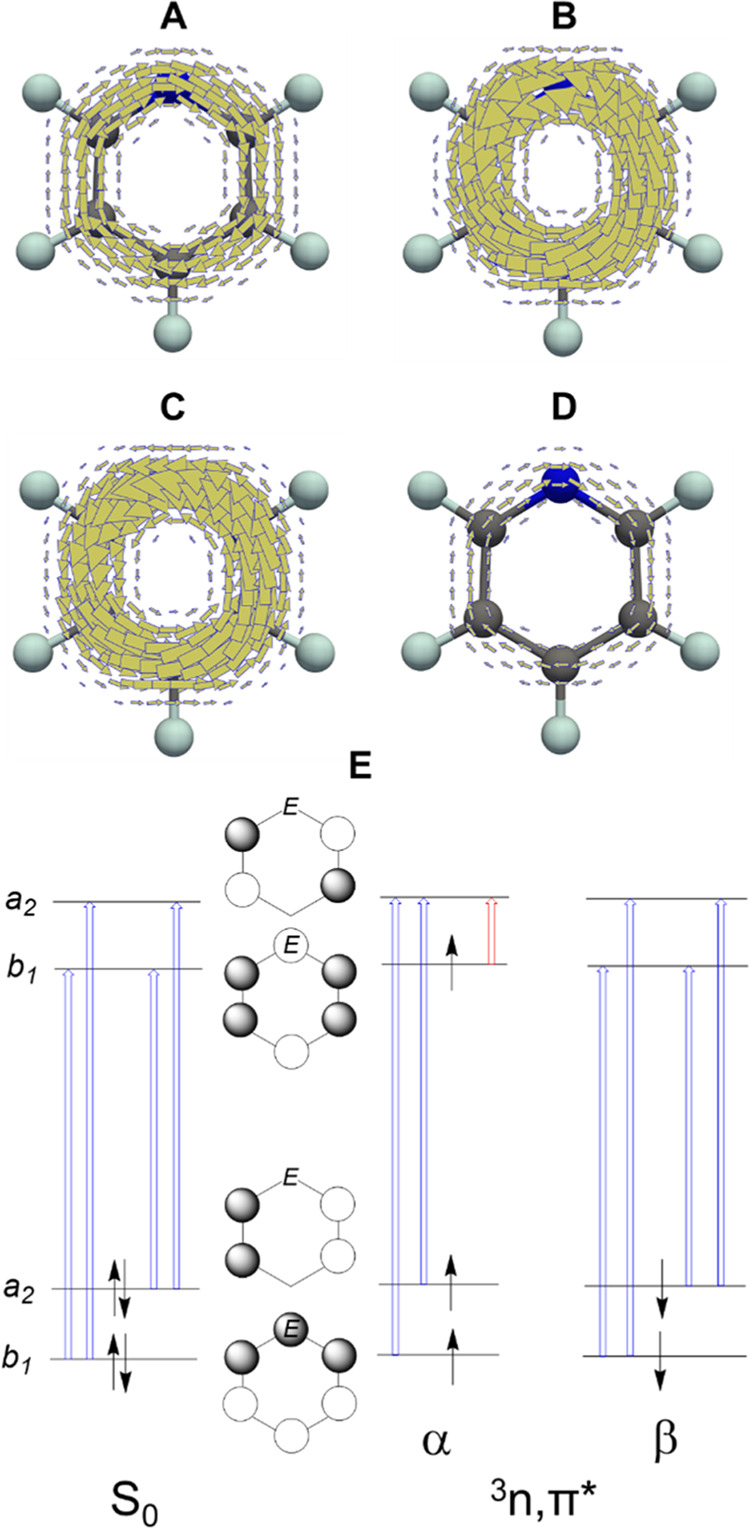
Maps of magnetically induced π-electron current densities calculated at 1 bohr above the molecular plane of 1: (A) S0 state, (B) 3n,π* state, (C, D) πα- and πβ-electron contributions to the 3n,π* state. Clockwise (anticlockwise) circulation corresponds to diatropic (paratropic) currents. (E) Qualitative energy level diagram for the frontier molecular orbitals in the S0 and 3n,π* states of monoheteroaromatics. Blue arrows indicate the translationally allowed transitions (inducing diatropic currents), and the red arrow indicates the rotationally allowed transition (inducing paratropic currents). Only the most relevant transitions, based on the values of the linear and angular momentum matrix elements, were selected.
Here it should be noted that the relative importance of the various orbital transitions within the πα-electron stack is related to the energy differences between the respective occupied and unoccupied orbitals, related to the electronegativity of the E atom (see above) and not to (anti)aromaticity. As a consequence, the magnetic (anti)aromaticity of the n,π* state may not agree with the electronic, energetic, and geometric aromaticity aspects, similarly as reported for the 3π,π* state of B4N4H861 and, in the S0 state, for (N6H6)2+ and C2N4H6.62 For a detailed analysis of the orbital transitions, see Table S20, SI. It can be noted that the NICS(1)zz values (Figure 5C) closely follow the trend of the MICD values, but they provide less information as they are not spin-separated. As a result, 3 in its 3n,π* state is the most antiaromatic among 1–6 with NICS, while the most aromatic with MCI.
Next, we analyze why there is a variation in the (anti)aromatic character of the 3n,π* states of 6-MR monoheteroaromatics. Both the E atom electronegativity and the molecular charge play roles as one can see that a low electronegativity of E and a negative charge lead to stronger aromatic character of the residual. The variation also seems to depend on the local pπ orbital overlap which differs among the monoheteroaromatics. For this reason, we analyzed the degree of uniformity in the π-electron distribution in the ring by calculating the root-mean-square deviation of π-electron distribution (RMSD(π)) obtained from a natural population analysis (NPA). Interestingly, there are good correlations between the MCI and RMSD(π) values for both S0 and 3n,π*, indicating that the more uniformly distributed the π-electrons, the higher the MCI values (Figure S4, SI). It is further notable that there is a reasonable correlation with the change in the RMSD(π) of the πβ-electron distribution when going from S0 to T1 and the degree of (anti)aromaticity of the residual, implying that if the πβ-electron distribution becomes more (less) uniformly distributed upon excitation, the residual of the system will become more aromatic (antiaromatic).
3.3. Diheteroaromatic 6-MRs (Group B)
The analysis becomes more complex for molecules with two heteroatoms as (i) there is a variation in the S0 aromaticity with the relative positions of the two heteroatoms,34,35 (ii) with two lone pairs there are several n,π* states since there are two (near-degenerate) lone-pair orbitals in addition to the two (near-degenerate) π* orbitals (potentially leading to multiconfigurational character), and (iii) there can be a variation among diheteroaromatics as to which n,π* state is lowest in energy. To facilitate, we split the diheteroaromatics in two subgroups: one composed of those with two different heteroatoms (10–14) and one of those with two equal heteroatoms (7–9 and 15–19). Additionally, we consider the protonated species of two compounds in the latter subgroup (9H+ and 19H+). Those with two different heteroatoms should, viewed simplistically, have the highest n orbital dominated by the least electronegative element, and their first n,π* state may resemble those of the monoheteroaromatics with the same heteroatom. Yet, we will see that this is not necessarily the case. We calculate MCI throughout the group and MICD for selected compounds.
Diheteroaromatic 6-MRs with E′ ≠ E
Starting with the three azaphosphinines 10–12 in their 3n,π* states computed at UCCSD(T) level, we found that these exhibit some multiconfigurational character (T1 diagnostics >0.044, the threshold for open-shell species).54−56 Accordingly, we explored these species also at UBD and CASSCF levels and found that multiconfigurational character does not impact on the aromaticity results (see Sections S2.1, S3.1, and S3.6 in the SI). Indeed, the trend in the MCI values computed with UCAM-B3LYP agrees with that of UBD.
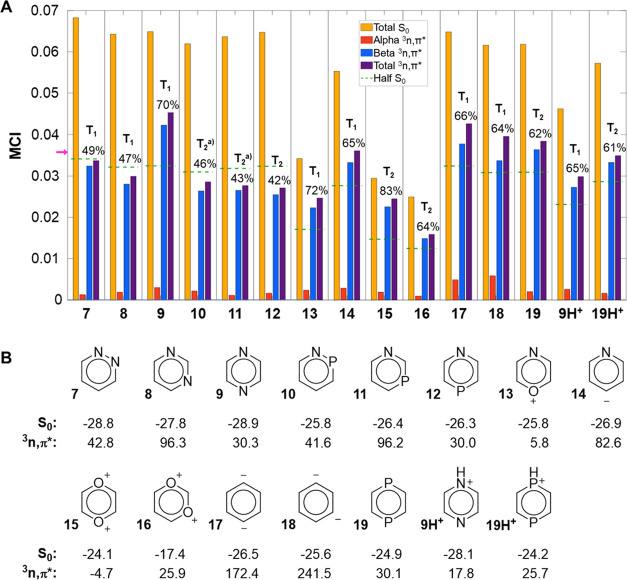
In S0, there is a minute increase in the aromaticity when going from 10 to 12 according to MCI, in line with earlier findings based on NICS,45,63−65 but in the lowest 3n,π* state, there is instead a minute decrease (Figure 7A). The MCI(3n,π*)tot values of 10–12 are similar to those of 1 and 2 (Figure 4A); however, their residuals (with MCI(3n,π*)tot at 42–47% of the MCI(S0) values) tend toward antiaromatic character whereby they resemble 1 more than 2. This is consistent with the fact that both C and P have low electronegativity, and that P has been labeled a “carbon copy”.66 With regard to the lone-pair orbitals, which are singly occupied in the lowest 3n,π* states, they are more localized on P than on N (Figure 8), but if one instead views the lone-pair orbital which is unoccupied it resembles the corresponding orbital in S0 and is more localized on N than on P.
Figure 7.
(A) MCI results (in a.u.) of diheteroaromatics in their triplet n,π* states (spin-separated) with UCAM-B3LYP/6-311+G(d,p). The purple arrow indicates the aromaticity threshold value for S0 (0.0358). The state orders Tn (n = 1, 2, 3,···) is given above the bars that represent the 3n,π* states. aT2 or higher (see SI Sections S2.1 and S3.1 for further details). (B) NICS(1)zz values in their S0 and 3n,π* states (in ppm).
Figure 8.
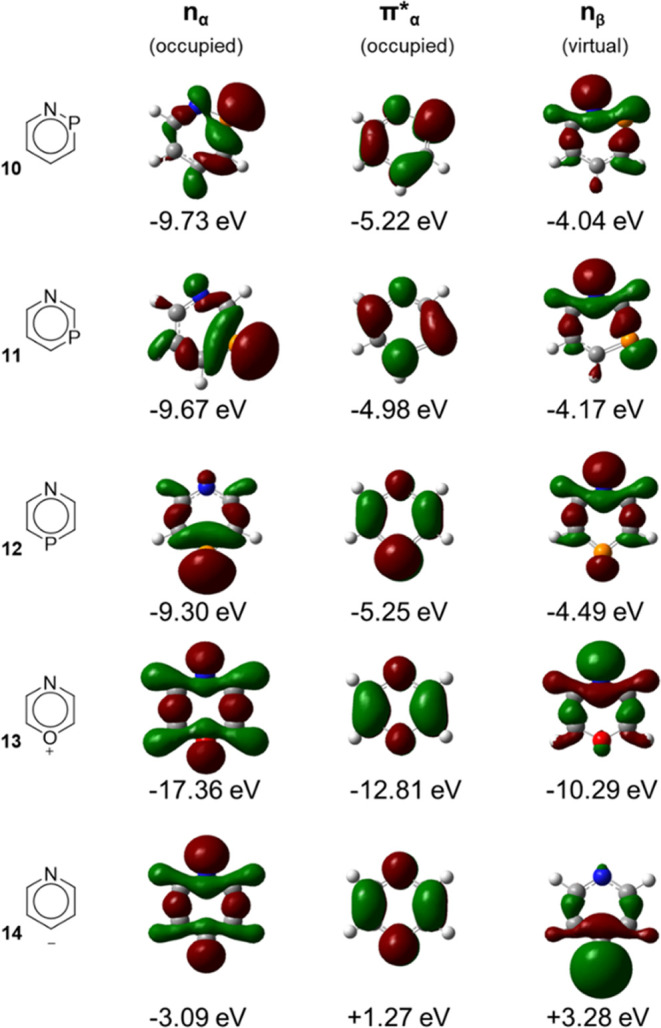
Singly occupied and unoccupied n and π* orbitals of 10–14 of the 3n,π* state, with orbital energies in eV. Noteworthy, the virtual lone-pair orbitals in the rightmost column resemble the doubly occupied lone-pair orbitals in S0. Isosurfaces of 0.040 au.
Although oversimplified, in Section 1, we put forth that the (anti)aromatic character of the residual and the vertical E(3n,π*) may correlate among isomers. Indeed, there is no extensive variation in the (anti)aromatic character neither in the S0 states of 10–12 nor in the residuals of their 3n,π* states, and the variation in their vertical E(3n,π*) is modest (3.34–3.60 eV), in line with the postulation. Furthermore, the 3n,π* states of 10–12 are not the T1 states but higher states (Figure 7A), a fact that might be explained by the non- or antiaromatic character of the residual of the n,π* state. The T1 states are instead of π,π* character.
Of the two other diheteroaromatics with E ≠ E′ (13 and 14), it is only 14 that exhibits a sufficiently aromatic character in S0 to satisfy our aromaticity criterion (MCI ≥ 0.0358). The 3n,π* state of 14 resembles that of 3, whereby also this excitation can be described as that of a monoheteroaromatic. Further support for this interpretation comes from the shape of the formal n orbital involved in the n,π* excitation since it has a marked localization at the anionic C atom (Figure 8). With regard to 13, it has a nonaromatic S0 state, yet, is still interesting as its MCI value in 3n,π* is significantly higher than half the S0 value. Thus, the MCI(3n,π*)tot value is intermediate between that of 5 and 1.
Diheteroaromatic 6-MRs with E′ = E
Among these species, the diazines and compounds 17 and 18 exhibit multiconfigurational character which should stem from near-degeneracy of the two lowest 3n,π* states (see Tables S25 and S53, SI). However, results from UBD calculations again corroborate that UCAM-B3LYP provides reliable aromaticity results and trends (Tables S8, S11, and S12, SI).
For the diazines 7–9, the aromaticity in S0 (Figure 7A) follows the established order pyridazine (7) > pyrimidine (8) ∼ pyrazine (9).67 Their lowest 3n,π* states are the T1 states and we find that the excitations are of similar type (Table S24, SI), although a comparison is ambiguous due to their different structures and symmetries. According to MCI, the 3n,π* state of 9 has a residual with clear aromatic character, while 7 and 8 have nonaromatic residuals (i.e., approximately half of the S0 values). Interestingly, although the largest difference in the MCI values between 7, 8, and 9 is due to the MCIβ-component, the MCIα of 9 is also larger than those of 7 and 8, indicating a weaker πα-antiaromatic contribution in the 3n,π* state of 9. These findings also agree with those of a recent study on the lowest excited states of the three diazines, yet, where these states were not differentiated as n,π* or π,π* states.24 It was argued that the more aromatic a molecule is in its S0 state, the more antiaromatic it will be in its first excited states. Such relationships were earlier found among the π,π* states of substituted fulvenes and related hyperconjugated compounds,68 i.e., specific compound classes. However, we find that this is not valid for the diazines because 7 is more aromatic than 8 in both its S0 and T1 (3n,π*) states.
The diazines make it clear that the hypothesis that E(3n,π*) is correlated with the (anti)aromaticity difference between S0 and the 3n,π* states is also oversimplified when regarding only isomers. Among 7–9, the largest difference in (anti)aromaticity between the two states is found for 7 while the smallest is found for 9 (Figure 7A), but 7 has the lowest E(3n,π*) (2.95 eV) and 8 the highest (4.13 eV). Further analysis reveals that the excitation energies are primarily influenced by the relative S0 energies of the three isomers because 8 is more stable than 7 by 1.03 eV (Table S24, SI), a feature that stems from repulsion between the lone-pair electrons of the two adjacent N atoms of 7.69
Here we explore why the 3n,π* state of 9 exhibits a highly aromatic residual according to MCI, and if the same trend among the diazines is found with magnetic and energetic aromaticity descriptors. An energy-based evidence of a higher aromatic character of the 3n,π* state of 9 than those of 7 and 8 comes from the relative energies, because 7 and 8 in their 3n,π* states are higher in energy than 9 by, respectively, 0.21 and 0.34 eV. Additionally, and in agreement with the MCI results, the calculated MICD for 7–9 demonstrate that only 9 exhibits a somewhat stronger diatropic πβ-electron ring current in its 3n,π* state compared to its S0 state. Moreover, the α-HSOMO of 9 has the least intensive paratropic contribution among 7–9, in accordance with the values of the α-HOMO–LUMO gap (Table S20, SI). Finally, the NICS values reflect a lower paratropicity of 9 (Figure 7B). Taken together, electronic and energetic descriptors thus support that the 3n,π* state of 9 has some aromatic character, and the magnetic indicators reveal that 9 has the least antiaromatic T1 state among the diazines. In this context, it is notable that perfluoropyridazine in its S1 state, which is of 1n,π* character, photorearranges to the corresponding pyrazine,70,71 possibly driven by a gain in aromatic character. Rewardingly, the same trends are found for the S1 states (all 1n,π*) of the diazines as for their T1 states (all 3n,π*), with 9 being the most stable and aromatic isomer also in S1 (Tables S13 and S28, SI).
Further clarity on the cause of the aromatic residual is gained by looking into the distribution of the π-electrons. The π-electron population in S0 is more evenly spread in 7, followed by 9, and last by 8, in line with the results of Figure 7. In contrast, in the 3n,π* state of 9 the π-electron distribution is clearly more uniform than in the other two species due to the high symmetry of the former (see Tables S35–S37, SI). In fact, the πβ-electron population is even more evenly distributed in this state than in the S0 state. Looking into the spin distributions, there is an accumulation of the excess πα-electrons around the N atoms of 9. For 7 and 8, both the πα- and the πβ-electrons are quite localized at the N atoms and at certain C atoms (different for each of the spins), leading to a less uniform π-electron distribution and lowered aromaticity for both spins. Conversely, in D2h symmetric 9, despite some accumulation around the N atoms, the distribution of πβ-electrons is forced by symmetry to be more uniform (all C atoms have the same π-electron population), which explains the aromaticity increase of the MCIβ-component.
Among the other compounds with E = E′, 15, 17, and 19 have residuals in their 3n,π* states with considerable aromatic character. Hence, it is obvious that the placement of two equal heteroatoms with in-plane lone-pairs in para-positions, leading to D2h symmetric molecules, provides for n,π* states with strong aromatic character of the residuals. For 17 and 18, it is also notable that the MCIα-components are significant, presumably a result of the fact that the excitation involves promotion of an α-electron into an orbital with diffuse character as a result of the low electronegativity of carbon. Although MICD was not computed for these species, NICS supports the MCI results as the para-isomers are the least antiaromatic isomers (Figure 7B).
One can note that the E atom electronegativity impacts on the S0 state aromaticity, and also on the total MCI value of the 3n,π* state. However, the main factor impacting the MCI value of the 3n,π* state, relative to the S0 state, is the placement of the heteroatoms as the para-isomers always have markedly aromatic residuals (Figure 7A). One can also note that the increase mainly occurs in the MCIβ-components. Furthermore, one may expect that an increased electrostatic repulsion could lead to a more even distribution of the πβ-electrons among atoms in the 6-MR. Yet, when regarding 9 and 17, which both are strongly aromatic in S0, and which also have strong aromatic character of the residual of the 3n,π* state, the two species have different π* orbitals and their n,π* states are thus of different types (B1 in 9 and A2 in 17). Hence, the type of π* orbital, and accordingly, the spatial distribution, seems unrelated to the aromatic character of the residual according to MCI. For these species, we did not explore spin-separated MICD, but with NICS the situation is opposite to that of MCI because with this index compounds 17 and 18 are strongly antiaromatic in their 3n,π* states (Figure 7B). This feature resembles that observed with NICS for 3 and stems from an extensive paratropic πα-contributions.
A further item to note is that compounds with electronegative E atoms (primarily O) which are weakly aromatic or nonaromatic in S0, gain some aromaticity in the MCIβ-component in the n,π* state (i.e., they obtain values that are more than half of that in S0). These species have rather localized π-electrons in S0 because of the highly electronegative and electron-deficient O+. Upon excitation to the n,π* state, the delocalization of the πβ-electrons increases due to the addition of one electron to the π-system, and the β-component of MCI increases (see Figures 4A and 7A).
Finally, for all diheteroaromatics, we also found a good correlation with the change in the RMSD(π) of the πβ-electron distribution when going from S0 to the 3n,π* state and the degree of (anti)aromaticity of the residual (Figure S6, SI). In particular, the π-electron distributions in the 3n,π* states of 9 and 15, with two equal E atoms in para-positions, are clearly more uniform than in their isomers due to their D2h symmetry.
Protonated Para-Diheteroaromatics
For the diheteroaromatics with E = E′ atoms at para-positions and with aromatic S0 states (9, 17, and 19) we also explored the changes in (anti)aromatic character upon protonation of their 3n,π* states. This leads to 9H+, 3, and 19H+, respectively. These three species remain aromatic in S0, but less than when unprotonated. Importantly, though, the residuals of their 3n,π* states remain aromatic in character in each of these species, indicating that protonation reduces the aromaticity of both the S0 and 3n,π* states to similar relative amounts. In contrast, when 14 is protonated at the negative C atom, leading to 1, there is no aromatic but rather an antiaromatic residual. From this, we conclude that the two features that lead to an aromatic residual are high symmetry (D2h or nearly so) and negative charge (excess of electrons).
3.4. Generalizations and Tentative Applications
The findings presented above can be generalized. In Section 2, we argued that in an n,π* state there is a tug-of-war between the antiaromatic πα-component and the aromatic πβ-component. Is there support for this hypothesis when considering all investigated molecules? We also discussed the potential correlation between the excitation energy and the (anti)aromatic character of the residual but pointed out factors unrelated to (anti)aromaticity that also affect excitation energies. Still, is the hypothesis valid for a limited set of compounds, e.g., substituted derivatives of a certain heteroaromatic? Figures 4 and 7 reveal that heteroaromatics with n,π* states with aromatic residuals often have these states as T1 or S1 states. Yet, is there a connection to the (anti)aromaticity of the residual of the n,π* state and the energy difference between the lowest n,π* and π,π* states? We further test if the knowledge gained on the (anti)aromatic character of the n,π* state can be expanded to other species that are not traditionally seen as heteroaromatics. Finally, we address molecules and features that tentatively can be useful for applications.
Our hypothesis on the molecular relaxation of the 3n,π* states is shown in Figure 3; the aromatic β-component strives to keep the S0 geometry whereas the α-component prefers to distort to release antiaromaticity. To analyze the effect of structural relaxation on the aromaticity of the 3n,π* states, we optimized the 3n,π* geometries of 1–9. Compound 5 is, however, not considered since it is nonaromatic in S0. In line with the tug-of-war hypothesis, two main behaviors were observed. First, in one set of heteroaromatics (1, 2, 4, 6, and 8, Section S3.5 in the SI), the antiaromaticity of the α-component is reduced significantly, but at the same time, the aromatic β-component is also clearly diminished. For example, during geometry optimization in its 3n,π* state, 1 puckers and becomes a mixed n,π*/π,π* state. In this process, the MCI(3n,π*)tot relative to the MCI(S0) value decreases from 45 to 22%, mainly due to aromaticity loss in the β-component, whereas the paratropic πα-electron current decreases from −25.5 to −4.9 nA T–1 and the diatropic πβ-electron current diminishes from 5.6 to 0.2 nA T–1. The change in α-contribution is not as pronounced with MCI, as this index cannot clearly differentiate between antiaromaticity and nonaromaticity (see discussions and examples in the MCI and EDDB sections in the SI). In the second set of compounds (3, 7, and 9), the aromatic β-component remains almost unaffected while the antiaromatic α-component is reduced slightly. For instance, 3 upon relaxation from its vertical 3n,π* state shifts to a planar, antiquinoidal structure. The residual remains unchanged (the MCI(3n,π*)tot relative to MCI(S0) only decreases from 59 to 58%) while the paratropic πα-electron current decreases (from −89.4 to −36.8 nA T–1) and the diatropic πβ-electron current remains almost the same (from 5.9 to 6.1 nA T–1). Unfortunately, classification in one or the other set is not related to the extent of (anti)aromatic character of the residual in the vertical 3n,π* state (e.g., 4 with an aromatic residual and 6 with a residual that tends toward antiaromaticity belong to the same set). Other factors, such as the preferred valence angle of a certain E atom or changes in exchange interaction upon excitation, should also play relevant roles.
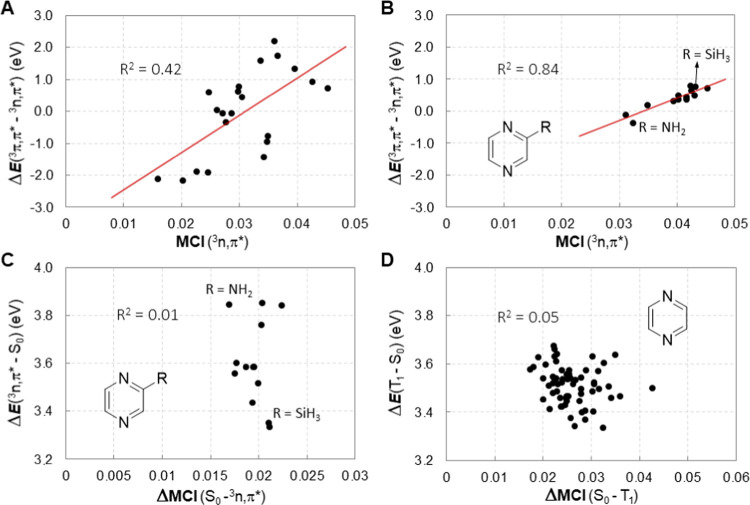
By jointly considering the investigated mono- and diheteroaromatics, one can conclude that as a rule-of-thumb a molecule with a high MCI(3n,π*)tot is likely to have its first 3n,π* state below the lowest 3π,π* state (Figure 9A), although the correlation is weak (R2 = 0.42). Yet, the energy difference between the 3n,π* and 3π,π* states should depend on both the (anti)aromatic character of the 3n,π* state and the destabilizing antiaromatic character of the 3π,π* state. Our focus herein is however on the n,π* states, while the π,π* states need a separate study.
Figure 9.
(A) ΔE(3π,π* – 3n,π*) vs MCI(3n,π*) for 1–19H+, (B) ΔE(3π,π* – 3n,π*) vs MCI(3n,π*) for 9 and monosubstituted pyrazines, (C) E(3n,π*) vs ΔMCI(S0 – 3n,π*) for 9 and monosubstituted pyrazines, and (D) distorted structures of 9 obtained through a normal mode following algorithm.
At this point, one can ask if the order between the 3n,π* and 3π,π* states instead (primarily) can be related to orbital energy differences? Indeed, the energy difference between the n and lowest π* orbital as compared to the highest π and lowest π* orbital is larger for pyrazine than for pyridine (the orbital energy differences are 8.29 and 8.83 eV for pyrazine and 9.08 and 9.11 eV for pyridine, respectively, Table S48, SI). Yet, there is also a clear effect by the (anti)aromatic character of the 3n,π* state because for 9 and monosubstituted pyrazines there is a clear correlation (R2 = 0.84, Figure 9B) between the ΔE(3π,π* – 3n,π*) and MCI(3n,π*), and there is a corresponding correlation between ΔE(3π,π* – 3n,π*) and NICS(3n,π*) although weaker (R2 = 0.58, Figure S11, SI). Hence, the lowest 3n,π* states of the species which have these states as their T1 states are more aromatic than in the species which have these states as higher excited states (Tables S55–S56, SI). Most monosubstituted pyrazines have T1 states of 3n,π* character (Figure 9B), yet, the π-donating amino substituent leads to a pyrazine with the 3π,π* state as T1. However, as stated above, to only use the (anti)aromatic character of the 3n,π* state is an approximation because also the antiaromatic character and energy of the 3π,π* state is influenced by substituents.72
We also considered 9 and the monosubstituted pyrazines when analyzing the hypothesis on a correlation between the vertical E(3n,π*) and ΔMCI(S0 – 3n,π*), but in this case there is no correlation (Figure 9C). One reason can be partial delocalization of the excitation onto the substituent, similar to previous findings on the 3π,π* state of substituted benzenes (vide supra).72 Still, the amino substituent leads to a pyrazine with high E(3n,π*) while the silyl group does the opposite. We also explored this for 9 at distorted structures with relative energies at most 10 kcal/mol above the optimum, and also in this case we find no correlation (R2 = 0.05, Figure 9D), likely due to a more significant loss of aromaticity in T1 upon distortion than in S0 (see SI, Section S3.9).
Our theoretical framework for analysis of n,π* states can be used to explore molecules with other types of excited states with an odd total number of π-electrons. Osmapyridinium complexes 20 and 21 (Figure 10A) have T1 states of 3π,σ* and 3σ,π* character, and were earlier found to be aromatic in both their S0 and T1 states (labeled adaptive aromatic).30 We now analyzed the spin-separated MCI and MICD of both vertical and relaxed 3σ,π* states (Figure 10 for MICD and Figure S14 in the SI for MCI results). Of the two species, 21 in 3σ,π* should be regarded as aromatic because its MCI(3σ,π*)tot value is 57% of the MCI(S0) value, while this state for 20 tends toward antiaromaticity (MCI(3σ,π*)tot is 39% of the MCI(S0) value), or alternatively, as nonaromatic if based on the previously reported MCI results.30 The results are mainly due to a relative increase and decrease of the MCIβ-component, respectively (see Section S3.11 in the SI for more details). Thus, by considering the α- and β-spin components separately, it becomes clear that the phenomenon labeled adaptive aromaticity and used for some metalla-aromatics can be rationalized within the same framework as that of the n,π* states of regular heteroaromatics. Thus, adaptive aromaticity is not a new form of aromaticity but a result of an imperfect cancellation of the antiaromatic α- and aromatic β-components as given by Mandado’s rule. Such situations will generally occur for electronic states described as excitations from an in-plane orbital to an out-of-plane orbital (or vice versa), or as a one-electron excitation to (or from) one annulenyl fragment from (or to) another fragment of a molecule, e.g., a metal-to-ligand charge transfer state.
Figure 10.
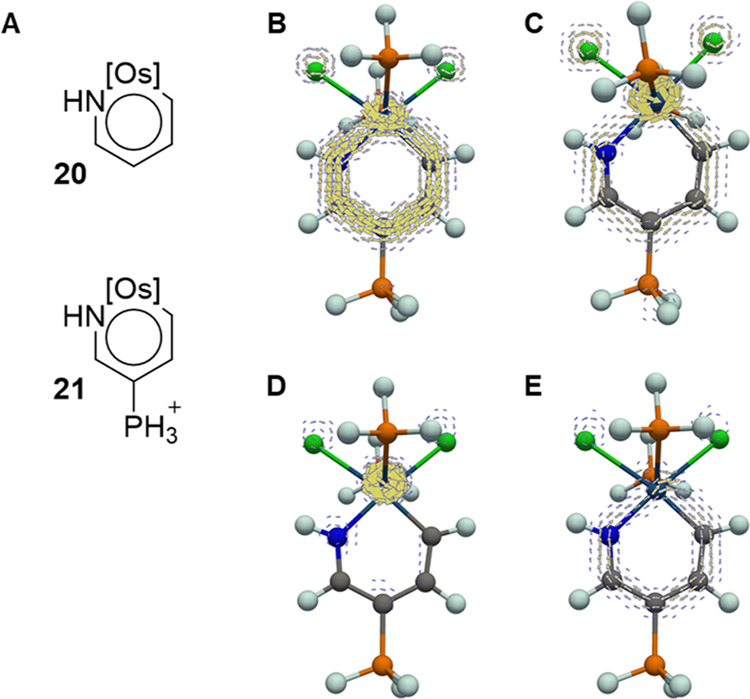
(A) Osmapyridinium complexes 20 and 21, and (B–E) π-electron MICD plots calculated 1 bohr above the molecular plane of 21: S0 state (B) and vertical 3σ,π* state (C) with the corresponding πα- and πβ-electron contributions (D, E). Clockwise circulation corresponds to diatropic (aromatic) currents. Full-scale plots in the SI.
Returning to pyrazine, the findings above can explain what we recently found for the photolabile drug amiloride.73 Amiloride is a pyrazine derivative with one π-electron withdrawing and three π-electron donating substituents, and this substituent pattern explains why its T1 state is of π,π* instead of n,π* character. Indeed, its light-induced degradation goes via a sequential two-step photoionization where the ionization step occurs from the antiaromatic T1 state of π,π* character.73 Such destructive photoionization can possibly be avoided by substituent patterns that instead lead to T1 states of 3n,π* character. For further examples on the tuning of excited state character, see Section S3.10 of the SI on polyazaacenes such as quinoxaline.
Above we found that the high symmetry of pyrazine leads to an 3n,π* state with an aromatic residual. In this context, 1,3,5-triazine (s-triazine) is a D3h symmetric N-containing heteroaromatic found in several agrochemicals.8 Interestingly, the s-triazine core in these agrochemicals is inert upon photoexcitation, whereas the substituents change positions. High-level computations also reveal that the lowest few excited states are of n,π* character.74 Thus, one may postulate that the photostability of s-triazine-based agrochemicals stems from aromatic residuals of their n,π* states. Yet, as these states are highly multiconfigurational (both the highest n orbitals and the lowest π* orbitals are doubly degenerate, Table S48, SI), a proper analysis requires an in-depth computational study.
4. Conclusions and Outlook
We examined the n,π* states of heteroaromatics with six π-electrons and in-plane lone-pairs (e.g., pyridine and the pyrylium ion), and applied Mandado’s 2n + 1 rule for aromaticity of separate spins. In their n,π* states, these species have four πα-electrons and three πβ-electrons, which leads to a tug-of-war between the antiaromatic πα-component and the aromatic πβ-component. The component that dominates varies between heteroaromatics and between aromaticity descriptors; the residuals between the two components can lean toward aromaticity or antiaromaticity. Yet, is there a pattern?
We first note that the n,π* states of 5-MR mono- and diheteroaromatics (e.g., thiophene and imidazole) lie far above the lowest excited states, which are of π,π* character, and we provide an explanation for this (see Section S3.7 in the SI). In contrast, for 6-MR heteroaromatics with one or two heteroatoms, the n,π* states that are T1 states often have rather aromatic character, mostly due to a larger β-component than in the Hückel-aromatic S0 state. Importantly, similar (anti)aromaticity trends were observed with both the magnetic and the electronic indices, but the antiaromatic character of the α-component is much more dominant in the results of the magnetic indices than in those of the electronic indices.
Also, the (anti)aromatic character of the residual is generally the same for the singlet and triplet n,π* states. The heteroaromatics that are likely to exhibit significant aromatic character in their lowest n,π* states are molecules with high symmetry (D2h), where electrons become more uniformly distributed, and/or with π-electron donating heteroatoms. Heteroaromatics with such n,π* states often have these as their T1 states. For the limited set of monosubstituted pyrazines, we observe a significant correlation between the energy difference between the lowest 3n,π* and 3π,π* states and the (anti)aromatic character of the 3n,π* state, yet, a comprehensive analysis must include also the antiaromatic destabilization of the 3π,π* state.
Although the vertical excitation energies of the n,π* states depend on several factors of both the S0 and n,π* states, the relative energies of isomeric heteroaromatics in their n,π* states vary in dependence of the aromatic character of the residuals. For example, the n,π* state of pyrazine (9) has a residual which is more aromatic than the n,π* state of pyrimidine (8), with the first being lower in energy than the latter by 0.34 eV.
Regarding the geometric relaxation of the n,π* state, there is a tug-of-war between the aromatic πβ-component, which tries to maintain the S0 state geometry, and the antiaromatic πα-component, which seeks to lessen its antiaromaticity through geometric distortions. Here, we identified two possible scenarios. In some systems, the antiaromaticity of the α-component and the aromaticity of the β-component are reduced significantly, while in others, the aromatic β-component remains almost unaffected while the antiaromatic α-component is reduced only slightly.
The approach described here for n,π* states of heteroaromatics can be generalized to analyze the aromaticity of other types of states with an odd total number of π-electrons. It can be utilized to understand the (anti)aromatic character of metallaaromatics which are not only aromatic in S0 but also in their triplet σ,π* and π,σ* states, earlier labeled as adaptive aromatic.29−33 Our analysis can also be extended to π-conjugated radical anions and cations such as C6H6+ or C8H8– with an even number of πα-electrons and an odd number of πβ-electrons, or vice versa. Indeed, radical cations or anions were analyzed by Mandado and co-workers who found by spin-separated NICS that their πα-component were antiaromatic and the πβ-components aromatic.19
Although the findings are fundamental in character, they can be applied. Earlier we found that amiloride-type drugs with central pyrazine moieties photodegrade along a two-step mechanism where the second step is a photoionization with an electron ejected from the antiaromatic T1 state of π,π* character.73 By knowing that the energetic order between the n,π* and π,π* states of pyrazines switch with substituents, and that the n,π* states have aromatic (stabilized) character, one may tailor amiloride-like compounds which have n,π* states as their T1 states. Moreover, with knowledge on how to rationally tune the order between the lowest n,π* and π,π* states through substituents, it also becomes clear how to design quinoxolines with lowest n,π* states, a feature that should be useful for the design of targeted species with interesting emission properties.
Acknowledgments
The authors are grateful to Mr. Fritz Deubel for performing initial computations, Dr. Ouissam El Bakouri and Dr. Eduard Matito for prompt responses on technical queries, and Prof. Per-Ola Norrby for valuable feedback. H.O. and N.P.V. acknowledge the Swedish Research Council for financial support (grant 2019-05618). M.S. and S.E. thank the Spanish Ministerio de Ciencia e Innovación for project PID2020-113711GB-I00/MCIN/AEI/10.13039/501100011033 and the Generalitat de Catalunya for project 2021SGR623. S.E. thanks Universitat de Girona and DIPC for an IFUdG2019 PhD fellowship. S.R. acknowledges support by the Serbian Ministry of Science, Technological Development and Innovation (Agreement No.451-03-47/2023-01/200122). Computations were enabled by resources of the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center (NSC), Linköping, Sweden.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.4c02580.
Aromaticity data; further analysis in terms of energy and electron distribution and additional data; including full-scale plots; input files; compound coordinates; and computational details (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Balaban A. T.; Oniciu D. C.; Katritzky A. R. Aromaticity as a Cornerstone of Heterocyclic Chemistry. Chem. Rev. 2004, 104, 2777–2812. 10.1021/cr0306790. [DOI] [PubMed] [Google Scholar]
- Baumann M.; Baxendale I. R.; Ley S. V.; Nikbin N. An Overview of the Key Routes to the Best Selling 5-Membered Ring Heterocyclic Pharmaceuticals. Beilstein J. Org. Chem. 2011, 7, 442–495. 10.3762/bjoc.7.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beverina L.; Pagini G. A. π-Conjugated Zwitterions as Paradigm of Donor–Acceptor Building Blocks in Organic-Based Materials. Acc. Chem. Res. 2014, 47, 319–329. 10.1021/ar4000967. [DOI] [PubMed] [Google Scholar]
- Luo D.; Jang W.; Babu D. D.; Kim M. S.; Wang D. H.; Kyaw A. K. K. Recent Progress in Organic Solar Cells Based on Non-Fullerene Acceptors: Materials to Devices. J. Mater. Chem. A 2022, 10, 3255–3295. 10.1039/D1TA10707K. [DOI] [Google Scholar]
- Chen X.; Tan D.; Yang D.-T. Multiple-Boron–Nitrogen (multi-BN) Doped π-Conjugated Systems for Optoelectronics. J. Mater. Chem. C 2022, 10, 13499–13532. 10.1039/D2TC01106A. [DOI] [Google Scholar]
- Huang J.; Yu G. Structural Engineering in Polymer Semiconductors with Aromatic N-Heterocycles. Chem. Mater. 2021, 33, 1513–1539. 10.1021/acs.chemmater.0c03975. [DOI] [Google Scholar]
- Lamberth C. Heterocyclic Chemistry in Crop Protection. Pest Manage. Sci. 2013, 69, 1106–1114. 10.1002/ps.3615. [DOI] [PubMed] [Google Scholar]
- Bioactive Heterocyclic Compound Classes: Agrochemicals; Lamberth C.; Dinges J., Eds.; Wiley-VCH Verlag Gmbh & Co: Weinheim, Germany, 2012. [Google Scholar]
- Baird N. C. Quantum Organic Photochemistry. II. Resonance and Aromaticity in the Lowest 3ππ* State of Cyclic Hydrocarbons. J. Am. Chem. Soc. 1972, 94, 4941–4948. 10.1021/ja00769a025. [DOI] [Google Scholar]
- Ottosson H. Organic Photochemistry: Exciting Excited-State Aromaticity. Nat. Chem. 2012, 4, 969–971. 10.1038/nchem.1518. [DOI] [PubMed] [Google Scholar]
- Karas L.; Wu J. I. Aromaticity: Baird’s Rules at the Tipping Point. Nat. Chem. 2022, 14, 723–725. 10.1038/s41557-022-00988-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg M.; Dahlstrand C.; Kilså K.; Ottosson H. Excited State Aromaticity and Antiaromaticity: Opportunities for Photophysical and Photochemical Rationalizations. Chem. Rev. 2014, 114, 5379–5425. 10.1021/cr300471v. [DOI] [PubMed] [Google Scholar]
- Papadakis R.; Ottosson H. The Excited State Antiaromatic Benzene Ring: A Molecular Mr Hyde?. Chem. Soc. Rev. 2015, 44, 6472–6493. 10.1039/C5CS00057B. [DOI] [PubMed] [Google Scholar]
- Oh J.; Sung Y. M.; Hong Y.; Kim D. Spectroscopic Diagnosis of Excited-State Aromaticity: Capturing Electronic Structures and Conformations upon Aromaticity Reversal. Acc. Chem. Res. 2018, 51, 1349–1358. 10.1021/acs.accounts.7b00629. [DOI] [PubMed] [Google Scholar]
- Liu C.; Ni Y.; Lu X.; Li G.; Wu J. Global Aromaticity in Macrocyclic Polyradicaloids: Hückel’s Rule or Baird’s Rule?. Acc. Chem. Res. 2019, 52, 2309–2321. 10.1021/acs.accounts.9b00257. [DOI] [PubMed] [Google Scholar]
- Kim J.; Oh J.; Osuka A.; Kim K. Porphyrinoids, a Unique Platform for Exploring Excited-State Aromaticity. Chem. Soc. Rev. 2022, 51, 268–292. 10.1039/D1CS00742D. [DOI] [PubMed] [Google Scholar]
- Solà M. Aromaticity Rules. Nat. Chem. 2022, 14, 585–590. 10.1038/s41557-022-00961-w. [DOI] [PubMed] [Google Scholar]
- Yan J.; Slanina T.; Bergman J.; Ottosson H. Photochemistry Driven by Excited-State Aromaticity Gain or Antiaromaticity Relief. Chem. - Eur. J. 2023, 29, e202203748 10.1002/chem.202203748. [DOI] [PubMed] [Google Scholar]
- Mandado M.; Graña A. M.; Pérez-Juste I. Aromaticity in Spin-Polarized Systems: Can Rings be Simultaneously Alpha Aromatic and Beta Antiaromatic?. J. Chem. Phys. 2008, 129, 164114 10.1063/1.2999562. [DOI] [PubMed] [Google Scholar]
- Valiev R. R.; Kurten T.; Valiulina L. I.; Ketkov S. Yu.; Cherepanov V. C.; Dimitrova M.; Sundholm D. Magnetically Induced Ring Currents in Metallocenothiaporphyrins. Phys. Chem. Chem. Phys. 2022, 24, 1666–1674. 10.1039/D1CP04779E. [DOI] [PubMed] [Google Scholar]
- Jorner K.; Feixas F.; Ayub R.; Lindh R.; Solà M.; Ottosson H. Analysis of a Compound Class with Triplet States Stabilized by Potentially Baird-Aromatic [10]Annulenyl Dicationic Rings. Chem. - Eur. J. 2016, 22, 2793–2800. 10.1002/chem.201504924. [DOI] [PubMed] [Google Scholar]
- Escayola S.; Tonellé C.; Matito E.; Poater A.; Ottosson H.; Solà M.; Casanova D. Guidelines for Tuning the Excited State Hückel-Baird Hybrid Aromatic Character of Pro-Aromatic Quinoidal Compounds. Angew. Chem., Int. Ed. 2021, 60, 10255–10265. 10.1002/anie.202100261. [DOI] [PubMed] [Google Scholar]
- Zeng W.; El Bakouri O.; Szczepanik D.; Bronstein H.; Ottosson H. Excited State Character of Cibalackrot-Type Compounds Interpreted in Terms of Hückel-Aromaticity: A Rationale for Singlet Fission Chromophore Design. Chem. Sci. 2021, 12, 6159–6171. 10.1039/D1SC00382H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen J.; Mikkelsen K. V. A Benchmark Study of Aromaticity Indexes for Benzene, Pyridine, and the Diazines - II. Excited State Aromaticity. J. Phys. Chem. A 2023, 127, 122–130. 10.1021/acs.jpca.2c07059. [DOI] [PubMed] [Google Scholar]
- Baranac-Stojanović M.; Stojanović M.; Aleksić J. Triplet State (Anti)Aromaticity of Some Monoheterocyclic Analogues of Benzene, Naphthalene and Anthracene. New J. Chem. 2021, 45, 5060–5074. 10.1039/D1NJ00207D. [DOI] [Google Scholar]
- Feixas F.; Poater J.; Matito E.; Solà M.. Aromaticity of Organic and Inorganic Heterocycles. In Structure, Bonding and Reactivity of Heterocyclic Compounds; Geerlings P., Ed.; Springer: Verlag, Berlin, 2014; pp 129–160. [Google Scholar]
- Guo S.; Wang L.; Deng Q.; Wang G.; Tian X.; Wang X.; Liu Z.; Zhang M.; Wang S.; Miao Y.; et al. Exploiting Heterocycle Aromaticity to Fabricate New Hot Exciton Materials. J. Mater. Chem. C 2023, 11, 6847–6855. 10.1039/D3TC01192E. [DOI] [Google Scholar]
- Foroutan-Nejad C. Magnetic Antiaromaticity – Paratropicity – Does Not Necessarily Imply Instability. J. Org. Chem. 2023, 88, 14831–14835. 10.1021/acs.joc.3c01807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D.; Shen T.; An K.; Zhu J. Adaptive Aromaticity in S0 and T1 States of Pentalene Incorporating 16 Valence Electron Osmium. Commun. Chem. 2018, 1, 18 10.1038/s42004-018-0018-y. [DOI] [Google Scholar]
- Shen T.; Chen D.; Lin L.; Zhu J. Dual Aromaticity in Both the T0 and S1 States: Osmapyridinium with Phosphonium Substituents. J. Am. Chem. Soc. 2019, 141, 5720–5727. 10.1021/jacs.8b11564. [DOI] [PubMed] [Google Scholar]
- Chen D.; Szczepanik D. W.; Zhu J.; Solà M. Probing the Origin of Adaptive Aromaticity in 16-Valence-Electron Metalla-pentalenes. Chem. - Eur. J. 2020, 26, 12964–12971. 10.1002/chem.202001830. [DOI] [PubMed] [Google Scholar]
- You F.; Qui R.; Zhu J. Adaptive Aromaticity in Osmapentalene and Osmapyridinium Complexes with Carbone Ligands. J. Phys. Org. Chem. 2023, 36, e4450 10.1002/poc.4450. [DOI] [Google Scholar]
- Ye Q.; Fang Y.; Zhu J. Adaptive Aromaticity in 18e Metallapentalenes. Inorg. Chem. 2023, 62, 14764–14772. 10.1021/acs.inorgchem.3c02223. [DOI] [PubMed] [Google Scholar]
- Dey S.; Manogaran D.; Manogaran S.; Schaefer H. F. III Quantification of Aromaticity of Heterocyclic Systems Using Interaction Coordinates. J. Phys. Chem. A 2018, 122, 6953–6960. 10.1021/acs.jpca.8b05041. [DOI] [PubMed] [Google Scholar]
- Feixas F.; Matito E.; Poater J.; Solà M. On the Performance of Some Aromaticity Indices: A Critical Assessment Using a Test Set. J. Comput. Chem. 2008, 29, 1543–1554. 10.1002/jcc.20914. [DOI] [PubMed] [Google Scholar]
- Flicker W. M.; Mosher O. A.; Kuppermann A. Electron Impact Investigation of Electronic Excitations in Furan, Thiophene, and Pyrrole. J. Chem. Phys. 1976, 64, 1315–1321. 10.1063/1.432397. [DOI] [Google Scholar]
- Lazzeretti P. Assessment of Aromaticity via Molecular Response Properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. 10.1039/B311178D. [DOI] [Google Scholar]
- Sundholm D.; Dimitrova M.; Berger R. J. F. Current Density and Molecular Magnetic Properties. Chem. Commun. 2021, 57, 12362–12378. 10.1039/D1CC03350F. [DOI] [PubMed] [Google Scholar]
- Bultinck P.; Ponec R.; Van Damme S. Multicenter Bond Indices as A New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. 10.1002/poc.922. [DOI] [Google Scholar]
- Feixas F.; Matito E.; Poater J.; Solà M. Quantifying Aromaticity with Electron Delocalisation Measures. Chem. Soc. Rev. 2015, 44, 6434–6451. 10.1039/C5CS00066A. [DOI] [PubMed] [Google Scholar]
- Szczepanik D. W. A New Perspective on Quantifying Electron Localization and Delocalization in Molecular Systems. Comput. Theor. Chem. 2016, 1080, 33–37. 10.1016/j.comptc.2016.02.003. [DOI] [Google Scholar]
- Szczepanik D. W.; Andrzejak M.; Dominikowska J.; Pawełek B.; Krygowski T. M.; Szatylowicz H.; Solà M. The Electron Density of Delocalized Bonds (EDDB) Applied for Quantifying Aromaticity. Phys. Chem. Chem. Phys. 2017, 19, 28970–28981. 10.1039/C7CP06114E. [DOI] [PubMed] [Google Scholar]
- Feixas F.; Jimenez-Halla J. O. C.; Matito E.; Poater J.; Solà M. A Test to Evaluate the Performance of Aromaticity Descriptors in All-Metal and Semimetal Clusters. An Appraisal of Electronic and Magnetic Indicators of Aromaticity. J. Chem. Theory Comput. 2010, 6, 1118–1130. 10.1021/ct100034p. [DOI] [Google Scholar]
- Schleyer P. v. R.; Maerker C.; Dransfeld A.; Jiao H.; van Eikema Hommes N. J. R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. 10.1021/ja960582d. [DOI] [PubMed] [Google Scholar]
- Chen Z.; Wannere C. S.; Corminboeuf C.; Puchta R.; Schleyer P. v. R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. 10.1021/cr030088+. [DOI] [PubMed] [Google Scholar]
- Gershoni-Poranne R.; Stanger A. Magnetic Criteria of Aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. 10.1039/C5CS00114E. [DOI] [PubMed] [Google Scholar]
- Yanai T.; Tew D. P.; Handy N. C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
- Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichromism Spectra Using Density Functional Force Fields. J. Phys. Chem. A 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
- Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Handy N. C.; Pople J. A.; Head-Gordon M.; Raghavachari K.; Trucks G. W. Size-Consistent Brueckner Theory Limited to Double Substitutions. Chem. Phys. Lett. 1989, 164, 185–192. 10.1016/0009-2614(89)85013-4. [DOI] [Google Scholar]
- Casida M. E.; Huix-Rotllant M. Progress in Time-Dependent Density-Functional Theory. Annu. Rev. Phys. Chem. 2012, 63, 287–323. 10.1146/annurev-physchem-032511-143803. [DOI] [PubMed] [Google Scholar]
- Lee T. J.; Taylor P. R. A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods. Int. J. Quantum Chem. 2009, 36, 199–207. 10.1002/qua.560360824. [DOI] [Google Scholar]
- Jayatilaka D.; Lee T. J. Open-Shell Coupled-Cluster Theory. J. Chem. Phys. 1993, 98, 9734–9747. 10.1063/1.464352. [DOI] [Google Scholar]
- Rienstra-Kiracofe J. C.; Allen W. D.; Schaefer H. F. III The C2H5 + O2 Reaction Mechanism: High-Level ab Initio Characterizations. J. Phys. Chem. A 2000, 104, 9823–9840. 10.1021/jp001041k. [DOI] [Google Scholar]
- Keith T. A.; Bader R. F. W. Calculation of Magnetic Response Properties Using a Continuous Set of Gauge Transformations. Chem. Phys. Lett. 1993, 210, 223–231. 10.1016/0009-2614(93)89127-4. [DOI] [Google Scholar]
- Keith T. A.; Bader R. F. W. Topological Analysis of Magnetically Induced Molecular Current Distributions. J. Chem. Phys. 1993, 99, 3669–3682. 10.1063/1.466165. [DOI] [Google Scholar]
- Lazzeretti P.; Malagoli M.; Zanasi R. Computational Approach to Molecular Magnetic Properties by Continuous Transformation of the Origin of the Current Density. Chem. Phys. Lett. 1994, 220, 299–304. 10.1016/0009-2614(94)00158-8. [DOI] [Google Scholar]
- Steiner E.; Fowler P. W. Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions. J. Phys. Chem. A 2001, 105, 9553–9562. 10.1021/jp011955m. [DOI] [Google Scholar]
- Preethalayam P.; Proos Vedin N.; Radekovic S.; Ottosson H. Azaboracyclooctatetraenes Reveal that the Different Aspects of Triplet State Baird-Aromaticity are Nothing but Different. J. Phys. Org. Chem. 2023, 36, e4455 10.1002/poc.4455. [DOI] [Google Scholar]
- Zhao L.; Grande-Aztazi R.; Foroutan-Nejad C.; Ugalde J. M.; Frenking G. Aromaticity, the Hückel 4n + 2 Rule and Magnetic Current. ChemistrySelect 2017, 2, 863–870. 10.1002/slct.201602080. [DOI] [Google Scholar]
- Frison G.; Sevin A.; Avarvari N.; Mathey F.; Le Floch P. The CH by N Replacement Effects on the Aromaticity and Reactivity of Phosphinines. J. Org. Chem. 1999, 64, 5524–5529. 10.1021/jo9903611. [DOI] [PubMed] [Google Scholar]
- Elguero E.; Alkorta I.; Elguero J. A Theoretical Study of the Properties of Ninety-Two “Aromatic” Six-Membered Rings Including Benzene, Azines, Phosphinines and Azaphosphinines. Heteroat. Chem. 2018, 29, e21441 10.1002/hc.21441. [DOI] [Google Scholar]
- McNeill J. N.; Bard J. P.; John D. W.; Haley M. M. Azaphophinines and Their Derivatives. Chem. Soc. Rev. 2023, 52, 8599–8634. 10.1039/d3cs00737e. [DOI] [PubMed] [Google Scholar]
- Dillon K. B.; Mathey F.; Nixon J. F.. Phosphorus: The Carbon. Copy: From Organophosphorus to Phospha-organic Chemistry; Wiley: Chichester, 1998. [Google Scholar]
- Mandado M.; Otero N.; Mosquera R. A. Local Aromaticity Study of Heterocycles Using n-Center Delocalization Indices: The Role of Aromaticity on the Relative Stability of Position Isomers. Tetrahedron 2006, 62, 12204–12210. 10.1016/j.tet.2006.10.022. [DOI] [Google Scholar]
- Jorner K.; Emanuelsson R.; Dahlstrand C.; Tong H.; Denisova A. V.; Ottosson H. Impact of Ground- and Excited-State Aromaticity on Cyclopentadiene and Silole Excitation Energies and Excited-State Polarities. Chem. - Eur. J. 2014, 20, 9295–9393. 10.1002/chem.201402577. [DOI] [PubMed] [Google Scholar]
- El-Hamdi M.; Tiznado W.; Poater J.; Solà M. An Analysis of the Isomerization Energies of 1,2-/1,3-Diazacyclobutadiene, Pyrazole/Imidazole, and Pyridazine/Pyrimidine with the Turn-Upside-Down Approach. J. Org. Chem. 2011, 76, 8913–8921. 10.1021/jo201639k. [DOI] [PubMed] [Google Scholar]
- Allison C. G.; Chambers R. D.; Cheburkov Yu. A.; MacBride J. A. H.; Musgrave W. K. R. J. The Isomerisation of Perfluoropyridazines to Perfluoropyrimidines and to Perfluoropyrazines. J. Chem. Soc. D 1969, 1200–1201. 10.1039/c29690001200. [DOI] [Google Scholar]
- Lemal D. M.; Johnson D. W.; Austel V.; et al. Pyridazine-Pyrazine Photorearrangement. J. Am. Chem. Soc. 1970, 92, 7505–7506. 10.1021/ja00728a063. [DOI] [Google Scholar]
- Baranac-Stojanović M. Substituent Effect on Triplet State Aromaticity of Benzene. J. Org. Chem. 2020, 85, 4289–4297. 10.1021/acs.joc.9b03472. [DOI] [PubMed] [Google Scholar]
- Jorner K.; Rabten W.; Slanina T.; Proos Vedin N.; Sillén S.; Ludvigsson J. W.; Ottosson H.; Norrby P.-O. Degradation of Pharmaceuticals through Sequential Photon Absorption and Photoionization in Amiloride Derivatives. Cell Rep. Phys. Sci. 2020, 1, 100274 10.1016/j.xcrp.2020.100274. [DOI] [Google Scholar]
- Clune R.; Shea J. A. R.; Hardikar T. S.; Tuckman H.; Neuscamman E. Studying Excited-State-Specific Perturbation Theory on the Thiel Set. J. Chem. Phys. 2023, 158, 224113 10.1063/5.0146975. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.