Recommendations on Methods for Assessing Multimorbidity Changes Over Time: Aligning the Method to the Purpose

Abstract

Background

The rapidly growing field of multimorbidity research demonstrates that changes in multimorbidity in mid- and late-life have far reaching effects on important person-centered outcomes, such as health-related quality of life. However, there are few organizing frameworks and comparatively little work weighing the merits and limitations of various quantitative methods applied to the longitudinal study of multimorbidity.

Methods

We identify and discuss methods aligned to specific research objectives with the goals of (i) establishing a common language for assessing longitudinal changes in multimorbidity, (ii) illuminating gaps in our knowledge regarding multimorbidity progression and critical periods of change, and (iii) informing research to identify groups that experience different rates and divergent etiological pathways of disease progression linked to deterioration in important health-related outcomes.

Results

We review practical issues in the measurement of multimorbidity, longitudinal analysis of health-related data, operationalizing change over time, and discuss methods that align with 4 general typologies for research objectives in the longitudinal study of multimorbidity: (i) examine individual change in multimorbidity, (ii) identify subgroups that follow similar trajectories of multimorbidity progression, (iii) understand when, how, and why individuals or groups shift to more advanced stages of multimorbidity, and (iv) examine the coprogression of multimorbidity with key health domains.

Conclusions

This work encourages a systematic approach to the quantitative study of change in multimorbidity and provides a valuable resource for researchers working to measure and minimize the deleterious effects of multimorbidity on aging populations.

Background and Objectives

Multimorbidity research has progressed rapidly over the last 20 years and is now turning toward understanding the dynamics of onset and progression with the goal of developing strategies to delay this progression and compress the period lived with high and deleterious morbidity levels (1). Abundant cross-sectional research has yielded important insights into the prevalence, correlates, and consequences of multimorbidity, but comparatively less is known about the dynamics of chronic disease accumulation or how changing longitudinal patterns of accumulation affect patient-centered outcomes. There is a growing recognition of the need to move beyond cross-sectional approaches to better understand trajectories and patterns of multimorbidity development and accumulation (2,3). To date, there is little published guidance on the application of specific quantitative methods to address key areas of inquiry in longitudinal multimorbidity research. The purpose of our work is to help fill this gap by describing the most relevant and useful statistical methods applicable to common research objectives, leading to more precise and advanced research questions that enhance our understanding of multimorbidity progression.

Specifically, the objectives of this Research Methods and Reporting article are to: (i) describe longitudinal statistical methods that are aligned to specific objectives in assessing multimorbidity, (ii) offer guidance on appropriate application of these methods for clinicians and applied researchers, and (iii) establish a common language for the analytic examination of multimorbidity progression. We propose an organizing typology for studying multimorbidity changes across the age span and match these common research objectives with appropriate analytic methods. We address both technical, data-related issues, such as operationalizing multimorbidity, variability in documenting diagnoses over a patient’s lifetime, and defining the scale of time over which change in multimorbidity is examined, as well as conceptual considerations that inform the selection of an analytic approach that best aligns with goals of multimorbidity researchers. Thus, an assessment of specific statistical methods that enable examination of multimorbidity changes over the life course can clarify the advantages, limitations, and scenarios under which these methods may advance our understanding of how multimorbidity evolves for individuals as they age.

General Considerations

There are several overarching methodological considerations when studying multimorbidity longitudinally. Principal among these are the measurement of multimorbidity itself, inconsistent reporting of chronic diseases over time, and decision-making around how to incorporate time-scale. First, estimates of change in multimorbidity and associations between multimorbidity and related health outcomes are dependent on which particular chronic conditions and instruments are chosen to measure multimorbidity (4). Lack of consensus on which conditions to include adds to the challenge of operationalizing multimorbidity (5). Several research teams and international experts have attempted to provide guidance on condition inclusion, with common inclusion criteria involving conditions that are chronic, require ongoing treatment, and are amenable to intervention (5–7). After identifying conditions that align with these general criteria, researchers must still operationalize the concept using a pre-existing summary measure to define multimorbidity (eg, weighted indices, simple counts, disease combination categories) that is best suited to their research objectives (8,9). As decisions around inclusions and operationalization are critical, providing rationale justifying the selection of conditions and instrumentation is central to conducting reproducible science and building the multimorbidity evidence base.

Second is the potential for conflicting information in self-reported diagnoses over repeated measurements in longitudinal survey data. Discrepancies in self-reported chronic conditions over time have been identified in as many as 30% of cases (10). As inconsistency in reporting is not identifiable in cross-sectional studies, the ability to address contradictory reports over time is a strength of longitudinal study design. Using adjudication methodologies to validate self-reports based on other available information on treatment and/or diagnosis date can reduce discrepancies in self-reports over time, with specific techniques including examination of prior wave responses for evidence of previous disease status to address inconsistent reporting, resolution of reversible, and nonreversible transitions (eg, prior stroke is considered nonreversible, whereas depressive symptomatology may vary over time), and missing data due to ambiguous responses (eg, “don’t know” or “refuse to answer”). Survey studies with administrative linkages to additional data sources also allow self-reports to be checked against medical claims or electronic health records.

Finally, a key consideration in longitudinal analyses of multimorbidity is how to define time. For example, time may alternatively be modeled as the number of years from study onset (time under observation) or as age at each observation point. If time under observation is the chosen time metric, it is important to adjust for baseline age differences—and potentially, cohort differences—in multimorbidity prevalence. When using age as the metric for time, potential difficulties include accounting for healthy participation bias and the challenge of disentangling age, period, and cohort (APC) effects. If a particular study uses age as an inclusion/exclusion criterion, older adults who are generally sicker and experience a greater number of chronic conditions are more likely to be excluded due to nonresponse, early-institutionalization, or mortality. This form of left-censoring can lead to bias in estimated associations, reduced statistical power due to diminished effect sizes, and reduced generalizability (11). Significant cohort effects in multimorbidity have been documented (12,13), implying that cohort effects may lead to biased estimates when modeling change in multimorbidity with advancing age. Several methods for estimating age effects while adjusting statistical models for period and cohort effects have been proposed, though the efficacy of these methods in addressing the APC identification problem is under debate (14,15) and guidance on the use of APC analyses may be found elsewhere (14,16,17). For a helpful and detailed discussion of issues related to time-scale in longitudinal studies, the exchange between Mendes de Leon (11) and Shaw and colleagues (18) provides a nice overview of the main considerations.

Statistical Approaches to Modeling Change in Multimorbidity

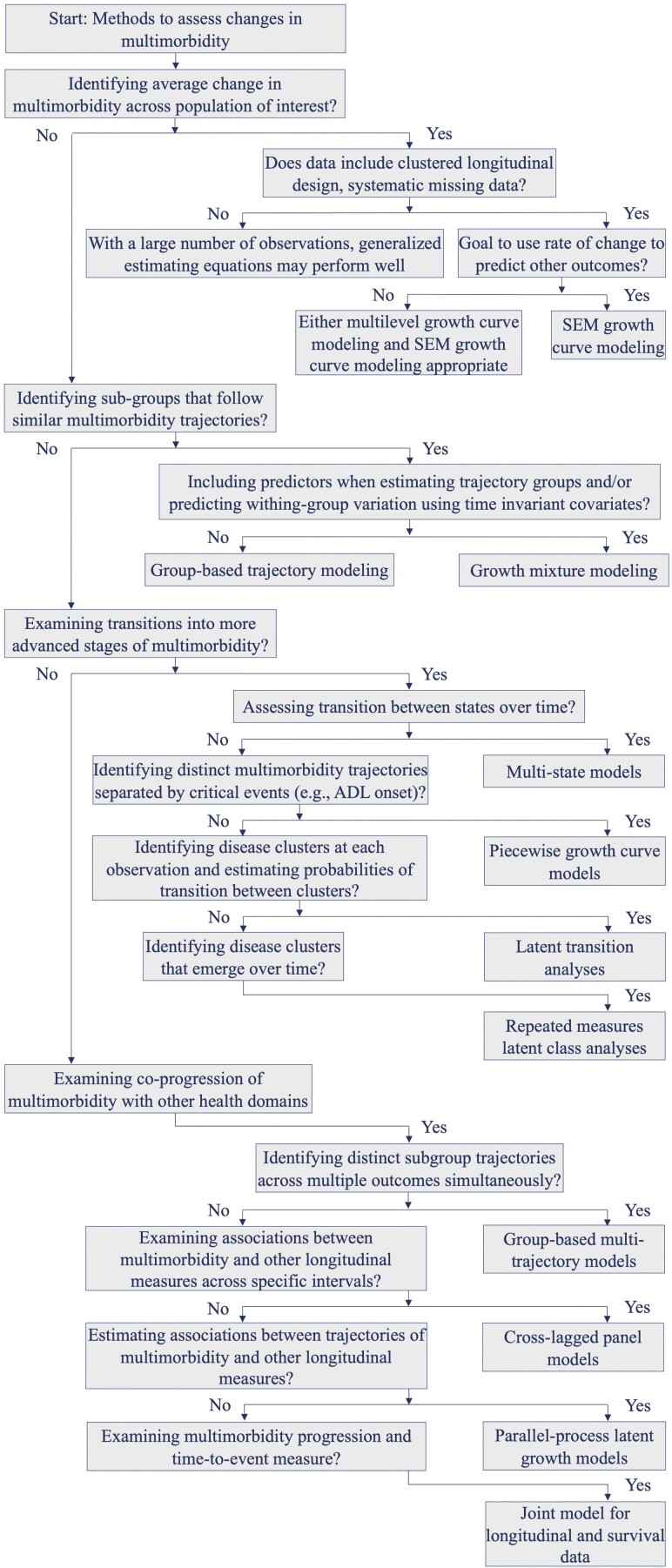
Once decisions are made on how best to operationalize multimorbidity, adjudicate inconsistent disease reporting, and define time, then the selection of an appropriate statistical method requires alignment with the research objective, keeping practical considerations and limitations in mind. To this end, we propose 4 general typologies of research objectives in the longitudinal study of multimorbidity: (i) examining individual multimorbidity trajectories; (ii) identifying subgroups that follow similar trajectories of multimorbidity progression; (iii) understanding when, how, and why individuals or groups shift to more advanced multimorbidity; and (iv) describing and examining the coprogression of multimorbidity with other key health domains over time. The following sections provide detail on appropriate statistical methods, organized according to these four typologies, for evaluating change in multimorbidity and related health outcomes. Each section focuses attention on a primary statistical method that can be used to address each research objective, using both conceptual models and illustrative examples to guide understanding of each approach. We limit our description to a prototypical statistical approach for each research objective. Thus, Table 1 presents additional methods that can be used to address each research objective, describes the purpose of each method, reviews important methodological considerations, and provides an illustrative research question for each approach. To help researchers identify the analytic method best suited to their research objectives, Figure 1 provides a decision tree organized around the 4 typologies to guide identification of a statistical method that fits their research goals.

Table 1.

Assessment of Longitudinal Methods Used to Evaluate Multimorbidity Changes

Method Family	Purpose	Important Methodological Considerations	Illustration
Examining individual change in multimorbidity
Growth curve models (GCM), implemented using mixed-effects regression models (also known as multilevel (MLM) or hierarchical linear modeling (HLM)) or structural equation models (SEM); generalized estimating equations (GEE)	Assessing changes in multimorbidity progression with an explicit interest in interindividual differences, accounting for hierarchal nesting (eg, within person, spatial grouping), and/or intraindividual change.	Can accommodate continuous (eg, weighted count), discrete (eg, count), or categorical (eg, dichotomous) outcomes; both measurement wave and age can be used to scale time; missing data on dependent and independent variables can be addressed through maximum likelihood estimation or multiple imputation; can be incorporated into general SEM framework (mixture models, using latent variables to predict outcomes, etc.). GEE: Intraindividual variation not estimated, requiring specification of within-person correlation structure; more stringent assumptions regarding missing data than GCM; does not easily accommodate clustered longitudinal data; less prone to convergence issues and faster computational time than GCM.	What is the average number of chronic conditions at initial measurement, and how does the number of conditions reported change over time? This allows us to evaluate whether changes in chronic diseases over time are different for adults from different backgrounds (eg, adults from different birth cohorts, minoritized groups, or underserved populations).
Identifying subgroups that follow similar trajectories of multimorbidity progression
Growth mixture models (GMM); group-based trajectory models (GBTM)	Identifying underlying subgroups that share distinct trajectories of multimorbidity.	Can accommodate continuous (eg, weighted count), discrete (eg, count), or categorical (eg, multimorbidity flag) outcomes; subgroups may have different functional forms; study attrition may affect group identification. GMM explicitly models and estimates intraindividual variation within defined trajectory groups; models may have greater estimation and convergence issues than GBTM; missing data handled using maximum likelihood estimation or multiple imputation. GBTM assumes no individual variation within defined trajectory groups; models less prone to convergence issues; maximum likelihood estimation or multiple imputation for missing data; probabilistic nature of group assignment should be accounted for in post-hoc analyses of group membership.	Are there subgroups within the general population that experience distinct trajectories of multimorbidity? Although the trajectory of multimorbidity is likely increasing for all study participants, there may be subgroups of older adults that have rapidly increasing multimorbidity and others who have low and very slowly increasing multimorbidity. Identifying characteristics associated with subgroup membership can provide actionable information for designing interventions or health promotion programs.
Understanding when, how, and why individuals or groups shift to more advanced stages of multimorbidity
Multistate models	Assessing the transition between states over time (eg, disease free, to single disease, to multimorbidity, to death).	Requires binary indicators of transition states defined a priori; assumes that right censoring process is independent of transition probabilities; allows for the inclusion of both time-invariant and time-varying covariates as predictors of transition probabilities.	What is the relationship between onset of specific disease combinations with timing or onset of more pernicious disease combinations (eg, those including dementia) and/or death? In midlife, most older adults have few diseases, transition to multimorbidity defined by common chronic conditions (eg, hypertension + arthritis) in their mid-60s, then transition to more pernicious disease combinations in their mid-80s (eg, hypertension + arthritis + dementia).
Piecewise growth curve models	Identify changes in multimorbidity associated with distinct temporal events.	Can accommodate continuous (eg, weighted count), discrete (eg, count), or categorical (eg, multimorbidity flag) outcomes, and binary indicators of events/knots; different ways to fit knots at temporal events; testing for differences in both levels and slopes.	Does the rate of chronic disease accumulation change following the occurrence of a specified event? Increases in additional chronic disease diagnoses—hence, multimorbidity accumulation—may occur more rapidly after onset of a functional disability.
Latent transition analysis (LTA)	Identify disease clusters at each observation and estimate probabilities of transition in cluster membership.	Best suited for several binary outcomes (eg, separate condition flags), but can also incorporate continuous (eg, weighted counts) and discrete (eg, count) outcomes; inclusion of low-incidence conditions can cause model convergence issues; estimating several classes and transitions rapidly increases dimensionality and likelihood of convergence issues.	(1) What are the most common disease combinations at each observation, (2) what is the likelihood that a patient transitions to a more serious disease combination, and (3) what patient characteristics predict such transitions? The specific multimorbidity patterns identified in a set of patients may center around early onset diseases, cardiovascular diseases, and mental health conditions, and over the course of a decade, patients in these patterns are more or less likely to transition to more complex patterns of disease.
Repeated measures latent class analysis (RMLCA)	Identification of subpopulations that follow similar patterns of disease clustering over an extended period of time; does not require specification of functional form (ie, linear, quadratic).	Best suited for several binary outcomes (eg, separate condition flags), but can also incorporate continuous (eg, weighted counts) and discrete (eg, count) outcomes; increasing number of follow-up observations and latent classes rapidly increases dimensionality and likelihood of nonconvergence.	(1) What are common disease clusters that emerge over repeated observations, (2) what percent of patients/respondents are included in classes that represent complex multimorbidity development, and (3) what characteristics are associated with membership in each longitudinal disease pattern? The most common multimorbidity patterns over time may be dominated by metabolic disorders or increasing complexity. Those experiencing obesity in middle old age tend to report diabetes and chronic kidney disease in later life.
Examining the coprogression of multimorbidity with key health domains over time
Group-based multitrajectory models	Identifying underlying subgroups of individuals that share a distinct pattern of progression in multiple outcomes (eg, multimorbidity, ADL/IADL disability, and hospital stays).	Can incorporate continuous (eg, weighted counts), discrete (eg, count), and binary (eg, separate condition flags) outcomes; determination of optimal number of groups is both computationally and empirically challenging, estimation of models including covariates can be difficult.	Are there subgroups in the population that share similar trajectories of multimorbidity, disability, and healthcare utilization? Identification of patient/respondent characteristics associated with membership in the highest-risk subgroups can inform clinical and policy interventions.
Cross-lagged panel models	Estimate the direction and strength of association between multiple variables across specific time intervals (eg, measurement waves in a panel study).	Can incorporate continuous (eg, weighted counts), discrete (eg, count), and binary (eg, multimorbidity flag) outcomes; testing for measurement invariance across waves; determine timing of lagged associations; identifying whether cross-lagged associations are consistent or vary across time; whether associations are unidirectional versus concurrent.	(1) Is variation in multimorbidity at a single point in time associated with change in mobility limitations at a later measurement and (2) is variation in mobility limitations at a single point in time associated with change in multimorbidity at a later measurement? A greater number of chronic conditions at initial measurement may increases the risk of mobility limitations at follow-up, and initial mobility limitations may be simultaneously associated with the number of chronic conditions reported at follow up.
Parallel-process growth models	Estimate the direction of association between multiple variables across continuous time intervals.	Can incorporate continuous (eg, weighted counts), discrete (eg, count), and binary (eg, multimorbidity flag) outcomes; requires nested model fit testing to identify parsimonious growth models for each outcome and to identify whether associations are unidirectional versus concurrent.	(1) Is variation in multimorbidity at baseline associated with the trajectory of mobility limitations and (2) are baseline mobility limitations associated with rate of change in multimorbidity? High multimorbidity at baseline increases the rate of increase in mobility limitations. More rapid increase in multimorbidity is associated with more rapid change in mobility limitations.
Joint model for longitudinal and survival data	Conjointly determine multimorbidity progression and time-to-event such as mortality. Examine relationship between development of multimorbidity and time to event outcome.	Can incorporate continuous (eg, weighted counts), discrete (eg, count), and binary (eg, multimorbidity flag) measures for outcome and binary indicators of survival outcome (eg, mortality); timing of longitudinal process can be concurrent with or preceding time to event outcome; inclusion of time to event outcome can be useful in addressing informative missingness in longitudinal model; approach is extensible to more complex survival methods (eg, competing risks), but models are computationally demanding and may be challenging to interpret.	Is rate of change in multimorbidity associated with subsequent time-to-onset of geriatric syndromes, such as frailty?

Figure 1.

Decision tree to guide selection of appropriate longitudinal methods to study multimorbidity changes over time.

Methods to Examine Individual Multimorbidity Trajectories

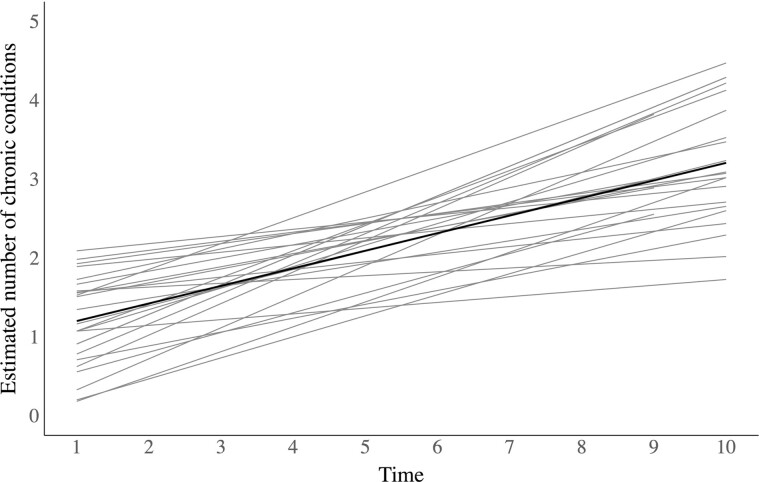
A major objective of longitudinal research on multimorbidity is to characterize the overall development and progression of multimorbidity among a defined population and, potentially, identify individual characteristics associated with an increase or decrease from the average level and rate of progression. The most widely used approach to address this objective is growth curve modeling (GCM) (3). Broadly speaking, this approach involves estimation of change in multimorbidity measured for each individual and averaged across individuals, essentially modeling both intraindividual and interindividual variations in change over time (19). This is graphically illustrated in Figure 2, which depicts both the individual and average trajectories of chronic disease accumulation in a hypothetical example of a growth curve model with random intercepts and slopes for each individual.

Figure 2.

Hypothetical example of estimated individual trajectories and overall mean trajectory of multimorbidity accumulation over time using growth curve modeling. Note: Individual trajectories are denoted by lighter lines.

There are 2 general approaches to the specification and estimation of GCM. The first is to estimate the model using mixed-effects regression (also known as multilevel (MLM) or hierarchical linear modeling), where observations over time are nested within individuals. The within-person trajectories (ie, the intercept and slope) are modeled at level-1 of the hierarchical model, and the between-person variation in these individual trajectories is modeled at level-2 through the inclusion of random effects for the intercept, slope, or both (20). The second approach uses structural equation modeling (SEM), in which the observed repeated measures are incorporated as multiple indicators on latent intercept and slope factors that characterize the unobserved growth trajectories (21). The objectives of both approaches are the same and they can be equivalently specified to produce the same results (22). Both can be used to estimate a variety of growth curve models of multimorbidity, including accounting for non-normal distributions (eg, count data, zero-inflated distributions). Further, both approaches can be extended to include additional levels of clustering beyond the individual; for example, observed groups of patients clustered within clinics or geographic locations. For a discussion of the similarities and differences between the 2 approaches, see Table 1 and Figure 1.

Example 1. Identifying racial/ethnic variation in multimorbidity trajectories

An early example of the use of GCM to examine multimorbidity trajectories over time is a study by Quiñones et al. (23) who examined racial/ethnic differences in multimorbidity among respondents to the Health and Retirement Study. Multimorbidity was operationalized as a count of chronic conditions assessed at each wave from 1995 to 2006. This study found significant racial/ethnic variation in multimorbidity trajectories, with Mexican Americans experiencing lower baseline levels of chronic disease and less rapid accumulation of multimorbidity, and Black Americans experiencing greater overall levels of multimorbidity but less rapid multimorbidity accumulation, relative to White Americans, respectively (23). This study illustrates several of the strengths of GCM for modeling longitudinal change. First, GCM can be used with unbalanced data structures, such as those that often occur in longitudinal cohort studies (ie, respondents are retained that contain missing observations at different waves of measurement) and are present in the Health and Retirement Study due to its cohort replenishment structure. Second, missing data can be addressed in GCM using either full information maximum likelihood or multiple imputation, both of which are robust to missing data under the condition that the probability of missingness is independent of the outcome after adjusting for observed covariates (24). In this example, the authors chose to utilize multiple imputation, replicating analyses across three fully imputed data sets and averaging across models to yield final estimates. Third, both time-invariant (eg, education) and time-varying (eg, marital status, self-rated health, functional limitations) covariates can be easily incorporated in GCM models. Finally, nonlinear trajectories can be incorporated in GCM through the inclusion of polynomial functions and assessed based on significance testing of the coefficients and comparison of model fit statistics, such as the Akaike information criteria and Bayesian information criteria (BIC) (25). In the current example, both quadratic and cubic terms were evaluated in the initial model-building phase but subsequently removed in favor of a simpler linear model based on fit statistics.

Common issues when using growth curve models

The SEM approach to GCM has more flexibility than the MLM approach because it allows specification of more complex models to test additional hypotheses (eg, mediation processes, predicting outcomes with the estimated trajectory, etc.) (22). This benefit of the SEM approach also allows examination of the concurrent progression of multimorbidity and other critical health outcomes simultaneously, potentially revealing clinically relevant associations. The SEM approach to GCM also enables the use of latent variables to measure (i) the outcome variables of interest prior to specification of the growth model and (ii) predictor variables of interest, giving the researcher the ability to account for measurement error in any latent variable specified. Finally, both approaches to GCM are relatively limited in their inability to model change in more nuanced measures of multimorbidity, such as specific disease combinations that emerge over time.

Additional approaches to examining individual change in multimorbidity

A closely related alternative to GCM is marginal modeling using generalized estimating equations (26,27). Like GCM, GEE is a regression-based approach that can be used to model the average longitudinal trajectory of an outcome as a function of both time-invariant and time-varying covariates while accounting for within-person clustering of observations. A primary difference between GEE and GCM is that, rather than attempting to model the within-person covariance structure through inclusion of random effects, GEE treats dependence of within-person observations as a nuisance factor to be adjusted for in the estimation of the population-averaged effects of covariates (28). In other words, the GEE approach does not permit estimation of the within-person variation in multimorbidity accumulation and precludes examination of factors potentially associated with that variability (eg, racial/ethnic differences in the rate of within-person change in multimorbidity cannot be estimated) (29).

Methods to Identify Subgroups That Follow Distinct Multimorbidity Trajectories

Both GCM and GEE are examples of variable-centered analyses, as the primary focus is on the relationships between variables (30). A basic assumption is that the sample is drawn from a homogenous population that can be characterized by a single set of parameters. In contrast, person-centered approaches assume a heterogeneous population composed of a finite number of subgroups with shared characteristics. The goals of the data-driven longitudinal methods that fall under person-centered approaches are to identify previously unknown subgroups that experience similar trajectories or patterns and to examine how subgroups differ in composition and outcomes (31). These person-centered approaches allow for identification of multiple, unique multimorbidity trajectories that exist in a population and the characteristics of persons with a higher likelihood of experiencing benign versus harmful trajectories of multimorbidity (ie, slow vs. rapid accumulation of chronic diseases).

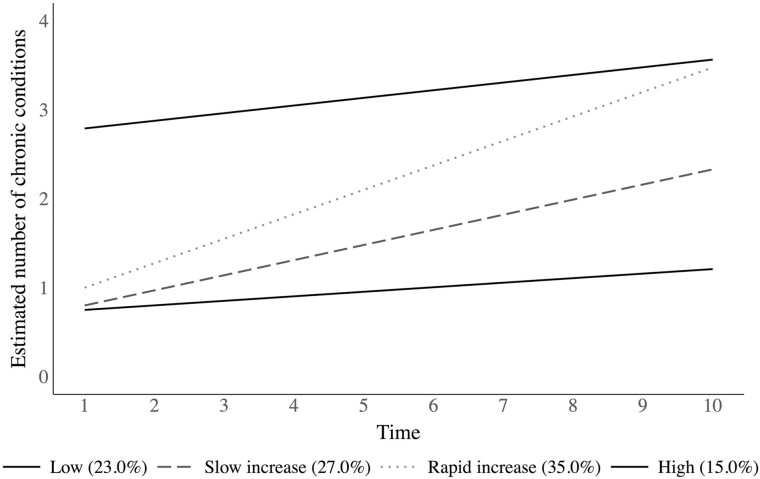
The longitudinal method most relevant to the goal of identifying subgroups that follow distinct multimorbidity trajectories is growth mixture modeling (GMM). GMM is based on the SEM approach to conventional GCMs but extends the SEM approach with the inclusion of a categorical latent factor to represent unobserved groups that share similar trajectories. Identifying the number of unique trajectories, the shape of each trajectory (represented by a unique latent intercept and latent slope for each subgroup), and the number and proportion of people within each trajectory are defining features of the GMM approach. Figure 3 presents a prototypical illustration of the underlying multimorbidity trajectories that could be estimated using a GMM. Once the optimal number of underlying trajectories is identified, researchers typically choose theoretically-relevant covariates to predict the likelihood of membership in the trajectory subgroups, or the categorical indicator of trajectory subgroup membership can be used to predict clinically relevant outcomes, such as disability onset or mortality.

Figure 3.

Hypothetical plot of latent multimorbidity trajectory subgroups identified using growth mixture modeling. Note: Percentages represent the proportion of sample that falls within each subgroup trajectory.

Example 2. Identifying heterogeneous multimorbidity trajectory groups

Using data from the Korean Longitudinal Study of Aging, Lee and colleagues (32) applied GMM to identify latent multimorbidity trajectories over 10 years, then examined the association between membership in the multimorbidity trajectory subgroups and respondents’ characteristics. The investigators operationalized multimorbidity as a cumulative 8-item index with interviews conducted biennially from 2006 to 2016 (n = 1 705), finding 4 unique multimorbidity trajectories that were differentially associated with sex/gender, depressive symptoms, life satisfaction, and frequency of contacts with others. This study provides a valuable illustration of how to determine the optimal number of latent trajectories, then regress trajectory subgroup membership on covariates of interest to identify characteristics of persons at the greatest risk of high or rapidly increasing multimorbidity.

The first step in GMM is to estimate and describe the optimal number of underlying trajectory groups. To identify the number of latent classes that best captures heterogeneity in multimorbidity trajectories, researchers engage in an iterative model-building process where models with a greater number of latent trajectories are compared with more parsimonious models with fewer latent trajectories. As there is no single criterion that can be used to identify the optimal number of latent trajectories, the consideration of several indicators of model fit and comparative indices are necessary to support model development. Using established guidance on model selection in latent class analyses (21,33,34), Lee and colleagues identified that growth in multimorbidity could be best characterized by 4 separate trajectories: those with consistently low multimorbidity (59.4%, n = 1 013), those with consistently high multimorbidity (7.5%, n = 127), those with moderately increasing multimorbidity (26.0%, n = 444), and finally those with rapidly increasing multimorbidity (7.1%, n = 121).

Once the optimal number of latent trajectories has been identified, indicators of each individual’s trajectory group membership can be regressed on explanatory variables, allowing researchers to identify how membership is associated with independent variables. Outcomes of interest (eg, mortality) can be regressed on indicators of membership in the latent trajectory subgroups (35) and can be extended to include time-invariant and time-varying covariates. In the example provided by Lee and colleagues, multinomial logistic regression was used to regress the indicator of latent trajectory membership on several sociodemographic and behavioral characteristics (eg, sex/gender, depressive symptoms, life satisfaction). Compared with the latent trajectory representing those with the fewest chronic conditions at baseline and who experienced little change in multimorbidity over time, the investigators found that women had a greater likelihood of membership in the consistently high multimorbidity group than men, and that greater depressive symptomatology and less-frequent social interaction were associated with membership in the consistently high multimorbidity subgroup. These findings demonstrate the unique benefits of the person-centered approach typified by GMM, namely the ability to (i) identify multimorbidity trajectory subgroups that pose the greatest risk to aging populations and (ii) determine which patient/respondent characteristics are associated with membership in the most adverse multimorbidity trajectories.

Common issues when using growth mixture models

A practical challenge to conducting GMM is the identification of the optimal number of underlying multimorbidity trajectories. This process is often complicated by conflicting substantive and inferential model fit information, identification of relatively rare subgroup trajectories that can lead to nonconvergence due to small subgroup sample sizes, and issues related to unequal variance across subgroups (36). Moreover, relatively large samples sizes are required (37) and the large number of parameters that must be estimated can be computationally intensive and result in convergence problems for more complex models.

Additional approaches to examining subgroup trajectories of multimorbidity

Though we emphasized the use of GMM to identify heterogeneity in trajectories of multimorbidity, group-based trajectory modeling (GBTM) is also a popular analytic approach to this type of research question. The goals of GMM and GBTM are similar, with the primary difference being that GMM includes random effects to model individual variation within trajectory groups, whereas GBTM does not estimate within-group variation of trajectories, and thus does not allow examination of the association between within-group variation and covariates of interest (38). Figure 1 and Table 1 weigh the relative strengths and limitations of the GMM and GBTM approaches.

Methods to Understand Transitions Into More Advanced Stages of Multimorbidity

In addition to modeling individual or subgroup trajectories of multimorbidity, investigators may be interested in modeling the risk of transition to more advanced multimorbidity states or how exposure to specific events may precede changes in multimorbidity. Alternately, the focus may be on person-centered research goals, such as identifying subgroups of patients that develop specific disease combinations (eg, combinations including dementia) and examining whether prior multimorbidity combinations or other characteristics serve as risk factors for transitions into such disease combinations. Approaches to address these questions include multistate models, piecewise growth curve models, latent transition analysis, and repeated measures latent class analysis (RMLCA).

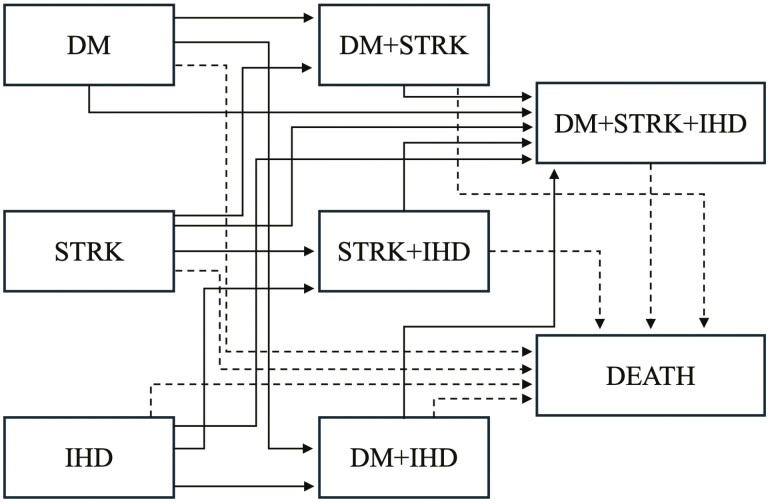
Multistate modeling can be used to evaluate the temporal development and progression of distinct multimorbidity clusters within the framework of survival analysis. This approach extends the general focus of survival analysis to allow for transitions through a finite set of intermediate states prior to some absorbing state of interest (eg, death) (39). Multistate modeling requires binary indicators of observed transition states that individuals may progress through, meaning that transition states must be defined a priori and are thus constrained to a relatively limited subset of possible states. Figure 4 presents a hypothetical example of the specific states and transitions that could be examined by a researcher interested in modeling transitions in cardiometabolic multimorbidity (based on diagnoses of diabetes mellitus, stroke, and ischemic heart disease) using a multistate model. The figure depicts 7 possible disease states, 12 possible transitions into more complex, nonabsorbing disease states, and 7 possible transitions into the absorbing state of death. The figure represents both the promise and complexity of multistate models, namely that several state probabilities and transitions across states representing advancing multimorbidity and mortality can be examined, with the reality that many statistical parameters and large sample sizes are required to perform such analyses.

Figure 4.

Hypothetical illustration of disease states and transitions that can be estimated in a multistate model of cardiometabolic multimorbidity and mortality. DM: diabetes mellitus; STRK: stroke; IHD: ischemic heart disease. Solid arrows depict transitions into nonabsorbing states and dashed arrows represent transitions into absorbing state of death.

Example 3. Examining progression of 3 chronic conditions in Hawaiian Medicare claims data with multistate modeling

Siriwardhana et al. (40) provide an application of multistate modeling examining multimorbidity progression and mortality risk among older adults diagnosed with 1 of 3 chronic conditions (diabetes mellitus, chronic kidney disease, and ischemic heart disease). Using claims data from the state of Hawaii with follow up from January 2009 to December 2013 (n = 23 030), the investigators restricted the analytic sample to Medicare beneficiaries entering the dataset through diagnosis of any of the 3 conditions. Initial descriptive statistics on transition counts provide evidence of the rate of transition between states and inform interpretation of later statistical estimates. As an example, patients with chronic kidney disease represented 23.4% of the initial sample, but the probability of occupying the state of singleton chronic kidney disease decreased to 12.7% after four years of observation. About 15% of the sample entered the absorbing state of mortality over the follow-up period.

Multistate models allow for estimation of several parameters that may be of substantive interest including the probability of occupying each state, the hazards of transition between states, and the association between transition probabilities and covariates of interest (41,42) Model specification of transitional probabilities depends on the complexity of transitions and type of data being analyzed and can include various Markov models (eg, time-homogenous or nonhomogenous models based on whether transition probabilities are dependent on time), as well as other non-Markov estimators that are generally less restrictive given fewer assumptions regarding the distribution of transition times (39,43). Estimating the cumulative transition hazards across states, Siriwardhana et al. identified several important transitions: respondents with chronic kidney disease as an initial disease state had the highest-risk of death and those who entered the intermediate state of chronic kidney disease + ischemic heart disease had a cumulative hazard of death 6 times greater than those who remained in the diabetes mellitus + ischemic heart disease state.

Typically, researchers are interested in the association between the duration of time spent in each state, hazards of transition across states, and patient/respondent characteristics, which can be estimated using Cox proportional hazards models or similar approaches. Both time-invariant and time-varying covariates can be incorporated into the models and time-varying covariates are often critical to consider given the association between time in state and transitional probabilities may be time dependent. Though using only covariates measured at baseline, Siriwardhana and colleagues accounted for the time-varying relationship between transition states and covariates by examining the impact of covariates at specific time points (eg, 365 days, 1 460 days). When examining the duration of time spent occupying a given state at these specific time points, the researchers found that age, sex/gender, race/ethnicity, chronic comorbidities, and financial status all displayed associations with the probability of state occupation, though the specific associations varied by time point and state. When modeling the cumulative hazard of transitions across the 16 possible states, age was associated with likelihood of transition to death, males were more likely to transition into more complex disease states than females, and the likelihood and nature of transitions were dependent on race/ethnicity, comorbid conditions, and financial status. As demonstrated by Siriwardhana and colleagues, the multistate model provides several opportunities to identify the risk of transitioning into more perilous forms of multimorbidity and experiencing mortality as a function of both prior disease states and characteristics of the individuals being studied.

Common issues when using multistate models

The application of methods for examining multimorbidity transitions is often constrained by the complexity of these approaches. Primary challenges in the construction of multistate models include the availability of detailed longitudinal data on both intermediate and absorbing states of interest and the requirement of a sufficiently large sample size to model potentially complex transition patterns. Missing data issues are especially important to consider when using multistate models as missingness can bias estimates of state probabilities, the transitions between states, and estimates of the association between covariates and these outcomes of interest (44,45). Both multiple imputation and maximum likelihood estimation offer potential solutions, though these methods assume randomness of missing data, which is often violated in longitudinal studies of health and aging (24).

Alternative approaches to examining transitions in multimorbidity

Several other statistical approaches are available for researchers interested in examining transitions into more complex and burdensome forms of multimorbidity. Piecewise growth curve modeling is an approach to examine the association of specific events (eg, hospitalization) with changes in the subsequent trajectory of multimorbidity, breaking the estimated trajectory into separate trajectories delineated temporally by the event of interest (eg, before and after hospitalization) (46). Latent transition analysis is a longitudinal extension of latent class analysis (21,47) allowing estimation of the probability of transition between clusters of individuals or unobserved groups over time conditional on previous group membership and covariates of interest. In contrast to latent transition analysis, which estimates latent subgroup membership at each observation then models transition in subgroup membership at adjacent observations, RMLCA estimates discrete longitudinal multimorbidity patterns across multiple waves of observation.

Methods to Examine Co-Progression of key Health Domains

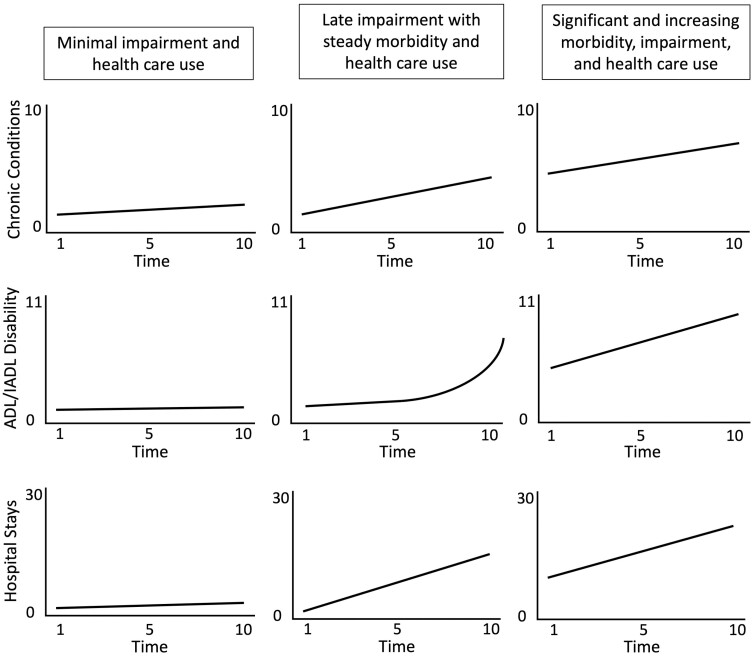
In addition to identification of developmental trends and patterns in multimorbidity, researchers are often interested in how trajectories of multimorbidity and other outcomes develop simultaneously, or how change in multimorbidity may be linked to progression in other clinical or policy-relevant outcomes. Risk/protective factors (eg, wealth or physical activity), health outcomes (eg, disablement or quality of life), and policy-relevant outcomes (eg, access to insurance or institutionalization) are themselves dynamic, requiring methods that can estimate change in multiple variables and allow researchers to model associations between the rate of change in multimorbidity and the concurrent processes of interest. Among the choices available to researchers, a recently developed extension of GBTM, known as group-based multitrajectory modeling, provides a novel and informative approach to the evaluation of multiple longitudinal processes. Like the single trajectory GBTM, the goal of the group-based multitrajectory model is to identify subgroups that share similar trajectories on some outcome of interest. In the group-based multitrajectory model, however, the subgroups are defined by their similarity across multiple outcomes of interest (48). In the hypothetical example depicted in Figure 5, three subgroups are identified based on their shared pattern of multimorbidity accumulation, disability progression, and number of hospitalizations.

Figure 5.

Hypothetical example of group-based multitrajectory model of 3 longitudinal outcomes: (1) count of chronic conditions; (2) count of limitations in activities of daily living (ADL) and instrumental activities of daily living (IADL); and (3) number of reported hospitalizations. The resulting 3-class solution is organized into columns and described in the text boxes at the top of the figure.

Example 4. Examining longitudinal patterns of multimorbidity and indicators of physical, cognitive, and emotional health among older adults

Research by Quinones et al. (49) provides an introduction to the use of group-based multitrajectory analysis to describe the coprogression of multimorbidity with concurrent changes in functional, cognitive, and emotional domains, and to examine the relationship of race/ethnicity with differential patterns of joint changes in these health domains. Using data from the Health and Retirement Study, the authors fit a group-based multitrajectory model to longitudinal measures of multimorbidity (measured as count of chronic conditions), ADL/IADL limitations, cognitive function, and depressive symptoms. This approach can be used with outcomes taking a variety of distributional forms, and the first step in the analysis is to use standard approaches to determine the correct specification for each outcome. In this case, the authors selected a censored normal model specification for count of chronic conditions and cognitive function score and a zero-inflated Poisson model for count of ADL/IADL limitations and count of depressive symptoms.

Following specification of the appropriate link function for each outcome (eg, logit link for binary outcomes, log link for count outcomes), the recommendation is to fit models iteratively using a 2-step approach (48). In the first step, a series of traditional GBTM models are fit to each outcome separately and the optimal number of trajectory groups and functional form (eg, linear, quadratic, cubic) is determined through comparison of fit indices. In this example, the number of trajectories was increased from 1 to 6 across each of the outcomes, with an optimal solution of 4–5 trajectories, modeled with a quadratic term allowing for nonlinear growth, was selected on the basis of the following criteria: (i) reduction in BIC, (ii) average posterior probability of trajectory group membership >0.7, (iii) odds of correct classification >5.0, and (iv) each trajectory group size >5% of total sample. In the second step, a series of multitrajectory models are fit across the range of optimal group numbers identified in the first step and the final model is selected by evaluating the above-mentioned criteria across multitrajectory models. In this example, this process yielded a solution indicating four distinct multitrajectory groups: (i) minimal impairment with low multimorbidity, (ii) minimal impairment with high multimorbidity, (iii) multidomain impairment with intermediate multimorbidity, and (iv) multidomain impairment with high multimorbidity. Groups 1 and 2 differed in multimorbidity burden over time but both had little deterioration in functional or cognitive scores. In contrast, Group 3 had lower multimorbidity accumulation than Group 2 but had moderate depressive symptomatology and worsening functional and cognitive performance. Finally, Group 4 had substantial functional limitation and high depressive symptomatology with worsening cognitive performance.

A notable strength of group-based multitrajectory models is the ability to employ the identified latent groups in subsequent analyses, identifying factors associated with group membership and/or whether group membership is predictive of outcomes such as mortality. This is facilitated by the estimation of posterior probabilities of group membership for each member of the sample which, similar to latent class analysis, permits assigning persons to the multitrajectory group for which they had the highest probability of membership. In the illustrative example, the authors conducted a multinomial logistic regression analysis to predict group membership from a range of sociodemographic and health-related factors, observing that Black and Hispanic race/ethnicity, lower wealth, lower education, male sex, and smoking history were significantly associated with membership in the 2 multitrajectory groups characterized by impairments across multiple domains.

Common issues when using group-based multitrajectory models

Modeling the bi-directional association between multimorbidity and health outcomes can identify modifiable factors that improve outcomes, yet the inclusion of additional health-related measures increases the need for an expert understanding of each health domain being studied and complicates statistical estimation of the desired models. The task of identifying the correct number and shapes of trajectories of interest is even more complex in group-based multitrajectory modeling than single trajectory approaches (ie, GMM and GBTM). As discussed above, these models are typically fit in an iterative manner beginning with specification of individual trajectory models and at each stage model fit criteria must be evaluated. Further, the complexity of these models necessitates large sample sizes and a relatively large number of repeated measurements to minimize issues of model nonconvergence. Finally, the treatment of assigned group as an individual-level observed variable in subsequent analysis is subject to bias resulting from the probabilistic nature of group assignment. This can be accounted for through various approaches to weighting individuals based on their calculated posterior probabilities of group membership and robustness to alternative specifications can be evaluated in sensitivity analyses.

Additional approaches to examining coprogression of multimorbidity with key health domains

In addition to the method described above, there are several alternative approaches to examining the co-occurrence of multimorbidity with other heath domains. An earlier extension of GBTM, commonly referred to as the joint trajectory model, was developed to allow simultaneous analysis of 2 longitudinal processes by linking estimated trajectories through a table of conditional probabilities (50). However, this approach is unwieldy in the context of multiple longitudinal processes and does not focus on identifying groups defined on the basis of similarities across multiple outcomes. Next, the cross-lagged panel model allows estimation of the incremental associations between 2 or more longitudinal variables of interest by incorporating both autoregressive and cross-lagged effects and is designed to investigate the causal direction of the relationship between variables across discrete time intervals (51,52). An extension of the GCM that allows for modeling of distinct trajectories for 2 or more outcomes is referred to as the parallel-process latent growth model. In this approach, 2 or more growth curves are modeled concurrently, each with a corresponding set of growth factors that can be correlated with or regressed on one another (21,53). This allows the researcher to assess potential relationships between the parameters (ie, intercepts and slopes) that describe the trajectories of multimorbidity and other simultaneously occurring health outcomes. Finally, a joint model for longitudinal and survival data (not to be confused with the joint GBTM model described above) can be used to examine the impact of a longitudinal process (such as multimorbidity accumulation) on a time-to-event outcome of interest (such as disability onset or nursing home entry). This involves simultaneous estimation of a GCM (or GMM) to estimate the longitudinal process and a survival model to estimate the hazard of event occurrence, with the 2 models linked via shared random effects (54).

Discussion and Implications

This paper describes various analytic approaches that may be particularly useful in understanding the critical processes of multimorbidity development and progression. There are a multitude of methods that serve unique and important purposes in the longitudinal study of multimorbidity, yet to date there has been little discussion and synthesis to weigh the merits and limitations of each approach. It is equally important to point out significant gaps in our understanding of how to trace out the evolution of multimorbidity across the lifespan, and how to apply existing methodologies to remedy these gaps. A more comprehensive and systematic approach to chronicling multimorbidity changes for middle-aged and older adults will contribute to a deeper understanding of the nature of multimorbidity progression with advancing age and may uncover more effective ways to deploy health and medical care resources to reduce multimorbidity burden and prolong years of healthy life (55). The specific studies used to demonstrate the application of the methods discussed illustrate the utility of applying such methods to advance the understanding of multimorbidity progression in diverse populations, though there are a variety of remaining questions that will require continued application of the methods described to yield actionable insights that can be leveraged to reduce the overall impact of multimorbidity. In addition, the development and application of advanced statistical methods to examine longitudinal change in multimorbidity is a relatively nascent field and there are several emerging and sophisticated state-of-science methods that will enable examination of complex and useful research questions in the future. It is important to emphasize that replicability of findings across studies and development of the multimorbidity research base depends on correct model choice and specification, and we hope our work proves a valuable resource in this respect. The application of the variety of methods discussed here presents opportunities for researchers to model the nature of changes in multimorbidity and link these changes to outcomes that underly health-related quality of life, burden of care on families and communities, and costs of multimorbidity-associated healthcare.

Funding

Research reported in this publication was supported by the National Institute on Aging of the National Institutes of Health (R01AG055681 and RF1AG058545 to ARQ and HGA who contributed from the Yale Claude D. Pepper Older Americans Independence Center P30AG021342). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Conflict of Interest

None.

Informed Consent and Institutional Review Board Approval

This study was approved by Oregon Health and Science University’s Institutional Review Board (IRB ID# STUDY00017034, STUDY00019414). We note that this article did not require the use of human subjects data and, therefore, no informed consent was required.