Application of marginalized zero-inflated models when mediators have excess zeroes

1. Introduction

Zero-inflated count variables are common in many fields of research; for example, in cardiovascular disease (CVD) research this could include risk factors such as number of cigarettes smoked and number of alcoholic beverages consumed or health outcomes such as number of arrythmias, surgery complication count, and coronary artery stenosis^1–3. Standard count regressions like Poisson and negative binomial models fail to accurately predict count outcomes with excess zeroes⁴. The Zero-Inflated Poisson (ZIP) model was developed based on a mixture distribution of a degenerative distribution at zero (excess zeroes) and a Poisson distribution⁴. Parameters from ZIP’s Poisson process are interpreted with respect to the non-excess zero population, but often researchers are interested in explaining effects with respect to the whole population⁵. In response the Marginalized Zero-Inflated Poisson (MZIP) model was developed by reparametrizing the likelihood of the ZIP model, to directly model the overall mean while addressing zero-inflation⁶.

Mediation analysis has become a powerful tool used in many fields to explore causal pathways that may suggest ways to lessen the burden of CVD related disparities, allowing investigators to quantify the portion of the association between an exposure and outcome that can be explained by a potential mediating factor (Figure 1). For example, in men, higher Southern diet scores (a potential mediating factor) explains approximately 46% of the association between Black race (an exposure) and incident hypertension (an outcome)⁷, and a portion of the educational disparities in CVD risk are attributable to smoking⁸. While mediation methods have been proposed for zero-inflated count outcomes^9,10, there is a dearth of methods for zero-inflated count mediators.

Figure 1:

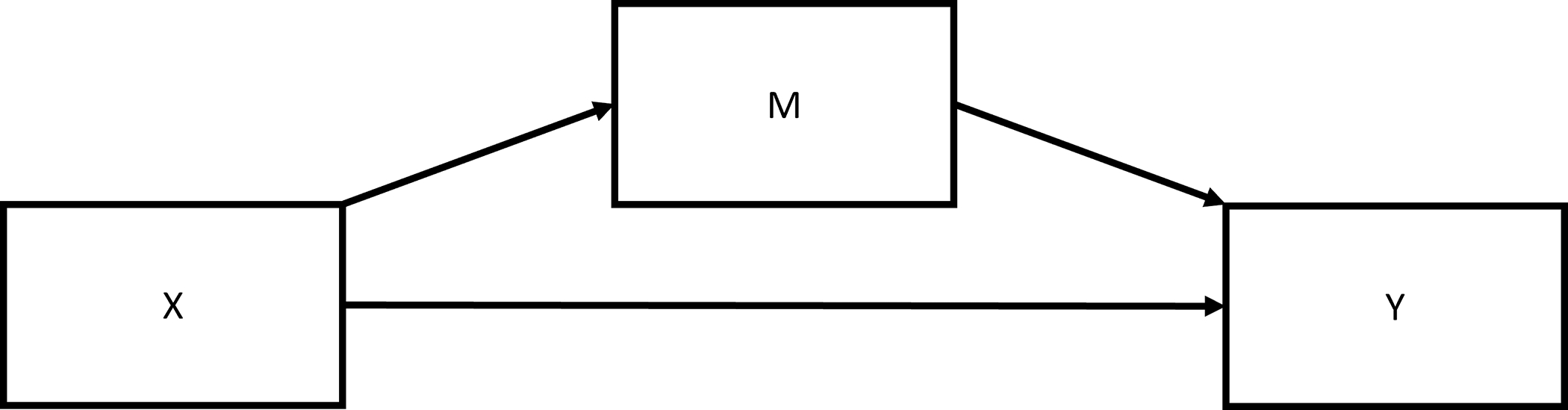
Pathways of a standard mediation analysis with exposure, X, mediator, M, and outcome, Y. No interaction is assumed.

The counterfactual approach to mediation provides definitions of mediation effects based on calculations of expectations for both outcome and mediator models, which are easily implementable and computationally straight-forward^11–13. Currently, the counterfactual approach to mediation has been adapted for binary, continuous and count outcomes and mediators¹³.

This article extends the counterfactual approach to mediation for zero-inflated count mediators utilizing the MZIP model for the mediator^6,13. Assuming all assumptions of causal mediation methods are satisfied, this method allows for easily derivable and computationally efficient mediation effects for the overall population mean. Section 2 reviews the counterfactual approach specification of mediation effects. Section 3 reviews the MZIP model. Section 4 extends the counterfactual approach to mediation where the mediator is a count variable with excess zeroes using MZIP. Section 5 presents a simulation study to examine the properties of the new MZIP counterfactual mediation model to compare to standard count counterfactual mediation methods. Section 6 presents analysis observing if gender differences in lipoprotein cholesterol can be explained by alcohol consumption. A discussion will follow in section 7.

2. Counterfactual Approach to Mediation

Traditional approaches to mediation such as the difference and product methods do not give causal interpretations when there are interactions or when outcome or mediator models beyond the identity link are fitted^13,14. Many frameworks have been developed to address the lack of flexibility of traditional method including the counterfactual approach to mediation^{11–13,15–18}. Assume $Y_i=Y$ is the observed value of the outcome, $M_i=M$ is the observed mediator, $\mathrm{X}$ the observed exposure, and $\mathrm{C}$ a vector of potential confounders for the i-th observation. First, standard counterfactual notation is introduced. Assume the exposure $X$ takes two levels, $x$ and $x^{\mathrm{*}}$, where we will call $x$ treatment and $x^{\mathrm{*}}$ control. If the exposure is binary, then it is standard to let $x=1$ and $x^{\mathrm{*}}=0$.

• $Y\left(x,m\right)={\mathrm{Y}}_{\mathrm{x}\mathrm{m}}:$ : is the counterfactual outcome for someone in the treatment group with the mediator fixed at $\mathrm{M}=\mathrm{m}$

• ${\mathrm{M}}_{\mathrm{x}\mathrm{*}}$: is the mediator value for someone in the control group

• $Y\left(x,M_{x\mathrm{*}}\right)=Y_{x{M}_{x^{\mathrm{*}}}}$ is the counterfactual outcome for someone if they received treatment, but the mediator was set to the value it would have taken under control (naturally)

The counterfactual approach involves fitting two regression equations: equation [1] regresses the outcome on the exposure, mediator, and any covariates and equation [2] regresses the mediator on the exposure and the same covariates as in the first model.

$$E\left[Y|X=x,M=m,\mathit{C}=\mathit{c}\right]=E\left[Y|x,m,\mathit{c}\right]={\beta }_0+{\beta }_{1}x+{\beta }_{2}m+{\mathit{\beta }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}$$ [1]

$$E\left[M|X=x,\mathit{C}=\mathit{c}\right]=E\left[M\right|x,\mathit{c}]={\tau }_0+{\tau }_{1}x+{{\mathit{\tau }}_{\mathbf{2}}}^{\mathit{\prime }}\mathit{c}$$ [2]

Using expected values based on parameter estimates from the outcome and mediator model the following important quantities can be derived:

$$NDE=E\left(Y_{x{M}_{x^{\mathrm{*}}}}-Y_{x^{\mathrm{*}}{M}_{x^{\mathrm{*}}}}|\mathit{c}\right)=\sum \left\{E\left[Y|x,m,\mathit{c}\right]-E\left[Y|x^{\mathrm{*}},m,\mathit{c}\right]\right\}P\left(m|x^{\mathrm{*}},\mathit{c}\right)$$

$$NIE=E\left(Y_{x{M}_x}-Y_{x{M}_x^{\mathrm{*}}}|\mathit{c}\right)=\sum E\left[Y|x,m,\mathit{c}\right]\left(P\left(m|x,\mathit{c}\right)-P\left(m|x^{\mathrm{*}},\mathit{c}\right)\right)$$

$$CDE\left(m\right)=E\left(Y_{xm}-Y_{x^{\mathrm{*}}m}|\mathit{c}\right)=E\left(Y|x,m,\mathit{c}\right)-E\left(Y\right|x^{\mathrm{*}},m,\mathit{c})$$

The natural direct effect (NDE) quantifies how much the outcome would change varying exposure from $x$ to $x^{\mathrm{*}}$, while the mediator is held constant for each individual at the value it would have taken at $X=x^{\mathrm{*}}$, or the exposure-outcome relationship not operating through the mediator. The natural indirect effect (NIE) quantifies how much on average the outcome would change if the mediator were changed from the value it would take at $X=x^{\mathrm{*}}$ to the value it would take given $X=x$, or often interpreted as the mediation effect. The controlled direct effect (CDE) quantifies how much the outcome would change if we varied the exposure from $x^{\mathrm{*}}$ to $x$ while the mediator was set to some pre-determined fixed value. The overall or total effect of the exposure on the outcome can be computed by summing NDE and NIE. CDE and NDE will be equivalent if there is no interaction between exposure and mediator in the outcome model.

Standard errors for effects in mediation analysis are typically computed using bootstrapping methods^19,20. In the case of large sample sizes, bootstrapping may be too computationally intensive, and standard errors using the delta method are alternatively available ^13,16.

The counterfactual approach to causal mediation requires the following assumptions about confounding be satisfied for accurate estimation of NDE and NIE:

• Assumption 1: No uncontrolled confounding of the exposure-outcome relationship ($Y_{xm}⫫X|C$)

• Assumption 2: No uncontrolled confounding of the mediator-outcome relationship ($Y_{xm}⫫M|\{X,C\}$)

• Assumption 3: No uncontrolled confounding of the exposure-mediator relationship ($M_x⫫X|C$)

• Assumption 4: No mediator-outcome confounder is affected by the exposure ($Y_{xm}⫫M_{x^{\mathrm{*}}}|C$).

Where $⫫$ denotes conditional independence. Assumptions are illustrated in Figure 2 for a properly specified mediation analysis. All four assumptions are needed for estimation of NIE and NDE, but only Assumption 1–2 are needed for estimation of CDE¹³. If the exposure is a randomized treatment assignment then Assumption 1 and 3 will be automatically satisfied. Violations of these assumptions may bias direct and indirect effect estimates and are discussed extensively elsewhere through sensitivity analyses^13,21,22. In addition to the confounding assumption, this framework also adopts the consistency assumption. That is when $X=x$ the counterfactual outcome $Y\left(x\right)$ and counterfactual mediator $M\left(x\right)$ are equal to their observed values $Y$ and $M$²³. In addition, when $X=x$ and $M=m$ the counterfactual outcome $Y(x,m)$ is equal to the observed outcome $Y$²³.

Figure 2.

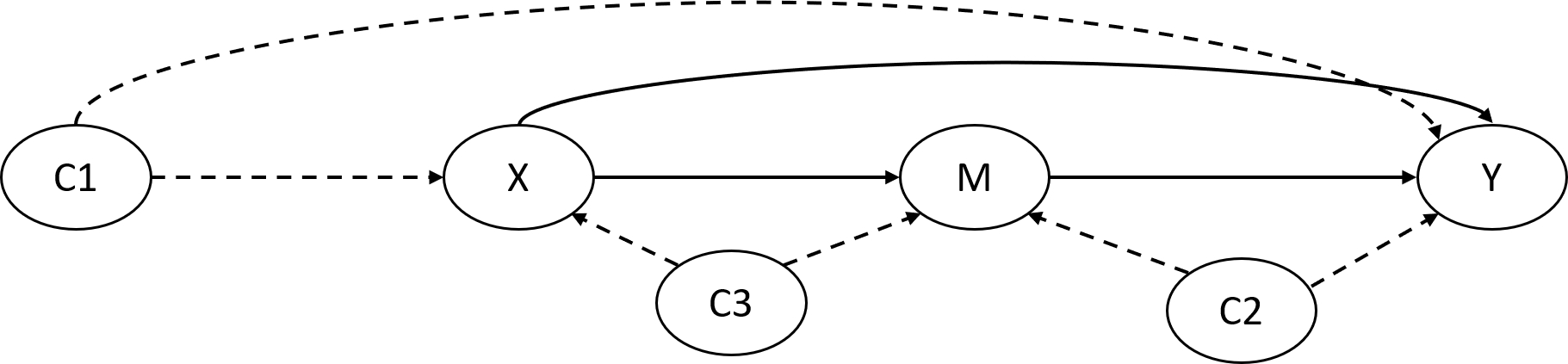
This DAG illustrates a scenario with proper control of confounders in a mediation analysis with an exposure X, mediator M, outcome Y, exposure–outcome confounder C1, mediator–outcome confounder C2, and exposure–mediator confounder C3.

3. MZIP Model

When a count variable has more zeroes than expected by a count distribution, this count is often referred to as ‘zero-inflated’ or having ‘excess zeroes’. When a count outcome has excess zeroes, Poisson and negative binomial model estimates will be biased⁴. While several models have been developed for excess zeroes in count data, many of these models do not provide inference comparable to standard count regression^4,24–26.. For example, the zero-inflated Poisson (ZIP) model allows the count variable of interest, $M_i,i=1,\dots n$, to take on the value of zero from a Bernoulli distribution with probability ${\psi }_i$ or be drawn from a Poisson distribution with mean ${\mu }_i$ with probability $1-{\psi }_i$⁴. ZIP estimates the probability of an individual being an excess zero and the mean of the non-excess zeroes, but doesn’t directly estimate the mean of the whole population^4,5. The latent class interpretations of these models are often misrepresented or overlooked by researchers interested in the overall population mean effect of the exposure⁵. Long et. al addressed this issue by transforming the latent class ZIP model to allow for marginal mean interpretations in the Marginalized Zero-Inflated Poisson Model (MZIP)⁶. The MZIP model uses a two-part modeling approach with the same Bernoulli component as ZIP, but the Poisson component models the overall population mean ${\nu }_i$, where ${\nu }_i=\left(1-{\psi }_i\right){\mu }_i$. MZIP model specifies:

$$logit\left({\psi }_i\right)={\mathit{Z}}_{\mathit{i}}^{\mathit{\prime }}\mathit{\gamma }$$

$$\log \left(v_i\right)={\mathit{Z}}_{\mathit{i}}^{\mathit{\prime }}\mathit{\alpha }$$

Where, $\mathit{\gamma }$ is a $(\rho \times 1)$ column vector of parameters associated with the probability of being an excess zero, $\mathit{\alpha }$ is a $\left(\rho \times 1\right)$ column vector of parameters associated with the overall population mean model, ${\mathit{Z}}_{\mathit{i}}$ is a $(\rho \times 1)$ vector of covariates for the $i$-th individual for both components of MZIP, and $\rho$ is the number of parameters including an intercept in the MZIP model. Note that we assume the same covariates are included in both components of MZIP, but this is not a requirement of the MZIP model. This allows for risk ratio or incidence density ratio interpretations equivalent to traditional Poisson regression, where $e^{{\alpha }_j}$ is the multiplicative increase in ${\nu }_i$ for a 1-unit increase in $z_j$. The logistic component parameters can be interpreted as the log-odds ratio of a 1-unit increase in $z_j$ on the probability of the outcome being an excess zero. The likelihood of the MZIP model is estimated using quasi-Newton optimization methods in statistical software such as SAS and STATA^27,28. Using the Poisson component of the MZIP model to obtain a single estimate of the association between exposure and mediator, mediation methodology can be extended to zero-inflated count mediators to obtain mediation effects for the overall population mean.

4. Mediation with Zero-Inflated Count Mediator

Using the counterfactual definitions of mediation effects allows for easily implementable and computationally straightforward estimations of NDE and NIE. Merging this framework with MZIP gives mediation effects interpreted with respect to the population mean while minimizing bias of mediation effects. In addition to the confounding and consistency assumptions needed for causal mediation discussed in Section 2, the proposed methods additionally require that the mediator and outcome model are correctly specified.

4.1. Continuous Outcome

Integrating the MZIP model into the counterfactual mediation framework results in derivations similar to the counterfactual approach with a Poisson model. When the mediator is a count variable with excess zeroes, first fit model a continuous outcome, Y, on the exposure, X, mediator, M, and a vector of covariates, C. Next, model the zero-inflated count mediator on the exposure and confounders, jointly modeling the probability of being an excess zero, ${\psi }_i$ and the overall mean count, ${\nu }_i$. An exposure-mediator interaction is included in the outcome model to fully assess the relationship between exposure, mediator, and outcome. The specified model is

$${E(Y}_i|x,m,\mathit{c})={\beta }_0+{\beta }_{1}x+{\beta }_{2}m+{\beta }_{3}xm+{{\mathit{\beta }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}$$

$$\log \left(v_i\left(M\right)|x,\mathit{c}\right)={\alpha }_0+{\alpha }_{1}x+{{\mathit{\alpha }}^{\mathit{\prime }}}_{\mathbf{4}}\mathit{c}$$

$$logit\left({\psi }_i\left(M\right)|x,\mathit{c}\right)={\gamma }_0+{\gamma }_{1}x+{{\mathit{\gamma }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}$$

The natural direct effect is calculated by

$$\begin{gathered} NDE={\text{Σ}}_m\left(E\left(Y_i\text{|}x,m,\mathit{c}\right)-E\left(Y_i\text{|}{x}^{*},m,\mathit{c}\right)\right)\left(P\left(m\text{|}{x}^{*},\mathit{c}\right)\right) \\ ={\text{Σ}}_m\left[\left({\beta }_0+{\beta }_{1}x+{\beta }_{2}m+{\beta }_{3}xm+{{\mathit{\beta }}_{\mathbf{4}}}^{\prime }\mathit{c}\right)-\left({\beta }_0+{\beta }_1{x}^{*}+{\beta }_{2}m+{\beta }_3{x}^{*}m+{{\mathit{\beta }}_{\mathbf{4}}}^{\prime }\mathit{c}\right)\right]P\left(M\text{|}{x}^{*},\mathit{c}\right) \\ ={\beta }_1\left(x-x^{*}\right)+{\beta }_3\left(x-x^{*}\right)\left[e^{{\alpha }_0+{\alpha }_{1}x*+{{\mathit{\alpha }}_{\mathbf{4}}}^{\prime }\mathit{c}}\right] \end{gathered}$$

The natural indirect effect is calculated by

$$\begin{gathered} NIE={\text{Σ}}_{m}E\left(Y_i|x,m,\mathit{c}\right)\left[P\left(M_i\text{|}x,\mathit{c}\right)-P\left(M_i\text{|}{x}^{*},\mathit{c}\right)\right] \\ ={\text{Σ}}_m\left({\beta }_0+{\beta }_{1}x+{\beta }_{2}m+{\beta }_{3}xm+{{\mathit{\beta }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}\right)\left(P\left(M\text{|}x,\mathit{c}\right)-P\left(M\text{|}{x}^{*},\mathit{c}\right)\right) \\ =\left({\beta }_0+{\beta }_{1}x+{\beta }_{2}E\left(M\text{|}x,\mathit{c}\right)+{\beta }_{3}xE\left(M\text{|}x,\mathit{c}\right)+{{\mathit{\beta }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}\right)-({\beta }_0+{\beta }_{1}x+{\beta }_{2}E(M|x^{*},\mathit{c})+{\beta }_{3}xE(M|x^{*},\mathit{c})+{{\mathit{\beta }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}) \\ =\left({\beta }_2+{\beta }_{3}x\right)\left[e^{{\alpha }_0+{\alpha }_{1}x+{{\mathit{\alpha }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}}-e^{{\alpha }_0+{\alpha }_{1}x*+{{\mathit{\alpha }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}}\right] \end{gathered}$$

If there is no interaction term, then ${\beta }_3$ can be set to zero simplifying model expression and formulas for NDE and NIE. Effects in this case are a function of the covariates $\mathit{C}$. A fixed value for each covariate will be required for estimating the NIE and NDE, and using the mean or median values of each covariate will yield marginal effects for the overall population¹³.

Summing NDE and NIE the total effect can be obtained. The proportion of the exposure-outcome relationship operating through the mediator, called the proportion mediated, can be derived by $\frac{NIE}{TE}$. The CDE is defined by

$$\begin{gathered} CDE=E\left(Y_i|x,m,\mathit{c}\right)-E\left(Y_i|x^{\mathrm{*}},m,\mathit{c}\right) \\ =\left({\beta }_0+{\beta }_{1}x+{\beta }_{2}m+{\beta }_{3}xm+{{\mathit{\beta }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}\right)-\left({\beta }_0+{\beta }_1{x}^{\mathrm{*}}+{\beta }_{2}m+{\beta }_3{x}^{\mathrm{*}}m+{{\mathit{\beta }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}\right) \\ =({\beta }_1+{\beta }_{3}m)(x-x^{\mathrm{*}}) \end{gathered}$$

The CDE is useful in the computation of the proportion eliminated (PE), which quantifies how much of the effect of the exposure on the outcome could be eliminated if we were to intervene and set the mediator at a fixed value for each individual. The proportion eliminated is computed by, $PE=\frac{TE-CDE\left(m\right)}{TE}$.

As in other applications of counterfactual mediation, standard errors and confidence intervals for the direct and indirect effects can derived through bootstrapping or delta method techniques (Appendix A1 and A2) Over-dispersion is often a concern of Poisson models mostly due to underestimation of variance. For zero-inflated counts, use of robust standard errors has been shown to alleviate this burden when using an MZIP model²⁵. When using the delta method for the proposed method one can use either model based or robust covariance structures for the MZIP mediator model to obtain effect estimates, minimizing the burden of overdispersion. For an outcome model specified using an identity link, the formulas of NDE and NIE will be the same for MZIP and Poisson mediator models, but the two models differ in distributional assumptions and estimation techniques.

4.2. Binary or Count Outcome

Derivations of mediation effects have also been computed for binary and count outcomes. Given the odds ratio is non-collapsible, it is not recommended to use a logistic regression outcome model for a non-rare binary outcome in a mediation framework²⁹. For non-rare binary outcomes it is recommended to use a log-binomial or Poisson model with robust standard errors to obtain risk ratio interpretations of effects³⁰. Since a log-link is used for the outcome model, NDE and NIE will be on a risk ratio scale. For binary (log-link) outcomes, the model is specified as:

$$\log \left(P\left(Y_i=1|x,m,\mathit{c}\right)\right)={\theta }_0+{\theta }_{1}x{+\theta }_{2}m+{\theta }_{3}xm+{{\mathit{\theta }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}$$

$$\log \left(v_i\left(M|x,\mathit{c}\right)\right)={\alpha }_0+{\alpha }_{1}x+{{\mathit{\alpha }}^{\mathit{\prime }}}_{\mathbf{4}}\mathit{c}$$

$$logit\left({\psi }_i\left(M|x,\mathit{c}\right)\right)={\gamma }_0+{\gamma }_{1}x+{{\mathit{\gamma }}_{\mathbf{4}}}^{\mathit{\prime }}\mathit{c}$$

Where $\mathit{\theta }$ are the parameters for the log-link model. For the log link outcome model, derivations of mediation effects require use of the moment-generating function of the mediator distribution, thus expressions will differ for varying mediator distributions. Mediation effect risk ratios then take the following formulas

$$R{R}^{NDE}=\frac{{\mathrm{e}}^{{\theta }_{1}x}\left(e^{{\gamma }_0+{\gamma }_1{x}^{\mathrm{*}}+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}+e^{\left(e^{{\alpha }_0+{\alpha }_1{x}^{\mathrm{*}}+{\mathit{\alpha }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}+\log \left(1+e^{{\gamma }_0+{\gamma }_1{x}^{\mathrm{*}}+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}\right)}\right)\left(\left(e^{{\theta }_2+{\theta }_{3}x}-1\right)\right)}\right)}{{\mathrm{e}}^{{\theta }_1{x}^{\mathrm{*}}}\left(e^{{\gamma }_0+{\gamma }_1{x}^{\mathrm{*}}+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}+e^{\left(e^{{\alpha }_0+{\alpha }_1{x}^{\mathrm{*}}+{\mathit{\alpha }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}+\log \left(1+e^{{\gamma }_0+{\gamma }_1{x}^{\mathrm{*}}+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}\right)}\right)\left(\left(e^{{\theta }_2+{\theta }_{3}x\mathrm{*}}-1\right)\right)}\right)}$$

$$R{R}^{NIE}=\frac{\left(1+e^{{\gamma }_0+{\gamma }_1{x}^{\mathrm{*}}+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}\right)\left(e^{{\gamma }_0+{\gamma }_{1}x+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}+e^{\left(e^{{\alpha }_0+{\alpha }_{1}x+{\mathit{\alpha }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}+\log \left(1+e^{{\gamma }_0+{\gamma }_{1}x+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}\right)}\right)\left(\left(e^{{\theta }_2+{\theta }_{3}x}-1\right)\right)}\right)}{\left(1+e^{{\gamma }_0+{\gamma }_{1}x+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}\right)\left(e^{{\gamma }_0+{\gamma }_1{x}^{\mathrm{*}}+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}+e^{\left(e^{{\alpha }_0+{\alpha }_1{x}^{\mathrm{*}}+{\mathit{\alpha }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}+\log \left(1+e^{{\gamma }_0+{\gamma }_1{x}^{\mathrm{*}}+{\mathit{\gamma }}_{\mathbf{4}}^{\mathit{\prime }}\mathit{c}}\right)}\right)\left(\left(e^{{\theta }_2+{\theta }_{3}x}-1\right)\right)}\right)}$$

$$R{R}^{CDE}=e^{\left({\theta }_1+{\theta }_{3}m\right)(x-x^{\mathrm{*}})}$$

Proofs of these effects are shown in the appendix (Appendix A3). Note the exposure-mediator interaction ${\theta }_3$ can be set to zero when interaction term is not indicated. Since these quantities are on a ratio scale, the risk ratio of the total effect is computed as the product of the NIE and NDE risk ratios. The proportion mediated is then computed by the following formula ¹³:

$$PM=\frac{R{R}^{NDE}\left(R{R}^{NIE}-1\right)}{R{R}^{NDE}\left(R{R}^{NIE}\right)-1}$$

The proportion mediated requires that the risk ratio of NDE and NIE both be either greater than or less than 1. The proportion eliminated is computed by ¹³:

$$PE=\frac{R{R}^{NDE}\left(R{R}^{NIE}\right)-R{R}^{CDE\left(m\right)}}{R{R}^{NDE}\left(R{R}^{NIE}\right)-1}$$

Standard errors can be computed through bootstrapping or by using delta method standard errors (Appendix A4). While the focus of the formulas in this section were for binary outcomes, the same formulas will apply to other log-link models such as Poisson or Negative Binomial models for count outcomes.

5. Simulation

To examine the properties of the proposed mediation methods, a simulation study was performed using the model and formulas for direct and indirect effects with a continuous outcome specified in section 4.1.

For each iteration, a binary exposure of interest $x$ is simulated from a Bernoulli distribution with probability 0.5. A covariate c, that is simulated from ${\chi }_2^2$ is also included in the simulation. A matrix of simulated exposure and covariate are merged into a $(n\times 3)$ matrix $\mathbf{Z}$ along with an intercept matrix, $\mathit{Z}=\left(\mathbf{1},x,c\right)$, where n is the sample size of the simulated data. The mediator values are then simulated from ZIP framework where:

$$\psi ~Bernoulli\left(\frac{\exp \left(Z\gamma \right)}{1+\exp \left(Z\gamma \right)}\right)$$

$$\mu ~Poisson\left(\exp \left(Z\alpha +\mathit{log}\left(1+Z\gamma \right)\right)\right)$$

Then the mediator value is derived by the product of $1-\psi$ and $\mu$. The outcome is subsequently simulated based on a linear equation of the exposure, mediator, covariates, and an error term $ϵ~N(0,{\sigma }^2)$.

Various parameter scenarios in which the natural direct and natural indirect effect are in the same direction were examined, meaning we can conveniently describe each scenario with the proportion mediated. Four scenarios of mediator data generation were considered as method performance may vary by zero-inflation levels, overall mean, and exposure effect on the probability of being an excess zero impact results (Table 1). Scenario 1 was used as a reference, scenario 2 decreased the zero-inflation, scenario 3 widened the gap between treatment and control for the probability of being an excess zero, and scenario 4 increased the overall mean (Figure 3). For each parameter scenario, different samples sizes (200, 600, 1 000) are considered with 5 000 iterations. Additionally, using equation 1 we assume $\mathit{\beta }=({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_4)=(23,\mathrm{3,1.5,0})$ with ${\sigma }^2=4$ for each scenario. ${\beta }_0$ is irrelevant to the estimation of NDE and NIE. Other parameters for the outcome model were chosen to ensure the NDE and NIE were in the same direction, linear model assumptions were mostly satisfied, and that effects and proportion mediated were values that would be plausible given ${\sigma }^2=4$. Note that the simulation study was set up such that all confounding assumptions are satisfied.

Table 1:

Scenarios for simulation study on zero-inflated mediator using MZIP

Scenario	Parameters	Excess Zero	Overall Mean	NIE	PM
1	$\mathrm{\gamma }$={0.35,-0.45,0.25}	Control=70%	Control=1.0	0.75	20%
	$\mathrm{\alpha }$={-0.5,0.41,0.25}	Treatment=60%	Treatment=1.5
2	$\mathrm{\gamma }$={-0.5,-0.45,0.25}	Control=50%	Control=1.0	0.75	20%
	$\mathrm{\alpha }$={-0.5,0.41,0.25}	Treatment=39%	Treatment=1.5
3	$\mathrm{\gamma }$={0.35,-1.5,0.25}	Control=70%	Control=1.0	0.75	20%
	$\mathrm{\alpha }$={-0.5,0.41,0.25}	Treatment=34%	Treatment=1.5
4	$\mathrm{\gamma }$={0.35,-0.45,0.25}	Control=70%	Control=2.5	0.75	20%
	$\mathrm{\alpha }$={0.42,0.18,0.25}	Treatment=60%	Treatment=3.0

^*The confounder variable is fixed at its mean level C=2 for these calculations

Figure 3.

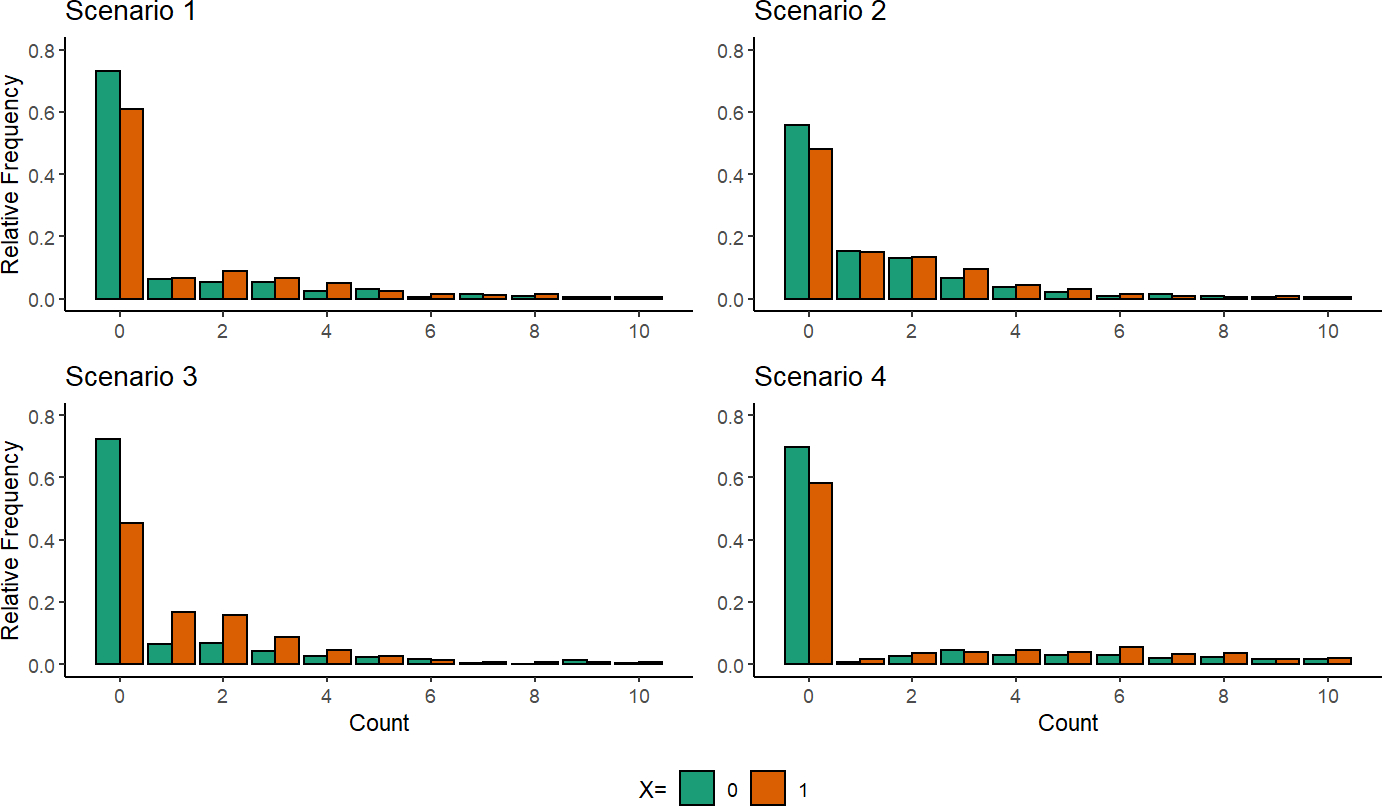
Distributions of simulated zero-inflated mediator by exposure group. From Scenario 1, Scenario 2 has a decreased probability of being an excess zero, Scenario 3 has a larger differential effect on the probability of being an excess zero in the unexposed group compared to the exposed group, and Scenario 4 has an increased overall population mean.

Given the lack of zero-inflated count mediation methods estimating marginalized effects, the proposed MZIP meditation method is compared to Poisson and linear mediator models which ignore the excess zeroes feature but provide estimation through modeling the overall mean. For each mediator modeling approach, the NDE will be the same as it relies solely on the outcome model. To compare methods in estimation of NIE, percent median bias, coverage, power, and median standard error using both the delta method and bootstrapped standard errors are calculated.

From Table 2, note that MZIP mediator models have the lowest bias. Poisson regression was not noticeably biased in scenarios with lower effect of exposure on excess zero probabilities. However, Poisson methods exhibited increased bias when there was a larger treatment effect on the probability of excess zero (scenario 3) and when the overall mean was increased (scenario 4). This is not unexpected as the Poisson model does not account for these differential effects in the treatment on the probability of being an excess zero. Linear regression yielded biased results in every scenario. For the MZIP mediator model bias decreased modestly as sample size increased. For Poisson and linear mediator models, this trend did not hold and in some cases with higher zero-inflation bias increased as sample size increased. This is likely reflective of bias converging to the population value based on the Poisson and normal distributions which are overestimating the mean of the zero-inflated mediator.

Table 2:

Comparison of median percent bias for estimation of NIE using MZIP, Poisson, and linear models for the mediator.

Scenario	Sample Size	MZIP	Poisson	Linear
1	200	0.09	1.74	9.93
	600	−0.79	3.71	12.54
	1000	−1.16	3.66	13.71
2	200	−0.88	0.48	9.81
	600	0.07	2.05	15.93
	1000	−0.51	4.17	16.86
3	200	−0.63	11.45	21.28
	600	−0.46	10.59	22.09
	1000	−0.03	8.73	20.75
4	200	−3.54	4.70	13.37
	600	−0.59	6.86	19.70
	1000	0.66	6.90	17.59

In Table 3 note that the delta method coverage probabilities for the NIE for Poisson and linear regression in a mediation framework are subpar and their bootstrap counterparts are slightly lower than the nominal 95%. Coverage for MZIP mediator models using both delta method and bootstrap standard errors were near 95% for all scenarios. Coverage was stable across sample size for all methods.

Table 3:

Comparison of coverage probabilities for NIE for MZIP, Poisson, and Linear mediator models

Scenario	Sample Size	MZIP		Poisson		Linear
		Delta	Boot-strap	Delta	Boot-strap	Delta	Boot-strap
1	200	95.12%	94.70%	47.22%	93.62%	81.42%	93.66%
	600	94.62%	94.42%	39.68%	92.96%	79.80%	92.86%
	1000	94.42%	94.46%	37.34%	92.98%	79.76%	92.52%
2	200	95.16%	95.02%	59.42%	93.86%	82.62%	93.39%
	600	94.78%	94.78%	50.48%	93.54%	80.00%	92.56%
	1000	94.89%	94.94%	46.90%	93.76%	78.70%	91.06%
3	200	95.08%	94.70%	54.04%	93.22%	79.82%	92.58%
	600	95.00%	94.66%	46.00%	92.16%	77.68%	90.92%
	1000	94.80%	94.46%	42.08%	91.40%	75.68%	89.20%
4	200	94.96%	95.02%	33.34%	93.00%	80.40%	93.16%
	600	94.88%	94.76%	28.14%	93.40%	79.94%	93.02%
	1000	95.10%	94.94%	26.26%	93.50%	80.68%	93.22%

Delta method and bootstrap errors for MZIP were comparable in terms of power (Table 4) and median standard error (Table 5) implying that bootstrap methods may not be necessary for MZIP application and delta method variance estimation is sufficient. Also, MZIP standard errors were close to the intrinsic standard error for the model (Table 5) implying that the model accurately estimates parameter variability. Poisson regression significantly underestimated standard errors which explains the poor coverage and high power of the model. Linear regression yielded a higher variance of NIE than other models, but still underestimated the true variance of NIE. The performance of linear regressions can be explained by linear regression tendency to not perform well due to skewness and sparsity of count data causing heteroskedasticity of standard errors³¹.

Table 4:

Comparison of power for NIE estimates using MZIP, Poisson, and linear regression mediator models

Scenario	Sample Size	MZIP		Poisson		Linear
		Delta	Boot-strap	Delta	Boot-strap	Delta	Boot-strap
1	200	40.22%	41.12%	73.64%	29.04%	45.06%	29.16%
	600	84.76%	84.80%	88.44%	49.32%	65.58%	49.34%
	1000	97.18%	97.20%	89.68%	64.01%	74.58%	60.84%
2	200	58.46%	58.84%	74.82%	40.08%	54.50%	39.80%
	600	96.66%	96.56%	91.82%	65.22%	77.70%	65.36%
	1000	99.84%	99.82%	96.06%	76.19%	85.04%	75.30%
3	200	51.30%	50.72%	77.98%	40.26%	55.42%	40.58%
	600	92.28%	92.10%	91.52%	61.28%	75.14%	62.20%
	1000	99.32%	99.26%	94.82%	70.14%	80.76%	70.64%
4	200	13.42%	13.22%	71.48%	12.18%	27.32%	12.40%
	600	32.50%	32.42%	81.28%	18.98%	35.78%	19.24%
	1000	48.50%	48.36%	83.82%	22.92%	39.72%	23.17%

Table 5:

Comparison of median standard errors for NIE estimates using MZIP, Poisson, and linear regression mediator models

Scenario	Sample Size	MZIP			Poisson			Linear
		Intrinsic	Delta	Boot-strap	Intrinsic	Delta	Boot-strap	Intrinsic	Delta	Boot-strap
1	200	0.43	0.44	0.44	0.76	0.24	0.60	1.55	0.47	0.68
	600	0.25	0.25	0.25	0.54	0.13	0.41	1.14	0.32	0.47
	1000	0.20	0.20	0.20	0.46	0.10	0.34	0.85	0.27	0.40
2	200	0.36	0.35	0.35	0.58	0.24	0.47	1.21	0.38	0.54
	600	0.20	0.20	0.20	0.45	0.14	0.32	1.45	0.26	0.38
	1000	0.16	0.16	0.16	0.36	0.10	0.26	0.65	0.21	0.31
3	200	0.39	0.38	0.39	0.67	0.24	0.51	1.95	0.41	0.59
	600	0.22	0.22	0.22	0.49	0.14	0.34	1.38	0.28	0.40
	1000	0.17	0.17	0.17	0.41	0.10	0.29	0.73	0.23	0.34
4	200	0.88	0.86	0.87	1.67	0.34	1.27	3.64	0.97	1.43
	600	0.51	0.50	0.50	1.90	0.20	0.89	2.94	0.68	1.02
	1000	0.39	0.39	0.39	1.03	0.15	0.74	2.2	0.59	0.86

Simulations were also completed for binary outcomes (Appendix A5) and for over-dispersed zero-inflated count mediators (Appendix A6). The simulations with binary outcomes were comparable to continuous outcomes. For over-dispersed mediators we observed that model-based delta method variance for MZIP did not provide adequate coverage; however, bootstrapping or use of robust delta method variance led to nominal coverage with robust errors having rapid computation speed. Additional simulations were conducted varying the value of ${\beta }_4$ with no measurable difference in model performance.

Overall, the proposed mediation method for zero-inflated count mediators using MZIP performed well in estimating the NIE and its corresponding variance in all sample sizes considered under both standard error estimation techniques. Poisson regression significantly underestimated the variance when using delta method errors. Delta method standard errors inherit distributional assumptions of the mediator model; for a Poisson model, the mean is equal to the variance. Notably for a mediator with a large number of zeroes, the overall mean is small resulting in small Poisson model variance estimates as well. Although computationally intensive bootstrap methods largely resolved the deficiencies of variance estimation for the Poisson mediator model, the biased estimation of mediation effects is problematic, particularly when there was a large treatment effect on the probability of being an excess zero and when the overall mean of the zero-inflated mediator was increased. Linear regression methods also performed poorly, indicating that jointly ignoring the zero-inflation and count nature of the mediator can lead to severely biased estimation. Linear regression assumes the mediator is unbounded, so it is not surprising that it behaved poorly with a bounded variable.

6. Illustrative Application

Cholesterol has long been associated with CVD events³². Using this novel mediation technique, we will observe if sex differences in lipid values can be explained by behavioral factors suitable to intervention. Studies have found relationships between alcohol consumption and low-density lipoprotein cholesterol (LDL-C), high-density lipoprotein cholesterol (HDL-C), and triglycerides^33–35. Alcohol consumption (e.g., number of drinks per week) is a zero-inflated count variable that could be intervened upon if this variable acts as a mediator between sex and cholesterol.

The REasons for Geographic And Racial Differences in Stroke (REGARDS) study is an ongoing, national cohort targeted at identifying factors that explain regional and race differences in stroke³⁶. REGARDS enrolled 30239 black and white individuals between 2003–2007 and continues to follow participants to understand why stroke incidence is higher among Black Americans and southerners particularly in regions with higher risk of stroke called the Stroke Belt and Stroke Buckle³⁶. REGARDS has intensive baseline and follow-up data on participants and is an ideal setting for exploring reasons for CVD-related disparities. Using this cohort, we observe how sex differences in lipid measures (9.5 years after cohort entry) can be explained by baseline alcohol consumption.

Triglycerides follow a skewed distribution, so they were log-transformed for analysis. Finally, adjustment is made for numerous covariates at baseline including race, urbanicity, geographical region (Stroke belt, Stroke buckle), income level, education level, and baseline statin use. After excluding people with missing baseline covariates and follow-up cholesterol, our analytic sample size is 12093. Alcohol consumption in REGARDS is self-reported as the number of drinks per week and contains about 70% zeroes (Figure 4). We assume that confounding and consistency assumptions are satisfied. In applied work, rigorous examination of these assumptions is necessary.

Figure 4.

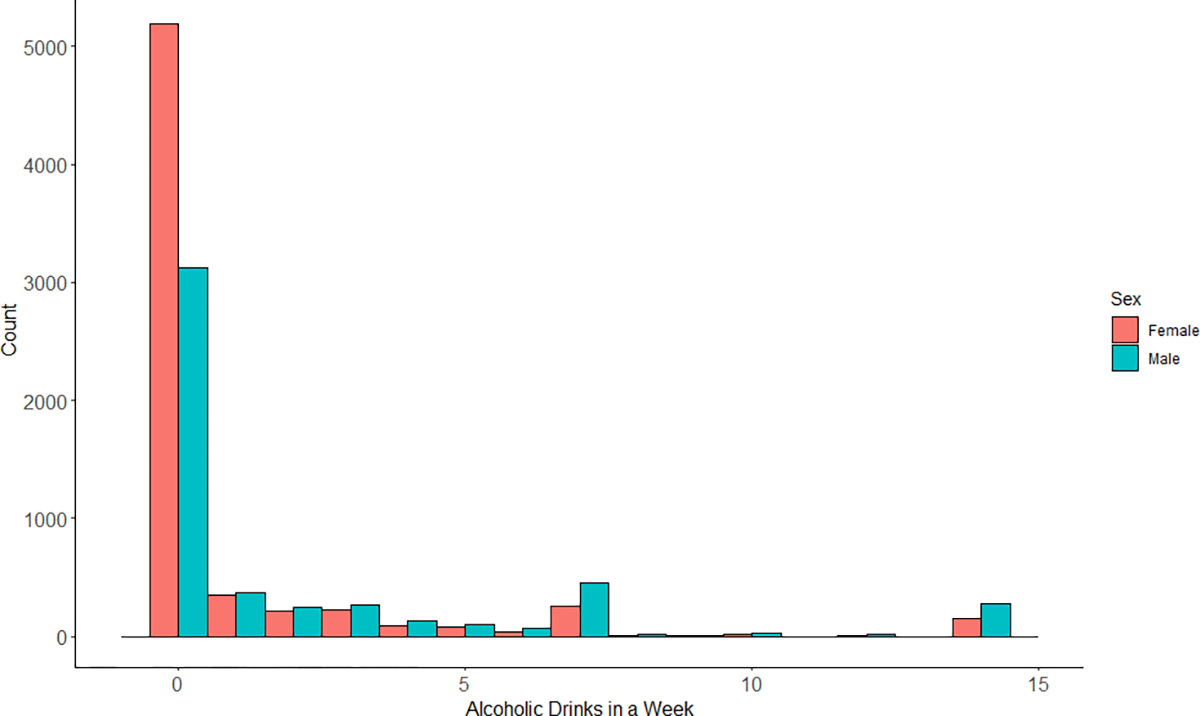
Distribution of number of alcoholic drinks in the last week by sex in the REGARDS study (n = 12,093). Over 70% of participants reported no drinks in the last week.

Shown in table 6 are the results of the analysis examining potential mediation of sex differences in log-triglycerides by alcohol consumption (Appendix A7). Due to the large sample size, variance estimates were similar for all methods except for indirect and total effects for linear regression mediator model without an interaction this is likely due to a combination of skewness in the mediator model causing heteroskedasticity of variance estimates and not including the interaction term in the outcome model to explain variability. From simulations in Section 5, we observe that Poisson and linear regression had higher estimates of NIE and are likely overestimating NIE and subsequently the proportion mediated. These results hold with and without exposure-mediator interaction effects, and estimated NIE was less when including the exposure-mediator interaction across all methods. Interaction terms were significant in the outcome model (P<0.0001). We found that the about 12% of sex disparities in triglycerides can be explained by alcohol consumption and that the relationship between sex and triglycerides varies by alcohol consumption.

Table 6:

Mediation results showing sex disparities in triglycerides (log) explained by alcohol consumption (female=reference group)

	MZIP	Poisson	Linear
NDE	0.0270(0.011,0.043)	0.0270(0.011,0.043)	0.0270(0.011,0.043)
NIE	0.0062(0.004,0.008)	0.0072(0.005,0.009)	0.0080(−0.213,0.229)
TE	0.0332(0.017,0.049)	0.0342(0.018,0.050)	0.0350(0.187,0.257)
PM	18.6%	21.10%	22.78%
With Interaction
NDE	0.0302(0.014,0.047)	0.0307(0.014,0.047)	0.0297(0.013,0.046)
NIE	0.0042(0.002,0.006)	0.0048(0.002,0.007)	0.0053(0.002,0.008)
TE	0.0344(0.018,0.051)	0.0355(0.019,0.052)	0.0350(0.019,0.051)
PM	11.96%	13.5%	15.00%

Sensitivity analysis stratifying by statin use examined whether mediation effects varied by medication usage and no significant differences were observed across strata. One limitation of this analysis is the potentially nonlinear relationship between alcohol consumption and cholesterol^33,34, but accounting for nonlinear relationship in mediation analysis is an area of future method development. Different specifications of alcohol consumption may be warranted to account for such nonlinearities through for example, categorization. Although methods for ordinal mediators exist they are not comparable to the proposed method and were not considered^37,38. We also considered robust standard errors for effect estimates given the seemingly over-dispersed outcome, but standard errors were equivalent to model based standard errors for MZIP.

While this application utilizes alcohol consumption as an example of a zero-inflated count mediator. Other zero-inflated variables that may act as mediators include healthcare utilization frequency³⁹, cigarette smoking⁴⁰, and the Charlson comorbidity index⁴¹.

7. Discussion

A mediation method for zero-inflated count mediators was proposed by incorporating the MZIP model into the counterfactual mediation framework. This novel causal mediation method for zero-inflated count mediators has marginal effect interpretations, options for rapid computation of variance, exposure-mediator interaction compatibility, and can accommodate continuous, binary and count outcomes. Given satisfaction of the confounding and consistency assumptions of causal mediation, this novel application of MZIP in mediation analysis yields unbiased population-average NIE estimates in a straightforward way compared to other two-part zero-inflated models. While previous work has developed methodology for zero-inflated count outcomes^9,10, the proposed method focuses on zero-inflated mediators.

The simulation study discussed in Section 5 demonstrated that other marginal mediator models (Poisson and linear regression) gave biased results, particularly given a large treatment effect on the probability of being an excess zero. This is because these models do not account for exposure differences in excess zeroes and subsequent impact on parameter estimation. Simulation results also showed that Poisson and linear regression underestimated variance of NIE. While mediation for Poisson and linear mediator models are readily available and easy to use^13,15, using these methods on a zero-inflated count variable should be avoided to prevent inaccurate and unreliable conclusions^4,5. Specifically, Poisson models tend to overestimate the overall mean of zero-inflated counts while underestimating variance. The assumption of normality in linear regression fails to be satisfied when the mediator has a large proportion of observations on a boundary space of the observed variable. The discussed method using MZIP yields unbiased estimates of NIE and its variance and is now readily available in a R package called `mzipmed` on the Comprehensive R Archive Network^42,43.

Standard errors for NDE and NIE are typically computed via bootstrap methods to account for multiple sources of model variability; however, this can be computationally intensive for large datasets such as the motivating REGARDS cohort. Using an MZIP mediator model, closed form expressions of variance via delta method that are comparable to bootstrapped variance estimation have been derived. Both delta and bootstrapping methods provide reliable estimates of variance and are both incorporated into the R package. Avoiding computationally intensive methods for reliable variance estimation can provide analytic efficiency, particularly for large datasets.

While we have shown that the proposed method performs better than more conventional approaches for zero-inflated counts, the use of MZIP model needs to be a justifiable modeling approach for the zero-inflated variable beyond mediation. As the MZIP model has significantly more parameters than a Poisson model, sufficient sample size is also needed. Without sufficient zero counts to warrant a zero-inflated model, mediation with a Poisson model will be more powerful and computationally efficient than the MZIP model^4,44.

One disadvantage of the proposed counterfactual approach to mediation is that added complexity to the mediator or outcome model requires new formulaic expressions of NDE and NIE¹³. Not all potential scenarios have been considered in the R package including cases with multiple mediator/exposures, covariate-exposure interactions, covariate-mediator interactions, and non-linear exposure/mediators associations. While these derivations are obtainable, they were not presently considered and are an area of future development. Other potential expansions to this method also will allow modeling of other types of outcomes such as time-to-event variables.. In addition, we only considered zero-inflated Poisson, but data could be zero-inflated negative binomial. While robust standard errors using MZIP seem to perform adequately in our simulations, future work will extend this methodology to other marginal zero-inflated models such as negative binomial²⁵.

8. Conclusion

In this paper we propose a causal mediation framework that takes into consideration zero-inflation of potential mediators by using MZIP for the mediator model, which provides marginal inference of the exposure on the mediator. Failure to consider the zero-inflation of a mediator with excess zeroes with traditional models like Poisson and linear regression can yield inaccurate results. Marginalized mean indirect effect estimates are not directly obtained with use of ZIP, meaning that inference on population effects is challenging to obtain. The proposed method circumvents these issues by minimizing bias of indirect effects, giving ideal coverage of standard errors, and providing marginal effect estimates. While we focused on alcohol consumption as a zero-inflated count mediator, cigarette use⁴⁰, sexual encounters⁶, dental caries⁵, healthcare utilization³⁹, and coronary artery stenosis⁴⁵ are other zero-inflated variables. Each of these variables could be reliably incorporated into the discussed method as mediators to describe, for example, health disparities in cardiovascular, dental, or healthcare research.