Regulating nanoscale directional heat transfer with Janus nanoparticles

Abstract

Janus nanoparticles (JNPs) with heterogeneous compositions or interfacial properties can exhibit directional heating upon external excitation with optical or magnetic energy. This directional heating may be harnessed for new nanotechnology and biomedical applications. However, it remains unclear how the JNP properties (size, interface) and laser excitation method (pulsed vs. continuous) regulate the directional heating. Here, we developed a numerical framework to analyze the asymmetric thermal transport in JNP heating under photothermal stimulation. We found that JNP-induced temperature contrast, defined as the ratio of temperature increase on the opposite sides in the surrounding medium, is highest for smaller JNPs and when a low thermal resistance coating covers a minor fraction of JNP surface. Notably, we discovered up to 20-fold enhancement of the temperature contrast based on thermal confinement under pulsed heating compared with continuous heating. This work brings new insights to maximize the asymmetric thermal responses for JNP heating.

Janus nanoparticles with heterogeneous interfacial thermal resistance can lead to nanoscale directional heating, particularly under pulsed heating.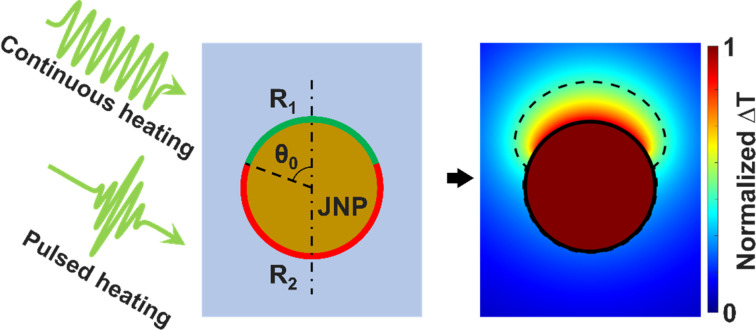

Introduction

Nanoparticle (NP) heating has enabled many applications,^1–4 including cancer treatment,^5–9 neuromodulation,^10,11 molecular hyperthermia,^12–15 point-of-care diagnosis,^16–18 contrast agents,^19,20 controlled release,²¹ energy harvesting,^22,23 and catalysis.^24,25 Janus nanoparticles (JNPs) refer to nanostructures with asymmetric structures, and have recently brought new opportunities to the field.^26–28 Two types of JNPs have been widely studied recently: the first type of JNPs consists of heterogeneous materials, such as combinations of metallic and non-metallic materials;^29–31 whereas the second type of JNPs is asymmetrically coated with different ligands, such as hydrophobic versus hydrophilic coatings.³² Upon laser excitation, the asymmetric structures of JNPs can lead to heterogeneous heating source,³³ or nonuniform NP–water interfacial thermal resistances (ITRs).³⁴ These asymmetries have been harnessed to regulate the thermal transport around the JNP and lead to directional heating.^34–37 Directional heating with the first type of JNPs has enabled novel applications with JNPs, such as thermophoretic nanomotors,^33,35,38 nano tweezers,^39,40 Janus nano pen injection,⁴¹ and energy management.⁴²

For the second type of JPNs, recent theoretical studies have shown the possibility of directional heating with significantly smaller (∼5 nm) than the first type JNPs (50–200 nm),³⁴ thus promising to open the new size range for potential applications. The central issue for JNP heating is a better understanding of thermal transport and temperature regulation.⁴⁰ Olarte-Plata et al. was among the first to analyze the directional heating of JNPs with heterogeneous coating and ITRs under continuous heating.³⁴ Using molecular dynamics (MD) simulation and continuous modelling, they demonstrated a temperature difference up to 10 K with hydrophilic/hydrophobic (octanethiolate/mercaptohexanol)-coated JNPs and estimated the temperature difference with a wide range of ITR combinations (0.1–100 × 10⁹ m² K W⁻¹) and sizes (5–100 nm, continuous modeling). Jiang et al. further utilized MD simulation to provide an atomic resolution of ITR variations of Au–water interface and demonstrate a temperature difference on the order of 5 K for with 20–30 nm NPs with 1 μW heating per NP.⁴³ While these studies have greatly advanced our knowledge of directional heating with JNP, several key questions remain unclear, specially how the distribution of heterogeneous ITR on JNP and the laser excitation duration (continuous vs. pulsed) regulate the nanoscale thermal transport.

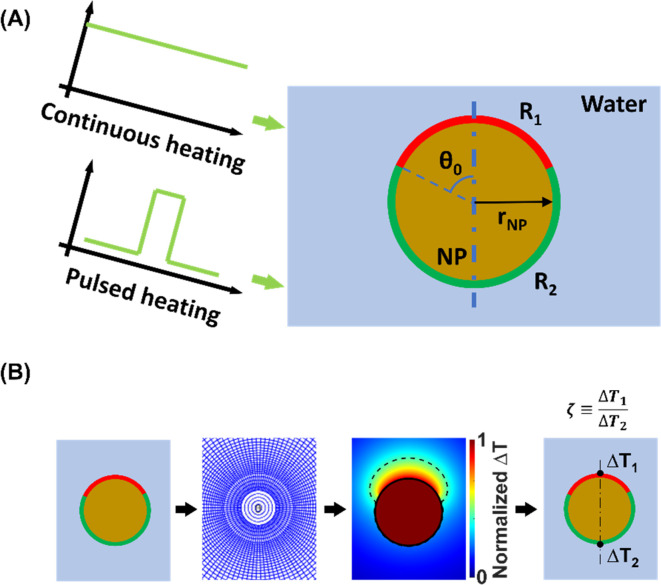
This work focuses on elucidating how the heterogeneous interface properties (ITRs), the area fraction of heterogeneous ITRs, and the laser excitation method (continuous vs. pulsed) regulate the nanoscale heat transfer (Fig. 1A) for JNPs with gold core and asymmetric surface coatings. Here we developed a numerical framework based on continuous models as it enables us scanning a wide range of parameter space, especially for the pulsed heating (transient process) scenarios. We defined a dimensionless parameter based on the ratio of asymmetric temperature increase (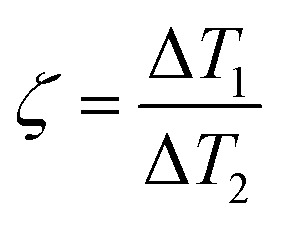, Fig. 1B) to quantify the magnitude of directional heating. Our modeling results suggest that increasing JNP size reduces the temperature contrast, additionally, an approximate solution is provided to estimate the JNP size-dependent temperature contrast. Furthermore, the distribution of interface thermal resistance (varying the surface coverage of low versus high interface thermal resistance) has a significant impact on the temperature contrast, with a minor coverage by low interface resistance leading to higher temperature contrast. Importantly, we demonstrate a significant enhancement of temperature contrast with pulsed JNP heating compared with continuous heating. Our work advances the understanding of directional heating with JNP by clarifying the contributions of various factors to JNP nanoscale thermal transport.

Fig. 1. Schematic illustration of the JNP heating modeling. (A) A spherical Janus nanoparticle (JNP) with gold core is heterogeneously coated, leading to nonuniform interfacial thermal resistance (ITR). The two ITRs on the JNP are R₁, covering the north pole, and R₂, covering the south pole. The polar angle (θ₀) defines the boundary between two different coatings and determines the fraction of the low thermal resistance coating vs. high thermal resistance coating. Continuous and pulsed heating was imposed on the JNP to model the steady-state and transient heating scenarios. (B) Schematic of the model under spherical coordinates. ΔT₁ and ΔT₂ indicate the temperature change in the water.

Results

Directional heating and temperature contrast under continuous heating

We first developed a numerical framework with finite difference methods (FDM) based on the continuous modeling of thermal transport (Fourier's law) to simulate thermal transport with the second type of JPN, which consists of a gold core and asymmetric coatings (Fig. 1A). It should be noted that continuous modeling are sufficiently accurate for estimating the JNP heating in an aqueous solution as the mean free path of phonon in the water (∼0.3 nm) is orders of magnitude smaller than the characteristic length in this work (5–100 nm).^14,44,45 Additionally, a recent study has shown that results from continuous modeling are in well consistence with the MD simulation even for small JNP (5 nm) heating.³⁴ We adopted constant thermal thermophysical properties (c, ρ, k) as we have shown in our previous work that temperature-dependent thermophysical properties have limited effect on the temperature profile compared that with the constant properties.¹⁴ The model (Fig. S1†) was vigorously validated including mesh independence and boundary effect analysis (ESI section “FDM model validation” and Fig. S2–S4†). To quantify the temperature contrast for JNP heating, we first define a dimensionless parameter:

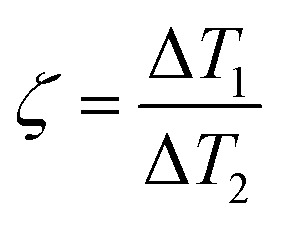1

where ΔT₁ and ΔT₂ indicate the representative temperature rise of the two coating parts (Fig. 1B). When ζ = 1, it indicates no temperature contrast or homogeneous heating, whereas when ζ < 1 or ζ > 1, it indicates directional heating.

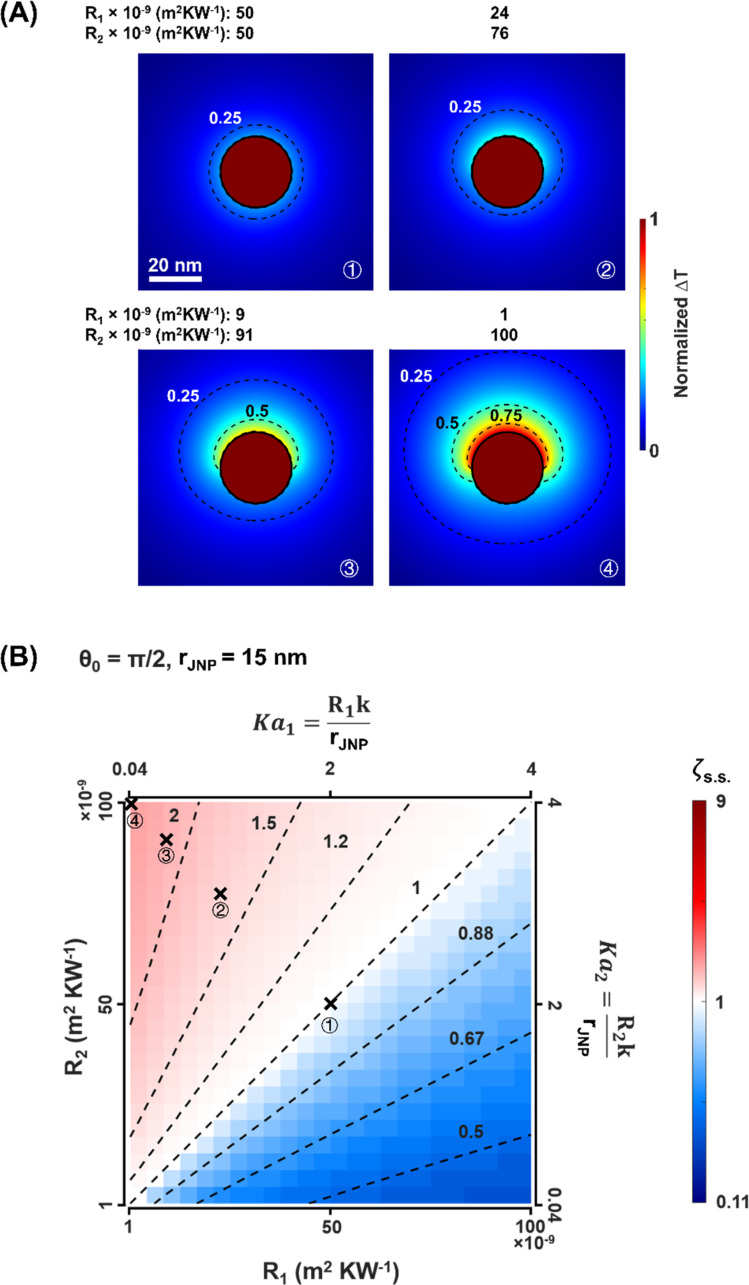
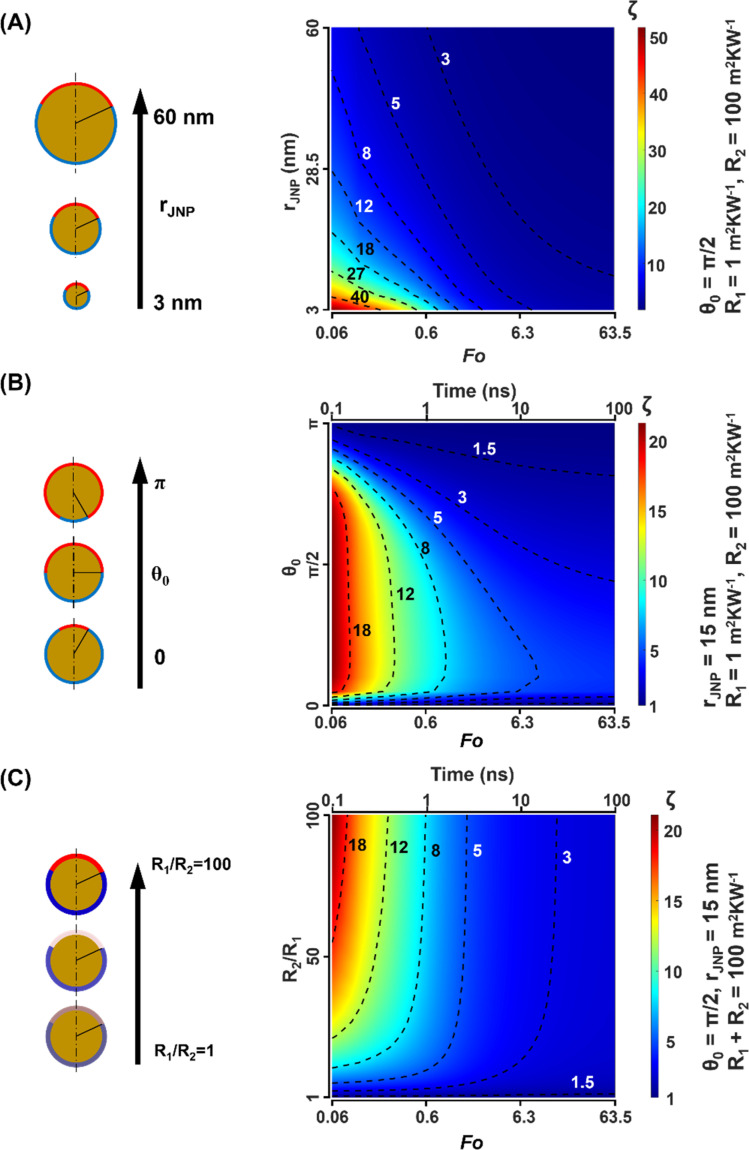
Several factors can affect the thermal transport and temperature profile during JNP heating, including the interfacial thermal resistance (ITR), the JNP size (r_JNP), the fraction of the low thermal resistance coating vs. high thermal resistance coating (as quantified by the polar angle θ₀ of the heterogeneous coatings, Fig. 1A), and the heating method (i.e., continuous heating vs. pulsed heating, can be quantified by heating time, t). First, we analyzed JNP heating under continuous heating and the simplest JNP with a symmetric geometry (polar angle θ₀ = π/2). Nonuniform interfacial properties can stem from the heterogeneous coating, including hydrophilicity that leads to different ITR values, and the contrast between ITRs can be tuned by altering the combination of surface coating materials or ligands.^46–48 Since the ITR values for NPs in an aqueous solution reported are in the order of 1–100 × 10⁻⁹ m² K W⁻¹ (Table S1†), or interfacial conductance: 0.01–1 × 10⁹ W m⁻² K⁻¹,^49–53 we will set our parameter range for ITRs as 1–100 × 10⁻⁹ m² K W⁻¹ throughout the paper. Fig. 2A shows that for a given JNP size (r_JNP = 15 nm), the combination of R₁ and R₂ significantly affects the temperature profile and temperature contrasts (ζ). With uniform ITR (case 1, R₁ = R₂ = 50 × 10⁻⁹ m² K W⁻¹), the temperature increase is uniform around the nanoparticle. With the increase in the ITR contrast (cases 2–4), we observed a higher temperature contrast, referred to as directional heating, in the surrounding water near the north pole and south pole (Fig. 2A). The maximum ITR ratio (R₂/R₁ = 100) gives a temperature contrast ζ = 2.5 (case 4). It should be noted that a uniform temperature profiled is observed inside JNP across all the combinations of the ITRs as the thermal conductivity and diffusivity of gold is much higher than those of water. To gain a complete picture of the temperature contrast as a function of ITRs, we constructed the 2D map of ζ_s.s. as a function of R₁ and R₂ (Fig. 2B), where the subscript s.s. indicates steady-state (i.e. continuous heating). The range for ITRs in Fig. 2B (1–100 × 10⁻⁹ m² K W⁻¹) is consistent with ITRs reported in the literature.¹⁴ζ_s.s. equals to 1 along the diagonal where R₁ = R₂ while ζ_s.s. deviates from 1 in the off-diagonal region (when R₁ ≠ R₂). Fig. 2B is symmetric along the diagonal line since exchanging the R₁ and R₂ should lead to the inverse of ζ_s.s..

Fig. 2. Temperature profile and contrast with Janus NP heating under the steady-state. (A) Normalized temperature rise (ΔT) with Janus nanoparticle (JNP) heating. The JNP size (r_JNP) is 15 nm, and the polar angle for the heterogeneous coating (θ₀) is π/2. (B) 2D map of ζ_s.s. in terms of the two ITRs, R₁, and R₂. Dotted lines are contour lines for ζ_s.s.. The Kapitza number (Ka) is defined as: 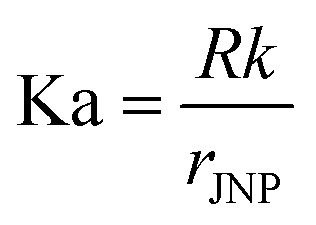, where R is the interfacial thermal resistance, k is the thermal conductivity of the media, r_JNP is the radius of JNP.

To further investigate how the combination of ITRs affects ζ_s.s., we developed a parallel circuit model (ESI section “Parallel circuit model”†) to analyze the JNP heating analytically. Here we assume no heat transfer across the polar angle (θ₀) of heterogeneous ITR in the water domain, and we simplified the model to a parallel circuit analogy (Fig. S5A†) with a set of linear equations to describe the temperature at the critical nodes (eqn (S2) and (S3)†). Based on this parallel circuit model, the temperature contrast under the steady-state can be estimated by:

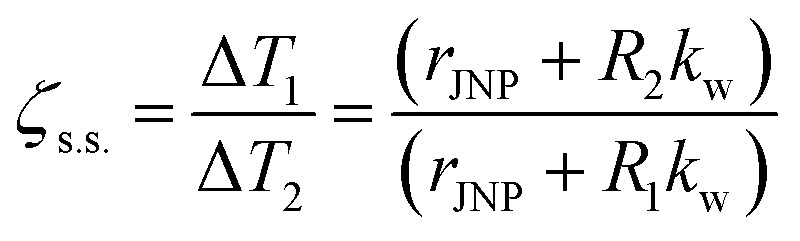2

Comparing results from the parallel circuit model with the FDM results (Fig. S5B†), the parallel circuit model overestimates ζ_s.s. and is more accurate with larger JNPs. This overestimation may arise from the assumption of no heat transfer across θ₀. The agreement between the numerical simulation and parallel circuit model improves for larger JNPs because heat flux in the θ direction becomes less important compared with the radial heat flux. Furthermore, eqn (2) demonstrates the size dependence of temperature contrast with JNP heating. For a given combination of R₁ and R₂, larger JNP size will yield less temperature contrast. This size dependence agrees with Kapitza number analysis,^52,54 where for larger NP, the ITR has a smaller effect on the heat dissipation 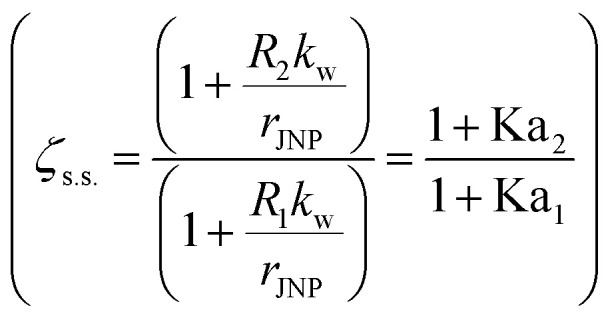. This size dependence of ζ_s.s. is also confirmed with the FDM model, and the ζ_s.s maps with r_JNP ranging from 3.75 to 60 nm (Fig. S6†).

Effect of JNP size and asymmetric coating on the temperature contrast under steady-state

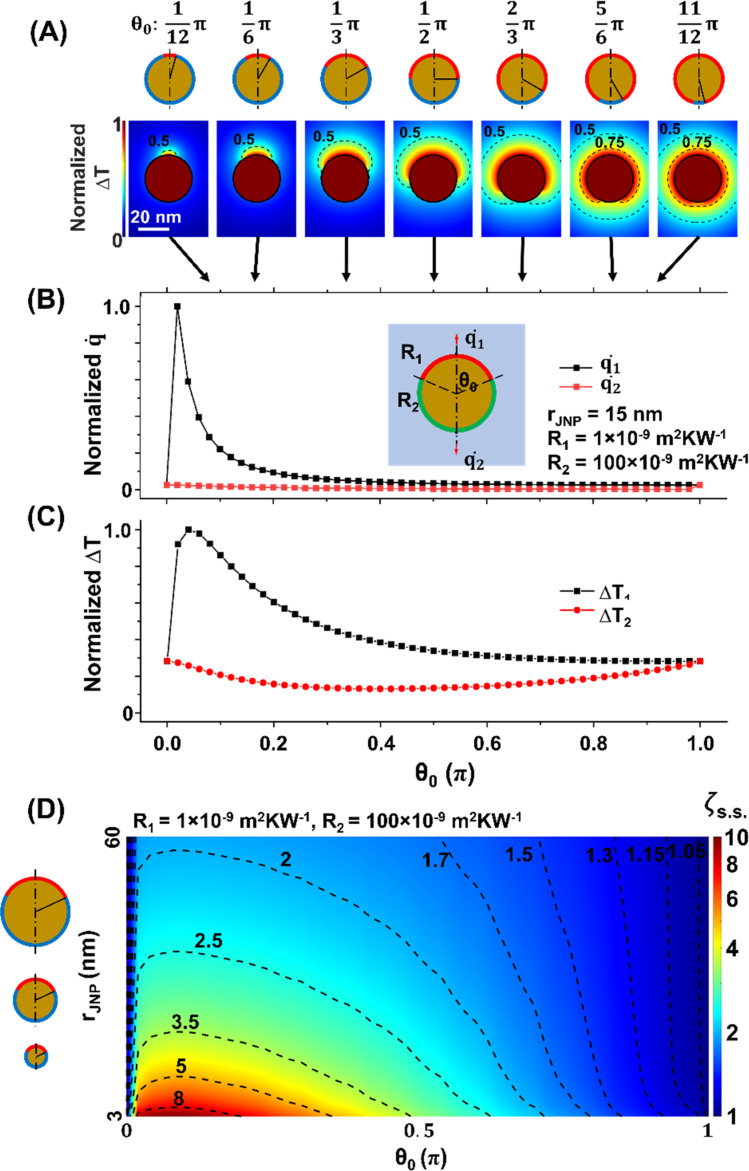
Next, we analyzed how the asymmetric surface coating impacts the temperature contrast. Under experimental conditions, the surface coating can be highly asymmetric with a major or minor fraction of the low thermal resistance coating vs. high thermal resistance coating, i.e., θ₀ deviates from π/2 (Fig. S7†).^31,55 Here, we investigated how the asymmetric coating impacts the temperature contrast by examining a range of polar angle θ₀ values (Fig. 3A). Fig. 3B shows that the asymmetric coating strongly affects the local heat flux rate across the interface (q̇). The local heat flux at the north pole (q̇₁) is significantly higher (∼50-fold at θ₀ = 0.02π) than that of the south pole (q̇₂) when θ₀ < π/2. The difference between q̇₁ and q̇₂ with smaller θ₀ leads to a remarkably higher ΔT₁ (Fig. 3C) than ΔT₂. We further examined the asymmetric coating for different JNP sizes (Fig. 3D). Our results suggest that smaller JNP size gives greater temperature contrast (e.g., ζ_s.s. = 10 for a 3 nm JNP with θ₀ ∼ π/12, area fraction for low thermal resistance ∼3%).

Fig. 3. Effect of the polar angle (θ₀) on the temperature contrast under steady-state. (A) Temperature profile of JNP heating with different θ₀. R₁ = 1 × 10⁻⁹ m² K W⁻¹ and R₂ = 100 × 10⁻⁹ m² K W⁻¹, r_JNP = 15 nm. (B) The local heat flux rate across the interface at the northern pole (q̇₁) and southern pole (q̇₂) as a function of θ₀. (C) ΔT₁ and ΔT₂ as a function of θ₀. (D) ζ_s.s. map as a function of r_JNP and θ₀. R₁ = 1 × 10⁻⁹ m² K W⁻¹, R₂ = 100 × 10⁻⁹ m² K W⁻¹. The dotted lines are contour lines for ζ_s.s..

Directional heating during pulsed heating

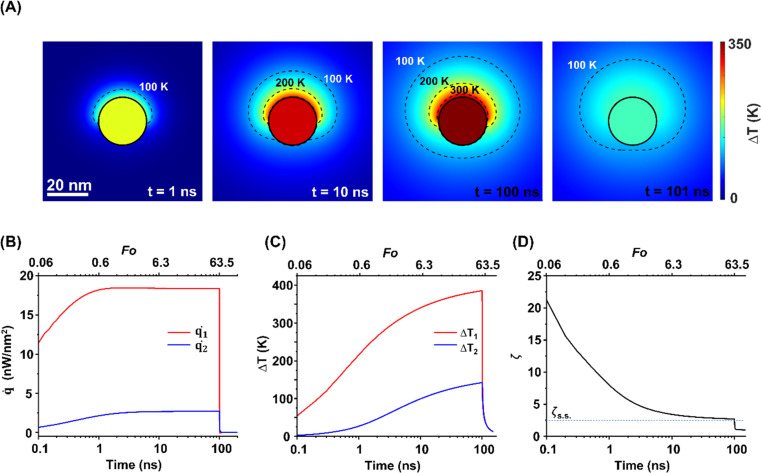
Recently, NP heating with femtosecond to nanosecond pulsed energy excitation has shown unique thermal responses and has played essential roles in various applications.^12,15,56 As the characteristic thermal relaxation time is on the order of nanoseconds (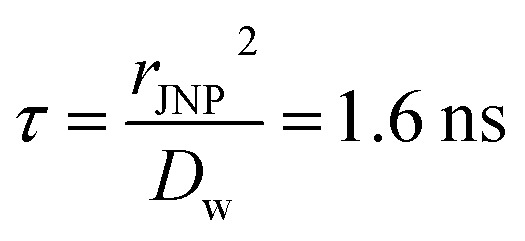 for 30 nm JNP), JNP heating with nanosecond or shorter pulsed heating is far from steady-state and can lead to thermal confinement. Here we imposed 100 ns laser pulse (constant heating) on a 30 nm JNP with R₂/R₁ = 100 and θ₀ = π/2. Fig. 4A illustrates the temperature profiles during the transient heating process. At t = 1 ns, only a thin layer of water adjacent to the JNP–water interface is heated along the northern hemisphere (ΔT ∼ 200 K). On the contrary, minimal heating is observed near the southern hemisphere (ΔT ∼ 25 K) due to higher ITR. By comparing the local heat flux at the north pole and south pole (q̇₁ and q̇₂), both the magnitude and slope for q̇₁(t) are significantly higher than those for q̇₂(t) for t < 1 ns, leading to enhanced temperature contrast (Fig. 4B–D, ζ ∼ 20 at 0.1 ns). Here we adopted the Fourier's number (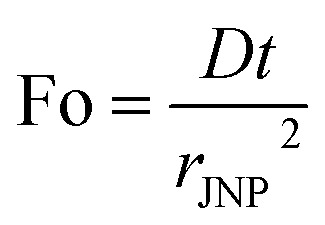, D: thermal diffusivity, t: time) as dimensionless time. As heating continues, thermal energy continuously diffuses and leads to reduced temperature contrast. At t = 100 ns, the maximum temperature is reached as it is the end time point for the pulsed heating and the heating asymptotically approaches the steady-state value (Fig. 4B, Fo = 63.5), and the temperature contrast ζ asymptotically falls to its steady-state level (Fig. 4C, ζ_s.s. = 2.5). After the pulsed heating (t > 100 ns), the whole system cools down rapidly, and both ΔT₁ and ΔT₂ drop to 0 with ζ approaching 1. Therefore, the thermal confinement under short ns pulse heating (Fo ≪ 1) leads to a 8-fold enhancement of temperature contrast under current conditions (Fo = 0.06, R₂/R₁ = 100, r_JNP = 15 nm, θ₀ = π/2).

Fig. 4. The temperature evolution during the transient heating. (A) ΔT profiles during the transient heating process with JNP. r_JNP = 15 nm, heating power (g) = 35.6 μW, heating time (t_heating) = 100 ns. R₁ = 1 × 10⁻⁹ m² K W⁻¹, R₂ = 100 × 10⁻⁹ m² K W⁻¹, θ₀ = π/2. (B) Temporal evolution of local heat flux rate (q̇)at the north pole and south pole, (C) ΔT and ΔT₂ and (D) ζ during the transient heating process. The blue dotted line in (D) indicates the corresponding ζ_s.s..

Effect of JNP size and asymmetric coating on the temperature contrast during the transient heating

Lastly, we investigated how the JNP size and asymmetric impacts the temperature contrast under pulsed heating. We started by analyzing JNP size (r_JNP) on the temperature contrast ζ and observe a strong size dependence (Fig. 5A). Smaller JNPs are more sensitive to heating time and hence have a stronger enhanced temperature contrast with pulsed heating (Fo = 0.06) compared with steady-state scenarios (14-fold enhancement for r_JNP = 3 nm and 4-fold for r_JNP = 60 nm). As shown in Fig. 5B, analysis of the asymmetric coating shows a strong enhancement for temperature contrast (13-fold) for a moderate θ₀ (π/12 < θ₀ < 3π/4) at short heating times (Fo < 1). Lastly, Fig. 5C demonstrates ζ in terms of ITR contrast and heating time and suggests that for high ITR contrast (R₂/R₁ > 25), the temperature contrast is significantly enhanced with short heating time (ζ ∼ 12–20 when Fo ∼ 0.1). Whereas for low ITR contrast (R₂/R₁ < 25), ζ is less sensitive to heating time, and for minimal ITR contrast (R₂/R₁ ∼ 1–2), ζ approximately keeps constant (ζ ∼ 1.5) throughout the transient process. In conclusion, our analysis gives a clear landscape of the transient temperature contrast due to JNP size (r_JNP) and ITR distribution (θ₀, R₂/R₁). Specifically, smaller-sized JNP with large ITR contrast and moderate polar angle has the maximal temperature contrast under pulsed heating.

Fig. 5. Effect of thermal resistance (R₂/R₁), asymmetric coating (θ₀), and particle size (r_JNP) on the temperature contrast during the transient heating. (A) ζ map as a function of r_JNP and Fo. (B) ζ map as a function of θ₀ and t. (C) ζ map as a ITR ratio and heating time (t). Here we regulate R₂ + R₁ = 100 m² K W⁻¹ and alter the R₂/R₁. The dotted lines are contour lines for ζ.

Discussion

Directional heating with the first kind of JNP

In this work, we focused on directional heating with the second type of Janus NP characterized by heterogeneous interfacial thermal resistances (ITRs). One key result from our model is a much-enhanced temperature contrast (ζ) with ultra-short pulsed heating compared with that of continuous heating. However, the mechanism behind this enhanced ζ remains elusive due to the formidable challenge of solving the analytical solution for the temperature function. We propose a potential explanation for the enhanced ζ observed during pulsed heating: the thermal confinement due to short heating time, leading to localized heating only around the north hemisphere, also known as thermal confinement, and consequently amplifying ζ during the pulsed heating.

Recently, FEM modeling has been used to investigate thermal transport with the first kind of JNP which consists of heterogeneous materials. González-Colsa et al. has shown a temperature gap of 10 K with a gold/polymer semi-shell nanostructure under pulsed heating, though the temperature gap under steady-state conditions with the semi-shell remains unclear.³⁶ Drawing parallels with the first type of JNP investigated in our study, we speculate a significantly enhanced directional heating potential for this type of JNP under ultra-fast pulsed heating compared to continuous heating, attributable to similar factors such as thermal confinement. We anticipate that ultra-fast pulsed heating could be an effective method for harnessing directional heating across various types of JNPs.

Effect of Brownian motion on JNP heating

The Brownian motion of particles in a liquid can have a significant impact on thermal transport around JNPs. For instance, the mean velocity associated with Brownian motion for a 10 nm particle in water is approximately 10 μm s⁻¹. Considering the time scale of our analysis (100 ns), this velocity suggests only minimal displacement (on the order of ∼1 pm). As a result, we anticipate that the influence of Brownian motion on thermal transport will be minimal under these conditions.

Conclusion

This work focuses on directional heating with Janus nanoparticle (JNP). Through computational modeling, we analyzed the effect of ITR contrast, JNP size, and asymmetric coating on the temperature contrast under steady-state and transient heating conditions. First, we found a significant size dependence of temperature contrast, where a smaller JNP can lead to greater temperature contrast. We further revealed the role of asymmetric coating and found higher temperature contrast when low thermal resistance coating covers a minor fraction of JNP surface. Importantly, we elucidated the temperature evolution near a JNP during a transient heating process and found up to 20-fold enhancement of the temperature contrast for pulsed JNP heating versus continuous heating. Our work provides the basis to design JNP and maximize the directional heating.

Methods

Theoretical model

Here we considered a JNP with two different surface coatings and interface thermal resistance values (Fig. 1A). The material of our JNP is gold and the JNP is submerged in an aqueous solution. Heat can transfer through the interface into the water when the JNP is excited by laser radiation.⁴⁰ To facilitate the investigation of thermal transport during the transient, we adopted square pulsed heating in our modeling. Recently, studies reported that heat conduction under the nanoscale could deviate from Fourier's law when the mean free path is comparable to the characteristic length.⁵⁷ In this work, the temperature profile in the water domain is our primary concern. Considering that the mean free path of phonons in the water (∼0.3 nm) is orders of magnitude smaller than the characteristic length (∼10 nm),⁴⁵ the Fourier law should be sufficient to model the thermal transport,^14,44 we applied Fourier's law with the governing equation:¹

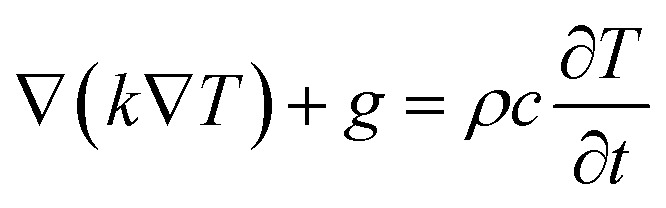3

Here, k is the thermal conductivity, g is the heat source, ρ is density, and c is the specific heat. We further expand the governing equation under spherical coordinates with azimuthal symmetry and simplify our model to a 2D problem (Fig. 1A and S1†). To further simplify the model, we assume constant thermal properties. Based on our previous work, the constant property assumption introduces minimal error.¹⁴ The theoretical model is shown as follows:

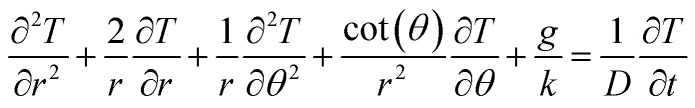4

where D refers to thermal diffusivity. Expanding the governing equation with spherical coordinates enables us to discretize the system with an orthogonal mesh (Fig. 1B and S1†). However, as shown in eqn (4), the system will have singularities when r → 0 and θ → 0 & π and is discontinuous at the center point where the two singularities meet (r = 0, θ = 0).⁵⁸ To overcome this, we assume the temperature is uniformly distributed in the θ direction near the center point. Thus, we can further reduce the governing equation in the region near the center point to a 1D problem (Fig. S1†). Since the thermal diffusivity of metal is much higher than that in water, the temperature profile inside the JNP is close to isothermal, and this 1D assumption is acceptable. Consequently, the temperature governing equation is given by:

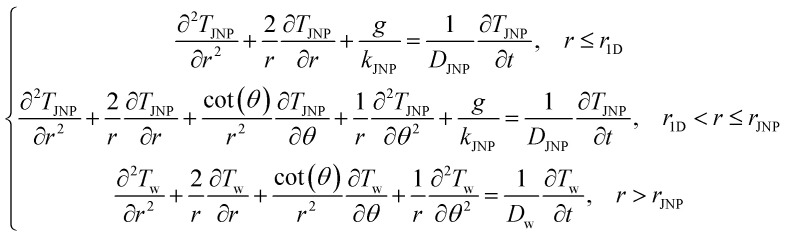5

The boundary and initial conditions are:

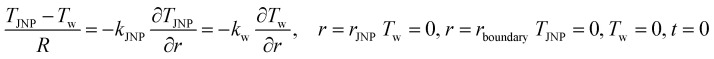6

r_1D refers to the radius of the 1D region (Fig. S2†), r_JNP refers to the radius of the JNP, and r_boundary refers to the radius of the boundary for the water domain. It should be noted that R is the interfacial thermal resistance (ITR), and it is a function of θ:

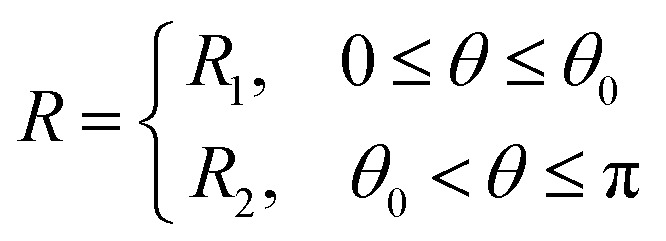7

where R₁ and R₂ indicate the ITR for the coating on the northern part and the ITR for the coating on the southern part, respectively, and θ₀ refers to the polar angle boundary between the heterogenous coatings (Fig. 1A).

Finite difference method model

Next, we used the finite difference method model and discretized eqn (5)–(7).⁵⁹ Here, we adopted a biased mesh in the radius direction in the water domain to achieve higher accuracy and save computational time (Fig. S1†). For the steady-state problem, the left-hand side of eqn (5) equals zero, and the discretized governing equation in the water domain is as follows:

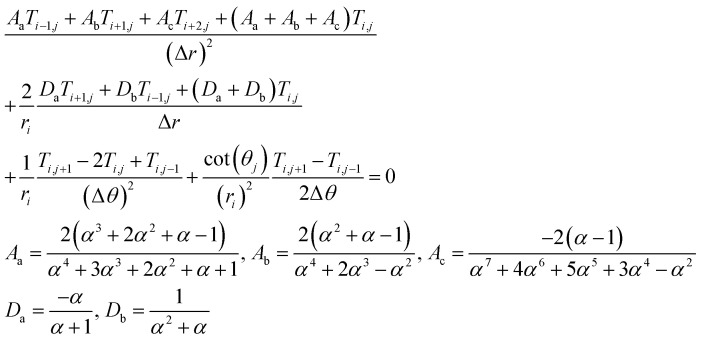8

where the subscript i indicates the ith node in the r direction, and j indicates the jth node in θ direction, α indicates the biased mesh factor (Δr_i+1 = αΔr_i). The system has a second order of accuracy, and we validated the model by conducting a mesh-independent analysis and boundary effect analysis (Fig. S2 and S3†).

For the transient problem, we discretized eqn (5)–(7) with a Crank–Nicolson scheme,⁶⁰ and the discretized governing equation in the water domain is:

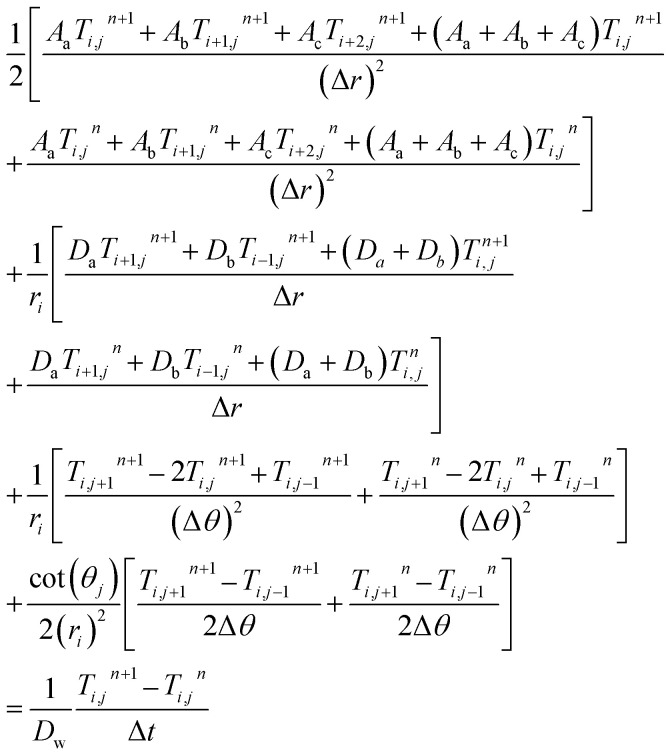9

where superscript n indicates the nth node in the time direction. We further validated the accuracy and stability of the model (Fig. S4†). Numerical results are consistent with analytical solutions. Eqn (8) and (9) are solved with MATLAB R2020b.

Abbreviations

JNP

Janus nanoparticle

ITR

Interfacial thermal resistance

MD

Molecular dynamic

FDM

Finite difference method

S.S.

Steady-state

Roman letters

R ₁

Interfacial thermal resistance along the north part of Janus nanoparticle, m² K W⁻¹

R ₂

Interfacial thermal resistance along the south part of Janus nanoparticle, m² K W⁻¹

k

Thermal conductivity, W m⁻² K⁻¹

k _JNP

Thermal conductivity in Janus nanoparticle, W m⁻² K⁻¹

k _w

Thermal conductivity in water, W m⁻² K⁻¹

T

Temperature, K

T _JNP

Temperature in the Janus nanoparticle, K

T _w

Temperature in water, K

g

Heating power, W m⁻³

c

Specific heat, J kg⁻¹

t

Time, s

r

Radius, m

r _1D

Radius of the 1D zone, m

r _JNP

Radius of the Janus nanoparticle, m

r _boundary

Radius of the water domain, m

D

Thermal diffusivity, m² s⁻¹

D _JNP

Thermal diffusivity in Janus nanoparticle, m² s⁻¹

D _w

Thermal diffusivity in water, m² s⁻¹

R

Interfacial thermal resistance, m² K W⁻¹

R ₁

Interfacial thermal resistance on the north hemisphere, m² K W⁻¹

R ₂

Interfacial thermal resistance on the southern hemisphere, m² K W⁻¹

Ka

Kaptiza number,

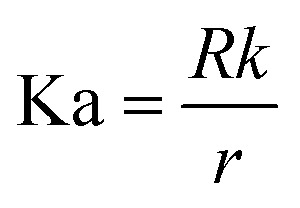
Ka₁

Kaptiza number on the north hemisphere,

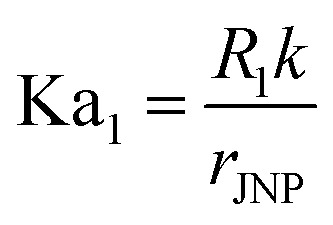
Ka₂

Kaptiza number on the southern hemisphere,

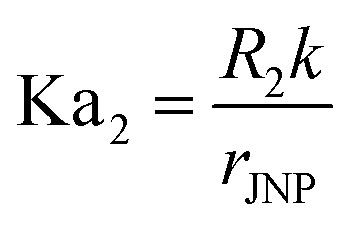
q

Heat flux, W

q ₁

Heat flux through the north hemisphere, W

q ₂

Heat flux through the southern hemisphere, W

q̇

Heat flux rate, W m⁻²

q̇ ₁

Heat flux rate at the north pole, W m⁻²

q̇ ₂

Heat flux rate at the south pole, W m⁻²

Fo

Fourier number,

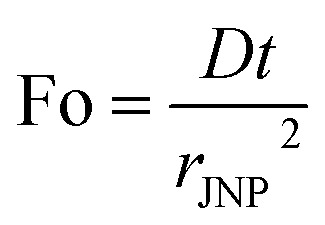
Greek symbols

θ

Polar angle

θ ₀

The critical polar angle that pinpoints the boundary between the heterogeneous interfacial thermal resistances

ζ

Dimensionless parameter to characterize the temperature contrast,

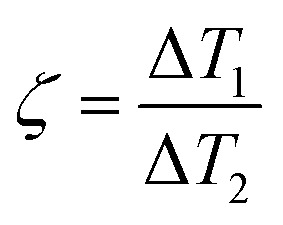
ζ _s.s.

Dimensionless parameter to characterize the temperature contrast for steady-state

ρ

Density, kg m⁻³

τ

Characteristic thermal relaxation time, 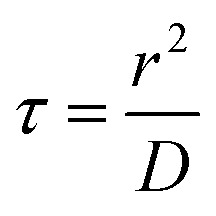, s

Author contributions

C. X. developed the numerical model and did the computational work and analysis. B. W. and Z. Q. participated in conceptualization and analysis. All authors contributed to the writing of the manuscript. Z. Q. directed the research.

Conflicts of interest

All authors declare that they have no conflicts of interest.