Abstract
Geometric frustration in the kagome lattice makes it a great host for the flat electronic band, nontrivial topological properties, and novel magnetism. Here, we use magnetotransport measurements to map out the field-temperature phase diagram of the centrosymmetric YMn6Sn6 with a Mn kagome lattice and show that the system exhibits the topological Hall effect (THE) with an in-plane applied magnetic field around 240 K. In addition, our neutron diffraction results demonstrate that the observed THE cannot arise from a magnetic skyrmion lattice, but instead from an in-plane field-induced double-fan spin structure with -axis components. This paper provides a platform to understand the influence of a field-induced novel magnetic structure on magnetoelectric response in topological kagome metals.
I. INTRODUCTION
Two-dimensional magnetic kagome lattice materials, composed of corner-sharing triangles and hexagons of magnetic ions separated by nonmagnetic buffer layers [Fig. 1(a)], are of great interest because they are candidates for quantum spin liquid [1], flat electronic bands [2–5], and topological electronic [6] and magnetic behavior [7,8]. For kagome metals [9], calculations using a simple tight-binding model with nearest-neighbor hopping reveal topologically protected linearly dispersive electronic bands near the Dirac point and dispersionless flat bands as confirmed by angle-resolved photoemission spectroscopy experiments [2,3,5,6]. The massive Dirac or Weyl node points in kagome metals exhibit striking magneto-electric phenomena, such as large intrinsic anomalous Hall effects (AHEs) and chiral anomalies [6,10–12]. On the other hand, a real-space Berry phase originating from a magnetic field-induced skyrmion lattice [Fig. 1(b)] or a noncollinear spin texture with nonzero scalar spin chirality [, where , , are the three nearest spins] [Fig. 1(c)] can act as a fictitious magnetic field for the conduction electrons to give rise to the topological Hall effect (THE) [13–20]. In contrast to the strong interplay between magnetism and topological electronic structure in momentum space, the noncollinear spin texture (real-space Berry phase)-induced electromagnetic responses of conduction electrons in kagome metals are still not well understood [13–20].
FIG. 1.
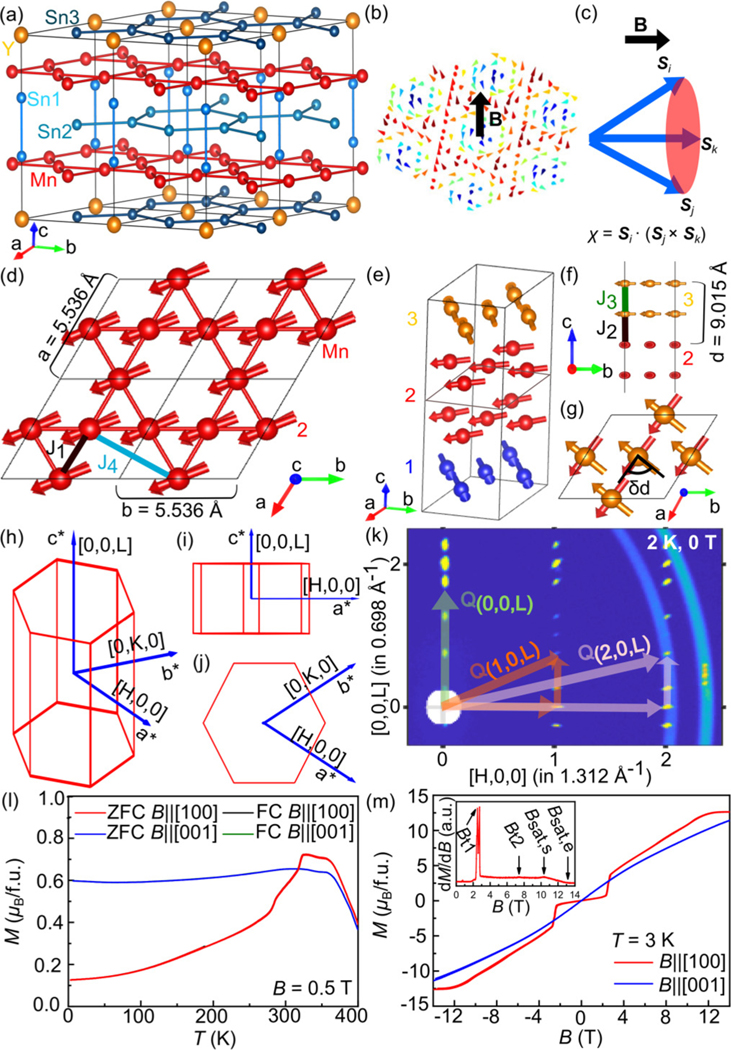
(a) Crystal structure of YMn6Sn6. The large yellow, medium red, and small blue (light blue and dark blue) balls represent Y, Mn, and Sn1 (Sn2 and Sn3) atoms, respectively. (b) A schematic of a nanoscale skyrmion lattice with field applied perpendicular to the kagome lattice plane. (c) A schematic of nonzero scalar spin chirality with three noncoplanar spins , , and . (d) Mn kagome bilayer top view in the YMn6Sn6 with nearest-neighbor and next-nearest-neighbor magnetic exchange couplings and , respectively. (e) Zero-field magnetic structure of YMn6Sn6. (f) Side view of structure shown in (e) where is the distance between kagome bilayers along the axis. The nearest-neighbor magnetic exchange couplings along the axis are and . The distance between collinear bilayers is 4.472 Å, and the distance between noncollinear layers is 4.547 Å, corresponding to and . (g) Top view of structure shown in (e) where is the rotation angle between kagome bilayers. (h)–(j) The definition of directions in reciprocal space. The momentum transfer in Å−1 is defined as , where , , and are Miller indices. (k) Single-crystal neutron diffraction in the plane at 2 K and 0 T. Incommensurate peaks are observed along (0, 0, L), (1, 0, L), and (2, 0, L) as indicated by , , and , respectively. (l) Temperature dependence of magnetization with zero-field-cooling (ZFC) and field-cooling (FC) modes at for and . (m) Field dependence of magnetization at for and . Inset: vs for .
In this paper, we report the discovery of the THE near room temperature in the antiferromagnetic (AFM) kagome metal YMn6Sn6, composed of a centrosymmetric Mn kagome lattice. The observed THE is strongly field-directional dependent and largest when the field is parallel to the Mn kagome plane, closely related to the formation of a double-fan spin structure with -axis components under the in-plane field. In addition, a large intrinsic AHE has also been observed when the spins are fully polarized at high field.
II. EXPERIMENTAL
YMn6Sn6 single crystals were grown by the Sn flux method. X-ray diffraction (XRD) patterns were performed using a Bruker D8 x-ray machine with radiation . Magnetization and electrical transport measurements were performed in Quantum Design PPMS-14 T. Small-angle neutron scattering (SANS) was performed at the NG7 SANS instruments at the NIST Center for Neutron Research (NCNR). Wide-angle single-crystal neutron diffraction measurements were performed on the CORELLI elastic diffuse scattering spectrometer at the Spallation Neutron Source, Oak Ridge Nation Laboratory (ORNL) and at the HB-3 thermal neutron triple-axis spectrometer at the High Flux Isotope Reactor, ORNL. Detailed experimental and data analysis methods are included in the Supplemental Material [21].
III. RESULTS AND DISCUSSION
YMn6Sn6 has a layered hexagonal MgFe6Ge6-type centrosymmetric structure (space group P6/mmm, No. 191) with lattice parameters of and [21–23]. As shown in Fig. 1(a), there are three kinds of Sn sites, and the crystal structure of YMn6Sn6 is composed of Y-Sn3, Mn-Sn1, and Sn2 layers stacking along the axis. The Sn2 and Sn3 atoms form the same graphenelike hexagon planes below or above the kagome layers of Mn atoms with . The Y and Sn1 atoms locate at the centers of Sn3 and Mn hexagons, respectively, but the occupancy of Y atoms in the Y-Sn3 layer expels the Sn1 atoms significantly away from the Mn kagome layer. Because of this unique structural feature, the magnetic properties of Mn6Sn6 (= rare earth elements) are very sensitive to both of the in the Mn kagome layer and the nature of elements. YMn6Sn6 shows a helical AFM (H-AFM) ground state below [Figs. 1(d)–1(g)] [23,24]. Defining the momentum transfer in reciprocal space [Figs. 1(h)–1(j)], at zero field and 2 and 240 K, the H-AFM structure is confirmed by refining the set of incommensurate magnetic Bragg peaks at , [Fig. 1(k)] [25]. While the Mn spins in each kagome bilayer (Mn-Sn1-Sn2-Sn1-Mn layer) are collinear ferromagnetic (FM) and confined within the layer [Fig. 1(d)], they rotate from one bilayer to the next bilayer by degrees, where is the distance between adjacent layers of moments aligned FM, and have no moment component along the axis [Fig. 1(f)]. This is because the double-flat-spiral magnetic structure has a strong FM exchange interaction through Sn1Sn2-Sn1 layers and a much weaker interaction through the Y-Sn3 layer [26]. At 240 K, , and at 2 K, . For , the magnetization curve at shows a paramagnetic-AFM transition at and a collinear to H-AFM transition at [Fig. 1(l)] [27,28]. In contrast, the curve for is rather flat below , indicating the magnetic moments of Mn atoms lie in the ab plane. The overlap of all zero-field-cooling (ZFC) and field-cooling (FC) curves indicates the absence of magnetic glassy state. For , the isothermal magnetization at increases smoothly because of gradual bending of the moments toward the axis [Fig. 1(m)]. However, the curve for shows a striking jump at derived from the curve [inset of Fig. 1(m)] and then increases gradually with field. The slope of the curve decreases when , and finally, the polarized FM (PFM) state is reached at . Note that there is another small kink located at [27,28]. The saturated moment for the Mn atom at 3 K is about 2.11 for .
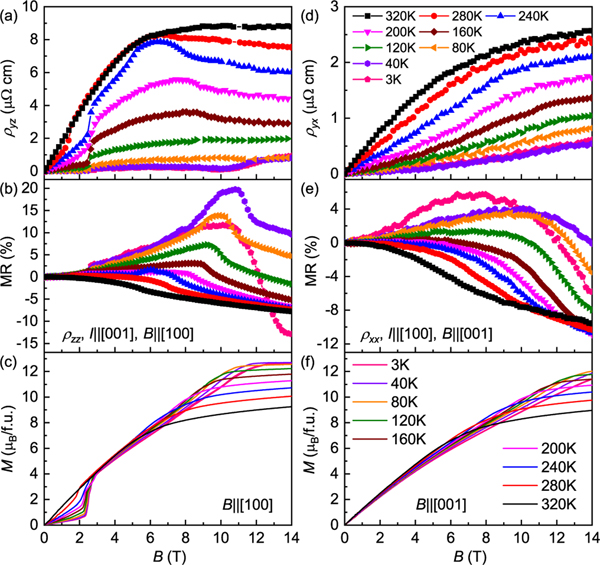
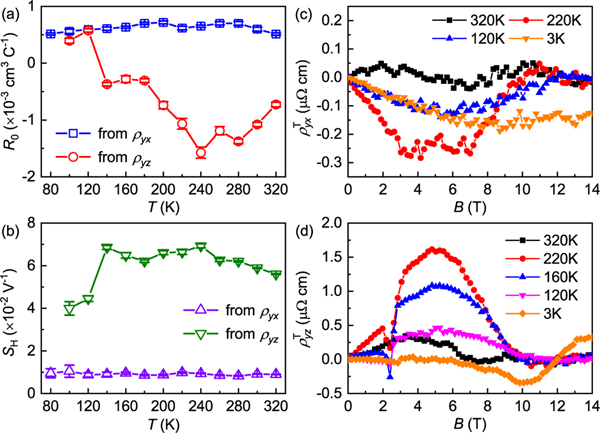
YMn6Sn6 exhibits metallic behaviors with weak anisotropy [21]. The Hall resistivity of YMn6Sn6 at 320 K increases and then saturates with increasing in-plane field [Fig. 2(a)]. With decreasing temperature, however, the curve shows a sharp jump at , followed by an obvious hump between and [Fig. 2(a)]. Such behavior is distinctly different from the nearly linear increase and gradual saturation behaviors of when [Fig. 2(c) and Fig. 3(a)]. This behavior weakens upon decreasing temperature with , dipping around 10 T, consistent with a previous paper [28]. The exhibits negative magnetoresistance (MR) at high temperatures, and when the temperature decreases, the positive MR appears at the low-field region but starts to decrease at the high-field region [Fig. 2(b)]. In contrast, the gradually increases and then saturates with increasing out-of-plane field [Fig. 2(d)], similar to the curves [Figs. 2(f) and 3(b)]. Upon lowering , the saturation field shifts to a higher field and is greater than 14 T when [Fig. 2(d)]. In general, shows a similar field dependence to throughout the temperature and field ranges [Fig. 2(e)], but it does not exhibit the obvious kinks observed in near characteristic fields, such as and etc. This implies that the magnetic configuration changes have remarkable influence on longitudinal resistivity, especially . In a magnetic system, the total Hall resistivity can usually be described as the sum of three contributions [19,29]:, where is the normal Hall resistivity due to the Lorentz force and is the ordinary Hall coefficient. Here, is the anomalous Hall resistivity, and should be a constant for the intrinsic anomalous Hall conductivity (AHC, ), which is linearly proportional to [29,30]. The last term represents the topological Hall resistivity, usually originating from noncollinear spin texture with nonzero scalar spin chirality. The scaling curves of vs show linear behaviors in the high-field region for both and when [Figs. 3(c) and 3(d)]. This undoubtedly indicates that the AHE is dominant when the THE vanishes in the PFM state. The and can be determined from the linear fit of the curves of vs when , as shown in Figs. 4(a) and 4(b). The derived from is positive and almost independent of temperature, similar to TbMn6Sn6 with a -axial-FM ground state and possibly related to the hole-type Dirac electrons near the Fermi energy level [31]. In contrast, the obtained from shows a strong temperature dependence with a sign change from negative to positive when . This implies that the direction of magnetic moments and magnetic structure may have significant effects on the electronic structure of YMn6Sn6, like in the case of Fe3Sn2 with Fe kagome bilayers, where the size of the Dirac gap can be tuned effectively by changing the direction of the external field [32]. Both obtained from and are positive. In addition, the relatively large values of and with weak dependence on longitudinal conductivity confirm the intrinsic AHE at high-field region [21]. These values of AHC are comparable with those in TbMn6Sn6 with Chern-gapped Dirac fermions [31], suggesting a possible similar contribution of Chern-gap-induced Berry curvature to AHC at the PFM state in YMn6Sn6. As shown in Figs. 4(c) and 4(d), both derived and [Figs. 3(e) and 3(f)] are small at high temperature. Their intensities increase with decreasing temperature at first, reaching the maximum values of and under at about 220 and 240 K, respectively, and then decrease quickly. At lower temperature, the shifts to a higher field. In contrast, the becomes negative when , located at .
FIG. 2.
(a) Hall resistivity , (b) magnetoresistance , and (c) as a function of magnetic field at various temperatures when . (d) Hall resistivity , (e) magnetoresistance , and (f) as a function of magnetic field at various temperatures when . The symbols in (a), (b), (d), and (e) have the same color codes. The colors of curves in (c) and (f) have the same definitions.
FIG. 3.
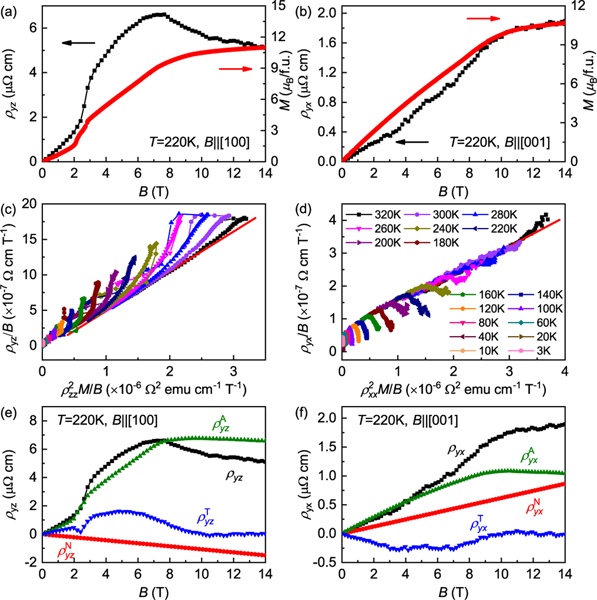
Field dependence of (a) Hall resistivity and for and (b) and for at 220 K. (c) vs and (d) vs at various temperatures. The red lines in (c) and (d) represent the fitting results of experimental curves above the saturation field at . The intercept and slope correspond to and , respectively. Accordingly, and can be calculated by and , respectively. Then is estimated after the subtraction of and from , i.e., and . Different estimated components of Hall resistivity at 220 K are shown in (e) and (f) for and , respectively. Because the emergence of upturn behavior for or the saturation region is beyond 14 T for , it cannot extract and from high-field linear fitting of vs curves. Thus, and at 100 K for and 80 K for are used to estimate and at the low-temperature region.
FIG. 4.
Temperature dependence of (a) and (b) derived from and . (c) and (d) as a function of B at selected temperatures.
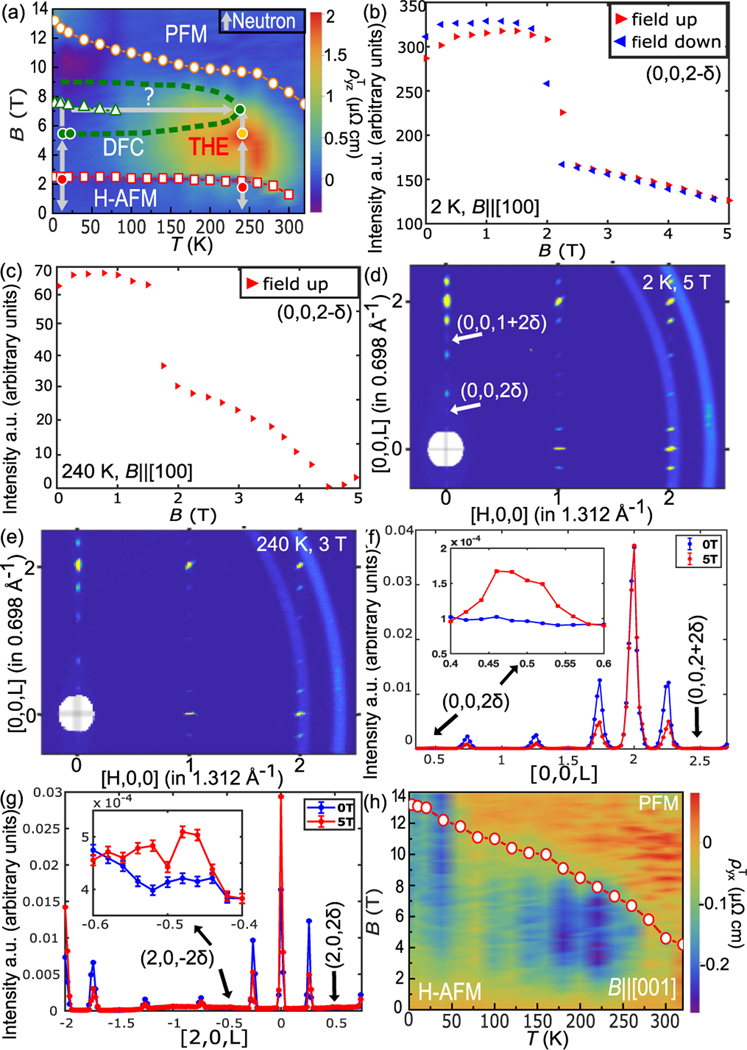
Our small-angle neutron diffraction measurements found no evidence for the expected field-induced skyrmion lattice [21]; thus, the THE for is not due to skyrmions. In contrast, the combined phase diagram of and magnetic transitions observed through neutron diffraction [Figs. 5(a)] provides a clear relation between in-plane-field-induced noncollinear magnetic structures and emergent electrodynamic responses. Here, is small at the H-AFM state with Mn moments lying in the ab plane. With , the Mn moments undergo a first-order spin-flop transition at at 2 K [Fig. 5(b)] and at 240 K [Fig. 5(c)] [21] to a new double-fan phase with a -axis component (DFC), contributing to the THE. This fanlike spin configuration is fully mapped by neutron diffraction measurements at 2 K, 5 T [Fig. 5(d)], and at 240 K, 3 T [Fig. 5(e)]. The -axis canting is due to interlayer weak AFM exchange coupling [33]. This is shown in the magnetic field dependence of the incommensurate peaks along the direction. Since neutron diffraction is only sensitive to the ordered moment component perpendicular to the wave vector , incommensurate peaks along the direction will not reveal any -axis canting [Fig. 5(f)]. On the other hand, for incommensurate peaks along the direction with [Fig. 5(g)], neutron diffraction measurements are sensitive to a field-induced -axis component. From our data, we conclude that an in-plane magnetic field induces a -axis component in the new magnetic ordered state. At low temperature and field , another unknown magnetic structure (denoted as “?”) is induced, leading to another weak THE with the opposite sign. Finally, when , the PFM state cannot host a topologically nontrivial spin structure; therefore, the THE disappears. On the other hand, the relatively small between H-AFM and PFM states could be ascribed to the possible noncollinear spin configuration when Mn moments tilt gradually toward the axis for [Fig. 5(h)].
FIG. 5.
(a) Phase diagram of YMn6Sn6 for with a contour plot of . data points are in white with colored outline, and neutron data points are in color with white outline. The orange circular, green triangular, and red square symbols represent , , and , respectively. Below ∼2 T, YMn6Sn6 forms a helical antiferromagnetic (H-AFM) structure; between ∼2–5.5 T, a double-fan phase with a -axis component (DFC) structure; at low temperature and field ∼5.5–9 T, a new unknown phase denoted “?”, and for higher, a polarized ferromagnetic (PFM) state. Gray arrows indicate neutron diffraction measurements. (b) Field dependence of peak intensity at 2 K. (c) Field dependence of peak intensity at 240 K. (d) and (e) Single-crystal neutron diffraction in the plane of a YMn6Sn6 single crystal at (d) 2 K, 5 T, and (e) 240 K, 3 T. Satellite peaks are observed at and . (f) and (g) Magnetic field dependence of (f) [0, 0, L] at 2 K and (g) [2, 0, L] at 2 K. Insets show the in (f) and peak in (g). (h) The contour plot of for between 3 and 320 K and from 0 to 14 T. The red circular symbols represent the .
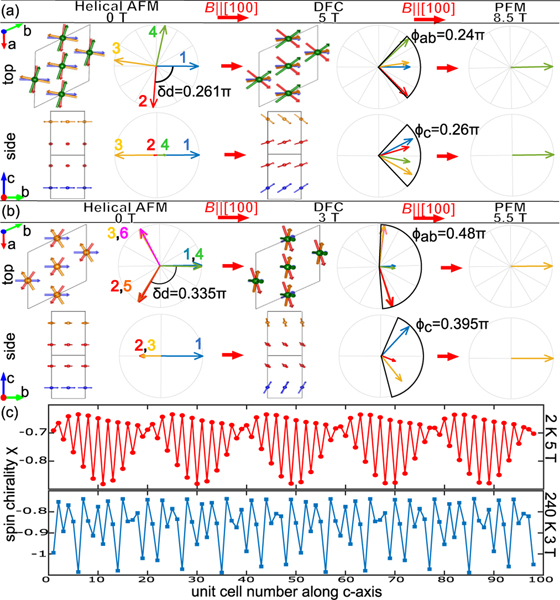
To model the DFC structure, we consider a double-fan structure with two sinusoidal functions representing the in-plane and out-of-plane components of the spin [21,34]. The angle of the ordered moment is , and , where and are the in-plane and -axis fan amplitudes, respectively, and is the phase difference between these two components. The refined results for 2 K, 5 T, are , , , and [Fig. 6(a)]. At 240 K, 3 T, the fits give , , , and [Fig. 6(b)]. The DFC structure modeled represents a spin texture that is clearly different from an intrinsically spin-inhomogeneous skyrmion lattice structure, which is expected to be field-direction independent, but consistent with the nonzero spin chirality requirement of the THE [19,20]. When choosing the three spins , , and from three consecutive unit cells, the spin chirality at 2 K, 5 T, and 240 K, 3 T, can be estimated [Fig. 6(c)]. Averaging over 100 unit cells, the at 2 K, 5 T, is −0.726, which increases in magnitude to −0.864 at 240 K, 3 T. If assuming the THE is also proportional to like in the skyrmion lattice [20,35], the vanishingly small THE with sign change at low temperature can be related to the decreased and the small with sign change below 100 K.
FIG. 6.
(a) The magnetic structure at 2 K with applied field from the top and side views. Numbers 1–4 represent Mn kagome bilayers stacked along the axis. Below 2.2 T, the helical antiferromagnetic (H-AFM) structure has in-plane rotation angle and no -axis canting. Above 2.2 T, the double-fan phase with a -axis component (DFC) spin structure emerges, described at 5 T within-plane fan spread and -axis spread . Above 8.5 T is the polarized ferromagnetic (PFM) state. (b) The magnetic structure at 240 K. Below 1.8 T, the H-AFM structure has . Above 1.8 T, the DFC spin structure is described at 3 T with and . Above 5.5 T is the PFM state. (c) Spin chirality as a function of unit cell number along the axis at 2 K, 5 T (red), and 240 K, 3 T (blue).
In the unified molecular field theory for an insulating H-AFM containing identical crystallographically equivalent spins with weak -axis magnetic exchange coupling [36], one would expect that an in-plane applied magnetic field should drive the helical structure into a fan structure without -axis spin component [34], which would result in zero spin chirality and therefore no THE. Our surprising discovery of an in-plane magnetic field applied on the metallic double-flat-spiral magnetic YMn6Sn6 inducing a fanlike -axis component is essential to understand the observed THE. Since YMn6Sn6 is a good metal, one would expect long-range magnetic exchange couplings including Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction where magnetic interactions on localized Mn moments are mediated through the conduction electrons. From a recent inelastic neutron scattering study of spin waves in YMn6Sn6, we see that the nearest-neighbor magnetic exchange couplings within the kagome layer and intrabilayer along the axis are and , respectively [Figs. 1(d) and 1(f)] [8]. Since the FM magnetic exchange couplings within the bilayer are expected to be much larger than interbilayer interaction , the comparable values of FM and suggest that there must be additional AFM exchange interactions along the axis to account for the in-plane field-induced -axis moment. These results are similar Ni-doped SrCo2As2, where helical incommensurate magnetic order is induced in Sr(Co1−xNix)2As2 near through RKKY interactions [37].
IV. CONCLUSIONS
In summary, centrosymmetric YMn6Sn6 with Mn kagome lattice shows a THE with in-plane magnetic field around 240 K, closely related to the field-induced DFC magnetic structure. Such a structure can only happen when the long-range -axial AFM exchange couplings are comparable with the in-plane ones. Moreover, in the PFM state, a relatively large intrinsic AHE and anisotropic carrier type under different field directions appear. These results indicate that, in addition to spin skyrmions, THE can also be induced from a uniform canted magnetic structure in a centrosymmetric lattice. Therefore, magnetic kagome metals can exhibit the rich tunability of various degrees of freedom and provide an excellent opportunity to study the strong entanglement among frustrated magnetism, electronic correlation, and topological electronic structure via spin-orbital coupling. After this work is submitted for publication, a related work reached a similar conclusion appeared [38].
Supplementary Material
ACKNOWLEDGMENTS
This paper was supported by the Beijing Natural Science Foundation (Grant No. Z200005), the National Key R&D Program of China (Grants No. 2018YFE0202600, 2016YFA0300504), the National Natural Science Foundation of China (No. 11774423, 11822412), the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (RUC; 18XNLG14, 19XNLG17). The neutron scattering work at Rice is supported by U.S. NSF-DMR-1700081 and by the Robert A. Welch Foundation under Grant No. C-1839 (P.D.). A portion of this research used resources at the Spallation Neutron Source and the High Flux Isotope Reactor, a DOE Office of Science User Facility operated by ORNL. H.H and S.F were supported by a MEXT Element Strategy Initiative to Form Core Research Center (Grant No. JPMXP0112101001).
References
- [1].Balents L, Spin liquids in frustrated magnets, Nature 464, 199 (2010). [DOI] [PubMed] [Google Scholar]
- [2].Ghimire NJ and Mazin II, Topology and correlations on the kagome lattice, Nat. Mater 19, 137 (2020). [DOI] [PubMed] [Google Scholar]
- [3].Kang M, Ye L, Fang S, You J-S, Levitan A, Han M, Facio JI, Jozwiak C, Bostwick A, Rotenberg E, Chan MK, McDonald RD, Graf D, Kaznatcheev K, Vescovo E, Bell DC, Kaxiras E, van den Brink J, Richter M, Prasad Ghimire M, Checkelsky JG, and Comin R, Dirac fermions and flat bands in the ideal kagome metal FeSn, Nat. Mater 19, 163 (2020). [DOI] [PubMed] [Google Scholar]
- [4].Yin J-X, Zhang SS, Chang G, Wang Q, Tsirkin SS, Guguchia Z, Lian B, Zhou H, Jiang K, Belopolski I, Shumiya N, Multer D, Litskevich M, Cochran TA, Lin H, Wang Z, Neupert T, Jia S, Lei H, and Hasan MZ, Negative flat band magnetism in a spin–orbit-coupled correlated kagome magnet, Nat. Phys 15, 443 (2019). [Google Scholar]
- [5].Lin Z, Choi J-H, Zhang Q, Qin W, Yi S, Wang P, Li L, Wang Y, Zhang H, Sun Z, Wei L, Zhang S, Guo T, Lu Q, Cho J-H, Zeng C, and Zhang Z, Flatbands and Emergent Ferromagnetic Ordering in Fe3Sn2 Kagome Lattices, Phys. Rev. Lett 121, 096401 (2018). [DOI] [PubMed] [Google Scholar]
- [6].Ye L, Kang M, Liu J, von Cube F, Wicker CR, Suzuki T, Jozwiak C, Bostwick A, Rotenberg E, Bell DC, Fu L, Comin R, and Checkelsky JG, Massive dirac fermions in a ferromagnetic kagome metal, Nature 555, 638 (2018). [DOI] [PubMed] [Google Scholar]
- [7].Chisnell R, Helton JS, Freedman DE, Singh DK, Bewley RI, Nocera DG, and Lee YS, Topological Magnon Bands in a Kagome Lattice Ferromagnet, Phys. Rev. Lett 115, 147201 (2015). [DOI] [PubMed] [Google Scholar]
- [8].Zhang H, Feng X, Heitmann T, Kolesnikov AI, Stone MB, Lu Y-M, and Ke X, Topological magnon bands in a room-temperature kagome magnet, Phys. Rev. B 101, 100405(R) (2020). [Google Scholar]
- [9].Sachdev S, Kagome and triangular-lattice heisenberg antiferromagnets: ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons, Phys. Rev. B 45, 12377 (1992). [DOI] [PubMed] [Google Scholar]
- [10].Kuroda K, Tomita T, Suzuki M-T, Bareille C, Nugroho AA, Goswami P, Ochi M, Ikhlas M, Nakayama M, Akebi S, Noguchi R, Ishii R, Inami N, Ono K, Kumigashira H, Varykhalov A, Muro T, Koretsune T, Arita R, Shin S, Kondo T, and Nakatsuji S, Evidence for magnetic Weyl fermions in a correlated metal, Nat. Mater 16, 1090 (2017). [DOI] [PubMed] [Google Scholar]
- [11].Wang Q, Xu Y, Lou R, Liu Z, Li M, Huang Y, Shen D, Weng H, Wang S, and Lei H, Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions, Nat. Commun 9, 3681 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Liu E, Sun Y, Kumar N, Muechler L, Sun A, Jiao L, Yang S-Y, Liu D, Liang A, Xu Q, Kroder J, Süß V, Borrmann H, Shekhar, Wang Z, Xi C, Wang W, Schnelle W, Wirth S,Chen Y, Goennenwein STB, and Felser C, Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal, Nat. Phys 14, 1125 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ueda K, Iguchi S, Suzuki T, Ishiwata S, Taguchi Y, and Tokura Y, Topological Hall Effect in Pyrochlore Lattice with Varying Density of Spin Chirality, Phys. Rev. Lett 108, 156601 (2012). [DOI] [PubMed] [Google Scholar]
- [14].Ueland BG, Miclea CF, Kato Y, Ayala-Valenzuela O, McDonald RD, Okazaki R, Tobash PH, Torrez MA, Ronning F, Movshovich R, Fisk Z, Bauer ED, Martin I, and Thompson JD, Controllable chirality-induced geometrical Hall effect in a frustrated highly correlated metal, Nat. Commun 3, 1067 (2012). [DOI] [PubMed] [Google Scholar]
- [15].Bruno P, Dugaev VK, and Taillefumier M, Topological Hall effect and Berry phase in magnetic nanostructures, Phys. Rev. Lett 93, 096806 (2004). [DOI] [PubMed] [Google Scholar]
- [16].Metalidis G and Bruno P, Topological Hall effect studied in simple models, Phys. Rev. B 74, 045327 (2006). [Google Scholar]
- [17].Onose Y, Ideue T, Katsura H, Shiomi Y, Nagaosa N, and Tokura Y, Observation of the magnon Hall effect, Science 329, 297 (2010). [DOI] [PubMed] [Google Scholar]
- [18].Fert A, Reyren N, and Cros V, Magnetic skyrmions: advances in physics and potential applications, Nat. Rev. Mater 2, 17031 (2017). [Google Scholar]
- [19].Nagaosa N and Tokura Y, Topological properties and dynamics of magnetic skyrmions, Nat. Nanotechnol 8, 899 (2013). [DOI] [PubMed] [Google Scholar]
- [20].Denisov KS, Rozhansky IV, Averkiev NS, and Lähderanta E, General theory of the topological hall effect in systems with chiral spin textures, Phys. Rev. B 98, 195439 (2018). [Google Scholar]
- [21].See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevB.103.014416 for additional information on experimental details. It also includes XRD pattern of YMn6Sn6, temperature dependence of longitudinal resistivity, scaling analysis between Hall and longitudinal conductivity, small-angle neutron diffraction, wide-angle neutron diffraction, and least square fitting. [Google Scholar]
- [22].Venturini G, Idrissi BCE, and Malaman B, Magnetic properties of RMn6Sn6 (R = Sc, Y, Gd-Tm, Lu) compounds with HfFe6Ge6 type structure, J. Magn. Magn. Mater 94, 35 (1991). [Google Scholar]
- [23].Venturini G, Fruchart D, and Malaman B, Incommensurate magnetic structures of RMn6Sn6 (R = Sc, Y, Lu) compounds from neutron diffraction study, J. Alloys Compd 236, 102 (1996). [Google Scholar]
- [24].Lefèvre C, Vernière A, Venturini G, and Malaman B, A neutron diffraction study of HfFe6Ge6-type YMn6Sn6−xInx compounds (0.03 ≤ x ≤ 0.72), J. Alloys Compd 361, 40 (2003). [Google Scholar]
- [25].Petříček V, Dušek M, and Palatinus L, Crystallographic computing system JANA2006: general features, Z. Kristallogr 229, 345 (2014). [Google Scholar]
- [26].Rosenfeld EV and Mushnikov NV, Double-flat-spiral magnetic structures: theory and application to the RMn6X6 compounds, Physica B 403, 1898 (2008). [Google Scholar]
- [27].Matsuo A, Suga K, Kindo K, Zhang L, Brück E, Buschow KHJ, Boer F. R. d., Lefèvre C, and Venturini G, Study of the Mn-Mn exchange interactions in single crystals of RMn6Sn6 compounds with R = Sc, Y and Lu, J. Alloys Compd 408–412, 110 (2006). [Google Scholar]
- [28].Uhlířová K, Sechovský V, de Boer FR, Yoshii S, Yamamoto T, Hagiwara M, Lefèvre C, and Venturini G, Magnetic properties and Hall effect of single-crystalline YMn6Sn6, J. Magn. Magn. Mater 310, 1747 (2007). [Google Scholar]
- [29].Nagaosa N, Sinova J, Onoda S, MacDonald AH, and Ong NP, Anomalous Hall Effect, Rev. Mod. Phys 82, 1539 (2010). [Google Scholar]
- [30].Zeng C, Yao Y, Niu Q, and Weitering HH, Linear Magnetization Dependence of the Intrinsic Anomalous Hall Effect, Phys. Rev. Lett 96, 037204 (2006). [DOI] [PubMed] [Google Scholar]
- [31].Yin J-X, Ma W, Cochran TA, Xu X, Zhang SS, Tien H-J, Shumiya N, Cheng G, Jiang K, Lian B, Song Z, Chang G, Belopolski I, Multer D, Litskevich M, Cheng Z-J, Yang XP, Swidler B, Zhou H, Lin H, Neupert T, Wang Z, Yao N, Chang T-R, Jia S, and Hasan MZ, Quantum-limit Chern topological magnetism in TbMn6Sn6, Nature 583, 533 (2020). [DOI] [PubMed] [Google Scholar]
- [32].Yin J-X, Zhang SS, Li H, Jiang K, Chang G, Zhang B, Lian B, Xiang C, Belopolski I, Zheng H, Cochran TA, Xu S-Y, Bian G, Liu K, Chang T-R, Lin H, Lu Z-Y, Wang Z, Jia S, Wang W, and Hasan MZ, Giant and anisotropic many-body spin-orbit tunability in a strongly correlated kagome magnet, Nature 562, 91 (2018). [DOI] [PubMed] [Google Scholar]
- [33].Balamurugan K, Lee S-H, Kim J-S, Ok J-M, Jo Y-J, Song Y-M, Kim S-A, Choi ES, Le MD, and Park J-G, Successive spin-flop transitions of a Neel-type antiferromagnet Li2MnO3 single crystal with a honeycomb lattice, Phys. Rev. B 90, 104412 (2014). [Google Scholar]
- [34].Johnston DC, Magnetic structure and magnetization of helical antiferromagnets in high magnetic fields perpendicular to the helix axis at zero temperature, Phys. Rev. B 96, 104405 (2017). [Google Scholar]
- [35].Neubauer A, Pfleiderer C, Binz B, Rosch A, Ritz R, Niklowitz PG, and Böni P, Topological Hall Effect in the A Phase of MnSi, Phys. Rev. Lett 102, 186602 (2009). [DOI] [PubMed] [Google Scholar]
- [36].Johnston DC, Unified molecular field theory for collinear and noncollinear Heisenberg antiferromagnets, Phys. Rev. B 91, 064427 (2015). [DOI] [PubMed] [Google Scholar]
- [37].Xie YF, Li Y, Yin ZP, Zhang R, Wang WY, Stone MB, Cao HB, Abernathy DL, Harriger L, Young DP, DiTusa JF, and Dai PC, Magnetic order and fluctuations in the quasi-two-dimensional planar magnet Sr(Co1−xNix)2As2, Phys. Rev. B 102, 214431 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Ghimire NJ, Dally RL, Poudel L, Jones DC, Michel D, Magar NT, Bleuel M, McGuire MA, Jiang JS, Mitchell JF, Lynn JW, and Mazin II, Competing magnetic phases and fluctuation-driven scalar spin chirality in the kagome metal YMn6Sn6, Sci. Adv 6, eabe2680 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.