Field-induced topological Hall effect and double-fan spin structure with a c-axis component in the metallic kagome antiferromagnetic compound YMn₆Sn₆

Abstract

Geometric frustration in the kagome lattice makes it a great host for the flat electronic band, nontrivial topological properties, and novel magnetism. Here, we use magnetotransport measurements to map out the field-temperature phase diagram of the centrosymmetric YMn₆Sn₆ with a Mn kagome lattice and show that the system exhibits the topological Hall effect (THE) with an in-plane applied magnetic field around 240 K. In addition, our neutron diffraction results demonstrate that the observed THE cannot arise from a magnetic skyrmion lattice, but instead from an in-plane field-induced double-fan spin structure with $c$-axis components. This paper provides a platform to understand the influence of a field-induced novel magnetic structure on magnetoelectric response in topological kagome metals.

I. INTRODUCTION

Two-dimensional magnetic kagome lattice materials, composed of corner-sharing triangles and hexagons of magnetic ions separated by nonmagnetic buffer layers [Fig. 1(a)], are of great interest because they are candidates for quantum spin liquid [1], flat electronic bands [2–5], and topological electronic [6] and magnetic behavior [7,8]. For kagome metals [9], calculations using a simple tight-binding model with nearest-neighbor hopping reveal topologically protected linearly dispersive electronic bands near the Dirac point and dispersionless flat bands as confirmed by angle-resolved photoemission spectroscopy experiments [2,3,5,6]. The massive Dirac or Weyl node points in kagome metals exhibit striking magneto-electric phenomena, such as large intrinsic anomalous Hall effects (AHEs) and chiral anomalies [6,10–12]. On the other hand, a real-space Berry phase originating from a magnetic field-induced skyrmion lattice [Fig. 1(b)] or a noncollinear spin texture with nonzero scalar spin chirality [$\text{χ}={\mathit{S}}_i\cdot \left({\mathit{S}}_j\times {\mathit{S}}_k\right)\ne 0$, where ${\mathit{S}}_i$, ${\mathit{S}}_j$, ${\mathit{S}}_k$ are the three nearest spins] [Fig. 1(c)] can act as a fictitious magnetic field for the conduction electrons to give rise to the topological Hall effect (THE) [13–20]. In contrast to the strong interplay between magnetism and topological electronic structure in momentum space, the noncollinear spin texture (real-space Berry phase)-induced electromagnetic responses of conduction electrons in kagome metals are still not well understood [13–20].

FIG. 1.

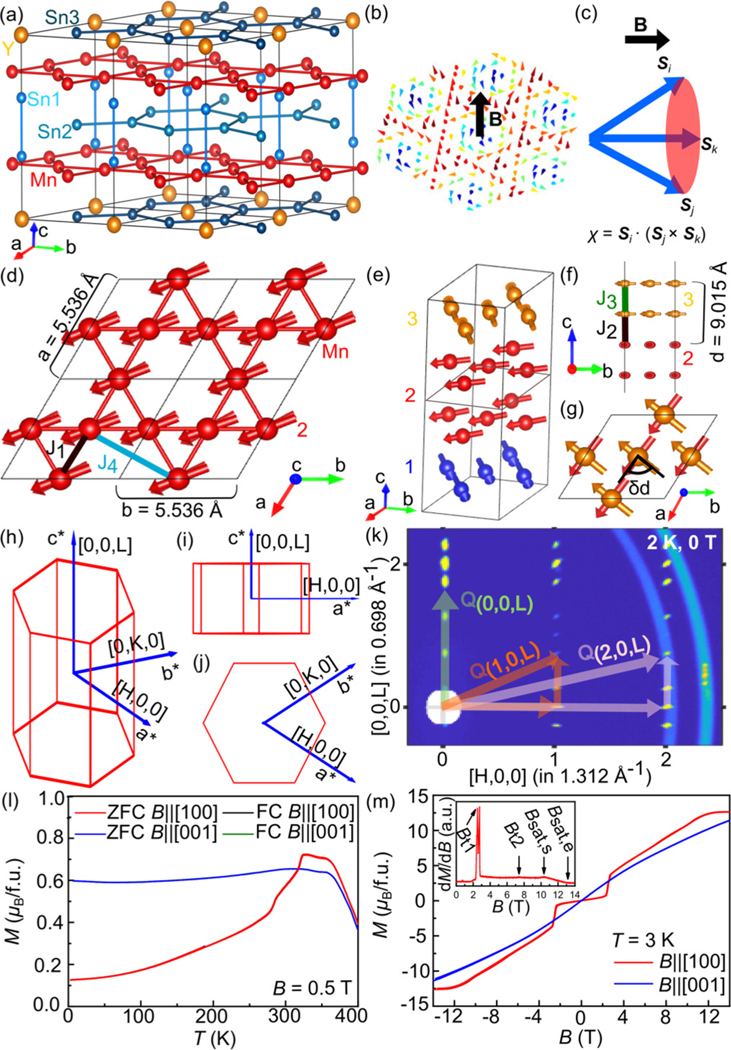
(a) Crystal structure of YMn₆Sn₆. The large yellow, medium red, and small blue (light blue and dark blue) balls represent Y, Mn, and Sn1 (Sn2 and Sn3) atoms, respectively. (b) A schematic of a nanoscale skyrmion lattice with field applied perpendicular to the kagome lattice plane. (c) A schematic of nonzero scalar spin chirality $\text{χ}$ with three noncoplanar spins ${\mathit{S}}_i$, ${\mathit{S}}_j$, and ${\mathit{S}}_k$. (d) Mn kagome bilayer top view in the YMn₆Sn₆ with nearest-neighbor and next-nearest-neighbor magnetic exchange couplings $J_1$ and $J_4$, respectively. (e) Zero-field magnetic structure of YMn₆Sn₆. (f) Side view of structure shown in (e) where $d$ is the distance between kagome bilayers along the $c$ axis. The nearest-neighbor magnetic exchange couplings along the $c$ axis are $J_2$ and $J_3$. The distance between collinear bilayers is 4.472 Å, and the distance between noncollinear layers is 4.547 Å, corresponding to $J_2$ and $J_3$. (g) Top view of structure shown in (e) where $\delta d$ is the rotation angle between kagome bilayers. (h)–(j) The definition of directions in reciprocal space. The momentum transfer $\mathit{Q}$ in Å⁻¹ is defined as $\mathit{Q}=H{\mathit{a}}^{\ast }+K{\mathit{b}}^{\ast }+L{\mathit{c}}^{\ast }$, where $H$, $K$, and $L$ are Miller indices. (k) Single-crystal neutron diffraction in the $\left[H,0,L\right]$ plane at 2 K and 0 T. Incommensurate peaks are observed along (0, 0, L), (1, 0, L), and (2, 0, L) as indicated by ${\mathit{Q}}_{(0,0,L)}$, $Q_{(0,0,L)}$, and $Q_{(2,0,L)}$, respectively. (l) Temperature dependence of magnetization $M(T)$ with zero-field-cooling (ZFC) and field-cooling (FC) modes at $B=0.5\text{T}$ for $B\Vert [100]$ and $B\Vert [001]$. (m) Field dependence of magnetization $M(B)$ at $T=3\text{K}$ for $B\Vert [100]$ and $B\Vert [001]$. Inset: $dM(B)/dB$ vs $B$ for $B\Vert [100]$.

In this paper, we report the discovery of the THE near room temperature in the antiferromagnetic (AFM) kagome metal YMn₆Sn₆, composed of a centrosymmetric Mn kagome lattice. The observed THE is strongly field-directional dependent and largest when the field is parallel to the Mn kagome plane, closely related to the formation of a double-fan spin structure with $c$-axis components under the in-plane field. In addition, a large intrinsic AHE has also been observed when the spins are fully polarized at high field.

II. EXPERIMENTAL

YMn₆Sn₆ single crystals were grown by the Sn flux method. X-ray diffraction (XRD) patterns were performed using a Bruker D8 x-ray machine with $\text{Cu}{K}_{\alpha }$ radiation $(\lambda =0.15418\text{nm})$. Magnetization and electrical transport measurements were performed in Quantum Design PPMS-14 T. Small-angle neutron scattering (SANS) was performed at the NG7 SANS instruments at the NIST Center for Neutron Research (NCNR). Wide-angle single-crystal neutron diffraction measurements were performed on the CORELLI elastic diffuse scattering spectrometer at the Spallation Neutron Source, Oak Ridge Nation Laboratory (ORNL) and at the HB-3 thermal neutron triple-axis spectrometer at the High Flux Isotope Reactor, ORNL. Detailed experimental and data analysis methods are included in the Supplemental Material [21].

III. RESULTS AND DISCUSSION

YMn₆Sn₆ has a layered hexagonal MgFe₆Ge₆-type centrosymmetric structure (space group P6/mmm, No. 191) with lattice parameters of $a=b=5.5362(2)\text{Å}$ and $c=9.0146(3)\text{Å}$ [21–23]. As shown in Fig. 1(a), there are three kinds of Sn sites, and the crystal structure of YMn₆Sn₆ is composed of Y-Sn3, Mn-Sn1, and Sn2 layers stacking along the $c$ axis. The Sn2 and Sn3 atoms form the same graphenelike hexagon planes below or above the kagome layers of Mn atoms with $d_{\text{Mn}-\text{Mn}}[\sim 2.76810(9)\text{Å}]$. The Y and Sn1 atoms locate at the centers of Sn3 and Mn hexagons, respectively, but the occupancy of Y atoms in the Y-Sn3 layer expels the Sn1 atoms significantly away from the Mn kagome layer. Because of this unique structural feature, the magnetic properties of $R$ Mn₆Sn₆ ($R$= rare earth elements) are very sensitive to both of the ${d_{\text{Mn}-\text{Mn}}}^{\text{intra}}$ in the Mn kagome layer and the nature of $R$ elements. YMn₆Sn₆ shows a helical AFM (H-AFM) ground state below $T_N\sim 333\text{K}$ [Figs. 1(d)–1(g)] [23,24]. Defining the momentum transfer $\mathit{Q}$ in reciprocal space [Figs. 1(h)–1(j)], at zero field and 2 and 240 K, the H-AFM structure is confirmed by refining the set of incommensurate magnetic Bragg peaks at $\mathit{Q}=(H,0,L\pm \delta )$, $H,L=\pm 1,2,\mathrm{...}$ [Fig. 1(k)] [25]. While the Mn spins in each kagome bilayer (Mn-Sn1-Sn2-Sn1-Mn layer) are collinear ferromagnetic (FM) and confined within the layer [Fig. 1(d)], they rotate from one bilayer to the next bilayer by $\delta d$ degrees, where $d$ is the distance between adjacent layers of moments aligned FM, and have no moment component along the $c$ axis [Fig. 1(f)]. This is because the double-flat-spiral magnetic structure has a strong FM exchange interaction through Sn1Sn2-Sn1 layers and a much weaker interaction through the Y-Sn3 layer [26]. At 240 K, $\delta =0.261(8)$, and at 2 K, $\delta =0.283(2)$. For $B\Vert [100]$, the magnetization curve $M(T)$ at $B=0.5\text{T}$ shows a paramagnetic-AFM transition at $T_N\sim 359\text{K}$ and a collinear to H-AFM transition at $T_t\sim 326\text{K}$ [Fig. 1(l)] [27,28]. In contrast, the $M(T)$ curve for $B\Vert [001]$ is rather flat below $T_N\sim 359\text{K}$, indicating the magnetic moments of Mn atoms lie in the ab plane. The overlap of all zero-field-cooling (ZFC) and field-cooling (FC) $M(T)$ curves indicates the absence of magnetic glassy state. For $B\Vert [001]$, the isothermal magnetization $M(B)$ at $T=3\text{K}$ increases smoothly because of gradual bending of the moments toward the $c$ axis [Fig. 1(m)]. However, the $M(B)$ curve for $B\Vert [100]$ shows a striking jump at $B_{t1}\sim 2.5\text{T}$ derived from the $\text{d}M(B)/\text{d}B$ curve [inset of Fig. 1(m)] and then increases gradually with field. The slope of the $M(B)$ curve decreases when $B>B_{\text{sat},s}(\sim 10.4\text{T})$, and finally, the polarized FM (PFM) state is reached at $B_{\text{sat},e}\sim 13.2\text{T}$. Note that there is another small kink located at $B_{t2}\sim 7.5\text{T}$ [27,28]. The saturated moment for the Mn atom at 3 K is about 2.11 ${\mu }_{\text{B}}/\text{Mn}$ for $B\Vert [100]$.

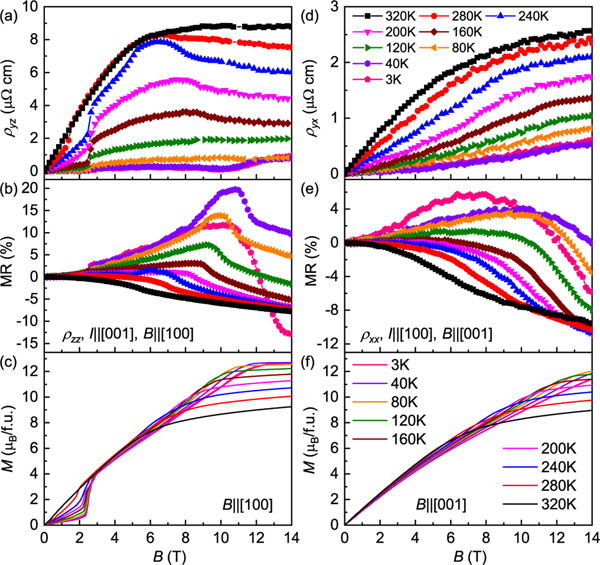
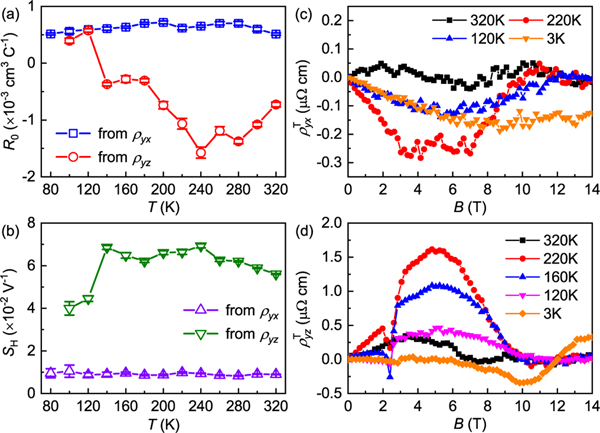
YMn₆Sn₆ exhibits metallic behaviors with weak anisotropy [21]. The Hall resistivity ${\rho }_{yz}(B)$ of YMn₆Sn₆ at 320 K increases and then saturates with increasing in-plane field [Fig. 2(a)]. With decreasing temperature, however, the ${\rho }_{yz}(B)$ curve shows a sharp jump at $B_{t1}$, followed by an obvious hump between $B_{t1}$ and $B_{\text{sat},e}$ [Fig. 2(a)]. Such behavior is distinctly different from the nearly linear increase and gradual saturation behaviors of $M(B)$ when $B>B_{t1}$ [Fig. 2(c) and Fig. 3(a)]. This behavior weakens upon decreasing temperature with ${\rho }_{yz}(B)$, dipping around 10 T, consistent with a previous paper [28]. The ${\rho }_{zz}(B)$ exhibits negative magnetoresistance (MR) at high temperatures, and when the temperature decreases, the positive MR appears at the low-field region but starts to decrease at the high-field region [Fig. 2(b)]. In contrast, the ${\rho }_{yx}(B)$ gradually increases and then saturates with increasing out-of-plane field [Fig. 2(d)], similar to the $M(B)$ curves [Figs. 2(f) and 3(b)]. Upon lowering $T$, the saturation field shifts to a higher field and is greater than 14 T when $T⩽80\text{K}$ [Fig. 2(d)]. In general, ${\rho }_{xx}(B)$ shows a similar field dependence to ${\rho }_{zz}(B)$ throughout the temperature and field ranges [Fig. 2(e)], but it does not exhibit the obvious kinks observed in ${\rho }_{zz}(B)$ near characteristic fields, such as $B_{t1}$ and $B_{\text{sat},s}$ etc. This implies that the magnetic configuration changes have remarkable influence on longitudinal resistivity, especially ${\rho }_{zz}$. In a magnetic system, the total Hall resistivity can usually be described as the sum of three contributions [19,29]:${\rho }_{\text{H}}={{\rho }_{\text{H}}}^N+{{\rho }_{\text{H}}}^A+{{\rho }_{\text{H}}}^T=R_{0}B+S_{\text{H}}{\rho }^{2}M+{{\rho }_{\text{H}}}^T$, where ${{\rho }_{\text{H}}}^N$ is the normal Hall resistivity due to the Lorentz force and $R_0$ is the ordinary Hall coefficient. Here, ${{\rho }_{\text{H}}}^A$ is the anomalous Hall resistivity, and $S_{\text{H}}$ should be a constant for the intrinsic anomalous Hall conductivity (AHC, ${\sigma }_{\text{H}}^{\text{A}}\sim {\rho }_{\text{H}}^{\text{A}}/{\rho }^2$), which is linearly proportional to $M$ [29,30]. The last term ${{\rho }_{\text{H}}}^T$ represents the topological Hall resistivity, usually originating from noncollinear spin texture with nonzero scalar spin chirality. The scaling curves of ${\rho }_{\text{H}}/\text{B}$ vs ${\rho }^{2}M/B$ show linear behaviors in the high-field region for both ${\rho }_{yx}(B)$ and ${\rho }_{yz}(B)$ when $T>80\text{K}$ [Figs. 3(c) and 3(d)]. This undoubtedly indicates that the AHE is dominant when the THE vanishes in the PFM state. The $R_0$ and $S_{\text{H}}$ can be determined from the linear fit of the curves of ${\rho }_{\text{H}}(B)/B$ vs $\rho {(B)}^{2}M(B)/B$ when $B>B_{\text{sat},e}$, as shown in Figs. 4(a) and 4(b). The $R_0\left(T\right)$ derived from ${\rho }_{yx}(B)$ is positive and almost independent of temperature, similar to TbMn₆Sn₆ with a $c$-axial-FM ground state and possibly related to the hole-type Dirac electrons near the Fermi energy level $E_{\text{F}}$ [31]. In contrast, the $R_0\left(T\right)$ obtained from ${\rho }_{yz}(B)$ shows a strong temperature dependence with a sign change from negative to positive when $T⩽120K$. This implies that the direction of magnetic moments and magnetic structure may have significant effects on the electronic structure of YMn₆Sn₆, like in the case of Fe₃Sn₂ with Fe kagome bilayers, where the size of the Dirac gap can be tuned effectively by changing the direction of the external field [32]. Both $S_{\text{H}}\left(T\right)$ obtained from ${\rho }_{yx}(B)$ and ${\rho }_{yz}(B)$ are positive. In addition, the relatively large values of ${{\sigma }_{xy}}^A\left(\sim 45\text{S}{\text{cm}}^{-1}\right)$ and ${{\sigma }_{zy}}^A\left(\sim 300{\text{Scm}}^{-1}\right)$ with weak dependence on longitudinal conductivity $\sigma (\sim 1/\rho )$ confirm the intrinsic AHE at high-field region [21]. These values of AHC are comparable with those in TbMn₆Sn₆ with Chern-gapped Dirac fermions [31], suggesting a possible similar contribution of Chern-gap-induced Berry curvature to AHC at the PFM state in YMn₆Sn₆. As shown in Figs. 4(c) and 4(d), both derived ${{\rho }_{yx}}^{\text{T}}(B)$ and ${{\rho }_{yz}}^{\text{T}}(B)$ [Figs. 3(e) and 3(f)] are small at high temperature. Their intensities increase with decreasing temperature at first, reaching the maximum values of ${{\rho }_{yx}}^{T,\text{max}}=-0.28\mu \text{Ω}\text{cm}$ and ${{\rho }_{yz}}^{T,\text{max}}=-2.0\mu \text{Ω}\text{cm}$ under $B\sim 5\text{T}$ at about 220 and 240 K, respectively, and then decrease quickly. At lower temperature, the ${{\rho }_{yx}}^{\text{T},\text{max}}$ shifts to a higher field. In contrast, the ${{\rho }_{yz}}^{\text{T},\text{max}}$ becomes negative when $T⩽80\text{K}$, located at $B\sim 10\text{T}$.

FIG. 2.

(a) Hall resistivity ${\rho }_{yz}(B)$, (b) magnetoresistance $\left\{\text{MR}=100\text{\%}\times \left[{\rho }_{zz}-{\rho }_{zz}(0)\right]/{\rho }_{zz}(0)\right\}$, and (c) $M(B)$ as a function of magnetic field at various temperatures when $B\Vert [100]$. (d) Hall resistivity ${\rho }_{yx}(B)$, (e) magnetoresistance $\left\{\text{MR}=100\text{\%}\times \left[{\rho }_{xx}-{\rho }_{xx}(0)\right]/{\rho }_{xx}(0)\right\}$, and (f) $M(B)$ as a function of magnetic field at various temperatures when $B\Vert [100]$. The symbols in (a), (b), (d), and (e) have the same color codes. The colors of curves in (c) and (f) have the same definitions.

FIG. 3.

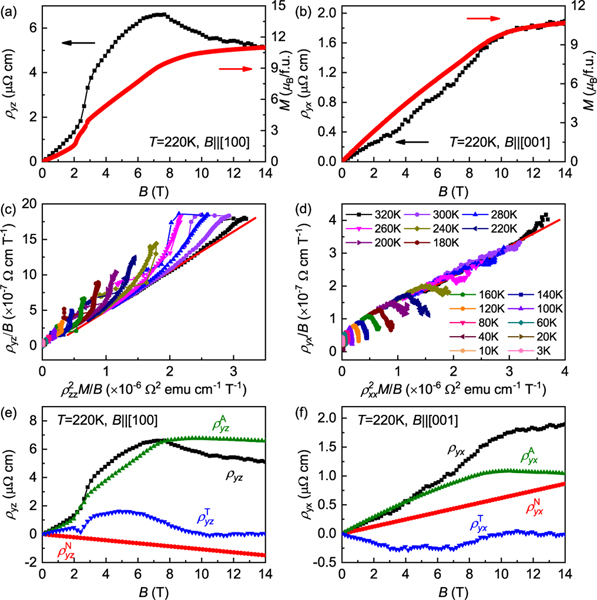
Field dependence of (a) Hall resistivity ${\rho }_{yz}$ and $M(B)$ for $B\Vert [100]$ and (b) ${\rho }_{yx}$ and $M(B)$ for $B\Vert [001]$ at 220 K. (c) ${\rho }_{yz}/B$ vs ${{\rho }_{zz}}^{2}M/B$ and (d) ${\rho }_{yx}/B$ vs ${\rho }_{xx}^{2}M/B$ at various temperatures. The red lines in (c) and (d) represent the fitting results of experimental curves above the saturation field at $T=320\text{K}$. The intercept and slope correspond to $R_0$ and $S_{\text{H}}$, respectively. Accordingly, ${{\rho }_{\text{H}}}^N$ and ${{\rho }_{\text{H}}}^A$ can be calculated by $R_{0}B$ and $S_{\text{H}}{\rho }^{2}M$, respectively. Then ${{\rho }_{\text{H}}}^T$ is estimated after the subtraction of ${{\rho }_{\text{H}}}^N$ and ${{\rho }_{\text{H}}}^A$ from ${\rho }_{\text{H}}$, i.e., ${\rho }_{yz}-{{\rho }_{yz}}^{\text{N}}-{{\rho }_{yz}}^{\text{A}}$ and ${{\rho }_{yx}}^{\text{T}}\equiv {\rho }_{yx}-{{\rho }_{yx}}^{\text{N}}-{{\rho }_{yx}}^{\text{A}}$. Different estimated components of Hall resistivity at 220 K are shown in (e) and (f) for ${\rho }_{yz}$ and ${\rho }_{yx}$, respectively. Because the emergence of upturn behavior for ${\rho }_{yz}(B)$ or the saturation region is beyond 14 T for ${\rho }_{yx}(B)$, it cannot extract $R_0$ and $S_{\text{H}}$ from high-field linear fitting of ${\rho }_{\text{H}}/B$ vs ${\rho }^{2}M/B$ curves. Thus, $R_0$ and $S_{\text{H}}$ at 100 K for ${\rho }_{yz}$ and 80 K for ${\rho }_{yx}$ are used to estimate ${{\rho }_{\text{yz}}}^T$ and ${{\rho }_{\text{yx}}}^T$ at the low-temperature region.

FIG. 4.

Temperature dependence of (a) $R_0(T)$ and (b) $S_{\text{H}}(T)$ derived from ${\rho }_{yx}(B)$ and ${\rho }_{yz}(B)$. (c) ${{\rho }_{yx}}^{\text{T}}(B)$ and (d) ${{\rho }_{yz}}^{\text{T}}(B)$ as a function of B at selected temperatures.

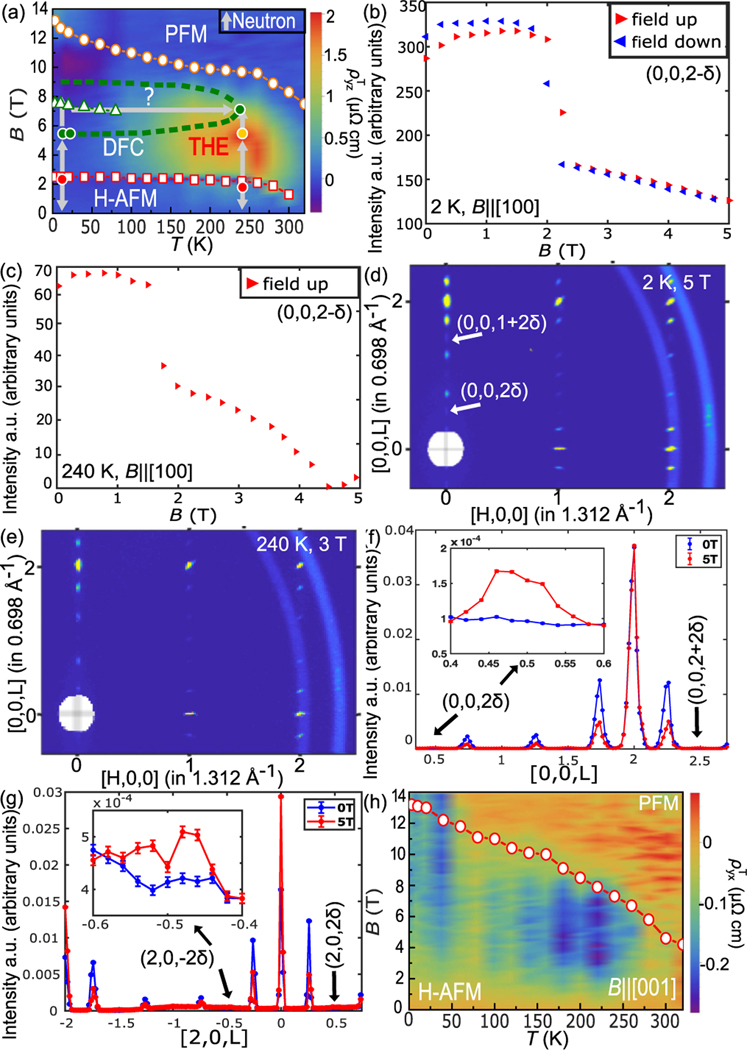
Our small-angle neutron diffraction measurements found no evidence for the expected field-induced skyrmion lattice [21]; thus, the THE for $B\Vert [100]$ is not due to skyrmions. In contrast, the combined phase diagram of ${{\rho }_{yz}}^{\text{T}}(B)$ and magnetic transitions observed through neutron diffraction [Figs. 5(a)] provides a clear relation between in-plane-field-induced noncollinear magnetic structures and emergent electrodynamic responses. Here, ${{\rho }_{yz}}^{\text{T}}(B)$ is small at the H-AFM state with Mn moments lying in the ab plane. With $B>B_{t1}$, the Mn moments undergo a first-order spin-flop transition at $B\sim 2.2\text{T}$ at 2 K [Fig. 5(b)] and $B\sim 1.8\text{T}$ at 240 K [Fig. 5(c)] [21] to a new double-fan phase with a $c$-axis component (DFC), contributing to the THE. This fanlike spin configuration is fully mapped by neutron diffraction measurements at 2 K, 5 T [Fig. 5(d)], and at 240 K, 3 T [Fig. 5(e)]. The $c$-axis canting is due to interlayer weak AFM exchange coupling [33]. This is shown in the magnetic field dependence of the incommensurate peaks along the $[H,0,L]$ $\left(H=1,2\right)$ direction. Since neutron diffraction is only sensitive to the ordered moment component perpendicular to the wave vector $\mathit{Q}$, incommensurate peaks along the $[0,0,L\pm n\delta ]$ $\left(n=1,2\right)$ direction will not reveal any $c$-axis canting [Fig. 5(f)]. On the other hand, for incommensurate peaks along the $\left[H,0,L\pm n\delta \right]$ direction with $H=1,2$ [Fig. 5(g)], neutron diffraction measurements are sensitive to a field-induced $c$-axis component. From our data, we conclude that an in-plane magnetic field induces a $c$-axis component in the new magnetic ordered state. At low temperature and field $B_{t2}<B<B_{\text{sat},e}$, another unknown magnetic structure (denoted as “?”) is induced, leading to another weak THE with the opposite sign. Finally, when $B>B_{\text{sat},e}$, the PFM state cannot host a topologically nontrivial spin structure; therefore, the THE disappears. On the other hand, the relatively small ${{\rho }_{yx}}^{\text{T}}(B)$ between H-AFM and PFM states could be ascribed to the possible noncollinear spin configuration when Mn moments tilt gradually toward the $c$ axis for $B\Vert [001]$ [Fig. 5(h)].

FIG. 5.

(a) Phase diagram of YMn₆Sn₆ for $B\Vert [100]$ with a contour plot of ${{\rho }_{yz}}^{\text{T}}(T,B)$. $M(B)$ data points are in white with colored outline, and neutron data points are in color with white outline. The orange circular, green triangular, and red square symbols represent $B_{\text{sat},e}$, $B_{t2}$, and $B_{t1}$, respectively. Below ∼2 T, YMn₆Sn₆ forms a helical antiferromagnetic (H-AFM) structure; between ∼2–5.5 T, a double-fan phase with a $c$-axis component (DFC) structure; at low temperature and field ∼5.5–9 T, a new unknown phase denoted “?”, and for higher, a polarized ferromagnetic (PFM) state. Gray arrows indicate neutron diffraction measurements. (b) Field dependence of $(0,0,2-\delta )$ peak intensity at 2 K. (c) Field dependence of $(0,0,2-\delta )$ peak intensity at 240 K. (d) and (e) Single-crystal neutron diffraction in the $\left[H,0,L\right]$ plane of a YMn₆Sn₆ single crystal at (d) 2 K, 5 T, and (e) 240 K, 3 T. Satellite peaks are observed at $(H,0,\pm 2\delta )$ and $(H,0,\pm \delta )$. (f) and (g) Magnetic field dependence of (f) [0, 0, L] at 2 K and (g) [2, 0, L] at 2 K. Insets show the $(0,0,2\delta )$ in (f) and $(2,0,-2\delta )$ peak in (g). (h) The contour plot of ${{\rho }_{yx}}^{\text{T}}(T,B)$ for $T$ between 3 and 320 K and $B$ from 0 to 14 T. The red circular symbols represent the $B_{\text{sat},s}$.

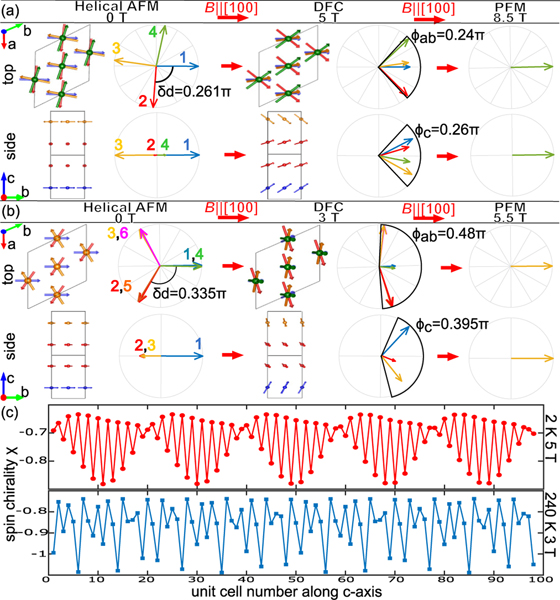
To model the DFC structure, we consider a double-fan structure with two sinusoidal functions representing the in-plane and out-of-plane components of the spin [21,34]. The angle ${\varphi }_{n,ab;n,c}$ of the ordered moment is ${\varphi }_{n,ab}={\varphi }_{ab}\text{sin}(n\delta d)$, and ${\varphi }_{n,c}={\varphi }_c\text{sin}(n\delta d-\phi )$, where ${\varphi }_{ab}$ and ${\varphi }_c$ are the in-plane and $c$-axis fan amplitudes, respectively, and $\phi$ is the phase difference between these two components. The refined results for 2 K, 5 T, are ${\varphi }_{\text{ab}}=0.24\pi$, ${\varphi }_c=0.26\pi$, $\phi =0.656\pi$, and $\delta d=0.261\pi$ [Fig. 6(a)]. At 240 K, 3 T, the fits give ${\varphi }_{ab}=0.455\pi$, ${\varphi }_c=0.379\pi$, $\phi =0.60\pi$, and $\delta d=0.335\pi$ [Fig. 6(b)]. The DFC structure modeled represents a spin texture that is clearly different from an intrinsically spin-inhomogeneous skyrmion lattice structure, which is expected to be field-direction independent, but consistent with the nonzero spin chirality $\text{χ}$ requirement of the THE [19,20]. When choosing the three spins $S_i$, $S_j$, and $S_k$ from three consecutive unit cells, the spin chirality $\text{χ}$ at 2 K, 5 T, and 240 K, 3 T, can be estimated [Fig. 6(c)]. Averaging over 100 unit cells, the $\text{χ}$ at 2 K, 5 T, is −0.726, which increases in magnitude to −0.864 at 240 K, 3 T. If assuming the THE is also proportional to $R_0$ like in the skyrmion lattice [20,35], the vanishingly small THE with sign change at low temperature can be related to the decreased $\text{χ}$ and the small $R_0$ with sign change below 100 K.

FIG. 6.

(a) The magnetic structure at 2 K with applied field from the top and side views. Numbers 1–4 represent Mn kagome bilayers stacked along the $c$ axis. Below 2.2 T, the helical antiferromagnetic (H-AFM) structure has in-plane rotation angle ${\delta }_d=0.261\pi$ and no $c$-axis canting. Above 2.2 T, the double-fan phase with a $c$-axis component (DFC) spin structure emerges, described at 5 T within-plane fan spread ${\varphi }_{ab}=0.24\pi$ and $c$-axis spread ${\varphi }_c=0.26\pi$. Above 8.5 T is the polarized ferromagnetic (PFM) state. (b) The magnetic structure at 240 K. Below 1.8 T, the H-AFM structure has ${\delta }_d=0.335\pi$. Above 1.8 T, the DFC spin structure is described at 3 T with ${\varphi }_{ab}=0.48\pi$ and ${\varphi }_c=0.395\pi$. Above 5.5 T is the PFM state. (c) Spin chirality $\text{χ}$ as a function of unit cell number along the $c$ axis at 2 K, 5 T (red), and 240 K, 3 T (blue).

In the unified molecular field theory for an insulating H-AFM containing identical crystallographically equivalent spins with weak $c$-axis magnetic exchange coupling [36], one would expect that an in-plane applied magnetic field should drive the helical structure into a fan structure without $c$-axis spin component [34], which would result in zero spin chirality and therefore no THE. Our surprising discovery of an in-plane magnetic field applied on the metallic double-flat-spiral magnetic YMn₆Sn₆ inducing a fanlike $c$-axis component is essential to understand the observed THE. Since YMn₆Sn₆ is a good metal, one would expect long-range magnetic exchange couplings including Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction where magnetic interactions on localized Mn moments are mediated through the conduction electrons. From a recent inelastic neutron scattering study of spin waves in YMn₆Sn₆, we see that the nearest-neighbor magnetic exchange couplings within the kagome layer and intrabilayer along the $c$ axis are $J_1\approx -28\text{meV}$ and $J_3\approx -23\text{meV}$, respectively [Figs. 1(d) and 1(f)] [8]. Since the FM magnetic exchange couplings within the bilayer $J_3$ are expected to be much larger than interbilayer interaction $J_2$, the comparable values of FM $J_1$ and $J_3$ suggest that there must be additional AFM exchange interactions along the $c$ axis to account for the in-plane field-induced $c$-axis moment. These results are similar Ni-doped SrCo₂As₂, where helical incommensurate magnetic order is induced in Sr(Co₁−xNi_x)₂As₂ near $x\approx 0.1$ through RKKY interactions [37].

IV. CONCLUSIONS

In summary, centrosymmetric YMn₆Sn₆ with Mn kagome lattice shows a THE with in-plane magnetic field around 240 K, closely related to the field-induced DFC magnetic structure. Such a structure can only happen when the long-range $c$-axial AFM exchange couplings are comparable with the in-plane ones. Moreover, in the PFM state, a relatively large intrinsic AHE and anisotropic carrier type under different field directions appear. These results indicate that, in addition to spin skyrmions, THE can also be induced from a uniform canted magnetic structure in a centrosymmetric lattice. Therefore, magnetic kagome metals can exhibit the rich tunability of various degrees of freedom and provide an excellent opportunity to study the strong entanglement among frustrated magnetism, electronic correlation, and topological electronic structure via spin-orbital coupling. After this work is submitted for publication, a related work reached a similar conclusion appeared [38].