Abstract
Diffusion Monte Carlo (DMC) is an exact technique to project out the ground state (GS) of a Hamiltonian. Since the GS is always bosonic, in Fermionic systems, the projection needs to be carried out while imposing antisymmetric constraints, which is a nondeterministic polynomial hard problem. In practice, therefore, the application of DMC on electronic structure problems is made by employing the fixed-node (FN) approximation, consisting of performing DMC with the constraint of having a fixed, predefined nodal surface. How do we get the nodal surface? The typical approach, applied in systems having up to hundreds or even thousands of electrons, is to obtain the nodal surface from a preliminary mean-field approach (typically, a density functional theory calculation) used to obtain a single Slater determinant. This is known as single reference. In this paper, we propose a new approach, applicable to systems as large as the C60 fullerene, which improves the nodes by going beyond the single reference. In practice, we employ an implicitly multireference ansatz (antisymmetrized geminal power wave function constraint with molecular orbitals), initialized on the preliminary mean-field approach, which is relaxed by optimizing a few parameters of the wave function determining the nodal surface by minimizing the FN-DMC energy. We highlight the improvements of the proposed approach over the standard single-reference method on several examples and, where feasible, the computational gain over the standard multireference ansatz, which makes the methods applicable to large systems. We also show that physical properties relying on relative energies, such as binding energies, are affordable and reliable within the proposed scheme.
1. Introduction
Ab initio electronic structure calculations, which compute the electronic structure of materials nonempirically, have become an essential methodology in the materials science and condensed matter physics communities. Density functional theory (DFT), a mean-field approach which was originally proposed by Kohn and Hohenberg,1 is the most widely used methodology for ab initio electronic structure calculations. DFT has enjoyed widespread success, despite its reliance on the so-called exchange–correlation (XC) functional, whose exact form is yet to be discovered. Although many XCs have been proposed, no functional that performs universally well for all materials is established.
Several methodologies transcend the mean-field paradigm. For example, in the quantum chemistry community, the coupled cluster method with single, double, and perturbative triple excitations,2 denoted as CCSD(T), is widely recognized as the gold-standard approach, balancing accuracy and computational efficiency. This technique has been employed as a reference in many benchmark tests, both for isolated and periodic systems.2−5 CCSD(T) is mostly applied in relatively small systems, as it becomes very computationally intensive as the simulated systems get larger (hundreds of electrons or more). Moreover, despite the many successes of CCSD(T), there are a few cases where CCSD(T) fails, mostly attributed to the multireference character of a chemical system (strong correlation) and where other methods, more expensive computationally, are needed.6 A different approach, adopted by the condensed matter community as the gold standard, is the diffusion Monte Carlo (DMC) method.7 DMC has good scaling with the system size and it uses algorithms that can be parallelized with little or no efficiency loss, fully exploiting modern supercomputers and making relatively large systems treatable.
CCSD(T) and DMC predictions typically show consensus in the computed physical properties, such as heats of formation and binding energies, and good agreement with experiments.5,8−13 It was believed that CCSD(T) and DMC would also agree on extended systems, but recent findings by Al-Hamdani et al.12 have unveiled discrepancies in binding energy calculations between these methods for large systems, such as a C60 buckyball inside a [6]-cycloparaphenyleneacetylene ring (C60@[6]CPPA). It is unclear which approach is to be trusted in these tricky cases. These findings raise a pivotal question: what is the reference approach for noncovalent interactions between large systems? To answer this question, Al-Hamdani et al.12 discussed possible discrepancy sources coming from uncontrollable errors existing in both CCSD(T) and DMC. Both approaches employ some approximations and have their weaknesses, and the debate is still open. To draw a more conclusive determination, one should develop a scheme which mitigates the impact of uncontrollable errors in the methods. In this work, we focus on improvements in the DMC approach that alleviate its largest source of error: the fixed-node (FN) approximation.
DMC yields the exact ground state (GS) in bosonic systems. In Fermionic systems (for instance, in electronic structure calculations), DMC suffers from the so-called negative sign problem, arising from the fact that the Fermionic GS has positive and negative regions. The negative sign problem in the DMC method for Fermions has been proven to be a nondeterministic polynomial hard problem;14 thus, it seems unrealistic to find a general solution at present. This problem is avoided, in practice, by modifying the DMC projection algorithm with the introduction of the FN approximation, where the projected wave function ΦFN is constrained to have the nodes of a predetermined guiding function ΨT. The FN approximation keeps the projected wave function ΦFN antisymmetric, but ΦFN is the exact GS Φ0 only if its nodes are exact. A general property of ΦFN is that it is always the closest function to Φ0 within the FN constraint. For trial functions obtained from mean-field approaches, such as Hartree–Fock (HF) or DFT, it is generally believed that the error associated with the FN approximation is small and benefits from a large error cancellation in the evaluation of binding energies.8 However, the FN error is typically not accessible, as Φ0 is unknown, and this yields an uncontrollable error in FN-DMC.
In standard FN-DMC simulations, the nodal surface is given by an approximate wave function, which is typically obtained starting from a mean-field approach, such as HF or DFT. The variational principle can still be applied to FN-DMC,a and so to go beyond the mean-field solution, one should optimize the given nodal surface by minimizing the FN-DMC energy EFN (which is the expectation value of ΦFN), going in the direction of the exact wave function Φ0 and the exact energy E0. This procedure is seldomly followed in DMC simulations, especially on large systems (say, with hundreds or thousands of electrons), as it is hardly affordable computationally and the uncertainty on the optimization of the FN surface could be easily comparable, if not larger, than the binding energy under consideration. Thus, the standard approach is to just keep the nodal surface of the Slater determinant (SD) built with the Kohn–Sham orbitals obtained from a DFT calculation. While the FN surface from DFT might be suboptimal, this approach typically yields quite reliable results, especially in the evaluations of noncovalent interactions, due to very favorable error cancellations.5,8
In smaller systems (with say, tens of electrons), it is possible to improve the nodal surface, and the most standard approach is to use an ansatz that has more degrees of freedom than the initial SD, such as the antisymmetrized geminal power (AGP),19−21 the Pfaffian,22−24 the complete active space,25,26 the valence bond,27,28 the backflow,23,29,30 and multideterminant expansions,31−38 including methods employing neural networks and machine learning techniques.39−45 The standard approach here is to optimize the wave function parameters at the level of theory of variational Monte Carlo (VMC).19,46−50 Indeed, optimization at the FN-DMC (FN-opt) level implies further difficulties, as we will discuss below. However, optimization at the VMC (VMC-opt) level has some flaws. In VMC-opt, the object that is optimized is the variational wave function ΨT, which is obtained from the product of one of the ansatzes discussed above and the Jastrow factor.b The closer ΨT gets to the GS Φ0, the smaller its VMC energy (variational principle) and its VMC variance (zero-variance property) are. VMC-opt explores the parameters’ variational space, seeking the set which minimizes the VMC energy or the VMC variance, and it is often done by employing the VMC gradient. It is not guaranteed that the parameters obtained from VMC-opt are those giving the best possible nodal surface allowed by the employed ansatz (unless we are in the limit case where ΨT yields VMC with zero variance, such that we know that ΨT is an eigenstate of the Hamiltonian). Although this approach, in practice, gives a better nodal surface than the DFT one, it sometimes gives unreasonable outcomes, e.g., it overestimates binding energies, as revealed in this work. It would be desirable, instead, to implement an optimization at the FN-DMC level of theory, where the parameters of the function ΨT giving the nodal surface are optimized so as to minimize the FN energy. This would guarantee to find the best nodal surface allowed by the adopted wave function ansatz. To the best of our knowledge, the first attempt to directly optimize the variational parameters included in a trial wave function at the FN-DMC level was done by Reboredo et al.51 in the ab initio framework. They proposed a way to iteratively generate new trial wave functions to get a better nodal surface. They generalized the method to excited states52 and finite temperatures53 and also applied for large systems such as C20.54 Very recently, McFarland and Manousakis55 reported successful energy minimizations with approximated and exact FN gradients. They proposed to optimize nodes using a combination of FN gradients and the projected gradient descent (PGD) method. The PGD method works for Be, Li2, and Ne using all-electron DMC calculations,55 while it has been successful only for small molecules.
When it comes to optimizing the nodal surface of a large system, the main problem is that the number of variational parameters determining the nodal surface often scales more than linearly with the size of the system. For instance, the number of variational parameters in the determinant part of the AGP ansatz scales with O(L2), where L is the number of basis functions in a system. It makes the parameter space to be optimized so complex that the optimization is easily trapped in local minima and one cannot find the true GS. Moreover, since the optimization algorithms are stochastic, there is always an additional uncertainty on the optimized parameters, which are not going to be exact and the corresponding DMC energy has therefore an optimization bias. The optimization bias increases with the system size and with the number of variational parameters and can be reduced only at the cost of increasing the statistical sampling (and the computational cost). The evaluation of binding energy implies the difference between two or more DMC energies, and it is often a tiny fraction of the total energy. Therefore, the optimization uncertainty can often be comparable to the binding energy, making the evaluation of the interaction energy unreliable. Moreover, we need to verify that the adopted approach satisfies basic physical properties, such as being size-consistent.c At the VMC level, the size consistency is a property of the wave function ansatz employed, and it depends on the optimization procedure. At the FN-DMC level, size consistency might depend on some choices on the algorithm,56 on the ansatz of the wave function providing the FN constraint, and on the optimization.
In this paper, we propose a scheme which aims to address these issues. In particular, our scheme satisfies the following points: (i) it is systematically more accurate than the standard approach of employing a single SD, (ii) it is size-consistent, and (iii) it is applicable also to large systems. The idea underlying the present work is the combination of the AGP wave function consisting of molecular orbitals (MOs), dubbed AGPn,21 the use of natural orbitals (NOs), and the optimization of its nodal surface using FN gradients on a selected subset of the AGPn parameters. In particular, we initialize the orbitals in the AGPn wave function using NOs, which are kept fixed afterward, such that only the coefficients combining them are optimized to relax the nodal surface. We call this scheme the fixed node antisymmetrized geminal power active space (FNAGPAS). Since the orbitals are fixed, this results in a much smaller number of variational parameters in the ansatz; thus, one can apply it for larger systems, such as C60 fullerene. We show that our scheme gives a better nodal surface (i.e., a lower energy in the FN-DMC calculation) compared to the typical Slater–Jastrow ansatz, and it reliably describes also strongly correlated systems (such as diradicals). We show that the use of FN-opt is important to fulfill the size-consistency property.
2. FNAGPAS Scheme
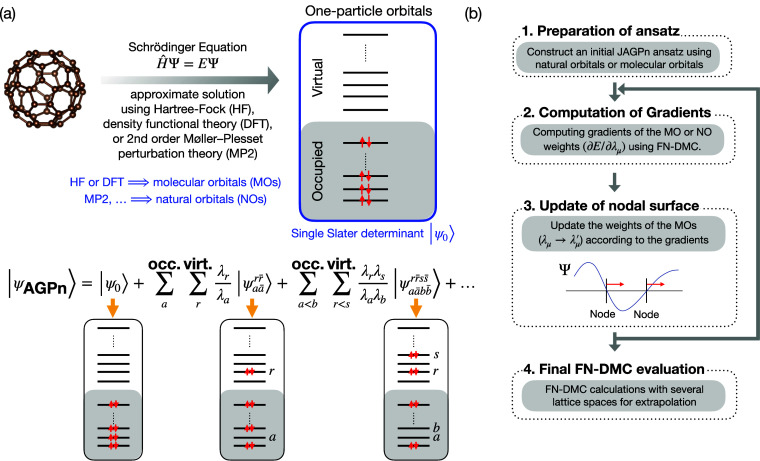
We describe here the scheme that we suggest to improve the accuracy of FN-DMC over the traditional single-determinant Slater–Jastrow ansatz. The key idea is the combination of the AGPn,21 which is the AGP wavefunction constraint with MOs, and the optimization of the ansatz using approximated FN gradients.55 We describe the ansatz in the following section, assuming an unpolarized system for simplicity. The schematic illustration explaining the key concept and its workflow is shown in Figure 1.
Figure 1.
Panel a: Schematic illustration of the FNAGPAS scheme. We perform a preliminary mean-field calculation to obtain MOs, followed by a correlated calculation yielding NOs. The AGPn ansatz corresponds to a multideterminant expansion built on the NOs and depending on the coefficients λi associated with each orbital i and optimized in order to minimize the FN energy. Panel b: Flowchart illustrating the FNAGPAS scheme workflow.
The real-space quantum Monte Carlo (QMC) typically employs a many-body wave function ansatz Ψ written as the product of two terms, ΨQMC = ΦAS × exp J. The term exp J, conventionally dubbed Jastrow factor, is symmetric, and the term ΦAS is antisymmetric. The Jastrow factor is explicitly dependent on electron–electron distance and often includes electron–nucleus and electron–electron–nucleus terms.d The nodal surface of a wave function is determined by the antisymmetric part ΦAS (because exp J ≥ 0). Thus, in FN-DMC, the accuracy of the results depends crucially on the quality of the nodes of ΦAS.
The antisymmetric part of a trial wave function is initially constructed from a mean-field self-consistent-field (SCF) approach, such as DFT or HF. The standard QMC setup in large systems is to define ΦAS as the single SD obtained from such preliminary SCF calculations. The corresponding ΨQMC is dubbed JSD. Therefore, the nodes of JSD are predefined before any QMC calculation and unrelaxed. Initializing the SD using different setups for the SCF calculations (e.g., different exchange–correlation functionals) leads to slightly different total energies, but most of the times, the interaction energies (which are evaluated from energy differences between two or more systems) are almost unaffected by the details of the preliminary SCF calculation, especially for weak noncovalent interactions. This is an indication that there is an almost perfect cancellation of the error induced by the FN approximation within the JSD ansatz, provided that the SD is initialized consistently in all systems.
However, changing the setup of the SCF calculation only allows the nodes to move within the variational freedom of a single SD. By contrast, giving ΦAS the variational freedom to relax the nodes beyond the JSD ansatz leads to an improvement of the FN-DMC total energy of the system,58 and possibly, also the interaction energies could change. The challenge that we take here is to generalize the ansatz in a way that large systems are still doable.
Here, we suggest to use the AGP ansatz as ΦAS. AGP is an implicitly multideterminant ansatz,56,59 which corresponds to a constrained zero-seniority expansion, as illustrated schematically in Figure 1. The evaluation of an AGP function can be reduced to the computation of a determinant; therefore, the AGP ansatz is computationally comparable to an SD (differently from explicitly multideterminant functions), thus ensuring the cubic scaling with the system size of both the variational and FN algorithms.e The AGP ansatz for a system of Nel electrons is
| 1 |
(we are assuming for simplicity an unpolarized
system with an even number of electrons, but the ansatz can be generalized
as discussed in ref (19)), where  is the antisymmetrization operator and
the function g is the geminal function
is the antisymmetrization operator and
the function g is the geminal function 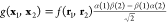 , which is a pairing function between two
electrons with coordinates x1 and x2 forming a spin singlet. The spatial part f(r1, r2) is symmetric,
and it can be written in terms of a basis set {χμ} for the single-electron orbital space as follows:
, which is a pairing function between two
electrons with coordinates x1 and x2 forming a spin singlet. The spatial part f(r1, r2) is symmetric,
and it can be written in terms of a basis set {χμ} for the single-electron orbital space as follows:
| 2 |
where μ and ν run over all the L basis orbitals and cμν are variational parameters. Notice that in general, L ≫ N, and the number of variational parameters cμν is equal to L2. The parameters define a L × L symmetric matrix C (the symmetry of f implies cμν = cνμ), so there is an orthogonal transformation U which diagonalizes C and allows rewriting f as
| 3 |
where ϕμ = ∑νUμνχν. With no loss of generality, we can assume
that λs are ranked in a decreasing order of their absolute value.
Notice that if only the first Nel/2 λs
are different from zero, then ΨAGP corresponds to
a single SD built on the orbitals 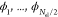 occupied with both spin-up and spin-down
electrons. Since such an SD built on orbitals from an SCF calculation
is the standard QMC setup, and it typically delivers good results,
we tried to relax the nodes by considering a subset norb (larger than Nel/2 but
≪ L) of the orbitals obtained from the SCF
calculation. This is what we call the AGPn ansatz.
occupied with both spin-up and spin-down
electrons. Since such an SD built on orbitals from an SCF calculation
is the standard QMC setup, and it typically delivers good results,
we tried to relax the nodes by considering a subset norb (larger than Nel/2 but
≪ L) of the orbitals obtained from the SCF
calculation. This is what we call the AGPn ansatz.
For efficient and effective use in QMC, the AGP and AGPn functions shall be multiplied by a Jastrow factor, yielding the so-called JAGP and JAGPn functions. The Jastrow factor can have the same variational form used also in JSD, which allows for the JSD, JAGP, and JAGPn functions to satisfy the cusp conditions and to effectively recover the dynamical correlations. Indeed, the main improvement of JAGP and JAGPn over JSD is their ability to capture static correlations, yielding to qualitatively different results on systems with an underlying multireference character, both at the variational and at the FN level of theory.56,59 The optimization of the parameters in the Jastrow is usually quite a feasible problem also on large systems, as their number does not grow uncontrollably with the size of the system. In practice, every QMC code implements a slightly different functional form of the Jastrow, but they share the general features mentioned above. The QMC code used in this work is TurboRVB,57 an open-source package. The Jastrow factor implemented in TurboRVB (described in ref (57)) has a number of parameters growing linearly with the size of the system (as shown in the Results and Discussion section).
In this work, we keep the orbital frozen and optimize the coefficients λ1, ..., λnorb of the JAGPn ansatz using FN-DMC gradients. A similar idea, but at the variational level, was also mentioned in a seminal work by Casula and Sorella to describe the BCS pairing function in iron-based superconductors.60 JAGPn dramatically reduces the number of variational parameters with respect to the JAGP ansatz, such that the optimization of the JAGPn function is doable even in pretty large systems, in contrast to JAGP which is affordable only on relatively small systems. Nevertheless, employing JAGPn significantly improves the FN-DMC energy (as well as the variational QMC energy) over the results within the traditional JSD function, as we will show in the results section. Of course, the JAGP ansatz has higher variational freedom than JAGPn, so JAGP can in principle improve further over JAGPn. However, in practice, we observe that FN-DMC energies obtained from the JAGP ansatz are comparable to those obtained from JAGPn on small systems (and both JAGP and JAGPn are significantly better that JSD), while, in large systems, JAGP is unaffordable because the optimization can be stuck at local minima at the variational level and can become unstable at the FN level. The latter instability is probably due to insufficient signal-to-noise ratios61 that the QMC optimization always suffers from, but the origin of the instability is yet unclear. On intermediate systems, we notice that JAGP FN-DMC energy is worse than the JAGPn FN-DMC energy, as a clear indication that despite the higher variational freedom on JAGP, the optimization of that many parameters is not converging and there is too much noise on the parameters.
The main problem of the AGP ansatz (and AGPn) is that it is not size-consistent at the variational level of theory, but JAGP (JAGPn) is size-consistent if we employ a very flexible Jastrow factor.62,63 Since the FN-DMC corresponds to applying an infinitely flexible Jastrow factor to the determinant part, optimizing the AGPn parameters at the FN level ensures the size consistency of our approach.
A crucial point to make JAGPn almost as accurate as JAGP, despite employing only a small number norb of parameters λs, is to carefully choose the orbitals. We notice that the virtual orbitals obtained from SCF calculations are typically not optimal, as we need a large number of them (of the order of L) to converge to the best JAGPn FN energy. Moreover, if we cannot afford a systematic test of the convergence of norb for each system of interest, it is difficult to define a sensible criterion to decide which norb to pick. We solved both the problems by employing NOs for expanding the pairing function, instead of using MOs. NOs were constructed from second-order Møller–Plesset (MP2) calculations. This is because the MP2 unoccupied orbitals incorporate perturbation effects and are physically better than those obtained with HF or DFT,64 as shown in the Supporting Information. More specifically, we constructed NOs by diagonalizing the density matrix obtained by MP2 calculations. We also notice that a method to construct NOs should be affordable also for large systems. This is also a reason why we chose MP2 for constructing NOs in this study. In practice, from the weight of the NOs, we can easily define a cutoff value to select norb on each system, and we notice that we get to converged results already with a value of n that is not much larger than Nel/2 (norb = Nel/2 would correspond to a single SD).
3. Computational Details
We applied our scheme to planar and twisted ethylenes, eight hydrocarbons (CH4, C2H4, C2H6, C6H6, C10H8, C14H10, C18H12, and C20H10), the C60 fullerene, and water–methane dimer (see Supporting Information for their coordinates). The number of valence electrons treated in this study is 12, 12, 8, 12, 14, 30, 48, 66, 84, 90, 240, and 16, respectively. The MP2 calculations (HF and DFT calculations for comparison) to generate nodal surfaces of trial wave functions were performed using PySCF v.2.0.1.65,66 The trial wave functions were converted to the TurboRVB wave function format using TurboGenius67 via TREXIO(68) files. We employed the cc-pVQZ basis set accompanied by the ccECP pseudopotentials69 for the eight hydrocarbons and C60 fullerene, while the cc-pVTZ basis set accompanied by the ccECP pseudopotentials69 for the water–methane and for the torsion calculation of ethylene. We employed [3s], [3s1p], and [3s1p] primitive Jastrow basis for H, C, and O atoms, respectively. The Jastrow factor and the weights of the NOs in the pairing function (i.e., the nodal surface of a wave function) were optimized using the stochastic reconfiguration method70 implemented in TurboRVB57 with an adaptive hyperparameter.71 The Jastrow factor was optimized only with VMC gradients, and it was held fixed during optimization with FN gradients. The FN gradients were computed from a standard walker distribution using mixed estimators, which corresponds to method A in ref (55). The lattice-discretized version of the FN-DMC calculations (LRDMC)72,73 was used in this study. The single-shot LRDMC calculations were performed by the single-grid scheme72 with lattice spaces a = 0.30, 0.25, 0.20, and 0.10 Bohr, and the energies were extrapolated to a → 0 using f(a2) = k4·a4 + k2·a2 + k0. The LRDMC calculations for computing those gradients were performed by the single-grid scheme72 with lattice space a = 0.20 Bohr. The determinant locality approximation (DLA)18 was employed for the LRDMC calculations.f We notice that the LRDMC framework guarantees the variational principle even with the presence of nonlocal pseudopotentials, as proven in the Appendix. The molecular structures are depicted using VESTA.74
4. Results and Discussion
4.1. FNAGPAS Captures Strong Correlation
We show that the proposed FNAGPAS is able to incorporate the correlation effect that the JSD ansatz cannot do at all. We apply our scheme for the torsion energy estimation of ethylene (C2H4). The torsion energy is defined as the energy difference between the GS ethylene structure (denoted as planar ethylene) and the orthogonally rotated ethylene structure (denoted as twisted ethylene), which are both shown in the inset of Figure 2. Here, we consider only the singlet states for both configurations. It was shown59 that the JSD ansatz cannot describe the torsion energy correctly since the ansatz cannot consider the static electronic correlation of the twisted ethylene, which has a diradical character. This is true both at the variational and at the FN level of theory.59 The lack of reliability in the FN results based on a JSD ansatz indicates that projection schemes cannot recover strong correlation if the FN constraints are given from a wave function with qualitative issues, due to the constraint on the projection coming from the trial wave function. Thus, the way to improve the quality of the FN results is to adopt a more general ansatz, able to improve the nodes of the trial wave function and enhance the reliability of FN estimations.
Figure 2.
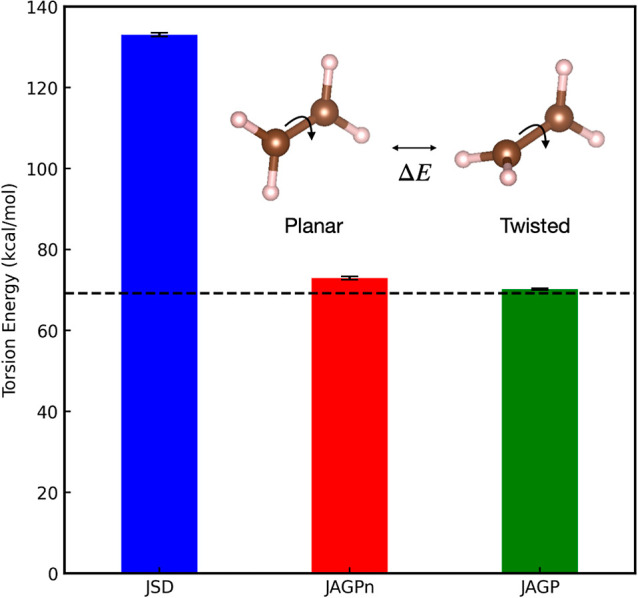
Torsion energy of ethylene from FN-DMC with JSD, JAGPn or JAGP wave functions. The values of JAGP and MR-CISD + Q (horizontal broken line) are taken from refs (59 and 76), respectively. The inset shows the structure of the planar and twisted ethylene.
The planar ethylene has an electronic structure characterized by a highest occupied MO (HOMO) of type π and a lowest unoccupied MO (LUMO) of type π*, and the HOMO–LUMO gap is finite. A single SD having two electrons of unlike spin on the HOMO and no electrons on the LUMO captures qualitatively well the nature of the wave function and there is no static correlation. However, when the molecule is twisted, the HOMO–LUMO gap decreases because the overlap between the p orbitals (orthogonal to the plane of the −CH2 atoms) of the two carbons decreases. At a torsional angle of 90° (i.e., twisted ethylene), the two p orbitals become orthogonal and the frontier orbitals become degenerate, forming two singly occupied MOs. We can define three independent (orthogonal) wave functions having two electrons on two degenerate orbitals forming a spin singlet, a diradical, and two zwitterionic states.75 Their wave functions imply the use of more than one SD, i.e., their electronic structure shows strong correlation. Thus, a multireference ansatz is needed to correctly describe the diradical character of the orthogonally twisted ethylene.59
Figure 2 shows the torsion energies of ethylene computed with the JSD ansatz with an HF nodal surface and the same energies computed with the JAGPn ansatz with HF MOs,g whose weights are optimized using DMC gradients. As a comparison, we also show results obtained with the full JAGP ansatz optimized using VMC gradients, which was taken from ref (59). The reference value in Figure 2 is taken from ref (76), and it is computed using MR-CISD + Q.h The JSD ansatz gives 133.1(4) kcal/mol for the torsion energy, which is far from the reference value obtained by MR-CISD + Q (i.e., 69.2 kcal/mol76). Our JAGPn ansatz gives an FN energy of 73.0(4) kcal/mol for the torsion energy, which is close to the reference values. This result demonstrates that the JAGPn ansatz optimized using FN gradients correctly describes the diradical character of the orthogonally twisted ethylene, something that the JSD ansatz cannot do.
4.2. Application of FNAGPAS to Small and Large Systems
We now show that the FNAGPAS scheme leads to a systematic improvement over the traditional JSD ansatz in molecular systems of increasing size, showing an accuracy in line with the full JAGP ansatz (and better on systems where the optimization error for the JAGP ansatz is large), while being affordable on much larger systems. We consider the eight hydrocarbons and the C60 fullerene, represented in Figure 3.
Figure 3.
Molecular systems considered in this work, whose FN energy has been computed with the traditional JSD ansatz and with the JAGPn ansatz (within the FNAGPAS scheme) discussed in this work. The energy gain (i.e., the improvement of the FNAGPAS scheme over the traditional scheme which employs the JSD ansatz) and the number of variational parameters in the wave function for each system are shown in Figure 4.
Figure 4 (top panel) shows the energy gain in the LRDMC total energies (a → 0) by the nodal-surface optimizations of JAGP and JAGPn over the traditional JSD ansatz (with the nodal surface taken from the DFT LDA calculations). Our proposed FNAGPAS scheme (JAGPn ansatz optimized using FN gradients) shows positive gains for all molecules, indicating that the nodal-surface optimizations improve the nodes of the SD obtained from DFT. Therefore, there is a systematic improvement in the description of the correlation energy. The energy gain scales linearly with the number of electrons in the system. The traditional JAGP ansatz (optimized using VMC gradients) was computationally affordable only on the four smallest systems, due to the rapid increase of the number of variational parameters (see the bottom panel in Figure 4), which makes the optimization unstable or not converging. In addition, we could only use VMC-opt for the JAGP ansatz because FN-opt is not stable. This highlights an additional crucial advantage of FNAGPAS over the traditional JAGP approach. In the four systems where we have both the traditional JAGP and the FNAGPAS results, the latter is equivalent to the former on ethane, and it recovers more correlation energy in methane, ethylene, and benzene. Larger systems were computationally unaffordable with JAGP, while JAGPn optimization remains feasible both at the variational and at the FN level. In fact, FNAGPAS has been successfully performed up to C60 fullerene. The gain in C60 is ∼2 meV/valence electron, as shown in the inset of Figure 4. This is a reasonable value, considering a previous study by Marchi et al. reporting ∼3 meV/valence electron for the finite-size graphene calculations with the same atoms as the C60.77
Figure 4.
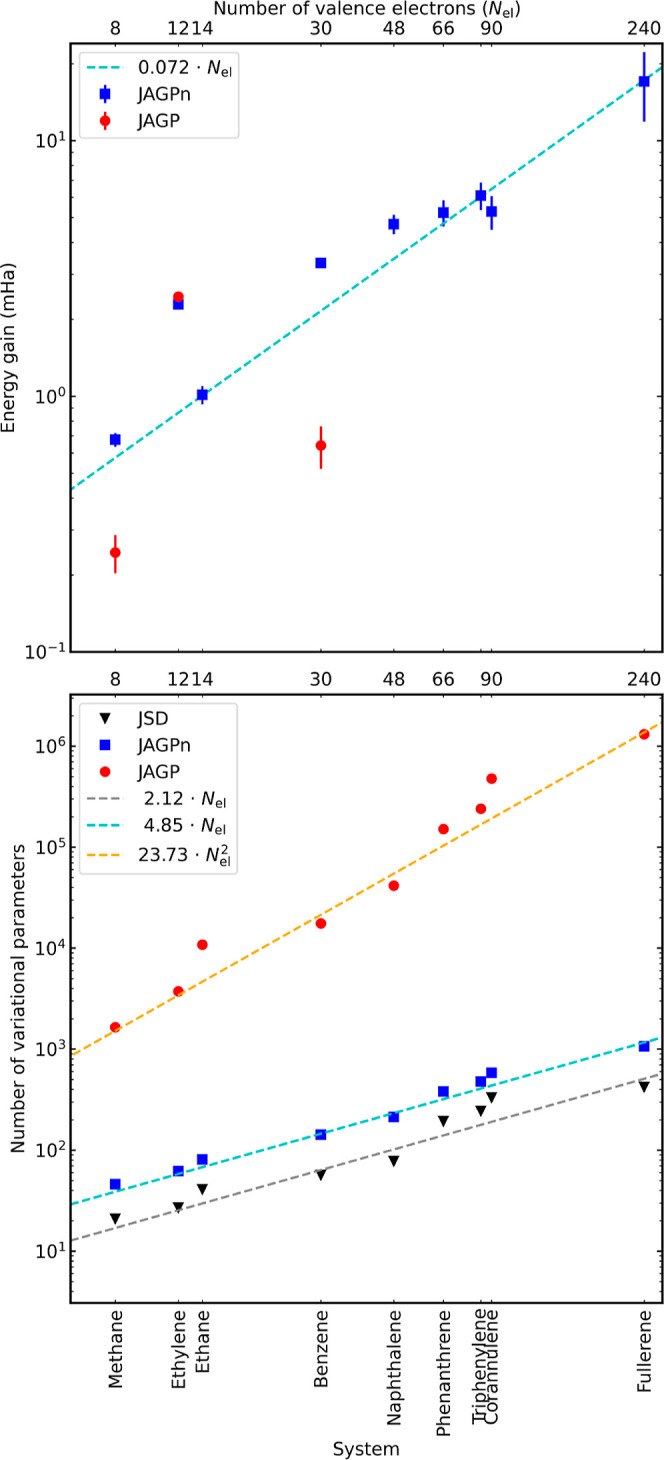
Top panel shows the improvement, dubbed energy gain, of the JAGP (red) and JAGPn (blue) ansatz with respect to the traditional JSD ansatz for each of the considered systems, as a function of the number of valence electrons. The energy gain is the difference between FN energy of the JSD ansatz and the JAGP (or JAGPn) ansatz. The bottom panel shows the number of parameters in the Jastrow factor, in the JAGP, and in the JAGPn wave functions. The dashed lines show the linear (gray for JSD and cyan for JAGPn) and quadratic (orange for JAGP) fitting curves.
Let us consider more closely the medium-size molecules. Figure 4 shows that the gains of JAGPn (optimized with FN gradients) are larger than those of JAGP (optimized using VMC gradients) in spite of the compactness of the AGPn ansatz. In fact, the number of variational parameters in the benzene molecule is 86 for the JAGPn ansatz and is 17,629 for the JAGP ansatz. Moreover, JAGP is a generalization of JAGPn. Therefore, one could naively expect that the larger the number of variational parameters, the lower the energy. Here, we observe an exception to this expectation. For this point, we recall that the calculations reported in Figure 4 are obtained with a quite small Jastrow factor, employing a [3s1p] basis set for C atoms and a [3s] for H atoms. This is because we target large systems with FNAGPAS, for which the use of large Jastrow factors is unaffordable. It has been reported that an incomplete Jastrow factor leads to misdirection of the nodal surface within the variational optimization of the JAGP ansatz in the square H4.78 To confirm if this is the case in the present calculations, we performed additional calculations with a larger Jastrow factor in the JAGP ansatz calculations (i.e., a basis set of [4s3p1d] and [3s1p] for C and H atoms, respectively) and obtained that the larger Jastrow factor leads to a much larger energy gain than that obtained with the JAGP ansatz with a small Jastrow [see results in the Supporting Information (Table S-I and Figure S-I)]. The result indicates that the small Jastrow factor leads to misdirection of the nodal surface of the JAGP ansatz also in this study. On the other hand, Figure 4 demonstrates that the FNAGPAS scheme works even with a small Jastrow factor and a minimal number of parameters in the antisymmetric part, making the approach applicable to larger systems.
As mentioned in the method part, see Section 2, the two main features over which FNAGPAS is built are (1) the AGPn ansatz and (2) the optimization of its nodal surface using FN gradients. To reveal which of the two is more crucial for the success of the method, i.e., the ansatz or the gradient, we tried the following combinations: (i) JAGPn with VMC-opt; (ii) JAGPn with FN-opt, (iii) JAGP with VMC-opt; and (iv) JAGP with FN-opt. Note that (ii) corresponds to FNAGPAS. The scheme (iv), unfortunately, is not possible as the JAGP has too many parameters and the FN optimization becomes unstable. Results obtained with schemes (i–iii) are reported in the Supporting Information (Table S-I and Figure S-I). We observe that scheme (ii) gives the best gains. Scheme (i) gives gains close to (ii), and they both are much better than (iii). Thus, it appears that freezing the orbitals to those obtained by a mean-field approach plays a crucial role in avoiding misdirection of the node optimization.
4.3. FNAGPAS Scheme Is Size-Consistent
We have shown that the AGPn ansatz is able to gain correlation energies at the FN level using very few variational parameters. In addition to their role in improving the nodal surface, FN gradients also appear to be crucial when calculating binding energies of molecules, preserving size consistency. As shown in Table 1 and discussed hereafter for the particular case of the water–methane dimer, this is not the case when VMC gradients are used. Therefore, when calculating binding energies of molecules, the use of VMC gradients in the JAGPn ansatz gives incorrect results, while the use of FN gradients plays a crucial role in it.
Table 1. FN Binding Energy Eb and Size-Consistency Energy Error ESCE, Computed with LRDMC a → 0, as Obtained with the JSD, JAGPn, and JAGP Wave Functionsa.
| ansatz | nodes opt | Eb (meV) | ESCE (meV) |
|---|---|---|---|
| JSD | –27(2) | –1(1) | |
| JAGPn | VMCopt | –46(2) | 10(2) |
| JAGPn | FNopt | –29(2) | –2(2) |
| JAGP | VMCopt | –41(3) | 11(3) |
| CCSD(T) | –27 | 0 |
For JAGPn, we consider both the case of using VMC and FN gradients to optimize the nodal surface. The latter is the scheme dubbed FNAGPAS in this work.
Table 1 contains the binding energies of the methane–water dimer computed with the JSD ansatz, with the JAGPn ansatz optimized using either VMC or FN gradients (the FNAGPAS approach), and with the JAGP ansatz optimized with VMC gradients. The binding energy is evaluated as the energy difference between the dimer and the sum of the energies of the two molecules: Eb = Ewater–methane – Ewater – Emethane. The reference value for the binding energy of the water–methane dimer, −27 meV, was computed by CCSD(T) implemented in the Orca(79,80) program.i We chose the CCSD(T) value as a reference because the bounded water–methane dimer is not a strongly correlated system, thus CCSD(T) should describe the binding energy correctly. In this system, the JSD ansatz gives a binding energy of −27(2) meV, which is in good agreement with the CCSD(T) values of −27.0 meV. Thus, a new DMC approach with nodal-surface optimization should lower the value of the total energies but should not affect the energy differences. The FNAGPAS scheme, which optimizes the JAGPn parameters with the FN gradients, behaves as expected, yielding a binding energy of −29(2) meV, still in good agreement with the reference value. However, this is not the case for the JAGPn ansatz optimized with the VMC gradients, which gives Eb = −46(2) meV, or for the JAGP ansatz (with VMC optimization), which gives Eb = −41(3) meV.
We can interpret the deterioration of the binding energy as follows: binding energies are computed from relative energies among two or more molecules; thus, the accuracy relies on its error cancellation. The error cancellation in DMC was reviewed and discussed by Dubecký in 2016.8 Their conclusion is that one can rely on error cancellation as long as one keeps the constructions and optimizations of the corresponding wave functions as systematic as possible. Indeed, this cancellation works when the nodes are kept at the same systematic accuracy at every step of the trial wave function constructions. In fact, for the water–methane dimer calculations in this study, our JSD ansatz fully satisfies the size consistency and gives satisfactory binding energy, which means that the error cancellation works with the DFT nodal surfaces. In this study, we found that error cancellation was deteriorated by the nodal-surface optimizations using the VMC gradients while recovered by those using the FN-DMC gradients. When one computes the binding energy of a complex system, one usually uses the same Jastrow basis sets for each element in the complex and the isolated systems. The use of the same Jastrow basis sets does not guarantee the same contribution to the total energy of both the complex and the isolated systems at the VMC level. Indeed, during the nodal-surface optimization at the VMC level, the incomplete Jastrow factor affects the nodal surface differently between the complex and isolated systems; thus, the resultant nodal surface gives the incorrect binding energy. The recovery should be because FN-DMC is a projection method to relax the amplitude of the AGPn ansatz, which corresponds to adding an unlimited flexible Jastrow factor to a given ansatz.
The Jastrow incompleteness is also related to the deterioration of the size consistency for JAGPn and JAGP with VMC optimization. The size consistency is a property that guarantees the consistency of the energy behavior when the interaction between the involved molecular system is nullified (e.g., by a long distance). If the size consistency is fulfilled, the energy of the far-away system should be equal to the sum of the energies of the two isolated molecules. The last column in Table 1 shows the difference in energies of the far-away water–methane complex (at a distance of ∼11 Å) and the sum of the isolated molecules, which can be considered the size-consistency error and is here dubbed ESCE. The JSD ansatz is size-consistent, as expected.81 The table clearly shows that the size consistency is deteriorated by the optimization using VMC gradients, i.e., the difference between the isolated and far-away energies is finite. In contrast, the size consistency is perfectly retrieved by the optimization using FN gradients. Neuscamman63 pointed out that the deterioration of the size consistency comes from an incomplete Jastrow factor. More specifically, the real-space three/four-body Jastrow factor, which was employed in the present study, cannot completely remove the size-consistency error unless we use unlimited flexibility in the Jastrow.63 To solve the problem, Goetz and Neuscamman proposed the so-called number-counting Jastrow factors that can suppress the unfavorable ionic terms and is able to solve the size-consistency problem82,83 within the VMC framework. In this regard, our proposed scheme can be interpreted as an alternative approach because, again, FN-DMC is a projection method to relax the amplitude of the AGPn ansatz, which corresponds to adding an unlimited flexible Jastrow factor to a given ansatz.
4.4. Discussion
First, we compare our approach with others that also target to go beyond the single-reference FN approximation. A well-established strategy is to use the multideterminant ansatz, which has witnessed numerous successes so far.84−92 The multideterminant approach offers the advantage of systematic improvement by increasing the number of SDs. Nonetheless, the number of SDs for a comprehensive representation exponentially scales with system size, imposing substantial computational demands for large systems. Therefore, this method has mainly been applied to small molecular systems.84−86 However, there have been successful efforts to reduce the number of required determinants by neglecting less important ones87,88 using, for instance, the configuration interaction using a perturbative selection made iteratively (CIPSI), which mitigates the exponential character of the multideterminant approach in practice.90,92 Recently, Benali et al. successfully applied the multideterminant approach for solids with more than a hundred electrons by combining the CIPSI technique with a restricted active space built using NOs,91 which is a similar idea as we present in this study. Indeed, they demonstrated that one can go beyond the single-reference nodal surface in large systems by the multideterminant approach in practice, though its naive asymptotic scaling is exponential. The multideterminant approach is becoming as practical and promising as the single-determinant approach.
Concerning the actual computational costs of our proposed methods, the choice of ansatz (i.e., JSD or AGPn) does not significantly affect the cost of wave function optimization, while the choice of gradients does. For instance, for C60, Jastrow optimization with the JSD ansatz and Jastrow + nodal-surface (i.e., weights of NOs) optimization with the JAGPn ansatz using VMC gradients require 11.9 and 43.6 core hours per optimization step with ∼7 mHa accuracy on the total energy evaluation at each optimization step, respectively.j However, if one uses FN gradients for wave function optimization, one needs more computational time. For instance, for C60, the nodal-surface (i.e., weights of NOs) optimization with the JAGPn ansatz using FN gradients with a = 0.20 au requires 195.3 core hours per optimization step with ∼7 mHa accuracy on the total energy evaluation at each optimization step. Thus, our FNAGPAS scheme using FN gradients shows the same scaling of the number of variational parameters as the single-reference FN DMC with JSD ansatz, while it increases the prefactor of computational cost.
Based on the results obtained in this work so far, we finally discuss how to improve a Fermionic ansatz in ab initio QMC calculations, in general. Recently, there have been many successful reports about machine-learning-inspired ansatz with a huge degree of freedom in describing electronic and spin states, such as deep neural networks,93 restricted Boltzmann machines,94−96 and transformers,97 which are utilized as ansatz of wave functions to solve the Schrödinger equation with lattice Hamiltonians. Also, in the ab initio community, ansatzes using deep neural networks have been successfully applied for realistic problems, such as PauliNet,42 FermiNet,39 and others.40,41,43−45 In light of the present results, let us consider exploiting an ansatz with a huge degree of freedom (i.e., many variational parameters) in ab initio QMC calculations to pursue an exact Fermionic GS. If we stop at the VMC level, we may apply such a flexible ansatz to Jastrow factors, the determinant part, or both parts, and it is expected that the larger the degree of freedom an ansatz has, the larger the energy gain should be. However, improvements at the VMC level do not necessarily lead to improvements at the FN level, especially if the determinant part is optimized at the variational level. A variational optimization improves the overall shape of the trial wave function ΨT, while the nodal surface might not be as optimized as the ΨT. In this work, indeed, we have seen how the JAGPn ansatz optimized at the FN level leads to much better results than the JAGP ansatz optimized at the VMC level, despite the latter having many more variational parameters and it is much better at the VMC level. Moreover, we also observed how the JAGPn (and JAGP, for that matter) ansatz itself yields a size-consistency error at the FN level if the parameters are optimized at the VMC level, while the same ansatz with parameters optimized at the FN level is not affected by this issue. Thus, caution should be used when employing these new highly flexible machine-learning-based wave function parameterizations, as it is not guaranteed that improvements in the VMC energy are reflected in improvements in the FN energy in a consistent way. Basic physical properties, which were present in the most standard wave functions (such as the JSD), might not appear in the fancier approaches, similar to the mentioned problem of size inconsistency in JAGP and JAGPn.
5. Conclusions and Perspectives
In this study, we propose a method for variational optimization of the AGP wave function expressed in terms of NOs, with pairing coefficients optimized using FN gradients. Within our scheme, the variational parameter space increases only linearly with the system size, as opposed to the quadratic scaling of the standard parameterization of AGP, with the result that our proposed method allows the optimization of the nodal surfaces for large systems, which has been difficult to achieve with conventional approaches. In addition to demonstrating that our scheme can be applied to systems as large as C60, we showed that our scheme also achieves better (i.e., lower) DMC energies than the single-reference FN DMC calculations. Moreover, we have shown that our approach is size-consistent and can be used to estimate binding energies.
We showed that the Jastrow incompleteness affecting nodal-surface optimizations can be mitigated by using FN gradients combined with the JAGPn ansatz. However, in this study, we did not investigate the effect of the basis set incompleteness on the determinant part (i.e., nodal surface). The basis set incompleteness is believed to be less severe in QMC calculations than in quantum chemistry methods because the Jastrow factor (at the variational level) or the projection (at the FN level) mitigates its error. However, to the best of our knowledge, no one has seriously investigated the error so far. Considering binding energy calculations done by DMC reported so far,8 the basis set incompleteness should have a small effect on small molecules, but it should be carefully considered when studying large molecules using DMC done with localized basis sets. This is one of the intriguing future works for applying the single-reference DMC and our proposed methods to large systems.
Acknowledgments
K.N. is grateful for computational resources from the Numerical Materials Simulator at the National Institute for Materials Science (NIMS). K.N. is grateful for computational resources of the supercomputer Fugaku provided by RIKEN through the HPCI System Research Projects (project IDs: hp220060 and hp230030). K.N. acknowledges financial support from the JSPS Overseas Research Fellowships, from Grant-in-Aid for Early Career Scientists (grant no. JP21K17752), from Grant-in-Aid for Scientific Research (grant no. JP21K03400), and from MEXT Leading Initiative for Excellent Young Researchers (grant no. JPMXS0320220025). D.A. and A.Z. acknowledge support from Leverhulme grant no. RPG-2020-038. D.A. and A.Z. also acknowledge support from the European Union under the NextGeneration EU (projects 20222FXZ33 and P2022MC742). The authors acknowledge the use of the UCL Kathleen High Performance Computing Facility (Kathleen@UCL), and associated support services, in the completion of this work. This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC05-00OR22725. Calculations were also performed using the Cambridge Service for Data Driven Discovery (CSD3) operated by the University of Cambridge Research Computing Service (www.csd3.cam.ac.uk), provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/T022159/1 and EP/P020259/1). This work also used the ARCHER UK National Supercomputing Service (https://www.archer2.ac.uk), the United Kingdom Car–Parrinello (UKCP) consortium (EP/F036884/1). We dedicate this paper to one of the authors, S.S. (SISSA), who passed away during the collaboration. He initially devised an idea to use FN gradients for wave function optimizations, which is one of the keys for the success of the present work. The QMC community will remember that he is one of the most influential contributors of the past and of the beginning of the present century to the community and in particular for deeply inspiring this work with his development of the ab initio QMC package, TurboRVB.57
Appendix
Proof for the Variational Principle of the LRDMC Optimization with DLA
As pointed out in seminal works by Casula et al.,72,98 the use of a pseudopotential that has the so-called nonlocal term induces an additional sign problem in the standard DMC approach with the LA; thus the variational principle, which justifies the energy minimization strategy, is deteriorated. Instead, one of the advantages of the LRDMC is that the use of pseudopotentials does not deteriorate the variational principle;72 thus, the energy minimization is justified. Recently, we implemented the DLA18 into the TurboRVB package. In this study, we combine the DLA with the LRDMC framework implemented in the TurboRVB package. We prove here that the variational principle holds also in the LRDMC with the DLA. This proof is inspired by the proof by Haaf et al.99 that the lattice Green’s function Monte Carlo method is variational.
In LRDMC calculations with the DLA, the effective Hamiltonian (i.e., the FN Hamiltonian) reads
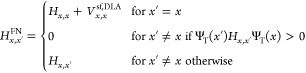 |
4 |
where 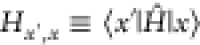 ,
, 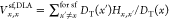 , by which the original term in the LRDMC
approach,
, by which the original term in the LRDMC
approach, 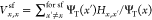 , is replaced, and sf means that all x′ (≠x) satisfy ΨT(x′)Hx,x′ΨT(x) > 0. Here, we omit the lattice-space dependency of
the
Hamiltonian (i.e., H ≡ Ha) because one can extrapolate energies to
the a → 0 limit. Notice that we assume that
a trial wave function can be decomposed into the Jastrow and determinant
parts, i.e., ΨT = JTDT. We also notice that
, is replaced, and sf means that all x′ (≠x) satisfy ΨT(x′)Hx,x′ΨT(x) > 0. Here, we omit the lattice-space dependency of
the
Hamiltonian (i.e., H ≡ Ha) because one can extrapolate energies to
the a → 0 limit. Notice that we assume that
a trial wave function can be decomposed into the Jastrow and determinant
parts, i.e., ΨT = JTDT. We also notice that
since the Jastrow factor does not affect the sign of a wave function. We define the following notations:
| 5 |
| 6 |
| 7 |
| 8 |
where |ΦFN⟩ is the FN GS of ĤFN. In the following, we will show that the following equations hold:
| 9 |
The first equality (EMA = EFN) holds because |ΦFN⟩ is the exact GS of HFN (i.e., ĤFN|ΦFN⟩ = EFN|ΦFN⟩). This is also true with the nonlocal terms of pseudopotentials. Now, we define the difference between the effective FN energy obtained with the effective Hamiltonian ĤFN and that obtained with the true Hamiltonian Ĥ:
| 10 |
We want to prove that ΔE ≥ 0 for
the FN state and that the equality holds for ΦFN =
ΨT = Ψ0, where we denote Ψ0 as the exact wave function of the original Hamiltonian Ĥ, i.e., 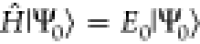 . Hereafter, we will do the same exercise
written in ref (99). We define the difference between the effective FN energy obtained
with the effective Hamiltonian HFN and
that obtained with the true Hamiltonian H:
. Hereafter, we will do the same exercise
written in ref (99). We define the difference between the effective FN energy obtained
with the effective Hamiltonian HFN and
that obtained with the true Hamiltonian H:
| 11 |
where we define a truncated Hamiltonian Htr and a spin-flip Hamiltonian Hsf by
| 12 |
and
| 13 |
Indeed, the matrix elements are
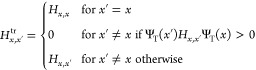 |
14 |
and
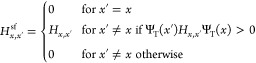 |
15 |
ΔE can be written explicitly in terms of the matrix elements:
| 16 |
This can be rewritten as
| 17 |
where sf means that all x′ (≠ x) satisfy ΨT(x′)Hx,x′ΨT(x) > 0. In this double summation, each pair of configurations (x, x′) appears twice. Therefore, we can combine these terms and rewrite it as a summation over the pairs:
| 18 |
Notice that the Hamiltonian is Hermitian: Hx,x′ = Hx′,x. Since all the pairs satisfy 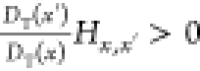 , we obtain
, we obtain
| 19 |
Then
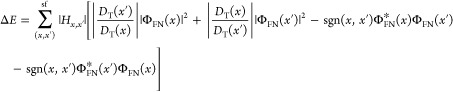 |
20 |
where sgn(x, x′) denotes the sign of Hx,x′. Finally, we get
| 21 |
indicating that ΔE is
positive for any wave function ΦFN. Thus, the GS
energy of HFN is an upper bound for the
GS energy of the original Hamiltonian H (i.e., EFN ≥ E). Hereafter,
we consider the case that one uses the true GS Ψ0 for the determinant of the trial wave function (i.e., ΨT = JT·Ψ0), to prove that EFN = E holds with ΨT = JT·Ψ0 (i.e., DT = Ψ0): For all the pairs (x, x′),
Ψ0Hx,x′Ψ0 > 0 is satisfied,
meaning
sgn(x, x′) → + and 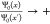 or sgn(x, x′) → – and
or sgn(x, x′) → – and 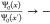 . Thus, the above condition is fulfilled
when the following condition is satisfied:
. Thus, the above condition is fulfilled
when the following condition is satisfied:
| 22 |
In the DLA approach, the spin-flip term is composed only of the determinant of the trial wave function. Therefore, the FN outcome with the DLA approach is not affected by the presence of the Jastrow factor in the trial wave function (in the a → 0 limit). Therefore, one gets ΦFN = Ψ0 with ΨT = JT·Ψ0. Thus, ΔE = 0 is fulfilled with ΨT = JT·Ψ0, and the following relations hold:
| 23 |
meaning that the effective Hamiltonian 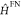 and the true Hamiltonian Ĥ have the same GS energy E0 and the same
GS ΦFN = Ψ0 with ΨT = JT ·Ψ0, where
the final equality E = E0 comes from the usual variational principle.
and the true Hamiltonian Ĥ have the same GS energy E0 and the same
GS ΦFN = Ψ0 with ΨT = JT ·Ψ0, where
the final equality E = E0 comes from the usual variational principle.
In the DLA approach,
we can update the trial wave function ΨT such that EMA goes down according
to the gradient ∂αEMA or using a more sophisticated optimization scheme. As written above,
the equals EFN = E = E0 are met when ΨT = J ·Ψ0. It implies that one can look
for the true GS energy and wave function by variation of the determinant
part of the trial wave function. Indeed, in the LRDMC calculations
with the DLA, one can access the mixed-average energy EMA and its derivative 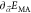 , where α⃗ is a set of the
variational parameters. Since EMA satisfies
the variational principle, i.e., EMA ≥ E0, the equality holds when ΨT = JT·Ψ0; as proven
above, one can update the determinant part of the trial wave function, DT, such that EMA goes down, then, it is expected that DT finally reaches DT → Ψ0 and EMA → E0.
, where α⃗ is a set of the
variational parameters. Since EMA satisfies
the variational principle, i.e., EMA ≥ E0, the equality holds when ΨT = JT·Ψ0; as proven
above, one can update the determinant part of the trial wave function, DT, such that EMA goes down, then, it is expected that DT finally reaches DT → Ψ0 and EMA → E0.
Data Availability Statement
The QMC kernel used in this work, TurboRVB, is available from its GitHub repository [https://github.com/sissaschool/turborvb].
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.4c00139.
Total energies and the number of variational parameters of hydrocarbons and fullerene, total energies of the methane–water complex and corresponding fragments and of the planar and twisted ethylene molecule, and discussion on the role of MOs or NOs in the AGPn ansatz and the size-consistency error (PDF)
Geometries, in xyz format, of all the systems studied (ZIP)
The authors declare no competing financial interest.
Footnotes
In all-electron calculations, FN-DMC is always variational, meaning that the lowest FN energy EFN is obtained when the exact nodal surface is used, otherwise EFN > E0. When pseudopotentials are employed, there are also nonlocal operators in the Hamiltonian. This yields to a problem similar to the sign problem, which requires a further approximation. There are a few alternatives to deal with pseudopotentials in DMC: the LA,15 the T-move (TM),16,17 the DLA, and the determinant locality TM (DLTM).18 TM and DLTM are variational, meaning that their energy (EFN,TM or EFN,DLTM) is an upper bound of the exact GS energy E0.
The Jastrow factor correlates explicitly all pairs of electrons; it is a symmetric positive function, so it recovers dynamical correlation and it does not change the nodal surface.
An approach is size-consistent if the energy of a system constituted by two or more noninteracting subsystems (e.g., two molecules far away) is the same of the sum of the energies of the subsystems.
See ref (57) for details about the functional form of terms implemented in the TurboRVB package used for this work.
It is generally claimed that the cost
of FN-DMC scales as the cube of the number of electrons Nel. This is true for simulations where the antisymmetric
part of the wave function can be computed as a determinant and Nel up to roughly a thousand. For larger systems,
the cost for a MC step is 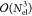 and therefore the cost of FN-DMC is quartic.
and therefore the cost of FN-DMC is quartic.
The use of DLA in LRDMC is equivalent to the DLTM18 scheme in standard DMC.
The HF orbitals obtained with the Fermi–Dirac smearing method were used for the occupied and the virtual orbitals of the JAGPn ansatz for the twisted ethylene because the HOMO and LUMO should have the same energies. Note, in this case, we did not use the NOs (introduced in the discussion above) because this system is characterized by strong correlation coming from the two frontier orbitals, which are easily derived already from the HF theory. Moreover, in the twisted ethylene case, we allowed the optimization of the off-diagonal coefficient of the AGP matrix that pairs the two frontier orbitals.
The twisted ethylene is a prototypical example of a system characterized by strong correlation where single-reference perturbative approaches, such as CCSD(T), fail and multireference approaches are needed.
In particular, we performed canonical CCSD(T) calculations with the automatic basis set extrapolation implemented in Orca (which assumes an exponential convergence for the HF energy and a polynomial convergence for the correlation energy) using Dunning correlation-consistent core-polarized basis sets, cc-pCVnZ, with quadruple-ζ (n = Q) and quintuple-ζ (n = 5) basis sets. We performed both estimations with and without counterpoise correction, both yielding a binding energy of −27.2 meV.
We measured the computational times on the Numerical Materials Simulator at the National Institute for Materials Science (NIMS) using 1536 cores [32 nodes × Intel Xeon Platinum 8268 (2.9 GHz, 24 cores) × 2 per node].
Supplementary Material
References
- Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- Bartlett R. J.; Musiał M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. 10.1103/RevModPhys.79.291. [DOI] [Google Scholar]
- Řezáč J.; Hobza P. Describing Noncovalent Interactions beyond the Common Approximations: How Accurate Is the “Gold Standard,” CCSD(T) at the Complete Basis Set Limit?. J. Chem. Theory Comput. 2013, 9, 2151–2155. 10.1021/ct400057w. [DOI] [PubMed] [Google Scholar]
- Řezáč J.; Hobza P. Benchmark Calculations of Interaction Energies in Noncovalent Complexes and Their Applications. Chem. Rev. 2016, 116, 5038–5071. 10.1021/acs.chemrev.5b00526. [DOI] [PubMed] [Google Scholar]
- Al-Hamdani Y. S.; Tkatchenko A. Understanding non-covalent interactions in larger molecular complexes from first principles. J. Chem. Phys. 2019, 150, 010901. 10.1063/1.5075487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szalay P. G.; Müller T.; Gidofalvi G.; Lischka H.; Shepard R. Multiconfiguration Self-Consistent Field and Multireference Configuration Interaction Methods and Applications. Chem. Rev. 2012, 112, 108–181. 10.1021/cr200137a. [DOI] [PubMed] [Google Scholar]
- Foulkes W. M. C.; Mitas L.; Needs R. J.; Rajagopal G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33–83. 10.1103/RevModPhys.73.33. [DOI] [Google Scholar]
- Dubecký M.; Mitas L.; Jurečka P. Noncovalent Interactions by Quantum Monte Carlo. Chem. Rev. 2016, 116, 5188–5215. 10.1021/acs.chemrev.5b00577. [DOI] [PubMed] [Google Scholar]
- Al-Hamdani Y. S.; Rossi M.; Alfè D.; Tsatsoulis T.; Ramberger B.; Brandenburg J. G.; Zen A.; Kresse G.; Grüneis A.; Tkatchenko A.; Michaelides A. Properties of the water to boron nitride interaction: from zero to two dimensions with benchmark accuracy. J. Chem. Phys. 2017, 147, 044710. 10.1063/1.4985878. [DOI] [PubMed] [Google Scholar]
- Brandenburg J. G.; Zen A.; Fitzner M.; Ramberger B.; Kresse G.; Tsatsoulis T.; Grüneis A.; Michaelides A.; Alfè D. Physisorption of Water on Graphene: Subchemical Accuracy from Many-Body Electronic Structure Methods. J. Phys. Chem. Lett. 2019, 10, 358–368. 10.1021/acs.jpclett.8b03679. [DOI] [PubMed] [Google Scholar]
- Zen A.; Brandenburg J. G.; Klimeš J.; Tkatchenko A.; Alfè D.; Michaelides A. Fast and accurate quantum Monte Carlo for molecular crystals. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, 1724–1729. 10.1073/pnas.1715434115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Hamdani Y. S.; Nagy P. R.; Zen A.; Barton D.; Kállay M.; Brandenburg J. G.; Tkatchenko A. Interactions between large molecules pose a puzzle for reference quantum mechanical methods. Nat. Commun. 2021, 12, 3927. 10.1038/s41467-021-24119-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi B. X.; Zen A.; Kapil V.; Nagy P. R.; Grüneis A.; Michaelides A. Many-Body Methods for Surface Chemistry Come of Age: Achieving Consensus with Experiments. J. Am. Chem. Soc. 2023, 145, 25372–25381. 10.1021/jacs.3c09616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troyer M.; Wiese U. J. Computational complexity and fundamental limitations to fermionic quantum Monte Carlo simulations. Phys. Rev. Lett. 2005, 94, 170201. 10.1103/PhysRevLett.94.170201. [DOI] [PubMed] [Google Scholar]
- Mitas L.; Shirley E. L.; Ceperley D. M. Nonlocal pseudopotentials and diffusion Monte Carlo. J. Chem. Phys. 1991, 95, 3467–3475. 10.1063/1.460849. [DOI] [Google Scholar]
- Casula M. Beyond the locality approximation in the standard diffusion Monte Carlo method. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 161102. 10.1103/PhysRevB.74.161102. [DOI] [Google Scholar]
- Casula M.; Moroni S.; Sorella S.; Filippi C. Size-consistent variational approaches to nonlocal pseudopotentials: Standard and lattice regularized diffusion Monte Carlo methods revisited. J. Chem. Phys. 2010, 132, 154113. 10.1063/1.3380831. [DOI] [PubMed] [Google Scholar]
- Zen A.; Brandenburg J. G.; Michaelides A.; Alfè D. A new scheme for fixed node diffusion quantum Monte Carlo with pseudopotentials: Improving reproducibility and reducing the trial-wave-function bias. J. Chem. Phys. 2019, 151, 134105. 10.1063/1.5119729. [DOI] [PubMed] [Google Scholar]
- Casula M.; Sorella S. Geminal wave functions with Jastrow correlation: A first application to atoms. J. Chem. Phys. 2003, 119, 6500–6511. 10.1063/1.1604379. [DOI] [Google Scholar]
- Casula M.; Attaccalite C.; Sorella S. Correlated geminal wave function for molecules: An efficient resonating valence bond approach. J. Chem. Phys. 2004, 121, 7110–7126. 10.1063/1.1794632. [DOI] [PubMed] [Google Scholar]
- Marchi M.; Azadi S.; Casula M.; Sorella S. Resonating valence bond wave function with molecular orbitals: Application to first-row molecules. J. Chem. Phys. 2009, 131, 154116. 10.1063/1.3249966. [DOI] [PubMed] [Google Scholar]
- Bajdich M.; Mitas L.; Drobný G.; Wagner L. K.; Schmidt K. E. Pfaffian Pairing Wave Functions in Electronic-Structure Quantum Monte Carlo Simulations. Phys. Rev. Lett. 2006, 96, 130201. 10.1103/PhysRevLett.96.130201. [DOI] [PubMed] [Google Scholar]
- Bajdich M.; Mitas L.; Wagner L. K.; Schmidt K. E. Pfaffian pairing and backflow wavefunctions for electronic structure quantum Monte Carlo methods. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 115112. 10.1103/PhysRevB.77.115112. [DOI] [Google Scholar]
- Genovese C.; Shirakawa T.; Nakano K.; Sorella S. General Correlated Geminal Ansatz for Electronic Structure Calculations: Exploiting Pfaffians in Place of Determinants. J. Chem. Theory Comput. 2020, 16, 6114–6131. 10.1021/acs.jctc.0c00165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toulouse J.; Umrigar C. J. Full optimization of Jastrow–Slater wave functions with application to the first-row atoms and homonuclear diatomic molecules. J. Chem. Phys. 2008, 128, 174101. 10.1063/1.2908237. [DOI] [PubMed] [Google Scholar]
- Zimmerman P. M.; Toulouse J.; Zhang Z.; Musgrave C. B.; Umrigar C. J. Excited states of methylene from quantum Monte Carlo. J. Chem. Phys. 2009, 131, 124103. 10.1063/1.3220671. [DOI] [PubMed] [Google Scholar]
- Anderson A. G.; Goddard W. A. Generalized valence bond wave functions in quantum Monte Carlo. J. Chem. Phys. 2010, 132, 164110. 10.1063/1.3377091. [DOI] [PubMed] [Google Scholar]
- Braïda B.; Toulouse J.; Caffarel M.; Umrigar C. J. Quantum Monte Carlo with Jastrow-valence-bond wave functions. J. Chem. Phys. 2011, 134, 084108. 10.1063/1.3555821. [DOI] [PubMed] [Google Scholar]
- Drummond N. D.; Ríos P. L.; Ma A.; Trail J. R.; Spink G. G.; Towler M. D.; Needs R. J. Quantum Monte Carlo study of the Ne atom and the Ne+ ion. J. Chem. Phys. 2006, 124, 224104. 10.1063/1.2204600. [DOI] [PubMed] [Google Scholar]
- Ríos P. L.; Ma A.; Drummond N. D.; Towler M. D.; Needs R. J. Inhomogeneous backflow transformations in quantum Monte Carlo calculations. Phys. Rev. E 2006, 74, 066701. 10.1103/PhysRevE.74.066701. [DOI] [PubMed] [Google Scholar]
- Toulouse J.; Umrigar C. J. Optimization of quantum Monte Carlo wave functions by energy minimization. J. Chem. Phys. 2007, 126, 084102. 10.1063/1.2437215. [DOI] [PubMed] [Google Scholar]
- Seth P.; Ríos P. L.; Needs R. J. Quantum Monte Carlo study of the first-row atoms and ions. J. Chem. Phys. 2011, 134, 084105. 10.1063/1.3554625. [DOI] [PubMed] [Google Scholar]
- Clark B. K.; Morales M. A.; McMinis J.; Kim J.; Scuseria G. E. Computing the energy of a water molecule using multideterminants: A simple, efficient algorithm. J. Chem. Phys. 2011, 135, 244105. 10.1063/1.3665391. [DOI] [PubMed] [Google Scholar]
- Morales M. A.; McMinis J.; Clark B. K.; Kim J.; Scuseria G. E. Multideterminant Wave Functions in Quantum Monte Carlo. J. Chem. Theory Comput. 2012, 8, 2181–2188. 10.1021/ct3003404. [DOI] [PubMed] [Google Scholar]
- Filippi C.; Assaraf R.; Moroni S. Simple formalism for efficient derivatives and multi-determinant expansions in quantum Monte Carlo. J. Chem. Phys. 2016, 144, 194105. 10.1063/1.4948778. [DOI] [PubMed] [Google Scholar]
- Scemama A.; Applencourt T.; Giner E.; Caffarel M. Quantum Monte Carlo with very large multideterminant wavefunctions. J. Comput. Chem. 2016, 37, 1866–1875. 10.1002/jcc.24382. [DOI] [PubMed] [Google Scholar]
- Dash M.; Moroni S.; Scemama A.; Filippi C. Perturbatively Selected Configuration-Interaction Wave Functions for Efficient Geometry Optimization in Quantum Monte Carlo. J. Chem. Theory Comput. 2018, 14, 4176–4182. 10.1021/acs.jctc.8b00393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scemama A.; Giner E.; Benali A.; Loos P.-F. Taming the fixed-node error in diffusion Monte Carlo via range separation. J. Chem. Phys. 2020, 153, 174107. 10.1063/5.0026324. [DOI] [PubMed] [Google Scholar]
- Pfau D.; Spencer J. S.; Matthews A. G. D. G.; Foulkes W. M. C. Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Phys. Rev. Res. 2020, 2, 033429. 10.1103/PhysRevResearch.2.033429. [DOI] [Google Scholar]
- Li X.; Fan C.; Ren W.; Chen J. Fermionic neural network with effective core potential. Phys. Rev. Res. 2022, 4, 013021. 10.1103/PhysRevResearch.4.013021. [DOI] [Google Scholar]
- Ren W.; Fu W.; Wu X.; Chen J. Towards the ground state of molecules via diffusion Monte Carlo on neural networks. Nat. Commun. 2023, 14, 1860. 10.1038/s41467-023-37609-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermann J.; Schätzle Z.; Noé F. Deep-neural-network solution of the electronic Schrödinger equation. Nat. Chem. 2020, 12, 891–897. 10.1038/s41557-020-0544-y. [DOI] [PubMed] [Google Scholar]
- Choo K.; Mezzacapo A.; Carleo G. Fermionic neural-network states for ab-initio electronic structure. Nat. Commun. 2020, 11, 2368. 10.1038/s41467-020-15724-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R.; Ye H.; Jiang D.; Wen X.; Wang C.; Li Z.; Li X.; He D.; Chen J.; Ren W. others Forward Laplacian: A New Computational Framework for Neural Network-based Variational Monte Carlo. arXiv 2023, arXiv:2307.08214. [Google Scholar]; preprint
- von Glehn I.; Spencer J. S.; Pfau D. A self-attention ansatz for ab-initio quantum chemistry. arXiv 2022, arXiv:2211.13672. [Google Scholar]; preprint
- Sorella S.; Seki K.; Brovko O. O.; Shirakawa T.; Miyakoshi S.; Yunoki S.; Tosatti E. Correlation-Driven Dimerization and Topological Gap Opening in Isotropically Strained Graphene. Phys. Rev. Lett. 2018, 121, 066402. 10.1103/PhysRevLett.121.066402. [DOI] [PubMed] [Google Scholar]
- Nakano K.; Maezono R.; Sorella S. All-Electron Quantum Monte Carlo with Jastrow Single Determinant Ansatz: Application to the Sodium Dimer. J. Chem. Theory Comput. 2019, 15, 4044–4055. 10.1021/acs.jctc.9b00295. [DOI] [PubMed] [Google Scholar]
- Genovese C.; Shirakawa T.; Nakano K.; Sorella S. General Correlated Geminal Ansatz for Electronic Structure Calculations: Exploiting Pfaffians in Place of Determinants. J. Chem. Theory Comput. 2020, 16, 6114–6131. 10.1021/acs.jctc.0c00165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ammar A.; Giner E.; Scemama A. Optimization of Large Determinant Expansions in Quantum Monte Carlo. J. Chem. Theory Comput. 2022, 18, 5325–5336. 10.1021/acs.jctc.2c00556. [DOI] [PubMed] [Google Scholar]
- Raghav A.; Maezono R.; Hongo K.; Sorella S.; Nakano K. Toward Chemical Accuracy Using the Jastrow Correlated Antisymmetrized Geminal Power Ansatz. J. Chem. Theory Comput. 2023, 19, 2222–2229. 10.1021/acs.jctc.2c01141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reboredo F. A.; Hood R. Q.; Kent P. R. C. Self-healing diffusion quantum Monte Carlo algorithms: Direct reduction of the fermion sign error in electronic structure calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 195117. 10.1103/PhysRevB.79.195117. [DOI] [Google Scholar]
- Reboredo F. A. Systematic reduction of sign errors in many-body problems: Generalization of self-healing diffusion Monte Carlo to excited states. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 80, 125110. 10.1103/PhysRevB.80.125110. [DOI] [Google Scholar]
- Reboredo F. A.; Kim J. Generalizing the self-healing diffusion Monte Carlo approach to finite temperature: A path for the optimization of low-energy many-body bases. J. Chem. Phys. 2014, 140, 074103. 10.1063/1.4861222. [DOI] [PubMed] [Google Scholar]
- Bajdich M.; Tiago M. L.; Hood R. Q.; Kent P. R.; Reboredo F. A. Systematic reduction of sign errors in many-body calculations of atoms and molecules. Phys. Rev. Lett. 2010, 104, 193001. 10.1103/physrevlett.104.193001. [DOI] [PubMed] [Google Scholar]
- McFarland J.; Manousakis E. Gradient-descent optimization of fermion nodes in the diffusion Monte Carlo technique. Phys. Rev. A 2022, 105, 032815. 10.1103/PhysRevA.105.032815. [DOI] [Google Scholar]
- Zen A.; Coccia E.; Gozem S.; Olivucci M.; Guidoni L. Quantum Monte Carlo Treatment of the Charge Transfer and Diradical Electronic Character in a Retinal Chromophore Minimal Model. J. Chem. Theory Comput. 2015, 11, 992–1005. 10.1021/ct501122z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakano K.; Attaccalite C.; Barborini M.; Capriotti L.; Casula M.; Coccia E.; Dagrada M.; Genovese C.; Luo Y.; Mazzola G.; Zen A.; Sorella S. TurboRVB: A many-body toolkit for ab initio electronic simulations by quantum Monte Carlo. J. Chem. Phys. 2020, 152, 204121. 10.1063/5.0005037. [DOI] [PubMed] [Google Scholar]
- Annaberdiyev A.; Melton C. A.; Bennett M. C.; Wang G.; Mitas L. Accurate Atomic Correlation and Total Energies for Correlation Consistent Effective Core Potentials. J. Chem. Theory Comput. 2020, 16, 1482–1502. 10.1021/acs.jctc.9b00962. [DOI] [PubMed] [Google Scholar]
- Zen A.; Coccia E.; Luo Y.; Sorella S.; Guidoni L. Static and dynamical correlation in diradical molecules by quantum monte carlo using the jastrow antisymmetrized geminal power ansatz. J. Chem. Theory Comput. 2014, 10, 1048–1061. 10.1021/ct401008s. [DOI] [PubMed] [Google Scholar]
- Casula M.; Sorella S. Improper s-wave symmetry of the electronic pairing in iron-based superconductors by first-principles calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 155125. 10.1103/PhysRevB.88.155125. [DOI] [Google Scholar]
- Becca F.; Sorella S.. Quantum Monte Carlo Approaches for Correlated Systems; Cambridge University Press, 2017. [Google Scholar]
- Sorella S.; Casula M.; Rocca D. Weak binding between two aromatic rings: Feeling the van der Waals attraction by quantum Monte Carlo methods. J. Chem. Phys. 2007, 127, 014105. 10.1063/1.2746035. [DOI] [PubMed] [Google Scholar]
- Neuscamman E. Size Consistency Error in the Antisymmetric Geminal Power Wave Function can be Completely Removed. Phys. Rev. Lett. 2012, 109, 203001. 10.1103/PhysRevLett.109.203001. [DOI] [PubMed] [Google Scholar]
- Grüneis A.; Booth G. H.; Marsman M.; Spencer J.; Alavi A.; Kresse G. Natural orbitals for wave function based correlated calculations using a plane wave basis set. J. Chem. Theory Comput. 2011, 7, 2780–2785. 10.1021/ct200263g. [DOI] [PubMed] [Google Scholar]
- Sun Q.; Berkelbach T. C.; Blunt N. S.; Booth G. H.; Guo S.; Li Z.; Liu J.; McClain J. D.; Sayfutyarova E. R.; Sharma S.; et al. PySCF: the Python-based simulations of chemistry framework. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1340 10.1002/wcms.1340. [DOI] [Google Scholar]
- Sun Q.; Zhang X.; Banerjee S.; Bao P.; Barbry M.; Blunt N. S.; Bogdanov N. A.; Booth G. H.; Chen J.; Cui Z. H.; Eriksen J. J.; Gao Y.; Guo S.; Hermann J.; Hermes M. R.; Koh K.; Koval P.; Lehtola S.; Li Z.; Liu J.; Mardirossian N.; McClain J. D.; Motta M.; Mussard B.; Pham H. Q.; Pulkin A.; Purwanto W.; Robinson P. J.; Ronca E.; Sayfutyarova E. R.; Scheurer M.; Schurkus H. F.; Smith J. E.; Sun C.; Sun S. N.; Upadhyay S.; Wagner L. K.; Wang X.; White A.; Whitfield J. D.; Williamson M. J.; Wouters S.; Yang J.; Yu J. M.; Zhu T.; Berkelbach T. C.; Sharma S.; Sokolov A. Y.; Chan G. K. L. Recent developments in the PySCF program package. J. Chem. Phys. 2020, 153, 024109. 10.1063/5.0006074. [DOI] [PubMed] [Google Scholar]
- Nakano K.; Kohulák O.; Raghav A.; Casula M.; Sorella S. TurboGenius: Python suite for high-throughput calculations of ab initio quantum Monte Carlo methods. J. Chem. Phys. 2023, 159, 224801. 10.1063/5.0179003. [DOI] [PubMed] [Google Scholar]
- Posenitskiy E.; Chilkuri V. G.; Ammar A.; Hapka M.; Pernal K.; Shinde R.; Borda E. J. L.; Filippi C.; Nakano K.; Kohulák O.; Sorella S.; de Oliveira Castro P.; Jalby W.; Ríos P. L.; Alavi A.; Scemama A. TREXIO: A file format and library for quantum chemistry. J. Chem. Phys. 2023, 158, 174801. 10.1063/5.0148161. [DOI] [PubMed] [Google Scholar]
- Bennett M. C.; Melton C. A.; Annaberdiyev A.; Wang G.; Shulenburger L.; Mitas L. A new generation of effective core potentials for correlated calculations. J. Chem. Phys. 2017, 147, 224106. 10.1063/1.4995643. [DOI] [PubMed] [Google Scholar]
- Sorella S. Green function Monte Carlo with stochastic reconfiguration. Phys. Rev. Lett. 1998, 80, 4558–4561. 10.1103/PhysRevLett.80.4558. [DOI] [Google Scholar]
- Sorella S.; Casula M.; Rocca D. Weak binding between two aromatic rings: Feeling the van der Waals attraction by quantum Monte Carlo methods. J. Chem. Phys. 2007, 127, 014105. 10.1063/1.2746035. [DOI] [PubMed] [Google Scholar]
- Casula M.; Filippi C.; Sorella S. Diffusion Monte Carlo method with lattice regularization. Phys. Rev. Lett. 2005, 95, 100201. 10.1103/PhysRevLett.95.100201. [DOI] [PubMed] [Google Scholar]
- Nakano K.; Maezono R.; Sorella S. Speeding up ab initio diffusion Monte Carlo simulations by a smart lattice regularization. Phys. Rev. B 2020, 101, 155106. 10.1103/PhysRevB.101.155106. [DOI] [Google Scholar]
- Momma K.; Izumi F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]
- Salem L.; Rowland C. The Electronic Properties of Diradicals. Angew Chem. Int. Ed. Engl. 1972, 11, 92–111. 10.1002/anie.197200921. [DOI] [Google Scholar]
- Barbatti M.; Paier J.; Lischka H. Photochemistry of ethylene: A multireference configuration interaction investigation of the excited-state energy surfaces. J. Chem. Phys. 2004, 121, 11614–11624. 10.1063/1.1807378. [DOI] [PubMed] [Google Scholar]
- Marchi M.; Azadi S.; Sorella S. Fate of the resonating valence bond in graphene. Phys. Rev. Lett. 2011, 107, 086807. 10.1103/PhysRevLett.107.086807. [DOI] [PubMed] [Google Scholar]
- Genovese C.; Meninno A.; Sorella S. Assessing the accuracy of the Jastrow antisymmetrized geminal power in the H4 model system. J. Chem. Phys. 2019, 150, 084102. 10.1063/1.5081933. [DOI] [PubMed] [Google Scholar]
- Neese F. The ORCA program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
- Neese F. Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, 4–9. 10.1002/wcms.1327. [DOI] [Google Scholar]
- Zen A.; Sorella S.; Gillan M. J.; Michaelides A.; Alfè D. Boosting the accuracy and speed of quantum Monte Carlo: Size consistency and time step. Phys. Rev. B 2016, 93, 241118. 10.1103/physrevb.93.241118. [DOI] [Google Scholar]
- Van Der Goetz B. W.; Neuscamman E. Suppressing Ionic Terms with Number-Counting Jastrow Factors in Real Space. J. Chem. Theory Comput. 2017, 13, 2035–2042. 10.1021/acs.jctc.7b00158. [DOI] [PubMed] [Google Scholar]
- Van Der Goetz B. W.; Otis L.; Neuscamman E. Clean and Convenient Tessellations for Number Counting Jastrow Factors. J. Chem. Theory Comput. 2019, 15, 1102–1121. 10.1021/acs.jctc.8b01139. [DOI] [PubMed] [Google Scholar]
- Booth G. H.; Alavi A. Approaching chemical accuracy using full configuration-interaction quantum Monte Carlo: A study of ionization potentials. J. Chem. Phys. 2010, 132, 174104. 10.1063/1.3407895. [DOI] [PubMed] [Google Scholar]
- Petruzielo F. R.; Toulouse J.; Umrigar C. J. Approaching chemical accuracy with quantum Monte Carlo. J. Chem. Phys. 2012, 136, 124116. 10.1063/1.3697846. [DOI] [PubMed] [Google Scholar]
- Morales M. A.; McMinis J.; Clark B. K.; Kim J.; Scuseria G. E. Multideterminant wave functions in quantum Monte Carlo. J. Chem. Theor. Comput. 2012, 8, 2181–2188. 10.1021/ct3003404. [DOI] [PubMed] [Google Scholar]
- Giner E.; Scemama A.; Caffarel M. Fixed-node diffusion Monte Carlo potential energy curve of the fluorine molecule F2 using selected configuration interaction trial wavefunctions. J. Chem. Phys. 2015, 142, 044115. 10.1063/1.4905528. [DOI] [PubMed] [Google Scholar]
- Caffarel M.; Applencourt T.; Giner E.; Scemama A. Communication: Toward an improved control of the fixed-node error in quantum Monte Carlo: The case of the water molecule. J. Chem. Phys. 2016, 144, 151103. 10.1063/1.4947093. [DOI] [PubMed] [Google Scholar]
- Yao Y.; Giner E.; Li J.; Toulouse J.; Umrigar C. J. Almost exact energies for the Gaussian-2 set with the semistochastic heat-bath configuration interaction method. J. Chem. Phys. 2020, 153, 124117. 10.1063/5.0018577. [DOI] [PubMed] [Google Scholar]
- Scemama A.; Giner E.; Benali A.; Loos P.-F. Taming the fixed-node error in diffusion Monte Carlo via range separation. J. Chem. Phys. 2020, 153, 174107. 10.1063/5.0026324. [DOI] [PubMed] [Google Scholar]
- Benali A.; Gasperich K.; Jordan K. D.; Applencourt T.; Luo Y.; Bennett M. C.; Krogel J. T.; Shulenburger L.; Kent P. R.; Loos P.-F.; et al. Toward a systematic improvement of the fixed-node approximation in diffusion Monte Carlo for solids—A case study in diamond. J. Chem. Phys. 2020, 153, 184111. 10.1063/5.0021036. [DOI] [PubMed] [Google Scholar]
- Malone F. D.; Benali A.; Morales M. A.; Caffarel M.; Kent P. R. C.; Shulenburger L. Systematic comparison and cross-validation of fixed-node diffusion Monte Carlo and phaseless auxiliary-field quantum Monte Carlo in solids. Phys. Rev. B 2020, 102, 161104. 10.1103/PhysRevB.102.161104. [DOI] [Google Scholar]
- Carleo G.; Nomura Y.; Imada M. Constructing exact representations of quantum many-body systems with deep neural networks. Nat. Commun. 2018, 9, 5322. 10.1038/s41467-018-07520-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carleo G.; Troyer M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. 10.1126/science.aag2302. [DOI] [PubMed] [Google Scholar]
- Nomura Y.; Darmawan A. S.; Yamaji Y.; Imada M. Restricted Boltzmann machine learning for solving strongly correlated quantum systems. Phys. Rev. B 2017, 96, 205152. 10.1103/PhysRevB.96.205152. [DOI] [Google Scholar]
- Nomura Y.; Imada M. Dirac-Type Nodal Spin Liquid Revealed by Refined Quantum Many-Body Solver Using Neural-Network Wave Function, Correlation Ratio, and Level Spectroscopy. Phys. Rev. X 2021, 11, 031034. 10.1103/PhysRevX.11.031034. [DOI] [Google Scholar]
- Viteritti L. L.; Rende R.; Becca F. Transformer Variational Wave Functions for Frustrated Quantum Spin Systems. Phys. Rev. Lett. 2023, 130, 236401. 10.1103/PhysRevLett.130.236401. [DOI] [PubMed] [Google Scholar]
- Casula M. Beyond the locality approximation in the standard diffusion Monte Carlo method. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 161102. 10.1103/PhysRevB.74.161102. [DOI] [Google Scholar]
- Ten Haaf D. F. B.; Bemmel H. J. M. V.; Eeuwen J. M. J. V. I.; Saarloos W. V.; Ceperley D. M. Proof for an upper bound in fixed-node Monte Carlo for lattice fermions. Phys. Rev. 1995, 51, 13039. 10.1103/PhysRevB.51.13039. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The QMC kernel used in this work, TurboRVB, is available from its GitHub repository [https://github.com/sissaschool/turborvb].