Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 May 30;146(23):16184–16193. doi: 10.1021/jacs.4c04045

Cavity Quantum Electrodynamics Enables para- and ortho-Selective Electrophilic Bromination of Nitrobenzene

Braden M Weight †,*, Daniel J Weix ‡, Zachary J Tonzetich , Todd D Krauss §,∥,*, Pengfei Huo §,∥,*
PMCID: PMC11177318  PMID: 38814893

Abstract

graphic file with name ja4c04045_0005.jpg

Coupling molecules to a quantized radiation field inside an optical cavity has shown great promise to modify chemical reactivity. In this work, we show that the ground-state selectivity of the electrophilic bromination of nitrobenzene can be fundamentally changed by strongly coupling the reaction to the cavity, generating ortho- or para-substituted products instead of the meta product. Importantly, these are products that are not obtained from the same reaction outside the cavity. A recently developed ab initio approach was used to theoretically compute the relative energies of the cationic Wheland intermediates, which indicate the kinetically preferred bromination site for all products. Performing an analysis of the ground-state electron density for the Wheland intermediates inside and outside the cavity, we demonstrate how strong coupling induces reorganization of the molecular charge distribution, which in turn leads to different bromination sites directly dependent on the cavity conditions. Overall, the results presented here can be used to understand cavity induced changes to ground-state chemical reactivity from a mechanistic perspective as well as to directly connect frontier theoretical simulations to state-of-the-art, but realistic, experimental cavity conditions.

Introduction

Coupling molecules to a quantized radiation field inside an optical cavity creates a set of photon–matter hybrid states called polaritons. These polariton states hold great promise for changing chemical reactivity in a general and facile way by tuning the properties of matter as well as the properties of photons. Despite the theoretical predictions of using polaritons for novel chemistry broadly,1 what has been demonstrated experimentally largely relates to polariton-modified reaction kinetics. For example, collective couplings between the electronic excited states of fulgide or similar molecules and quantized photonic modes inside an optical cavity, so-called electronic strong coupling (ESC), were shown to both enhance or suppress photochemical isomerization reactions.2,3 In another example, vibrational excitations collectively coupled to the photonic excitations of a microcavity, commonly referred to as vibrational strong coupling (VSC), resulted in chemical kinetics that can be enhanced4,5 or suppressed.6−8 In these two collective coupling regimes, the kinetics of the reactions are changed, but importantly, there is no new type of product generated compared to the same reactions outside the cavity.

Recent theoretical investigations1,9 have suggested that the ground state of a molecular system can be significantly modified by coupling the electronic states of a molecule to a cavity photon mode.10−20 In particular, it has been shown that the cavity can modify the endo/exo selectivity of Diels–Alder reactions,21,22 modify the ground-state proton transfer reaction barriers and driving forces,15,16 and selectively control the product of a click reaction.23 Note that the cavity frequency in these studies is chosen to be in the range of electronic excitations in molecules (in terms of energy, on the order of eV), and thus, the resulting polaritonic effects are expected to be different than the more commonly explored VSC regime.6,8

In addition, for this case cavity modified ground-state chemistry does not require the usual resonance effects of light–matter interactions (i.e., frequency matching between light and matter excitations) since the cavity can directly modify how the ground state of the hybrid system couples to the molecular system through the cavity mode’s vacuum fluctuations, referred to as quantum vacuum fluctuation modified chemistry.15,21 Importantly, predictions based on single molecules coupled to a cavity are also within the reach of the magnitude of the strong coupling shown in recent experiments using a plasmonic nanocavity.24 A conceptual understanding of these recently proposed ground-state modifications due to cavity vacuum fluctuations9,15,17,21,25−27 is provided in the Theoretical Methods section. From an experimental perspective, cavity vacuum fluctuations have already been shown to modify the work function of materials inside the cavity,28 as predicted by early theory work.20

The molecule–cavity hybrid system can be described by the Hamiltonian1,9,29 in eq 2. The light–matter coupling strength is expressed as

graphic file with name ja4c04045_m001.jpg 1

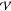where Inline graphic is the effective mode volume of the cavity, ε is the permittivity inside the cavity, and ωc is the cavity frequency. Through light–matter interactions, various photon-dressed electronic states will be coupled to each other. For example, the ground electronic state with 1 photon in the cavity and an excited electronic state with 0 photons in the cavity will couple through the light–matter interaction. When the energy of these two basis states become close, they interact (mathematically similar to the interaction of atomic orbitals to form molecular orbitals), leading to the formation of excited polariton states. These (and all similar) interactions represent the result of resonant, strong light–matter coupling, causing the formation of new eigenstates, i.e., polaritons.

Through nonresonant light–matter interactions, the cavity can directly modify the ground state of a molecule coupled to the cavity. In order to understand this effect, which is important for understanding how cavities can modify ground-state chemical reactivity, one has to go beyond the predictions of the simple Jaynes–Cummings model for light–matter interactions.30 Direct modification of polariton ground states can be caused by two physical processes:1,9,31 (i) off-resonance light–matter interactions (third term in eq 2) through the ground-state permanent dipole and optical transition dipoles between the ground and excited states and (ii) a dipole self-energy (DSE) term. The detailed theoretical arguments are provided in the Theoretical Methods section below eq 2.

In this work, we demonstrate that the strong coupling between molecule and cavity can dramatically change the reaction outcome of the bromination of nitrobenzene in its ground state. The bromination of nitrobenzene is a textbook electrophilic aromatic substitution (EAS) reaction,32,33 where meta bromination is the predominant product under many standard conditions.34−39 The observation of exclusively meta bromination has been well-explained by the relative stability of the three possible cationic intermediates of BrC6H4NO2+ (see Scheme 1) using resonance structure analysis.33,40,41 These and similar reactions have also been explored with density functional theory; although in some cases alternative mechanisms have been proposed,42−46 the Wheland intermediate explains the regiochemistry for nitrobenzene bromination in polar solvents well.

Scheme 1. Mechanism and Regiochemistry for the Bromination of Nitrobenzene.

Scheme 1

Open in a new tab

This reaction generally results in meta-substituted nitrobenzene (blue) with small or no detectable amounts of ortho- and para-products. The depicted mechanism, via a cationic intermediate, is generally used to explain this selectivity. Coupling this reaction to the cavity is predicted to change selectivity to favor the para (yellow) or ortho (orange) products.

We apply a recently developed ab initio polariton chemistry approach16 and theoretically demonstrate that coupling nitrobenzene to an optical cavity can fundamentally change the selectivity of the electrophilic bromination reaction of nitrobenzene, making ortho- or para-substituted products possible. We emphasize that these modifications are achieved for highly off-resonant cavities which generate products inside the cavity that cannot be generated under the same conditions outside the cavity. We have further provided an analysis of how coupling to the cavity will change the charge distribution of the cationic intermediate, which therefore causes a modification to the preferred bromination site. As such, strong couplings between molecules inside the cavity offer a promising tool14 to fundamentally change the outcome of known chemical reactions.

Results and Discussion

Scheme 1 presents the classic reaction mechanism of the electrophilic bromination of nitrobenzene, which first proceeds through a cationic intermediate (the so-called Wheland intermediate) PhNO2–Br+ that undergoes subsequent deprotonation to afford the product. In this work, we focus on the cavity modification of the energies of these positively charged reaction intermediates PhNO2–Br+. This molecule is accepted as the quasi-stable intermediate species in the kinetics of the bromination of nitrobenzene, and the site selectivity of halogenations of aryl species is largely dictated by this intermediate.32,40,41,47 However, recent experimental and theoretical explorations have demonstrated that other pathways, such as an addition–elimination route, maybe more favored under certain conditions.42,48,49

Outside the cavity, the meta intermediate is the most stable for nitrobenzene and provides nearly 100% selectivity due to a favorable set of possible resonance structures. On the other hand, the para- and ortho-substituted products are not observed due to the presence of high-energy resonance structures. In the case of bromination outside of the cavity, which corresponds to the parameters A0 = 0.0 a.u. and ωc = 0.0 eV in eq 2, the meta-substituted intermediate species is more thermodynamically stable compared to the ortho and para species by roughly 2 and 5 kcal/mol, respectively, confirming this classic reaction mechanism.

Coupling this intermediate with the optical cavity, we find that the energy of the ortho- and para-substituted intermediates can be lower than that of the meta-substituted species under a range of coupling strengths A0 and cavity frequencies ωc. The relative energies of different intermediates depend on the orientation of the intermediate relative to the electric field of the cavity. A more stable ortho-substituted intermediate is formed if the cavity polarization is along one direction of the molecule (blue regions in Figure 1a; Cartesian directions are defined in the inset to Scheme 1a), while the para substituent becomes stabilized for a different polarization direction (blue regions in Figure 1b).

Figure 1.

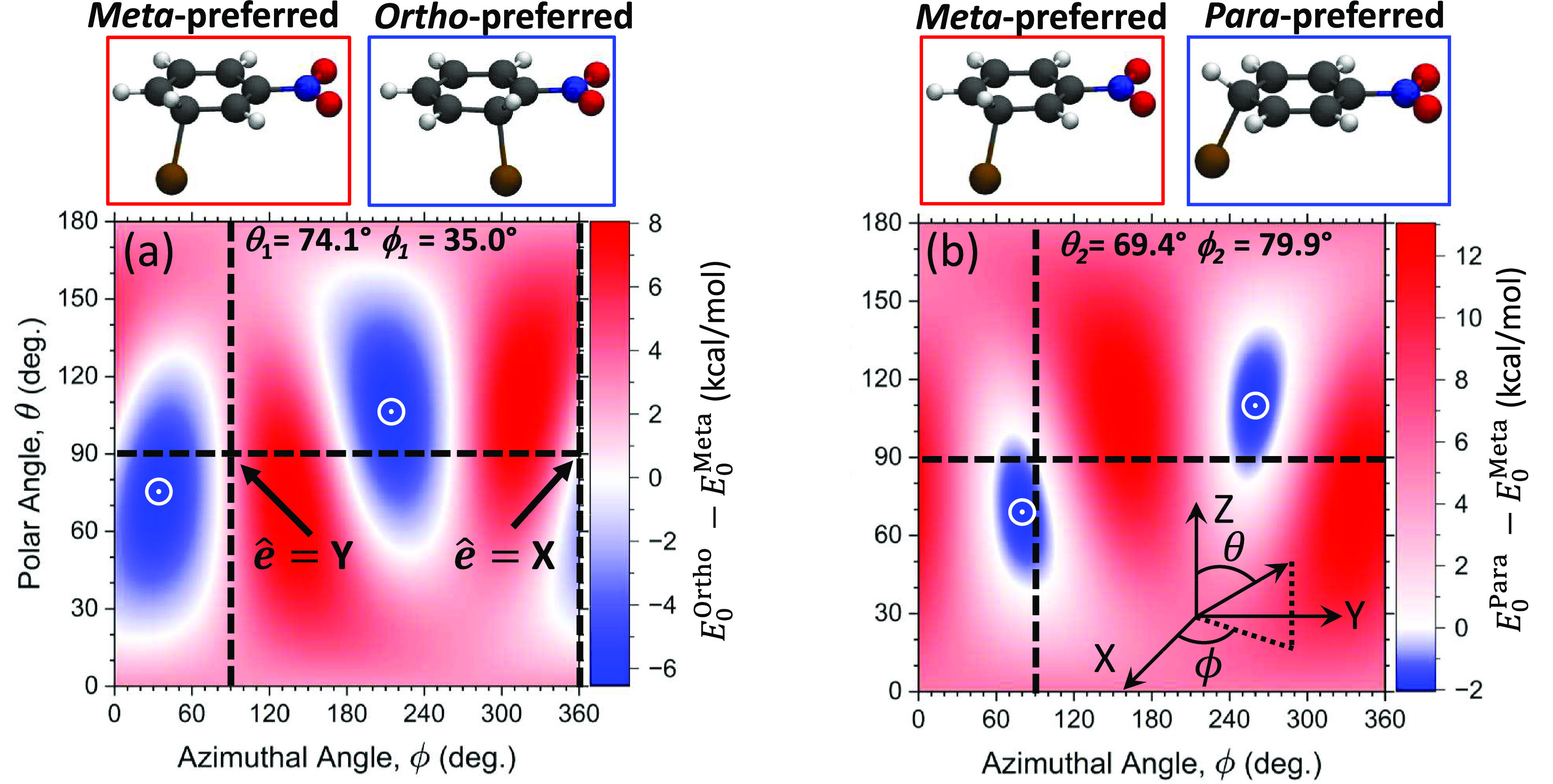
Figure 1

Open in a new tab

Relative energy of the polaritonic ground states between (a) ortho-BrC6H4NO2+ and meta-BrC6H4NO2+ and between (b) para-BrC6H4NO2+ and meta-BrC6H4NO2+ as a function of the azimuthal ϕ ∈ [0, 2π) and polar θ ∈ [0, π) angles of the cavity polarization vector with respect to the molecular Cartesian axes in the inset of panel (b). The cavity frequency and coupling strength are fixed at ωc = 1.8 eV and A0 = 0.3 a.u. (corresponding to a cavity volume of 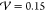Inline graphic nm3 or a field strength of 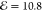Inline graphic V/nm). The minimum values of the relative energies in each case are (a) −6.43 and (b) −1.97 kcal/mol, which are denoted by white open circles.

To observe a significant change in the polaritonic ground state (due to the nonresonant light–matter coupling terms in the Hamiltonian), it generally requires a very strong light–matter interaction strength between a single molecule and the cavity mode.9,15,21 This light–matter coupling regime can be realized by using state-of-the-art plasmonic nanocavities, which provide realistic experimental parameters that were used for these simulations. In these systems,50,51 the cavity mode volume is extremely small, on the order of Å3. 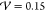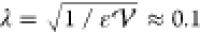For example, a recent nanocavity achieved a mode volume52 of Inline graphic nm3. The coupling strength typically required21 to observe any interesting changes to the ground state is Inline graphic a.u., corresponding to A0 ≈ 0.3 a.u. 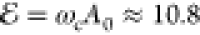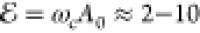or a field strength of Inline graphic V/nm that can be experimentally accomplished.24 Experimentally, the nanoparticle-on-mirror (NPoM) cavity structure53 can achieve such coupling strengths with electric field intensities Inline graphic V/nm. For the specific case of a gold plasmonic nanocavity,50,51 the cavity frequency is ωc = 1.8 eV. 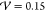These coupling strengths from NPoM cavities are also consistent with a mode volume of Inline graphic nm3.

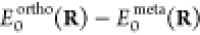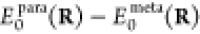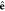Figure 1a presents the relative energetic stability of the meta and ortho cationic intermediate species, computed as Inline graphic inside the cavity as a function of θ and ϕ. Figure 1b presents the results of Inline graphic. The cavity polarization direction Inline graphic with respect to the X-, Y-, and Z-directions of the molecule is defined by the polar angle θ and the azimuthal angle ϕ (see inset to Scheme 1a and the inset of Figure 1b). 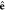In Figure 1, all possible spatial orientations of the cavity polarization direction Inline graphic with respect to the molecule are presented. 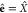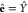When θ = 90° and ϕ = 0° (or equivalently, ϕ = 360°), Inline graphic, and when θ = 90° and ϕ = 90°, Inline graphic. Note that in the experimental setup, the cavity polarization direction is fixed50 and is related to the cavity design, whereas the molecular orientation is expected to be random unless using additional geometrical confinement.50 We want to explore all possible relative orientations between the molecule and cavity polarization. To have a simple coordinate system, we fix the molecular orientation (equivalent to defining the coordinate system with respect to the molecule) and subsequently vary the cavity polarization direction with respect to the molecular orientation, which is equivalent to having a fixed cavity polarization and varying the molecular orientation.

From Figure 1, we can see the regions (blue) of θ and ϕ where ortho- or para-substituted intermediates are more stable than the meta-substituted isomer. For example, the most stable energy for the ortho-substituted complex is achieved when θ ≈ 75° and ϕ ≈ 35°, which is 6.4 kcal/mol lower in energy than the meta-substituted complex. The most stable energy for the para-substituted complex is achieved when θ ≈ 70° and ϕ ≈ 80°, which is 2.0 kcal/mol more stable compared to the meta-substituted complex. When θ = 0° for 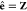Inline graphic or θ = 180° for 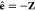Inline graphic, the cavity polarization is along Z-direction, where the molecular dipole is nearly zero and the cavity modification diminishes, as expected. The room-temperature thermal energy is kBT ≈ 0.58 kcal/mol, and for the case of bromination outside the cavity, the meta-substituted intermediate species is thermodynamically stable compared to the ortho and para species by roughly 2 and 5 kcal/mol, respectively (see Figure 4). Thus, these results suggest that by coupling the nitrobenzene molecule to an optical cavity, the preferred bromination sites can be tuned to either ortho-substituted or para-substituted, whereas outside the cavity, meta-substituted products dominate under standard conditions.32,33 As such, coupling to the cavity allows one to obtain “impossible products” (para- and ortho-substituted BrC6H4NO2+) outside the cavity. For additional comparison, Figure S10 shows the energy difference between the ortho and para species.

Figure 4.

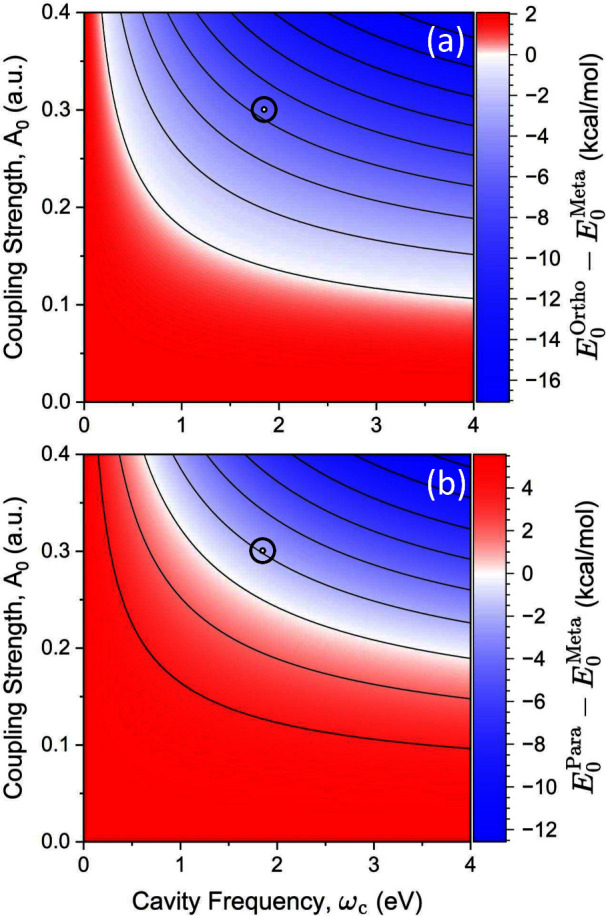
Figure 4

Open in a new tab

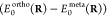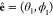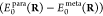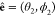(a) Relative energy of the polaritonic ground states between the ortho intermediate and the meta intermediate Inline graphic when the cavity polarization is Inline graphic. (b) Relative energy of the para intermediate and the meta intermediate Inline graphic for Inline graphic. These relative energies are reported as functions of the light–matter coupling strength A0 and cavity frequency ωc. The color scales indicate the relative energy, with red showing thermodynamic favorability for the meta-substituted cation and blue for the other. 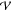The black open circles correspond to a cavity volume of Inline graphic = 0.15 nm3 and a cavity frequency of ωc = 1.8 eV. This volume corresponds to A0 = 0.3 a.u. 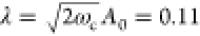and Inline graphic a.u.

For the single molecule strong coupling case, one often has to control the molecular orientation with respect to the cavity field polarization direction in order to see polaritonic effects on the chemistry. For example, recent theoretical work suggests that only when coupling to the cavity along particular electric field directions can one selectively obtain the endo or exo products of a Diels–Alder reaction,21 whereas an isotropic random orientation of the molecule will likely end up giving an equal mixture of both isomers, a situation similar to that obtained outside the cavity. Experimentally, it has been shown for a single molecule–NPoM cavity system that controlling the molecular orientation to align the molecule with the cavity field is possible.50 Nevertheless, perfectly controlling the molecular orientation in all cases is exceptionally challenging.

The currently proposed bromination reaction, on the other hand, does not require precise control of the orientation of molecules, if the goal is to obtain non-meta-substituted products in order to demonstrate the use of a cavity to enable novel bromination selectivity under standard reaction conditions. As such, randomly orientated molecules strongly coupled to the nanocavity will bias the selectivity to favor ortho- and para-substituted nitrobenzene products. On the other hand, if the objective is to only obtain either ortho- or para-substituted pure species, then one would need to either control the molecular orientation along the cavity field polarization or separate the mixture of products post-reaction, as is common for bromination of activated arenes.

To further understand the role of the optical cavity in inducing these chemical changes, we compute the ground-state electron density difference between molecules placed inside the cavity and outside the cavity. This comparison allows for a direct visualization of the cavity mediated changes to the electron density and facilitates chemical insights into the relative stability of the various substituted reaction intermediates. The difference density function of the ground state is defined as 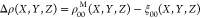Inline graphic, where 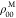Inline graphic is the polaritonic ground-state electronic density (with the photonic degrees of freedom integrated out), and ξ00 is the bare electronic ground-state density. 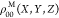Theoretical details for computing Inline graphic and ξ00(X, Y, Z) are provided in the Supporting Information. Further, a discussion regarding the contributions to the polaritonic ground-state density matrix with respect to the calculated the electronic densities can be found in the Supporting Information. To help visualize the density difference, we further integrate out the Z-direction (perpendicular to the plane of the benzene ring) and present the two-dimensional density differences, Δρ(X, Y) = ∫ dZΔρ(X, Y, Z).

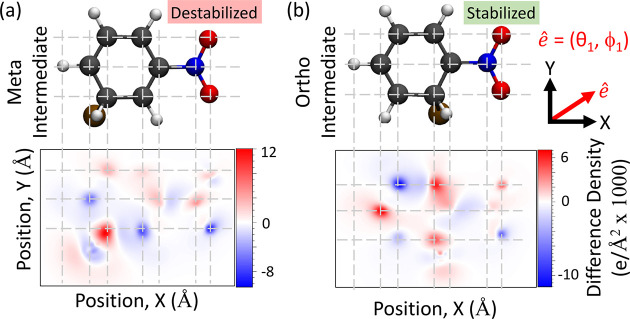
Figure 2 shows the electron density difference when the cavity polarization is along 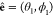Inline graphic (see Figure 1a and the inset of Figure 2b for the polarization direction projected onto the XY-plane). The rest of the parameters are the same as in Figure 1, with A0 = 0.3 a.u. and ωc = 1.8 eV. Under these conditions, the ortho-substituted Wheland intermediate becomes more stable than the meta-substituted intermediate (see Figure 1a) by ∼6.4 kcal/mol. Figure 2a shows the density difference for the meta-substituted reaction intermediate, while Figure 2b presents the density difference for the ortho-substituted reaction intermediate. The color scheme of this plot is as follows: red (positive values) indicates the accumulation of electron density, and blue (negative values) indicates the depletion of electron density upon coupling of the molecule into the cavity. Figure S3 in the Supporting Information shows data for the meta- (Figure S3a) and para-substituted (Figure S3b) intermediate species.

Figure 2.

Figure 2

Open in a new tab

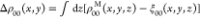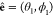Ground-state density difference Inline graphic of (a) the meta cationic intermediate and (b) the ortho cationic intermediate with a light–matter coupling strength of A0 = 0.3 a.u. and cavity frequency ωc = 1.8 eV. The cavity polarization is along Inline graphic, defined in the inset of Figure 1b, showing the projection of the polarization onto the XY-plane. The color bar indicates the magnitude and sign of the difference density Δρ00(x, y), where positive (red) indicates electron charge accumulation and negative (blue) indicates electron charge depletion upon coupling the molecule with the cavity.

Figure 2 presents the electron density difference contour maps for the meta-substituted and ortho-substituted intermediate species, depicting the cavity induced localization of the electron density accumulation (red) and depletion (blue). For the meta-substituted intermediate species, the bromine-connected carbon accumulates a large amount of electron density when coupling to the cavity, while the adjacent carbons (ortho and para carbons relative to the nitro group) exhibit strong electron density depletion. On the other hand, the ortho intermediate species in Figure 2b shows a delocalized electron density accumulation on the bromine-connected carbon and the two carbons in the meta position relative to the bromine-connected carbon. However, the electron density becomes depleted only at the para carbon relative to the bromine-connected carbon (i.e., the carbon opposite the bromine-connected carbon).

This reorganization of the electron density allows for the cavity mediated selectivity of the three cationic intermediate species. In fact, for the ortho intermediate species, one can make a direct connection to a resonance structure for the Wheland intermediate that contains a partial positive charge on the carbon opposite the bromine-connected carbon. Thus, the cavity stabilizes the ortho Wheland intermediate by shifting the electronic density to a stable resonance structure, depicted in Scheme 1d(ii), in contrast to the destabilizing resonance structure that occurs outside the cavity with a partial positive charge in the nitrogen-connected carbon, depicted in Scheme 1d(i). In other work, the reorganization of the ground-state electronic distribution inside the cavity has been theoretically observed11,14,22,54 and attributed to the exchange of character between molecular orbitals.14,22 This effect is highly system-dependent since the observed effects depend on the relative orientation and strengths of the permanent and transition dipole moments of the molecular orbitals as well as their squares through the DSE. While a general theory for how the electronic density changes inside the cavity remains unknown, it will be the subject of future work to figure out design principles for at least a given class of reactions. On the other hand, in the collective VSC regime (when ωc ≈ 0.1 eV), recent experiments55 show that the nuclear magnetic resonance (NMR) spectrum of molecules is not modified inside the cavity (i.e., there are no apparent NMR shifts under VSC), implying that the electronic density is not perturbed by the cavity under VSC conditions. This is an important distinction between the ESC and VSC coupling regimes.

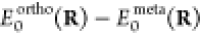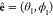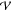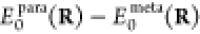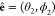Figure 3a presents the relative energetics of the ortho- and meta-substituted intermediates Inline graphic when the cavity polarization is Inline graphic (see Figure 1a) as a function of the cavity frequency ωc and the cavity mode volume Inline graphic (in units of nm3). Figure 3b presents the relative energetics of the para- and meta-substituted intermediates Inline graphic when Inline graphic (see Figure 1b). Here, we focus on the range of frequency ωc ≈ 1–4 eV, which is within the typical range possible of nanocavity designs. The cavity frequency of the NPoM cavity depends on the materials of the nanoparticle, the size of the nanoparticle, and the gap size between the particle and the mirror surface. The typical value for a gold nanoparticle is about ωc ≈ 2 eV (600 nm). The typical value for a silver nanoparticle is about ωc ≈ 2.5 eV (500 nm), and that for an aluminum nanoparticle is about ωc ≈ 3 eV (400 nm).24

Figure 3.

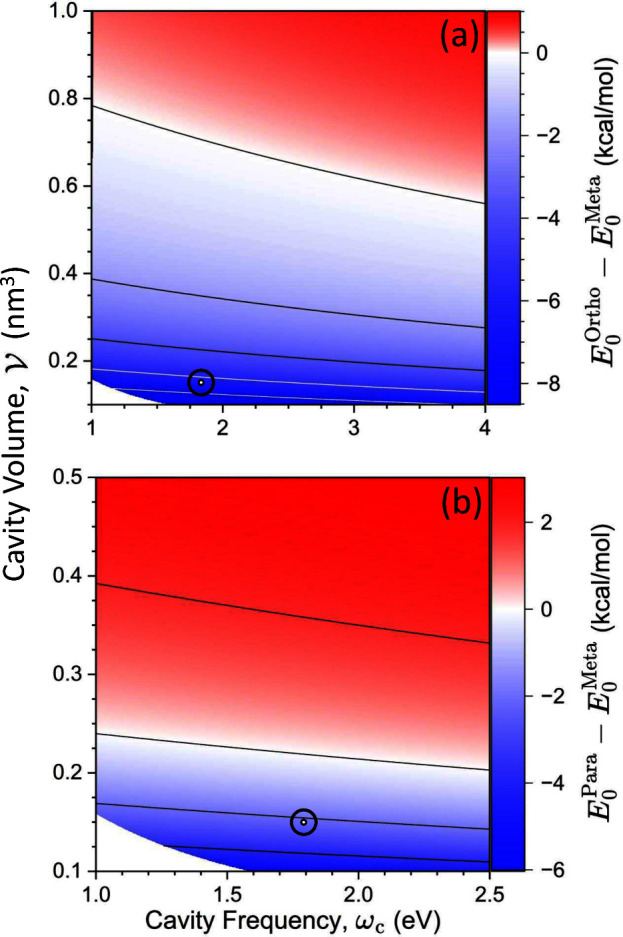
Figure 3

Open in a new tab

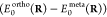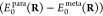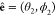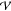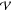(a) Relative energy of the polaritonic ground states between the ortho intermediate and the meta intermediate Inline graphic when the cavity polarization is Inline graphic. (b) Relative energy of the para intermediate and the meta intermediate Inline graphic for Inline graphic. These relative energies are reported as functions of the cavity mode volume Inline graphic and cavity frequency ωc. The color scales indicate the relative energy, with red showing thermodynamic favorability for the meta-substituted cation and blue for the other. 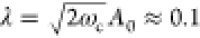The black open circles correspond to a cavity volume of Inline graphic = 0.15 nm3 and a cavity frequency of ωc = 1.8 eV. This volume corresponds to A0 = 0.3 a.u. and Inline graphic a.u.

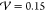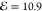In particular, for the recent experiments50,51 on a single emitter strongly coupled to the plasmonic nanocavity, with a gold nanoparticle the cavity has a frequency of ωc = 1.8 eV. Assuming a mode volume equivalent to those previously reported (Inline graphic nm3), the equivalent coupling strength is A0 = 0.3 a.u. (or λ = 0.1 a.u.), and the field intensity is Inline graphic V/nm. With these parameters, one can lower the energy of the ortho complex by 6.74 kcal/mol compared to the meta-substituted intermediate and lower the energy of the para-substituted intermediate by 2.24 kcal/mol compared to the meta-substituted intermediate. Although coupling to the cavity does not dramatically lower the energy of the ortho/para-substituted intermediates, these computed coupling strengths indicate favorability for the ortho or para products, and thus, one should expect to obtain the mixtures of these products together with the meta-substituted product.

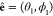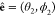Figure 4 presents the relative stability of the three positively charged intermediate species when the cavity is polarized along the Inline graphic direction (Figure 4a) or along the Inline graphic direction (Figure 4b). 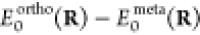Similarly to Figure 3, the relative stability is reported as the difference in the polaritonic ground state energies between the ortho and meta cationic intermediate species in Figure 4a, denoted as Inline graphic, and those between the para and meta cationic intermediate species in Figure 4b, denoted as 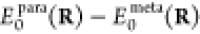Inline graphic. In addition Figure 4 depicts the stability as functions of the cavity frequency ωc and light-matter coupling strength A0.

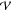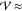The cavity induces a stabilization of the ortho (para) species in comparison to the meta by up to ∼8 kcal/mol (6 kcal/mol) with a cavity frequency of ωc = 4.0 eV (2.5 eV) and a cavity volume of Inline graphic = 0.1 nm3 (0.1 nm3). For reference, the volume of a single molecule (roughly the size of benzene) is ∼0.1 nm3. The white region indicates the turning point of the cavity mediated selectivity for each polarization. 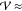For ortho/meta selectivity, the cavity is required to have a mode volume of Inline graphic 0.70 nm3 (for ωc ≈ 1.8 eV) in order to favor ortho selectivity. 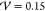For para to be the favored product over meta, the cavity is required to have (for ωc ≈ 1.8 eV) a mode volume of Inline graphic 0.225 nm3. In both panels, the open circles indicate currently accessible cavity parameters based on state-of-the-art NPoM plasmonic cavities24 and correspond to a cavity volume of Inline graphic nm3 and a cavity frequency of ωc = 1.8 eV. At these parameters and in both polarizations, we predict that the cavity is already able to provide the selectivity of this bromination reaction away from the expected meta product. Thus, our theoretical predictions should be experimentally realizable with current experimental cavity designs. The typical single molecule cavity setup in experiments is constructed by assembling an ensemble of gold nanoparticles on top of a gold mirror, creating a small confinement and large field strength between each nanoparticle and Au surface.50 Thus, there will be a large ensemble of Au particle–molecule hybrid systems on the gold surface.50 Experimentally, one should be able to characterize the non-meta product.

As an important note for the experimental design of cavities, we want to emphasize that light–matter resonance effects are not the primary mechanisms in these cavity induced modifications (Figures 3 and 4). The cavity frequency only plays a role in optimizing the magnitude of the light–matter coupling strength (eq 1). From an experimental perspective, this implies that one does not need to design the cavity with a frequency to match certain optical transitions. We expect this feature of ground state modifications via cavity quantum electrodynamics to alleviate the usual experimental difficulties associated with tuning the resonance condition between the cavity and the molecular absorption frequencies.

Conclusions

In this work, we used the ab initio cavity quantum electrodynamics (QED) approach to investigate a chemical reaction, the bromination of nitrobenzene, coupled to an optical cavity. Our approach is based on the previously developed parametrized QED (pQED) method, which uses the QED Pauli–Fierz Hamiltonian to describe light and matter interactions and uses adiabatic electronic states and all dipole matrix elements between them as inputs to compute the polariton eigenenergies.16

The bromination of nitrobenzene exhibits near 100% selectivity, favoring the meta-substituted isomer. Upon coupling to the cavity, we theoretically calculated the relative energies of the meta-, ortho-, and para-substituted cationic intermediates BrC6H4NO2+, which are key intermediates that dictate the outcome of the reaction. Outside the cavity, the meta-substituted intermediate is 2 kcal/mol lower than the ortho-substituted intermediate and about 5 kcal/mol lower than the para-substituted intermediate, in agreement with reported experimental results. 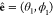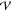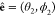Upon coupling to the cavity and aligning the cavity polarization direction along Inline graphic (see Figure 1a), the ortho-substituted intermediate is energetically more stable than the meta-substituted intermediate by up to 6 kcal/mol for a cavity frequency ωc and cavity volume Inline graphic chosen to match state-of-the-art plasmonic cavity designs.24 When the cavity polarization direction is along Inline graphic (see Figure 1b), the para-substituted intermediate is energetically more stable than the meta-substituted intermediate, with up to −2 kcal/mol. These changes in the selectivity of the various substituted intermediates are due to the quantum light–matter interactions between the molecules and cavity, which mixes the character of electronic excited states into the polariton ground state. These changes were characterized by using the electronic density difference of the system inside and outside the cavity. We thus have theoretically shown that one can obtain ortho- or para-substituted bromonitrobenzene when coupling the reaction to an optical cavity, flipping the selectivity compared to outside the cavity.

To probe the possibility of experimental realization of our theoretical prediction, we focused on the currently available plasmonic nanocavity parameters for the cavity frequency and field strength. We further scanned all possible polarization directions. Interestingly, we can find finite regions in the configuration space of polar angle and azimuthal angle that make the ortho- or para-substituted species more stable than the meta-substituted intermediate, with the largest stabilization energy of 6.43 kcal/mol (11.24 kBT at room temperature) for ortho and 1.97 kcal/mol (3.42 kBT) for para. 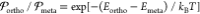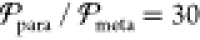The relative probability of forming the ortho- and para-substituted species is Inline graphic = ∼7 × 105 for ortho and Inline graphic for para. This implies that with the nanocavity and fully isotropic orientations of the molecule inside, one should expect to generate a non-meta-substituted product (in addition to the usual meta species), demonstrating that coupling to the cavity can make the nonstandard product, which cannot be easily obtained otherwise. More importantly, we have explicitly shown that coupling to a photonic cavity will dramatically change the selectivity. Furthermore, from an experimental perspective, detection of these anomalous products will provide conclusive evidence of the cavity mediated effects in the ground state.

From a synthetic perspective, coupling to the cavity flips the selectivity expected for electrophilic aromatic substitution in two important and useful ways. First, it flips the normal selectivity of the nitrogroup to make it an ortho/para director. Second, this approach appears to stabilize ortho substitution over para substitution. As noted above, this is also a rare selectivity that would complement existing approaches well.56

Additionally, we note that there are no obvious resonance effects in the observables presented in this work. This is because the molecule interacts through nonresonant terms such as the DSE and the indirect bilinear interactions (with examples discussed in the Theoretical Methods section). Further, when coupling N > 1 molecules with the cavity, there will be upper and lower polaritonic states, together with a dense manifold of “dark” states that contain negligible amounts of photonic character.1,57 While these dark states have been suggested to be important for excited-state dynamics, the exploration in the current work is focused on ground-state reactivities on the ground polariton state. Thus, the formation of dark states will have minimal impact on the cavity modified reactivities presented here.

Overall, this work demonstrates the possibility of polariton-mediated changes to the selectivity of well-known chemical reactions. The theoretical prediction can, in principle, be experimentally verified using state-of-the-art plasmonic nanocavity designs.

Theoretical Methods

We use the ab initio polariton approach we developed in a previous work, which we refer to as the pQED approach.16 The pQED approach uses the Pauli–Fierz Hamiltonian in the Born–Oppenheimer approximation (see eq 2) to describe light and matter interactions and uses adiabatic electronic states as the basis for the electronic degrees of freedom and Fock states as the basis for the photonic degree of freedom.

The light–matter interaction Hamiltonian under the dipole gauge1,9,29 is expressed as

graphic file with name ja4c04045_m040.jpg 2

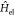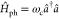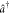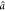where Inline graphic is the electronic Hamiltonian under the Born–Oppenheimer approximation (i.e., without the nuclear kinetic energy operator), Inline graphic is the Hamiltonian of the cavity field, Inline graphic and Inline graphic are the raising and lowering operators of the cavity field, respectively, 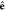Inline graphic is a unit vector indicating the field polarization direction, and 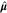Inline graphic is the dipole operator of the molecule, including, for example, permanent dipole 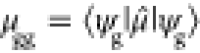Inline graphic, transition dipole 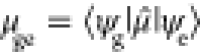Inline graphic and all other possible dipole matrix elements. Through the light–matter coupling terms in eq 2, various photon-dressed electronic states will be coupled to each other. 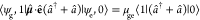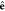For example, |ψg, 1⟩ ≡ |ψg⟩ ⊗ |1⟩ (the ground electronic state with 1 photon) and |ψe, 0⟩ ≡ |ψe⟩ ⊗ |0⟩ (an excited electronic state with 0 photons) will couple through Inline graphic, where μge is the transition dipole between the ground state and excited state projected along the Inline graphic direction. When the energy of these two basis states become close, the |ψg, 1⟩ and |ψe, 0⟩ states hybridize, leading to the formation of excited polariton states. This is the typical resonant light–matter coupling induced hybridization and generating new eigenstates and polaritons.

The direct modification of polariton ground states can be caused by two other physical processes:1,9,31 (i) off-resonance light–matter interactions (third term in eq 2) through the ground-state permanent dipole and optical transition dipoles between the ground and excited states and (ii) a dipole self-energy (DSE) term (final term in eq 2). 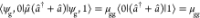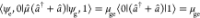For example, in (i), similarly to above, |ψg, 0⟩ will couple to the |ψg, 1⟩ state through a term proportional to Inline graphic, and |ψg, 1⟩ will couple to |ψe, 0⟩ through Inline graphic. Importantly, note that there may be many such electronic excited states ψe that contribute to the ground state through these off-resonant interactions (see the Supporting Information for details on the specific interaction terms depicted through an analysis of the ground-state density matrix). 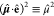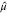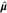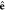In (ii), the DSE term allows for extensive coupling through the square of the electronic dipole matrix Inline graphic, where we denote Inline graphic as the projection of Inline graphic along the cavity polarization direction Inline graphic. 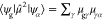The matrix elements between the ground state |ψg⟩ and any electronic state |ψα⟩ due to the DSE coupling can be expressed as Inline graphic, where α and γ include the ground and excited electronic states. The direct coupling (i) is responsible for the accumulation of photons in the ground state,10 while DSE (ii) is largely responsible for the modifications to the ground-state energy.58

The polariton eigenstates and eigenenergies are obtained by solving the following equation:

graphic file with name ja4c04045_m058.jpg 3

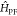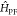where Inline graphic is given in eq 2, Ej(R) is the Born–Oppenheimer polaritonic potential energy surfaces (which parametrically depend on the nuclear coordinates R), and |Ej(R)⟩ is the polariton state. We directly diagonalize the polaritonic Hamiltonian Inline graphic matrix and obtain the eigenvalues. 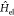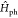The basis is constructed using the tensor product of electronic adiabatic states |ψα(R)⟩ (i.e., the eigenstates of the electronic Hamiltonian Inline graphic) and the Fock states |n⟩ (i.e., the eigenstates of the photonic Hamiltonian Inline graphic), expressed as |ψα(R)⟩ ⊗ |n⟩ ≡ |ψα(R), n⟩. 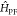This basis is used to evaluate the matrix elements of Inline graphic, and diagonalizing it provides Ej(R) and the corresponding polariton states

graphic file with name ja4c04045_m064.jpg 4

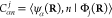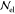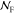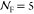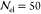where Inline graphic. Here, the number of included electronic states, Inline graphic, and photonic Fock/number states, Inline graphic, are treated as convergence parameters. A convergence test is provided in the Supporting Information, and the typical numbers of states are Inline graphic and Inline graphic. Further details regarding the pQED approach are provided in the Supporting Information. The accuracy of the above-described pQED approach has been benchmarked16 with the more accurate self-consistent QED coupled-cluster (scQED-CC) approach, where the pQED method generates nearly quantitative agreement with the scQED-CC approach.

The observations presented here, including the DSE mentioned above, go beyond the often-used classical field Hamiltonian59−62

graphic file with name ja4c04045_m070.jpg 5

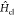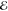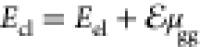where E is the classical electric field, which has also been shown to modify ground-state reactivities.59−62 Note that Inline graphic only includes a frequency independent field Inline graphic that couples only to the ground-state permanent dipole μgg of the molecule. Often, the energy of the classical Hamiltonian can be fit to a linear model: Inline graphic.59 In this case, the changes to transition state barrier heights, for example, depend on the difference in the permanent dipole moments between the reactant and transition-state geometries:59,62 ΔΔEclass ∝ Δμgg = μgg(RTS) – μgg(RReact). 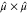As discussed above, the QED Pauli–Fierz Hamiltonian includes many other effects, such as the direct coupling between light and matter through the third term in eq 2 (resonant and off-resonant contributions), which accounts for all possible dipole matrix elements and the DSE term (fourth term in eq 2) that strongly couples the electronic states through the square of the total dipole operator Inline graphic and is thus mixing all of the electronic states. Additionally, others have noted that the inclusion of the DSE term in the Hamiltonian results in a guaranteed ground state due to the quadratic confinement of the DSE term in the dipole gauge.1,29,58,63,64 It is thus interesting to find the distinct difference between the classical field effect and the QED effect on ground-state modification in the future.

Finally, we want to mention that the DSE has the dominant contribution to the ground-state energy modifications in this work. In Figure S1 in the Supporting Information, we have analyzed energy contributions from all terms in the Pauli–Fierz QED Hamiltonian, and DSE closely follows the changes of the total energy given by the full Pauli–Fierz Hamiltonian, and all other terms cancel. Alternatively, the DSE effect can be understood from the self-consistent treatment of the ab initio QED11 from considering the mean-field approach (i.e., QED Hartree–Fock) to the Pauli–Fierz Hamiltonian. From this perspective and in the coherent state representation of the cavity mode,11,65 the bilinear light–matter coupling term can be shifted away,1 leaving only the DSE term, representing the dipole fluctuations 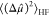Inline graphic, where 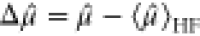Inline graphic. From this mean-field electronic perspective, cavity induced modifications only arise due to the DSE term itself. However, the pQED approach we used in the current work goes well beyond the mean-field level due to the exact diagonalization of the Pauli–Fierz Hamiltonian.16

Computational Details

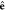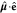All electronic structure calculations were performed using the QCHEM software package66 using linear response time-dependent density functional theory (LR-TD-DFT) and the ωB97XD hybrid exchange-correlation functional with the 6-311+G* basis set. The geometries of the BrC6H4NO2+ intermediate with various substitution positions are optimized in its electronic ground states. For cavity polarization Inline graphic along a particular direction with (θ, ϕ) angles, the Inline graphic term in eq 2 is evaluated as follows:

graphic file with name ja4c04045_m079.jpg 6

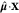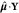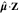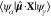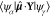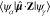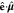where Inline graphic, Inline graphic, and Inline graphic are the dipole operators projected along the X-, Y-, and Z-directions, respectively. The matrix elements of these projected dipole operators, Inline graphic, Inline graphic, and Inline graphic, are obtained from electronic structure calculations and are used to evaluate the Inline graphic term in eq 2. The electronic excited-state energies and the molecular transition dipole matrix were computed using the QCHEM package.66

Acknowledgments

This work was supported by the National Science Foundation’s “Center for Quantum Electrodynamics for Selective Transformations (QuEST)” under Grant CHE-2124398. P.H. appreciates the support of the Cottrell Scholar Award (a program by the Research Corporation for Science Advancement). Computing resources were provided by the Center for Integrated Research Computing (CIRC) at the University of Rochester. We appreciate the helpful discussions with Arkajit Mandal, Yu Zhang, Jonas Widness, Julianna Mouat, Rachel Bangle, Rose Kennedy, and Joe Dinnocenzo.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.4c04045.

  • Details of theoretical approaches, theoretical analysis of the energy contributions for polariton ground state, additional results on density difference, convergence of the calculation with adiabatic-Fock basis, additional analysis of the ground-state density matrix, and additional results on cavity polarization (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja4c04045_si_001.pdf (4.7MB, pdf)

References

  1. Mandal A.; Taylor M. A. D.; Weight B. M.; Koessler E. R.; Li X.; Huo P. Theoretical Advances in Polariton Chemistry and Molecular Cavity Quantum Electrodynamics. Chem. Rev. 2023, 123, 9786–9879. 10.1021/acs.chemrev.2c00855. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Zeng H.; Pérez-Sánchez J. B.; Eckdahl C. T.; Liu P.; Chang W. J.; Weiss E. A.; Kalow J. A.; Yuen-Zhou J.; Stern N. P. Control of Photoswitching Kinetics with Strong Light–Matter Coupling in a Cavity. J. Am. Chem. Soc. 2023, 145, 19655–19661. 10.1021/jacs.3c04254. [DOI] [PubMed] [Google Scholar]
  3. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
  4. Lather J.; Bhatt P.; Thomas A.; Ebbesen T. W.; George J. Cavity Catalysis by Cooperative Vibrational Strong Coupling of Reactant and Solvent Molecules. Angew. Chem., Int. Ed. 2019, 58, 10635–10638. 10.1002/anie.201905407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Lather J.; Thabassum A. N. K.; Singh J.; George J. Cavity catalysis: modifying linear free-energy relationship under cooperative vibrational strong coupling. Chem. Sci. 2021, 13, 195–202. 10.1039/D1SC04707H. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Thomas A.; George J.; Shalabney A.; Dryzhakov M.; Varma S. J.; Moran J.; Chervy T.; Zhong X.; Devaux E.; Genet C.; Hutchison J. A.; Ebbesen T. W. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angew. Chem., Int. Ed. 2016, 55, 11462–11466. 10.1002/anie.201605504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Thomas A.; Jayachandran A.; Lethuillier-Karl L.; Vergauwe R. M. A.; Nagarajan K.; Devaux E.; Genet C.; Moran J.; Ebbesen T. W. Ground state chemistry under vibrational strong coupling: dependence of thermodynamic parameters on the Rabi splitting energy. Nanophotonics 2020, 9, 249–255. 10.1515/nanoph-2019-0340. [DOI] [Google Scholar]
  8. Thomas A.; Lethuillier-Karl L.; Nagarajan K.; Vergauwe R. M. A.; George J.; Chervy T.; Shalabney A.; Devaux E.; Genet C.; Moran J.; Ebbesen T. W. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science 2019, 363, 615–619. 10.1126/science.aau7742. [DOI] [PubMed] [Google Scholar]
  9. Mandal A.; Taylor M. A. D.; Huo P. Theory for Cavity-Modified Ground-State Reactivities via Electron–Photon Interactions. J. Phys. Chem. A 2023, 127, 6830–6841. 10.1021/acs.jpca.3c01421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Flick J.; Schäfer C.; Ruggenthaler M.; Appel H.; Rubio A. Ab Initio Optimized Effective Potentials for Real Molecules in Optical Cavities: Photon Contributions to the Molecular Ground State. ACS Photonics 2018, 5, 992–1005. 10.1021/acsphotonics.7b01279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Haugland T. S.; Ronca E.; Kjønstad E. F.; Rubio A.; Koch H. Coupled Cluster Theory for Molecular Polaritons: Changing Ground and Excited States. Phys. Rev. X 2020, 10, 041043. 10.1103/PhysRevX.10.041043. [DOI] [Google Scholar]
  12. Mordovina U.; Bungey C.; Appel H.; Knowles P. J.; Rubio A.; Manby F. R. Polaritonic coupled-cluster theory. Phys. Rev. Research 2020, 2, 023262. 10.1103/PhysRevResearch.2.023262. [DOI] [Google Scholar]
  13. DePrince A. E. Cavity-modulated ionization potentials and electron affinities from quantum electrodynamics coupled-cluster theory. J. Chem. Phys. 2021, 154, 094112. 10.1063/5.0038748. [DOI] [PubMed] [Google Scholar]
  14. Riso R. R.; Haugland T. S.; Ronca E.; Koch H. Molecular orbital theory in cavity QED environments. Nat. Commun. 2022, 13, 1368. 10.1038/s41467-022-29003-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Pavošević F.; Hammes-Schiffer S.; Rubio A.; Flick J. Cavity-Modulated Proton Transfer Reactions. J. Am. Chem. Soc. 2022, 144, 4995–5002. 10.1021/jacs.1c13201. [DOI] [PubMed] [Google Scholar]
  16. Weight B. M.; Krauss T. D.; Huo P. Investigating Molecular Exciton Polaritons Using Ab Initio Cavity Quantum Electrodynamics. J. Phys. Chem. Lett. 2023, 14, 5901–5913. 10.1021/acs.jpclett.3c01294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Weight B. M.; Tretiak S.; Zhang Y. Diffusion quantum Monte Carlo approach to the polaritonic ground state. Phys. Rev. A 2024, 109, 032804. 10.1103/PhysRevA.109.032804. [DOI] [Google Scholar]
  18. Severi M.; Zerbetto F. Polaritonic Chemistry: Hindering and Easing Ground State Polyenic Isomerization via Breakdown of σ – π Separation. J. Phys. Chem. Lett. 2023, 14, 9145–9149. 10.1021/acs.jpclett.3c02081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Weight B. M.; Li X.; Zhang Y. Theory and modeling of light-matter interactions in chemistry: current and future. Phys. Chem. Chem. Phys. 2023, 25, 31554–31577. 10.1039/D3CP01415K. [DOI] [PubMed] [Google Scholar]
  20. Ciuti C.; Bastard G.; Carusotto I. Quantum vacuum properties of the intersubband cavity polariton field. Phys. Rev. B 2005, 72, 115303. 10.1103/PhysRevB.72.115303. [DOI] [Google Scholar]
  21. Pavošević F.; Smith R. L.; Rubio A. Computational study on the catalytic control of endo/exo Diels-Alder reactions by cavity quantum vacuum fluctuations. Nat. Commun. 2023, 14, 2766. 10.1038/s41467-023-38474-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wang J.; Weight B.; Huo P. Investigating Cavity Quantum Electrodynamics-Enabled Endo/Exo- Selectivities in a Diels-Alder Reaction. ChemRxiv 2024, 1. 10.26434/chemrxiv-2024-6xsr6-v2. [DOI] [Google Scholar]
  23. Pavosevic F.; Smith R. L.; Rubio A. Cavity Click Chemistry: Cavity-Catalyzed Azide-Alkyne Cycloaddition. J. Phys. Chem. A 2023, 127, 10184–10188. 10.1021/acs.jpca.3c06285. [DOI] [PubMed] [Google Scholar]
  24. Akselrod G. M.; Huang J.; Hoang T. B.; Bowen P. T.; Su L.; Smith D. R.; Mikkelsen M. H. Large-Area Metasurface Perfect Absorbers from Visible to Near-Infrared. Adv. Mater. 2015, 27, 8028–8034. 10.1002/adma.201503281. [DOI] [PubMed] [Google Scholar]
  25. Vu N.; Mejia-Rodriguez D.; Bauman N.; Panyala A.; Mutlu E.; Govind N.; Foley J. Cavity Quantum Electrodynamics Complete Active Space Configuration Interaction Theory. J. Chem. Theory Comput. 2024, 20, 1214–1227. 10.1021/acs.jctc.3c01207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Li X.; Zhang Y. First-principles molecular quantum electrodynamics theory at all coupling strengths. arXiv 2023, 1. 10.48550/arXiv.2310.18228. [DOI] [Google Scholar]
  27. Cui Z.-H.; Mandal A.; Reichman D. R. Variational Lang–Firsov Approach Plus Møller–Plesset Perturbation Theory with Applications to Ab Initio Polariton Chemistry. J. Chem. Theory Comput. 2024, 20, 1143–1156. 10.1021/acs.jctc.3c01166. [DOI] [PubMed] [Google Scholar]
  28. Hutchison J. A.; Liscio A.; Schwartz T.; Canaguier-Durand A.; Genet C.; Palermo V.; Samorì P.; Ebbesen T. W. Tuning the Work-Function Via Strong Coupling. Adv. Mater. 2013, 25, 2481–2485. 10.1002/adma.201203682. [DOI] [PubMed] [Google Scholar]
  29. Taylor M. A. D.; Mandal A.; Zhou W.; Huo P. Resolution of Gauge Ambiguities in Molecular Cavity Quantum Electrodynamics. Phys. Rev. Lett. 2020, 125, 123602. 10.1103/PhysRevLett.125.123602. [DOI] [PubMed] [Google Scholar]
  30. Jaynes E. T.; Cummings F. W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. 10.1109/PROC.1963.1664. [DOI] [Google Scholar]
  31. Mandal A.; Montillo Vega S.; Huo P. Polarized Fock States and the Dynamical Casimir Effect in Molecular Cavity Quantum Electrodynamics. J. Phys. Chem. Lett. 2020, 11, 9215–9223. 10.1021/acs.jpclett.0c02399. [DOI] [PubMed] [Google Scholar]
  32. Loudon M.; Parise J. In Organic Chemistry; Macmillan Learning, 2015. [Google Scholar]
  33. Anslyn E. V.; Dougherty D. A. In Modern Physical Organic Chemistry; University Science Books, 2006. [Google Scholar]
  34. Harrison J. J.; Pellegrini J. P.; Selwitz C. M. Bromination of deactivated aromatics using potassium bromate. J. Org. Chem. 1981, 46, 2169–2171. 10.1021/jo00323a039. [DOI] [Google Scholar]
  35. Rozen S.; Brand M.; Lidor R. Aromatic bromination using bromine fluoride with no Friedel-Crafts catalyst. J. Org. Chem. 1988, 53, 5545–5547. 10.1021/jo00258a030. [DOI] [Google Scholar]
  36. Tanemura K.; Suzuki T.; Nishida Y.; Satsumabayashi K.; Horaguchi T. Halogenation of Aromatic Compounds by N-chloro-, N-bromo-, and N-iodosuccinimide. Chem. Lett. 2003, 32, 932–933. 10.1246/cl.2003.932. [DOI] [Google Scholar]
  37. Eguchi H.; Kawaguchi H.; Yoshinaga S.; Nishida A.; Nishiguchi T.; Fujisaki S. Halogenation Using N-Halogenocompounds. II. Acid Catalyzed Bromination of Aromatic Compounds with 1,3-Dibromo-5,5-dimethylhydantoin. Bull. Chem. Soc. Jpn. 1994, 67, 1918–1921. 10.1246/bcsj.67.1918. [DOI] [Google Scholar]
  38. Wang W.; Yang X.; Dai R.; Yan Z.; Wei J.; Dou X.; Qiu X.; Zhang H.; Wang C.; Liu Y.; Song S.; Jiao N. Catalytic Electrophilic Halogenation of Arenes with Electron-Withdrawing Substituents. J. Am. Chem. Soc. 2022, 144, 13415–13425. 10.1021/jacs.2c06440. [DOI] [PubMed] [Google Scholar]
  39. de Almeida L.; de Mattos M.; Esteves P. Tribromoisocyanuric Acid in Trifluoroacetic Acid: An Efficient System for Smooth Brominating of Moderately Deactivated Arenes. Synlett 2013, 24, 603–606. 10.1055/s-0032-1317795. [DOI] [Google Scholar]
  40. Chemical Reactivity Theory: A Density Functional View; Chattaraj P. K., Ed.; CRC Press, Boca Raton, Florida, U.S., 2009. [Google Scholar]
  41. Arrieta A.; Cossıo F. P. Loss of aromaticity and π-electron delocalization in the first step of the electrophilic aromatic nitration of benzene, phenol and benzonitrile. Journal of Molecular Structure: THEOCHEM 2007, 811, 19–26. 10.1016/j.theochem.2007.03.007. [DOI] [Google Scholar]
  42. Deraet X.; Desmedt E.; Van Lommel R.; Van Speybroeck V.; De Proft F. The electrophilic aromatic bromination of benzenes: mechanistic and regioselective insights from density functional theory. Phys. Chem. Chem. Phys. 2023, 25, 28581–28594. 10.1039/D3CP03137C. [DOI] [PubMed] [Google Scholar]
  43. Rohrbach S.; Murphy J. A.; Tuttle T. Computational Study on the Boundary Between the Concerted and Stepwise Mechanism of Bimolecular SNAr Reactions. J. Am. Chem. Soc. 2020, 142, 14871–14876. 10.1021/jacs.0c01975. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Moors S. L. C.; Deraet X.; Van Assche G.; Geerlings P.; De Proft F. Aromatic sulfonation with sulfur trioxide: mechanism and kinetic model. Chem. Sci. 2017, 8, 680–688. 10.1039/C6SC03500K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Van Lommel R.; Moors S. L. C.; De Proft F. Solvent and Autocatalytic Effects on the Stabilisation of the σ-Complex during Electrophilic Aromatic Chlorination. Chemistry A European J. 2018, 24, 7044–7050. 10.1002/chem.201800385. [DOI] [PubMed] [Google Scholar]
  46. Stuyver T.; Danovich D.; De Proft F.; Shaik S. Electrophilic Aromatic Substitution Reactions: Mechanistic Landscape, Electrostatic and Electric-Field Control of Reaction Rates, and Mechanistic Crossovers. J. Am. Chem. Soc. 2019, 141, 9719–9730. 10.1021/jacs.9b04982. [DOI] [PubMed] [Google Scholar]
  47. Makhloufi A.; Belhadad O.; Ghemit R.; Baitiche M.; Merbah M.; Benachour D. Theoretical and conceptual density functional theory (DFT) study on selectivity of 4-hydroxyquinazoline electrophilic aromatic nitration. J. Mol. Struct. 2018, 1152, 248–256. 10.1016/j.molstruc.2017.09.001. [DOI] [Google Scholar]
  48. Kong J.; Galabov B.; Koleva G.; Zou J.-J.; Schaefer H. F.; Schleyer P. v. R. The Inherent Competition between Addition and Substitution Reactions of Br2 with Benzene and Arenes. Angew. Chem., Int. Ed. 2011, 50, 6809–6813. 10.1002/anie.201101852. [DOI] [PubMed] [Google Scholar]
  49. Galabov B.; Koleva G.; Simova S.; Hadjieva B.; Schaefer H. F.; Schleyer P. v. R.. Arenium ions are not obligatory intermediates in electrophilic aromatic substitution. In Proceedings of the National Academy of Sciences; 2014; Vol. 111, p 10067–10072. [DOI] [PMC free article] [PubMed]
  50. Chikkaraddy R.; de Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Santhosh K.; Bitton O.; Chuntonov L.; Haran G. Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit. Nat. Commun. 2016, 7, ncomms11823. 10.1038/ncomms11823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Wu T.; Yan W.; Lalanne P. Bright Plasmons with Cubic Nanometer Mode Volumes through Mode Hybridization. ACS Photonics 2021, 8, 307–314. 10.1021/acsphotonics.0c01569. [DOI] [Google Scholar]
  53. Chen S.; Xiao Y.-H.; Qin M.; Zhou G.; Dong R.; Devasenathipathy R.; Wu D.-Y.; Yang L. Quantification of the Real Plasmonic Field Transverse Distribution in a Nanocavity Using the Vibrational Stark Effect. J. Phys. Chem. Lett. 2023, 14, 1708–1713. 10.1021/acs.jpclett.2c03818. [DOI] [PubMed] [Google Scholar]
  54. Flick J.; Ruggenthaler M.; Appel H.; Rubio A. Kohn–Sham approach to quantum electrodynamical density-functional theory: Exact time-dependent effective potentials in real space. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 15285–15290. 10.1073/pnas.1518224112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Patrahau B.; Piejko M.; Mayer R. J.; Antheaume C.; Sangchai T.; Ragazzon G.; Jayachandran A.; Devaux E.; Genet C.; Moran J.; Ebbesen T. W. Direct Observation of Polaritonic Chemistry by Nuclear Magnetic Resonance Spectroscopy. Angew. Chem., Int. Ed. 2024, 63, e202401368 10.1002/anie.202401368. [DOI] [PubMed] [Google Scholar]
  56. Srivastava S. K.; Chauhan P. M. S.; Bhaduri A. P. Novel site-specific one-step bromination of substituted benzenes. Chem. Commun. 1996, 2679–2680. 10.1039/cc9960002679. [DOI] [Google Scholar]
  57. Qiu L.; Mandal A.; Morshed O.; Meidenbauer M. T.; Girten W.; Huo P.; Vamivakas A. N.; Krauss T. D. Molecular Polaritons Generated from Strong Coupling between CdSe Nanoplatelets and a Dielectric Optical Cavity. J. Phys. Chem. Lett. 2021, 12, 5030–5038. 10.1021/acs.jpclett.1c01104. [DOI] [PubMed] [Google Scholar]
  58. Rokaj V.; Welakuh D. M.; Ruggenthaler M.; Rubio A. Light–matter interaction in the long-wavelength limit: no ground-state without dipole self-energy. J. Phys. B: At. Mol. Opt. Phys. 2018, 51, 034005. 10.1088/1361-6455/aa9c99. [DOI] [Google Scholar]
  59. Hoffmann N. M.; Wang X.; Berkelbach T. C. Linear Free Energy Relationships in Electrostatic Catalysis. ACS Catal. 2022, 12, 8237–8241. 10.1021/acscatal.2c02234. [DOI] [Google Scholar]
  60. Shaik S.; Danovich D.; Joy J.; Wang Z.; Stuyver T. Electric-Field Mediated Chemistry: Uncovering and Exploiting the Potential of (Oriented) Electric Fields to Exert Chemical Catalysis and Reaction Control. J. Am. Chem. Soc. 2020, 142, 12551–12562. 10.1021/jacs.0c05128. [DOI] [PubMed] [Google Scholar]
  61. Aragonès A. C.; Haworth N. L.; Darwish N.; Ciampi S.; Bloomfield N. J.; Wallace G. G.; Diez-Perez I.; Coote M. L. Electrostatic catalysis of a Diels–Alder reaction. Nature 2016, 531, 88–91. 10.1038/nature16989. [DOI] [PubMed] [Google Scholar]
  62. Hanaway D. J.; Kennedy C. R. Automated Variable Electric-Field DFT Application for Evaluation of Optimally Oriented Electric Fields on Chemical Reactivity. J. Org. Chem. 2023, 88, 106–115. 10.1021/acs.joc.2c01893. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Schäfer C.; Ruggenthaler M.; Rokaj V.; Rubio A. Relevance of the Quadratic Diamagnetic and Self-Polarization Terms in Cavity Quantum Electrodynamics. ACS Photonics 2020, 7, 975–990. 10.1021/acsphotonics.9b01649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Taylor M. A. D.; Mandal A.; Huo P. Resolving ambiguities of the mode truncation in cavity quantum electrodynamics. Opt. Lett. 2022, 47, 1446. 10.1364/OL.450228. [DOI] [PubMed] [Google Scholar]
  65. Philbin T. G. Generalized coherent states. Am. J. Phys. 2014, 82, 742–748. 10.1119/1.4876963. [DOI] [Google Scholar]
  66. Epifanovsky E.; Gqilbert A. T. B.; Feng X.; Lee J.; Mao Y.; Mardirossian N.; Pokhilko P.; White A. F.; Coons M. P.; Dempwolff A. L.; et al. Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package. J. Chem. Phys. 2021, 155, 084801. 10.1063/5.0055522. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja4c04045_si_001.pdf (4.7MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES