Abstract
The occurrence of wildfire threats has increased in the last few decades creating serious challenges for thousands of communities around the world. Understanding the physical and social dynamics imposed by wildfires is fundamental to assessing and reducing the ensuing risk to different communities. Although, several studies investigating household wildfire risk perception and decision-making are available in the literature, modelling solutions to predict household behaviour in wildfire scenarios are still in their early stages. Hence the lack of a behavioural model suitable for embedding within a simulation tool.
In this paper, we propose a mathematical framework aimed at simulating how householders perceive the risk associated to wildfires and how they take protective actions in response to such threats. A conceptual Wildfire Decision Model, based on nine assumptions derived from existing literature on human behaviour in wildfires, is introduced. A mathematical framework is then proposed to implement such a model within a simulation tool. The proposed modelling solution can help identify the information required to generate new dynamic and behavioural travel demand models for wildfire evacuation.
Keywords: wildfire, human behaviour, decision-making, householder, modelling
1. Introduction
The threat of wildfires and the related damage to the area where development and infrastructure are located within or adjacent to wildland vegetation, known as Wildland Urban Interface (WUI) fires, is a growing global concern [1,2]. The occurrences of these natural threats have increased in the last few decades [3,4]. Wildfires are creating serious challenges for fire and emergency response services and thousands of communities around the world [5] – in terms of required resources, responses and planning.
Understanding the physical and social dynamics characterizing wildfires is fundamental to effectively and safely respond to wildfire threats. To date, several wildfire models have been proposed in the literature to simulate fire development. Further, several engineering tools have been proposed to simulate the pedestrian and traffic evacuation dynamics of communities affected by wildfires [5]. A review of engineering tools for fire pedestrian and traffic evacuation dynamics is available in these two works [5,6]. However, these models are typically assessed based on their performance within their subject domain, rather than their potential contribution to understanding the outcome of an incident in total.
One of the major challenges in determining the outcome of an wildfire incident is understanding how households perceive wildfires and respond to them [7]. Several behavioural studies have been carried out to address this challenge by investigating household behaviours in wildfires (see for instance [8–10]), and using hypothetical studies, where participants are asked how they would behave in hypothetical wildfire scenarios [11–13]. A review of those behavioural studies and factors affecting household perception and response to wildfire is available in the work by Folk et al. [7].
Even with of the availability of several wildfire behavioural studies and engineering tools to simulate wildfire pedestrian and traffic dynamics, a complete set of tools integrating household decision-making models and large scale evacuation models is still lacking [14]. Those integrated tools, also known as dynamic travel demand models for vehicular traffic models, have been proposed for other disasters such as hurricanes and tsunami [15–19]. However, applications for wildfire emergencies are still in the early stages [5]. This is likely due to the lack of a comprehensive modelling framework aimed at providing a set of integrated tools to quantify household risk perception and response to wildfire emergencies [14,20]. A general framework has been recently proposed by Ronchi et al. [5] and Folk et al. [7]. Ronchi et al. [5] examine the type of conceptual model functionality required to produce an integrated modelling approach to wildfire evacuation. Folk et al. [7] examined the factors that should be included within a model of residential response to wildfires. However, neither developed computational structures that might quantify the response. Therefore, a mathematical framework modelling those decision-making processes is still unavailable in the literature. A model that connects external physical conditions with householder decision-making and their protective response is fundamental to the creation of an integrated approach.
As such, there is the need for a numerical framework to bridge this gap. This framework will have practical significance in the field as it will allow for the quantitative assessment of the wildfire risk by running more evidence-based wildfire evacuation simulations. Moreover, such a framework, once calibrated using data-sets from different case studies, will allow for the identification of the factors that affect decision-making during wildfires and how these people respond to different information provided by authorities (via warnings, etc.). As such this framework may help emergency planning and for the design of warnings and education campaigns to community currently under threat of wildfire, as well as to identify people who need more support and guidance in future wildfire events.
The goal of this paper is to present a mathematical framework aimed at simulating how householders perceive the risk associated with wildfires and how they take protective actions to respond to such threats. In this paper, we introduce a conceptual Wildfire Decision Model based on nine assumptions. These assumptions are inspired and guided by the literature on human behaviour in wildfires. The proposed modelling framework is a tool that is useful to generate new dynamic travel demand models for large-scale wildfire evacuations. Further, this work provides mathematical specifications that are based on the existing engineering models developed for other large-scale emergencies such as hurricanes. As such, this represents one of the first attempts to develop a mathematical framework that can be used for engineering purposes, once it is calibrated for different case studies, to identify the decisions made by householders while threatened by a wildfire emergency. The proposed solution will enhance wildfire evacuation simulations allowing modellers to predict the decision to stay or leave and the decision of when to leave. To date, these decisions are only assumed by the modeller as an input instead of being simulated [21–26].
By identifying gaps in our current understanding, the development of the modelling framework also suggests data sources required in future data collection exercises. To date, several data-sets have been collected to investigate specific aspects of householders’ attitudes [8,12], decision delay [13,27], and response strategies [9–11,28,29]. However, those data-sets are not sufficient to calibrate and validate a comprehensive householder decision-making model.
2. Background
Models that address human behaviour in wildfires are key to assessing the safety of communities affected by those natural threats. To date, several studies are available that present conceptual models and behavioural results which identify factors affecting householder decision-making.
One of the most well know conceptual models describing individual responses to environmental hazards and disaster scenarios is the Protective Action Decision Model (PADM) by Lindell and Perry [30], which. identifies the flow of information from the receipt of a cue to individual protective action. This model has been modified by Cova et al. [31] to represent specifically householders’ behaviour facing a wildfire emergency. This was achieved by developing a flow chart consisting of a series of binary decisions (i.e., yes vs no) aimed at identifying whether a householder will choose to Shelter in Place (SIP), defend the property, shelter in a refuge, or evacuate.
There are a number of conceptual models presented in the research literature [32–36] that attempt to describe or explain human behaviour in fire. These models tend to focus on one of the following: the overall process (e.g. [37–40]) providing limited detail about decision-making processes in any given situation, a single aspect of the decision-making process [41], or one specific incident (e.g. [34]).Each type of model needs to be coupled with other data sources and theories to support the development of a more comprehensive conceptual model.
For instance, the work of Breaux et al. identified key stages in the individual decision-making process (recognition/interpretation, behaviour, and the outcome of the action), with inputs such as, past experiences, situational factors, and the individual’s current status included as factors that impact the recognition/interpretation process [39]. Following this, Canter et al. produced a theoretically-based model to represent the major evacuation action sequences, based on a person receiving information, interpreting the information, preparing to act on the information and then performing the action [37,38]. Although an important advance in understanding evacuee decision-making, the Canter et al. model cannot be implemented given the lack of detailed information on specific elements and the subsequent influence on action phases.
Research into disasters, based on theories from the social sciences, has led to the development of conceptual models describing the decision-making process for public warning response, where people go through several phases (e.g. hearing, understanding, believing, and personalizing the warning) [32,33,42–44].
Ronchi et al. [5] reviewed numerous articles (including the work of Lindell et al. and Cova et al.) that present alternative descriptions of the resident decision-making process and the factors that affect them. For instance, Murray-Tuite and Wolshon [45], Trainor et al. [46], and Wachinger et al. [47] each produced a set of factors that might influence the residential decision-making process when confronted by external threats (including wildfire threats). This review was designed to establish the types of factors that might be required (and therefore be represented in information exchange between fire, pedestrian and traffic components) and where these might influence the decision-making process. Decision-making processes outlined by Wachinter et al. and others (including the work of Trainor et al. [46], Taylor and Freeman [48], Hess and Gotham [49], and Naghawi and Wolshon [50]) were then used as a basis for highlighting where these factors have an impact on the evacuee response timeline. For example, the structure of Lindell and Perry’s PADM model [30] has been transformed into one that is more readily applied to simulation [51]. Another recently developed wildfire response conceptual model by Folk et al. [7], adopts the PADM to represent householders’ decision-making steps and the factors affecting those steps.
Given the approaches examined (and following the recent work by Folk et al. [5]), the intended application area and the use of the PADM model in both evacuation from individual structures and larger scale incidents, the PADM is used in this paper as the conceptual framework for model development.
Several studies have investigated households’ behaviours during wildfires (post-event) and identified factors that affected their risk perceptions, decision-making, and response. Folk et al. [7], associated the identified factors with the decision-making stages of the PADM that they affect (i.e. pre-decisional stages (receipt, attention, and comprehension), threat credibility, risk assessment and protective action decision). In most of those studies, the factors affecting households’ behaviours have been identified by using simple statistical tests to verify if there were statistical differences between people deciding to leave, defend or Shelter-In-Place (SIP). As such, these existing studies do not provide information about (1) the impact of each factor on the protective action decision (i.e. how much a single parameter changes the probability to choose one strategy over another); or (2) the combined impact of several factors through a multivariate analysis (i.e. what is the probability of choosing a strategy given a set of factors). Only a few studies have attempted to quantify the impact of the factors on performance [52,53]. Paveglio et al. [52] estimated a multinomial logit to predict the protective strategies while McLennan et al. [53] presented two negative binomial regression models predicting the strength of the intention to leave. The benefit of this approach is that it provides values to help determine the likelihood and impact of a stage in the decision-making process.
The existing literature lacks modelling studies and engineering tools to predict how householders perceive wildfires and respond to them. Such models and tools are key to the safety assessment of communities threatened by wildfire as they allow for the identification of the proportion of householders intending to stay (i.e., to defend or SIP) or leave and when they take those actions. Householder decision-making models and transportation models need to be merged to enable the actual evacuation process to be simulated [5]. This paper aims at addressing this need by proposing a mathematical framework for householder decision-making in wildfire emergencies aimed at answering two key questions: “When do householders start taking a response action?” and “Which response action is taken by householders”
3. Modelling Assumptions
This work introduces a new Wildfire Decision Model aimed at simulating the human decision-making process in response to wildfire emergencies at the resident or householder level. This model employs a simplified version of the Protective Action Decision Model proposed by Lindell and Perry [30], which is developed to reflect an algorithmic formulation to be implemented in future largescale evacuation simulation tools. The proposed model is also inspired by the Evacuation Decision Model introduced by Reneke [54], which was expanded by Lovreglio et al. [43], to simulate evacuee decision-making in building fires based on the qualitative findings by Kuligowski [55] and behavioural guidelines introduced by Gwynne [35]. As such, the original model assumptions proposed in these references [43,54] are listed here, and are modified and adapted to wildfire emergencies. The assumptions underpinning the Wildfire Decision Modelare summarized below.
1. The purpose of the Wildfire Decision Model is to introduce a mathematical framework for future engineering models aimed at predicting the how and when households respond to an emergency in terms of what to do (i.e. leave or stay) and when to do it.
The prediction of household response to wildfires is the result of the combination of two modelling stages. The first stage aims to predict household responses to a wildfire (i.e. how individuals/groups perceive and interpret the cues, assess the threat, perceive risk, and select a set of actions). This first modelling stage predicts how many households decide to leave or to stay and the time required to make such a decision. The second stage focuses on vehicular and pedestrian movement to safety using as inputs the results of the first stage (i.e. how many households decide to leave and the time to start leaving). Most wildfire studies have failed to recognise that human behaviour and transportation aspects are intertwined – bidirectionally coupled [46]. As such, there is a division of the wildfire evacuation research into a behavioural perspective focusing on qualitative and quantitative aspects related to human behaviour and an engineering perspective focusing on traffic modelling [31]. The proposed mathematical framework aims at reducing this gap by establishing a foundation for new engineering solutions to simulate human behaviour in wildfires by predicting protective actions and response times. As such, this model is a step towards the creation of dynamic (i.e. time dependent) travel demand models for wildfire evacuations [17].
2. Perceived risk is the main factor to predict the decision to take protective actions and the timing required for such a decision.
The perceived risk is the foundation of the proposed model as existing disaster research and conceptual studies have shown that the perception of personal risk (i.e. the expectation of exposure to injury, death or property damage and loss) is deeply connected with the decision to take protective actions [30,47,56]. In fact, before taking any protective actions, householders typically need to identify and assess the risk by asking the following two questions: “Is there a real threat I need to pay attention to?” and “Do I need to take protective actions?” [1 pp. 47]. Depending on the quantification of the risk, decision-makers decide if it is necessary to stop their routine activities and start taking protective actions following this behavioural rule: the greater the certainty, severity, and immediacy of the perceived risk, the greater the likelihood of householders to perform protective actions [1 pp. 50,10].
3. It is assumed that householders adopt one of four behavioural states:
Normal State;
Investigating State;
Vigilant State;
Protective State.
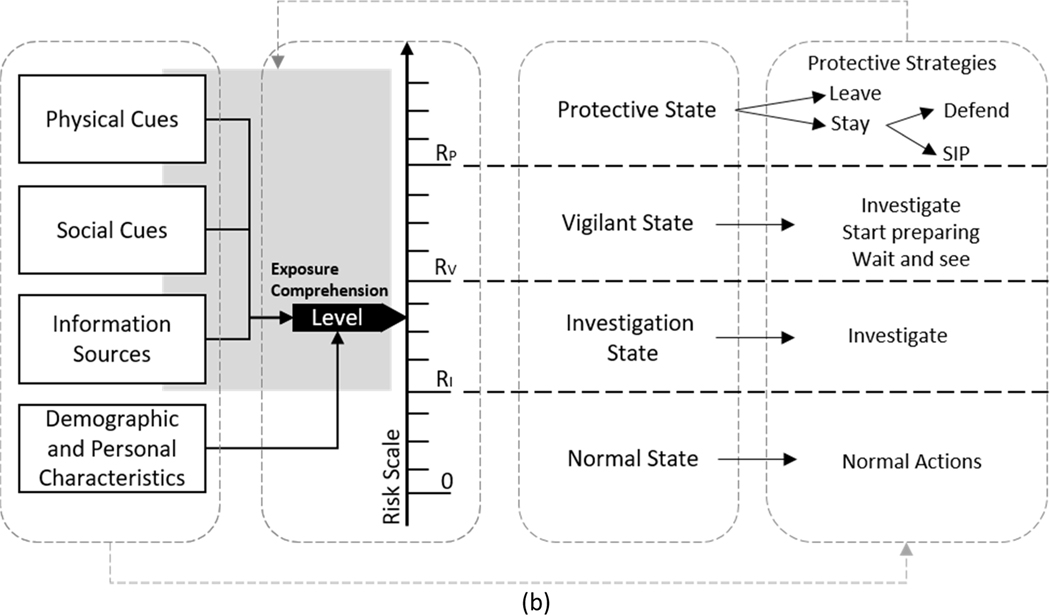
The concept of behavioural states was introduced by Reneke [2] in his decision model to address the findings by Kuligowski [55] in her evacuation model. Those findings highlight the existence of several major types of behavioural states, and in turn, types of behaviours, based on perceived risk. Each behavioural state is characterized by a different threat credibility. As such, householders take specific types of actions depending on their behavioural state and threat credibility. In the proposed model, those who do not perceive any risk or a relatively low level of risk, continue routine activities believing that there is no credible threat (Normal State). Those who may be uncertain about the threat, but perceive some risk, start seeking additional information to understand the situation (Investigating State). Once the threat is identified (i.e. a credible threat is perceived), but the perceived risk has not reached a specific (pre-determined) threshold level, householders continue gathering information before making a decision on whether to take protective action or not (Vigilant State). If/when the perceived risk reaches a critical value, householders decide to take protective actions, choosing between several possible strategies (Protective State).
Vigilant State is not included in the Reneke model for building fire; however, it is added here to address other types of decisions/behaviours typical of wildfire decision-making and action – i.e., to extend the model for the new application area. For example, several recent studies indicated that many decision-makers do not want or intend to evacuate automatically in the event of a wildfire as they prefer to “wait and see” before making their final decision to leave or stay [9,12,28]. This distinction is important because it can account for differences in protective actions and associated timing of these actions; e.g., households in a Vigilant State “tend to carry out fewer preparations both for defending and for evacuating compared with people who have decided on one of these concrete actions” [27]. Vigilant householders still remain in their property but are effectively primed for new information and are therefore more attentive and sensitive to it if it should arrive.
4. Householders perform actions following one or a combination of multiple protective strategies.
Several studies indicate that three main protective strategies can be identified: stay-defend, stay-shield or leave [9,12,28]. Householders, who decided to stay, can have either a defend strategy or shelter in place (SIP) strategy. The former is the option chosen by householders who want to protect their property and/or its occupants. Although, the main intent of this strategy is defending, the residence may also be used for protection during the passage of the wildfire front. The latter is defined by the absence of attempts to regularly monitor conditions inside and outside the shelter as well as by the absence of defensive actions – the property is used purely for protection [9]. The strategy to leave consists of moving towards a safe place. This is generally done using a vehicle and can be the result of a sequence of preparatory actions such as packing a vehicle, picking others up, or gathering with others before starting the actual movement toward a safe place [5].
The last householder behaviour can be the result of a combination of these three strategies. For instance, some householders may have attempted to evacuate or defend their property prior to choosing to SIP. As such, SIP is often used as a backup strategy [9]. In other scenarios, householders who previously decided to defend their property may ultimately decide to evacuate because of an increase in perceived risk, failure of equipment used to defend the home, or because their house catches fire [28].
5. The change in perceived risk is proportional to the intensity of external factors (i.e. physical and social cues and the information sources) the household receives and the householder’s internal factors (i.e. demographic, perspectives, memories of previous experiences and attitudes).
The external stimuli perceived by decision-makers are converted into a risk level which can lead to the protective action decisions. Those external factors can be divided into cues from the physical and social environment (especially sights and sounds) and socially transmitted information such as disaster alerts and warnings [1 pp. 46]. Moreover, existing literature on human behaviour in wildfire have highlighted that several internal factors, such as previous experience, affects how a decision-maker converts external factors into perceived threat credibility and risk [7]. Internal factors can either have an impact on the pre-decision process or the final risk assessment as illustrated in other types of emergencies, such as building fires [58,59].
6. The impact of cues and information sources is influenced by weights accounting for decision-maker exposure and comprehension.
According to the Protective Action Decision Model proposed by Lindell and Perry, external factors such as environmental and social cues and warnings, are subject to pre-decisional processes [1 pp. 48]. External factors need to be sensed, paid attention to, and comprehended by a decision-maker, before an individual can assess threat credibility and risk. Psychological theories can be used to explain those aspects. For instance, the Theory of Affordances [60,61] argues that the impact of a warning or a cue on decision-making is mediated by the Sensory Affordance and Cognitive Affordance. Sensory Affordance refers to how a warning or a cue supports seeing or hearing to catch households’ attention. Cognitive Affordance supports the understanding of a sensed warning or cue.
7. The effects of the external and internal factors affecting the perception of risk are additive according to a linear formulation.
This model assumes that physical cues and socially transmitted information are independent of each other. As such, some decision-makers might observe and assess some combination of environmental and social cues, whereas others might act only on the basis of warnings [1 pp. 49]. This is included in the model by assuming that the perceived risk consists of additive risk terms associated with each external factor. The additive assumption is known in a regression context and in econometrics as a linearity assumption [62]. However, it is worth highlighting that this assumption does not necessarily refer to the relationship among the dependent and the independent variables . Instead, linearity refers to the way in which the parameters associated with these dependent variables enter the equation as illustrated in Equation 1.
| Eq. 1 |
The linearity assumption has been used in many previous studies investigating the factors affecting decision-making during disasters, such as fire evacuations [63,64]. However, it is important to acknowledge that this is a simplifying assumption that may obscure the complex relationship between the factors represented.
8. Both internal and external factors affect the choice of actions and strategies taken at each stage.
Assumption 3 argues that when in a behavioural state, a decision-maker needs to choose between a set of protective actions and strategies. This decision to select between available actions is affected by both the external factors that characterize the threat as well as the internal factors characterizing the decision-maker. Several studies have shown that the choice of protective actions and strategies is affected by decision-makers’ socio-demography, preparation for and experiences with wildfire, as well as the nature and source of the cues [9–11,28,29].
9. The level of perceived risk of decision-makers facing the same situation may not be equal.
This assumption is based on the concept of behavioural uncertainty in evacuation models [65,66]. Behavioural uncertainty refers to the impossibility for an external observer to achieve a full understanding (deterministic knowledge) of an evacuation process given the complexity of this phenomenon [67]. For instance, Lindell and Perry argue that “[…] some of those at risk who are exposed to environmental cues will heed this information, but others will not.” [30]. Therefore, stochastic or semi stochastic approaches are suggested to develop novel wildfire behavioural models [5].
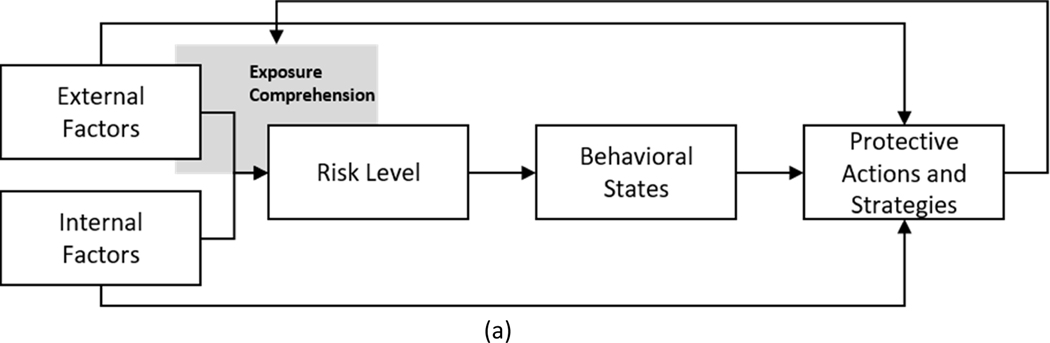
The conceptual block model derived by these assumptions is illustrated in Figure 1.a. While an expanded version of the conceptual model is presented in Figure 1.b. This model illustrates the relation among the cues perceived by evacuees and their actions using perceived risk and the definition of four behavioural states (normal, investigating, vigilant and protective). The model indicates that the perceived risk is affected by several external factors (namely, physical cues, social cues, information sources) and decision-makers’ internal factors (namely, demographics and characteristics). The external factors need to be sensed, paid attention to and comprehended in order to influence perceived risk through threat credibility. Perceptions of cues and their combined effects can both increase and decrease the level of perceived risk. In several disasters, perceiving lower intensity cues, conflicting cues, and cues that were decreasing in intensity caused decision-makers without a firm understanding of the event to underestimate their risk [67].
Figure 1 –
Conceptual model: (a) block version and (b) expanded version.
The decision-makers’ behavioural state depends upon the risk perceived in a wildfire scenario. Once the perceived risk exceeds the three thresholds (i.e., , and , see Figure 1.b) the decision-makers change their behavioural state accordingly; i.e. move to the next state. Depending on their states, evacuees can take different types of actions or strategies (i.e. series of actions) to meet objectives associated with that state. The selection of those action and strategies is affected by both external and internal factors as indicated by the segmented arrows at the bottom of Figure 1.b. The selected actions could have feedback effects on the perception of cues (for instance, searching actions can modify the exposure and comprehension of some cues) as is indicated by the segmented arrows at the top of Figure 1.b.
The proposed conceptual model is dynamic over time. From an implementation view point, this can be achieved by a time-based or event-based approach. The former approach assumes that the perceived risk and protective actions are estimated at each time-step. The latter approach implies that the perceived risk and protective actions are estimated for each event, changing the state of the system (i.e. an evacuee receives a new source of information or perceives a new social or physical cue).
4. Model Specification
Starting from the assumptions listed in the previous section, model parameters are proposed to define how cues affect the level of risk, , of a householder at time and modifies the behavioural states and the time required to reach the four behavioural states (Assumption 2–3, Normal, Investigating, Vigilant, Protective states). According to Assumption 5 and 7, the equation defining the relation between , the intensity of external factors (i.e. physical and social cues and the information sources), the internal factors (i.e. demographic, perspective, memories of previous experiences and socio-economic characteristics) can be defined as:
| Eq.2 |
where is a function of all the external factors and internal factors . The internal factors (i.e., demographic, perspectives, memories of previous experiences and attitudes) are assumed constant within the current wildfire event given it time frame. By contrast, the intensity of the external factors can vary over time. Considering the linear assumption, Equation 2 can be rewritten as:
| Eq.3 |
where and are the parameters assessing the impact of external and internal factors on the level of risk respectively. can be affected by the credibility of threat for the householders. As such, their value might vary when householders change their behavioral states and thus level of threat credibility (Assumption 3). is a weight parameter accounting for householder exposure (i.e., perception and attention paid to the cues) and comprehension of the external factor, (Assumption 6). Therefore, positive values of and indicate that the related factors increase the perceived risk while negative ones indicate that those factors reduce the perceived risk. The parameters are always positive and are equal to one when the related factors are perceived and zero otherwise.
The following sections discuss several key aspects of the model in more detail: external factors (Section 4.1), internal factors (Section 4.2), how to account for the behavioral uncertainty (Section 4.3), the definition of the risk thresholds (Section 4.4) and how to model the action and strategy selection (Section 3.5).
4.1. External Factors
Few studies are available in the literature showing which external factors had impact on households’ risk perception and, in turn, their decisions and actions during wildfires. To achieve a more comprehensive list of factors we also consider factors observed during hurricane emergencies [7]. Despite the clear difference in the nature of the emergencies, both wildfires and hurricanes have the capacity to displace communities and evolve over similar timescales (i.e. the public does have some amount of time over which they are receiving cues and they can make decisions). [7]. Based on such background, we propose in Table 1 a list of independent variables that need to be considered and included in the proposed model based on the review in this work [7]. It is worth highlighting that this list might not be comprehensive as there might be other factors that have not been identified in existing studies.
Table 1 –
External factors affecting households risk perception (“+” indicates a positive impact; “−“ indicates a negaLve impact)
All identified factors have a positive impact on the risk perception; i.e. increase perceived risk. However, the credibility of those cues might depend on the credibility of the information channel – the source and arrival mode of the information. As such it might be expected that information provided by trusted institutes or organizations (such as government and firefighters) have a higher impact on the increment of risk perception than other information channels. As such, the credibility and thus the impact of external factors are dependent on the information channels. A list of those channels have been identified in this paper [8] and include: environmental cues, radio, television, fire agency website, Twitter1, Facebook1, face-to-face interactions with family and/ or friends, neighbours and others.
Two other elements affecting this process is the households’ exposure to external factors (i.e., perception and attention paid to the cues) and their comprehension. To date, there is very little research on such topics in the wildfire field. Whittaker et al. [28] identified that extreme hot weather reduced the householders’ exposure to environmental cues and warnings during the Australian Black Saturday. It is also reasonable to assume that the time of the day could have impact on households’ exposure. For instance, the exposure to external factors can be dramatically reduced overnight. Such a trend has been observed and modelled in a few hurricane decision models [16,72]. Such an effect is included in the proposed model through the parameters in Equation 3. Such parameters need to be zero when an external factor is not sensed, attended to, or comprehended and “1”, otherwise. A probabilistic approach can be used to assign. Considering the binary structure, a simple Bernoulli distribution could be used to simulate the parameters:
| Eq.4 |
where is the probability that external factor is sensed, paid attention to, and understood. Such a probability might vary depending on variables such as weather and time of the day.
4.2. Internal Factors
Previous wildfire emergencies have shown that several internal factors can impact households’ risk perception. Those factors, , are listed in Table 2. The proposed list is based on the review work proposed in this paper [7].
Table 2 –
Internal factors affecting households risk perception (“+” indicates a positive impact; “−“ indicates a negaLve impact)
The proposed list indicates that there are several factors that might reduce the risk perception and thus delay the response actions. Age is one of those factors affecting householders’ response to hurricane Ike [71]. The length of time householders have lived in an area (i.e. residence time) can reduce their risk perception while householders living in suburban locations might not consider themselves at risk [28,70,73]. The levels of education and income show differing impacts on risk perception depending on the type of emergency. As such, further investigations and theories are necessary to explain those trends. Generally, previous experience has been shown to increase levels of risk perception [70,71,75]. However, experiencing unnecessary evacuations is shown to have a negative impact on risk perception [71].
Most of the proposed internal factors have a direct impact on risk perception. However, some of these factors have indirect influences. For instance, Benight [70] observed that women are more sensitive to evacuation warnings and orders in wildfire emergencies while Huang [71] identified that previous experience has an impact on the perception of threat credibility which has an impact on risk perception. Therefore, interaction terms might need to be included in Equation 3.
4.3. Behavioural Uncertainty
Behavioural uncertainty is another key component of the proposed model (see Assumption 9). Such uncertainty can be accounted for in the model assuming that the perceived risk of households is not a purely deterministic quantity. The behavioural uncertainty can be then simulated by introducing a random term into Equation 2 since it is not possible to obtain a complete understanding on how evacuees behave. This term allows the modelling of differences among households facing the same situation as the current description of households’ characteristics is not able to capture all of the variables affecting their behaviour. This means that different agents facing the same situation can have different perceived risks. Therefore, Equation 2 can be rewritten using the sum of a deterministic term, , and a random term, , as indicated in Equation 5.
| Eq. 5 |
where is the vector of all the parameters affecting the deterministic aspects, such as and in Equation 3. The random term is a distribution having mean equal to zero and a constant standard deviation . Different distributions can be chosen to define , such as normal distribution and logistics distributions, depending on the calibration and implementation issues discussed in Section 4.
A further possibility to model the behavioural uncertainty is by assuming that the parameters are not constant among householders. We can assume that those parameters have their own probability distributions PDF where is the vector of parameters characterizing the probability distribution. In other words, this allows for the simulation of different households’ sensitivity to the same external factors. This type of formulation is typical for random parameters models and has been implemented to investigate the heterogeneity of decision makers in several disasters such as building fires [77–79], tsunami [15] and hurricanes [18,19,80]. The incorporation of this is left for future work.
4.4. Risk Thresholds and Behavioural States
According to Assumption 3, the householders can have four different behavioural states (Normal State, Investigating State, Vigilant State, and Protective State) and the passage from one state to another depends upon the level of perceived risk. As such, it is necessary to identify three thresholds (, , and ) that a householder needs to pass to progress to another state - investigating, vigilant and then protective state as illustrated in Figure 1.b. Using those thresholds is possible to define the behavioural rules in Table 3.
Table 3 –
Relationship between behavioural states and risk value
| Behavioural state | Risk Value | ||
|---|---|---|---|
| Normal | |||
| Investigating | |||
| Vigilant | |||
| Protective | |||
Because of the behavioural uncertainty, is not a deterministic quantity. As such, it is not possible to evaluate the agent’s state with a deterministic approach. However, it is possible to define the probability that the householder is in each behavioural state as illustrated by Equations 6.
| Eq.6 |
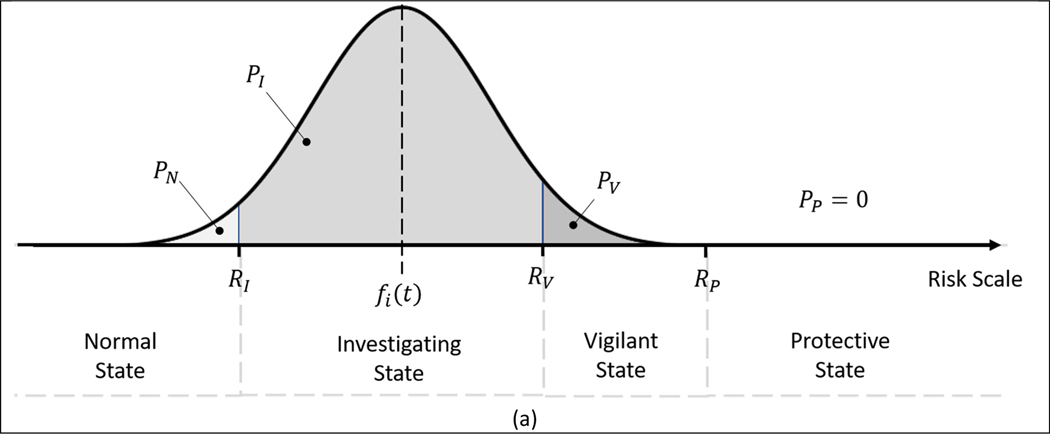
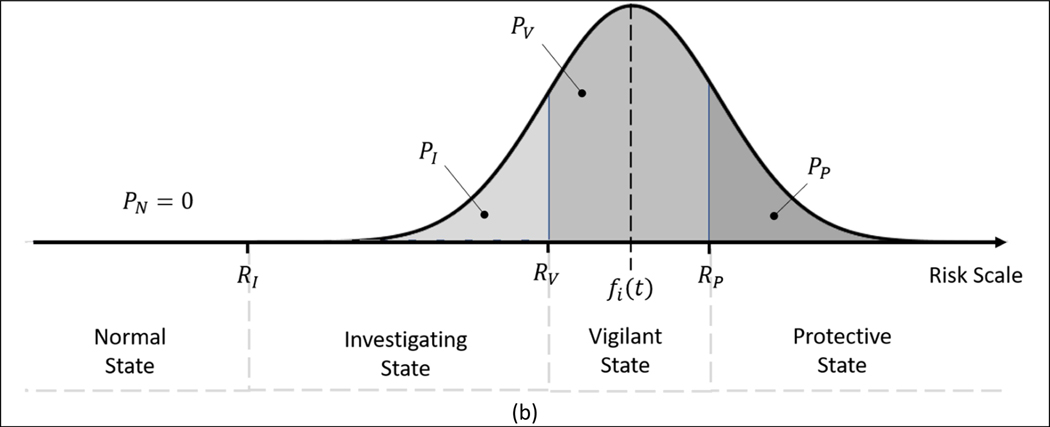
where , , , and are the probabilities of the householder to be in the normal, investigating, vigilant and protective states, respectively, given the cues experienced and their interpretation of them. is the cumulative distribution of the random term, , introduced in Equation 5. Figure 2 provides a graphical representation of Equation 6. In Figure 2, it is possible to observe that that , , , and , depend on the value of deterministic part, , of risk. Those probabilities are graphically represented by the area under the bell curve representing random term, . decreases when the bell curve moves toward higher values of risk while gradually increases.
Figure 2 –
Visual representation of Equations 5 when the determinist part of the perceived risk is in (a) the investigating state and in (b) the vigilant state.
Equation 6 can have either a closed formulation or can be estimated using numeric algorithms depending on the distribution of the random term. For instance, assuming that the random term has a standardized logistic distribution, has a logistic function, and the formulation defined in Equation 6 represents an Ordered Logit model [81].
4.5. Action and Strategy Selection
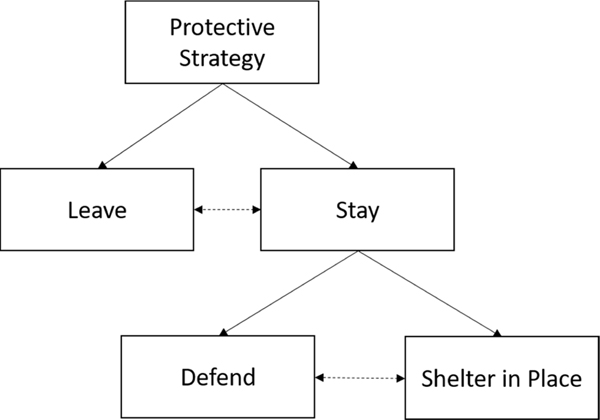
Once householders have reached the protective state (see Section 4.4), they need to select a protective strategy (Assumption 4). Many authors have investigated the possible strategies used by householders to respond to wildfire threats [9–11,28,29]. According to this body of literature, the main protective strategies that can be identified are: leave, defend or SIP. As such, it is possible to identify the decision tree depicted in Figure 3. This tree is a nested tree including binary options.
Figure 3 –
Protective strategy decision tree.
The literature also indicates that the final householder behaviour can be the result of a combination of these three strategies (see Assumption 4) as the decision-making could be dynamic over time. The possibility to change decision is represent in Figure 3 by the dash arrows. From implementation point of view, this decision-making process can be simulated using either time based or event based pproach. In fact, the information source and cues can change the kind of protective action that the householder might take.
A possible solution to model such a decision tree can be defined assuming that such a decision is affected by both the external factors that characterize the threat as well as the internal factors characterizing the decision-maker (Assumption 8). As such, each householder can make an assessment of each option based on these factors that is expressed in terms of utility (i.e. the overall satisfaction derived by each option). Considering Assumption 9, those utilities cannot be entirely assessed and measured. From a modelling point of view, this can be addressed by dividing the utilities associated with each option into a deterministic part and a random part (consistent with the approach adopted previously). A closed formulation can be used to simulate such a decision, such as the nested-logit models [82]. Under those assumptions, the probabilities of the householder to leave , defend or SIP can be calculate as illustrated in Equation 7.
| Eq.7 |
where is the degree of independence in unobserved utility among the alternatives in the ‘stay’ nest and is the probability to stay (i.e.)., and are the deterministic utility terms utility that the householder associates with the leave, fight and SIP strategies. According to Assumption 9, those quantities are a function of both the internal and external factors . A list of those factors is shown in Table 4. Such a list of internal (INT) and external (EXT) factors is based on the review proposed in this review [7]. It is worth highlighting that this list might not be comprehensive as there might be other factors that have not been identified in existing studies.
Table 4 –
Internal and external factors affecting protective action decision-making (“+” indicates a positive impact; “−“ indicates a negative impact)
| ID | Factor | Nature | Leave | Defend | SIP | Reference |
|---|---|---|---|---|---|---|
| 1 | Risk perception | INT | + | + | [12,27,73,75,85] | |
| 2 | Gender (female) | INT | + | [28,52,73,76,83,86–88] | ||
| 3 | Gender (male) | INT | + | |||
| 4 | Political leaning (democratic) | INT | + | [73] | ||
| 5 | Government supporter | INT | + | + | [52] | |
| 6 | Age | INT | + | [88] | ||
| 7 | Income | INT | + | [52] | ||
| 8 | Existing household plan | EXT | + | + | [12,29,88] | |
| 9 | Preparedness (self and property) | INT | + | [29,73,84,88] | ||
| 10 | Bushfire knowledge | INT | + | [88] | ||
| 11 | Previous experience | INT | ± | [70,75,76,83] | ||
| 12 | Self-efficacy | INT | + | [85][53] | ||
| 13 | Response-efficacy | INT | + | |||
| 14 | Self-characterization | INT | + | |||
| 15 | House-preparedness and survivability | INT | + | [84] | ||
| 16 | Having children | EXT | + | [85,88] | ||
| 17 | Family safety | INT | + | [12] | ||
| 18 | Self-safety | INT | + | [85] | ||
| 19 | Having pets | EXT | + | [73,85] | ||
| 20 | Having livestock | EXT | + | [73,84,85] | ||
| 21 | Community attachment | INT | + | [12,29,88] | ||
| 22 | Property attachment | INT | + | [12,29,83,85,88] | ||
| 23 | Working for wood and insurance industries | INT | + | [52] | ||
| 24 | Having more than one helper in the home to defend | EXT | + | [84] | ||
| 25 | Self-responsibility | INT | + | [29,52] | ||
| 26 | Received warning | EXT | + | [75] | ||
| 27 | Advice to leave from friend and family | EXT | + | [86] | ||
| 28 | Advice to leave from neighbours* | EXT | + | [86,88] | ||
| 29 | Advice to leave from emergency service* | EXT | + | [73,86,88] | ||
| 30 | Mandatory evacuation order | EXT | + | [73] | ||
| 31 | Presence of firefighters in the area | EXT | + | [84] | ||
| 32 | Living in a rural area | EXT | + | [88] |
face to face interactions
Table 4 illustrates whether each fact has a positive or negative impact on the decision to leave, defend or SIP. However, in some instances, further information is available in the original reference that helps modelling householder behaviour. For instance, Strawderman [75], focusing on the decision to leave, observed that receiving advice to leave from friends, family, neighbours and/or emergency services had more impact on women and the advice from friends, relatives and neighbours had less impact than advice from authorities. Mozumder [73] showed that mandatory evacuation orders had greater impact than evacuation advice on the choice to leave. Moreover, having livestock has a stronger impact than having pets on the decision to leave [73]. Finally, householders, who planned to stay in hotel/motel (i.e. household plan), were more likely to evacuate than those planned to stay in a shelter [73].
The results present in the literature are not always consistent. For example, previous experience, such as false alarms, can have an negative impact on the decision to evacuate. [76,83]. However, such a trend was not observed by Benight [70]. According to Tibbits et al. [84], the presence of firefighters have a positive impact on the decision to stay and defend while McLennan et al. [10] did not identify this factor as having significant impact on actions. It is assumed that the precise impact of such experience would be affected by the outcome associated with the experience.
A final consideration regarding the protective action strategy selection is that factors can vary over time (i.e. risk perception). Therefore, the probabilities defined in Equation 7 can change over time. Such a behaviour is supported by many findings showing that householders have changed their protective strategy over time because of the change of the threat perceptions [9,28].
5. Model Calibration
In this section, a component of the proposed model is calibrated using the data collected by Strahan et al. [8]. Given the available data in this reference [8], it is possible to calibrate a model predicting householders’ decision to leave or stay using a subsection of factors listed in Table 4. As such, this calibration study allows us to confirm the positive or negative impact of the available factors on the decision to leave and to stay. Moreover, the proposed model allows (1) the investigation of the impact of each factor on the protective action decision: leave vs. stay (i.e., how much a single parameter changes the probability to choose each strategy); and (2) the investigation of the combined impact of several factors through a multivariate analysis (i.e. what is the probability to choose a strategy given a set of factors). As such, the proposed model represents a novel tool to predict individual household’s decisions to leave or stay given their demographics, attitudes, perceived risk and the warnings they receive.
5.1. Survey
The survey by Strahan et al. [8] was designed to identify self-evacuation archetypes using data from 457 Australian householders who had recently experienced a bushfire. In this study, this data is used to investigate the strategy selection described in Section 4.5; i.e., identifying the factors that impacted the decision to leave their property, or instead, stay to defend or SIP. Therefore, the overall survey data is used to calibrate the model and then the actions predicted by the model are compared against individual survey responses to determine the validity of individual model predictions.
Strahan et al. [8] developed a telephone survey to collect data from randomly selected residents living in areas that had been directly affected by 1) the January 2014 bushfire in Parkerville, Stoneville and Mt Helena in the Perth Hills and 2) the January 2015 bushfire that affected thirteen towns and surrounding rural areas in the Adelaide Hills. The survey was based on the theoretical framework provided by Protective Action Decision Model [30]. It included 94 questions aimed at collecting the following information:
Intended and actual responses to bushfire (i.e. leave or stay);
Household demographics;
Proximity to the bushlands;
Self-efficacy and self-responsibility;
Previous experience in bushfires including property damage, injury, death or evacuation;
Intrusiveness of the bushfire threat;
Threat perceptions and perceptions of impact;
Perceptions of the attributes of hazard adjustments2;
Long-run hazard adjustments undertaken3;
Perceptions of neighbours, media and emergency services involved in the bushfire event;
Sources of information and warnings about the bushfire;
Protective action processes of the interviewees during the event;
Impediments to evacuation.
Details of the questionnaire are available in the supplement material provided in this work [30]. For all instances, the full data-set is employed for calibration and validation. The data is used to calibrate the model and identify the coefficient values that best approximate the impact of these factors on the decision to leave or stay – generating a function connecting the underlying surveyed factors and associated coefficients with a predicted outcome. The calibrated model is then used to predict the response decision of individual respondents based on their other survey answers.
5.2. Participants
A total of 457 residents in wildfire prone areas affected by the two wildfire events were surveyed by telephone, achieving an overall response rate of 54.1%. The sample consists of 182 men (39.8%) and 275 women (60.2%) aged 18–65 years of age. Many (69%) lived in households without dependents, of those who did live with dependents, 68.7% had dependent children and 31.3% housed dependent adults. 11.6% had a household member with a disability who required assistance or care. More than 80% had lived in the locality for over 10 years. 71% of respondents lived in homes within 100 m of the bushlands and 21% lived between 100 m and 500 m of bushlands.
5.3. Model Specification and Estimation
The model proposed in this paper is a binary logit model predicting the probability of a householder to leave or stay. This decision represents part of the decision tree in Figure 3. Although it is also important to estimate the probability to defend or SIP (within the stay strategy), such a decision cannot be estimated using this data-set as this information was not collected via the survey. These two outcomes are combined in this analysis. The dependent variable used in this calibration study is the decision to either leave or stay taken by the 457 respondents.
The model is illustrated in Table 5. This model is specified assuming that the utility function of leaving includes all the variables listed in Table 5 while the utility function of stay is equal to zero. As such, a positive value of the estimated parameters indicates that the associated variables increase the probability of leaving while negative ones reduce it. Equation 8 shows how it is possible to calculate the probability to leave or stay for the householder simplifying the formulation Equation 7 since the probability to defend or SIP cannot be estimated.
| Eq.8 |
where are the factors (i.e., independent variables) included in the models and are the estimated parameters.
Table 5 –
Full choice model predicting the probability of householders to leave or stay (positive values indicates an increment of the probability to leave while negative values a decrease of this probability)
| Number of observations= 454 | |||||
|---|---|---|---|---|---|
| AdjR2 =0 .06 | |||||
|
| |||||
| ID* | Parameter | Description | Value | P-value | Marginal Effect |
| 1 | Self and Family Risk | from 1 (low) to 6 (high) | −0.325 | 0.132 | −6.9% |
|
| |||||
| 1 | Property Risk | from 1 (low) to 6 (high) | 0.516 | 0.005 | 10.9% |
|
| |||||
| 1 | Pet/Livestock Risk | from 1 (low) to 6 (high) | 0.098 | 0.546 | 2.0% |
|
| |||||
| 2 | Gender | 1=female; 0=male. | 0.361 | 0.229 | 7.6% |
|
| |||||
| 6 | Age1 | 1 if 18–24 years, 0 if others | −1.840 | 0.033 | −38.9% |
|
| |||||
| 6 | Age2 | 1 if 25–34 years, 0 if others | −0.509 | 0.588 | −10.4% |
|
| |||||
| 6 | Age3 | 1 if 35–44 years, 0 if others | −0.351 | 0.652 | −7.3% |
|
| |||||
| 6 | Age4 | 1 if 45–54 years, 0 if others | −0.332 | 0.563 | −6.9% |
|
| |||||
| 6 | Age5 | 1 if 55–64 years, 0 if others | −0.588 | 0.255 | −12.3% |
|
| |||||
| 6 | Age6 | 1 if 65–74 years, 0 if others | −0.183 | 0.723 | −3.9% |
|
| |||||
| 9 | Self-preparedness | from 0 (low) to 4 (high) | −0.250 | 0.023 | −5.2% |
|
| |||||
| 9 | House preparedness | from 0 (low) to 9 (high) | −0.023 | 0.778 | −0.5% |
|
| |||||
| 10 | Bushfire knowledge | from 0 (low) to 5 (high) | 0.195 | 0.393 | 4.1% |
|
| |||||
| 13 | Leaving efficacy | from 1 (low) to 5 (high) | 0.725 | 0.001 | 14.10% |
|
| |||||
| 13 | Staying efficacy | from 1 (low) to 5 (high) | −0.717 | 0.001 | −16.20% |
|
| |||||
| 16 | Having children | 1=yes; 0=no. | −0.013 | 0.977 | −0.2% |
|
| |||||
| 19 | Having pets | 1=yes; 0=no. | −0.019 | 0.964 | −0.6% |
|
| |||||
| 20 | Having livestock | 1=yes; 0=no. | 0.487 | 0.225 | 10.2% |
|
| |||||
| 25 | Self-responsibility | from 1 (low) to 5 (high) | −0.481 | 0.093 | −10.5% |
|
| |||||
| 26 | Receiving warning to leave or defend | 1=yes; 0=no. | 0.690 | 0.039 | 14.4% |
ID as shown in Table 4
The independent variables introduced in this calibration are selected based on the list of factors provided in Table 4. When such factors were measured in the survey, they were included in the calibrated model in Table 5. This table identifies the variables affecting the decision. The variables found to be significant in Table 5 are then used to estimate the final model proposed in Table 6.
Table 6 –
Partial choice model predicting the probability of householders to leave or stay (positive values indicates an increment of the probability to leave while negative values a decrease of this probability)
| Number of observations= 454 | |||||
|---|---|---|---|---|---|
| AdjR2 =0 .09 | |||||
|
| |||||
| ID* | Parameter | Description | Value | P-value | Marginal Effect |
| 1 | Property Risk | from 1 (low) to 6 (high) | 0.34907 | 0.006 | 7.30% |
|
| |||||
| 6 | Age1 | 1 if 18–24 years, 0 if others | −1.287 | 0.065 | −27.90% |
|
| |||||
| 9 | Self-preparedness | from 0 (low) to 4 (high) | −0.28047 | 0.003 | −5.90% |
|
| |||||
| 13 | Leaving efficacy | from 1 (low) to 5 (high) | 0.77214 | 0 | 12.90% |
|
| |||||
| 13 | Staying efficacy | from 1 (low) to 5 (high) | −0.65598 | 0.001 | −17.20% |
|
| |||||
| 25 | Self-responsibility | from 1 (low) to 5 (high) | −0.47554 | 0.074 | −11.30% |
|
| |||||
| 26 | Receiving warning to leave or defend | 1=yes; 0=no. | 0.51721 | 0.098 | 10.60% |
Goodness of fit is assessed based on a comparison of the likelihood that a model includes only a constant , the likelihood of the proposed models in Table 5 and 6, and the adjusted McFadden R squared (AdjR2)4. The value of AdjR2 for the model in Table 5 indicate that the variables included in the model significantly improve the intercept model [89]. Moreover, the AdjR2 for the model in Table 6 has a higher value than the one for the model in Table 5. This indicates that the model has a better fit when only the variables that significantly affect the decision are included. Finally, several likelihood ratio tests are used to compare the models in Table 5 and 6 with the intercept model and to compare both models against each other. Both models provide a statistical improvement over the intercept model , while the model in Table 5 (having more parameters) does not provide a significant improvement over the model shown in Table 6 (having fewer parameters). These results indicate that the simpler model in Table 6 might be used for future implementations.
The capability of the model to predict the choice made by the 457 interviewees is calculated using the following steps (known in the literature as cross validation):
The data collected by Strahan et al. [6] is analyzed to identify a subset of factors, from those in Table 4, were included in the survey and thus can be used in the calibration process.
Regress the response data from the survey on the independent variables (derived from the set suggested in the proposed model) to generate coefficients for the independent variables; i.e. their unit impact on the likelihood of an individual responding.
These general coefficients are embedded and represent the impact of the factors within the model.
The model is then applied to calculate the probability of each interviewee choosing to leave or stay using the parameters (and the coefficients generated in a) calculated in Table 5; i.e. the model configured using the overall data-set is applied to each individual to predict their response
The model prediction for each individual is established by identifying the predicted outcome with the highest probability;
The predicted and actual actions across the population are compared to determine the number of times the simulated actions match the actual choice made by the householders;
This count is divided by the number obtained in (c) by the sample size to generate a percentage.
Given steps (a) – (f) are completed, the models proposed in Table 5 and 6 predicts 83% of the choice made by the interviewees. This represent further evidence that that the simplest model in Table 6 can be used for future implementations.
Although several parameters are not statistically significant, those parameters are left in the model in Table 5 as (1) the existing literature suggests that they have an impact and (2) such results could be also affected by the relatively small sample size. Considering that p-values is just “the tip of the iceberg” [90], it is possible to use many other statistics to assess the impact of each variable on the probability to leave or stay [91]. Marginal effects are proposed in Table 5 to investigate those impacts5.
In this paper, marginal effects measure the change in the probability of a householders to leave when an independent variable is changed, holding all other independent variables constant to the sample average [89]. For binary variables, marginal effects indicate how the probabilities change as the binary independent variable changes from 0 to 1 while, for continuous variables, those provide a good approximation of the amount of change in probability that will be produced by a 1-unit change of a continuous variable. For instance, it is possible to observe that the probability to leave for a (binary variable) female householder is 7.6% higher than the one for a male householder while 1-unit change of (continuous variable) householders’ bushfire knowledge produces an increment of 4.1% of their probability to leave. Analysing the marginal effects in Table 5, it is possible to observe that many variables can have a notable impact on the probability to leave, although their associated parameters are not different from zero to a statistically significant degree. The only exceptions are the following factors: house preparedness, having children and having pets. In fact, those variables generate variation of probabilities smaller than 1%.
Finally, it is possible to observe that the sign of the estimated parameter for the models in Table 5 and 6, which indicate whether the probability to leave or stay increases or decreases, shows consistent results. Moreover, the sign and meaning of these parameters are in agreement with the trends observed in previous studies (see, Table 4) showing the robustness of the proposed model.
The first exception is for the householders’ age. In fact, according to the literature [88], younger householders prefer to leave while the proposed model indicate that they prefer to stay. As such, there is need for more confirmatory studies to finally assess the impact of age on the protective strategy selection. The last exception is the sign of the “having livestock” parameter. According to the literature (see Table 4), householders that have livestock are less likely to leave while the proposed model in Table 5 shows an opposite trend. This could be due to the fact that such a variable could be a proxy of householders’ wildfire exposure as householders having livestock are potentially likely to live in rural areas and/or be more exposed to a wildfire front. As such, future research is required to shed light on this discrepancy.
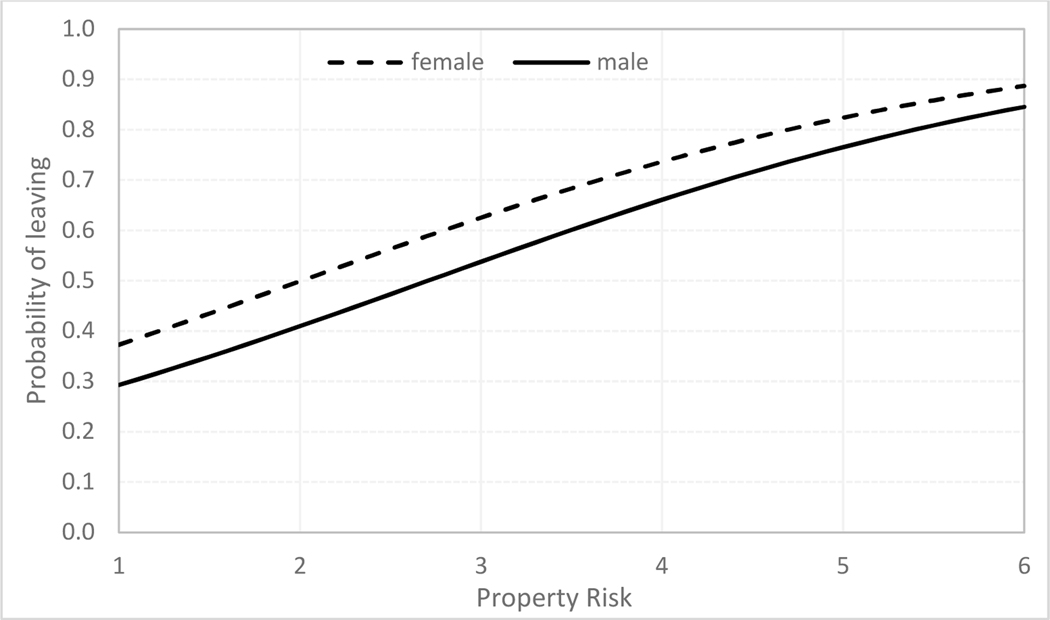
A simple implementation of the proposed model is illustrated in Figure 4 using Equation 8. This figure illustrates how the probability that a householder will leave is sensitive to his/her perceived property risk and gender6. In line with the sign in Table 5, it is possible to observe that the probability of leaving increases with the risk. Moreover, this application shows that the change in probabilities can be greater than 40% going from low to higher levels of property risk. Finally, this table allows the visualization of the impact of gender on the decision, which is in line with the marginal effect shown in Table 5.
Figure 4 –
Impact of property risk and gender on the probability of a household to leave
6. Discussion and Conclusion
This paper introduces a mathematical framework aimed at predicting how householders perceive the risk associated to wildfires and how they take protective actions in response to such threats. This is done by presenting a conceptual Wildfire Decision Model based on nine assumptions which rely on the existing literature on human behaviour in wildfires. The proposed modelling framework allows the behavioural state of a householder (i.e., four possible states - normal, investigating, vigilant and response) to be identified and the protective action response of each householder (i.e. leave, SIP or defend). As such the proposed framework, once embedded within a simulation platform, will provide a tool that generates new dynamic travel demand models for large-scale evacuations due to wildfires. This mathematical framework can be adjusted for different contexts and countries and calibrated using the datasets available in the literature. As such, future calibration may or may not include all the protective actions listed in this work (i.e. leave, SIP or defend), depending on whether these are available options for householders.
The Wildfire Decision Model has been specified based on the nine assumptions derived from the research literature and on the existing engineering models developed for other large-scale emergencies such as hurricanes. Different modelling solutions are available in the literature to simulate human decision-making during disasters, such as Fuzzy Theory, Neural Network, rule based models, etc. [67]. In this work, the model was specified to reach a structural approximation of PADM and to embed a probabilistic structure allowing the simulation of the behavioural uncertainty. As such, the proposed model belongs to the broad family of random utility models [92]. We identified a set of internal and external factors that have an impact on protective action decision-making and that then needed to be included in the model. Although it is not possible to state whether this set is exhaustive; however, it is representative of current understanding. Finally the proposed model focuses only on individual decision-making and future development may seek to integrate and simulate group decision-making following existing solutions, such as [93,94].
In this work, a component of the proposed model is calibrated using the data collected by Strahan et al. [8]. The data was analysed to generate representative coefficients within the model representing the impact of the factors already embedded within the model. The calibrated model can simulate the householders’ decision to stay or leave as a function of several internal and external factors (see Table 5). As such, this calibrated model represents the first tool available to predict householder protective strategy for a wildfire emergency. The results produced by the calibrated model were then compared against the individual actions taken by individual respondents to the survey; i.e. on an individual level. In effect, the model calibrated with summary data from the overall data-sets was asked to predict individual responses, as a means of model validation. The validation results show an overall agreement with the existing literature and it is capable of predicting 83% of the choices made by the 457 householders interviewed by Strahan et al. [8].
The main limitation of the data set used in this paper is the inability to distinguish between defend or SIP actions among those who decided to stay, as this information was not collected. Another limitation of this dataset is the limited sample size and the limited heterogeneity of the sample. Only 457 were interviewed and the data refers only to Australian householders. There may be cultural, situational and behavioural differences between this sample and others of interest. Using data from different wildfire-prone countries might generate different calibration results since there are different evacuation strategies/policies in Australia and the US. As such, new data is necessary to quantify those differences.
The intention of this work was to develop a provisional model capable of predicting residential response in wildfires. It is recognized that this is a first step at making such a predictive model and that further data is required to make the model both more robust and representative. However, the identification and implementation of the behavioural factors as well as the quantification of the impact of these factors on the individual decision-making process represents a significant step. With the availability of additional data, from different incidents and locations, the model’s representation of residential decision-making in wildfire events can be further developed, calibrated and tested. Moreover, future work is required to expand the proposed model to predict householder behaviour in different large scale natural disasters such as hurricanes and flood.
Footnotes
Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose.
Perceptions of short-run hazard adjustments or protective action perceptions are perceptions of evacuating or remaining in protecting personal safety or property.
Long run hazard adjustments are the preparatory actions taken in advance of a bushfire to prepare property, establish fire-fighting equipment and organise personal protective equipment [8].
Those are standard parameters used to evaluate the goodness of fit for random utility models [89,92].
The remaining variables are set on the sample average.
Publisher's Disclaimer: This is a PDF file of an article that has undergone enhancements after acceptance, such as the addition of a cover page and metadata, and formatting for readability, but it is not yet the definitive version of record. This version will undergo additional copyediting, typesetting and review before it is published in its final form, but we are providing this version to give early visibility of the article. Please note that, during the production process, errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Boustras G, Ronchi E, Rein G, Fires: fund research for citizen safety, Nature. 551 (2017) 300–300. doi: 10.1038/d41586-017-06020-6. [DOI] [PubMed] [Google Scholar]
- [2].Evers CR, Ager AA, Nielsen-Pincus M, Palaiologou P, Bunzel K, Archetypes of community wildfire exposure from national forests of the western US, Landsc. Urban Plan 182 (2019) 55–66. doi: 10.1016/J.LANDURBPLAN.2018.10.004. [DOI] [Google Scholar]
- [3].Liu Y, Stanturf J, Goodrick S, Trends in global wildfire potential in a changing climate, For. Ecol. Manage 259 (2010) 685–697. doi: 10.1016/J.FORECO.2009.09.002. [DOI] [Google Scholar]
- [4].Schoennagel T, Balch JK, Brenkert-Smith H, Dennison PE, Harvey BJ, Krawchuk MA, Mietkiewicz N, Morgan P, Moritz MA, Rasker R, Turner MG, Whitlock C, Adapt to more wildfire in western North American forests as climate changes., Proc. Natl. Acad. Sci. U. S. A 114 (2017) 4582– 4590. doi: 10.1073/pnas.1617464114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Ronchi E, Rein G, Gwynne S, Wadhwani R, Intini P, Bergstedt A, e-Sanctuary: Open MultiPhysics Framework for Modelling Wildfire Urban Evacuation - Fire Protection Research Foundation, 2017. [Google Scholar]
- [6].Pel AJ, Bliemer MCJ, Hoogendoorn SP, A review on travel behaviour modelling in dynamic traffic simulation models for evacuations, Transportation (Amst). 39 (2011) 97–123. doi: 10.1007/s11116-011-9320-6. [DOI] [Google Scholar]
- [7].Folk L, et al. , A Provisional Conceptual Model of Human Behavior in Response to Wildland-Urban Interface Fires, Fire Technol. (2019). [Google Scholar]
- [8].Strahan K, Whittaker J, Handmer J, Self-evacuation archetypes in Australian bushfire, Int. J. Disaster Risk Reduct. (2017). doi: 10.1016/J.IJDRR.2017.10.016. [DOI] [Google Scholar]
- [9].Whittaker J, Blanchi R, Haynes K, Leonard J, Opie K, Experiences of sheltering during the Black Saturday bushfires: Implications for policy and research, Int. J. Disaster Risk Reduct. 23 (2017) 119–127. doi: 10.1016/J.IJDRR.2017.05.002. [DOI] [Google Scholar]
- [10].McLennan J, Elliott G, Omodei M, Householder decision-making under imminent wildfire threat: stay and defend or leave?, Int. J. Wildl. Fire 21 (2012) 915. doi: 10.1071/WF11061. [DOI] [Google Scholar]
- [11].Alsnih R, Rose J, Stopher P, Understanding household evacuation decisions using a stated choice survey: case study of bush fires, in: Transp. Res. Board Annu. Meet. 84th, 2005. [Google Scholar]
- [12].McLennan J, Paton D, Beatson R, Psychological differences between south-eastern Australian householders’ who intend to leave if threatened by a wildfire and those who intend to stay and defend, Int. J. Disaster Risk Reduct. 11 (2015) 35–46. doi: 10.1016/J.IJDRR.2014.11.008. [DOI] [Google Scholar]
- [13].McLennan J, Elliott G, Wait and see’: the elephant in community bushfire safety room, in: Bushfire CRC AFAC 2012. Conf. Res. Forum, 2012: pp. 56–69. [Google Scholar]
- [14].Russo F, Chilà G, Integrated travel demand models for evacuations: a bridge between social science and engineering, Int. J. Saf. Secur. Eng 4 (2014) 19–37. doi: 10.2495/SAFE-V4-N1-19-37. [DOI] [Google Scholar]
- [15].Urata J, Pel AJ, People’s Risk Recognition Preceding Evacuation and Its Role in Demand Modeling and Planning, Risk Anal. (2017). doi: 10.1111/risa.12931. [DOI] [PubMed] [Google Scholar]
- [16].Fu H, Wilmot C, Survival Analysis-Based Dynamic Travel Demand Models for Hurricane Evacuation, Transp. Res. Rec. J. Transp. Res. Board 1964 (2006) 211–218. doi: 10.3141/1964-23. [DOI] [Google Scholar]
- [17].Fu H, Wilmot C, Sequential Logit Dynamic Travel Demand Model for Hurricane Evacuation, Transp. Res. Rec. J. Transp. Res. Board 1882 (2004) 19–26. doi: 10.3141/1882-03. [DOI] [Google Scholar]
- [18].Hasan S, Mesa-Arango R, Ukkusuri S, A random-parameter hazard-based model to understand household evacuation timing behavior, Transp. Res. Part C Emerg. Technol 27 (2013) 108–116. doi: 10.1016/J.TRC.2011.06.005. [DOI] [Google Scholar]
- [19].Sadri AM, Ukkusuri SV, Murray-Tuite P, A random parameter ordered probit model to understand the mobilization time during hurricane evacuation, Transp. Res. Part C Emerg. Technol 32 (2013) 21–30. doi: 10.1016/J.TRC.2013.03.009. [DOI] [Google Scholar]
- [20].Dixit V, Wilmot C, Wolshon B, Modeling Risk Attitudes in Evacuation Departure Choices, Transp. Res. Rec. J. Transp. Res. Board 2312 (2012) 159–163. doi: 10.3141/2312-17. [DOI] [Google Scholar]
- [21].Beloglazov A, Almashor M, Abebe E, Richter J, Steer KCB, Simulation of wildfire evacuation with dynamic factors and model composition, Simul. Model. Pract. Theory 60 (2016) 144–159. doi: 10.1016/J.SIMPAT.2015.10.002. [DOI] [Google Scholar]
- [22].Cova TJ, Johnson JP, Microsimulation of Neighborhood Evacuations in the Urban–Wildland Interface, Environ. Plan. A 34 (2002) 2211–2229. doi: 10.1068/a34251. [DOI] [Google Scholar]
- [23].Gan H-S, Richter K-F, Shi M, Winter S, Integration of simulation and optimization for evacuation planning, Simul. Model. Pract. Theory 67 (2016) 59–73. doi: 10.1016/J.SIMPAT.2016.07.001. [DOI] [Google Scholar]
- [24].Li D, Cova TJ, Dennison PE, Setting Wildfire Evacuation Triggers by Coupling Fire and Traffic Simulation Models: A Spatiotemporal GIS Approach, Fire Technol. (2018) 1–26. doi: 10.1007/s10694-018-0771-6. [DOI] [Google Scholar]
- [25].Veeraswamy A, Galea ER, Filippidis L, Lawrence PJ, Haasanen S, Gazzard RJ, Smith TEL, The simulation of urban-scale evacuation scenarios with application to the Swinley forest fire, Saf. Sci 102 (2018) 178–193. doi: 10.1016/J.SSCI.2017.07.015. [DOI] [Google Scholar]
- [26].Wolshon B, Marchive E, Emergency Planning in the Urban-Wildland Interface: Subdivision-Level Analysis of Wildfire Evacuations, J. Urban Plan. Dev 133 (2007) 73–81. doi: 10.1061/(ASCE)0733-9488(2007)133:1(73). [DOI] [Google Scholar]
- [27].McNeill IM, Dunlop PD, Skinner TC, Morrison DL, Predicting delay in residents’ decisions on defending v. evacuating through antecedents of decision avoidance, Int. J. Wildl. Fire 24 (2015) 153–161. doi: 10.1071/WF12213. [DOI] [Google Scholar]
- [28].Whittaker J, Haynes K, Handmer J, McLennan J, Community safety during the 2009 Australian “Black Saturday” bushfires: an analysis of household preparedness and response, Int. J. Wildl. Fire 22 (2013) 841. doi: 10.1071/WF12010. [DOI] [Google Scholar]
- [29].McLennan J, Elliott G, Omodei M, Whittaker J, Householders’ safety-related decisions, plans, actions and outcomes during the 7 February 2009 Victorian (Australia) wildfires, Fire Saf. J 61 (2013) 175–184. doi: 10.1016/J.FIRESAF.2013.09.003. [DOI] [Google Scholar]
- [30].Lindell MK, Perry RW, Communicating Environmental Risk in Multiethnic Communities, 2004. [Google Scholar]
- [31].Cova TJ, Drews FA, Siebeneck LK, Musters A, Protective Actions in Wildfires: Evacuate or Shelter-in-Place?, Nat. Hazards Rev 10 (2009) 151–162. doi: 10.1061/(ASCE)1527-6988(2009)10:4(151). [DOI] [Google Scholar]
- [32].Gwynne SMV, Kuligowski ED, Kinsey MJ, Hulse LM, Modelling and influencing human behaviour in fire, Fire Mater. 41 (2017) 412–430. doi: 10.1002/fam.2391. [DOI] [Google Scholar]
- [33].Gwynne SM, Hulse LM, Kinsey MJ, Guidance for the Model Developer on Representing Human Behavior in Egress Models, Fire Technol. (2015) 1–26. doi: 10.1007/s10694-015-0501-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Kuligowski ED, The Process of Human Behavior in Fires - NIST Technical Note 1632, 2008. [Google Scholar]
- [35].Gwynne SMV, Translating Behavioral Theory of Human Response into Modeling Practice - Report NISTGCR 12–972, 2013. [Google Scholar]
- [36].Sime JD, Escape behaviour in fires : “panic” of affiliation?, (1984). http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.332982 (accessed March 7, 2018). [Google Scholar]
- [37].Canter D, Fire and Human Behaviour - an Introduction, in: Canter D. (Ed.), Fires Hum. Behav, John Wiley & Sons, 1980. [Google Scholar]
- [38].Tong D, Canter D, The decision to evacuate: a study of the motivations which contribute to evacuation in the event of fire, Fire Saf. J 9 (1985) 257–265. [Google Scholar]
- [39].Breaux J, Canter D, Sime JD, Psychological aspects of behaviour of people in fire situations, in: Psychol. Asp. Behav. People Fire Situations, 1976: pp. 39–50. [Google Scholar]
- [40].Canter D, Donald I, Chalk J, Pedestrian Behaviour during Emergencies Underground: The psychology of crowd control under life threatening circumstances, in: Saf. Road Rail Tunnels, 1992: pp. 135–150. [Google Scholar]
- [41].Proulx G, A stress model for people facing a fire, J. Environ. Psychol 13 (1993) 137–147. doi: 10.1016/S0272-4944(05)80146-X. [DOI] [Google Scholar]
- [42].Lovreglio R, Fonzone A, dell’Olio L, Borri D, A study of herding behaviour in exit choice during emergencies based on random utility theory, Saf. Sci 82 (2016). doi: 10.1016/j.ssci.2015.10.015. [DOI] [Google Scholar]
- [43].Lovreglio R, Ronchi E, Nilsson D, An Evacuation Decision Model based on perceived risk, social influence and behavioural uncertainty, Simul. Model. Pract. Theory 66 (2016) 226–242. doi: 10.1016/j.simpat.2016.03.006. [DOI] [Google Scholar]
- [44].J.. Bryan, Behavioral Response to Fire and Smoke, in: DiNenno JD, Al E. (Eds.), SFPE Handb. Fire Prot. Eng 3th Ed., National Fire Protection Association, 2002: p. 3.315–3.341. [Google Scholar]
- [45].Murray-Tuite P, Wolshon B, Evacuation transportation modeling: An overview of research, development, and practice, Transp. Res. Part C Emerg. Technol 27 (2013) 25–45. doi: 10.1016/J.TRC.2012.11.005. [DOI] [Google Scholar]
- [46].Trainor JE, Murray-Tuite P, Edara P, Fallah-Fini S, Triantis K, Interdisciplinary Approach to Evacuation Modeling, Nat. Hazards Rev 14 (2013) 151–162. doi: 10.1061/(ASCE)NH.1527-6996.0000105. [DOI] [Google Scholar]
- [47].Wachinger G, Renn O, Begg C, Kuhlicke C, The Risk Perception Paradox-Implications for Governance and Communication of Natural Hazards, Risk Anal. 33 (2013) 1049–1065. doi: 10.1111/j.15396924.2012.01942.x. [DOI] [PubMed] [Google Scholar]
- [48].Taylor MAP, Freeman SK, A review of planning and operational models used for emergency evacuation situations in Australia, Procedia Eng. 3 (2010) 3–14. doi: 10.1016/J.PROENG.2010.07.003. [DOI] [Google Scholar]
- [49].Hess DB, Gotham JC, Multi-Modal Mass Evacuation in Upstate New York: A Review of Disaster Plans, J. Homel. Secur. Emerg. Manag 4 (2007). doi: 10.2202/1547-7355.1317. [DOI] [Google Scholar]
- [50].Naghawi H, Wolshon B, Operation of multimodal transport system during mass evacuations, Can. J. Civ. Eng 42 (2015) 81–88. doi: 10.1139/cjce-2014-0177. [DOI] [Google Scholar]
- [51].Lindell MK, EMBLEM2: An empirically based large scale evacuation time estimate model, Transp. Res. Part A Policy Pract. 42 (2008) 140–154. doi: 10.1016/J.TRA.2007.06.014. [DOI] [Google Scholar]
- [52].Paveglio TB, Prato T, Dalenberg D, Venn TJ, Understanding evacuation preferences and wildfire mitigations among northwest Montana residents, Int. J. Wildl. Fire 23 (2014) 435–444. doi: 10.1071/WF13057. [DOI] [Google Scholar]
- [53].McLennan J, Cowlishaw S, Paton D, Beatson R, Elliott G, Predictors of south-eastern Australian householders’ strengths of intentions to self-evacuate if a wildfire threatens: two theoretical models, Int. J. Wildl. Fire 23 (2014) 1176. doi: 10.1071/WF13219. [DOI] [Google Scholar]
- [54].Reneke PA, Evacuation Decision Model, 2013. doi: 10.6028/NIST.IR.7914. [DOI] [Google Scholar]
- [55].Kuligowski ED, Terror Defeated: Occupant Sensemaking, Decision-making and Protective Action in the 2001 World Trade Center Disaster, University of Colorado at Boulder, 2011. [Google Scholar]
- [56].Kuligowski E, Predicting Human Behavior During Fires, Fire Technol. 49 (2013) 101–120. doi: 10.1007/s10694-011-0245-6. [DOI] [Google Scholar]
- [57].E Drabek T, Understanding disaster warning responses, Soc. Sci. J 36 (1999) 515–523. doi: 10.1016/S0362-3319(99)00021-X. [DOI] [Google Scholar]
- [58].Kinateder MT, Kuligowski ED, Reneke PA, Peacock RD, Risk perception in fire evacuation behavior revisited: definitions, related concepts, and empirical evidence, Fire Sci. Rev 4 (2015) 1. doi: 10.1186/s40038-014-0005-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Lovreglio R, Ronchi E, Nilsson D, A model of the decision-making process during pre-evacuation, Fire Saf. J 78 (2015). doi: 10.1016/j.firesaf.2015.07.001. [DOI] [Google Scholar]
- [60].Gibson J, The theory of affordances, in: Giesking JJ, Mangold W. (Eds.), People, Place, Sp. Read, 1977: pp. 56–60. [Google Scholar]
- [61].Hartson R, Cognitive, physical, sensory, and functional affordances in interaction design, Behav. Inf. Technol 22 (2003) 315–338. doi: 10.1080/01449290310001592587. [DOI] [Google Scholar]
- [62].Greene WH, Econometric Analysis - 7th Edition, Pearson, 2011. [Google Scholar]
- [63].Kuligowski ED, Mileti DS, Modeling pre-evacuation delay by occupants in World Trade Center Towers 1 and 2 on September 11, 2001, Fire Saf. J 44 (2009) 487–496. doi: 10.1016/j.firesaf.2008.10.001. [DOI] [Google Scholar]
- [64].Sherman MF, Peyrot M, Magda LA, Gershon RRM, Modeling pre-evacuation delay by evacuees in World Trade Center Towers 1 and 2 on September 11, 2001: A revisit using regression analysis, Fire Saf. J 46 (2011) 414–424. doi: 10.1016/j.firesaf.2011.07.001. [DOI] [Google Scholar]
- [65].Ronchi E, Reneke PA, Peacock RD, A Method for the Analysis of Behavioural Uncertainty in Evacuation Modelling, Fire Technol. (2013). doi: 10.1007/s10694-013-0352-7. [DOI] [Google Scholar]
- [66].Lovreglio R, Ronchi E, Borri D, The validation of evacuation simulation models through the analysis of behavioural uncertainty, Reliab. Eng. Syst. Saf 131 (2014) 66–174. doi: 10.1016/j.ress.2014.07.007. [DOI] [Google Scholar]
- [67].Lovreglio R, Modelling Decision-Making in Fire Evacuation based on the Random Utility Theory, Politecnico of Bari, Milan and Turin, 2016. [Google Scholar]
- [68].Dow K, Cutter SL, Public orders and personal opinions: household strategies for hurricane risk assessment, Glob. Environ. Chang. Part B Environ. Hazards 2 (2000) 143–155. doi: 10.1016/S14642867(01)00014-6. [DOI] [Google Scholar]
- [69].Whitehead JC, Edwards B, Van Willigen M, Maiolo JR, Wilson K, Smith KT, Heading for higher ground: factors affecting real and hypothetical hurricane evacuation behavior, Glob. Environ. Chang. Part B Environ. Hazards 2 (2000) 133–142. doi: 10.1016/S1464-2867(01)00013-4. [DOI] [Google Scholar]
- [70].Benight CC, Collective efficacy following a series of natural disasters, Anxiety, Stress Coping. 17 (2004) 401–420. doi: 10.1080/10615800512331328768. [DOI] [Google Scholar]
- [71].Huang S-K, Lindell MK, Prater CS, Wu H-C, Siebeneck LK, Household Evacuation Decision Making in Response to Hurricane Ike, Nat. Hazards Rev 13 (2012) 283–296. doi: 10.1061/(ASCE)NH.1527-6996.0000074. [DOI] [Google Scholar]
- [72].Fu H, Wilmot C, Static vs. dynamic and aggregate vs. disaggregate: a comparison between practice and research in hurricane evacuation travel demand modeling, in: 86th Annu. Meet. Transp. Res. Board, 2007. [Google Scholar]
- [73].Mozumder P, Raheem N, Talberth J, Berrens RP, Investigating intended evacuation from wildfires in the wildland–urban interface: Application of a bivariate probit model, For. Policy Econ 10 (2008) 415–423. doi: 10.1016/J.FORPOL.2008.02.002. [DOI] [Google Scholar]
- [74].Bateman JM, Edwards B, Gender and Evacuation: A Closer Look at Why Women Are More Likely to Evacuate for Hurricanes, Nat. Hazards Rev 3 (2002) 107–117. doi: 10.1061/(ASCE)1527-6988(2002)3:3(107). [DOI] [Google Scholar]
- [75].Strawderman L, Salehi A, Babski-Reeves K, Thornton-Neaves T, Cosby A, Reverse 911 as a Complementary Evacuation Warning System, Nat. Hazards Rev 13 (2012) 65–73. doi: 10.1061/(ASCE)NH.1527-6996.0000059. [DOI] [Google Scholar]
- [76].Whittaker J, Handmer J, Community bushfire safety: a review of post-Black Saturday research, Aust. J. Emerg. Manag 35 (2010). [Google Scholar]
- [77].Lovreglio R, Fonzone A, dell’Olio L, A mixed logit model for predicting exit choice during building evacuations, Transp. Res. Part A Policy Pract. 92 (2016). doi: 10.1016/j.tra.2016.06.018. [DOI] [Google Scholar]
- [78].Lovreglio R, Fonzone A, Dell’Olio L, Borri D, A Study of Herding Behaviour in Exit Choice during Emergencies based on Random Utility Theory, Saf. Sci 82 (2016) 421–431. doi: 10.1016/j.ssci.2015.10.015. [DOI] [Google Scholar]
- [79].Lovreglio R, Borri D, Dell’Olio L, Ibeas A, A discrete choice model based on random utilities for exit choice in emergency evacuations, Saf. Sci 62 (2014) 418–426. doi: 10.1016/j.ssci.2013.10.004. [DOI] [Google Scholar]
- [80].Hasan S, Ukkusuri S, Gladwin H, Murray-Tuite P, Behavioral Model to Understand Household-Level Hurricane Evacuation Decision Making, J. Transp. Eng 137 (2011) 341–348. doi: 10.1061/(ASCE)TE.1943-5436.0000223. [DOI] [Google Scholar]
- [81].Greene WH, Hensher DA, Modeling Ordered Choices: A Primer, Cambridge University Press, 2010. [Google Scholar]
- [82].Train K, Discrete choice methods with simulation, Cambridge university press, 2003. [Google Scholar]
- [83].Cohn PJ, Carroll MS, Kumagai Y, Evacuation behavior during wildfires: results of three case studies, West. J. Appl. For 21 (2006) 39–48. [Google Scholar]
- [84].Tibbits A, Whittaker J, Stay and defend or leave early: Policy problems and experiences during the 2003 Victorian bushfires, Environ. Hazards 7 (2007) 283–290. doi: 10.1016/j.envhaz.2007.08.001. [DOI] [Google Scholar]
- [85].McNeill IM, Dunlop PD, Skinner TC, Morrison DL, A value- and expectancy-based approach to understanding residents, Int. J. Wildl. Fire 25 (2016) 378–389. doi: 10.1071/WF15051. [DOI] [Google Scholar]
- [86].Whittaker J, Eriksen C, Haynes K, Gendered responses to the 2009 Black Saturday bushfires in Victoria, Australia, Geogr. Res 54 (2016) 203–215. doi: 10.1111/1745-5871.12162. [DOI] [Google Scholar]
- [87].Eriksen C, Gill N, Head L, The gendered dimensions of bushfire in changing rural landscapes in Australia, J. Rural Stud 26 (2010) 332–342. doi: 10.1016/J.JRURSTUD.2010.06.001. [DOI] [Google Scholar]
- [88].McLennan J, Elliott G, Omodei M, Issues in Community Bushfire Safety: Analyses of Interviews Conducted by the 2009 Victorian Bushfires Research Task Force, 2011. [Google Scholar]
- [89].Hensher DA, Rose JM, Greene WH, Applied Choice Analysis: A Primer, Cambridge University Press, 2005. [Google Scholar]
- [90].Leek JT, Peng RD, Statistics: P values are just the tip of the iceberg, Nature. 520 (2015) 612–612. doi: 10.1038/520612a. [DOI] [PubMed] [Google Scholar]
- [91].Levine TR, Weber R, Park HS, Hullett CR, A Communication Researchers’ Guide to Null Hypothesis Significance Testing and Alternatives, Hum. Commun. Res 34 (2008) 188–209. doi: 10.1111/j.1468-2958.2008.00318.x. [DOI] [Google Scholar]
- [92].Train KE, Discrete Choice Methods with Simulation, Cambridge University Press, Cambridge, 2009. doi: 10.1017/CBO9780511805271. [DOI] [Google Scholar]
- [93].Zha Q, Zhang H, Consensus reaching in social network group decision making: Research paradigms and challenges, Knowledge-Based Syst. 162 (2018) 3–13. doi: 10.1016/J.KNOSYS.2018.06.036. [DOI] [Google Scholar]
- [94].Li G, Kou G, Peng Y, A Group Decision Making Model for Integrating Heterogeneous Information, IEEE Trans. Syst. Man, Cybern. Syst 48 (2018) 982–992. doi: 10.1109/TSMC.2016.2627050. [DOI] [Google Scholar]
- [95].Qian Hang, Toolkit on Econometrics and Economics Teaching, Https://Www.Mathworks.Com/Matlabcentral/Fileexchange/32601-Toolkit-on-Econometrics-andEconomics-Teaching?Focused=5197845&tab=function. (2011). [Google Scholar]