Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2024 Jun 6;9(24):26149–26158. doi: 10.1021/acsomega.4c01576

Cobalt(II) Single-Ion Magnet Coordinated by Double Deprotonation of 2,2′-Bipyridine-6,6′-diol Ligands

En-Che Yang †,*, Yu-Tung Tsai †, Po-Ya Chang ‡, Mykhaylo Ozerov §, Jurek Krzystek §, Su-Ying Chien ∥, Jun-Xian He †, Ting-Shen Kuo ⊥, Hwo-Shuenn Sheu ‡,*
PMCID: PMC11190935  PMID: 38911747

Abstract

graphic file with name ao4c01576_0010.jpg

In this study, we synthesized a new Co(II) complex, [NMe4]2[Co(bpyO2)2] (1), using deprotonated 2,2′-bipyridine-6,6′-diol ligands (bpyO22–). This compound exhibits a significant zero-field splitting (D) value. The far-infrared magneto spectroscopy and high-frequency and field electron paramagnetic resonance (HFEPR) measurements indicated that compound 1 possesses D = −54.8 cm–1 and E ∼ 0 cm–1. These findings were subsequently confirmed by other experimental data, including DC magnetic susceptibilities and variable temperature and variable magnetic field reduced magnetizations. Additionally, we conducted a series of AC magnetic susceptibility measurements to investigate the kinetics of magnetization relaxation. Below 6.6 K and under zero external magnetic field, fast quantum tunneling of magnetization (QTM) dominates (∼570 Hz), and temperature-independent out-of-phase signals are observed. Above 8.1 K, temperature-dependent behavior is observed. Furthermore, we examined the AC magnetic susceptibility behavior under external magnetic fields ranging from 300 to 4000 G. The effect of QTM is significantly reduced in the presence of an external magnetic field. Temperature-dependent behavior is primarily governed by Raman relaxation. Through structural analysis of compound 1 and a series of pure nitrogen-coordinated single-ion magnets (SIMs), we propose that the oxo substituents from the double-deprotonated form of the 2,2′-bipyridine-6,6′-diol ligands donate their negative charge to the pyridine ring, forming amido anion sites. This triggers a more pronounced out-of-phase signal than that observed in pure pyridine-coordinated compounds. Moreover, we observed intermolecular interactions, including intermolecular hydrogen bonding, which, to some extent, influenced the slow relaxation of molecules. Therefore, we speculate that the slow relaxation phenomenon of compound 1 may be attributed to the combination of oxo back-donating effects and intermolecular interactions.

Introduction

Extensive research has been undertaken in the realm of molecular magnets1 due to their potential applications in data storage and quantum computing. These molecules possess significant magnetic anisotropy, which refers to the variance in energy levels between distinct magnetic states. Anisotropy plays a crucial role in establishing enduring magnetic states, a fundamental characteristic of molecular magnets.2 In molecular magnets, the energy barrier for spin-flip is determined by both the magnetic anisotropy (D) and the spin value (S). For integer spin values, the energy barrier is represented by |D|S2, whereas for half-integer spin values, it takes the form of |D|(S2 – 1/4).3 Up until 2010, most research endeavors centered on increasing the number of metal ions within a cluster to achieve a giant spin number, thereby augmenting the magnitude of the energy barrier.4 However, this approach encountered a bottleneck as the molecular D value decreased more rapidly than the increase in molecular spin, resulting in only a modest enhancement of the effective energy barrier for spin-flip.5 An alternative approach, involving a single metal ion with high magnetic anisotropy and an appropriate spin value (S), has effectively achieved the creation of single-ion magnets (SIMs). The pioneering instance of SIMs was exemplified by the [TbPc2]− complex, developed by Ishikawa et al. in 2003.6 This achievement demonstrated that a single metal ion with substantial magnetic anisotropy has the potential to yield a molecular magnet with out-of-phase signals reaching record-high temperatures of approximately 40 K.

Prior to 2007, research on molecular magnets primarily focused on first-row transition metals due to their high abundance and accessibility.7 Among them, Co(II) possesses strong spin–orbital coupling, making it prone to generating larger magnetic anisotropy and rendering it an ideal candidate for single-ion magnet (SIM) studies.8 In 2011, Long and colleagues reported a successful SIM using [Ph4P]2 [Co(SPh)4], demonstrating slow magnetization relaxation and out-of-phase signals up to 7 K without an applied DC magnetic field.9 This indicated when a single Co(II) ion combined with suitable ligands in a pseudotetrahedral geometry, it could exhibit SIM behavior. Subsequently, ligands containing sulfur,10 phosphorus,11 and pure oxygen12 were investigated. Regarding pure nitrogen ligands, Slageren and his colleagues reported a Co(II) SIM chelated with two bis-sulfonamide ligands,13 which exhibited out-of-phase signals reaching a record high of 20 K and magnetization hysteresis at 1.8 K. In 2019, Chen and colleagues extended the ligands to include amides,14 resulting in more significant hysteresis loops observed at 1.8 K and out-of-phase signals exceeding 20 K. These instances indicated that whether stabilized by sulfone or carbonyl groups, amide anion ligands can effectively create dramatic Co(II) SIM compounds. In 2019, Zheng and colleagues successfully prepared SIMs by combining sulfonamide and pyridine moieties on the same ligand, displaying out-of-phase signals at about 12 K.15 In 2022, our laboratory combined chelating sulfonamide ligands with monodentate pyridine and chelating 2,9-diphenyl-phenanthroline ligands. The results showed that only the rigid and chelating ligand 2,9-diphenyl-phenanthroline exhibited out-of-phase signals up to 12 K without an applied DC magnetic field.16 While pyridine-like ligands typically act as π donors in the angular overlap model (AOM),17 these two cases suggest that replacing two of the four amido anion ligands with pyridines can decrease the temperatures at which out-of-phase signals occur. In 2020, we employed only 2,9-diphenyl-phenanthroline as the ligand. Without an applied DC magnetic field, no out-of-phase signals were observed.18 After applying a 1000 G DC magnetic field frequency-dependent out-of-phase signals were observed, reaching a maximum of 6 K. These findings collectively highlight the significance of amide anion ligands in enabling pure nitrogen-coordinated ligands to exhibit SIM behavior. In contrast, pure pyridine ligands alone are ineffective in triggering SIM behavior. In this study, we aim to extend our investigation by testing bipyridine ligands with substituted oxo groups on the pyridine moiety to determine if the resonance pathway can induce an amide anion form, resulting in SIM characteristics.

Results and Discussion

Synthesis and Structure

We used deprotonated 2,2′-bipyridine-6,6′-diol (abbreviated as bpyO22–) as a ligand to synthesize compound 1, [NMe4]2[Co(bpyO2)2]. The synthesis process involved mixing Co(ClO4)2·6H2O and bpyO2H2 in dimethylformamide (DMF) at room temperature, followed by the dropwise addition of 25% (NMe4)OH/MeOH as a base. The reaction proceeded for 2 h, and then diethyl ether vapor was diffused into the resulting solution to obtain dark pink crystals of compound 1. There are two independent complexes in the lattice. The structure of compound 1 is shown in Figure 1. The Co(II) ion in compound 1 coordinates with two doubly deprotonated ligands that are roughly perpendicular. The two independent complexes form a distorted tetrahedral geometry with dihedral angles of 83.29 and 83.34°. Additionally, the two C2 axes of the bipyridine ligands are not colinear but twisted at angles of 17.56 and 16.19°. The N–Co–N angles on both ligands are significantly smaller than the ideal tetrahedron (109.47°), measuring 81.24 and 81.90°, respectively. The four Co(II)–N bonds have bond lengths in the range of 1.985–2.032 Å. The bond-valence-sum (BVS) calculation (Table 2S) confirms the charge on the cobalt ion is +2. The two pyridine planes on the same ligand in compound 1 roughly remain on the same plane but with a small twist of 8.341 to 12.52°. The most notable feature of complex 1 is the C–O, C–N, and C–C bond lengths on the ligands. The eight C–O bonds exhibit bond lengths in the range of 1.256–1.275 Å, strongly indicating C=O double bond characteristics. The immediate C–C bonds are in the range of 1.445–1.427 Å, deviating largely from the average value of 1.40 Å for C–C bond lengths in pyridine. All of the other C–C bond lengths are in the range of 1.353–1.408 Å, which are quite agreeable or slightly shorter than the average C–C bond lengths in pyridine. The N–C bonds in the pyridine rings have bond lengths in the range of 1.355–1.381 Å, which are relatively longer than the typical C–N bond length (1.34 Å) in pyridine. Based on these observations, it is suggested that the negative charges do not reside on the oxy-group but on the N atoms, which delocalize onto the pyridine rings to some extent. Thus, it is more reasonable to treat it as an amide anion stabilized by both the C=O group and the resonance effect of the pyridine ring (Scheme 1S).

Figure 1.

Figure 1

Open in a new tab

Ortep plot of complex 1, [NMe4]2[Co(bpyO2)2] [H2O]2. Purple denotes cobalt, blue nitrogen, red oxygen, gray carbon, and white hydrogen atoms.

Magnetic Resonance Measurements

In order to accurately measure the zero-field splitting energy of compound 1, we conducted far-infrared magneto spectroscopy (FIRMS) experiments, which allowed us to directly probe the transition from the Ms = |±3/2⟩ ground to the Ms = |±1/2⟩ first excited Kramers’ doublet.19 The infrared transmission spectra were measured for the powder sample at a temperature of 5.5 K and in the magnetic field range of 0.0–17.5 T. To discern the magnetic absorptions, the spectra were divided by the reference spectrum, which is the average spectrum for all magnetic fields. Such a normalization process effectively removes nonmagnetic contributions to the transmission intensity, revealing spectral features sensitive to the magnetic field. The resulting spectra are shown in Figure 2 (top) as a heatmap in the magnetic field and energy (frequency) domain. The transition energy between Kramers’ doublets is similar for all randomly oriented microcrystallines at low magnetic fields, yielding the strongest spectral feature seen as a blue area on the heatmap. Although this area is obscured by noise due to low intensity below 140 cm–1 (Figure 2, bottom), magnetic absorption is fairly resolvable at zero field. In high magnetic fields, Zeeman term spreads the magnetic absorption over a broad frequency range, whose high-frequency edge is well resolved at 145 cm–1 due to increased intensity of the transmission signal. We assign the energy of 109.6 (±0.5) cm–1 to the zero-field inter-Kramers transitions. With this information, we will next use high-frequency and -field electron paramagnetic resonance (HFEPR) to determine the sign of D and the magnitude of E.

Figure 2.

Figure 2

Open in a new tab

(Top) 2D FIRMS plot of compound 1, [NMe4]2[Co(bpyO2)2], showing the zero-field magnetic transition originating from 109.6(0.5) cm–1. (Bottom) Transmittance line plot of FIRMS data for compound 1. Data obtained at 9.8 G and 17.15 T.

To complement the FIRMS experiment and possibly obtain the sign of D and magnitude of E, we performed high-frequency and -field electron paramagnetic resonance (HFEPR) in the 270–500 GHz frequency range at 10 K. The resulting spectra are shown in Fig. 5S in the Supporting Information. The only resonances observed originated from solid molecular dioxygen, a common contaminant in low-temperature HFEPR, and an unidentified g = 2.00 species. There appeared faint traces of other resonances at some frequencies; however, they were of extremely low intensity and most likely do not represent the bulk properties of the complex. Compound 1 is thus essentially EPR-silent in the conditions listed above. This indicates two things. First, it suggests that the D value is negative because, if it were positive, the allowed ΔMs = 1 EPR intra-Kramers transition within the ground Ms = ±1/2 doublet would prominently show in the spectra. Second, it implies that the zero-field splitting (zfs) tensor is axial. If it were not axial, we would observe the ΔMs = 3 transition within the ground Ms = ±3/2 Kramers doublet. Although strictly forbidden according to the EPR selection rules, this transition becomes increasingly allowed through the finite rhombic parameter E. This phenomenon has been observed in the literature related to Co(II) SIMs.20 Therefore, the value of E must be very small. We can thus safely assume that the two-dimensional (2D)* value obtained from FIRMS is equal to 2D. This result is also consistent with the structure. From Fig. 2S, we obtained a dihedral angle of approximately 83° between the planes of the two ligands, close to being perpendicular bisectors of each other. Based on the results of FIRMS and HFEPR, we will subsequently perform curve fitting of DC magnetization and reduced magnetization using parameters D = −54.8 cm–1 and E ∼ 0 cm–1.

Magnetic Properties and Calculation

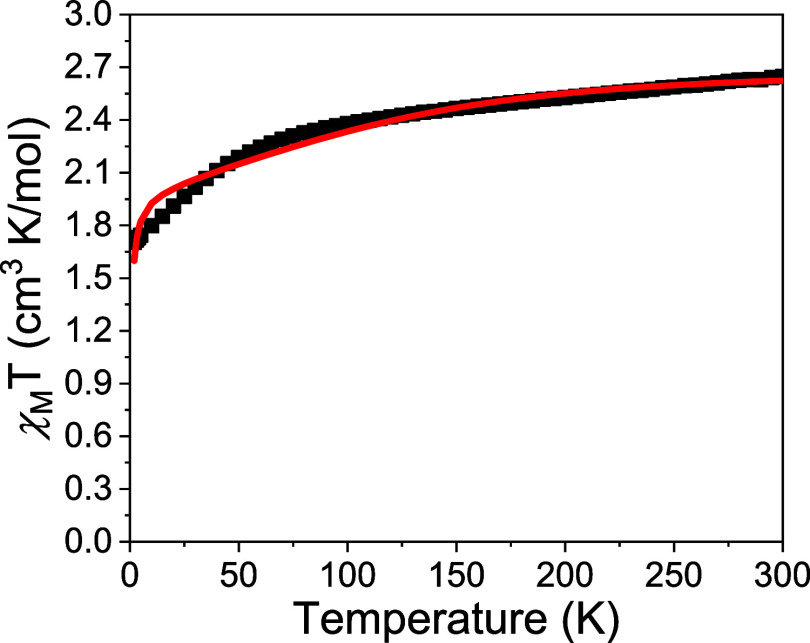
DC magnetic susceptibility measurement was then employed to study the magnetic properties of this material. In this study, a polycrystalline sample of compound 1 was utilized, and its magnetic susceptibility was measured within the temperature range of 2–300 K under a magnetic field strength of 1000 G. The results are presented in Figure 3, where it is observed that compound 1 exhibited a χMT value of 2.65 cm3 mol–1 K at 300 K. This value is notably higher than the theoretical spin-only value of 1.88 cm3 mol–1 K for an S = 3/2 system. Subsequently, the χMT value of compound 1 gradually decreased to 2.27 cm3 mol–1 K at 65 K and further declined to 1.7 cm3 mol–1 K at 2 K. Upon careful examination of the lattice packing, it was determined that two water molecules interacted with the oxygen atoms on the ligand through hydrogen bonding (as depicted in Fig. 6S). The unconventional hydrogen bonds were identified between the proton of the methyl group of the cation [NMe4]+ and the oxygen atom on the bpyO22– ligand. Additionally, the closest Co···Co distance is measured as 9.222 Å. As a result, it is believed that the overall behavior of χMT is influenced not only by the substantial zero-field splitting resulting from strong spin–orbit coupling but also by intermolecular interactions. However, due to the involvement of multiple processes within intermolecular interactions, quantifying them with limited parameters presents a challenge. Consequently, we employed a mean-field semiquantitative approach to interpret the behavior of χMT when utilizing the PHI program21 for curve fitting. The solid line in Figure 3 illustrates the fitting result obtained using the PHI program. A good alignment between the fitting outcomes and data is apparent above 30 K. Deviations observed below 30 K are likely attributed to the divergence of multiple intermolecular interaction mechanisms from the mean-field model. This behavior was also reported in the literature.22 The fitting uses the results of FIRMS and HFEPR of D = −54.8 cm–1, E ∼ 0 cm–1, and an intermolecular interaction strength of −0.064 cm–1.

Figure 3.

Figure 3

Open in a new tab

Magnetic susceptibility measurements for compounds 1, [NMe4]2[Co(bpyO2)2], where χMT vs T was measured from 2 to 300 K under 1000 G. The red solid line represents the fitting using the PHI program.

We then conducted variable temperature and variable magnetic field reduced magnetization experiments.23 We applied magnetic fields within the range of 1–6 T and varied the temperature between 2 and 4 K. The results of the reduced magnetization experiments are presented in Figure 4. The colored dots represent experimental data, while the solid red lines indicate the fitting results. In this context, the y-axis is M/Nβ, where M stands for magnetization, N represents Avogadro’s number, and β represents the Bohr magneton. The x-axis represents H/T, where H represents magnetic field strength in Tesla and T is the absolute temperature in Kelvin. By fixing the D and E values obtained from FIRMS and HFEPR, we conducted fitting solely for the g value. The fitting results perfectly match the experimental data, yielding a g value of 2.37.

Figure 4.

Figure 4

Open in a new tab

Experimental results (scatter) and simulation curve (the solid line) of reduced magnetization experiment, (1–6 T, 2–4 K) which are based on the parameters obtained from FIRMS measurements.

Subsequently, we employed the OpenMolcas program24 to conduct ab initio calculations in order to determine the transition moment for this S = 3/2 system. For this calculation, we utilized the ANO-RCC-VTZP basis set (referred to as VTZP) for Co(II) while employing the ANO-RCC-VDZ basis set for all other atoms. The input for the calculations was directly based on the X-ray structure. Angular momentum was set on the Co(II) metal center. RASSCF procedures were performed with 7 active electrons distributed across 5 orbitals, encompassing all 10 quartet and 40 doublet states.25 Subsequently, the RASSI procedure was utilized to compute spin–orbit interactions.26 The Single_Aniso method was employed to calculate the transition moments. The main outcomes of the Single_Aniso process are listed in Table 3S, which includes the following tables: “Energy of Spin–Orbit States”, “g Tensor”, “ZFS Hamiltonian”, and “D Tensor”. The direction of the g-axis is shown in the Supporting Information on page 12S. These results yield a D value of −73.04 cm–1 and an E value of +1.68 cm–1. Finally, the Ubar function was employed to generate an energy level plot and estimate the transition moments between different spin states (see Figure 5). Due to the significant discrepancy between the previously mentioned D value and the experimental value, we conducted additional calculations using ORCA 5.0.4.27 The calculations used scalar relativistic Douglas–Kroll–Hess (DKH) theory and were performed at the CASSCF/NEVPT2/def2-TZVPP level, incorporating spin–orbit mean-field (SOMF). NEVPT2 calculations were carried out for 7 electrons in five 3d orbitals [CAS(7, 5)]. At the same time, we also use Ab initio Ligand Field Theory (AILFT) to estimate d-orbital splitting, crystal field strength, ZFS, and the direction of the g-axis. Their main outputs are listed in Table 6S. The d-orbital splitting is shown in Fig. 16S. Since the direction of the g-axis is in close agreement with the results of OpenMolcas calculations, we will not redraw it. The resulting D value was −61.4 cm–1, which showed a much closer alignment with the experimental value compared to the previous calculation.

Figure 5.

Figure 5

Open in a new tab

Transition moment diagrams for compounds 1, [NMe4]2[Co(bpyO2)2], were obtained based on ab initio calculations using OpenMolcas. The numbers represent the magnitudes of the transition moments. Cobalt(II) was treated with the ANO-RCC-VTZP basis set.

In order to investigate the fundamental mechanism responsible for the observed slow magnetization relaxation in compound 1, [NMe4]2[Co(bpyO2)2], we conducted alternating current (AC) magnetic susceptibility measurements on polycrystalline samples of compound 1 in a temperature range of 1.9–15 K. The measurements involved applying an AC magnetic field within the frequency range of 1–1000 Hz at 3.5 G. As shown in Figure 6a, the out-of-phase signals of compound 1 under a zero direct current (DC) magnetic field are presented. Notably, below 6.6 K, the frequencies of the out-of-phase signals remain relatively constant at around 570 Hz across various temperatures. Above 6.9 K, the peak frequencies gradually increase with temperature, reaching approximately 918 Hz at 9.6 K. The temperature-independent behavior observed below 6.6 K indicates that the dominant process is quantum tunneling of magnetization (QTM).28 The rate of QTM falls within the frequency window of the AC oscillating field, making it observable.

Figure 6.

Figure 6

Open in a new tab

Out-of-phase signals of compound 1, [NMe4]2 [Co(bpyO2)2], in AC magnetic susceptibility measurements. (a) Top: under 0 G applied external magnetic field. (b) Bottom: under 300 G applied external magnetic field.

Conversely, due to the compound’s substantial zero-field splitting value (D = −54.8 cm–1), as mentioned in the literature,29 the Orbach process for compound 1 is nearly negligible below 10 K. Consequently, the observed temperature-dependent magnetization relaxation above 6.9 K is likely associated with the Raman process. In order to demonstrate that the temperature-independent behavior observed below 6.6 K is attributed to QTM, we applied a relatively small DC magnetic field (300 G) to the system. We conducted AC magnetic susceptibility measurements using the same frequency range of 1–1000 Hz within a temperature range of 1.9–13 K. Figure 6b illustrates the out-of-phase signals of compound 1 under a 300 G DC magnetic field. In comparison to the conditions with zero DC magnetic field shown in Figure 6a, it is evident that under a 300 G DC magnetic field, the out-of-phase signals across the frequency range of 1–1000 Hz are significantly distributed between 2.5 and10.5 K. This clearly indicates a temperature-dependent behavior. In other words, the presence of an external field substantially reduces the QTM process.

To understand the influence of external magnetic fields on magnetization relaxation, we conducted a series of AC magnetic susceptibility measurements on compound 1 under various applied DC magnetic fields. The applied magnetic fields included 0, 300, 500, 1000, 1500, 2000, 3000, and 4000 G. We used frequencies ranging from 1 to 1000 Hz within a temperature range of 1.9–13.0 K. Detailed in-phase and out-of-phase spectra are provided in Figs. 7S−14S. We plotted the natural logarithm of relaxation time vs inverse of temperature of the out-of-phase peaks under different magnetic fields in Figure 7. Quantifying magnetization relaxation processes under different external fields typically involves direct, Raman, Orbach, and QTM processes.30 Some literature employs formulas that incorporate Raman, Orbach, and QTM processes.13 However, in our case, the contribution of the Orbach process is nearly negligible due to its high energy barrier. The three-term formula is challenging to accurately quantify the magnitude of the Orbach process within this range. Similar to our case, literature often utilizes eq 1 to quantify spin relaxation processes,29 considering only Raman and QTM processes.

graphic file with name ao4c01576_m001.jpg 1

Figure 7.

Figure 7

Open in a new tab

Plot of ln(τ) versus 1/T for compound 1, [NMe4]2[Co(bpyO2)2], under different DC magnetic fields. The solid lines correspond to the fits to eq 1.

In eq 1, the first term corresponds to QTM, and the second term corresponds to Raman relaxation. Under the condition of zero magnetic field, the value of parameter B is quite large, at 570 s–1. The exponent of the Raman term is 6.16, with a constant C of 2.2 × 10–4 s–1 K–n. This indicates that QTM predominantly governs the phenomenon of magnetization relaxation. After the application of a small DC magnetic field (300 G), the exponent n of the Raman term generally remains around 6.64, and the constant C experiences a slight decrease to 1.4 × 10–4 s–1 K–n. Meanwhile, the value of parameter B experiences a significant reduction to 1.15 s–1. Hence, it strongly indicates that QTM exhibits a notable decrease under an applied magnetic field. When an applied DC magnetic field of 500 G is introduced, the exponent n of the Raman term remains at around 6.86, with the constant C being 7.84 × 10–5 s–1 K–n. The value of parameter B further decreases to 0.65 s–1. Within the range of applied DC magnetic fields from 1000 to 4000 G, the constant C remains between 1.67 × 10–5 and 3.26 × 10–5 s–1. The exponent n increases to the range of 7.21–7.52. The value of parameter B remains between 0.36 and 1.00 s–1 for applied DC magnetic fields of 1000 to 3000 G. This implies that the Raman process dominates the magnetization relaxations. At 4000 G, the value of parameter B bounces back to approximately 0.93 s–1. This behavior might be attributed to the participation of the unconsidered direct relaxation process under high magnetic field conditions (See Table 5S).

We also performed Argand (Cole–Cole) plots for the AC magnetic susceptibility. The Cole–Cole plots for the cases of zero external field and applied external fields above 1000 G (1000–4000 G) could all be well fitted using a single Debye model (eqs 2 and 3).31 Here, χS and χT represent the adiabatic (ω → ∞) and isothermal (ω → 0) susceptibilities, respectively. The parameter α is the distribution parameter, with values ranging from 0 to 1. A larger α value leads to a flatter curve. The results of these analyses are provided in Fig. 15S.

graphic file with name ao4c01576_m002.jpg 2
graphic file with name ao4c01576_m003.jpg 3

However, at low DC magnetic fields (300 and 500 G), the Cole–Cole plot exhibits a double-peak phenomenon at low temperatures, as shown in Figure 8. This double-peak behavior indicates the presence of two relaxation processes. According to the approach described in the literature,32 they can be well fitted using eqs 4 and 5. Under the condition of 300 G, between 2.5 and 6.3 K, the curve displays a peak at higher frequencies and another larger peak at lower frequencies. The peak at higher frequencies is likely attributed to the fast quantum tunneling of magnetization (QTM). When the temperature exceeds 7.8 K, only a single peak is observed, which can be attributed to a thermally activated process. With a DC magnetic field of 500 G, the QTM process is further suppressed. Nevertheless, we can still observe a significant tailing phenomenon at higher frequencies between 3.4 and 4.5 K. Beyond the applied magnetic field of 1000 G, this phenomenon essentially disappears, and the magnetization relaxation process is dominated by thermally activated processes. We speculate that this fast QTM process, similar to other Co(II) tetrahedra single-ion magnets (SIMs), is induced by the intermolecular interactions.

graphic file with name ao4c01576_m004.jpg 4
graphic file with name ao4c01576_m005.jpg 5

Figure 8.

Figure 8

Open in a new tab

Cole–Cole plots of compound 1, [NMe4]2[Co(bpyO2)2], under DC magnetic fields of 300 G (top) and 500 G (bottom). The left-hand side represents measurements at lower temperatures, while the right-hand side represents measurements at higher temperatures.

Scheme 1 presents a comparative analysis of compound 1 with other single-ion magnets (SIMs) containing pure nitrogen ligands. Subscripts denote the D values in their zero-field splitting (zfs), the temperature (To) at which their out-of-phase signals roughly appear at around 1000 Hz, and the applied magnetic field strength required to observe the out-of-phase signals. Additionally, we have marked the N–Co–N angles on top. In the literature, some have related the splitting of the d orbitals and the D value to the N–Co–N angle.33 However, from our computational results (see Fig. 16S), the pattern of d-orbital splitting does not match or correlate with patterns in the literature. This indicates that analyzing the d-orbital splitting pattern solely based on angles as variables is not suitable. In addition, in Scheme 1, it can be observed that the correlation between the N–Co–N angle and the D value is not apparent. Instead, among the substituents, the presence of amide anion shows significant differences in D values and the temperature of out-of-phase signals appearing in the absence of an external field. The first row includes three compounds (including 1) with substituted Co(II) complexes of bipyridine34 and phenanthroline.18 In these three compounds, D values range from −46 to −57 cm–1. However, it is notable that compound 1 is the only one displaying out-of-phase signals without the need for an applied DC magnetic field. The second row includes three SIMs obtained by coordinating sulfonamide or amide anions in a chelating manner.13,14 These three complexes all have four amide anions coordinating. They exhibit zfs, with D values ranging from −115 to −144 cm–1. Their out-of-phase signals appear above 20 K in zero DC magnetic field, making them the strongest Co(II) SIMs in all cases. The last four compounds involve amide anions combined with pyridine or imine moieties.15,16,35,36 Their D values typically fall between −50 and −60 cm–1, with a case of D = −94 cm–1 also reported. Regardless of the D value, their out-of-phase signals mostly appear around 10 K. From the analysis in Scheme 1, it can be inferred that among pseudotetrahedral configurations, SIMs coordinating four sulfonamide or amide anions exhibit the highest out-of-phase temperatures, followed by compounds with amide anions combined with pyridine or imine moieties. Generally, pure pyridine or phenanthroline ligands do not exhibit out-of-phase signals in zero DC magnetic field. What causes compound 1 to be an exception among the compounds in the first row? Structural analysis of compound 1 reveals that its oxo group has a C=O bond (1.256–1.275 Å), resembling a double bond between carbon and oxygen, suggesting resonance of the negative charge to the pyridine ring. As nitrogen has the highest electronegativity in pyridine, the negative charge is considerably distributed on the nitrogen atom. Thus, despite being a pyridine ligand, compound 1 is similar to amide anions to a significant extent. Consequently, it has a higher temperature for the appearance of out-of-phase signals under zero applied DC magnetic field. However, compared to pure amide or sulfonamide anion ligands, compound 1 has both a lower zero-field splitting |D| value and a lower temperature for the appearance of out-of-phase signals. This can be attributed to the delocalization of the negative charge on nitrogen in the electronic cloud of the pyridine ring, reducing nitrogen’s π donor ability. The comparisons among this series of compounds allow us to draw this reasonable postulation.

Scheme 1. Comparison of Compound 1, [NMe4]2[Co(bpyO2)2] (A), with Other Pseudotetrahedral SIMs Reported in the Literature (B–J), Featuring Pure Nitrogen Coordination.

Scheme 1

Open in a new tab

Conclusions

In this study, we synthesized compound 1, [NMe4]2 [Co(bpyO2)2], using double-deprotonated 2,2′-bipyridine-6,6′-diol as a ligand. Compound 1 transfers negative charge from the oxo substituent onto the pyridine ring through resonance, causing the ligands to resemble amide anions. However, compared to genuine amide anion ligands, compound 1 exhibits a lower |D| value and out-of-phase signal than expected. This difference may be attributed to the negative charge delocalizing onto the pyridine ring, thereby weakening its π-donating ability. Furthermore, within the text, we also observed intermolecular interactions, including intermolecular hydrogen bonding. We postulate that the combination of oxo back-donating effects and a certain extent of intermolecular interactions may be the reason for its pronounced slow magnetization relaxation under zero DC magnetic field. Further studies on compounds in this series will be conducted to determine the true cause of this observation.

Experimental Section

All commercially available chemicals were utilized without any further purification.

[NMe4]2[Co(bpyO2)2] (1)

A solution was prepared by dissolving 0.188 g (1 mmol) of 2,2-bipyridine-6,6′-diol in 6 mL of dimethylformamide (DMF). Separately, another solution containing 0.183 g of Co(ClO4)2·6H2O (0.5 mmol) in 6 mL of DMF was added dropwise to the first solution. While stirring, 0.728 g of TMAOH ((NMe4)OH 25% in MeOH) (2 mmol) was slowly added to the mixture. The reaction was allowed to proceed for 2 h at room temperature. Upon completion of the reaction, solid residues were removed through gravity filtration. Diethyl ether vapor was then introduced into the filtrate solution, resulting in the formation of dark pink crystals suitable for X-ray analysis. IR (KBr cm–1) spectra exhibited peaks at 3015 (s), 2343 (s), 1641 (s), 1598 (m), 1462 (m), 1364 (m), 1254 (s), 1156 (s), 1129 (s), 1087 (s), 948 (m), 861 (s), 788 (s), 628 (s), 604 (s), 541 (s), and 456 (s) cm–1. Elemental analysis for C28H43CoN6O7.5 yielded theoretical (experimental) values of N, 13.08 (13.11)%, C, 52.33 (52.31)%, and H, 6.74 (6.69)%. The yield was 35.2%. The synchrotron powder diffraction pattern of compound 1, shown in Fig. 17S, matches well with the simulated pattern of the single crystal structure.

X-ray Crystallography

The crystal structures of compounds 1 were analyzed using a Bruker D8 Venture diffractometer equipped with a Mo-target (Kα = 0.71073 Å) microfocus X-ray generator and a PHOTON-II CMOS detector. Experimental temperature was adjusted with a nitrogen flow (Oxford Cryosystems). The detector was placed 75 mm away from the crystalline samples, and a hemisphere of data was collected with a 10 s exposure time. Absorption corrections were carried out using semiempirical methods from equivalents for all three compounds. The full-matrix least-squares method was used for the structure solution and refinement of non-hydrogen atoms with the SHELX-2019/1 program.37 Anisotropic refinement was performed on all non-hydrogen atoms, while hydrogen atoms were calculated and refined using the riding model. Further details of the refinement for compounds 1 can be found in CCDC 2333572.† The powder X-ray diffraction pattern was collected at the BL01C2 beamline of the National Synchrotron Radiation Research Center, Taiwan, and shown in Fig. 17S.

Physical Property Measurements

Infrared spectra were recorded with KBr pellets using a PerkinElmer 1600 spectrometer. Elemental analysis was performed using a Heraeus Vario III-NCH instrument. DC magnetic measurements were carried out using a Quantum Design MPMS7 system, with the samples secured in an eicosane to prevent torque. The magnetic background was subtracted by blank measurements, and the diamagnetism correction was estimated from Pascal’s constant. AC magnetic measurements were conducted using a Quantum Design MPMS-XL system.

The FIRMS experiment was conducted at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee, Florida. A Bruker Vertex 80v FT-IR spectrometer was used in conjunction with a 17.5 T vertical bore superconducting magnet for data collection. The instrument utilized a mercury lamp and a composite silicon bolometer (infrared lab) as incoherent subterahertz radiation sources and detectors, respectively. HFEPR spectra were obtained at NHMFL using a custom-built spectrometer with a 17 T superconducting magnet. The experiment employed low-frequency (8–20 GHz) microwave sources, supplemented by cascade amplifiers and multipliers (Virginia Diodes, Charlottesville, Virginia), to generate higher harmonic frequencies.38

Computational Details

The computational calculations were performed using (a) OpenMolcas version 23.02. The RASSCF and RASSI procedures were utilized in the calculations, considering all 10 quartet states and 40 doublet states to obtain the spin energies. The energy barrier and corresponding g, D, and E values were calculated using the SINGLE_ANISO procedure based on the obtained results. (b) ORCA 5.0.4: calculations used DKH and were conducted at the CASSCF/NEVPT2/def2-TZVPP level. The AILFT sequence was employed to estimate the splitting of d orbitals, ZFS, and crystal field parameters.

Acknowledgments

The authors would like to express their gratitude to several institutes for their contributions. The National Taiwan University Instrument Centre, College of Science, was responsible for conducting elemental analysis and DC magnetic susceptibility measurements. The National Yang Ming Chiao Tung University provided AC magnetic susceptibility data. The X-ray structural analysis was conducted at the Instrumentation Centre College of Science, National Taiwan University. The powder X-ray diffractions were measured at the National Synchrotron Radiation Research Center of Taiwan. FIRMS and HFEPR experiments were carried out at the National High Magnetic Field Laboratory, Tallahassee, Florida.

Glossary

Abbreviations

bpyO22–

deprotonated 2,2′-bipyridine-6,6′-diol.

TMAOH

(NMe4)OH

FIRMS

far-infrared magneto spectroscopy

HFEPR

high-frequency and -field electron paramagnetic resonance

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c01576.

  • Geometry analysis; the main output of computational calculations; HFEPR spectra; AC magnetic susceptibility measurements; and powder X-ray diffraction plot (PDF)

  • ic22335 (CIF)

The Ministry of Science and Technology of Taiwan (MOST 111–2113-M-030–006) and the Ministry of Education of Taiwan (A0112005) provided support for this study. Work performed at the NHMFL was supported by the U.S. National Science Foundation (Cooperative Agreement DMR-2128556) and by the State of Florida.

The authors declare no competing financial interest.

Supplementary Material

ao4c01576_si_001.pdf (4.8MB, pdf)
ao4c01576_si_002.cif (1.9MB, cif)

References

  1. Coronado E. Molecular magnetism: from chemical design to spin control in molecules, materials and devices. Nat. Rev. Mater. 2020, 5, 87–104. 10.1038/s41578-019-0146-8. [DOI] [Google Scholar]
  2. a Guo F.-S.; He M.; Huang G.-Z.; Giblin S. R.; Billington D.; Heinemann F. W.; Tong M.-L.; Mansikkamäki A.; Layfield R. A. Discovery of a Dysprosium Metallocene Single-Molecule Magnet with Two High-Temperature Orbach Processes. Inorg. Chem. 2022, 61 (16), 6017–6025. 10.1021/acs.inorgchem.1c03980. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Ying X.; Zhu Z.; Zhao C.; Zhang Y.-Q.; Tang J. Five-Coordinated Dysprosium Single-Molecule Magnet Functionalized by the SMe Group. Inorg. Chem. 2022, 61 (50), 20547–20551. 10.1021/acs.inorgchem.2c03375. [DOI] [PubMed] [Google Scholar]
  3. Christou G.; Gatteschi D.; Hendrickson D. N.; Sessoli R. Single-Molecule Magnets. MRS Bull. 2000, 25 (11), 66–71. 10.1557/mrs2000.226. [DOI] [Google Scholar]
  4. a Zabala-Lekuona A.; Seco J. M.; Colacio E. Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time. Coord. Chem. Rev. 2021, 441, 213984 10.1016/j.ccr.2021.213984. [DOI] [Google Scholar]; b Murugesu M.; Habrych M.; Wernsdorfer W.; Abboud K. A.; Christou G. Single-Molecule Magnets: A Mn25 Complex with a Record S = 51/2 Spin for a Molecular Species. J. Am. Chem. Soc. 2004, 126 (15), 4766–4767. 10.1021/ja0316824. [DOI] [PubMed] [Google Scholar]
  5. a Bencini A.; Gatteschi D.. EPR of Exchange Coupled Systems; Dover, 2012. [Google Scholar]; b Boča R.Theoretical Foundations of Molecular Magnetism; Elsevier, 1999. [Google Scholar]
  6. Ishikawa N.; Sugita M.; Ishikawa T.; Koshihara S.-Y.; Kaizu Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125 (29), 8694–8695. 10.1021/ja029629n. [DOI] [PubMed] [Google Scholar]
  7. a Stamatatos T. C.; Abboud K. A.; Wernsdorfer W.; Christou G. Spin Tweaking” of a High-Spin Molecule: An Mn25 Single-Molecule Magnet with an S = 61/2 Ground State. Angew. Chem., Int. Ed. 2007, 46, 884–888. 10.1002/ange.200603254. [DOI] [PubMed] [Google Scholar]; b Milios C. J.; Vinslava A.; Wernsdorfer W.; Moggach S.; Parsons S.; Perlepes S. P.; Christou G.; Brechin E. K. A Record Anisotropy Barrier for a Single-Molecule Magnet. J. Am. Chem. Soc. 2007, 129, 2754–2755. 10.1021/ja068961m. [DOI] [PubMed] [Google Scholar]; c Yang E.-C.; Kirman C.; Lawrence J.; Zakharov L. N.; Rheingold A. L.; Hill S.; Hendrickson D. N. Single-Molecule Magnets: High-Field Electron Paramagnetic Resonance Evaluation of the Single-Ion Zero-Field Interaction in a Zn3IINiII Complex. Inorg. Chem. 2005, 44 (11), 3827–3836. 10.1021/ic0482279. [DOI] [PubMed] [Google Scholar]
  8. Murrie M. Cobalt(ii) single-molecule magnets. Chem. Soc. Rev. 2010, 39, 1986–1995. 10.1039/b913279c. [DOI] [PubMed] [Google Scholar]
  9. a Zadrozny J. M.; Long J. R. Slow Magnetic Relaxation at Zero Field in the Tetrahedral Complex [Co(SPh)4]2-. J. Am. Chem. Soc. 2011, 133 (51), 20732–20734. 10.1021/ja2100142. [DOI] [PubMed] [Google Scholar]; b Zadrozny J. M.; Telser J.; Long J. R. Slow magnetic relaxation in the tetrahedral cobalt(II) complexes [Co(EPh)4]2–(E: O S Se). Polyhedron 2013, 64, 209–217. 10.1016/j.poly.2013.04.008. [DOI] [Google Scholar]
  10. Vaidya S.; Tewary S.; Singh S. K.; Langley S. K.; Murray K. S.; Lan Y.; Wernsdorfer W.; Rajaraman G.; Shanmugam M. What Controls the Sign and Magnitude of Magnetic Anisotropy in Tetrahedral Cobalt(II) Single-Ion Magnets?. Inorg. Chem. 2016, 55, 9564–9578. 10.1021/acs.inorgchem.6b01073. [DOI] [PubMed] [Google Scholar]
  11. a Mondal A. K.; Sundararajan M.; Konar S. A new series of tetrahedral Co(ii) complexes [CoLX2] (X = NCS, Cl, Br, I) manifesting single-ion magnet features. Dalton Trans. 2018, 47, 3745–3754. 10.1039/C7DT04007E. [DOI] [PubMed] [Google Scholar]; b Hrubý J.; Dvořák D.; Squillantini L.; Mannini M.; van Slageren J.; Herchel R.; Nemec I.; Neugebauer P. Co(II)-Based single-ion magnets with 1,1′-ferrocenediyl-bis(diphenylphosphine) metalloligands. Dalton Trans. 2020, 49, 11697–11707. 10.1039/D0DT01512A. [DOI] [PubMed] [Google Scholar]
  12. Yang R.-C.; Wang D.-R.; Liu J.-L.; Wang Y.-F.; Lin W.-Q.; Leng J.-D.; Zhou A.-J. Phosphine Oxide Ligand Based Tetrahedral CoII Complexes with Field-induced Slow Magnetic Relaxation Behavior Modified by Terminal Ligands. Chem. - Asian J. 2019, 14, 1467–1471. 10.1002/asia.201900280. [DOI] [PubMed] [Google Scholar]
  13. a Rechkemmer Y.; Breitgoff F. D.; van der Meer M.; Atanasov M.; Hakl M.; Orlita M.; Neugebauer P.; Neese F.; Sarkar B.; van Slageren J. A four-coordinate cobalt(II) single-ion magnet with coercivity and a very high energy barrier. Nat. Commun. 2016, 7, 10467 10.1038/ncomms10467. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Bamberger H.; Albold U.; Midlíková J. D.; Su C. Y.; Deibel N.; Hunger D.; Hallmen P. P.; Neugebauer P.; Beerhues J.; Demeshko S.; Meyer F.; Sarkar B.; van Slageren J. Iron(II), Cobalt(II), and Nickel(II) Complexes of Bis(sulfonamido)benzenes: Redox Properties, Large Zero-Field Splittings, and Single-Ion Magnets. Inorg. Chem. 2021, 60 (5), 2953–2963. 10.1021/acs.inorgchem.0c02949. [DOI] [PubMed] [Google Scholar]
  14. Cui H.-H.; Lu F.; Chen X.-T.; Zhang Y.-Q.; Tong W.; Xue Z.-L. Zero-Field Slow Magnetic Relaxation and Hysteresis Loop in Four-Coordinate CoII Single-Ion Magnets with Strong Easy-Axis Anisotropy. Inorg. Chem. 2019, 58 (19), 12555–12564. 10.1021/acs.inorgchem.9b01175. [DOI] [PubMed] [Google Scholar]
  15. Wu T.; Zhai Y.-Q.; Deng Y.-F.; Chen W.-P.; Zhang T.; Zheng Y.-Z. Correlating magnetic anisotropy with the subtle coordination geometry variation of a series of cobalt(ii)-sulfonamide complexes. Dalton Trans. 2019, 48, 15419–15426. 10.1039/C9DT01296F. [DOI] [PubMed] [Google Scholar]
  16. Lou Y.-S.; Lin B.-R.; Wu C.-M.; Chien S.-Y.; Yang E.-C. Phonon-induced relaxation mechanisms are changed by a chelating effect in a CoII single-ion magnet. Dalton Trans. 2022, 51, 6646–6653. 10.1039/D1DT03515K. [DOI] [PubMed] [Google Scholar]
  17. Figgis B. N.; Hitchman M. A.. Ligand Field Theory and Its Applications; Wiley-VCH, 1999. [Google Scholar]
  18. Wu C.-M.; Tsai J.-E.; Lee G.-H.; Yang E.-C. Slow magnetization relaxation in a tetrahedrally coordinated mononuclear Co(ii) complex exclusively ligated with phenanthroline ligands. Dalton Trans. 2020, 49, 16813–16820. 10.1039/D0DT03481A. [DOI] [PubMed] [Google Scholar]
  19. Tin P.; Bone A. N.; Bui N. N.; Zhang Y.-Q.; Chang T.; Moseley D. H.; Ozerov M.; Krzystek J.; Cheng Y.; Daemen L. L.; Wang X.; Song L.; Chen Y.-S.; Shao D.; Wang X.-Y.; Chen X.-T.; Xue Z.-L. Advanced Spectroscopic and Computational Studies of a Cobalt(II) Coordination Polymer with Single-Ion-Magnet Properties. J. Phys. Chem. C 2022, 126 (31), 13268–13283. 10.1021/acs.jpcc.2c03083. [DOI] [Google Scholar]
  20. Sottini S.; Poneti G.; Ciattini S.; Levesanos N.; Ferentinos E.; Krzystek J.; Sorace L.; Kyritsis P. Magnetic Anisotropy of Tetrahedral CoII Single-Ion Magnets: Solid-State Effects. Inorg. Chem. 2016, 55, 9537–9548. 10.1021/acs.inorgchem.6b00508. [DOI] [PubMed] [Google Scholar]
  21. Chilton N. F.; Anderson R. P.; Turner L. D.; Soncini A.; Murray K. S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. 10.1002/jcc.23234. [DOI] [PubMed] [Google Scholar]
  22. a Ali B.; Li X. L.; Gendron F.; Guennic B. L.; Tang J. A new class of DyIII-SIMs associated with a guanidine-based ligand. Dalton Trans. 2021, 50, 5146–5153. 10.1039/D1DT00260K. [DOI] [PubMed] [Google Scholar]; b Hu Z.-B.; Jing Z.-Y.; Li M.-M.; Yin L.; Gao Y.-D.; Yu F.; Hu T.-P.; Wang Z.; Song Y. Important Role of Intermolecular Interaction in Cobalt(II) Single-Ion Magnet from Single Slow Relaxation to Double Slow Relaxation. Inorg. Chem. 2018, 57, 10761–10767. 10.1021/acs.inorgchem.8b01389. [DOI] [PubMed] [Google Scholar]
  23. Aubin S. M. J.; Sun Z.; Eppley H. J.; Rumberger E. M.; Guzei I. A.; Folting K.; Gantzel P. K.; Rheingold A. L.; Christou G.; Hendrickson D. N. Single-Molecule Magnets: Jahn–Teller Isomerism and the Origin of Two Magnetization Relaxation Processes in Mn12 Complexes. Inorg. Chem. 2001, 40 (9), 2127–2146. 10.1021/ic000911+. [DOI] [PubMed] [Google Scholar]
  24. Galván I. F.; Vacher M.; Alavi A.; Angeli C.; Aquilante F.; Autschbach J.; Bao J. J.; Bokarev S. I.; Bogdanov N. A.; Carlson R. K.; Chibotaru L. F.; Creutzberg J.; Dattani N.; Delcey M. G.; Dong S. S.; Dreuw A.; Freitag L.; Frutos L. M.; Gagliardi L.; Gendron F.; Giussani A.; González L.; Grell G.; Guo M.; Hoyer C. E.; Johansson M.; Keller S.; Knecht S.; Kovačević G.; Källman E.; Manni G. L.; Lundberg M.; Ma Y.; Mai S.; Malhado J. P.; Malmqvist P. Å.; Marquetand P.; Mewes S. A.; Norell J.; Olivucci M.; Oppel M.; Phung Q. M.; Pierloot K.; Plasser F.; Reiher M.; Sand A. M.; Schapiro I.; Sharma P.; Stein C. J.; Sørensen L. K.; Truhlar D. G.; Ugandi M.; Ungur L.; Valentini A.; Vancoillie S.; Veryazov V.; Weser O.; Wesołowski T. A.; Widmark P.-O.; Wouters S.; Zech A.; Zobel J. P.; Lindh R. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. 10.1021/acs.jctc.9b00532. [DOI] [PubMed] [Google Scholar]
  25. Malmqvist P. A.; Rendell A.; Roos B. O. The restricted active space self-consistent-field method, implemented with a split graph unitary group approach. J. Phys. Chem. A 1990, 94, 5477–5482. 10.1021/j100377a011. [DOI] [Google Scholar]
  26. Malmqvist P. Å.; Roos B. O.; Schimmelpfennig B. The restricted active space (RAS) state interaction approach with spin–orbit coupling. Chem. Phys. Lett. 2002, 357, 230–240. 10.1016/S0009-2614(02)00498-0. [DOI] [Google Scholar]
  27. Neese F. Software update: The ORCA program system—Version 5.0. Wiley Comput. Mol. Sci. 2022, 12, e1606 10.1002/wcms.1606. [DOI] [Google Scholar]
  28. Gunther L.; Barbara B.. Quantum Tunneling of Magnetization- QTM ’94; Springer, 1994. [Google Scholar]
  29. Zhang Y.-Z.; Gómez-Coca S.; Brown A. J.; Saber M. R.; Zhang X.; Dunbar K. R. Trigonal antiprismatic Co(ii) single molecule magnets with large uniaxial anisotropies: importance of Raman and tunneling mechanisms. Chem. Sci. 2016, 7, 6519–6527. 10.1039/C6SC02035F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Zadrozny J. M.; Atanasov M.; Bryan A. M.; Lin C.-Y.; Rekken B. D.; Power P. P.; Neese F.; Long J. R. Slow magnetization dynamics in a series of two-coordinate iron(II) complexes. Chem. Sci. 2013, 4 (1), 125–138. 10.1039/C2SC20801F. [DOI] [Google Scholar]
  31. a Cole K. S.; Cole R. H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. 10.1063/1.1750906. [DOI] [Google Scholar]; b Cole K. S.; Cole R. H. Dispersion and Absorption in Dielectrics II. Direct Current Characteristics. J. Chem. Phys. 1942, 10, 98–105. 10.1063/1.1723677. [DOI] [Google Scholar]
  32. Tang J.-K.; Zhang P.. Lanthanide Single-Molecule Magnets; Springer, 2015. [DOI] [PubMed] [Google Scholar]
  33. Legendre C. M.; Damgaard-Møller E.; Overgaard J.; Stalke D. The Quest for Optimal 3 d Orbital Splitting in Tetrahedral Cobalt Single-Molecule Magnets Featuring Colossal Anisotropy and Hysteresis. Eur. J. Inorg. Chem. 2021, 2021, 3108–3114. 10.1002/ejic.202100465. [DOI] [Google Scholar]
  34. Vallejo J.; Pardo E.; Viciano-Chumillas M.; Castro I.; Amorós P.; Déniz M.; Ruiz-Pérez C.; Yuste-Vivas C.; Krzystek J.; Julve M.; Lloret F.; Cano J. Reversible solvatomagnetic switching in a single-ion magnet from an entatic state. Chem. Sci. 2017, 8, 3694–3702. 10.1039/C6SC05188J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ferreira P. S.; Cerdeira A. C.; Cruz T. F. C.; Bandeira N. A. G.; Hunger D.; Allgaier A.; van Slageren J.; Almeida M.; Pereira L. C. J.; Gomes P. T. Single-ion magnet behaviour in homoleptic Co(ii) complexes bearing 2-iminopyrrolyl ligands. Inorg. Chem. Front. 2022, 9, 4302–4319. 10.1039/D2QI00601D. [DOI] [Google Scholar]
  36. Carl E.; Demeshko S.; Meyer F.; Stalke D. Triimidosulfonates as Acute Bite-Angle Chelates: Slow Relaxation of the Magnetization in Zero Field and Hysteresis Loop of a CoII Complex. Chem. - Eur. J. 2015, 21, 10109–10115. 10.1002/chem.201406083. [DOI] [PubMed] [Google Scholar]
  37. Sheldrick G. M. SHELXT - Integrated space-group and crystal-structure determination. Acta Crystallogr., Sect. A: Found. Adv. 2015, 71, 3–8. 10.1107/S2053273314026370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Hassan A. K.; Pardi L. A.; Krzystek J.; Sienkiewicz A.; Goy P.; Rohrer M.; Brunel L. C. Ultrawide band multifrequency high-field EMR technique: A methodology for increasing spectroscopic information. J. Magn. Reson. 2000, 142, 300–312. 10.1006/jmre.1999.1952. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao4c01576_si_001.pdf (4.8MB, pdf)
ao4c01576_si_002.cif (1.9MB, cif)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES