Abstract
Background
HALE is now a regular strategic planning indicator for all levels of the Chinese government. However, HALE measurements necessitate comprehensive data collection and intricate technology. Therefore, effectively converting numerous diseases into the years lived with disability (YLD) rate is a significant challenge for HALE measurements. Our study aimed to construct a simple YLD rate measurement model with high applicability based on the current situation of actual data resources within China to address challenges in measuring HALE target values during planning.
Methods
First, based on the Chinese YLD rate in the Global Burden of Disease (GBD) 2019, Pearson correlation analysis, the global optimum method, etc., was utilized to screen the best predictor variables from the current Chinese data resources. Missing data for predictor variables were filled in via spline interpolation. Then, multiple linear regression models were fitted to construct the YLD rate measurement model. The Sullivan method was used to measure HALE. The Monte Carlo method was employed to generate 95% uncertainty intervals. Finally, model performances were assessed using the mean absolute error (MAE) and mean absolute percentage error (MAPE).
Results
A three-input-parameter model was constructed to measure the age-specific YLD rates by sex in China, directly using the incidence of infectious diseases, the incidence of chronic diseases among persons aged 15 and older, and the addition of an under-five mortality rate covariate. The total MAE and MAPE for the combined YLD rate were 0.0007 and 0.5949%, respectively. The MAE and MAPE of the combined HALE in the 0-year-old group were 0.0341 and 0.0526%, respectively. There were slightly fewer males (0.0197, 0.0311%) than females (0.0501, 0.0755%).
Conclusion
We constructed a high-accuracy model to measure the YLD rate in China by using three monitoring indicators from the Chinese national routine as predictor variables. The model provides a realistic and feasible solution for measuring HALE at the national and especially regional levels, considering limited data.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12889-024-19112-6.
Keywords: China, Years lived with disability rate, Health-adjusted life expectancy, Practical model, Uncertainty intervals
Background
Economic and social development has shifted individuals’ focus toward not only living longer but also living better. Healthy life expectancy is a significant measure of a population’s lifespan and quality of life [1]. In 2000, the World Health Organization (WHO) explicitly included healthy life expectancy as a health system performance evaluation indicator to quantify the health status of populations [2]. The WHO has since routinely published healthy life expectancy surveillance values for countries worldwide. In 2004, the European Union adopted the healthy life expectancy as a structural indicator for monitoring health trends [3]. France, the United Kingdom, and Sweden even made this a policy goal prior to the European Union. The first planning goal of the “Healthy China 2030” Plan [4], released by the Chinese Communist Party State Council in 2016, states that “by 2030, healthy life expectancy will be significantly improved”.
healthy life expectancy is typically measured following the Sullivan methodology, which combines unhealthy status within a life table framework [5]. With the diversity of health concepts, unhealthy health conditions with different meanings correspond to different healthy life expectancies such as disability-free life expectancy [6], healthy life expectancy without specific diseases [7], and self-rated healthy life expectancy [8]. These metrics are easily calculable, and unhealthy rate data are readily available, with numerous corresponding studies. However, since these healthy life expectancies solely concentrate on the number of years of survival with a specific health condition, they fail to offer a comprehensive and integrated assessment of the quality of health survival and are difficult to compare with each other.
However, the healthy life expectancy indicator in China’s national planning is generally a composite indicator that discounts life expectancy by considering various illnesses and disabilities. Currently, this indicator is dominated by health-adjusted life expectancy (HALE) from the Global Burden of Disease (GBD) study led by The Institute for Health Metrics and Evaluation. For instance, GBD 2019 [9] categorizes all illnesses and disabilities into three major groups and 369 causes for comprehensive discounting, and evaluates the HALE of 204 countries or regions worldwide, including China. This provides an essential point of reference for assessing the quality of comprehensive health levels and formulating policies for each country. The GBD HALE was also calculated using the Sullivan method [10]. The unhealthy rate is the years lived with disability (YLD) rate converted from a combination of all the different types of diseases, for which full prevalence data are needed. However, given the scarcity of data and variety of country-specific problems, GBD has devised a complicated process to estimate the YLD rate. In particular, the technical approach represented by DisMod-MR [11] is difficult to generalize and apply globally.
With the development of GBD YLD rate measurement techniques [12–14], there are now other methods of measurement both domestically and internationally. One method involves collecting disease prevalence data through surveys, and calculating YLD rates by combining the disability weights of each illness [15, 16]. However, the questionnaire is not comprehensive and captures data on only a few diseases. Another approach is to extract prevalence rates for various diseases from electronic medical records in hospitals, again combined with disability weights to compute YLD rates [17, 18]. Nevertheless, determining the full prevalence of nonfatal diseases in a specific area using electronic medical records is likely to lead to underreporting. Moreover, as the data are derived from hospitals and utilize techniques such as big data, the applicability of these methods is limited. Additionally, the WHO [19] proposed using the indirect method to calculate YLD rates, assuming that the ratio of YLD rate to years of life lost is the same in the study and reference areas. Its applications exist in Guangdong Province, China [20, 21]. However, the distribution of disease burden may differ significantly among regions, introducing bias into estimation outcomes [22]. These limitations greatly constrain the measurement and applicability of HALEs in China.
In 2022, China’s 14th Five-Year Plan for National Health [23] further proposed the goal of “increasing HALE in the same proportion as expectancy by 2025”. Subgovernments at all levels in China, including provinces and municipalities, have also set regional HALE goals accordingly. Therefore, how to measure the YLD rate in China and its provinces and cities, based on the current status of the actual data in China, has become the most important challenge for HALE measurements in China.
Therefore, this study utilized the GBD technique and database as a basis for identifying the best predictor variables among the current data resources in China to construct a simple model for measuring China’s YLD rate. This approach aims to simplify China’s HALE calculation. In the absence of domestic data resources in China, this provides a practical and feasible solution for measuring national-level HALEs, especially regional-level HALEs, and offers technical assistance for the quantitative evaluation of health policies.
Methods
Sources of data
The GBD database
The YLD rates and 95% UI, life tables, HALEs, and corresponding sex-specific data for 21 age groups (0, 1–4, 5–9, 10–14,……, 90–94, and 95+) in China for 1990–2019 were obtained from GBD 2019 data from the Global Health Data Exchange query tool (https://vizhub.healthdata.org/gbd-results/).
Domestic data available in China
The data for China’s health care system come mainly from disease surveillance, maternal and child health surveillance, cause-of-death surveillance, censuses, sample surveys (e.g., the National Health Service Survey), and residents’ health records, among others. These data are publicly available through vehicles such as the National Health Service Survey and Analysis Report, the China Health and Health Statistics Yearbook, and the China Statistical Yearbook. The National Health Service Survey and Analysis Report offers data on resident prevalence, long-term disabling and disability conditions, etc. The China Health and Health Statistics Yearbook includes data on morbidity and mortality from infectious diseases and maternal and child health (neonatal mortality rate, infant mortality rate, under-five mortality rate (U5MR). The China Statistical Yearbook contains data on national accounting, socioeconomic indicators, educational attainment per capita, and urbanization rate.
Treatment and screening of independent variables
We filled in missing data for certain variables within China using spline interpolation. Additionally, we harmonized individual indicators with age ranges that were inconsistent across different years.
To screen independent variables, we utilized multiple linear regression, Pearson correlation analysis, collinearity statistics, etc., to screen four variables using the global optimum method. The data included the incidence of infectious diseases (IID), the incidence of chronic diseases among persons aged 15 and older (PCDPF), the two-week incidence of impairment poisoning, and the U5MR. After careful consideration of the model’s applicability, we ultimately selected three independent variables (IID, PCDPF, and U5MR). For reference, the four-input-parameter model has been included in the Appendix, along with additional information. In addition, it should be noted that IID, as referenced in this study, represents the incidence of A and B statutory infectious diseases. See also the Appendix for specific classifications.
Model construction
Modeling of YLD rates by sex and age in China
The model was developed by inputting 3 predictor variables (IID, PCDPF, U5MR) and outputting them to obtain 21 age-specific YLD rates. The details are as follows:
(1) Twenty-one multiple linear regression models were constructed:
 |
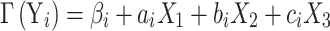1 |
In this model,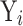 
represents the YLD rate for 21 age groups (age Group 0, 1–4, 5–9, 10–14,…, 90–94, and 95+); 
, 
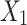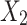, and 
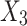correspond to IID, PCDPF, and U5MR, respectively; 
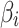is the intercept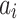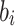; and 
, 
, and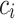 
are the corresponding independent variable regression coefficients. Model (1) included 21 multiple linear regression models corresponding to each age group. After testing different transformations, 
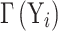chooses the logit transformation:
 |
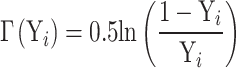2 |
(2) In building Model (1) for different genders, except for the PCDPF, the two independent variables are directly modeled by substituting the aggregate rate for the subgender rate.
Sullivan method for measuring HALE[24]
Uncertainty intervals (UIs)
We assessed the uncertainty of the model coefficients, YLD rates and HALE estimates based on the uncertainty of the GBD data. Monte Carlo methods were utilized to generate 95% UIs. The GBD YLD rate, following logit transformation, was assumed to conform to a multivariate normal distribution. With the GBD-reported YLD rates and 95% UIs, we constructed 30 multivariate normal distributions from which we randomly generated 1000 
s. Then, we obtained the 95% UIs for the YLD rate estimates, HALE estimates,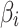 
, 
, 
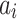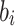, and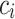 
using the 2.5th and 97.5th quartiles. More details are given in the Appendix.
Error assessment
This study evaluated the accuracy of this simple model on the basis of the YLD rate and HALE dimensions. The model-measured YLD and HALE were used as model fit values. HALEs were calculated using model-measured YLD rates and GBD life tables through the Sullivan method. The YLD rate and HALE published by GDB served as true reference values. The data were assessed in three ways: (a) Drawing residual plots. (b) The mean absolute error (MAE) and mean absolute percentage error (MAPE) were calculated. The formulas are as follows [25], where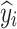 
, 
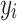, and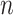 
denote the model fitted value, the true reference value, and the total number of estimates, respectively. (c) Plotting line plots of model-fitted and true reference values with 95% UI.
 |
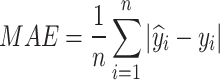3 |
 |
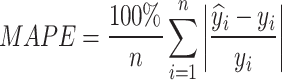4 |
Statistical software
R-4.2.2 software (packages reshape2, MASS, splines, pracma, gplot2, gcookbook, dplyr, gpubr, gsci) was used throughout this study.
Results
Model construction
Descriptive analysis of three predictor variables
Table 1 shows the descriptive analysis of the three predictor variables IID, PCDPF (both male and female populations), and U5MR using 4 metrics: maximum, minimum, median, and mean.
Table 1.
Descriptive analysis of three predictor variables
| variables | maximum | minimum | median | mean |
|---|---|---|---|---|
| IID | 0.0030 | 0.0017 | 0.0022 | 0.0023 |
| PCDPF_both | 0.5371 | 0.1862 | 0.2043 | 0.2656 |
| PCDPF_male | 0.5289 | 0.1678 | 0.1864 | 0.2463 |
| PCDPF_female | 0.5423 | 0.2057 | 0.2250 | 0.2846 |
| U5MR | 0.0610 | 0.0078 | 0.0238 | 0.0289 |
Coefficients of the YLD rate measurement models
Table 2 displays the coefficients and their 95% UIs for Model (1), the YLD rate measurement model, across various genders and age groups. To ensure accurate model parameters, the regression coefficients were rounded to four decimal places. For age-specific models, all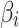 
values are positive, while 
, 
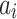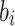, and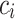 
values may be positive or negative. The 
, 
, 
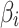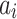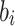, and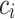 
values of the combined model are situated between the corresponding values of the male and female models. After all the coefficients are substituted into Model (1), only three independent variables—IID, PCDPF, and U5MR—are needed to calculate the 21 age-specific YLD rates for males, females, and the combined population in a region. Additionally, the results of the four-parameter model can be found in the Appendix.
Table 2.
Coefficients of the YLD rate measurement model for different genders and age groups
| Age groups | Male | Female | Both | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
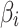
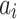
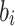
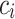
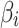
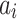
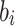
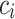
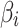
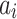
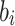
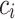
| 0- | 1.8615(1.5676,2.1686) | 8.9296(-89.86,104.4651) | 0.0749(-0.3495,0.5163) | -3.4638(-6.2056,-0.6767) | 1.9244(1.6017,2.2606) | 1.4015(-89.2012,98.5111) | -0.0339(-0.5089,0.4189) | -4.0875(-6.7341,-0.9566) | 1.8893(1.5782,2.2044) | 5.0838(-95.0983,98.3153) | 0.0277(-0.3935,0.4767) | -3.7456(-6.4152,-0.8885) |
| 1–4 | 1.9694(1.6564,2.282) | -5.1199(-105.66,89.3598) | -0.2137(-0.6211,0.2179) | -2.7403(-5.311,0.1668) | 2.0788(1.7471,2.4175) | -9.8239(-103.8426,90.4263) | -0.3049(-0.7628,0.1747) | -3.5109(-6.3764,-0.5827) | 2.0151(1.6647,2.3346) | -6.7746(-108.6964,93.8619) | -0.2498(-0.6564,0.2006) | -3.0582(-5.7274,-0.1229) |
| 5–9 | 1.8413(1.525,2.1515) | -0.8975(-101.7561,94.1937) | -0.1547(-0.569,0.2849) | -1.9308(-4.5082,1.0019) | 1.9073(1.5992,2.2224) | -0.0878(-89.1423,95.2822) | -0.1897(-0.6449,0.2733) | -2.3390(-5.0928,0.4604) | 1.8688(1.5419,2.19) | -0.1318(-97.964,99.0181) | -0.1682(-0.5808,0.2811) | -2.0884(-4.6995,0.8061) |
| 10–14 | 1.6316(1.3374,1.9374) | 1.9377(-97.2023,95.3694) | -0.0537(-0.4723,0.3893) | -0.8173(-3.4299,2.0455) | 1.5875(1.2654,1.9069) | 1.5146(-83.0149,99.3105) | -0.0599(-0.5111,0.391) | -0.7935(-3.4908,1.9591) | 1.6099(1.2935,1.9257) | 1.9764(-90.8264,97.9303) | -0.0552(-0.4808,0.3775) | -0.8259(-3.3644,1.7507) |
| 15–19 | 1.5261(1.2449,1.8354) | 3.7940(-93.8766,94.1744) | -0.0335(-0.4508,0.3749) | -0.6617(-3.3066,2.0369) | 1.4563(1.1364,1.7867) | -1.4657(-92.6654,94.5287) | -0.0635(-0.5362,0.4028) | -1.2921(-4.0064,1.5633) | 1.4898(1.171,1.7968) | 0.9114(-91.2431,95.0335) | -0.0420(-0.4779,0.4019) | -1.0058(-3.4936,1.5461) |
| 20–24 | 1.4536(1.1914,1.738) | 4.2732(-82.274,88.3974) | -0.0374(-0.4256,0.3432) | -1.2270(-3.6582,1.2982) | 1.3738(1.0737,1.6944) | -2.7204(-89.8365,88.28) | -0.0654(-0.5239,0.3675) | -2.0357(-4.5894,0.7386) | 1.4092(1.115,1.698) | 0.2690(-86.5912,85.2794) | -0.0420(-0.4448,0.3843) | -1.6123(-4.0458,0.7989) |
| 25–29 | 1.3981(1.145,1.6852) | -0.6930(-92.0414,85.5352) | -0.0710(-0.4481,0.3159) | -1.2683(-3.7395,1.239) | 1.2745(0.9582,1.6023) | -3.5984(-95.8204,89.5813) | -0.0426(-0.5183,0.4044) | -1.9072(-4.5349,1.0659) | 1.3340(1.0227,1.6283) | -3.0808(-92.6824,84.617) | -0.0532(-0.4668,0.3865) | -1.5637(-4.0372,0.9158) |
| 30–34 | 1.3550(1.0825,1.6537) | -3.8105(-99.3002,86.6227) | -0.0995(-0.5006,0.292) | -1.2241(-3.7556,1.476) | 1.1988(0.8692,1.5326) | -3.6009(-98.9042,89.4311) | -0.0307(-0.5154,0.4211) | -1.7896(-4.459,1.2694) | 1.2725(0.9508,1.5746) | -3.3793(-97.621,90.2346) | -0.0623(-0.489,0.3835) | -1.4924(-4.0047,1.1893) |
| 35–39 | 1.3017(1.0351,1.5927) | -4.8401(-99.3466,81.1911) | -0.1094(-0.4948,0.2805) | -1.2015(-3.6518,1.3679) | 1.1471(0.8328,1.4698) | -5.9297(-98.9376,87.4883) | -0.0362(-0.5058,0.4076) | -1.7220(-4.3229,1.2322) | 1.2219(0.9178,1.5141) | -5.4039(-94.3819,84.6567) | -0.0707(-0.4856,0.3752) | -1.4605(-3.9564,1.1055) |
| 40–44 | 1.2235(0.9435,1.5236) | -3.9177(-98.8668,84.7891) | -0.1054(-0.4978,0.3085) | -0.9989(-3.4551,1.6916) | 1.0765(0.7607,1.4012) | -6.3659(-101.6396,87.6795) | -0.0302(-0.5097,0.4269) | -1.4290(-4.0477,1.5179) | 1.1470(0.8339,1.4453) | -4.9543(-98.126,85.1809) | -0.0656(-0.4943,0.3699) | -1.1952(-3.738,1.4064) |
| 45–49 | 1.1470(0.8608,1.4537) | -4.3704(-101.06,85.1792) | -0.0855(-0.4893,0.3345) | -0.8279(-3.3536,1.938) | 1.0049(0.6872,1.3301) | -5.0810(-99.3075,88.5691) | -0.0269(-0.5162,0.4319) | -1.1509(-3.7588,1.7713) | 1.0716(0.7573,1.3766) | -3.9819(-98.1502,89.3272) | -0.0542(-0.4911,0.4001) | -0.9499(-3.5559,1.6995) |
| 50–54 | 1.0640(0.7779,1.3822) | -5.0987(-101.6711,86.558) | -0.0629(-0.4766,0.3672) | -0.6543(-3.2642,2.1167) | 0.9263(0.6099,1.2474) | -5.3515(-98.0374,89.4413) | -0.0176(-0.5021,0.4305) | -0.9582(-3.5471,1.9832) | 0.9918(0.6765,1.2982) | -4.8706(-101.1156,87.1881) | -0.0399(-0.4833,0.4161) | -0.7512(-3.3769,1.9276) |
| 55–59 | 0.9734(0.6885,1.2923) | -6.1668(-100.2057,90.1042) | -0.0428(-0.458,0.3824) | -0.5263(-3.1987,2.1742) | 0.8550(0.5407,1.1749) | -7.3568(-103.2215,83.4189) | -0.0097(-0.4922,0.4641) | -0.7126(-3.3674,2.1542) | 0.9136(0.5897,1.2317) | -7.0781(-101.4935,83.6403) | -0.0272(-0.4707,0.4594) | -0.5775(-3.2193,2.072) |
| 60–64 | 0.8716(0.5849,1.1754) | -7.2787(-103.3529,89.184) | -0.0142(-0.4208,0.416) | -0.3027(-2.9157,2.3396) | 0.7680(0.4397,1.0843) | -8.3920(-103.148,87.0003) | 0.0077(-0.4696,0.4859) | -0.4027(-3.0952,2.5065) | 0.8216(0.5069,1.1228) | -8.2262(-100.3827,80.3776) | -0.0086(-0.4604,0.4812) | -0.3444(-3.0742,2.4549) |
| 65–69 | 0.7501(0.4676,1.0324) | -7.0827(-95.9519,79.0654) | 0.0298(-0.3817,0.4741) | -0.1241(-2.8241,2.5645) | 0.6620(0.3442,0.9885) | -7.7256(-101.1817,90.0398) | 0.0263(-0.4443,0.4832) | -0.2158(-2.9427,2.6614) | 0.7091(0.4118,1.001) | -7.7619(-94.8636,77.8574) | 0.0199(-0.4051,0.4821) | -0.2119(-2.8057,2.4425) |
| 70–74 | 0.6373(0.3512,0.9403) | -6.3963(-97.9173,82.0546) | 0.0507(-0.346,0.4975) | 0.0401(-2.8468,2.8818) | 0.5604(0.2521,0.8764) | -6.6255(-97.2704,91.4211) | 0.0292(-0.4452,0.4706) | -0.0710(-2.7701,2.7855) | 0.6016(0.3059,0.9141) | -6.9564(-99.3681,76.6746) | 0.0330(-0.3856,0.4962) | -0.0923(-2.7044,2.6144) |
| 75–79 | 0.5494(0.2213,0.8751) | -5.3748(-105.2794,88.8814) | 0.0363(-0.4093,0.4931) | 0.2235(-2.8412,3.175) | 0.4713(0.1574,0.7996) | -5.5550(-101.808,90.0585) | 0.0143(-0.4464,0.4868) | 0.0803(-2.7465,2.8094) | 0.5094(0.1977,0.8408) | -5.5586(-97.4039,87.087) | 0.0228(-0.4503,0.4946) | 0.0533(-2.5135,2.9136) |
| 80–84 | 0.4613(0.1199,0.7939) | -3.3880(-101.8622,102.616) | 0.0117(-0.4504,0.4671) | 0.4306(-2.4492,3.3016) | 0.3734(0.0518,0.6938) | -2.7735(-95.5256,93.9542) | -0.0082(-0.4921,0.4961) | 0.2355(-2.7983,3.0682) | 0.4092(0.0962,0.7623) | -2.8768(-99.8572,93.4903) | 0.0049(-0.4803,0.4952) | 0.2370(-2.6374,3.2957) |
| 85–89 | 0.3952(0.0485,0.7345) | -0.6385(-102.0297,112.085) | -0.0151(-0.4789,0.4497) | 0.4766(-2.5766,3.5764) | 0.3067(-0.0217,0.6456) | 1.3770(-99.3191,99.616) | -0.0421(-0.5589,0.4754) | 0.0682(-2.9729,3.0247) | 0.3354(0.0222,0.6869) | 0.0632(-100.3999,98.5852) | -0.0277(-0.5356,0.4512) | 0.1716(-3.0417,3.2445) |
| 90–94 | 0.3365(-0.0128,0.6713) | 3.5145(-96.6604,114.9733) | -0.0338(-0.5164,0.4335) | 0.6014(-2.3655,3.638) | 0.2523(-0.0798,0.5816) | 6.5459(-87.0686,108.0101) | -0.0812(-0.615,0.4209) | -0.1256(-3.2322,2.9552) | 0.2702(-0.0434,0.5961) | 5.1485(-93.6325,106.3527) | -0.0843(-0.5841,0.3881) | 0.0399(-3.0837,3.047) |
| 95+ | 0.2630(-0.0767,0.5999) | 8.7173(-92.0022,121.9523) | -0.0469(-0.5513,0.4205) | 0.6455(-2.3148,3.64) | 0.1828(-0.1644,0.5225) | 12.5105(-86.6712,113.2924) | -0.1043(-0.6223,0.3976) | -0.3791(-3.5573,2.5804) | 0.1937(-0.1699,0.5055) | 12.2797(-87.3525,121.4148) | -0.1106(-0.6319,0.3815) | -0.2437(-3.0914,2.9493) |
Values in parentheses are 95% uncertainty intervals
Error assessment
Results of YLD rate error assessment
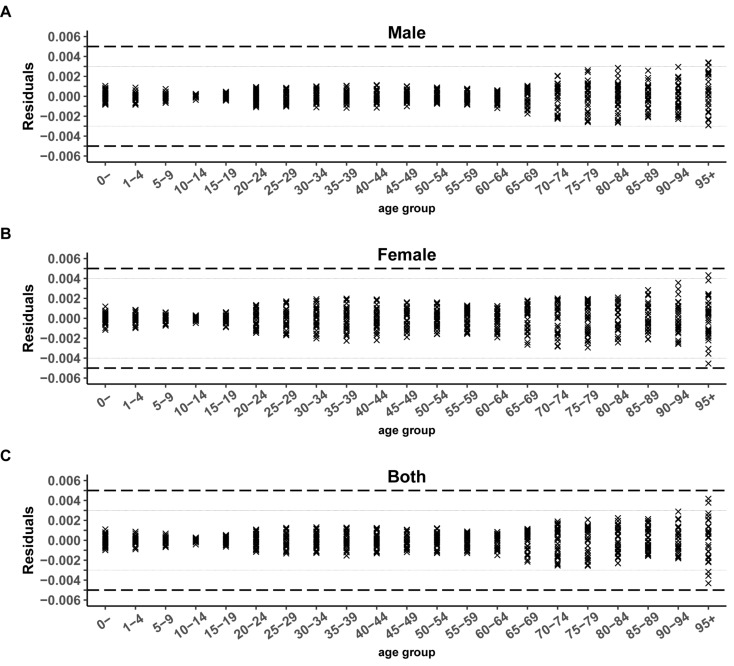
Figure 1 shows the YLD rates for different sexes and age groups. The residuals for males, females, and the combined group fluctuated above and below zero, ranging from (-0.003, 0.003), (-0.004, 0.004), and (-0.003, 0.003), respectively. Table 3 displays the error assessment results for YLD rates across sexes and age groups, with a total MAE and MAPE of 0.0007 and 0.5949%, respectively, for the combined YLD rates. The total MAE and MAPE for males were 0.0006 and 0.5522%, respectively, which were lower than those for females (0.0008 and 0.6762%, respectively). The MAPEs were slightly lower in males than in females in all age groups, except for those aged 0 years. Among the various age groups, there was a general trend of increasing MAE with age, and the MAPE exhibited a general decreasing trend with age.
Fig. 1.
Residuals of YLD rates by genders and age groups
Table 3.
Results of error assessment of YLD rates by genders and age groups
| age groups | Male | Female | Both | |||
|---|---|---|---|---|---|---|
| MAE | MAPE | MAE | MAPE | MAE | MAPE | |
| 0- | 0.0005 | 1.7540 | 0.0004 | 1.5975 | 0.0004 | 1.6616 |
| 1–4 | 0.0003 | 0.9893 | 0.0003 | 1.3444 | 0.0003 | 1.1323 |
| 5–9 | 0.0002 | 0.7038 | 0.0002 | 0.8305 | 0.0002 | 0.7539 |
| 10–14 | 0.0001 | 0.2634 | 0.0002 | 0.3706 | 0.0001 | 0.3190 |
| 15–19 | 0.0002 | 0.3781 | 0.0003 | 0.5477 | 0.0002 | 0.4717 |
| 20–24 | 0.0005 | 0.8592 | 0.0007 | 0.9664 | 0.0006 | 0.8944 |
| 25–29 | 0.0005 | 0.7652 | 0.0008 | 1.0014 | 0.0006 | 0.8637 |
| 30–34 | 0.0005 | 0.6411 | 0.0009 | 0.9424 | 0.0006 | 0.7739 |
| 35–39 | 0.0005 | 0.5793 | 0.0009 | 0.8863 | 0.0006 | 0.6839 |
| 40–44 | 0.0005 | 0.5437 | 0.0009 | 0.7656 | 0.0006 | 0.6220 |
| 45–49 | 0.0004 | 0.4308 | 0.0008 | 0.6231 | 0.0005 | 0.4329 |
| 50–54 | 0.0004 | 0.3567 | 0.0008 | 0.5509 | 0.0006 | 0.4418 |
| 55–59 | 0.0004 | 0.2952 | 0.0008 | 0.4699 | 0.0006 | 0.3736 |
| 60–64 | 0.0004 | 0.2325 | 0.0008 | 0.4186 | 0.0005 | 0.3110 |
| 65–69 | 0.0007 | 0.3499 | 0.0011 | 0.4924 | 0.0008 | 0.4154 |
| 70–74 | 0.0011 | 0.4852 | 0.0013 | 0.5373 | 0.0012 | 0.5097 |
| 75–79 | 0.0012 | 0.4643 | 0.0014 | 0.4795 | 0.0012 | 0.4607 |
| 80–84 | 0.0011 | 0.3956 | 0.0012 | 0.3591 | 0.0012 | 0.3951 |
| 85–89 | 0.0009 | 0.2834 | 0.0011 | 0.3086 | 0.0010 | 0.2918 |
| 90–94 | 0.0012 | 0.3509 | 0.0012 | 0.3190 | 0.0010 | 0.2775 |
| 95+ | 0.0017 | 0.4751 | 0.0016 | 0.3896 | 0.0017 | 0.4076 |
| Total | 0.0006 | 0.5522 | 0.0008 | 0.6762 | 0.0007 | 0.5949 |
mean absolute error (MAE), mean absolute percentage error (MAPE), MAE is in units of 1 and MAPE is in %
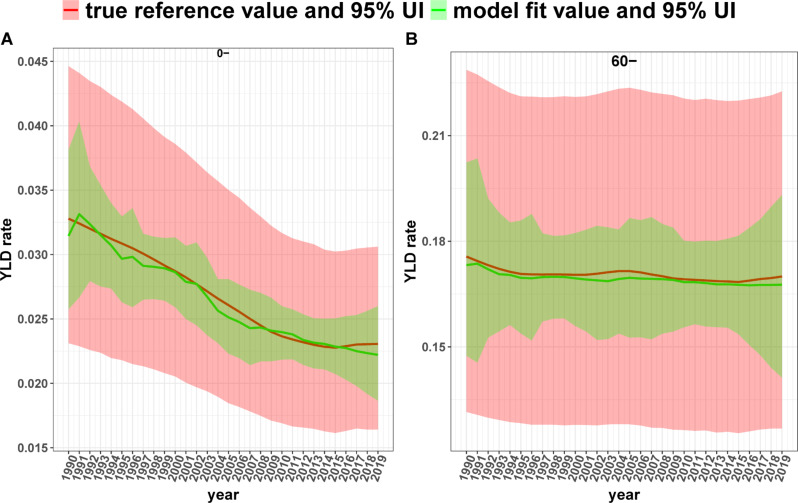
In addition, Fig. 2 illustrates the model fit and true reference values of the combined YLD rates for different years for the 0- and 60–64 age groups. Notably, the two lines almost overlap. Comparable observations are observed in other age groups (see Figure S4 in the Appendix).
Fig. 2.
Comparison of model-fitted values and true reference values of the combined YLD rate for different age groups, 1990–2019 (A) and (B) indicate the 0- age group and 60–64 age group separately. Shaded areas indicate the corresponding 95% uncertainty intervals
Results of HALE error assessment
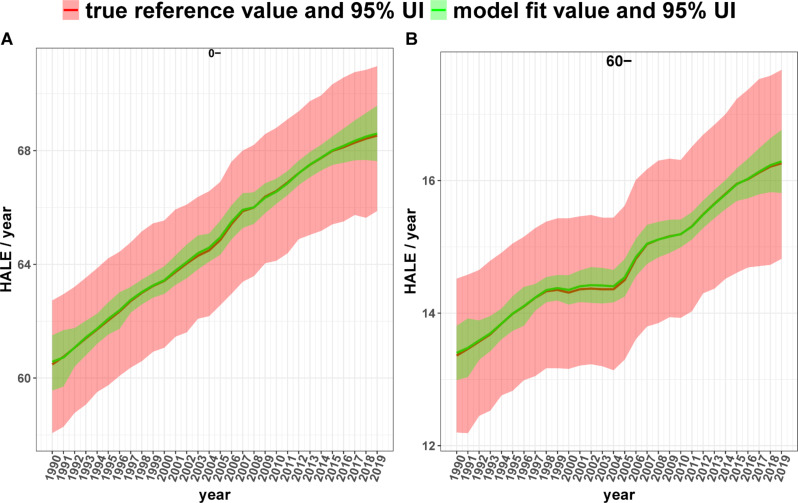
The residuals for males, females, and patients with combined HALE also fluctuated above and below 0, with ranges of (-0.05, 0.05), (-0.10, 0.10), and (-0.08, 0.08), respectively (see Fig. 3). The MAE and MAPE of the combined HALE in the 0-year age group were 0.0341 years and 0.0526%, respectively. These metrics were lower for males (0.0197 years, 0.0311%) than for females (0.0501 years, 0.0755%). In the 60-year-old group, the MAE and MAPE of the combined HALE were 0.0170 and 0.1154%, respectively, and were lower in males (0.0126, 0.0912%) than in females (0.0226, 0.1433%). The male MAPEs were slightly lower than the female MAPEs in all age groups, except for the 95 + years group. Refer to Table 4. Again, the model fit values for the combined HALE and the true reference values nearly overlap. See Fig. 4 and Appendix (Figure S5).
Fig. 3.
Residuals of HALE by genders and age groups
Table 4.
Results of error assessment of HALE by genders and age groups
| age groups | Male | Female | Both | |||
|---|---|---|---|---|---|---|
| MAE | MAPE | MAE | MAPE | MAE | MAPE | |
| 0- | 0.0197 | 0.0311 | 0.0501 | 0.0755 | 0.0341 | 0.0526 |
| 1–4 | 0.0200 | 0.0313 | 0.0508 | 0.0762 | 0.0346 | 0.0529 |
| 5–9 | 0.0194 | 0.0321 | 0.0504 | 0.0797 | 0.0341 | 0.0551 |
| 10–14 | 0.0189 | 0.0339 | 0.0498 | 0.0852 | 0.0337 | 0.0590 |
| 15–19 | 0.0187 | 0.0365 | 0.0493 | 0.0917 | 0.0333 | 0.0635 |
| 20–24 | 0.0180 | 0.0386 | 0.0480 | 0.0976 | 0.0323 | 0.0675 |
| 25–29 | 0.0163 | 0.0388 | 0.0450 | 0.1008 | 0.0301 | 0.0694 |
| 30–34 | 0.0147 | 0.0391 | 0.0414 | 0.1030 | 0.0272 | 0.0699 |
| 35–39 | 0.0134 | 0.0403 | 0.0381 | 0.1063 | 0.0248 | 0.0720 |
| 40–44 | 0.0125 | 0.0429 | 0.0345 | 0.1094 | 0.0227 | 0.0752 |
| 45–49 | 0.0127 | 0.0507 | 0.0310 | 0.1132 | 0.0212 | 0.0814 |
| 50–54 | 0.0126 | 0.0602 | 0.0280 | 0.1202 | 0.0199 | 0.0902 |
| 55–59 | 0.0128 | 0.0739 | 0.0252 | 0.1295 | 0.0184 | 0.1003 |
| 60–64 | 0.0126 | 0.0912 | 0.0226 | 0.1433 | 0.0170 | 0.1154 |
| 65–69 | 0.0123 | 0.1155 | 0.0199 | 0.1609 | 0.0160 | 0.1391 |
| 70–74 | 0.0111 | 0.1410 | 0.0162 | 0.1733 | 0.0136 | 0.1575 |
| 75–79 | 0.0084 | 0.1467 | 0.0122 | 0.1783 | 0.0103 | 0.1636 |
| 80–84 | 0.0057 | 0.1456 | 0.0082 | 0.1705 | 0.0069 | 0.1576 |
| 85–89 | 0.0035 | 0.1352 | 0.0060 | 0.1775 | 0.0047 | 0.1534 |
| 90–94 | 0.0037 | 0.1784 | 0.0050 | 0.2059 | 0.0039 | 0.1683 |
| 95+ | 0.0038 | 0.2565 | 0.0045 | 0.2797 | 0.0046 | 0.2871 |
| Total | 0.0129 | 0.0838 | 0.0303 | 0.1323 | 0.0211 | 0.1072 |
mean absolute error (MAE), mean absolute percentage error (MAPE), MAE is in units of 1 and MAPE is in %
Fig. 4.
Comparison of model-fitted values and true reference values of the combined HALE for different age groups, 1990–2019 (A) and (B) indicate the 0- age group and 60–64 age group separately. Shaded areas indicate the corresponding 95% uncertainty intervals
Discussion
This study employed the GBD Chinese YLD rate as a benchmark to identify three commonly used indicators, IID, PCDPF and U5MR, from available data resources within China. A model for measuring the Chinese YLD rate with these three variables as predictors was then constructed. The model will have significant applications in the measurement of HALE in mainland China.
Since the HALE incorporated into Chinese government planning in the document ‘Healthy China 2030’ in 2016 [4]. It has become standard practice for all levels of government in China, including the entire country, 34 provinces and 333 municipalities, to propose target planning for HALE. Nevertheless, the calculation of HALE in planning is subject to conversion to YLD rates using prevalence data for the full range of causes. Consequently, the high data requirements have become a significant obstacle for Chinese governments at all levels in measuring YLD, which in turn constrains their ability to measure HALE. The three-parameter YLD measurement model proposed in this study addresses the key issue of HALE measurement in China, particularly at the provincial and municipal levels. It is possible for provincial and municipal governments at all levels to obtain the IID from infectious disease surveillance data, PCDPF from chronic disease survey data, and U5MR from maternal and child surveillance data. These data can then be substituted into the ‘model (1)’ constructed in this study to obtain the YLD rate of the region by age. Once this has been done, the YLD rate can be combined with life expectancy to calculate the HALE of the region using the Sullivan method.
Currently, the GBD study leads in measuring HALE worldwide [9, 27, 28]. However, the measurement process of GBD’s HALE is quite complex, particularly the calculation process of YLD, which necessitates the use of global data resources and a sophisticated methodology. This makes it challenging to apply the methodology in different regions within China. The China YLD rate measurement model in this study was constructed on the basis of the GBD structure. Despite some deviations from GBD published values, this model greatly improves its applicability in China. This is due to the fact that the three predictor variables utilized in the model proposed in this study are more prevalent in China’s domestic provincial and municipal data resources, and the model is straightforward to implement. The IID data originates from China Infectious Disease Surveillance, and the U5MR data is derived from the Maternal and Child Surveillance and Coroner’s Surveillance programs, which collectively encompass all urban areas within the country. The PCDPF data is derived from two sources: the National Health Service Survey, conducted every five years in China, and the Chronic Disease and Risk Factor Surveillance Survey, conducted every three years [26].
All of the error values for YLD rates and HALEs are very small and approach zero, regardless of whether the models are sex specific or combined. This indicates a highly accurate model with estimates closely aligned with published GBD values. This indicates that the YLD measurement model constructed in this study is more reliable than several other YLD rate measures mentioned in the introduction. Nonetheless, we still present the four-parameter model for different genders in the Appendix. This is because the addition of the two-week incidence of impairment poisoning to the IID, PCDPF, and U5MR parameters led to a decrease in the total MAPE of the combined YLD rate and HALE by 14.12% and 32.18%, respectively.
The modeled errors by age showed that YLD MAEs increased and that MAPEs decreased with age, probably because YLD rates increase with age. Furthermore, the modeled errors by sex indicate that although the MAPEs of YLD rates and HALEs are lower for males than for females at almost all ages, the difference is almost negligible given the magnitude of YLD rates and HALEs values for both sexes. Similar findings were reported in previous studies performed by Jonker Marcel F. et al. [29] using the Bayesian random-effects approach to estimate healthy life expectancy.
The predictor variables we used to model the subsexed YLD rates in this study were as follows: only the PCDPF was split-sex. For IID and U5MR (including the two-week incidence of impairment poisoning for the four-parameter model in the Appendix), the combined rates were employed in the subsexed model. This is mainly because the MAE and MAPE of the sex-specific YLD rate are very close to those of the combined YLD rate in the sex-specific model, although only the PCDPF variable is sex specific. In fact, we also tried to include sex-specific IID and U5MR in the corresponding models, but the model errors hardly improved substantially. Another factor is that the aggregate values employed exhibit greater stability than the gender-specific values of the variables, without gender bias. In addition, using aggregate variables is more convenient than using gender-specific variables in model application. The official publicly released data for variables such as IID and the U5MR within China are all aggregated values, with few gender-specific values [30, 31].
Furthermore, it is worth noting that, compared with those of the GBD study, our study found narrower 95% UIs for the YLD rate and HALE model-fitted values. This disparity may be attributed to the differing calculation processes of UIs. The UIs of GBDs are based on a global data source and are estimated using many different estimation methods. There are large uncertainties inherent in this approach [32]. In contrast, our UIs are based on the YLD rates of GBD and their 95% UIs, computed using Monte Carlo methods. This is used to measure the overall reliability of the estimates.
This study employs the YLD rate data up to 2020, which does not incorporate the impact of the novel coronavirus (COVID-19) [33]. Notwithstanding this, the impact of the YLDs associated with the COVID-19 on the YLD rate in this study was minimal. This is due to the fact that the GBD 2021 results indicate that the majority of COVID-19-induced DALYs are deaths rather than YLDs [34]. Moreover, the global incidence of COVID-19-induced YLDs represents a mere 0.56% of the total YLD rate in 2020 and 1.6% in 2021. Indeed, it has been demonstrated that the impact of the COVID-19 pandemic on life expectancy in China has been relatively minimal [35].
The findings of this study indicate two potential avenues for future research. Firstly, it should be noted that the variables included in the model of this study are only applicable to the measurement of all-cause YLD rates in China. Nevertheless, the methodology employed in this study also indicates that other countries, particularly those with limited data resources, may utilize the same process to identify suitable variables for their regions and construct corresponding YLD rate measurement models. Secondly, the model proposed in this study is unable to differentiate between the YLD rates for different etiologies. Consequently, it is only capable of measuring the total YLD rate for all etiologies. In the future, further investigation can be conducted to ascertain the decomposition of the YLD measured by the model in this study into the YLD of the major etiologies.
Finally, the main limitation of this study is that our model simplifies the YLD rate measurement technique in GBD, relying on the GBD database. Hence, the accuracy of the estimates in this study is largely dependent on the reliability of YLD rate estimates in China provided by GBD. However, the GBD study is currently acknowledged as one of the most widely recognized and accepted research programs in HALE [36].
Conclusion
Based on data from the GBD Study and domestic sources in China, this study constructed a three-input-parameter model to estimate YLD rates and HALEs by sex and age group in China. That is, to obtain the 21 age-specific YLD rates, the 3 predictor variables IID, PCDPF, and U5MR were inputted for some regions. These rates were combined with life tables to obtain HALEs. The results showed that the HALE measurement model we developed in China possesses a simple methodology, strong applicability and high accuracy. With limited data resources in China, our research provides a realistic and feasible solution for computing the national HALE, particularly at the provincial, city, and county levels.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
We thank the Global Burden of Disease study for providing a rich resource of valuable data for our research.
Abbreviations
- HALE
Health-Adjusted Life Expectancy
- YLD
Years lived with disability
- GBD
Global Burden of Disease
- MAE
Mean absolute error
- MAPE
Mean absolute percentage error
- WHO
World Health Organization
- U5MR
Under-five mortality rate
- IID
Incidence of infectious diseases
- PCDPF
Incidence of chronic diseases among persons aged 15 and older
- UIs
Uncertainty intervals
Author contributions
HSB provided research design ideas. CY provided research methodology guidance. MJJ and ZXC organized and processed the data. CSQ organized and analyzed the data and wrote the manuscript. All authors had access to all the data in the study, contributed to manuscript writing, and approved the final version.
Funding
This work was supported by grants from the Natural Science Foundation of Jiangxi Province(20224BAB206094), the Science and Technology Plan Project of Jiangxi Province Health Commission (202211345), the National Natural Science Foundation of China(81960618).
Data availability
Domestic data available in China are from National Health Service Survey and Analysis Report , the China Health and Health Statistics Yearbook, and the China Statistical Yearbook . GBD 2019 data are from the Global Health Data Exchange query tool (https://vizhub.healthdata.org/gbd-results/).
Declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors have no relevant financial or non-financial interests to disclose.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Walsh D, Wyper GMA, McCartney G. Trends in healthy life expectancy in the age of austerity. J Epidemiol Commun H. 2022;76(8):743–5. doi: 10.1136/jech-2022-219011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.The world health. report 2000 – Health systems: improving performance [https://apps.who.int/iris/handle/10665/268209]].
- 3.Evaluating the Uptake of the Healthy Life Years Indicator. Final report [https://www.rand.org/content/dam/rand/pubs/technical_reports/2007/RAND_TR453.pdf].
- 4.Healthy China 2030 Outline of the, Plan. [http://www.gov.cn/zhengce/2016-10/25/content_5124174.htm].
- 5.Robine JM, Ritchie K. Healthy life expectancy: evaluation of global indicator of change in population health. BMJ. 1991;302(6774):457–60. doi: 10.1136/bmj.302.6774.457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Norman P, Exeter D, Shelton N, Head J, Murray E. (Un-) healthy ageing: Geographic inequalities in disability-free life expectancy in England and Wales. Health Place. 2022;76:102820. doi: 10.1016/j.healthplace.2022.102820. [DOI] [PubMed] [Google Scholar]
- 7.Hu Z, Liu XT, Jiang F, Ma LX, Yang J, Chen Y, Zhu LH, Mao ZX, Hou J, Wang CJ. Multidimensional evaluation of healthy life expectancy indicators based on mental health among the rural older population: a large-scale cross-sectional study. J Affect Disorders. 2022;319:318–24. doi: 10.1016/j.jad.2022.09.033. [DOI] [PubMed] [Google Scholar]
- 8.Moreno X, Lera L, Albala C. Disability-free life expectancy and life expectancy in good self-rated health in Chile: gender differences and compression of morbidity between 2009 and 2016. PLoS ONE. 2020;15(4):e0232445. doi: 10.1371/journal.pone.0232445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Collaborators GD. Global age-sex-specific fertility, mortality, healthy life expectancy (HALE), and population estimates in 204 countries and territories, 1950–2019: a comprehensive demographic analysis for the global burden of Disease Study 2019. Lancet. 2020;396(10258):1160–203. doi: 10.1016/S0140-6736(20)30977-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murray CJL, Ezzati M, Flaxman AD, Lim S, Lozano R, Michaud C, Naghavi M, Salomon JA, Shibuya K, Vos T, et al. GBD 2010: design, definitions, and metrics. Lancet. 2012;380(9859):2063–6. doi: 10.1016/S0140-6736(12)61899-6. [DOI] [PubMed] [Google Scholar]
- 11.Vos T, Flaxman AD, Naghavi M, Lozano R, Michaud C, Ezzati M, Shibuya K, Salomon JA, Abdalla S, Aboyans V, et al. Years lived with disability (YLDs) for 1160 sequelae of 289 diseases and injuries 1990–2010: a systematic analysis for the global burden of Disease Study 2010. Lancet. 2012;380(9859):2163–96. doi: 10.1016/S0140-6736(12)61729-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Collaborators GP. The state of health in Pakistan and its provinces and territories, 1990–2019: a systematic analysis for the global burden of Disease Study 2019. Lancet Glob Health. 2023;11(2):E229–43. doi: 10.1016/S2214-109X(22)00497-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xi JY, Zhang WJ, Chen Z, Zhang YT, Chen LC, Zhang YQ, Lin X, Hao YT. Potential gains in Health-Adjusted Life Expectancy by reducing Burden of Noncommunicable diseases in 188 countries: a Population-based study. Value Health. 2023;26(6):802–9. doi: 10.1016/j.jval.2022.12.008. [DOI] [PubMed] [Google Scholar]
- 14.Angell B, Sanuade O, Adetifa IMO, Okeke IN, Adamu AL, Aliyu MH, Ameh EA, Kyari F, Gadanya MA, Mabayoje DA, et al. Population health outcomes in Nigeria compared with other west African countries, 1998–2019: a systematic analysis for the global burden of Disease Study. Lancet. 2022;399(10330):1117–29. doi: 10.1016/S0140-6736(21)02722-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee JY, Ock M, Kim SH, Go DS, Kim HJ, Jo MW. Health-Adjusted Life Expectancy (HALE) in Korea: 2005–2011. J Korean Med Sci. 2016;31:S139–45. doi: 10.3346/jkms.2016.31.S2.S139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kim YE, Jung YS, Ock M, Park H, Kim KB, Go DS, Yoon SJ. The gaps in Health-Adjusted Life Years (HALE) by income and region in Korea: A National Representative Bigdata Analysis. Int J Env Res Pub He. 2021;18(7):3473. doi: 10.3390/ijerph18073473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ruan XW, Li Y, Jin XH, Deng P, Xu JY, Li N, Li X, Liu YQ, Hu YY, Xie JW, et al. Health-adjusted life expectancy (HALE) in Chongqing, China, 2017: an artificial intelligence and big data method estimating the burden of disease at city level. Lancet Reg Health-W. 2021;9:100110. doi: 10.1016/j.lanwpc.2021.100110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Miao X, Chen J, Wu Q, Meng W, Ren L, Wu Z, Guo X, Zhang X, Meng Q. Estimation of the population, death, and quality of life in Shaanxi Province, western China: a cross-sectional study. Chin Med J (Engl) 2023;136(15):1832–8. doi: 10.1097/CM9.0000000000002524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.National burden of disease studies. : a practical guide [https://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=615C74FCAC6855487513C525A468DA1C?doi=10.1.1.120.8776&rep=rep1&type=pdf]
- 20.Xi JY, Chen YY, Zhang YQ, Luo A, Du ZC, Liang BH, Dong H, Lin X, Qin PZ, Hao YT. Key social determinants to narrow the gap between Health-adjusted life expectancy and life expectancy in megacities. Biomed Environ Sci. 2022;35(9):773–81. doi: 10.3967/bes2022.102. [DOI] [PubMed] [Google Scholar]
- 21.Zheng XY, Xu XJ, Liu YY, Xu YJ, Pan SX, Zeng XY, Yi Q, Xiao N, Lin LF. Age-standardized mortality, disability-adjusted life-years and healthy life expectancy in different cultural regions of Guangdong, China: a population-based study of 2005–2015. BMC Public Health. 2020;20(1):858. doi: 10.1186/s12889-020-8420-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Murray CJ, Lopez AD. Alternative projections of mortality and disability by cause 1990–2020: global burden of Disease Study. Lancet. 1997;349(9064):1498–504. doi: 10.1016/S0140-6736(96)07492-2. [DOI] [PubMed] [Google Scholar]
- 23.The 14th Five-Year. Natl Health Plan [https://www.gov.cn/zhengce/content/2022-05/20/content_5691424.htm].
- 24.Sullivan DF. A single index of mortality and morbidity. HSMHA Health Rep. 1971;86(4):347–54. doi: 10.2307/4594169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhao D, Zhang H, Zhang R, He S. Research on hand, foot and mouth disease incidence forecasting using hybrid model in mainland China. BMC Public Health. 2023;23(1):619. doi: 10.1186/s12889-023-15543-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang QQ, Yu SC, Xu CD, Liu JJ, Li YQ, Zhang MH, Long XJ, Liu YN, Bi YF, Zhao WH, et al. Association between Selenium in Soil and diabetes in Chinese residents aged 35–74 years: results from the 2010 National Survey of Chronic diseases and behavioral risk factors Surveillance. Biomed Environ Sci. 2020;33(4):260–8. doi: 10.3967/bes2020.035. [DOI] [PubMed] [Google Scholar]
- 27.Collaborators GDH. Global, regional, and national disability-adjusted life-years (DALYs) for 333 diseases and injuries and healthy life expectancy (HALE) for 195 countries and territories, 1990–2016: a systematic analysis for the global burden of Disease Study 2016. Lancet. 2017;390(10106):1260–344. doi: 10.1016/S0140-6736(17)32130-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Collaborators GDH. Global, regional, and national disability-adjusted life-years (DALYs) for 359 diseases and injuries and healthy life expectancy (HALE) for 195 countries and territories, 1990–2017: a systematic analysis for the global burden of Disease Study. Lancet. 2018;392(10159):1859–922. doi: 10.1016/S0140-6736(18)32335-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jonker MF, Congdon PD, van Lenthe FJ, Donkers B, Burdorf A, Mackenbach JP. Small-area health comparisons using health-adjusted life expectancies: a bayesian random-effects approach. Health Place. 2013;23:70–8. doi: 10.1016/j.healthplace.2013.04.003. [DOI] [PubMed] [Google Scholar]
- 30.Chen L, Wang Z. The Urban-Rural gap in under-5 mortality rate narrowed in China, 1991–2019. Iran J Public Health. 2021;50(8):1722–3. doi: 10.18502/ijph.v50i8.6820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jiang Y, Dou X, Yan C, Wan L, Liu H, Li M, Wang R, Li G, Zhao L, Liu Z, et al. Epidemiological characteristics and trends of notifiable infectious diseases in China from 1986 to 2016. J Glob Health. 2020;10(2):020803. doi: 10.7189/jogh.10.020803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Permanyer I, Villavicencio F, Trias-Llimos S. Healthy lifespan inequality: morbidity compression from a global perspective. Eur J Epidemiol. 2023;38(5):511–21. doi: 10.1007/s10654-023-00989-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bai R, Liu Y, Zhang L, Dong W, Bai Z, Zhou M. Projections of future life expectancy in China up to 2035: a modelling study. Lancet Public Health 2023, S2468–2667(22):00338–00333. [DOI] [PMC free article] [PubMed]
- 34.GBD2021-Diseases-and-Injuries-Collaborators. Global incidence, prevalence, years lived with disability (YLDs), disability-adjusted life-years (DALYs), and healthy life expectancy (HALE) for 371 diseases and injuries in 204 countries and territories and 811 subnational locations, 1990–2021: a systematic analysis for the Global Burden of Disease Study 2021. Lancet (London, England) 2024. [DOI] [PMC free article] [PubMed]
- 35.GBD2021-Diseases-and-Injuries-Collaborators. Global age-sex-specific mortality, life expectancy, and population estimates in 204 countries and territories and 811 subnational locations, 1950–2021, and the impact of the COVID-19 pandemic: a comprehensive demographic analysis for the Global Burden of Disease Study 2021. Lancet (London, England) 2024. [DOI] [PMC free article] [PubMed]
- 36.Chen LJ, Wang L, Qian Y, Chen H. Changes and Trend disparities in Life Expectancy and Health-Adjusted Life Expectancy attributed to disability and mortality from 1990 to 2019 in China. Front Public Health. 2022;10:925114. doi: 10.3389/fpubh.2022.925114. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Domestic data available in China are from National Health Service Survey and Analysis Report , the China Health and Health Statistics Yearbook, and the China Statistical Yearbook . GBD 2019 data are from the Global Health Data Exchange query tool (https://vizhub.healthdata.org/gbd-results/).