Ultrafast reversible self-assembly of living tangled matter

Abstract

Tangled active filaments are ubiquitous in nature, from chromosomal DNA and cilia carpets to root networks and worm collectives. How activity and elasticity facilitate collective topological transformations in living tangled matter is not well understood. We studied California blackworms (Lumbriculus variegatus), which slowly form tangles in minutes but can untangle in milliseconds. Combining ultrasound imaging, theoretical analysis, and simulations, we developed and validated a mechanistic model that explains how the kinematics of individual active filaments determines their emergent collective topological dynamics. The model reveals that resonantly alternating helical waves enable both tangle formation and ultrafast untangling. By identifying generic dynamical principles of topological self-transformations, our results can provide guidance for designing classes of topologically tunable active materials.

Editor’s summary

Anyone who has ever packed away rope without coiling it properly knows how easily it gets tangled and how difficult it can be to untangle. By contrast, California blackworms will migrate into a tangled ball over the course of minutes to regulate temperature or moisture but then disentangle and scatter within milliseconds upon sensing danger. Patil et al. combined ultrasound studies of worms with theory to develop a model of how the movement of individual worms (or filaments) affects the collective dynamics (see the Perspective by Panagiotou). In particular, they found that alternating helical waves enabled both tangle formation and ultrafast untangling. —Marc S. Lavine

Knots determine the robustness and function of filamentous matter across a wide range of scales, from the intertwined yarns in ropes and fabrics (1) to the tangled polymers in rubbers (2, 3) and gels (4). The extraordinary stability of knotted materials arises from the intricate interplay of mutual mechanical obstruction (5) and contact friction (6) between adjacent filaments (7, 8). As any fisherman or long-haired creature can confirm, creating knotty structures (9) is not difficult: When soft elastic fibers are randomly mixed together (10), they naturally tend to form a highly disordered tangled state (11, 12). By contrast, untangling a complex knot presents a daunting and historically infamous (13) task. Certain biological species such as the California blackworm (Lumbriculus variegatus) (14) have evolved to solve both the tangling and the untangling problem with great efficiency by using only a relatively basic set of neurons and muscles. Exactly how they are able to do this remains poorly understood.

When considered from an active matter perspective, worm tangles constitute an archetypal example of an autonomous filamentous material that can self-assemble, shape-shift, and exhibit emergent collective functions (15, 16). In minutes, a group of initially dispersed California blackworms (14) can self-organize into a persistent three-dimensional (3D) tangled structure, but they require only a few tens of milliseconds to disentangle upon sensing danger (movie S1). Blackworms, as well as some of their relatives (17), use the tangled state to efficiently execute a range of essential biological functions, such as temperature maintenance, moisture retention, and collective locomotion (18, 19). Perhaps more importantly, the ability to escape rapidly (20) from the tangle can often be a lifesaving escape response from predators (14) and environmental threats (16). Motivated by an interest to understand the biophysical mechanisms by which filamentous organisms can achieve both robust tangling and ultrafast untangling, we combined ultrasound imaging experiments and elasticity theory to explain how individual worm gaits give rise to collective topological dynamics and transitions between tangled and untangled states. By mapping worm tangling to percolation (21) and picture-hanging puzzles (22), we show how resonantly tuned helical waves can enable self-assembly and rapid unknotting of filamentous matter, thus revealing a generic dynamical principle that can guide the design of new active materials.

Ultrasound experiments

Blackworms can assemble into topologically intricate tangles consisting of anywhere from 5 to 50,000 worms (Fig. 1A) (16). Our ultrasound experiments, conducted on worm tangles immobilized in gelatin (movie S2), allowed for the reconstruction of the 3D structure of a living tangle (Fig. 1, B and C, and supplementary materials, materials and methods). This revealed a picture of the tangle as a strongly interacting system, in which the worms are tightly packed (Fig. 1D) and most worms are in contact with most other worms (Fig. 1E). In addition to describing the arrangement of contact, the nontopological structure of the worm tangle can also be described on the basis of the variation of geometric quantities both within and between different worms. To analyze the tangle geometry, we approximated each worm as a curve, $\mathit{x}(s)$, parameterized by arc length, $s$, which can be characterized by local in-plane curvature, $\text{κ}(s)$, and an out-of-plane 3D torsion, $\text{τ}(s)$. These geometric quantities give rise to bending strain, $ϵ=\text{κ}h$ (Fig. 1F), and chirality, $\chi ={\text{κ}}^2\text{τ}$ (Fig. 1G), where $h$ is the worm radius (23). The 3D distributions of both strain and chirality are primarily heterogeneous (Fig. 1, F and G) and decay rapidly as functions of the spatial separation, $\text{|}\mathit{x}-\mathit{y}\text{|}$ (Fig. 1, H and I). For small values of $\text{|}\mathit{x}-\mathit{y}\text{|}$, the correlation functions are dominated by intraworm interactions, but decorrelation occurs once ${\text{ρ}}_{\text{C}}$ begins to include interworm effects. In particular, ${\text{ρ}}_{\text{C}}\approx 0$ for both strain and chirality once $\text{|}\mathit{x}-\mathit{y}\text{|}>2.5h$, which indicates the existence of an effective radius, $h_{\text{eff}}=1.25h$. This effective radius is a signature of the ultrasound protocol (23), which requires the tangles to undergo a small dilation. The rapid decorrelation demonstrates that strain and chirality are not described by 3D continuum fields, illustrating the difficulty of constructing a continuum theory for the living tangle. Understanding the mesoscale structure of the tangle requires moving beyond purely geometrical properties.

Fig. 1. Three-dimensional ultrasound data reveal the mechanical structure of active, biological worm tangles.

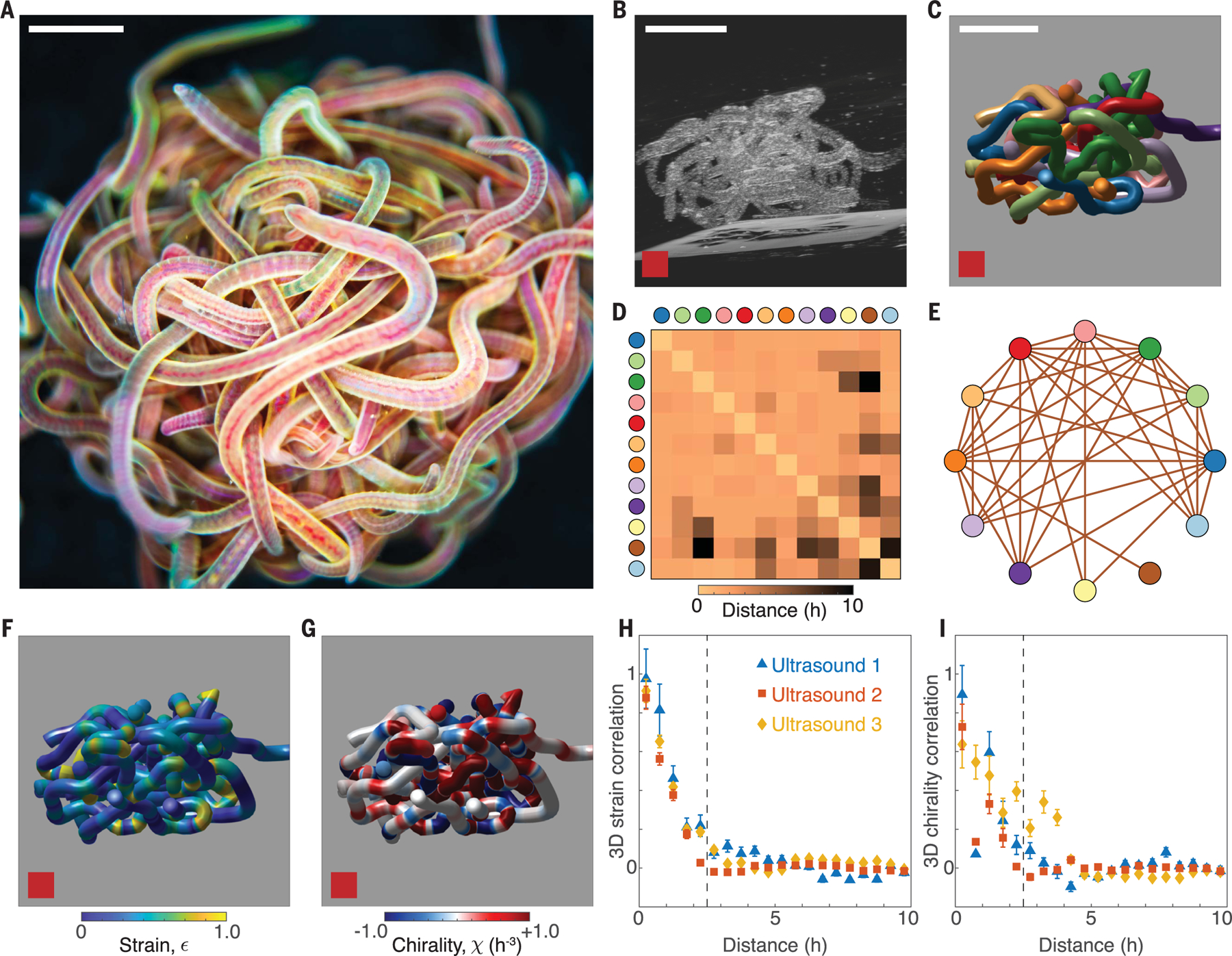
(A) Topologically complex tangle formed by Lumbriculus variegatus consisting of approximately 200 worms. Scale bar, 3 mm. (B and C) Ultrasound imaging reveals the interior structure of a 12-worm tangle. Scale bar, 5 mm. (D and E) The contact matrix and contact graph confirm that the worm tangle is a strongly interacting system. (F and G) Three-dimensional experimental data enable the visualization of strain $ϵ$, and chirality $\chi$, fields within the tangle, revealing that the worms form achiral tangles. (H and I) Decorrelation of strain, ${\text{ρ}}_C[ϵ(\mathit{x}),ϵ(\mathit{y})]$, and chirality, ${\text{ρ}}_{\text{C}}[\chi (\mathit{x}),\chi (\mathit{y})]$, over distances of $\text{|}\mathit{x}-\mathit{y}\text{|}\approx 2.5h$ (dotted lines) demonstrates the limits of a continuum elastic theory for worm tangles. The decorrelation length scale indicates the existence of an effective radius, $h_{\text{eff}}~1.25h$, arising from the preparation of tangles for ultrasound (23).

Topological analysis of the tangle geometry allows us to distinguish between different forms of contact. The intuitive notion that worms that intertwine should interact more strongly than worms that simply touch can be captured by considering the linking number (24), $Lk$, of the $i$th worm and the $j$th worm

$$L{k}_{ij}=\frac{1}{4\pi }\text{∫}dsd\text{σ}{\mathrm{\Gamma }}_{ij}\cdot \left({\partial }_s{\mathrm{\Gamma }}_{ij}\times {\partial }_{\sigma }{\mathrm{\Gamma }}_{ij}\right)$$ (1)

where ${\mathrm{\Gamma }}_{ij}(s,\text{σ})=\left[{\mathit{x}}_i(s)-{\mathit{x}}_j(\text{σ})\right]\text{/}\left[\left|{\mathit{x}}_i(s)-{\mathit{x}}_j(\text{σ})\right|\right]$, and ${\mathit{x}}_i$ and ${\mathit{x}}_j$ are the curves representing the $i$th and $j$th worms. Although traditionally defined only for closed curves, the linking number of open curves quantifies entanglement by taking an average of the amount of intertwining in every 2D projection (23, 25). Visually, pairs of worms with $\text{|}Lk\text{|}>1\text{/}2$ appear to wind around each other (Fig. 2, A and B). However, $Lk$ is not sensitive to contact, which must ultimately mediate every worm–worm interaction. Accordingly, we defined a more sensitive measure called “contact link,” or $cLk$, by setting $cLk=\text{|}Lk\text{|}$ for worms in contact and $cLk=0$ otherwise. In contrast to the contact matrix (Fig. 1D), the contact link matrix (Fig. 2C) identifies a far smaller number of key interactions, thus providing a sparser representation of tangle state. This is evident from the tangle graph (Fig. 2D), which shows worm–worm interactions with $cLk>1\text{/}2$. Despite being a function of pairwise tangling as opposed to a function of total entanglement, the robustness of contact link as a tangling measure is evident through its behavior across different ultrasound datasets. For example, the probability distribution of the contact link between two worms, a measure of topological interaction strength, retains a characteristic shape across worm tangles (Fig. 2E). Additionally, the total contact link (23), obtained by summing all the pair contact links from Fig. 2C, is sensitive to the contact structure of the tangle. When treated as a collection of tubes, the contact structure of a tangle can be altered by modifying the tube radius. The total contact link as a function of tube radius behaves similarly across datasets as the tubes are thickened from zero radius to larger radii (Fig. 2F). Thus, by incorporating topological information (25, 26) as well as geometric information, $cLk$ captures core structural motifs that are reproducible across different experiments, enabling us to compare experimentally observed worm tangles with tangled structures generated from dynamical simulations.

Fig. 2. Topological structure of worm tangles.

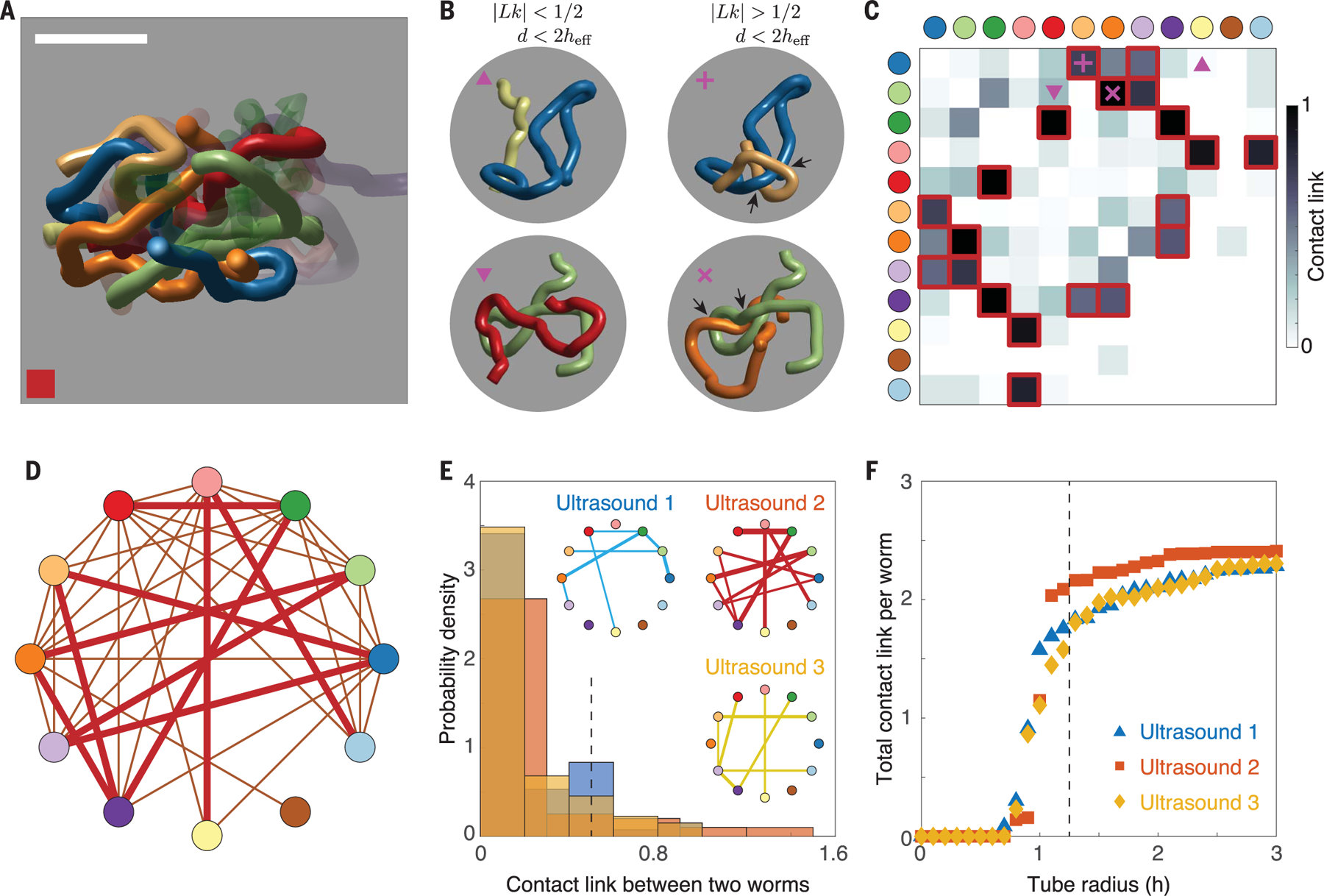
(A) Individual topological interactions between chosen worms (solid color) mapped in detail by 3D ultrasound reconstructions (as in Fig. 1, B and C). Scale bar, 5 mm. (B) Topological analysis enables the classification of tangle structure by distinguishing between (left column) contact and (right column) linking interactions, which are defined by having linking number $\text{|}Lk\text{|}>1\text{/2}$. (C) Contact link, $cLk$, defined as the absolute value of the link between worms separated by at most $2h_{\text{eff}}$, identifies the strongest topological interactions within the tangle. The contact link between nontouching worms is 0. Pairs of worms with $cLk>\text{1/2}$ are highlighted in red. (D) The tangle graph provides a sparser representation of tangle state than does the contact graph. Edges are present between pairs of worms with $cLk>\text{1/2}$, that is, worms that both touch and have $\text{|}Lk\text{|}>1\text{/2}$ [red bordered squares in (C)]. (E) The probability distribution of the contact link between two worms is stable across ultrasound datasets. Pairs of worms with contact link greater than $1\text{/}2$ (dotted line) lead to edges in the corresponding tangle graphs (inset), with edge thickness given by the value of the contact link. (F) Increasing the tube radius of the worm curves modifies the contact structure of the tangle and thus increases the total contact link (23). The radius dependence of total contact link is similar across different tangles and indicates the presence of an effective radius, as in Fig. 1, H and I, that is distinct from the true radius, $h$.

Worm dynamics

The ability of the blackworm to form tangles in minutes (Fig. 3A) but rapidly unravel in milliseconds (Fig. 3B) is a key biological and topological puzzle (27, 28). To understand the dynamical process that gives rise to tangle formation, we experimentally studied the head trajectories of single worms (Fig. 3, A to D, and supplementary materials, materials and methods). Because these experiments were performed in a shallow fluid well (height ~2 mm), the projection of the trajectories into 2D (Fig. 3, A to D) did not cause substantial information loss. To capture the winding motions associated with tangling and untangling, we assumed the worm head has a preferred speed, $v=\langle \text{|}\dot{\mathit{x}}(t)\text{|}\rangle$, and focused on the worm turning direction, $\text{θ}(t)=\arg \dot{\mathit{x}}(t)$. The $\text{θ}$ trajectories can be described approximately in terms of two parameters, the average angular speed, $\text{α}=\langle \left|\dot{\text{θ}}\right|\rangle$ (Fig. 3, A and B), and the rate, $\text{λ}$, at which $\dot{\text{θ}}$ changes sign. These quantities can be estimated from the noisy trajectory data (23). Although the characteristic timescales for slow tangling and ultrafast untangling, ${\text{α}}^{-1}$, differ by two orders of magnitude, rescaling the $\text{θ}$ trajectories for each gait by ${\text{α}}^{-1}$ revealed similar underlying dynamics (Fig. 3, A and B). This similarity reflects the biological constraints on locomotion machinery (29) and indicates that tangling and untangling can be captured by the same mathematical model. To confirm this, we first formulated a minimal 2D model of worm-head dynamics, which we then generalized to a full 3D dynamical picture.

Fig. 3. Resonant helical worm-head dynamics give rise to numerically reproducible weaving and unweaving gaits.

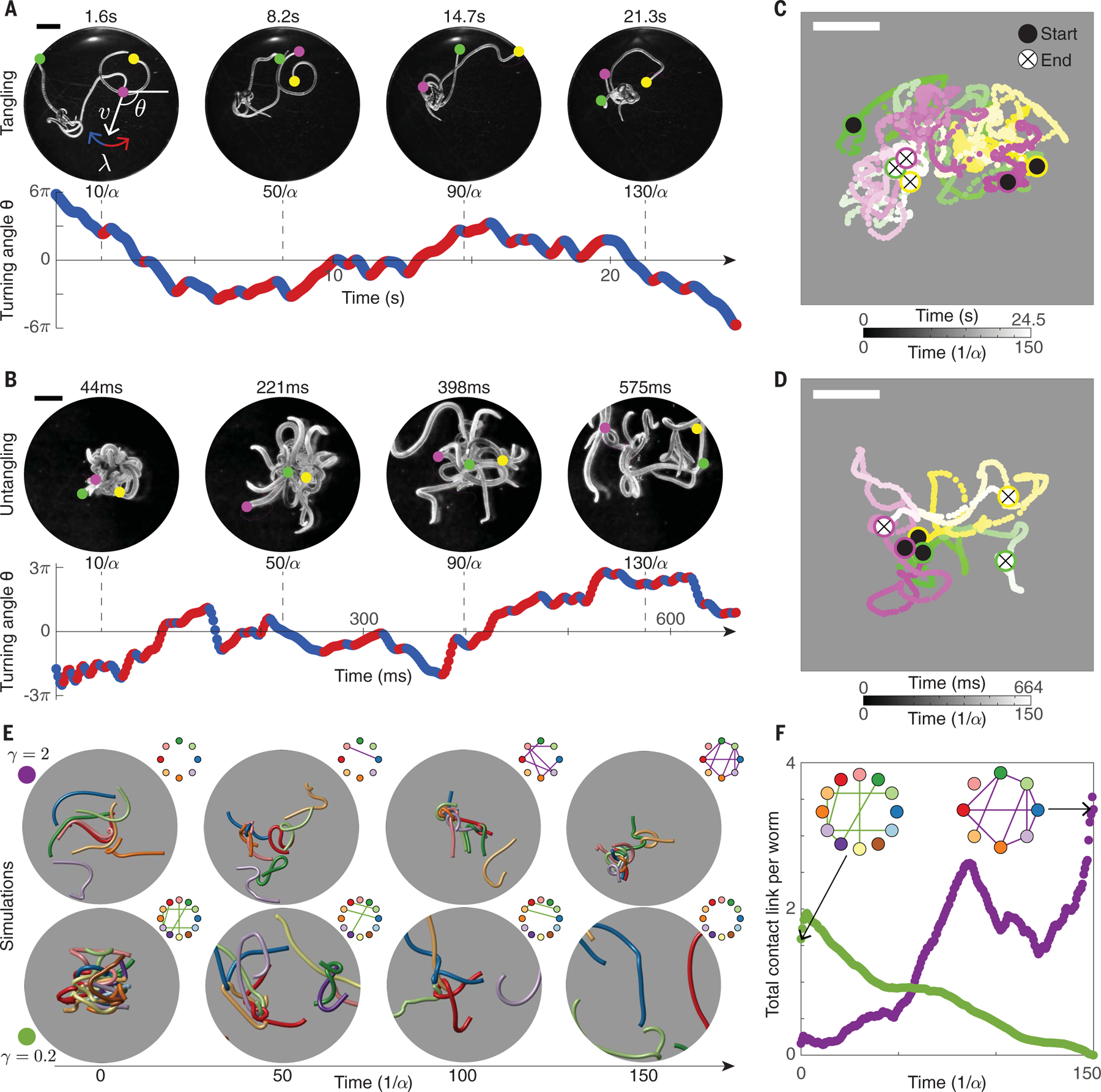
(A and B) Experimentally observed worm-head trajectories projected into 2D can be approximated by their angular direction, $\text{θ}(t)=\arg \dot{\mathit{x}}(\text{t})$, in both the (A) tangling and (B) untangling cases (movie S3). $\text{θ}$ is characterized by an average turning rate, $\text{α}=\langle \left|\dot{\text{θ}}\right|\rangle$, and a rate of switching from left turning (red points, $\dot{\text{θ}}>0$) to right turning (blue points, $\dot{\text{θ}}<0$). The chirality number, $\text{γ}=\text{α/}2\text{πλ}$, captures the difference between weaving $(\text{γ}=0.68)$ and unweaving $(\text{γ}=0.36)$ gaits. ${\text{α}}^{-1}$ defines an intrinsic timescale for tangle assembly and disassembly. Scale bars, 3 mm. (C and D) Experimentally measured head trajectories of three worms (different colors) executing the (C) tangling and (D) untangling gaits demonstrate the (C) formation or (D) removal of topological obstructions within a similar time in units of ${\text{α}}^{-1}$. Scale bars, 5 mm. (E) Simulations of active Kirchhoff filaments demonstrate that the gaits described in (A) and (B) are sufficient for reversible tangle self-assembly (movie S3). The topological state is quantified with tangle graphs (inset). Tangling filaments have large $\text{γ}$ [(E), top row, and (A)], and untangling filaments have small $\text{γ}$ [(E), bottom row, and (B)]. The initial tangled state [(E), bottom row] is obtained from 3D ultrasound reconstruction. Average worm lengths range from 40 mm (top row) to 28 mm (bottom row), with a radius of 0.5 mm throughout. Displayed worms are thickened to aid visualization. (F) The total contact link per worm (Fig. 2) obtained from simulations reveals the rate at which tangles form [(E), top row, purple dots] and unravel [(E), bottom row, green dots].

A minimal 2D model can be constructed by focusing on the helical worm-head dynamics that we identified experimentally (Fig. 3). The quantities $\text{α}$, $\text{λ}$, and $v$ motivate the following stochastic differential equation (SDE) model for a worm-head trajectory (23)

$$\dot{\mathit{x}}=v{\mathit{n}}_{\text{θ}}+{\text{ξ}}_T,\dot{\text{θ}}=\text{σ}(t;\text{λ})\text{α}+{\text{ξ}}_R$$ (2)

where ${\text{ξ}}_T$ and ${\text{ξ}}_R$ are noise terms, ${\mathit{n}}_{\text{θ}}$ is a unit vector in the $\text{θ}$ direction, and $\text{σ}(t;\text{λ})$ switches between +1 and −1 at rate $\text{λ}$. These trajectories can be further classified by dimensionless parameters. The chirality number, $\text{γ}=\text{α/}2\text{πλ}$, distinguishes between the tangling and untangling gaits (Fig. 3, A and B). This nondimensional parameter corresponds to the average number of right- or left-handed loops traced out by the worm before changing direction and provides an intuitive way of understanding the topological properties of each gait. When $\text{γ}$ is large, worms wind around each other before switching direction, producing a coherent tangle. By contrast, for small $\text{γ}$, the worms change direction before they are able to wind around one another and so remain untangled. This relationship between tangle state and chirality can be thought of as a form of resonance. Our trajectory model thus explains how the characteristic helical waves produced by untangling worms mediate topology (movie S3).

We next showed that these conclusions generalize to a full 3D mechanical model of worm gaits. To model the worms, we performed elastic-fiber simulations in which the worms were treated as Kirchhoff filaments (5, 30–34) with active head dynamics. The head motions were prescribed by the SDE model (2) together with additional 3D drift (23); the body responded elastically. The resulting worm collectives could form 3D tangled structures (Fig. 3E) consistent with those seen in our experiments, as quantified by contact link (Fig. 3F). The tangling and untangling behavior in these simulations appears to be a function of the chirality number, $\text{γ}$, further confirming its importance (Fig. 3, E and F, and movie S3). This formulation of a 3D dynamical model allows us to understand how the dynamics of single worms produces worm collectives with distinct topologies.

Mean-field theory

On the basis of our analysis of the worm trajectories, we built a mean-field tangling model, which establishes a mapping between tangling and percolation (Fig. 4). To formulate an analytically tractable model, we treat the worm motion as essentially 2D, so each worm effectively moves in a 2D slice of the 3D tangle (Fig. 4, A and B). As a given worm moves in a plane, its head traces out a curve, $\mathit{x}(t)$ (Fig. 4B, purple and green curves), described by Eq. 2. The worm can encounter a set of obstacles, $\mathrm{\Lambda }$, that indicate intersections of the other worms with the given plane (Fig. 4B, colored circles). The 3D notion of contact link between worms can be mapped to this 2D picture (22) by considering the winding of the trajectory, $\mathit{x}(t)$, around the obstacles, $p\in \mathrm{\Lambda }$. We can assign a value to each obstacle, $p$, that measures how much $\mathit{x}(t)$ winds around $p$ and how close the trajectory gets to $p$ (Fig. 4B). We call this value the “contact winding” of $\mathit{x}(t)$ about $p$ and denote it $c{W}_p$ (23). Thresholding and averaging all the contact winding numbers yields a tangling index

$$𝒯=〈\sum _{p\in \mathrm{\Lambda }}\Theta \left(c{W}_p-1\right)〉$$ (3)

where the step function $\Theta$ returns 1 if $c{W}_p>1$ and 0 otherwise. The tangling index therefore counts the number of obstacles that a worm winds around and illustrates that worm-head trajectories with different chirality number, $\text{γ}$, are topologically distinct (Fig. 4B). For example, by changing direction frequently, trajectories with small $\text{γ}$ have smaller overall contact winding (Fig. 4B, bottom row). Because the tangling index counts entanglements, it can also be interpreted as a measure of the mean degree of a tangle graph. Because connected graphs asymptotically have a mean degree of at least 2, we identify ${𝒯}^{\ast }\approx 2$ as the critical tangling index separating tangled states, with $𝒯>2$, from loose states, with $𝒯<2$. Near-critical trajectories (23) bear a notable resemblance to curves that solve the famous picture-hanging puzzle (22), which asks how to hang a picture on two pegs so that it falls if either peg is removed. Critical worm gaits could therefore be associated with such topological quick-release mechanisms; our tomographic reconstructions do indicate that worms form near-critical tangles (Fig. 2F), thus balancing tangle stability with ability to disentangle rapidly.

Fig. 4. Bioinspired tangling model reveals phase diagram underlying topological assembly and manipulation of generic tangles.

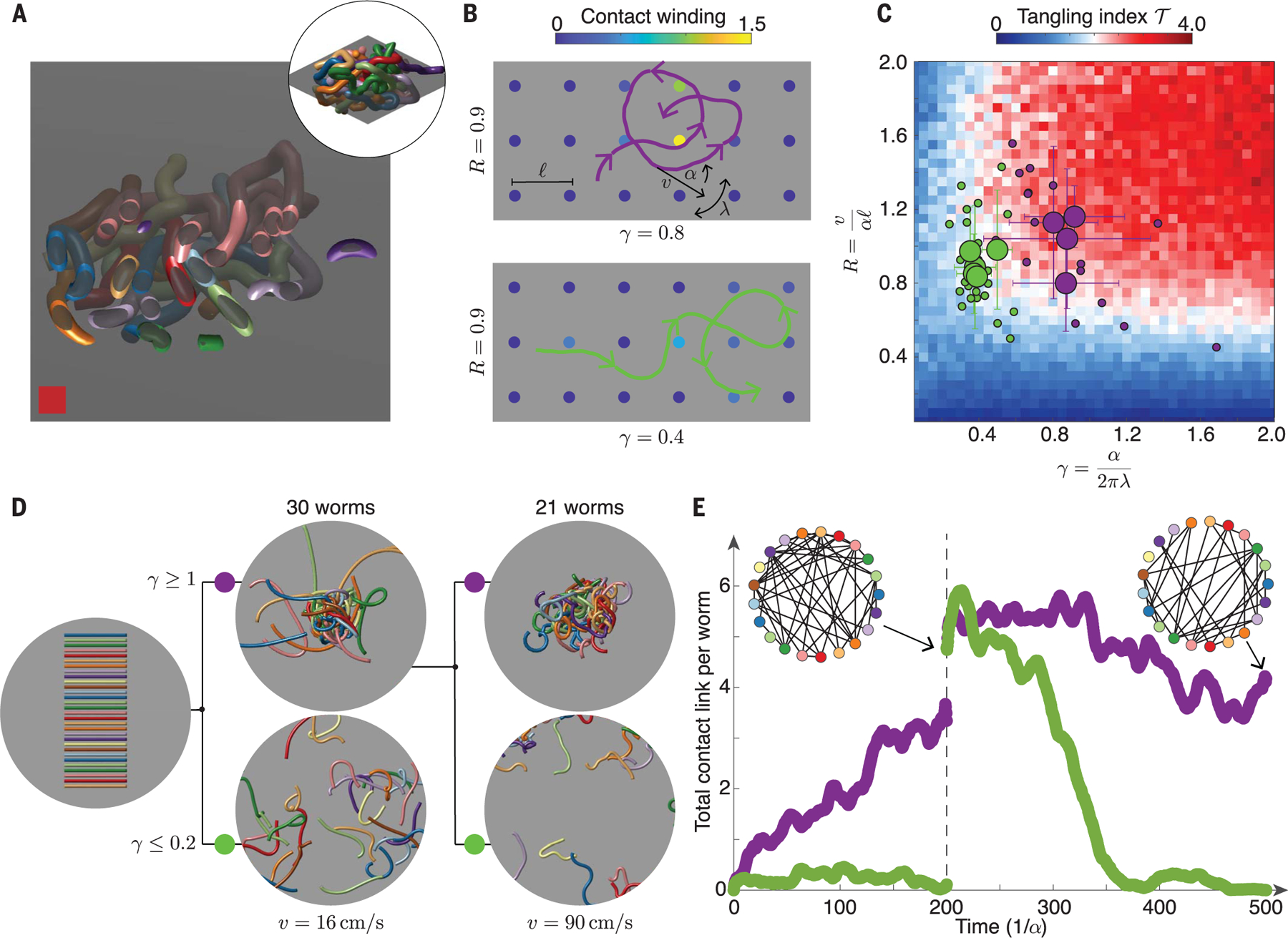
(A) Two-dimensional cross sections of 3D ultrasound reconstructions indicate the obstacle landscape faced by a worm exhibiting quasi-2D motion. (B) A 2D mean-field tangling model measures the winding of a worm-head trajectory (purple and green curves) around fixed obstacles in the plane (solid circles). Contact winding, $cWp$, around obstacles that are far from the trajectory (23) is 0. Points with $cWp>1$ contribute to the tangling index, $𝒯$, of a trajectory (Eq. 3). Trajectories with small chirality number, $\text{γ}$, have smaller overall contact winding. (C) Measured values of $\text{γ}$ and $R$ for blackworms undergoing tangling (purple disks) or untangling (green disks) dynamics lie in regions of the tangle phase space corresponding to tangling (red, $𝒯>2$) and untangling (blue, $𝒯<2$), where the critical value ${𝒯}^{\ast }<2$ corresponds to a connected tangle graph, and hence a minimally tangled state. The untangling data consists of $n=25$ worms (small green disks) from $n=5$ separate 12-worm untangling experiments, and the tangling data consists of $n=18$ worms (small purple disks) from $n=4$ separate 5-worm tangling experiments. The large disks show mean values of $\text{γ}$ and $R$ obtained by averaging over all worms in a given experiment (23). Error bars show standard deviation. (D) Worm gaits predicted by the tangling phase diagram enable robust control of topological transitions (movie S4). Tangle formation and avoidance can be controlled at fixed $R$ by varying $\text{γ}$, both for low worm speeds $v$, (middle, $R=3.4$) and high worm speeds (right, $R=1.0$). Worms have a length of 40 mm and a radius of 0.5 mm. Displayed worms are thickened to aid visualization. (E) Timescales of tangling and untangling from simulations in (D) are set by ${\text{α}}^{-1}$, which varies from the low $v$ simulations ($t<200\text{/α}$, ${\text{α}}^{-1}\approx 0.1\text{s}$) to the high $v$ simulations ($t<200\text{/α}$, ${\text{α}}^{-1}\approx 4\text{ms}$). The largest cluster of touching worms produced by the low $v$, large $\text{γ}$ simulation is used as the initial condition for the high $v$ simulations (23), causing an apparent jump in total contact link per worm at $t<200\text{/α}$. Tangle graphs (insets) illustrate the topological structure of the simulated tangles.

The tangling index enables the topological state to be predicted from worm motion and spacing (Fig. 4C). Assuming small noise terms (23), the worm-head trajectories are characterized by speed $v$, turning rate $\text{α}$, and angular switching rate $\lambda ;\ell$ captures the worm spacing. This leads to two dimensionless quantities, the chirality number, $\text{γ}=\text{α/}2\text{πλ}$, and the loop number, $R=v\text{/α}\ell$, which measures the size of the loops produced by the worm trajectory in units of $\ell$. The resulting phase diagram, $𝒯(\gamma ,R)$, explains the observed values of $\text{γ}$ and $R$ for worms executing tangling and untangling gaits (Fig. 4C). The timescale of these topological transformations depends on ${\text{α}}^{-1}$, which can take any value for fixed $\text{γ}$ and $R$. Because ${\text{α}}^{-1}=R\ell v^{-1}$, the associated topological transformation timescale is small for fast worms and large for slow worms, which is in agreement with observed worm behavior (Fig. 3, A and B), provided that $R$ and $\ell$ stay approximately constant. The tangling phase diagram further demonstrates that the loop number, $R$, can also be used to control topological state. For example, larger values of $R$ allow a worm to wind around more obstacles, increasing topological complexity. However, for $R>0.5$, the chirality number, $\text{γ}$, is the key determinant of tangle state (Fig. 4C), indicating that tangle topology can be controlled purely by changing the rate, $\text{λ}$, at which the turning direction switches. The validity of this intuitive picture was confirmed with 3D simulations, demonstrating that by tuning $\text{γ}$, active filaments can be programmed to reversibly tangle and untangle at any head speed $v$ (Fig. 4D and movie S4). The phase diagram therefore reveals how tangle topology can be robustly controlled by manipulating only the chiral dynamics of the constituent filaments (Fig. 4, D and E, and movie S4).

Discussion

Blackworm locomotion lies close to the critical tangling threshold (Fig. 4C), indicating that blackworm gaits are mechanically optimized for crossing the tangling–untangling barrier. However, our mean-field tangling model predicts a large space of tangling and untangling strategies, within which blackworms occupy a relatively small region. In addition, at fixed $\text{γ}$ and $R$, the tangling and untangling timescale, ${\text{α}}^{-1}$, can take any value, underscoring the size of the locomotion space. Accounting for energetics helps identify the topological strategies that are inefficient for blackworms. For example, untangling with small $R$ requires forming small, energetically costly loops. Similarly, untangling by means of the linear trajectories corresponding to large $R$ gaits requires braids to be unraveled by pulling rather than unweaving, a motion associated with a higher friction penalty (7, 23). Furthermore, blackworm dynamics are necessarily multifunctional, and topological requirements must be balanced with the need to support efficient, biologically feasible locomotion (14, 32, 35). For example, the helical waves of alternating chirality that promote untangling have also been identified in the context of worm swimming (14). However, the highly entangled region of phase space with $\text{γ}>\text{1}$, $R>0.5$ suggests that there are stable tangle topologies not accessed by the worm collectives. Such a tangle could contain chiral filaments, in contrast to our observed living worm tangles (Fig. 1G). The chirality number and loop number thus demonstrate how complex topologies may be created and tested beyond the biologically feasible regime.

Active helical waves produced by the motion of individual worms facilitate collective tangling and ultrafast untangling. Because the underlying mechanisms are generic, and because the predictions of elasticity theory are known to generalize across a wide range of scales (31), it is relevant to ask whether the results of our mean-field tangling model could apply to other systems of packed and tangled fibers. Our model additionally demonstrates methods for fine control of tangle topology, opening up the possibility of programming a wide range of behaviors into a single topologically adaptive material by harnessing the large internal state space of tangles. The framework developed here could help in better understanding the mechanical advantages of specific classes of tangles and aid in the development of multifunctional materials based on topological properties.

Data and materials availability:

The code used for numerical simulations is available at Zenodo (36). Additional datasets are available at Zenodo (37).