Abstract
Johnson noise thermometers infer thermodynamic temperature from measurements of the thermally-induced current fluctuations that occur in all electrical conductors. This paper reviews the status of Johnson noise thermometry and its prospects for both metrological measurements and for practical applications in industry. The review begins with a brief description of the foundations and principles of Johnson noise thermometry before outlining the many different techniques and technological breakthroughs that have enabled the application of JNT to high-accuracy, cryogenic, and industrial thermometry. Finally, the future of noise thermometry is considered. As the only purely electronic approach to thermodynamic temperature measurement, Johnson noise thermometry has appeal for metrological applications at temperatures ranging from below 1 μK up to 800 K. With the rapid advances in digital technologies, there are also expectations that noise thermometry will become a practical option for some industrial applications reaching temperatures above 2000 K.
Keywords: Johnson noise, temperature measurement, noise thermometer
1. Introduction
Johnson noise is the electronic noise caused by the random thermal motion of charge carriers that occurs within all electrical conductors. Einstein predicted Johnson noise in his 1905 explanation of Brownian motion [1], more than two decades before Johnson reported measurements of the noise in 1927 [2, 3] and Nyquist provided the theoretical description in 1928 [4]. Brownian motion and Johnson noise are examples of microscopic fluctuations related to temperature and macroscopic dissipative phenomena, viscosity and electrical resistance in these cases, because both the fluctuations and the dissipative phenomena arise from the random thermal motion of charge carriers, atoms, or molecules. Einstein’s and Nyquist’s explanations were the first examples of the fluctuation-dissipation theorem developed in 1951 by Callen and Welton [5] (see also [6]).
For Johnson noise, the fluctuation-dissipation theorem relates the power spectral density of the noise voltage, across a conductor in terms of the real part of the conductor impedance, , and its temperature, ,
| (1) |
where is Planck’s constant, is frequency, and is the Boltzmann constant. This expression, derived by Nyquist, is a one-dimensional form of the Planck blackbody law [4, 7]. A second term representing the quantum mechanical zero-point energy is often included in (1), however, the inclusion of the term is controversial and there are thermodynamic arguments suggesting it should not be there [8–10]. The presence or absence of the term is relevant only for high-accuracy measurements at temperatures below 1 mK (see Sec. 3.2).
Usually, Johnson noise is characterized by its mean-square voltage, , conventionally called the noise power. For temperatures above 25 K and frequencies below 1 MHz, the noise power is approximated with a relative error of less than by Nyquist’s law,
| (2) |
where is the bandwidth over which the noise voltage is measured. If the conductor is a pure resistance, , the power spectral density is independent of frequency and the noise is described as “white”. A convenient rule of thumb is that the spectral density of the voltage noise from a 1 resistor at room temperature is about . When integrated over a 1 MHz bandwidth, the noise voltage totals about 4 rms.
Nyquist’s law, (2), which is the foundation for most Johnson noise thermometry (JNT), shows that the thermodynamic temperature can be inferred from measurements of the noise power produced by a resistor of known resistance. One of the main attractions of JNT is that so long as the sensor resistance can be measured, (2) is insensitive to chemical, mechanical, and even nuclear changes in the sensor, and therefore the sensor does not require independent calibration. No other temperature sensor has such immunity to material changes. Indeed, JNT sensors do not need to be metallic conductors; electrolytic solutions [4], graphite rope [11], and even the plasma of combustion processes have been used as sensors [12].
Nyquist’s law also applies to real systems, with very high accuracy and without the need for correction terms. This contrasts with the equations of state used for gas thermometry where the behaviour of real gasses is very much more complicated than the ideal-gas models imply.
Noise thermometry has been applied at temperatures ranging from below 50 nK to 2200 °C, a range far exceeding that of any other temperature sensor. The electronic nature of Johnson noise also means that JNT sensors are easily interfaced to electronic measurement and control systems.
Despite the attractions, noise thermometry is not a practical option for most applications. Measuring such a small signal is a challenge when it must be amplified by a factor of 105 or more, and filtered and rectified with minimal distortion and corruption. The random nature of the noise also means the statistical uncertainty in a temperature measurement decreases as the square root of the measurement bandwidth and measurement time, and large amounts of data are required to make useful measurements. JNT is not suited to applications requiring both high accuracy and fast measurements.
The greatest interest in JNT is found where conventional contact thermometers are unreliable, or knowledge of the thermodynamic temperature is important, i.e., the long-term stability or reproducibility of a temperature measurement method is not sufficient. The long-term aim of many temperature metrologists has been to replace the recipes of the international temperature scales [13, 14] with primary thermometry, and noise thermometry is amongst the most promising candidates. In recent years, this aim has been furthered by the research supporting the planned redefinition of the kelvin and the introduction of the revised SI in May 2019 [15]. Instead of the current definition, based on the triple point of water, the kelvin is to be defined by fixing a value for the Boltzmann constant. For the last decade or so, many of the world’s national measurement institutes have been making exacting measurements of the Boltzmann constant, with several contributing measurements made by JNT [16–19].
Noise thermometry has also been of interest at cryogenic temperatures where other thermodynamic techniques lose sensitivity or cease to operate. At least five distinct JNT methods have been developed for use at cryogenic temperatures, with several exploiting superconducting electronics.
Because any change in resistance of the JNT sensor can be measured in situ, JNT sensors can be calibrated in situ. JNT is therefore well suited to industrial applications requiring long-term stability and where removal of the sensor for recalibration is impracticable. Examples can be found in the nuclear power industry where traditional temperature sensors exposed to radiation are unstable and become too radioactive to be safely withdrawn for recalibration [20–24]. For similar reasons, JNT has also been considered for power systems in satellites [25, 26]. It is also being considered for the control of some high-value-manufacturing processes at temperatures, above 400 °C or so where the cost of shutdowns for recalibrations is high. Here, the requirements for the reliability and accuracy of measurements have increased over recent decades, but there has been no corresponding improvement in the performance of the thermocouples and resistance thermometers traditionally used to control such processes.
This paper reviews the progress and prospects of JNT, focussing on the wide variety of techniques and identifying the major sources of measurement uncertainty. The review begins in Section 2 with a summary of the basic principles of JNT. The following sections then describe the techniques used for high-accuracy, cryogenic, and industrial applications. The review omits detailed discussion of non-thermometric applications of Johnson noise measurements, including microwave radiometry e.g., [27], spin noise spectroscopy [28], cryptography [29, 30], and the measurement of material properties e.g., [31], in part because the principles and techniques are very similar, and in part because these applications make lesser demands in respect of accuracy. Throughout, there is an emphasis on technological advances as other perspectives are covered by the earlier reviews by Kamper [32], Blalock and Shepard [33], and White et al. [34]. For a detailed overview of industrial noise thermometry see the review by Brixy [11].
2. Basic Measurement Principles
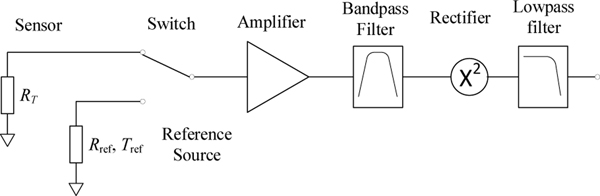
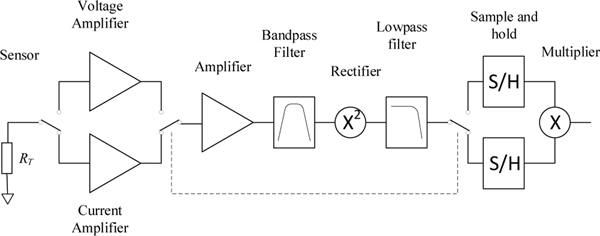
Figure 1 shows a simple schematic diagram of a Johnson noise thermometer, comprising a resistor as the temperature sensor, a low-noise amplifier, a band-pass filter, a square-law rectifier, and a low-pass filter. The output signal of the low-pass filter is ideally proportional to the mean-square noise voltage produced by the resistor, (2). Because the gain and bandwidth of the noise thermometer can be difficult to quantify precisely, it is usual to make two measurements, one with a resistor at the unknown temperature, and another with a reference noise source. Usually the reference noise source is a resistor at a known temperature as in Figure 1, but shot noise from diodes [35, 36], multi-resistor and thermistor networks [37, 38], and synthetic noise sources [39, 40] have also been used. The temperature is calculated from the ratio of the measured noise powers, which is ideally independent of the amplifier gain and bandwidth:
| (3) |
where , , and are respectively the temperature, resistance, and average noise power of the reference resistor, and and are the resistance and average noise power of the sensing resistance at the unknown temperature. Because the bandwidth is the same for the two measurements, the ratio of the noise powers is also the ratio of the power spectral densities. Often, because of concerns with the linearity of the thermometer, either by design or adjustment, the two noise powers are made equal so that in many noise thermometers
| (4) |
Figure 1.
A simplified schematic diagram of a switched-rectifier Johnson noise thermometer.
Application of the propagation-of-uncertainty law [41] to (3) shows that the relative uncertainty in the inferred temperature is related to the relative uncertainties in the various measurements by
| (5) |
In almost all applications, because of the random nature of Johnson noise, the measurement uncertainty is dominated by the two terms describing the relative uncertainty in the measured noise powers. The Johnson noise voltage is distributed according to a normal distribution with the probability density
| (6) |
The square-law rectified noise voltage therefore has a chi-square distribution with a mean , and variance . If independent samples of the rectified voltage are averaged, then the mean noise power is distributed as a chi-square distribution with degrees of freedom, and the relative uncertainty is given by
| (7) |
Further, if the JNT passband is rectangular with a bandwidth and the voltage is sampled uniformly for a measurement period according to the Nyquist-Shannon theorem so that , the relative uncertainty is given by Rice’s formula [42]:
| (8) |
Note that (7) and (8) apply only when a square-law rectifier is used. If a linear rectifier (or any other rectifier) is used, the measurement is less statistically efficient, and the relative uncertainty is higher [43].
Where the bandwidth of a thermometer is defined by analogue filters realising a non-rectangular pass-band with a frequency response, , the effective bandwidth for calculating the relative uncertainty, (8), is the correlation bandwidth [7, 44–47]:
| (9) |
Equation (9) is a form of the Welch-Satterthwaite formula for the equivalent degrees of freedom [41] for linear combinations of variances, so that is the number of degrees of freedom per second acquired by the thermometer [44, 47].
Equation (8) gives the minimum uncertainty for absolute temperature measurements, but when making temperature ratio (relative) measurements according to (3), two noise-power measurements are made, which doubles both the measurement time and the variance, so that the minimum uncertainty in the relative temperature measurement is given by
| (10) |
where is the total measurement time, and is the minimum number of degrees of freedom required to achieve the given relative uncertainty. In most noise power measurements, there are influence factors that cause the uncertainty to be larger than given by (10). Amplifier noise is always a major contributor and may more than double the uncertainty.
For a good industrial measurement requiring an uncertainty of 1 K at 1000 K (relative uncertainty of 0.1%), the minimum number of degrees of freedom (minimum number of independent samples in an average) is about 107. If the measurements are acquired at 100 kHz, the measurement time is more than a minute. In the highest accuracy JNT measurements, the integration time may exceed 100 days, and the total data acquired may exceed 100 TB.
2. High-Accuracy Noise Thermometry
This section considers the three JNT techniques that have been applied over wide temperature ranges and used to make measurements with the lowest relative uncertainties, usually below 0.1%. The techniques illustrate the main technological advances that have contributed to high-accuracy JNT.
3.1. The Switched Rectifier
The first noise thermometers were switched rectifiers, as shown in Figure 1. Dicke, in 1946, recognised the close relationship between Johnson noise and blackbody radiation and built the first noise thermometer to measure the microwave radiation from astronomical objects [7]. Microwave radiometers with similar operating principles continue to be used to measure the temperatures of astronomical objects as well as the cosmic microwave background remaining from the Big Bang [27, 48]. For JNT, the most important feature of the Dicke radiometer is the use of a switch to toggle the radiometer between the signal of interest and the reference signal, to eliminate the effects of drifts in the noise, gain, and bandwidth of the JNT. The same switching technique is exploited in many noise thermometers today.
Garrison and Lawson, inspired by Dicke’s investigations, in 1949 built the first noise thermometer to infer temperature from measurements of Johnson noise in a resistor [49]. Contrary to the requirements of (3), switched rectifiers do not measure or , instead the measured noise powers include the extraneous amplifier noise, , and Johnson noise due to the resistance of the connecting leads to the sensors, , so that the thermometer output is proportional to or . For this reason, the two measured noise powers are adjusted to be equal and the unknown temperature is given by the ratio of the resistances, (4).
The unwanted noise from the amplifier and lead wires contributes significantly to the measurement uncertainty and, for the switched rectifier, (8) must be replaced by
| (11) |
which shows a strong dependence on the amplifier signal-to-noise ratio and favours the use of slightly larger values of sensing resistance than with other methods.
Garrison and Lawson identified and discussed most of the limitations of the switched-rectifier; the two-wire definition of resistance, the errors due to noise from lead resistances at different temperatures, stray capacitances in the connecting leads to the resistors modifying the frequency response, the dependence of the amplifier gain on source resistance, the input noise currents of the amplifiers, electromagnetic interference, and the frequency dependence of the sensor resistance.
Switched-rectifier noise thermometers have been used for both industrial and metrological measurements spanning temperatures from 2 K to 1250 K [50,51]. In some of the measurements, the square-law rectifier is replaced by a linear rectifier, which sacrifices a little statistical efficiency for circuit simplicity. The best measurements to date include measurements of the temperatures of metal freezing points used as temperature references [51], and measurements of the thermodynamic temperature in the range of 90 K and 100 K with an uncertainty of about 3 mK [52].
3.1. The Cross-Correlator
In 1959, Fink introduced correlators to JNT to measure temperatures using a three-resistor pi network in which the cross-correlation between two of the noise voltages across the network can be made zero [53], and the temperature inferred from the null condition. Jones developed a similar thermometer based on correlation and the setting of a measurement null [54]. Following a demonstration of a simpler correlator system by Brophy et al. [55], other researchers proposed the use cross-correlators for JNT [20, 56–59].
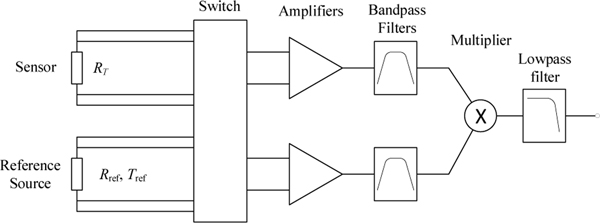
Figure 2 shows a schematic diagram for the switched correlator system developed by Brixy et al. [11, 20, 60–62]. The switch has the same benefits as in the switched rectifier; the elimination of the effects of gain and bandwidth drift.
Figure 2.
A simplified schematic diagram of the switched-correlator noise thermometer.
The correlator has three significant advantages over the switched rectifier. Firstly, as Figure 2 shows, the correlator has a natural four-wire definition of the resistance, which eliminates errors due to lead resistances in both the resistance measurement and the measurement of the noise power.
The main benefit of the correlator is that it eliminates the systematic error due to the extraneous noise voltages arising in the amplifier and the lead resistances. If the input voltages to the two channels are and respectively, where and are respectively the equivalent input noise voltages and noise currents of the two amplifiers, then the average output of the correlator is proportional to
| (12) |
so that the output is proportional to the mean noise power as required, with (typically) very small errors due to the input noise currents of the amplifiers.
Most correlating noise thermometers use a preamplifier with a common-source FET and bipolar-cascode input stage [63–65] with high transconductance FETs to give a very low noise current and low equivalent-input noise voltage. The input stage should be operated without feedback to minimise the current noise [64] and the cascode stage must present a purely resistive load to the FET to maintain a 90° phase shift between the FET input noise current and noise voltage [64, 66], and therefore ensure zero correlation between them. The most recent preamplifier designs have good common-mode rejection and bandwidths exceeding 1 MHz [65].
Thirdly, the correlator has the advantage of a lower statistical uncertainty than the square-law rectifier (compare to (5))
| (13) |
so that the dependence on the amplifier signal-to-noise ratio has halved [47, 67].
The first significant metrological application of correlators to JNT was by Klein et al. who measured the temperature dependence of the vapour pressure of liquid 4He with a relative uncertainty of about 10−4 [63]. The accuracy was limited in part by imperfections in the analogue multiplier used in the correlator. If the output of the multiplier is modelled by
| (14) |
so that in addition to the ideal output, , the averaged output includes small errors proportional to products of all the various moments of the distributions for and (i.e., linear combinations of , , and ). The only way to ensure the noise-power ratio in (3) is immune to such errors, is to ensure that , so that all the errors are the same for the two measurements [47, 63]. That is, the reference noise voltage must have the same statistical distribution as the sensor voltage, and the amplifier noise voltages, and , must be the same during the two measurements. Thus, despite the much-improved immunity of the correlator to amplifier noise, it is still necessary to operate the thermometer with equal noise powers of the measurement resistor and the reference source, if low uncertainties are required.
The switched-correlator noise thermometer was developed initially by Brixy for use in medium- and high-temperature ranges in nuclear reactors [20], and over a couple of decades significant improvements were made, especially to the sensing resistor design (see Sec. 5.3.2 and Sec. 5.3.3 below) and thermometers were trialled in reactors in several countries.
With the advent of fast high-resolution analogue-to-digital converters (ADC) in the 1980s, analogue multipliers in correlators were rapidly replaced by digital multipliers [68, 69]. The move to digital signal processing enabled several significant advances including frequency-domain cross-correlation, digital definition of the bandwidth, compact data storage as averaged cross spectra, computation of autocorrelation spectra for diagnostic purposes, and the ability to recognise some types of electromagnetic interference in the measured spectra [62, 70, 71].
Storm constructed a digital switching correlator with the aim of measuring the Boltzmann constant [67] while White and Pickup [72] investigated the effects of quantisation and ADC non-linearity on the accuracy of the JNTs. The dithering effect of the noise significantly attenuates the effects of ADC non-linearities so that quantization effects are practically zero, and the effects of non-linearity are substantially reduced. Brixy et al. demonstrated total uncertainties of 0.002% in measurements of the freezing point of zinc [62], and Edler et al., using one of Brixy’s thermometers, successfully measured thermodynamic temperatures of the fixed points of indium (~156 °C), gold (~1064 °C), copper (~1085 °C) and palladium (~1555 °C) [37, 73–75].
Electromagnetic interference remains one of the most difficult sources of uncertainty in JNT. While it is possible to construct powerful statistical tests for narrow-band stationary EMI, it is not always possible to recognise broadband or non-stationary EMI [71]. The only conclusive test for EMI is to operate the noise thermometer with a four-terminal-zero resistance and confirm that the correlation is zero [70]. Because the correlated noise is ideally zero, these tests have a relatively low uncertainty and can be carried out in a short time. For guidance on electronic design for low EMI susceptibility see [76] and [77].
A significant remaining difficulty with the switched-correlator is the conflict between the requirement to operate with equal noise powers to minimise the effects of non-linearity, which requires the sensing resistances to be different (from (3))
| (15) |
and the requirement for the frequency response of the sensor and connecting leads to be the same. If it is assumed that the connecting leads between the sensors and input impedance of the preamplifiers are modelled by a single lumped capacitance , then the frequency response match requires
| (16) |
so that the sensing resistances must be the same. A simple resolution to the conflict is to increase the capacitance on the leads to the sensor with the lower resistance to ensure the time constants are the same [52], but this solution neglects higher order effects due to stray inductance [64, 78], and sometimes the inductive effects are larger.
3.3. The QVNS Thermometer
In 1999, Benz et al. [79] developed a superconducting pulse-density delta-sigma digital-to-analog converter exploiting the Josephson effect to produce voltage pulses, , so that they have quantized area
| (17) |
where is an integer ( under typical operating conditions), is Planck’s constant, and is the charge of the electron. The Josephson junctions are driven by a programmed sequence of pulses at a frequency of a few gigahertz to produce any desired waveform with an accuracy well beyond that available from conventional arbitrary waveform synthesisers.
When applied to JNT, the synthesiser is used to produce pseudo-random noise constructed as a sequence of equal-amplitude odd-harmonic sinusoids with random phase (see Figure 3). The quantum-accurate voltage-noise source (QVNS) can be programmed to produce voltage noise of any desired average spectral density, and because the noise is constructed as the sum of a large number of sinusoids of random phase, it has a normal probability distribution. In this way, the QVNS can be programmed to produce a deterministic reference signal that closely matches both the spectral density and voltage distribution of the thermal noise.
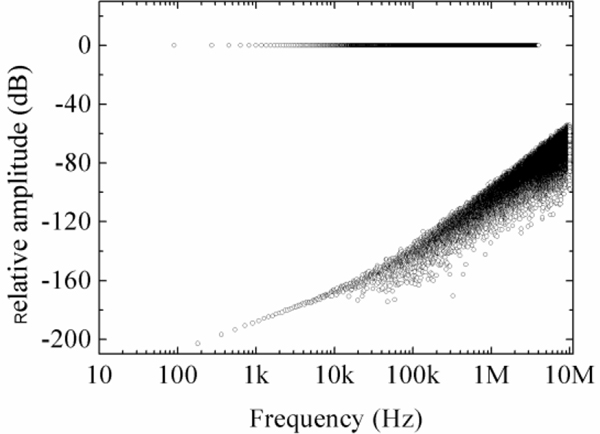
Figure 3.
The QVNS spectrum calculated from the QVNS code sequence. The upper branch shows the odd harmonics and the lower branch shows the even harmonics. The amplitudes of the even harmonics are indicative of the variation of the amplitudes of the odd harmonics from the target voltage.
The use of the QVNS as the reference noise source for JNT has several important advantages. Firstly, and most importantly, the QVNS has the ability to synthesize different voltages appropriate for different temperatures in a perfectly linear fashion over many decades of voltage and temperature, with no other changes in the operating conditions. No other reference noise source can do this.
Secondly, with the addition of on-chip lead resistors maintained at 4 K to minimise additional uncorrelated noise, the QVNS can be built with any desired output resistance. This enables a simultaneous match of the noise powers and the source impedances of the sources, thereby enabling a match of frequency responses of the lead wires between the preamplifiers and the two noise sources, which in turn enables a substantial increase in bandwidth [39].
Thirdly, the effect of any non-linearity can be measured directly by programming the QVNS to produce noise with different amplitudes and observing the trend in the measured temperature with different noise power ratios.
Fourthly, the QVNS can be switched off so it produces zero volts enabling a measurement of the error caused by EMI. This eliminates the need for a separate four-terminal zero-resistance probe for the reference source and means that one of the two EMI tests can be conducted without changing any other aspect of the JNT operation.
Fifthly, because the QVNS output is deterministic rather than stochastic, the uncertainty in the measurement of the reference noise power is less than for the thermal noise (compare to Equation (13))
| (18) |
Note that the uncertainty is zero when the amplifier noise is zero. The uncertainty in the measurement of the ratio of the noise powers (combining (13) and (18)) is therefore
| (19) |
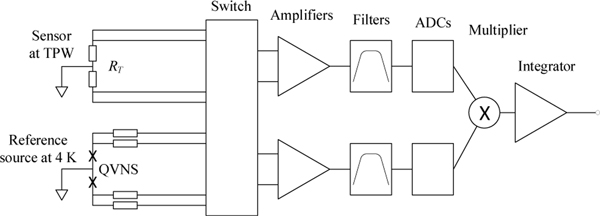
Finally, and most importantly, the QVNS enables measurement of temperature directly in terms of electrical measurement units and the Boltzmann constant. Figure 4 shows a simplified schematic diagram of the QVNS-JNT. The thermal noise from the sensor has a spectral density
| (20) |
where the sensing resistance is expressed as the ratio in units of the von Klitzing resistance where is the charge of the electron, and is Planck’s constant. The QVNS produces a pseudo-random noise for which the calculable power spectral density is
| (21) |
where , is the Josephson constant, is a clock frequency, is the bit length of the digital code for the noise waveform, is an adjustable parameter of the software that sets the amplitude of the synthesized QVNS waveform, and is the number of junctions in the Josephson array used in the QVNS [80, 81].
Figure 4:
The QVNS thermometer. When measuring the Boltzmann constant, the thermal sensor is maintained at the triple point of water.
The output of the correlator is proportional to the noise powers of the thermal or the QVNS signals, and since the bandwidth of the system is the same in the two configurations, the ratio of the measured noise powers is the ratio of the spectral densities . The inferred temperature is therefore
| (22) |
Although some measurements of thermodynamic temperature have been made using a QVNS thermometer [82–84], to date, the main application of QVNS thermometers has been to make low-uncertainty measurements of the Boltzmann constant [17, 81, 85] in support of the planned redefinition of the kelvin, with the best measurement achieving an uncertainty of 0.00027%. The measurement configuration for the Boltzmann constant determinations is shown in Figure 4 with the sensing resistor for the thermal noise source maintained at the triple point of water, the current kelvin definition. A QVNS thermometer has also been built at NMIJ (Japan) using a simpler quantum-accurate noise source that does not produce normally distributed noise [19], and Callegaro [86] describes a noise thermometer of a similar design using a non-quantized reference source.
Second to the statistical uncertainty, the major remaining source of uncertainty is the frequency response mismatch between the two sets of lead wires between the noise sources and the correlator. Ideally, the two sets of leads should be identical, and the resistors in the QVNS leads should be twice the resistance of the sensing resistor [78]. However, some mismatch effects remain due to the temperature dependence of the inductance and capacitance of the leads, and corrections must be applied. This results in a compromise, between the complexity of the correction model and the bandwidth over which the corrections are applied, to obtain the lowest uncertainty [78, 85, 87].
Other, much smaller contributions to the uncertainty include the uncertainties in the QVNS clock frequency, the Boltzmann constant, the Planck constant, and the resistance measurement. The remaining parameters in (14) are known exactly and contribute no uncertainty. From May 2019, following the promulgation of the revised SI, the uncertainty in the Boltzmann constant and the Planck constant will be zero.
4. Cryogenic Noise Thermometry
One of the major factors affecting the speed and accuracy of JNTs, especially at low temperatures where Johnson noise is small, is the intrinsic noise of the amplifiers. The development in the mid-1960s of superconducting quantum interference devices (SQUIDs), which have sensitivities six orders of magnitude better than the best JFET amplifiers, enabled the development of several types of cryogenic noise thermometer.
SQUIDs exploit the extraordinary properties of superconductors and Josephson junctions. Josephson junctions are formed by two weakly coupled superconductors, for example, where two superconductors are separated by a thin non-superconducting layer. The junctions have properties that include quantum-accurate voltage-to-frequency and frequency-to-voltage conversion, and a current-voltage characteristic whereby currents less than the ‘critical current’ tunnel across the junction and generate no voltage.
In any superconducting loop, formed from wire significantly thicker than the magnetic field penetration depth, the magnetic flux through the loop is quantized to integer multiples of the flux quantum Wb, and, therefore, the magnetic field within the loop is also quantized. SQUIDs are a loop of superconductor interrupted by one or two Josephson junctions. The junctions enable flux quanta to enter or leave the loop accompanied by changes in the voltage across the junction(s), so that changes in magnetic fields can be measured by counting flux quanta. When accompanied by the appropriate electronics, SQUIDs can be used to measure changes in magnetic flux with a resolution below 10−6 . For further information on SQUIDs, how they are used, and their capabilities, see [88, 89].
Superconductivity is limited to a select group of materials and occurs at temperatures below 30 K for conventional metallic superconductors, and below 130 K for high-temperature superconductors. Therefore, SQUIDs are generally only suitable for cryogenic thermometry.
At the very lowest temperatures, Nyquist’s law may not be a sufficient approximation of the fluctuation dissipation relation (1). The relative error in Nyquist’s law is given by the series expansion of the Planck factor (see (2))
| (23) |
so that a JNT using Nyquist’s law at temperatures near 1 mK and with an average operating frequency of 100 kHz is accurate to about 0.24%.
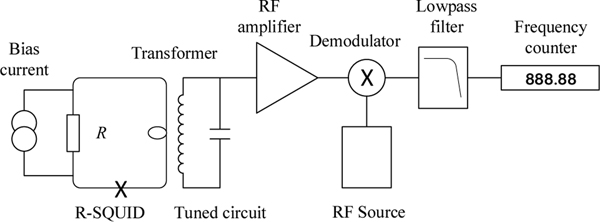
4.1. Josephson or R-SQUID Thermometer
The first cryogenic noise thermometer, proposed and demonstrated by Kamper and Zimmerman in the 1970s [90], uses the voltage-to-frequency conversion characteristics of Josephson junctions; the ac Josephson effect. The Josephson junction is shunted by a small resistance, , through which a bias current is passed, as shown in Figure 5. The circuit configuration is also known as an R-SQUID. The dc voltage, , across the resistor causes the junction to oscillate at the frequency
| (24) |
Figure 5.
Schematic diagram of the R-SQUID noise thermometer
The Johnson noise in the resistor modifies the bias voltage and therefore also the oscillation frequency of the junction. If the radiation from the junction is detected, amplified, and measured by a frequency counter with an integration time , then the variance in the measured frequency is
| (25) |
so the temperature may be determined from the measurement of variance and resistance, and knowledge of the integration time of the frequency counter. Because the transduction constant for the R-SQUID is determined by fundamental constants and , the thermometer is an absolute primary thermometer, and no independent calibration is required. If measurements of frequency are taken, then the relative uncertainty in the measured temperature is
| (26) |
with a minimum measurement time of .
Because the thermometer is absolute, ratio measurements are not necessary and a single sequence of measurements of frequency is sufficient, and the number of samples required to achieve a given relative uncertainty is one quarter of that required for the thermometers of Sec. 3.1.
Inevitably, (25) is idealised. Firstly, the equation is derived assuming that the bandwidth of the frequency counter, , is very much smaller than the bandwidth of both the R-SQUID and the electronics following the R-SQUID. This requirement means that the measurements of frequency are taken relatively slowly, and the thermometer is correspondingly slow. If the thermometer is made faster by decreasing the counter integration period, then it is necessary to consider the frequency responses of the R-SQUID sensor loop and the SQUID electronics [91], and unless the responses are well characterised, the thermometer is no longer absolute and a reference measurement is required for calibration.
Secondly, the frequency counter usually counts an integer number of cycles of the waveform, so that an additional variance, due to the quantization error of the counter, must be added to (25) [92]. Better implementations of the thermometer measure the period of the waveform to infer frequency and make the quantization effects negligible.
Thirdly, there is additional noise in the R-SQUID arising from the current source and the SQUID electronics, which add a small variance term to (25), causing an offset to the inferred temperature. The offset is typically no more than a few tens of microkelvin. Finally, the value of the sensing resistance used in (25) should include the shunting resistance of the Josephson junction and the output impedance of the current source [92–94].
The R-SQUID noise thermometer played an important role in extending the International Temperature Scale to low temperatures. Soulen et al. used the thermometer to establish a temperature scale between 6 mK and 740 mK with an accuracy of about 0.1% [92, 95]. Schuster et al. also built an R-SQUID thermometer to establish a scale below 0.6 K [96].
R-SQUID noise thermometers have largely been replaced by current-sensing noise thermometers since the mid-1990s due to much reduced measurement times and the increasing availability of low-cost SQUIDs. Some efforts have been made to manufacture R-SQUID noise thermometers with thin-film high temperature superconductors, but so far, the efforts have proved to be unsuccessful [94, 97].
4.2. Current-Sensing Noise Thermometer
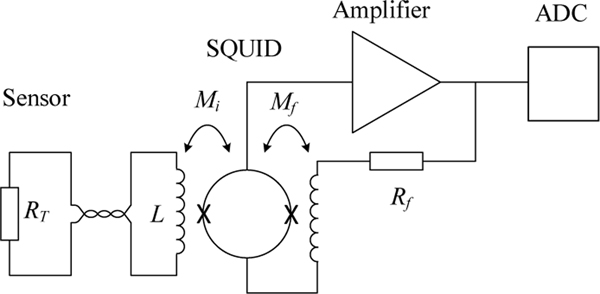
Because SQUIDs are magnetic field or flux sensors, they are best suited to measurements of noise currents rather than noise voltages. Figure 6 shows the schematic diagram of the current-sensing noise thermometer (CSNT) developed by Giffard et al., also in the early 1970s [98, 99]. The first block in Figure 6 shows the sensing resistor, typically a few micro-ohms to milli-ohms, which generates a noise current with a spectral density
| (27) |
where is the sensing resistance, and is the inductance of the sensor loop. The first term of (27) is the current-noise equivalent of Nyquist’s law, (2), and the second term is the first-order low-pass frequency response of the sensor loop. The −3 dB cut-off frequency of the loop is , and typically ranges from a few tens of hertz to several hundred kilohertz. The magnetic field generated by the noise current is detected by the SQUID, which is coupled to the sensor coil via the input mutual inductance . The signal from the SQUID is then used by the flux-locked-loop electronics to stabilise the magnetic flux in the SQUID by circulating a feedback current, coupled to the SQUID via the mutual inductance , that is equal and opposite to the sensor noise current. So long as the loop gain in the feedback loop is sufficiently high, the spectral density of voltage generated at the output of the flux-locked-loop electronics is
| (28) |
where is the feedback resistance.
Figure 6.
The current-sensing noise thermometer.
To measure the temperature absolutely, it is necessary to know the values of the two mutual inductances and the feedback resistance. The resistance is easily measured by conventional four-wire techniques. The input mutual inductance can be found by replacing the sensing resistance with a current source and using the SQUID output to count the change in the number of flux quanta coupled to the SQUID circuit as the current is changed. Similarly, the mutual inductance in the feedback circuit is found by applying a voltage to the feedback resistance and again counting the change in flux quanta coupled to the SQUID. In both cases the mutual inductance is given by , where is the change in the number of flux quanta observed with a change in current,. In practice, (28) is approximate because of the coupling between the input coil and the feedback coil, which results in depending on the resistance of the sensor coil [100]. However, with care, the uncertainties can be reduced below 1%.
The output voltage of the flux-locked-loop can be measured using conventional amplification and signal processing techniques. In most measurements, the voltage is sampled rapidly and processed in the frequency domain by least-squares fitting (28) to the observed noise spectra. At least one of the resistance, , or the inductance, , must be known accurately for the least-squares fit to yield the temperature.
There are several variations on the sensor construction. Figure 6 shows superconducting wires connecting the sensing resistance to the inductor. This rearrangement enables the sensing resistance to be at a different location and different temperature to the SQUID. In some versions, the SQUID and the sensing loop are manufactured on the same substrate so that the sensing resistance and the SQUID are the sensing element. In others, the sensor loop is non-superconducting and may be a simple copper or gold ring or cylinder.
The measurement time and the relative uncertainty depend on the way the thermometer is operated. In the fastest mode, the sampling frequency is high enough to ensure the highest frequency resolved in the FFT (the Nyquist frequency) is very much greater than the −3 dB bandwidth of the sensor-inductor loop. The correlation bandwidth is then determined entirely by the frequency response of the sensor loop, and, from (9)
| (29) |
so that the least uncertainty in an absolute temperature measurement is given by
| (30) |
where is the total measurement time. The uncertainty will be at least twice this value for relative measurements. Equation (30) shows that the fastest measurements are made when the sensing resistance is large (~ 1 ohm), and the inductance is small (~ 1 μH).
There are several factors that may lead to a higher uncertainty than indicated by (30). For practical measurements, it may be necessary to include high-pass filters to eliminate noise at low frequencies, and low-pass filters to prevent aliasing at high frequencies. The effect of both is to reduce the correlation bandwidth. Aliasing, due to an insufficiently high sampling frequency, not only reduces the correlation bandwidth, it also folds high-frequency SQUID noise into the pass-band increasing the apparent spectral density of the noise [46, 101]. The bandwidth and/or loop gain of the flux-locked-loop may also limit the bandwidth of the measurements. Finally, least-squares fits of (28) to the measured spectrum yield the lowest uncertainty for the temperature when both the resistance and inductance are known.
The fastest measurements to date have been reported by Casey et al. [102], with uncertainties near 1% for measurement times of 0.1 s, only about a factor of two larger than indicated by (32). Such measurement times require very wide-band systems with fast sample rates; the −3dB bandwidth of the sensor loop was 245 kHz.
As with most noise thermometers, other noise sources, especially electromagnetic interference, are a major concern. To minimize the effect of EMI, the sensing resistor, the SQUID, and all associated wiring should be within a superconducting shield. Any remaining EMI may be identifiable as discrete peaks in the measured spectrum, and may be eliminated by removing the corresponding bin in the FFT [103].
The noise from the SQUID and the electronics also contribute to the measured noise power. Usually such noise is characterised as an equivalent device temperature since it appears as a constant offset to measured temperatures. With modern SQUID electronics, device noise temperatures are usually only a few microkelvin, so are significant only at the very lowest temperatures. In [103], the SQUID noise contribution was measured at frequencies higher than the bandwidth of the sensor loop, where the noise is white, and then subtracted from the noise spectrum as a frequency-independent offset.
Amongst the best measurements to date are those of Shibahara et al. [103], who made primary measurements below 1 K. A relative uncertainty of 1.53% was obtained along with good agreement with PLTS-2000.
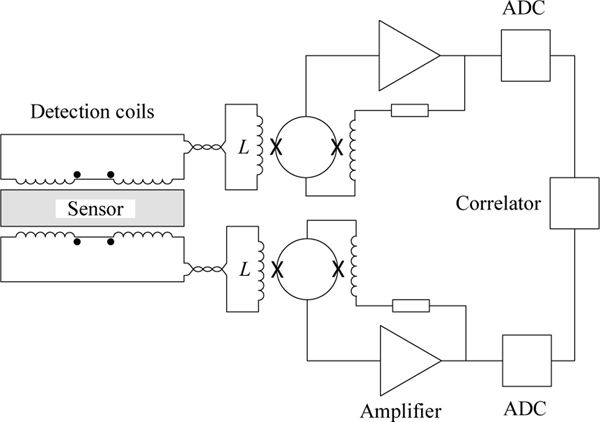
Rothfuss et al. [104] describe an interesting variation of the current-sensing noise thermometer that uses two SQUIDs and two sets of flux-locked-loop electronics as a correlator (see Figure 7). This has the effect of reducing the device noise temperature by a factor of 15 or so, improving the accuracy of measurements at very low temperatures. They report uncertainties of about 1% for temperatures between 42 μK and 800 mK. Measurements below 1 mK or so have the additional problem of poor thermalisation, i.e, a poor thermal connection between the electrons, which are responsible for the noise, and the phonons of the atomic lattice meaning that the temperatures of the electron gas and the lattice are not the same. Overcoming this effect may require a direct electronic connection between the sensor loop and the (metallic) object of interest.
Figure 7.
Schematic of a cross-correlating current-sensing noise thermometer with gradiometer (differential) sensing coils.
Operation of current-sensing noise thermometers in relative mode, i.e., measuring the ratio of the noise power with respect to the noise power from a reference temperature, simplifies the calibration of the thermometer at the expense of increased measurement time. A wide range of superconducting fixed points are available. Lusher et al. [105] and Casey et al. [102, 106] successfully operated relative mode CSNTs over a wide temperature range from 4.2 K down to 1 mK and achieved a statistical uncertainty of about 1% with measuring time of about 10 s.
4.3. Magnetic Field Fluctuation Thermometer
In recent years, another JNT closely related to the current-sensing noise thermometer and known as a magnetic field fluctuation thermometer (MFFT), has been developed [100, 107–113]. Unlike the current-sensing noise thermometer, in which the SQUID is closely coupled to a well-defined sensor loop, the SQUID in a MFFT is coupled to a relatively large metallic object in which the current paths are not defined.
The advantage of MFFT, by comparison with the CSNT, is that no wiring connections are necessary between temperature sensor and the SQUID, and therefore it largely eliminates both thermal and electrical errors due to connecting wires and contact resistances. Also, the inductive coupling offers greater flexibility with respect to the choice of sensor materials, sensor shapes and volumes, and enables larger temperature differences between the sensor and the SQUID.
The power spectrum of the magnetic field fluctuations generated by the random currents in the sensor is a function of the geometry and electrical resistivity of the sensor material, the distance between the SQUID coils and the surface of the sensor, and the temperature of the sensor. The power spectrum is usually modelled as
| (31) |
where is the spectral density of the flux noise at zero-frequency and is directly proportional to temperature and in accordance with Nyquist’s law. The parameters , , and describe the frequency dependence of the measured power spectrum, and provided that both the configuration of the MFFT and the electrical conductivity of the sensor are constant over the temperature range of interest, the spectral shape is temperature-independent. The first MFFTs were operated as relative thermometers so that the unknown temperature is determined in terms of a reference temperature fixed by another thermometer calibrated according to ITS-90 or PLTS-2000, or a superconducting fixed point, so that
| (32) |
where and are determined by fitting (31) to the measured noise spectra.
Engert et al. demonstrated better than 1% accuracy temperature measurements over the range of PLTS-2000 with a MFFT working in relative mode with a measurement time of some tens of seconds [108]. Beyer et al. also developed a MFFT to realize reference measurements at temperatures directly traceable to the PLTS-2000 via superconducting fixed points, in which relative uncertainties of less than 1% were achieved with system bandwidths of 100 Hz to 1 kHz and measurement times of about 10 s [100]. The uncertainties in relative measurements are increased by the need to fit several parameters in the spectral model, and the need to make a ratio measurement.
Kirst et al. developed a primary MFFT for measurements in range from 5 K down to 1 mK using a detailed electromagnetic model to calculate the magnetic field fluctuation spectra for an infinite conducting plate [113]. The MFFT also used a pair of gradiometric SQUIDs to perform a correlation measurement and an additional calibration coil to measure the conductivity of the senor [114]. The measurement times and uncertainties are reduced because there is no need to fit the spectral model or make a second ratio measurement. Kirst et al. reported measurements in temperature range of 16 mK to 700 mK with a relative uncertainty of 0.59%, and with very good agreement between the measured and calculated spectra [113]. Their results also showed a good agreement with the PLTS-2000. The most significant uncertainties arose from measurements of the distances between the detection coils and calibration coil and between the detection coils and surface of the sensor.
A commercial MMFT is now available [115] with a range of 1 mK to 1 K, 1% accuracy, and a measurement time of 30 s.
4.4. Quantum-Roulette Noise Thermometer
In 1997 Gallop et al. [88, 116–122] suggested a very different current sensing noise thermometer that eliminates the need to independently characterise the SQUID and its electronics.
In a conductive loop with inductance and resistance , the total noise current is, from (28)
| (33) |
which is simply a restatement of the Boltzmann equipartition theorem requiring the average energy of the inductor, with its single degree of freedom, to be . The result applies to all sensor loops, independent of their resistance.
Suppose now, the loop is superconducting and has an element that can be switched between the resistive and superconducting states. In the resistive state, the current evolves randomly, characterised by the time constant of the loop,. When the loop is switched into the superconducting state, the magnetic flux trapped in the loop must be an integer multiple of the flux quantum , and have a mean square fluctuation again described by Boltzmann’s equipartition theorem
| (34) |
The temperature of the sensor loop can therefore be determined from knowledge of the loop inductance and by repeatedly switching the loop between normal and superconducting states and measuring the variance of the sampled flux. In effect, the switched loop behaves as a combined sensor, sample-and-hold, and analogue-to-digital converter for the flux noise. The calibration of the electronics exploits the knowledge that the sampled flux is quantized in multiples of .
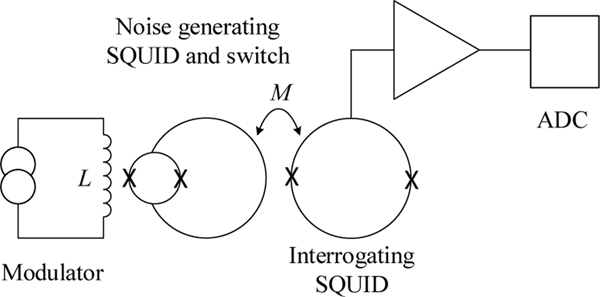
Figure 8 shows a simple schematic diagram of the quantum roulette noise thermometer. The temperature sensing loop is a dc SQUID with Josephson junctions exposed to a small rf coil that modulates the critical current of the junctions and switches the loop between the superconducting and normally-conducting states. A full description of the switching mechanism is given by Lee et al. [122]. A second dc SQUID is used to measure the flux of the first SQUID, and a second coil driven by a dc current is used to alter the external flux. The interrogating SQUID need only be magnetically coupled to the sensor SQUID, so can be operated at 77K, and the two loops may differ in temperature by up to 50 K or more.
Figure 8.
The quantum-roulette noise thermometer. The modulator switches the Josephson junctions between superconducting and normal states.
The QRNT is relatively slow due to the time taken for the loop current to change, which is determined by the time constant,. In early experiments, the sample rates were about 1 Hz [122], but more recent studies report measurements at 10 kHz with suggestions that samples rates of 1 MHz may be possible [88].
Because each measurement is a single sample, the measurement uncertainty follows (7) relating the relative uncertainty to the number of measurements. With sample rates of 10 kHz, the measurement time required to achieve statistical uncertainties of 1% is 2 s. Other contributions to the measurement uncertainty remain unexplored. Lee et al. [122] indicate concerns about how current-evolution dynamics within the loop, especially during the transitions to the quantized state, affect the measured flux distribution, but these effects have yet to be fully investigated. The thermometer has been used to measure temperatures in the range from about 20 K to 90 K.
4.5. Shot Noise Thermometer
Shot noise originates from the discrete nature of electric charge. The descriptive term was introduced by Schottky in his 1918 study on vacuum tube noise with the analogy of the random impulses of acoustic noise made by lead shot hitting a target [123]. The first shot noise thermometer, developed by Spietz et al, was operated over temperatures spanning four and a half decades from 10 mK to nearly 300 K, a wider range than for any other noise thermometer [124].
All the JNTs considered above use linear sensing resistances, i.e., sensors for which the current through the device is directly proportional to the voltage across the device. With non-linear sensors, the noise processes and their models are more complicated than for simple resistors. Wyatt and Coram [125] show that in non-linear devices, the noise processes must be described in terms of noise currents rather than noise voltages, have Poisson statistics rather than Gaussian statistics, and depend on distinct forward and reverse currents through the device. The net dc current through the device is the difference between the forward and reverse currents, while the spectral density of the noise depends on the sum of the two currents. The ratio of the forward and reverse currents must also exhibit a simple exponential dependence on the device temperature. The theory spans linear resistors, pn-junctions, as well as tunnel junctions.
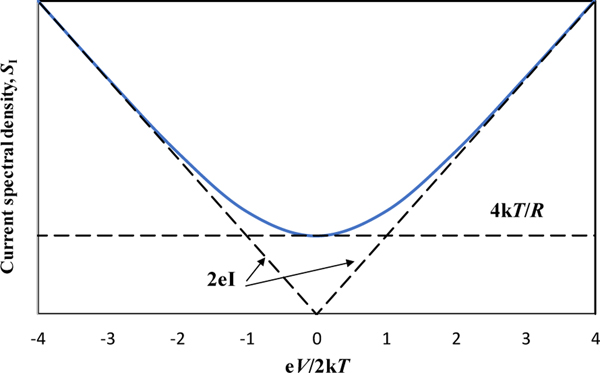
A tunnel junction is formed where two sections of normal (i.e., non-superconducting) conductor are separated by a thin insulating barrier. If the insulation is sufficiently thin, electrons tunnel across the junction, in both directions, generating a shot-noise impulse when they arrive and depart. If a bias voltage is applied to the junction, the current in one direction increases while the current in the other direction decreases. The noise current has the spectral density [124, 126]
| (35) |
where is the dc current through the junction, and is the voltage across the junction. The characteristic for the tunnel junction is hyperbolic and symmetric about (see Figure 9). When the junction is unbiased , the spectral density of the noise is
| (36) |
so that the junction behaves like a linear resistance and the noise is described by Nyquist’s law. When the bias voltage is large ,
| (37) |
which is the conventional formula for shot noise. Because the transition between the two regimes changes with temperature, the junction temperature can be inferred from measurements of the characteristic at different bias voltages. Additionally, because the shot noise part of the characteristic (37) is known, no additional calibration of the amplifier and electronics is necessary, and the measurement is absolute. The only requirements are for accurate measurements of the bias voltage and current.
Figure 9.
Normalised plot of the spectral density of the tunnel junction shot noise versus bias voltage showing the limiting behaviours for small and large bias voltages.
Because tunnel junctions have a very wide bandwidth, shot noise thermometers can operate at high frequencies and with bandwidths of hundreds of megahertz to achieve short measurement times. It is, however, necessary to consider the amplifier noise, which adds a large offset to the measurement of noise power. Additionally, directional couplers are required to minimise the reflection of the amplifier noise currents by the device resistance which depends on the bias voltage [127, 128]. The high operating frequency of the thermometer also means that Planckian corrections, (23), for the non-negligible photon energies, are necessary when the thermometer is used at temperatures below 50 mK or so, depending on the operating frequency and the accuracy required [127]:
| (38) |
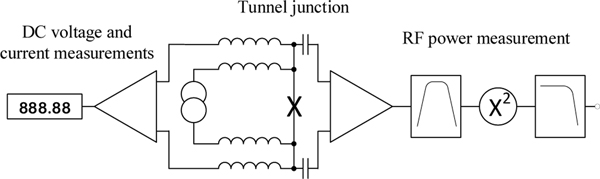
Figure 10 shows a schematic diagram of the first shot noise thermometer as described by Spietz et al. [124]. Inductive and capacitive filtering is used to isolate the dc and rf parts of the measurement circuit. On the dc side of the measurement, a variable current source is used to bias the temperature sensor, an Al-AlOx-Al tunnel junction, and a DVM is used to measure the bias voltage. The rf side of the measurement system includes the amplifier chain providing about 70 dB of gain, a 300 MHz wide bandpass filter centred on 450 MHz, a Schottky diode rectifier, low-pass filter and DVM to measure the averaged noise power.
Figure 10.
Schematic diagram of the shot noise thermometer.
The initial measurements between 37 mK and 295 K included comparisons with calibrated secondary thermometers indicating an accuracy of better than 1% over most of the range, a best accuracy of about 0.1% near 0.5 K, and a resolution of 0.02%. Spietz et al. also describe several of the major sources of error and means by which accuracies of better than 0.1% might be readily achieved. Later measurements by Spietz et al. [127] demonstrated the need to consider the photon energies, (38), when measuring near 10 mK. Sayer et al. [129] investigated the effects of departures of the current noise from the simple shot noise model including 1/f noise and non-Poisson shot noise. Park et al. [128, 130–132] developed and operated a similar shot noise thermometer operating near 1 GHz for the temperature range from 500 mK to 100 K and demonstrated an accuracy of the order of 1%. In a more recent paper, they have considered the need to carefully manage the operating point of the diode rectifier in order to ensure an accurate square-law characteristic [131].
4.6. Bosonic Junction Noise Thermometer
Since 1995 when the first Bose-Einstein condensate (BEC) was produced at a temperature of 170 nK [133], there has been intense interest in BECs as a means of understanding macroscopic quantum phenomena. Because the mass of material maintained at these temperatures is extremely small, only a few thousand atoms, the temperature of the BEC must be determined from the BEC properties rather than by using an external sensor. Amongst the techniques available at these temperatures is the bosonic Josephson junction noise thermometer, first demonstrated by Gaiti et al. in 2006 [134–137].
As the name suggests, the thermometer is an analogue of the Josephson junction, and is formed when a BEC is confined to a double-well potential:
| (39) |
The first term of (39) describes a three-dimensional ellipsoidal potential well within which the BEC is confined, while the second term imposes a long-period potential that places a weak energy barrier at the centre of the ellipsoid and separates the BEC into left- and right-hand parts approximately apart (a few micrometers). The trapping frequencies, , , and , indicate the energy levels of the ground states for wavefunctions in the three directions, or equivalently, the degree of confinement imposed by the potential well in those directions. The BEC-barrier-BEC structure is analogous to the superconductor-insulator-superconductor structure of the Josephson junction.
Once the BEC has formed and has separated into two parts, it will continue to behave as a single coherent object due to coupling via atoms tunnelling through the weak barrier. The coherence is increased by increasing the tunnelling current, which occurs with greater numbers of atoms and a low barrier height. The coherence is weakened by thermal fluctuations, so that the balance between the processes provide a direct measure of the temperature. The coherence factor is
| (40) |
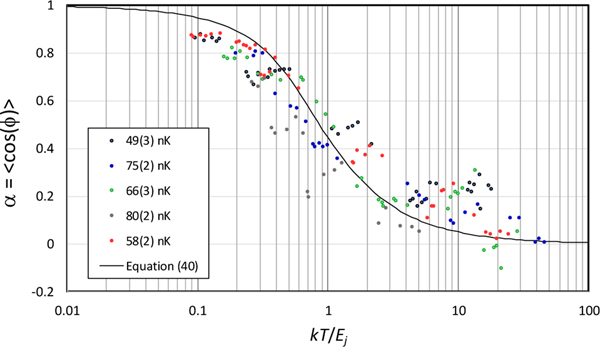
where and is the quantum mechanical phase difference between the wavefunctions for the two groups, is the measure of the coupling between the two groups, and the functions in (40) are modified Bessel functions of the first kind. Since for small phase differences, , the coherence factor is related to the variance of the fluctuating phase differences.
Gati et al. demonstrated the thermometer for at temperatures ranging between 50 nK and 80 nK for a range of different values, achieving uncertainties of the order of 30% (see Figure 11). The uncertainties arise in part from the small number of measurements of phase difference averaged (typically 40) and uncertainties in the measurement of the phase differences. Detailed theoretical description of the thermometer is given in [137], and details of the experiment are given in Gati [134–136].
Figure 11.
The measured coherence factor versus normalised energy for the bosonic junction thermometer, compared with theory. The scatter is due to the small number of measurements made for each point.
5. Industrial Noise Thermometry
The main motivations for the application of Johnson noise thermometry to industrial temperature measurement are improved reliability and freedom from the need to remove the sensor for recalibration. This is especially true at temperatures above 1000 °C where thermocouples are the only viable contact thermometer, yet their instability at these temperatures makes regular replacement or recalibration essential for longterm installations. Additionally, there may be good logistical reasons why recalibration or replacement is not practical. In nuclear installations, thermometers may be too radioactive to be withdrawn, in satellite applications the installation too remote to be accessed, and in high-value manufacturing environments, the cost of frequent shutdowns may be prohibitive.
Despite the compelling arguments in favour of JNT for a few selected applications, often supported by successful trials, we know of no permanent JNT installation in any commercial enterprise. In the following subsections we review the different applications where JNT has been explored, the technical challenges for JNT in an industrial environment, and the different JNT techniques that have been explored.
5.1. Other Methods
5.1.1. Threshold noise thermometer.
In 1960, Brodski and Savateev suggested the use of a threshold detector in the place of the square-law detector in the basic switching rectifier JNT (Figure 1) [138]. Threshold detectors exploit the Gaussian probability distribution of the noise voltage and measure the frequency that the noise exceeds some threshold voltage,. The expected count rate is half the threshold-crossing frequency and given by [139]:
| (41) |
where is the frequency response of the thermometer. The maximum sensitivity of the count rate to changes in the thermal noise voltage is achieved with the threshold set to [140]
| (42) |
The count rate is sensitive to mismatches in the frequency response to the two noise sources, and to mismatches in the noise powers, including differences in the noise powers from the lead wires and the amplifiers. As with the switched-rectifier noise thermometer, the reference resistor is adjusted so that the count rates from the two noise sources are the same, which ideally ensures the thermal noise powers are the same and the temperature can be found from the ratio of the resistances, (4).
Savateev successfully evaluated the thermometer at the oxygen point (−218.8 °C) [140]. The technique was also developed independently by Fujishiro et al. [141] who measured temperatures in a pressure vessel and achieved accuracies of better than 0.3% from room temperature to 630 °C. A basic uncertainty analysis of the technique has yet to be carried out, but because only a small part of the signal is used, the method is less statistically efficient than a square-law detector.
5.1.2. Dual thermocouple noise thermometer.
One of the major obstacles to the adoption of noise thermometry for industrial applications is the slow measurement time, and, as noted Sec. 2, measurement times of the order of minutes may be required to achieve a resolution of 0.1 %. Such measurement times are long compared to the response times of thermocouples and resistance thermometers and may be too long to enable satisfactory control over plant temperatures.
Brixy et al. [60] developed a solution that combined the rapid response of the thermocouple and the long-term accuracy and stability of the noise thermometer. As shown in Figure 12, the sensor uses a four-wire resistor as the noise sensor, with the four lead wires made from two thermocouples.
Figure 12.
Combined noise-thermocouple sensor.
The thermocouples measure temperature continuously, while the noise thermometer operates periodically to calibrate the thermocouples in-situ. The in-situ calibration has the additional benefit of eliminating thermocouple errors caused by temperature gradients across inhomogeneous regions within the thermocouple wires, thereby solving a notorious problem with thermocouples [11, 61].
Brixy successfully trialled the TC-NT thermometer with different sensing elements at temperatures ranging from below 300 °C in pressure water reactors, to 1000 °C in gas-cooled reactors, petrochemical reformers, glass works, and hot isostatic presses at 1800 °C. Some trials with boron-carbide thermocouples and graphite rope sensing elements were also carried out at 2200 °C [11].
5.1.3. Dual resistance noise thermometer.
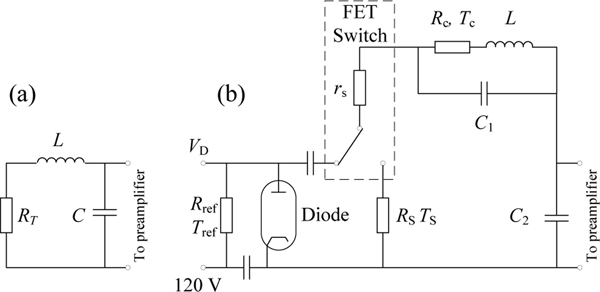
Following the same principle as the dual thermocouple-noise thermometer, it is also possible to combine the short response time of resistance thermometers and the long-term stability of the noise thermometer by using the same sensor for both measurements. This technique must accommodate a sensing element with a large temperature coefficient, rather than the more usual sensing element designed to have a low temperature coefficient.
The first application of the technique was by Soulen et al. who used it to calibrate a rhodium-iron resistance thermometer for cryogenic thermometry below 500 mK [142]. The first industrial application was in 1984 by Blalock et al. [143] who used a 200 platinum resistance thermometer to achieve an accuracy of about 0.1% when measuring the water circulated in a nuclear facility at about 300 °C. Britton et al. also evaluated the technique for use around 300 °C [144–146]. De Groot et al. used a switched-correlator noise thermometer with a molybdenum-silicide resistance element operating between 1000 °C and 1600 °C [147]. They found that the thermometer could be calibrated to better than 0.3% for temperatures up to 1500 °C, but temperature cycling of the sensor induced changes of up to 1%.
5.1.4. Noise power thermometer.
The need to measure the resistance of the JNT sensor, especially at high temperatures where the drift in sensor resistance can be significant, is an inconvenience that costs additional measurement time. Borkowski, Blalock, Shepard et al. [38, 143, 148, 149] described and evaluated a noise power thermometer that measures both the noise current and the noise voltage of the sensing resistor. The measured noise voltage is
| (43) |
where is the voltage gain of the voltage amplifier, and the measured noise current is
| (44) |
where is the trans-impedance of the current amplifier. The measured noise power is then
| (45) |
which is directly proportional to temperature and independent of the sensing resistance. The thermometer requires calibration to determine the overall gain of the thermometer, but that can be carried out in the laboratory. The stability of the thermometer instrumentation is unaffected by the factors causing the sensor to drift.
One of the problems with this technique is the intrinsic noise voltage and currents of the amplifiers, the effects of which depend on the sensor resistance. Borkowski and Blalock substantially reduced the effects by designing the current amplifier so that the trans-impedance depends on the sensor resistance in a manner that compensates the amplifier noises. Using this technique and a dual sensor platinum resistance thermometer connected either singly, in series, or in parallel, between 0 °C and 1000 °C, they demonstrated that the thermometer errors were typically within 1 % [148].
5.1.4. Capacitive noise thermometer.
Another method avoiding the need to measure the JNT sensor resistance exploits the fact that the total noise power produced by a sensing resistor in an RLC low-pass filter (Figure 14(a)) is
| (46) |
so that the noise power is independent of the sensing resistance and the inductance. This result is another example of Boltzmann’s equipartition theorem (see also (33)).
Figure 14.
The band-pass capacitive noise thermometer (a) the principle, (b) a practical realisation.
A practical implementation of such a thermometer, developed by Pepper and Brown [35], and shown in Figure 14(b), is essentially a switched-rectifier JNT with a high-Q RLC filter constraining most of the noise to a narrow band. To overcome problems with the amplifier noise currents and noise voltages, the thermometer switches between the sensor and a reference noise source with nominally the same resistance as the sensor. The operation of the thermometer is complicated by the self-capacitance and resistance of the inductor which modify the frequency response of the RLC circuit. The total noise power is determined by the combined capacitance of and in figure 14(b), which does not need to be known in ratio measurements, and a weighted average of the temperatures of the inductor resistance and the sensor resistance. Instead of altering the reference resistance to match the noise powers, the circuit includes a shot-noise source, the diode of figure 14(b), with the diode current determined by the voltage across the reference resistor,. When the noise powers are matched, the temperature is determined as
| (47) |
where the various resistance are as indicated in Figure 14(b), is the electronic charge and is the Boltzmann constant. With the reference resistor and the sensor resistance closely matched, the absolute temperature is largely determined by the reference temperature (with ) and the diode voltage, with a modest correction due to the circuit resistances. While the measured temperature does depend on the sensing resistance, the effects are second order, and the sensor resistance need not be known with low uncertainty.
The thermometer was operated with a resonant frequency of 7 MHz and a of 15, and an rf amplifier with a bandwidth of 2 MHz to 10 MHz. The thermometer achieved statistical uncertainties of about 0.3% with an averaging time of just 1 s and measured temperatures up to 1500 °C.
5.1.5. Inductive noise thermometer.
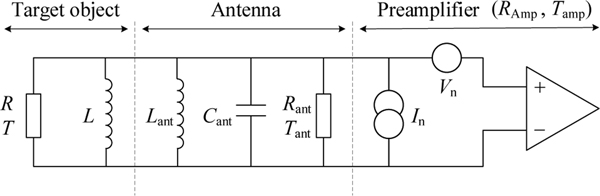
Most thermometers are installed with the sensing element in thermal contact with the object of interest. However, such installations are not practical where the surface of the object is moving or deteriorating due to corrosion, as is often the case with hotmetals processing. Seppa and Varpula describe and demonstrate a non-contact method of noise thermometry that measures temperature of metallic objects via inductive coupling [144, 145]. The technique is similar in principle to the magnetic field fluctuation thermometers of Sec 4.3, except that instead of using a SQUID to measure the magnetic field, the thermometer uses a high-Q antenna. As shown in Figure 15, the method also shares some similarity with the capacitive method (sec 5.1.5).
Figure 15.
Equivalent circuit for the inductive noise thermometer.
The unknown temperature is determined by measuring the total noise power of the resonant circuit and its impedance at resonance.
| (48) |
where, is the amplifier noise voltage, and are the resistance and temperature of the target object, and are the temperature and resistance of the antenna, and and are the equivalent noise resistance and noise temperature of the amplifier, and
| (49) |
is the mean-square impedance of the antenna and the object averaged over the frequency response of the thermometer. Theoretical aspects of the inductive noise thermometer are presented in [150], and a simpler description and the results of experiments are presented in [151].
Using a thermometer operated at 1.5 MHz and with a noise bandwidth of 5 kHz, Varpula and Seppa demonstrated agreement with conventional thermocouple thermometry within 1% for temperatures up to 1300 K. Since the integration time was only 13 s, the thermometer is a feasible solution for real-time temperature monitoring in metals processing industries.
The thermometer was also tested on a continuous casting process, and compared with an optical pyrometer, to evaluate it in an industrial environment. The temperature indications from the JNT were higher than indicated by the optical pyrometer in part because they were not measuring at the same position, in part due to occasional extraneous noise from EMI, and perhaps also in part because the JNT measured the temperature beneath the cooler oxidised surface of the metal.
5.1.6. Superposition thermometer.
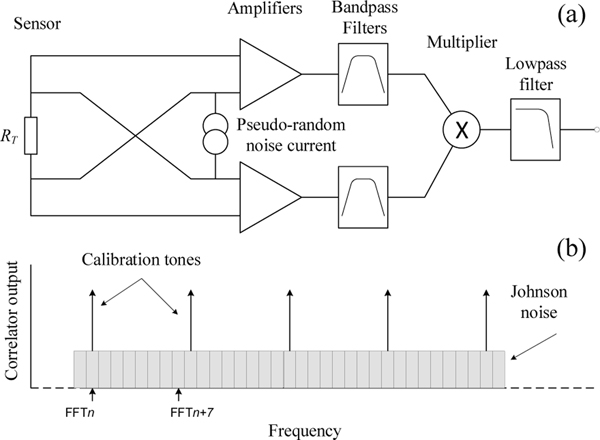
The superposition thermometer replaces the time-domain multiplexing of the switched correlator, by frequency-domain multiplexing [152, 153]. As shown in Figure 16(a), a current source, connected to one pair of the sensing-resistor lead wires, injects a pseudorandom calibration signal in the form of a frequency comb with randomised phases (see Sec. 3.3). The spectrum of the signal seen by the preamplifiers is as shown in Figure 16(b). The signals are sampled synchronously with the calibration signal to ensure there is no spectral leakage and that each calibration tone is located in a single FFT bin.
Figure 16.
(a) The superposition noise thermometer. (b) The power spectrum seen by the amplifiers.
By processing the spectra in the frequency domain, it is possible to simultaneously (i) measure the resistance of the sensing element, (ii) measure the thermal noise power, (iii) calibrate the noise power measurement, and (iv) extend the bandwidth by compensating for the low-pass frequency response of the connecting leads. In the prototype thermometer, the tones are separated by 1220 Hz intervals between 10 kHz and 1.2 MHz and occupy FFT bins 152 Hz wide. Because only 1/8 of the FFT bins contain the calibration tones, only 1/8 of the bandwidth is sacrificed for the noise-power calibration and the resistance measurement. The thermometer also uses a high sensing resistance of 5 kΩ to minimise the contribution of the amplifier noise to the statistical uncertainty. With all of these strategies, the thermometer achieves a statistical uncertainty very close to that given by Rice’s formula (8) and is about 20 times faster than a switching correlator with a 100 kHz bandwidth. Measurements with the JNT have a statistical uncertainty of about 0.05% with an integration period of just 7 seconds. Measurements were found to be within 0.3% in the range from −20 °C to 120 °C. A commercial version of the thermometer is under development [154].
5.2. Applications
5.2.1. Nuclear.
Historically, the greatest industrial interest in noise thermometry has been for core- and coolant-temperature measurements in nuclear reactors. In addition to the problems of servicing sensors that have become radioactive, reactor cores are amongst the most difficult environments. Sensors may be subjected to pressures of 20 MPa or more, temperatures as high as 2200 °C, thermal neutron fluxes causing transmutation of the sensor materials, and fast neutron and gamma fluxes causing extreme crystallographic dislocations, embrittlement, and swelling [23]. Shepard et al. [21] describe several examples of the sensor damage occurring in reactors cores, including one where 90% of the rhenium in a sensor was transmuted to osmium within one year’s exposure. In another example they report tungsten-rhenium thermocouples, exposed to 1250 °C, drifting at rates of 1.5 °C/h and totalling 130 °C over a period of 1000 h. In the same reactor, a noise thermometer with measurement uncertainty of about 10 °C showed no signs of drift.
Much of the research into nuclear applications of JNT has been carried out at two locations. The Nuclear Research Centre (KFA, now FZ) in Jülich, Germany, has produced several generations of noise thermometer that have been successfully evaluated in different types of reactors and over a range of applications from cooling water to in-core measurements [11, 61, 62, 155–158]. Much of their work has been focussed on development of the dual thermocouple-noise thermometer (Sec. 5.1.2), and on the development of suitable sensors. The KFA team carried out all the early development on switched correlators, which laid much of the foundation for recent progress in metrological noise thermometry using correlators (Sec 3.2). The dual thermocouple noise thermometer developed at KFA has also been considered for application by the Commissariat à l’Energie Atomique (CEA) [159]. The KFA group is no longer active in noise thermometry, but a good review of their activities and conclusions can be found in [11] and [61].
The second major research group is a long standing and still active collaboration between the Oak Ridge National Laboratory (ORNL) and the University of Tennessee, both at Knoxville, USA [25, 33, 38, 144, 148, 160–167]. Much of the early research focussed on the development of the noise power thermometer (Sec 5.1.4) and trials to establish the utility and reliability of noise thermometry under a wide variety of the conditions experienced in nuclear installations. Most recently, their work has shifted to investigations of correlator-based thermometers and signal processing methods to minimise the effects of electromagnetic interference.
Other nuclear research has been carried out at the CEN/SCK nuclear Research Centre at Mol, Belgium [24, 168, 169], and at the Hanford Engineering Laboratory in Richland, USA [23, 170], both of which investigated the noise power thermometer (Sec. 5.1.4) and developed sensors for exposure at very high temperatures. Both groups demonstrated accuracies of about 0.3% for temperatures above 1500 °C in laboratory conditions, but neither investigated JNT performance in reactors.
5.2.2. Space.
Nuclear power supplies, at present, are the only practical solution for high-power, long-range, or long-duration space missions [171]. Between 1983 and 1994, the US Department of Energy and NASA participated in a joint project to develop the SP-100 scalable nuclear reactor, designed to supply 100 kW of electrical power for a range of civil and military space applications [172, 173]. Control of the SP-100 reactor required temperature measurement accurate to better than 1% at 1100 °C for a minimum of 7 years with a measurement time of less than 7 s and a 95% reliability. Infrared radiation thermometry and Johnson noise thermometry are the only two techniques capable of meeting this specification [167, 174, 175].
From 1987 to 1991, the SP-100 programme supported Johnson noise thermometry development at ORNL, following earlier investigations into terrestrial nuclear applications (see Sec. 5.2.1). Initial experiments focussed on the noise power thermometer (Sec 5.1.4), but later experiments explored the capacitive noise power thermometer (Sec 5.1.5) [176]. Terrestrial experiments in reactors showed that both systems achieved uncertainties of the order of 0.4% [167, 174, 175], which met the SP-100 specification. At the time the SP-100 project was concluded, 1993, the reactor thermometer used tungsten-rhenium thermocouples and JNT separately to achieve the required 7 s measurement time. ORNL continue to investigate space applications of noise thermometers using correlating noise thermometers [162]. The current proposal for a flexible reactor for space applications [177], has a nominal core temperature of only 800 °C, which avoids the need for the exotic technologies and materials required for higher temperature operation.
Johnson noise thermometry was also considered for the control of crystal growth experiments on the International Space Station [26]. The study investigated the suitability of JNT for application for medium-term experiments (months) at temperature above 1500 °C, where precision of 0.1 °C might be required. Experiments with tungsten-rhenium thermocouples under the same conditions exhibited drifts of 100 °C over a 20-hour period. Much of the effort was devoted to finding suitable insulation materials for the sensor. The noise thermometer operated satisfactorily at 1800 °C without problems and with an uncertainty of about 10 °C.
5.2.3. Plasma and hot gas thermometry.
The fluctuation dissipation theorem applies to all conductors. Therefore, Johnson noise can also be found in the highly ionised gas of plasmas and combustion processes. Ivashchenko et al. [12] describes a model of the two ionisation mechanisms in a hydrocarbon flame, and measurements of the temperature of an oxy-acetylene flame using two different sensing modes operating between 5 MHz and 30 MHz. They recorded noise temperatures in the range 1000 K to 1950 K, depending on the combustion conditions, the method of measurement, and the measurement mode. Korobchenk and Ivashchenk later considered how well the measured electron temperature relates to the gas temperature [178].
Baum et al. [179] evaluated the suitability of JNT for hot gas measurements by constructing a gaseous sensor using a hot-air chamber seeded with caesium-chloride. The resistance of the gas sensor was in the range 100 to 10 depending on the temperature and pressure of the gas. They performed a series of experiments to confirm the theory by comparing measurements made by thermocouple with those from the noise thermometer operating near 20 MHz with a hot wire sensor, and with the hot-gas sensor. The measurements with the hot-gas sensor spanned the range 1070 K to 1550 K and achieved an uncertainty of about 1%.
Gill et al. [180] compared the performance of a noise thermometer with a tungsten-rhenium thermocouple in an oxy-hydrocarbon flame in the range 1500 K to 2100 K and found that the JNT indicated a temperature 4% to 7% higher than the thermocouple, most likely caused by radiative cooling of the thermocouple when located in the flame. They discuss in some detail the calibration of the noise thermometer, measurements of the sensor resistance, and contributions of the measuring instruments to the uncertainty.
5.2.4. Nano-scale thermometry.
Accurate temperature measurement is important for both research and manufacture of micro- and nano-scale objects and structures. In particular, the very low heat capacities of one- and two-dimensional objects can restrict measurements to passive techniques such as thermocouple thermometry or Johnson noise thermometry [35], and Johnson noise thermometry has the advantage of not requiring additional sensors.
Dobson et al. [181] describe the calibration of an integrated thermocouple using noise thermometry over the range 300 K to 600 K. An uncertainty below 1 K was achieved with a small metallic resistor of 1.5 kΩ measured over a 1 kHz bandwidth. They also calibrated a nano-scale resistance thermometer used for temperature measurements in atomic force microscopy probe. Crossno et al. [182] describe a very wide band radiofrequency (RF) Johnson noise thermometer used to measure the conductance of a graphene device. The thermometer operated at 2 GHz with a correlation bandwidth of 328 MHz, and achieved a sensitivity of 5.5 mK for an integration time of 1 s over the range 3 K to 300 K. Bunyan et al. describe the measurement of the temperature of a micron-scale MOSFET transistor as a function of power, and Glatti et al. [183] describe the measurement of the temperature of a single electron tunnelling device at temperatures below 500 mK with an uncertainty of about 10 mK.
5.3. Technical challenges
5.3.1. Measurement time.
Johnson noise thermometry is unlikely to be adopted as a routine industrial technique until measurement uncertainties of 0.1 % or less can be obtained in a few seconds, enabling JNT to replace thermocouple and platinum resistance thermometry for temperature control applications. Rice’s equation, (8), shows JNTs should have bandwidths 1 MHz or more. Additionally, the factor of four increase in measurement time required to compensate for the increased uncertainty with switching thermometers, (10), is costly, as is the multiplying factor due to amplifier noise (11) or (19).
At present only three JNT techniques meet the industrial needs in respect of speed:
the superposition thermometer (Sec. 5.1.6), which operates close to the limit prescribed by Rice’s equation, combines a high statistical efficiency with a bandwidth of 1 MHz.
the dual noise thermometers (Secs. 5.1.1, 5.1.2) that combine a noise thermometer with a much faster conventional thermometer, either a resistance thermometer or thermocouple,
very wide-band radio-frequency noise thermometers. for which the measurement uncertainty is limited to about 1% by amplifier noise and uncertainties associated with measurement and calibration of noise powers.
Scandurra et al. [184] and Hrbek [58] describe a technique that increases the sensitivity of the noise thermometer enabling faster measurements than implied by Rice’s equation. Consider a sensing resistance with a temperature dependence . According to Nyquist law, the noise power is
| (50) |
The sensitivity of the thermometer, which measures the percentage change in noise power for a 1% change in the temperature, is
| (51) |
For a noise thermometer operating with a constant sensor resistance (n = 0), the normal mode of operation for a JNT, the sensitivity is 1.0. If the sensor is pure-metal such as platinum, copper or nickel, the resistance is approximately proportional to the absolute temperature [185], , the sensitivity doubles, and the measurement uncertainty can be halved. Even greater gains can be made with semiconductors with a very high temperature coefficient of resistance. Unfortunately, it is not obvious how the effect can be exploited. If the resistance of the sensor is a stable function of temperature, it is simpler and more efficient to simply treat the sensor as any other resistance thermometer and infer the temperature directly from the measured resistance. If the sensor is not stable, the dual resistance-noise thermometer is a better alternative.
Equation (51) also highlights the possibility of using a resistor with a 1/T temperature dependence (n = −1) to make a stable reference noise source, since the noise power is independent of temperature [38].
5.3.2. Sensors.
The sensors for JNTs have only a few essential requirements. Ideally, they should have a flat frequency response, and this means they should be noninductively wound, and therefore commercially manufactured platinum resistance thermometers are not ideal. For high-accuracy applications, the conductors should also be thin enough to avoid the skin effect. Brixy describes examples of high-temperature sensors of the birdcage design, which are suitable for lower accuracy industrial noise thermometry [11, 61].
Ferromagnetic materials carry the risk of introducing Barkhausen noise. Barkhausen noise occurs with the rapid changes in magnetic domains and the resulting magnetic field fluctuation induces a voltage or current in a measuring circuit. The effect occurs in response to a changing external magnetic field but can also occur with vibration. Brixy [1996] cites instances where Barkhausen noise has been observed. Ferromagnetic materials should be avoided for the sensing element, the leadwires, and any shielding material located near the sensor or leadwires.
The sensors should also be fully supported to prevent mechanical movement and avoid microphonic effects. If there is a dc voltage across the lead wires for example, perhaps due to thermoelectric effects or the input offset voltage of the preamplifier, changes in the capacitance between conductors will cause a small current. Powder insulation around the leadwires is useful for preventing the mechanical movement [11].
At low temperatures and up to 150 °C or so, most noise thermometers have used metal-film resistors, usually manufactured on a ceramic substrate and printed in a meander pattern. The meander pattern is designed to balance the inductive and capacitive effects within the resistor, so these sensors have a low temperature coefficient, negligible skin effect, and a wide flat frequency response. Care should be taken in the selection of resistors, to avoid resistors packaged with ferromagnetic materials because of the potential for Barkhausen noise and for parasitic inductance effects.
For temperatures above 150 °C there are no suitable commercially manufactured resistors. The most suitable sensors are made from either nickel-chromium alloys or noble metals threaded into a short section of multi-bore (2 to 36 hole) alumina ceramic insulator; the ‘bird-cage’ design (see [11, 61, 156, 186, 187] for examples and details). Nichrome alloys with 70% to 80% nickel have a low temperature coefficient and may be used in an oxidising atmosphere, due to a passivating oxide layer that allows use at temperatures up to about 1200 °C. The noble metals such as pure platinum, platinum-rhodium alloys, platinum-tungsten alloy will tolerate higher temperatures, up to 1500 °C. Alloys have the advantage of a lower temperature coefficient.
At temperatures beyond 1500 °C, the best sensors operate in vacuum or a reducing environment. Rhenium and tungsten-rhenium alloys have been used successfully, also wound onto a birdcage-style ceramic insulator [11, 61]. They can be used successfully up to 2200 °C. Brixy also experimented with braided graphite rope sensors, which have the advantage of immunity to breakage caused by thermal expansion and contraction [11].
5.3.3. Signal transmission.
The lead wires between the sensor and the JNT electronics are nearly always a source of error. Figure 17 shows a simplified model of the sensor, the connecting leads represented as a transmission line, and a preamplifier represented simply by its input capacitance. The transmission line is characterised by an inductance per meter, L, capacitance per meter, C, series resistance per meter, R, and parallel conductance per meter, G. In reality, the connecting lead assembly is more complicated than the model implies as it may be constructed as multiple coaxial leads, twisted pairs, shielded pairs, or shielded 4-wire lines, and different sections of the leads may have different constructions.
Figure 17.
Model of the sensor, connecting leads, and the preamplifier.
The connecting leads cause two distinct problems, dispersion distortion and loss. Dispersion distortion arises from the frequency dependent transfer function of the leads when combined with the sensor and preamplifier impedance, and this is primarily a function of the inductance and capacitance of the transmission line. Dispersion distortion occurs to some degree in all noise thermometers and becomes an increasingly difficult problem for systems with long lead lengths and operating at high frequencies. Loss occurs where energy is dissipated in the line, so is primarily caused by the series resistance and parallel conductance and results in the reduction in amplitude of the noise signals.
For many applications, the model need not be as complicated as shown in Figure 17. The simplest variation is applicable at low temperatures (no loss), low frequencies, and for short line lengths,. Then the model can be simplified to Figure 18 and the measured noise power, , has the relative spectral shape
| (52) |
Figure 18.
a simplified models (a) first order in frequency, (b) third-order in frequency.
This equation shows that the frequency response changes with the resistances of the sensor and the reference noise source. At first glance, it may seem that a solution is to switch the preamplifier capacitance along with the noise sources to maintain the same RC time constant [52, 188–190]. However, this neglects the transmission line inductance, as shown in figure 19 [64, 78], so matching the time constants is an approximation that works only at very low frequencies. At higher frequencies, matches are only possible if all the elements of the model are matched [78], i.e., use the same transmission line construction for both noise sources. It is also helpful to use sensor resistances close to the characteristic impedance, , of the transmission line:
| (53) |
as this ensures the frequency response of the system is as flat and as wide as practical. Commercial cables normally have a characteristic impedance in the range from 35 to 150 , with many near 50 .
Figure 19.
simplified model of the effect of poor electrical insulation at high temperatures.
At sufficiently high temperatures, all insulation materials become electrically conductive, with the resistance falling exponentially with temperature, and this leads to three significant problems. The simplified model in Figure 19 shows, firstly, that a high conductance between any of the main conductors of the connecting leads causes attenuation of the signal from the JNT sensor, and the attenuation is dependent on the sensor resistance and the conductance of the insulation, which also depends on the temperature profile along the connecting leads. The unwanted cable conductance also biases measurements of the sensor resistance. Above 1500 °C, it is necessary to use a low sensor resistance, in the range from 1 to 10 , and exotic insulation materials such as hafnia, beryllia, and boron nitride [11, 61].
The second difficulty is the Johnson noise generated by the cable conductance. Even in correlating noise thermometers, the effects of the extraneous noise currents injected into the sensor result an unwanted correlated signal. For high-accuracy measurements, it is necessary to model the imperfect insulation as a complex admittance , where the dc conductance is and the ac losses are described by a temperature- and frequency-dependent loss tangent . The lossy capacitance of the insulator produces both a frequency-dependent attenuation of the thermal sensor noise and an independent parallel source of thermal noise. The two effects both result in measurement errors, but are opposite in sign, with the net effect usually resulting in a negative error [79]. Errors of this type have been observed above 700 K in probes using fused-silica insulators previously subjected to flame processing [191]. The effects may be mitigated by geometrical arrangements that minimize the capacitance with the fused silica dielectric and by avoiding flame-treated fused silica.
The third difficulty relates to electromagnetic interference causing by unwanted currents flowing in the measurement circuit.
5.3.4. Electromagnetic Interference.
Electromagnetic interference (EMI) is a major technical challenge. With high-accuracy laboratory applications, there appears to be no alternative to the use of heavy magnetic screening, often in addition to a screened room [17, 85, 192], but with industrial applications, such precautions are impossible. Instead, a combination of careful layout, electronic design, and signal processing is essential.
EMI can be classified in two forms. The first is caused by direct connections and unwanted currents flowing in the measurement circuit. This happens for example in any of the connecting-lead models of Sec 5.3.3. If there are unwanted currents flowing in the shield of the transmission line, the voltage generated there will cause unwanted currents to flow through the cable conductance and capacitance to the sensing resistance. Therefore, all efforts must be made to ensure no currents flow in the shields of the transmission lines.
The second form of EMI arises from unwanted electromagnetic fields and may be classified as electrostatic, magnetic, or plane-wave [76]. With electrostatic EMI, the coupling mechanism can be modelled as a capacitance linking the interfering object and the circuit of interest. The current induced in the measurement circuit is proportional to the rate of change of voltage on the nearby object. Magnetic EMI is the conjugate effect with voltages induced by distant currents and the coupling determined by the mutual inductance between the two circuits. If the interfering source is sufficiently distant, then the interference takes the form of an electromagnetic wave.
The screening of electromagnetic fields takes two main forms, reflection and absorption. Reflection dominates at low frequencies and arises from the movement of charge in the screen in response to the field and cancelling the effect of the field within the screen. Absorption dominates at high frequencies and arises from the absorption of energy as the field propagates through the screen material. The effectiveness of these two effects is very different for electrostatic, magnetic and plane waves, and has a strong frequency dependence, as shown qualitatively in Figure 20.
Figure 20.
The frequency dependence of the effectiveness of electromagnetic screens depends on the nature of the source, frequency, and distance to the source [76].
The most problematic EMI is caused by magnetic fields generated at close proximity. Examples include digital telephone and security systems, computers, fluorescent lamps, and mains cables. Mains cables carry currents from switch-mode power supplies, electric motors, temperature controllers, digital electronics, etc, with harmonics extending to frequencies well into the hundreds of kilohertz. The difficulty of effectively shielding magnetic interference is the reason that the frequencies up to a few kilohertz are usually removed from the noise power measurement.
The most effective measure against magnetic EMI is to minimise mutual inductance by minimising the cross-sectional area of the two circuits and maximising the distance between them. JNT cables should not be routed close to power cables, and certainly not close to cables carrying rapidly changing currents. Coaxial cables present the lowest area to a magnetic field, and radiate the smallest magnetic fields, because the geometric centre of the inner and outer conductors are co-located. Coaxial cable also has the advantage of a complete outer conductor to eliminate electrostatic interference. Twisted pair cables also work well [76, 77] for magnetic fields. The construction of balanced or differential sensors (e.g., a centre-tapped resistors) and the use of differential amplifiers with a good common-mode rejection ratio (CMRR) also help.
The signal processing used to combat EMI typically consists of the ‘blanking’ of spikes detected in the time-domain signals and frequency-domain blanking where strong spectral lines characteristic of single-frequency interference are detected [62, 174, 175, 193]. Sometimes the bias due to EMI can be detected by summing spectral elements at multiples of the local mains frequency, for example, and comparing the sum to the results from the rest of the spectrum [194]. However, there are no statistical tests guaranteed to detect all broadband or non-stationary EMI [71], so every precaution must be used to prevent the EMI from affecting the measurement.
6. Progress and Prospects
Johnson noise thermometry has made very significant advances in the last two decades. Perhaps the most significant advances have been in metrological applications where noise thermometry has been used to make thermodynamic measurements with uncertainties comparable to the best of other thermodynamic techniques. Measurements of the Boltzmann constant by JNT also made a small but very important contribution to the recent CODATA adjustments of the fundamental constants [16, 17], by providing a measurement with a relative uncertainty of just 2.7×10−6 and by demonstrating consistency with two other thermodynamic techniques and ruling out the possibility of large systematic errors in all three methods. Notably, it was the only purely electronic measurement. Future research is likely to capture the benefits of recent advances by developing thermometers that operate at temperatures up to 400 °C or more with millikelvin accuracy.
Recent developments in current sensing and magnetic field fluctuation noise thermometers (Secs 4.2, 4.3) have made a significant contribution to cryogenic thermometry by providing a thermodynamic measurement technique supported by commercial instrumentation and spanning at least three decades in temperature. With the anticipated adoption of a new kelvin definition based on a defined value for the Boltzmann constant in May 2019, greater adoption of noise thermometry can be expected in this temperature range.
Another possibility is an integrated-circuit noise thermometer. Zhang and Chen [195] have simulated the performance of a unswitched rectifier JNT that included the sensor, a four-stage amplifier, filters, and a 6-bit flash ADC on the same chip. Advantages of IC JNTs include wide bandwidths due to low stray capacitance and inductance, and low EMI due to the small circuit areas. Despite the simplicity of the design, the simulation suggests uncertainties of no more than 0.6 °C over the range −40 °C to 105 °C. Perhaps with a correlator-based design, uncertainties below 0.2 °C are possible
Although there have been significant developments in industrial noise thermometry, the benefits of the research, in the form of a readily available commercial instruments and sensors, has yet to be realized. For the moment, JNT appears to be attractive only for the most difficult measurements and environments. However, the recent development of the superposition technique (Sec 5.1.7), which offers significant speed advances over past techniques, and the continuing advances in miniaturization of digital signal processing instruments, suggest that useful commercial instruments may not be far away.
Figure 13.
The noise-power thermometer measures the product of the noise current and the noise voltage.
References
- [1].Einstein A 1905. Investigations on the theory of the Brownian movement Ann. der Physik 19 371–81. [Google Scholar]
- [2].Johnson JB 1927. Thermal agitation of electricity in conductors Nature. 119 50–1. [Google Scholar]
- [3].Johnson JB 1928. Thermal agitation of electricity in conductors Phys. Rev 32 97–109. [Google Scholar]
- [4].Nyquist H 1928. Thermal agitation of electric charge in conductors Phys. Rev 32 110–3. [Google Scholar]
- [5].Callen HB and Welton TA 1951. Irreversibility and generalized noise Phys. Rev 83 34–40. [Google Scholar]
- [6].Kubo R 1966. The fluctuation-dissipation theorem Rep. Prog. Phy 29 255–284. [Google Scholar]
- [7].Dicke RH 1946. The measurement of thermal radiation at microwave frequencies Rev. Sci. Inst 17 268–75. [DOI] [PubMed] [Google Scholar]
- [8].Abbott D, Davis BR, Phillips NJ and Eshraghian K 1996. Simple derivation of the thermal noise formula using window-limited Fourier transforms and other conundrums IEEE Trans. Ed 39 1–13. [Google Scholar]
- [9].Kish LB, Niklasson G and Granqvist CG 2016. Zero Thermal Noise in Resistors at zero temperature. Fluct. Noise Lett. 15,1640001 [Google Scholar]
- [10].Reggiani L and Alfinito E 2017. The puzzling of zero-point energy contribution to black-body radiation spectrum: The role of Casimir force Fluct. Noise. Lett 16, 1771002 [Google Scholar]
- [11].Brixy H and Kakuta T 1996. Noise Thermometer, Japan Atomic Energy Research Institute, JAERI Review 96–003. [Google Scholar]
- [12].Ivashchenko YS, Korobchenko YG and Bondarenko TS 1975. Electron temperature of a hydrocarbon flame Combustion Explosion & Shock Waves. 11 703–7. [Google Scholar]
- [13].Preston-Thomas H 1990. The International Temperature Scale of 1990 (ITS-90) Metrologia. 27 3. [Google Scholar]
- [14].Rusby RL, Durieux M, Reesink AL, Hudson RP, Schuster G, Kühne M, Fogle WE, Soulen RJ and Adams ED 2002. The provisional low temperature scale from 0.9 mK to 1 K, PLTS‐2000 J Low Temp. Phys 126 633–42. [Google Scholar]
- [15].Fischer J, et al. 2018. The Boltzmann Project Metrologia. 55 R1–R20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Newell DB, et al. 2018. The CODATA 2017 Values of h, e, k, and NA for the Revision of the SI Metrologia. 55 L13. [Google Scholar]
- [17].Qu JF, Benz SP, Coakley K, Rogalla H, Tew WL, White R, Zhou KL and Zhou ZY 2017. An improved electronic determination of the Boltzmann constant by Johnson noise thermometry Metrologia. 54 549–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Flowers-Jacobs NE, Pollarolo A, Coakley KJ, Fox AE, Rogalla H, Tew WL and Benz SP 2017. A Boltzmann constant determination based on johnson noise thermometry Metrologia. 54 730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Urano C, Yamazawa K and Kaneko NH 2017. Measurement of the Boltzmann constant by Johnson noise thermometry using a superconducting integrated circuit Metrologia. 54 847–55. [Google Scholar]
- [20].Brixy HG 1971. Temperature measurement in nuclear reactors by noise thermometry Nucl. Inst. and Meth 97 75–80. [Google Scholar]
- [21].Shepard RL, Borkowski CJ, East JK, Fox RJ, Horton JL, Hardt PVD, Zeisser P and Mason F. 1974. Ultrasonic and Johnson noise fuel center-line thermometry. in Proc. International Colloquium on High-Temperature in-pile Thermometry, Petten, Netherlands, 12 Dec 1974. [Google Scholar]
- [22].Anderson RL Kollie TG Guildner LA 1976. Problems in High Temperature Thermometry, CRC Critical Reviews in Analytical Chemistry 6.2 171–221 DOI: 10.1080/10408347608542692 [DOI] [Google Scholar]
- [23].Cannon CP 1981. A 2200 C fuel center-line Johnson noise power thermometer IEEE Trans Nucl. Sci 28 763–6. [Google Scholar]
- [24].Decreton MC 1982. High temperature noise thermometry for industrial applications, in Temperature: Its measurement and Control in Science and Industry, Vol. 5, Ed Schooley JF (AIP, New York: ) pp 1293–1243 [Google Scholar]
- [25].Shepard RL, Carroll RM, Falter DD, Blalock TV and Roberts MJ, 1992, Tuned-circuit dual-mode Johnson noise thermometers, in Temperature: Its Measurement & Control in Science & Industry, Vol. 6, Ed Schooley JF, (AIP; New York: ) pp 997–1002 [Google Scholar]
- [26].Stenzel C, Meyer T, Krause H and Brixy H 2003. Noise thermometry in crystal growth facilities for the international space station (iss) Crystal Research and Technology. 38 697–706. [Google Scholar]
- [27].Fixsen DJ 2009. The temperature of the cosmic microwave background. Astrophys. J 707, 916–920. [Google Scholar]
- [28].Sinitsyn NA Pershin YV 2016. Rep. Prog. Phys 79 106501 [DOI] [PubMed] [Google Scholar]
- [29].Kish LB 2006. Totally secure classical communication utilizing Johnson (-like) noise and Kirchoff’s law, Phys. Lett. A 352 178–182 [Google Scholar]
- [30].Vadai G Mingesz R Gingl Z 2015. Generalized Kirchhoff-law-Johnson-noise (KLJN) secure key exchange system using arbitrary resistors. Sci. Rep, 5, 13653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Crossno J Liu X Ohki TA Kim P Fong KC 2015. Development of high frequency and wide bandwidth Johnson noise thermometry, Appl. Phys. Lett 106 023121 [Google Scholar]
- [32].Kamper RA 1972, Survey of Noise Thermometry, in Temperature: Its Measurement and Control in Science and Industry. Vol. 4. Ed. Rubin LG (ISA, Pittsburg: ) 349–354 [Google Scholar]
- [33].Blalock TV and Shepard RL 1982. Decade of progress in high-temperature Johnson noise thermometry in Temperature: Its measurement and control in science and industry. Vol 5 Ed Schooley JF (AIP, New York: ) 1219–23. [Google Scholar]
- [34].White DR, et al. 1996. The status of Johnson noise thermometry Metrologia. 33 325. [Google Scholar]
- [35].Pepper MG and Brown JB 1979. Absolute high-temperature Johnson noise thermometry J. Phys. E Sci. Inst 12 31 [Google Scholar]
- [36].Imamura M Ohte A 1982. A new method of noise thermometry, in Temperature: Its Measurement and Control in Science and Industry Vol 5 Ed. Schooley JF (AIP, New York: ) 139–142 [Google Scholar]
- [37].Neuer G, Fischer J, Edler F and Thomas R 2001. Comparison of temperature measurement by noise thermometry and radiation thermometry Measurement. 30 211–21 [Google Scholar]
- [38].Blalock T, Horton J and Shepard R 1982. Johnson noise power thermometer and its application in process temperature measurement, in Temperature: Its Measurement and Control in Science and Industry. Vol 5 Ed Schooley JF (AIP, New York: ) 1249–1259. [Google Scholar]
- [39].Benz SP, Martinis JM, Dresselhaus PD and Nam S-W 2003. An ac Josephson source for Johnson noise thermometry IEEE Trans. Instrum. Meas. 52 545–9. [Google Scholar]
- [40].Callegaro L, D’Elia V, Pisani M and Pollarolo A 2009. A Johnson noise thermometer with traceability to electrical standards Metrologia. 46 409–415 [Google Scholar]
- [41].BIPM 2008. Guide to the Expression of Uncertainty in measurement JCGM 100:2008 (BIPM Paris; ) [Google Scholar]
- [42].Rice SO 1944. Mathematical analysis of random noise Part 1. Bell Sys. Tech. J 23 282–332 [Google Scholar]
- [43].Van der Ziel A 1954. Noise: Sources, Characterisation, Measurement. Prentice-Hall. Englewood Cliffs NJ [Google Scholar]
- [44].Blackman RB and Tukey JW 1958. The measurement of power spectra from the point of view of communications engineering Part 1 Bell Syst. Tech. J 37 185–282. [Google Scholar]
- [45].Burdic WS 1968. Radar Signal Analysis Prentice-Hall, Englewood Cliffs NJ [Google Scholar]
- [46].White DR 1989. The noise bandwidth of sampled data systems IEEE Trans. Instrum. Meas 38 1036–43. [Google Scholar]
- [47].White DR, Benz SP, Labenski JR, Nam SW, Qu JF, Rogalla H and Tew WL 2008. Measurement time and statistics for a noise thermometer with a synthetic-noise reference Metrologia. 45 395–405. [Google Scholar]
- [48].Jarosik N, et al. 2003. Design, implementation, and testing of the microwave anisotropy probe radiometers Ast. J. Supp 145 413. [Google Scholar]
- [49].Garrison JB and Lawson AW 1949. An absolute noise thermometer for high temperatures and high pressures Rev. Sci. Inst 20 785–94. [DOI] [PubMed] [Google Scholar]
- [50].Patronis ET, Marshak H, Reynolds CA, Sailor VL and Shore FJ 1959. Low‐temperature thermal noise thermometer Rev. Sci. Inst 30 578–80 [Google Scholar]
- [51].Crovini L and Actis A 1978. Noise thermometry in the range 630–962 °C Metrologia 14 69 [Google Scholar]
- [52].Pickup CP 1975. A high-resolution noise thermometer for the temperature range 90–100 K Metrologia 11 151. [Google Scholar]
- [53].Fink HJ 1959. A new absolute noise thermometer at low temperatures Can. J. Phy 37 1397–406. [Google Scholar]
- [54].Jones BK 1978. Electrical noise thermometer Appl. Phys 16 99–102. [Google Scholar]
- [55].Brophy JJ, Epstein M and Webb SL 1965. Correlator‐amplifier for very low-level signals Rev. Sci. Inst 36 1803–6. [Google Scholar]
- [56].Storm L. Measurement of small noise signals with a correlator and noise thermometry at low temperatures. Zeitscrift fur Angewandte Physik. 1970;28:331. [Google Scholar]
- [57].Rubin LG 1970. Cryogenic thermometry: A review of recent progress Cryogenics. 10 14–22. [Google Scholar]
- [58].Hrbek J 1972. The measurement of low temperatures by means of a noise thermometer with a semiconductor sensor Czech. J. Phys. B 22 633–40. [Google Scholar]
- [59].Kraftmakher YA and Cherevko AG 1972. Noise correlation thermometer Phys. Stat. Sol. A 14 K35K38. [Google Scholar]
- [60].Brixy H, Hecker R, Oehmen J, Barbonus P and Hans R. 1982. Temperature Measurement, in Proc Specialist meeting on Gas Cooled Reactor Core and High Temperature Instrumentation. International Atomic Energy Commission IAEA-TC-389/6–7 [Google Scholar]
- [61].Brixy H, Hecker R, Oehmen J and Zimmermann E 1990. Temperature measurements in the high-temperature range (1000–2000 °C) by means of noise thermometry High Temp.-High Press. 23 625–31. [Google Scholar]
- [62].Brixy H, Hecker R, Oehmen J, Rittinghaus KF, Setiawan W and Zimmermann E 1992. Noise thermometry for industrial and metrological applications at KFA Jülich, in Temperature, Its Measurement and Control in Science and Technology. Vol 5 Ed Schooley JF (AIP, New York: ) 993–6. [Google Scholar]
- [63].Klein HH, Klempt G and Storm L 1979. Measurement of the thermodynamic temperature of 4He at various vapour pressures by a noise thermometer Metrologia. 15 143–54. [Google Scholar]
- [64].White DR and Zimmermann E 2000. Preamplifier limitations on the accuracy of Johnson noise thermometers Metrologia. 37 11–23. [Google Scholar]
- [65].Qu J, Benz SP, Rogalla H and White DR 2009. Reduced non-linearities and improved temperature measurements for the NIST Johnson noise thermometer Metrologia. 46 512–24. [Google Scholar]
- [66].Callegaro L, D’Elia V, Manta F, Ortolano M and Pisani M 2010. Short communication: Improvements to INRIM Johnson noise thermometer Int. J. Thermophys 31 1396–8. [Google Scholar]
- [67].Storm L 1986. Precision measurements of the Boltzmann constant Metrologia. 22 229–34. [Google Scholar]
- [68].Klempt G 1982. Errors in Johnson noise thermometry in Temperature: Its Measurement and Control in Science and Industry Vol 5 Ed Schooley JF (AIP, New York: ) 125–8. [Google Scholar]
- [69].White DR 1984. Systematic errors in a high-accuracy Johnson noise thermometer Metrologia. 20 1. [Google Scholar]
- [70].White D, Mason R and Saunders P 2001. Progress towards a determination of the indium freezing point by Johnson noise thermometry Proc. TEMPMEKO 2001 Ed Fellmuth B (VDE; Verlag Gmbh, Berlin: ) 129–34. [Google Scholar]
- [71].Willink R and White DR 1998. Detection of corruption in Gaussian processes with application to noise thermometry Metrologia. 35 787–98. [Google Scholar]
- [72].White DR and Pickup CP 1987. Systematic errors in digital cross correlators due to quantization and differential nonlinearity IEEE Trans. Instrum. & Meas. 36 47–53. [Google Scholar]
- [73].Edler F, Kühne M and Tegeler E. Noise thermometry above 960 °C. in Proc. TEMPMEKO 1999 Ed. Dubbledam JF (VSL, Delft: ) 394–399 [Google Scholar]
- [74].Edler F 2003. Thermodynamic temperature of the freezing point of copper measured by noise thermometry, in Temperature: Its measurement and Control in Science and Industry, Ed Ripple DC, (AIP, New York: ) 13–8. [Google Scholar]
- [75].Edler F, Kühne M and Tegeler E 2004. Noise temperature measurements for the determination of the thermodynamic temperature of the melting point of palladium Metrologia. 41 47–55. [Google Scholar]
- [76].Ott HW Noise reduction techniques in electronic systems 2nd Ed. (John Wiley & Sons, New York: ) 1988 [Google Scholar]
- [77].Awan S Kibble B and Schurr J 2011. Coaxial electrical circuits for interference-free measurements (IET, London: ) [Google Scholar]
- [78].White DR and Qu JF 2018. Frequency-response mismatch effects in Johnson noise thermometry Metrologia. 55 38–49. [Google Scholar]
- [79].Benz SP, Burroughs CJ and Dresselhaus PD 2000. Low harmonic distortion in a Josephson arbitrary waveform synthesizer Applied Physics Letters. 77. [Google Scholar]
- [80].Benz SP, Jifeng Q, Rogalla H, White DR, Dresselhaus PD, Tew WL and Sae Woo N 2009. Improvements in the NIST Johnson noise thermometry system IEEE Trans. Instrum. Meas 58 884–90. [Google Scholar]
- [81].Benz S, White DR, Qu J, Rogalla H and Tew W 2009. Electronic measurement of the Boltzmann constant with a quantum-voltage-calibrated Johnson noise thermometer Comptes Rendus Physique. 10 849–58. [Google Scholar]
- [82].Tew WL, Labenski JR, Nam SW, Benz SP, Dresselhaus PD and Burroughs CJ 2007. Johnson noise thermometry near the zinc freezing point using resistance-based scaling Int J Thermophys. 28 62945. [Google Scholar]
- [83].Labenski JR, Tew WL, Benz SP, Nam SW and Dresselhaus P 2008. A determination of the ratio of the zinc freezing point to the tin freezing point by noise thermometry Int J Thermophys. 29 1–17. [Google Scholar]
- [84].Tew WL, Benz SP, Dresselhaus PD, Coakley KJ, Rogalla H, White DR and Labenski JR 2010. Progress in noise thermometry at 505 K and 693 K using quantized voltage noise ratio spectra Int. J. Thermophys 31 1719–38. [Google Scholar]
- [85].Qu J, Benz SP, Pollarolo A, Rogalla H, Tew WL, White R and Zhou K 2015. Improved electronic measurement of the Boltzmann constant by Johnson noise thermometry Metrologia. 52 S242–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Callegaro L, D’Elia V, Pisani M and Pollarolo A 2009. A noise thermometer with traceability to electrical standards, Metrologia 46 409–415 [Google Scholar]
- [87].Coakley KJ and Qu J 2017. Spectral model selection in the electronic measurement of the Boltzmann constant by Johnson noise thermometry Metrologia. 54 204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Gallop J 2003. SQUIDs: Some limits to measurement Supercond. Sci. Tech. 16 1575–82. [Google Scholar]
- [89].Fagaly RL 2006. Superconducting quantum interference device instruments and applications Rev. Sci. Inst 77 101101 [Google Scholar]
- [90].Kamper RA and Zimmerman J 1971. Noise thermometry with the Josephson effect Journal of Applied Physics. 42 132–6. [Google Scholar]
- [91].Soulen RJ, Vechten DV and Seppä H 1982. Effect of additive noise and bandpass filter on the performance of a Josephson junction noise thermometer Rev. Sci. Inst. 53 1355–62. [Google Scholar]
- [92].Soulen RJ, Fogle WE and Colwell JH 1994. Measurements of absolute temperature below 0.75 K using a Josephson-junction noise thermometer J Low Temp Phys. 94 385–487. [Google Scholar]
- [93].Soulen RJ and Giffard RP 1978. Josephson‐effect absolute noise thermometer: Resolution of unmodeled errors Appl. Phys. Lett 32 770–2. [Google Scholar]
- [94].Gallop JC and Petley BW 1995. Josephson noise thermometry with HTS devices IEEE Trans. Instrum. Meas 44 234–7. [Google Scholar]
- [95].Soulen R, Fogle W and Colwell J 1992. A decade of absolute noise thermometry at NIST using a resistive squid Temperature: Its Measurement and Control in Science and Industry. Vol 6 Ed. Schooley JF (AIP, New York: ) 983–8. [Google Scholar]
- [96].Schuster G, Hechtfischer D, Buck W and Hoffmann A 1990. Consistency of low temperature scales and the temperature of the 3He melting pressure minimum Phys. B Physics of Cond. Mat 165 31–2. [Google Scholar]
- [97].Peden DA, Macfarlane JC, Hao L, Reed RP and Gallop JC 1999. YbCo-noble metal resistors for HTS Josephson noise thermometry IEEE Trans. Appl. supercond 9 4408–11. [Google Scholar]
- [98].Giffard RP, Webb RA and Wheatley JC 1972. Principles and methods of low-frequency electric and magnetic measurements using an rf-biased point-contact superconducting device J Low Temp Phys. 6 533–610. [Google Scholar]
- [99].Webb RA, Giffard RP and Wheatley JC 1973. Noise thermometry at ultralow temperatures J Low Temp Phys. 13 383–429. [Google Scholar]
- [100].Beyer J, Kirste A and Schurig T 2016. Squid-based thermometers in Encyclopaedia of Applied Physics (Wiley and VCH; Verlag Gmbh: ). [Google Scholar]
- [101].Vaughan RG, Scott NL and White DR 1991. The theory of bandpass sampling IEEE Trans. Sig. Proc 39 1973–84. [Google Scholar]
- [102].Casey A, et al. 2014. Current sensing noise thermometry: A fast practical solution to low temperature measurement J Low Temp Phys. 175 764–75. [Google Scholar]
- [103].Shibahara A, et al. 2016. Primary current-sensing noise thermometry in the millikelvin regime Philos Trans A Math Phys Eng Sci. 374 20150054. [DOI] [PubMed] [Google Scholar]
- [104].Rothfuss D, Reiser A, Fleischmann A and Enss C 2016. Noise thermometry at ultra-low temperatures Phil. Trans A Math Phys Eng Sci 374 20150051. [DOI] [PubMed] [Google Scholar]
- [105].Lusher CP, et al. 2001. Current sensing noise thermometry using a low tc dc squid preamplifier Meas. Sci. and Technol. 12 1 [Google Scholar]
- [106].Casey A 2003. Current-sensing noise thermometry from 4.2 k to below 1 mK using a dc squid preamplifier Physica B: Condensed Matter. 329–333 1556–9. [Google Scholar]
- [107].Beyer J, Drung D, Kirste A, Engert J, Netsch A, Fleischmann A and Enss C 2007. A magnetic-field-fluctuation thermometer for the mK range based on squid-magnetometry IEEE Trans. Appl. Supercond 17 760–3. [Google Scholar]
- [108].Engert J, Beyer J, Drung D, Kirste A and Peters M 2007. A noise thermometer for practical thermometry at low temperatures Int J Thermophys. 28 1800–11. [Google Scholar]
- [109].Engert J, Beyer J, Drung D, Kirste A, Heyer D, Fleischmann A, Enss C and Barthelmess HJ 2009. Practical noise thermometers for low temperatures J. Phys. Conf. Ser 150 012012 [Google Scholar]
- [110].Engert J, Heyer D, Beyer J and Barthelmess HJ 2012. Noise thermometry at low temperatures: MFFT measurements between 1.6 K and 1 mK J. Phys. Conf. Ser 400 052003 [Google Scholar]
- [111].Engert J, Heyer D and Fischer J 2013. Low-temperature thermometry below 1 K at PTB. AIP Conf. Proc 1552 136–41. [Google Scholar]
- [112].Kirste A, Regin M, Engert J, Drung D and Schurig T 2014. A calculable and correlation-based magnetic field fluctuation thermometer J. Phys.: Conf. Sers 568 032012 [Google Scholar]
- [113].Kirste A and Engert J 2016. A squid-based primary noise thermometer for low-temperature metrology Phil. Trans A Math Phys Eng Sci. 374 20150050. [DOI] [PubMed] [Google Scholar]
- [114].Kirste A, Drung D, Beyer J and Schurig T 2008. Optimization of squid magnetometers and gradiometers for magnetic-field-fluctuation thermometers J. Phys.: Conference Series. 97. [Google Scholar]
- [115].MAGNICON, MFFT-1 Noise Thermometer, http://www.magnicon.com/fileadmin/download/datasheets/Magnicon_MFFT-1.pdf Downloaded October 21 2018.
- [116].Gallop J, Hao L and Reed R 1997. Qrnt: A primary thermometer based on an HTS SQUID Physica C: Superconductivity and its Applications. 282–287 2485–6. [Google Scholar]
- [117].Gallop JC, Hao L and Reed RP 1997. The quantum roulette noise thermometer Appl. Supercon 5 285–9. [Google Scholar]
- [118].Hao L, Gallop JC, Reed RP, Peden DA and Macfarlane JC 1998. The quantum roulette noise thermometer, in 1998 Conference on Precision Electromagnetic Measurements Digest p649–650 [Google Scholar]
- [119].Hao L, Gallop JC, Reed RP, Peden DA and Macfarlane JC 1999. HTS SQUID application as a quantum roulette noise thermometer IEEE Trans. Appl. Supercon 9 2971–4. [Google Scholar]
- [120].Hao L, Gallop JC, Macfarlane JC, Peden DA and Reed RP 1999. The quantum roulette noise thermometer IEEE Trans. Instrum. Meas 48 659–62. [Google Scholar]
- [121].Ling H, Peden DA, Macfarlane JC and Gallop JC 2001. Characterization of YbCo/Au/YbCo resistors for HTS Josephson noise thermometry IEEE Transactions on Instrumentation and Measurement. 50 314–7. [Google Scholar]
- [122].Lee RAM, Hao L, Peden DA, Gallop JC, Macfarlane JC and Romans EJ 2001. Quantum roulette noise thermometer: Progress and prospects IEEE Transactions on Applied Superconductivity. 11 859–62. [Google Scholar]
- [123].Schottky W 1918. Über spontane stromschwankungen in verschiedenen elektrizitätsleitern Ann. phys 362 541–67. [Google Scholar]
- [124].Spietz L, Lehnert KW, Siddiqi I and Schoelkopf RJ 2003. Primary electronic thermometry using the shot noise of a tunnel junction Science. 300 1929–32. [DOI] [PubMed] [Google Scholar]
- [125].Wyatt JL and Coram GJ 1999. Nonlinear device noise models: Satisfying the thermodynamic requirements IEEE Trans. Elec. Dev 46 184–93. [Google Scholar]
- [126].Callegaro L 2006. Unified derivation of Johnson and shot noise expressions Am. J. Phys 74 438–40. [Google Scholar]
- [127].Spietz LF, 2006. The shot noise thermometer, PhD dissertation, Yale University. [Google Scholar]
- [128].Song W, Chong Y and Kim K. Setup of shot noise measurement in a tunnel junction for noise thermometry. in 2008 Conference on Precision Electromagnetic Measurements Digest. p 138–39 [Google Scholar]
- [129].Sayer RA, Engerer JD, Sen S, Vidhyadhiraja NS and Fisher TS 2011. Low-frequency electrical noise thermometry for micro- and nano-scale devices, in Proc. ASME Congress p411–21. [Google Scholar]
- [130].Park J, Rehman M, Choi JS, Khim ZG, Ryu SW, Song W and Chong Y. 2010. Development of a broadband shot noise measurement system at low-temperature for noise thermometry. in Conference on Precision Electromagnetic Measurements Digest p510–511 [Google Scholar]
- [131].Park JH, Rehman M, Choi JS, Ryu S-W, Khim ZG, Song W and Chong Y 2012. Broadband shot noise measurement system at low temperature for noise thermometry using a tunnel junction IEEE Trans. Instrum. Meas 61 205–11. [Google Scholar]
- [132].Park JH, 2012. Noise thermometry using a broadband radio-frequency measurement at low temperatures, PhD dissertation Seoul National University [Google Scholar]
- [133].Anderson MH, Ensher JR, Matthews MR, Wieman CE and Cornell EA 1995. Observation of bose-einstein condensation in a dilute atomic vapor Science. 269 198–201. [DOI] [PubMed] [Google Scholar]
- [134].Gati R, Esteve J, Hemmerling B, Ottenstein TB, Appmeier J, Weller A and Oberthaler MK 2006. A primary noise thermometer for ultracold bose gases New J. Phys 8 189 [Google Scholar]
- [135].Gati R, Hemmerling B, Folling J, Albiez M and Oberthaler MK 2006. Noise thermometry with two weakly coupled bose-einstein condensates Phys Rev Lett. 96 130404. [DOI] [PubMed] [Google Scholar]
- [136].Gati R and Oberthaler MK 2007. A bosonic Josephson junction J. Phys. B: 40 R61–R89. [DOI] [PubMed] [Google Scholar]
- [137].Gottlieb AD and Schumm T 2009. Quantum noise thermometry for bosonic Josephson junctions in the mean-field regime Phys. Rev. A 79 063601 [Google Scholar]
- [138].Brodskii AD and Savateev AV 1960. A new method of absolute temperature measurements Meas. Tech 3 397–402. [Google Scholar]
- [139].Papoulis A 1984. Probability, Random Variables, and Stochastic Processes (McGraw-Hill, New York: ) p345–347. [Google Scholar]
- [140].Savateev AV 1962. Compensated thermal noise pulse thermometer Meas. Tech 5 114–20. [Google Scholar]
- [141].Fujishiro I, Mii H, Senowo M 1970. Noise thermometry for very high pressure use. In Proc Les propriétés physiques des solides sous pression: Grenoble, 8–10 septembre 1969 188: 457–460. [Google Scholar]
- [142].Jr RJS, Rusby RL and Vechten DV 1980. A self-calibrating rhodium-iron resistive SQUID thermometer for the range below 0.5 K J Low Temp Phys. 40 553–69. [Google Scholar]
- [143].Blalock TV, Roberts MJ and Shepard RL 1985. In situ calibration of nuclear plant resistance thermometers using Johnson noise, in Proc. of the Industrial Temperature Measurement Symposium. 1985. [Google Scholar]
- [144].Britton CL Jr., Roberts M, Bull ND, Holcomb DE and Wood RT 2012. Johnson noise thermometry for advanced small modular reactors. ORNL/TM-2012/346, SMR/ICHMI/ORNL/TR-2012/01. [Google Scholar]
- [145].Britton CL Jr, Bull ND and Roberts M 2014. Amplifiers module prototype for the Johnson noise thermometry system. ORNL/TM-2013/192, SMR/ICHMI/ORNL/TR-2012/03. [Google Scholar]
- [146].Britton C, Bull Ezell N D, Roberts M, Holcomb D and Wood R 2014. Johnson noise thermometry for drift-free measurements in Proc. ASME 2014 Small Modular Reactors Symposium pp. V001T02A010-V001T02A010 [Google Scholar]
- [147].De Groot M, Dubbeldam J, Brixy H, Edler F, Dhupia G and Chattle M. Development of a high temperature resistance thermometer using noise thermometry. in Proc. TEMPMEKO 1996, Ed. Marcarino P (Levrotto & Bell, Torino: ) [Google Scholar]
- [148].Borkowski CJ and Blalock TV 1974. A new method of Johnson noise thermometry Rev. Sci. Inst 45 151–62. [Google Scholar]
- [149].Oakes LC, Shepard RL 1988. Johnson noise thermometer for high radiation and high temperature environments, In Transactions of the Fifth Symposium on Space Nuclear Power Systems. [Google Scholar]
- [150].Seppä H and Varpula T 1993. Inductive noise thermometer: Theoretical aspects J. Appl. Phys 74 771–6. [Google Scholar]
- [151].Varpula T and Seppä H 1993. Inductive noise thermometer: Practical realization Rev. Sci. Inst 64 1593–600. [Google Scholar]
- [152].Pearce J, Greenen A, Bramley P and Cruickshank D. 2015. Towards a practical Johnson noise thermometer for long-term measurements in harsh environments. in Proc. 4th International Conference on Advancements in Nuclear Instrumentation Measurement Methods and their Applications p1–4 [Google Scholar]
- [153].Bramley P, Cruickshank D and Pearce J 2017. The development of a practical, drift-free, Johnson-noise thermometer for industrial applications Int J Thermophys 38 25 [Google Scholar]
- [154].Johnson Noise thermometer Metrosol, URL: http://www.johnson-noisethermometer.com/index.html (21 Oct. 2018)
- [155].Brixy H, Rittinghaus KF, Gaertner KJ and Hecker R, 1974. Developments in the area of noise thermometry at KFA-Juelich; In Proc. International high temperature, in-pile thermometry colloquium, Petten Netherlands, 23–13 Dec 1974; ORNL-TR-2904; CONF-741226–2. KFA Julich (Germany) [Google Scholar]
- [156].Brixy H, Hecker R, Rittinghaus K and Howener H 1982. Application of noise thermometry in industry under plant conditions In Temperature, Its Measurement and Control in Science and Industry, Vol 5. Ed. Schooley JF (AIP, New York: ) 1225–37. [Google Scholar]
- [157].Brixy H, Mallinckrodt DV and Lynen A 1983. Creamics as materials for measurement resistors in noise thermometry High Temperatures-High Pressures. 15 139–46. [Google Scholar]
- [158].Brixy H, Hecker R, Oehmen J and Zimmermann E 1991. Temperature measurements in the high-temperature range (1000–2000 °c) by means of noise thermometry. High Temperatures-High Pressures. 23 625–631 [Google Scholar]
- [159].Lopez Legrand A and Villard JF 2011. Noise thermometry for nuclear applications IEEE Trans. Nucl Sci 58 156–60. [Google Scholar]
- [160].Blalock TV and Borkowski CJ 1978. High-level noise source for the calibration of Johnson noise power thermometers Rev. Sci. Instrum 49 1046. [DOI] [PubMed] [Google Scholar]
- [161].Roberts MJ 1987. Cable parameter estimation based on impedance measurements at one end Rev. Sci. Inst 58 681–6. [Google Scholar]
- [162].Roberts MJ 1988. Comparison between two‐wire and three‐wire models for shielded twisted‐pair cables used in Johnson noise thermometry Rev. Sci. Inst 59 298–303. [Google Scholar]
- [163].Ezell NDB, Britton CL and Roberts M 2017. Authentication of electromagnetic interference removal in Johnson noise thermometry ORNL/TM-2017/011. [Google Scholar]
- [164].Kisner R, Britton CL, Jagadish U, Wilgen JB, Roberts M, Blalock TV, Holcomb D, Bobrek M Ericson MN 2004. Johnson noise thermometry for harsh environments. in Proc. 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No.04TH8720). [Google Scholar]
- [165].Korsah Kofi, Ramuhalli Pradeep, Vlim Kisner, Roger A, Britton CL 2016. Assessment of sensor technologies for advanced reactors. ORNL/TM-2016/337 R1 [Google Scholar]
- [166].Holcomb DE, Johnson noise thermometry for space reactor temperature measurement, in AIP Conference Proceedings. 2004. p. 567–73. [Google Scholar]
- [167].Holcomb DE, Kisner RA, Bryan WL and Hardy JE 2006. Evaluation of the measurement technologies required for the Jupiter icy moons orbiter (JIMO) reactor, in Proc. 5th International Topical Meeting on Nuclear Plant Instrumentation Controls, and Human Machine Interface Technology. [Google Scholar]
- [168].Decreton M, Binard L, Delrez C, Hebel W and Schubert W 1980. High temperature measurements by noise thermometry High Temperatures - High Pressures, 12 395–402 [Google Scholar]
- [169].Decreton MC 1982. High temperature noise thermometry for industrial applications, In Temperature: Its measurement and control in science and Industry Vol 5, Ed. Schooley JF (AIP, New York: ) p1239–1243 [Google Scholar]
- [170].Billeter TR and Cannon CP 1982. Dual high-temperature measurements using Johnson-noise thermometry. In Temperature: Its measurement and control in science and Industry Vol 5, Ed. Schooley JF (AIP, New York: ) pp 1245–1247 [Google Scholar]
- [171].International Atomic Energy Agency 2005. The role of nuclear power and nuclear propulsion in the peaceful exploration of space. (IAEA, Vienna: ) [Google Scholar]
- [172].Truscello VC 1983. SP-100: The us space nuclear reactor power program. JPL9–1-88 [Google Scholar]
- [173].Demuth SF 2003. SP-100 Space reactor design Prog. Nucl. Energy 42 323–59. [Google Scholar]
- [174].Holcomb DE, Kisner RA and Britton CL 2005. Ab initio thermometry for long-term unattended space reactor operation. Proc, Space Nuclear Conference, San Diego, paper 1170 [Google Scholar]
- [175].Holcomb DE, Kisner RA, Britton CL 2006. Fundamental thermometry for long-term and high-temperature deployment in generation IV reactors. Proc. International Symposium on Future Instrumentation and Controls 2005. [Google Scholar]
- [176].Shepard RL and Weiss J M Use of SP-100 thermometry technology to improve operation of electric power plants. in Proc Energy Conversion Engineering Conference, 1996. [Google Scholar]
- [177].Gibson MA, Oleson SR, Poston DI and McClure P 2017. NASA’s kilopower reactor development and the path to higher power missions. NASA/TM—2017–219467 [Google Scholar]
- [178].Korobchenko YG and Ivashchenko YS 1982. Selectivity in measuring the thermodynamic temperature of an ionized gas with a noise thermometer based on a capacity transducer Meas. Tech. 25 240–1. [Google Scholar]
- [179].Baum DW, Gill SP, Shimmin WL and Watson JD 1981. Thermal noise emissions from a hot gas No. FR-153 ARTEC Associates Inc. Hayward Calif. CALIF, 1981. [Google Scholar]
- [180].Gill SP, Shimmin WL, and Watson JD. 1983. Noise Thermometry Measurements in Combustion Processes. No. ARTEC-13–176. ARTEC Associates Inc. Hayward Calif. CALIF, 1983. [Google Scholar]
- [181].Dobson PS, Mills G and Weaver JMR 2005. Microfabricated temperature standard based on Johnson noise measurement for the calibration of micro- and nano-thermometers Review of Scientific Instruments. 76. [Google Scholar]
- [182].Crossno J, Liu X, Ohki TA, Kim P and Fong KC 2015. Development of high frequency and wide bandwidth Johnson noise thermometry Appl. Phys. Lett 106.2, 023121. [Google Scholar]
- [183].Glattli DC, Jacques P, Kumar A, Pari P and Saminadayar L 1997. A noise detection scheme with 10 mK noise temperature resolution for semiconductor single electron tunnelling devices J. Appl. Phys 81 7350–7356. [Google Scholar]
- [184].Scandurra G, Cannatà G and Ciofi C. Fast johnson noise thermometry using a temperature dependent sensor. in 2012 IEEE International Instrumentation and Measurement Technology Conference. 2012. [Google Scholar]
- [185].Nicholas JV and White DR, 2001. Traceable Temperatures: An introduction to temperature measurement and calibration (John Wiley & Sons, New York: ) [Google Scholar]
- [186].Von Mallinckrodt D, Hausser H and Brixy H 1985. Ceramic resistors for noise thermometers High Temperatures.--High Pressures. 17 639–45. [Google Scholar]
- [187].Kerkhof O, Houtzager E, Wensveen J v and Maloney E 2008. Thermal noise sensor insulation using ultrathin ceramic coatings Int J Thermophys. 29 1156–65. [Google Scholar]
- [188].Pickup C 1982. A high-accuracy noise thermometer for the range 100–150 °C range, In Temperature: Its Measurement and Control in Science and Industry Vol 5, ED Schooley JF, (AIP, New York: ) p129–131. [Google Scholar]
- [189].Crovini L and Actis A. Systematic errors in high temperature noise thermometry. in Inst. Phys. Conf. Ser. 1975. pp398–408 [Google Scholar]
- [190].Crovini L and Actis A 1975. A precise variable level binary noise generator Alta Frequenza. 44 617–21. [Google Scholar]
- [191].Yamazawa K, Tew WL, Pollarolo A, Rogalla H, Dresselhaus PD, and Benz SP, 2013. Improvements to the Johnson Noise Thermometry System for Measurements at 505 – 800 K Temperature: Its Measurement and Control in Science and Industry. 8 (AIP Conf. Proc. 1552) 50–55. [Google Scholar]
- [192].Benz SP, Dresselhaus PD and Burroughs CJ 2011. Multitone waveform synthesis with a quantum voltage noise source IEEE Trans. Appl. Supercon 21 681–6. [Google Scholar]
- [193].Ezell NDB, Britton C, Ericson N, Holcomb D, Roberts MJ, Djouadi S and Wood R 2018. A novel technique applying spectral estimation to Johnson noise thermometry Nucl Technol. 202 173–9. [Google Scholar]
- [194].White D and Mason R 2004. An EMI test for Johnson noise thermometry Proc. TEMPMEKO 2004 Ed. Zvizdic D (university of Zagreb, Zagreb: ) pp485–90. [Google Scholar]
- [195].Zhang X, Chen D 2015. An integrated circuit solution of thermal noise thermometer with cascaded pre-amplifier and 6-bit resolution analog-to-digital converter. IEEE Circuits and Systems (ISCAS), 2015 IEEE International Symposium. [Google Scholar]