Abstract
Time-resolved functional connectivity (trFC) assesses the time-resolved coupling between brain regions using functional magnetic resonance imaging (fMRI) data. This study aims to compare two techniques used to estimate trFC to investigate their similarities and differences when applied to fMRI data. These techniques are the sliding window Pearson correlation (SWPC), an amplitude-based approach, and phase synchronization (PS), a phase-based technique.
To accomplish our objective, we used resting-state fMRI data from the Human Connectome Project (HCP) with 827 subjects (repetition time: 0.72s) and the Function Biomedical Informatics Research Network (fBIRN) with 311 subjects (repetition time: 2s), which included 151 schizophrenia patients and 160 controls.
Our simulations reveal distinct strengths in two connectivity methods: SWPC captures high-magnitude, low-frequency connectivity, while PS detects low-magnitude, high-frequency connectivity. Stronger correlations between SWPC and PS align with pronounced fMRI oscillations. For fMRI data, higher correlations between SWPC and PS occur with matched frequencies and smaller SWPC window sizes (~30s), but larger windows (~88s) sacrifice clinically relevant information. Both methods identify a schizophrenia-associated brain network state but show different patterns: SWPC highlights low anti-correlations between visual, subcortical, auditory, and sensory-motor networks, while PS shows reduced positive synchronization among these networks.
In sum, our findings underscore the complementary nature of SWPC and PS, elucidating their respective strengths and limitations without implying the superiority of one over the other.
Keywords: phase synchrony, sliding window Pearson correlation, dynamic functional connectivity, time-resolved functional network connectivity, amplitude demodulation, phase demodulation
1. INTRODUCTION.
The study of functional connectivity (FC) offers significant insights into inter-network communication within the brain using functional magnetic resonance imaging (fMRI) (Biswal, Yetkin et al. 1995, Lowe, Dzemidzic et al. 2000, Fingelkurts, Fingelkurts and Kähkönen 2005, Bastos and Schoffelen 2016). FC and functional network connectivity (FNC) - functional connectivity between whole brain intrinsic fMRI networks have uncovered several key findings about intrinsic blood oxygenation level-dependent (BOLD) brain activity, particularly through resting-state fMRI (rsfMRI), and have provided valuable information about various brain disorders, including but not limited to schizophrenia (Calhoun, Kiehl et al. 2004, Lynall, Bassett et al. 2010, Sheffield and Barch 2016), Alzheimer’s disease (Allen, Barnard et al. 2007, Chhatwal, Schultz et al. 2013, Sheline and Raichle 2013), and depression (Veer, Beckmann et al. 2010, Zeng, Shen et al. 2012, Mulders, van Eijndhoven et al. 2015). Numerous methods exist for quantifying FC/FNC between brain network time series, including Pearson correlation (Greicius, Krasnow et al. 2003, Damoiseaux, Rombouts et al. 2006), partial correlation (Sun, Miller and D’esposito 2004), mutual information (Calhoun, Kim and Pearlson 2003, Wang, Alahmadi et al. 2015, Salman, Vergara et al. 2019, Mohanty, Sethares et al. 2020, Motlaghian, Belger et al. 2022), phase locking value (Zhang, Pan et al. 2016), and dynamic time warping (Meszlényi, Hermann et al. 2017, Linke, Mash et al. 2020, Wiafe, Faghiri et al. 2024, Wiafe, Faghiri et al. 2024, Wiafe, Kinsey et al. 2024), among others.
Over the past few years, there has been a growing body of research extending FC studies to capture FC in a temporally resolved manner (Chang and Glover 2010, Sakoğlu, Pearlson et al. 2010, Hutchison, Womelsdorf et al. 2013, Allen, Damaraju et al. 2014). This approach, often referred to as time-resolved functional connectivity (trFC) (Calhoun, Miller et al. 2014, Iraji, Faghiri et al. 2020), time-varying functional connectivity (Lurie, Kessler et al. 2020), or dynamic functional connectivity (dFC) (Hutchison, Womelsdorf et al. 2013), reveals how brain networks are coupled over time. Supported by the notion that the brain is a highly complex dynamic system (Kelso 1995, Telesford, Simpson et al. 2011) with intricate inter-network connections (Achard, Salvador et al. 2006, Van den Heuvel and Sporns 2013, Sporns 2016) across different spatiotemporal scales (Majeed, Magnuson and Keilholz 2009, Iraji, Fu et al. 2019), trFC has provided a deeper understanding of brain function and organization (Hutchison, Womelsdorf et al. 2013, Allen, Damaraju et al. 2014) and complex concepts such as consciousness (López-González, Panda et al. 2021, Panda, Thibaut et al. 2022). The term ‘time-resolved functional network connectivity’ (trFNC) is typically used when intrinsic networks from the fMRI data are used.
Several methods for estimating trFC exist, such as sliding window Pearson correlation (SWPC) (Allen, Damaraju et al. 2014, Leonardi and Van De Ville 2015), cross wavelet coherence (Chang and Glover 2010, Yaesoubi, Allen et al. 2015), phase synchrony (PS) (Pedersen, Omidvarnia et al. 2018, Honari, Choe et al. 2020), coactivation patterns (Eickhoff, Bzdok et al. 2011, Liu, Zhang et al. 2018), hidden Markov models (Zhang, Cai et al. 2020, Hussain, Langley et al. 2023) and other window-based approaches based on Spearman and Kendall correlation (Savva, Mitsis and Matsopoulos 2019, Torabi, Mitsis and Poline 2024), and mutual information (Savva, Mitsis and Matsopoulos 2019, Torabi, Mitsis and Poline 2024),
Traditionally recognized as a prominent measure of time-resolved functional connectivity in the field of neuroscience, SWPC excels in quantifying the time-varying connectivity of different brain regions (Sakoğlu, Pearlson et al. 2010, Handwerker, Roopchansingh et al. 2012, Jones, Vemuri et al. 2012, Tagliazucchi, Von Wegner et al. 2012, Hutchison, Womelsdorf et al. 2013, Hutchison, Womelsdorf et al. 2013, Keilholz, Magnuson et al. 2013, Allen, Damaraju et al. 2014, Calhoun, Miller et al. 2014, Zalesky, Fornito et al. 2014, Du, Fryer et al. 2018, Faghiri, Stephen et al. 2018, Mokhtari, Akhlaghi et al. 2019, Iraji, Faghiri et al. 2020, Faghiri, Adali and Calhoun 2022, Kazemivash and Calhoun 2022, Faghiri, Yang et al. 2023). While SWPC has gained considerable acceptance as a reliable measure for brain connectivity, it is important to note that it specifically captures linear co-variations related to the signal. This means that SWPC is adept at identifying instances where brain regions activate simultaneously in a linear and directly proportional manner.
Recently, Pedersen et al. compared SWPC with a more recently used technique for fMRI data, phase synchrony (Pedersen, Omidvarnia et al. 2018). PS measures the synchronization of neural activities based on the timing of their phase relationships (Lachaux, Rodriguez et al. 1999, Mormann, Lehnertz et al. 2000, Laird, Carew and Meyerand 2001, Varela, Lachaux et al. 2001, Laird, Rogers et al. 2002, Deshmukh, Shivhare et al. 2004, Costa, Rognoni and Galati 2006, Pockett, Bold and Freeman 2009, Fell and Axmacher 2011, Glerean, Salmi et al. 2012, Sun, Hong and Tong 2012, Bolt, Nomi et al. 2018, Kumar, Reddy and Behera 2018, Pedersen, Omidvarnia et al. 2018, Honari, Choe et al. 2020). PS is typically computed by estimating the phase of the signal and finding the phase difference. The most commonly used approach to estimating the instantaneous phase of a signal is to employ the analytic signal approach based on the Hilbert transform (Bedrosian 1962) , while others use wavelet transforms (Boashash 1992).
Pedersen et al. compared these two methods by quantifying the average Spearman correlation between PS and SWPC with varying window sizes, highlighting their similarities using fMRI data (Pedersen, Omidvarnia et al. 2018). However, the PS method they used employed an all-positive phase synchronization measure, overlooking anti-synchronization estimations. To make PS comparable to SWPC, Pedersen et al. computed the correlation between the all-positive PS measure and the absolute values of SWPC (Pedersen, Omidvarnia et al. 2018). Honari et al. emphasized the benefits of using a PS measure that accounts for both positive and negative values by employing the cosine function instead of the sine function (Honari, Choe et al. 2020). Additionally, while Pedersen’s findings are insightful, averaging the correlations between the two methods does not provide insights into their temporal dependencies. In magnetoencephalography (MEG) studies, the concepts of amplitude coupling and phase coupling have been shown to reflect at least partially distinct neuronal mechanisms (Siems and Siegel 2020). Furthermore, previous study shows that the correlation between SWPC and PS is time-dependent (Wiafe, Fu et al. 2023) in fMRI data, indicating the need for a more nuanced analysis to understand the time-resolved relationships between these measures.
Our primary objective is to compare these two methods in a time-varying manner while addressing the above concerns. In contrast to earlier work claiming that phase synchrony is preferable to SWPC (Pedersen, Omidvarnia et al. 2018), we show through simulations and fMRI analysis that these two methods offer complementary insights into time-resolved functional connectivity. Also, from the perspective of signals and communication theory, these methods depend on different fundamental aspects of a signal: SWPC is amplitude-based, while PS is phase-based. By studying trFC through the lens of communication theory, we aim to shed more light on the complementary information offered by these two methods. This approach can provide deeper insights into how brain networks communicate and interact over time, shedding light on their time-resolved relationships and functional organization. Our study employs independent component analysis (ICA) to extract intrinsic brain networks from the fMRI data (Calhoun, Adali et al. 2001, Du, Fu et al. 2020).
Our paper is structured as follows: we continue with a background section comparing the two methods to communication system demodulation techniques. We then present simulations to highlight the complementary information identified by each method. We demonstrate the consistency of time-resolved correlations between SWPC and PS with the spectral properties of fMRI data across two datasets. We also explore the clinically relevant insights each method offers for Schizophrenia. Finally, we discuss the complementary nature of the approaches, noting that neither is superior. We provide MATLAB code for all analyses.
2. BACKGROUND.
Some studies have suggested the similarity between the trFNC measures: SWPC with amplitude demodulation (Faghiri, Iraji et al. 2022) and PS with phase demodulation (Wang and Da 2012). In communication theory, modulation is a technique used to transmit signals effectively from one point to another (Haykin and Moher 1989). Modulation is a process where some property of a waveform, often called the carrier wave, which usually has a single frequency component (monochromatic), is changed by a signal wave containing information, a message/modulating signal, to be transmitted (Haykin and Moher 1989, Roden 1991). This process is often necessary to allow for multiple message signals, such as voice or video, to be transmitted without interfering with one another. Given this, the message signal is modulated onto a high-frequency carrier signal. The modulation can occur in various forms, such as amplitude modulation (AM), frequency modulation (FM), or phase modulation (PM), each affecting a different aspect of the carrier wave – its amplitude, frequency, or phase, respectively (Smillie 1999, Sharma, Mishra and Saxena 2010). These are the types of modulation schemes under analog modulation. The basic components of the analog modulation schemes are presented below.
| (1) |
Where is the carrier signal is the carrier signal amplitude, is the carrier signal frequency, is the message signal, Am is the message signal amplitude and is the message signal frequency.
2.1. Amplitude demodulation and sliding window Pearson correlation.
Amplitude modulation (AM) involves varying the strength of a carrier signal in proportion to a message signal. An amplitude-modulated signal can be expressed below:
| (4) |
The amplitude modulation method is a linear modulation scheme that is characterized by and relies on the superposition principle. When two modulating signals are summed and used to modulate a carrier, the resulting AM signal is equivalent to the sum of the AM signals produced by each modulating signal individually (Haykin and Moher 1989, Proakis, Salehi et al. 1994). This property demonstrates the linear behavior of AM in terms of superposition.
SWPC and amplitude modulation share similar subsystems with amplitude demodulation (Faghiri, Iraji et al. 2022). Based on this similarity, the application of a time-varying correlation method like the sliding window Pearson correlation is valuable for analyzing signals in accordance with the time-varying nature of the message signal . In this approach, segments where the carrier aligns closely with the modulated signal are highly correlated, indicating high amplitudes in the message signal. Conversely, segments with low correlation indicate where the carrier does not align closely with the modulated signal, suggesting a lower amplitude value in the message signal. This method highlights the efficacy of correlation in amplitude modulation (AM) demodulation. Given a message signal , carrier signal , and amplitude modulated signal , the relationship between and is given below:
| (5) |
Where is the message signal across the selected window size . It can be seen from the proof (see supplementary material 1) that SWPC estimates a normalized version of the message signal by assessing the degree of linear alignment between the carrier (i.e., ) and the modulated signal ().
2.2. Phase demodulation and phase synchrony
Phase modulation (PM) modulates the carrier signal’s phase with the message signal’s amplitude. Applying the superposition theorem, phase modulation introduces non-linearity due to the cosine function (Haykin and Moher 1989, Proakis, Salehi et al. 1994) and is shown in supplementary material 2. In PM, the modulated signal’s phase carries the information, and this phase must be decoded to retrieve the original message signal, phase demodulation. The phase synchrony method of finding the relation between the estimated phase two signals has a similar baseline of logic as phase demodulation. Comparing the instantaneous phase of the carrier signal with that of the modulated signal, the difference between their phases directly corresponds to the message signal. Mathematically, considering as the phase-modulated signal, the instantaneous phase of this signal is . By extracting this phase and comparing it with the phase of the unmodulated carrier wave, the message signal can be retrieved:
| (10) |
This method of demodulation relies on the precise measurement of phase differences. Small phase changes can lead to significant changes in position within the cycle, especially near the wrapping points where phase values repeat after a full cycle (360° or radians). Dealing with these wrap-around effects introduces non-linearity absent in linear amplitude variations.
2.3. SWPC and phase synchrony.
SWPC and phase synchrony represent distinct approaches in the analysis of neural activity. SWPC primarily examines relationships of brain networks’ signal strengths, aiding in the identification of co-activated brain regions over time. In contrast, phase synchrony delves into timing and phase relationships, offering insights into the synchronization of neural activities. Understanding these differences is essential for comprehending the complexity of neural dynamics and brain function.
We hypothesize that contrasting these two methods will shed light on the diverse nature of cognitive and functional processes in the brain, considering that they extract different information from a signal pair. For instance, certain cognitive tasks may demand precise timing synchronization between brain regions without necessitating simultaneously high levels of activation. Recognizing these patterns may help us understand the intricate workings of the brain and how different tasks mobilize neural networks in distinct ways.
3. DATA & DATA PROCESSING.
3.1. fMRI data
This study received approval from an ethics board, and all participants provided consent by signing a form approved by the institutional review board (IRB).
The first dataset used is the Function Biomedical Informatics Research Network (fBIRN) study, which includes resting fMRI data collected from schizophrenia patients and controls. Scans were collected at a repetition time (TR) of 2 seconds. The study led to a total of 160 controls with an average age of 37.04 ± 10.86 years, ranging from 19 to 59 years. Among these, 45 were female and 115 were male. Additionally, there were 151 patients diagnosed with schizophrenia, with an average age of 38.77 ± 11.63 years, ranging from 18 to 62 years. In this group, 36 were female and 115 were male. The typical controls and schizophrenic patients were meticulously matched in terms of age, gender distribution, and mean framewise displacement during scans (age: p = 0.18; gender: p = 0.39; mean framewise displacement: p = 0.97). Schizophrenic patients were in a clinically stable condition during the time of their scans. The fBIRN dataset is used to assess the similarity between SWPC and PS in relation to its clinical relevance to schizophrenia brain disorder.
The second dataset used in our study is the resting-state fMRI dataset collected from 827 subjects via the Human Connectome Project (HCP) database (Van Essen, Ugurbil et al. 2012, Van Essen, Smith et al. 2013). We utilized the first-session scans acquired using a Siemens Skyra 3T scanner with a multiband accelerated, gradient-echo echo-planar imaging (EPI) sequence. The scanning parameters were set to a repetition time (TR) of 0.72s, 72 slices, an echo time (TE) of 58ms, and a flip angle of 90°. A voxel size of 2 × 2 × 2 mm was used to acquire 1200 time points of fMRI data for each subject. Given the HCP dataset has an extensive participant pool, we use it as a validation dataset for the similarity between SWPC and PS.
3.2. fMRI pre-processing
fMRI data require extensive preprocessing to correct for various sources of noise and artifacts before analysis. The preprocessing steps commonly applied in fMRI studies include slice timing correction, realignment, spatial normalization, and spatial smoothing (Turner, Howseman et al. 1998, Penny, Friston et al. 2011, Esteban, Markiewicz et al. 2019). Following preprocessing, (Fu, Batta et al. 2024) we implemented the NeuroMark pipeline, a fully automated spatially constrained ICA on the preprocessed fMRI data (Du, Fu et al. 2020). Using the neuromark_fMRI_1.0 template (available in GIFT at http://trendscenter.org/software/gift or http://trendscenter.org/data) we generated 53 intrinsic connectivity networks (ICNs) for each subject. These ICNs are grouped into brain functional domains, including Subcortical (SC), Auditory (Aud), Sensorimotor (SM), Visual (Vis), Cognitive Control (CC), Default Mode (DM), and Cerebellum (Cb).
3.3. fMRI post-processing
To enhance the quality of these ICNs, we implemented detrending and despiking methods to eliminate drifts, sudden fluctuations, and significant artifacts that may have persisted after the initial preprocessing stages. The time series of the ICNs were bandpass-filtered in the range of 0.01 to 0.15 Hz, a frequency range in fMRI research that is suggested to be relevant for identifying brain domain BOLD signals (Braun, Plichta et al. 2012, Yaesoubi, Allen et al. 2015). An infinite impulse response (IIR) filter was designed using the butter function in MATLAB and applied via the filtfilt function to ensure zero phase shifts and preserve phase information (Oppenheim 1999, Proakis 2007, Caballero-Gaudes and Reynolds 2017). The optimal filter order was estimated using the Buttord function in MATLAB, which returns the lowest order of the Butterworth filter with no more than 3dB ripple in the passband and at least 30dB of attenuation in the stopband. Finally, we performed z-scoring on the ICNs. The MATLAB version used was MATLAB R2022a for all steps of the analysis.
4. METHOD
4.1. Sliding window Pearson correlation.
As previously discussed in the background section, the SWPC method calculates the Pearson correlation between signal pairs, sliding a defined window by one time point until covering all time points. This method is a standard approach for computing trFNC between brain regions (Hutchison, Womelsdorf et al. 2013, Allen, Damaraju et al. 2014, Mokhtari, Akhlaghi et al. 2019, Iraji, Faghiri et al. 2020, Faghiri, Iraji et al. 2022, Wiafe, Fu et al. 2023). Given a time series pair, and the sliding window Pearson correlation over a defined window of length is given below:
| (11) |
A key challenge in using SWPC is determining the optimal window length to effectively capture connectivity between a signal pair. SWPC’s sensitivity to window length has been well-documented (Hutchison, Womelsdorf et al. 2013). The selected window must be large enough to detect low connectivity yet small enough to identify transient connectivity (Sakoğlu, Pearlson et al. 2010, Leonardi and Van De Ville 2015). Leonardi and Van De Ville recommend using a minimum window length longer than the longest wavelength of the signal, approximately 100 seconds, particularly when the low-frequency cutoff is 0.01 Hz. Other studies have suggested that shorter window lengths, ranging from 20 to 60 seconds, could be viable for estimating trFNC in fMRI data (Shirer, Ryali et al. 2011, Zalesky and Breakspear 2015, Liégeois, Ziegler et al. 2016, Preti, Bolton and Van De Ville 2017, Pedersen, Omidvarnia et al. 2018).
In our study, we opt for a window size aligned with the −3dB cutoff frequency of the high-pass rectangular window filter subsystem of SWPC (Faghiri, Iraji et al. 2021, Faghiri, Yang et al. 2023, Wiafe, Fu et al. 2023), as detailed below:
| (2) |
where N is the window size and Fs is the sampling frequency (1/0.72s =1.39hz for HCP and 1/2s = 0.5hz for fBIRN). Due to the application of a bandpass filter, the high-pass cutoff should be higher than 0.01Hz, which results in a minimum N value of ~123 samples (~88s) for HCP and ~45 samples (~88s) for fBIRN.
4.2. Phase Synchrony.
Phase synchrony or synchronization is a phenomenon where the phases of two oscillating signals align over time. This concept has been instrumental in exploring functional connectivity, as evidenced by various studies (Lachaux, Rodriguez et al. 1999, Fell and Axmacher 2011, Glerean, Salmi et al. 2012, Omidvarnia, Pedersen et al. 2016, Bolt, Nomi et al. 2018, Pedersen, Omidvarnia et al. 2018). There are two primary approaches for analyzing phase synchrony: one involves a window-based approach, like SWPC, while the second method involves using the estimated instantaneous phase of signal pairs. The window-based approaches include techniques like phase locking value (Tass, Rosenblum et al. 1998, Rebollo, Devauchelle et al. 2018), circular-circular correlation (Jammalamadaka, Sengupta and Sengupta 2001), and Toroidal-Circular Correlation (Sojakova 2016, Zhan, Ma et al. 2019). The instantaneous phase approach employs metrics such as phase coherence, where the sine of the phase difference is employed (Pedersen, Omidvarnia et al. 2017, Pedersen, Omidvarnia et al. 2018) , and the cosine of relative phase, where the cosine of phase difference is employed (Cabral, Vidaurre et al. 2017, Honari, Choe et al. 2020, Vohryzek, Deco et al. 2020, Hancock, Cabral et al. 2022, Wiafe, Fu et al. 2023). Honari et al. provide comprehensive details on these methods and approaches.
In our study, we adopt the instantaneous phase approach, which necessitates estimating the instantaneous phase of signals for analyzing phase synchrony. We specifically utilize the cosine of the phase difference because it provides a readily comparable measure to SWPC. Positive values indicate high synchronization, while negative values suggest anti-synchronization, akin to correlation coefficients. Given a narrow-banded time series pair, and , phase synchrony computed by the cosine of relative phase is given below:
| (13) |
Where and represents the Hilbert transform. The Hilbert transform is commonly used for this estimation, provided that the Bedrosian theorem’s conditions are met. According to the Bedrosian theorem, successful phase extraction requires the spectral properties of the signal’s envelope and phase to be separate and distinct from each other (Bedrosian 1962, Xu and Yan 2006). The narrower the bandwidth of the signal, the more likely the Hilbert transform accurately models the signal (Boashash 1992, Delprat, Escudié et al. 1992, Picinbono 1997, Chavez, Besserve et al. 2006).
In this study, where the primary focus is to compare the performance of SWPC and phase synchrony, we adhere to standard practices concerning the choice of frequency band and bandwidth in fMRI analysis in phase synchrony measures. Extensive research suggests that the frequency band [0.04, 0.07]Hz is commonly regarded as the most reliable and functionally relevant for capturing meaningful neural activity (Biswal, Yetkin et al. 1995, Achard, Salvador et al. 2006, Glerean, Salmi et al. 2012). Glerean, Salmi et al. specifically employed this frequency band for computing phase synchrony due to its characteristics of yielding robust fMRI signals least affected by noise, as supported by prior studies (Biswal, Yetkin et al. 1995, Achard, Salvador et al. 2006, Buckner, Sepulcre et al. 2009). Furthermore, some studies have utilized a slightly broader frequency band of [0.03, 0.07]Hz (Pedersen, Omidvarnia et al. 2017, Pedersen, Omidvarnia et al. 2018). Pedersen, Omidvarnia et al. compared SWPC to phase synchrony using a measure based on 1 − abs(sin (φx(t) − φy(t))) emphasizing the strong relationship between SWPC and phase synchrony within the frequency band [0.03, 0.07]Hz. We opt for the same frequency band [0.03, 0.07]Hz to highlight both the disparities and complementary aspects between SWPC and phase synchrony methods rather than focusing on their similarities, as demonstrated by Pedersen, Omidvarnia, et al., given our study’s alignment with their objectives.
4.3. SWPC and PS using synthesized data.
We assessed SWPC and phase synchrony using synthesized data across three scenarios to highlight their complementary nature. In the first scenario, we show that phase synchrony effectively captures connectivity characterized by weak coupling at high frequencies, where SWPC may not perform as well. Phase-based methods excel in examining synchronization among weakly coupled oscillators, supported by studies like the Kuramoto model and others (Rosenblum, Pikovsky and Kurths 1996, Kopell and Ermentrout 2002, Dorfler and Bullo 2012, Schwemmer and Lewis 2012, Thümler, Srinivas et al. 2023). This aligns with findings that weak coupling is best explained by “phase-only” models (Fagerholm, Moran et al. 2020) and that weak synaptic coupling can show high-frequency synchronization (Lee and Sepulchre 2024). We generated time-resolved connectivity ground truth with low magnitudes and high frequencies to demonstrate phase synchrony’s superiority over SWPC.
In the second scenario, we show that SWPC captures low-frequency connectivity with strong coupling, which phase synchrony may miss. Fagerholm et al. found that anesthetized brain states depend on oscillator amplitudes, favoring “amplitude-only” models (Fagerholm, Moran et al. 2020). This aligns with studies showing simpler, more stable anesthetic neuronal dynamics (Scott, Fagerholm et al. 2014, Fagerholm, Scott et al. 2016). They also demonstrated that phase models fail with strong coupling (Fagerholm, Moran et al. 2018). Thus, we generated connectivity ground truth with high magnitudes and low frequencies to highlight SWPC’s advantages.
In the third scenario, we aimed to merge scenarios 1 and 2 by creating time-resolved connectivity characterized by mid-strength and mid-frequency range. Both phase synchrony and SWPC are anticipated to accurately estimate connectivity in this scenario.
4.3.1. Scenario 1: Weak high-frequency connectivity encoded in phase.
We initiate the procedure by generating two bandlimited signals and . and are expressed below:
| (14) |
For we generate a high-frequency bandlimited phase signal in the frequency range of from a Gaussian distribution with a mean of zero, expressed as Here denotes the central frequency, represents a random phase deviation signal, and is the connectivity signal which is a high-frequency bandlimited signal with frequency range of with a maximum amplitude of 0.3 also generated from a Gaussian distribution with a mean of zero. We encode the connectivity into the phase of by combining with within . Concurrently, we generate a low-frequency random signal , bandlimited to the frequency range of so that its frequency does not overlap with . The signal is created similarly, where we generate another low-frequency random signal and a high frequency phase signal . We use a cosine function for to ensure that the phase synchrony using the cosine of the phase difference yields . This scenario creates a phase modulation scenario where the message signal (time-resolved connectivity) is encoded in the phase of the signal. The process of generating scenario one is illustrated in Figure 1. Finally, Gaussian noise is added to both and to achieve a signal-to-noise ratio (SNR) of 20dB, which is within the reported SNR range of the fMRI time series (Welvaert and Rosseel 2013). To assess SWPC and phase synchrony in this scenario, we compute SWPC across multiple window sizes and phase synchrony across multiple filtering frequency bands between 100 randomized iterations of and and compare their respective results to the ground truth connectivity .
Figure 1.
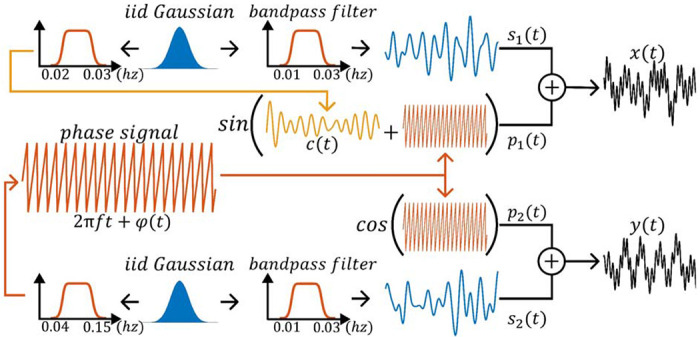
illustrates the pipeline for Scenario 1. A weak high-frequency time-resolved connectivity is encoded in the phase of the output signals. To prevent the amplitude of the signals from encoding the low-amplitude high-frequency time-resolved connectivity ground truth, random Gaussian signals with non-overlapping frequencies are introduced and added to the phase signals.
4.3.2. Scenario 2: Strong low-frequency connectivity encoded in amplitude.
In scenario 2, we adhere to the methodology utilized by Faghiri, Yang et al. for generating time-resolved connectivity between pairs of band-limited signals encoded in their amplitudes using Cholesky decomposition (Schmittmann, Jahfari et al. 2015, Kang, Ombao et al. 2017, Pedersen, Omidvarnia et al. 2018, Faghiri, Yang et al. 2023). This methodology involves the creation of two random time series, which are subsequently bandlimited to a frequency range of . To establish a time-resolved connectivity in the amplitudes of and , we generate as a low-frequency time-resolved connectivity signal, bandlimited to the frequency range of , with an amplitude of 0.9. Subsequently, is utilized to construct a time-varying covariance matrix in the following form:
| (15) |
Cholesky decomposition is employed to decompose this covariance matrix at each time point. The resulting upper triangular matrix is then multiplied by and , thereby encoding a time-resolved connectivity of at time t between and . This scenario creates an amplitude modulation scenario where the message signal (connectivity) is encoded in the amplitude of a signal. The process of scenario 2 is illustrated in Figure 2. Similarly to scenario 1, Gaussian noise with a mean of zero and a standard deviation corresponding to an SNR of 50dB is added to and . We evaluate SWPC and phase synchrony by computing SWPC across multiple window sizes and phase synchrony across multiple bandwidths between 100-sample pairs of and and compared their respective results to the ground truth connectivity .
Figure 2.
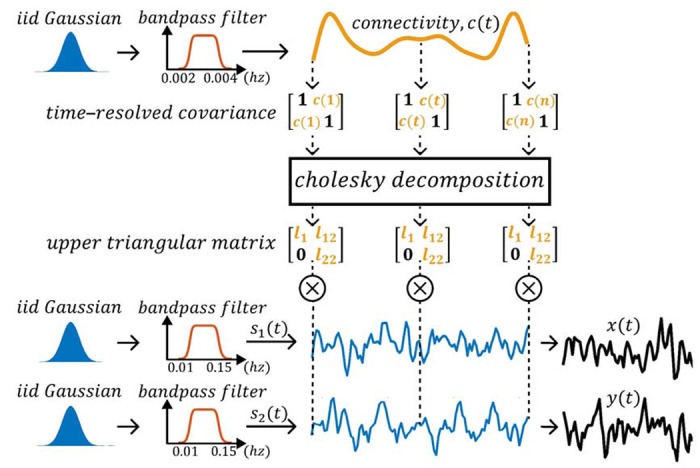
illustrates the pipeline for Scenario 2. Strong low-frequency time-resolved connectivity, modulated by the amplitude of the signals using Cholesky decomposition, is depicted. Firstly, two bandlimited random signals are generated and modulated by the time-resolved upper triangular Cholesky decomposed matrices derived from the strong low-frequency time-resolved connectivity. This process generates two signals with the ground truth time-resolved connectivity encoded in their amplitudes.
4.3.3. Scenario 3: Mid-strength mid-frequency connectivity encoded in both amplitude and phase.
In scenario 3, we follow a methodology similar to scenario 1. However, in this case, after encoding into such that the phase difference between and yields c(t), we also encode into the low-frequency signal such that is not random like in scenario 1. We employ the technique used in scenario two by utilizing the upper triangular matrix from the Cholesky decomposed covariance matrix to generate and such that their amplitudes exhibit time-resolved connectivity . Here, we select a midfrequency band range for in the range of with a mid-coupling amplitude of 0.6. Subsequently, similar to scenarios 1 and 2, and are constructed by summing their respective and signals. As in the previous scenarios, Gaussian noise is added to achieve an SNR of 50dB. We then evaluate Sliding Window Pearson Correlation (SWPC) and phase synchrony between 100-sample pairs of and across multiple window sizes and bandwidths, respectively.
All filtering is done with a Butterworth bandpass filter. The filter’s design aims for a maximum attenuation of 3 decibels in the passband and a minimum of 30 decibels in the stopband. The window sizes used for evaluating SWPC are 15s, 45s, 75s, 105s, and 135s, while the bandwidths used for evaluating phase synchronization are 0.01-0.04Hz, 0.03-0.07Hz, 0.05-0.09Hz, 0.07-0.11Hz, and 0.09-0.13Hz.
4.4. Matching parameters
Comparing amplitude-based SWPC with phase-based PS poses challenges due to their inherent differences. SWPC requires a window size, resulting in a shorter time-resolved connectivity time series compared to the original length. PS, employing the Hilbert transform, offers instantaneous measurement, complicating alignment for comparison. Without imposing a window for PS, studying time-resolved similarity becomes impractical. Yet, enforcing a window alters the measure, potentially skewing comparison accuracy. For a low-frequency cutoff of 0.01 Hz, a window size exceeding 88 seconds is recommended to capture the signal’s lowest frequency content (Faghiri, Iraji et al. 2021). To align SWPC with PS, we select two bandwidths (0.01-0.15 Hz and 0.03-0.07 Hz) and corresponding window sizes. Utilizing equation (2) for a low-frequency cutoff of 0.03 Hz, we derive a 30-second window size suited to capture activity within the narrower bandwidth of 0.03-0.07 Hz.
Comparing PS, typically focused on a narrow bandwidth (around 0.03-0.07 Hz) for fMRI data, with SWPC, which operates across all frequencies, presents challenges. While PS limits analysis to a specific frequency range, potentially excluding relevant neuronal information in broader frequency bands, SWPC captures connectivity across all frequencies without such constraints. This discrepancy complicates the comparison. Should SWPC be adjusted to match PS’s narrow bandwidth, sacrificing its ability to capture broad connectivity? Alternatively, maintaining SWPC’s full bandwidth may introduce biases. For PS, we adhere to the standard 0.03-0.07 Hz bandwidth. For SWPC, we compute connectivity across the broader BOLD-relevant frequency range (0.01-0.15 Hz) and within the same narrow band used for PS, enabling direct comparison.
Using cosine in PS raises concerns about potential information loss, which is not always justified in the literature. While it offers interpretability by indicating strong synchrony for small phase differences, it masks true differences. For example, the cosine of or 7 both yield approximately 0.7. Despite aligning with SWPC, cosine diminishes information from phase differences.
To align PS with windowed SWPC, a moving median is more suitable than a moving average. It ensures alignment while preserving PS’s ability to capture transient interactions. Some information loss occurs, but it’s less severe than with a moving average.
4.5. Time-resolved comparison between SWPC and PS.
For each subject, trFNC is computed using both PS and SWPC methods. These computations are carried out with the specified parameters and the moving median matching technique described above. The computation is conducted across all 53 unique intrinsic brain network pairs obtained from the Neuromark pipeline. To compare the two methods, the brain network pairs are vectorized for each subject, resulting in a time(window) × features matrix. Here, features represent the vectorized brain network pairs. For each time window of trFNC, the Spearman correlation between SWPC and PS features is computed, yielding time-resolved correlation coefficients between SWPC and PS across features. Spearman correlation was used to compare SWPC and PS because their distributions do not follow a normal distribution (see supplementary material 3) (Hauke and Kossowski 2011). These temporal correlation coefficients depict how SWPC and PS correlate over time for each subject. After obtaining the time-resolved correlation between PS and SWPC for all subjects, these correlation coefficients are separated into five bins based on their values: 0-0.2, 0.2-0.4, 0.4-0.6, 0.6-0.8, and 0.8-1 (no negative values were estimated in our data). These bins illustrate the time windows of trFNC where SWPC and PS are highly correlated and where they are not, according to their discretized correlation bins. For each correlation coefficient bin, the trFNC estimates of SWPC and PS are segregated into their respective bins of correlations, resulting in five sets of trFNC estimates for each method, representing each correlation bin.
To gain insight into the differences between the two methods from the fMRI data, we extract fMRI time points within the windowed trFNC that fall within each Spearman correlation bin. Subsequently, for each timepoint corresponding to a respective correlation bin, we define the same window size applied in trFNC estimations to the fMRI time series centered at that time point. We then computed the power spectral density (PSD) for these windows. Specifically, we conducted a short-time Fourier transform of the fMRI data utilizing the identical window size employed in the trFNC methods. Next, we averaged all power spectra across all time windows, brain networks, and subjects that fall into a given correlation bin. This process resulted in a single PSD representing each correlation bin of interest. This approach allows us to observe how the PSD patterns change based on the correlation between the two methods, potentially providing insight into why these methods may be similar or dissimilar from the data’s power spectrum.
Given the significance of window size selection in short-time power spectrum analysis and its impact on frequency resolution in PSD estimations, we delineate three distinct cases for comparative analysis. In case 1, we utilize the fMRI BOLD relevant frequency range of 0.01-0.15 Hz with a corresponding window size of 88 seconds for SWPC, while a frequency band of 0.03-0.07 Hz is employed for PS, as discussed previously. For case 2, we align the frequency content of both methods by utilizing the 0.03-0.07 Hz frequency band, with a corresponding window size of 30 seconds. To address concerns regarding frequency resolution in case 2, we introduce the third case. In case 3, we maintain the same frequency band as in case 2 but opt for a window size of 88 seconds as in case 1. We conduct all subsequent analyses using these three cases to offer a more comprehensive understanding of their complementary nature, recognizing that no single matching or compensation technique may be adequate to represent the complementary nature of the two methods.
4.6. Group analysis with SWPC and PS.
To explore the complementary advantages of SWPC and PS, our goal is to leverage the complementary aspects of both methods to gain insights into brain disorders, specifically schizophrenia. Firstly, we compute the average trFNC within each correlation, which is estimated by both SWPC and PS independently. By computing the average connectivity across correlation bins, we can observe the differences in connectivity estimation between the two methods, thereby gaining insights into their average estimations within each correlation bin. For this analysis, we use the fBIRN dataset, focusing specifically on case 1 as described above. In this case, the bandwidth of fMRI for SWPC is set to 0.01 – 0.15 Hz with a window size of 88 seconds, while the bandwidth for PS is set to 0.03 – 0.07 Hz, using a median window of 88s to match it to SWPC.
Furthermore, we extend our analysis of trFNC by incorporating additional steps involving clustering. The aim is to extract recurring patterns (k-means cluster centroids), commonly referred to as brain functional states (Allen, Damaraju et al. 2014). Therefore, after computing the SWPC and PS for the fBIRN dataset, we independently apply k-means clustering to the time-resolved connectivity estimations obtained from each method to identify these recurring patterns.
For this analysis, we continue to use the parameters from case 1: the bandwidth of fMRI for SWPC is set to 0.01 – 0.15 Hz with a window size of 88 seconds, while for PS, the bandwidth is set to 0.03 – 0.07 Hz. However, unlike previous steps, we do not crop the PS estimation using a moving median window. This approach ensures that the results from PS are not compromised by forcing them to match the windowing parameters of SWPC, thereby maintaining the integrity of the PS method and allowing for a fair comparison of the recurring patterns identified by each method.
The k-means clustering is employed with the city-block distance metric, which is preferable for high-dimensional data (Aggarwal, Hinneburg and Keim 2001). We chose 4 clusters for PS and SWPC based on the ratio of the within-cluster sum of squared distances (WSS) to the between-cluster sum of squared distances (BSS) (see supplementary material 4 for elbow criteria plots).
The k-means clustering is performed on the full fBIRN dataset, including controls (CN) and schizophrenia (SZ) groups. After clustering, we segregate the clusters based on group membership (CN and SZ) to allow for a direct comparison between the two groups. Two-sample t-tests are further performed on the clusters obtained from PS and SWPC to compare the CN and SZ groups. To control for false positives induced by multiple comparisons, we employ false discovery rate (FDR) correction using the Benjamini-Hochberg procedure (Benjamini and Hochberg 1995). Following common conventions, we employed a significance threshold set at an FDR-adjusted p-value of less than 0.05. This is used for all statistical tests employed in this study.
Furthermore, we computed the average duration that each subject remains within a cluster/state after entering it, known as the mean-dwell time (MDT) (Iraji, Faghiri et al. 2020), and the average percentage of time a subject stays within a cluster/state, known as the fraction rate (FR) (Iraji, Faghiri et al. 2020). To assess the differences between the CN and SZ groups captured by SWPC and PS, we performed a two-sample t-test on the MDT and FR metrics between schizophrenic patients and controls.
Finally, to highlight the complementary nature of SWPC and PS, we analyze how the two methods vary in similarity by quantifying the occupancy of each state obtained from k-means clustering based on the correlation between SWPC and PS. Using the same correlation bins employed in the previous analysis, for each state, we quantify the percentage of each correlation bin that is comprised in that state. In this analysis, a few time points will not belong to any correlation bin in the states obtained from PS since we do not crop PS using a moving median to match it to SWPC before performing k-means clustering. We observed that applying a moving median cropping technique to match PS to SWPC results in a loss of significant information, particularly in the significant differences identified by the PS method in all three cases used in previous analyses (see supplementary material 5). Therefore, to preserve the integrity of PS, we retain these time points. This approach ensures that the PS method’s unique insights are not compromised, allowing for a robust comparison of the complementary aspects of SWPC and PS.
5. RESULTS.
5.1. SWPC and PS using synthesized data.
The evaluation of SWPC and PS across various window sizes and frequency bandwidths aims to demonstrate their complementary nature by highlighting their strengths, weaknesses, and similarities. In scenario 1, the ground truth time-resolved connectivity has a low magnitude (indicating weak coupling) and is characterized by a high frequency. Figure 3, under scenario 1, reveals consistently low correlation values below 0.4 across all window sizes for the correlations of each 100 sample signal pair of the SWPC estimations and their respective ground truths, indicating poor and unreliable estimation. Notably, the window size of 15s shows a slightly higher correlation coefficient range between 0.18 to 0.36 compared to other window sizes, which fall below 0.2. This slight improvement in the correlation coefficient for the smallest window size is logical, as it allows for more rapid changes in connectivity due to its smaller temporal span. Nonetheless, the estimation remains unreliable. PS demonstrates effective estimation of the ground truth time-resolved connectivity, particularly within the frequency bandwidths of 0.05-0.09Hz, 0.07-0.11Hz, and 0.09-0.13Hz, with correlation coefficients exceeding 0.6, approximately 0.75, and approximately 0.7, respectively. Lower frequency bands for PS fail to effectively estimate the ground truth connectivity, as depicted by the low correlation coefficient distribution under scenario 1 of Figure 3. This outcome is expected since the ground truth connectivity is high frequency. It is intuitive to anticipate higher frequency connectivity within the higher frequencies of the signals rather than within lower frequencies.
Figure 3.
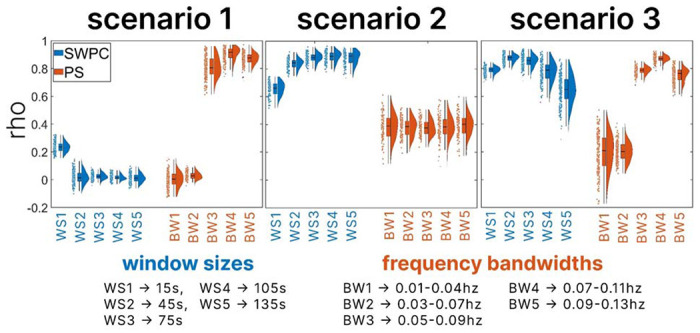
illustrates the results from the simulation analysis of all three scenarios. For each scenario, the correlation between each sample signal pair’s time-resolved connectivity estimations and their respective ground truth time-resolved connectivity is computed. The window sizes used for evaluating SWPC are 15s, 45s, 75s, 105s, and 135s, while the bandwidths used for evaluating phase synchronization are 0.01-0.04Hz, 0.03-0.07Hz, 0.05-0.09Hz, 0.07-0.11Hz, and 0.09-0.13Hz. The boxplots, kernel density, and scatter plots of correlation coefficients across all samples for each scenario are displayed, with SWPC results shown in blue and PS results shown in orange. Note that PS performs better in scenario 1, and SWPC performs better in scenario 2, emphasizing the complementary nature of the two approaches.
In scenario 2, where the time-resolved connectivity exhibits high magnitude (indicating strong coupling) and low frequency (reflecting stable connectivity), higher correlation coefficients are observed between the SWPC estimations and their respective ground truths across all window sizes in Figure 3. However, the 15s window size shows a slightly lower distribution of correlation coefficients compared to other window sizes. Despite this slight decrease, the correlation coefficients against the PS estimations remain higher for the 15s window size under scenario 2 in Figure 3. SWPC demonstrates a reliable estimation of high magnitude, low-frequency time-resolved connectivity. In contrast, the correlation coefficients between PS estimations and the ground truth are more spread out, centered around 0.4, indicating an unreliable estimation of strong low-frequency time-resolved connectivity.
Scenario 3 was designed to depict a scenario where the time-resolved connectivity is encoded in the amplitude of the signal pairs rather than the phase, with the characteristics of the time-resolved connectivity representing a compromise between scenarios 1 and 2. This entails mid-strength and mid-frequency time-resolved connectivity. Both SWPC and PS estimations demonstrate high correlation coefficients when compared with their respective ground truths, particularly for window sizes of 15s, 45s, and 75s, as well as frequency bandwidths of 0.05-0.09Hz, 0.07-0.11Hz, and 0.09-0.13Hz, respectively.
The simulation results compared using the root mean squared error between the SWPC and PS estimations with their respective ground truths are given in supplementary material 6.
5.2. Time-resolved comparison of SWPC and PS
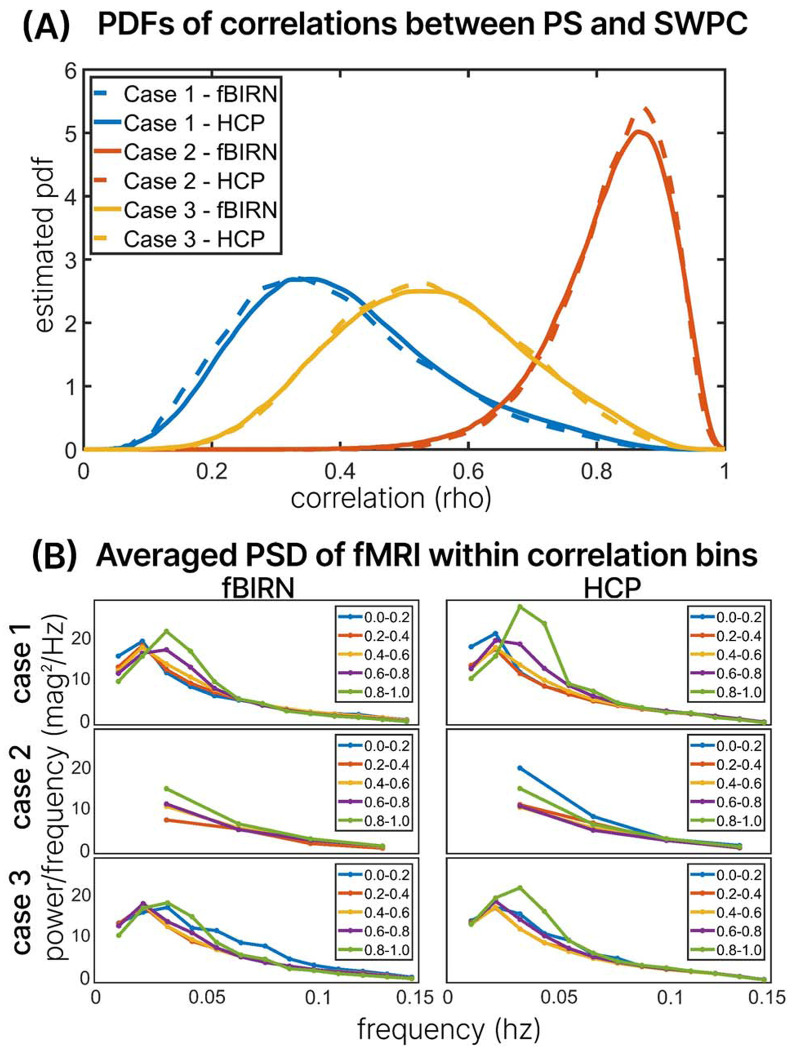
The comparative analysis between SWPC and PS methodologies, looking into the distinctions between these approaches and their relationship to the dynamic activity of brain networks, is displayed in Figure 4. Figure 4 illustrates the outcomes of temporal correlation assessments between SWPC and PS across pairs of brain networks and subjects. The analysis is performed for three distinct cases: Case one employs a bandwidth of 0.01 to 0.15 Hz for SWPC with a window size of 88 seconds, while cases two and three utilize a bandwidth of 0.03 to 0.07 Hz for SWPC. However, case two employs a window size of 30 seconds, corresponding to the low-frequency cutoff of the fMRI data, while case three retains the window size of 88 seconds. For all cases, PS utilizes the fMRI bandwidth of 0.03 to 0.07 Hz. The PDFs of the time-resolved correlation coefficients between SWPC and PS are depicted in Figure 4 (A) for all cases and both the fBIRN and HCP datasets. Notably, the PDFs derived from both the fBIRN and HCP datasets exhibit very high similarity, with substantial overlap within each case.
Figure 4.
presents results from segregating phase synchrony (PS) and sliding window Pearson correlation (SWPC) into five temporal correlation bins (0-0.2, 0.2-0.4, 0.4-0.6, 0.6-0.8, and 0.8-1) across three cases. In Case 1, SWPC has a bandwidth of 0.01-0.15 Hz with a window size of 88 seconds, while PS uses 0.03-0.07 Hz. In Case 2, both SWPC and PS use a bandwidth of 0.03-0.07 Hz with a window size of 30 seconds. In Case 3, both methods utilize a bandwidth of 0.03-0.07 Hz, but the window size is 88 seconds. (A) depicts the probability density function (PDF) of SWPC-PS correlation coefficients for each case. Additionally, the Power Spectral Density (PSD) of the fMRI data from HCP and fBIRN datasets across varying correlation bins is shown in (B). The averaged PSD across windows of the fMRI time series, brain networks, and subjects corresponding to each correlation bin is displayed for each case. This highlights that SWPC and PS are most similar (within high correlation bins) when the frequency range accessed by both approaches is close, particularly when the fMRI data exhibits a strong dominant frequency.
In the context of case one, the time-resolved correlation between PS and SWPC is notably lower compared to the other cases, which aligns with the different frequency content accessible to each method (0.01 to 0.15 Hz for SWPC and 0.03 to 0.07 Hz for PS). Conversely, in case two, where the frequency contents are the same, the correlation between PS and SWPC is significantly higher, as expected. Finally, in case three, the time-resolved correlation coefficients fall between those of case one and case two, indicating an intermediary relationship between SWPC and PS correlations. These findings reveal the nuanced interplay between the parameters and their impact on the comparative analysis of PS and SWPC in relation to trFNC of the brain.
In Figure 4(B), the averaged PSDs corresponding to the correlation bins are presented for each case. In case 1, the PSD patterns exhibit consistency between the fBIRN and HCP datasets. Notably, for bins indicating a high correlation between SWPC and PS, there is a discernible peak around 0.033 Hz in the fMRI data, particularly within correlation bins of 0.8-1 and 0.6-0.8. Conversely, for bins indicating lower correlations between SWPC and PS, a peak in PSD is observed at 0.022 Hz of the fMRI data. These patterns persist across datasets. In case 2, the PSD patterns show slight discrepancies between the fBIRN and HCP datasets. Specifically, in the HCP dataset, there exists a PSD plot for the lowest correlation bin, which is absent in the fBIRN dataset. Upon examining the PDFs in Figure 4(A) for case 2, it becomes evident that very few subjects fall within the low correlation bins. Consequently, there are minimal subjects within correlation bins below 0.6, rendering the PSD estimations below 0.6 unreliable. The observed high power at a frequency around 0.033 Hz in the correlation bin of 0-0.2 for case two in the HCP dataset may be attributed to a small subject size, as there are no subjects in the fBIRN dataset for this correlation bin. This poses a challenge in interpreting the results of case 2, especially considering the window size of 30 seconds, which results in poorer frequency resolution. However, for the reliable bins in case 2, namely 0.8-1 and 0.6-0.8, the patterns remain consistent across both datasets: higher correlation bins correspond to higher peak power at 0.033 Hz.
In case 3, where the window size is 88 seconds, and the frequency content matches in SWPC and PS (0.03-0.07hz), the PSD patterns exhibit consistency between the fBIRN and HCP datasets. Notably, for the highest correlation bin (0.8-1.0), there is a peak of PSD at 0.033 Hz, mirroring the findings observed in case 1. When examining lower correlation bins—specifically, bins of 0.6-0.8, 0.4-0.6, and 0.2-0.4—a peak at 0.022 Hz in the PS is evident, with the highest correlation bin among these three (0.6-0.8) exhibiting a slightly higher peak. This consistency is observed across both datasets. However, multiple peaks at various frequencies are observed for the lowest correlation bin, 0-0.2. While this pattern is consistent with both datasets, it is more prominent in the fBIRN dataset.
5.3. Group differences with SWPC and PS.
The averaged trFNC across subjects and time (windows) for each correlation bin is computed on the fBIRN dataset to observe how the functional connectivity estimated using SWPC and PS varies as a function of the similarity between the two methods. The results are depicted in Figure 5. Specifically, Figure 5(A) shows the averaged trFNC within each correlation bin, segmented into five segments from correlation coefficients from 0 to 1. The trFNC patterns exhibit strongly connected brain networks within the bins where correlation is highest, such as in the 0.8-1 and 0.6-0.8 correlation coefficient bins. For the lower correlation bins, both SWPC and PS showcase reduced levels of connectivity estimations, with PS exhibiting lower levels of connectivity patterns compared to SWPC. This indicates that the dissimilarities between SWPC and PS in estimating trFNC are more pronounced in scenarios with low connectivity patterns. In this analysis, the frequency band for SWPC is 0.01-0.15 Hz with a window size of 88 seconds, while the frequency band for PS is 0.03-0.07 Hz with a cropping moving median to match PS to SWPC.
Figure 5.
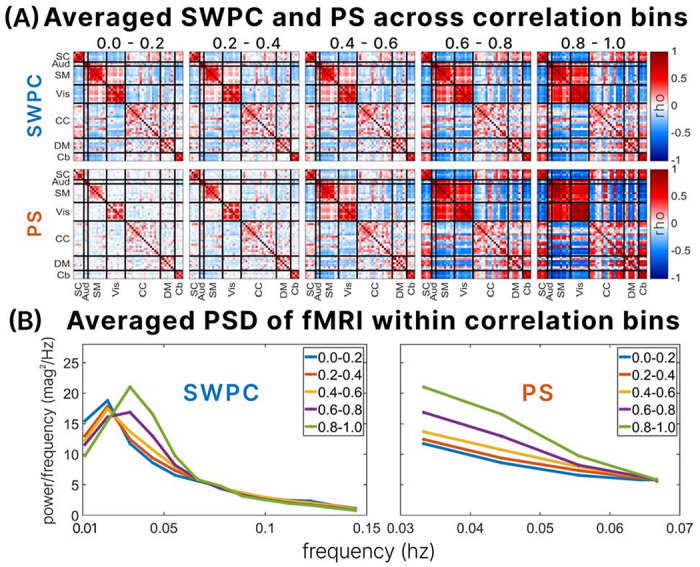
shows the averaged trFNC across brain network pairs within each correlation bin, depicting the similarity/dissimilarity between the trFNC estimated by SWPC and PS based on Spearman correlation. For each correlation bin, the average trFNC is displayed in (A), while the average power spectral density (PSD) across all brain networks and subjects is shown in panel (B). For each time point within a correlation bin, a window is defined as centered at that time point of the fMRI data across all brain networks with a window size of 88 seconds. The PSD is then computed for these windows. All PSDs are averaged across all subjects, time/windows, and brain networks within each correlation bin to obtain a single PSD corresponding to each correlation bin. Considering that PS utilizes a bandwidth of 0.03 - 0.07 Hz, we display the PSD within this range in panel (B) for PS. Note that the lower the correlation between SWPC and PS, the less connected the trFNC estimations derived from SWPC and PS are, with this effect being more pronounced for PS. Also, when the correlation between SWPC and PS is strong, the dominant frequency of the fMRI data accessed by SWPC closely matches that of PS, which is 0.033 Hz. For lower correlations, the dominant frequency of the fMRI data accessed by SWPC is around 0.022 Hz, indicating that the connectivity varies across different frequency bands as accessed by the two methods.
The PSD of the fBIRN fMRI frequency band accessed by SWPC and PS within each correlation bin is displayed in Figure 5 (B). The dominant frequency component of the fBIRN fMRI data across subjects and brain networks is 0.033 Hz for all correlation bins in PS, but it shows reduced power as the correlation bins decrease. The high power in high correlation bins at the dominant frequency indicates high synchronization at the 0.033 Hz frequency, suggesting a form of oscillatory behavior, which explains the strongly connected patterns observed within the high correlation bins in Figure 5 (A) for PS.
For SWPC, the dominant frequency within the highest correlation bin is around 0.033 Hz, which implies matched information between the two methods, considering this is the same dominant frequency observed in the case of using PS. However, for lower correlation bins, the averaged PSD accessed by SWPC still shows oscillatory properties but with a dominant frequency of 0.22 Hz instead. Considering that PS does not have access to this frequency range, it is expected that at a dominant frequency of 0.22 Hz, the similarities between SWPC and PS will be reduced.
These observations suggest that the differences between SWPC and PS are more evident in lower connectivity states and are also due to the different frequency bands utilized by the two methods. This highlights the complementary nature of SWPC and PS in capturing different aspects of brain connectivity, with each method providing unique insights that the other might miss.
To further explore the complementary nature of SWPC and PS, we perform a group analysis on the states estimated by the two methods between SZ and CN groups using the fBIRN dataset. Figure 6 displays the results from the group analysis, showcasing the complementary functional relevance to brain disorder between the two methods. Figure 6 (A) shows the cluster centroids of SZ (upper triangle) and CN (lower triangle) for SWPC and PS.
Figure 6.
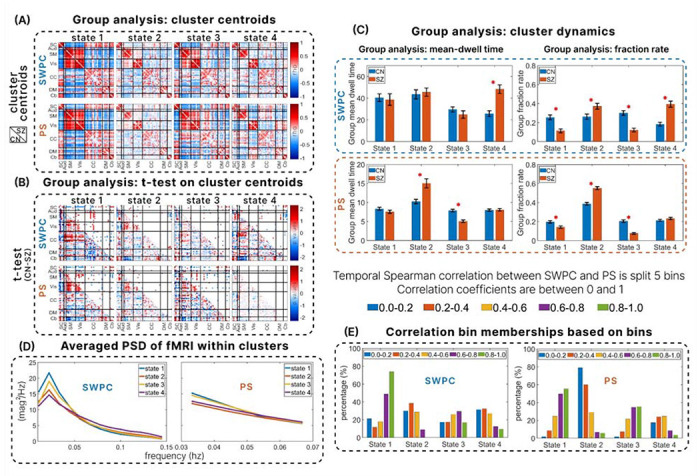
illustrates the group analysis results obtained from computing k-means clustering on SWPC and PS. The states derived from k-means clustering for SWPC and PS are depicted in (A). In these matrices, the upper triangle represents the states of brain network pairs for the schizophrenic (SZ) group, while the lower triangle represents the states of brain network pairs for the control (CN) group. (B) shows the results of a two-sample t-test performed on the estimated states to identify significant differences between SZ and CN groups in the brain network pairs within the states for SWPC and PS independently. The lower triangle displays the −log(pvalue) * sign(CN – SZ), indicating both the direction and significance of the differences. The upper triangle shows the thresholded p-value, with a threshold of less than 0.05. Note how the significant differences identified by SWPC and PS vary across states, highlighting their complementary nature. (C) displays the mean-dwell time (MDT) and fraction rate (FR) of SWPC and PS between SZ and CN groups, with significant differences indicated by an asterisk based on a p-value threshold of less than 0.05. (D) depicts the average power spectral density (PSD) of the fMRI data utilized by SWPC (0.01 - 0.15hz) and PS (0.03-0.07hz), averaged across subjects and time within each cluster/state. Note that MDT of SWPC finds significant differences in states 2 and 3, while PS identifies significant differences in state 4, indicating the complementary nature of the information they provide. (E) shows the percentage of the membership of each correlation bin within a cluster/state for both SWPC and PS, indicating the percentage each correlation bin forms a cluster.
In the states derived from the k-means clustering of SWPC and PS, there are two high connectivity/anti-connectivity states and two low connectivity/anti-connectivity states for both methods, as shown in Figure 6(A). These states are supported by the fMRI power spectral density (PSD) accessed by each method, illustrated in Figure 6(D). The low power of the dominant frequencies is observed in states 2 and 4, emphasizing these as the states with the least level of synchrony across brain network pairs. Given that the difference between the two methods is more evident in low connectivity states, we expect these low connectivity states for both SWPC and PS to be occupied by a larger percentage of low correlation bins, specifically the 0-0.2 and 0.2-0.4 correlation coefficient bins. Figure 6 (E) confirms this expectation, showing that states 2 and 4 have the highest percentage occupancy of those correlation bins for both PS and SWPC, further emphasizing these as the least connected states. Conversely, states 1 and 3 exhibit the highly connected brain network paired states. This is also supported by the PSDs of PS and SWPC, which exhibit the highest power at the dominant frequencies in Figure 6(D). Additionally, in Figure 6(E), states 1 and 3 show the highest percentage occupancy of the highest correlation bins, specifically in the 0.6-0.8 and 0.8-1 bins.
Figure 6(B) presents the results of a two-sample t-test with FDR correction. The lower triangle indicates , providing both the direction and a continuous representation of the significant differences. The upper triangle shows the thresholded FDR-corrected p-values, also indicating the direction of the differences as in the lower triangle.
These significant differences between SZ and CN, as captured by PS and SWPC, are complementary. For example, in the most connected state, state 1 in Figure 6(B), PS captures significant differences between the sensory-motor and visual network pairs, which are missed by SWPC. This indicates that controls exhibit significantly higher synchronization than schizophrenic groups between sensory-motor and visual networks. Conversely, in state 1 of SWPC, there is a significant difference between SZ and CN in the connectivity between sensory-motor networks and cognitive networks, which is missed by PS. This indicates that CNs exhibit significantly higher correlations than SZ groups between their sensory-motor and cognitive networks.
The mean dwell time and fraction rate between SZ and CN further emphasize the complementary nature of these methods, as depicted in Figure 6(C). The asterisks in Figure 6(C) indicate significant p-values between the MDT and FR of SZ and CN using the two methods, with a threshold of less than 0.05. PS captures significant differences between SZ and CN groups in MDT for states 2 and 3. As shown in Figure 6(A), state 2 is less synchronized, while state 3 is a high synchronization/anti-synchronization state. These significant differences are not detected by SWPC in its corresponding states. Conversely, SWPC captures significant differences between SZ and CN groups in MDT for state 4, another less connected state, which PS does not detect. Schizophrenia has been widely associated with less connected brain networks (Lynall, Bassett et al. 2010, Nejad, Ebdrup et al. 2012, Damaraju, Allen et al. 2014, Rabany, Brocke et al. 2019). Consequently, we expect significant differences between SZ and CN groups in the MDT of the less synchronized/connected states. According to Figure 6(A), state 4 is the least connected in SWPC and shows the lowest dominant frequency in Figure 6(D). Thus, it is anticipated that schizophrenic patients are more likely to remain in state 4 once they enter it, compared to controls in SWPC.
Interestingly, in PS, the least synchronized state, according to Figure 6(A), and the one with the lowest dominant frequency in Figure 6(D), is state 2. As expected, schizophrenic patients are more likely to stay in this state longer than controls. The differences in the least connected states identified by SWPC and PS are noteworthy. Although both methods identify a disconnected state, these states are different, suggesting that schizophrenic patients exhibit different types of functionally disconnected brain network patterns detected by PS and SWPC, particularly when examining the mean dwell time of trFNC.
In terms of FR, SWPC captures significant differences between SZ and CN in all four states, while PS captures significant differences in the first three states. In state 4, SWPC exhibits the least connected brain networks, whereas the PS counterpart shows some modular positive, relatively low synchrony patterns between sub-cortical, auditory, and sensory-motor brain networks. State 4 of PS is primarily occupied by correlation bins 0.2-0.4 and 0.4-0.6, as shown in Figure 6(E). This implies that, for the mid-range similarity between SWPC and PS, specifically the correlation bins 0.2-0.4 and 0.4-0.6, PS identifies some unique patterns that SWPC does not detect. However, while these patterns are interesting, they do not provide any significant difference between schizophrenic patients and controls in terms of FR.
These results further highlight the complementary insights provided by each method. Each method reveals unique aspects of connectivity dynamics, with PS being more sensitive to certain states and SWPC to others, thereby providing a more comprehensive understanding when used together.
6. DISCUSSION.
From a communication theory perspective, phase synchronization can be viewed as a phase demodulation technique (Wang and Da 2012), while sliding window Pearson correlation can be seen as an amplitude demodulation technique, (Faghiri, Iraji et al. 2022) as discussed extensively in the background section. These two techniques are fundamentally different and offer complementary strengths and limitations. This distinction emphasizes that PS and SWPC, as time-resolved functional network connectivity measures, capture different information: PS extracts shared information through the phase of the BOLD activity, whereas SWPC captures shared information through the amplitude of the BOLD activity.
Moreover, these methods differ in their ability to capture various kinds of connectivity between a pair of signals. Our simulations demonstrate that PS more accurately estimates low-amplitude fast-varying connectivity between narrow-band signal pairs, as shown in scenario 1 of Figure 3 and consistent with previous findings (Fagerholm, Moran et al. 2018, Lee and Sepulchre 2024). On the other hand, high-amplitude slow-varying connectivity between broadband activity signal pairs is better estimated by SWPC, as illustrated in scenario 2, and is consistent with previous findings (Scott, Fagerholm et al. 2014, Fagerholm, Scott et al. 2016, Fagerholm, Moran et al. 2020). These findings highlight the differences in the types of connectivity each method captures.
While the distinction between the two methods is clear, it is not uncommon to expect phase and amplitude information to be similar at certain times and in specific scenarios. This leads to an interest in comparing SWPC and PS in the context of trFNC. However, comparing these two measures is not straightforward due to their differing nature. For instance, PS operates as an instantaneous measure, while SWPC functions as a window-based measure. In our study, we compare these two methods across several cases, window sizes, and bandwidths in fMRI data, acknowledging that no single comparison case is the best. We aim to link differences between the two methods with the power spectral density estimation of fMRI data. This approach allows us to understand variations in trFNC by analyzing the spectral properties of fMRI data across Spearman correlation bins corresponding to the two methods.
In case 1, we use standard practices of an 88-second window and a frequency band of 0.01-0.15 Hz for SWPC and match PS using a median window of the same window and a frequency band of 0.03-0.07 Hz. To address the frequency range mismatch between SWPC and PS, we use a frequency band of 0.03-0.07 Hz for SWPC with a corresponding window size of 30 seconds in case 2. However, the 30-second window significantly reduces the frequency resolution of the PSD estimation. To counter this, we create Case 3 from Case 2 by using an 88-second window instead of 30 seconds. While these cases aim to balance the compromises of the two methods, we acknowledge that neither of them is the most appropriate case for comparison. Nonetheless, we find consistency in the PSD estimations across all cases and two different fMRI datasets in relation to the correlation bins between SWPC and PS.
As shown in Figure 4(A), the estimated PDF of the Spearman correlation between SWPC and PS is consistent across the fBIRN and HCP datasets, suggesting that the time-varying correlations between SWPC and PS are not biased by a single dataset. The correlation between SWPC and PS is highest in Case 2, which is expected since a smaller window size for SWPC aligns more closely with the instantaneous nature of PS. However, it is important to note that amplitude correlations are best suited for amplitude estimation (Van Den Heuvel and Pol 2010, Engel, Gerloff et al. 2013, Fu, Tu et al. 2018, Mostame and Sadaghiani 2020), which requires a low-pass filter to extract the relevant slow-varying amplitude of the signal (Faghiri, Iraji et al. 2021), as done in amplitude demodulation (Haykin and Moher 1989, Proakis, Salehi et al. 1994) and consequently by SWPC. Therefore, while SWPC closely matches PS in Case 2, SWPC is not reliable in this case due to the conceptual inconsistency and the reduced statistical power of correlation estimations (Schönbrodt and Perugini 2013).
The PSD estimations of the fMRI data across correlation bins show consistency with the concept of phase and amplitude being synced under strong oscillatory conditions (Fagerholm, Moran et al. 2020). Intuitively, if two sine waves have the same frequency and phase shifts, phase synchronization and amplitude correlations will be synced. If two signals are strongly coupled, their dominant frequencies tend to align (Rosenblum, Pikovsky and Kurths 1996, Boccaletti, Kurths et al. 2002), giving rise to oscillations at the same or near the same frequencies (oscillatory conditions) (Lowet, Roberts et al. 2016, Sivarajah, Steinbacher et al. 2019, He, Xu et al. 2022). This oscillatory behavior can be observed when the average power spectral density across all brain networks reflects a dominant frequency. Consequently, we expect SWPC and PS to be closely matched when the fMRI PSD across all subjects and brain networks is closer to an oscillatory condition, which is observed in the higher correlation bins (0.6-0.8 and 0.8-1.0). This is observed in Figure 4(B) across all cases and both datasets, especially for the correlation bin 0.8-1.0, except in Case 2 of the HCP dataset where the lowest correlation bin (0.0-0.2) yields the highest power of the dominant frequency in the PSD estimation, implying strong oscillatory behavior. This anomaly can be explained by the low-frequency resolution in that case, making the PSDs unreliable. Another possible reason could be drawn from scenario 2 of our simulation results, which shows that SWPC outperforms PS when connectivity is encoded in the amplitude of the signals (Van Den Heuvel and Pol 2010, Engel, Gerloff et al. 2013, Mostame and Sadaghiani 2020) with a high amplitude of connectivity (Fagerholm, Moran et al. 2020). This suggests that the strong oscillatory component is encoded in the amplitude of the brain networks at those times. However, this is not observed in the fBIRN dataset. In the fBIRN dataset, no samples exist within the 0-0.2 correlation bin in case 2 (Figure 4A) and, thus, have no corresponding PSD estimation (Figure 4B). Due to this, the reason for the strong oscillatory component being encoded in the amplitude in the HCP dataset remains conjectural since it cannot be validated in the fBIRN dataset.
Another reason for the difference between SWPC and PS is the mismatch of frequency bands: SWPC utilizes a range of 0.01-0.15 Hz, while PS utilizes 0.03-0.07 Hz. This discrepancy is evident in Figure 5. Figure 5 shows the average trFNC and average PSD of the fBIRN fMRI dataset across correlation bins between SWPC and PS.
From Figure 5(A), the higher the correlation bin between the methods, the more connected or synchronized the brain network pairs are for both methods. Conversely, the lower the correlation bin, the less connected the brain network pairs appear, especially in PS. The low level of connectivity of brain networks in the low correlation bins is supported by the estimated PSD within these bins. In Figure 5(B), it is evident that the lower the correlation bin, the lower the power of the dominant frequency at 0.033 Hz, implying that lower correlation bins correspond to less oscillatory properties of the fMRI data. This aligns with the observation that PS shows a lower level of synchronization in lower correlation bins. For lower correlation bins, the fMRI data accessed by SWPC shifts from the 0.03 Hz frequency to lower dominant frequencies around 0.022 Hz. Despite this shift, the PSDs for these lower correlation bins still exhibit oscillatory properties, explaining why low correlation bins in SWPC still show a relatively higher level of connectedness in Figure 5(A). This underscores one of the reasons SWPC and PS differ: the mismatch of frequency bands. This observation is also consistent with the notion that functional connectivity varies across different frequency bands (Luo, He et al. 2020, Faghiri, Iraji et al. 2021, Ziaeemehr and Valizadeh 2021, Li, Cheng et al. 2022, Kajimura, Margulies and Smallwood 2023).
To explore the clinical relevance of the disparities between SWPC and PS, we conducted k-means clustering on the trFNC estimated by SWPC and PS independently to obtain functional connectivity states, as displayed in Figure 6(A). The composition of each correlation bin in each cluster/state is displayed in Figure 6(E). One notable distinction between SWPC and PS is evident in state 4. Despite being a low-connected state, PS exhibits an observable modular structure more prominently than SWPC. PS detects low levels of synchronization between sub-cortical, auditory, and sensory-motor brain networks, which are not detected by SWPC. Connecting this observation to the similarities between the two methods, it can be seen from Figure 6(E) that state 4 has a high percentage of mid-range correlation bins for PS, specifically the 0.2-0.4 and 0.4-0.6 bins. This highlights that at mid-range correlations between the two methods, PS identifies synchrony patterns that are missed by SWPC. Considering that this state is a low-connected/synchronized state, a plausible reason why this pattern is found for PS could be drawn from our simulation analysis, which suggests that PS is more appropriate for capturing low-amplitude time-resolved connectivity than SWPC (Fagerholm, Moran et al. 2018, Lee and Sepulchre 2024), as demonstrated in scenario 1 of Figure 3.
The state with the least connected brain networks for SWPC is state 4, while for PS, it is state 2, as shown in Figure 6(A) and validated by the PSD estimation of the fBIRN fMRI dataset across the states in Figure 6(D). The state with the lowest PSD at the dominant frequency is shown as state 4 (purple plot) for SWPC and as state 2 (red plot) for PS. One striking observation is that the least connected states manifest differently in SWPC and PS, highlighting their complementarity. The patterns of state 4 in SWPC are characterized by low anti-correlations between visual networks and subcortical, auditory, and sensory-motor networks. In contrast, state 2 in PS is characterized by low synchronization between the same brain networks. We detect significant differences between schizophrenia and control groups in state 2 of PS and state 4 of SWPC, with SZ groups showing a higher mean-dwell time in these states than CN groups, as shown in Figure 6 (C). This finding aligns with previous studies indicating that individuals with schizophrenia are more associated with low connectivity levels (Friston and Frith 1995, Friston 1998, Kim, Burge et al. 2008, Lynall, Bassett et al. 2010, Pettersson-Yeo, Allen et al. 2011, Nejad, Ebdrup et al. 2012, Williamson and Allman 2012, Damaraju, Allen et al. 2014, Miller, Yaesoubi et al. 2016, Iraji, Deramus et al. 2019, Iraji, Fu et al. 2019). These results suggest that while SZ groups tend to stay longer in the least connected/synchronized states (Damaraju, Allen et al. 2014, Du, Pearlson et al. 2016, Fu, Caprihan et al. 2019, Faghiri, Iraji et al. 2020, Weber, Johnsen et al. 2020, Fu, Iraji et al. 2021, Hyatt, Wexler et al. 2022, Bostami, Lewis et al. 2024), there are multiple low connected/synchronized states associated with schizophrenia. One state is characterized by low anti-correlations between visual networks and subcortical, auditory, and sensory-motor networks, as detected by SWPC (Damaraju, Allen et al. 2014, Du, Pearlson et al. 2016, Faghiri, Yang et al. 2023). The other state is characterized by low positive synchronization between the same brain networks, as detected by PS in Figure 6(A). This dual pattern of low connectivity states highlights the complexity of functional connectivity alterations in schizophrenia and underscores the importance of using both SWPC and PS to capture different aspects of brain network dysfunction in this disorder.
Another clinically relevant difference between SWPC and PS can be observed in state 3. In state 3 of SWPC, most cognitive control networks exhibit anti-correlations with sensory-motor and visual networks, while in PS, there exists positive synchronization among some networks within those domains, as depicted in Figure 6(A). We observe more significant differences between schizophrenia and control groups in state 3 of PS than we detect in state 3 of SWPC, as illustrated in Figure 6(B). For instance, CN exhibits significantly higher synchronization between some sensory-motor networks and visual networks, indicated by the red dots in state 3 of PS in Figure 6(B). Additionally, we detect significant differences between SZ and CN groups in state 3 of PS, with CN groups showing a higher mean-dwell time in this state than SZ groups, as shown in Figure 6(C), an observation undetected by SWPC. According to Figure 6(E), state 3 constitutes declining percentages of correlation bins from high to low. This pattern is similar to state 1 and validated by Figure 6(D), where states 1 and 2 are the most connected states, with state 1 being slightly higher than state 3. This demonstrates that even for highly connected/modular states and states mostly characterized by a high correlation between SWPC and PS, the clinically relevant information is complementary. This observation is further made evident in state 1 for both methods, as the significant differences between SZ and CN groups are complementary, as shown in Figure 6(B). SWPC indicates that in state 1, CN groups exhibit stronger correlations between sensory-motor networks and cognitive control networks, undetected by PS, while PS identifies stronger synchronization between sensory-motor networks and visual networks, undetected by SWPC.
Based on our results, it is strongly evident that the two methods are complementary, each with their strengths and weaknesses. The suggestion to use PS instead of SWPC due to the absence of a window size requirement (Glerean, Salmi et al. 2012, Omidvarnia, Pedersen et al. 2016, Pedersen, Omidvarnia et al. 2018, Zhou, Zhu et al. 2023) does not take into account the sensitivity of PS to bandwidth and frequency band selection. For instance, in our simulation analysis (Figure 3), bandwidths BW1 and BW2 perform poorly in Scenario 1, where PS was expected to outperform SWPC, highlighting PS’s sensitivity to bandwidth selection. The concept of the “right” bandwidth for PS remains unresolved, making it challenging to recommend PS over SWPC for time-resolved functional connectivity analysis, especially when there is evidence that suggests the bandwidth of neural relevant information varies across subjects (Handwerker, Ollinger and D’Esposito 2004, Grady and Garrett 2014). Furthermore, although a 30-second window size for PS shows a high correlation with SWPC, as demonstrated in Figure 4 (A), the clinical relevance provided by SWPC using a longer window size, such as 88 seconds, is not captured by PS (see supplementary material 5). This indicates that the similarities between the two methods do not inherently make one superior to the other.
Moreover, the concept of instantaneous phase is straightforward to interpret for monochromatic (single-frequency) signals, whereas the notion of a single-valued instantaneous frequency and phase is not meaningful for all types of signals (Boashash 1992, Picinbono 1997). This underscores the necessity of narrowband filtering when employing the Hilbert transform (Boashash 1992, Chavez, Besserve et al. 2006) for computing PS in fMRI studies. Therefore, selecting an appropriate narrow frequency band is essential to obtain a meaningful interpretation of phase synchronization from fMRI data. The recommendation to use PS (Glerean, Salmi et al. 2012, Omidvarnia, Pedersen et al. 2016, Pedersen, Omidvarnia et al. 2017, Pedersen, Omidvarnia et al. 2018) overlooks the critical parameter of frequency band selection. It suggests that PS is superior to SWPC because it does not require choosing a window size, yet it neglects the necessity of constricting the frequency band of the fMRI signal for meaningful PS analysis (Glerean, Salmi et al. 2012). Note that window size and shape selection in SWPC is, in essence, a filter design procedure (Faghiri, Iraji et al. 2022) and, therefore, is quite similar to the filter design step that is necessary for estimating PS using the Hilbert transform. Additionally, estimating the instantaneous phase based on the analytic signal definition is possible for specific types of signals, which makes it inapplicable to all types of signals (Picinbono 1997). Future works need to investigate if fMRI signals match these assumptions.
Considering the limitations highlighted for the phase synchronization method, we propose an alternative perspective on SWPC and PS: neither method holds superiority over the other. We conclude that the fundamental differences between PS and SWPC necessitate that they be studied separately to uncover complementary insights into time-resolved functional network connectivity and the brain. Thus, we recommend further studies explore phase-amplitude trFNC measures to fully leverage their unique contributions.
A limitation of this study was our inability to quantify the exact reasons for the dissimilarities observed between the two methods in some cases. We propose several possible reasons, such as necessary frequency mismatches, the oscillatory properties of the fMRI data, and different connectivity properties, as demonstrated in our simulations. However, it remains unclear how each of these factors contributes to the observed differences and to what degree. To address this, we recommend that future research focuses on quantifying the effects of these factors to better understand their influence on trFNC analyses. Additionally, future studies should undertake a more comprehensive comparison of the strengths and weaknesses of these two methods with other time-varying approaches, such as time-varying phase-amplitude coupling, co-activation patterns, and the integration of directed connectivity. Furthermore, incorporating graph-theoretical features, such as network integration, segregation, and efficiency, would help establish a broader conceptual framework for applying these methods to dynamic functional connectivity.
7. CONCLUSION.
In conclusion, our study underscores the complementary nature of SWPC and PS, each leveraging distinct signal properties—amplitude and phase, respectively—to illuminate brain network interactions. Integrating the strengths of both methods promises a more comprehensive understanding of time-resolved functional connectivity in fMRI research.
Supplementary Material
Highlights:
We compare sliding window Pearson correlation (SWPC) and phase synchrony (PS).
SWPC depends on window size, while PS needs narrow bands, losing key information.
SWPC captures slow amplitude connectivity; PS captures fast phase connectivity.
Both detect disconnected states in schizophrenia but show complementary patterns.
SWPC and PS are complementary tools, chosen based on study focus and constraints.
11. ACKNOWLEDGMENT.
This work was supported by the National Institutes of Health (NIH) grant (R01MH123610) and the National Science Foundation (NSF) grant #2112455.
Footnotes
DECLARATION OF COMPETING INTEREST.
None.
10. DATA & CODE AVAILABILITY STATEMENT.
The codes for all our analyses in MATLAB language can be accessed through GitHub (https://github.com/Sirlord-Sen/studying_trFNC_via_communication_theory). The data was not collected by us and was provided in a deidentified manner. The IRB will not allow sharing of data or individual derivatives as a data reuse agreement was not signed by the subjects during the original acquisition.
12. REFERENCES.
- Achard S., Salvador R., Whitcher B., Suckling J. and Bullmore E. (2006). “A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs.” Journal of Neuroscience 26(1): 63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggarwal C. C., Hinneburg A. and Keim D. A. (2001). On the surprising behavior of distance metrics in high dimensional space. Database Theory—ICDT 2001: 8th International Conference London, UK, January 4–6, 2001 Proceedings 8, Springer. [Google Scholar]
- Allen E. A., Damaraju E., Plis S. M., Erhardt E. B., Eichele T. and Calhoun V. D. (2014). “Tracking whole-brain connectivity dynamics in the resting state.” Cereb Cortex 24(3): 663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen G., Barnard H., McColl R., Hester A. L., Fields J. A., Weiner M. F., Ringe W. K., Lipton A. M., Brooker M. and McDonald E. (2007). “Reduced hippocampal functional connectivity in Alzheimer disease.” Archives of neurology 64(10): 1482–1487. [DOI] [PubMed] [Google Scholar]
- Bastos A. M. and Schoffelen J.-M. (2016). “A tutorial review of functional connectivity analysis methods and their interpretational pitfalls.” Frontiers in systems neuroscience 9: 175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bedrosian E. (1962). Product theorem for Hilbert transforms, Rand Corporation. [Google Scholar]
- Benjamini Y. and Hochberg Y. (1995). “Controlling the false discovery rate: a practical and powerful approach to multiple testing.” Journal of the Royal statistical society: series B (Methodological) 57(1): 289–300. [Google Scholar]
- Biswal B., Yetkin F. Z., Haughton V. M. and Hyde J. S. (1995). “Functional connectivity in the motor cortex of resting human brain using echo-planar MRI.” Magn Reson Med 34(4): 537–541 [DOI] [PubMed] [Google Scholar]
- Boashash B. (1992). “Estimating and interpreting the instantaneous frequency of a signal. I. Fundamentals”. Proceedings of the IEEE 80(4): 520–538. [Google Scholar]
- Boccaletti S., Kurths J., Osipov G., Valladares D. and Zhou C. (2002). “The synchronization of chaotic systems.” Physics reports 366(1-2): 1–101. [Google Scholar]
- Bolt T., Nomi J. S., Vij S. G., Chang C. and Uddin L. Q. (2018). “Inter-subject phase synchronization for exploratory analysis of task-fMRI.” NeuroImage 176: 477–488. [DOI] [PubMed] [Google Scholar]
- Bostami B., Lewis N., Agcaoglu O., Turner J. A., van Erp T. G., Ford J. M., Calhoun V. and Iraji A. (2024). “Time-varying Spatial Propagation of Brain Networks in fMRI data.” bioRxiv: 2024.2002. 2012.579169. [Google Scholar]
- Braun U., Plichta M. M., Esslinger C., Sauer C., Haddad L., Grimm O., Mier D., Mohnke S., Heinz A., Erk S., Walter H., Seiferth N., Kirsch P. and Meyer-Lindenberg A. (2012). “Test-retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures.” NeuroImage 59(2): 1404–1412. [DOI] [PubMed] [Google Scholar]
- Buckner R. L., Sepulcre J., Talukdar T., Krienen F. M., Liu H., Hedden T., Andrews-Hanna J. R., Sperling R. A. and Johnson K. A. (2009). “Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer’s disease.” Journal of neuroscience 29(6): 1860–1873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero-Gaudes C. and Reynolds R. C. (2017). “Methods for cleaning the BOLD fMRI signal.” NeuroImage 154:128–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabral J., Vidaurre D., Marques P., Magalhães R., Silva Moreira P., Miguel Soares J., Deco G., Sousa N. and Kringelbach M. L. (2017). “Cognitive performance in healthy older adults relates to spontaneous switching between states of functional connectivity during rest.” Scientific reports 7(1): 5135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun V., Kim J. and Pearlson G. (2003). FMRI connectivity measured by mutual information and correlation: Linear dependence vs. General dependence. Proceedings of the 7th ISMRM Scientific Meeting. [Google Scholar]
- Calhoun V. D., Adali T., Pearlson G. D. and Pekar J. J. (2001). “A method for making group inferences from functional MRI data using independent component analysis.” Human brain mapping 14(3): 140–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun V. D., Kiehl K. A., Liddle P. F. and Pearlson G. D. (2004). “Aberrant localization of synchronous hemodynamic activity in auditory cortex reliably characterizes schizophrenia.” Biological psychiatry 55(8): 842–849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun Vince D., Miller R., Pearlson G. and Adalı T. (2014). “The Chronnectome: Time-Varying Connectivity Networks as the Next Frontier in fMRI Data Discovery.” Neuron 84(2): 262–274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C. and Glover G. H. (2010). “Time-frequency dynamics of resting-state brain connectivity measured with fMRI.” NeuroImage 50(1): 81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chavez M., Besserve M., Adam C. and Martinerie J. (2006). “Towards a proper estimation of phase synchronization from time series.” Journal of Neuroscience methods 154(1–2): 149–160 [DOI] [PubMed] [Google Scholar]
- Chhatwal J. P., Schultz A. P., Johnson K., Benzinger T. L., Jack C. Jr, Ances B. M., Sullivan C. A., Salloway S. P., Ringman J. M. and Koeppe R. A. (2013). “Impaired default network functional connectivity in autosomal dominant Alzheimer disease.” Neurology 81(8): 736–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costa T., Rognoni E. and Galati D. (2006). “EEG phase synchronization during emotional response to positive and negative film stimuli.” Neuroscience letters 406(3): 159–164. [DOI] [PubMed] [Google Scholar]
- Damaraju E., Allen E. A., Belger A., Ford J. M., McEwen S., Mathalon D. H., Mueller B. A., Pearlson G. D., Potkin S. G., Preda A., Turner J. A., Vaidya J. G., van Erp T. G. and Calhoun V. D. (2014). “Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia.” NeuroImage: Clinical 5: 298–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux J. S., Rombouts S. A., Barkhof F., Scheltens P., Stam C. J., Smith S. M. and Beckmann C. F. (2006). “Consistent resting-state networks across healthy subjects.” Proceedings of the national academy of sciences 103(37): 13848–13853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delprat N., Escudié B., Guillemain P., Kronland-Martinet R., Tchamitchian P. and Torresani B. (1992). “Asymptotic wavelet and Gabor analysis: Extraction of instantaneous frequencies.” IEEE transactions on Information Theory 38(2): 644–664. [Google Scholar]
- Deshmukh A. V., Shivhare V., Gadre V. M., Patkar D. P., Shah S. and Pungavkar S. (2004). A phase based method for investigating the functional connectivity in the fMRI data. Proceedings of the IEEE INDICON 2004. First India Annual Conference, 2004., IEEE. [Google Scholar]
- Dorfler F. and Bullo F. (2012). “Synchronization and transient stability in power networks and nonuniform Kuramoto oscillators.” SIAM Journal on Control and Optimization 50(3): 1616–1642 [Google Scholar]
- Du Y., Fryer S. L., Fu Z., Lin D., Sui J., Chen J., Damaraju E., Mennigen E., Stuart B. and Loewy R. L. (2018). “Dynamic functional connectivity impairments in early schizophrenia and clinical high-risk for psychosis.” Neuroimage 180: 632–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Y., Fu Z., Sui J., Gao S., Xing Y., Lin D., Salman M., Abrol A., Rahaman M. A., Chen J., Hong L. E., Kochunov P., Osuch E. A. and Calhoun V. D. (2020). “NeuroMark: An automated and adaptive ICA based pipeline to identify reproducible fMRI markers of brain disorders.” Neuroimage Clin 28:102375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Y., Pearlson G. D., Yu Q., He H., Lin D., Sui J., Wu L. and Calhoun V. D. (2016). “Interaction among subsystems within default mode network diminished in schizophrenia patients: a dynamic connectivity approach.” Schizophrenia research 170(1): 55–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff S. B., Bzdok D., Laird A. R., Roski C., Caspers S., Zilles K. and Fox P. T. (2011). “Co-activation patterns distinguish cortical modules, their connectivity and functional differentiation.” Neuroimage 57(3): 938–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel A. K., Gerloff C., Hilgetag C. C. and Nolte G. (2013). “Intrinsic coupling modes: multiscale interactions in ongoing brain activity.” Neuron 80(4): 867–886. [DOI] [PubMed] [Google Scholar]
- Esteban O., Markiewicz C. J., Blair R. W., Moodie C. A., Isik A. I., Erramuzpe A., Kent J. D., Goncalves M., DuPre E. and Snyder M. (2019). “fMRIPrep: a robust preprocessing pipeline for functional MRI.” Nature methods 16(1): 111–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagerholm E. D., Moran R. J., Violante I. R., Leech R. and Friston K. J. (2018). “Breaking the bonds of weak coupling: the dynamic causal modelling of oscillator amplitudes.” arXiv preprint arXiv:1812.06315 [Google Scholar]
- Fagerholm E. D., Moran R. J., Violante I. R., Leech R. and Friston K. J. (2020). “Dynamic causal modelling of phase-amplitude interactions.” NeuroImage 208: 116452. [DOI] [PubMed] [Google Scholar]
- Fagerholm E. D., Scott G., Shew W. L., Song C., Leech R., Knöpfel T. and Sharp D. J. (2016). “Cortical entropy, mutual information and scale-free dynamics in waking mice.” Cerebral cortex 26(10): 3945–3952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faghiri A., Adali T. and Calhoun V. D. (2022). Single Sideband Modulation as a Tool To Improve Functional Connectivity Estimation. 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI). [Google Scholar]
- Faghiri A., Iraji A., Damaraju E., Belger A., Ford J., Mathalon D., Mcewen S., Mueller B., Pearlson G. and Preda A. (2020). “Weighted average of shared trajectory: A new estimator for dynamic functional connectivity efficiently estimates both rapid and slow changes over time.” Journal of neuroscience methods 334: 108600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faghiri A., Iraji A., Damaraju E., Turner J. and Calhoun V. D. (2021). “A unified approach for characterizing static/dynamic connectivity frequency profiles using filter banks.” Network Neuroscience 5(1): 56–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faghiri A., Iraji A., Duda M., Adali T. and Calhoun V. D. (2022). A Unified Framework for Modularizing and Comparing Time-Resolved Functional Connectivity Methods. 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC). [DOI] [PubMed] [Google Scholar]
- Faghiri A., Stephen J. M., Wang Y. P., Wilson T. W. and Calhoun V. D. (2018). “Changing brain connectivity dynamics: from early childhood to adulthood.” Human brain mapping 39(3): 1108–1117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faghiri A., Yang K., Ishizuka K., Sawa A., Adali T. and Calhoun V. (2023). Frequency modulation increases the specificity of time-resolved connectivity: A resting-state fMRI study. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fell J. and Axmacher N. (2011). “The role of phase synchronization in memory processes.” Nature Reviews Neuroscience 12(2): 105–118. [DOI] [PubMed] [Google Scholar]
- Fingelkurts A. A., Fingelkurts A. A. and Kähkönen S. (2005). “Functional connectivity in the brain—is it an elusive concept?” Neuroscience & Biobehavioral Reviews 28(8): 827–836 [DOI] [PubMed] [Google Scholar]
- Friston K. J. (1998). “The disconnection hypothesis.” Schizophrenia research 30(2): 115–125 [DOI] [PubMed] [Google Scholar]
- Friston K. J. and Frith C. D. (1995). “Schizophrenia: a disconnection syndrome.” Clin Neurosci 3(2): 89–97. [PubMed] [Google Scholar]
- Fu Z., Batta I., Wu L., Abrol A., Agcaoglu O., Salman M. S., Du Y., Iraji A., Shultz S., Sui J. and Calhoun V. D. (2024). “Searching Reproducible Brain Features using NeuroMark: Templates for Different Age Populations and Imaging Modalities.” Neuroimage 292: 120617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Z., Caprihan A., Chen J., Du Y., Adair J. C., Sui J., Rosenberg G. A. and Calhoun V. D. (2019). “Altered static and dynamic functional network connectivity in Alzheimer’s disease and subcortical ischemic vascular disease: shared and specific brain connectivity abnormalities.” Human brain mapping 40(11): 3203–3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Z., Iraji A., Turner J. A., Sui J., Miller R., Pearlson G. D. and Calhoun V. D. (2021). “Dynamic state with covarying brain activity-connectivity: On the pathophysiology of schizophrenia.” Neuroimage 224: 117385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Z., Tu Y., Di X., Du Y., Pearlson G. D., Turner J. A., Biswal B. B., Zhang Z. and Calhoun V. D. (2018). “Characterizing dynamic amplitude of low-frequency fluctuation and its relationship with dynamic functional connectivity: An application to schizophrenia.” NeuroImage 180: 619–631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glerean E., Salmi J., Lahnakoski J. M., Jääskeläinen I. P. and Sams M. (2012). “Functional magnetic resonance imaging phase synchronization as a measure of dynamic functional connectivity.” Brain Connect 2(2): 91–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grady C. L. and Garrett D. D. (2014). “Understanding variability in the BOLD signal and why it matters for aging.” Brain Imaging Behav 8(2): 274–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius M. D., Krasnow B., Reiss A. L. and Menon V. (2003). “Functional connectivity in the resting brain: a network analysis of the default mode hypothesis.” Proceedings of the national academy of sciences 100(1): 253–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock F., Cabral J., Luppi A. I., Rosas F. E., Mediano P. A., Dipasquale O. and Turkheimer F. E. (2022). “Metastability, fractal scaling, and synergistic information processing: What phase relationships reveal about intrinsic brain activity.” NeuroImage 259:119433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handwerker D. A., Ollinger J. M. and D’Esposito M. (2004). “Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses.” Neuroimage 21(4): 1639–1651. [DOI] [PubMed] [Google Scholar]
- Handwerker D. A., Roopchansingh V., Gonzalez-Castillo J. and Bandettini P. A. (2012). “Periodic changes in fMRI connectivity.” Neuroimage 63(3): 1712–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauke J. and Kossowski T. (2011). “Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data.” Quaestiones geographicae 30(2): 87–93 [Google Scholar]
- Haykin S. and Moher M. (1989). “Analog & Digital Communications.” Canada: John Wiley & Sons Inc [Google Scholar]
- He Z., Xu C., He W., He J., Zhou Y. and Li F. (2022). “Principle and applications of multimode strong coupling based on surface plasmons.” Nanomaterials 12(8): 1242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honari H., Choe A. S., Electrical M. A. L. D. o., Engineering C., University J. H., Imaging U. F. M. K. R. C. f. F. B., Institute K. K., Injury U. I. C. f. S. C., Radiology U. D. o., Science R., Medicine J. H. U. S. o., Biostatistics U. D. o. and Usa (2020). “Evaluating phase synchronization methods in fMRI: A comparison study and new approaches.” NeuroImage 228: 117704 – 117704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussain S., Langley J., Seitz A. R., Hu X. P. and Peters M. A. K. (2023). “A Novel Hidden Markov Approach to Studying Dynamic Functional Connectivity States in Human Neuroimaging.” Brain Connect 13(3): 154–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison R. M., Womelsdorf T., Allen E. A., Bandettini P. A., Calhoun V. D., Corbetta M., Delia Penna S., Duyn J. H., Glover G. H., Gonzalez-Castillo J., Handwerker D. A., Keilholz S., Kiviniemi V., Leopold D. A., de Pasquale F., Sporns O., Walter M. and Chang C. (2013). “Dynamic functional connectivity: promise, issues, and interpretations.” Neuroimage 80: 360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison R. M., Womelsdorf T., Allen E. A., Bandettini P. A., Calhoun V. D., Corbetta M., Penna S. D., Duyn J. H., Glover G. H., Gonzalez-Castillo J., Handwerker D. A., Keilholz S. D., Kiviniemi V. J., Leopold D. A., Pasquale F. d., Sporns O., Walter M. and Chang C. (2013). “Dynamic functional connectivity: Promise, issues, and interpretations.” NeuroImage 80: 360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison R. M., Womelsdorf T., Gati J. S., Everling S. and Menon R. S. (2013). “Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques.” Human brain mapping 34(9): 2154–2177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyatt C. J., Wexler B. E., Pittman B., Nicholson A., Pearlson G. D., Corbera S., Bell M. D., Pelphrey K., Calhoun V. D. and Assaf M. (2022). “Atypical dynamic functional network connectivity state engagement during social-emotional processing in schizophrenia and autism.” Cerebral Cortex 32(16): 3406–3422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iraji A., Deramus T. P., Lewis N., Yaesoubi M., Stephen J. M., Erhardt E., Belger A., Ford J. M., McEwen S. and Mathalon D. H. (2019). “The spatial chronnectome reveals a dynamic interplay between functional segregation and integration.” Human brain mapping 40(10): 3058–3077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iraji A., Faghiri A., Lewis N., Fu Z., Rachakonda S. and Calhoun V. D. (2020). “Tools of the trade: estimating time-varying connectivity patterns from fMRI data.” Social Cognitive and Affective Neuroscience 16(8): 849–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iraji A., Fu Z., Damaraju E., DeRamus T. P., Lewis N., Bustillo J. R., Lenroot R. K., Belger A., Ford J. M. and McEwen S. (2019). “Spatial dynamics within and between brain functional domains: A hierarchical approach to study time-varying brain function.” Human brain mapping 40(6): 1969–1986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jammalamadaka S. R., Sengupta A. and Sengupta A. (2001). Topics in circular statistics, world scientific [Google Scholar]
- Jones D. T., Vemuri P., Murphy M. C., Gunter J. L., Senjem M. L., Machulda M. M., Przybelski S. A., Gregg B. E., Kantarci K. and Knopman D. S. (2012). “Non-stationarity in the “resting brain’s” modular architecture.” PloS one 7(6): e39731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kajimura S., Margulies D. and Smallwood J. (2023). “Frequency-specific brain network architecture in resting-state fMRI.” Scientific Reports 13(1): 2964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang H., Ombao H., Fonnesbeck C., Ding Z. and Morgan V. L. (2017). “A Bayesian double fusion model for resting-state brain connectivity using joint functional and structural data.” Brain connectivity 7(4): 219–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazemivash B. and Calhoun V. D. (2022). “A 5D approach to study spatio-temporal dynamism of resting-state brain networks in schizophrenia.” Annu Int Conf IEEE Eng Med Biol Soc 2022: 3737–3740. [DOI] [PubMed] [Google Scholar]
- Keilholz S. D., Magnuson M. E., Pan W.-J., Willis M. and Thompson G. J. (2013). “Dynamic properties of functional connectivity in the rodent.” Brain connectivity 3(1): 31–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelso J. S. (1995). Dynamic patterns: The self-organization of brain and behavior, MIT press. [Google Scholar]
- Kim D., Burge J., Lane T., Pearlson G. D., Kiehl K. A. and Calhoun V. D. (2008). “Hybrid ICA-Bayesian network approach reveals distinct effective connectivity differences in schizophrenia.” Neuroimage 42(4): 1560–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopell N. and Ermentrout G. B. (2002). “Mechanisms of phase-locking and frequency control in pairs of coupled neural oscillators.” Handbook of dynamical systems 2: 3–54. [Google Scholar]
- Kumar S., Reddy T. and Behera L. (2018). EEG based motor imagery classification using instantaneous phase difference sequence. 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), IEEE. [Google Scholar]
- Lachaux J. P., Rodriguez E., Martinerie J. and Varela F. J. (1999). “Measuring phase synchrony in brain signals.” Human brain mapping 8(4): 194–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird A., Carew J. and Meyerand M. E. (2001). Analysis of the instantaneous phase signal of a fMRI time series via the Hilbert transform. Conference Record of Thirty-Fifth Asilomar Conference on Signals, Systems and Computers (Cat. No. 01CH37256), IEEE. [Google Scholar]
- Laird A. R., Rogers B. P., Carew J. D., Arfanakis K., Moritz C. H. and Meyerand M. E. (2002). “Characterizing instantaneous phase relationships in whole-brain fMRI activation data.” Human brain mapping 16(2): 71–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J. G. and Sepulchre R. J. (2024). “Rapid and robust synchronization via weak synaptic coupling.” Automatica 160: 111416. [Google Scholar]
- Leonardi N. and Van De Ville D. (2015). “On spurious and real fluctuations of dynamic functional connectivity during rest.” Neuroimage 104: 430–436. [DOI] [PubMed] [Google Scholar]
- Li J., Cheng L., Chen S., Zhang J., Liu D., Liang Z. and Li H. (2022). “Functional Connectivity Changes in Multiple-Frequency Bands in Acute Basal Ganglia Ischemic Stroke Patients: A Machine Learning Approach.” Neural Plast 2022: 1560748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liégeois R., Ziegler E., Phillips C., Geurts P., Gómez F., Bahri M. A., Yeo B. T. T., Soddu A., Vanhaudenhuyse A., Laureys S. and Sepulchre R. (2016). “Cerebral functional connectivity periodically (de)synchronizes with anatomical constraints.” Brain Structure and Function 221(6): 2985–2997 [DOI] [PubMed] [Google Scholar]
- Linke A. C., Mash L. E., Fong C. H., Kinnear M. K., Kohli J. S., Wilkinson M., Tung R., Jao Keehn R. J., Carper R. A., Fishman I. and Müller R. A. (2020). “Dynamic time warping outperforms Pearson correlation in detecting atypical functional connectivity in autism spectrum disorders.” NeuroImage 223: 117383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X., Zhang N., Chang C. and Duyn J. H. (2018). “Co-activation patterns in resting-state fMRI signals.” Neuroimage 180: 485–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-González A., Panda R., Ponce-Alvarez A., Zamora-López G., Escrichs A., Martial C., Thibaut A., Gosseries O., Kringelbach M. L., Annen J., Laureys S. and Deco G. (2021). “Loss of consciousness reduces the stability of brain hubs and the heterogeneity of brain dynamics.” Communications Biology 4(1): 1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe M. J., Dzemidzic M., Lurito J. T., Mathews V. P. and Phillips M. D. (2000). “Correlations in low-frequency BOLD fluctuations reflect cortico-cortical connections.” Neuroimage 12(5): 582–587 [DOI] [PubMed] [Google Scholar]
- Lowet E., Roberts M. J., Bonizzi P., Karel J. and De Weerd P. (2016). “Quantifying neural oscillatory synchronization: a comparison between spectral coherence and phase-locking value approaches.” PloS one 11(1): e0146443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Y., He H., Duan M., Huang H., Hu Z., Wang H., Yao G., Yao D., Li J. and Luo C. (2020). “Dynamic functional connectivity strength within different frequency-band in schizophrenia.” Frontiers in Psychiatry 10: 995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lurie D. J., Kessler D., Bassett D. S., Betzel R. F., Breakspear M., Kheilholz S., Kucyi A., Liégeois R., Lindquist M. A., McIntosh A. R., Poldrack R. A., Shine J. M., Thompson W. H., Bielczyk N. Z., Douw L., Kraft D., Miller R. L., Muthuraman M., Pasquini L., Razi A., Vidaurre D., Xie H. and Calhoun V. D. (2020). “Questions and controversies in the study of time-varying functional connectivity in resting fMRI.” Netw Neurosci 4(1): 30–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynall M.-E., Bassett D. S., Kerwin R., McKenna P. J., Kitzbichler M., Muller U. and Bullmore E. (2010). “Functional connectivity and brain networks in schizophrenia.” Journal of Neuroscience 30(28): 9477–9487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majeed W., Magnuson M. and Keilholz S. D. (2009). “Spatiotemporal dynamics of low frequency fluctuations in BOLD fMRI of the rat.” Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine 30(2): 384–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meszlényi R. J., Hermann P., Buza K., Gál V. and Vidnyánszky Z. (2017). “Resting State fMRI Functional Connectivity Analysis Using Dynamic Time Warping.” Frontiers in Neuroscience 11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller R. L., Yaesoubi M., Turner J. A., Mathalon D., Preda A., Pearlson G., Adali T. and Calhoun V. D. (2016). “Higher dimensional meta-state analysis reveals reduced resting fMRI connectivity dynamism in schizophrenia patients.” PloS one 11(3): e0149849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohanty R., Sethares W. A., Nair V. A. and Prabhakaran V. (2020). “Rethinking measures of functional connectivity via feature extraction.” Scientific reports 10(1): 1298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mokhtari F., Akhlaghi M. I., Simpson S. L., Wu G. and Laurienti P. J. (2019). “Sliding window correlation analysis: Modulating window shape for dynamic brain connectivity in resting state.” Neuroimage 189: 655–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mormann F., Lehnertz K., David P. and Elger C. E. (2000). “Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients.” Physica D: Nonlinear Phenomena 144(3-4): 358–369. [Google Scholar]
- Mostame P. and Sadaghiani S. (2020). “Phase- and amplitude-coupling are tied by an intrinsic spatial organization but show divergent stimulus-related changes.” NeuroImage 219: 117051. [DOI] [PubMed] [Google Scholar]
- Motlaghian S. M., Belger A., Bustillo J. R., Ford J. M., Iraji A., Lim K., Mathalon D. H., Mueller B. A., O’Leary D., Pearlson G., Potkin S. G., Preda A., van Erp T. G. M. and Calhoun V. D. (2022). “Nonlinear functional network connectivity in resting functional magnetic resonance imaging data.” Hum Brain Mapp 43(15): 4556–4566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulders P. C., van Eijndhoven P. F., Schene A. H., Beckmann C. F. and Tendolkar I. (2015). “Resting-state functional connectivity in major depressive disorder: a review.” Neuroscience & Biobehavioral Reviews 56: 330–344. [DOI] [PubMed] [Google Scholar]
- Nejad A. B., Ebdrup B. H., Glenthøj B. Y. and Siebner H. R. (2012). “Brain connectivity studies in schizophrenia: unravelling the effects of antipsychotics.” Curr Neuropharmacol 10(3): 219–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omidvarnia A., Pedersen M., Walz J. M., Vaughan D. N., Abbott D. F. and Jackson G. D. (2016). “Dynamic regional phase synchrony (DRePS) An Instantaneous Measure of Local fMRI Connectivity Within Spatially Clustered Brain Areas.” Human Brain Mapping 37(5): 1970–1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oppenheim A. V. (1999). Discrete-time signal processing, Pearson Education India. [Google Scholar]
- Panda R., Thibaut A., Lopez-Gonzalez A., Escrichs A., Bahri M. A., Hillebrand A., Deco G., Laureys S., Gosseries O., Annen J. and Tewarie P. (2022). “Disruption in structural-functional network repertoire and time-resolved subcortical fronto-temporoparietal connectivity in disorders of consciousness.” eLife 11: e77462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen M., Omidvarnia A., Walz J. M., Zalesky A. and Jackson G. D. (2017). “Spontaneous brain network activity: Analysis of its temporal complexity.” Network Neuroscience 1(2): 100–115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen M., Omidvarnia A., Zalesky A. and Jackson G. D. (2018). “On the relationship between instantaneous phase synchrony and correlation-based sliding windows for time-resolved fMRI connectivity analysis.” NeuroImage 181: 85–94. [DOI] [PubMed] [Google Scholar]
- Penny W. D., Friston K. J., Ashburner J. T., Kiebel S. J. and Nichols T. E. (2011). Statistical parametric mapping: the analysis of functional brain images, Elsevier. [Google Scholar]
- Pettersson-Yeo W., Allen P., Benetti S., McGuire P. and Mechelli A. (2011). “Dysconnectivity in schizophrenia: where are we now?” Neurosci Biobehav Rev 35(5): 1110–1124. [DOI] [PubMed] [Google Scholar]
- Picinbono B. (1997). “On instantaneous amplitude and phase of signals.” IEEE Transactions on signal processing 45(3): 552–560. [Google Scholar]
- Pockett S., Bold G. E. and Freeman W. J. (2009). “EEG synchrony during a perceptual-cognitive task: Widespread phase synchrony at all frequencies.” Clinical Neurophysiology 120(4): 695–708 [DOI] [PubMed] [Google Scholar]
- Preti M. G., Bolton T. A. W. and Van De Ville D. (2017). “The dynamic functional connectome: State-of-the-art and perspectives.” NeuroImage 160: 41–54. [DOI] [PubMed] [Google Scholar]
- Proakis J. G. (2007). Digital signal processing: principles, algorithms, and applications, 4/E, Pearson Education India. [Google Scholar]
- Proakis J. G., Salehi M., Zhou N. and Li X. (1994). Communication systems engineering. Prentice Hall New Jersey. [Google Scholar]
- Rabany L., Brocke S., Calhoun V. D., Pittman B., Corbera S., Wexler B. E., Bell M. D., Pelphrey K., Pearlson G. D. and Assaf M. (2019). “Dynamic functional connectivity in schizophrenia and autism spectrum disorder: Convergence, divergence and classification.” NeuroImage: Clinical 24: 101966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebollo I., Devauchelle A.-D., Béranger B. and Tallon-Baudry C. (2018). “Stomach-brain synchrony reveals a novel, delayed-connectivity resting-state network in humans.” Elife 7: e33321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roden M. S. (1991). Analog and digital communication systems, Prentice-Hall, Inc. [Google Scholar]
- Rosenblum M. G., Pikovsky A. S. and Kurths J. (1996). “Phase synchronization of chaotic oscillators.” Physical review letters 76(11): 1804. [DOI] [PubMed] [Google Scholar]
- Sakoğlu U., Pearlson G. D., Kiehl K. A., Wang Y. M., Michael A. M. and Calhoun V. D. (2010). “A method for evaluating dynamic functional network connectivity and task-modulation: application to schizophrenia.” Magma 23(5-6): 351–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakoğlu Ü., Pearlson G. D., Kiehl K. A., Wang Y. M., Michael A. M. and Calhoun V. D. (2010). “A method for evaluating dynamic functional network connectivity and task-modulation: application to schizophrenia.” Magnetic Resonance Materials in Physics, Biology and Medicine 23: 351–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salman M. S., Vergara V. M., Damaraju E. and Calhoun V. D. (2019). “Decreased cross-domain mutual information in schizophrenia from dynamic connectivity states.” Frontiers in Neuroscience 13: 457620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savva A. D., Mitsis G. D. and Matsopoulos G. K. (2019). “Assessment of dynamic functional connectivity in resting-state fMRI using the sliding window technique.” Brain Behav 9(4): e01255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmittmann V. D., Jahfari S., Borsboom D., Savi A. O. and Waldorp L. J. (2015). “Making large-scale networks from fMRI data.” PloS one 10(9): e0129074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schönbrodt F. D. and Perugini M. (2013). “At what sample size do correlations stabilize?” Journal of Research in Personality 47(5): 609–612. [Google Scholar]
- Schwemmer M. A. and Lewis T. J. (2012). “The theory of weakly coupled oscillators.” Phase response curves in neuroscience: theory, experiment, and analysis: 3–31. [Google Scholar]
- Scott G., Fagerholm E. D., Mutoh H., Leech R., Sharp D. J., Shew W. L. and Knöpfel T. (2014). “Voltage imaging of waking mouse cortex reveals emergence of critical neuronal dynamics.” Journal of Neuroscience 34(50): 16611–16620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma D. K., Mishra A. and Saxena R. (2010). “Analog & digital modulation techniques: an overview.” International Journal of Computing Science and Communication Technologies 3(1): 2007 [Google Scholar]
- Sheffield J. M. and Barch D. M. (2016). “Cognition and resting-state functional connectivity in schizophrenia.” Neuroscience & Biobehavioral Reviews 61: 108–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheline Y. I. and Raichle M. E. (2013). “Resting state functional connectivity in preclinical Alzheimer’s disease.” Biological psychiatry 74(5): 340–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirer W. R., Ryali S., Rykhlevskaia E., Menon V. and Greicius M. D. (2011). “Decoding Subject-Driven Cognitive States with Whole-Brain Connectivity Patterns.” Cerebral Cortex 22(1): 158–165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siems M. and Siegel M. (2020). “Dissociated neuronal phase- and amplitude-coupling patterns in the human brain.” NeuroImage 209: 116538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivarajah P., Steinbacher A., Dastrup B., Lu J., Xiang M., Ren W., Kamba S., Cao S. and Nelson K. A. (2019). “THz-frequency magnon-phonon-polaritons in the collective strong-coupling regime.” Journal of Applied Physics 125(21). [Google Scholar]
- Smillie G. (1999). Analogue and digital communication techniques, Elsevier. [Google Scholar]
- Sojakova K. (2016). “The equivalence of the torus and the product of two circles in homotopy type theory.” ACM Transactions on Computational Logic (TOCL) 17(4): 1–19 [Google Scholar]
- Sporns O. (2016). Networks of the Brain. MIT press. [Google Scholar]
- Sun F. T., Miller L. M. and D’esposito M. (2004). “Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data.” Neuroimage 21(2): 647–658. [DOI] [PubMed] [Google Scholar]
- Sun J., Hong X. and Tong S. (2012). “Phase synchronization analysis of EEG signals: an evaluation based on surrogate tests.” IEEE Transactions on Biomedical Engineering 59(8): 2254–2263. [DOI] [PubMed] [Google Scholar]
- Tagliazucchi E., Von Wegner F., Morzelewski A., Brodbeck V. and Laufs H. (2012). “Dynamic BOLD functional connectivity in humans and its electrophysiological correlates.” Frontiers in human neuroscience 6: 339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tass P., Rosenblum M., Weule J., Kurths J., Pikovsky A., Volkmann J., Schnitzler A. and Freund H.-J. (1998). “Detection of n: m phase locking from noisy data: application to magnetoencephalography.” Physical review letters 81(15): 3291. [Google Scholar]
- Telesford Q. K., Simpson S. L., Burdette J. H., Hayasaka S. and Laurienti P. J. (2011). “The brain as a complex system: using network science as a tool for understanding the brain.” Brain connectivity 1(4): 295–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thümler M., Srinivas S. G., Schröder M. and Timme M. (2023). “Synchrony for weak coupling in the complexified Kuramoto model.” Physical Review Letters 130(18): 187201. [DOI] [PubMed] [Google Scholar]
- Torabi M., Mitsis G. D. and Poline J.-B. (2024). “On the variability of dynamic functional connectivity assessment methods.” GigaScience 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner R., Howseman A., Rees G. E., Josephs O. and Friston K. (1998). “Functional magnetic resonance imaging of the human brain: data acquisition and analysis.” Exp Brain Res 123(1-2): 5–12. [DOI] [PubMed] [Google Scholar]
- Van Den Heuvel M. P. and Pol H. E. H. (2010). “Exploring the brain network: a review on resting-state fMRI functional connectivity.” European neuropsychopharmacology 20(8): 519–534. [DOI] [PubMed] [Google Scholar]
- Van den Heuvel M. P. and Sporns O. (2013). “Network hubs in the human brain.” Trends in cognitive sciences 17(12): 683–696. [DOI] [PubMed] [Google Scholar]
- Van Essen D. C., Smith S. M., Barch D. M., Behrens T. E. J., Yacoub E. and Ugurbil K. (2013). “The WU-Minn Human Connectome Project: An overview.” NeuroImage 80: 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen D. C., Ugurbil K., Auerbach E., Barch D., Behrens T. E., Bucholz R., Chang A., Chen L., Corbetta M., Curtiss S. W., Delia Penna S., Feinberg D., Glasser M. F., Harel N., Heath A. C., Larson-Prior L., Marcus D., Michalareas G., Moeller S., Oostenveld R., Petersen S. E., Prior F., Schlaggar B. L., Smith S. M., Snyder A. Z., Xu J. and Yacoub E. (2012). “The Human Connectome Project: a data acquisition perspective.” Neuroimage 62(4): 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varela F., Lachaux J.-P., Rodriguez E. and Martinerie J. (2001). “The brainweb: phase synchronization and large-scale integration.” Nature reviews neuroscience 2(4): 229–239. [DOI] [PubMed] [Google Scholar]
- Veer I. M., Beckmann C. F., Van Tol M.-J., Ferrarini L., Milles J., Veltman D. J., Aleman A., Van Buchem M. A., van der Wee N. J. and Rombouts S. A. (2010). “Whole brain resting-state analysis reveals decreased functional connectivity in major depression.” Frontiers in systems neuroscience 4: 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vohryzek J., Deco G., Cessac B., Kringelbach M. L. and Cabral J. (2020). “Ghost attractors in spontaneous brain activity: Recurrent excursions into functionally-relevant BOLD phase-locking states.” Frontiers in systems neuroscience 14: 20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C. and Da F. (2012). “Phase demodulation using adaptive windowed Fourier transform based on Hilbert-Huang transform.” Optics Express 20(16): 18459–18477. [DOI] [PubMed] [Google Scholar]
- Wang Z., Alahmadi A., Zhu D. and Li T. (2015). Brain functional connectivity analysis using mutual information. 2015 IEEE global conference on signal and information processing (GlobalSIP), IEEE [Google Scholar]
- Weber S., Johnsen E., Kroken R. A., Løberg E.-M., Kandilarova S., Stoyanov D., Kompus K. and Hugdahl K. (2020). “Dynamic functional connectivity patterns in schizophrenia and the relationship with hallucinations.” Frontiers in psychiatry 11: 498643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welvaert M. and Rosseel Y. (2013). “On the definition of signal-to-noise ratio and contrast-to-noise ratio for FMRI data.” PLoS One 8(11): e77089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiafe S.-L., Faghiri A., Fu Z., Miller R. and Calhoun V. (2024). Capturing Stretching and Shrinking of Inter-Network Temporal Coupling in FMRI Via WARP Elasticity. [Google Scholar]
- Wiafe S.-L., Faghiri A., Fu Z., Miller R., Preda A. and Calhoun V. D. (2024). “The dynamics of dynamic time warping in fMRI data: a method to capture inter-network stretching and shrinking via warp elasticity.” Imaging Neuroscience. [Google Scholar]
- Wiafe S.-L., Kinsey S., Iraji A., Miller R. and Calhoun V. D. (2024). “Normalized Dynamic Time Warping Increases Sensitivity In Differentiating Functional Network Connectivity In Schizophrenia.” bioRxiv: 2024.2010.2031.621415. [Google Scholar]
- Wiafe S. L., Fu Z., Calhoun V. D. and Faghiri A. (2023). “Phase and amplitude, two sides of functional connectivity.” Annu Int Conf IEEE Eng Med Biol Soc 2023: 1–4. [DOI] [PubMed] [Google Scholar]
- Williamson P. C. and Allman J. M. (2012). “A framework for interpreting functional networks in schizophrenia.” Frontiers in human neuroscience 6: 184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y. and Yan D. (2006). “The Bedrosian identity for the Hilbert transform of product functions.” Proceedings of the American Mathematical Society 134(9): 2719–2728. [Google Scholar]
- Yaesoubi M., Allen E. A., Miller R. L. and Calhoun V. D. (2015). “Dynamic coherence analysis of resting fMRI data to jointly capture state-based phase, frequency, and time-domain information.” NeuroImage 120: 133–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A. and Breakspear M. (2015). “Towards a statistical test for functional connectivity dynamics.” NeuroImage 114: 466–470. [DOI] [PubMed] [Google Scholar]
- Zalesky A., Fornito A., Cocchi L., Gollo L. L. and Breakspear M. (2014). “Time-resolved resting-state brain networks.” Proceedings of the National Academy of Sciences 111(28): 10341–10346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng L.-L., Shen H., Liu L., Wang L., Li B., Fang P., Zhou Z., Li Y. and Hu D. (2012). “Identifying major depression using whole-brain functional connectivity: a multivariate pattern analysis.” Brain 135(5): 1498–1507. [DOI] [PubMed] [Google Scholar]
- Zhan X., Ma T., Liu S. and Shimizu K. (2019). “On circular correlation for data on the torus.” Statistical papers 60: 1827–1847. [Google Scholar]
- Zhang G., Cai B., Zhang A., Stephen J. M., Wilson T. W., Calhoun V. D. and Wang Y. P. (2020). “Estimating Dynamic Functional Brain Connectivity With a Sparse Hidden Markov Model.” IEEE Trans Med Imaging 39(2): 488–498. [DOI] [PubMed] [Google Scholar]
- Zhang Y., Pan X., Wang R. and Sakagami M. (2016). “Functional connectivity between prefrontal cortex and striatum estimated by phase locking value.” Cognitive neurodynamics 10: 245–254 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J., Zhu H., Wang J. and Sun J. (2023). “Dynamic Characteristics of Local Functional Connectivity Revealed by Dynamic Regional Phase Synchrony.” IEEE Transactions on Neural Systems and Rehabilitation Engineering 31: 2507–2517. [DOI] [PubMed] [Google Scholar]
- Ziaeemehr A. and Valizadeh A. (2021). “Frequency-Resolved Functional Connectivity: Role of Delay and the Strength of Connections.” Front Neural Circuits 15: 608655. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The codes for all our analyses in MATLAB language can be accessed through GitHub (https://github.com/Sirlord-Sen/studying_trFNC_via_communication_theory). The data was not collected by us and was provided in a deidentified manner. The IRB will not allow sharing of data or individual derivatives as a data reuse agreement was not signed by the subjects during the original acquisition.