Skip to main content
PMC home page

This is a preprint.

It has not yet been peer reviewed by a journal.

The National Library of Medicine is running a pilot to include preprints that result from research funded by NIH in PMC and PubMed.

bioRxiv logoLink to bioRxiv
[Preprint]. 2024 Jun 14:2024.06.12.598645. [Version 1] doi: 10.1101/2024.06.12.598645

The Roles of Drift and Selection on Short Stamen Loss in Arabidopsis thaliana along an Elevational Gradient in the Spanish Pyrenees

Sophia F Buysse 1,2,3, Samuel G Pérez 1,2,3, Joshua R Puzey 4, Ava Garrison 1,2,3, Gideon S Bradburd 5, Christopher G Oakley 6, Stephen J Tonsor 7, F Xavier Picó 8, Emily B Josephs 1,2,9,*, Jeffrey K Conner 1,2,3,*
PMCID: PMC11195200  PMID: 38915635

Abstract

Traits that have lost function sometimes persist through evolutionary time. These traits may be maintained by a lack of standing genetic variation for the trait, if selection against the trait is weak relative to drift, or if they have a residual function. To determine the evolutionary processes shaping whether nonfunctional traits are retained or lost, we investigated short stamens in 16 populations of Arabidopsis thaliana along an elevational cline in the Spanish Pyrenees. We found a cline in short stamen number from retention of short stamens in high elevation populations to incomplete loss in low elevation populations. We did not find evidence that limited genetic variation constrains the loss of short stamens at high elevations nor evidence for divergent selection on short stamens between high and low elevations. Finally, we identified loci associated with short stamens in the Spanish Pyrenees that are different from loci associated with variation in short stamen number across latitudes from a previous study. Overall, we did not identify the evolutionary mechanisms maintaining an elevational cline in short stamen number but did identify different genetic loci underlying the variation in short stamen along similar phenotypic clines.

Keywords: genetic drift, trait loss, selection, effective population size, stamen, elevational cline

Introduction

Traits that have lost function are often lost through evolutionary time, yet some persist. Nonfunctional traits could be lost through direct selection against the trait (Dorken et al., 2004; Lahti et al., 2009), correlated responses to selection on other traits caused by pleiotropy or linkage disequilibrium (Yoshizawa et al., 2012), or the accumulation of selectively neutral mutations (Fong et al., 1995). In contrast, nonfunctional traits may be maintained by evolutionary constraint if the nonfunctional trait is genetically correlated with a different, functional trait (Lande, 1979; Walsh & Blows, 2009). Nonfunctional trait loss could also be prevented if there is not enough standing genetic variation for selection to act on the trait (Lahti et al., 2009) or if weak selection against the trait is unable to overcome drift (Charlesworth, 2009). Both of these processes may be pronounced in species with small effective population sizes. Determining the evolutionary processes shaping whether nonfunctional traits are retained or lost will have broad implications for our understanding of the interplay of direct selection, correlated responses to selection, and genetic drift (reviewed in Futuyma, 2010).

Here, we use an elevational cline in short stamen number in Arabidopsis thaliana to investigate how evolutionary processes interact to shape variation in a trait that has lost function. Almost all of the 3,700 species in the Brassicaceae family have flowers with four long and two short stamens (Endress, 1992). While the function of short stamens is unknown, maintaining the stamen length difference is likely adaptive in wild radish, Raphanus raphanistrum, an outcrossing species within Brassicaceae (Conner et al., 2003; Waterman et al., 2023). However, A. thaliana evolved to be almost entirely self-fertilizing from an outcrossing ancestor between 0.5 – 1 million years ago (Durvasula et al., 2017; Tang et al., 2007). In flowering plants, a transition from outcrossing to self-pollination and subsequent relaxation of selection for pollination often results in a suite of trait changes, called the ‘selfing syndrome’, that includes smaller flowers and reduced distance between the anthers and stigma (Sicard & Lenhard, 2011). Self-pollination also decreases local effective population size (Caballero, 1994), increasing the effects of genetic drift.

Short stamens in A. thaliana do not contribute significantly to self-fertilized seed number, but have nonetheless been retained in most natural populations (Royer et al., 2016). In particular, southern European populations are more likely to lose short stamens while northern European populations retain both short stamens. Because northern European populations of A. thaliana have undergone repeated bottlenecks that reduced effective population size, and thus standing genetic variation (Beck et al., 2008; François et al., 2008; Lewandowska-Sabat et al., 2010), short stamens may be retained in these populations because there is insufficient genetic variation for stamen number and/or weak selection against stamens cannot overcome drift. Alternatively, the latitudinal cline of the European populations could be maintained by local adaptation for short stamen number or another correlated trait. The same evolutionary processes may shape elevational clines in short stamen number. High elevations were glaciated, even at southern latitudes (Hughes et al., 2006) and while the Spanish Pyrenees do include putative refugia regions (Médail & Diadema, 2009), prior work in the Pyrenees has shown high elevation montane populations have less genetic variation and smaller effective population sizes than lower elevation coastal populations (Gomaa et al., 2011; Montesinos et al., 2009). Further, because environmental factors vary similarly with latitude and elevation, selection may result in similar phenotypic clines. Yet, latitudinal and elevational phenotypic clines are not always parallel (Daco et al., 2021; Kooyers et al., 2015) and when parallel phenotypic clines are identified, they may not have a parallel genetic basis (Fulgione et al., 2022; Gamba et al., 2022).

To understand the processes shaping variation in short stamen loss, we assessed 16 populations of A. thaliana along an elevational gradient in the Spanish Pyrenees. We counted short stamen number in a growth-chamber common garden and sequenced multiple individuals per population to quantify genetic variation. We identified an elevational cline in short stamen number in the Spanish Pyrenees, with more stamen loss at low elevation, similar to the previously described latitudinal cline (Royer et al., 2016). We then used multiple regression, polygenic adaptation detection, and genome wide association studies to address possible mechanisms for maintaining the cline:

  1. Is the short stamen loss cline maintained by variation in effective population size? Less stamen loss in populations with less genetic variation after accounting for variation due to elevation would be consistent with the hypothesis that stamen loss is constrained by a lack of genetic variation and less effective selection.

  2. Is the short stamen loss cline maintained by local adaptation? Evidence for divergent selection on short stamen number between high and low elevation populations would support local adaptation maintaining the cline.

  3. What genomic loci are associated with short stamen number? If we identify loci within the three previously identified QTL (Royer et al., 2016), then this would support parallel genomic evolution between the latitudinal and elevational clines in short stamen number.

Materials and Methods

Seed Collection

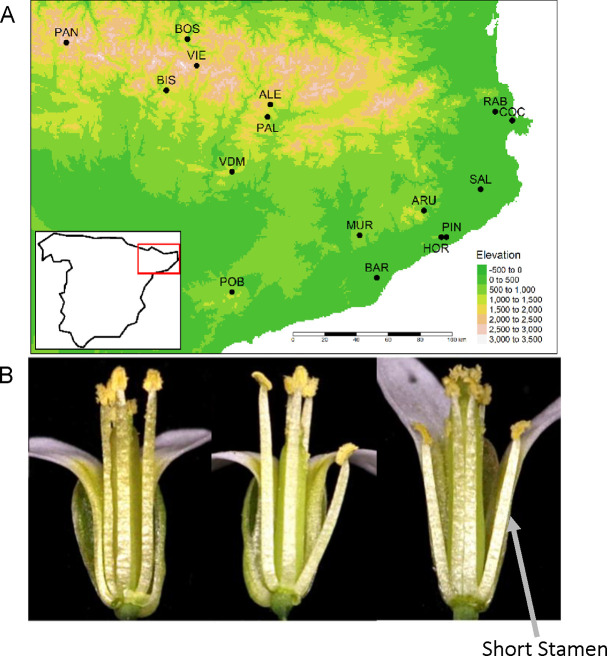
Population collection sites are along an elevation gradient across the Pyrenees and along the Mediterranean coast (Fig. 1A, Table S1). Seeds from five to nine individuals were haphazardly collected from multiple patches in each of 16 populations (n = 112 genotypes) in northeast Spain (Montesinos-Navarro et al., 2011). These lineages are also used in Montesinos-Navarro et al. (2011), Montesinos-Navarro et al. (2012), and Wolfe and Tonsor (2014). They include the 10 populations from Montesinos et al. (2009) and the 9 populations from Gomaa et al. (2011).

Figure 1: Short stamen number increases with elevation.

Figure 1:

Open in a new tab

A) Each point represents the seed collection site for 16 populations of A. thaliana across the Spanish Pyrenees. The map coloring indicates elevation from green at low elevation to white at high elevation. B) Natural variation in short stamen number. Flowers have 0 (left), 1 (center), or 2 (right) short stamens. Photos by Frances Whalen.

Phenotyping

To assess genetic differentiation for short stamen number, plants were grown in chamber common gardens in three blocks at Michigan State University, East Lansing, MI. Seeds were stratified at 4°C for five days before we increased temperatures to 22°C:18°C for 16-hour days at a constant 60% humidity for four weeks. After emergence, plants were thinned to one seedling per cell in a 200 cell plug tray. One to four plants from each of the 112 genotypes (median = 2, n= 230 plants) were vernalized at 4°C with 10-hour days for six weeks before returning to 22°C:18°C for 16-hour days through flowering.

On each plant, we counted stamen number (Fig. 1B) on up to three flowers at each of up to three timepoints throughout the duration of flowering to estimate short stamen number (1 to 9 flowers per plant, median = 6, n= 1,423 flowers). Population mean short stamen number was calculated as the arithmetic mean from all flowers phenotyped in a population (42 to 169 flowers per population, mean = 88.9, median = 99.5). The arithmetic population means were highly correlated with estimated marginal means for each population calculated with the emmeans package (Lenth, 2021) in R (v4.2.2 (R Core Team, 2021)) from a model with population as a fixed effect, random effects of flowering timepoint nested within plant nested within genotype which is nested within population, and random effect for block (r= 0.975, p < 0.001).

We sequenced the entire genomes of a subset of 61 genotypes (see below). The 61 genotypes include representatives from all 16 populations (3 or 4 different genotypes per population). In the sequenced genotypes, stamen number was counted on up to four plants per genotype (median = 2, n = 141) and up to nine flowers per plant (median = 7, n = 971). For all analyses that incorporate both phenotypic and SNP information, arithmetic population means were recalculated as the mean from flowers scored for short stamen number from sequenced genotypes (18 to 118 flowers per population, median = 63). The population means from all flowers and the population means from only the sequenced genotypes are highly correlated (r = 0.985, p < 0.001) indicating the sequenced genotypes are representative of all plants scored for short stamen number.

Sequencing

A subset of 61 genotypes (3–4 per population) were chosen for Ilumina paired-end whole-genome 150bp sequencing using the WGS-Novogene platform. Nextera adapter sequences were trimmed from the raw sequence data with Trim Galore (Krueger, 2019). We also clipped the first 15 bp of each read because quality checks with FastQC (Andrews, 2019) and MultiQC (Ewels et al., 2016) showed an identical, unusual, pattern in the first 10 bases of each read: GTTTTAAACT. Reads were mapped to the TAIR10 reference genome (Berardini et al., 2015) using BWA mem with default settings (Li & Durbin, 2009). The mean mapping rate for properly paired reads was 96.6% with a mean of 15,224,790 properly paired and mapped reads per genotype and a total of 943,936,960 mapped and paired reads in the dataset. The median depth across genotypes was low but acceptable at 8X. There is variation in coverage, missing data, and quality scores between genotypes, but no genotypes were excluded on this basis (Table S2). Duplicate reads were marked with the Genome Analysis Toolkit (GATK) v4.1.4.1 (Van der Auwera & O’Connor, 2020) MarkDuplicates Spark. After an initial round of Haplocaller and GenotypeGVCF, the dataset was filtered with the parameters suggested by GATK best practices (Van der Auwera & O’Connor, 2020): QD <2, FS > 60, MQ < 40, ReadPosRankSum < −8, and MQRankSum < −12.5. The filtered file was used as a known variants file for base quality score recalibration (BQSR). Variants were then called again with HaplotypeCaller using the GVCF flag to keep all sites before combining samples for GenotypeGVCF with the all-sites flag to create a dataset that includes both variant and invariant sites (116,855,685 total sites).

Testing the drift hypotheses

To estimate the effects of past drift and gene flow in each population, genome-wide pairwise nucleotide diversity (pi) was calculated for each population as an approximate measure of effective population size with pixy v1.0.4 (Korunes & Samuk, 2021) from a filtered dataset containing variant and invariant sites based on the pixy protocol. We used quality filters to remove all indels and low-quality sites that met the following criteria: quality score less than 20, mean depth less than 3, and more than 25% missing data. The filtered dataset contains 99,202,614 sites. A peak in nucleotide diversity was observed in the centromere of each chromosome, likely caused by fewer mapped sites (Korunes and Samuk, pers. com.). However, excluding previously published centromeres (Clark et al., 2007) did not meaningfully change genome-wide nucleotide diversity (r = 0.998, p <0.001), so centromeres are included in all of the following analyses (results excluding the centromeres can be found in Figs. S5–S7).

To test if variation in effective population size is maintaining a cline in short stamen number, we used multiple regression to identify how short stamen number was predicted by nucleotide diversity and elevation. While elevation is correlated with climatic variables such as precipitation and temperature (Montesinos-Navarro et al., 2011) that could be selective agents for plant traits, we used elevation because previous work in these same 16 populations demonstrated that elevation explained 54% of the variance in trait principal component 1 (traits include: phenology, water use efficiency, instantaneous CO2 and H2O exchange, PSII quantum efficiency, and specific leaf area) while the climate PC1 only explained 36% of the trait variation (Wolfe & Tonsor, 2014). We then visualized these results by using the residuals of single regression models. We used lme4 in R for all models (Bates et al., 2015).

A negative relationship between nucleotide diversity and short stamen number after correcting for elevation would support the hypothesis that smaller effective population sizes are constraining trait loss due to low standing variation and less effective selection. A relationship between short stamen number and elevation after correcting for nucleotide diversity could be evidence for divergent selection because it indicates the short stamen number cline persists beyond the variation explained by nucleotide diversity. However, this relationship could also result from shared evolutionary history, sometimes called shared genetic drift, if relatedness among populations is associated with elevation (Colautti & Lau, 2015). Therefore, we further investigated evidence for divergent selection by testing for local adaptation in short stamen number.

Testing for local adaptation

We used plink v1.9 (Chang et al., 2015) to filter the all-sites output from GATK to a “variant sites only” dataset for conducting genetic principal component analysis (PCA). The “variant sites only” dataset was also used for a genome-wide association study (GWAS; see below). We used quality filters to remove all indels and non-biallelic sites in addition to low quality sites that met the following criteria: minor allele frequency less than 5%, quality score less than 25, mean depth less than 5, and more than 25% missing data. The variant sites dataset contains 1,858,706 SNPs. Filtering parameters were chosen to maintain the same percent nonsynonymous sites (annotated by snpEff (Cingolani et al., 2012)) as stricter parameters while retaining more variants in the dataset. Genetic PCA was calculated for the first 20 PCs with plink v1.9 (Chang et al., 2015) to characterize genetic relatedness within, and differentiation between, populations. We looked for correlations between the population average PC value and elevation for the first 4 PCs to identify population structure associated with elevation.

We tested for divergent selection across populations on short stamen number, i.e., selection for more stamens at high elevation and/or fewer stamens at low elevation than expected due to genetic drift, with Qpc using the quaint R package (Josephs et al., 2019). Qpc is an extension of Qst-Fst analysis that uses genetic PCs to estimate additive genetic variance within and between populations (Josephs et al., 2019), and tests for phenotypic differentiation due to selection beyond that expected from neutral evolution. This differs from the multiple regression test for the drift hypothesis described above because Qpc explicitly considers among population differentiation. Qpc incorporates genetic relatedness within and among populations through a kinship matrix, rather than a single measure of population differentiation as in Qst-Fst. Qpc then tests for excess phenotypic divergence along major axes of genetic relatedness (principal components of the kinship matrix) rather than excess phenotypic divergence between populations as in Qst-Fst (Josephs et al., 2019). The input kinship matrix was generated from a random subset of 50,000 SNPs that had no missing data. This kinship matrix is slightly different from the kinship matrix used for genetic PCA because Qpc requires a kinship matrix standardized across all loci, not each locus individually as in plink, and quaint is not capable of dealing with missing data.

Using genome wide association studies (GWAS) to identify loci associated with short stamen loss

We performed GWAS to find genomic regions associated with short stamen number. Mean short stamen number was not normally distributed (Shapiro-Wilk w=0.85, p = 3.27×10−6; Fig. S1). Arcsine transformation made the distribution closer to normal but still skewed (Shapiro-Wilk w = 0.91, p = 2.72×10−4; Fig. S1). Phenotypic and genotypic data were merged in plink v1.9 (Chang et al., 2015). GWAS was conducted in gemma v0.98.4 with the Wald hypothesis test for each SNP against the alternate allele and a centered kinship matrix to account for population structure (Zhou & Stephens, 2012). The output was visualized with the qqman (Turner, 2018) and ggplot2 (Wickham et al., 2019) R packages. SNPs were further investigated if they passed a significance threshold specified using a false discovery rate (FDR) < 0.05 determined with p.adjust in R.

Additional GWAS were conducted due to the remaining skew in the arcsine-transformed data. We ran a GWAS with untransformed mean short stamen number and another with mean short stamen number coded as a binary trait. In the latter, genotypes with no short stamen loss (mean short stamen number = 2) were coded as controls and genotypes with any amount of short stamen loss (mean short stamen number < 2) were coded as cases. Finally, a fourth GWAS was conducted on the subset of genotypes that experience short stamen loss (i.e., only the genotypes with mean short stamen number < 2; Shapiro-Wilk w=0.93, p=0.0132) to ameliorate the zero-inflated-like distribution in the other continuous GWAS caused by excess genotypes with a mean short stamen number equal to 2 (Fig. S1).

We identified genetic regions with SNPs associated with short stamen number in at least two GWAS to find candidate regions for further study (“shared” SNPs). We identified overlapping regions associated with stamen loss among the four GWAS analyses by creating a 1kb window centered on each SNP that had an FDR adjusted p-value below 0.10 in any GWAS and searching for SNPs within that window that were also below an FDR adjusted p-value of 0.10 in at least one other GWAS. We chose a more lenient FDR of 0.10 for this analysis because we have higher confidence SNPs are associated with short stamen number if they pass a significance threshold in multiple analyses. We chose a window of 1kb to include regions flanking the associated SNP, although we recognize that A. thaliana genes can be larger than 1kb and that linkage disequilibrium (LD) begins to drop off around 50kb in our individuals (Fig. S2), so this is a conservative overlap criterion. SNPs in overlapping stamen loss associated regions were investigated with the TAIR10 genome browser.

All figures were created with ggplot2 (Wickham et al., 2019) and ggpubr (Kassambara, 2023) unless otherwise noted.

Results

Short stamen loss is more common at low elevation

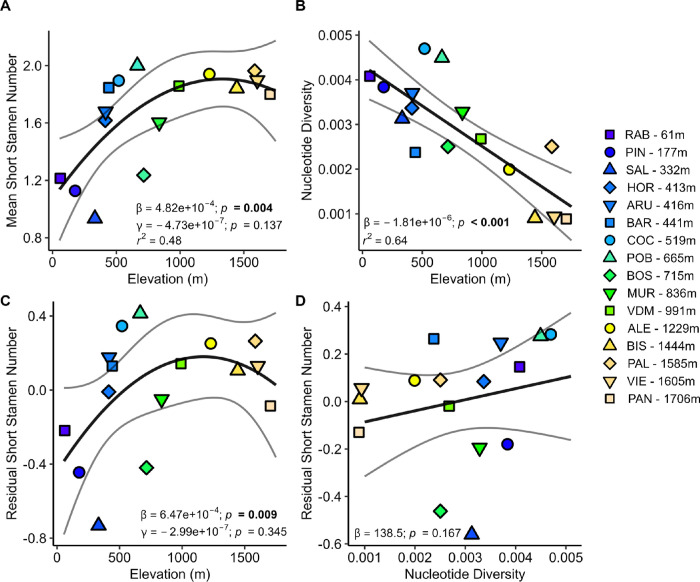
Mean short stamen number, when measured in a common garden, increases with the elevation of the source population until reaching close to two stamens around 1300m (β = 4.84×10−4, p = 0.004; γ = −4.73×10−7, p = 0.137; Fig. 2A; Table S3). Thus, short stamen retention is more common in populations from higher elevations and loss is more common at low elevations in the Spanish Pyrenees. This elevational cline is similar to the previously identified latitudinal cline where short stamen loss is more common at southern latitudes (Royer et al., 2016).

Figure 2: Effective population size does not explain retention of short stamens at high elevation.

Figure 2:

Open in a new tab

A) Mean short stamen number shows a quadratic elevational cline. B) Elevation strongly predicts population mean pairwise nucleotide diversity, our measure of effective population size. C) The residuals of the model of short stamen number regressed on nucleotide diversity then regressed on elevation and D) the residuals of the model of short stamen number regressed on quadratic elevation then regressed on nucleotide diversity. In C and D, statistics from the full model (r2 = 0.50; Table S3) are displayed on the figures. In all panels, the color of each point represents the population elevation, black lines are the regression, and grey lines are 95% confidence intervals.

Nucleotide diversity decreases with elevation, but there is no evidence that variation in effective population size maintains the cline in short stamen number

Consistent with expectations that A. thaliana in the Pyrenees experienced repeated founder effects after the last glaciation, high elevation populations have less nucleotide diversity than low elevation populations (β = −1.81×10−6, p < 0.001; Fig. 2B; Table S3). The three populations with the lowest nucleotide diversity are high elevation populations BIS, VIE, and PAN. The results are consistent with prior findings that genetic diversity and effective population size decrease with elevation in this region (Gomaa et al., 2011; Montesinos et al., 2009). Population nucleotide diversity is comparable to nucleotide diversity of A. thaliana across the Iberian Peninsula and the European range (Alonso-Blanco et al., 2016).

We hypothesized a negative relationship between nucleotide diversity and short stamen number if variation in effective population size was maintaining the short stamen cline, but nucleotide diversity did not significantly predict short stamen number when accounting for elevation (β = −138.5, p =0.167; Fig. 2D; Table S3). Further, the relationship between short stamen number and elevation is similar whether nucleotide diversity is included or not (Fig. 2C, compare to Fig. 2A; Table S3). These results suggest the short stamen number cline is not maintained by variation in effective population size but may be maintained by local adaptation, correlated responses to selection, or shared evolutionary history.

There is no evidence for divergent selection on short stamen number along the elevational cline

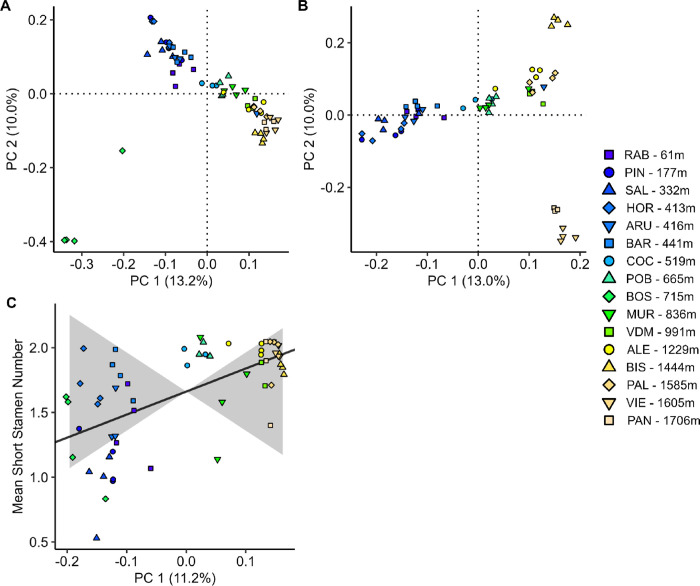
An elevational cline in short stamen number could result from local adaptation to different optima at high and low elevations. To demonstrate evidence of local adaptation resulting from divergent selection, we would need to show that the cline in short stamen number is stronger than what could be generated by neutral evolution alone. Genetic structure, here measured using genetic PCA, shows a strong pattern of genetic differentiation by elevation; both PC1 (r = −0.75, p = 9.22×10−4) and PC2 (r = −0.54, p = 0.03) are correlated with elevation (Fig. 3A). Neither PC3 nor PC4 are correlated with elevation (Fig. S3). The BOS population is an outlier along both PC1 and PC2 (Fig. 3A). This aligns with geographic information because BOS is located on a northern face of the Spanish Pyrenees while the other populations are on southern faces, and prior work identified BOS in the Northwestern genetic cluster of the Iberian Peninsula while the other 15 populations belong to the Northeast cluster or are classified as mixed (Castilla et al., 2020). The PCA was conducted a second time after removing the BOS population (Fig. 3B). These results continue to show an elevational cline along PC1 (r = −0.92, p = 1.15×10−6), though PC2 (r = −0.17, p = 0.55) separates the four highest elevation populations from each other with the closest clustering of PAN and VIE. The strong genetic differentiation across elevation we observed means that we have low power to test for even greater differentiation in stamen loss as evidence for divergent selection. Not surprisingly, we did not find evidence for divergent selection on short stamen number with Qpc. Differences in short stamen number between high and low elevation populations were not larger than could be explained by neutral evolution (Fig. 3C, p=0.257).

Figure 3: Genetic variation is correlated with elevation, but there is no evidence for divergent selection on short stamen number.

Figure 3:

Open in a new tab

A) Genetic PCA for PC1 and PC2 from 1,858,706 SNPs. B) Genetic PCA for PC1 and PC2 with BOS individuals excluded. C) Qpc results showing the relationship between mean short stamen number and genetic differentiation (black line, p=0.26) is within expectations due to neutral evolution (grey shading). The fill color of each point represents the population elevation. Panels A and C used slightly different input data (see Methods).

Few SNPs across the genome are associated with short stamen number

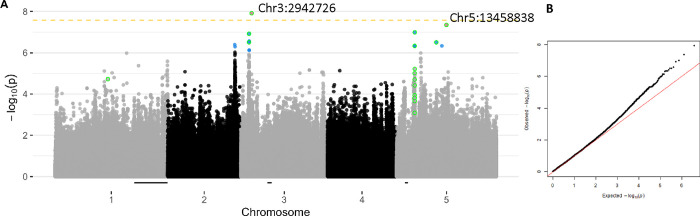
We conducted GWAS to identify loci associated with short stamen number. Because short stamen number was not normally distributed (Fig. S1), we conducted GWAS on arcsine-transformed mean short stamen number, untransformed mean short stamen number, a binary trait of whether or not individuals lacked any short stamens, and an untransformed subset of only genotypes that lack some short stamens. Each GWAS found different SNPs associated with the trait. The qqplot for the arcsine-transformed GWAS shows most p-values close to the 1:1 line between Expected and Observed (Fig. 4) but the p-values in the binary GWAS deviate early from the 1:1 line, indicating a high false positive rate in identifying SNPS associated with any short stamen loss (Fig. S4). In accordance with this observation, the binary GWAS had 1,707 SNPs associated with short stamen loss at FDR < 0.05 while the other analyses only had two or three (Figs. 4, S4). Only two SNPs are associated with arcsine-transformed short stamen number (FDR < 0.05; Fig. 4). The SNP at Chr3:2942726 is within a FAD/NAD(P)-binding oxidoreductase family protein (AT3G09580) that localizes in the chloroplast (Tomizioli et al., 2014). The SNP at Chr5:13458838 is not within a gene; the closest gene, PICALM3 (AT5G35200), is just over 3kb away.

Figure 4. Few SNPs are associated with short stamen number.

Figure 4.

Open in a new tab

Manhattan plot (A) and QQ plot (B) for arcsine-transformed mean short stamen number. The yellow dashed line indicates significance at p=0.05 after Bonferroni correction. Blue points are significant below a FDR of 0.10. Pink labelled points are significant below a FDR of 0.05. Points with a green outline are shared between at least two short stamen GWAS below FDR 0.10 (n = 20). The black bars on the x axis are Bayes 95% credible intervals for short stamen number QTL identified by Royer et al. (2016).

We identified top candidates for loci associated with short stamen number by identifying 1kb windows that have SNPs associated with short stamen number in multiple GWAS (“shared” SNPs). To do so, we calculated 1kb windows centered on all SNPs associated with short stamen number (FDR < 0.10) and searched for other SNPs that fit the same criteria and fell within each window. Twenty SNPs were associated with short stamen number in more than one GWAS from 9 different 1kb windows (Table S4). None of the SNPs fall within genes with known stamen function. However, a shared SNP at Chr3:2253161 is approximately 40kb away, thus within LD (Fig. S2), from FHA2 (AT3G07220), a SMAD/FHA domain containing protein involved in stamen development (Ahn et al., 2013; Gu et al., 2020). Mutating FHA2 proteins can cause plants to have fewer stamens, though flowers sometimes lose long stamens and sometimes lose short stamens (Ahn et al., 2013). The two SNPs associated with arcsine-transformed short stamen number (FDR < 0.05) are included in the shared SNPs (Fig. 4; Table S4).

All of the SNPs associated with variation in short stamen number fall outside the 95% credible intervals of previously identified QTL for stamen loss using recombinant inbred lines with parents from the extremes of the latitudinal stamen loss gradient (Royer et al., 2016). The closest intersection is on chromosome 5, where SNPs associated with short stamens are approximately 2,000kb further into the chromosome than the previously identified stamen loss QTL. This is beyond the start of LD decay we estimated of 50kb (Fig. S2).

Discussion

In this study, we tested for an elevation cline in short stamen loss. We found that short stamen number increased with elevation (Fig. 2A), similar to the latitudinal cline observed by Royer et al. (2016). Short stamen number is one of many traits that show an elevational cline in this region (Montesinos et al., 2009; Montesinos-Navarro et al., 2011; Wolfe & Tonsor, 2014). Of these traits, days to bolting shows similar elevational and latitudinal clines with delayed bolting at high elevations and northern latitudes (Montesinos-Navarro et al., 2011; Stinchcombe et al., 2004). Thus, short stamen number joins a growing database of traits with an elevational cline in the Spanish Pyrenees and a much smaller set of traits with parallel elevational and latitudinal clines. These clines could be maintained by effective population sizes because both high elevation populations and northern latitude populations may have undergone repeated bottlenecks that reduced effective population size since the last glaciation (Beck et al., 2008; François et al., 2008; Hughes et al., 2006; Lewandowska-Sabat et al., 2010). While the Pyrenees do include putative glacial refugia regions (Médail & Diadema, 2009), none of the 16 populations analyzed here have been classified as relict lineages that predate the last glaciation (Castilla et al., 2020). Selection could also maintain similar latitudinal and elevational clines because environmental factors such as temperature often vary in the same away across latitude and elevation.

We then tested if the cline in short stamen loss was maintained by variation in effective population size if a combination of low genetic variation and less effective selection in high elevation populations hinders a response to selection against short stamens. We found variation in genetic diversity across elevations consistent with expectations from repeated founder effects during range expansion after the last glaciation and/or low gene flow (Fig. 2B). However, the multiple regression suggests that variation in genetic diversity is not maintaining the short stamen number cline (Fig. 2C and 2D). Instead, the multiple regression suggests that elevation can explain both variation in genetic diversity and in stamen number. It is important to note that our clines show populations with low genetic diversity maintain two stamens. This is opposite to the hypothesis that genetic drift would cause trait loss which has been shown in other systems (Eckert et al., 1996; Lahti et al., 2009).

Next, we tested if the cline in short stamen loss was maintained by local adaptation using Qpc, an extension of Qst-Fst (Josephs et al., 2019). We found no evidence of local adaptation maintaining the cline in short stamen number (Fig. 3C). One caveat to our findings is that Qst-Fst struggles to identify selection when there is large genetic differentiation between populations or weak selection that results in similar values for Qst and Fst (Whitlock & Guillaume, 2009). This is also potentially an issue for Qpc in this study as there is a great deal of genetic differentiation between high and low elevation populations (Fig. 3A). However, the Qst-Fst approach has identified local adaptation contributing to elevational clines in leaf succulence and specific leaf area in 14 populations of A. thaliana from the Swiss Alps where there is also a great deal of genetic differentiation (Luo et al., 2015). Qpc has also previously been used to identify local adaptation in 249 natural A. thaliana accessions from across the European native range; local adaptation was identified in initial size, growth rate at 16°C, and temperature response (Clauw et al., 2022). Ultimately, reciprocal transplant studies across elevations in the field will provide the strongest evidence for or against local adaptation.

Finally, we used GWAS to identify loci associated with short stamen number. We identified 20 SNPs associated with short stamen number in multiple GWAS (FDR < 0.10). These SNPs lie outside the QTL for short stamens that were previously identified in a cross between a northern European and southern European accession (Royer et al., 2016). The effect sizes of the Royer et al. (2016) QTL (range from 0.05 to 0.15) and our loci (Table S4) are comparable, suggesting that we would be able to identify these QTL if they segregated at intermediate frequency in the populations used here. Instead, the populations studied here may be fixed for the southern allele identified in Royer et al (2016). However, our GWAS effect sizes may be inflated due to winner’s curse (Göring et al., 2001; Josephs et al., 2017). In addition, the QTL identified in Royer et al. (2016) were epistatic, which could make them harder to detect through standard GWAS approaches. Overall, our results suggest that the latitudinal cline in short stamen number across Europe has a different genetic basis than the elevational cline in short stamen number observed in the Pyrenees.

While the short stamen loss clines are similar between latitude and elevation, the lack of overlap between the associated loci suggests that short stamen loss is caused by mutations at different genes in different geographic regions. These results are consistent with other findings that the chromosome regions underlying the same phenotypic cline can differ by region. For example, elevational clines of A. thaliana in different geographic regions show delayed flowering at higher elevations but the genetic basis of this cline varies by global region (Gamba et al., 2022). Additionally, parallel clines in flowering time in A. thaliana in the Cape Verde Islands arose from mutations at different genes (FRI and FLC) (Fulgione et al., 2022).

In conclusion, short stamen loss is occurring in low elevation populations more than in high elevation populations. Our results suggest that retention of two short stamens in high elevation populations are not explained by reduced effective population sizes or by local adaptation to different optima in high and low elevation populations. Thus, the evolutionary mechanisms underlying variation in short stamen number are excitingly complex and deserve further study. A third hypothesis is that correlated responses to selection may maintain the cline in short stamen number (Futuyma, 2010; Lande, 1979). However, correlated responses to selection on other locally adapted traits could result in weak evidence for divergent selection; we did not find this. Future work should better characterize direct selection and correlated responses to selection on short stamens in the field by measuring fitness of plants with natural variation in short stamen number and experimental manipulation of stamens, like that done by Royer et al. (2016), in the field. Further, refining the short stamen number QTL to candidate genes and comparing to genetic regions underlying locally adapted traits could uncover the role of linked or pleiotropic genes leading to correlated responses to selection. These additional studies across both latitudinal and elevational gradients will characterize the interplay of direct selection, correlated responses to selection, and genetic drift in trait loss and identify parallel evolutionary forces at play across environmental contexts.

Supplementary Material

Supplement 1
media-1.pdf (1.6MB, pdf)

Teaser text.

The evolutionary mechanisms underlying loss or retention of traits that have lost function are poorly understood. Short stamens in Arabidopsis thaliana provide a compelling system to investigate the roles of genetic drift and selection in trait loss across latitudinal and elevational clines. This study investigates the role of drift and selection in short stamen loss in 16 populations of A. thaliana along an elevational gradient in the Spanish Pyrenees. An investigation of the genetic loci underlying variation in short stamen number suggests mutations in different genes may cause trait loss in similar phenotypic clines within a species.

Acknowledgements:

We thank D. Schemske for guidance throughout the initial stages of the project, N. Zhang for library preparation, and A. Platts for bioinformatics assistance. This manuscript was improved by comments from Conner lab and Josephs lab members.

Funding:

Research reported was supported by the National Institute of General Medical Sciences of the National Institutes of Health (NIH) under award R35GM137919 (awarded to GSB) and R35GM142829 (awarded to EBJ), and by National Science Foundation awards DEB 0919452 (to JKC) and DEB 2223962 (to JKC and GSB). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or NSF.

Footnotes

Conflict of Interest: The authors declare no conflicts of interest.

Data Availability:

These sequence data will be submitted to the GenBank database upon manuscript acceptance. All phenotypic data and code will be made available on GitHub upon acceptance. GWAS output files will be made available on figshare upon acceptance.

References

  1. Ahn E.-R., Cho H.-K., & Pai H.-S. (2013). The forkhead-associated domain 2 (FHA2) in Arabidopsis plays a role in plant fertility by regulating stamen development. Planta, 237(4), 1015–1023. 10.1007/s00425-012-1815-7 [DOI] [PubMed] [Google Scholar]
  2. Alonso-Blanco C., Andrade J., Becker C., Bemm F., Bergelson J., Borgwardt K. M. M., Cao J., Chae E., Dezwaan T. M. M., Ding W., Ecker J. R. R., Exposito-Alonso M., Farlow A., Fitz J., Gan X., Grimm D. G. G., Hancock A. M. M., Henz S. R. R., Holm S., … Zhou X. (2016). 1,135 Genomes Reveal the Global Pattern of Polymorphism in Arabidopsis thaliana. Cell, 166(2), 481–491. 10.1016/j.cell.2016.05.063 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Andrews S. (2019). FastQC (0.11.9) [Computer software]. Babraham Bioinformatics. https://www.bioinformatics.babraham.ac.uk/projects/fastqc/ [Google Scholar]
  4. Bates D., Mächler M., Bolker B., & Walker S. (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67(1), 1–48. 10.18637/JSS.V067.I01 [DOI] [Google Scholar]
  5. Beck J. B., Schmuths H., & Schaal B. A. (2008). Native range genetic variation in Arabidopsis thaliana is strongly geographically structured and reflects Pleistocene glacial dynamics. Molecular Ecology, 17(3), 902–915. 10.1111/j.1365-294X.2007.03615.x [DOI] [PubMed] [Google Scholar]
  6. Berardini T. Z., Reiser L., Li D., Mezheritsky Y., Muller R., Strait E., & Huala E. (2015). The arabidopsis information resource: Making and mining the “gold standard” annotated reference plant genome. Genesis, 53(8), 474–485. 10.1002/dvg.22877 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Caballero A. (1994). Developments in the prediction of effective population size. Heredity, 73(6), Article 6. 10.1038/hdy.1994.174 [DOI] [PubMed] [Google Scholar]
  8. Castilla A. R., Méndez-Vigo B., Marcer A., Martínez-Minaya J., Conesa D., Picó F. X., & Alonso-Blanco C. (2020). Ecological, genetic and evolutionary drivers of regional genetic differentiation in Arabidopsis thaliana. BMC Evolutionary Biology, 20(1). 10.1186/s12862-020-01635-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chang C. C., Chow C. C., Tellier L. C., Vattikuti S., Purcell S. M., & Lee J. J. (2015). Second-eneration PLINK: rising to the challenge of larger and richer datasets. GigaScience, 4(1), 7. 10.1186/S13742-015-0047-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Charlesworth B. (2009). Effective population size and patterns of molecular evolution and variation. Nature Reviews Genetics, 10(3), 195–205. 10.1038/nrg2526 [DOI] [PubMed] [Google Scholar]
  11. Cingolani P., Platts A., Wang L. L., Coon M., Nguyen T., Wang L., Land S. J., Lu X., & Ruden D. M. (2012). A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff. Fly, 6(2), 80–92. 10.4161/fly.19695 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Clark R. M., Schweikert G., Toomajian C., Ossowski S., Zeller G., Shinn P., Warthmann N., Hu T. T., Fu G., Hinds D. A., Chen H., Frazer K. A., Huson D. H., Schölkopf B., Nordborg M., Rätsch G., Ecker J. R., & Weigel D. (2007). Common sequence polymorphisms shaping genetic diversity in Arabidopsis thaliana. Science, 317(5836), 338–342. 10.1126/science.1138632 [DOI] [PubMed] [Google Scholar]
  13. Clauw P., Kerdaffrec E., Gunis J., Reichardt-Gomez I., Nizhynska V., Koemeda S., Jez J., & Nordborg M. (2022). Locally adaptive temperature response of vegetative growth in Arabidopsis thaliana. eLife, 11, e77913. 10.7554/eLife.77913 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Colautti R. I., & Lau J. A. (2015). Contemporary evolution during invasion: Evidence for differentiation, natural selection, and local adaptation. Molecular Ecology, 24(9), 1999–2017. 10.1111/mec.13162 [DOI] [PubMed] [Google Scholar]
  15. Conner J. K., Rice A. M., Stewart C., & Morgan M. T. (2003). Patterns and mechanisms of selection on a family-diagnostic trait: Evidence from experimental manipulation and lifetime fitness selection gradients. Evolution, 57(3), 480–486. 10.1111/j.0014-3820.2003.tb01539.x [DOI] [PubMed] [Google Scholar]
  16. Daco L., Colling G., & Matthies D. (2021). Altitude and latitude have different effects on population characteristics of the widespread plant Anthyllis vulneraria. Oecologia, 197(2), 537–549. 10.1007/s00442-021-05030-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dorken M. E., Neville K. J., & Eckert C. G. (2004). Evolutionary vestigialization of sex in a clonal plant: Selection versus neutral mutation in geographically peripheral populations. Proceedings of the Royal Society B: Biological Sciences, 271(1555), 2375–2380. 10.1098/rspb.2004.2875 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Durvasula A., Fulgione A., Gutaker R. M., Alacakaptan S. I., Flood P. J., Neto C., Tsuchimatsu T., Burbano H. A., Picó F. X., Alonso-Blanco C., & Hancock A. M. (2017). African genomes illuminate the early history and transition to selfing in Arabidopsis thaliana. Proceedings of the National Academy of Sciences, 114(20), 5213–5218. 10.1073/pnas.1616736114 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Eckert C. G., Manicacci D., & Barrett S. C. H. (1996). Genetic Drift and Founder Effect in Native Versus Introduced Populations of an Invading Plant, Lythrum Salicaria (lythraceae). Evolution, 50(4), 1512–1519. 10.1111/j.1558-5646.1996.tb03924.x [DOI] [PubMed] [Google Scholar]
  20. Endress P. K. (1992). Evolution and Floral Diversity: The Phylogenetic Surroundings of Arabidopsis and Antirrhinum. International Journal of Plant Sciences, 153(3), S106–S122. [Google Scholar]
  21. Ewels P., Magnusson M., Lundin S., & Käller M. (2016). MultiQC: Summarize analysis results for multiple tools and samples in a single report. Bioinformatics, 32(19), 3047–3048. 10.1093/bioinformatics/btw354 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fong D. W., Kane T. C., & Culver D. C. (1995). VESTIGIALIZATION AND LOSS OF NONFUNCTIONAL CHARACTERS. Annual Review of Ecology and Systematics, 26(1), 249–268. 10.1146/annurev.es.26.110195.001341 [DOI] [Google Scholar]
  23. François O., Blum M. G. B., Jakobsson M., & Rosenberg N. A. (2008). Demographic History of European Populations of Arabidopsis thaliana. PLOS Genetics, 4(5), e1000075. 10.1371/journal.pgen.1000075 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Fulgione A., Neto C., Elfarargi A. F., Tergemina E., Ansari S., Göktay M., Dinis H., Döring N., Flood P. J., Rodriguez-Pacheco S., Walden N., Koch M. A., Roux F., Hermisson J., & Hancock A. M. (2022). Parallel reduction in flowering time from de novo mutations enable evolutionary rescue in colonizing lineages. Nature Communications, 13(1), 1461. 10.1038/s41467-022-28800-z [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Futuyma D. J. (2010). EVOLUTIONARY CONSTRAINT AND ECOLOGICAL CONSEQUENCES. Evolution, 64(7), 1865–1884. 10.1111/J.1558-5646.2010.00960.X [DOI] [PubMed] [Google Scholar]
  26. Gamba D., Lorts C., Haile A., Sahay S., Lopez L., Xia T., Kulesza E., Elango D., Kerby J., Yifru M., Bulafu C. E., Wondimu T., Glowacka K., & Lasky J. R. (2022). The genomics and physiology of abiotic stressors associated with global elevation gradients in Arabidopsis thaliana (p. 2022.03.22.485410). bioRxiv. 10.1101/2022.03.22.485410 [DOI] [PubMed] [Google Scholar]
  27. Gomaa N. H., Montesinos-Navarro A., Alonso-Blanco C., & Picó F. X. (2011). Temporal variation in genetic diversity and effective population size of Mediterranean and subalpine Arabidopsis thaliana populations. Molecular Ecology, 20(17), 3540–3554. 10.1111/j.1365-294X.2011.05193.x [DOI] [PubMed] [Google Scholar]
  28. Göring H. H. H., Terwilliger J. D., & Blangero J. (2001). Large Upward Bias in Estimation of Locus-Specific Effects from Genomewide Scans. The American Journal of Human Genetics, 69(6), 1357–1369. 10.1086/324471 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gu B.-W., Tan L.-M., Zhang C.-J., Hou X.-M., Cai X.-W., Chen S., & He X.-J. (2020). FHA2 is a plant-specific ISWI subunit responsible for stamen development and plant fertility. Journal of Integrative Plant Biology, 62(11), 1703–1716. 10.1111/jipb.12945 [DOI] [PubMed] [Google Scholar]
  30. Hughes P. D., Woodward J. C., & Gibbard P. L. (2006). Quaternary glacial history of the Mediterranean mountains. Progress in Physical Geography: Earth and Environment, 30(3), 334–364. 10.1191/0309133306pp481ra [DOI] [Google Scholar]
  31. Josephs E. B., Berg J. J., Ross-Ibarra J., & Coop G. (2019). Detecting Adaptive Differentiation in Structured Populations with Genomic Data and Common Gardens. 10.1534/genetics.118.301786 [DOI] [PMC free article] [PubMed]
  32. Josephs E. B., Stinchcombe J. R., & Wright S. I. (2017). What can genome-wide association studies tell us about the evolutionary forces maintaining genetic variation for quantitative traits? New Phytologist, 214(1), 21–33. 10.1111/nph.14410 [DOI] [PubMed] [Google Scholar]
  33. Kassambara A. (2023). ggpubr: “ggplot2” Based Publication Ready Plots (R package version 0.6.0) [Computer software]. <https://CRAN.R-project.org/package=ggpubr>.
  34. Kooyers N. J., Greenlee A. B., Colicchio J. M., Oh M., & Blackman B. K. (2015). Replicate altitudinal clines reveal that evolutionary flexibility underlies adaptation to drought stress in annual Mimulus guttatus. New Phytologist, 206(1), 152–165. 10.1111/nph.13153 [DOI] [PubMed] [Google Scholar]
  35. Korunes K. L., & Samuk K. (2021). pixy: Unbiased estimation of nucleotide diversity and divergence in the presence of missing data. Molecular Ecology Resources. 10.1111/1755-0998.13326 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Krueger F. (2019). Trim Galore (0.6.5) [Computer software]. Babraham Bioinformatics. https://www.bioinformatics.babraham.ac.uk/projects/trim_galore/ [Google Scholar]
  37. Lahti D. C., Johnson N. A., Ajie B. C., Otto S. P., Hendry A. P., Blumstein D. T., Coss R. G., Donohue K., & Foster S. A. (2009). Relaxed selection in the wild. Trends in Ecology and Evolution, 24(9), 487–496. 10.1016/j.tree.2009.03.010 [DOI] [PubMed] [Google Scholar]
  38. Lande R. (1979). Quantitative Genetic Analysis of Multivariate Evolution, Applied to Brain: Body Size Allometry. Evolution, 33(1), 402–416. [DOI] [PubMed] [Google Scholar]
  39. Lenth R. V. (2021). emmeans: Estimated marginal Means, aka Least Squares Means (R package version 1.6.2–1) [Computer software]. https://CRAN.R-project.org/package=emmeans
  40. Lewandowska-Sabat A. M., Fjellheim S., & Rognli O. A. (2010). Extremely low genetic variability and highly structured local populations of Arabidopsis thaliana at higher latitudes. Molecular Ecology, 19(21), 4753–4764. 10.1111/j.1365-294X.2010.04840.x [DOI] [PubMed] [Google Scholar]
  41. Li H., & Durbin R. (2009). Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics, 25(14), 1754–1760. 10.1093/bioinformatics/btp324 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Luo Y., Widmer A., & Karrenberg S. (2015). The roles of genetic drift and natural selection in quantitative trait divergence along an altitudinal gradient in Arabidopsis thaliana. Heredity, 114(2), 220–228. 10.1038/hdy.2014.89 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Médail F., & Diadema K. (2009). Glacial Refugia Influence Plant Diversity Patterns in the Mediterranean Basin. Journal of Biogeography, 36(7), 1333–1345. [Google Scholar]
  44. Montesinos A., Tonsor S. J., Alonso-Blanco C., & Picó F. X. (2009). Demographic and genetic patterns of variation among populations of Arabidopsis thaliana from contrasting native environments. PLoS ONE, 4(9). 10.1371/journal.pone.0007213 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Montesinos-Navarro A., Picó F. X., & Tonsor S. J. (2012). CLINAL VARIATION IN SEED TRAITS INFLUENCING LIFE CYCLE TIMING IN ARABIDOPSIS THALIANA. Evolution, 66(11), 3417–3431. 10.1111/j.1558-5646.2012.01689.x [DOI] [PubMed] [Google Scholar]
  46. Montesinos-Navarro A., Wig J., Xavier Pico F., & Tonsor S. J. (2011). Arabidopsis thaliana populations show clinal variation in a climatic gradient associated with altitude. New Phytologist, 189(1), 282–294. 10.1111/j.1469-8137.2010.03479.x [DOI] [PubMed] [Google Scholar]
  47. R Core Team. (2021). R: A language and environment for statistical computing [Computer software]. R Foundation for Statistical Computing. https://www.R-project.org/. [Google Scholar]
  48. Royer A. M., Kremer C., George K., Pérez S. G., Schemske D. W., & Conner J. K. (2016). Incomplete loss of a conserved trait: Function, latitudinal cline, and genetic constraints. Evolution, 70(12), 2853–2864. 10.1111/evo.13096 [DOI] [Google Scholar]
  49. Sicard A., & Lenhard M. (2011). The selfing syndrome: A model for studying the genetic and evolutionary basis of morphological adaptation in plants. Annals of Botany, 107(9), 1433–1443. 10.1093/aob/mcr023 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Stinchcombe J. R., Weinig C., Ungerer M., Olsen K. M., Mays C., Halldorsdottir S. S., Purugganan M. D., & Schmitt J. (2004). A latitudinal cline in flowering time in Arabidopsis thaliana modulated by the flowering time gene FRIGIDA. Proceedings of the National Academy of Sciences, 101(13), 4712–4717. 10.1073/pnas.0306401101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Tang C., Toomajian C., Sherman-Broyles S., Plagnol V., Guo Y. L., Hu T. T., Clark R. M., Nasrallah J. B., Weigel D., & Nordborg M. (2007). The evolution of selfing in Arabidopsis thaliana. Science, 317(5841), 1070–1072. 10.1126/SCIENCE.1143153/SUPPL_FILE/TANG.SOM.REVISION.1.PDF [DOI] [PubMed] [Google Scholar]
  52. Tomizioli M., Lazar C., Brugière S., Burger T., Salvi D., Gatto L., Moyet L., Breckels L. M., Hesse A.-M., Lilley K. S., Seigneurin-Berny D., Finazzi G., Rolland N., & Ferro M. (2014). Deciphering Thylakoid Sub-compartments using a Mass Spectrometry-based Approach *. Molecular & Cellular Proteomics, 13(8), 2147–2167. 10.1074/mcp.M114.040923 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Turner S. D. (2018). qqman: An R package for visualizing GWAS results using Q-Q and manhattan plots. Journal of Open Source Software, 3(25), 731. 10.21105/JOSS.00731 [DOI] [Google Scholar]
  54. Van der Auwera G., & O’Connor B. (2020). Genomics in the Cloud: Using Docker, GATK, and WDL in Terra (1st Edition). O’Reilly Media. [Google Scholar]
  55. Walsh B., & Blows M. W. (2009). Abundant genetic variation + strong selection = multivariate genetic constraints: A geometric view of adaptation. Annual Review of Ecology, Evolution, and Systematics, 40, 41–59. 10.1146/annurev.ecolsys.110308.120232 [DOI] [Google Scholar]
  56. Waterman R., Sahli H., Koelling V. A., Karoly K., & Conner J. K. (2023). Strong evidence for positive and negative correlational selection revealed by recreating ancestral variation. Evolution, 77(1), 264–275. 10.1093/evolut/qpac001 [DOI] [PubMed] [Google Scholar]
  57. Whitlock M. C., & Guillaume F. (2009). Testing for Spatially Divergent Selection: Comparing QST to FST. Genetics, 183(3), 1055–1063. 10.1534/genetics.108.099812 [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wickham H., Averick M., Bryan J., Chang W., McGowan L., François R., Grolemund G., Hayes A., Henry L., Hester J., Kuhn M., Pedersen T., Miller E., Bache S., Müller K., Ooms J., Robinson D., Seidel D., Spinu V., … Yutani H. (2019). Welcome to the Tidyverse. Journal of Open Source Software, 4(43), 1686. 10.21105/joss.01686 [DOI] [Google Scholar]
  59. Wolfe M. D., & Tonsor S. J. (2014). Adaptation to spring heat and drought in northeastern Spanish Arabidopsis thaliana. New Phytologist, 201(1), 323–334. 10.1111/nph.12485 [DOI] [PubMed] [Google Scholar]
  60. Yoshizawa M., Yamamoto Y., O’Quin K. E., & Jeffery W. R. (2012). Evolution of an adaptive behavior and its sensory receptors promotes eye regression in blind cavefish. BMC Biology, 10(108). 10.1186/1741-7007-11-82 [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Zhou X., & Stephens M. (2012). Genome-wide efficient mixed-model analysis for association studies. Nature Genetics 2012 44:7, 44(7), 821–824. 10.1038/ng.2310 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplement 1
media-1.pdf (1.6MB, pdf)

Data Availability Statement

These sequence data will be submitted to the GenBank database upon manuscript acceptance. All phenotypic data and code will be made available on GitHub upon acceptance. GWAS output files will be made available on figshare upon acceptance.

Articles from bioRxiv are provided here courtesy of Cold Spring Harbor Laboratory Preprints

RESOURCES