Genuine high-order interactions in brain networks and neurodegeneration

Abstract

Brain functional networks have been traditionally studied considering only interactions between pairs of regions, neglecting the richer information encoded in higher orders of interactions. In consequence, most of the connectivity studies in neurodegeneration and dementia use standard pairwise metrics. Here, we developed a genuine high-order functional connectivity (HOFC) approach that captures interactions between 3 or more regions across spatiotemporal scales, delivering a more biologically plausible characterization of the pathophysiology of neurodegeneration. We applied HOFC to multimodal (electroencephalography [EEG], and functional magnetic resonance imaging [fMRI]) data from patients diagnosed with behavioral variant of frontotemporal dementia (bvFTD), Alzheimer’s disease (AD), and healthy controls. HOFC revealed large effect sizes, which, in comparison to standard pairwise metrics, provided a more accurate and parsimonious characterization of neurodegeneration. The multimodal characterization of neurodegeneration revealed hypo and hyperconnectivity on medium to large-scale brain networks, with a larger contribution of the former. Regions as the amygdala, the insula, and frontal gyrus were associated with both effects, suggesting potential compensatory processes in hub regions. fMRI revealed hypoconnectivity in AD between regions of the default mode, salience, visual, and auditory networks, while in bvFTD between regions of the default mode, salience, and somatomotor networks. EEG revealed hypoconnectivity in the γ band between frontal, limbic, and sensory regions in AD, and in the δ band between frontal, temporal, parietal and posterior areas in bvFTD, suggesting additional pathophysiological processes that fMRI alone can not capture. Classification accuracy was comparable with standard biomarkers and robust against confounders such as sample size, age, education, and motor artifacts (from fMRI and EEG). We conclude that high-order interactions provide a detailed, EEG- and fMRI compatible, biologically plausible, and psychopathological-specific characterization of different neurodegenerative conditions.

1. Introduction

Brain dynamics reflect an exquisite orchestration of neural activity at different spatial and temporal scales (Avena-Koenigsberger et al., 2017; Lynn and Bassett, 2019), which can be tracked at millisecond temporal resolution by magneto/electroencephalography (M/EEG), and at millimeter spatial resolution by functional magnetic resonance imaging (fMRI). A hallmark of brain dynamics - and self-organized systems more generally (Seif et al., 2020) - is to exhibit emergent collective behavior (Tognoli and Kelso, 2014), which refers to functional patterns of activity that are better described as a whole rather than as the sum of their parts.

Theoretical (Grasso et al., 2021; Rosas et al., 2019), methodological (Ince et al., 2017), and empirical (Delis et al., 2022; El-Gaby et al., 2021; Gatica et al., 2021; Luppi et al., 2020; Shahidi et al., 2019) studies support collective behavior as a biologically plausible signature of the brain in health and disease (Kragel et al., 2018). Nevertheless, accurately characterizing collective dynamics in brain networks has been hindered by the technical impossibility of assessing the exponentially increasing number of high-order interactions (Roebroeck et al., 2011). The simple but popular strategy to avoid this combinatorial explosion is to focus only on pairwise interactions, and extract information about collective phenomena from their overall topology via metrics derived from network science (Bullmore and Sporns, 2009). This strategy leads to functional connectivity, which captures the degree of covariation of the activity between pairs of regions. Although some functional connectivity approaches can capture nonlinear dependencies (Ince et al., 2017; King et al., 2013), the rich coordination displayed by brain function makes this approach severely limited: genuine higher-order functional interactions cannot be retrieved from networks built solely from pairwise statistics (Mazade and Alonso, 2019; Rosas et al., 2019). Thus, it is plausible that the unsatisfying performance of fMRI functional connectivity in association studies (Marek et al., 2022) may be improved not only by increasing the sample size of the corresponding datasets, but also assessing collective neural activity that goes beyond pairwise effects.

The collective dynamics of the brain — and its disruption in neuro-degeneration — can be addressed by high-order functional connectivity (HOFC), which accounts for functional interactions involving three and more brain regions, conferring HOFC more biological plausibility compared to its pairwise counterpart. An effective approximation to the computation of genuine HOFC should successfully address the problem of combinatorial explosion and open the door to the rich information encoded in the high-order interactions of the brain. While some HOFC approaches have been proposed (Chen et al., 2021; Zhang et al., 2019, 2017), these have important methodological and theoretical limitations: i) they are fundamentally pairwise, as they are based on pairwise correlations between abstract representations of the activity of groups of regions, such as the correlation of correlations (Zhang et al., 2017); ii); they have not solved the combinatorial problem and hence the analysis has been restricted to triplets (Camino-Pontes et al., 2018) or to small brain parcellations (Gatica et al., 2021), neglecting important spatial details of brain networks and iii) they have not been applied in a multimodal setting with high temporal (EEG) and spatial (fMRI) resolution, missing complementary information present in different scales (Uludağ and Roebroeck, 2014).

Examining higher order interactions has been demonstrated in neuroimaging studies (Gatica et al., 2021; Luppi et al., 2022). However, for HOFC to represent a substantial advance, it should afford new insights into disorders of brain connectivity. The anatomical substrate of brain functional patterns – the connectome – is already known to be disrupted by neurodegenerative diseases (Fornito et al., 2015; van den Heuvel and Sporns, 2019) resulting in widespread functional alterations (Alderson et al., 2018; Pievani et al., 2014). Furthermore, the mechanism for this disruption is well described. For example, the pathogenic protein spread hypothesis (Frisoni et al., 2022; Walsh and Selkoe, 2016) suggests that pathological protein aggregates spread in the brain through the connectome via cell-to-cell contacts, triggering widespread brain hub dysfunctions (Crossley et al., 2014; Walsh and Selkoe, 2016). This strongly suggests that it should be possible to effectively track neurodegenerative diseases by assessing appropriate patterns of coordinated brain activity. Currently, there is a lack of integrative and robust frameworks that can describe the specific pathophysiological signatures of neurodegeneration in terms of hypo and hyper connectivity of HOFC of different spatiotemporal scales (Schultz et al., 2017). Bridging this gap would directly impact the reliability of neuroimaging biomarkers to detect, predict, and characterize the effect of neurodegeneration in brain networks.

Here, we provide a novel, multimodal, and systematic framework to characterize genuine HOFC in brain networks from resting state EEG and fMRI recordings, leveraging recent advances in multivariate information theory (Ince et al., 2017; Rosas et al., 2019). Furthermore, this framework was applied to two diseases with known disrupted connectivity – behavioral variant frontotemporal dementia (bvFTD, Ibañez and Manes, 2012) and Alzheimer’s disease (AD, Zhou and Seeley, 2014) – to investigate high-order brain functional networks involving up to 20 brain regions as a whole functional unit. Our approach overcomes the combinatorial problem by introducing a novel greedy search algorithm (Wilt et al., 2010), finding the most compromised high-order networks in a specific disease or condition. The greedy search algorithm was used in combination with machine learning techniques to characterize brain network dysfunction. A feature selection procedure found the smallest set of multimodal networks - combined from source space EEG and fMRI recordings - that yielded the strongest discriminative power. This set was characterized in terms of the number and identity of the regions involved, the relevance of each modality, and the changes in HOFC, controlling for potential confounding variables. Results show that HOFC was for more effective, and identified more parsimonious markers, of the pathophysiological signatures of neurodegeneration, compared to traditional pairwise functional connectivity approaches. By integrating these efforts, this work provides convergent multimodal evidence of HOFC disruptions across neurodegenerative diseases by accounting for collective behavior in the development of biologically plausible biomarkers of brain health.

2. Materials and methods

2.1. Experimental design

The study comprised a total of 173 participants, including 99 healthy controls (CN), 25 bvFTD, and 49 CE patients from an ongoing analytical framework of multimodal neuroimaging (Birba et al., 2022; Díaz-Rivera et al., 2022; Legaz et al., 2021; Salamone et al., 2021) led by BrainLat (Duran-Aniotz et al., 2022) and including resting-state electroencephalography (EEG) and f/MRI recordings. For the CN group, 95 patients were recorded using fMRI, 46 EEG, and 42 using both. For the bvFTD and AD groups, 22 and 43 subjects were recorded using fMRI, 18 and 31 using EEG, and 15 and 25 subjects with both modalities, respectively. Recruitment was conducted in clinical centers of Chile(GERO/CMYN, Universidad de Chile), Argentina (CNC, Universidad de San Andrés), and Colombia (Pontificia Universidad Javeriana) by a multidisciplinary team, following a multicentric database with a common protocol for recruitment and diagnosis as provided elsewhere (Díaz-Rivera et al., 2022; Salamone et al., 2021). Diagnoses were conducted by a consensus group including different expert neurologists, according to the current criteria for probable bvFTD (Rascovsky et al., 2011) and NINCDS-ADRDA clinical criteria for AD (McKhann et al., 2011), and supported by extensive neurological, neuropsychiatric, and neuropsychological examinations (Baez et al., 2014; Melloni et al., 2016; Piguet et al., 2011; Santamaría-García et al., 2017) (Table S3, S4, and S5). Patients of each group displayed their expected atrophy pattern (Krueger et al., 2010) (see Table S1 and S2). Examinations were conducted in accordance with the standardized protocol provided by the Multi-Partner Consortium to Expand Dementia Research in Latin America (ReDLat) (Ibanez et al., 2021a, 2021b). This assessment ensures that harmonized evaluations are carried out by certified examiners, with extensive training for clinical and cognitive evaluations, based on a quality assurance checklist. Participants and their informants reported no history of neurological, or psychiatric disorders, primary language deficits, or substance abuse. Demographic information for the full and matched samples is provided in Tables 3 and 4, respectively. All the subjects gave written informed consent before participating. The experimental protocol was approved by the Research and Ethics Committee of all relevant institutions in compliance with the Helsinki declaration for research with human subjects.

Table 3.

Unimodal classification statistics for the peak AUC values.

	fMRI				EEG
	bvFTD vs CN		AD vs CN		bvFTD vs CN (δ)		AD vs CN (θ)
AUC	0.904	(0.017)	0.900	(0.014)	0.955	(0.021)	0.867	(0.024)
Precision	0.922	(0.017)	0.892	(0.014)	0.931	(0.022)	0.793	(0.025)
Specificity	0.655	(0.042)	0.761	(0.069)	0.818	(0.064)	0.683	(0.049)
Sensitivity	0.944	(0.016)	0.894	(0.014)	0.957	(0.023)	0.816	(0.033)
Accuracy	0.890	(0.017)	0.853	(0.016)	0.918	(0.024)	0.762	(0.027)
F1-score	0.933	(0.012)	0.893	(0.010)	0.944	(0.017)	0.804	(0.023)

Data is presented as mean (standard deviation) out of 300 iterations of the classifier.

Table 4.

Multimodal classification statistics.

	bvFTD vs CN	AD vs CN
AUC	0.975 (0.0111)	0.953 (0.0102)
Precision	0.9431 (0.0133)	0.9091 (0.0167)
Specificity	0.7667 (0.0572)	0.8118 (0.0374)
Sensitivity	0.9731 (0.0098)	0.9287 (0.0175)
Accuracy	0.9315 (0.0147)	0.890 (0.0178)
F1-score	0.9578 (0.009)	0.9186 (0.0132)

Data is presented as mean (standard deviation) out of 300 iterations of the classifier.

2.2. Neuroimaging recordings

2.2.1. fMRI acquisition and processing

We acquired and pre-processed three-dimensional volumetric and ten-minute-long resting-state MRI sequences following OHBM recommendations (Poldrack et al., 2017). Data were recorded in 3 different centers (Supplementary section fMRI acquisition and processing).

Resting state recordings were obtained by instructing participants not to think about anything in particular while remaining still, awake, and with eyes closed. Then, to ensure that magnetization achieved a steady-state, we discarded the first five volumes of each subject’s resting-state recording. Images were then preprocessed using the Data Processing Assistant for Resting-State fMRI (DPARSF V2.3), an open access toolbox that generates an automatic pipeline for fMRI analysis. DPARFS works by calling the SPM12 and the Resting-State fMRI Data Analysis Toolkit (REST V.1.7). Preprocessing steps included slice-timing correction (using the middle slice of each volume as the reference scan) and realignment to the first scan of the session to correct head movement (SPM functions) (García-Cordero et al., 2016). We regressed out six motion parameters, cerebrospinal fluid (CSF) and white matter (WM) signals to reduce potential effects of movement-related, physiological, and cardio-respiratory effects (REST v.1.7 toolboxes). Motion parameters were estimated during realignment, and CFS and WM masks were derived from the tissue segmentation of each subject’s T1 scan in native space with SPM12 (after co-registration of each subject’s structural image with the functional image). None of the participants showed head movements >3 mm and/or rotations higher than 3° and no differences in head motion among groups were found (Table S6). Finally, images were normalized to the MNI space using the echo-planar imaging (EPI) template from SPM12, smoothed using an 8-mm full-width-at-half-maximum isotropic Gaussian kernel, and bandpass filtered between 0.01 and 0.1 Hz to correct and remove low-frequency drifts from the MRI scanner. Data was parcellated with the AAL90 (Tzourio-Mazoyer et al., 2002) removing the subcortical regions, using only 84 regions.

2.2.2. EEG acquisition and processing

The participants sat in a comfortable chair, inside a dimly lit sound-attenuated and electromagnetically-shielded EEG chamber. As for fMRI, participants were instructed to remain still and awake. Ongoing, eyes-closed EEG was recorded for 5 min from 128 scalp locations using a radial electrode placement system. The reference electrodes were set to linked mastoids. Electrodes were also placed in periocular locations to record eye blinks and eye movements. The EEG was recorded using a Biosemi Active-two acquisition system. Analog filters were set at 0.03 and 100 Hz. Signals were sampled at 1024 Hz, and preprocessed offline using standard procedures implemented in a costume processing pipeline. Recordings were band-pass filtered between 0.5 and 40 Hz using a zero-phase shift Butterworth filter, and re-referenced to the average of all channels. Malfunctioning channels were identified and replaced using weighted spherical interpolation. Data were down-sampled to 512 Hz, and independent component analysis was used for correcting EEG artifacts induced by eye movements. No significant difference in eye movements between groups were found (ANOVA, p-value>0.1, Table S7).

2.2.3. EEG source localization

The source analysis of the EEG was conducted using the standardized Low-Resolution Electromagnetic Tomography method (sLORETA (Pascual-Marqui et al., 2002)). The sLORETA uses a particular scalp voltage distribution of the EEG to compute the standardized current density at each of a number of predefined virtual sensors located in the cortical gray matter and the hippocampus of a reference brain (MNI 305, Brain Imaging Centre, Montreal Neurologic Institute) based on the linear, weighted sum of the scalp electric potentials. The electrodes layout (Biosemi 128) was registered onto the scalp MNI152 coordinates. Landmarks for registering the electrode locations were Nasion (Nz), Inion (Iz), the left preauricular point (LPP) and the right preauricular point (RPP). Location of landmark and recording electrodes were expressed in millimeters, using the Cartesian coordinate system. A signal to noise ratio of 1 was the choice for the regularization method used to compute the sLORETA transformation matrix (forward operator for the inverse solution problem). The lead field in sLORETA is calculated for a fixed set of 316 scalp electrodes from the 5% location system (Pascual-Marqui et al., 2002). The standardized current densities maps were obtained using a head model of three concentric spheres, in a predefined source space of 6242 voxels (voxel size of 5x5x5 mm3) of the MNI average brain. Data was also parcellated using the AAL90 (Tzourio-Mazoyer et al., 2002) removing the subcortical regions. Current densities were estimated for each of the 153.600 voltage distributions comprising the five minutes rsEEG (sampling frequency of 512 Hz). Time-varying current densities computed at a particular point in time were averaged among voxels belonging to the same AAL90 region, such that a single (mean) time series was obtained for each cortical region.

2.3. Data analysis

All analyses were carried out using custom scripts written in MAT-LAB 2021.

2.4. Dual total correlation

Consider a system of $n$ random variables denoted by $X^n=(X_1,\dots ,X_n)$. The dual total correlation is a non-negative generalization of the mutual information (MI) (Rosas et al., 2019), which and can be expressed as:

$$DTC(X^n)=H(X_1,\dots ,X_n)-{\sum }_{i=1}^{n}H(X_i\mid X_{-i}^n)$$ (1)

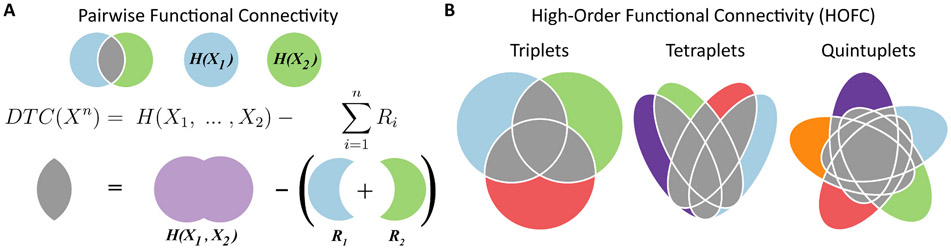
where $H(X_1,\dots ,X_n)$ is the joint Shannon’s entropy of the $n$ variables, and $H(X_i\mid X_{-i}^n)$ is the the entropy of the $i\text{-}th$ region conditioned by the activity of the whole system without it - which is known as “residual entropy,” and is denoted as $R_i$ in Fig. 1. Above, $X_{-i}^n$ is a shorthand notation for the vector of all variables except $X_i$ (i.e., $(X_1,\dots ,X_{i-1},X_{i+1},\dots ,X_n)$). A visual representation of the DTC for groups of 2, 3, 4 and 5 variables is shown (gray zone) on the Venn diagrams of Fig. 1.

Fig. 1.

An information-theoretic metric of high-order functional connectivity (HOFC). A) The traditional pairwise functional connectivity is represented by Venn diagrams. The light blue (green) circle corresponds to the Shannon’s entropy ($H(\cdot )$) of brain region 1 (2), and their intersection to their pairwise functional connectivity, here measured by the dual total correlation (DTC, gray). B) Illustration of the high-order functional connectivity (HOFC) for triplets, tetraplets, and quintuples. The gray zone also represents the DTC, which measures the functional connectivity for 3 or more regions. $X^n$: $n$-variable system. $X_i$: $i\text{-}th$ variable of $X^n$. $R_i$ residual entropy of the $i\text{-}th$ region.

The calculation of information-theoretic quantities from continuous data - as the one obtained in resting state neuroimaging recordings (temporal signals of fMRI and source space EEG, Fig. 2A) has important challenges (Lizier, 2014). One robust way to address these challenges is to use the Gaussian copula method (Gatica et al., 2021; Ince et al., 2017), which enables an efficient and robust estimation of information-theoretic quantities in general, and the DTC in particular, from continuous data. This method transforms the distribution of each single variable into Gaussian while preserving the copula between them. A notable advantage of this method, compared to non-parametric ones (Lizier, 2014), is that all the information-theoretic quantities have closed form (including the estimation biases) and can be reliably estimated for Gaussian variables.

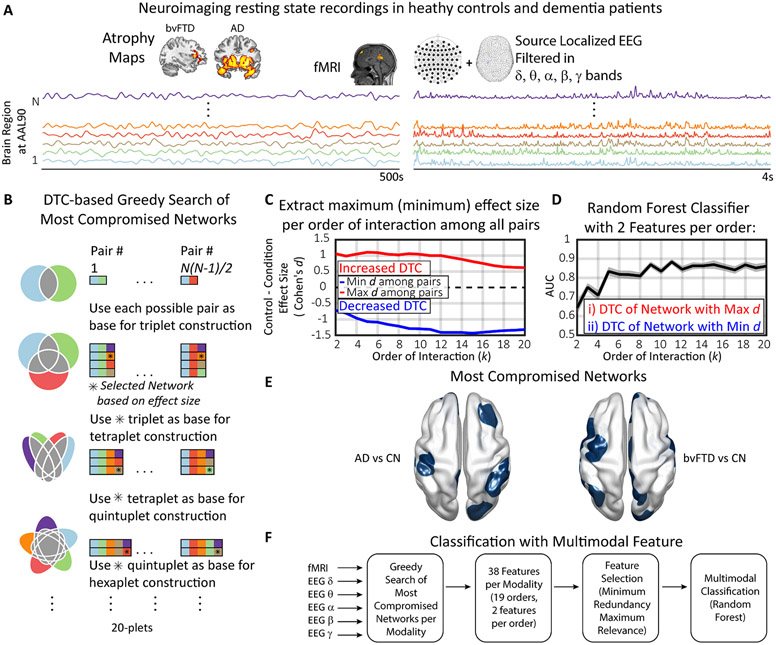
Fig. 2.

Workflow overview. A) Two neuroimaging modalities (fMRI and EEG) were obtained for control subjects and dementia patients (bvFTD and AD). Atrophy maps in the inset show expected gray matter loss in fronto-temporo-insular regions (bvFTD), and in middle-temporal and posterior regions (AD; Table S1 and S2 for details). The EEG recordings were source localized and bandpass filtered in the canonical EEG bands. B) A greedy search algorithm (GSA) was implemented to find the network whose DTC maximizes (minimizes) the effect size for each order of interaction. In the Venn diagrams, also displayed in Fig. 1, each square represents one brain region, each row is a specific n-plet, and each column a different pair. C) For each order of interaction, the network with the maximum (red) and the minimum (blue) effect size is obtained. D) Area under the receiver operating characteristic (ROC) curve obtained from a random forest classifier trained using 2 features per order of interaction: the DTC of the network with maximal and minimal effect size, respectively. E) For each comparison between groups, the most compromised networks per order of interactions were obtained. F) Finally, as the GSA was applied to each data modality, a set of the most compromised networks for each of them was obtained. A total of 228 features (19 orders of interaction, 2 features per order, and 6 data types) were used as inputs for a feature selection algorithm that gives the optimal multimodal biomarker for each condition. fMRI: functional magnetic resonance imaging; EEG: electroencephalogram; bvFTD: behavioral variant frontotemporal dementia; AD: Alzheimer’s disease; CN: healthy controls group; DTC: dual total correlation; AUC: Area under the receiver operating characteristic curve; $d$: Cohen’s effect size.

2.5. Effect size

To find the most compromised networks associated with each pathology, the changes in HOFC were quantified via the Cohen’s $d$ measure of the effect size (Sawilowsky, 2009):

$$d=\frac{{\mu }_{condition}-{\mu }_{control}}{s},s=\sqrt{\frac{(m-1)s_{condition}^2+(m_{control}-1)s_{control}^2}{m_{condition}+m-2}},$$ (2)

where ${\mu }_{control}$and ${\mu }_{condition}$ are the average DTC of the control and neurodegenerative disease group, respectively, and $s$ is the pooled standard deviation where $s_{control}^2(s_{condition}^2)$ and $m_{control}(m_{condition})$ are the variance of the control (condition) group and their sample sizes, respectively, and $m$is the total sample size given by $m_{condition}+m_{control}$. This metric measures a standardized mean difference between groups, and its sign indicates the direction of the effect: a positive value of $d$ indicates DTC increases in the neurodegenerative diseases, while a negative value indicates decreases. Instead of using p-values to assess the group differences, metrics of classification performance were used to validate these differences (see Methods: Random Forest classifier).

2.6. Greedy search algorithm (GSA)

To approximate the set of most compromised brain networks (largest changes in the DTC), we developed a greedy search algorithm (GSA) to find the networks with the largest DTC increase associated with a neurodegenerative condition. Here, we used k to denote the order of interaction, i.e. the number of regions involved on each network, with k = 2 being the smallest order. The GSA searches in a stepwise manner the networks associated to the maximum (minimum) effect size (measured with the Cohen’s $d$, see Methods: effect size) at each order of interaction, starting the search from each possible pair of regions. As illustrated in Fig. 2B, the process proceeded, for each pair of regions, by calculating the DTC of all the triples with two of the three regions belonging to a given pair, and then selecting the triplet with the largest effect size. Then, all the tetraplets with three of the four regions belonging to the triplet with the largest effect size were evaluated, selecting the one with the largest effect size, and so forth (the latter procedure worked analogously but follows the networks with the largest negative effect sizes). These steps were repeated until reaching networks of 20 regions, up to which the estimations of the DTC are still reliable (Gatica et al., 2021).

2.7. Pairwise metrics

For fMRI and EEG the Pearson correlation coefficients between pairs of brain regions was used as a measure of linear correlation (Prado et al., 2022), and it were computed following cov(X,Y)/(σx σy), where cov(X, Y) was the covariance between the time series X and Y, and σx(y) was the standard deviation of X (Y). The non-linear correlation metric used was the mutual information (MI), which was computed via the Gaussian copula method (Ince et al., 2017). Eq. 1 was used to compute MI, as the DTC is equivalent to the MI for two variables.

2.8. Random forest classifier

The fitcensemble MATLAB function was used with default parameters to train a random forest classifier. LogitBoost was used as a boosting method, with 100 learning cycles, 10 maximum splits, and each split used the square root of the number of predictors. Node classification error was used as split criterion. To perform cross-validation, the data set was randomly partitioned with stratification into 5 groups with approximately the same number of subjects. Then, the model was fit using 4 of these groups, and its performance (ROC curve and confusion matrix) was tested using the group that remained, and repeated this process until all groups were used for testing and training. This procedure was repeated 60 times (unless other is specified) to obtain distributions and average measures of performance. For the case of the multi-modal data set, the missing data were handled using surrogate splits (Feelders, 1999). Area under the ROC curve (AUC) was used to summarize the classification performance, and a detailed statistical analysis was provided by the precision, sensitivity, specificity, accuracy, and F-score (Moguilner et al., 2022).

2.9. Maximum relevance minimum redundancy

The fsmrmr MATLAB function was used to compute the maximum relevance minimum redundancy (MRMR) score for each feature (Peng and Ding, 2005). This algorithm sorted the features according to a ratio between the maximum relevance (measured by the MI between a feature and a response variable) and the redundancy (measured by the MI between two features). Instead of using these scores to select the number of features, we used the scores in descending order to sequentially add features one by one until a maximum in the average AUC was obtained.

2.10. Multivariate linear regression of confounders

The mvregress Matlab function was used to remove the effect of diverse confounders on the features based on HOFC. Two separate procedures were performed: one to remove the effect of demographics (age and education) and other to remove recording artifacts (fMRI head movements and EEG eye artifacts). For the first case, age and education were used as explanatory variables, and the response variables were the HOFC features. For the second case, only the features obtained from fMRI were regressed by fMRI head movements (translation and rotation) while only features obtained from EEG were regressed by eye artifacts. In both cases the residuals of the fit were used as a new set of features where the effect of demographics and recording artifacts were removed, respectively. The fit used an intercept, only diagonal terms of the covariance matrix were used, and missing values were imputed using the expected value of the missing observation given the observed data.

2.11. Additional statistical analysis

Categorical variables were analyzed with Pearson’s chi-squared (χ²) test. Continuous variables were analyzed through ANOVA and post-hoc pairwise comparisons. For atrophy maps, a cluster-correction for multiple comparisons was used in AlphaSim. Changes in HOFC in EEG and fMRI were assessed using Cohen’s $d$ effect size (eq. 3). Comparisons between AUC distributions were carried out using non-parametric Mann-Whitney test.

3. Results

3.1. High-order functional connectivity (HOFC)

The first contribution was the development of a principled framework to assess genuine HOFC which overcame the combinatorial problem. The framework assessed the HOFC between 3 or more brain regions via a multivariate extension of Shannon’s mutual information (MI) known as dual total correlation (DTC, Fig. 1 and eq. 1) (Rosas et al., 2019). Intuitively, the DTC captures the shared information - i.e., the part of the activity that is common to two or more brain regions. The DTC is equal to the MI for two variables (i.e., when n = 2), and it is zero if and only if all the considered variables are jointly independent (i.e., their joint distribution is equal to the product of their marginals). The Venn diagram (Fig. 1) illustrates the natural extension from pairwise functional connectivity to HOFC using the DTC, which represents the core metric to capture brain network dysfunction in bvFTD and AD. A conceptual advantage of this perspective is that brain networks are not defined as a collection of pairwise relationships; they are defined according to their overall interdependence as a group, accounting for pairwise to n-th order interactions.

Our aim was to identify the high-order networks that were more affected by neurodegeneration in bvFTD and AD. Any data-driven approach to identify these networks faces a combinatorial problem: for a moderate parcellation of 82 brain regions (we used 82 cortical regions of the Automated Anatomical Labeling atlas, AAL90), there are 3.321 possible pairs, 88.560 possible triplets, 1.749.060 tetraplets, 28.285.336 quintuplets, and so on. Hence, an evaluation of each of the possible interactions of all orders –whose number is on the order of 10³⁰– is not feasible. To address this combinatorial challenge, we introduced an efficient algorithm to investigate the differences between a healthy control group (CN) and bvFTD and AD groups, respectively, which is explained in the next section.

3.2. Overcoming the combinatorial explosion with a greedy search algorithm (GSA)

The combinatorial explosion represents an important obstacle when adopting the high-order perspective, and the naive perspective (i.e., random sampling) is sub optimal for a moderate network of 82 brain regions. In the face of a daunting combinatorial challenge, greedy search algorithms (GSA) represent a natural compromise between an inefficient random search and an infeasible exhaustive search (Wilt et al., 2010). Following the principles of GSA, our proposed procedure identified compromised networks (changes in HOFC) for each neurodegenerative condition (bvFTD and AD) and modality (EEG and fMRI, Fig. 2A). In the following, we describe our greedy search algorithm that approximates the set of networks that maximizes/minimizes the effect size between conditions. With maximization we aim to find the largest DTC increase, while with minimization we aim the opposite, this is, to find hyper and hypo connectivity, respectively. To ease the notation, we use n to denote the total number of regions and k to denote the number of brain regions (i.e., the order of interaction) involved in a given network (Fig. 2B).

Our approach employs a step-wise search by selecting, on each step, the most compromised (i.e., largest effect size) brain network, and then using it as a starting point for the next step. First, given a n-variable system, all the possible duplets (pairs) were generated, i.e., k = 2. Then, each pair was used as the base for generating its corresponding list of n – 2 triplets (k = 3). For instance, if the algorithm started with the duplet (1,2), the following triplets would be generated: (1,2,3), (1,2,4), (1,2,5), …, and (1,2,n), where the triplet (1,2,1) and (1,2,2) are not considered due to the repetition of one of the elements. Once all the triplets were generated for a specific pair, the associated dual total correlation (DTC) was computed for all the subjects, altogether with the effect size (Cohen’s d, see eq. 2) between conditions. Then, if the aim was to find DTC increase (decrease), the triplet that maximizes (minimizes) the effect size between conditions was used for the construction of all the possible n – 3 tetraplets (k = 4) that used this triplet as base. Accordingly, the tetraplet that maximized (minimized) the effect size between conditions was used as base for the construction of all the possible n – 4 quintuplets (k = 5). This accumulative procedure was performed until k = 20, a size that has been previously used in the analysis of high-order interactions in neuroimaging data (Gatica et al., 2021) and where the estimations can still be reliable considering the short sample size of fMRI data specially. Thus, for each possible pair, the maximum and minimum effect size at each order of interactions was extracted, resulting in sequences of networks of different sizes with their corresponding effect size as illustrated in Fig. 2C. Finally, to obtain the set of networks that best captured the differences between conditions, the maximum (minimum) effect size among all pairs was extracted at each order of interaction. In summary, our algorithm identified one hyper and one hypo connected network per order of interaction: one with a maximal increase of HOFC and one with a maximal decrease. The DTC values of these compromised networks were then used as features for a machine learning classifier to assess the predictive power of HOFC to classify the groups (see next section and Methods for details) (Fig. 2D).

Leveraging the multimodal application of this framework, the GSA was separately applied to fMRI and source space EEG filtered in 5 canonical bands (δ, θ, α, β, and γ) (Laufs, 2008). A total of 228 networks were obtained: 2 networks per order of interaction (the maximum and minimum $d$), 19 orders (2 to 20), and 6 different data types (one for fMRI and 5 for EEG bands, Fig. 2A,F). In order to find the top predictors, a feature selection algorithm (Methods: maximum relevance minimum redundancy) identified the smallest set of networks that maximizes the classifier’s performance (Fig. 2F). Thus, by coupling the GSA with feature selection, we aimed to obtain robust and parsimonious multimodal potential biomarkers for neurodegeneration based on HOFC, whose interpretation informs the brain functional networks that become hypo- or hyper- connected in bvFTD and AD, respectively.

3.3. Neurodegenerative conditions are reliably characterized and predicted by HOFC in EEG and fMRI signals

To investigate the power of HOFC to identify subjects from the healthy controls, bvFTD, and AD groups, the GSA was separately applied to fMRI and source space EEG. We found that both neurodegenerative conditions exhibited highly compromised networks, evidenced in both neuroimaging modalities (i.e., large effect size, absolute value of Cohen’s $d$ > 1, Fig. 3A). There were increases and decreases (large positive and negative effect sizes, respectively) in dual total correlation (DTC; intuitively, capturing the part of the activity that is common to two or more brain regions). Although $d$ varied among comparisons, the maximum/minimum effect size was always obtained at orders of interaction larger than 2. This suggests that HOFC captures more variance in data than the traditional pairwise connectivity (Results: HOFC involves a more parsimonious characterization of neurodegeneration than standard pairwise metrics). In each comparison, the largest absolute effect size was associated with DTC decrease, suggesting a larger relevance of hypo than hyper connectivity.

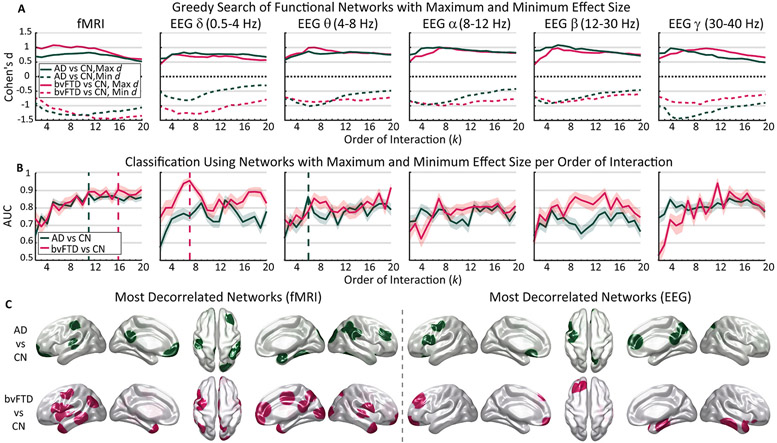
Fig. 3.

The predictive power of the HOFC for neurodegeneration. A) The GSA yields networks associated with large effect sizes magnitudes for both modalities (fMRI and filtered EEG), and condition comparison (CN vs. AD, CN vs. bvFTD). Solid (dashed) lines show the maximum (minimum) effect size obtained by the algorithm. B) Using the DTC of the two most compromised networks per order of interaction as features for a random forest classifier, we found that HOFC strongly predicts neurodegeneration in both modalities. Solid lines and shaded areas represent the average ± 1 standard deviation of 60 runs of the classifier, respectively. Dashed vertical lines indicate the maximum AUC for each condition comparison in each modality. C) Most decorrelated networks for fMRI (left) and EEG (right) value, i.e., the hypo connected networks associated with the dashed vertical lines in B. fMRI: functional magnetic resonance imaging; EEG: electroencephalogram; bvFTD: behavioral variant frontotemporal dementia; AD: Alzheimer’s disease; CN: healthy controls group; DTC: dual total correlation; AUC: Area under the receiver operating characteristic curve; $d$: Cohen’s effect size; GSA: greedy search algorithm.

To evaluate the predictive power of these highly compromised networks in each recording modality, a random forest algorithm was trained (60 random partitions of data, see Methods: random forest classifier) for each order of interaction, using the two most compromised networks per order. The performance of the classifier was measured with the area under the (AUC) receiver operator characteristic (ROC) curve, the precision, sensitivity, specificity, accuracy, and F1-score, obtaining one average value per order of interaction, and modality (Table 3).

Orders of interaction beyond 2 best discriminated patients from controls (consistent with the effect size magnitudes). For fMRI data, the average AUC increased with the order of interaction for both conditions, reaching a peak of AUC = 0.904 ± 0.017 at k = 16 for bvFTD, and AUC = 0.900 ± 0.014 at k = 11 for AD (Fig. 3B). For EEG, the average AUC of bvFTD peaked at 0.955 ± 0.021 for k = 7 in the δ band, while AD peaked at 0.867 ± 0.024 for k = 6 in the θ band. The repeated random partitions of data to train and test the classifier, and the small confidence intervals, ensures the reliability of our approach. These results suggest that HOFC robustly captures pathophysiological signatures for bvFTD and AD, respectively, in terms of spatiotemporal brain networks, their changes in functional connectivity, and the number of regions involved.

Since our aim was to characterize the specific pathophysiological signatures of each disease with respect to the controls, we did not delve into the differences between bvFTD and AD. However, excellent average AUC values were found in both the unimodal and multimodal case (AUC ~ 0.95, Supplementary Fig. S1), demonstrating that our approach is also useful to distinguish between subtle differences in neurodegenerative diseases.

3.4. HOFC reveals the core pathophysiology of neurodegeneration

To uncover the specific pathophysiological signatures of each neurodegenerative condition, the smallest subset of networks with the strongest predictive power was selected among all the networks found by the GSA (Fig. 2F), including both fMRI and EEG functional networks. This multimodal subset was characterized in terms of number of features, modalities (fMRI and the 5 EEG frequency bands), changes in DTC, the orders of interaction, and regions involved. A maximum relevance minimum redundancy algorithm (Methods: maximum relevance minimum redundancy (Peng and Ding, 2005)) was implemented to sort features in descending order (Fig. 4A). Sorted features were sequentially included in the random forest classifier, with a subsequent selection of the maximum in the average AUC (Fig. 4B). This maximum represented the simplest and most accurate description of data that our approach could obtain solely from multimodal neuroimaging recordings, despite missing data (Methods: participants).

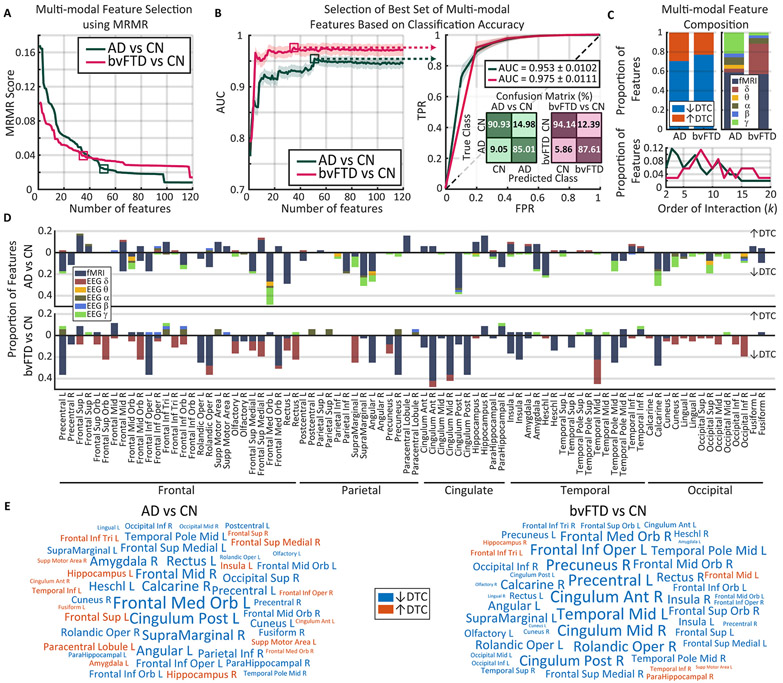
Fig. 4.

Specific pathophysiological signatures of neurodegeneration revealed by multimodal biomarkers. A) The scores of each feature (sorted in descending order) were obtained using the MRMR feature selection algorithm. Squares are the best points obtained in B. B) AUC values correspond to classifications based on the accumulation of the sorted features obtained by MRMR. Solid lines are the average among 180 runs of a 5-fold cross-validated random forest, and shaded areas represent the corresponding standard deviation. Squares represent the maximum average AUC value, i.e. the optimal number of features for each condition (bvFTD = 35, AD = 51), with their associated ROC curve and the confusion matrices. Values of the legend were obtained from 300 runs of the classifier. C) Dementias were characterized mainly by decreases in connectivity and high-order networks. The selected multimodal feature was characterized in terms of DTC increase (red) and decrease (blue), the data modality (colors in the right most panel), and the order of interaction of the compromised networks (bottom panel). D) The bvFTD and AD groups exhibited different pathophysiological signatures. The participation of each region in the multimodal feature was quantified in terms of how many features included a given region, how many features were related to DTC increase or decrease, and to each data modality (same colour code of C). E) Word clouds with the 50 AAL regions with largest participation. Size represents the data of the bar charts of D, and colors indicate if the region was more related to DTC increase (red) or decreases (blue). fMRI: functional magnetic resonance imaging; EEG: electroencephalogram; bvFTD: behavioral variant frontotemporal dementia; AD: Alzheimer’s disease; CN: healthy controls group; DTC: dual total correlation; AUC: Area under the receiver operating characteristic curve; TPR: true positive rate; FPR: false positive rate; L: left hemisphere; R: right hemisphere; MRMR: maximum relevance minimum redundancy; ↑: Increase. ↓: decrease.

High average AUC values (>0.95) were obtained using 35 and 51 features, for bvFTD and AD groups, respectively (Fig. 4B). A better classification for bvFTD (AUC = 0.975 ± 0.0111) than for AD (AUC = 0.953 ± 0.0102) was found (Table 4, for classification details). For both bvFTD and AD, the multimodal classification involved ~60% of fMRI features. Regarding EEG, all the filtering bands were represented in the multimodal subset for AD, with stronger presence of the γ band. The bvFTD group exhibited more presence of δ band and no participation of θ band (Fig. 4C). Consistent with the larger magnitude of negative effect sizes in the unimodal case (Fig. 3A), ~70% of the features were associated with DTC decrease (Fig. 4C, upper panel). As also suggested by the unimodal case (Fig. 3B), the multi-modal biomarkers were composed of networks of different orders, with a larger presence of intermediate orders (3 < k < 15, Fig. 4C, lower panel). Notably, the multimodal subset of AD had more low-order features in comparison with that of bvFTD.

To confirm that the multimodal composition was necessary to capture differential information from different recording modalities, the same procedure described above for the full multimodal combination of feature selection was applied to 4 alternative set of features: i) only fMRI, ii) only EEG, iii) only DTC increase, and iv) only DTC decrease. The full multimodal combination was significantly more accurate than all the alternatives (Mann-Whitney p-value <10⁻⁶, Supplementary Fig. S2). As expected, the fMRI was the closest alternative, followed by the alternative that contained only DTC decrease. Using only EEG or only DTC increase worsened the results (Mann-Whitney p-value <10⁻⁶, Supplementary Fig. S2). So, despite the larger importance of fMRI, and of DTC decrease for the multimodal biomarkers, the highest predictive power was a result of a synergy between DTC increase and decrease obtained from both modalities.

To characterize the brain regions of the multimodal biomarkers, the participation of each region was measured by counting the number of features in which each region is represented (Fig. 4D and E). In agreement with previous multimodal results, most of the represented regions were related to DTC decrease, with few regions involved in DTC increase (Fig. 4E). However, some hub regions were involved both in increase and decrease: left frontal regions, right precuneus, and right temporal pole in bvFTD; right middle frontal regions and right amygdala in AD. Notably, frontal, temporal, and default mode network-associated regions were highly represented in both bvFTD and AD. Nevertheless, each patient group displayed a specific topographical pattern, where the highest MRMR score was associated with DTC decrease in large fMRI networks: 12 regions for bvFTD and 15 regions for AD. The former included regions of the default mode (frontal, posterior cingulate, angular cortices and precuneus), salience (insula and anterior cingulate cortices), and somatomotor networks (Rolandic operculum and precentral), while the latter included regions of the default mode (frontal, posterior cingulate, and angular cortices), salience (amygdala), visual (calcarine), and auditory (Heschl) networks. These regions were highly represented in the multimodal features as well (Fig. 4E). The contribution of EEG to the DTC decrease, albeit small, was specific to the δ band in bvFTD with a similar pattern to the one found for fMRI, with the addition of occipital regions. For AD, EEG contributed to DTC decrease mainly in the γ band, with a similar pattern to fMRI. Regarding DTC increase, bvFTD networks included frontal and temporal regions, as well as insula, amygdala and hippocampal regions; AD was associated to large fMRI networks involving frontal, temporal, occipital, cingulate, and hippocampal regions, in addition to the insula and amygdala, while in EEG networks were more associated to intra-frontal networks. In agreement with the higher importance of fMRI and DTC decrease, the topographical pattern of each condition partially resembles the most decorrelated networks detected in fMRI (previously reproduced in Fig. 3C).

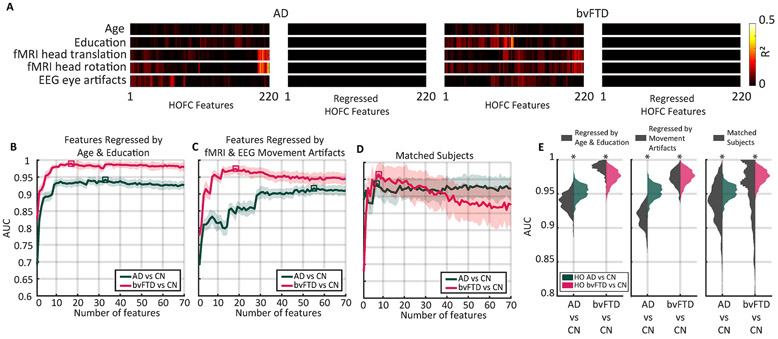
3.5. HOFC is robust against demographic and motor confounders

To rule out the potential influence of confounders on the predictive power of HOFC, we controlled for the influence of demographics and motor artifacts on the HOFC features. First, demographics, age and education (Table 1) were controlled using two approaches: i) a multivariate linear regression to remove the joint effect of age and education from the HOFC features (Fig. 5A), and ii) subsample analysis using a dataset where age and education were matched across groups (Table 2, Fig. 5D). Both approaches resulted in comparable magnitudes, but significantly different AUC values to the ones obtained in the main analysis (Mann-Whitney p-value <10–6, Fig. 5B, F, E).

Table 1.

Demographics of full population.

	CN (N = 99)	bvFTD (N = 25)	AD (N = 49)	Statistics		Post-hoc Comparison
				χ2	DF	Groups	p
Sex (F/M)	54/44*	7/18	28/20*	6,51	170	CN vs bvFTD	0,03
				p = 0,03		CN vs AD	0,9
						bvFTD vs AD	0,03
				Statistics (ANOVA)
Age (mean)	67,74	67,20	76,55	F = 18,53	171	CN vs bvFTD	0,78
Standard Deviation	8,37	11,35	7,74	p < 0,001		CN vs AD	<0,001
						bvFTD vs AD	<0,001
Years of education (mean)	14,34	14,48	10,38	F = 13	171	CN vs bvFTD	0,89
Standard Deviation	4,28	4,78	5,25	p < 0,001		CN vs AD	<0,001
						bvFTD vs AD	<0,001

^*1 subject did not inform. Categorical variables were analyzed with Pearson’s chi-squared (χ²) test. Continuous variables were analyzed through ANOVAs and post-hoc pairwise comparisons. See Table S5 for cognitive and functional evaluations. DF: Degrees of freedom. AD: Alzheimer’s disease; bvFTD: behavioral variant frontotemporal dementia; CN: healthy controls.

Fig. 5.

HOFC is robust against the linear influence of demographics and motor artifacts on HOFC. A) Variance of HOFC features (220 features) explained by age, education, fMRI head movements (translation and rotation), and EEG eye artifacts before and after multivariate linear regression. Colour scale is the R2 (square of the Pearson’s correlation coefficient). B) Classifiers’ performance using HOFC features where the effect of age and education was removed by multivariate linear regression. Solid lines and shaded areas represent the average and standard deviation, respectively. Squared denotes the maximal AUC obtained following the feature selection procedure. C) Same as B, but with features regressed by fMRI head artifacts and EEG eye artifacts. D) Classifier’s performance using raw HOFC features for a subsample of the population where age and education were matched (Table 2). E) Distributions of AUC values associated with the squares in B, C, and D. Sixty independent random splits were used for cross-validation. Asterisks denote Mann-Whitney p-value <10–6. bvFTD: behavioral variant of frontotemporal dementia; AD: Alzheimer’s disease; R2: coefficient of determination; CN: healthy controls group; HO: high-order; HOFC: high-order functional connectivity; AUC: Area under the receiver operating characteristic curve.

Table 2.

Demographics of matched subpopulation.

	CN (N = 19)	bvFTD (N = 19)	AD (N = 19)	Statistics	DF
Sex (F/M)	10/9	5/14	12/7	χ2 = 3.61 p = 0,16 Statistics (ANOVA)	54
Age (mean)	68,89	68,57	73,16	F = 0,84	55
Standard Deviation	7,48	1,92	6,11	p = 0,43
Years of education (mean)	14,77	14,57	12,9	F = 1,26	55
Standard Deviation	3,42	0,91	5,36	p = 0,29

Categorical variables were analyzed with Pearson’s chi-squared (χ²) test. Continuous variables were analyzed through ANOVAs and post-hoc pairwise comparisons. DF: Degrees of freedom. AD: Alzheimer’s disease; bvFTD: behavioral variant frontotemporal dementia; CN: healthy controls.

Second, to control for movement artifacts, a multivariate linear regression was used to remove the influence of fMRI head movements (translation and rotation, Supplementary Table 6) and EEG eye artifacts (Supplementary Table 7) on HOFC (Fig. 5A). Even when these artifacts showed no significant differences between groups (Supplementary Table 6 and 7), we aimed to provide a more robust and complementary result by regressing out these variables on the groups’ comparison. Again, the predictive power obtained using the set of regressed features was comparable but significantly different to the one obtained in the main analysis (Mann-Whitney p-value <10–6, Fig. 5). Thus, we showed that although some of the changes in high-order brain connectivity could be associated with the population’s demographics and motor artifacts, their association was negligible in terms of the predictive power achieved by our approach solely based on brain resting state activity.

HOFC involves a more parsimonious characterization of neurodegeneration than standard pairwise metrics.

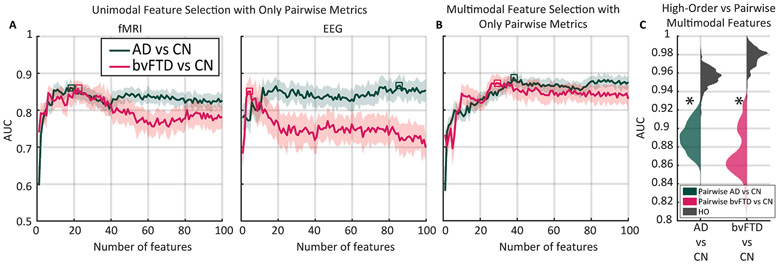
To investigate whether the high-order approach is simpler - in terms of number of features - and performs better than using standard pairwise-based connectivity, pairwise functional connectivity was computed for both modalities, using linear and nonlinear metrics of dependence. For both modalities the Pearson correlation coefficient was used as the linear metric (Prado et al., 2022), and the mutual information (MI) (Ince et al., 2017) as the nonlinear one. To make the pairwise approach comparable to HOFC, for each modality (and EEG frequency bands), and metric, the 50 pairwise features with the largest absolute effect size were selected, such that we ended up with an initial set of 100 and 500 features for fMRI and EEG, respectively. Furthermore, we used the feature selection algorithm to find the minimal set of pairwise features that gave the highest predictive power for both the unimodal and multimodal cases. The maximal possible number of features was constrained to 100 to result in a fair comparison with the HOFC approach.

In both unimodal cases, the AUC values were lower than 0.9 in bvFTD and AD (Fig. 6A). In the specific case of fMRI, the maximum was found using approximately 20 features for both conditions. In the case of EEG, bvFTD peaked using 5 features and AD using 86. Compared to the HOFC, the performance obtained in the unimodal case with the pairwise approach was lower (Mann-Whitney p-value <10⁻⁶). However, the unimodal EEG case with pairwise metrics used information from all the frequency bands, whereas in the HOFC unimodal approach each frequency band was evaluated separately. Remarkably, the HOFC used only 2 features, leading to a more parsimonious and interpretable description of the specific pathophysiology than the unimodal case.

Fig. 6.

Classification using only pairwise metrics. A) Feature selection for the unimodal case using only pairwise metrics. Solid lines and shaded areas represent the average and standard deviation, respectively. B) Same as A) but for the multi-modal case. C) HOFC outperformed pairwise FC, as shown by the distributions of AUC values for 300 random data splits for the cross-validation procedure. Gray distributions represent the features obtained by the high-order (HO) approach, while the colored ones represent the corresponding distribution obtained using pairwise metrics. Asterisks denote Mann-Whitney p-value <10⁻⁶. fMRI: functional magnetic resonance imaging. EEG: electroencephalogram. bvFTD: behavioral variant frontotemporal dementia. AD: Alzheimer’s disease; CN: healthy controls group; AUC: Area under the receiver operating characteristic curve; HO: high-order.

For the multimodal case, AUC values were lower than 0.9 for both conditions, with ~30 features for bvFTD and ~ 40 features for AD (Fig. 6B). The HOFC outperformed the pairwise metric in terms of predictive power (Mann-Whitney p-value <10⁻⁶, Fig. 6C). These results support the hypothesis that neurodegeneration impacts connectivity in a distributed way (Agosta et al., 2013; Jalilianhasanpour et al., 2019; Pievani et al., 2014; Rossini et al., 2020b; Walsh and Selkoe, 2016), rather than restricted to local and low-order changes.

4. Discussion

We proposed a multimodal high-order interactions framework to characterize brain functional networks at different spatiotemporal scales. This framework produced biologically plausible multimodal HOFC markers of two neurodegenerative diseases, captured via multivariate information theory. A first result was the analysis of several orders of interaction by using a novel greedy search algorithm, which overcame the combinatorial explosion. In spite of the different physiological processes captured by fMRI and the canonical EEG frequency bands, we showed that neurodegeneration is characterized by a combination of hyper- and hypo-connectivity, with disruptions in specific brain hubs, and a larger relevance of slow timescales. In contrast to other HOFC measures used to characterize brain disorders (Zhang et al., 2019), our approach is not based on pairwise relationships (e.g. correlation of correlations, or other methods of network analysis) but on assessing genuine high-order statistical relationships. Despite the fundamental differences between our approach and traditional approaches, many of the regions and networks previously reported to be impaired in AD and bvFTD (Jalilianhasanpour et al., 2019) were identified. In bvFTD, regions from the salience and default mode networks, and hypoconnectivity in the δ band were the most relevant features, while AD mainly involved regions from the default mode and sensory networks, and hypoconnectivity in the γ band. The high discriminative performance obtained by our HOFC framework for AD and bvFTD from neuroimaging data was similar or even higher than standard biomarkers, such as PET (Ossenkoppele et al., 2021; Smailagic et al., 2015) or plasma (Chouliaras et al., 2022; Thijssen et al., 2021). However, the former is less sensitive to bvFTD and very limited in terms of accessibility, while the latter is sensible to both, but it is not directly indicative of the brain function, and not yet widely available. In contrast, our approach captures specific brain signatures of both neurodegenerative diseases, and has the potential to be widely applicable in low-cost unimodal settings as EEG. Moreover, the biological plausibility, computational efficiency, and the statistical soundness of our framework demonstrate its potential as an affordable and scalable solution for identification and diagnosis, as well as for future investigation of prognosis and early stages of the disease. The applicability of this approach opens the door to further characterizations of brain collective behavior in health and disease.

Despite the potential of pseudo-HOFC as plausible biomarkers for brain disorders (Zhang et al., 2019), these approaches are not able to capture the nonlinear statistical dependencies between multiple variables in their native space. In fact, these approaches compute the linear correlation between a pair of variables, where each variable represents the activity of a separate group of brain regions. In turn, our approach is able to measure nonlinear interactions between groups of variables without using abstract representation of their joint activity, leading to proper estimates of nonlinear and genuine high-order interactions in brain recordings.

The proposed framework contributes computational and theoretical advantages with respect to previous approaches. First, the approach leverages advances in multivariate information theory (Rosas et al., 2019) to propose a natural extension of the traditional pairwise functional connectivity to a genuine measure of HOFC, using the DTC as a general and nonlinear metric that captures the statistical dependence between 3 or more variables as a whole. Second, our approach overcomes the combinatorial explosion of high-order interactions via a deterministic greedy search algorithm designed to find highly compromised networks. A remarkable outcome of the algorithm was the presence of peaks on the positive and negative effect sizes at specific scales, suggesting that the difference between groups is neither maximized using pairs nor the biggest order (k = 20). Third, we obtained the simplest set of features that robustly predicted neurodegeneration using MRMR (Peng and Ding, 2005) to rank the feature’s importance, and validated its discriminative power with the classification performance. The maxima in the AUC values closely matched the cut-off on the MRMR scores (Fig. 4A-B), suggesting that the latter provides a useful and efficient approximation for finding the relevant set of features for discriminating between groups.

Neurodegeneration represents a clinical, social, and economic burden upon patients, families, and health systems, especially in underrepresented settings (Ibanez et al., 2021b), with the two conditions assessed here being among the most common and critical ones - AD is the most frequent dementia and bvFTD is one of the most impactful because of its early onset and associated behavioral changes (Jalilianhasanpour et al., 2019; Piguet and Kumfor, 2020). The overlap between AD and bvFTD (Du et al., 2007), and also with other neurodegenerative diseases, requires the development of affordable, scalable, and biologically relevant biomarkers which allow accurate diagnosis. Our results show promising evidence supporting applications of low-cost EEG in clinical settings, progressing in the international calls for cost-efficient biomarkers in dementia research (Dottori et al., 2017; Parra et al., 2021). In fact, the current international recommendations for research in our region (Latin America), suggest the development of affordable neuro-imaging biomarkers potentially linked in the future to plasma biomarkers (Parra et al., 2022). Indeed, the large effect sizes, AUC values and related measures observed at networks of intermediate orders substantially outperformed what could be attained by traditional pairwise functional connectivity approaches in terms of parsimony and predictive power - for both unimodal and multimodal cases. In resonance with the network degeneration hypothesis (Drzezga, 2018), our results support the idea that the effect of neurodegeneration on brain activity is better characterized as a dysfunction in collective patterns of brain dynamics, rather than as a low-order dysfunction.

Our results suggest that both hyper and hypo connectivity are associated with late neurodegenerative processes, but with a lesser contribution of the former (Brown et al., 2021). Indeed, hyperconnectivity has been proposed to be focal, possibly as an initial compensatory process (e. g., connectivity overload (Jones et al., 2016)), and to wane with disease progression (Bonanni et al., 2021). The novel finding that highly-connected regions (in terms of structural connectivity, (Crossley et al., 2014)) are involved both in hypo and hyperconnectivity suggests that the consequences of these compensatory processes could also be present at advanced stages of disease progression especially in brain hubs. The hyper and hypoconnectivity in the amygdala, insula and frontal regions could be associated with plasticity accompanying pathological processes (Benussi et al., 2016) which could derive in a reorganization of functional networks (van den Heuvel and Sporns, 2019). However, AD exhibited more pronounced simultaneous hyper and hypo connectivity in fMRI in the amygdala and middle frontal gyrus consistent with more advanced disease. Conversely, bvFTD exhibited mixed effects including both fMRI and EEG, especially in frontal and insular regions. Thus, the specific regions and temporal scales involved in hyper and hypo-connectivity could reflect different disease stages and degree of heterogeneity in the psychopathological mechanisms, consistent with the heterogeneous pattern described in bvFTD (Migeot et al., 2022). This needs to be confirmed with further studies that may allow to track disease progression and heterogeneity with HOFC.

Despite multiple inconsistent results regarding brain connectivity disruptions in neurodegeneration, AD and bvFTD have been characterized by hypoconnectivity mainly in the default mode network in AD, and in the salience network for bvFTD (Jalilianhasanpour et al., 2019). In this last condition, the default mode and salience network hypoconnectivity have been associated with allostatic interoceptive network and overload mechanisms (Birba et al., 2022). In agreement with these effects, both diseases were associated with hypoconnectivity in large fMRI networks, where bvFTD involved regions of the allostatic interoceptive network (Birba et al., 2022), combining the default mode and salience, and somatomotor networks. In turn, AD involved regions of the default mode, salience, visual, and auditory networks. Noteworthy, the specific contribution of the δ band to hypoconnectivity between frontal, temporal, parietal and sensory regions in bvFTD may reflect structural changes in large-scale networks (Wirsich et al., 2017), which resonates with the atrophy and hypometabolism reported in some of these regions (Bejanin et al., 2020). However, considering that this band has been also related to pairwise hypoconnectivity in this disease (Govaarts et al., 2022; Yu et al., 2016), further research is needed to unveil the characteristic spatial scales in which different oscillatory bands are disrupted, and what are their corresponding underlying pathophysiological processes.

In spite of the lesser contribution of hyperconnectivity to the multimodal features, it was associated with large-scale networks that included hippocampus, amygdala and insula, which may be related to the disruptions of processes of recognition and emotional memory of salient information (Zheng et al., 2017; Ibañez et al., 2010). Furthermore, the hyperconnectivity in the α and β EEG bands between frontal and parietal regions for bvFTD, and between intra-frontal regions in AD may suggest a disease-selective increased recurrence of the frontoparietal network in neurodegenerative diseases. Moreover, the focal and concomitant presence of hypoconnectivity in frontal regions suggests that part of the hypoconnectivity of neurodegeneration could be explained by an increased recurrence between frontal regions that impairs connectivity with remote regions. Also, the larger prevalence of hypoconnectivity in the γ band in AD suggests that, in this disease, impairments in bottom-up processing (Richter et al., 2017) could be due to disconnectivity between integrative (frontal and limbic) and sensory areas (posterior and temporal). In turn, in bvFTD this band was involved only in one feature associated with hyperconnectivity in a large-scale network including frontal, temporal, limbic and posterior regions, pointing towards disparate mechanisms of cognitive impairment in the two conditions.

These findings provide a rich and complex characterization of spatiotemporal dynamics that is often inconsistent in pairwise connectivity reports (Jalilianhasanpour et al., 2019). Most of the critical regions observed in AD and bvFTD (Fig. 4D) overlap with highly connected hubs selectively compromised by neurodegeneration identified in >20,000 subjects (Crossley et al., 2014). These data-driven results also resonate with the idea that neurodegeneration disrupts large-scale brain communication (Seeley et al., 2009), with more heterogeneous networks disrupted in bvFTD than in AD (Fig. 4C), in agreement with the disruption of the large-scale allostatic-interoceptive network in bvFTD (Birba et al., 2022; Migeot et al., 2022). Finally, such highly-dimensional spatiotemporal dynamics revealed by HOFC may provide a potential mechanism to explain the usually ignored synergetic blending across multiple cognitive and brain processes in brain health and disease (Ibanez, 2022).

Our work highlights the relevance of combining different sources of information (Uludağ and Roebroeck, 2014) by demonstrating that the top classification results from a synergy between both neuroimaging modalities (Fig. S2), and by showing that demographic information, motor artifacts, sample size, and missing data do not explain the classification results (Fig. 5). This last observation is of critical relevance for future scalability and expansion of this approach to clinical settings. Slow brain dynamics measured with fMRI contributed more to the multimodal feature than EEG. Indeed, fMRI and slow EEG activity may reflect structural damage in the connectome (Wirsich et al., 2017; Wodeyar et al., 2020) triggered by neurodegeneration (Zhou and Seeley, 2014). However, the high discrimination performance obtained with unimodal EEG supports its use as a more scalable and low-cost screening tool (Rossini et al., 2020a). Moreover, education (Katzman, 1993) and age (Hou et al., 2019) are known risk factors and confounders for neurodegeneration. By combining matched sample analysis, and multivariate approaches (Fig. 5), we confirmed that the redundancy between HOFC and demographics is neglectable, as well as with motor artifacts. These results suggest that neurodegeneration could be effectively tracked mainly with HOFC. In addition, missing data — common in multicentric and multimodal studies —was handled by using random forest classifier with surrogate splits. Robust replication was obtained with the matched subsample having no missing data, thus controlling for the effect of missing data. Finally, large classification performance and robust effect size was convergently found in a smaller subsample (Fig. 5), suggesting that the requirement of very large datasets in fMRI association studies (Marek et al., 2022) could be relaxed by leveraging more biologically plausible and robust analytical tools.

Our framework has a number of limitations and brings a novel agenda for future research. First, our data-driven approach focuses on analyzing high-order patterns, giving no direct indications about the potential underlying high-order mechanisms (Rosas et al., 2022). However, the lack of mechanistic information is not an obstacle for building robust discriminant methods to identify specific pathophysiological signatures. Furthermore, identifying spatiotemporal HOFC across neurodegenerative conditions is the first step to develop subsequent mechanistic insights with whole-brain modeling (Deco et al., 2018). Second, our approach currently limits the orders of interaction that are assessed, and also does not carry out a full exploration of those interactions. Greedy algorithms have well-known limitations, as a piecewise selection of local optima may not reach the global optima. However, the large effect sizes and AUC values suggest that the approximated optima found by the GSA captures relevant information for a robust characterization of neurodegeneration. Future work may use larger orders of interactions to initialize the GSA (e.g., triplets, tet- raplets, or higher) which could improve the exploration of the combinatorial space. Third, although many other feature selection algorithms are available (Li et al., 2017), the computational efficiency and simple interpretation of MRMR made it suitable for our demonstrative purposes. Fourth, longer and longitudinal recordings and larger sample sizes could allow for a robust identification of even higher-order networks, which - we speculate - could provide an even simpler and more robust characterization of neurodegeneration. Finally, the main empirical limitation was our modest sample size, which nevertheless was similar to or larger than other reports. However, such limitation is tempered by the robust effect sizes obtained, the strict control of clinical variables, and using detailed diagnostic procedures and systematic assessments (Melloni et al., 2016; Piguet et al., 2011; Rascovsky et al., 2011). Future studies should replicate present results in larger samples and assess the temporality of HOFC in neurodegeneration from early (prodromal, preclinical) to late (severe disorganization) stages.

Present work demonstrates that embracing the study of genuine high-order interactions in the brain is neither a theoretical whim nor a haunting technical problem, but is a promising avenue for developing markers for characterizing brain function. Our HOFC framework is theoretically principled, biologically plausible, and feasible for a broad range of scenarios involving multimodal neuroimaging data, providing a promising new approach to characterize neurodegeneration. We show how this framework can provide affordable, specific, scalable, and biologically plausible candidate biomarkers of AD and bvFTD, whose performance can be enhanced in the presence of multimodal recordings. Finally, our work opens a new agenda where the potential of brain collective behavior will need to be tested in multiple scenarios, including early stages of neurodegeneration, progression, phenotypic heterogeneity, and responses to interventions. We hope that this work will motivate future larger longitudinal studies, which may lead the way to a more extended clinical application of HOFC as a biologically plausible marker of neurodegeneration and brain dynamics in general.

Supplementary data to this article can be found online at https://doi.org/10.1016/j.nbd.2022.105918.

Data availability

Data will be made available on request.