Anisotropic Network Analysis of Open/Closed HCN4 Channel Advocates Asymmetric Subunit Cooperativity in cAMP Modulation of Gating

Abstract

Hyperpolarization-activated cyclic nucleotide-modulated (HCN) channels are opened in an allosteric manner by membrane hyperpolarization and cyclic nucleotides such as cAMP. Because of conflicting reports from experimental studies on whether cAMP binding to the four available binding sites in the channel tetramer operates cooperatively in gating, we employ here a computational approach as a promising route to examine ligand-induced conformational changes after binding to individual sites. By combining an elastic network model (ENM) with linear response theory (LRT) for modeling the apo-holo transition of the cyclic nucleotide-binding domain (CNBD) in HCN channels, we observe a distinct pattern of cooperativity matching the “positive–negative–positive” cooperativity reported from functional studies. This cooperativity pattern is highly conserved among HCN subtypes (HCN4, HCN1), but only to a lesser extent visible in structurally related channels, which are only gated by voltage (KAT1) or cyclic nucleotides (TAX4). This suggests an inherent cooperativity between subunits in HCN channels as part of a ligand-triggered gating mechanism in these channels.

Introduction

Hyperpolarization-activated cyclic nucleotide-gated (HCN) channels are encoded by the closely related HCN1–4 gene family. They conduct the I_f/I_h current, a mixed K⁺/Na⁺ conductance that generates and modulates the automaticity of firing in pacemaker cells in heart and brain.^1,2 For their function, they employ a complex dual mechanism of gating in which hyperpolarizing voltages open the channel and binding of cAMP to a cytosolic binding site shifts the channel opening to more depolarized voltages. The latter links the control over channel activity with cytosolic signaling cascades for a fine-tuning of HCN gating.

High-resolution structural information on HCN channels from cryo-electron microscopy (cryo-EM) confirmed that the architecture of HCN channels is overall similar to that of voltage-dependent K⁺ (Kv) channels.^3,4 Also, HCNs are tetrameric proteins in which each monomer is built of six α-helical (S1–S6) transmembrane (TM) segments. The first four TM segments (S1–S4) assemble as the voltage sensor domain (VSD) while the remaining S5 and S6 elements form the pore module including the selectivity filter. At the N-terminus, the S1 TM segment extends directly into the cytosolic HCN domain. The C-terminus of the S6 segments is connected via the so-called C-linker to the cytosolic cyclic nucleotide–binding domain (CNBD).

The general tetrameric arrangement of HCN channels is similar to that of the related cyclic nucleotide-gated (CNG) and Ether-a-go-go (Eag) channels, as well as to the plant ortholog KAT1, with four subunits adopting, relative to the pore, the so-called nondomain-swapped arrangement of the voltage sensor.⁵⁻⁷ The cytosolic domains, in contrast, are assembled in a “swapped” manner in the sense that the C-linker of one subunit rests on the C-linker of its direct neighbor.⁸ The HCN domain, wedged between the C-linker/CNBD and the transmembrane domains, interacts not only with the adjacent subunit but also with the opposite subunits.⁹ This distinct mechano-coupling in the cytosolic domains is thought to translate the initial signal of cAMP binding to the CNBD to the membrane-embedded part of the channel.⁹

Despite an apparent 4-fold symmetry in the membrane-embedded part of the channel and in the C-linker/CNBD, several functional data advocate a pronounced asymmetry in cAMP binding. Ulens and Siegelbaum linked four subunits of HCN2 in a concatemer in which they were able to introduce between 0 and 4 mutations in the cAMP binding site to prevent ligand association with CNBD.¹⁰ Systematic functional testing of these constructs with respect to cAMP-enhanced channel opening showed that the four CNBDs do not contribute independently to channel gating. Instead, the data advocated cooperativity in binding between the subunits in which pairs of subunits form two functional dimers. Only after an interaction of the latter dimers does the channel acquire full opening. This cooperative nature of cAMP binding sites in HCN channel gating was further detailed by patch clamp fluorometric recordings in which the binding of a fluorescent cAMP analogue to its binding site is monitored simultaneously with channel activation in the same membrane patch.¹¹ Kinetic analysis of the functional data suggests a complex scheme of cooperative gating in which the binding of one cAMP molecule affects the affinity for the binding of a subsequent molecule. The authors extract from their data a sequential model with a “positive–negative–positive“ cooperativity meaning that the affinity for the second and fourth cAMP is enhanced, while association of the third molecule is penalized by the preceding binding.¹¹

Cooperativity in ligand binding was recently challenged for detergent solubilized resting HCN channels by high-resolution optical studies in which the binding dynamics of cAMP to individual tetrameric HCN1 and HNC2 channels was monitored with single-molecule resolution.¹² The authors observed that the ligand molecules were binding independently to all four subunits, suggesting that HCN channels in the resting state (0 mV) exhibit no cooperativity in cAMP binding. The authors propose that the evidence for cooperativity reported in previous studies could be an artifact of extracting single protein behavior from macroscopic measurements. Alternatively, secondary interaction partners, which are not part of the channel protein itself, could, in a cellular context, affect the mechanism of cAMP binding to the HCN channels.¹² Indeed, more recently, a purely positive cooperativity was reported in a study in which the resting HCN2 channel was embedded in native cell membranes.¹³ This suggests that environmental conditions, like the membrane, might be important for the cooperative behavior of the channel.

Here, we employ the analysis of anisotropic network models (ANM) of HCN structures as an independent test for cooperative versus noncooperative binding patterns of cAMP to these channel proteins.^14,15 Despite being a coarse-grained model with a simplistic potential energy function—with amino acids modeled as single nodes connected by springs—ANMs are able to predict global, functionally relevant motions of water-soluble proteins as well as of membrane proteins.¹⁶⁻¹⁹ This coarse-grained method has already been used successfully in the past, in combination with linear response theory (LRT), for uncovering mechanical coupling and conformational changes associated with ligand binding in various proteins.²⁰⁻²³ In the specific case of HCN channels, which are in the center of interest here, the cAMP-induced movements in the single chain and in the whole tetramer were correctly predicted by these coarse-grained method methods before being finally confirmed by cryo-EM structures.^24,25,9,20

To tackle the question of cooperativity, in the present study, we took advantage of the procedure described in Kunzmann to apply a force mimicking the conformational changes induced by cAMP on one CNBD of either the HCN1 or HCN4 channel structure.²⁶ This local impact in one subunit would have no consequences on the remaining subunits if ligand binding is noncooperative. In the case of cooperativity between CNBDs, the force applied to one CNBD would impact the others. Analysis of our data agrees with the latter scenario in that a stepwise binding produces the same sequence of positive, negative, and positive cooperativity that was reported in experiments.¹¹ The data suggest that binding of the first cAMP imposes in HCN channels an asymmetry in the subsequent binding steps with a peculiar cooperative pattern. Our results indicate that this feature must be an inherent property of the channel protein and be independent of cellular factors. Taken together, the computational results support experimental data on a cooperative modulation of HCN channel activity by cAMP. Detailed insights into the complex pattern of cooperativity will provide valuable information for systems biological modeling of these channels in pace making cells such as the sinoatrial node, with dynamic variations in membrane voltage and cAMP concentrations.

Methods

Preparation of Models

Resolved cryo-EM structures were downloaded from the RCSB PDB. The loop modeling procedure implemented in MODELER v. 10.2 was applied to model missing residues in HCN1 (5U6O/5U6P), the single KAT1 structure (6V1X), and TAX4 (6WEJ/6WEK).²⁷ All modeled residues are situated in loop regions (see Table 1). The four HCN4 structures (7NP3/7NP4, 6GYN/6GYO) without missing amino acids were directly used in subsequent steps. All atoms that were neither part of the protein nor part of the bound ligand cAMP/cGMP were removed. The amino acid sequences of apo-holo pairs (all channels but KAT1) were aligned with penalized internal gaps to obtain the same number of residues by removing nonoverlapping N- or C-terminal stretches in the longer sequence. KAT1 was aligned in the same manner with apo HCN4 in the open state (7NP3) to obtain corresponding residue IDs within the CNBD.

Table 1. Overview of PDB-IDs of Channels, Sequence Regions of Closed Gaps in Loop Regions, CNBD Residues, and Residues Designated as Ligand-Binding Residues within the CNBD.

PDB-ID	identifier	closed gaps	CNBD residues	ligand-binding residues
5U6O	apo HCN1, closed	201–202, 243–251	466–585	503, 522, 527,530, 532, 537–545, 548–553
5U6P	holo HCN1, closed			503, 522, 527,530, 532, 537–545, 548–553
6GYN	apo HCN4, closed		593–706	624, 643, 645, 651, 653, 658–664, 669–674
6GYO	holo HCN4, closed
7NP3	apo HCN4, open			624, 632, 643, 645, 651, 653, 658–664, 669–672, 674
7NP4	holo HCN4, closed
6WEJ	apo TAX4, closed	162–164	593–706	521, 527, 529, 540, 549, 550, 552, 557–563, 574–579, 616, 617
6WEK	holo TAX4, open	161–166
6V1X	KAT1, closed	158–160	374–491	405, 413, 426, 428, 436, 438, 443–449, 454–457, 459

Coarse-Grained Elastic Network Models of Ion Channels

In coarse-grained ENMs, single amino acid residues are commonly represented as nodes placed at the position of their respective Cα atoms.²⁸ Interactions between amino acid pairs are modeled by a harmonic potential function.

1

where Δr_ij is the displacement of a given node pair ij from its equilibrium distance r_ij,0 (generally corresponding to the initial structure used to create the ENM) and γ_ij is the force constant.

In the anisotropic variant of ENMs (i.e., as anisotropic network models), the direction of oscillations during normal-mode analysis (NMA) is taken into account in the form of the Hessian matrix H:¹⁴

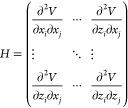2

with x, y, and z the subsets of the displacement vector Δr⃗_ij along the main Cartesian axes.

Matrix quasi-inversion of the Hessian as Moore–Penrose pseudoinverse yields the covariance matrix H^–1, which contains information regarding the linear relation between fluctuations in x, y, and z directions.^29,30

ENM/ANM variants differ in the parametrization of γ_ij and the chosen distance cutoff, for interactions between nodes.³¹ In this work, a standard anisotropic network with invariant force constants of 1 kcal/mol with a cutoff range of 15 Å was employed.¹⁴

As a control, a range of parameter sets was chosen in conjunction with 7NP3:

The sequence- and distance-dependent (sdENM) parameter set as well as the extended ANM (eANM), together with the parameter-free ANM and the Hinsen-C_α force field were applied with their standard parameters.^15,32,33 Additionally, varying cutoff distances were tested for invariant ANMs (8, 45, and 150 Å) and pfANMs (15 Å).

As a vibrational subsystem analysis approach, which considers the lipid environment around the protein, the explicit ANM (exANM) was also included as reference:³⁴ Here, a cutoff of 15 Å was selected, with a membrane diameter of 29.6 Å for the preoriented 7NP3 with a membrane radius in the xy-plane (orthogonal to the channel’s main axis) of 160 Å. The channel was preoriented using the PPM Web server (v. 3.0; https://opm.phar.umich.edu/ppm_server3_cgopm).³⁵

Following Zhang et al., a higher xy-plane radius for the membrane was chosen compared to the original exANM publication, together with an invariant force constant for both the membrane environment as well as the embedded ion channel.^34,36

Linear Response Induced by cAMP-Binding

LRT has been previously applied to protein ANMs to model binding of ligands and allosteric rearrangements.^20,25

Starting from the covariance matrix H^–1 for a given ANM and with acting forces F⃗ modeling binding/unbinding of the ligand, predicted displacements Δp⃗ are computed following a linear approximation:

3

To simulate binding of cAMP to CNBDs, forces were applied along displacement vectors Δq⃗_exp between Cα atoms of cAMP binding residues found in the apo

and holo structure after “local” chainwise superimposition (CNBD residues in each chain were superimposed separately; see Table 1 for selected residues). Displacement vectors were computed for binding residues (located within 6 Å of cAMP in the holo structure; see Table 1) in all four subunits after superimposition with the apo structure. In the “local” case, superimposition of CNBDs and displacement computation were conducted for each subunit separately.

Perturbing forces ΔF⃗ were applied to single subunits in the same direction as Δq⃗_exp.

The relative absolute values of the atom-specific displacement vectors in Δq⃗_exp were retained in ΔF⃗, with arbitrary force units due to the inherent coarse-grained nature of ANMs.

For KAT1 as the only channel investigated in this work without a corresponding apo-holo pair, displacement vectors were transferred to residues from the same relative position within the CNBD as designated binding residues in apo HCN4 in the open state (7NP3) after chainwise superimposition of the CNBDs in apo HCN4 and KAT1.

Residues in KAT1 corresponding to binding residues and CNBD residues in apo HCN4 were obtained from the KAT1/apo HCN4 sequence alignment with penalized internal gaps described above.

From induced displacements for CNBD-perturbations in single subunits Δp⃗_LRT,i, LRT-induced displacements Δp⃗_LRT for different combinations of perturbed CNBDs were computed directly as sums.²⁶

This is equivalent to the computed displacements for forces directly acting on multiple subunits following eqs 3 and 4, with as the force for the individual subunit i:

4

5

6

LRT Multiresidue Null Model

1000 LRT perturbations drawn from a spherical arrangement around the coordinate origin of the investigated structure were applied to all binding residues as multiresidue LRT null model, based on the single residue LRT null model.²⁵ Iterating over all directions, all binding residues were perturbed at the same time in the same general direction and with the same arbitrary force unit. To obtain evenly spaced displacements in a spherical shape, 1000 points were generated by using a Fibonacci lattice.

Overlap between Experimental and Induced Displacements

The relative orientation of resulting LRT-displacements for the apo structure and apo-holo displacements observed for the superimposed cryo-EM structures in the CNBD of different subunits was analyzed by computing their overlap.

Here, the overlap is defined as the cosine of angle α between the two vectors Δp⃗_LRT and Δq⃗_exp:

7

Equation 7 is adapted from Sanejouand, in which the absolute of the numerator is additionally computed.

This metric quantifies the relative orientation and alignment of two vectors, with vectors pointing in the same or opposite directions (Ω = 1 and Ω = −1, respectively) and perpendicular vectors (Ω = 0) as edge cases.

Programs and Software Libraries

The whole procedure outlined above was conducted using the Biotite Python library for bioinformatics in conjunction with the Springcraft extension package for ENMs.^37,38

Covariance matrices for the membrane-embedded proteins according to the exANM parameter set were computed with ProDy(39) Additional Python libraries were used for data analysis, visualization, and workflow integration.⁴⁰⁻⁴⁵

Results and Discussion

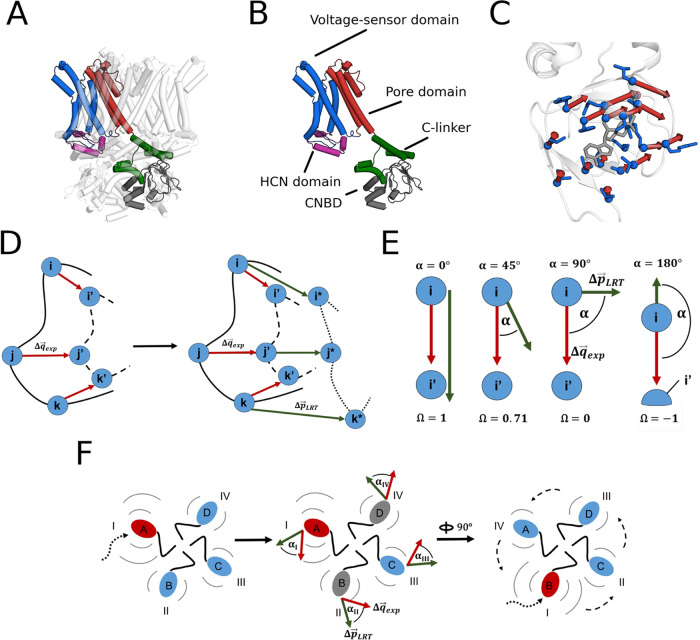
To answer the question whether sequential cAMP binding to the CNBDs affects their conformation in an independent or cooperative manner, we created an ANM of the available cryo-EM structures of HCN1 (5U6O, 5U6P)³ and HCN4 (7NP3, 7NP4; 6GYN, 6GYO)^4,46 channels in their cAMP free and bound states, hereafter “apo” and “holo”, respectively. In the case of HCN4, we included two different apo structures in the analysis, as they display a closed (6GYN) and an open conductive pore (7NP3). This will provide additional information about whether pore opening has an impact on cooperativity. Figure 1A shows, as an example, the structure of apo HCN4 obtained from 7NP3. For clarity, one chain is colored based on the domains composing it. In Figure 1B, the latter chain is isolated from the tetramer and domains are labeled.

Figure 1.

Structures of the HNC channel and representation of ligand-induced CNBD displacements with a schematic representation of the LRT procedure and computation of overlaps for LRT-induced displacements. Structural overview of the apo HCN4 channel in the open state (7NP3), with colored functional subunits in the tetrameric channel (A) and for a single monomer (B): The N-terminal HCN domain is illustrated in violet, the voltage sensor containing domains in blue, pore domains in red, the C-linker in green and the CNBD in dark gray. cAMP-induced displacements in the CNBD of HCN4 (C). The CNBD of the apo structure is shown in the cartoon representation, with red arrows as displacement vectors, pointing toward the location of the ligand-binding residues (blue) in the holo structure. The ligand (gray, stick-representation) is shown in its bound position in the holo state. A schematic overview is depicted in (D): LRT forces are applied along displacement vectors (red arrows, Δq⃗_exp) on one subunit, pointing from the residue’s initial apo to their holo position (i and i′ respectively). As a consequence of all interactions in the ANM model, the perturbation yields a predicted LRT-induced displacement vector (green arrow, Δp⃗_LRT), pointing from the apo to the LRT-induced displacement position (i and i*, respectively). The alignment of experimental apo-holo displacements and those induced by LRT on one subunit is evaluated using the overlap Ω, which is the Cosine of the angle α between both vectors (E). The whole procedure is depicted in (F) in an overview of the homotetramer: Single subunits are acutely perturbed (red sphere, perturbing force as dotted curved arrow) and overlaps evaluated separately for the acutely perturbed subunit (I) as well as for the remaining subunits (II–IV). Subunits II and IV are neighboring subunit I directly (cis-located), and subunit III is located opposite of I (trans-located monomer). Each structural subunit is perturbed independently (depicted as 90° rotation of the relative positions I–IV); results for relative positions II–IV are averaged.

Like HCN channels, also CNG and KAT1 channel monomers are subdivided into 6 transmembrane domains with a conserved cyclic nucleotide-binding site (CNBD) in the cytosolic C-terminus. Despite their similar architecture, these channels are from a functional point of view distinctly different: While HCN channels are primarily gated by negative voltage and modulated in their activity by cAMP binding, the KAT1 channel is insensitive to cAMP and only opened by membrane hyperpolarization.⁴⁷ The activation of CNG channels reveals the opposite dependencies; it is insensitive to voltage, and opening is exclusively achieved by cyclic nucleotide binding. Also this occurs in some kind of a cooperative manner⁴⁸ via distinct interactions between their four binding sites.⁴⁹ To address the question on both general and channel-specific cooperativities in the three types of structurally similar but functionally different channels, LRT responses were also computed for an apo-closed (6WEJ) and cGMP-bound open TAX4 (6WEK) structure pair,⁵⁰ and for KAT1 in the closed state (6V1X).⁵¹

We reason that the linear responses mimicking cyclic nucleotide binding will generate a conformational change resembling the experimental holo structure, when imposed on a CNBD of the ENM models of HCN1/4, TAX4, and KAT1. Based on this assumption, we derive the force vector, in the framework of an LRT (see the Methodssection), for the displacement of the CNBD residues involved in the apo-holo transition. For calculation of these forces, each monomeric CNBD chain of the holo structure was, first, superimposed on the apo CNBD in the corresponding chain. For the superimposition of holo and apo CNBDs, a “local” method for each separate chain was chosen over a “global” superimposition of all amino acids. The reason is that our analysis is focused on displacements that occur in response to ligand binding within the CNBD in each subunit. Changes in the orientation of the CNBDs relative to the channel pore region are not important in this context. Because KAT1 is not binding cyclic nucleotides, only the apo structure is available.⁵¹ The missing holo state was approximated by applying to the CNBD the same perturbing force vector F⃗ computed for HCN4.

Next, the displacement vectors Δq⃗_exp between the apo and holo positions of the Cα atoms of the designated residues were computed (Methods, Table 1 and Figure 1C).

To recreate ligand-induced conformational changes in the CNBD, a perturbing force vector F⃗ with the same direction as Δq⃗_exp, but in arbitrary force units, was applied to the Cα atoms of the designated residues. The four subsets of F⃗ corresponding to the four individual CNBDs in different subunits were applied separately to study cooperativity between these sites (see the Methods section and Figure 1D,E).

To compare the LRT-induced displacements Δp⃗_LRT with the corresponding experimental displacements Δq⃗_exp between the apo and holo conformations, we calculated the displacement overlap (Figure 1E). This overlap Ω is equal to the Cosine of angle α between Δp⃗_LRT and Δq⃗_exp, with a maximum value of 1 when the two vectors Δp⃗_LRT and Δq⃗_exp point in the same direction, a minimum value of −1 when they point in opposite directions, and a value of 0 that indicates orthogonality between both vectors.

In agreement with experimental data,⁵²⁻⁵⁴ we interpret Ω values approaching 1 in nonperturbed CNBDs as indirect evidence of positive cooperativity in the sense that those CNBDs undergo conformational changes matching the experimental apo-holo displacement and, therefore, display an increased cAMP binding affinity.

Following the same rationale, an Ω value of −1 indicates a negative cooperativity, whereas a value close to zero indicates no cooperativity between binding sites in nonperturbed monomers.

Induced displacements Δp⃗_LRT computed with the ENM-LRT method are linear approximations: They are exactly valid for only short deviations from the unperturbed apo structure. Therefore, results for Δp⃗_LRT obtained with this method are to be interpreted qualitatively. The overlap between Δp⃗_LRT and Δq⃗_exp is an indication of cooperativity insofar, as it describes the propensity of the apo structure CNBDs to move into the direction of the holo structure CNBDs, after the perturbation of a single apo CNBD.

This procedure was repeated with all four monomers A–D after rotating them one by one into LRT perturbed relative position I (Figure 1F). The results of the analysis are reported as mean overlaps for the four rotations. As expected for C4-symmetrized structures, the standard deviations are therefore neglectable (below ±0.1) excluding any hidden asymmetry between multimers.

Figure 2A shows exemplary LRT-induced displacements (green arrows) for apo HCN4 in the open-pore state, after perturbing CNBD I, in the two cis- (II + IV) and trans-located CNBD (III) with respect to I, together with experimental displacements (red arrows).

Figure 2.

Comparisons between LRT-induced displacements and experimental displacements reveal a robust pattern for HCN as well as for KAT1 and TAX4. Experimental displacements Δq⃗_exp (red) and LRT-induced displacements Δp⃗_LRT (green) of the apo HCN4 structure in the open state are shown as arrows in subunit IV, III, I, and II (A). Overlaps Ω between LRT-computed displacements and experimental apo-holo displacement vectors (arbitrary units) after perturbation of a single subunit in relative position I (B). A clear pattern is visible with positive overlaps for the trans subunit (III) compared to negative overlaps for cis-located subunits (II, IV). Overall higher absolute overlaps are observed for HCN channels compared with TAX4 and KAT1. The average overlaps for all single perturbed subunits and their corresponding relative conditions are plotted as bars. Standard deviations for these values are below ±0.1.

The overlaps from the perturbed monomer I and the experimental holo structure of the same subunit show values of about 0.8. This underscores that perturbation of the apo structure by externally applied forces can approximate the experimental holo structure. Notably, the procedure does not perfectly convert the apo CNBD into the holo one, e.g., the overlap Ω is not reaching 1, presumably because we applied forces only CNBD residues located in the vicinity of the ligand (see the Methodssection, Table 1, and Figure 1C). Furthermore, all LRT-induced transitions are predicted for an ANM of the initial structure, while intermediate states in the apo-to-holo transitions (with 1–3 ligands bound) are not considered.

The overlap values from the remaining CNBDs show that they are significantly different from zero for HCN1, as well as for both open and closed HCN4, meaning that the LRT analysis suggests cooperativity in ligand binding. Scrutiny of the individual overlap values uncovers that the CNBD in subunit III, which lies diagonally opposite (trans position) to CNBD I, exhibits a strong positive cooperativity; the two proximate CNBDs II, and IV (cis position) show, in contrast, a negative cooperativity (Figure 2B).

Similar overlap values and patterns for HCN1 and HCN4 furthermore indicate structurally highly conserved mechanical coupling between the four subunits composing HCN channels. HCN4 in the open- and closed-pore state, with an inactive voltage-sensing domain in both cases, have similarly high overlaps. This indicates a negligible influence of the difference in the pore-opening state on the CNBD interactions.

Application of the same procedure to the KAT1 and TAX4 channels generates a similar pattern of positive cooperativity for the trans subunit and negative cooperativities for cis subunits (Subunits II and III/IV respectively, Figure 2B). However, while the pattern in these channels is conserved, the absolute values of the overlaps are much smaller than in the HCN channels. Despite a similar global architecture shared between HCN, KAT1, and CNG, we observed intrinsic mechanical coupling between CNBDs with a high degree of cooperativity only for HCN channels. Lower overlaps indicate a weaker or no coupling between CNBDs in different subunits. It is worth noting that results for KAT1 must be treated with some caution: Without an available ligand-bound structure for this purely voltage-gated channel, the perturbation vectors were inferred from apo-holo transitions in HCN4.

As a control for our results, we addressed the question of whether the pattern of responses as in Figure 2B are robust toward changes of ENM force constants and parameters used for the calculation.

To this end, we applied a wide range of ENM parameter sets with and without an explicit cutoff value. We also performed an additional evaluation of the critical distance between two amino acids in the force constant value and/or an amino acid specificity. Finally, since HCN channels are membrane proteins, also the impact of explicit surrounding lipids on the presumed cooperativity in these channels was analyzed (Table 2).

Table 2. Overlaps Ω between LRT-Derived Displacements and Apo-holo Displacements Computed for HCN4 with Different ENM Parameters^a.

ENM parameter set	II	III	IV	rc, Å	AA specific	NB distance dependence
invariant*	–0.84	0.75	–0.55	8	false
invariant	–0.63	0.71	–0.69	15
invariant*	–0.46	0.69	–0.51	45
invariant*	–0.51	0.68	–0.26	150
sdENM	–0.66	0.72	–0.67		true	binned distance categories
eANM	–0.67	0.72	–0.70	14	true
pfANM	–0.57	0.68	–0.37		false	dij–2
pfANM*	–0.63	0.71	–0.69	15
Hinsen	–0.63	0.72	–0.68		false	dij–6
exANM	–0.61	0.74	–0.72	15	false

^aAverage overlap values after perturbation of the CNBD in subunits A–D (position I) are given in arbitrary units, rounded to two decimals. Standard deviations are below 0.01. The chosen cutoff value (r_c) as well as absence or presence of an amino acid-specific evaluation of interactions (AA specific) are also listed. Short notes regarding the distance dependence of nonbonded interactions as part of the parameter set are listed in the last column (NB distance dependence). The dependence on that distance between node pair ij (d_ij) is directly given if part of the functional form of the ENM. sdENMs evaluate nonbonded distances for specific amino acid pairs and specific distance bins (binned distance categories). ENM parameter sets with a nonstandard r_c are marked with an asterisk (*). Additional information regarding the listed ENM parameters is available in the Methods section.

The respective control runs with different force fields generated qualitatively similar results for the 7NP3 structural model. The only two exceptions out of the 10 individually tested parameter sets are found for pfANMs and invariant ANMs without any effective cutoff distance; in the latter case, the cutoff of invariant ANMs was set to 150 Å, which exceeds the maximum pairwise atom distance in 7NP3. These results are consistent with data from a comparative method study. Also in this systematic investigation, pfANMs and ENM variants with overly large cutoff values or without any cutoff value and slowly decaying long-range nonbonded interactions (like pfANMs), reproduced results from MD simulations with lower fidelity than variants with lower cutoffs.¹⁹ When tested as cross-checks, pfANMs with an enforced distance cutoff of 15 Å and the Hinsen-FF, a parameter set without explicit cutoff but fast-decaying nonbonded interactions, both reproduced the negative/positive pattern for trans/cis subunits.

Our control data confirm that for reasonable cutoffs or fast-decaying long-ranging nonbonded interactions, the ENM parameters only have a slight influence on the results. Modeling effects of the lipid membrane with exANMs also only minimally affected the obtained overlaps.

Hence, on the basis of these control experiments, we can conclude that the observed cooperative patterns seem to be a feature of the HCN channel structure itself.

For the remainder of the analysis, an invariant ANM with a cutoff value of 15 Å was chosen, consistent with the robustness of results with cutoffs between 8 and 15 Å for 7NP3 (Table 2).

Next, we asked to what extent the pattern of positive and negative subunit cooperativity is related to the structural changes from the apo to the holo conformation in perturbed subunit I. We reasoned that an arbitrary perturbation of subunit I, not mimicking the conformational changes of ligand binding, should not create the same pattern of cooperativity if the latter is causally linked to structural deviations induced by ligand-binding. Such a random perturbation would be expected for overlaps of around 0 in relative position I, e.g., when the vector of the imposed displacement is orthogonal to that of the apo-holo transition. To test this assumption, we perturbed in a multiresidue LRT null model all C_α atoms involved in ligand binding within the CNBD of subunit I in the same general direction and at the same time. For this purpose, force vectors were subsequently applied in 1000 spherically arranged directions while maintaining the general direction of perturbation at each C_α position (see the Methods section).

As for Figure 2, we estimated from the overlap the impact of this perturbation first on subunit I and then on the remaining binding sites II–IV. The overlap values in Figure 3A report the deviation between the experimental structure of the CNBD in the holo configuration and that obtained in response to different parallel LRT null model perturbations. The overlap values for positions II–IV are plotted relative to those in position I.

Figure 3.

Parallel LRT null model perturbations of cAMP binding residues in HCN. Overlaps in subunits II–IV (columns 1–3, respectively, denoted as Ω_II–Ω_IV) are plotted as a function of overlap values in subunit I (Ω_I) after randomized perturbation of cAMP binding residues in the latter (A). For a better visual distinction, dots are color coded according to the overlaps Ω_II–Ω_IV, respectively (minimum: blue; maximum: red). Distinct channels are plotted in row order: HCN4 (7NP3/7NP4), the alternative HCN4 structure pair (6GYN/6GYO) (HCN4-alter.), and HCN1 (5U6O/5U6P). The Pearson coefficient and its associated P value are shown above each subplot. An approximately linear relationship between the overlap at position I and those at other positions can be observed. Here, positions II and IV (cis) are negatively correlated with those in I, while those in III (trans) are positively correlated. Overlap distributions for HCN4 are shown in (B), with the 100 highest (Max. Ω_I, red) and lowest (Min. Ω_I, blue) overlap distributions as well as those 100 with an overlap closest to zero (Min |Ω_I|, gray) shown as stripplot. Boxes denote the interquartile range and the median of the category. Opposing subunits are highlighted with the same color (I + III: dark gray; II + IV: light gray).

The data show for all channel proteins a linear correlation between overlap values in subunits II–IV relative to those in subunit I. For overlaps close to zero in subunit I, a higher variability can be observed in other subunits compared to those with a high positive or negative overlap. This is better seen in Figure 3B: Both the 100 distributions with the highest overlap in subunit 1 and the 100 with the lowest overlap produce a distinct pattern (respectively, positive for trans-located and negative for cis-located subunits and vice versa). In comparison, the 100 smallest absolute values (i.e., close to an overlap of zero in subunit I) produce a mix of patterns. This indicates that motions in a ligand binding site which best mimic ligand association or ligand dissociation produce a distinct pattern of cooperativity in the remaining subunits. Motions in a single binding site, which are neither mimicking ligand binding nor dissociation, are also influencing the conformation of the remaining subunits. But in these cases, the reaction of the remaining subunits is more random with respect to the absolute value of the overlap as well as its quality of impact e.g., whether the impact on other subunits is positive or negative.

For TAX4 and KAT1, the relation between random displacements in subunit I and induced displacements is more dispersed. Overlaps are generally lower for induced displacements on sites II–IV compared with those observed for HCN channels (Figures S1A and 3A).

Additionally, in comparison to HCN, there are overall lower differences in overlaps between movements induced by the 100 perturbation directions with the highest/lowest overlap in subunit I and those 100 with the smallest absolute values (Figures S1B and 3B).

In summary, the data highlight that cooperative conformational changes in the remaining subunits II–IV occur in a very reproducible manner whenever a displacement in subunit I mimics the conformational change of either ligand binding (positive values) or dissociation (negative values) in this subunit. This is true for members of the HCN family, while this relation is less stringent for TAX4 and KAT1. Hence, any conformational transition in the CNBD of HCN channels, which is sufficiently similar to the one generated by ligand binding, will eventually cause some kind of positive conformational impact on the trans CNBD and negative impacts on the cis-located CNBDs (Figure 3A,B). This finding is compatible with experimental data in HCN channels according to which ligand binding occurs in a cooperative manner.^11,13 The data are also compatible with data on HCN channel modulation by cGMP and cAMP analogues, e.g., molecules that are not identical to cAMP.^55,56 Even though the latter bind with a lower affinity to the CNBD and presumably cause distinctly different conformational changes in the ligand binding site than cAMP, they are still able to modulate HCN channel gating.

Implications for HCN Channel Gating

The results suggest that after binding of the first cAMP molecule, the trans binding site is on average populated as second site by the ligand because the binding affinity of the latter site is increased due to a positive cooperative behavior between the diagonally located CNBDs. This step is followed by sequential binding of the third and fourth ligands to the CNBDs that are cis-located with respect to the first liganded CNBD. This information can be translated into the cooperative binding pattern shown in Figure 4. cAMP binding displays a positive cooperativity between trans-located CNBDs (I and III in Figure 4). Once liganded, trans CNBDs induce negative cooperativity to their adjacent (cis-located) empty sites II and IV. Once a third ligand binds to either of the two sites (II in Figure 4), cAMP binding to the last open site (IV in Figure 4) is again favored by positive trans cooperativity.

Figure 4.

LRT-modeled sequential binding patterns of HCN channels show the same pattern as the experimentally derived Ka values for HCN2. The overlap for 1–4 bound cAMP/cGMP molecules (solid lines) shows a qualitatively similar behavior between LRT-simulated subsequent binding of ligands in I–III–II–IV and the experimentally derived association constant K_a of HCN2 channels in the open state (dotted yellow line) from Kusch et al.¹¹ (A). The perturbed subunit in the current step is depicted in red, previously perturbed subunits in blue, and unperturbed subunits in gray (B).

Several experimental studies with HCN channels have provided indirect structural and functional support for such a scenario. Two laboratories have independently shown with concatamers of HCN2 that two cAMP bound to the CNBDs in the trans position had a different impact on channel activity compared to a situation in which the ligands were bound to two subunits in a cis configuration.^10,57 Such a preferential mechanical connection between subunits in a trans versus cis configuration, which is also predicted from our LRT simulations, is supported by additional structural and computational data. In two independent studies, it was shown that the cationic side chain of K464 in the C-linker of HCN2 forms a hydrogen bond with the backbone of M155.^9,58 This results in a functionally important connection between the elbow structure of one subunit and the HCN domain on the trans subunit. While this underscores the mechanical coupling between trans-oriented subunits, it also provides a link to the mechanism of cAMP-modulated channel gating. The critical connection between the trans subunits serves as a key player in the transmission of conformational information from the CNBD via the C-linker to the gates in the channel forming part of the protein.^9,58

A plot of the overlap values from the LRT analysis as a function of the number of subunits binding cAMP agrees very well with the experimentally measured affinity of cAMP for HCN2 in the voltage-activated state (Figure 4). Both independent approaches exhibit the same “positive–negative–positive” cooperative pattern of cAMP binding. The only difference between the experimental and computational data is that the binding affinity for the fourth cAMP binding is lower than in the experimental data. In both cases, there is a positive trend for binding to the last free site after the third side is populated. But the absolute value is in the computational analysis lower than for the first binding and the displacement overlap after the third binding step is still negative. This deviation between experimental and computational data must be taken with caution.

In contrast to HCN channels, TAX4 and KAT1 show weaker sequential overlap patterns with lower absolute values (Figure 4). Together with the lower binding patterns in cis- and trans-located CNBDs for these channels induced by singular perturbations, this suggests a lower intersubunit coupling of the ligand-binding regions of these channels compared to HCN.

It is worth mentioning that the actual structure progressively deviates with increasing numbers of bound cAMP molecules from the apo structure, which was taken as input structure for the ANM. This may with each binding step limit the accuracy of LRT-ENM predicted deviations for the starting apo structure, because this model operates with harmonic approximations and can thus only predict deviations well for small perturbances of the starting structure.²⁰ Therefore, intermediate structures between apo and holo with partial binding of a ligand to CNBDs cannot be modeled with this approach directly. The employed method has limitations inasmuch as both the harmonic approximation and the coarse-grained potential function in ANMs only predict global movements of the channel; small local structural changes due to ligand-CNBD interactions or the sequence of binding kinetically are not resolved by this approach.³¹

Conclusions

This work was motivated by conflicting results in which one study claims that cAMP-mediated gating in resting HCN2 channels is not cooperative, while other studies report a distinct cooperativity in cAMP binding. The results of our LRT analysis now support from a structural point of view the latter mechanism. The LRT-induced conformational changes in the CNBDs shown in Figure 4 suggest “tectonics” in HCN channels in such a way that ligand-induced conformational change in one subunit influences the conformation of the remaining sites; we interpret this as an indication for cooperativity. Modeling of single ligand-binding events by LRT-ENM uncover positive interactions between CNBDs in trans-located subunits and inhibitory interactions between cis-located subunits. With this information, the data support a scenario in which the second binding step occurs more likely in the trans position, which is induced to follow a motion favorable for ligand-binding by the first binding event. Binding of the third ligand should be disfavored because the two empty subunits in the cis position are suppressed in binding. While previous experimental data in Kusch et al. as well as the present computational study support such distinct cooperativity in HCN channels, its physiological role is not clear.¹¹ It can only be speculated that the complex interplay between membrane voltage and ligand binding on channel gating provides cells with a wide range of possibilities to fine-tune HCN activation in the context of dynamic changes in membrane voltage and cAMP concentrations.

A full interpretation of the LRT results in the context of HCN channel function is not straightforward. The pattern of alternating “positive–negative–positive” cooperativity seen in the LRT analysis was also reported from functional experiments with HCN2 but only in the case when the channel was activated by negative voltage.¹¹ In the resting channel, only positive cooperativity was observed.¹³ Since all of the HCN structures used for LRT were obtained at 0 mV, i.e., in the resting state, and since we found no difference between the HCN4 structures in the open and closed configuration, we cannot directly interpret the present data in the context of HCN channel gating. At this point, the data only suggest that the HCN channels possess intrinsic sets of motions, which can lead to the observed complex pattern of conformational changes in the ligand binding domains. These intrinsic motions are triggered by the binding of individual ligands to their binding sites. In the entire protein embedded in the membrane bilayer, these intrinsic motions are presumably functionally relevant only in a condition in which the protein is in its voltage-activated configuration.

The distinct pattern of cooperativity in HCN channels was less pronounced in the structurally related CNG channel TAX4 and the plant ortholog channel KAT1. While binding of a single ligand causes in all HCN channels the same degree of conformational changes in the remaining three CNBDs, the conformational impact onto these open binding sites is less pronounced in the voltage-insensitive TAX4 and the cyclic nucleotide-insensitive KAT1. It is tempting to speculate that these channels lack the evolved sophisticated mechanism of coupling the CNBD and the transmembrane region, both via the C-linker and the HCN domain, in comparison to HCN channels. More generally, subunit cooperativity could be an inherent property of tetrameric channels with a 6TMD architecture. The basis for these distinct subunit interactions might originate from the fact that the functional tetramers are presumably assembled in cells as dimers of dimers.^59,60 This could also be the basis for the widespread cooperativity of gating between distinct channel proteins found in clusters.⁶¹

Data Availability Statement

Input files and Python scripts used for analysis and plotting as part of a Snakemake workflow are freely available via Zenodo (https://doi.org/10.5281/zendo.10691716) this is the final link in zendo.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.4c00360.

• Additional overlaps Ω between experimental displacements according to CNBD-superimposed structures and those according to the LRT for KAT1 and TAX4 result in lower overlaps Ω compared to HCN (PDF)

Author Contributions

^# P.K. and J.H.K. contributed equally. K.H. and G.T. designed the research studies; K.H., A.M., and G.T. obtained the funding; P.K. and J.H.K. conducted computational work; P.K. and J.H.K. analyzed the data; P.K., J.H.K., A.M., A.S., and G.T. wrote the manuscript; all of the authors read, corrected, and approved the manuscript.

The work was funded in part by the Deutsche Forschungsgemeinschaft (Grants HA5261/6-1 to J.H.K. and K.H., and TH558/34-1 to G.T.), a Fondazione Telethon grant GGP200221 (to A.M.) and Project Leducq Foundation for Cardiovascular Research “Fighting against sinus node dysfunction and associated arrhythmias (FANTASY)”–LFCR 219CVD03 (A.M.).

The authors declare no competing financial interest.