Structural Insights into DNA-Stabilized Silver Clusters

Abstract

Despite their great promise as fluorescent biological probes and sensors, the structure and dynamics of Ag complexes derived from single stranded DNA (ssDNA) are less understood than their double stranded (dsDNA) counterparts. In this work, we seek new insights into the structure of single Ag_NssDNA clusters using analytical ultracentrifugation (AUC), nuclear magnetic resonance spectroscopy, infrared spectroscopy and molecular dynamics simulations (MD) of a fluorescent (Ag_NssDNA)⁸⁺ nanocluster. The results suggest that the purified (Ag_NssDNA)⁸⁺ nanocluster is a mixture of predominantly Ag₁₅ and Ag₁₆ species that prefer two distinct long-lived conformational states: one extended, the other approaching spherical. However, the ssDNA strands within these clusters are highly mobile. Ag(I) interacts preferentially with the nucleobase rather than the phosphate backbone, causing a restructuring of the DNA strand relative to the bare DNA. Infrared spectroscopy and MD simulations of (Ag_NssDNA)⁸⁺ and model nucleic acid homopolymers suggest that Ag(I) has a higher affinity for cytosine over guanine bases, little interaction with adenine, and virtually none with thymine. Ag(I) shows a tendency to interact with cytosine N3 and O2 and guanine N7 and O6, opening the possibility for a Ag(I)-base bifurcated bond to act as a nanocluster nucleation and strand stabilizing site. This work provides valuable insight into nanocluster structure and dynamics which drive stability and optical properties, and additional studies using these types of characterization techniques are important for the rational design of single stranded AgDNA nanocluster sensors.

Introduction

Noble-metal clusters with sizes approaching their Fermi wavelengths (≈0.5 nm for Ag and Au) display remarkable optical properties owing to the discretization of states. Within this quantum regime, the number of non-radiative decay paths fall off leading to a large increase in fluorescence quantum yields. In recent years, efforts to stabilize few-atom clusters have seen success with the use of various ligands^1–5. Among these ligand-stabilized quantum-sized clusters, silver clusters stabilized by single stranded DNA (Ag_NssDNA) stand out for their exceptional stability and tunability⁶. Selection of the stabilizing DNA or RNA⁷ sequence controls the formation of Ag_NssDNA clusters, with identified sizes ranging from (10 to 24) Ag atoms⁸. By varying the sequence of the stabilizing strand, cluster sizes can be tuned to produce fluorescence colors ranging from blue to near infrared ⁹. The unique relationship between DNA sequence and cluster color makes Ag_NssDNA nanoclusters exciting for a number of sensing schemes including detection of single base mutations^10–12, metal ions¹³, and target DNA¹⁴ and RNA¹⁵ strands while their dual metallic/molecular-like optical properties make them promising candidates for novel nanophotonic elements¹⁶.

However, many applications involving Ag_NssDNA nanoclusters remain limited by the lack of mechanistic understanding regarding their photo-physical and folding pathways. This lack of understanding is largely due to challenges in obtaining structural information. Recently, it was shown that Ag_NssDNA made from single stranded (ss) DNA displayed optical properties that can be rationalized by a rod-like structure^{17, 18} consistent with subsequent studies demonstrating their polarization-dependent behavior¹⁹, preference for forming non-spherical magic numbers²⁰ and their low-energy chiroptical responses²¹. However, the detailed secondary and tertiary structure of a majority of Ag_NssDNA nanoclusters remains incomplete, thus hindering their use in applications for which a deeper understanding of Ag-base binding is required.

To gain new conformational insights into these intriguing Ag_NssDNA nanoclusters, analytical and modeling characterization was performed on a 28 oligonucleotide unit DNA oligomer previously shown to stabilize an Ag atom nanocluster (Ag_NssDNA). This Ag_NssDNA nanocluster has a quantum yield of 0.75, an excitation maximum at 600 nm (2.07 eV) and an emission maximum of 670 nm (1.85 eV) ^17,21. Analytical ultracentrifugation (AUC) and nuclear magnetic resonance spectroscopy (NMR) were performed on purified solutions of Ag_NssDNA Attenuated total reflection infrared (ATR-IR) spectra were collected on bare DNA (ssDNA), on a purified solution of Ag_NssDNA as it transitioned from liquid to film and on solutions of DNA homopolymers with and without Ag(I). Lastly, MD simulations were employed to examine Ag(I) ion occupancies for various nucleobase atoms of ssDNA in solution.

Results and Discussion

Previous work on Ag_NssDNA nanoclusters demonstrated the likelihood for a rod-like configuration in which a neutral silver atom core is stabilized within a DNA shell, supported by Ag(I) bond mediation ^{16, 17}. Among these clusters, the Ag_NssDNA species containing the 5’-CACCGCTTTTGCCTTTTGGGGACGGATA-3’ strand was chosen for further characterization here owing to its relatively high stability, up to 30 days at 20 ^oC. Following high performance liquid chromatography purification, electrospray ionization mass spectrometry (ESI-MS) was used to confirm a mixture of (Ag_NssDNA)⁸⁺ species in solution (Figure S1) ²¹, where N=15, 16, 17. Numerical integration of the predominant (Ag_NssDNA)⁸⁺ species resulted in a relative ratio of Ag₁₅:Ag₁₆:Ag₁₇ to be 7.1:4.9:1, assuming ionization probabilities to be the same for all three nanoclusters, where 8⁺ is the cluster charge.

To independently characterize the in situ shape distribution of (Ag_NssDNA)⁸⁺ clusters, AUC sedimentation velocity experiments were performed. Particles experiencing centrifugal acceleration sediment at rates that depend on their size, density and shape. For dilute, non-interacting particles, the contributions of these factors can be described by a simple force balance, equating the applied centrifugal force to the resistive buoyancy and frictional forces. Rearrangement of this force balance to solve for the acceleration scaled velocity defines a particle’s sedimentation coefficient, s, in the Svedberg equation (particle formalism):

$$s=\frac{v}{{\omega }^{2}r}=\frac{V({\rho }_p-\rho )}{6\pi \mathrm{\eta }{R}_0(f/f_0)}$$ (1)

where ν is the particle velocity, $\omega$ is the rotor angular velocity, $r$ is the radial distance from the center of rotation, V is the particle volume, ${\rho }_p$ is the particle density, $\rho$ and $\eta$ are the solvent density and viscosity. $R_0$ is the radius of an equivalent mass hard, smooth sphere with frictional coefficient $f_0$, and $f$ is the frictional coefficient of the sedimenting particle. The ratio $f/f_0$ is thus a measure of deviation from spherical symmetry. Equation 1 shows that particles of equal mass or volume may be separated by AUC if they have different densities and/or shapes.

To determine the distribution of s-values present in a sample, the signal-weighted radial concentration distribution of the particles is measured as a function of time through either absorbance or interference optical systems. In the absence of convection, and for diffuse, non-interacting particles, one can derive, from a mass balance on a sector-shaped cell, the differential equation relating the change in concentration with time to the diffusional and sedimentation contributions using the Lamm equation:

$$\frac{\partial c}{\partial t}=D\left(\frac{{\partial }^{2}c}{\partial r^2}+\frac{1}{r}\frac{\partial c}{\partial r}\right)-{\omega }^{2}s\left(r\frac{\partial c}{\partial r}+2c\right)$$ (2)

wherein $c$ is the particle concentration, $D$ the diffusion coefficient and $t$ is time. Although an analytical solution to Equation 2 does not exist, the time-dependent concentration profiles measured in the experiment can be numerically fit to extract the sedimentation coefficient distribution with various software packages. For this work, SEDFIT version 15.01b was utilized to fit the data using the c(s) and c(s, ff0) models.^{22, 23}

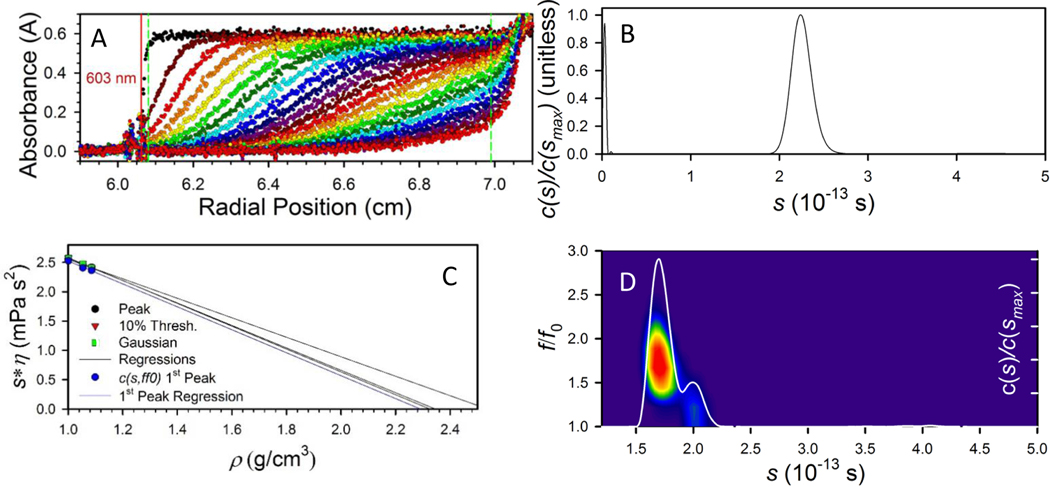
Figure 1A shows representative sedimentation profiles of our (Ag_NssDNA)⁸⁺ nanoclusters measured in 0.001 mol/L phosphate buffer saline (PBS) at peak absorbance of 603 nm. Fitting this data using SEDFIT, known solution parameters, and an estimate for the density of the complex leads to the sedimentation coefficient distribution shown in Figure 1B. A narrow distribution of sedimentation coefficients, such as in Figure 1B, is consistent with a near monomodal population of particles expected for the chromatography selected (Ag_NssDNA)⁸⁺ nanoclusters. More accurate fitting of the data, including extraction of shape information, requires better characterization of the particle density. The functional anhydrous density of the (Ag_NssDNA)⁸⁺ complex can be determined by collecting sedimentation data in systematically varied mixtures of H₂O/D₂O and using SEDFIT to calculate sedimentation coefficients as a function of bulk density. Per Equation 1, extrapolating a plot of $\rho$ vs s* $\eta$ to a sedimentation value of zero yields the particle density (Figure 1C). For the (Ag_NssDNA)⁸⁺ nanoclusters in PBS, this value was approximately 2.3 g/cm³, regardless of whether the extrapolation was done using the peak s-value, a signal-weighted average, or a Gaussian fit to the c(s) fit. This value was furthermore consistent with the value of (2.36 to 2.9) g/cm³ estimated from the mass-weighted average of Ag₁₅ssDNA. This analysis implicitly assumed that the shape and density distributions of the particle were not affected by the transition from H₂O to D₂O, and that the isotopes were distributed uniformly through the bulk at constant molar ratio.

Figure 1. Analytical Ultracentrifuge Results.

A. Absorbance profiles capturing particle sedimentation information measured as a function of time (changing colors) of the (Ag_NssDNA)⁸⁺ in H₂O-PBS. Only every 4^th curve is shown. The red vertical line indicates the best-fit meniscus position, and the green, vertical dashed lines indicate the region of fit data. B. Sedimentation coefficient distribution calculated from the data in A using the c(s) model in SEDFIT, demonstrating the narrow range of sedimentation coefficients observed for the (Ag_NssDNA)⁸⁺ nanoclusters. However, this model assumes a single frictional coefficient reflects contributions from all observed species. C. The effective (Ag_NssDNA)⁸⁺ nanocluster anhydrous density was found through extrapolation of the peak, 10% Thresh (signal averaged), and Gaussian-fit sedimentation coefficients in different compositions of H₂O and D₂O-PBS to zero sedimentation of the (Ag_NssDNA)⁸⁺ nanoclusters after iteration of the c(s) fit to include the determined density. Variation of the intercept density at the level observed in C did not significantly affect further analysis. D. Sedimentation coefficient distribution (line) and friction coefficient heat map for the (Ag_NssDNA)⁸⁺ nanoclusters measured in 80:20 by vol D₂O-PBS:H₂O-PBS solution. At these conditions, the shape and density contributions to the sedimentation are separated enough to allow determination of two populations within the Ag_NssDNA nanocluster population; a dominant extended morphology with an $f/f_0$ ratio of ≈ 1.61, and a minor, compact, morphology with $f/f_0$ ratio of ≈ 1.2 with an uncertainty of ≤ 0.02 based on the variation of peak position.

With the density value for the (Ag_NssDNA)⁸⁺ nanoclusters determined, the distribution of friction coefficients within the s-value distribution was solved by simultaneously fitting the s and $f/f_0$ values for the (Ag_NssDNA)⁸⁺ nanoclusters in 80:20 D₂O/H₂O (Figure 1D). In changing the solvent isotope composition, both ballistic and diffusional motion are reduced identically by the change in viscosity, but only ballistic motion is decreased by the change in solvent density, thus the ratio of diffusional motion to ballistic motion increases somewhat, providing a better estimate of frictional contributions. The fit clearly shows two distinct populations of clusters. The dominant population, with $f/f_0$ = ~1.61, implies that the primary morphology of the (Ag_NssDNA)⁸⁺ nanoclusters was significantly anisotropic. Interpreting the results as an oblate (prolate) spheroidal morphology, the values imply an oblate (prolate) aspect ratio of approximately 7.3 (6.7) depending on the level of hydration and its effect on the location of the plane of shear. A reasonable lower limit for interpretation is ≈ 6.8 (6.2). For these calculations, a density of 0.3 g water/g, commonly used as a hydration estimate for biomolecules, was utilized. This value is not independently discernable from the performed density contrast experiments. The second population displays a much smaller friction factor, $f/f_0$ = 1.2, implying the presence of a second, significantly more compact, morphology of (Ag_NssDNA)⁸⁺ nanoclusters in the solution with an aspect ratio of 1.3 (1.3). The hydrated nanocluster is more likely since X-ray diffraction has shown that water molecules are binding with Ag(I) in nucleobase complexes ²⁴. This second population, based on integration of the absorbance signal contributions to the s-value distribution, comprises ≈ 20 % of the total dispersed mass. Based on the small change in composition across the distribution of Ag₁₅:Ag₁₆:Ag₁₇ nanoclusters, it is more likely that the bi-modal population distribution represents a distinct conformational structure of the (Ag_NssDNA)⁸⁺ nanoclusters, rather than a difference caused by the Ag stoichiometry.

Further structural elucidation by NMR methods confirmed a structured (Ag_NssDNA)⁸⁺ cluster as observed by the sharpening of the ¹H imino peaks in the 1D ¹H spectrum relative to the imino spectrum of the bare DNA (Fig. 2A). Of the 17 expected ¹H imino resonances, approximately 15 peaks can be visually counted, the majority of which are in the non-canonical region (approximately 9.0 ppm to 11.5 ppm). The observed lack of resonances in the canonical region between 11.5 ppm and 14.0 ppm suggests that the (Ag_NssDNA)⁸⁺ has not folded back to form Watson-Crick base pairing and may be in some kind of extended conformation, although these data do not rule out more compact non-canonical interactions.

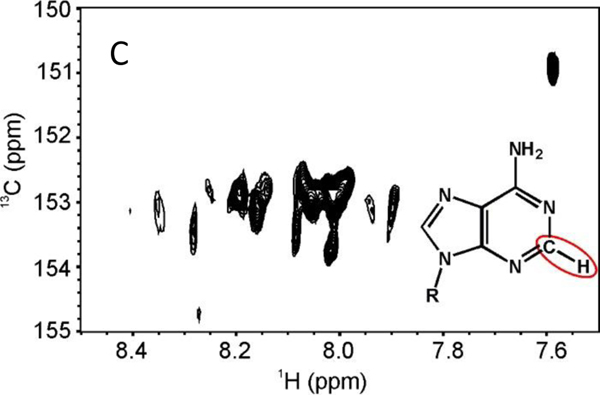
Figure 2. Representative NMR Spectral Fingerprint Regions of the Ag₁₅ssDNA Cluster.

A. Imino fingerprint region from the 1D ¹H NMR spectra of bare ssDNA (bottom) and (Ag_NssDNA)⁸⁺ (top) at 5 °C in 97 % H₂O, 3 % D₂O. B. H6-H5 deoxycytidine fingerprint 2D-¹H,¹H TOCSY (τ_mix = 60 ms) in 99.96% D₂O. C. H2-C2 deoxyadenosine fingerprint from the 2D ¹H,¹³C-HMQC spectrum in 99.96% D₂O. Both B. and C. were collected at 25 °C. See Materials and Methods for additional experimental details.

Collection of further spectra unexpectedly afforded cross peaks that were on the slow-to-intermediate exchange regime on the NMR time scale. In the ¹H,¹H TOtal Correlation SpectroscopY (TOCSY), the dC H6-H5 fingerprint region should only have 7 cross peaks, one for each dC. Yet at least 20 peaks, most with broad linewidths, can be visually counted, with the intensity of many peaks at the noise threshold due to the intermediate exchange regime on the NMR time scale (Fig. 2B). Similarly, in the H2-C2 region for dA in the ¹H,¹³C Heteronuclear Multiple Quantum Coherence spectroscopy (HMQC), only 4 correlations should be observed, whereas there are myriad of cross peaks (Fig. 2C). Such observations indicate the existence of multiple unique (Ag_NssDNA)⁸⁺ conformational states with exchange rates ranging from the millisecond-to-second regime. These observations of conformational heterogeneity from the significant line broadening are consistent with the previous report of AgssDNA clusters⁶. Since the (Ag_NssDNA)⁸⁺ cluster has 7 neutral Ag and the dC-Ag is a known site of Ag dehydration and complexation to the N3 of cytosine ²⁵, it is conceivable that the sharper cross peaks in the H6-H5 region of the TOCSY are indicative of dC-Ag clustering; however, the quality of the NMR spectra precluded further detailed analysis. Taken together, the NMR spectra suggest that very dynamic microstates exist that are intrinsic to longer lived populations found by AUC. While conformational changes in AgDNA clusters have been implicated in the past, they have typically been associated with notable optical transitions in response to environmental changes^{21, 26}. It is beyond the scope of our study to determine how these putative microstates may impact fluorescence or the two different observed macromolecular nanoclusters observed by AUC.

Infrared spectra were gathered to elucidate specific interactions between Ag(I) and the DNA oligomers. Although Ag(0) is also present, Ag(I) interacts with DNA bases with substantially higher affinity than Ag(0) ²⁷. Association of Ag(I) with ssDNA was reflected in changes in the solution vibrational spectrum (Figure 3). There are four spectral regions of interest that provide information about backbone and sugar orientation, base identity and hydrogen bonding: the (800 to 1000) cm⁻¹ region contains coupled sugar and phosphodiester vibrations; (1000 to 1250) cm⁻¹ has strong absorptions of the phosphate and sugar; (1250 to 1500) cm⁻¹ are base-sugar bands that are sensitive to the glycosidic torsion angle and sugar conformation; and the bands from (1500 to 1800) cm⁻¹ originate from C=O, C=N and C=C stretch and -NH₂ bending modes ^28–30 with varying degrees of coupling. Although previous IR work has been done to interpret interactions between Ag with dsDNA, care must be taken not to assume that Ag interacts identically with ssDNA ^{31, 32}.

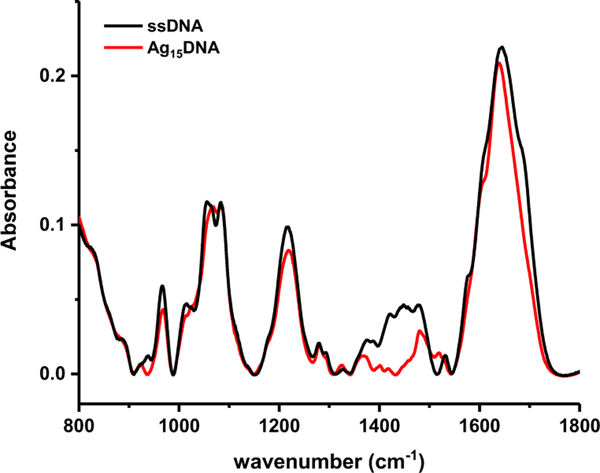
Figure 3. ATR-IR infrared spectra.

Bare DNA (black) and Ag₁₅DNA (red) before complete evaporation of buffer. The strong, broad feature between 800 cm⁻¹ and 900 cm⁻¹ is residual water.

The bare ssDNA and (Ag_NssDNA)⁸⁺ IR-ATR spectra were selected for analysis just prior to complete buffer evaporation (Figure 3). For both spectra, peaks in the region from (800 to 1250) cm⁻¹ are very similar with minor differences occurring in position and relative intensity for the O-P-O bending mode (965 cm⁻¹), the phosphodiester stretch (1055 cm⁻¹ and 1063 cm⁻¹), as well as the symmetric (1085 cm⁻¹) and asymmetric (1220 cm⁻¹) PO₂ stretching mode. The PO₂ stretches are very typical of single stranded DNA and have been observed to maintain their frequency under conditions ranging from 0 % to 100 % relative humidity ³³. The absence of substantial peak shifts in this region demonstrates that the silver ions are not likely to bound to the sugar-phosphate backbone, consistent with previous work ^{31, 34–36}.

The effect of Ag on the bases is more pronounced in the (1300 to 1800) cm⁻¹ region. Peaks from (1300 to 1500) cm⁻¹ have been used as indicators of DNA conformation since methylene and methine deformation peaks are located here³⁷. An intensity decrease was observed from (1340 to 1465) cm⁻¹ upon complexation with Ag (Figure 3). Although peaks in this region have been used to identify the presence of A, B and Z DNA glycosidic bond rotations, and N- and S- type sugar conformers ²⁹, confident assignments of conformational changes induced by Ag cannot be made here given the large number of conformers, as is evident by NMR. However, Ag mediated DNA base pairs have been shown to preferentially adopt enhanced propeller twist conformations relative to B-DNA as well as a variety of sugar puckering modes ³⁸. Given the large spectral changes observed here, it is reasonable to assume that Ag and DNA binding would similarly lead to changes in the glycosidic bond angles of the DNA and sugar conformations.

Peak shifts and intensity changes were evident in the (1500 to 1800) cm⁻¹ nucleic acid region where in-plane C=O, C=N, C=C and NH₂ deformation modes are located. Gaussian peak fitting only afforded 6 peaks in this region for solution ssDNA and (Ag_NssDNA)⁸⁺ (Figure S2), although there are more than 14 vibrational modes in this region³⁹. Peaks 1650 cm⁻¹ and above are mainly carbonyl stretching while the peaks between 1500 cm⁻¹ and 1650 cm⁻¹ derive from C=N and C=C in-plane ring stretching. -NH₂ scissoring appears from 1500–1600 cm⁻¹. There is a red shift of peaks in the Ag₁₅DNA spectra compared to ssDNA. Taken together, peak intensity loss and red shifting in this region is characteristic of silver complexation ³².

To investigate the role of Ag/DNA interactions in these observed spectral changes, we first address the possibility of base-base hydrogen bonding in the ssDNA spectra of homopolymer films. Figure 4 displays the experimentally measured ssDNA film spectrum and the calculated spectrum using the weighted average homopolymer spectra ($\overline{S}).\overline{S}$ was calculated as:

$$\overline{S}=s_C\left(\frac{n_C}{n_{TOT}}\right)+s_G\left(\frac{n_G}{n_{TOT}}\right)+s_A\left(\frac{n_A}{n_{TOT}}\right)+s_T\left(\frac{n_T}{n_{TOT}}\right)$$ (3)

where $s_x$ and $n_x$ are the baseline corrected infrared spectrum and number of residues for C, G, A or T, respectively, and $n_{TOT}$ is the total number of residues. The peak positions of the ssDNA follow very closely with the homopolymer $\overline{S}$, indicating that the ssDNA is likely adopting a random conformation with weak or non-existent nucleic acid hydrogen bonding, although the 1710 cm⁻¹ peak in the weighted polymer film could be from protonated cytosine undergoing hydrogen bonding ^{29, 40}. The random coil conformation is consistent with the circular dichroism curves for this particular ssDNA ²¹. Random conformation is also consistent with the ¹H NMR results that do not show Watson Crick or Hoogsteen hydrogen bonded imino protons and indicates that the IR-ATR spectral changes observed in (Ag_NssDNA)⁸⁺ (Figure 3) are not due to decoupling of hydrogen bonds, which would result in shifts toward higher frequencies.

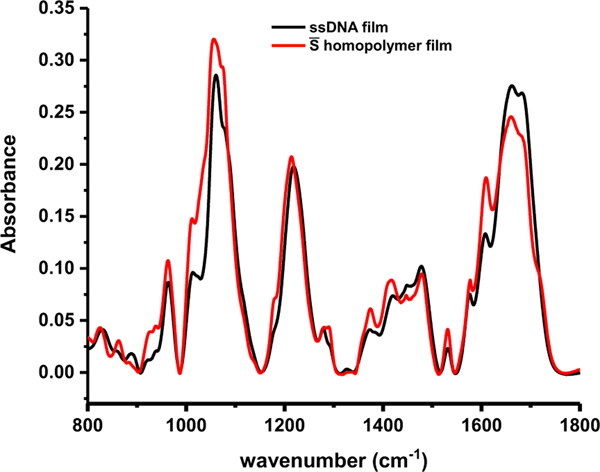
Figure 4. Comparison of experimentally measured and calculated spectra of ssDNA film.

ssDNA (black), $\overline{\mathrm{S}}$ homopolymer (red). The peak positions and relative intensities of the ssDNA film are very similar to those of the $\overline{\mathrm{S}}$ homopolymer film, indicating a random conformation.

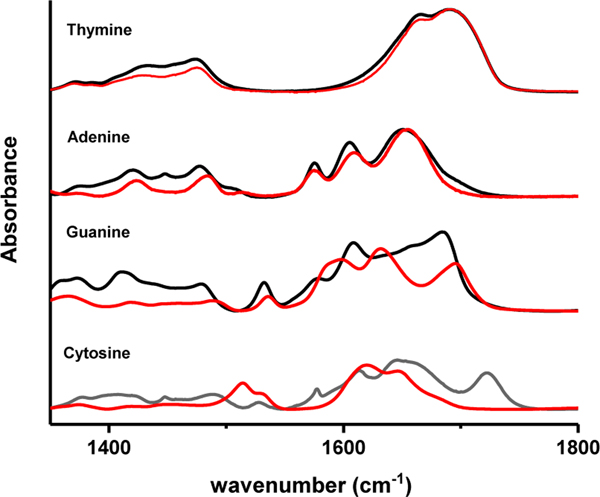
To gain insight into the how Ag(I) interacts with the individual bases, infrared spectroscopy was performed on homopolymers of all four base types with and without Ag(I) present (Figure 5). In this figure, AgNO₃ was incubated at 1 Ag(I)/base, and the spectra are reflective of Ag(I) and base affinity. The poly(dT) spectra with and without Ag(I) are almost identical in peak position and intensity, indicating that there is negligible interaction between Ag(I) and the thymine, consistent with ESI-MS results ⁴¹. There is also minimal interaction between Ag(I) and the adenine homopolymer. However, spectral changes at 1375 cm⁻¹ and 1450 cm⁻¹ are attributed to aliphatic deformation modes of the sugar syn A conformation. Previous work using hairpin strands with single base loops shows that dC and dG loops fluoresce after reduction of Ag(I), dA fluoresces weakly, and dT does not fluoresce at all ⁹. Whereas the addition of Ag(I) to poly(dA) and poly(dT) only produces minimal spectral changes in the sugar region of the spectra, addition of Ag(I) to poly(dC) and poly(dG) affords a complete restructuring of the spectra. Apparently, Ag(I) interacts directly with C and G bases, whereas the addition of Ag(I) to A and T primarily alters the glycosidic bonds and sugar conformations at this Ag(I)/base ratio. However, assignment of specific Ag(I)-dC and Ag(I)-dG base interaction sites was not straightforward due to the interdependent nature of the vibrational modes in this base spectral region.

Figure 5. ssDNA homopolymers.

Bare strand (black) and incubated with 1 Ag(I)/nucleobase (red).

A recent paper by Peng et al.³⁹ has shed light on the complexity and dependency of vibrational modes which obscure assignments of specific Ag(I)/base atom interactions in this region. In their work, polarization-dependent 2D IR was used in conjunction with density functional theory modeling of nucleotide monophosphates in D₂O to characterize the in-plane vibrational energies, anharmocities and couplings, and transition dipoles. Their results reveal a very complex region with a total of 14 ring in-plane vibrations for all four bases plus 3 NH₂ bending vibrations, not counting additional carbonyl peaks that could exist due to Watson Crick or Hoogsten bonding. According to Peng et al., guanine has 4 modes. Three are highly coupled C=N, C=C and ring modes while the other mode is the C=O vibration not strongly coupled to the others. The interactions of Ag(I) with specific cytosine ring atoms are also unclear. Peng showed that the 5 cytosine modes are highly coupled, including the C=O to the N=C, C=C and in-plane ring modes. These spectra show that Ag(I) interacts strongly with cytosine and guanine, but specific Ag interaction sites cannot be ascertained. Molecular dynamics (MD) simulations were performed to provide insight into specific interactions between Ag(I) and base atoms prior to and after nanocluster growth.

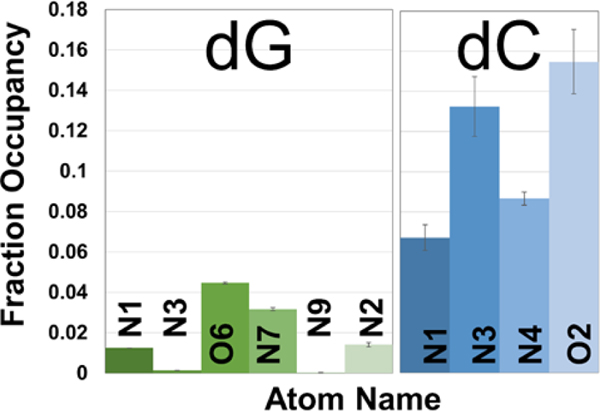
MD simulations were performed by running microsecond length simulations on six base oligomers of homopolymer dA, dC, and dG ssDNA constructs, starting from both canonical B-form and random conformations in pure water. Five Ag(I) ions, parameterized to reproduce hydration free energies and ion-oxygen distances in TIP4P-Ew water, were added to neutralize DNA charge.⁵⁰ Thymine oligonucleotide was omitted due to its very weak interaction with Ag(I). Through the use of a 0.4 nm cutoff for interacting atoms, Ag(I) ions that associate with DNA via first hydration shell water molecules were captured as well as Ag(I) ions that chelate directly to DNA base atoms. Though the Ag(I) ions have the highest calculated occupancies for the negatively charged phosphate backbone oxygens during the simulations (Figure S3), the MD simulations allow the examination of where the ions associate with nucleobase atoms when this interaction does occur (Figure 6), over several binding events per simulation. (shown in Figure S4). The fractional occupancy of Ag(I) for base atoms for each of the oligomers shows differential base-dependent occupancy (Figure S5). For adenine, the Ag(I) occupancy is extremely low across all base nitrogen atoms. The probability of Ag(I) interacting with cytosine is about 10 times higher than with guanine. These trends are reproducible for cytosine and guanine bases in ssDNA strand subset hexamers (Figure S6). In other work, a modest preference for guanine over cytosine was found when the Ag(I)/base interaction was simulated using density functional theory where a strong preference for Ag(I) to cytosine or guanine over adenine and thymine was also evident ⁴². Swasey et al.⁴¹ used quantum chemical calculations to relate Ag(I) interaction preference to homobase binding energies and found the following trend: G>C>A>T. Our results suggest that there is a strong preference for Ag(I) to associate with cytosine over the three other bases in the context of single strand stabilization.

Figure 6. MD simulations showing average Ag(I) fractional occupancies for dG and dC base atoms of ssDNA central 4 bases of 6 base oligomers.

Averages are reported for the central four bases over two runs, and the error bars show the sum of squares of the standard deviations between two runs. The highest nucleobase interaction probability with Ag(I) is shown between the nitrogen and oxygen atoms on guanine (N7, O6) and on cytosine (N3, O2).

Examining specific atom preferences for repeat units 2–5 in Figure 6, Ag(I) interacts with similar probability with guanine O6 and N7, with some affinity to N2 in residue on -NH₂. With cytosine, Ag(I) also interacts with O2 and the adjacent N3 with similar affinity, occupying N1 and N4 in lesser amounts. Since Ag(I) is seen to associate with adjacent O and N sites in both cytosine and guanine, it is possible that Ag(I) may be shared between both N and O atoms within each base. Figure 7 shows the Ag(I) occupancy probability density for cytosine for fractional occupancies > 10 % within 0.4 nm of the base atoms. These computational results support the possibility of Ag(I) bridging between cytosine N3 and O2 atoms (Figure 7) and as well guanine O6 and N7 atoms, although at a much reduced fractional occupancy. This Ag(I) bridging for cytosine or guanine bases represents the most stable state with the highest binding energy for the five possible interaction sites on guanine (N7-O6>O6>N3>N3’>NH₂) and two possible binding sites on cytosine (N3-O2>O2) ⁴². Ag(I) N7 and O6 chelation was also seen for guanosine in very early work ³⁶. These results deviate from the reported N7 guanine and N3 cytosine binding sites in the context of double stranded DNA and tetramers ^{24, 38, 41, 43}.

Figure 7. MD simulations of Ag(I) ion density for dC base atoms.

Bridging density between the N3 (blue) and O2 (red) atoms is shown in gray. Density is reported at 10 % occupancy and is calculated from two independent simulations.

The purified (Ag_NssDNA)⁸⁺ nanocluster consists of a mixture of clusters with 15 and 16 silver atoms in comparable proportions and a minor amount of Ag₁₇DNA. The fact that the Ag₁₅ and Ag₁₆ species were not isolated during the HPLC purification step implies that the surface energies for both species are very similar. The AUC results reveal two distinct populations of clusters: one with a very elongated aspect ratio at ≈ 80 mass % and the other at ≈ 20 mass % taking on a much more spherical shape, assuming the nanocluster is highly hydrated. The high aspect ratio particle agrees well with the picture of a rod-like chain that supports fluorescence emission, as proposed in earlier work ¹⁷. This small change in the number of neutral silver atoms seen in the mass spectra is not believed to cause the drastic change in shape seen in the minor component. It has been shown that more spherical AgssDNA clusters have higher energy transitions than corresponding rod shaped clusters ¹⁶, and these higher energy transitions are not present here. It is interesting that this particular nanocluster has a reported quantum yield of 0.75 and the elongated nanocluster is similar in abundance (≈ 80 mass %), hinting that the spherical nanocluster could be a nonfluorescent species. The (Ag_NssDNA)⁸⁺ clusters exhibit conformational heterogeneity between the rod and sphere shaped populations, but their mobility is likely constrained by chelation of Ag(I) to primarily cytosine and then guanine. Both MD simulations and structural data implicate DNA chain flexibility where Ag(I) has the opportunity to chelate to the most energetically stable state, bonding to both the oxygen and adjacent nitrogen of each cytosine and guanine nucleobase.

Conclusions

Here we have gained insight into the structure of (Ag_NssDNA)⁸⁺ nanoclusters on multiple length scales. We have shown that the purified (Ag_NssDNA)⁸⁺ species consists of comparable amounts of Ag₁₅ and Ag₁₆. AUC data reveal two long-lived global, conformational states of the (Ag_NssDNA)⁸⁺ cluster, one more rod-shaped and the other spherical. The two long-lived global states are believed to be conformationally distinct species whose tertiary structure is fundamentally different. The nanocluster structure exhibited too much conformational heterogeneity to elucidate a secondary structure using NMR, although the observation of multiple microstates demonstrates the highly dynamic nature of the DNA. Lastly, we confirm that Ag(I) clusters interact directly with DNA bases, rather than the phosphate backbone, and further show that cluster stabilization has a profound impact on sugar geometries. Cytosine and guanine bases in homopolymer strands are seen to directly couple with Ag(I), whereas the presence of Ag(I) primarily affects sugar geometries in poly(dA) and poly(dT) strands. IR results also imply that Ag(I) does interact with the guanine O6 in addition to other ring nitrogens while no specific Ag(I) ring interactions can be gleaned from the cytosine IR results. MD simulations support Ag(I)/base associations shown in the IR data and indicate a strong preference of Ag(I) for cytosine over guanine with very little interaction with adenine. Ag(I) has a similar preference for nitrogen (N3) or oxygen (O2) on cytosine, and nitrogen (N7) or oxygen (O6) on guanine, implying a possible bifurcated Ag(I)-N-O bond in each of these nucleobases. The MD simulations imply that cytosine may provide a nanocluster nucleation site prior to reduction and a DNA strand stabilizing site post reduction, where the ssDNA moiety is dominant. More in-depth NMR studies coupled with AUC could provide an important toolbox for monitoring, understanding and eventually predicting the long term stability of these Ag_NDNA nanoclusters as promising biological fluorescent probes.

Materials and Methods

(Ag_NssDNA)⁸⁺ Nanocluster Preparation

(Ag_NssDNA)⁸⁺ solutions were prepared by reducing silver ions in the presence of the ssDNA templating strand, 5’-CACCGCTTTTGCCTTTTGGGGACGGATA-3’ (Integrated DNA Technologies) in aqueous buffer. Final solution concentrations were: 15 × 10⁻⁶ mol/L ssDNA, 187.5 × 10⁻⁶ mol/L AgNO₃, 94 × 10⁻⁶ mol/L NaBH₄, and 0.01 mol/L NH₄OAc. Each 30 mL reaction was allowed to proceed overnight at room temperature in the dark. To prepare the IR and NMR samples, 300 mL of starting material was purified by high performance liquid chromatography⁸ using triethyl ammonium acetate (TEAA) as the ion-pairing agent in a mobile phase consisting of A: 0.035 mol/L TEAA/H₂O, B: 0.035 mol/L TEAA/93% MeOH. Linear gradients from (12 to 22) % by vol B were run at a rate of 0.33 % by vol B/min on a Gemini (Phenomenex) 5 μm C18 column (110 Å pore size; 50 mm long; 10 mm inner diameter) with a flow rate of 5 mL/min at room temperature. The purified material was collected, concentrated and exchanged into 0.001 mol/L phosphate buffer saline, pH 7, using 15 mL Amicon Ultra (Millipore) centrifugal filters with a 3 kDa cutoff. The final concentration of the purified solution was approximately 0.7 × 10⁻³ mol/L in 300 μL based on the DNA extinction coefficient. Silver cluster size was verified by ESI-MS (SI Figure 1). 10 μL of this solution was drop-cast onto a diamond prism for infrared measurements. For NMR experiments in 99.9 % by vol D₂O, (Ag_NssDNA)⁸⁺ was exchanged five times in D₂O in a 4 mL 3 kDa Amicon centrifugal filter. Lyophilization changed the fluorescence spectra of the (Ag_NssDNA)⁸⁺ complex, so exchange into D₂O could not be performed by this manner. Final NMR sample concentrations were 0.82 × 10⁻³ mol/L and 0.85 × 10⁻³ mol/L for the ssDNA and (Ag_NssDNA)⁸⁺, respectively, in 5 % by vol D₂O, 95 % by vol deionized water. (Ag_NssDNA)⁸⁺ nanoclusters were stable up to 30 days stored at −20 ^oC.

Analytical Ultracentrifuge

Sedimentation velocity experiments were performed in a Beckman Coulter XL-I analytical ultracentrifuge using an AN-50 rotor loaded with 12 mm optical path length, 2-sector, Epon-charcoal centerpieces at a rotor speed of 45000 RPM or 50000 RPM. All experiments were performed at 15.0 °C, after a minimum 2 h equilibration time and with reference buffers of the same composition as the sample solutions. A filling volume of 400 mL was employed in each sector of appropriate reference or sample. Radial absorbance scans were collected at 260 nm or 603 nm depending on the experiment; scans were collected at (4 to 5) min intervals, with sedimentation occurring over 100 to 160 scans. Density and viscosity values for buffer solutions in H₂O and D₂O were measured independently using an Anton Paar 5000 M densitometer/ Lovis ME viscometer combination instrument; values for intermediate concentrations were obtained by linear interpolation. Analysis of the interference data was conducted using the C(s) model in SEDFIT version 15.01b ^{22, 23}. The partial specific volume of the complex was initially estimated from the particle composition and refined after the densitometry experiment.

NMR Spectroscopy

NMR experiments were performed on a 900 MHz Bruker Avance III spectrometer (Bruker BioSpin, Inc) equipped with triple resonance cryogenically-cooled TCI probe with a z-axis gradient system. Exchangeable protons were visualized using a 1D ¹H water flip-back Watergate with 32 scans, a recycling delay of 2.0 s, a sweep width of 22 ppm, 200 ms acquisition time, and the ¹H transmitter on water. The optimum temperature to visualize the imino protons of the Ag₁₅DNA was determined to be 5 °C. After the (Ag_NssDNA)⁸⁺ complex was exchanged into D₂O, a 2D ¹H,¹H TOCSY (τ_mix = 60 ms) was collected with uniform sampling in t₁, spectral width of 12 ppm, acquisition time of 23.4 ms x 189.2 ms in t₁ and t₂, respectively, recycling delay of 1.5 s, and 32 scans per increment. The 2D ¹H,¹³C HMQC was performed at ¹³C natural abundance with 50 % non-uniform sampling (NUS) with the NUS schedule generated by the Poisson Gap sampling method ⁴⁴ . The acquisition time was 7.1 ms x 140 ms and sweep widths of 40 ppm x 10 ppm in t₁ (¹³C) and t₂ (¹H), respectively. For the aromatic region, the ¹³C transmitter was placed at 145 ppm. The recycling delay was 1.5 s, and 2048 scans per increment were collected. Due to the conformational equilibrium on the slow to intermediate exchange on the NMR time scale, spectral assignments could not be performed.

All 2D spectra were processed with NMRPipe V8.9 ⁴⁵. The 2D HMQC was reconstructed using iterative soft thresholding embedded within the software. Spectra were visualized with NMRFAM-Sparky V1.4 ⁴⁶. The 1D spectra were processed within Topspin 3.2 (Bruker BioSpin, Inc).

Fourier Transform Infrared Spectroscopy

A GladiATR (Pike Technologies) diamond attenuated total internal reflection accessory was mounted inside a Nicolet Nexus 870 Fourier transform infrared spectrometer (IR-ATR). The accessory and spectrometer were purged with dry air, and 128 background scans were collected at 1 cm⁻¹ resolution. 10 μl solutions of either ssDNA, (Ag_NssDNA)⁸⁺, or homopolymers in 0.001 mol/L PBS were deposited at room temperature onto the ATR crystal. The homopolymers were 15 repeat units of either cytosine, guanine, adenine or thymine (Integrated DNA Technologies). Acquisition of 8 co-added scans was immediately initiated and ran continuously for 25 minutes until the water completely evaporated, leaving a uniform film.

Molecular Dynamics Simulations

ssDNA was built in a B-form helical conformation and in a random extended conformation using the nab and tLeap program in Amber16⁴⁷, respectively. The sequences used were dA6, dC6, and dG6 for the homogenous sequences and 5’CACCGC3’, 5’GACGGA3’, and 5’TGCCTT3’ for the heterogeneous sequences. The OL15DNA force field was used^48–50. TIP4P-Ew waters⁵¹ were added, with 5 neutralizing Ag (I) ions⁵², using a 0.1 nm buffer between the solute and edges of the truncated octahedron solvent box, and ion positions were randomized 0.6 nm from the solute and 0.4 nm from each other. Simulations were performed with the graphics processing unit version of PMEMD MD engine⁵³ from the Amber simulation suite of programs. Initial structures were minimized and equilibrated as described previously ⁵⁴. For production dynamics, a canonical ensemble (NVT) was used with temperature set to 300 K and controlled by a Langevin thermostat with a collision frequency of 2 ps^{−1 55}. A direct space cutoff of 0.9 nm was used with particle mesh Ewald for long range electrostatics⁵⁶. Masses of heavy atoms bonded to hydrogen atoms were repartitioned, shifting each hydrogen’s mass to 3.024 Da and allowing for a longer integration time step of 4 fs ⁵⁷. Production dynamics were run for a microsecond per sequence per starting conformation. CPPTRAJ⁵⁸ hbond command was used to analyze Ag (I) ions within 0.4 nm of all solute atoms. Results from hbond were averaged for each atom over two independent trajectories, yielding an average and standard deviation per atom, and are reported in Supporting Figure S3 and S6. These averages were combined into averages for atoms in each of the four central bases in Figure 6 and averages over all base atoms for dA, dC, and dG in Figure S5, where the error is propagated as the sum of squares of the standard deviations between the two independent trajectories.