A previously unknown magnetic fluctuation origin is identified for the topological Hall effect in the kagome YMn6Sn6 system.
Abstract
Identification, understanding, and manipulation of novel magnetic textures are essential for the discovery of new quantum materials for future spin-based electronic devices. In particular, materials that manifest a large response to external stimuli such as a magnetic field are subject to intense investigation. Here, we study the kagome-net magnet YMn6Sn6 by magnetometry, transport, and neutron diffraction measurements combined with first-principles calculations. We identify a number of nontrivial magnetic phases, explain their microscopic nature, and demonstrate that one of them hosts a large topological Hall effect (THE). We propose a previously unidentified fluctuation-driven mechanism, which leads to the THE at elevated temperatures. This interesting physics comes from parametrically frustrated interplanar exchange interactions that trigger strong magnetic fluctuations. Our results pave a path to chiral spin textures, promising for novel spintronics.
INTRODUCTION
Topologically nontrivial magnetic and electronic structures have attracted extraordinary attention in the past few years. Kagome-net magnets are one of the popular classes of these materials (1–5). It was recently realized that highly nontrivial physics can come from noncollinear interplanar ordering between ferromagnetic (FM) kagome planes, such as topological Hall effect (THE) in the absence of crystallographic inversion symmetry breaking (6, 7). As opposed to anti-FM (AF) kagome materials, for FM kagome planes formed by the metals such as Fe or Mn, the in-plane exchange interaction is strongly FM and not magnetically frustrated but still forms characteristics of kagome geometry: Dirac cones, and flat bands (8–12). The interesting physics comes from the fact that, by virtue of the Mermin-Wagner theorem, the FM ordering in the two-dimensional planes is strongly suppressed, with the magnetic dynamics being controlled by weak interplanar exchange interactions, which, on the contrary, can be and usually are frustrated. Thus, these materials are strongly magnetically fluctuating and provide fertile ground for interesting new phenomena.
YMn6Sn6 is a prototype for this materials class. It forms a hexagonal P6/mmm structure (a = 5.541 Å and c = 9.035 Å) consisting of kagome planes [Mn3Sn] separated by two inequivalent Sn3 and Sn2Y layers, i.e., [Mn3Sn][Sn3][Mn3Sn][Sn2Y] (Fig. 1, A and B) (13, 14). YMn6Sn6 is a good metal (15, 16), as can be seen in our resistivity data shown in Fig. 1C, and, hence, is expected to have relatively long-range exchange interactions, possibly including Ruderman-Kittel-Kasuya-Yosida coupling (Fig. 1A). All Mn planes and in-plane nearest-neighbor Mn─Mn bonds are crystallographically equivalent, but the interplanar Mn─Mn bonds along c are markedly different, with an FM exchange interaction across the Sn3 layers and AF across the Sn2Y layers. These are frustrated by the second-neighbor interaction across an intermediate Mn3Sn layer (J1 and J3 are FM, while J2 is AF) and result in complex magnetic behaviors (14, 15). Below TN ≈ 345 K (Fig. 1D), a commensurate collinear AF structure first forms with the propagation vector k = (0, 0, 0.5). On cooling, an incommensurate phase quickly appears, which coexists with the commensurate phase in a narrow temperature range and becomes the only phase below 300 K (14, 17). On the basis of powder diffraction, the incommensurate state has been reported to have two (and even three at room temperature) nearly equal wave vectors (14), which can be described as a staggered spiral, also dubbed the “double flat spiral,” (18) as depicted in Fig. 1E. A magnetic field applied in the ab plane induces multiple transitions seen in the magnetization and Hall resistivity (15). An enigmatic THE is observed at elevated temperatures, with the largest value around 245 K and a magnetic field of 4 T (16). Here, we determine the microscopic origin of the magnetic field–induced phases of YMn6Sn6 and develop a theory describing the observed THE.
Fig. 1. Crystal structure and electrical and magnetic properties of YMn6Sn6.
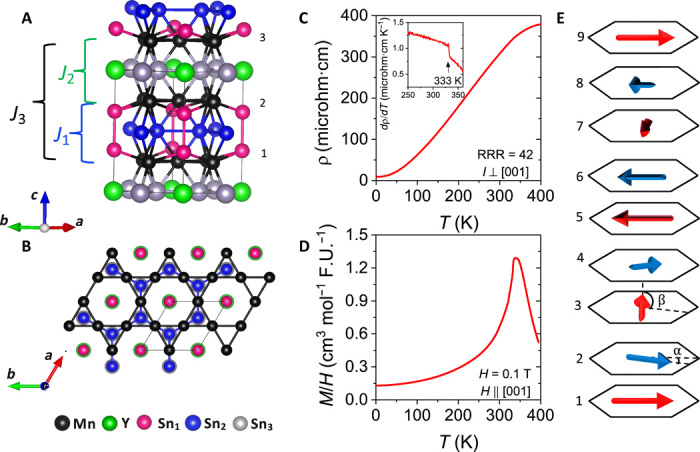
(A) Sketch of the crystal structure of YMn6Sn6. (B) Top view of the structure shown in (A). Within a unit cell shown by the grey solid lines, there are two kagome planes with the formula Mn3Sn that are separated by Sn3 and YSn2 layers. The symbols Ji are the exchange constants between different Mn layers. (C) Electrical resistivity of YMn6Sn6 as a function of temperature with the electric current applied in the ab plane. Inset shows the temperature derivative of the electrical resistivity in the vicinity of TN, which shows a jump at 333 K below which an incommensurate spiral state develops. The residual resistivity ratio (RRR = ρ400K/ρ2K) is 42 indicating a good sample quality. (D) Magnetic susceptibility (M/H) of YMn6Sn6 as a function of temperature. (E) Incommensurate magnetic structure of YMn6Sn6 in the absence of external magnetic field. Arrows represent the direction of FM spins within a kagome plane. There are small constant angles α between the FM-coupled spins across the Sn3 layer, and β between the AF ones across the Sn2Y, which result in a spiral spin arrangement, where every other Mn layer forms a spiral with the pitch defined by α + β ≈ 90° and the two spirals rotated by α with respect to each other. The incommensurate spirals repeat after about four crystallographic unit cells or about nine Mn layers that are indicated by the numbers 1 to 9.
RESULTS AND DISCUSSION
We first present the different field-induced magnetic phases of YMn6Sn6 via bulk measurements. Figure 2A shows the magnetization measurements of YMn6Sn6 at two representative temperatures: 5 and 245 K. For the magnetic field applied along the c axis (red curve), the magnetization increases smoothly with field and, for 5 K, saturates slightly above 12 T, while the 245-K data show that the saturation field clearly decreases with increasing temperature. The effect of a magnetic field applied in the ab plane (Hab) shown by the blue curves is more marked. At 5 K, we see a sharp increase at 2 T, indicative of a metamagnetic transition. A closer look reveals two close transitions, more apparent in the ac susceptibility measurement (Fig. 2B). Since the two transitions are very close, we denote the metamagnetic transition field by a single variable, H1, for the remainder of the paper. As the field is further increased, the magnetization changes slope and increases continuously until H2 = 7 T. Above H2, the magnetization grows slower and saturates at H3 = 9.8 T. As temperature is increased, H1, H2, and H3 all shift to lower fields, and H2 and H3 become closer and merge. A phase diagram constructed from the ac susceptibility is depicted in Fig. 2B, with four main phases: (i) 0 < H < H1, (ii) H1 < H < H2, (iii) H2 < H < H3, and (iv) H > H3. We denote them as distorted spiral (DS), transverse conical spiral (TCS), fan-like (FL), and forced FM (FF), respectively, based on the magnetic structures as detailed below. The narrow intermediate phases between FL and FF and between TCS and FF are labeled “I” and “II,” respectively.
Fig. 2. Magnetization and Hall effect of YMn6Sn6.
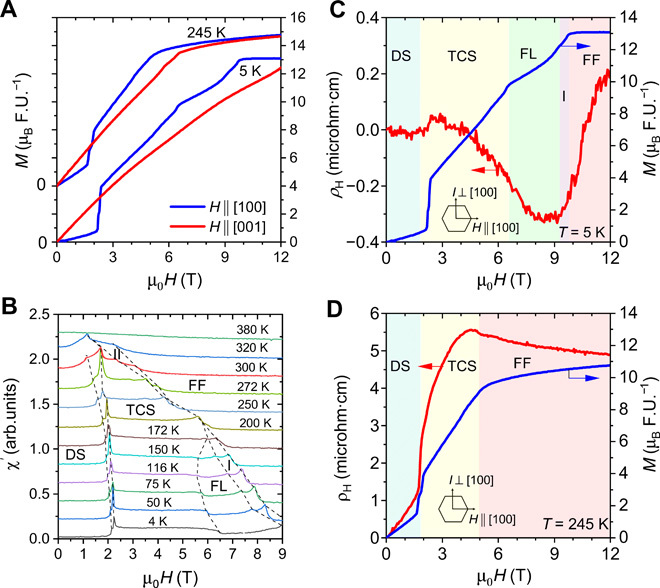
(A) Magnetization as a function of external magnetic field at 5 and 245 K with the magnetic field applied parallel and perpendicular to the c axis. Data have been offset as indicated. (B) Phase diagram of YMn6Sn6 constructed from ac susceptibility measurements. Arb. units, arbitrary units. (C and D) Hall resistivity (left axis) and magnetization (right axis) as a function of magnetic field applied in the ab plane at 5 K (C) and 245 K (D). The arrows in the hexagon in (C and D) indicate the filed and current direction in the basal plane of the hexagonal lattice of YMn6Sn6.
The Hall resistivity (ρH) and magnetization (M) as a function of Hab at 5 and 245 K are compared in Fig. 2 (C and D), respectively. At 5 K, ρH has a very small negative slope in the DS phase. At H1, ρH shows a small jump but then decreases before increasing rapidly to saturation in the FF state, forming a remarkable minimum in the FL phase. The behavior of ρH is notably different at 245 K, where it exhibits a positive slope in the DS phase. At the metamagnetic transition (H1), it shows a sizable jump and then increases nonlinearly with the magnetization in the TCS phase, which has been interpreted as the THE (16).
The zero-field neutron diffraction data are plotted in Fig. 3A. A commensurate magnetic Bragg peak is observed at the onset of long-range magnetic order, where k = (0, 0, 0.5) and TN = 345 K, which quickly transforms into two distinct incommensurate wave vectors. These two incommensurate structures coexist from their onset to the base temperature (12 K) determined by high-resolution measurements (inset in Fig. 3A). The two wave vectors (0, 0, kz,1) and (0, 0, kz,2) with kz,1 < kz,2 evolve smoothly with temperature along L, and ∣kz,1 − kz,2∣ decreases with cooling. The two magnetic structures stemming from kz,1 and kz,2 are consistent with previous reports (14, 18) (see Fig. 1E) but with slightly different periodicities (fig. S4A).
Fig. 3. Single-crystal neutron diffraction of YMn6Sn6.
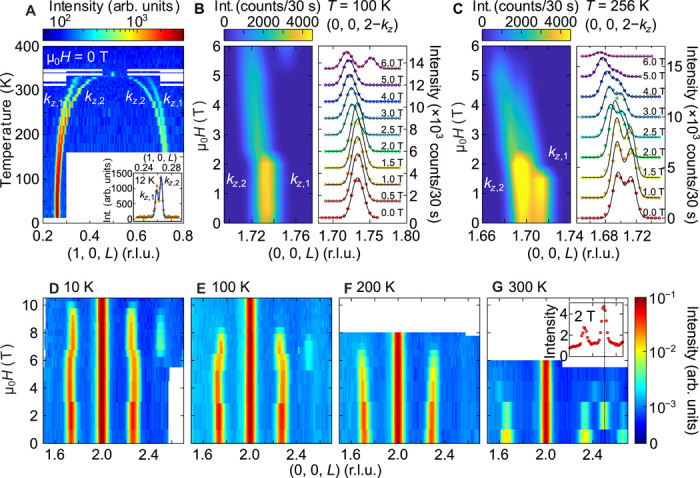
(A) Magnetic Bragg peaks tracked as a function of temperature. A commensurate magnetic peak at L = 0.5 appears between 345 and 330 K, and the two incommensurate magnetic structures stemming from the wave vectors kz,1 and kz,2 appear at 330 K and persist to the base temperature measured (12 K). The inset, taken with high instrumental resolution, shows that the two wave vectors do not converge, even as they get closer with decreasing temperature. (B and C) Incommensurate magnetic Bragg peaks (0, 0, 2 − kz,n) (n = 1,2) tracked at 100 and 256 K, respectively, as a function of applied magnetic field. The solid black lines in the right-hand panels of (B) and (C) are Gaussian fits to the data described in Materials and Methods. An offset was added between individual L scans for clarity. Offsets are 1500 counts/30 s for (B) and 2000 counts/30 s for (C). (D to G) Neutron diffraction data taken up to higher fields with a position sensitive detector and coarse resolution for (D) 10 K, (E) 100 K, (F) 200 K, and (G) 300 K. In these data, kz,1 and kz,2 are not resolvable, but the high fields at which the data were taken reveal the field ranges at which each of the magnetic phases are present. The inset of (G) is a cut taken from the main panel at 2 T, where the dashed black line shows that the new peak appearing at this field is commensurate at L = 2.5.
We now focus on the multiple magnetic phases induced via application of an external magnetic field in the ab plane. Figure 3 (B and C) shows data taken about (0, 0, 2 − kz,n) (n = 1, 2) for 100 and 256 K, respectively. We find that kz, n are almost field independent, except for an abrupt shift to larger momentum for both magnetic peaks at H1, which lies between 2.0 and 2.5 T (between 1.5 and 2.0 T for H1 at 256 K). Concomitant with these shifts are pronounced decreases in intensity of the Bragg peaks at (0, 0, L ± kz, n) positions. The T = 100 K data show a new commensurate structure emerging at H2 (6 T), with the wave vector (0, 0, kc), where kc = 0.25 and a satellite at 2kc-type positions, which can be seen in Fig. 3E (discussed more below). These commensurate peaks coexist with the incommensurate peaks at 6 T and emerge at the cost of the incommensurate intensities (see section S2 for details).
A 15-T magnet was used to focus on the high-field behavior, where coarse instrumental resolution was used to compensate for the reduced intensities. The two incommensurate wave vectors are not resolvable with this resolution, but the data satisfactorily capture the overall high-field behavior. Figure 3F shows that, at 200 K, the incommensurate peaks disappear above 7 T, similar to the observation that they are almost fully suppressed by 6 T in the 256-K high-resolution data (Fig. 3C). The k = (0, 0, 0.25) commensurate structure at 100 K and 6 T in Fig. 3B can be seen at the same field in Fig. 3E at Q = (0, 0, 2.25) with a satellite peak at Q = (0, 0, 2.50). In addition, we see that all but the FF structures disappear above 8 T as the spins become fully polarized. The high-field commensurate phase persists down to 10 K, shown in Fig. 3D, but is shifted higher in field and is present between 6.5 and 9.5 T.
The neutron data capture all the features observed in bulk magnetic measurements (Fig. 2). Below H1, there is very little change to the incommensurate peaks. At H1, the wave vector positions change by ∼3%, and intensity drops as much as 60% (see fig. S4). The H1 transition, which spans almost the entire temperature range of zero-field incommensurability, resembles a spin-flop transition, deduced from the magnetization data in Fig. 2A. As discussed further in the theoretical section, this is a spin flop from a helical to cycloidal spiral. Comparison of the structure factor calculations for each magnetic structure to the data supports this assignment (see section S2 and fig. S5 for details). At H2, commensurate peaks with k = (0, 0, 0.25)–type positions, as well as satellites at 2kc, emerge at the cost of the incommensurate structures. The commensurate peaks only appear in the FL phase. Curiously, however, a commensurate phase with propagation vector k = (0, 0, 0.5) is seen to emerge at 300 K and low field (2 T) as seen in Fig. 3G. This temperature and field reside within region II of the phase diagram in Fig. 2B.
To understand the microscopic origin and nature of the different magnetic phases, we performed first-principles density functional theory (DFT) calculations and used the results to construct a mean field theory at T = 0. The details are presented in Materials and Methods and section S3, and here, we summarize the main findings. First, DFT total energy calculations were performed and fit to the Hamiltonian (Eq. 1)
| (1) |
where H is the external field and n is a unit vector along the local magnetization direction. The first sum runs over six nearest neighbors along the c axis, the second sum runs over the first neighbors in the ab plane, and the last three sums run over all atoms (i + 1 denotes the nearest c-axis neighbor). K is the easy-plane single-ion anisotropy, and the Ising-type anisotropic exchange, Jz, is the only one allowed by symmetry for the vertical bonds. To account for Hubbard correlations, we added a DFT + U correction (see section S3). We found that the best description of the ground state is attained for U − J = 0.4 to 0.6 eV, and in the following, we use 0.4 eV (not unreasonable for a good metal). The results are shown in the table S2 for three models: “full,” “reduced,” where J4 − 6 are absorbed into modified J2 − 3, and “minimal,” where Jz is, in addition, combined with K. The full model has a staggered spiral as a ground state, as shown in Fig. 1E, with the two angles α = − 22° and β = 138°, in reasonable agreement with the low-temperature experimental k ≈ (0, 0, 0.25) described by the pitching angles α = −20° and β = 110° (α + β = 90°). These angles were used in the reduced model, J2 − 3, calculations.
We now present the mean field theory results for the minimal and reduced models at T = 0. At H = 0, one gets a staggered spiral (14). Without K, the minimal model uniquely defines (14) the propagation vector kz but is degenerate with respect to the plane in which the magnetic moments rotate. The anisotropy K locks the spins to the ab plane. Results for the mean field theory are shown in Fig. 4 (A to C) (see section S4 for details). The behavior for H‖c is trivial: The helical spiral becomes a longitudinal conical spiral (LCS) and gradually transforms into a field-polarized FM phase. For H‖a, if there were no magnetic anisotropy (K = 0), then the staggered spiral would immediately flop from spins rotating in the ab plane (helical) to those rotating in the bc plane (cycloidal), which would then gradually cant into a TCS state, and eventually saturate. The magnetic anisotropy sets a finite spin-flop field , where ⟨J⟩ is the appropriately averaged J1 − 3 parameters. Below H1, the spiral remains flat but distorts slightly by canting each spin a little toward a (this is the DS phase). At H1, the magnetization increases discontinuously. However, when the conical angle in the TCS phase above H1 becomes rather small, at the field H2, not that far from the saturation field, further canting gains too little energy, and it becomes energetically favorable to flop back into the ab plane, gaining back some of the anisotropy energy. The resulting phase, found by minimization of the minimal Hamiltonian, is a very unusual commensurate FL phase, depicted in Fig. 4B. It can be described as a quadrupled structure along the c axis, with spins deviating from the x direction, the direction of the magnetic field, by the angles γ, γ, −δ, δ, −γ, −γ, δ, −δ, which gradually decrease until the FF state, γ = δ = 0, is reached (see section S4 for details). The FL phase has a different periodicity for Mx, the projection of Mn moments onto the x axis, and for My, the projection onto the perpendicular in-plane axis. The latter corresponds to kc = 0.25, the former to kc = 0.5, and the variation of amplitude of Mx is much smaller. The calculations (Fig. 4C) capture all features of the measured magnetization (Fig. 2A). The predictions are also confirmed by our neutron data: The first spin flop from a nearly helical to a nearly cycloidal spiral leads to about 50% loss in the scattering intensity for (0, 0, L ± kn, z)–type Bragg peaks (neutrons do not scatter off the Mz component in our geometry when the scattering vector is along L), consistent with the discontinuous loss of intensity in the experiment (see section S2). In the minimal model, the first spin flop does not alter the periodicity; experimentally, however, kz slightly increases in the TCS phase. To understand this, we need to step back to the reduced model that retains separation of K and Jz. Then, the mean field theory predicts a tiny shortening of the spiral pitch at H = H1, on the scale of ≈0.36Jz/J1 ∼ 1% (see section S4). The FL phase also finds full confirmation in the experiment: At H = H2, as predicted, kz changes discontinuously to kc = 0.25, and the predicted weaker satellite at 2kc is observed as well.
Fig. 4. First-principles calculation and phenomenological model of spin chirality for THE.
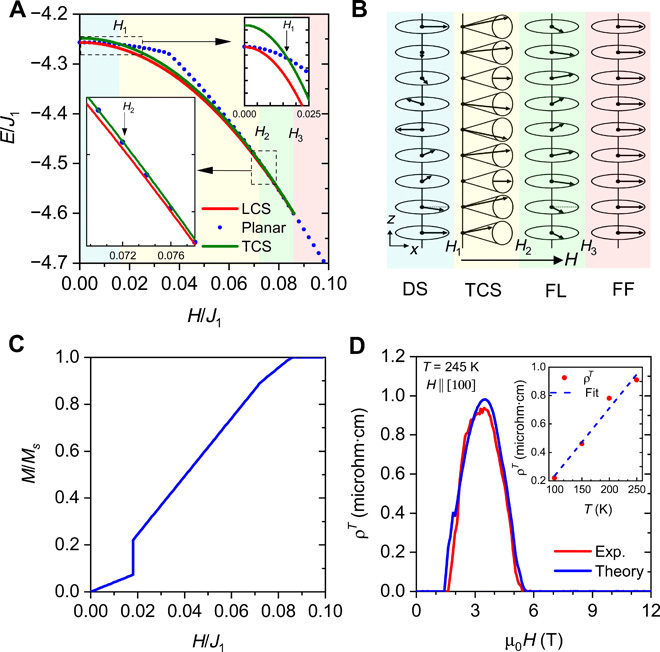
(A) Energy for different magnetic states as a function of reduced magnetic field obtained in mean field calculations. The planar state represented by the blue dotted line has DS structure below the kink and FL structure above the kink. (B) Sketch of different field-induced magnetic structures. (C) Calculated magnetization as a function of in-plane field. (D) Experimental and theoretical topological Hall resistivity given by Eq. 2 as a function of external magnetic field at 245 K. Inset shows the temperature variation of the THE at 4 T below 250 K. The dashed line is a linear fit to the experimental data.
We now focus on the THE and show its origin in a fluctuation-driven chirality. The THE appears in the TCS phase only. The fact that the THE is observed only at elevated temperatures, while the TCS phase exists in the entire temperature range below 330 K, strongly suggests the key role of thermal fluctuations. It is worth remembering that the system is strongly two-dimensional, with nearly two orders of magnitude difference between the ab and c couplings. In this case, by virtue of the Mermin-Wagner theorem, the mean field transition temperature of several thousand kelvin is markedly suppressed by large and relatively slow in-plane fluctuations. This is reminiscent of the famous nematic transition in the planar J1 − J2 Heisenberg mode (19), where these fluctuations can give rise to a new, nonmagnetic order parameter without a long-range magnetic order. This so-called nematic phase is realized in many Fe-based superconductors (20) and maybe in other materials as well (21).
We will argue now that similar physics may be realized in the TCS phase. The detailed theory is provided in section S5. Here, we present a summary of the results. In a continuous approximation, the TCS can be described as M = Mx + m, where is the induced magnetic moment and is a constant, and is a cycloidal spiral. It is also assumed that while the direction of the Mn moment can change and fluctuate, the amplitude stays the same. The topological chiral field given by the standard expression (2) bx = M · (∂yM × ∂zM) = ∂yM · (∂zM × M) is thus zero in the TCS phase (or in any phase) where ∂yM = 0, and hence, there is no THE. However, addition of a magnon fluctuation, propagating along y with wave vector ky, gives M = Mxx + m + μ where, as mentioned, m ⊥ x and μ represents a magnon propagating along y (to have nonzero ∂yM) in a plane defined by a vector ω, such that ω ∝ ky. Then, , and . Using these equations on bx, keeping only the terms quadratic in μ and averaging over y, gives bx = −kymzμ2, and, unless , bx ≠ 0.
The physical meaning of this result is very simple; the TCS is one independent magnon short of a chiral combination of static magnons. Of all possible magnons, there are some that generate positive chirality, but, by crystallographic symmetry, for each such magnon, there is a partner with the same energy and opposite chirality. These two partners will be thermally excited with the same probability, and their effect will cancel each other, in the absence of an external field. However, in an applied field, they create nonzero chiral susceptibility, reminiscent of the nematic susceptibility in Fe-based superconductors. We find the chiral field in such a case to be
| (2) |
The topological Hall resistivity (ρT) is proportional to ⟨bx⟩, and hence, ρT can be calculated by Eq. 2 using experimental parameters. Note that this expression is valid only for H1 < Hx < H2 and the topological Hall resistivity is zero outside these limits. The theoretical ρT is plotted together with the measured data at T = 245 K in Fig. 4D. The inset shows the temperature dependence of ρT at a constant field of 4 T, which is linear in temperature as expected from Eq. 2 (Mz depends on the temperature very weakly, as one can see from the experimental data in fig. S17). The details of the experimental and theoretical ρT are provided in the section S6. The remarkable agreement of the experimental data with this phenomenological model provides insight into the microscopic origin of the THE as stabilized by the thermal fluctuations, creating an imbalance in the right- and left-handed TCSs, a nematic spin chirality. We want to point out that the exceptional agreement between theory and experimental THE may be, to some extent, fortuitous, given the simplicity of the model and partitioning of the total ρH (discussed in detail in section S6), but provides strong support to the presented physical picture, describing the observed THE. Note that quantization of the Hall effect has been discussed in two-dimensional kagome-lattice ferromagnets (22), where the spin tilting provides the necessary scalar chirality. The mechanism we propose here, however, is different since the observed chiral response arises from preferentially exciting spin fluctuations propagating in one direction (at the expense of those moving in the opposite direction) within a particular spiral state.
We have identified two unique magnetic phases, TCS and FL, in YMn6Sn6, which emerge from the competitions between exchange interactions, the magnetic anisotropies, and Zeeman energy, with a remarkable agreement between bulk measurements, neutron diffraction, and first-principles calculations. The THE in the TCS phase is of particular interest. As opposed to noncoplanar and skyrmionic materials, this spiral magnet without static spin chirality forms a nonzero internal skyrmionic magnetic field dynamically, through preferential excitation of chiral fluctuations with a given handedness. This field deflects the conducting charge and thus produces the extra component to the Hall effect, the THE. Our results not only provide a new mechanism for the THE but also open promising avenues in looking for chiral spin fluctuations in new materials and at temperatures relevant for practical applications. Moreover, it is well known that spin-orbit coupling in kagome-lattice magnets can mediate the entanglement of the electronic and magnetic topology giving rise to more exotic correlated phenomena (12, 23). Recently, a novel electronic topological phenomenon has been realized in the isostructural compound TbMn6Sn6 (24). Thus, this family of compounds may provide prototypes to study the interplay of topological properties simultaneously arising both in real and momentum space.
MATERIALS AND METHODS
Crystal growth and characterization
Single crystals of YMn6Sn6 were grown by the self-flux method. Y pieces (Alfa Aesar; 99.9%), Mn pieces (Alfa Aesar; 99.95%), and Sn shots (Alfa Aesar; 99.999%) were loaded in a 2-ml aluminum oxide crucible in a molar ratio of 1:1:20. The crucible was then sealed in a fused silica ampoule under vacuum. The sealed ampoule was heated to 1175°C over 10 hours, homogenized at 1175°C for 12 hours, and then cooled to 600°C over 100 hours. Once the furnace reached 600°C, the excess flux was decanted from the crystals using a centrifuge. Well-faceted hexagonal crystals as large as 100 mg were obtained. The crystal structure of the compound was verified by x-ray powder diffraction at room temperature using a Rigaku MiniFlex diffractometer. A few crystals from each growth batch were ground into powder, and x-ray diffraction patterns were collected on those powder samples. Rietveld refinement (25) of a representative powder x-ray pattern using FullProf software (26) is shown in fig. S1. Magnetic and transport measurements were carried out on oriented single crystals.
Magnetic and transport property measurements
dc susceptibility measurements were made using a Quantum Design VSM SQUID. dc magnetization and transport measurements were measured using a physical property measurement system (PPMS). ac susceptibility measurements were carried out using a Quantum Design DynaCool PPMS. Resistivity and Hall measurements were performed following the conventional 4-probe method. Pt wires of 25 μm in diameter were attached to the sample with EPO-TEK H20E silver epoxy. An electric current of 1 mA was used for the transport measurements. In magnetoresistance measurements, the contact misalignment was corrected by field symmetrizing the measured data.
Neutron diffraction measurements
A single crystal was oriented in either the (H, 0, L) or (H, H, L) scattering plane on the triple-axis neutron spectrometer BT-7 (27) at the National Institute of Standards and Technology Center for Neutron Research. Elastic diffraction data were taken with Ei = Ef = 14.7 meV and 25′ − 10′ − 10′ − 25′ full width at half maximum (FWHM) collimators were used before and after the sample, before the analyzer, and before the detector, respectively (unless otherwise noted). A superconducting 7-T vertical field magnet system with a top-loading closed cycle refrigerator was used at the sample position such that the applied field was parallel to the crystallographic direction. Bragg peaks were resolution limited and Gaussian in shape. Peaks were therefore fit to Gaussians with the FWHMs constrained to be that of the spectrometer resolution as determined by the program ResLib (28). Data using a superconducting 15-T vertical field magnet system were taken in the (H, H, L) scattering plane, where the magnetic field was also parallel to . Moderately coarse resolution was used with open −50′ − 40′R − 120′ collimators (where “R” indicates radial) and a position-sensitive detector. Throughout the manuscript, momentum is reported in reciprocal lattice units (r.l.u.) denoted using H, K, and L, where .
First-principles calculations
Most calculations were performed using the projected augmented wave pseudo-potential code VASP (29) and the gradient-dependent density functional of (30). For control purposes, some calculations were also repeated using the all-electron linearized augmented plane wave code WIEN2k (31). Hubbard correlations were taking into account using the DFT + U with the fully localized double counting prescription and the spherically averaged correction U − J, with the values of U − J given in Results and Discussion section.
Acknowledgments
We thank P. Nikolic and C. Batista for insightful discussions. Funding: N.J.G. and I.I.M. acknowledge start-up funding from George Mason University. I.I.M. additionally acknowledges support from the U.S. Department of Energy through the grant #DE-SC0021089. Work in the Materials Science Division at Argonne National Laboratory (J.F.M. and J.S.J.) was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Science, and Engineering Division. Work at ORNL (M.A.M.) was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences, and Engineering Division. The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology. Author contributions: N.J.G. conceived and coordinated the project. N.J.G. and N.T.M. grew the crystals. N.J.G., N.T.M., D.M., and D.C.J. characterized the samples. N.J.G. and M.A.M. performed the magnetic and magnetotransport measurements. J.F.M. contributed to the magnetic and transport measurements. J.S.J. contributed to the transport measurements. L.P., R.L.D., and J.W.L. carried out neutron diffraction experiments. L.P., M.B., N.J.G., and J.W.L. performed small angle neutron scattering experiment. I.I.M. carried out the first-principles calculations and devised the phenomenological theory. N.J.G. wrote the manuscript with contributions from R.L.D., J.W.L., and I.I.M. All authors contributed to the discussion of the results. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/51/eabe2680/DC1
REFERENCES AND NOTES
- 1.J. Zang, V. Cros, A. Hoffmann, Topology in Magnetism (Springer, 2018). [Google Scholar]
- 2.Nagaosa N., Tokura Y., Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Nagaosa N., Yu X. Z., Tokura Y., Gauge fields in real and momentum spaces in magnets: Monopoles and skyrmions. Phil. Trans. R. Soc. A 370, 5806–5819 (2012). [DOI] [PubMed] [Google Scholar]
- 4.Bradlyn B., Cano J., Wang Z., Vergniory M. G., Felser C., Cava R. J., Bernevig B. A., Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science 353, aaf5037 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Armitage N. P., Mele E. J., Vishwanath A., Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 15001 (2018). [Google Scholar]
- 6.Kübler J., Fesler C., Non-collinear antiferromagnets and the anomalous Hall effect. Europhys. Lett. 108, 67001 (2014). [Google Scholar]
- 7.Nakatsuji S., Kiyohara N., Higo T., Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015). [DOI] [PubMed] [Google Scholar]
- 8.Ghimire N. J., Mazin I. I., Topology and correlations on the kagome lattice. Nat. Mater. 19, 137–138 (2020). [DOI] [PubMed] [Google Scholar]
- 9.Kang M., Ye L., Fang S., You J.-S., Levitan A., Han M., Facio J. I., Jozwiak C., Bostwick A., Rotenberg E., Chan M. K., Mc Donald R. D., Graf D., Kaznatcheev K., Vescovo E., Bell D. C., Kaxiras E., van den Brink J., Richter M., Ghimire M. P., Checkelsky J. G., Comin R., Dirac fermions and flat bands in the ideal kagome metal FeSn. Nat. Mater. 19, 163–169 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Ye L., Kang M., Liu J., von Cube F., Wicker C. R., Suzuki T., Jozwiak C., Bostwick A., Rotenberg E., Bell D. C., Fu L., Comin R., Checkelsky J. G., Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Liu E., Sun Y., Kumar N., Muechler L., Sun A., Jiao L., Yang S.-Y., Liu D., Liang A., Xu Q., Kroder J., Süß V., Borrmann H., Shekhar C., Wang Z., Xi C., Wang W., Schnelle W., Wirth S., Chen Y., Goennenwein S. T. B., Felser C., Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yin J. X., Zhang S. S., Chang G., Wang Q., Tsirkin S. S., Guguchia Z., Lian B., Zhou H., Jiang K., Belopolski I., Shumiya N., Multer D., Litskevich M., Cochran T. A., Lin H., Wang Z., Neupert T., Jia S., Lei H., Hasan M. Z., Negative flat band magnetism in a spin–orbit-coupled correlated kagome magnet. Nat. Phys. 15, 443–448 (2019). [Google Scholar]
- 13.Lefèvre C., Verniere A., Venturini G., Malaman B., A neutron diffraction study of HfFe6Ge6-type YMn6Sn6−xInx compounds (0.03≤x≤0.72). J. Alloys Compd. 361, 40–47 (2003). [Google Scholar]
- 14.Venturini G., Fruchart D., Malaman B., Incommensurate magnetic structures of RMn6Sn6(R = Sc, Y, Lu) compounds from neutron diffraction study. J. Alloys Compd. 236, 102–110 (1996). [Google Scholar]
- 15.K. Uhlíová, F. R. deoer, V. Sechovský, G. Venturini, Magnetism of YMn6Sn6 and DyMn6Ge6: Single-crystal study, in WDS’06 Proceedings of Contributed Papers Part III (Matfyzpress, 2006), pp. 48–53. [Google Scholar]
- 16.Q. Wang, Q. Yin, S. Fujitsu, H. Hosono, H. Lei, Near-room-temperature giant topological Hall effect in antiferromagnetic kagome metal YMn6Sn6. arXiv: 1906.07986 [cond-mat.str-el] (19 June 2019).
- 17.Zhang H., Feng X., Heitmann T., Kolesnikov A. I., Stone M. B., Lu Y.-M., Ke X., Topological magnon bands in a room-temperature kagome magnet. Phys. Rev. B 101, 100405 (2020). [Google Scholar]
- 18.Rosenfeld E. V., Mushnikov N. V., Double-flat-spiral magnetic structures: Theory and application to the compounds. Physica B 403, 1898–1906 (2008). [Google Scholar]
- 19.Chandra P., Coleman P., Larkin A. I., Ising transition in frustrated Heisenberg models. Phys. Rev. Lett. 64, 88–91 (1990). [DOI] [PubMed] [Google Scholar]
- 20.Fernandes R. M., Chubukov A. V., Schmalian J., What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014). [Google Scholar]
- 21.Zhang G., Glasbrenner J. K., Flint R., Mazin I. I., Fernandes R. M., Double-stage nematic bond ordering above double stripe magnetism: Application to BaTi2Sb2O. Phys. Rev. B 95, 174402 (2017). [Google Scholar]
- 22.Ohgushi K., Murakami S., Nagaosa N., Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 62, R6065–R6068 (2000). [Google Scholar]
- 23.Kuroda K., Tomita T., Suzuki M.-T., Bareille C., Nugroho A. A., Goswami P., Ochi M., Ikhlas M., Nakayama M., Akebi S., Noguchi R., Ishii R., Inami N., Ono K., Kumigashira H., Varykhalov A., Muro T., Koretsune T., Arita R., Shin S., Kondo T., Nakatsuji S., Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090–1095 (2017). [DOI] [PubMed] [Google Scholar]
- 24.Yin J.-X., Ma W., Cochran T. A., Xu X., Zhang S. S., Tien H.-J., Shumiya N., Cheng G., Jiang K., Lian B., Song Z., Chang G., Belopolski I., Multer D., Litskevich M., Cheng Z.-J., Yang X. P., Swidler B., Zhou H., Lin H., Neupert T., Wang Z., Yao N., Chang T.-R., Jia S., Hasan M. Z., Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 583, 533–536 (2020). [DOI] [PubMed] [Google Scholar]
- 25.McCusker L. B., Von Dreele R. B., Cox D. E., Louër D., Scardi P., Rietveld refinement guidelines. J. Appl. Cryst. 32, 36–50 (1999). [Google Scholar]
- 26.Rodriguez-Carvajal J., Recent advances in magnetic structure determination by neutron powder diffraction. Physica B 192, 55–69 (1993). [Google Scholar]
- 27.Lynn J. W., Chen Y., Chang S., Zhao Y., Chi S., Ratcliff W. II, Ueland B. G., Erwin R. W., Double-focusing thermal triple-axis spectrometer at the NCNR. J. Res. Natl. Inst. Stand. Technol 117, 61–79 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.A. Zheludev, ResLib 3.4 software (Oak Ridge National Laboratory, Oak Ridge, Tennessee, 2007).
- 29.Kresse G., Furthmüller J., Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
- 30.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- 31.P. Blaha, K. Schwarz, G. K. H. Madsen, D. Luitz, J. Laskowsk, F. Tran, L. Marks, L. Marks, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties (Vienna Univ. of Technology, 2001).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/51/eabe2680/DC1


