宏观压痕测量血管壁力学性能方法的研究

Abstract

在动脉疾病的诊断和治疗中，有效评估血管壁局部生物力学特性至关重要。压痕测量可用于评估动脉局部力学性能，但压头的几何结构和分析理论对测量结果的影响尚不清楚。本文采用4种压头对猪的肺动脉、胸主动脉近心端和胸主动脉远心端进行测量，并通过斯内登（Sneddon）和瑟尔吉（Sirghi）理论计算动脉弹性模量，探究压头几何结构和分析理论对弹性模量测量值的影响。结果显示，圆柱形压头测量的动脉弹性模量值低于球形压头测量值；其次，与Sirghi理论计算结果相比，通过不考虑黏附力的Sneddon理论获得的动脉弹性模量值略大。综上，本研究可为毫米级压痕技术有效测量动脉局部力学特性提供参数支持。

0. 引言

美国心脏病学会数据显示，全球心血管患者从1990年的2.71亿人增加到2019年的5.23亿人，其中死亡人数从1990年的1 210万增加到2019年的1 860万^[1]。心血管疾病已成为导致人类死亡和残疾的主要原因。常见心血管疾病包括动脉粥样硬化、动脉瘤和动脉夹层等，它们的发生和发展与血管壁局部力学性能的改变密切相关^[2-6]。因此，有效评估动脉局部力学性能成为动脉疾病诊断和治疗的关键，特别是在评估斑块的发展、预测夹层破裂位置等方面尤为重要。

拉伸实验^[7-9]和灌流实验^[10]是测量动脉力学性能的常用方法，可表征实验样本的整体力学性能。与拉伸实验和灌流实验相比，压痕实验更适合测量动脉的局部力学性能。目前，压痕技术在不同研究领域以及不同尺度上均有应用。其中，微米或纳米级压头可以测量微观组织力学性能，如动脉内皮细胞^[11-13]、平滑肌细胞^[14]以及细胞外基质^[15]等；毫米级压头可以从宏观角度测量组织力学性能，如动脉粥样硬化中的纤维帽组织^[16]和脂质组织^[17]等。除此之外，毫米级压痕实验还能在传统开放式手术中有效区分健康组织和病变组织，帮助外科医生准确定位缝合线位置^[18]。

随着压痕技术不断发展，其应用也日益广泛。在不同文献报道中，使用压痕技术测得的弹性模量值存在很大差异。例如，微米和纳米级压痕实验中，Pesen等^[11]测量的牛肺动脉内皮细胞弹性模量值在0.2～2.0 kPa之间；Viswanathan等^[12]测量的人肺动脉内皮细胞平均弹性模量值为2.9 kPa；此外，Wang等^[13]测量的人肺动脉内皮细胞细胞核、细胞质、细胞边缘的弹性模量分别是26～29 kPa、18～19 kPa、4～6 kPa。据报道，微米和纳米级压痕实验测量结果的差异主要源于不同的压头几何结构^[19-20]以及不同的分析理论^[21]。相对而言，毫米级压痕实验中，压头几何结构和分析理论对测量结果是否产生影响，目前尚不清楚。

为能在毫米级实验中准确、有效地表征动脉组织局部力学性能，探究压头几何结构和分析理论对压痕测量结果的影响，本研究使用4种压头[包括：直径为1 mm的圆柱形压头（圆柱形-1 mm）；直径为0.5、1、2 mm的球形压头（球形-0.5 mm、球形-1 mm、球形-2 mm）]对猪的肺动脉、胸主动脉近心端和胸主动脉远心端进行测量，并使用忽略黏附力的斯内登（Sneddon）理论^[22]和考虑黏附力的瑟尔吉（Sirghi）理论^[21]计算动脉弹性模量，并对测量结果进行统计分析。此外，本研究还通过压痕实验和拉伸实验分别测量了动脉生物力学性能，验证并比较两种实验方法测量结果的差异，以期更深入地了解动脉组织力学性能。

1. 材料与方法

1.1. 样本的制备

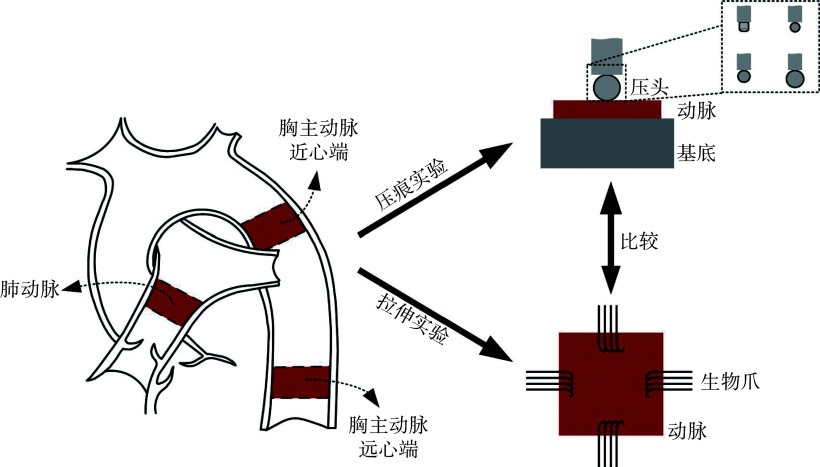
本研究使用当地屠宰场健康猪的动脉作为研究材料。如图1所示，对猪肺动脉、胸主动脉近心端和胸主动脉远心端进行力学实验。实验前，去除样本上多余的脂肪和结缔组织，并使用激光位移传感器LK-G5000（Keyence Corp.，日本）测量样本厚度。所有样本在力学检测前保存在4 °C生理盐水中不超过6 h。

图 1.

Schematic diagram of arterial anatomy and mechanical tests

动脉解剖示意图及力学实验示意图

1.2. 力学实验

1.2.1. 压痕实验

使用力学实验机5544（Instron Corp.，美国）进行测试，最大量程为5 N。为研究压头几何结构对测量结果的影响，采用4种不同的压头（圆柱形-1 mm、球形-0.5 mm、球形-1 mm、球形-2 mm）对猪肺动脉、胸主动脉近心端和胸主动脉远心端进行力学性能评估。实验时需将样本置于基底上，手动调整压头高度使其接近样本且不相互接触。为防止样本干燥变硬，使用生理盐水浸润样本。实验中，压头以0.5 mm/min速率沿垂直于动脉内膜层方向施加载荷，最大加载位移（压痕深度）为0.2 mm（小于样本厚度的10%），随后开始卸载，直至压头与样本完全分离，记录此过程中的载荷和位移数据。

1.2.2. 拉伸实验

本研究将样本置于37 ℃生理盐水中进行拉伸实验，使用双轴循环测试系统IPBF-300（凯尔测控试验系统有限公司，中国）对猪肺动脉、胸主动脉近心端和胸主动脉远心端进行测试，最大量程为5 N。如图1所示，使用生物爪对样本进行固定，并将水平和垂直方向与样本的轴向和周向对齐。测试区域为20 mm×20 mm的正方形范围。在水平与垂直两个方向同时施加0%～5%应变范围的预拉伸处理，共进行10次。正式实验时采用等轴加载条件，收集20%应变范围内的应力—应变曲线。预拉伸实验和正式实验均采用位移控制，拉伸速率为20 mm/min。

1.3. 生物力学特性分析

1.3.1. 压痕实验数据分析

样本的弹性模量由压痕实验中获得的力、位移数据计算得到。Sneddon^[22]研究表明，使用轴对称刚性压头测量各向同性半无限体材料生物力学性能时，如果材料发生小变形，则可根据压头所施加力F的绝对值和压痕深度h获得材料弹性模量E，其计算过程如式(1)所示：

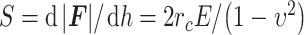1

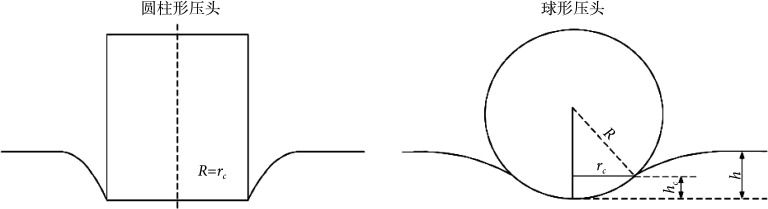
其中，S为材料刚度。υ是被测材料的泊松比，本研究假设动脉是不可压缩材料，υ = 0.5。r_c是压头与样本的接触半径。如图2所示，圆柱形压头接触半径r_c = R，R是压头半径^[23]，则力F的绝对值如式(2)所示：

图 2.

Contact profile between indenter and material

压头与材料接触轮廓图

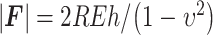2

球形压头压痕实验中压头与材料之间产生球形接触，压头附近的材料下沉。根据Sneddon理论，球形压头与样本的实际接触深度h_c = 0.5∙h，接触半径r_c如式(3)所示：

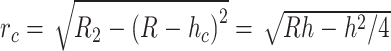3

则球形压头所施加力F的绝对值和材料压痕深度h的关系如式(4)所示：

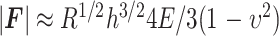4

上述理论忽略了压头与样本之间的黏附力。当考虑黏附力时，根据Sirghi理论，外部载荷F由压头与样本接触部分的弹性力F_e与黏附力F_a组成，如式(5)所示：

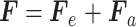5

通过黏附力影响实验测量绘制力—位移曲线，且黏附力可在卸载过程中观察并测得^[24]，因此本研究对卸载部分数据进行分析。考虑到压头与样本接触面积A_c和卸载过程中黏附能W_a不断变化，黏附力F_a的绝对值如式(6)所示：

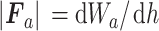6

黏附能W_a的计算过程如式(7)所示：

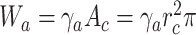7

其中，γ_a是压头与样本之间的黏附功；π为圆周率。则黏附力F_a的绝对值如式(8)所示：

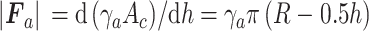8

综上，对于球形压头，若不考虑压头与材料接触区域的黏附力，外部施加载荷F的绝对值与压痕深度h的关系如式(9)所示：

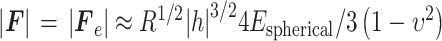9

若考虑压头与材料之间的黏附力，F的绝对值与h之间的关系如式(10)所示：

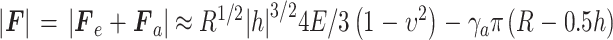10

1.3.2. 拉伸实验数据分析

拉伸实验中样本的工程应力σ（即载荷除以横截面面积）如式(11)所示：

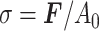11

样本工程应变ε的绝对值（即位移除以样品的初始厚度）如式(12)所示：

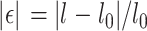12

其中，F为施加载荷，A₀为样本初始横截面积，l₀是样本初始长度，l是实验结束时的样本长度。

根据样本应力—应变曲线，可获得应变为0.10时的动脉切线模量E，其计算过程如式(13)所示：

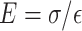13

1.4. 统计学分析

弹性模量值用平均值±标准差表示。使用统计分析软件SPSS v.24.0（International Business Machines Corp.，美国）进行统计学处理，两组间比较采用独立样本t检验，多组间比较采用单因素方差分析和最小显著差异法（least significant difference，LSD）、塔姆黑尼T2（Tamhane’s T2）事后多重比较；检验水准为0.05。

1.5. 组织学染色

采用弹性范吉森染色法（elastica van Gieson staining，EVG）对动脉弹性纤维进行染色。首先用石蜡将样本包埋切片，然后通过EVG染液浸染切片。使用显微镜IX71（Olympus Corp.，日本）观察并采集染色图像DP71（Olympus Corp.，日本），其中动脉弹性纤维呈黑色。

2. 结果

2.1. 压头几何结构对动脉力学性能测量值的影响

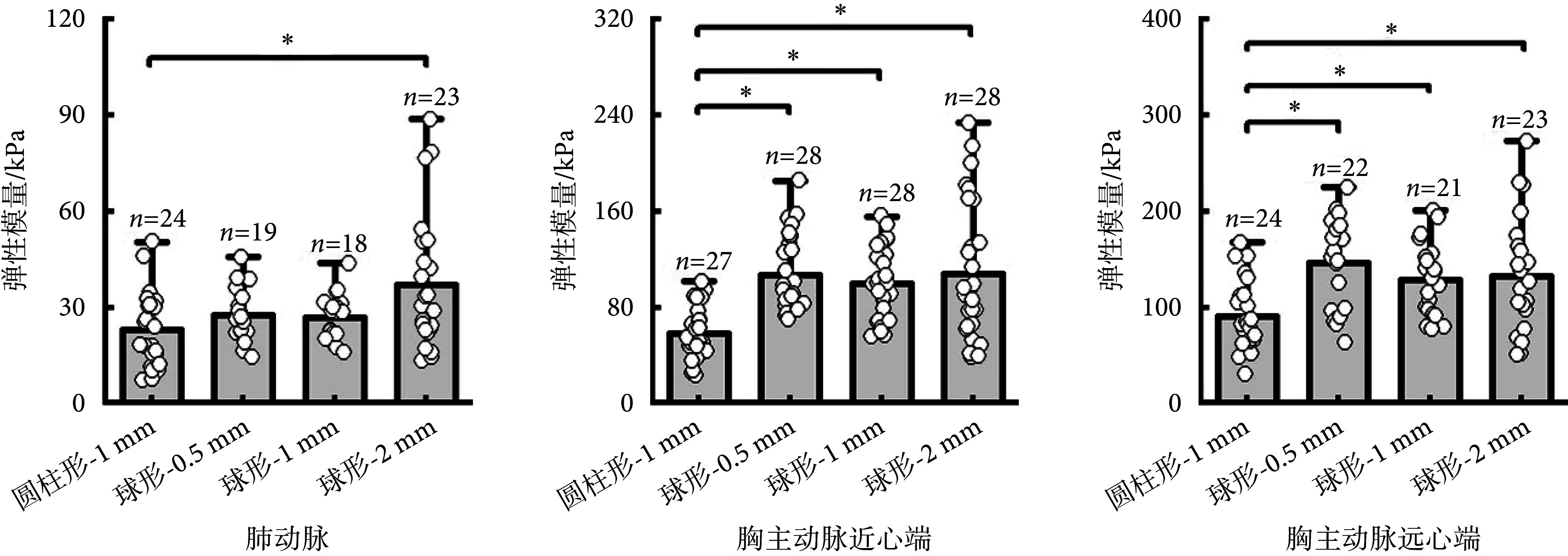
如图3所示，在三个测量区域中，使用圆柱形-1 mm、球形-0.5 mm、球形-1 mm、球形-2 mm压头测量的弹性模量值之间均存在差异，并且该差异有统计学意义（肺动脉：F = 4.583，P < 0.01；胸主动脉近心端：F = 10.709，P < 0.01；胸主动脉远心端：F = 16.024，P < 0.01）。在肺动脉处，使用球形-2 mm压头测量的弹性模量值大于圆柱形-1 mm压头测量的弹性模量值[MD = − 14.361（− 28.323，− 0.399），P = 0.041]；在胸主动脉近心端，对比圆柱形-1 mm压头的弹性模量测量值，使用球形-0.5 mm、球形-1 mm、球形-2 mm压头测量的弹性模量值均较大[球形-0.5 mm：MD = − 48.822（− 68.989，− 28.655），P < 0.01；球形-1 mm：MD = − 6.867（− 60.570，− 22.947），P < 0.01；球形-2 mm：MD = − 49.375（− 81.797，− 16.952），P < 0.01]；胸主动脉远心端与胸主动脉近心端测量结果趋势一致，均显示使用球形-0.5 mm、球形-1 mm、球形-2 mm压头测量的弹性模量值大于圆柱形-1 mm压头测量值[球形-0.5 mm：MD = − 55.044（− 89.623，− 20.465），P < 0.01；球形-1 mm：MD = − 38.114（− 68.662，− 7.565），P < 0.01；球形-2 mm：MD = − 41.046（− 81.604，− 0.488），P = 0.046]。

图 3.

The values of arterial elastic modulus measured with four indenters

使用4种压头测量的动脉弹性模量值

^*P < 0.05

^*P < 0.05

2.2. 分析理论对动脉力学性能测量值的影响

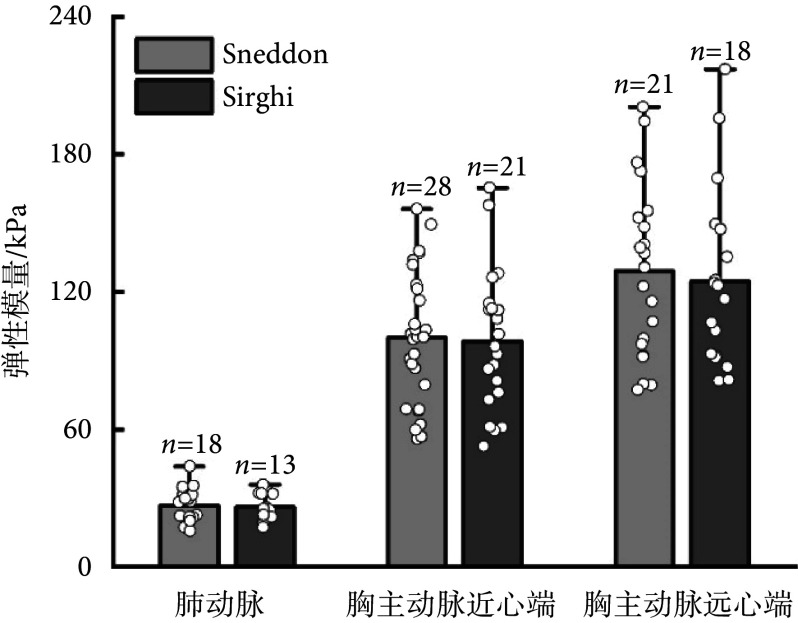
如图4所示，使用两种分析理论（忽略黏附力的Sneddon理论、考虑黏附力的Sirghi理论），分别计算球形-1 mm压头测量的动脉弹性模量值。结果显示，与Sirghi理论计算结果相比，Sneddon理论获得的动脉弹性模量值略大，差异无统计学意义（肺动脉：t = 0.211，P = 0.834；胸主动脉近心端：t = 0.181，P = 0.857；胸主动脉远心端：t = 0.377，P = 0.708）。

图 4.

Comparison of elastic modulus values obtained by Sneddon theory^[22] and Sirghi theory^[21]

通过Sneddon^[22]理论和Sirghi等^[21]理论获得的弹性模量值对比

2.3. 压痕实验与拉伸实验测量动脉力学性能值的对比

如表1所示，压痕实验测量的弹性模量和拉伸实验测量的轴向、周向弹性模量值的差异有统计学意义（肺动脉：F = 43.756，P < 0.01；胸主动脉近心端：F = 88.720，P < 0.01；胸主动脉远心端：F = 100.658，P < 0.01），且压痕实验测量的动脉弹性模量值小于拉伸实验测量值；其中，拉伸实验测量肺动脉轴向弹性模量值约是压痕实验测量值的4倍，胸主动脉近心端和胸主动脉远心端轴向弹性模量值约是压痕实验测量值的3倍；拉伸实验测量肺动脉、胸主动脉近心端周向弹性模量值约是压痕实验测量值的5倍，胸主动脉远心端周向弹性模量值约是压痕实验测量值的4倍。此外，压痕实验和拉伸实验测量结果均显示，肺动脉、胸主动脉近心端和胸主动脉远心端弹性模量值差异有统计学意义，表现为胸主动脉远心端，胸主动脉近心端和肺动脉三者弹性模量依次减小。（压痕实验：F = 65.903，P < 0.01；轴向拉伸实验：F = 17.934，P < 0.01；周向拉伸实验：F = 52.945，P < 0.01）

表 1. The values of arterial elastic modulus (kPa) measured by the indentation test and the tensile test.

The values of arterial elastic modulus (kPa) measured by the indentation test and the tensile test

压痕实验和拉伸实验测量的动脉弹性模量值

动脉	压痕实验			拉伸实验					F值	P值
				轴向			周向
	n	弹性模量/kPa		n	弹性模量/kPa		n	弹性模量/kPa
肺动脉	18	26.75 ± 7.36		9	108.96 ± 39.35		9	141.39 ± 51.67	43.756	< 0.01
胸主动脉近心端	28	99.99 ± 28.90		8	338.89 ± 131.06		7	458.98 ± 100.71	88.720	< 0.01
胸主动脉远心端	21	129.03 ± 37.66		7	384.96 ± 115.58		8	522.49 ± 91.47	100.658	< 0.01
F值	—	65.903		—	17.934		—	52.945	—	—
P值	—	< 0.01		—	< 0.01		—	< 0.01	—	—

2.4. 动脉的组织学特征

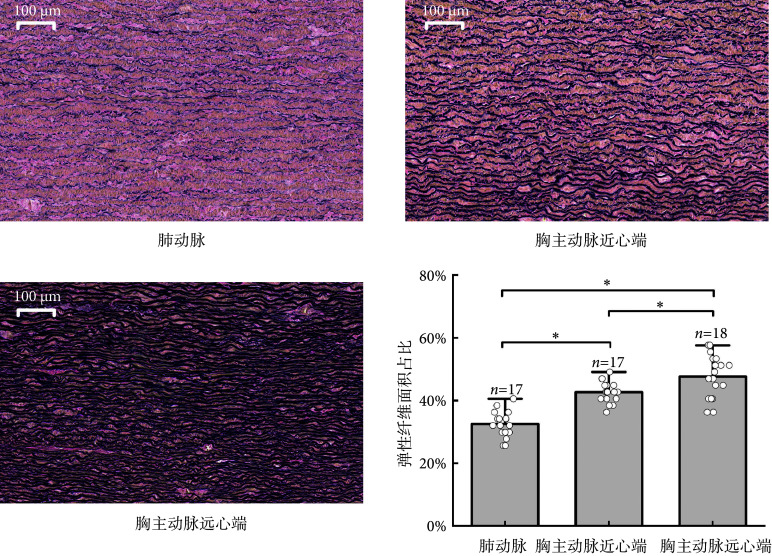
如图5所示，肺动脉、胸主动脉近心端和胸主动脉远心端中的弹性纤维含量差异具有统计学意义（F = 40.471，P < 0.01），EVG染色图和弹性纤维面积占比显示，肺动脉弹性纤维含量低于胸主动脉近心端和胸主动脉远心端[胸主动脉近心端：MD = − 10.161（− 13.445，− 6.876），P < 0.01；胸主动脉远心端：MD = − 15.139（− 19.959，− 10.318），P < 0.01]，胸主动脉近心端弹性纤维含量低于胸主动脉远心端[MD = − 4.978（− 9.593，− 0.362），P = 0.032]。

图 5.

Arterial EVG staining and elastic fiber area proportion

动脉EVG染色图及弹性纤维面积占比

^*P < 0.05

^*P < 0.05

3. 讨论

3.1. 分析与讨论

动脉局部力学性能的评估在动脉疾病的预测和治疗方面具有重要意义。本研究旨在通过毫米级压痕技术测量肺动脉、胸主动脉近心端和胸主动脉远心端组织的局部力学性能，以评估压头几何结构和分析理论对动脉弹性模量测量值的影响；此外，比较了压痕实验与拉伸实验测量的动脉弹性模量，分析了两种实验方法获得的测量值之间的差异。

压痕实验中，胸主动脉近心端和胸主动脉远心端测量结果显示，圆柱形-1 mm压头测量的弹性模量值低于球形-0.5 mm、球形-1 mm、球形-2 mm压头测量值。这可能是由于圆柱形压头边缘与样本表面接触产生应力集中现象^[25]，进而导致测量结果偏小。考虑到球形压头不易发生应力集中^[26]，故其更适于测量动脉或其他软组织的力学性能。结果显示，使用球形-2 mm压头测量的弹性模量标准差在三个测量区域均大于球形-0.5 mm和球形-1 mm压头测量值。当样本泊松比和压痕深度确定时，压头与样本之间的摩擦力与r_c/h值呈正相关^[27]，球形-2 mm压头与样本表面会产生较大的摩擦力，导致弹性模量测量值的分散程度较大。此外，使用球形-0.5 mm压头测量时需要高精度传感器和稳定的操作技术。综上，使用球形-1 mm压头能相对方便、准确地测量动脉力学性能。

压痕实验结果显示，与Sneddon^[22]的理论结果相比，依据Sirghi等^[21]的理论获得的弹性模量测量值偏小，但两者差异无统计学意义。差异产生的原因是由于Sirghi等^[21]的理论假设外部载荷由弹性力和黏附力组成，黏附力会导致压头与样本的接触半径增大^[15]。同时，Sneddon^[22]的理论表明，样本弹性模量与接触半径成反比，因此忽略黏附力导致测量的动脉弹性模量值略大。

拉伸实验测量的弹性模量值高于压痕实验测量值，这可能与动脉弹性纤维分布和实验加载方式有关。动脉中膜含有丰富的弹性纤维^[28]，其中71%以板层形态沿血管壁周向分布，27%包围层间平滑肌细胞形成笼状结构，剩余2%沿径向分布连接弹性纤维板层^[29]。径向压痕实验中，部分纤维受外部载荷作用而产生小变形，而拉伸实验中有更多的纤维响应载荷^[30]，导致两种实验方法测得的动脉弹性模量值存在差异。此外，考虑到动脉更适合抵抗沿纤维方向的拉力^[30]，压痕实验中载荷垂直于弹性纤维层，而拉伸实验中载荷平行于弹性纤维层，这导致压痕实验弹性模量测量值偏小。

压痕实验和拉伸实验结果显示，肺动脉的弹性模量值低于胸主动脉近心端和远心端，而胸主动脉近心端的弹性模量值又低于远心端，这与之前的研究结果一致^[31]。其原因在于肺动脉、胸主动脉近心端和远心端的弹性纤维含量不同，导致了相应的弹性模量差异。同时，动脉微结构的差异也导致了压痕实验和拉伸实验测量的相应动脉弹性模量值存在倍数差异。

3.2. 研究局限性

在压痕实验测量动脉力学性能时，假设血管壁是各项同性材料，但动脉组织内部结构和性质通常是非均质的，这可能导致测量结果产生偏差。此外，本研究在室温条件下对动脉进行压痕实验测试，未能考虑温度对动脉壁生物力学性能的影响。最后，虽然本研究初步证实了压痕实验和拉伸实验测量的动脉弹性模量值存在倍数关系，且随着动脉在动脉树中的位置而变化，但目前尚未确立两种实验方法所测动脉弹性模量值之间的转化公式，这需要进行更深入的实验验证和数据分析。

4. 结论

本研究探讨了毫米级压痕实验中，压头几何结构和分析理论对动脉弹性模量测量值的影响。结果表明，压头几何结构明显影响弹性模量测量值，而Sneddon^[22]和Sirghi等^[21]的理论对测量结果影响不大。通过球形-1 mm压头和Sneddon^[22]理论能有效计算动脉弹性模量。本研究有助于理解不同文献中报道的弹性模量值，并为使用压痕技术有效测量动脉或其他软组织弹性模量值提供参数支持。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：曹祎凡、高志鹏、陈凌峰主要负责实验设计、数据记录与分析；曹祎凡、石怡柯、赵雅威负责图片绘制；曹祎凡主要负责论文撰写；李芬、宋辉、张倩倩、陈凌峰、李晓娜、陈维毅负责论文审阅修订。

Funding Statement

国家自然科学基金(12002231，12072218)；山西省国家卫生健康委员会重点科研计划(20410710100)