肿瘤治疗电场对细胞微管蛋白的介观动力学影响研究

Abstract

Tumor treatment fields (TTFields) can effectively inhibit the proliferation of tumor cells, but its mechanism remains exclusive. The destruction of cellular microtubule structure caused by TTFields through electric field force is considered to be the main reason for inhibiting tumor cell proliferation. However, the validity of this hypothesis still lacks exploration at the mesoscopic level. Therefore, in this study, we built force models for tubulins subjected to TTFields, based on the physical and electrical properties of tubulin molecules. We theoretically analyzed and simulated the dynamic effects of electric field force and torque on tubulin monomer polymerization, as well as the alignment and orientation of α/β tubulin heterodimer, respectively. Research results indicate that the interference of electric field force induced by TTFields on tubulin monomer is notably weaker than the inherent electrostatic binding force among tubulin monomers. Additionally, the electric field torque generated by the TTFileds on α/β tubulin dimers is also difficult to affect their random alignment. Therefore, at the mesoscale, our study affirms that TTFields are improbable to destabilize cellular microtubule structures via electric field dynamics effects. These results challenge the traditional view that TTFields destroy the microtubule structure of cells through TTFields electric field force, and proposes a new approach that should pay more attention to the "non-mechanical" effects of TTFields in the study of TTFields mechanism. This study can provide reliable theoretical basis and inspire new research directions for revealing the mesoscopic bioelectrical mechanism of TTFields.

0. 引言

肿瘤治疗电场（tumor treating fields，TTFields）是一类中频（100～300 kHz）、低强度（100～300 V/m）正弦电场，对多种肿瘤细胞的增殖具有抑制效应^[1]。临床试验证实了TTFields对多种实体肿瘤具有良好的治疗效果，有效提高了患者生存期，并具有无侵入、副作用低等优点^[2]。据此，美国食品药品监督管理局（U.S. Food and Drug Administration，FDA）分别于2011年、2015年和2019年授权了TTFields在复发性胶质瘤^[3]、新诊断性胶质瘤^[3]和间皮瘤^[4]治疗中的应用。虽然TTFields在临床中表现良好，但其抑制肿瘤细胞增殖的内在机制尚不明晰，部分医疗人员和患者对该技术持保守甚至怀疑态度。另外，机制不清也不利于临床应用中的治疗方案优化和疗效提高，限制了该技术的发展和推广。

在现有较成熟的电磁场肿瘤治疗技术中，电磁场的力学作用和热效应是杀伤肿瘤细胞的主要机制，例如：电穿孔通过电场力破坏细胞膜结构^[5-7]，微波消融通过电磁热烧蚀肿瘤细胞^[8]。目前，在TTFields的机制研究中，电场通过电场力、力矩破坏细胞微管的结构，进而抑制肿瘤细胞有丝分裂被认为是TTFields抑制肿瘤细胞增殖的主要原因。这一猜想观点基于以下事实：细胞骨架是真核细胞中重要的亚结构，在维持细胞正常形态、有丝分裂和胞内物质运输中发挥着重要作用，细胞骨架由大量的微管构成，而单个微管是由一种具有强电偶极矩的α/β异二聚体微管蛋白（以下简称为：微管蛋白二聚体）聚合而成^[9]；一方面，在微管解聚和聚合活动十分活跃的有丝分裂前中期，TTFields电场通过库仑力破坏微管蛋白二聚体的正常聚合；另一方面，电场对微管蛋白二聚体电偶极子的力矩将促使微管蛋白二聚体与外电场平行，干扰微管蛋白二聚体在细胞内部正常的排列取向，从而影响微管生长及其结构稳定性，导致有丝分裂失败^[10]。虽然在离体细胞实验中，已有研究通过荧光图像观察到细胞骨架形态异常、子细胞染色体分配不均等现象^[10]，但这不足以证明TTFields是通过电场力、力矩破坏了微管结构，而有可能是电场所激发的细胞内化学环境失衡等“非力”原因所造成。

针对TTFields对细胞微管电生理活动的潜在影响，为厘清TTFields是否能够产生足够强的电场力、力矩效应来破坏细胞微管结构稳定性，本文建立TTFields对微管蛋白单体聚合和微管蛋白二聚体排列取向干扰的力学模型，从生物物理角度，理论研究介观层面上TTFields对微管蛋白的动力学效应。研究结果表明，肿瘤细胞暴露于TTFields中时，微弱的电场库仑力和电场力矩对细胞内微管蛋白单体之间的聚合及微管蛋白二聚体的排列取向影响甚微，从而不足以破坏微管结构稳定性，以往细胞实验现象中所观察到的细胞骨架异常原因更可能来自于其他“非力”效应。

1. 细胞微管蛋白介观物理模型

1.1. 几何模型

如图1所示，细胞微管是真核细胞中一种圆柱管状蛋白质结构，其内、外径分别约为15 nm和25 nm，其长度一般为几十纳米（nm）到几十微米（μm）^[11]。单个微管一般由13条原丝构成，每一条原丝由微管蛋白二聚体首尾聚合而成，微管蛋白二聚体长度约8 nm，单个微管蛋白二聚体由直径约5 nm的近似球形微管蛋白单体聚合而成^[11]。

图 1.

Mesoscopic model of cell microtubule and tublin

细胞微管及微管蛋白介观模型

1.2. 电学特性

由于氨基酸残基的存在和非均匀分布，微管蛋白二聚体表面有部分残余电荷，表现出电极性。在生理条件下的弱碱性环境中，微管蛋白二聚体整体呈负电性^[11]。微管蛋白二聚体的整体电极性可以等效为电磁理论中的电偶极子，但其电偶极矩并不是单方向的。在如图1所示的直角坐标系下，通过分子动力学计算，得到微管蛋白二聚体的电偶极矩分布如表1所示^[12]。其中，微管蛋白二聚体的y方向电偶极矩最大，约为1 700 D[单位：德拜（D），1 D ≈ 3.33 × 10⁻³⁰ C·m]。

表 1. The electric dipole of tubulin dimer.

The electric dipole of tubulin dimer

微管蛋白二聚体的电偶极矩

电偶极矩方向	数值/D
x 方向	337
y 方向	− 1 669
z 方向	198
整体	1 714

2. TTFields作用下细胞内电场分布

为研究TTFields对细胞微管的影响，首先需要明确TTFields在单细胞内部的分布状态，由于现有实验技术难以对细胞内部的电场直接测量，本文将对肿瘤细胞处于TTFields中时细胞内部的电场强度分布状态进行仿真模拟。

人体大多数细胞一般呈不规则梭形，大小在几十微米左右，典型TTFields的频率在几百千赫兹（kHz），因此电磁波的波长远大于细胞尺度，电磁场的辐射效应可以忽略。当细胞暴露于TTFields中时，由电流连续性原理和全电流定律可以得出细胞内部电场的控制方程，如式(1)所示：

1

电场与电位之间的关系，如式(2)所示：

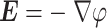2

其中，E和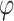分别为电场强度和电位分布，γ和ε分别为细胞仿真计算场域的电导率和介电常数分布，t为时间，∇为哈密顿算子。考虑到电场频率非高频，TTFields可简化为准静态电磁场，即式(1)中第二项位移电流项可以忽略。

为了更加真实地模拟细胞内电场分布，以宫颈癌HeLa肿瘤细胞（来自加州大学伯克利分校Life Science Addition Storeroom）（以下简称为：肿瘤细胞）为例，根据其真实显微形态，建立不规则肿瘤细胞群体模型如图2所示。在肿瘤细胞建模中，由于微管结构处于细胞质中，因此忽略了细胞核，并将细胞质等效为各向同性的电解质媒质，单细胞的几何参数和电学参数如表2所示^[13-14]。在仿真模型中，设置TTFields电场方向为水平方向，其频率和幅值设置为典型值（200 kHz、200 V/m），在多物理场仿真软件COMSOL（5.3，COMSOL Inc.，瑞士）中，通过交流电（alternating current，AC）/直流电（direct current，DC）模块频域稳态求解器对细胞内电场进行计算，得到肿瘤细胞内部的电场分布情况如图2所示。

图 2.

TTFields intensity distribution in HeLa cells

HeLa细胞内的TTFields强度分布

表 2. The geometrical and electrical parameters of single cell model.

The geometrical and electrical parameters of single cell model

单细胞模型几何和电参数

参数		数值
尺寸/μm	细胞大小	10～30
	细胞膜厚度	5 × 10−3
电导率/(S∙m−1)	细胞膜	5 × 10−6
	细胞质	0.5
	细胞外液	0.6
相对介电常数	细胞膜	9.8
	细胞质	60
	细胞外液	80

根据欧姆定律的微分形式，在电场作用下，场域内电流密度计算如式（3）所示：

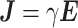3

其中，J为电流密度，E为电场强度，γ为计算场域的电导率分布。

由于细胞膜的电导率极低，在电流密度一定的情况下，肿瘤细胞膜内的电场强度远大于细胞质内电场强度，因此仿真结果仅展示细胞质内的电场强度大小分布。从仿真结果看出，当肿瘤细胞处于TTFields中时，由于肿瘤细胞形态的不同，其内部电场大小略有不同。在肿瘤细胞密集处，较大的电压降落在细胞膜上，导致肿瘤细胞内电场较低，且当肿瘤细胞长轴越倾向于与外电场方向平行时，肿瘤细胞内部电场较强。实际人体组织中，肿瘤细胞以三维形式存在，在同一TTFields作用下，三维肿瘤细胞与二维肿瘤细胞模型中的电场仿真结果略有不同，但整体上肿瘤细胞内电场强度均约为100～300 V/m^[15]，不会对后续电场力和力矩分析结果产生数量上的差异，因此为简化建模、提高数值计算效率，本文采用上述二维肿瘤细胞模型进行电场仿真研究。

3. TTFields对微管蛋白的动力学影响

3.1. 对微管蛋白单体聚合的影响

在介观层面上，细胞内蛋白质之间的聚合依赖于电荷或极性分子之间的静电力。在微管的装配过程中，α或β微管蛋白单体先聚合成微管蛋白二聚体，然后微管蛋白二聚体再首尾相接排列装配形成管状微管。在上述过程中，α或β微管蛋白单体之间的静电吸引力发挥着重要作用。当细胞处于外电场中时，外电场对微管蛋白单体的电场力是否有潜在“拉开”微管蛋白单体之间的正常聚合状态，进而破坏微管稳定聚合结构的影响，是值得探究的。如表1所示，已经表明微管蛋白二聚体有较强的电偶极矩，其x方向电偶极矩约为337 D，且外电场作用在x方向电偶极矩上的电场力最有可能影响微管蛋白聚合稳定性。假设微管蛋白的残余电荷分布于近似球形的蛋白表面，其面密度分布为σ。由于电偶极矩的存在，可等效为α或β微管蛋白单体带异种电荷，则在TTFields作用下，微管蛋白α和β单体的受力模型如图3所示。

图 3.

The force model of tubulin monomers subjected to TTFields

TTFields对微管蛋白单体的电场力受力模型

由图3右图中的几何关系，对微管蛋白单体球体模型微元化，可得球台微元侧面积，如式(4)所示：

4

TTFields对α微管蛋白单体的球台微元的电场力计算，如式(5)所示：

5

积分可得α微管蛋白单体整体所受电场力，如式(6)所示：

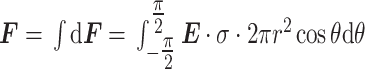6

一般地，微管蛋白表面的电荷分布并不均匀，即σ是坐标的函数，如式(6)所示，为简化积分计算，可认为电荷均匀分布于微管蛋白表面，则可得α微管蛋白单体受到TTFields的电场力，如式(7)所示：

7

在式(4)～(7)中，dS，dF分别为微管蛋白单体微元球台侧面积及其受到的电场力，E和F分别为TTFields电场强度和微管蛋白单体整体受到的电场力，σ为微管蛋白单体表面电荷密度，r和θ分别为微管蛋白单体半径及其与水平向左方向的夹角。

由微管蛋白二聚体的x方向电偶极矩可估算得出α微管蛋白单体表面电荷密度约为5.6 mC/m²，若考虑三维方向上的全部电偶极矩，这一数据将与文献[16]十分吻合。因此，将电荷密度数5.6 mC/m²据代入式（7）可计算得到：强度为200 V/m的典型TTFields对α微管蛋白单体的电场力约为8.8 × 10⁻⁵ pN，由于TTFields是交变电场，这也是TTFields在一个作用周期中对微管蛋白单体产生的最大电场力，或称之为破坏力上限。

在正常的微管聚合活动中，α和β微管蛋白单体之间的静电吸引力F_αβ在皮牛（pN）级别^[17]，更有文献指出，只有当微管受到的张力大于6.59 pN时^[18]，才有可能破坏微管结构稳定性。从TTFields对微管蛋白单体的电场力计算结果与微管蛋白单体正常聚合的静电力对比分析来看，TTFields电场力远小于正常的微管蛋白单体聚合静电力，因此TTFields难以通过电场力来破坏微管蛋白单体之间的正常聚合。

3.2. 对微管蛋白二聚体取向的影响

从电磁场角度看，电场不仅对电偶极子正负电荷有相反的电场力，若外电场与电偶极矩方向不平行，电场力还会产生改变电偶极子取向的电场力扭矩。在TTFields作用下，电场力难以破坏微管蛋白单体之间的正常聚合，但电场力矩是否会改变微管蛋白二聚体的随机排列取向，从而干扰微管蛋白二聚体装配成微管的生理过程，是值得探究的另一个问题。

在电场作用下，只有微管蛋白二聚体轴向（x方向）电偶极矩所受的电场力矩有可能改变微管蛋白二聚体的排列取向，因此对微管蛋白二聚体在TTFields作用下进行受力分析如图4所示。

图 4.

The rotation model of tubulin dimer subjected to TTFields torque

微管蛋白二聚体受TTFields电场力矩模型

将微管蛋白二聚体视为不可形变的刚体，由刚体转动定律可得其在电场力矩和阻力矩作用下的转动方程，如式(8)所示：

8

其中，M_E为电场力矩，M_f为微管蛋白二聚体在细胞质中运动受到的粘滞阻力矩，I为微管蛋白二聚体转动惯量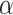，为转动角加速度。

TTFields电场对微管蛋白二聚体产生的力矩，如式(9)所示：

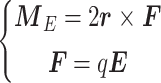9

其中，E为TTFields电场，F为微管蛋白单体受到的电场力，r为旋转中心指向α微管蛋白单体质心的向量，q为微管蛋白单体所带电荷量大小。

微管蛋白二聚体旋转运动受到的细胞质粘滞阻力矩，如式(10)所示：

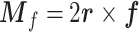10

其中粘滞阻力由斯托克斯公式^[19]给出，如式(11)所示：

11

式中，f为微管蛋白单体受到的细胞质粘滞阻力，r为微管蛋白单体半径，η为细胞质粘滞系数，v为微管蛋白二聚体旋转的线速度，其与角速度的大小关系为v = ωr。

结合几何关系可得微管蛋白二聚体在电场力矩作用下的旋转控制方程，如式(12)所示：

12

其中，θ为微管蛋白二聚体x方向电偶极矩与竖直方向的夹角，t为旋转时间，m为微管蛋白单体的质量，r为微管蛋白单体半径，η为细胞质粘滞系数，p_x为微管蛋白二聚体x方向电偶极矩大小，E为TTFields电场大小。

由于TTFields是交变电场，上式（12）中电场大小E是关于时间的函数，为简化计算，令E为TTFields电场的幅值，以此来计算电场力矩扭转微管蛋白二聚体角度的上限。

α和β微管蛋白单体具有相似的球体形状，且具有近似的质量，约55 kDa（1 Da ≈ 1.66 × 10⁻²⁷ kg）^[20]，细胞质的粘滞系数约为3 mPa·s^[21]，TTFields电场强度大小E取典型幅值200 V/m，设初始角度θ = 0，将上述数据代入式（12），由2/3阶龙格—库塔法解得一个TTFields周期内微管蛋白二聚体扭转角度数值解如图5所示。

图 5.

Rotation angle of tubulin dimer within one TTFields period

一个TTFields周期内微管蛋白二聚体扭转角度

从计算结果看出，在前半个周期内，微管蛋白二聚体扭转角度最大达到约6.4 × 10⁻⁵ rad，半个周期后，电场发生改变，微管蛋白二聚体反向旋转，削弱微管蛋白二聚体的扭转取向，但整体上，微管蛋白二聚体几乎保持着原有初始取向。因此可以证明，在TTFields作用下，微管蛋白二聚体受到电场力矩和粘滞阻力矩的共同作用，其扭转角度极小、可以忽略，TTFields电场力矩将难以对微管蛋白二聚体的排列取向产生实质性的影响，其正常排列取向更多地依赖于随机热运动。

4. 仿真模拟与讨论

对细胞内部的介观力学进行直接测量需要极其精密的实验条件和先进技术，在基础研究中，仿真模拟往往是验证理论分析的重要研究方法。本文将建立有限元仿真模型，仿真模拟TTFields对微管蛋白的电场力和力矩分布，从而印证电场对微管蛋白单体聚合和微管蛋白二聚体排列取向的影响。

4.1. TTFields对微管蛋白单体的电场力

在多物理场分析软件COMSOL（5.3，COMSOL Inc.，瑞士）中按照真实尺寸建立微管蛋白二聚体模型，设定其相对介电常数为2、电导率为0.5 S/m^[17]，电荷密度为±5.6 mC/m²（α微管蛋白单体为正，β微管蛋白单体为负），计算场域其他参数设置如表2所示，当设置平行于微管蛋白二聚体轴向的典型TTFields时，微管蛋白二聚体所受电场力分布如图6所示。

图 6.

TTFields electric field force on tubulin dimer

TTFields作用于微管蛋白二聚体的电场力

从电场力仿真结果来看，由于电场在微管蛋白二聚体两端集中，因此所产生的电场力略大，但整体上微管蛋白单体受到的电场力大小在10⁻⁴～10⁻⁵ pN数量级，远远小于皮牛级的微管蛋白单体之间正常静电吸引力。另外，在生物体内，细胞亚结构自身的抗破坏强度一般在皮牛级，例如DNA双螺旋之间的结合力强度大约在12 pN^{[22 ]}，单个微管原丝的抗弯刚度大约为2.3 pN^[23]，侧面印证了TTFields电场力难以破坏微管正常结构。

4.2. TTFields对微管蛋白二聚体的电场力矩

为验证TTFields对微管蛋白二聚体的排列取向影响，对微管蛋白二聚体在典型TTFields作用下所受到的电场力矩进行了仿真模拟。由于单个微管蛋白二聚体在细胞质中的排列具有随机性，其轴线方向可能与外界施加的电场呈0～π rad夹角，因此对不同初始排列取向的微管蛋白二聚体受到的TTFields电场力矩进行仿真计算分析，得到力矩分布如图7所示。其中，仿真模型参数的设置与4.1小节中一致。

图 7.

TTFields electric field force torque on tubulin dimer

TTFields作用于微管蛋白二聚体的电场力矩

从仿真结果看出，当电场方向与微管蛋白二聚体轴向垂直时，微管蛋白二聚体受到的电场力矩最大，约为2.5 × 10⁻²⁵ Nm，随着电场方向与微管蛋白二聚体轴线夹角的增大，由于力臂的减小，力矩也逐渐减小，并呈现余弦衰减规律。整体上，仿真模拟得到的典型TTFields对微管蛋白二聚体的扭转力矩在10⁻²⁵ Nm数量级，这一数值与式(8)计算得到的电场最大力矩2.2 × 10⁻²⁵ Nm近似。并且10⁻²⁵ Nm级别的电场力矩远小于细胞处于正常生理条件下的随机热运动能量E_T = k_BT = 4.3 × 10⁻²¹ J（k_B为玻尔兹曼常数，T为生理温度310 K）^[15]。另外，有实验表明，要通过交流电场旋转随机排列的微管，其电场强度需达到约10⁷ V/m^[24]，远高于典型TTFields的电场强度（200 V/m）。因此，TTFields的电场力矩作用难以对细胞质内游离的微管蛋白二聚体排列取向造成可观影响。

5. 结论

本文从生物物理角度，开展TTFields对细胞微管蛋白聚合和排列取向干扰的介观动力学影响研究，进而揭示TTFields对细胞微管结构稳定性影响的力学效应。研究结果表明：

（1）典型TTFields对微管蛋白单体的电场力约在10⁻⁵ pN数量级，这一数值远小于皮牛级别的微管蛋白单体之间的正常静电聚合力；

（2）典型TTFields对微管蛋白二聚体的电场力矩约在10⁻²⁵ Nm数量级，这一数值远小于10⁻²¹ J级别的正常生理随机热运动能量；

（3）在电场力矩和细胞质粘滞阻力矩的共同作用下，典型TTFields对微管蛋白二聚体的扭转角度约在10⁻⁵ rad级别。

因此，在介观水平上，TTFields难以对微管蛋白单体的正常聚合和微管蛋白二聚体随机取向造成干扰，从而难以通过力学效应破坏细胞微管结构的稳定性，TTFields对细胞骨架的破坏更有可能是通过“非力”效应造成。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：李星负责仿真建模、理论分析和论文撰写；刘开达、郭琮负责仿真数据处理、论文修订；房天瑞负责图表制作；杨帆负责整体研究指导。

致谢

感谢加州大学伯克利分校Bio-thermal实验室Boris Rubinsky教授对本文研究工作的支持。

Funding Statement

科技部外国专家项目（G2023181006L）；江苏省创新训练项目（202310287127Y）

Jiangsu Province Innovation Training Program; State Administration of Foreign Experts Affairs project