Abstract
为实现人体心率的非接触式测量并提高其测量的精准度，本文提出一种基于多通道雷达数据融合的人体心率测量方法。雷达数据首先依次对每个通道数据进行人体位置识别、相位提取与解缠绕、相位差分、功率谱熵优化的带通滤波以及快速独立成分分析提取。再将四通道数据叠加融合后，使用霜冰优化的变分模态分解分离出心跳信号。最后引入线性调频Z变换进行心率估计。经过40组数据验证，本文方法的平均均方根误差为2.35次/分，平均错误率为2.39%，皮尔逊相关系数为0.97，置信区间为[–4.78, 4.78]次/分，一致性误差为–0.04次/分。实验结果显示，本文提出的测量方法在准确性、相关性、一致性方面表现出色，能够实现人体心率的精准测量。
Keywords: 雷达信号处理, 多通道数据融合, 非接触心率测量
Abstract
To achieve non-contact measurement of human heart rate and improve its accuracy, this paper proposes a method for measuring human heart rate based on multi-channel radar data fusion. The radar data were firstly extracted by human body position identification, phase extraction and unwinding, phase difference, band-pass filtering optimized by power spectrum entropy, and fast independent component analysis for each channel data. After overlaying and fusing the four-channel data, the heartbeat signal was separated using frost-optimized variational modal decomposition. Finally, a chirp Z-transform was introduced for heart rate estimation. After validation with 40 sets of data, the average root mean square error of the proposed method was 2.35 beats per minute, with an average error rate of 2.39%, a Pearson correlation coefficient of 0.97, a confidence interval of [–4.78, 4.78] beats per minute, and a consistency error of –0.04. The experimental results show that the proposed measurement method performs well in terms of accuracy, correlation, and consistency, enabling precise measurement of human heart rate.
Keywords: Radar signal processing, Multi-channel data fusion, Non-contact heart rate measurement
0. 引言
连续监测心率对于心率失常、猝死、心肌炎等心脏突发疾病的发现和预防尤为重要[1]。连续监测心率仪器分为接触式与非接触式两种。传统的接触式仪器对于烧伤患者、婴儿、受困人员等无法接触人体的情况无能为力，而且长时间佩戴仪器也会引起人体不适[2]。而非接触式仪器中的生物雷达因高穿透性、无光照影响、可连续性等优点被应用到人体心率检测领域[3]。
生物雷达应用于连续监测心率领域的重点在于雷达信号分离，通常会使用数字滤波器[4]、经验模式分解（empirical mode decomposition，EMD）[5]、变分模态分解（variational mode decomposition，VMD）[6]、小波分解[7]等方法。Higashi等[8]对多普勒雷达的时域信号使用维纳滤波和多逻辑回归，测量出的心率平均错误率为4.48%。胡锡坤等[9]利用自适应尺度小波从雷达信号分离出心跳信号，静坐情况下25 s内的准确率保持在95%以上。Qi等[10]使用多阶差分增强的VMD算法对超宽带雷达信号提取人体心率，真实人体数据估计结果的平均错误率为4.24%。
现行国家标准GB 9706.227-2021中，心率监测的准确性应为±10%或±5次/分中的较大者[11]。为获取更高的测量精准度，本文提出一种基于多通道雷达数据融合的人体心率精准测量方法。首先通过优化后的预处理方法得到多通道雷达数据，然后使用优化后的变分模态分解算法分离出心跳信号，最后通过线性调频Z变换（cadmium zinc telluride，CZT）估计出心率[12]。本文将通过一系列实验证实算法的可靠性、鲁棒性和准确性。
1. 雷达测量人体心率的原理
本文使用的雷达是调频连续波（frequency modulation continuous wave，FMCW）雷达，具有信噪比高、指向精度高、多普勒灵敏度高等优势。雷达发射信号是线性调频脉冲（linear frequency modulation，LFM）信号，其最小单元称之为脉冲，公式表示为：
 |
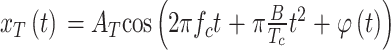1 |
其中AT为脉冲的幅度，fc为起始的频率，B为带宽，Tc为周期，t为时间，φ(t)为相位噪声。若人站在距离R米处，雷达回波信号与发射信号混频后，得到的中频（intermediate frequency，IF）信号为
 |
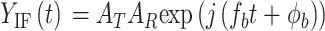2 |
其中AR为回波信号幅度；IF信号的频率fb = (4πBRt)/(cTc)，c为光速；IF信号的相位ϕb = (4πR)/λ，λ为波长，毫米波雷达的波长通常为1～10 mm。人体心脏跳动会伴随着0.1～0.5 mm的胸腔伏动，通过计算不难发现IF信号的相位比频率对微小伏动更加敏感，所以选用相位信号作为心率测量的原始信号[13-15]。
2. 实验方法
2.1. 雷达数据的采集
实验雷达数据使用德州仪器公司的IWR1642BOOST和DCA1000EVM进行采集。实验中IWR1642BOOST雷达的起始频率为77 GHz，调频斜率为65 GHz/μs，快时间采样点数为256，帧数为14 400，帧周期为5 ms，脉冲数为2。实验中雷达使用1根发射天线和4根接收天线。不同接收天线具有不同方向的敏感度差异，可以保留目标的不同特征信息[16]。DCA1000EVM为高速数据采集卡，可将数据传输到电脑中，数据按照帧模式进行采集。实验标准数据使用力康集团的KS-CM01血氧探头进行采集，探头每秒获取一次心率，测量误差符合YZB/粤0303-2014《血氧探头》的标准要求。
实验共招募无心血管疾病的志愿者20名，志愿者具体信息见附件1。采集时为避免志愿者大幅度晃动，每位志愿者坐在距离雷达0.4～0.5 m处，且胸部正对雷达。实验采用举哑铃提升心率的方式保证心率分布范围。每位志愿者连续进行两次数据采集，每次采集72 s数据，总共收集40组雷达数据和标准数据，心率范围为58～106次/分，数据编号参见附件1。在雷达和血氧探头采集数据时，均会自动记录开始时间戳，借此保证数据的时间对齐。由于雷达启动前期性能不稳定，将删除前2 s数据。在CZT频率估计时，以10 s为滑窗进行心率估计，最终每组数据将获取60 s的估计心率。
2.2. 雷达信号的预处理
2.2.1. 人体位置识别
静态物体在不同时间的雷达回波相同，因此可采用相量均值相消算法去除静态物体的回波[17]。将所有IF信号求算术平均得到参考IF信号，相量均值相消算法的数学表达为：
 |
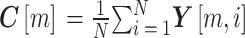3 |
其中m为快时间采样点数，N为脉冲总数，Y为IF信号被采样后的矩阵，大小为m × N。然后求取IF信号与参考IF信号的差值，得到相量均值相消后数据可表示为：
 |
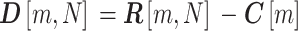4 |
人体位置识别普遍采用快速傅里叶变换（fast Fourier transform，FFT）法[18]。由于不同距离的目标物体会产生不同的多普勒频移，所以不同的频率对应着不同距离的物体。为随时间变化准确地选取距离单元，以帧为组，取累加后幅度最大值时的复数数据，组成微动信号。
2.2.2. 相位解缠绕方法及差分
对于复数类型的微动信号，利用反正切函数法即可得到其相位，公式为：
 |
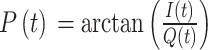5 |
其中，I(t)和Q(t)为微动信号的实部、虚部。但是反正切函数法得到的相位会出现跳跃大于或等于π弧度的情况，即相位缠绕。相位缠绕时不能反映相位的真实变化趋势。因此选用线性解调（linear demodulation，LD）算法[19]进行相位解缠绕，算法是对实部和虚部组成的混合矩阵M进行奇异值分解（singular value decomposition，SVD），然后计算主成分矩阵，第一个主分量即为所求相位信号[20]，用公式可表示为：
 |
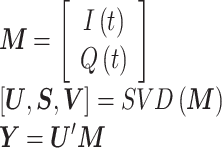6 |
其中，U、S、V分别是分解后的左奇异向量、奇异值、右奇异向量；Y是主成分矩阵。通过LD算法得到的信号容易存在波动性较大的问题，为降低这种不规则性波动并使信号趋于平稳，采取一阶差分法优化后得到最终相位信号[10]。
2.2.3. 带通滤波器
心率的频率范围为0.8～3.0 Hz，为滤除其他频率的噪声并满足极窄过渡带宽和较小阻带波动的需要，选用无限冲击响应滤波器中的椭圆滤波器[21]。实验所采用椭圆滤波器的具体参数以及幅频与相频特性曲线参见附件2。功率谱熵是一种表示信号复杂度的特征量，功率谱熵越小代表信号的混乱度越小[22]。所以功率谱熵越小的信号中，包含的噪声越小，相位信号的信噪比越高。根据雷达帧周期、心率频率以及奈奎斯特采样定律，实验将在10～200 Hz的范围内搜索最优采样率，确保较高的信噪比。
2.2.4. 快速独立成分分析
快速独立成分分析（fast independent component analysis，FastICA）作为一种盲源分离技术，借助信号自身的非高斯性和独立性进行分离。算法首先对输入信号X(t)进行均值和白化处理，以此去除其相关性，再采用牛顿迭代的方法不断修正解混矩阵W直至目标函数值满足收敛条件λ。本文FastICA的目标函数是采用负熵，其中负熵的函数可简化为：
 |
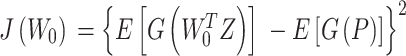7 |
其中E[·]为均值运算，G(·)为非线性函数，W0为解混矩阵初始值，P为零均值的高斯随机变量且与W0TZ具有相同协方差值[23–25]。因此可使用FastICA技术提取出雷达信号的主成分信号，去除其中高斯杂乱信号。
2.3. 心跳信号的分离
2.3.1. 变分模态分解
VMD算法[26–27]首先确定K个中心频率为wk的模态分量（intrinsic mode functions，IMF），记作vk(t)，然后对vk(t)进行希尔伯特变换构造约束变分问题，过程由公式呈现为：
 |
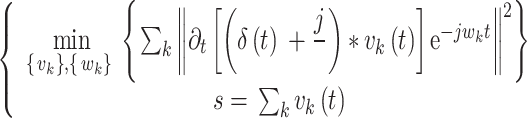8 |
其中，vk为模态分量，wk为模态分量的中心频率，s为输入信号。首先使用惩罚因子和拉格朗日乘子将问题变为无约束变分问题，同时保证严格约束条件，过程表示为
 |
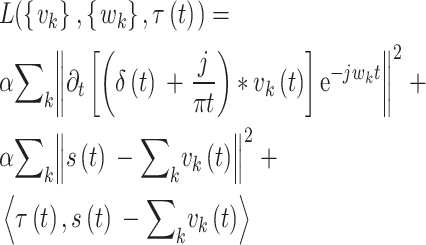9 |
其中α为惩罚因子，τ(t)为拉格朗日乘子。利用交替方向乘法迭代得到问题的最佳解，所有模态可表示为：
 |
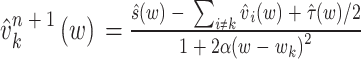10 |
其中ω为频率，^为其傅里叶变换。迭代过程中模态中心频率wkn + 1更新、拉格朗日乘子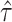
n + 1(w)更新、迭代停止条件的数学表达分别为：
 |
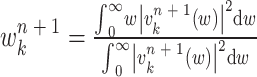11 |
 |
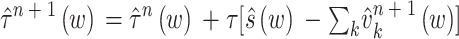12 |
 |
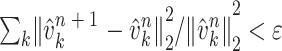13 |
VMD算法对不同的信号应当采用不同的模态数K和惩罚因子α，针对此问题本文采用霜冰优化算法对两个参数进行优化。
2.3.2. 霜冰优化算法
在2023年，Su等[28]以雾凇生长为灵感，提出霜冰（RIME）算法。算法整体由颗粒集群的初始化、软雾凇搜索策略、硬雾凇穿刺机制和正贪婪选择机制组成。五种颗粒凝结情形组成软雾凇搜索策略，用公式表示为：
 |
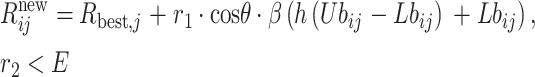14 |
其中Rijnew为第i个软雾剂的第j个颗粒；Rbest,j为更新后的颗粒位置；r1为颗粒方向；h为附着力；Ubij和Lbij为上下界；r2为判定是否凝聚成软雾剂的随机值，取值范围为(0, 1)；β = 1 − [wt/T]/w为环境因素，w为分段数，[·]为取整函数，t为当前迭代次数，T为最大迭代次数。增强算法的收敛性与局部最优跳出性的硬雾凇穿刺机制，用公式表示为：
 |
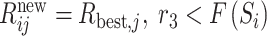15 |
其中Rijnew为更新后颗粒位置；r3为判定是否凝聚成软雾剂的随机值，取值范围为(0, 1)；F(Si)为归一化后最佳的适应度。针对每一组数据都进行VMD的参数优化，参数的搜索范围为K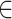
[2, 10]，α
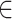[1 000, 20 000]。霜冰优化中通过设置适应度函数确定算法优化方向，适应度函数设置为与原信号相关性最大的IMF的功率谱熵[29]。
2.4. 心率估计算法
CZT是对信号Z变换后的螺旋线周线上等间隔取点，以此达到对指定区间频率进行细化的目的。本文使用CZT方法将心跳信号的0.8～3.0 Hz进行频谱细化，同时以10 s为滑窗，完成对心跳信号的心率估计。
2.5. 评价指标
实验的评价指标主要采用均方根误差（root mean square error，RMSE）和平均错误率（average error rate，ACE），其计算公式为：
 |
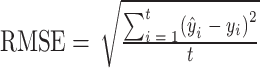16 |
 |
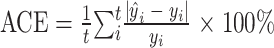17 |
其中t为估计时间长度，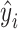
为第i秒心率估计值，yi为第i秒的心率真实值。RMSE和ACE越小代表估计值越准确，算法越可靠[30]。本文采用40组RMSE和ACE的统计结果来整体评估算法性能，主要包括效果提升组数、效果提升率、效果提升组均值、效果降低组均值等。效果提升组数是指第二种算法相较于第一种算法在评价指标上有所优化的组别个数；效果提升率是指效果提升组数占总组数的比例；效果提升组均值是指所有效果提升组评价指标提升的平均值；效果降低组均值是指所有效果降低组评价指标降低的平均值。
3. 结果展示与讨论
3.1. 结果展示
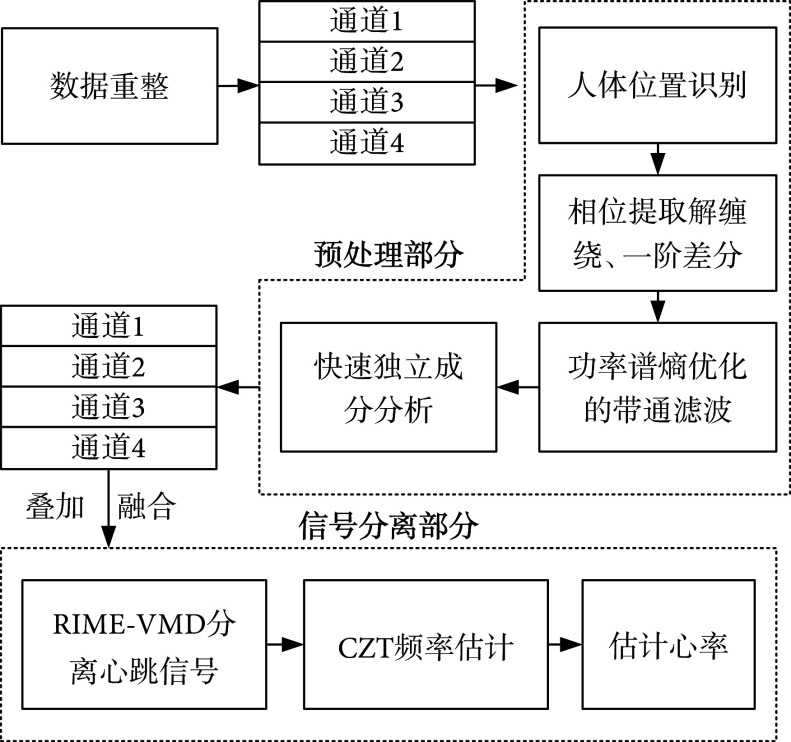
以01组数据为例，依次展示雷达信号的预处理、心跳信号分离的过程结果以及使用CZT算法得到预估心率的过程，具体流程如图1所示。
图 1.
Overall flow chart of the algorithm
算法整体流程图
对01组数据的通道1先采用2.2.1小节的相量均值相消算法去除静态物体回波（结果参见附件3），随后以帧为组提取出通道1的微动信号（结果参见附件4）。然后根据反正切函数提取的相位信号，使用LD法进行解缠绕，并采取一阶差分法降低通道1相位信号的无规则波动（结果参见附件5）。随后使用2.2.3节的带通滤波器，对通道1的相位信号进行滤波，再利用FastICA法得到通道1的主成分信号（结果参见附件6）。
为保留更多方向、速度特征信息和降低信噪比，以按照上述方式完成四个通道的主成分信号提取，并进行叠加处理得到多通道融合数据，结果如图2的原信号所示。随后使用RIME-VMD方法完成对多通道融合数据的分解，结果如图2所示。其中，RIME优化后的模态数K为3，惩罚因子α为6 919。所有的模态分量中模态分量3的相关性最大，相关系数为0.591，因此选用模态分量3作为分离出的心跳信号。
图 2.
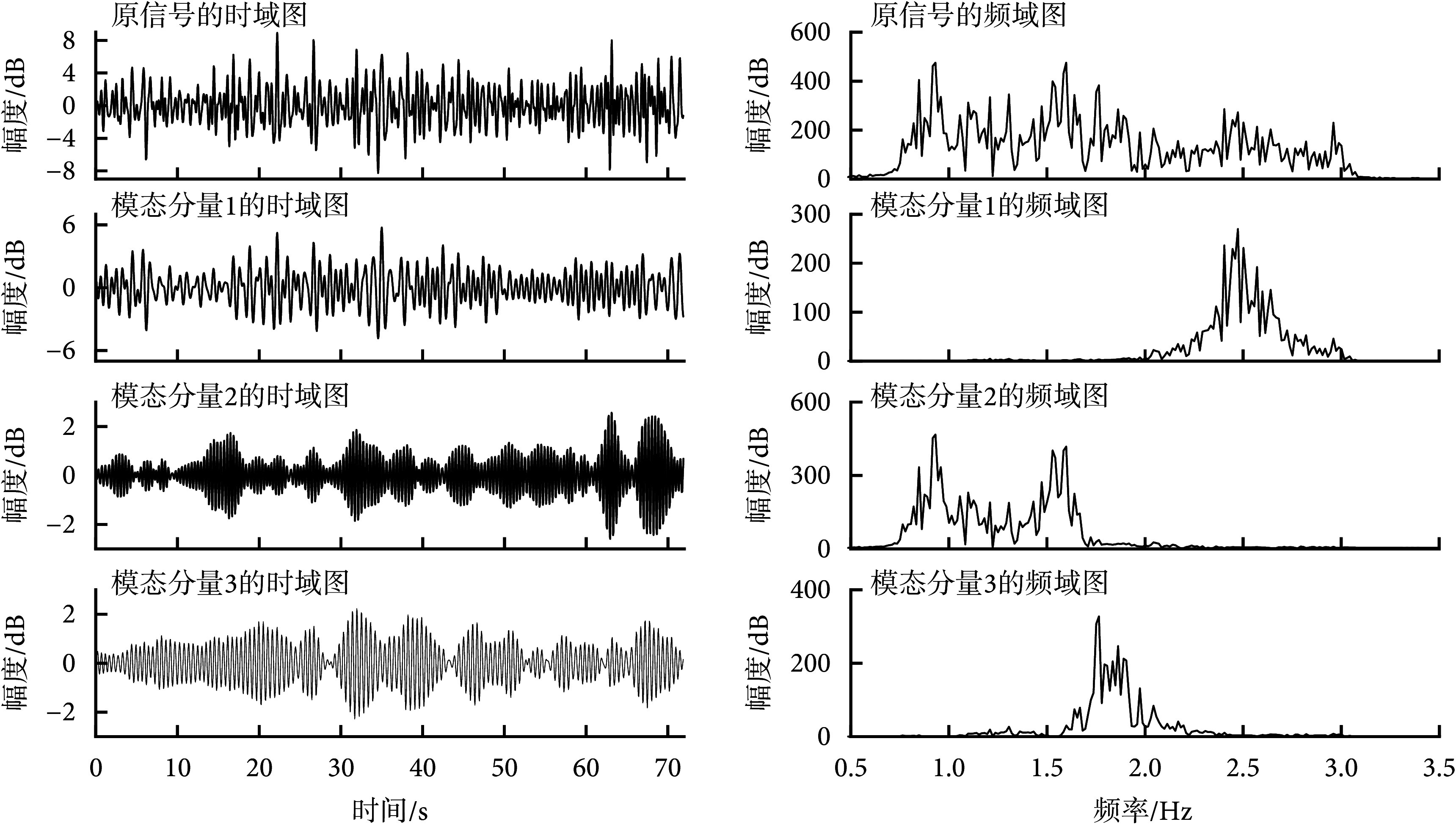
RIME-VMD decomposition diagram
RIME-VMD算法分解结果
最后以10 s滑窗的方式，使用CZT法完成心率的估计。第1 s滑窗数据的频谱图如图3左图所示，其中最高峰的频率为1.52 Hz，因此第1 s的估计心率为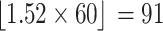
次/分。以此类推，完成组01数据60 s的心率估计，结果如图3右图所示。
图 3.
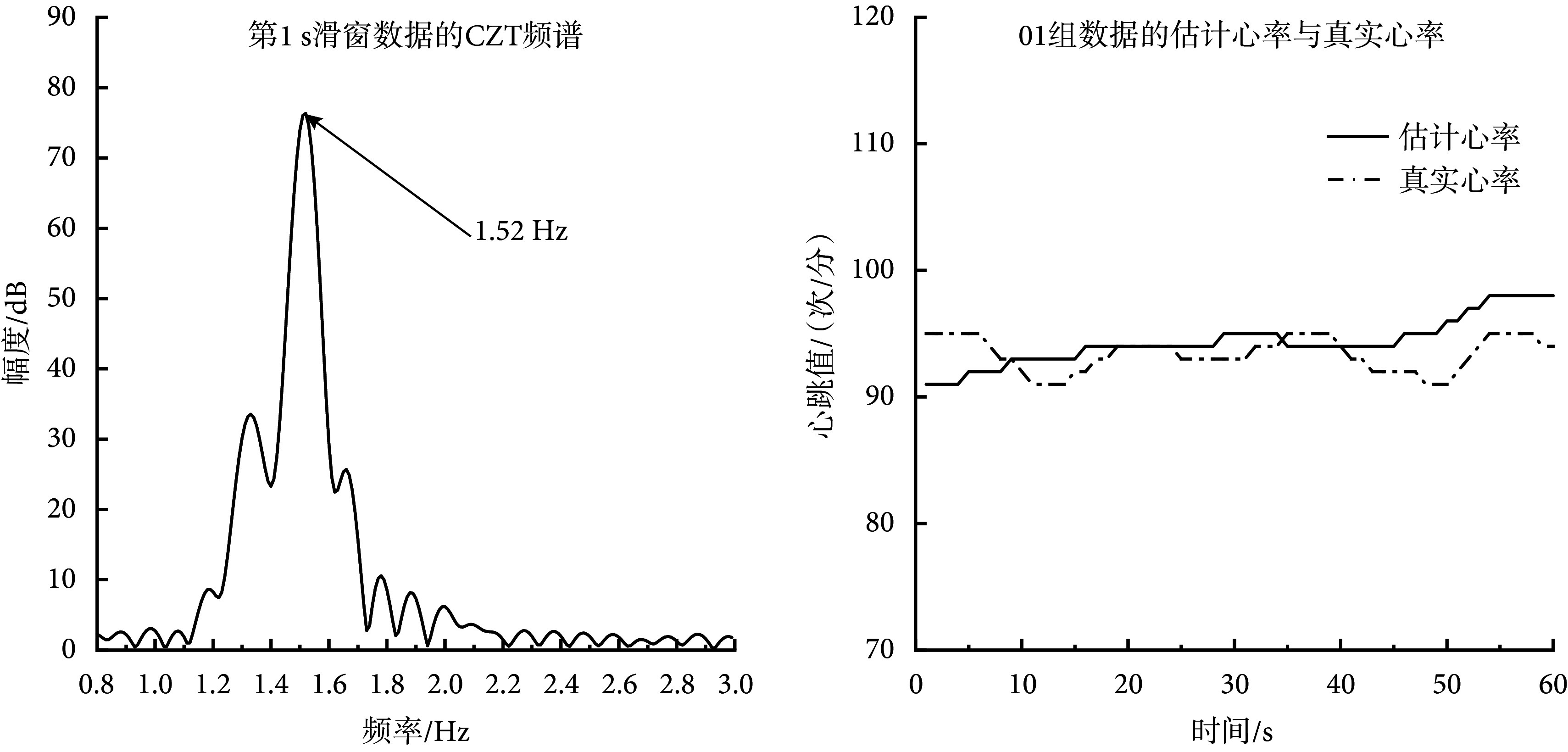
Heart rate estimation process and results for group 01 data
01组数据心率估计过程以及结果
3.2. 采样率寻优验证对比
根据奈奎斯特抽样定律，心跳信号采样率至少为1.6～6.0 Hz，才会不发生混叠现象。同时功率谱熵越小代表信号的混乱度越小，即信号越可能存在周期信号。因此以01、02组的单通道雷达数据为例，设置采样率为10～200 Hz，计算滤波后信号的功率谱熵和算法的RMSE，归一化处理后的结果如图4所示。
图 4.
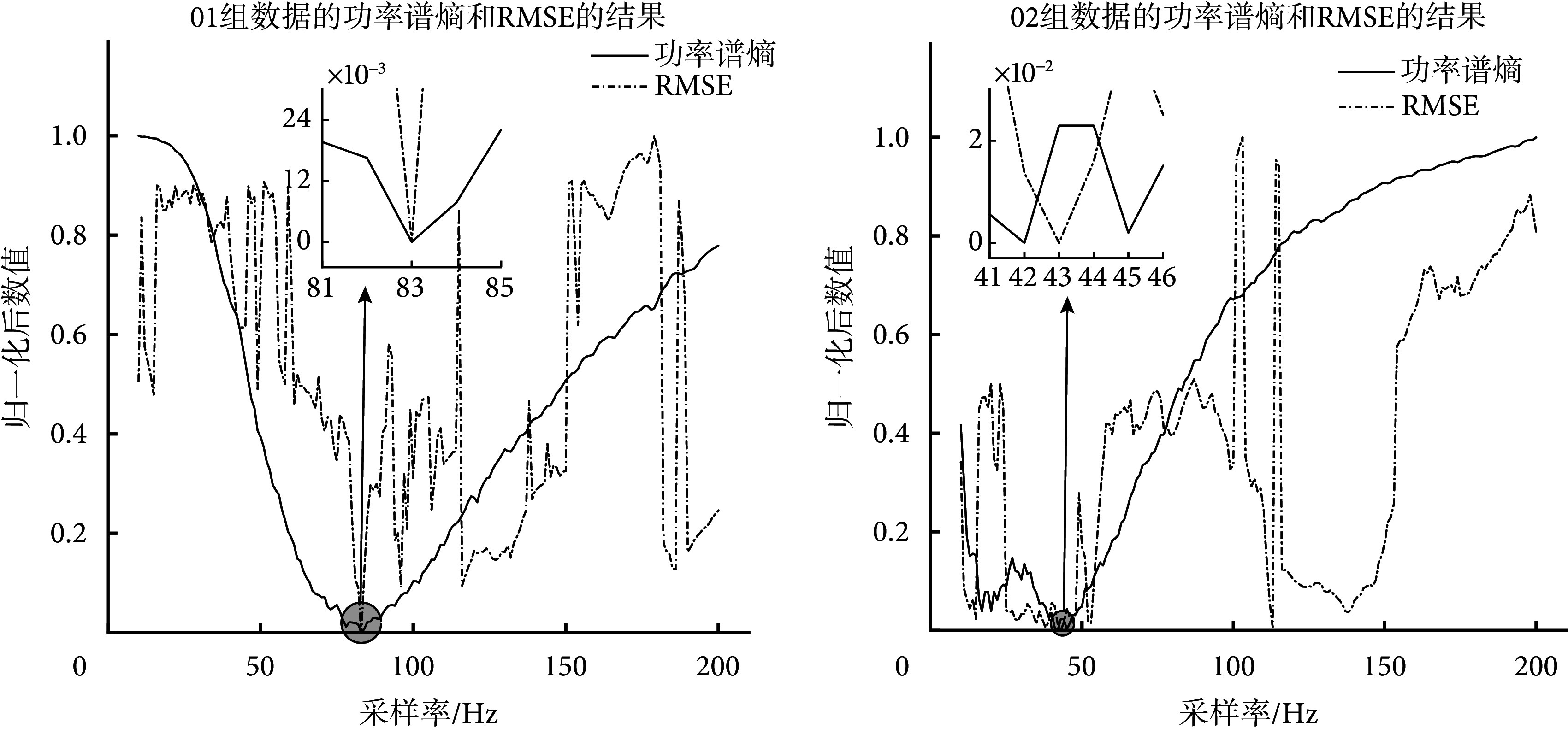
Normalized power spectrum entropy and RMSE plot
归一化的功率谱熵和RMSE关系图
从图4可知，01组在采样率为83 Hz时，功率谱熵和RMSE均最小。02组在采样率为42 Hz时功率谱熵最低，在采样率为43 Hz时RMSE最低，尽管采样率不一致，但十分接近。因此通过最小功率谱熵的方式确定采样率可以减少信号的混乱度，从而提高整体算法精度。
3.3. FastICA算法验证对比
使用FastICA算法能够将独立源信号分离出来，因此选取多通道融合数据为样本，以是否使用FastICA算法为唯一变量，验证采用FastICA算法的必要性，统计结果如表1所示，各组原始结果参见附件7。
表 1. Statistical results before and after using the FastICA algorithm.
Statistical results before and after using the FastICA algorithm
FastICA算法使用前后的统计结果
| 评价指标 | 效果提升 组数 |
效果提升率 | 效果提升组 均值 |
效果降低组 均值 |
| RMSE | 36 | 90% | − 10.29次/分 | 0.47次/分 |
| ACE | 38 | 95% | − 11.96% | 0.85% |
从表1可以看出，采用FastICA算法对于90%的数据都有提升效果，仅对于少量数据产生较小的不良影响。其中，效果提升组的RMSE平均降低10.29次/分，ACE平均降低11.96%；效果降低组的RMSE平均升高0.47次/分，ACE平均升高0.85%。总体而言，FastICA算法能够提升心率估计的准确度，有效降低其他噪声信号对实验的不良影响。
3.4. 单通道数据与多通道融合数据对比
多通道融合数据相较于单通道数据含有更多的信息，但同时也可能引入干扰。为验证多通道融合数据的适用性和可靠性，实验将对比单一通道数据的估计结果与多通道融合数据的估计结果，其中单一通道数据共计160个。统计结果如表2所示，各组原始实验结果参见附件8。
表 2. Statistical results of single-channel data and multi-channel fusion data.
Statistical results of single-channel data and multi-channel fusion data
单通道数据与多通道融合数据的统计结果
| 评价指标 | 效果提升 组数 |
效果提升率 | 效果提升组 均值 |
效果降低组 均值 |
| RMSE | 135 | 84.40% | –4.55次/分 | 0.31次/分 |
| ACE | 126 | 78.80% | –4.87% | 0.47% |
从表2可以看出，相比于单通道数据，78.80%的多通道融合数据都具有更好的估计效果，效果提升组的RMSE平均降低4.55次/分，ACE平均降低4.87%。反观剩余单通道数据的RMSE平均升高0.31次/分，ACE平均升高0.47%。如果选用单通道数据，将无法保证每次都会有最优异的效果。综上所述，多通道数据融合具有很好的适用性和可靠性，能够保证后续算法的优异效果。
3.5. 整体算法结果与讨论
为验证本文RIME-VMD算法的优劣性，将它与EMD算法、集合经验模态分解（ensemble empirical mode decomposition，EEMD）算法进行对比。三种算法的实验结果和对比如表3、表4所示，各组原始实验结果参见附件9。
表 3. Experimental results of RIME-VMD, EMD and EEMD.
Experimental results of RIME-VMD, EMD and EEMD
RIME-VMD、EMD、EEMD的实验结果
| 算法 | 平均RMSE/（次/分） | 平均ACE（%） | 平均运行时间/s |
| EMD | 16.71 | 17.13 | 13.26 |
| EEMD | 19.36 | 20.87 | 18.00 |
| RIME-VMD | 2.35 | 2.39 | 38.07 |
表 4. Comparison between RIME-VMD and EMD and EEMD.
Comparison between RIME-VMD and EMD and EEMD
RIME-VMD与EMD、EEMD的比较结果
| 评价指标 | 比较算法 | 统计指标 | |||
| 效果提升 组数 |
效果 提升率 |
效果提升组 均值 |
效果降低组 均值 |
||
| RMSE | EMD | 40 | 100% | –14.35次/分 | 0次/分 |
| EEMD | 40 | 100% | –17.00次/分 | 0% | |
| ACE | EMD | 40 | 100% | –14.73% | 0% |
| EEMD | 40 | 100% | –17.47% | 0% | |
从表3和表4可以看出，RIME-VMD算法的平均RMSE为2.35次/分，平均ACE为2.39%，符合心电监护仪的国家标准，比引言中提到的算法具有更高的准确度。同时，RIME-VMD算法与EMD算法、EEMD算法相比在准确性上均有提升，其中RMSE平均降低14.35次/分、17.00次/分，ACE平均降低14.73%、17.47%。因此可以得出RIME-VMD算法效果优于EMD算法和EEMD算法的结论。但是，从平均运行时间来看，RIME-VMD算法需要更长的时间，所以在实时检测时需要减少RIME-VMD算法寻优用时。此外，RIME-VMD算法相关性与一致性的结果，如图5所示。
图 5.
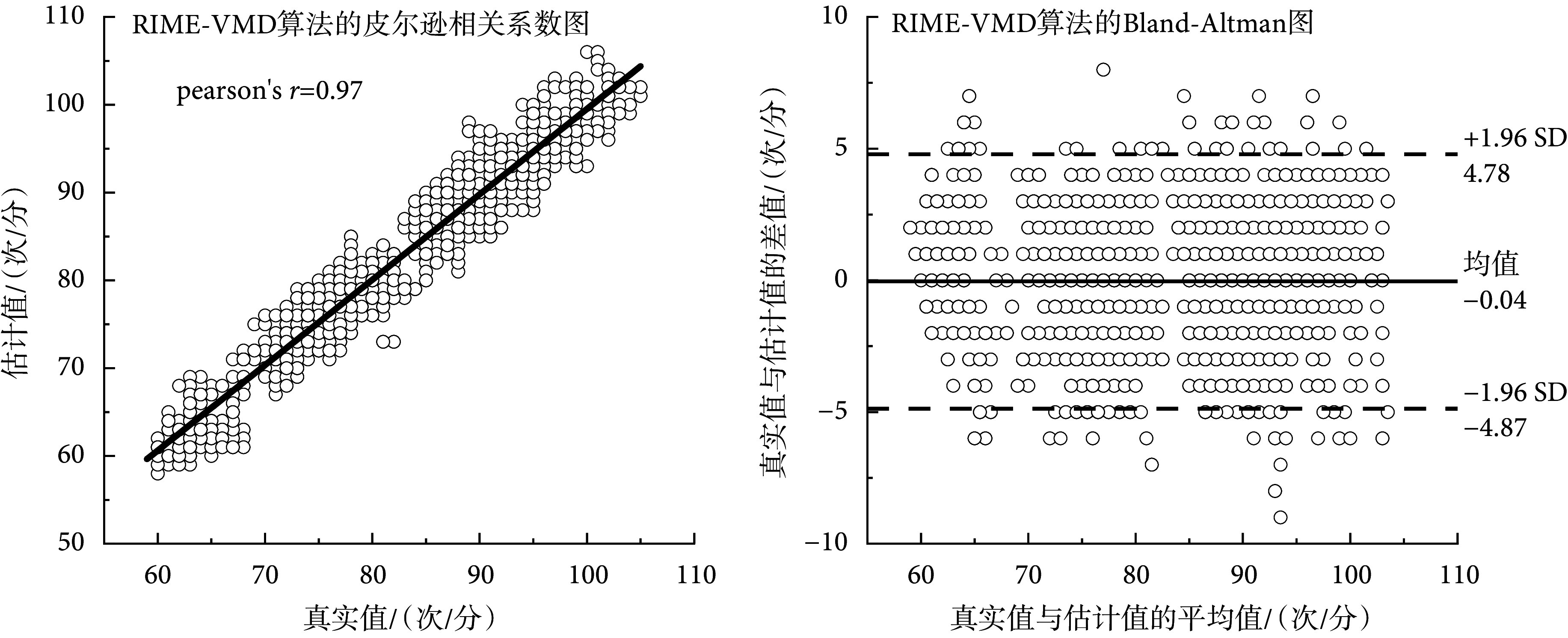
Correlation and consistency graph of RIME-VMD
RIME-VMD算法的相关性与一致性图
图5左图是RIME-VMD算法的皮尔逊相关系数图，相关系数为0.97，说明估计值与真实值具有强相关性。图5右图为RIME-VMD算法的Bland-Altman图，置信区间为[–4.78, 4.78]次/分，误差值为–0.04次/分，大约有95.96%的数据在置信区间内，说明估计值与真实值具有极强的一致性。
4. 结论
本文提出一种FMCW雷达的多通道融合心率测量方法，该方法首先对人体微动信号进行探究，使用以功率谱熵为优化指标的IIR带通滤波器和FastICA算法分别对四通道数据进行降噪处理。然后将四通道数据叠加融合后，以功率谱熵作为RIME的适应度，采用RIME-VMD分离出心跳信号，最后使用CZT频率估计心率。实验结果显示，40组心率估计结果RMSE平均值为2.35，ACE平均值为2.39%，皮尔逊相关系数为0.97，置信区间为[–4.78, 4.78]次/分，一致性误差为–0.04次/分。综上所述，本文提出的多通道融合心率测量算法有着优异的精准性、可靠性和鲁棒性，同时也为雷达信号处理提供了一种新的思路和解决方案。
重要声明
利益冲突声明：本文全体作者均声明不存在利益冲突。
作者贡献声明：郭洪瑞主要负责算法程序设计与编写、数据记录与分析以及论文撰写；曹汇敏、张朱珊莹主要负责实验流程、协调沟通、计划安排、提供实验指导以及论文审阅修订；杨克奇主要负责协助完成实验以及数据的初步分析。
伦理声明：本研究通过了中南民族大学科研伦理与科技安全委员会的审批（批文编号：2024-SCUEC-055）。
本文附件见本刊网站的电子版本（biomedeng.cn）。
Funding Statement
国家自然科学基金（61178087）
National Natural Science Foundation of China
References
- 1.方震, 简璞, 张浩, 等 基于FMCW雷达的非接触式医疗健康监测技术综述. 雷达学报. 2022;11(3):499–516. doi: 10.12000/JR22019. [DOI] [Google Scholar]
- 2.Kranjec J, Begus S, Gersak G, et al Non-contact heart rate and heart rate variability measurements: A review. Biomed Signal Process Control. 2014;13:102–112. doi: 10.1016/j.bspc.2014.03.004. [DOI] [Google Scholar]
- 3.Seflek I, Yaldiz E A comprehensive study about low-cost and limited bandwidth FMCW bio-radar: detailed analyses on vital signs measurements. Frequenz. 2022;76(9-10):505–520. doi: 10.1515/freq-2021-0241. [DOI] [Google Scholar]
- 4.Phuoc N S. Variable IIR digital band-pass and band-stop filters// 2018 2nd International Conference on Imaging, Signal Processing and Communication (ICISPC). Kuala Lumpur: IEEE, 2018: 132-137.
- 5.余明, 陈锋, 张广, 等 基于经验模态分解与独立成分分析的心肺复苏伪迹自适应滤除算法. 生物医学工程学杂志. 2016;33(5):834–841. [PubMed] [Google Scholar]
- 6.Li C, Wu Y, Lin H, et al ECG denoising method based on an improved VMD algorithm. IEEE Sens J. 2022;22(23):22725–22733. doi: 10.1109/JSEN.2022.3214239. [DOI] [Google Scholar]
- 7.Jaros R, Nedoma J, Kepak S, et al Fiber-optic interferometry-based heart rate monitoring. IEEE Trans Instrum Meas. 2022;71:1–15. [Google Scholar]
- 8.Higashi K, Sun G, Ishibashi K. Precise heart rate measurement using non-contact Doppler radar assisted by machine-learning-based sleep posture estimation// 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Berlin: IEEE, 2019: 788-791.
- 9.胡锡坤, 金添 基于自适应小波尺度选择的生物雷达呼吸与心跳分离方法. 雷达学报. 2016;5(5):462–469. doi: 10.12000/JR16103. [DOI] [Google Scholar]
- 10.Qi Q, Zhao Y, Zhang L, et al Research on ultra-wideband radar echo signal processing method based on P-order extraction and VMD. Sensors. 2022;22(18):6726. doi: 10.3390/s22186726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.国家药品监督管理局. 医用电气设备: GB 9706.227-2021. 北京: 国家药品监督管理局,2021.
- 12.Yan X, Huiyue Y, Wuxiong Z, et al An improved CZT algorithm for high-precision frequency estimation. Appl Sci. 2023;13(3):1907. doi: 10.3390/app13031907. [DOI] [Google Scholar]
- 13.Ni P, Miao C, Tang H, et al Small foreign object debris detection for millimeter-wave radar based on power spectrum features. Sensors. 2020;20(08):2316. doi: 10.3390/s20082316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.卢炤宇, 葛春风, 王肇颖, 等 频率调制连续波激光雷达技术基础与研究进展. 光电工程. 2019;46(7):7–20. [Google Scholar]
- 15.Zhang Z, Qiu Z, Hu W, et al Research on wingtip distance measurement of high-speed coaxial helicopter based on 77 GHz FMCW millimeter-wave radar. Meas Sci Technol. 2023;34(8):085111. doi: 10.1088/1361-6501/acc5fd. [DOI] [Google Scholar]
- 16.Huang X, Cheena H, Thomas A, et al Indoor detection and tracking of people using mmWave sensor. J Sen. 2021;2021:6657709. [Google Scholar]
- 17.Eder Y, Eldar Y C Sparsity-based multi-person non-contact vital signs monitoring via FMCW radar. IEEE J Biomed Health Inform. 2023;27(6):2806–2817. doi: 10.1109/JBHI.2023.3255740. [DOI] [PubMed] [Google Scholar]
- 18.Cooley J W, Tukey J W An algorithm for the machine calculation of complex Fourier series. Math Comput. 1965;19(90):297–301. doi: 10.1090/S0025-5718-1965-0178586-1. [DOI] [Google Scholar]
- 19.Park B K, Boric-Lubecke O, Lubecke V M Arctangent demodulation with dc offset compensation in quadrature Doppler radar receiver systems. IEEE Trans Microw Theory Tech. 2007;55(5):1073–1079. doi: 10.1109/TMTT.2007.895653. [DOI] [PubMed] [Google Scholar]
- 20.Mercuri M, Lorato I R, Liu Y H, et al Vital-sign monitoring and spatial tracking of multiple people using a contactless radar-based sensor. Nat Electron. 2019;2:252–262. doi: 10.1038/s41928-019-0258-6. [DOI] [Google Scholar]
- 21.Ge Z, Guo H, Wang T, et al Universal graph filter design based on Butterworth, Chebyshev, and Elliptic functions. Signal Process. 2023;42(1):564–579. [Google Scholar]
- 22.Li X, Wan S, Huang X, et al Milling chatter detection based on VMD and difference of power spectral entropy. Int J Adv Manuf Technol. 2020;111(7-8):2051–2063. doi: 10.1007/s00170-020-06265-y. [DOI] [Google Scholar]
- 23.Shahshahani S M R, Mahdiani H R FiCA: A fixed-point custom architecture FastICA for real-time and latency-sensitive applications. IEEE Trans Neural Syst Rehabil Eng. 2022;30:2896–2905. doi: 10.1109/TNSRE.2022.3213010. [DOI] [PubMed] [Google Scholar]
- 24.杨蕾, 王慧琴, 王可, 等 基于聚类优化FastICA的混合颜料光谱信息解混算法. 光学学报. 2020;40(5):205–213. [Google Scholar]
- 25.杨玉瑶, 郝婧宇, 吴水才 结合快速独立成分分析算法和卷积神经网络的胎儿心电信号提取与分析方法. 生物医学工程学杂志. 2023;40(1):51–59. doi: 10.7507/1001-5515.202210071. [DOI] [Google Scholar]
- 26.Li J, Liu Z, Qiu M, et al Fault diagnosis model of rolling bearing based on parameter adaptive VMD algorithm and Sparrow Search Algorithm-Based PNN. Appl Intell. 2023;25(2):3150–3165. [Google Scholar]
- 27.Chengbo Y, Youyu M Optimised VMD based on improved Grey Wolf for human pulse wave characterisation. J Phys Conf Ser. 2022;2356(1):12–23. [Google Scholar]
- 28.Su H, Zhao D, Heidari A A, et al RIME: A physics-based optimization. Neurocomputing. 2023;523(203):183–214. [Google Scholar]
- 29.Zhao N, Zhang J, Mao Z, et al Time-frequency feature extraction method of the multi-source shock signal based on improved VMD and bilateral adaptive Laplace wavelet. Chin J Mech Eng-En. 2023;36(1):36. doi: 10.1186/s10033-023-00859-9. [DOI] [Google Scholar]
- 30.任彧, 刘稳, 高志刚 一种改进的用于心率估计的峰值提取方法. 生物医学工程学杂志. 2019;36(5):834–840. doi: 10.7507/1001-5515.201810041. [DOI] [PMC free article] [PubMed] [Google Scholar]